Helium II phase: superfluid, supersolid, liquid crystal or spin ice?

Abstract

Experimentally observed physical properties of condensed He II phase of the simplest atomic matter ${}^4$He are reviewed and analysed in view of the governing Shubnikov's idea about spatial and spin ordering in ${}^4$He below λ transition. The matter has been considered within the framework of the unitary quantum mechanical concept for interatomic interaction between helium atoms based on principal role of the spin subsystem which is a real nature of the commonly accepted helium quanticity widely discussed over the last century.

Keywords:

• He II phase
• ${}^4$He–${}^4$He interatomic interaction
• superfluid
• supersolid
• spin–spin interaction
• microwave absorption
• spin–phonon interaction
• polytypism
• superplasticity

1. Introduction

An active discussion on the physical nature of the Helium II phase has been going on for last 80 years but no essential success in explanation of so-called ‘superfluid’ behaviour was reached, except of several phenomenological models without determined microscopical background. In contrast with superconductivity (which means an anomalous jump in physically measured and well-defined conduction of some metals which can be interpreted quantum-mechanically as microscopic coherent state with order parameter), the ‘superfluidity’ introduced within some hydrodynamic scheme is hardly to be interpreted microscopically, because ‘fluidity’ is a feature of macroscopic continuum with parameters averaged over ‘physically infinitesimal volume’ which principally prevents the real microscopic description. The microscopic coherent states are possible only if the continuum possesses translational symmetry (crystal) which means a spatial ordering in the system of microscopically interacting atoms or molecules. In this situation, the mechanical ‘fluidity’ means yield of the crystal which is controlled by mobility of the crystal lattice defects (dislocations and vacancies) interacting with electrons and phonons. As an example we refer to mechanical softening of superconductors during NS-transition which is due to increase in mobility of dislocations in superconductors as compared to the normal state. Dielectric helium has no conducting electrons, but electrons of valence zone and electronic spins produce the spin–phonon interaction which is background for different properties of the He II phase if the spatial ordering below λ-transition will be clarified.

In 1936, Shubnikov published in Nature [1] the paper where he claimed the direct analogy between λ-transition in liquid ${}^4$He (transition from He I to He II phase) and ferromagnetic transition near Curie point. He wrote [1]:

The anomaly in the specific heat of liquid helium at 2.19${}^{\circ }$K has the same shape as that of the λ-point anomaly in crystalline substances. In crystalline bodies, the λ-point anomaly, similar to that shown by ferromagnetic bodies at the Curie point, is due to some process connected with a change of order in the crystal. It is natural to suppose that in the case of liquid helium II, we also have to do with some form of order. As this type of transition is observed in liquids when liquid crystals are formed, it is not impossible that liquid helium at temperatures below 2.19${}^{\circ }$K also forms liquid crystals.

Experimentalist of genius, Shubnikov was, among them, the expert in crystallophysics (the Shubnikov–de Haas effect [2] was discovered on the Bi monocrystals prepared by L.V. Shubnikov). Despite the experiments had not shown a visible crystalline effect, Shubnikov had no doubt in his concept and planned further researches of the corresponding matter, including into scientific plans of his cryogenic laboratory in UFTI [3] the necessary tasks. However, in August 1937 he was arrested, and in November, 1937 executed by Stalin's NKVD [4], so these plans had not been realised. Shubnikov's idea is rather evident: He I phase is undoubtedly structureless simple liquid (it has no order parameter associated with any regular spatial structure of the medium, but only density fluctuations), so that the He II phase must possess some structural order parameter (like translation periodicity or spatial symmetry groups of crystalline structures) because, physically, two simple liquids cannot be divided by phase transition boundary at all.

In 1938, Kapitza [5] introduced the term ‘superfluid’, and since that the problem of the He II phase for many years was developed, in fact, within the framework of hydrodynamical concept. The progress of the superfluid ideology has been perfectly analysed in the fundamental paper of Balibar [6]. For the first time, the interphase transition between He I and He II was optically researched by McLennan [7] (he had noted that the λ-transition as itself was described by Keesom and Wolfke in 1927), and their experiments on Reileigh scattering and Raman effect gave evidence of λ-transition, but no conclusions about ordering in He II phase were made. Based on theoretical assumption of F. London [8,9], Tisza [10,11] proposed two-liquid model, which was a subject of strong discussions with Landau [12,13]. The most essential step made by Landau [14–16] was introducing phonons and ‘rotons’ to interpret the experimentally observed properties of He II phase (as noted Landau [14,15], the term ‘roton’ was introduced by I.E. Tamm, and we have to note that the term ‘phonon’ is known also by suggestion of I.E. Tamm). However, despite the phonons are collective excitations in the system of strongly interacted and spatially ordered atoms, the Landau's theory does not provide an account of potential energy of interatomic interaction. Nevertheless, because of the linear phonons as the normal excitation modes over a spatially ordered ground state with translation symmetry can be treated as an ideal Bose gas, the system can be successfully described closely to the initial London and Tisza suggestions, but with special assumptions about hypothetic ‘rotons’ to modify the linear phonon spectrum for understanding of experimentally observed phenomena. It is remarkably that initially suggested phenomenological roton spectrum was hereafter found in a number of experiments [17] which is an evidence of the deep physical intuition of Landau. Bogoliubov [18] and Feynman [19–21] had made some improvements in Landau theory.

An important step in understanding of the properties of He II was attempted by Nozières [22] proposition: ‘…we must treat the superfluid and the solid in a common language’. It seems to be a direct development of the Shubnikov's idea about crystalline nature of He II phase. Nozières drawn the quantum lattice gas model [23,24] with off-diagonal long range order as a specific ‘ pre-crystallisation’ state of the superfluid (for this specifically ordered state Matsuda and Tsuneto [24] introduced the term ‘supersolid’, which hereafter will be used by E. Kim and M.H.W. Chan to determine, in fact, the superplastic behaviour of the normal solid helium under alternative loading in torsion oscillator [25–27]). The quantum lattice gas of hard core bosons reduces the problem to the pseudospin anisotropic Heisenberg model which predicts the existence of a superfluid phase [28,29]. However, here we shall interpret the specific properties of the He II phase from an alternative point of view, closer to the Shubnikov's idea about crystalline ordering in this system.

Now, it is evident that all the variety of the properties of helium, despite its imaginary simplicity, is determined namely by specifics of its atomic construction and interatomic interaction, especially by contribution from its spin subsystem [30–32]. We are sure that the real helium quanticity consists in the governing role of its spin subsystem within a resonant valence bond [33,34]. Here we will consider the condensed helium recognising the features which are common to all others molecular crystals. We would like to show that all the observable helium properties are typical for different molecular cryocrystals.

2. Helium I and Helium II

For the first step, we compare the phase diagram of ${}^4$He in Figure 1 with the phase diagram of simple water from Figure 2 (the both diagrams are plotted with normative data known from the literature [35–39]). Even a cursory examination shows that there is a deep analogies between two diagrams, Figures 1 and 2, and, consequently, we can suppose a deep analogies between corresponding physical properties of ${}^4$He and H${}_2$O. Sometimes one says that the negative slop of the λ-line ($\mathrm{\partial }P/\mathrm{\partial }T<0$ along λ-line) is a feature belonging exclusively to phase diagram of ${}^4$He, and it can be an indicator of the special quantum nature of helium. Indeed, the liquid–solid boundaries of other rare gases and a number of molecular systems like N${}_2$, CO, CO${}_2$, etc. have a positive slop, but, however, the boundary Liquid-Ice I on the phase diagram of simple water H${}_2$O (Figure 2) demonstrates the behaviour completely similar to ${}^4$He, and it is a question about such an analogy in physical behaviour of these two, at first sight, quite different molecular systems. The character of phase transitions is principally defined by details of interatomic interactions in the molecular system, so that we have to attend to the specific peculiarities and similarity of interactions in ${}^4$He and H${}_2$O.

Figure 1. Phase diagram of ${}^4$He replotted from data of [35–37].

Figure 2. Phase diagram of H${}_2$O replotted from data of [38].

The familiar intrinsic property of the H${}_2$O molecule is very large electric dipole momentum $d_{{\mathrm{H}}_2\mathrm{O}}=1.8546D=6.186\times {10}^{-30}$ Cm [40], so that we can expect an essential contribution of the direct anisotropic dipole–dipole interaction [41,42], $U_{dd}\left(R\right)=\frac{{\mathbf{\text{d}}}_1{\mathbf{\text{d}}}_2}{R^3}-3\frac{\left({\mathbf{\text{d}}}_1\mathbf{\text{R}}\right)\left({\mathbf{\text{d}}}_2\mathbf{\text{R}}\right)}{R^5},$ where ${\mathbf{\text{d}}}_1$ and ${\mathbf{\text{d}}}_2$ are point dipoles with coordinates ${\mathbf{\text{r}}}_1$ and ${\mathbf{\text{r}}}_2$, $\mathbf{\text{R}}={\mathbf{\text{r}}}_2-{\mathbf{\text{r}}}_1$ is the distance between dipoles, and just the similar form has magnetic (relativistic) spin–spin interaction [43] within the ${}^4$He${}_2$-dimer electronic shell [30–32] (see Equation (6(6) $\begin{array}{rl}& {\hat{H}}_{\mathrm{S}\mathrm{S}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)\\ & =\frac{g_s^2{\alpha }_s^2}{4}\{-\frac{8\pi }{3}\sum _{s\ne s^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}\delta ({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}})\\ & +\sum _{s\ne s^{\mathrm{\prime }}}\frac{1}{r_{s{s}^{\mathrm{\prime }}}^3}[{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}-3\frac{\left({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s\right)\left({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}\right)}{r_{s{s}^{\mathrm{\prime }}}^2}]\}\end{array}$(6) ), Section 3.1). Thus we find the similarity of interatomic interaction in H${}_2$O and helium condensed phases with only difference that magnetic interaction is of five order weaker (as the relativistic effect of order $1/c^2$) than dipole–dipole electrostatics, but the λ-transition in ${}^4$He occurs at sufficiently lower temperature (∼2.17 K) than the liquid water solidifies (∼273 K). Another example of an exceptional properties of the water is the negative coefficient of thermal expansion in the vicinity of the Liquid-Ice I boundary, but the similar behaviour of the ${}^4$He at λ-line is observable as well [44]. Analogies between thermomechanical effects in helium and water were intimated by Landau [14,15] in 1941. It is known existence of so-called ice-like structures in water above triple point (i.e. in still formally liquid state) which correlates with the experimentally observed peaks of inelastic neutron scattering in He I phase [17,45].

It is evident that the quantum ${}^4$He, as to its observable physical properties, in some sense seems to be a deep analog of the simple water (and a number of other condensed molecular systems), and this fact gives us reasons to interpret the properties of helium basing on some observable properties of molecular liquids and molecular solids with respect to specific quantum features of helium. The real quanticity of helium is due to its spin subsystem, it can be seen, among them, if comparing ${}^3$He and ${}^4$He: the only difference in one nuclear spin, but the great dissimilarity in the physical properties.

During the λ-transition the simple liquid He I (with only short-range ordering) undergo the transformation into He II phase which evidently demonstrates features of the long-range order and coexists with its own saturated vapour as a smooth well-defined interface without boiling (opposite to the surface of He I). On the other hand, the He II phase demonstrates mechanical compliance typical to superplastic solids (for example for water ice), and for this reason L.V. Shubnikov characterised it as ‘liquid crystal’. Thus from the very beginning we have all the reasons to suspect some special (not a purely liquid-like, but most likely liquid-crystalline, water-ice-like) behaviour of the He II phase. It is evident that all the specifics of He I→He II phase transition (and, correspondingly, of the He II structure) is determined by the details of ${}^4$ He–${}^4$He interatomic interactions [32].

3. Interatomic interaction in the helium condensed phases

The most important topic in view of the problems discussed above is the nature of interatomic interaction in helium which is commonly supposed to be an extremely quantum system (by the way, the hydrogen demonstrate a series of really quantum features that are no less important than well-known helium effects [46]). The main question is the root of the quantum basis of helium–helium interatomic interaction.

The real quantum nature of helium is the role of its spin subsystem in the helium–helium interatomic interaction. This role becomes quite evident when compare with the quite different observable properties of two helium isotopes, ${}^3$He and ${}^4$He. Despite the only one-half nuclear spin of ${}^3$He (spin of ${}^4$He nucleus is equal to zero), it behaves radically different as compared to ${}^4$He. The main characteristic feature of ${}^4$He is λ-transition from simple liquid (He I) to so-called ‘superfluid’ (He II) phase at 2.171 K under saturated vapour pressure [44]. It is clear that two simple liquids cannot be neighboured along the λ-line by the second order phase transition, so that, according to general physical reasons, the He II phase should be provided by a nonzero specific structural order parameter which can be realised only through the physical degrees of freedoms belonging to the corresponding matter. The only difference between ${}^3$He and ${}^4$He (except of insufficient difference in atomic masses) is nuclear spin of ${}^3$He. Each phase transition observed in condensed matter is resulted inevitably by some details of interatomic interactions in this matter, and in the case of helium we have to conclude that the λ-transition, in all likelihood, is an effect of the spin subsystem of the ${}^4$He isotope. L. Shubnikov [1] was the first who pointed out the fact that the λ-transition seems to be a close analog of magnetic Curie transformation and proposed to interpret the He II phase as a liquid crystal, so that as the system with structural ordering (the Shubnikov's proposition was made well before than the term ‘superfluid’ had been introduced by P. Kapitza [5]). Here we briefly consider the problem of ${}^4$ He–${}^4$He interaction [32].

3.1. Two interacting atoms of ${}^4$He (${}^4$He${}_2$-dimer [30–32])

We consider the ${}^4$He${}_2$-dimer as the system of six charged particles [30–32]: two nuclei with the positive charges ${\mathcal{Z}}_1={\mathcal{Z}}_2={\mathcal{Z}}_0=+2$ and coordinates ${\mathbf{\text{R}}}_1=0$, ${\mathbf{\text{R}}}_2=R_0(\sin {\mathrm{\Theta }}_0\cos {\mathrm{\Phi }}_0,\sin {\mathrm{\Theta }}_0\sin {\mathrm{\Phi }}_0,\cos {\mathrm{\Theta }}_0)={\mathbf{\text{R}}}_0,$ as well as four electrons with charges ${\mathcal{Z}}_a={\mathcal{Z}}_b={\mathcal{Z}}_c={\mathcal{Z}}_d=-1$ and coordinates ${\mathbf{\text{r}}}_a$, ${\mathbf{\text{r}}}_b$, ${\mathbf{\text{r}}}_c$, ${\mathbf{\text{r}}}_d$, 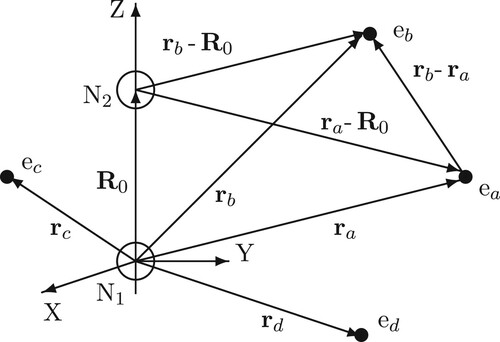respectively. Here and below the Hartree atomic units have been used. Figure 3 shows the configuration of the system (for simplicity, only electrons ‘a’ and ‘b’ are marked, and the internuclear distance ${\mathbf{\text{R}}}_0$ has been combined with $0z$-axis).

Figure 3. The scheme of interaction between helium atoms. Vector ${\mathbf{\text{R}}}_0$ is displayed schematically as a part of $0z$-axis, i.e. at ${\mathrm{\Theta }}_0=0$.

The Hamiltonian of the problem has the form [30–32] (1) $\begin{array}{rl}& {\hat{H}}_{tot}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)=-\frac{1}{2\mu }{\mathrm{\Delta }}^{\left(\mathrm{n}\mathrm{u}\mathrm{c}\right)}({\mathbf{\text{R}}}_0)+\frac{{\mathcal{Z}}_0^2}{R_0}\\ & +H^{\left(e\right)}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)+{\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & +{\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0),\end{array}$(1) where $\mu =M_{\mathrm{n}\mathrm{u}\mathrm{c}}/m_e$ ($M_{\mathrm{n}\mathrm{u}\mathrm{c}}$ is nuclear mass), $H^{\left(e\right)}$ is the pure electronic part of the problem (four mutually repulsing electrons in the attractive Coulomb central fields of the both first and second nuclei), (2) $\begin{array}{r}{\hat{H}}^{\left(e\right)}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)=-\frac{1}{2}\sum _s{\mathrm{\Delta }}^{\left(e\right)}\left({\mathbf{\text{r}}}_s\right)-{\mathcal{Z}}_0\sum _s\frac{1}{r_s}\end{array}$(2) and (3) $\begin{array}{r}{\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)=-{\mathcal{Z}}_0\sum _s\frac{1}{|{\mathbf{\text{r}}}_s-{\mathbf{\text{R}}}_0|}+\frac{1}{2}\sum _{s\ne s^{\mathrm{\prime }}}\frac{1}{r_{s{s}^{\mathrm{\prime }}}},\end{array}$(3) where ${\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}={\mathbf{\text{r}}}_s-{\mathbf{\text{r}}}_{s^{\mathrm{\prime }}}$, $s,s^{\mathrm{\prime }}=a,b,c,d$. Furthermore, ${\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}$ describes the relativistic corrections due to spin–orbit and spin–spin interactions [30–32], (4) $\begin{array}{rl}{\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)& ={\hat{H}}_{\mathrm{S}\mathrm{O}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & +{\hat{H}}_{\mathrm{S}\mathrm{S}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d).\end{array}$(4) The spin–orbit term has the form (cmp. with $H_3$ in Equation (39.14) of the book Ref. [43]) (5) $\begin{array}{rl}& {\hat{H}}_{\mathrm{S}\mathrm{O}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & =-i\frac{{\mathcal{Z}}_0{g}_S{\alpha }_S^2}{4}\{\sum _s{\hat{\mathit{\sigma }}}_s[\frac{{\mathbf{\text{r}}}_s}{r_s^3}\times {\mathrm{\nabla }}_s]\\ & +\sum _s{\hat{\mathit{\sigma }}}_s[\frac{{\mathbf{\text{r}}}_s-{\mathbf{\text{R}}}_0}{|{\mathbf{\text{r}}}_s-{\mathbf{\text{R}}}_0{|}^3}\times {\mathrm{\nabla }}_s]\\ & -\frac{1}{{\mathcal{Z}}_0}\sum _s{\hat{\mathit{\sigma }}}_s\sum _{s^{\mathrm{\prime }}\ne s}[\frac{{\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}}{r_{s{s}^{\mathrm{\prime }}}^3}\times ({\mathrm{\nabla }}_s-{\mathrm{\nabla }}_{s^{\mathrm{\prime }}}\left)\right]\}\end{array}$(5) where ${\alpha }_S=1/137.039$ is the Sommerfeld constant, $g_S=1.001145$ is the spin g-factor, and $\hat{\mathit{\sigma }}$ is the vector with components built of Pauli matrices, and the Thomas–Frenkel factor 1/2 has been taken into account in Equation (5(5) $\begin{array}{rl}& {\hat{H}}_{\mathrm{S}\mathrm{O}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & =-i\frac{{\mathcal{Z}}_0{g}_S{\alpha }_S^2}{4}\{\sum _s{\hat{\mathit{\sigma }}}_s[\frac{{\mathbf{\text{r}}}_s}{r_s^3}\times {\mathrm{\nabla }}_s]\\ & +\sum _s{\hat{\mathit{\sigma }}}_s[\frac{{\mathbf{\text{r}}}_s-{\mathbf{\text{R}}}_0}{|{\mathbf{\text{r}}}_s-{\mathbf{\text{R}}}_0{|}^3}\times {\mathrm{\nabla }}_s]\\ & -\frac{1}{{\mathcal{Z}}_0}\sum _s{\hat{\mathit{\sigma }}}_s\sum _{s^{\mathrm{\prime }}\ne s}[\frac{{\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}}{r_{s{s}^{\mathrm{\prime }}}^3}\times ({\mathrm{\nabla }}_s-{\mathrm{\nabla }}_{s^{\mathrm{\prime }}}\left)\right]\}\end{array}$(5) ) as well. The spin–spin interaction term describes the pair interaction between magnetic moments of individual electrons (cmp. with $H_5$ in Equation (39.14) of the book Ref. [43]), (6) $\begin{array}{rl}& {\hat{H}}_{\mathrm{S}\mathrm{S}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)\\ & =\frac{g_s^2{\alpha }_s^2}{4}\{-\frac{8\pi }{3}\sum _{s\ne s^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}\delta ({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}})\\ & +\sum _{s\ne s^{\mathrm{\prime }}}\frac{1}{r_{s{s}^{\mathrm{\prime }}}^3}[{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}-3\frac{\left({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s\right)\left({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}\right)}{r_{s{s}^{\mathrm{\prime }}}^2}]\}\end{array}$(6) (nuclear spin of the ${}^4$He atom is equal to zero). It is quite evident that the spin–spin Hamiltonian ${\hat{H}}_{ss}^{\hat{\mathit{\sigma }}}$ is explicitly independent on the internuclear distance ${\mathbf{\text{R}}}_0$ (inexplicit dependence of spin–spin exchange is only due to $R_0$-dependent electronic matrix elements [30]).

It should be noted that the Hamiltonian Equation (4(4) $\begin{array}{rl}{\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)& ={\hat{H}}_{\mathrm{S}\mathrm{O}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & +{\hat{H}}_{\mathrm{S}\mathrm{S}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d).\end{array}$(4) ) ignores so important relativistic corrections as retarded potentials for electromagnetic interactions within the intra- and interatomic bonds [43], but the proper treatment of the corresponding problem needs special relativistic approach based on Pauli equation with spinor basis. However, here we shall restrict our consideration to the non-relativistic problem of the helium–helium interatomic interactions, taken into account spin contribution only through parity and degeneration of the four-spin system on the helium–helium interatomic bond. The relativistic corrections will be taken into account as perturbation using spatial matrix elements calculated with the ground state wave function of the non-relativistic problem (see Section 3.2.3).

According to this suggestions the Hamiltonian Equation (1(1) $\begin{array}{rl}& {\hat{H}}_{tot}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)=-\frac{1}{2\mu }{\mathrm{\Delta }}^{\left(\mathrm{n}\mathrm{u}\mathrm{c}\right)}({\mathbf{\text{R}}}_0)+\frac{{\mathcal{Z}}_0^2}{R_0}\\ & +H^{\left(e\right)}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)+{\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & +{\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0),\end{array}$(1) ) leads to the spinless Schrödinger equation, (7) $\begin{array}{rl}& \{-\frac{1}{2\mu }{\mathrm{\Delta }}^{\left(\mathrm{n}\mathrm{u}\mathrm{c}\right)}({\mathbf{\text{R}}}_0)+\frac{{\mathcal{Z}}_0^2}{R_0}\\ & +H^{\left(e\right)}+{\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\}\mathrm{\Psi }({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & =\mathcal{E}\mathrm{\Psi }({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0),\end{array}$(7) which describes an exact non-relativistic dynamics of the system, including internuclear motion, and spin contributions can be taken into account speculatively through parity and degeneration of the four-spin states on the interatomic helium–helium bond. First, we have built the solution

In reality, when solving Equation (7(7) $\begin{array}{rl}& \{-\frac{1}{2\mu }{\mathrm{\Delta }}^{\left(\mathrm{n}\mathrm{u}\mathrm{c}\right)}({\mathbf{\text{R}}}_0)+\frac{{\mathcal{Z}}_0^2}{R_0}\\ & +H^{\left(e\right)}+{\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\}\mathrm{\Psi }({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & =\mathcal{E}\mathrm{\Psi }({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0),\end{array}$(7) ) within exact diagonalisation approach [30,31,47], we have to take into account properly the dynamics of heavy repulsive nucleus and, thus, to use a basis incorporate the functions of continuous spectrum (with $\mathcal{E}>0$), whereas the electronic part of the problem is based only on functions of discrete spectrum [47]. However, if we are interested in some specific applications restricted to only interatomic interactions in condensed helium matter, then the interatomic distance ${\mathbf{\text{R}}}_0$ has a rather narrow range of variation in the region of finite motion ($\mathcal{E}<0$), and the system can be treated on the semi-quantitative level within Heitler–London (HLA) approximation [48], where effective interatomic interaction $U\left(R_0\right)$ is built as a parametric function of $R_0$ with following treatment of $R_0$ as dynamic variable in the one-dimensional $R_0$-dependent Schrödinger equation. Thus, below we will derive from Equation (7(7) $\begin{array}{rl}& \{-\frac{1}{2\mu }{\mathrm{\Delta }}^{\left(\mathrm{n}\mathrm{u}\mathrm{c}\right)}({\mathbf{\text{R}}}_0)+\frac{{\mathcal{Z}}_0^2}{R_0}\\ & +H^{\left(e\right)}+{\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\}\mathrm{\Psi }({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & =\mathcal{E}\mathrm{\Psi }({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0),\end{array}$(7) ) the density matrix $\mathrm{\Psi }\left(R_0\right)$ which depends only on the internuclear distance $R_0$. On the first step, in the next section we neglect the relativistic corrections $H_{\mathrm{r}\mathrm{e}\mathrm{l}}$ and discuss the corresponding corrections in Subsection 3.2.3.

Thus, applying the exact diagonalisation approach [30,31,47] to the linear equation Equation (7(7) $\begin{array}{rl}& \{-\frac{1}{2\mu }{\mathrm{\Delta }}^{\left(\mathrm{n}\mathrm{u}\mathrm{c}\right)}({\mathbf{\text{R}}}_0)+\frac{{\mathcal{Z}}_0^2}{R_0}\\ & +H^{\left(e\right)}+{\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}\}\mathrm{\Psi }({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & =\mathcal{E}\mathrm{\Psi }({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0),\end{array}$(7) ) with basis of 1134 functions (direct product of 81 electronic functions and 14 nuclear functions), we obtain the spectrum of the bound states of the ${}^4$He${}_2$ dimer. The basis set is the direct product, (8) $\begin{array}{rl}& u_p^{NLM}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|R_0,{\mathrm{\Theta }}_0,{\mathrm{\Phi }}_0)\\ & \equiv |\begin{array}{ccc}{n}_a& l_a& m_a\\ n_b& l_b& m_b\\ n_c& l_c& m_c\\ n_d& l_d& m_d\end{array}〉\otimes |NLM〉,\end{array}$(8) of electronic four-electron composition, (9) $\begin{array}{rl}{u}_p({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)& \equiv |\begin{array}{ccc}{n}_a& l_a& m_a\\ n_b& l_b& m_b\\ n_c& l_c& m_c\\ n_d& l_d& m_d\end{array}〉\\ & =\prod _s{\psi }_{n_s{l}_s{m}_s}(\alpha r_s,{\vartheta }_s,{\phi }_s),s=a,b,c,d,\end{array}$(9) and nuclear wave function $|NLM〉$. All one-particle functions are vectors built of standard hydrogen-like states [30,31,47], (10) $\begin{array}{r}{\psi }_{nlm}\left(\alpha \mathbf{\text{r}}\right)={\mathcal{R}}_{nl}\left(\alpha r\right)Y_{lm}(\vartheta ,\phi )\equiv |nlm〉,\end{array}$(10) and (11) $\begin{array}{r}{\psi }_{NLM}\left({\mathbf{\text{R}}}_0\right)={\mathcal{R}}_{NL}\left(R_0\right)Y_{LM}(\mathrm{\Theta },\mathrm{\Phi })\equiv |NLM〉.\end{array}$(11) The 25 lowest levels of the obtained spectrum are presented in Table 1. Except the ground and first excited states, all the levels are degenerate, and each sub-level has a specific value of $〈R_0〉$ which means a quantum fluctuation of internuclear distance within a stable degenerated state. In other words, we have the ‘quantum oscillations’ within the bound state of dimer.

Table 1. Lowest levels of the complete ${}^4$He–${}^4$He spectrum calculated with basis of 1134 elements.

Level	Energy (a.u.)	State (deg.)	Nuclear quantum numbers $〈NLM|$	$〈R_0〉$ (Bohr)	$〈R_0〉$ (Å)
1	−4.19415	1g	$〈210|$	3.229	1.708
2	−4.13701	1g	$〈100|$	4.382	2.318
3a	−4.11761	2u	$〈21\pm 1|$	3.243	1.715
3b	−4.11761			3.401	1.799
4a	−3.76090	3g	$〈200|$	3.464	1.885
4b	−3.76090	3g		3.796	2.008
4c	−3.76090	3g		3.826	2.024
5a	−3.72043	3g	$〈210|$	3.209	1.698
5b	−3.72043	3g		3.255	1.722
5c	−3.72043	3g		3.315	1.753
6a	−3.61646	6u	$〈21\pm 1|$	3.074	1.626
6b	−3.61646	6u		3.330	1.772
6c	−3.61646	6u		3.422	1.810
6d	−3.61646	6u		3.426	1.812
6e	−3.61646	6u		3.492	1.847
6f	−3.61646	6u		3.922	2.075
7a	−3.59904	6u	$〈21\pm 1|$	3.260	1.725
7b	−3.59904	6u		3.271	1.731
7c	−3.59904	6u		3.291	1.741
7d	−3.59904	6u		3.305	1.749
7e	−3.59904	6u		4.008	2.120
7f	−3.59904	6u		4.010	2.121
8a	−3.59493	3u	$〈210|$	3.458	1.829
8b	−3.59493	3u		3.410	1.804
8c	−3.59493	3u		3.411	1.805

As it is seen from Table 1 the ground state of dimer is realised on non-spherical state $|210〉$ of the nuclear subsystem, and, in view of screening of the nuclear field by electronic density from four electrons, belong simultaneously for two nuclei (see Hamiltonian equation (1(1) $\begin{array}{rl}& {\hat{H}}_{tot}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)=-\frac{1}{2\mu }{\mathrm{\Delta }}^{\left(\mathrm{n}\mathrm{u}\mathrm{c}\right)}({\mathbf{\text{R}}}_0)+\frac{{\mathcal{Z}}_0^2}{R_0}\\ & +H^{\left(e\right)}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)+{\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & +{\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0),\end{array}$(1) )). The total picture seems to be like as two interacting multiples centred on the distance $R_0$ (and in the main order on $R_0^{-n}$ the multiples can be treated as superposition of the parallel and oppositely oriented dipoles from individual electrons formally belong to the separate nuclei). It is evident that there is no longer any compositions of the ground states of independent atoms, but superposition of elements built as direct composition (see Equation (8(8) $\begin{array}{rl}& u_p^{NLM}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|R_0,{\mathrm{\Theta }}_0,{\mathrm{\Phi }}_0)\\ & \equiv |\begin{array}{ccc}{n}_a& l_a& m_a\\ n_b& l_b& m_b\\ n_c& l_c& m_c\\ n_d& l_d& m_d\end{array}〉\otimes |NLM〉,\end{array}$(8) )) of all elements belong to complete individual spectra of the interacting atoms.

It can be seen that the ground state energy of the system under study is higher than the energy of two independent non-interacting ${}^4$He atoms in their ground states [47] ($2\times -2.86=-5.72$ a.u.) which is consequence of the contribution to the total energy of ${}^4$He${}_2$ dimer from internuclear repulsion and repulsion between oppositely oriented dipoles mutually inducted for each other by interacting atoms. The opposite orientation of the inducted dipolar momenta within the complete diatomic ground state is evident from the simple reasons of the spatial symmetry of the ground state wave function relative to the plane $z=R_0/2$. Attraction between two dipoles exists if the dipoles are parallel and lying along a common axis, but such configuration is in contradiction to the conditions of spatial symmetry for the ground state wave function. More detailed this problem of atom-atom interaction will be discussed in the next subsection.

As it is shown by the data of Table 1, the average distance between nuclei is in good agreement with typical values of minima on potential curves known from the literature [49–53]. But the most noticeable fact is that within degenerated states (the energies of sublevels have been calculated with a high accuracy) the average internuclear distances $〈R_0〉$ on the sublevels are evidently different, and this means the existence of an ‘oscillatory state’ of the corresponding degenerated level where the average internuclear distance $〈R_0〉$ is ‘wandering’ around the equivalent states of the degenerated level (degeneracy of the level is statistical weight of the degenerated state).

The obtained ground state ($\sim -4.19$ a.u., see spectrum of Table 1) is the ‘bound state energy’ higher than the ‘vacuum level’ of approximately $-5.72$ a.u. (the energy of two independent helium atoms [47]), and in this connection the result seems to be corresponded to a certain ‘metastable’ state of the helium–helium bond. Physically, this fact is due to the total Hamiltonian of the problem Equation (1(1) $\begin{array}{rl}& {\hat{H}}_{tot}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)=-\frac{1}{2\mu }{\mathrm{\Delta }}^{\left(\mathrm{n}\mathrm{u}\mathrm{c}\right)}({\mathbf{\text{R}}}_0)+\frac{{\mathcal{Z}}_0^2}{R_0}\\ & +H^{\left(e\right)}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)+{\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & +{\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0),\end{array}$(1) ) contains, in addition to the energy of two independent atoms (Equation 2(2) $\begin{array}{r}{\hat{H}}^{\left(e\right)}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)=-\frac{1}{2}\sum _s{\mathrm{\Delta }}^{\left(e\right)}\left({\mathbf{\text{r}}}_s\right)-{\mathcal{Z}}_0\sum _s\frac{1}{r_s}\end{array}$(2) ), the internuclear repulsion and the interaction Hamiltonian equation (3(3) $\begin{array}{r}{\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)=-{\mathcal{Z}}_0\sum _s\frac{1}{|{\mathbf{\text{r}}}_s-{\mathbf{\text{R}}}_0|}+\frac{1}{2}\sum _{s\ne s^{\mathrm{\prime }}}\frac{1}{r_{s{s}^{\mathrm{\prime }}}},\end{array}$(3) ) with pair interelectronic repulsion and attractions of each electron to the second nucleus proportional to the nuclear charge ${\mathcal{Z}}_0$. Thus the corrections to the vacuum level are determined by the fine balance between attraction-repulsion within the many-body quantum system which is quite difficult to be reproduced properly at $R_0\to \mathrm{\infty }$ using truncated basis of finite dimension. In the strict sense, the corresponding problem cannot be solved rigorously only with the basis of discrete spectrum equation (8(8) $\begin{array}{rl}& u_p^{NLM}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|R_0,{\mathrm{\Theta }}_0,{\mathrm{\Phi }}_0)\\ & \equiv |\begin{array}{ccc}{n}_a& l_a& m_a\\ n_b& l_b& m_b\\ n_c& l_c& m_c\\ n_d& l_d& m_d\end{array}〉\otimes |NLM〉,\end{array}$(8) ), but a basis of continuous spectrum must be included, and a Green functions formalism should be applied. Such a scheme is beyond the scope of our consideration, and in the next section we analyse this problem from a certain semi-quantitative point of view to obtain some plausible estimations and clarify the corresponding facts on a qualitative level. To do this we return to the Born–Oppenheimer–Heitler–London approximation which allow us analysing the interatomic interaction as a function of interatomic distance $R_0$ [30–32].

3.2. Born–Oppenheimer–Heitler–London approximation

3.2.1. Hamiltonian

Here we suggest that electrons ‘a’ and ‘b’ belong to the first nucleus, and electrons ‘c’ and ‘d’ belong to the second one, and re-write the Hamiltonian Equation (1(1) $\begin{array}{rl}& {\hat{H}}_{tot}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)=-\frac{1}{2\mu }{\mathrm{\Delta }}^{\left(\mathrm{n}\mathrm{u}\mathrm{c}\right)}({\mathbf{\text{R}}}_0)+\frac{{\mathcal{Z}}_0^2}{R_0}\\ & +H^{\left(e\right)}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)+{\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & +{\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0),\end{array}$(1) ) in the form [32] (12) $\begin{array}{rl}& {\hat{H}}_{\mathrm{t}\mathrm{o}\mathrm{t}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)={\hat{H}}_1({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b)+{\hat{H}}_2({\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)\\ & +{\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)+{\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0),\end{array}$(12) where ${\hat{H}}_1({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b)$ and ${\hat{H}}_1({\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)$ are Hamiltonians of independent helium atoms with ${\mathcal{Z}}_0=2$, (13) $\begin{array}{rl}{\hat{H}}_1({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b)& =-\frac{1}{2}{\mathrm{\Delta }}^{\left(e_a\right)}\left({\mathbf{\text{r}}}_a\right)-\frac{1}{2}{\mathrm{\Delta }}^{\left(e_b\right)}\left({\mathbf{\text{r}}}_b\right)\\ & -\frac{{\mathcal{Z}}_0}{r_a}-\frac{{\mathcal{Z}}_0}{r_b}+\frac{{\mathcal{Z}}_0}{|{{\mathbf{\text{r}}}_a-\mathbf{\text{r}}}_b|}\end{array}$(13) and (14) $\begin{array}{rl}{\hat{H}}_2({\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)& =-\frac{1}{2}{\mathrm{\Delta }}^{\left(e_c\right)}\left({\mathbf{\text{r}}}_c\right)-\frac{1}{2}{\mathrm{\Delta }}^{\left(e_d\right)}\left({\mathbf{\text{r}}}_d\right)\\ & -\frac{{\mathcal{Z}}_0}{r_c}-\frac{{\mathcal{Z}}_0}{r_d}+\frac{{\mathcal{Z}}_0}{|{{\mathbf{\text{r}}}_c-\mathbf{\text{r}}}_d|}\end{array}$(14) the Hamiltonian ${\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)$ is mutual interaction, (15) $\begin{array}{rl}& {\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & =+\frac{{\mathcal{Z}}_0^2}{R_0}-\frac{{\mathcal{Z}}_0}{|{\mathbf{\text{r}}}_a-{\mathbf{\text{R}}}_0|}-\frac{{\mathcal{Z}}_0}{|{\mathbf{\text{r}}}_b-{\mathbf{\text{R}}}_0|}\\ & -\frac{{\mathcal{Z}}_0}{|{\mathbf{\text{r}}}_c+{\mathbf{\text{R}}}_0|}-\frac{{\mathcal{Z}}_0}{|{\mathbf{\text{r}}}_d+{\mathbf{\text{R}}}_0|}\\ & +\frac{1}{|{\mathbf{\text{R}}}_0+{\mathbf{\text{r}}}_c-{\mathbf{\text{r}}}_a|}\\ & +\frac{1}{|{\mathbf{\text{R}}}_0+{\mathbf{\text{r}}}_d-{\mathbf{\text{r}}}_a|}+\frac{1}{|{\mathbf{\text{R}}}_0+{\mathbf{\text{r}}}_c-{\mathbf{\text{r}}}_b|}\\ & +\frac{1}{|{\mathbf{\text{R}}}_0+{\mathbf{\text{r}}}_d-{\mathbf{\text{r}}}_b|},\end{array}$(15) and ${\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)$ is the relativistic (spin–orbit and spin–spin) part of interaction, according to Equation (4(4) $\begin{array}{rl}{\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)& ={\hat{H}}_{\mathrm{S}\mathrm{O}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & +{\hat{H}}_{\mathrm{S}\mathrm{S}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d).\end{array}$(4) ). In fact, ${\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\hat{\mathit{\sigma }}}$ is a really small correction, proportional to the small parameter ${\alpha }^2/4\simeq 4.2$ K, where $\alpha =1/137$ is Sommerfeld (fine structure) constant [43,54]. As it can be seen from Equation (15(15) $\begin{array}{rl}& {\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & =+\frac{{\mathcal{Z}}_0^2}{R_0}-\frac{{\mathcal{Z}}_0}{|{\mathbf{\text{r}}}_a-{\mathbf{\text{R}}}_0|}-\frac{{\mathcal{Z}}_0}{|{\mathbf{\text{r}}}_b-{\mathbf{\text{R}}}_0|}\\ & -\frac{{\mathcal{Z}}_0}{|{\mathbf{\text{r}}}_c+{\mathbf{\text{R}}}_0|}-\frac{{\mathcal{Z}}_0}{|{\mathbf{\text{r}}}_d+{\mathbf{\text{R}}}_0|}\\ & +\frac{1}{|{\mathbf{\text{R}}}_0+{\mathbf{\text{r}}}_c-{\mathbf{\text{r}}}_a|}\\ & +\frac{1}{|{\mathbf{\text{R}}}_0+{\mathbf{\text{r}}}_d-{\mathbf{\text{r}}}_a|}+\frac{1}{|{\mathbf{\text{R}}}_0+{\mathbf{\text{r}}}_c-{\mathbf{\text{r}}}_b|}\\ & +\frac{1}{|{\mathbf{\text{R}}}_0+{\mathbf{\text{r}}}_d-{\mathbf{\text{r}}}_b|},\end{array}$(15) ), we do not include into ${\hat{H}}_{\mathrm{i}\mathrm{n}\mathrm{t}}$ the $R_0$-independent interelectron repulsion within the pairs ‘ a–b’ and ‘c–d' which suppose to be prescribed to the first and second nuclei separately and are the parts of their own intrinsic (‘vacuum’) energy.

3.2.2. Non-relativistic (van der Waals) He–He interaction

The necessary solutions can be built in two asymptotical limiting cases, $R_0\to 0$ and $R_0\to \mathrm{\infty }$ [32] and energy of the system as a function of interatomic distance for the both cases is plotted on Figure 4). As it can be seen, the right well for helium is deeper than the left one, but, more importantly, it is much broader and evidently nonharmonic. As a result, the inherent ground level of the left well (red level on Figure 4) lies much higher than the vacuum level $U_{\mathrm{v}\mathrm{a}\mathrm{c}}=-5.72$ a.u., whereas the corresponding level of the right well (blue level on Figure 4) is only rough approximately $10÷50$ K below the $U_{\mathrm{v}\mathrm{a}\mathrm{c}}$. Exact numerical data cannot be produced within the developed approach in view of, at least, two reasons: (i) the curves 1 and 2 on the Figure 4 are divergent asymptotics obtained for immobile nuclei (the internuclear distance $R_0$ is not accounted as dynamical variable of the problem, but only free parameter in the Schrödinger equation) and (ii) the potential curves specified in a numerical form give no way to extract properly an effect of several Kelvins in magnitude against a vacuum background of several atomic units [32]. The complete energy curve combined of asymptotics from Figure 4 has been shown in Figure 5. The barrier on the potential curve of ${}^4$ He–${}^4$He interaction was first discussed in review of R.A. Buckingham [55] and supported by a number of calculations [49–53]. In our case the barrier in Figure 5 cannot change essentially the value of the ground level of the right well except of possibly splitting of order 5K. In addition, the average interatomic distance in the well of Figure 5 can be estimated as $〈R_0〉=6.35$ Bohr ≈3.36 Å which is in good agreement with molar volume ∼28 cm${}^3$/mol known for ${}^4$He liquid [44]. Under external pressure, the barrier is lowered down the well and the ground state becomes lower, so that helium transfers into solid phase. Anyway, despite the semi-quantitative approach used in the above-mentioned considerations, we can see that all the estimated values are in good agreement with experimentally obtained data for helium liquid [44].

Figure 4. (Colour online) Curve (1): The total interaction energy calculated with short-range repulsion asymptotics [32] for He${}_2$ dimer. The ‘intrinsic’ level in the short-range well is −1.37 a.u. with $〈R_0〉=2.1$ Bohr. Curve (2): The total interaction energy calculated with long-range repulsion asymptotics [32] for He${}_2$ dimer. The ‘intrinsic’ level in the long-range well is −5.85 a.u. with $〈R_0〉=6.35$ Bohr ≈3.36 Å, it is in good agreement with known molar volume of ${}^4$He [44] (see text). Dashed line corresponds to the ‘vacuum’ level $U_{\mathrm{v}\mathrm{a}\mathrm{c}}=-5.72$ a.u. as the ground state energy of two independent ${}^4$He atoms [47].

Thus we can conclude that the non-relativistic energy of the bound state for ${}^4$He${}_2$ dimer lies in the vicinity of the vacuum level $U_{\mathrm{v}\mathrm{a}\mathrm{c}}$, so that the corresponding condensed phase must be constructed as simple boiling liquid with only short-range order (He I phase). In this connection some formally small relativistic corrections (of order $\sim 1/c^2$) should play an essential role in the total balance of interactions in quantum helium matter.

Figure 5. (Colour online) Curve (1): The total interaction energy composed of corves (1) and (2) from Figure 4 as a unitary dependence for He${}_2$ dimer [32]. The both curves are built up within different approximation procedures [32], so that the composition can be fulfilled only on a qualitative level. The left well of the double-well potential is much narrower than the right one which, in addition, is extremely wide and smooth. As a result, the ground-state level of the double-well lies only a bit higher than the blue level of the right well, approaching from the bottom to the ‘vacuum’ level $U_{\mathrm{v}\mathrm{a}\mathrm{c}}=-5.72$ a.u. It means a ‘softening’ of the non-relativistic van der Waals interaction on this ground the relativistic spin–spin interaction with energy of order 10 kelvin becomes a leading factor (see text).

3.2.3. Spin-dependent interaction

The difference in observable physical properties between condensed phases of two helium isotopes testifies undoubtedly that different spin subsystems of ${}^3$He and ${}^4$He are principal background of interatomic interactions in the mentioned substances. Here we consider in some details only ${}^4$He with total nuclear spin equal to zero. The spin-dependent relativistic corrections of order $\sim 1/c^2$ are really small perturbation with a measure of the coefficient ${\alpha }_S^2/4\sim 4.2$ K (where ${\alpha }_S=1/137$ is Sommerfeld constant). In this connection, for simplicity, the interelectronic interaction of the required relativistic Hamiltonian ${\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)$ Equation (4(4) $\begin{array}{rl}{\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)& ={\hat{H}}_{\mathrm{S}\mathrm{O}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & +{\hat{H}}_{\mathrm{S}\mathrm{S}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d).\end{array}$(4) ) can be written in the limit $R_0=0$ which just corresponds to condensed helium phase. This Hamiltonian includes only four electron coordinates ${\mathbf{\text{r}}}_s$ (originate from the point $R_0=0$) with four electronic spins ${\hat{\mathit{\sigma }}}_s$ (s = a, b, c, d) of two helium shells and can be written as the superposition of spin–orbital ${\hat{H}}_{\mathrm{S}\mathrm{O}}^{\hat{\mathit{\sigma }}}$ (Equation 5(5) $\begin{array}{rl}& {\hat{H}}_{\mathrm{S}\mathrm{O}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & =-i\frac{{\mathcal{Z}}_0{g}_S{\alpha }_S^2}{4}\{\sum _s{\hat{\mathit{\sigma }}}_s[\frac{{\mathbf{\text{r}}}_s}{r_s^3}\times {\mathrm{\nabla }}_s]\\ & +\sum _s{\hat{\mathit{\sigma }}}_s[\frac{{\mathbf{\text{r}}}_s-{\mathbf{\text{R}}}_0}{|{\mathbf{\text{r}}}_s-{\mathbf{\text{R}}}_0{|}^3}\times {\mathrm{\nabla }}_s]\\ & -\frac{1}{{\mathcal{Z}}_0}\sum _s{\hat{\mathit{\sigma }}}_s\sum _{s^{\mathrm{\prime }}\ne s}[\frac{{\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}}{r_{s{s}^{\mathrm{\prime }}}^3}\times ({\mathrm{\nabla }}_s-{\mathrm{\nabla }}_{s^{\mathrm{\prime }}}\left)\right]\}\end{array}$(5) ) and spin–spin ${\hat{H}}_{\mathrm{S}\mathrm{S}}^{\hat{\mathit{\sigma }}}$ Equation (6(6) $\begin{array}{rl}& {\hat{H}}_{\mathrm{S}\mathrm{S}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)\\ & =\frac{g_s^2{\alpha }_s^2}{4}\{-\frac{8\pi }{3}\sum _{s\ne s^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}\delta ({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}})\\ & +\sum _{s\ne s^{\mathrm{\prime }}}\frac{1}{r_{s{s}^{\mathrm{\prime }}}^3}[{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}-3\frac{\left({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s\right)\left({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}\right)}{r_{s{s}^{\mathrm{\prime }}}^2}]\}\end{array}$(6) ) contributions [30–32,43]. To obtain the spin density matrix for our problem, we have to calculate the average $〈G.S.|{\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\hat{\mathit{\sigma }}}|G.S.〉$ over the spatial ground state of the four-electron system on the ${}^4$ He–${}^4$He interatomic bond, and as he ground state wave function we choose $|G.S.〉=|100{〉}_a|100{〉}_b|100{〉}_c|100{〉}_d.$ In this case, due to symmetry reasons, the matrix elements of $〈G.S.|{\hat{H}}_{\mathrm{S}\mathrm{O}}^{\hat{\mathit{\sigma }}}|G.S.〉$ are equal to 0, and the spin density matrix has the form: (16) $\begin{array}{rl}& \rho ({\hat{\mathit{\sigma }}}_a,{\hat{\mathit{\sigma }}}_b,{\hat{\mathit{\sigma }}}_c,{\hat{\mathit{\sigma }}}_d|R_0)=〈G.S.|{\hat{H}}_{\mathrm{S}\mathrm{S}}^{\hat{\mathit{\sigma }}}|G.S.〉\\ & =\frac{g_S^2{\alpha }_S^2}{4}\{-\frac{8\pi }{3}\sum _{s\ne s^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}〈G.S|\delta ({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}})|G.S〉\\ & +\sum _{s\ne s^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}〈G.S.\left|\frac{1}{r_{ss\mathrm{\prime }}^3}\right|G.S.〉\\ & -3〈G.S.\left|\frac{\left({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s\right)\left({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}\right)}{r_{s{s}^{\mathrm{\prime }}}^5}\right|G.S.〉\}.\end{array}$(16) It is reasonable to suggest that magnetic moments of the four electrons on the common interatomic bond will be oriented preferable perpendicular to this bond, it means that ${\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s\simeq 0$, and last term in Equation (16(16) $\begin{array}{rl}& \rho ({\hat{\mathit{\sigma }}}_a,{\hat{\mathit{\sigma }}}_b,{\hat{\mathit{\sigma }}}_c,{\hat{\mathit{\sigma }}}_d|R_0)=〈G.S.|{\hat{H}}_{\mathrm{S}\mathrm{S}}^{\hat{\mathit{\sigma }}}|G.S.〉\\ & =\frac{g_S^2{\alpha }_S^2}{4}\{-\frac{8\pi }{3}\sum _{s\ne s^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}〈G.S|\delta ({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}})|G.S〉\\ & +\sum _{s\ne s^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}〈G.S.\left|\frac{1}{r_{ss\mathrm{\prime }}^3}\right|G.S.〉\\ & -3〈G.S.\left|\frac{\left({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s\right)\left({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}\right)}{r_{s{s}^{\mathrm{\prime }}}^5}\right|G.S.〉\}.\end{array}$(16) ) can be omitted. As a result we have [32] (17) $\begin{array}{r}\rho ({\hat{\mathit{\sigma }}}_a,{\hat{\mathit{\sigma }}}_b,{\hat{\mathit{\sigma }}}_c,{\hat{\mathit{\sigma }}}_d|R_0)={\mathcal{E}}_1\left(R_0\right)+\frac{J}{2}\sum _{s\ne s^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}},\end{array}$(17) where ${\mathcal{E}}_1(〈R_0〉)$ is the energy of the ground state, and J is the magnitude of spin–spin pair exchange (Heisenberg exchange constant) represented through the corresponding spatial matrix elements, (18) $\begin{array}{rl}J& =\frac{g_S^2{\alpha }_S^2}{4}\{-\frac{8\pi }{3}〈G.S|\delta ({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}})|G.S〉+\\ & +〈G.S.\left|\frac{1}{r_{ss\mathrm{\prime }}^3}\right|G.S.〉-3〈G.S.\left|\frac{({\mathbf{\text{r}}}_s-{\mathbf{\text{r}}}_{s^{\mathrm{\prime }}}{)}^2}{3r_{ss\mathrm{\prime }}^5}\right|G.S.〉\}\end{array}$(18) Whereas the energy of the spatial ground state can be calculated with high enough accuracy [30–32], the calculation of J is much problematic because only the first term in Equation (18(18) $\begin{array}{rl}J& =\frac{g_S^2{\alpha }_S^2}{4}\{-\frac{8\pi }{3}〈G.S|\delta ({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}})|G.S〉+\\ & +〈G.S.\left|\frac{1}{r_{ss\mathrm{\prime }}^3}\right|G.S.〉-3〈G.S.\left|\frac{({\mathbf{\text{r}}}_s-{\mathbf{\text{r}}}_{s^{\mathrm{\prime }}}{)}^2}{3r_{ss\mathrm{\prime }}^5}\right|G.S.〉\}\end{array}$(18) ) (so-called ‘contact interaction’, see also Ref. [41]) can be calculated exactly with use of the corresponding representation [56] for δ-function, (19) $\begin{array}{r}\frac{8\pi }{3}〈G.S.|\delta ({\mathbf{\text{r}}}_a-{\mathbf{\text{r}}}_b)|G.S.〉=\frac{1}{3}({\mathcal{Z}}_0-\sigma {)}^3,\end{array}$(19) where σ is the screening constant [54,57], the corresponding calculations for helium atom [47] give $\sigma \simeq 0.2323$ (in the literature [58,59] are known other estimations of $\sigma \simeq 0.3125$). Other two terms in Equation (18(18) $\begin{array}{rl}J& =\frac{g_S^2{\alpha }_S^2}{4}\{-\frac{8\pi }{3}〈G.S|\delta ({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}})|G.S〉+\\ & +〈G.S.\left|\frac{1}{r_{ss\mathrm{\prime }}^3}\right|G.S.〉-3〈G.S.\left|\frac{({\mathbf{\text{r}}}_s-{\mathbf{\text{r}}}_{s^{\mathrm{\prime }}}{)}^2}{3r_{ss\mathrm{\prime }}^5}\right|G.S.〉\}\end{array}$(18) ) contain Coulomb irregularities which must be renormalised using a certain procedure of quantum electrodynamics [60]. In 1930, E. Fermi proposed an approach [61] which allowed to get an estimation for the spatial matrix element $〈r_{ss\mathrm{\prime }}^{-3}〉$, and here we use some similar procedure [32] with the simplest ground state wave function. As a result, we have the estimation (20) $\begin{array}{r}J\simeq -11.716\mathrm{K}\end{array}$(20) Note that this value is just the depth of the Lennard–Jones potential well for helium [55], but the most essential fact is the negative sign of the Heisenberg constant J which means that the spin exchange within the ${}^4$ He–${}^4$He bond is ferromagnetic, and we immediately keep in mind the Shubnikov's analogy [1] of the λ-line with Curie transition in ferromagnets. In reality situation is much more complicated because exchange constant Equation (18(18) $\begin{array}{rl}J& =\frac{g_S^2{\alpha }_S^2}{4}\{-\frac{8\pi }{3}〈G.S|\delta ({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}})|G.S〉+\\ & +〈G.S.\left|\frac{1}{r_{ss\mathrm{\prime }}^3}\right|G.S.〉-3〈G.S.\left|\frac{({\mathbf{\text{r}}}_s-{\mathbf{\text{r}}}_{s^{\mathrm{\prime }}}{)}^2}{3r_{ss\mathrm{\prime }}^5}\right|G.S.〉\}\end{array}$(18) ) (see also Equation 16(16) $\begin{array}{rl}& \rho ({\hat{\mathit{\sigma }}}_a,{\hat{\mathit{\sigma }}}_b,{\hat{\mathit{\sigma }}}_c,{\hat{\mathit{\sigma }}}_d|R_0)=〈G.S.|{\hat{H}}_{\mathrm{S}\mathrm{S}}^{\hat{\mathit{\sigma }}}|G.S.〉\\ & =\frac{g_S^2{\alpha }_S^2}{4}\{-\frac{8\pi }{3}\sum _{s\ne s^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}〈G.S|\delta ({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}})|G.S〉\\ & +\sum _{s\ne s^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}〈G.S.\left|\frac{1}{r_{ss\mathrm{\prime }}^3}\right|G.S.〉\\ & -3〈G.S.\left|\frac{\left({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s\right)\left({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}\right)}{r_{s{s}^{\mathrm{\prime }}}^5}\right|G.S.〉\}.\end{array}$(16) ) consists of three terms with different signs, and, in addition, only the first term of Equation (18(18) $\begin{array}{rl}J& =\frac{g_S^2{\alpha }_S^2}{4}\{-\frac{8\pi }{3}〈G.S|\delta ({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}})|G.S〉+\\ & +〈G.S.\left|\frac{1}{r_{ss\mathrm{\prime }}^3}\right|G.S.〉-3〈G.S.\left|\frac{({\mathbf{\text{r}}}_s-{\mathbf{\text{r}}}_{s^{\mathrm{\prime }}}{)}^2}{3r_{ss\mathrm{\prime }}^5}\right|G.S.〉\}\end{array}$(18) ) (contact interaction) can be calculated exactly. The next two terms in Equation (18(18) $\begin{array}{rl}J& =\frac{g_S^2{\alpha }_S^2}{4}\{-\frac{8\pi }{3}〈G.S|\delta ({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}})|G.S〉+\\ & +〈G.S.\left|\frac{1}{r_{ss\mathrm{\prime }}^3}\right|G.S.〉-3〈G.S.\left|\frac{({\mathbf{\text{r}}}_s-{\mathbf{\text{r}}}_{s^{\mathrm{\prime }}}{)}^2}{3r_{ss\mathrm{\prime }}^5}\right|G.S.〉\}\end{array}$(18) ) are spatial matrix elements with Coulomb irregularities which can be only roughly estimated. Moreover, each atom is surrounded by neighbouring atoms, and the electronic array from neighbours creates a valence bond with collectivised electrons, so that the sign of exchange within the bond in condense phase can be both ferromagnetic and antiferromagnetic depending on atomic configuration of the medium and possible contribution of multispin exchange.

Spectrum ${\mathcal{E}}_i^{\left(s\right)}$ of the spin density matrix equation (17(17) $\begin{array}{r}\rho ({\hat{\mathit{\sigma }}}_a,{\hat{\mathit{\sigma }}}_b,{\hat{\mathit{\sigma }}}_c,{\hat{\mathit{\sigma }}}_d|R_0)={\mathcal{E}}_1\left(R_0\right)+\frac{J}{2}\sum _{s\ne s^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}},\end{array}$(17) ) has been presented in Table 2. The spin spectrum ${\mathcal{E}}_i^{\left(s\right)}$ consists of three degenerate levels with quintuply degenerate ground state ${\mathcal{E}}_0^{\left(s\right)}=6J=-70.3$ K. The spin–spin interaction lowers the bound energy ${\mathcal{E}}_1\left(R_0\right)$ on the He–He interatomic bond and at $T\to 0$ stabilises a helium condensed phase near the labile equilibrium level of spatial bond presented on Figure 5. If suppose that the spins are distributed among sites of a spatial lattice (regular or irregular) with coordinates $\mathbf{\text{f}}$, then the spin contribution to the interatomic interaction in condensed helium phases can be presented in the standard Heisenberg form [31] (21) $\begin{array}{rl}{\hat{H}}_{\mathrm{s}\mathrm{p}\mathrm{i}\mathrm{n}}& =\frac{J\left(R_0\right)}{2}\sum _{\mathbf{\text{f}},\mathit{\delta }}[{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}}^{\left(a\right)}{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}}^{\left(b\right)}+{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}}^{\left(a\right)}{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}+R_0\mathit{\delta }}^{\left(a\right)}+{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}}^{\left(a\right)}{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}+R_0\mathit{\delta }}^{\left(b\right)}\\ & +{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}}^{\left(b\right)}{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}+R_0\mathit{\delta }}^{\left(a\right)}\\ & +{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}}^{\left(b\right)}{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}+R_0\mathit{\delta }}^{\left(b\right)}+{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}+R_0\mathit{\delta }}^{\left(b\right)}{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}+R_0\mathit{\delta }}^{\left(b\right)}]\end{array}$(21) where $\mathit{\delta }$ is a unit vector directed to the corresponding nearest neighbour from the first coordination sphere of the site $\mathbf{\text{f}}$ (‘a’ and ‘b’ denote electrons prescribed to the site $\mathbf{\text{f}}$ and, for simplicity, we suppose that the length of all interatomic bonds is equal to $R_0$). Thus each bond with the neighbouring atom from the first coordination sphere contains four spins bonded by mutual exchange of spin pairs and, probably, by four-spin exchange [31]. The further consideration of the spin-possessed properties of condensed ${}^4$He phases will be continued in Section 7.

Table 2. Spin states within ${}^4$He–${}^4$He bond at ferromagnetic exchange.

State	Energy, ${\mathcal{E}}_i^{\left(s\right)}/J$	Parity	Degeneration
1	−6	even	5
2	2	odd	9
3	6	even	2

4. Anomalies in solid ${}^4$He

Following Nozières' recommendations [22], we start discussing the ‘superfluid’ state from overlook of the high-pressure HCP solid phase in regard to just anomalously ‘supersolid’ behaviour in mechanical and thermodynamical properties of the ${}^4$He, and then enter through the solid–liquid boundary into He II region where superfluid and supersolid ideologies were applied originally to interpret the experimentally observed properties of the He II phase. We will consider the three most essential phenomena: (i) excessive heat capacity at 0.1–0.5 K [62,63], (ii) non-monotonic behaviour of $P\left(T\right)$ [64,65] at 0.1–0.5 K, and (iii) anomalous softening of ${}^4$He crystal at 0.1 –1.0K [66–69]. The common feature united all these phenomena is demand for macroscopically great amount of microscopic spatial degrees of freedom which can be typically excited within the temperature interval of 0.1–1.0 K. It should be noted that all the mentioned features can be evidence of the solid phase transition ‘normal solid’→‘supersolid’ predicted by Kim and Chan in Ref. [26] (see Subsection 5.2).

4.1. What are the low-temperature degrees of freedom?

Lin et al. [62,63] reported anomalous heat capacity peak at 0.05 –0.15 K (excessive heat capacity on the standard phonon $\sim T^3$ dependence) in the ${}^4$He solid with different amounts of ${}^3$He impurities (they specially emphasise that under their experimental conditions the heat capacity peak cannot be associated with phase separation in a mixture of helium isotopes). It is evident that excessive heat capacity at very low temperature (where the density of phonon states is rather small) needs a resource of macroscopic degrees of freedom, and such degrees (at certain conditions) could be supplied by dislocations, but the necessary density of dislocations seems to be enormously high for the perfect quantum crystal. Another suggestion [70] is based on the possible contribution of two-level tunnelling states (so-called glassy contribution) in the highly disordered crystalline medium, but the nature of this ‘glassy phase’ remains unclear.

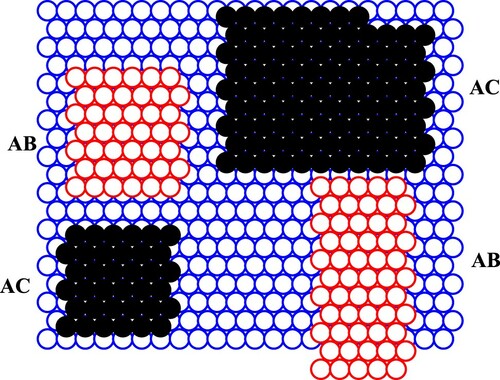
We developed the model for excessive heat capacity built [71–73] on real structural peculiarities of solid ${}^4$He. A perfect monoatomic HCP crystal can be built as multilayered system [74–77] which is a stack of close-packed basal planes on triangular lattice (Figure 6). According to the standard crystallographic procedure, we denote one of the planes as A and place a second element over the first one in such a way as not to destroy the closest packing of neighbouring atoms in the whole stack.

Figure 6. (Colour online) Three monoatomic layers on triangular lattice in two different position: $\dots ABC\dots$ stack (a) and $\dots ACB\dots$ stack (b).

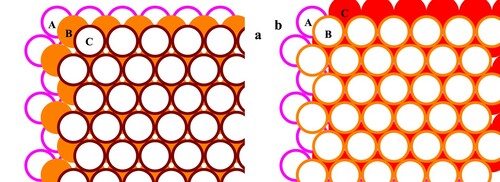
This can be done in one of two positions as it is illustrated by Figure 6(a) (B-position over A layer) and Figure 6(b) (C-position over A layer). Thus, placing N two-dimensional basal elements in the mentioned manner, we can produce 2${}^N$ different polytype modifications of monoatomic crystal lattice where each atom has 12 nearest neighbours in the first coordination sphere and 12 next-nearest neighbours in the second coordination sphere, respectively, at any arbitrary sequence of A, B, C elements (and neighbourhood of two coinciding elements is forbidden). The closest-packing principle is provided for any type of the polytypic structure [75] and the limited entropy of the totally random packing of the polytype built of N 2D layers on triangular lattice is equal to $N\ln 2$. The two-plane periodic structure $\dots B|AB|A\dots$ is hexagonal close-packed (HCP or 2H) lattice, the three-plane period $\dots C|ABC|A\dots$ means face-centred cubic crystal (FCC or 3C). The next periodic polytypes are twinned hexagonal structures $\dots C|ABAC|A\dots$ (4H), and $\dots B|ABCAB|A\dots$ (5H) as well as six-layered modifications $\dots B|ABCACB|A\dots$ (6H${}_1$) and $\dots C|ABABAC|A\dots$ (6H${}_2$). Then are seven 9-periodic structures (9T${}_{1\dots 6}$ and 9R), 12-periodic (12R), etc., up to a sequence of unlike-pairs with period formally tending to infinity [74–76] (the so-called random stacking faults or chaotic stacking faults structure). Any polytypic system can be obtained from the simplest 2H structure due to coherent elementary glide along the basal directions. In fact, it is the well-known mechanism of martensitic transformations in crystalline solids, [75,76] and this fact can be illustrated by Figure 7.

Figure 7. (Colour online) Different positions of B-type and C-type clusters on an A-type layer (schematic). The clusters divided by Shockley's partial dislocations (see text).

Figure 7 shows the layer A with ‘islands’ of B and C types (for simplicity, we suppose the third overlayer is of A-type similar to the first one). It can be seen that each island is surrounded by a channels due to incompatibility between B and C positions on the same A-substrate. These channels are network of Shockley's partial dislocations [78]. If one boundary atom from island B jumps between two equivalent potential wells along the groove of the potential relief of the substrate (layer A) onto boundary of layer C, it means an elementary displacement of the dislocation line through the distance $a/\sqrt{3}$ (where a is interatomic distance). After this act the island C increases, but island B decreases by one atom. Due to low energy of the barrier between neighbouring B and C positions the mentioned displacement can be realised by quantum tunnelling without thermal activation. This mechanism produces additional (as compared with phonon ones) degrees of freedom. Mechanically, it is a one-dimensional Frenkel–Kontorova dislocation [79,80]. The $AB\to AC$ transformation due to successive jumping of the atoms from AB to AC positions (like zipping-unzipping) means a motion of an elementary kink along the line of the partial dislocation, and the current of these kinks leads to the shift of the front of transformation in the complete analogy with kink-generated motion of perfect dislocation. The quantum tunnelling of the kinks along the real channel of the partial dislocation can be interpreted according to Andreev–Lifshits mechanism [81], which is quantum-mechanical generalisation of the ‘crowdion’ model [82] proposed for description of self-diffusion in alkali metals. This gives us a physical explanation of restricted one-dimensional diffusion evidently observed in helium crystals [48,83,84] (cmp. with kink dynamics on the perfect dislocations [78,85]). It should be noted that atomic configurations quite analogous to the pictured on Figure 7 (related to the stacking faults and Shockley partials) were obtained in Ref. [86] through PIMC computer simulations (see also literature cited therein). As it is seen from Figure 7, the obtained configuration is a network of the Shockley partial dislocations which can move in the basal plane due to atomic kinks (Frenkel–Kontorova solitons or Andreev–Lifshits excitons) migration stimulated by thermal fluctuations or internal stresses.

In this connection, the polytype of arbitrary structure is the HCP lattice with a certain one-dimensional distribution of ‘stacking faults’ in a hexagonal or cubic positions [75,76] along c-axis of hexagonal cell (perpendicular to basal planes). The faults are 2D defects packed without breaking of the closest packing principle, but only a certain arrangement and re-arrangement in succession of these two-type crystalline planes with triangular lattice is a mechanism of 3D deformation of the crystal. The re-arrangement of such a stacks needs to get a certain stacking-fault energy (SFE) [77] and packing entropy, so that it is thermodynamically specified process with an average packing period in z-direction as the order parameter of the spatially disordered crystal. The SFE is typically small in atomic and molecular cryocrystals, especially for solid helium and another solidified rare gases [87], so that we can expect that the polytype model is perfectly suitable for solid ${}^4$He.

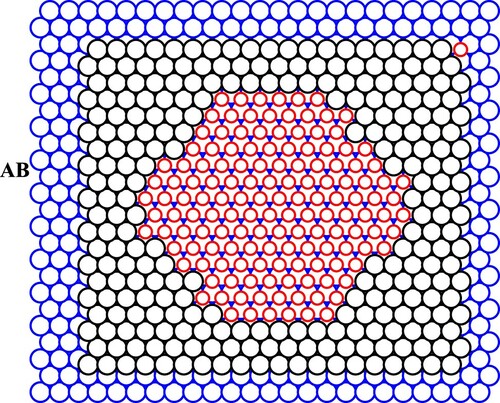
If the layers shown in Figure 7 are covered by 2D basal plane of A-type, then we have the local defect structure built of four prismatic dislocation loops (so-called Frank prismatic loops [78,88]). In a perfect HCP (or 2H) crystal lattice, the prismatic dislocation of such kind can, in principle, glide along c-axis (i.e. perpendicularly to the basal planes [78]), but in reality this process is possible only at very specific distribution of internal stresses, so that the evolution of the prismatic loops (Frank dislocations) is mainly due to diffusive atomic migration [78] (in the quantum crystals it is, certainly, quantum diffusion). In a polytype with a number of stacking faults the glide of prismatic loops is almost forbidden (or at least essentially impeded) due to intersection of the gliding loop with others incommensurate prismatic dislocations located in the neighbouring basal planes, so that atomic diffusion is the only mechanism to move the loops. It should be noted that the kinks on the partial dislocations are the direct analog of ‘invisible vacancies’ predicted for colloidal crystals [89]. The anomalous mobility of the crowdion-like kinks should be a reason of analogy between condensed helium and colloidal systems stated in Ref. [90].

Figure 8 shows schematically a possible distribution of the prismatic loops within an array of the prismatic dislocations built as clusters of atoms in B or C positions and placed on the same A-basal plane. The dislocations divided by rather wide stripes of vacant positions, so that an atomic exchange between neighbouring clusters will be fulfilled by tunnelling within quasi-2D geometry. And Figure 9 shows the prismatic dislocation loop built as a vacancy disc [78,88] with atomic kinks on the internal contour (edge of extra-plane) of the loop. The diffusive tunnelling of the kinks under external loading leads to the healing of the defect with simultaneous relaxation of internal stresses. This is a basis of so-called Nabarro–Herring–Lifshits mechanism of dislocation-diffusive creep of crystals [91–93] and hypothetic quantum-diffusive creep in helium [94] (contribution of the prismatic dislocation loops to the diffusive creep in crystals was studied theoretically [95,96] and experimentally [97,98] during 60s).

Figure 8. (Colour online) Prismatic Frank dislocations built of atomic B-type and C-type clusters on an A-type substrate (schematic). The clusters divided by wide vacant regions which are 2D vacant space for atomic migration between neighbouring clusters (see text).

Figure 9. (Colour online) Prismatic dislocation loop built of vacancies (vacansion disc, see text). Atomic kinks can be seen on the internal contour of the loop. The kinks can migrate due to tunnelling in the 2D relief of the vacant interior of the prismatic loop.

4.2. Heat capacity of multilayered polytype

To classify the polytypic structure, we use below the more compact notation system of Ewald–Belov–Jagodzinski [75,76] which takes into account directly the local symmetry of crystalline environment for each site of a chosen 2D layer. So, if any layer A is surrounded by like-pair of neighbours (as BAB or CAC, etc.) then it means the position with local hexagonal symmetry, and this position we denote as h-layer. If the layer is surrounded by unlike-pair (as BAC or CAB, etc.), we denote it as cubic or c-layer. With this notation, for example, the 6H${}_1$ polytype should be denoted as $\dots |hcchcc|\dots$, etc., and this notation system is used below.

The stack of basal planes with totally aperiodic (random) packing without breaking the closest-packing principle is the system of random (or chaotic) stacking-faults (RSF) [76]. Evidently, this system does not possess a microscopic translation symmetry along c-axis, but even in this case the direction perpendicular to basal planes remains the crystallographic axis of the third-order rotation symmetry. Thus all the long-periodic polytypic structures (up to RSF) belong to hexagonal symmetry subgroup $C_{3v}$. As a result, in long-wave limit (it is just the case of solid ${}^4$He) the polytype is crystallographically perfect anisotropic elastic medium with hexagonal symmetry and specific dispersion of acoustic (phononic) excitation along c-direction. Each variant of the polytypic stack has a specific intrinsic energy (due to SFE of individual elements in stack) and specific entropy (due to variety of packing configurations among N planes). In general, it is a complicated problem to be solved exactly, but in reality the anomalous heat capacity peak is comparably small, so that it is reasonable to suggest [70] that the total specific heat of the system is a result of additive contributions from phonons and some extraneous (non-phononic) degrees of freedom. The only question is the nature of these extraneous degrees which are supposed in [70] to be built of hypothetic two-level Andreev systems [99].

We will keep, in fact, the similar point of view but with the only difference that we propose the real physical mechanism of extraneous degrees based on a structural transformation in HCP crystalline polytype [75,76]. In this connection, we need also recalculate the spectrum of phonon excitations in a polytypic crystal. By this means the free energy $F(T,V)$ of the polytype consists of two parts, (22) $\begin{array}{r}F(T,V)=F_{ex}(T,N)+F_{\mathrm{p}\mathrm{h}}(T,V),\end{array}$(22) where $F_{\mathrm{p}\mathrm{h}}(T,V)$ is the ‘dynamic’ part due to phonon excitation in anisotropic lattice, and $F_{ex}(T,N)$ is the excessive or ‘static’ part as the free energy of a multilayered stack built of two-dimensional closely-packed atomic layers on triangular lattice. Successive transformation with temperature and pressure in solid polytype is realised as a continuous solid phase transition of martensitic type through a chain of phases with different spatial periods along c-axis. The phases can be short-periodic, long-periodic [100–103] and even aperiodic (RSF). It means that phonon spectrum of the crystal depends on the details of its polytypic structure and, as a result, the free energy Equation (22(22) $\begin{array}{r}F(T,V)=F_{ex}(T,N)+F_{\mathrm{p}\mathrm{h}}(T,V),\end{array}$(22) ) could not be, in general, presented as superposition of phonon and polytypic part. However, taking into account that any polytypic transformation in the stack of the layers with triangular lattice do not destroy the close packing of the crystal which remains macroscopically perfect elastic medium, and only long-wave phonons are essential for thermodynamics of helium solids, we conclude that the model of Equation (22(22) $\begin{array}{r}F(T,V)=F_{ex}(T,N)+F_{\mathrm{p}\mathrm{h}}(T,V),\end{array}$(22) ) is valid to describe the system under study.

4.2.1. Phonon part of heat capacity

The general expression for the function $F_{\mathrm{p}\mathrm{h}}\left(T\right)$ is well known [104–106] (23) $\begin{array}{r}{F}_{\mathrm{p}\mathrm{h}}\left(T\right)=\sum _{\mathbf{\text{k}},\alpha }\{\frac{{\omega }_{\alpha }\left(\mathbf{\text{k}}\right)}{2}+T\ln [1-\exp (-\text{β}{\omega }_{\alpha }(\mathbf{\text{k}}\left)\right)]\},\end{array}$(23) where the summation is over all states in the Brillouin zone, and all three acoustic frequency branches ${\omega }_{\alpha }\left(\mathbf{\text{k}}\right)$ of the spectrum in monoatomic lattice (the system of units with Planck and Boltzmann constants equal to 1 is used, $\mathbf{\text{k}}$ is three-dimensional wave vector), $\text{β}=1/T$. To get the spectrum ${\omega }_{\alpha }\left(\mathbf{\text{k}}\right)$ we have to solve the corresponding problem of lattice dynamics [106]. The Hamiltonian of this problem, according to the layered structure of the polytype, can be presented as a sum of N partial Hamiltonians $H_j$ describing 2D crystal lattices on triangular lattice (basal planes of HCP structure) [107] (24) $\begin{array}{r}{H}_{\mathrm{p}\mathrm{h}}(\mathbf{\text{p}},\mathbf{\text{u}})=\sum _{j=1}^N{H}_j({\mathbf{\text{p}}}_{{\mathbf{\text{f}}}_j},{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}).\end{array}$(24) Below we use harmonic approximation with only interaction of the nearest neighbours [71,107]. In this approximation, we have [73] (25) $\begin{array}{rl}{H}_j({\mathbf{\text{p}}}_{{\mathbf{\text{f}}}_j},{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j})& =\frac{1}{2m}\sum _{{\mathbf{\text{f}}}_j}{\mathbf{\text{p}}}_{{\mathbf{\text{f}}}_j}^2\\ & +\frac{\kappa \left(a\right)}{2}\sum _{{\mathbf{\text{f}}}_j,{\mathbf{\text{n}}}^{\left(\nu \right)}}\left[\right({\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}-{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j+a{\mathbf{\text{n}}}^{\left(\nu \right)}}){\mathbf{\text{n}}}^{\left(\nu \right)}{]}^2\\ & +\frac{\lambda \left(a\right)}{2}\sum _{{\mathbf{\text{f}}}_j,a{\mathbf{\text{n}}}^{\left(\nu \right)}}({\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}-{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j+a{\mathbf{\text{n}}}^{\left(\nu \right)}}{)}^2\\ & +\frac{\kappa \left(b\right)}{2}\sum _{{\mathbf{\text{f}}}_j,{\mathit{\delta }}_{j+1}^{\left(\nu \right)}}\left[\right({\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}-{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j+a{\mathit{\delta }}_{j+1}^{\left(\nu \right)}}){\mathit{\delta }}_{j+1}^{\left(\nu \right)}{]}^2\\ & +\frac{\lambda \left(b\right)}{2}\sum _{{\mathbf{\text{f}}}_j,{\mathit{\delta }}_{j+1}^{\left(\nu \right)}}({\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}-{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j+a{\mathit{\delta }}_{j+1}^{\left(\nu \right)}}{)}^2+\\ & +\frac{\kappa \left(b\right)}{2}\sum _{{\mathbf{\text{f}}}_j,{\mathit{\delta }}_{j-1}^{\left(\nu \right)}}\left[\right({\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}-{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j+a{\mathit{\delta }}_{j-1}^{\left(\nu \right)}}){\mathit{\delta }}_{j-1}^{\left(\nu \right)}{]}^2\\ & +\frac{\lambda \left(b\right)}{2}\sum _{{\mathbf{\text{f}}}_j,{\mathit{\delta }}_{j-1}^{\left(\nu \right)}}({\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}-{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j+a{\mathit{\delta }}_{j-1}^{\left(\nu \right)}}{)}^2,\end{array}$(25) where ${\mathbf{\text{p}}}_{{\mathbf{\text{f}}}_j}$ and ${\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}$ are momentum and displacement of the atom with the mass m in the site ${\mathbf{\text{f}}}_j$ of 2D triangular lattice with interatomic distance a. The unit vectors ${\mathbf{\text{n}}}^{\left(\nu \right)}$ set the directions to the nearest neighbours in the plane of the layer j, and unit vectors ${\mathit{\delta }}_{j\pm 1}^{\left(\nu \right)}$ are directed toward the neighbours of the first coordination sphere in upper (j + 1) or lower (j−1) adjacent planes (we use the Cartesian coordinate system in which the z-axis is directed perpendicular to the basal planes, and the $(x,y)$ coordinate plane coincides with the 2D triangular lattice of the number j). Therefore, the coordinates of the neighbours in the j-plane are $a{\mathbf{\text{n}}}^{\left(\nu \right)}$, with (26) $\begin{array}{r}{\mathbf{\text{n}}}^{(1,4)}=(\pm 1,0,0),{\mathbf{\text{n}}}^{(2,3,5,6)}=\frac{1}{2}(\pm 1,\pm \sqrt{3},0),\end{array}$(26) and the coordinates of the neighbours in adjacent layers are $a{\mathit{\delta }}_{j\pm 1}^{\left(\sigma \right)}$, where the unit vectors ${\mathit{\delta }}_{j\pm 1}^{\left(\sigma \right)}$ have the form (27) $\begin{array}{rl}{\mathit{\delta }}_{j\pm 1}^{\left(1\right)}& =\frac{1}{2}(1,\frac{1}{\sqrt{3}},\pm \gamma ),{\mathit{\delta }}_{j\pm 1}^{\left(2\right)}=\frac{1}{2}(-1,\frac{1}{\sqrt{3}},\pm \gamma ),\\ {\mathit{\delta }}_{j\pm 1}^{\left(3\right)}& =(0,-\frac{1}{\sqrt{3}},\pm \frac{\gamma }{2})\end{array}$(27) (B-configuration on Figure 6) and (28) $\begin{array}{rl}{\mathit{\delta }}_{j\pm 1}^{\left(1\right)}& =(0,\frac{1}{\sqrt{3}},\pm \frac{\gamma }{2}),{\mathit{\delta }}_{j\pm 1}^{\left(2\right)}=-\frac{1}{2}(1,\frac{1}{\sqrt{3}},\mp \gamma ),\\ {\mathit{\delta }}_{j\pm 1}^{\left(3\right)}& =\frac{1}{2}(1,-\frac{1}{\sqrt{3}},\pm \gamma )\end{array}$(28) (C-configuration on Figure 6). The distance between layers j + 1 and j−1 is equal to c, and $\gamma =c/a$ (for simplicity, we assume that the interplanar distance between the layers j and j + 1, as well as between j and j−1 are identical and equal to c/2). For an ideal packing of hard spheres, [74] ${\gamma }^2=8/3$. However, generally speaking, the interplanar distances can be different for $\dots h\dots$ ($\dots BAB\dots$) or $\dots c\dots$ ($\dots BAC\dots$) configurations of the j-plane environment, but we ignore this fact in the present study.

Furthermore, $\kappa \left(r\right)$ and $\lambda \left(r\right)$ are the force constants, responsible for the ‘central’ (directed along $\mathbf{\text{n}}$ or $\mathit{\delta }$) and ‘off-central’ part of the interatomic interaction, defined by the potential $U\left(r\right)$, (29) $\begin{array}{r}\kappa \left(r\right)=\frac{1}{2}\left[U^{\mathrm{\prime }\mathrm{\prime }}\right(r)-2\lambda (r\left)\right],\lambda \left(r\right)=\frac{U^{\mathrm{\prime }}\left(r\right)}{2r}.\end{array}$(29) Here r = a corresponds to interaction within the layer, whereas r = b corresponds to the interaction with neighbours in the neighbouring layers, (30) $\begin{array}{r}{b}^2=\frac{a^2}{3}(1+\frac{3}{4}{\gamma }^2).\end{array}$(30) If ${\gamma }^2=8/3$ then b = a. The terms in the Hamiltonian, proportional to $U^{\mathrm{\prime }}\left(r\right)$, are essential for crystals under external pressure (solid helium is just the same type of solids), when the interatomic distances do not correspond to the minimum of the pair interatomic interaction potential $U\left(r\right)$. It is plausible that the contribution from the terms depending on $U^{\mathrm{\prime }}\left(r\right)$ is the main determinant in the value of the shear modulus of solid helium. It is natural to assume that the interatomic distance in the compressed helium lattice is shifted toward the repulsive branch of the potential $U\left(r\right)$, and, consequently, $\lambda <0$, so that the value of the bulk modulus increases with increasing in external pressure acting on the crystal.

The last four terms in the Hamiltonian equations (24(24) $\begin{array}{r}{H}_{\mathrm{p}\mathrm{h}}(\mathbf{\text{p}},\mathbf{\text{u}})=\sum _{j=1}^N{H}_j({\mathbf{\text{p}}}_{{\mathbf{\text{f}}}_j},{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}).\end{array}$(24) ), (25(25) $\begin{array}{rl}{H}_j({\mathbf{\text{p}}}_{{\mathbf{\text{f}}}_j},{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j})& =\frac{1}{2m}\sum _{{\mathbf{\text{f}}}_j}{\mathbf{\text{p}}}_{{\mathbf{\text{f}}}_j}^2\\ & +\frac{\kappa \left(a\right)}{2}\sum _{{\mathbf{\text{f}}}_j,{\mathbf{\text{n}}}^{\left(\nu \right)}}\left[\right({\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}-{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j+a{\mathbf{\text{n}}}^{\left(\nu \right)}}){\mathbf{\text{n}}}^{\left(\nu \right)}{]}^2\\ & +\frac{\lambda \left(a\right)}{2}\sum _{{\mathbf{\text{f}}}_j,a{\mathbf{\text{n}}}^{\left(\nu \right)}}({\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}-{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j+a{\mathbf{\text{n}}}^{\left(\nu \right)}}{)}^2\\ & +\frac{\kappa \left(b\right)}{2}\sum _{{\mathbf{\text{f}}}_j,{\mathit{\delta }}_{j+1}^{\left(\nu \right)}}\left[\right({\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}-{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j+a{\mathit{\delta }}_{j+1}^{\left(\nu \right)}}){\mathit{\delta }}_{j+1}^{\left(\nu \right)}{]}^2\\ & +\frac{\lambda \left(b\right)}{2}\sum _{{\mathbf{\text{f}}}_j,{\mathit{\delta }}_{j+1}^{\left(\nu \right)}}({\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}-{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j+a{\mathit{\delta }}_{j+1}^{\left(\nu \right)}}{)}^2+\\ & +\frac{\kappa \left(b\right)}{2}\sum _{{\mathbf{\text{f}}}_j,{\mathit{\delta }}_{j-1}^{\left(\nu \right)}}\left[\right({\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}-{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j+a{\mathit{\delta }}_{j-1}^{\left(\nu \right)}}){\mathit{\delta }}_{j-1}^{\left(\nu \right)}{]}^2\\ & +\frac{\lambda \left(b\right)}{2}\sum _{{\mathbf{\text{f}}}_j,{\mathit{\delta }}_{j-1}^{\left(\nu \right)}}({\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}-{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j+a{\mathit{\delta }}_{j-1}^{\left(\nu \right)}}{)}^2,\end{array}$(25) ) are the energy of random j-plane interaction with the rest of the crystal. Obviously, for each realisation within the RSF system, the components ${\delta }_{j\pm 1,x}^{\left(\alpha \right)}$ and ${\delta }_{j\pm 1,y}^{\left(\alpha \right)}$ of the corresponding vectors will be randomly taken as one from a set from (27(27) $\begin{array}{rl}{\mathit{\delta }}_{j\pm 1}^{\left(1\right)}& =\frac{1}{2}(1,\frac{1}{\sqrt{3}},\pm \gamma ),{\mathit{\delta }}_{j\pm 1}^{\left(2\right)}=\frac{1}{2}(-1,\frac{1}{\sqrt{3}},\pm \gamma ),\\ {\mathit{\delta }}_{j\pm 1}^{\left(3\right)}& =(0,-\frac{1}{\sqrt{3}},\pm \frac{\gamma }{2})\end{array}$(27) ) or (28(28) $\begin{array}{rl}{\mathit{\delta }}_{j\pm 1}^{\left(1\right)}& =(0,\frac{1}{\sqrt{3}},\pm \frac{\gamma }{2}),{\mathit{\delta }}_{j\pm 1}^{\left(2\right)}=-\frac{1}{2}(1,\frac{1}{\sqrt{3}},\mp \gamma ),\\ {\mathit{\delta }}_{j\pm 1}^{\left(3\right)}& =\frac{1}{2}(1,-\frac{1}{\sqrt{3}},\pm \gamma )\end{array}$(28) ). Of course, the spectrum ${\omega }_{\nu }\left(\mathbf{\text{k}}\right)$ of the problem will depend significantly on the accounting method for the randomness in the stacking of the layers in the RSF crystal. In any case, it is clear that the system of this type loses the microscopic periodicity along the z-axis (the 2D crystallographic translation symmetry along any direction in a basal plane on the perfect triangular lattice remains unchanged), and therefore it is impossible to construct directly a regular mode, associated with a strong translational symmetry of the lattice. On the other hand, even in a random sequence $\dots h\dots c\dots$ of planes A, B, C, the close-packing principle is never destroyed, so that each atom has 12 neighbours in both the first and second coordination spheres, and only the local symmetry of the environment (hexagonal or cubic) changes randomly. For each of the j-planes, the transverse components, ${\delta }_{j\pm 1,x}^{\left(\sigma \right)}$ and ${\delta }_{j\pm 1,y}^{\left(\sigma \right)}$, of the vectors ${\mathit{\delta }}_{j+1}^{\left(\sigma \right)}$ are random, setting the direction toward the neighbours in the adjacent planes, whereas all the components of ${\delta }_{j\pm 1,z}^{\left(\sigma \right)}$ are not random (if the possible variation of γ in the cubic and hexagonal positions can be ignored, and ideal value of $\gamma =\sqrt{8/3}$ is chosen). In addition, the stack of the basal planes is transversally isotropic crystal, and the summation over transverse components ${\mathit{\delta }}_{j+1}^{\left(\sigma \right)}$ with high accuracy can be replaced by integration over azimuthal angle in the basal plane [107].

Finally, the phonon heat capacity can be written in the form [104–106] (31) $\begin{array}{rl}\frac{C_{\mathrm{p}\mathrm{h}}\left(T\right)}{k_B}& =\frac{\sqrt{3}}{4{\pi }^2}{N}_{1D}{N}_{2D}\sum _{\alpha =1,2,3}{\int }_0^{a{k}_D}q\mathrm{d}q{\int }_0^{\pi }\mathrm{d}{q}_z\\ & \times {\left(\frac{\text{β}{\omega }_{\alpha }(q,q_z)}{2}\right)}^2{\sinh }^{-2}\left(\frac{\text{β}{\omega }_{\alpha }(q,q_z)}{2}\right),\end{array}$(31) where $N_{2D}$ is the number of atoms in an individual basal plane on triangular lattice, $N_{1D}$ is the number basal planes in the stack (so that $N_{1D}{N}_{2D}$ is the total number of atoms in the crystal), $q^2=a^2(k_x^2+k_y^2)$ is two-dimensional wave vector in a basal xy-plane, $q_z=a{k}_z$, and $k_D=\frac{1}{a}\sqrt{\frac{8\pi }{\sqrt{3}}}.$ is the approximate Debye vector for the first Brillouin zone of triangular lattice [71,107] (it appears when the exact hexagonal zone of 2D lattice is replaced by an equivalent circular area in $\mathbf{\text{k}}$-space). The spectrum is [71–73] (32) $\begin{array}{r}{\omega }_{1,2,3}(q,q_z)=\sqrt{Z_0\left({ϵ}_{{\omega }_{1,2,3}}^2\right(q,q_z)+D\frac{q^2}{4})}.\end{array}$(32) Here $Z_0=6$ is the coordination number in basal plane, $D=U^{\mathrm{\prime }}\left(a\right)/2ma$ ($U\left(r\right)$ is the energy of interatomic interaction, and m is the atomic mass), $\begin{array}{rl}{ϵ}_{{\omega }_1}^2\left(q\right)& =\rho \cos \frac{\tau }{3};\\ {ϵ}_{{\omega }_{2,3}}^2\left(q\right)& =\rho (-\cos \frac{\tau }{3}\pm \sqrt{3}\sin \frac{\tau }{3}),\end{array}$ where $\rho =\sqrt[6]{{\mathcal{Q}}^2+|\mathcal{D}|}$, $\tau =\arctan \frac{\sqrt{|\mathcal{D}|}}{\mathcal{Q}},$ with (33) $\begin{array}{rl}\mathcal{D}& ={\mathcal{Q}}^2+{\mathcal{P}}^3,\mathcal{Q}=\frac{c_2^3}{27c_3^3}-\frac{c_2{c}_1}{6c_3^2}+\frac{c_0}{2c_3},\\ \mathcal{P}& =\frac{3c_3{c}_1-c_2^2}{9c_3^2},\end{array}$(33) and $\begin{array}{rl}{c}_3& =-1;c_2=\frac{9}{36}{\mathrm{\Omega }}^2{q}^2+({\mathrm{\Delta }}_z^2+2{\mathrm{\Delta }}^2)r_0^2;\\ c_1& =-\frac{7}{36}{\mathrm{\Omega }}^4{q}^4-\frac{9}{36}{\mathrm{\Omega }}^2({\mathrm{\Delta }}^2+{\mathrm{\Delta }}_z^2)q^2{r}_0^2\\ & -{\mathrm{\Delta }}^2({\mathrm{\Delta }}^2+2{\mathrm{\Delta }}_z^2)r_0^4+{\left(\frac{{\mathrm{\Omega }}^2}{12}\gamma \right)}^2{q}^2{q}_z^2;\\ c_0& ={\mathrm{\Delta }}^4{\mathrm{\Delta }}_z^2{r}_0^6+\frac{9}{36}{\mathrm{\Delta }}^2{\mathrm{\Delta }}_z^2{\mathrm{\Omega }}^2{q}^2{r}_0^4\\ & +\frac{7}{36}{\mathrm{\Delta }}^2{\mathrm{\Delta }}_z^2{\mathrm{\Omega }}^2{q}^4{r}_0^2-{\left(\frac{{\mathrm{\Omega }}^2}{12}\gamma \right)}^2\left({\mathrm{\Omega }}^2{q}^2+{\mathrm{\Delta }}^2{r}_0^2\right)q^2{q}_z^2;\\ r_0^2& =\frac{1}{2}(q_z^2+\frac{q^2}{6}).\end{array}$ The force constants are determined as (34) $\begin{array}{rl}{\mathrm{\Omega }}^2& =\frac{1}{2m}\left(U^{\mathrm{\prime }\mathrm{\prime }}\right(a)-\frac{U^{\mathrm{\prime }}\left(a\right)}{a}),\\ {\mathrm{\Delta }}^2& =\frac{1}{6}{\mathrm{\Omega }}^2+\frac{U^{\mathrm{\prime }}\left(a\right)}{2ma},\\ {\mathrm{\Delta }}_z^2& =\frac{{\gamma }^2}{4}{\mathrm{\Omega }}^2+\frac{U^{\mathrm{\prime }}\left(a\right)}{2ma}.\end{array}$(34) In reality, ${\mathrm{\Omega }}^2\gg \frac{U^{\mathrm{\prime }}\left(a\right)}{2ma},$ and with enough accuracy we can suppose that Ω is the only elastic modulus for transversally-isotropic polytype [30,71,72].

Figure 10 shows the temperature run of the heat capacity Equation (31(31) $\begin{array}{rl}\frac{C_{\mathrm{p}\mathrm{h}}\left(T\right)}{k_B}& =\frac{\sqrt{3}}{4{\pi }^2}{N}_{1D}{N}_{2D}\sum _{\alpha =1,2,3}{\int }_0^{a{k}_D}q\mathrm{d}q{\int }_0^{\pi }\mathrm{d}{q}_z\\ & \times {\left(\frac{\text{β}{\omega }_{\alpha }(q,q_z)}{2}\right)}^2{\sinh }^{-2}\left(\frac{\text{β}{\omega }_{\alpha }(q,q_z)}{2}\right),\end{array}$(31) ) at different values Ω [30,71,72]. It can be seen from Figure 10(a) that the heat capacity equation (31(31) $\begin{array}{rl}\frac{C_{\mathrm{p}\mathrm{h}}\left(T\right)}{k_B}& =\frac{\sqrt{3}}{4{\pi }^2}{N}_{1D}{N}_{2D}\sum _{\alpha =1,2,3}{\int }_0^{a{k}_D}q\mathrm{d}q{\int }_0^{\pi }\mathrm{d}{q}_z\\ & \times {\left(\frac{\text{β}{\omega }_{\alpha }(q,q_z)}{2}\right)}^2{\sinh }^{-2}\left(\frac{\text{β}{\omega }_{\alpha }(q,q_z)}{2}\right),\end{array}$(31) ) tends to equipartition law at $T\to \mathrm{\infty }$ with accuracy of about 2% ($C_{\mathrm{p}\mathrm{h}}\left(\mathrm{\infty }\right)=3.058N_{1D}{N}_{2D}{k}_B$) which seems to be quite acceptable, taken into account the made above approximations and the fact that we need to describe only the low-temperature run of the solid ${}^4$He heat capacity. The low-temperature heat capacity (Figure 10a,b) demonstrates the perfect $T^3$-dependence which is characteristic to an ideal Debye lattice.

Figure 10. The phonon part of the heat capacity of the polytype stack [30,71,72] (per atom) for three values of Ω: $\mathrm{\Omega }=10$ K (curve 1), $\mathrm{\Omega }=7.5$ K (curve 2), $\mathrm{\Omega }=5$ K (curve 3). The inset on (a) presents the initial part of the corresponding dependences. (b) Shows this part of the graph versus $T^3$-abscissa.

4.2.2. Anomalous (excessive) heat capacity

Here we consider only anomalous (or excessive) heat capacity from polytypic degrees of freedom. We consider a quasi-one-dimensional stack of $N_{1D}$ two-dimensional crystalline layers packed in arbitrary order, for example, $\dots hchhhcchcchh\dots$, etc. It is reasonable to suggest that interaction in like-pairs $\dots hh\dots$ and $\dots cc\dots$ should be different from one another, and both are different from interaction in unlike-pair $\dots hc\dots$. The Hamiltonian of such system can be written as one-dimensional lattice gas model in the nearest neighbours approximation [72,73], (35) $\begin{array}{r}{H}_{\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{y}}=-{ϵ}_0\sum _i{\hat{\sigma }}_i-V\sum _i{\hat{\sigma }}_i{\hat{\sigma }}_{i+1},\end{array}$(35) where ${\hat{\sigma }}_i$ are ‘non-integer occupation numbers’, (36) $\begin{array}{r}{\hat{\sigma }}_i=\left(\begin{array}{c}{\sigma }_c\\ {\sigma }_h\end{array}\right)\end{array}$(36) which can take one of two values, ${\sigma }_c=1-{\xi }_c$ or ${\sigma }_h=1+{\xi }_h$ (${\xi }_c,{\xi }_h\ll 1$), where ${ϵ}_0$ is the average energy per site, and V >0 is an interaction energy between neighbouring sites. This approach is a direct analog of exactly solving Ising model [108] as a chain of mutually coupled two-state systems. The difference between the proposed polytype model and an array of simple independent two-level systems (see [70,99,109]) is an account of interaction between neighbouring basal planes.

The solution of the problem Equation (35(35) $\begin{array}{r}{H}_{\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{y}}=-{ϵ}_0\sum _i{\hat{\sigma }}_i-V\sum _i{\hat{\sigma }}_i{\hat{\sigma }}_{i+1},\end{array}$(35) ) can be obtained easily within transfer matrix approach [108,110]. The canonical partition function of the 1D problem is (37) $\begin{array}{r}{Z}_{1D}=\mathrm{S}\mathrm{p}{\widehat{\mathbf{\text{T}}}}^{N_{1D}},\widehat{\mathbf{\text{T}}}=\left(\begin{array}{cc}{\tau }_{11}& {\tau }_{12}\\ {\tau }_{21}& {\tau }_{22}\end{array}\right),\end{array}$(37) where (38) $\begin{array}{rl}{\tau }_{11}& =\exp (a{\sigma }_h+K{\sigma }_h^2),{\tau }_{22}=\exp (a{\sigma }_c+K{\sigma }_c^2)\\ {\tau }_{12}& ={\tau }_{21}=\exp \left[\frac{a}{2}\right({\sigma }_h+{\sigma }_c)+K{\sigma }_h{\sigma }_c],\end{array}$(38) and $a=\text{β}{ϵ}_0$, $K=\text{β}V$. If $N_{1D}\gg 1$ then the excessive part of the free energy in Equation (22(22) $\begin{array}{r}F(T,V)=F_{ex}(T,N)+F_{\mathrm{p}\mathrm{h}}(T,V),\end{array}$(22) ) is equal to (39) $\begin{array}{r}{F}_{ex}(T,N_{1D})=-T\ln Z_{1D}=-N_{1D}T\ln \mathrm{\Lambda }\left(T\right),\end{array}$(39) where $\mathrm{\Lambda }=\mathrm{m}\mathrm{a}\mathrm{x}\{{\lambda }_1,{\lambda }_2\}$ is the greatest eigenvalue of the transfer-matrix $\widehat{\mathbf{\text{T}}}$. In the case of $2\times 2$ matrix (Equation (39(39) $\begin{array}{r}{F}_{ex}(T,N_{1D})=-T\ln Z_{1D}=-N_{1D}T\ln \mathrm{\Lambda }\left(T\right),\end{array}$(39) )) we have [111], (40) $\begin{array}{r}{\lambda }_1={\tau }_{11}-{\tau }_{12}v,{\lambda }_2={\tau }_{22}+{\tau }_{12}v,\end{array}$(40) where (41) $\begin{array}{r}v=p+\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}p\sqrt{1+p^2},p=\frac{{\tau }_{22}-{\tau }_{11}}{2{\tau }_{12}}.\end{array}$(41) As a result, the static part of the heat capacity (per one basal plane) can be written in the form (42) $\begin{array}{rl}\frac{C_{ex}\left(T\right)}{k_B{N}_{1D}}& =T\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{T}^2}\{T\ln \mathrm{\Lambda }(T\left)\right\}\\ & =\frac{T}{\mathrm{\Lambda }\left(T\right)}\\ & \times \left\{\frac{\mathrm{\partial }\mathrm{\Lambda }\left(T\right)}{\mathrm{\partial }T}\left[2-\frac{T}{\mathrm{\Lambda }\left(T\right)}\frac{\mathrm{\partial }\mathrm{\Lambda }\left(T\right)}{\mathrm{\partial }T}\right]+T\frac{{\mathrm{\partial }}^2\mathrm{\Lambda }\left(T\right)}{\mathrm{\partial }{T}^2}\right\}.\end{array}$(42) The comparison our theoretical results [73] with experimental measurements [62,63] shows Figure 11. The choice of the fitting parameters is discussed in Ref. [73]. As it is shown from Figure 11, the behaviour of $C_{ex}\left(T\right)$ at $T\to \mathrm{\infty }$ is evidently exponential, whereas experimental heat is probably power-like. This fact indicates that the lattice gas model with only next-neighbours interaction (Equation 35(35) $\begin{array}{r}{H}_{\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{y}}=-{ϵ}_0\sum _i{\hat{\sigma }}_i-V\sum _i{\hat{\sigma }}_i{\hat{\sigma }}_{i+1},\end{array}$(35) ) has a restricted applicability to description of the system in the limit $T\to 0$ as it take place for two-level models [70,109]. This limitation can be improved within approach with next-nearest-neighbours interactions, for example, within so-called ANNNI model [102,103,112–115].

Figure 11. (Colour online) Theoretical fitting of the excessive heat capacity $C_{ex}$ (solid line) [73]. The phonon part $C_{\mathrm{p}\mathrm{h}}$ is extremely small at given temperatures, it is represented by dashed line, the scattered points are experimental data [62,63].

In 1935, Landau [116] proposed an interpretation of the anomalies of heat capacity within solid state as a continuous transition between phases of different crystallographic symmetry [104]. Krishna and Sebastian [117] observed experimentally with X-ray scattering the continuous phase transformation in long-periodic polytypes.

4.3. Anomalies in $P\left(T\right)$

Just simultaneously with discussed above anomalies in the heat capacity, the research group from B. Verkin Institute [64,65] (see also [118,119]) reported experimentally observed anomalies in phonon pressure $P_{\mathrm{p}\mathrm{h}}\left(T\right)$ of ${}^4$He solid at the same temperature region 0.2 –0.5K and explained the observations by existence of a hypothetic disordered ‘glassy phase’. In [71,72], we presented more physical explanation based on structural evolution of the HCP polytype as a model for ${}^4$He crystal.

The phonon pressure in the ${}^4$He polytype can be written in the form [71] ($P_0$ is the crystallisation pressure at T = 0) (43) $\begin{array}{rl}{P}_{\mathrm{p}\mathrm{h}}\left(T\right)& =P_0-\frac{2T}{\pi \gamma a^3}\sum _{\nu =1,2,3}{\int }_0^{q_D}q\mathrm{d}q{\int }_0^{\pi /2}\mathrm{d}{q}_z\\ & \times \ln \{1-\exp [-\frac{{\omega }_{\nu }(q,q_z)}{T}]\}.\end{array}$(43) Using our theoretical approach, we interpret here the experimental dependences of $P\left(T\right)$ obtained in [64,65] and plotted on Figure 12(a,b) with scattered points. The experiment was performed as follows: liquid ${}^4$He in the cell at initial pressure $P_0$ is cooled with blocking capillary down to temperature of about 0.1 K and the dependence $P\left(T\right)$ during the first run demonstrates the break in the vicinity of 0.25–0.3 K, so that the slope of the $P\left(T\right)$ below the breaking point becomes twice higher than at T>0.3 K (full boxes on Figure 12(a,b)). If we believe that the pressure in ${}^4$He crystal is of phonon nature, $P\left(T\right)-P_0\sim T^4$, then it is reasonable to suppose that elastic constant of the low-temperature branch (in our case it is Ω determined by Equation (34(34) $\begin{array}{rl}{\mathrm{\Omega }}^2& =\frac{1}{2m}\left(U^{\mathrm{\prime }\mathrm{\prime }}\right(a)-\frac{U^{\mathrm{\prime }}\left(a\right)}{a}),\\ {\mathrm{\Delta }}^2& =\frac{1}{6}{\mathrm{\Omega }}^2+\frac{U^{\mathrm{\prime }}\left(a\right)}{2ma},\\ {\mathrm{\Delta }}_z^2& =\frac{{\gamma }^2}{4}{\mathrm{\Omega }}^2+\frac{U^{\mathrm{\prime }}\left(a\right)}{2ma}.\end{array}$(34) )) is approximately twice lower than the corresponding value of the high-temperature branch, and the necessary fitting [71,72] gives $\mathrm{\Omega }=4.71$ K and $\mathrm{\Omega }=8.51$ K for the regions below and above 0.3 K, respectively (in addition, for the low-temperature branch the initial pressure $P_0$ must be shifted on $\mathrm{\Delta }{P}_0=-0.25$ mbar along the pressure axis). This phenomenon has all characteristic features of solid state (martensitic) phase transition [120,121] (in polytypes the martensitic transformation was experimentally discovered by Krishna [117]). On the other hand, this phenomenon is a complete analog of ${}^4$He softening discovered in Refs. [68,69] and discussed with more details in Subsection 4.4.

Figure 12. (Colour online) The temperature dependence of phonon pressure $P_{\mathrm{p}\mathrm{h}}\left(T\right)$ (a) and $P_{\mathrm{p}\mathrm{h}}\left(T^4\right)$ (b) in a ${}^4$He crystal during thermocycling from crystallisation temperature down to 0.1 K and back to the pre-melting point (annealing). Scattered points – experiment [64,65]: full boxes – the crystal at first cooling during crystallisation from liquid phase, open circles – annealed crystal. Solid lines – present theory for annealed specimen at $\mathrm{\Omega }=8.91$ K (see text for details). The experimental dependence for the first cooling has evident break of the curve at $T\sim 0.3$ K and can be fitted by two theoretic dependences [71,72] with two different Ω (see Equation (34(34) $\begin{array}{rl}{\mathrm{\Omega }}^2& =\frac{1}{2m}\left(U^{\mathrm{\prime }\mathrm{\prime }}\right(a)-\frac{U^{\mathrm{\prime }}\left(a\right)}{a}),\\ {\mathrm{\Delta }}^2& =\frac{1}{6}{\mathrm{\Omega }}^2+\frac{U^{\mathrm{\prime }}\left(a\right)}{2ma},\\ {\mathrm{\Delta }}_z^2& =\frac{{\gamma }^2}{4}{\mathrm{\Omega }}^2+\frac{U^{\mathrm{\prime }}\left(a\right)}{2ma}.\end{array}$(34) )) and $P_0$, correspondingly: for low-temperature branch (below 0.3 K) the frequency $\mathrm{\Omega }=4.71$ K at $\mathrm{\Delta }{P}_0=0$ and for the high-temperature branch (above 0.3 K) $\mathrm{\Omega }=8.51$ K with shift $\mathrm{\Delta }{P}_0=+0.25$ mbar along the pressure axis (see text for details).

During the return warming from the lower temperature the dependence $P\left(T\right)$ runs along the bottom curve (empty circles on Figure 12(a,b)) and demonstrates the perfect $\sim T^4$ behaviour. Thus the system demonstrates hysteretic behaviour within simple thermodynamic process at constant volume (it is noticeable that the similar hysteresis was observed at heat capacity measurements reported in Ref. [63]). In Refs. [64,65], the hysteresis was explained by a defect structure which is produced at far from equilibrium process of solidification and successive annealing of this structure during the first cooling of the sample down to the lowest temperature. As a result, at the lower temperature of the cycle the defect structure has been annealed completely and the next warming-cooling cycles will be performed along the smooth bottom curve in Figure 12(a,b). This phenomenon can be easily interpreted in the framework of above-mentioned approach of Section 4.1. It is reasonable to suggest that at the crystallisation the defect structure will be built not of edge dislocation with open extra-planes which must be squeezed off the crystal lattice due to large external compression, but mainly of prismatic dislocation loops (closed disks of vacancies) or network of Shockley's partials (see Figures 7–9) which are able to survive under the uniform external compression necessary for solidification. The presence of the vacancies in the crystal sample of N atoms at fixed volume V of the experimental cell means existence of a certain excessive ‘free volume’ $\mathrm{\Delta }V=V-N{v}_0$ inevitable connected with free volume (dilatation) of vacancies ($v_0$ is specific volume of the helium atom). The relaxation of the defect structure is formation of the thermodynamically equilibrium lattice structure through low-dimensional migration of atoms (quantum diffusion) among the partial clusters to build the perfect crystal lattice and remove the excessive free volume from the crystal. The evident feature of the free volume relaxation is the drop $\mathrm{\Delta }P$ of the initial basic pressure (see Figures 12(a,b) and additional clarifications in Refs. [64,65,71–73]). If the perfect lattice had been built, the lattice does not contain the excessive vacancy free volume, and the thermodynamic phonon process $P\left(T\right)$ runs strongly along the curve belonging to the perfect lattice (empty circles on Figure 12 a,b) with $\mathrm{\Omega }=8.91$ K. In addition, it is possible that the drop of the pressure can be an evidence of penetration into metastable region during a solid phase transition like the ‘normal solid’→‘supersolid’ phase transition predicted in Ref. [26].

Another example of hysteretic behaviour of $P\left(T\right)$ dependence is given by results of our measurements within a region of BCC-HCP transformation (it is a first-order phase transition) at the phase boundary between ${}^4$He solid and He II phase [122] (see Figure 13). The $P\left(T\right)$ measurements were performed by thermocycling through the region of BCC-HCP mixed structures between the boundary temperatures correspond to the monophase system (Figure 13). 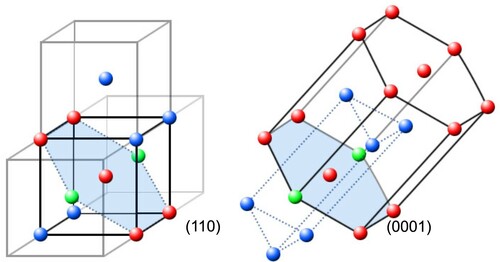The most characteristic feature of the process is asymmetry of the $P\left(T\right)$ dependence in the boundary tails of the hysteresis loop (see Figure 14 a,b). In Ref. [122], we explain this fact by specific crystallography of the forward and reverse HCP$\leftrightarrows$BCC transformations (Figure 15). To undergo from HCP to BCC, the crystal must obtain some dilatation within the only (0001)-basal plain, whereas at BCC→HCP transition the dilatation can be supplied in one of the six equivalent (110) glide systems. The solid state transformation provides typically the formation of some heterophase structure where the individual crystallites are conjugated crystallographically into a complete system. The formation of the HCP lattice around the basal system of the only one possible (0001) orientation is more hindered as compared to BCC nucleation which is possible in six glide systems of different orientations [122]. As a result, the transition into HCP phase demonstrates a certain delay (Figure 14a), whereas return to the BCC configuration is quite easy (Figure 14a).

Figure 13. (Colour online) Hysteresis of the $P\left(T\right)$ dependence during reversible HCP$\leftrightarrows$BCC transformations [122]. Enumeration corresponds to successive cooling (empty boxes) and warming (full boxes).

Figure 14. (Colour online) Detailed configuration of the $P\left(T\right)$ hysteresis near the boundary tails at upper (a) and lower (b) temperatures of the measurements [122].

Figure 15. (Colour online) Schematic crystallography of HCP$\leftrightarrows$BCC transformations.

It is the only way (down P-axis at temperature T<1.65 K) to enter He II phase directly from high-pressure HCP region. Any other way provides first entering simple liquid He I region and then undergoing λ-transition into He II. It means that direct transformation from ${}^4$He solid into He II superfluid (supersolid or liquid crystal) presumes quite complicated crystallographic reconstruction which includes the formation of a certain structural ordering within the low-pressure He II phase, whereas at higher temperatures (above 1.65 K) the ${}^4$He crystal→He I liquid is a simple solid–liquid melting into structureless phase without long-range order.

4.4. Mechanical properties: temperature-dependent internal friction

Special area of interest are anomalies in mechanical properties of solid ${}^4$He which were discussed intensively last two decades mainly in view of specific ‘supersolid’ problem [69], but simultaneously a number of important features typical for the standard solid state behaviour have being discovered on helium crystals. Moreover, now becomes evident that the some ‘extraordinary’ properties of the helium condensed phases seem to be manifestations of well-known physical events. Here we are focusing on the phenomena which clearly demonstrate the close relationship between solid helium and the rest of the solid state community.

When considering the deformation mechanism of solid helium we must be aware of the fact that it crystallises with uniform compression under external static pressure $P_0>25$ bar within a closed cell (at restricted constant volume), so that the specimen is formed without free surfaces which are necessary (as at usual testing conditions) to detect both reversible or irreversible (plastic) deformation of HCP crystal due to basal or pyramidal glide of perfect (non-splitted) edge or screw dislocations [78,123]. It should be remembered that under uniform compression the most part of the edge dislocations will be squeezed out from the lattice during crystallisation [124,125], so that the crystal could be practically free of gliding edge dislocations [126–129]. Moreover, in HCP polytype the pyramidal glide systems are forbidden because of stacking faults microscopic disorder along the c-axis, so that only basal glide is possible. In view of mentioned condition, the only possible basal deformation is ‘rotation’ of any basal plane in stack on $\pi /6$ around the c-axis without breaking the close-packing rule in the whole lattice. It means formation of a new local stacking faults, and, hence, changing of a sequence of A, B, C objects with only unlike pair neighbours allowed (the total number of the planes in the whole stack is fixed). Physically, this process can be realised by so-called spiral dislocation source (rotating screw dislocation [75,78]), but in general it should be considered as a continuous solid phase (martensitic) transformation controlled by temperature and pressure. If the polytype contains stacking fault clusters divided by Shockley's partial dislocations (see Figure 7), the process is due to tunnelling of atoms from the core of the Shockley's into neighbouring clusters which are more preferable energetically at given T and P. The partials which divide the stacking fault clusters on Figure 7 form the network of partial dislocations. It should be emphasised that the partials are not channels for direct atomic motions (as it usually supposed within a primitive models of ‘superfluid’ dislocation cores [130–133]). The motion of the partial dislocation is due to successive displacement (tunnelling) of bordering atoms from neighbouring clusters through the barrier of microscopic distance $a/\sqrt{3}$ (a is the lattice parameter) in direction transversal to the dislocation line, and, simultaneously, along dislocation moves an eigenexcitation, or a kink which in fact is one-dimensional Frenkel–Kontorova dislocation [79,80] (or, within quantum treatment, Andreev–Lifshits exciton [81]). If the kink runs along all the length of the dislocation segment, this dislocation segment will be displaced on the elementary step from one to the neighbouring valley of its Peierls relief. Thus the mechanism of expansion of the partial dislocations is the motion of dislocation kinks which can be created or annihilated due to thermal fluctuation or external stresses, but general driving force for this process can be interpret as a gradient of chemical potential which stimulates the solid state structural transition in polytipic crystal during changing in external conditions [117].

Another advantage of the above-described mechanism can be an explanation for one-dimensional quantum self-diffusion and heterodiffusion predicted and discovered experimentally in solid ${}^4$He and hydrogen [48,83,84,134].

The most direct evidence of the dislocation phenomena in solid helium is experimentally observed temperature-dependent internal friction [66,67,69] which in reality is well-known Bordoni peak [135,136] (see for all details the book [137]). In HCP ${}^4$He the comparable narrow peak of internal friction [66,67,69] (registered within the frequency range 20 Hz÷2 kHz) has a maximum localised within the temperature interval 0.1–0.15 K, and with frequency the maximum shifts to higher temperature but the magnitude of the maximum decreases, just as it is known for the standard Bordoni phenomenon [136]. In solid ${}^3$He with BCC lattice the much more wider peak [67,69] with maximum localised approximately at 0.25 K has a maximal magnitude at the lowest frequency (22 Hz) and decreases rapidly with frequency, so that we consider a structurally-sensitive phenomenon.

Mason [138] and Seeger [139] suggested a model for temperature dependent internal friction (Bordoni peak) based on dynamics of double kinks on dislocation lines (long before Read [140] proved experimentally dislocation mechanism of internal friction in kHz-diapason). Physically, the creation and expansion of a dynamic double kink means jumping of an atomic group from the dislocation extra-plane into the neighbouring valley of Peierls relief [141]. Expanding like zipper double kink is, in fact, motion of an one-dimensional Frenkel–Kontorova dislocation, and, as a result it is an elementary act of dislocation glide. Creation and motion of the double kinks are supported by thermal fluctuations and applied stress [78]. The double kink to be created needs a certain energy $W_k$ and mechanical work $\sigma v_k$ (where σ is the mechanical stress and $v_k$ is the activation volume [78]), and then it expands due to Peach–Koehler force [78,142]. As a result the partition function of the kinks ‘gas’ can be written in the standard form (44) $\begin{array}{r}\mathcal{Z}\sim \exp (-\frac{F_k}{T}),\end{array}$(44) where $F_k=W_k-\sigma v_k$ is the free energy. The quantum mechanical approach to calculate $W_k$ has been attempted in Ref. [143] (as to quantum motion of kinks along dislocations in ${}^4$He, see also Ref. [144]). If the kinks creation process manifests only one characteristic energy, then we expect the most intensive rate of the kinks multiplication at $T\sim W_k$, and, correspondingly, the rather narrow peak of the internal friction, as it is in ${}^4$He [66,67,69] where we have only one easy glide system $\left\{0001\right\}$ in HCP lattice (Figure 15). On the other hand, in BCC lattice we have six $\left\{001\right\}$ glide systems (Figure 15) which in a real polycrystal will be randomly oriented relative to external loading σ, so that in the BCC polycrystal we have a wide spectrum of the creation free energies $F_k$ in the partition function equation (44(44) $\begin{array}{r}\mathcal{Z}\sim \exp (-\frac{F_k}{T}),\end{array}$(44) ) and the sum over this spectrum, as a result, leads to the wide maximum of the internal friction registered in the BCC ${}^3$He crystals [67,69] (the corresponding results for classical BCC crystals and the difference between Bordoni peaks in HCP and BCC structures are fundamentally discussed in Ref. [137]).

The most intriguing feature of the newest researches in ${}^4$He solid is registration of acoustic emission (AE) which accompanies the helium crystal deformation process [145]. It is known that AE is a powerful tool to detect the dynamical dislocation processes during plastic deformation in crystals [146]. The spectral composition of AE registered in ${}^4$He solid (Figure 3b in Ref. [145]) shows that three most essential peaks of AE spectral density fall on the frequency interval 10–20 MHz whereas the driving force of the internal friction experiments has the frequency of 20 Hz–2 KHz. Moreover, the most pronounced response manifests the Bordoni peak just at 20 Hz drive [67,69] where at the most low-frequent driving force the attenuation dependence $Q^{-1}\left(T\right)$ demonstrates extremely jagged run which can be an evidence of a current of galloping (high-frequent, short-period) AE events triggered by the low-frequency alternating load. The most plausible candidates for the sources of high-frequent AE are dynamic kinks on dislocations. The kinks creation, annihilation and motion [146] are the governing processes in the 10 mega-Hertz AE which is evidently of pre-microscopic nature (AE produced through oscillations of macroscopic dislocation segments (strings) is typically of 50–100 kHz region). If the frequency of driving force increases than the activation volume of the kink creation decreases, so that the contribution of the kink dynamics into partition function equation (44(44) $\begin{array}{r}\mathcal{Z}\sim \exp (-\frac{F_k}{T}),\end{array}$(44) ) (proportional to $\exp \left(\sigma v_k/T\right)$) becomes inessential, and the magnitude of the Bordoni peak decreases. As can be seen from Equation (44(44) $\begin{array}{r}\mathcal{Z}\sim \exp (-\frac{F_k}{T}),\end{array}$(44) ), the kinked density of states changes the most rapidly at $T\sim W_k$ [147] and this causes the maximum in $Q^{-1}\left(T\right)$. At $T\to \mathrm{\infty }$ the concentration of the double kinks on dislocation lines tends to unity [78], and dislocation segment can be considered as a smooth (macroscopic) dislocation string [148].

4.5. Brief summary of Section 4

In 1935, Landau published in [116] the anomalous heat capacity is caused by certain ordering phenomena in the physical system (the theory of λ-point or second-order phase transition, see also [104]). Landau introduced the order parameter as a macroscopic thermodynamic parameter of the system, and at present it is the generally accepted approach for the treatment of structural transformations in structurally ordered (and, certainly, disordered) solids and liquids. In the context of this trend, we have to interpret the above-discussed anomalies of solid ${}^4$He as evolution of crystalline order, and polytypism is a quite convenient model to describe the peculiarities of the close-packed crystalline structures with a great variety of modifications and continuous mutual transformations among them realising through evolution of Shockley's partial dislocations (by zipping of Frenkel–Kontorova kinks or Andreev–Lifshits excitons along the dislocation lines) due to thermal fluctuations and under internal stresses. In a certain meaning, this process is a low-dimensional quantum-diffusional creep which causes the giant plasticity of ${}^4$He (and shear modulus softening) in the interval 0.1<T<0.3 K.

Thus we can see that even in solid HCP and BCC phases ${}^4$He demonstrates a number of peculiar phenomena which testify to the presence of easily excited degrees of freedom and the low-temperature solid phase transformations caused by such degrees. In this connection, we have to attend to the Frenkel's conclusion [149] that a liquid state inherits the ordering characters appropriate to its solid state (as example, we refer to the ice-like structures in water [40]). Principally, such phenomena are well known in the condensed matter physics, but in the case of solid HCP and BCC ${}^4$He all the phenomena becomes quite visible on the background of isotopic purity and mechanical compliance of condensed helium which as usual is attributed to ‘quantum effects’, whereas the real quantum nature of helium consists in the character of its interatomic interaction and namely this fact is the governing factor for all experimentally observable helium properties. Yield in solid helium state is easy glide of dislocations which, microscopically, is creation-annihilation of kinks, and, as a result, it determines the success in interpretation of helium properties on the basis of dislocation ideology [69].

And, in addition, it should be noted that the low-temperature softening of elastic moduli is a well-known effect in superconductors [150].

5. Superfluid and supersolid

To start discussing the ‘superfluid’ in some convenient meaning we have to take into account that all famous ‘superfluid’ effects were discovered on the equilibrium line of the condensed He II phase with its saturated vapour (see phase diagram Figure 1). It means that the properties of the He II phase as itself drop out of the problem under consideration.

There is a main question: is the He II phase liquid with solid-like behaviour or solid with liquid-like peculiarities? Following the Nozières approach we will consider the He II phase properties moving down through the phase diagram of Figure 1 from the solid HCP and BCC phases left-of-λ-line just into He II region. When considering the properties of He II phase, F. London wrote [151] in 1939:

Below the λ-point the entropy difference between the liquid and the solid phase decreases rapidly toward zero with falling temperature, which indicates that the liquid phase goes into a peculiar state of order. This change towards an ordered state begins at the λ-point and occurs continuously in a relatively small temperature range. It would be interesting to know what kind of order is realised in this liquid state.

Certainly, it is a direct support of the initial Shubnikov's idea [1]. London [151] discussed a qualitative scheme based on atom–atom ‘van der Waals’ interaction to interpret the possible structural ordering in the ‘liquid’ He II phase as a chain of structural configurations (including simple cubic, BCC, diamond and HCP lattices [151]) depending on potential energy of two helium atoms as a function of interatomic distance. Simultaneously was established an idea to interpret the λ-transition He I→He II as a disorder→order transformation, and on this way the ODLRO (off-diagonal long range order) concept was developed.

5.1. Supersolid according to Matsuda and Tsuneto

In 1962, Yang [152], based on Penrose and Onsager approach [153,154], derived the concept ODLRO for reduced density matrix in the coordinate space representation applied to a many-body system of bosons or fermions in view of assumption that superfluid He II and the superconductors are phases characterised by the existence of such an order. On the ground of the quantum lattice gas (QLG) model with forbidden of the double occupation of the lattice site proposed for He II by Matsubara and Matsuda in 1956 [23], Matsuda and Tsuteto [24] derived the ODLRO approach for He II within the pseudo-spin formulation which they called as ‘supersolid’. Subsequently the QLG acquired more adequate designation as the model of hard core bosons (HCB) [155–166], and here we show several results [28,29] of the HCB description applied to the ordered He II phase.

We represent the Hamiltonian of the hard-core bosons [22] (Bose–Hubbard model) in the form [28,29] (45) $\begin{array}{rl}{H}_B& =-\frac{t}{2}\sum _{\mathbf{\text{f}},\mathit{\delta }}(a_{\mathbf{\text{f}}}^{+}{a}_{\mathbf{\text{f}}+\mathit{\delta }}+a_{\mathbf{\text{f}}+\mathit{\delta }}^{+}{a}_{\mathbf{\text{f}}})+\frac{V_1}{2}\sum _{\mathbf{\text{f}},\mathit{\delta }}{n}_{\mathbf{\text{f}}}{n}_{\mathbf{\text{f}}+\mathit{\delta }}\\ & -\frac{V_2}{2}\sum _{\mathbf{\text{f}},\mathit{\gamma }}{n}_{\mathbf{\text{f}}}{n}_{\mathbf{\text{f}}+\mathit{\gamma }}-\mu \sum _{\mathbf{\text{f}}}{n}_{\mathbf{\text{f}}},\end{array}$(45) where t is the nearest-neighbour hopping, $V_{1,2}>0$ are the interparticle interactions with nearest neighbours (nn, first coordination sphere) and next-nearest neighbours (nnn, second coordination sphere), respectively, $\mathit{\delta }$ ($\mathit{\gamma }$) is the vector connecting nn (nnn), μ is the chemical potential, $a_{\mathbf{\text{f}}}^{+},a_{\mathbf{\text{f}}}$ are Pauli creation and annihilation operators of a hard-core boson at site $\mathbf{\text{f}}$, satisfying the following commutation relations: $\begin{array}{rl}[a_{\mathbf{\text{f}}}^{+},a_{\mathbf{\text{g}}}^{+}]& =[a_{\mathbf{\text{f}}},a_{\mathbf{\text{g}}}]=[a_{\mathbf{\text{f}}},a_{\mathbf{\text{g}}}^{+}]=0,(\mathbf{\text{f}}\ne \mathbf{\text{g}})\\ [a_{\mathbf{\text{f}}}^{+},a_{\mathbf{\text{f}}}^{+}{]}_{+}& =[a_{\mathbf{\text{f}}},a_{\mathbf{\text{f}}}{]}_{+}=0,[a_{\mathbf{\text{f}}},a_{\mathbf{\text{f}}}^{+}{]}_{+}=1,\end{array}$ so that the double occupation of a lattice site is forbidden, and the occupation number $n_{\mathbf{\text{f}}}=a_{\mathbf{\text{f}}}^{+}{a}_{\mathbf{\text{f}}}$ is equal either 1 or 0. In our consideration, $V_1$ is always positive while $V_2$ can be positive or negative.

This model is equivalent to a 1/2-spin XXZ magnet [24]. A down spin corresponds to an occupied site, while an up spin corresponds to an empty site [23] (46) $\begin{array}{r}{a}_{\mathbf{\text{f}}}^{+}\to S_{\mathbf{\text{f}}}^{-},a_{\mathbf{\text{f}}}\to S_{\mathbf{\text{f}}}^{+},n_{\mathbf{\text{f}}}\to \frac{1}{2}-S_{\mathbf{\text{f}}}^z.\end{array}$(46) Substituting (46(46) $\begin{array}{r}{a}_{\mathbf{\text{f}}}^{+}\to S_{\mathbf{\text{f}}}^{-},a_{\mathbf{\text{f}}}\to S_{\mathbf{\text{f}}}^{+},n_{\mathbf{\text{f}}}\to \frac{1}{2}-S_{\mathbf{\text{f}}}^z.\end{array}$(46) ) into the Hamiltonian (45(45) $\begin{array}{rl}{H}_B& =-\frac{t}{2}\sum _{\mathbf{\text{f}},\mathit{\delta }}(a_{\mathbf{\text{f}}}^{+}{a}_{\mathbf{\text{f}}+\mathit{\delta }}+a_{\mathbf{\text{f}}+\mathit{\delta }}^{+}{a}_{\mathbf{\text{f}}})+\frac{V_1}{2}\sum _{\mathbf{\text{f}},\mathit{\delta }}{n}_{\mathbf{\text{f}}}{n}_{\mathbf{\text{f}}+\mathit{\delta }}\\ & -\frac{V_2}{2}\sum _{\mathbf{\text{f}},\mathit{\gamma }}{n}_{\mathbf{\text{f}}}{n}_{\mathbf{\text{f}}+\mathit{\gamma }}-\mu \sum _{\mathbf{\text{f}}}{n}_{\mathbf{\text{f}}},\end{array}$(45) ), we get $H_B=H_M-N{E}_0,$ where $H_M$ is the Hamiltonian of an anisotropic XXZ model [28,29], (47) $\begin{array}{rl}{H}_M& =-\frac{J}{2}\sum _{\mathbf{\text{f}},\mathit{\delta }}(S_{\mathbf{\text{f}}}^{+}{S}_{\mathbf{\text{f}}+\mathit{\delta }}^{-}-\mathrm{\Delta }{S}_{\mathbf{\text{f}}}^z{S}_{\mathbf{\text{f}}+\mathit{\delta }}^z)\\ & -\frac{J\alpha \mathrm{\Delta }}{2}\sum _{\mathbf{\text{f}},\mathit{\gamma }}{S}_{\mathbf{\text{f}}}^z{S}_{\mathbf{\text{f}}+\mathit{\gamma }}^z-\mathcal{H}\sum _{\mathbf{\text{f}}}{S}_{\mathbf{\text{f}}}^z,\end{array}$(47) with the ferromagnetic transverse exchange J = 2t. The longitudinal exchange for nn is antiferromagnetic and equal to $J\mathrm{\Delta }$. The nnn exchange $J\alpha \mathrm{\Delta }$ can be either ferro- or antiferromagnetic, $\mathrm{\Delta }=V_1/2t$, $\alpha =V_2/V_1$, and $\mathcal{H}=-\mu +{\gamma }_0(V_1-V_2)/2$ is an external magnetic field, ${\gamma }_0$ is the coordination number (for 2D square lattice ${\gamma }_0=4$ in both nn and nnn cases, for 2D triangular lattice ${\gamma }_0=6$ in both nn and nnn cases), $E_0=[\mu -{\gamma }_0(V_1-V_2\left)/4\right]/2$, and N is the total number of lattice sites. At $\alpha =0$ the Hamiltonian (47(47) $\begin{array}{rl}{H}_M& =-\frac{J}{2}\sum _{\mathbf{\text{f}},\mathit{\delta }}(S_{\mathbf{\text{f}}}^{+}{S}_{\mathbf{\text{f}}+\mathit{\delta }}^{-}-\mathrm{\Delta }{S}_{\mathbf{\text{f}}}^z{S}_{\mathbf{\text{f}}+\mathit{\delta }}^z)\\ & -\frac{J\alpha \mathrm{\Delta }}{2}\sum _{\mathbf{\text{f}},\mathit{\gamma }}{S}_{\mathbf{\text{f}}}^z{S}_{\mathbf{\text{f}}+\mathit{\gamma }}^z-\mathcal{H}\sum _{\mathbf{\text{f}}}{S}_{\mathbf{\text{f}}}^z,\end{array}$(47) ) reduces to an anisotropic Heisenberg model. Here we will discuss only 2D square and triangular lattices [28,29], because just these cases are in main importance for the polytypic model of the condensed He II phase.

In this section, we present a part of the spin-wave dispersion results [29] for HCB on a triangular lattice. The spectra calculated with and without account for NLSW (non-linear spin wave) corrections along the directions indicated in Figure 16 are shown for different filling ρ in Figure 17. The directions are chosen in a similar way as it is done in Ref. [167]. As it is seen from Figure 17(a) the NLSW corrections lead to an increase of the frequency along all the directions as compared to that found in the LSW (linear spin wave) approximation. For $V_2=0$ and −0.3 the excitation spectrum has well-defined minima at the equivalent points Q and C which correspond to the corners of the Brillouin zone (see Figure 17a). Note that in the case of $V_2=0$ in the linear spin-wave approximation the frequency goes to zero at $V_1=4t$. With increase in $V_2$ the minima of ${\tilde{\omega }}_{\mathbf{\text{k}}}$ at points Q and C shallow, and change into maxima at $V_2\simeq 0.12$.

Figure 16. The first Brillouin zone of the triangular lattice.

Figure 17. (Colour online) Spin-wave dispersion for HCB on triangular lattice [28,29] at different filling ρ: (a) 0.5, (b) 0.4, (c) 0.3. The parameters t = 0.5, $V_1=1$, and $V_2=$ 0 (1), 0.3 (2), -0.3 (3). The present theory: NLSW (solid) and LSW (dashed).

Another special point is located in the middle of the face of the Brillouin zone (point B). It is known that for a Heisenberg antiferromagnet on a triangular lattice there exists a true minimum at this point [168–171]. Our analysis of the HCB model at half-filling $\rho =0.5$ (see Figure 18) shows that at point B the true minimum develops only if nnn interaction is repulsive. Indeed, as it is seen from Figure 17(a), at $V_2=-0.3$ point B is not an extremum. At $V_2=0$, as our calculations show, a very shallow minimum exists when point B is approached along the direction QB (the similar behaviour was found in Ref. [167]), but along the segment AB the spectrum is disperionless due to the constancy of the structure factor ${\mathrm{\Gamma }}_{\mathbf{\text{k}}}=-1/3$, and therefore point B is not a true minimum. At last if $V_2=0.3$ point B is the true minimum that deepens with further increase in $V_2$. Note that with the change in interaction parameters the spectrum of a triangular lattice HCB near the corner points and midpoints of the faces of the Brillouin zone behaves much like the spectrum of a square lattice HCB near the corner ($\pi ,\pi$) and mid-face ($\pi ,0$) points of the corresponding Brillouin zone. The vanishing of the frequency at points B and C indicates the transitions from superfluid into new phases, correspondingly, collinear and dominant $V_1$ supersolid [172].

Figure 18. (Colour online) Spin-wave dispersion along the OB direction [29] at half-filling $\rho =0.5$, t = 0.5, $V_2=1.4$, and different $V_1$: $V_1=0.7$ (curve 1), $V_1=0.3$ (curve 2), $V_1=0$ (curve 3). The present theory: NLSW (solid) and LSW (dashed).

Figure 18 displays the spin wave dispersion along the OB direction when the roton minimum develops. As it is seen the account for NLSW corrections makes the minimum shallower and shifts its position to the centre of the Brillouin zone. The LSW frequency curves calculated for different values of $V_1$ intersect at point K (this fact is due to vanishing ${\mathrm{\Gamma }}_{\mathbf{\text{k}}}$ at this point). The pseudo-spin XXZ Hamiltonian Equation (47(47) $\begin{array}{rl}{H}_M& =-\frac{J}{2}\sum _{\mathbf{\text{f}},\mathit{\delta }}(S_{\mathbf{\text{f}}}^{+}{S}_{\mathbf{\text{f}}+\mathit{\delta }}^{-}-\mathrm{\Delta }{S}_{\mathbf{\text{f}}}^z{S}_{\mathbf{\text{f}}+\mathit{\delta }}^z)\\ & -\frac{J\alpha \mathrm{\Delta }}{2}\sum _{\mathbf{\text{f}},\mathit{\gamma }}{S}_{\mathbf{\text{f}}}^z{S}_{\mathbf{\text{f}}+\mathit{\gamma }}^z-\mathcal{H}\sum _{\mathbf{\text{f}}}{S}_{\mathbf{\text{f}}}^z,\end{array}$(47) ) is the equivalent representation for bosonic system Equation (45(45) $\begin{array}{rl}{H}_B& =-\frac{t}{2}\sum _{\mathbf{\text{f}},\mathit{\delta }}(a_{\mathbf{\text{f}}}^{+}{a}_{\mathbf{\text{f}}+\mathit{\delta }}+a_{\mathbf{\text{f}}+\mathit{\delta }}^{+}{a}_{\mathbf{\text{f}}})+\frac{V_1}{2}\sum _{\mathbf{\text{f}},\mathit{\delta }}{n}_{\mathbf{\text{f}}}{n}_{\mathbf{\text{f}}+\mathit{\delta }}\\ & -\frac{V_2}{2}\sum _{\mathbf{\text{f}},\mathit{\gamma }}{n}_{\mathbf{\text{f}}}{n}_{\mathbf{\text{f}}+\mathit{\gamma }}-\mu \sum _{\mathbf{\text{f}}}{n}_{\mathbf{\text{f}}},\end{array}$(45) ), so that we believe that the obtained XXZ-spectra. Figures 17 and 18 describe properly the system of interacting bosons with repulsion on the first coordination sphere and attraction in the second coordination sphere (just in accordance with original repulsive Bogolubov model [18], see also Refs. [173,174]), and this approach gives naturally the spectrum with real ‘rotonic’ minimum, whereas the phenomenological Landau's phonon spectrum (certainly, phonons are the Bose-gas) needs to be supplied by artificial ‘roton’ branch to describe the real properties of the He II phase. The lattice gas model Equation (45(45) $\begin{array}{rl}{H}_B& =-\frac{t}{2}\sum _{\mathbf{\text{f}},\mathit{\delta }}(a_{\mathbf{\text{f}}}^{+}{a}_{\mathbf{\text{f}}+\mathit{\delta }}+a_{\mathbf{\text{f}}+\mathit{\delta }}^{+}{a}_{\mathbf{\text{f}}})+\frac{V_1}{2}\sum _{\mathbf{\text{f}},\mathit{\delta }}{n}_{\mathbf{\text{f}}}{n}_{\mathbf{\text{f}}+\mathit{\delta }}\\ & -\frac{V_2}{2}\sum _{\mathbf{\text{f}},\mathit{\gamma }}{n}_{\mathbf{\text{f}}}{n}_{\mathbf{\text{f}}+\mathit{\gamma }}-\mu \sum _{\mathbf{\text{f}}}{n}_{\mathbf{\text{f}}},\end{array}$(45) ) takes into account some realistic features of interatomic interaction (repulsion $V_1$ with nn and attraction $-V_2$ with nnn, and, if necessary, an interaction with coordination spheres of higher order can be included), but, in fact, the interatomic interaction in the helium condensed phases is more complicate (see Section 3.2), in particular, it is spin-dependent (certainly, it means the real electronic spin, but not pseudo-spin of Equation 46(46) $\begin{array}{r}{a}_{\mathbf{\text{f}}}^{+}\to S_{\mathbf{\text{f}}}^{-},a_{\mathbf{\text{f}}}\to S_{\mathbf{\text{f}}}^{+},n_{\mathbf{\text{f}}}\to \frac{1}{2}-S_{\mathbf{\text{f}}}^z.\end{array}$(46) ). Moreover, the interacting ${}^4$He atoms are no longer being considered as elementary bosons, but only as composite of fermions (valence electrons with one-half spin) and spinless bosons (${}^4$He nuclei, α-particles). The motion of nuclei means the presence of phonon excitations (see Sections 4.2.1, 4.2.2) and solidification due to spin subsystem on the λ-line means strong spin–spin correlations within valence bond at spin–phonon coupling (see Section 7).

5.2. Supersolid according to Kim and Chan

In 2004, Kim and Chan [25–27], based on more recent research [175], reported an effect which they called ‘supersolid’ because it seems to be a superfluid behaviour within presumably solid phase. The solid ${}^4$He crystallised in cylindric cell of torsion oscillator at different pressures was treated by alternative torsion deformation and had been found that the resonant frequency of the oscillator (at certain regimes) drops when the temperature decreases, so that it seems that moment of inertia of the system reduces. Authors of Refs. [25–27] called the phenomenon as NCRI – ‘non-classical rotational inertia’, and explained it as existence of specific low-temperature supersolid phase with superfluid behaviour within a specific solid state. This report initiated a wide discussion with a number explanation of the observed phenomenon.

The most constructive interpretation of the ‘supersolid’ effect in crystalline solids seems to be superplastic behaviour, well-known in solid state physics. Dash and Wettlaufer [176] suggested that ‘supersolid’ in the torsion oscillator can be resulted by slippage in the contact of the crystal with the cylindric wall of the cell (many years ago the corresponding effect was considered by Yu. Kosevich and S. Svatko [177]). Hereafter this concept was developed within a model of superfluidity in grain boundaries of a polycrystal [178,179], which is quite analogous to the above-mentioned Nabarro–Herring–Lifshits model [91–93] (in this connection it should be noted that, among cryocrystals, the superplastic behaviour demonstrates para-hydrogen [180–183] and simple water ice [40]).

Here we interpret the experiments [25–27] as the amplitude-dependent internal friction in a crystalline polytypic structure. Let us consider the cylindric helium sample with bases radius $r_0$ and height $h_0$, the cylindric coordinates of the sample elements are $r,\phi ,z$ ($0\le r\le r_0,0\le \phi \le 2\pi ,0\le z\le h_0$). If into cell is placed the layer of thickness $h_l=r_0-r_l$ ($r_l$ is the radius of the internal cylindric surface, $r_l\le r\le r_0$). When the sample is involved into periodic oscillations with frequency Ω around z-axis, then (48) $\begin{array}{r}\phi \left(t\right)={\mathrm{\Phi }}_0\sin \mathrm{\Omega }t,\end{array}$(48) where ${\mathrm{\Phi }}_0$ is the angular amplitude of oscillations. The linear (tangential) velocity of the point $(r,\phi (t\left)\right)$ in the laboratory coordinate system is (49) $\begin{array}{r}{v}_{\phi }\left(t\right)=r\dot{\phi }\left(t\right)=r{\mathrm{\Phi }}_0\mathrm{\Omega }\cos \mathrm{\Omega }t,\end{array}$(49) where the dot-accent means the time derivative and the maximal linear velocity of the rim points $r=r_0$ is $v_{\mathrm{m}\mathrm{a}\mathrm{x}}=r_0{\mathrm{\Phi }}_0\mathrm{\Omega }$. The points of the involved into rotation helium sample experience the normal $w_n=w_r(r,t)$ and tangential $w_{\tau }=w_{\phi }(r,t)$ accelerations, (50) $\begin{array}{rl}{w}_r(r,t)& =-\frac{v_{\phi }^2\left(t\right)}{r}=-r{\mathrm{\Phi }}_0^2{\mathrm{\Omega }}^2{\cos }^2\mathrm{\Omega }t,\\ w_{\phi }(r,t)& =r\dot{\phi }\left(t\right)=-r{\mathrm{\Phi }}_0{\mathrm{\Omega }}^2\sin \mathrm{\Omega }t.\end{array}$(50) As a result, there are two components of the volume force density $\mathbf{\text{f}}(r,t)=\rho \mathbf{\text{w}}(r,t)$ (ρ is the density of the sample), (51) $\begin{array}{rl}{f}_r(r,t)& =-\frac{v_{\phi }^2\left(t\right)}{r}=-\rho r{\mathrm{\Phi }}_0^2{\mathrm{\Omega }}^2{\cos }^2\mathrm{\Omega }t,\\ f_{\phi }(r,t)& =r\dot{\phi }\left(t\right)=-\rho r{\mathrm{\Phi }}_0{\mathrm{\Omega }}^2\sin \mathrm{\Omega }t.\end{array}$(51) The next step is to find the distribution of internal stresses within the helium sample in the torsion oscillatory cell. He first problem is configuration of the cell interior (e.g. porous matrix with channels of different length and diameter [25–27]). For definite estimations, we shall suppose that the sample is a solid ${}^4$He crystal rigidly bound with the cell rim at $r=r_0$ and the internal boundary of the sample is a free of external loading cylindric surface $r=r_l$. It is reasonable to build the desirable estimations for isotropic elastic sample of the described configuration. According to the symmetry of the problem, we consider the displacement field of two components, $u_r(r,t)$ and $u_{\phi }(r,t)$, which can be calculated within the quasi-static approximation because the maximal rim velocities in the experiments [25–27] are much lower than the sound velocity in helium. Thus we can exploit the standard equations of the isotropic elasticity [184], (52) $\begin{array}{rl}& G(\mathrm{\Delta }{u}_r-\frac{u_r}{r^2})+(\lambda +G)\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left[\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\right(r{u}_r\left)\right]+f_r(r,t)=0,\\ & G(\mathrm{\Delta }{u}_{\phi }-\frac{u_{\phi }}{r^2})+f_{\phi }(r,t)=0,\end{array}$(52) where G is the shear modulus, λ is the parameter, and Δ is the radial part of Laplacian, $\mathrm{\Delta }=\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{r}^2}+\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}.$ The boundary conditions are (53) $\begin{array}{rl}& u_r{|}_{r=r_0}=0,u_{\phi }{|}_{r=r_0}=0,\\ & {\sigma }_{rr}{|}_{r=r_l}={\left[\right(\lambda +2G)\frac{\mathrm{\partial }{u}_r}{\mathrm{\partial }r}+\lambda \frac{u_r}{r}]}_{r=r_l}=0,\\ & {\sigma }_{\phi r}{|}_{r=r_l}=G{(\frac{\mathrm{\partial }{u}_{\phi }}{\mathrm{\partial }r}-\frac{u_{\phi }}{r})}_{r=r_l}=0,\end{array}$(53) where ${\sigma }_{rr}$ ${\sigma }_{\phi r}$ are the components of the stress tensor [184]. The solution of the system equations (52(52) $\begin{array}{rl}& G(\mathrm{\Delta }{u}_r-\frac{u_r}{r^2})+(\lambda +G)\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left[\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\right(r{u}_r\left)\right]+f_r(r,t)=0,\\ & G(\mathrm{\Delta }{u}_{\phi }-\frac{u_{\phi }}{r^2})+f_{\phi }(r,t)=0,\end{array}$(52) ), (53(53) $\begin{array}{rl}& u_r{|}_{r=r_0}=0,u_{\phi }{|}_{r=r_0}=0,\\ & {\sigma }_{rr}{|}_{r=r_l}={\left[\right(\lambda +2G)\frac{\mathrm{\partial }{u}_r}{\mathrm{\partial }r}+\lambda \frac{u_r}{r}]}_{r=r_l}=0,\\ & {\sigma }_{\phi r}{|}_{r=r_l}=G{(\frac{\mathrm{\partial }{u}_{\phi }}{\mathrm{\partial }r}-\frac{u_{\phi }}{r})}_{r=r_l}=0,\end{array}$(53) ) makes it possible to find the shear component ${\sigma }_{\phi r}(r,t)$ of the stress tensor and to calculate the Peach–Koehler force which stimulates the edge dislocation glide in φ-direction, that is a yield of the matter within the cell or, in other words, a loss in rotational inertia. Of course, it is possible to introduce the more tricky boundary conditions which take into account a slippage in the contact between the sample and rim. Certainly, the more tricky model for the sample deformation (e.g. a variant of viscous-elastic medium), but anyway the model must be based on the real polytypic nature of the He II phase.

Thus the ${}^4$He ‘supersolid’ in torsion oscillator cell should be considered as the HCP ${}^4$He solid within an amplitude-dependent internal friction experiment under radially non-uniform alternative shear loading. However, the most significance and advantage of the experiments [25–27] is the prediction of a phase boundary between ‘supersolid’ and ‘normal solid’ phases at 230–350 mK and 25–40 bar [26] which is close analog of the λ-line between He I and He II phases (up to the negative slope of the supersolid-normal-solid boundary line). This prediction completely coincides with the observable features of ${}^4$He just in this temperature-pressure region (such as anomalous heat capacity [62,63], softening of shear modulus [66–69] and non-monotonic behaviour of $P\left(T\right)$ [64,65,118,119]).

When treating the supersolid problem, Balibar et al. [185] formulated several questions which can be answered (at least, partially) in view of the above consideration of Subsections 4.1 and 4.4 (the questions of Ref. [185] are cited in their original form):

1. ‘We would like to know in more detail the differences between the behaviour of solid ${}^4$He and solid ${}^3$He. In what ways do the dislocations in these two quantum solids differ? And, what similarities and differences exist between the helium quantum solids and solid hydrogen?’ and ‘…more details about the manner in which flow depends on the driving chemical potential?’

   • Principally, the only difference between ${}^4$He and ${}^3$He atoms is the nuclear spin of ${}^3$He, but structurally the crystal lattices of the two isotopes at low pressures are radically different (HCP for ${}^4$He and BCC for ${}^3$He). BCC ${}^3$He monocrystal has three intersecting basal glide systems (110), (101), (011), whereas the HCP ${}^4$He has only one system (0001) of basal easy glide. Under loading, the presence of the multiple slip leads to an intensive work hardening [78,123] in the high-symmetric cubic ${}^3$He, whereas the yield along the unique HCP basal system of ${}^4$He is working easily. In addition, the dislocations in HCP are splitted in the basal plane, and partials contain kinks (see Subsection 4.1) which are extremely mobile in the gradient of chemical potential $\mu (T,P)$ as a driving force, $\mathrm{\nabla }\mu (T,P)=\frac{\mathrm{\partial }\mu (T,P)}{\mathrm{\partial }T}\mathrm{\nabla }T+\frac{\mathrm{\partial }\mu (T,P)}{\mathrm{\partial }P}\mathrm{\nabla }P,$ that is in the gradient of temperature (thermodiffusion) and pressure (barodiffusion) [186]. Para-hydrogen p-H${}_2$ with HCP lattice demonstrates superplastic and superelastic behaviour which was experimentally observed in a series of works [180–183]. It should be noted that by neutron measurements [46] phonon spectrum of the para-H${}_2$ in pre-melting region is the complete analog of the well-known spectrum of the superfluid ${}^4$He.

2. ‘For instance, which dislocations are split into partials? Is this critical to their mobility? What is the stacking fault energy and resulting splitting? What is the difference in the binding energy for 3He to screw versus edge dislocations and to partials? At what temperatures will kinks and kink motion be thermally activated? Can we calculate the kink energy by including quantum fluctuations and quantum tunnelling so that one gets some prediction for the existence of zero-point kinks?’

   ∙∙

   The split perfect dislocation consists of two Shockley's partials which restrict the 2D region of a stacking fault [77,78]. The benefit of this configuration is determined by both energy and packing entropy of the stacking fault. The Calculation of the stacking fault energy (SFE) is relatively complicated problem which includes a knowledge about atom–atom interaction in the matter under study. As to noble gas solids, the corresponding calculation of SFE is known for argon [87], it is estimated as $\sim -0.022$ erg/cm${}^2$. It seems that for helium the corresponding value must be, at least, of order smaller. Anyway, it is noticeable that the SFE in argon is a negative value, so that the splitting can be advantageous energetically (of course, without account of entropy contribution). The mobility of the partials due to kinks creation-annihilation has been discussed above (Subsection 4.4). The kinks can be excited either thermally or mechanically (because the chemical potential $\mu (T,P)$ is a function of the temperature and pressure) but the probability of the kink creation depends on the energy of the creation act. The quantum mechanical calculation of the kink creation probability was given in Ref. [143]. The formation of zero-point kinks presumes the presence of a quantum (athermic) fluctuation, and an example of such fluctuation has been given in Section 3.1. As we can see from Table 1, within a group of degenerated states of ${}^4$He${}_2$-dimer all sublevels have the same energy, but each of them corresponds to his own average interatomic distance $〈R_0〉$. It means that the interatomic distance fluctuates athermically at the constant energy on the degenerated level (walking about the degenerated sublevels) but to put the system into degenerated excited state we have, anyway, to supply the system with a portion of energy to transfer it to the excited level over the low-lying non-degenerated ground state.

3. In a number of the experiments, there is an irreversible behaviour. What is responsible for this and just how does annealing or stress influence this irreversibility? There are only a few rotation experiments that have been directed to the study of solid helium and the behaviour that these experiments reveal is complex and not at all understood. What is the relevance of vortices to solid helium? Can we exploit some of the superfluid vortex experimental technology to study dislocations? A disadvantage of solid helium as a material science model system is the inability to directly image and count dislocations. For example, can He2* or other excited stable states (or dopant impurities) be excited and imaged in solid helium? Could you decorate and light up dislocations? Could a charge be injected and currents used to learn something about dislocations, e.g. see a current moving down a single dislocation?

   ∙∙∙

   The irreversible behaviour means the real plastic deformation produced by gliding dislocations [123], but the reversible means the martensitic transformation in the multilayered polytypic structure [75,76] which is realised due to re-shuffling of the closely packed basal planes under control of corresponding thermodynamic conditions on the energy and packing entropy in the stack (see Subsections 4.1, 4.2 and 4.4). In view of this construction of the 2D closely packed basal plane with relatively weak interplane binding, the polytypic stack is extremely sensitive and compliable to the shear deformation, especially at oscillatory cell rotations. Such an interlayer motion is typical for the standard model of fluid mechanics [186], so that both ‘superfluid’ and ‘supersolid’ can be attested as a ‘liquid crystal’ and this proposed by Shubnikov model (including the vortex problem) we will consider in the following section.

Eventually, the supersolid according to Kim and Chan means superplasticity, the phenomenon well known in traditional materials science. Such an alternative was first proposed by Dash and Wettlaufer [176]. As to molecular cryocrystals in general, the superplasticity has been demonstrated, among them, by above-mentioned para-hydrogen [180,181] and water ice [40]. The excellent example of superplasticity in helium is reported in Ref. [187] experiments on compression-driven mass flow of solid helium in Vycor.

6. He II as liquid crystal

Shubnikov [1] introduced the term ‘liquid crystal’ to coincide the mechanical compliance of He II with its observable behaviour as a spatially ordered matter. Landau [12,14–16] proposed phonon description which is based on a tacit assumption that the medium possesses a translational symmetry that is, in fact, a crystalline lattice. This approach was derived hereinafter by Bogoliubov [18] and Feynman [19–21]. Tisza's model of the two-fluidity presumes implicitly the presence of two types of coupled excitations, and this demand can be satisfied, for instance, within the concept of spin–phonon interaction (see Section 7). All the mentioned mechanisms are typical only for the spatially ordered (crystalline) systems, and for this reason the concept of liquid crystal or supersolid (in its original sense introduced by Matsuda and Tsuneto [24]) can be applied unambiguously to the He II phase. Microscopic spatial ordering in a condensed matter means formation of a regular valence bond with long-range translation symmetry, and, as a result, creation of the condensed phase with all the necessary features of the macroscopic crystalline state. The best form of the condensed system which combines the partial crystalline ordering with high deformation ability is multilayered polytype (see Subsection 4.1). The polytype is a stack of 2D crystalline plates one-dimensionally disordered in direction perpendicular to the basal plane (the direction of c-axis). The plytype transforms easily due to basal glide (yield) without breaking the closest packing principle of the stack (‘supersolid’), just like the incompressible flow of an ideal liquid (‘superfluid’) without violation of continuity [186]. Thus all the above discussed properties of the ${}^4$He solid can be extended to the He II phase with only difference in degrees of one-dimensional ordering along c-direction and density of partials or associated stacking faults which increases the mechanical compliance of He II phase relative to interplane shift or rotation within the basal system.

In addition, as it shown in Refs. [31,32] (see Section 3.2), the spin subsystem takes an essential contribution into atom-atom interaction of ${}^4$He, and we can suppose the spin ordering within each 2D basal plane with presumable triangular lattice [29] (see Section 5.1). In view of Equation (20(20) $\begin{array}{r}J\simeq -11.716\mathrm{K}\end{array}$(20) ), we can expect that the spin exchange in a basal plane is of ferromagnetic type, so that the spins of each 2D triangular lattice in the ground state must have a mutual parallel orientation transversally to the basal 2D plane. The spins of the neighbouring 2D elements must be preferentially in opposite orientation (like domain magnetisation in macroscopic ferromagnet) to minimise the macroscopic magnetisation, so that along c-axis the up-down spin chains are formed. In this connection, between the neighbouring basal planes exists some additional magnetic repulsion, and it is an additional factor for the interplane softening and the basal easy glide behaviour. Some additional properties of the spin subsystem will be discussed in Section 7.

Here it should be made a notation about vortices in the He II phase. The standard way to introduce the quantised vortex [188–190] is to apply the Bohr–Sommerfeld quantisation rule (54) $\begin{array}{r}{\gamma }_n=m_{He}{\oint }_L{\mathbf{\text{v}}}_s\mathrm{d}\mathbf{\text{l}}=2\pi n\hslash \end{array}$(54) which, however, contradicts to the hypothesis about potentiality of the superfluid velocity ${\mathbf{\text{v}}}_s$, that is to necessary condition on circulation $\mathrm{r}\mathrm{o}\mathrm{t}{\mathbf{\text{v}}}_s=0$ or ${\oint }_L{\mathbf{\text{v}}}_s\mathrm{d}\mathbf{\text{l}}\equiv 0.$ In addition, the circulation Equation (54(54) $\begin{array}{r}{\gamma }_n=m_{He}{\oint }_L{\mathbf{\text{v}}}_s\mathrm{d}\mathbf{\text{l}}=2\pi n\hslash \end{array}$(54) ) is not an adiabatic invariant because the hydrodynamic velocity ${\mathbf{\text{v}}}_s$ is not an element of any Hamiltonian's system (in fact, the velocity ${\mathbf{\text{v}}}_s$ is not a good determined dynamical variable and integration contour L is not a trajectory of a separate atom within any phase space). The only question is the nature of stable (long-lived) vortices in He II, but absence of such vortices in He I. If the condition Equation (54(54) $\begin{array}{r}{\gamma }_n=m_{He}{\oint }_L{\mathbf{\text{v}}}_s\mathrm{d}\mathbf{\text{l}}=2\pi n\hslash \end{array}$(54) ) would be appreciated, then we can expect the circulation has a discrete spectrum corresponding to $n=1,2,3,\dots$, and this result is not quite understood mechanically because the hydrodynamic field of velocities (remember that ${\mathbf{\text{v}}}_s$ is governed by two-fluid hydrodynamic equations [186,190]) must lie to a certain macroscopic flow of helium atoms which evidently contradicts to the idea of spatial ordering in He II phase. Thus the ‘quantisation’ of the hydrodynamic vortex motion seems to be an artificial procedure which hardly ever can obtain easily a distinct physical background. The real microscopical degrees of freedom with properties of angular momentum in condensed helium phases are electronic spins within valence zone (and, in addition, nuclear spins in ${}^3$He). Through electronic shells these spin rotational degrees are strongly coupled with phonons, and as a result the ‘roton minimum’ appears on the dispersion curve of the longitudinal phonons [150]. Certainly, if the two different types of excitations are shown along the common spectrum brunch, then there are two types of degrees of freedom strongly coupled within the system, and in our case they are phonons (translation degrees) and spins (rotational degrees).

The real quantised vortices in the quantum system are Abrikosov's vortices in the type-II superconductors [191,192], and in the literature is known a number of attempts [193–195] to draw the corresponding concept for explanation of superfluid vorticity. In the type-II superconductors, the vortices are filaments of normal state where magnetic field penetrates into superconducting matrix, and it is the structure of the Shubnikov phase [196] discovered by Shubnikov's research group in Kharkov UFTI [197–200] (see also Bardeen [201] and the books [3,4]). The Abrikosov's vortex lattice is a coherent state with quantised flux of magnetic field determined by Maxwell equations in opposite to hydrodynamic vortices with configuration determined by mechanical equations of motion for continuous medium [202,203]. There is an essential difference between the vortex in type-II superconductor and the vortex in the He II phase: the filament of Abrikosov's vortex follows strongly to the force lines of the magnetic field penetrate into Shubnikov phase [196], whereas the orientation of the vortex filaments in the He II phase do not correspond typically to any field characters (except of boundary conditions and an effect of centrifugal forces in rotating cells) and do not form typically any spatially regular systems, as it is in the case of Abrikosov lattice [191,192]. Moreover, the vortex system in He II demonstrates an entanglement [193] which seems to be a random structure of curved vortex lines. To describe the vortex–vortex interaction in Refs. [193–195] was used an ‘electromagnetic analogy’ where the ‘ quantised’ vortex is considering as a curvilinear ‘current’ which produced a velocity fields governing by the by the familiar Biot–Savart relation [41,204]. In this case, the interaction energy between two ‘superfluid’ vortices can be presented as [195] (55) $\begin{array}{r}{E}_{1,2}=\frac{\rho {\gamma }_n^2}{4\pi }\iint \frac{\mathrm{d}{\mathbf{\text{s}}}_1\mathrm{d}{\mathbf{\text{s}}}_2}{|{\mathbf{\text{r}}}_1-{\mathbf{\text{r}}}_2|}\end{array}$(55) where ρ is the density of the fluid and ${\gamma }_n$ is the circulation Equation (54(54) $\begin{array}{r}{\gamma }_n=m_{He}{\oint }_L{\mathbf{\text{v}}}_s\mathrm{d}\mathbf{\text{l}}=2\pi n\hslash \end{array}$(54) ). However, it should be noted that the result Equation (55(55) $\begin{array}{r}{E}_{1,2}=\frac{\rho {\gamma }_n^2}{4\pi }\iint \frac{\mathrm{d}{\mathbf{\text{s}}}_1\mathrm{d}{\mathbf{\text{s}}}_2}{|{\mathbf{\text{r}}}_1-{\mathbf{\text{r}}}_2|}\end{array}$(55) ) can hardly be applied to the ‘superfluid’ vorticity, because it is obtained on the superposition principle, the main principle of the linear Maxwell's electrodynamics. The hydrodynamic vorticity is governing by non-linear equations [186], and the superposition principle cannot be applied to the hydrodynamic vortices.

Just the different pictures appears if we consider the He II phase in some sense as ‘liquid’ (yield, easy glide), but nevertheless built of 2D spatially ordered crystallites on triangular lattice. As it is considered above, the best concept of the corresponding system is multilayered polytype with strong crystalline ordering within 2D basal planes and easy mutual glide (yield) between neighbouring elements (see Section 4.1). The most familiar crystal lattice defect in this structure is dislocation [75] that is linear singularity of the total displacement field $\mathbf{\text{u}}\left(\mathbf{\text{r}}\right)$ which satisfies the condition [42] (56) $\begin{array}{r}{\oint }_{\mathcal{L}}\mathrm{d}{u}_i=-b_i,\end{array}$(56) where $\mathbf{\text{b}}$ is Burgers vector which takes the discrete values proportional to the discrete lattice parameters. Thus the dislocation is the stable vortex of the displacement field with ‘spatially quantised’ magnitude $\mathbf{\text{b}}$. The condition equation (56(56) $\begin{array}{r}{\oint }_{\mathcal{L}}\mathrm{d}{u}_i=-b_i,\end{array}$(56) ) is quite similar to Equation (54(54) $\begin{array}{r}{\gamma }_n=m_{He}{\oint }_L{\mathbf{\text{v}}}_s\mathrm{d}\mathbf{\text{l}}=2\pi n\hslash \end{array}$(54) ) with the only difference that the circulation of displacements (even time-dependent) around dislocation, and the circulation of the displacements generate by dislocation has the strongly determined constant value coincided with lattice structure and type of dislocation (and independent of a local curvature of the dislocation line whose position and curvature are, in general, time-dependent). The linear screw, edge or mixed dislocations are moving linear vortices, the Frank loops are circular vortices, the dislocations due to entanglement create the complicate defect structure which provides, however, easy deformation of the crystalline system. In addition, the definition Equation (56(56) $\begin{array}{r}{\oint }_{\mathcal{L}}\mathrm{d}{u}_i=-b_i,\end{array}$(56) ) has a strong physical sense which allows the determined electromagnetic analogies [78] based on superposition principle, and the interaction between two dislocations can be described properly by the Equation (55(55) $\begin{array}{r}{E}_{1,2}=\frac{\rho {\gamma }_n^2}{4\pi }\iint \frac{\mathrm{d}{\mathbf{\text{s}}}_1\mathrm{d}{\mathbf{\text{s}}}_2}{|{\mathbf{\text{r}}}_1-{\mathbf{\text{r}}}_2|}\end{array}$(55) ). Thus the dislocation concept of the He II vorticity can be quite naturally built into Shubnikov's concept of liquid crystal.

7. He II as spin ice

In this section we combine all the above-described features of condensed ${}^4$He into a universal concept of semi-ordered phase (‘liquid crystal’, according to the Shubnikov's definition [1]). It is evident that the best model for the condensed matter which naturally includes extremal yielding of structurally stable spatially-ordered elements is only multilayered polytype stacked of 2D crystalline planes with triangular lattice (in general, randomly, but without breaking the closest packing principle). Each atom of such system has six nearest in-plane neighbours, but only three nearest neighbours from the upper or lower planes. It means that in-plane interatomic bonds are greater than interplane ones, and this fact is especially important for helium where interatomic interaction is highly specified, especially due to principal role of the spin subsystem (Section 3.2). The crystalline polytypic construction allows mutual easy glide between neighbouring 2D crystallites with long-range translational order which leads, as a result, to all the observable ‘superfluid’ or ‘supersolid’ phenomena, and the spatial order exists, undoubtedly, in the spin subsystem of the He II phase, because the sins are strongly coupled with their electrons distributed among ordered atomic shells (spin–phonon coupling). The spin excitations (spin waves) in the spin-ordered subsystem of the He II play an extremely important role in view of rather weak contribution from non-relativistic (van der Waals) interactions, and namely spins are the necessary rotational degrees of freedom to interpret so-called ‘roton’ minimum in phonon spectrum of He II (thus, the rotons introduced by Tamm [14] are simply electronic spins strongly coupled with translational phonon modes through correlation among atomic shells which is a basis of the phonon excitations). Finally the proper Hamiltonian for polytypic He II phase must include three terms (57) $\begin{array}{r}{\hat{H}}_{\mathrm{r}\mathrm{e}\mathrm{l}}=H_{\mathrm{p}\mathrm{h}}+{\hat{H}}_{\mathrm{s}\mathrm{p}\mathrm{i}\mathrm{n}}+{\hat{H}}_{\mathrm{s}\mathrm{p}\mathrm{h}},\end{array}$(57) where the first term, $H_{\mathrm{p}\mathrm{h}}$, is the phonon Hamiltonian equation (24(24) $\begin{array}{r}{H}_{\mathrm{p}\mathrm{h}}(\mathbf{\text{p}},\mathbf{\text{u}})=\sum _{j=1}^N{H}_j({\mathbf{\text{p}}}_{{\mathbf{\text{f}}}_j},{\mathbf{\text{u}}}_{{\mathbf{\text{f}}}_j}).\end{array}$(24) ) [30,71–73], the second term is the spin Hamiltonian equation (21(21) $\begin{array}{rl}{\hat{H}}_{\mathrm{s}\mathrm{p}\mathrm{i}\mathrm{n}}& =\frac{J\left(R_0\right)}{2}\sum _{\mathbf{\text{f}},\mathit{\delta }}[{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}}^{\left(a\right)}{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}}^{\left(b\right)}+{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}}^{\left(a\right)}{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}+R_0\mathit{\delta }}^{\left(a\right)}+{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}}^{\left(a\right)}{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}+R_0\mathit{\delta }}^{\left(b\right)}\\ & +{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}}^{\left(b\right)}{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}+R_0\mathit{\delta }}^{\left(a\right)}\\ & +{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}}^{\left(b\right)}{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}+R_0\mathit{\delta }}^{\left(b\right)}+{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}+R_0\mathit{\delta }}^{\left(b\right)}{\hat{\mathit{\sigma }}}_{\mathbf{\text{f}}+R_0\mathit{\delta }}^{\left(b\right)}]\end{array}$(21) ) and the third term, ${\hat{H}}_{\mathrm{s}\mathrm{p}\mathrm{h}}$ describes the spin–phonon coupling [30,31] which can be obtained through expansion of the exchange constant $J\left(R_0\right)$ (Equation 18(18) $\begin{array}{rl}J& =\frac{g_S^2{\alpha }_S^2}{4}\{-\frac{8\pi }{3}〈G.S|\delta ({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}})|G.S〉+\\ & +〈G.S.\left|\frac{1}{r_{ss\mathrm{\prime }}^3}\right|G.S.〉-3〈G.S.\left|\frac{({\mathbf{\text{r}}}_s-{\mathbf{\text{r}}}_{s^{\mathrm{\prime }}}{)}^2}{3r_{ss\mathrm{\prime }}^5}\right|G.S.〉\}\end{array}$(18) ) on atomic displacements of atoms in neighbouring sites. It is the standard mechanism of spin-phonon interaction [205] applied to the spin-ordered He II phase. As a result, taking into account Equation (6(6) $\begin{array}{rl}& {\hat{H}}_{\mathrm{S}\mathrm{S}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d)\\ & =\frac{g_s^2{\alpha }_s^2}{4}\{-\frac{8\pi }{3}\sum _{s\ne s^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}\delta ({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}})\\ & +\sum _{s\ne s^{\mathrm{\prime }}}\frac{1}{r_{s{s}^{\mathrm{\prime }}}^3}[{\hat{\mathit{\sigma }}}_s{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}-3\frac{\left({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_s\right)\left({\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}{\hat{\mathit{\sigma }}}_{s^{\mathrm{\prime }}}\right)}{r_{s{s}^{\mathrm{\prime }}}^2}]\}\end{array}$(6) ), (58) $\begin{array}{rl}{\hat{H}}_{\mathrm{s}\mathrm{p}\mathrm{h}}& =\frac{\mathrm{\partial }J\left(R_0\right)}{\mathrm{\partial }{R}_0}\sum _{\mathbf{\text{f}},\mathit{\delta }}\left[\right({\mathbf{\text{u}}}_{\mathbf{\text{f}},R_0\mathit{\delta }}-{\mathbf{\text{u}}}_{\mathbf{\text{f}}}\left)\mathit{\delta }\right]\\ & \times [{\hat{\mathit{\sigma }}}_a^{\mathbf{\text{f}}}{\hat{\mathit{\sigma }}}_a^{\mathbf{\text{f}},R_0\mathit{\delta }}+{\hat{\mathit{\sigma }}}_a^{\mathbf{\text{f}}}{\hat{\mathit{\sigma }}}_b^{\mathbf{\text{f}},R_0\mathit{\delta }}+{\hat{\mathit{\sigma }}}_b^{\mathbf{\text{f}}}{\hat{\mathit{\sigma }}}_a^{\mathbf{\text{f}},R_0\mathit{\delta }}+{\hat{\mathit{\sigma }}}_b^{\mathbf{\text{f}}}{\hat{\mathit{\sigma }}}_b^{\mathbf{\text{f}},R_0\mathit{\delta }}],\end{array}$(58) where ${\mathbf{\text{u}}}_{\mathbf{\text{f}}}$ and ${\mathbf{\text{u}}}_{\mathbf{\text{f}},\mathit{\delta }}$ are the displacements of the lattice sites $\mathbf{\text{f}}$ and $\mathbf{\text{f}}+R_0\mathit{\delta }$, respectively. The spin–phonon interaction is proportional to the both gradient of the lattice sites displacements and bilinear superpositions of the spin operators [205–207] within a He–He bond, and this situation is just a direct analog of translation-rotation interaction in molecular cryocrystals with molecular rotational degrees of freedom [107,208–210].

It can be seen from Equation (58(58) $\begin{array}{rl}{\hat{H}}_{\mathrm{s}\mathrm{p}\mathrm{h}}& =\frac{\mathrm{\partial }J\left(R_0\right)}{\mathrm{\partial }{R}_0}\sum _{\mathbf{\text{f}},\mathit{\delta }}\left[\right({\mathbf{\text{u}}}_{\mathbf{\text{f}},R_0\mathit{\delta }}-{\mathbf{\text{u}}}_{\mathbf{\text{f}}}\left)\mathit{\delta }\right]\\ & \times [{\hat{\mathit{\sigma }}}_a^{\mathbf{\text{f}}}{\hat{\mathit{\sigma }}}_a^{\mathbf{\text{f}},R_0\mathit{\delta }}+{\hat{\mathit{\sigma }}}_a^{\mathbf{\text{f}}}{\hat{\mathit{\sigma }}}_b^{\mathbf{\text{f}},R_0\mathit{\delta }}+{\hat{\mathit{\sigma }}}_b^{\mathbf{\text{f}}}{\hat{\mathit{\sigma }}}_a^{\mathbf{\text{f}},R_0\mathit{\delta }}+{\hat{\mathit{\sigma }}}_b^{\mathbf{\text{f}}}{\hat{\mathit{\sigma }}}_b^{\mathbf{\text{f}},R_0\mathit{\delta }}],\end{array}$(58) ) that spin subsystem plays the role of an external force for phonon excitations, and when approaching some ‘resonant’ wavelength the phonon dispersion curve will be ‘subsided’ due to loading from spin degrees of freedom (roton minimum of dispersion curve). Mechanically, the translation–rotation interaction could be a justification for the phonon–‘roton’ coupling in He II (phonons are translation excitations in the medium, but spin degrees of freedom have the well-known transformation properties of angular momentum). In this connection the physical sense of term ‘roton’, introduced by I.E. Tamm [14] in 1941 could be clarified. The phenomenon of microwave resonant absorption is the manifestation of direct interaction between macro- and microscopic degrees of freedom in condensed helium phases, and concept of the spin–phonon interaction is quite realistic as the mechanism for a number of experimentally observed effects.

7.1. Temperature-dependent spin ordering

There are two main problems in the statement of the nature of an ordering in the spin subsystem of the He II phase: (i) spatial ordering of electronic shells of individual atoms spatially ordered within a crystal lattice and (ii) the sign of spin exchange constant. In our case, we suppose that He II phase is multilayered polytype with principal role of spin subsystem for interatomic interaction and, certainly, we can expect that the He II phase will be stacked of 2D ferromagnetically ordered (in view of ferromagnetic type of the estimated exchange Equation (20(20) $\begin{array}{r}J\simeq -11.716\mathrm{K}\end{array}$(20) ) for the spin contribution into He–He interaction) crystalline planes on triangular lattice connected by comparably weak inter-plane interaction which can be interpreted as an ‘effective’ external magnetic field (or mean field) applied to the given 2D plane from the neighbouring layers. Just the same model is considered in Ref. [211], and here we apply it for further explanations. It seems to be rather unexpected that electronic spins on the He–He bond prefer the ferromagnetic ordering (just as between simple permanent magnets connected with the contact interaction) whereas within the unitary shell of the ${}^4$He ground state two electrons keep the opposite spins. It is due to the fact that mutual spin orientation within ${}^4$He atom with central symmetry of the nucleus Coulomb field is controlled by the conservation law of the total (orbital plus spin) angular momentum of the spherically symmetric atom, but it does not hold in the case of the ${}^4$He${}_2$-dimer with two attractive centres and the only contact interaction between spin pairs remains essential.

Thus we consider briefly the HFM on a triangular lattice in an external magnetic field [211] with peculiar attention concentrated on small and intermediate external field h magnitudes. Figure 19 represents the temperature dependences of the magnetisation at different values of h/J. These results obtained through the Green function formalism [212–214] agree closely with high temperature series expansion (HTSE [211]), just up to the point of HTSE applicability, and with the random phase approximation (RPA [215]) which coincides with HTSE only at relatively high temperatures. We have also calculated the magnetisation at low temperatures using the renormalisation group technique (RGT [211]). The results are obtained in a good agreement within both our approaches [211]. At a given magnetic field, the magnetisation for the triangular lattice exceeds $〈S^z〉$ for the square one [211] within the whole temperature range. This result seems quite natural because the local field for a spin of the triangular lattice ferromagnet is higher than that for a spin of the square FM due to the greater coordination number of the triangular lattice. This result demonstrates the important role of the in-plane interaction strongly connected with the number of the nearest neighbours in the 2D subsystem. Of course the results of Figure 19 at low temperatures agree exactly to the so-called Bloch $T^{3/2}$-law [216,217].

Figure 20 demonstrates the temperature dependence of the heat capacity $C\left(T\right)$ of the 2D HFM [211]. With increase in an external field the position of the maximum on the curve $C\left(T\right)$ shifts to higher temperatures and its value $C_m^{tr}$ first increases rapidly and then decreases. A similar behaviour occurs for the heat capacity maximum $C_m^{sq}$ on a square lattice [211]. It should be noted that the HFM heat capacity with maximum at $T\sim J$ could be drawn to the explanation of the excessive heat (Section 4.2.2) in the HCP solid ${}^4$He but for the estimated exchange constant Equation (20(20) $\begin{array}{r}J\simeq -11.716\mathrm{K}\end{array}$(20) ) is too high to satisfy the experimental data [62,63].

Figure 19. Temperature dependence of the magnetisation (per spin) for HFM on a triangular lattice [211] at $h/J=0.1$, 0.3, 0.5, 0.7, 1.0, 1.5 (from left to right). The theory [211] (solid), HTSE (dashed), RGT (thin lines), and RPA [211] (dotted).

Figure 20. Temperature dependence of the heat capacity for HFM on a triangular lattice [211] at $h/J=0.1$, 0.5, 1.0, 1.5 (from left to right). The theory [211] (solid), HTSE (dashed), and RPA [211] (dotted). Thin lines correspond to $h=$0.

Another fact to be taken into account is spin–orbital splitting. Spin–orbital contribution (Equation (5(5) $\begin{array}{rl}& {\hat{H}}_{\mathrm{S}\mathrm{O}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & =-i\frac{{\mathcal{Z}}_0{g}_S{\alpha }_S^2}{4}\{\sum _s{\hat{\mathit{\sigma }}}_s[\frac{{\mathbf{\text{r}}}_s}{r_s^3}\times {\mathrm{\nabla }}_s]\\ & +\sum _s{\hat{\mathit{\sigma }}}_s[\frac{{\mathbf{\text{r}}}_s-{\mathbf{\text{R}}}_0}{|{\mathbf{\text{r}}}_s-{\mathbf{\text{R}}}_0{|}^3}\times {\mathrm{\nabla }}_s]\\ & -\frac{1}{{\mathcal{Z}}_0}\sum _s{\hat{\mathit{\sigma }}}_s\sum _{s^{\mathrm{\prime }}\ne s}[\frac{{\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}}{r_{s{s}^{\mathrm{\prime }}}^3}\times ({\mathrm{\nabla }}_s-{\mathrm{\nabla }}_{s^{\mathrm{\prime }}}\left)\right]\}\end{array}$(5) )) in view of symmetry reasons has a rather small value in the ground state, but due to explicit dependence on $R_0$ it has a strong effect on spin–lattice (spin–phonon) coupling. Spin dynamics (with transformation properties of angular momentum) ‘loads’ phonon modes, and this leads to the minimum in phonon spectrum just similar to the translation-rotation coupling in molecular crystals [107].

7.2. The first Rybalko effect

In 2004, Rybalko [218,219] had discovered an electrical activity of the He II phase which implies that excited by oscillating heater a second sound stationary wave produces between two electrically isolated bases of the measuring cell (the cell electric capacitor) an alternative electromotive force with frequency exactly corresponded to the double frequency of the heater power supply (recently, the phenomenon was confirmed in the independent experiments [220,221]). This phenomenon initiated a wide discussion which was concentrated around an active searching for possible electric sources in helium which unlikely can be found in the electrically neutral medium with extremely low atomic polarisability. Unfortunately, none of the attempts took into account the discussed above features specified namely to the He II phase. Here we propose an interpretation based directly on the spin-ordered model which does not demand any external electric charges or effects of electric polarisability for explanation of the observable events.

The second sound in He II is the heat wave [222] which in magnetically ordered systems must be accompanied with ‘magnetic second sound’ [205–207], an excitation created due to temperature dependence of the saturated magnetisation in the spin-ordered system (so-called Bloch $T^{3/2}$-law [216,217], see also previous Subsection 7.1). To define the temperature distribution within the experimental cell, Peshkov [222] used the known solution of the heat transfer equation [186,223], (59) $\begin{array}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }t}\mathrm{\Theta }(z,t)=\kappa \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{z}^2}\mathrm{\Theta }(z,t),\end{array}$(59) where $\mathrm{\Theta }(z,t)=T(z,t)-T_0$ is the overheating temperature of the cell interior over the constant thermostat temperature $T_0$ produced by the external heater placed at z = 0 (the problem is considered as one-dimensional one for cylindric cell with generatrix of length h along z-axis). The heater is supplied with alternative current ${\mathcal{I}}_0\sin \mathrm{\Omega }t$ and produced the heat current, (60) $\begin{array}{r}q=k_0{\mathcal{I}}_0^2{\mathcal{R}}_0{\sin }^2\mathrm{\Omega }t,\end{array}$(60) where ${\mathcal{R}}_0$ is the active resistance of the heater and the transfer coefficient $k_0<1$ accounts Kapitza's loses (and any others loses) on the boundary between heater and helium bath. Thus, we have the boundary condition at z = 0, (61) $\begin{array}{rl}{\frac{\mathrm{\partial }\mathrm{\Theta }(z,t)}{\mathrm{\partial }z}|}_{z=0}& =\frac{k_0}{c_p}{\mathcal{I}}_0^2{\mathcal{R}}_0{\sin }^2\mathrm{\Omega }t\\ & =\frac{k_0}{2c_p}{\mathcal{I}}_0^2{\mathcal{R}}_0(1-\cos 2\mathrm{\Omega }t),\end{array}$(61) where $c_p$ is the isobaric heat capacity. From the boundary condition Equation (61(61) $\begin{array}{rl}{\frac{\mathrm{\partial }\mathrm{\Theta }(z,t)}{\mathrm{\partial }z}|}_{z=0}& =\frac{k_0}{c_p}{\mathcal{I}}_0^2{\mathcal{R}}_0{\sin }^2\mathrm{\Omega }t\\ & =\frac{k_0}{2c_p}{\mathcal{I}}_0^2{\mathcal{R}}_0(1-\cos 2\mathrm{\Omega }t),\end{array}$(61) ) is quite evident the fact of the temperature oscillations with the double frequency $2\mathrm{\Omega }$. It should be noted that the boundary heat Equation (61(61) $\begin{array}{rl}{\frac{\mathrm{\partial }\mathrm{\Theta }(z,t)}{\mathrm{\partial }z}|}_{z=0}& =\frac{k_0}{c_p}{\mathcal{I}}_0^2{\mathcal{R}}_0{\sin }^2\mathrm{\Omega }t\\ & =\frac{k_0}{2c_p}{\mathcal{I}}_0^2{\mathcal{R}}_0(1-\cos 2\mathrm{\Omega }t),\end{array}$(61) ) consists not only of the alternative component but also of the constant average current $\sim {\mathcal{I}}_0^2{\mathcal{R}}_0/2$. The boundary condition at z = h means heat current from the cell into thermostat with the transfer coefficient $k_h$, (62) $\begin{array}{r}{\frac{\mathrm{\partial }\mathrm{\Theta }(z,t)}{\mathrm{\partial }z}|}_{z=h}=\frac{k_h}{c_p}\mathrm{\Theta }(h,t).\end{array}$(62) The problem equations (59(59) $\begin{array}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }t}\mathrm{\Theta }(z,t)=\kappa \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{z}^2}\mathrm{\Theta }(z,t),\end{array}$(59) )–(61(61) $\begin{array}{rl}{\frac{\mathrm{\partial }\mathrm{\Theta }(z,t)}{\mathrm{\partial }z}|}_{z=0}& =\frac{k_0}{c_p}{\mathcal{I}}_0^2{\mathcal{R}}_0{\sin }^2\mathrm{\Omega }t\\ & =\frac{k_0}{2c_p}{\mathcal{I}}_0^2{\mathcal{R}}_0(1-\cos 2\mathrm{\Omega }t),\end{array}$(61) ) can be solved by standard approaches of mathematical physics [223], and the obtained solution is in some reasons different from the used by Peshkov [222] (in view of exact account of the boundary conditions Equations (61(61) $\begin{array}{rl}{\frac{\mathrm{\partial }\mathrm{\Theta }(z,t)}{\mathrm{\partial }z}|}_{z=0}& =\frac{k_0}{c_p}{\mathcal{I}}_0^2{\mathcal{R}}_0{\sin }^2\mathrm{\Omega }t\\ & =\frac{k_0}{2c_p}{\mathcal{I}}_0^2{\mathcal{R}}_0(1-\cos 2\mathrm{\Omega }t),\end{array}$(61) ), (62(62) $\begin{array}{r}{\frac{\mathrm{\partial }\mathrm{\Theta }(z,t)}{\mathrm{\partial }z}|}_{z=h}=\frac{k_h}{c_p}\mathrm{\Theta }(h,t).\end{array}$(62) )). In addition, the real experimental cell is a cylinder of height h and radii of bases ${\rho }_0$, so that the temperature field within the cell $\mathrm{\Theta }(\rho ,\phi ,z,t)$ is, in general, a function of three spatial coordinates $\rho ,\rho ,\phi ,z$ and must be determined not only by the boundary conditions at z = 0 and z = h, but also by the boundary conditions (heat transfer between the cell and the thermostat) at the lateral surface $\rho ={\rho }_0$ of the experimental cell. As a result, the temperature field within the cylindrically symmetric cell will be a function $\mathrm{\Theta }(\rho ,z,t)$ not only of longitudinal coordinate $0\le z\le h$ but also of the radial coordinate $0\le \rho \le {\rho }_0$. The further consideration of this problem is beyond the purpose of our paper, and the only fact that the periodic heating excited within the cell a periodically time-dependent (with the frequency $2\mathrm{\Omega }$) spatially inhomogeneous temperature field $\mathrm{\Theta }(\rho ,z,t)$ of the second sound which is accompanied with coupled stationary spin wave in the spin-ordered system [205].

The creation of the spin wave in the inhomogeneous temperature field we demonstrate is based on the results of the paper [211] (see Subsection 7.1 and Figure 19). As can be seen from Figure 19, the low temperature magnetisation $\mathbf{\text{M}}\left(T\right)$ of 2D triangular spin lattice is just the Bloch $T^{3/2}$-law [217], (63) $\begin{array}{r}\mathbf{\text{M}}\left(T\right)\sim \mathbf{\text{M}}\left(0\right)-\frac{g{\mu }_b}{v_0}{\left(\frac{T}{J}\right)}^{3/2},\end{array}$(63) where ${\mu }_b$ is Bohr magneton, g is Landé factor, $v_0$ is specific volume per spin and $\mathbf{\text{M}}\left(0\right)$ is the saturation magnetisation at zero temperature. Following the time-dependent temperature distribution $\mathrm{\Theta }(\mathbf{\text{r}},t)$, we obtain the time-dependent magnetisation inside the cell, $\mathbf{\text{M}}\left(\mathrm{\Theta }\right(\mathbf{\text{r}},t\left)\right)$ and, finally, the magnetic induction $\mathbf{\text{B}}(\mathbf{\text{r}},t)=4\pi \mathbf{\text{M}}\left(\mathrm{\Theta }\right(\mathbf{\text{r}},t\left)\right)$ which, according to the Maxwell equation (Faraday electromagnetic induction law), is a vortex of the alternative electric field $\mathbf{\text{E}}(\mathbf{\text{r}},t)$ (electromotive force), (64) $\begin{array}{r}\mathrm{r}\mathrm{o}\mathrm{t}\mathbf{\text{E}}(\mathbf{\text{r}},t)=-\frac{1}{c}\frac{\mathrm{\partial }\mathbf{\text{B}}(\mathbf{\text{r}},t)}{\mathrm{\partial }t}=-\frac{4\pi }{c}\frac{\mathrm{\partial }\mathbf{\text{M}}\left(\mathrm{\Theta }\right(\mathbf{\text{r}},t\left)\right)}{\mathrm{\partial }t},\end{array}$(64) which is registered in the experiment [218].

In 2005, Rybalko [224] reported the mechanoelectric effect which is an another variant of the electrical activity of He II phase which is quite different from described above. It was shown that electric induction can be produced in the torsion oscillator with the He II film entrained by the wall of the torsion cell (the experiments were performed both in auto-generator regime and under external oscillatory drive). Authors of Ref. [224] interpreted the effect as a result of ‘dynamic polarisation of the liquid’, but we propose another explanation of the effect. Taking into account the developed here model of He  II phase as a spin-ordered system with ferromagnetic type of exchange (see Equation 20(20) $\begin{array}{r}J\simeq -11.716\mathrm{K}\end{array}$(20) ) we can treat the observation of Ref. [224] as the standard Barnett effect [225] (the gyroscopic spin response from the rotating sample, see also [226]). Under alternative rotation of the torsion oscillator cell the spins within the He II film deposited on the inner surface of the cell must by twice re-oriented during a period of the cell oscillations, and, as a result, we have the alternative magnetisation directed along/opposite the rotation axis and, consequently, an inducted alternative electric field according to the Faraday law (Equation 64(64) $\begin{array}{r}\mathrm{r}\mathrm{o}\mathrm{t}\mathbf{\text{E}}(\mathbf{\text{r}},t)=-\frac{1}{c}\frac{\mathrm{\partial }\mathbf{\text{B}}(\mathbf{\text{r}},t)}{\mathrm{\partial }t}=-\frac{4\pi }{c}\frac{\mathrm{\partial }\mathbf{\text{M}}\left(\mathrm{\Theta }\right(\mathbf{\text{r}},t\left)\right)}{\mathrm{\partial }t},\end{array}$(64) ). The described above experiments [218,219,224] provide support for our suggestion about principal role of the spin subsystem in observable physical properties of the He II phase.

7.3. Barnett effect and transversal electromotive force in torsion oscillator with ${}^4$He film

This section has been written through the decisive collaboration with Dr. A. Rybalko. The Barnett effect [225,227] (in common with Einstein–de Haas effect [228]) gives a direct evidence of the spin-produced magnetisation in a rotated condensed matter. The rotation of a sample with an angular velocity $\mathbf{\Omega }$ leads, due to gyromagnetic coupling, to generation in the sample the magnetisation (magnetic moment per volume unit) $\mathbf{\text{M}}=N_s\mathbf{\Omega }/\mathrm{\Gamma }$, where $N_s$ is the number of active spins in the experimental sample, $\mathrm{\Gamma }=-ge/2m_{e}c$ is the gyromagnetic ratio, and g is Landé factor (here and below we use the Gauss units). Thus the points of the rotating around $\mathbf{\Omega }$-axis system have the linear velocities $\mathbf{\text{v(f{r})}}=[\mathbf{\Omega }\times \mathbf{\text{r}}]$ and, due to well-known relation of the Lorentz transformation [41], possess in the stationary laboratory system the dynamic dielectric polarisation $\mathbf{\text{P}}(\mathbf{\text{r}},t)$ (time-dependent dipole moment of the volume unity) (65) $\begin{array}{r}\mathbf{\text{P}}(\mathbf{\text{r}},t)=\frac{1}{c}\left[\mathbf{\text{v}}\right(\mathbf{\text{r}})\times \mathbf{\text{M}}(\mathbf{\text{r}},t\left)\right]=\frac{1}{c}\left[\right[\mathbf{\Omega }\times \mathbf{\text{r}}]\times \mathbf{\text{M}}(\mathbf{\text{r}},t\left)\right].\end{array}$(65) As a result, the Barnett effect in the rotating system must be accompanied by transversal electromotive force $\mathbf{\text{E}}(\mathbf{\text{r}},t)=-4\pi \mathbf{\text{P}}(\mathbf{\text{r}},t)$ which is perpendicular to both $\mathbf{\text{M}}(\mathbf{\text{r}},t)$ and $\mathbf{\text{v}}\left(\mathbf{\text{r}}\right)$.

The corresponding phenomenon on ${}^4$He film cooled below λ-point at T<2.186 K (Helium II phase) has been discovered in Ref [224]. The experimental cell is filled with ${}^4$He gas until on the cooled inner surface of the rotating bob [224] of height $h=$1cm and inner diameter $D=2R_0=1$ cm is formed the perfectly deposited helium film [229] with thickness of $d=300--350\text{Å}\ll R_0$ (the adsorbed ${}^4$He film with just the similar thickness is still strongly coupled with accurately polished metallic substrate of the torsional bob). The bob is mounted on the vertical rod built of thin steel capillary with external and internal diameters 0.8 and 0.5 mm, respectively [224]. It had been involving into oscillations from external generator by capacitive driver at the resonant frequency of the filled system $f_0=136$ Hz [224]. The bob rotation angle $\phi \left(t\right)$ under external harmonic driving with frequency $f_0$ and amplitude Φ is $\phi \left(t\right)=\mathrm{\Phi }\sin {\omega }_{0}t$, where ${\omega }_0=2\pi f_0$. The angular velocity of the bob rotation is $\mathbf{\Omega }=\mathbf{\text{n}}{\omega }_0\mathrm{\Phi }\cos {\omega }_{0}t$ (the unit vector $\mathbf{\text{n}}$ determines the direction of the rotation axis, ${\mathbf{\text{n}}}^2=1$). In view of $d\ll R_0$ we can suppose that all the points of the ${}^4$He dielectric layer have the same linear velocities $\mathbf{\text{v}}=[\mathbf{\Omega }\times {\mathbf{\text{R}}}_0]$ or $v={\omega }_0{R}_0\mathrm{\Phi }\cos {\omega }_{0}t$ perpendicularly to the rotation axis. In cylindric coordinates $(\mathbf{\text{R}},z)$ where the bob rotates around z-axis, the thin dielectric layer adsorbed on the interior $({\mathbf{\text{R}}}_0,z)$ of the bob produces the transverse (relative to the rotation axis) polarisation Equation (65(65) $\begin{array}{r}\mathbf{\text{P}}(\mathbf{\text{r}},t)=\frac{1}{c}\left[\mathbf{\text{v}}\right(\mathbf{\text{r}})\times \mathbf{\text{M}}(\mathbf{\text{r}},t\left)\right]=\frac{1}{c}\left[\right[\mathbf{\Omega }\times \mathbf{\text{r}}]\times \mathbf{\text{M}}(\mathbf{\text{r}},t\left)\right].\end{array}$(65) ) (66) $\begin{array}{rl}\mathbf{\text{P}}(\mathbf{\text{R}},z,t)& =\frac{N_s}{c\mathrm{\Gamma }}\left[\right[\mathbf{\Omega }\times {\mathbf{\text{R}}}_0]\times \mathbf{\Omega }]=-\frac{2m_e{N}_s}{ge}{\mathrm{\Omega }}^2{\mathbf{\text{R}}}_0\\ & =-\frac{2m_e{v}^2{N}_s}{ge{R}_0^2}{\mathbf{\text{R}}}_0\\ & =-\frac{m_e{N}_s}{ge{R}_0^2}{\mathbf{\text{R}}}_0{v}_{\mathrm{m}\mathrm{a}\mathrm{x}}^2(\cos 2{\omega }_{0}t+1),\end{array}$(66) where $v_{\mathrm{m}\mathrm{a}\mathrm{x}}={\omega }_0{R}_0\mathrm{\Phi }$ is the amplitude of linear velocity of the He II layer (the linear velocity of the inner bob surface). It can be seen that the transverse polarisation oscillates with the double frequency $2{\omega }_0=4\pi f_0$. The registered alternative part of the transversal potential difference $\mathrm{\Delta }U\left(t\right)=-4\pi P\left(t\right)d$ across the layer is (67) $\begin{array}{r}\mathrm{\Delta }U\left(t\right)=U_0\cos 2{\omega }_{0}t;U_0=\frac{4\pi m_e{v}_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{ge{R}_0}{N}_{s}d.\end{array}$(67) It can be seen that the alternative TEMF is a signal with double frequency $2{\omega }_0$ of the driving torque [224].

The signal of transverse electromotive force (TEMF) $\mathrm{\Delta }U$ between isolated electrode which penetrate inside the rod into cell and the external surface of the bob was registered after amplification by digital memory oscilloscope. The typical oscillogram is presented on Figure 21 where plot (a) shows the registered TEMF $\mathrm{\Delta }U$ and plot (b) is the voltage of frequency $f_0$ on the bob driver. An elementary Fourier analysis shows that the signal is the linear superposition of two components with frequencies $2{\omega }_0$ and ${\omega }_0$, (68) $\begin{array}{r}\mathrm{\Delta }U\left(t\right)=U_0(\cos 4\pi f_{0}t+0.5\sin 2\pi f_{0}t).\end{array}$(68) Just now we focus our attention on the double-frequency electromotive response of the torsion oscillations which is characteristic namely for the Barnett effect. The driving-frequency component of the registered signal will be discussed below.

Figure 21. (Colour online) (a) The typical oscillogram of the TEMF [224] in comparison with (b) driving voltage (see text).

The most pronounced feature of the observed effect is the temperature dependence of the TEMF [224]. Figure 22 presents the temperature dependence of the amplitudes $U_0$ of TEMF (see Equation 67(67) $\begin{array}{r}\mathrm{\Delta }U\left(t\right)=U_0\cos 2{\omega }_{0}t;U_0=\frac{4\pi m_e{v}_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{ge{R}_0}{N}_{s}d.\end{array}$(67) ) for three different linear velocities $v_{\mathrm{m}\mathrm{a}\mathrm{x}}$ of the ${}^4$He layer in the temperature range 1.5–2.5 K. It is evident that the registered electromotive force strongly indicates the λ-transition [44] between He I (at $T>T_{\lambda }$) and He II (at $T<T_{\lambda }$) phases. Structureless simple liquid He I demonstrates no TEMF (and, correspondingly, no Barnett effect), whereas these effects observed below λ-point suggest that He II phase is spatially ordered and spin-ordered system [30–32,240,241] (‘liquid crystal’, according to the known Shubnikov's determination [1]). The temperature dependence of the Barnett effect means that the spin–spin and spin–orbit interaction is an essential factor which controls the spin compliance relative to noninertial influence from spin–lattice coupling under external rotation. Of course, this picture can be realised only within spatially ordered atomic system where spins are not completely free rotors, but gyroscopes in frames (atomic orbitals) interacting with nearest neighbours and rotating as a whole with an external angular velocity $\mathbf{\Omega }$. In this connection we have to suggest that relation between macroscopic magnetisation $\mathbf{\text{M}}$ and $\mathbf{\Omega }$ must be proportional with coefficient of the dynamic magnetic susceptibility $\chi \left(T\right)$ (see [227,230]), (69) $\begin{array}{r}\mathbf{\text{M}}=\chi \left(T\right)\frac{\mathbf{\Omega }}{\mathrm{\Gamma }},\end{array}$(69) and this susceptibility must be evidently temperature-dependent because it controls the dynamic of revolution of the spin and orbital magnetic moments under external alternative magnetic field. This susceptibility is determined by the coupling of electronic spins with atomic orbitals involved into rotation of the sample in the torsion oscillator (whose angular velocity plays the role of an external magnetic field) and, as a result, it is the nature of the experimentally registered temperature-dependent TEMF, (70) $\begin{array}{r}{U}_0\left(T\right)=\frac{4\pi m_e{v}_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{ge{R}_0}\chi \left(T\right)N_{s}d.\end{array}$(70) Figure 22 shows the temperature dependence $U_0\left(T\right)$ for three values of the maximal linear velocity of the layer, $v_{\mathrm{m}\mathrm{a}\mathrm{x}}$. It is seen that the TEMF appears just in the point of the λ-transition, and at $T<T_{\lambda }$ the run of $U_0\left(T\right)$ is quite similar to standard dependence of susceptibility $\chi \left(T\right)$ for magnetically ordered systems [216,226] (this fact supports the Shubnikov's analogy [1] between λ-transition He I→He II and Curie point in magnetics and proves the spin-supported mechanism of interatomic interaction in the quantum He II phase [32,231,232]).

Figure 22. (Colour online) Temperature dependences of the TEMF at different driving velocities of the ${}^4$He layer [224]: full circles – $v_{\mathrm{m}\mathrm{a}\mathrm{x}}=744\mu$m/s, open triangles – $v_{\mathrm{m}\mathrm{a}\mathrm{x}}=620\mu$m/s, full triangles – $v_{\mathrm{m}\mathrm{a}\mathrm{x}}=434\mu$m/s (see text).

Table 3 presents the amplitudes of TEMF as a function of linear velocity of the ${}^4$He layer in the torsion oscillator at temperature T = 2.02 K which corresponds the maximums on the curves of Figure 23. These data allow us to verify the relation Equation (71(71) $\begin{array}{r}\chi \left(T\right)=\frac{ge{R}_0}{4\pi m_e{v}_{\mathrm{m}\mathrm{a}\mathrm{x}}^2{N}_{s}d}{U}_0\left(T\right),\end{array}$(71) ), and, as it is seen from Figure 23, the function $U_0$ vs. $v_{\mathrm{m}\mathrm{a}\mathrm{x}}^2$ demonstrates the ideal linear dependence.

Figure 23. (Colour online) Amplitude of the TEMF vs. square of layer velocity: it can be seen the ideal linear dependence [224]. Blue circles – no signal from liquid ${}^4$He (He I phase above λ-transition).

Table 3. Transversal electromotive force [224] as a function of oscillation velocity at T = 2.02 K.

Amplitude of oscillation velocity $v_{\mathrm{m}\mathrm{a}\mathrm{x}}$ (μm/s)	Transversal electromotive force (nV)
78.0	1.6
155.0	6.5
310.0	26.0
372.0	37.0
403.0	45.0
434.0	51.0
465.0	59.0
496.0	67.0
527.0	75.0
558.0	84.0
589.0	94.0
620.0	104.0
651.0	115.0
663.0	119.0
713.0	138.0
744.0	150.0

To compare the obtained experimental data with expression Equation (71(71) $\begin{array}{r}\chi \left(T\right)=\frac{ge{R}_0}{4\pi m_e{v}_{\mathrm{m}\mathrm{a}\mathrm{x}}^2{N}_{s}d}{U}_0\left(T\right),\end{array}$(71) ) we estimate the TEMF amplitude for free spins (neglecting spin–spin, spin–orbit and spin–phonon interactions), i.e. for the case $\chi \left(T\right)=1$. First of all, we estimate the number of spins within the ${}^4$He film of volume $\pi Dhd=9.42\times {10}^{-6}$ cm${}^3$. Taking into account the volume density of ${}^4$He near the λ-line [44], $\rho =0.146$ g/cm${}^3$, and ${}^4$He mass, $m_{\mathrm{H}\mathrm{e}}=3.32\times {10}^{-24}$ g, we find $N_s\sim 8.3\times {10}^{17}$ spins within the layer. Using the known values of $e/m_e$, we get for $v_{\mathrm{m}\mathrm{a}\mathrm{x}}=744\mu$m/s the TEMF amplitude $U_0\simeq 3.3\times {10}^{-7}\mathrm{C}\mathrm{G}\mathrm{S}\mathrm{E}=99\mu$V which is nearly three order higher than the experimentally observed value $U_0=150$ nV (see Table 3), and the difference between experimental results and simple estimation based on the model of free spins is naturally due to dynamic susceptibility $\chi \left(T\right)$. From Equation (71(71) $\begin{array}{r}\chi \left(T\right)=\frac{ge{R}_0}{4\pi m_e{v}_{\mathrm{m}\mathrm{a}\mathrm{x}}^2{N}_{s}d}{U}_0\left(T\right),\end{array}$(71) ) we have (71) $\begin{array}{r}\chi \left(T\right)=\frac{ge{R}_0}{4\pi m_e{v}_{\mathrm{m}\mathrm{a}\mathrm{x}}^2{N}_{s}d}{U}_0\left(T\right),\end{array}$(71) and, as a result, all three curves from Figure 22 merge together into universal dependence $\chi \left(T\right)$ as it illustrates by Figure 24. It can be seen that the obtained function $\chi \left(T\right)$ is quite similar to the standard susceptibility of typical magneto-ordered materials [216,226], and this fact supports the conclusion about spin nature of the λ-transition in ${}^4$He [31,32,231,232].

Figure 24. (Colour online) Dynamic susceptibility of the Barnett magnetisation vs. temperature (see text). Symbols on the graph correspond to those from Figure 23.

A somewhat different (but principally equivalent) way of getting the obtained results is to find rigorously the electromagnetic fields produced within the cylindric resonator (the closed bob of the torsion oscillator) under external rotation. At such an approach, we would have to solve the equation of motion for spins on the orbitals of the mutually interacting atoms coupled within the condensed ${}^4$He layer rotating with non-inertial torsion cell. This scheme allows us principally to build an exact solution of the problem: if the time evolution of the point magnetic moment ${\mathbf{\text{m}}}_i({\mathbf{\text{r}}}_i,t)$ (placed in the point ${\mathbf{\text{r}}}_i$) is known, then the magnetic induction $\mathbf{\text{B}}(\mathbf{\text{r}},t)$ as superposition of the quasi-stationary (in view of the smallness of the bob rotating frequency Ω as compared to intra-atomic frequencies) alternative fields from individual dynamic spins using the standard electrodynamic formula [41], (72) $\begin{array}{r}\mathbf{\text{B}}(\mathbf{\text{r}},t)=\sum _i\{\frac{3{\mathbf{\text{n}}}_i\left({\mathbf{\text{n}}}_i{\mathbf{\text{m}}}_i\right)-{\mathbf{\text{m}}}_i}{|\mathbf{\text{r}}-{\mathbf{\text{r}}}_i{|}^3}+4\pi {\mathbf{\text{m}}}_i\delta (\mathbf{\text{r}}-{\mathbf{\text{r}}}_i\left)\right\},\end{array}$(72) where ${\mathbf{\text{n}}}_i=(\mathbf{\text{r}}-{\mathbf{\text{r}}}_i)/|\mathbf{\text{r}}-{\mathbf{\text{r}}}_i|$ (of course, the geometry of the resonator and the boundary conditions must be taken into account). Then the law of electromagnetic induction, (73) $\begin{array}{r}[\mathrm{\nabla }\times \mathbf{\text{E}}(\mathbf{\text{r}},t\left)\right]=-\frac{1}{c}\frac{\mathrm{\partial }\mathbf{\text{B}}(\mathbf{\text{r}},t)}{\mathrm{\partial }t},\end{array}$(73) gives us the distribution of the electric field and, correspondingly, the electromotive force within the resonator interior. In reality, this problem is principally solvable, but rather cumbersome in view of necessity to operate with complicate boundary problem and (what is more important) to solve the extraordinary complicate equation of motion for spin under spin-spin and spin-orbital interaction in the non-inertial rotating system. So, despite the mentioned approach gives principally exact solution, we restrict ourselves here by the half-quantitative (but well substantiated) consideration of the problem under study with only one essential remark in conclusion. S.J. Barnett in his initial works [225] paid a special attention to the dynamic revolution of a bound magnetic moment inside the frame with several degrees of freedom within a system globally rotating with angular velocity Ω. He found that the mechanical torque acting on the magnetic moment consists of two summands: first of them proportional to Ω, and second − proportional to ${\mathrm{\Omega }}^2$. This fact means that the signal of TEMF must contain, at least, two harmonics with frequencies both $f_0$ and $2f_0$, as it can be seen from Figure 21. Thus the observed TEMF is produced by spin currents formed due to spin precession and nutations in a rotating body [233–235] and entangled spin revolutions due to spin-spin and spin-orbital coupling within non-inertial rotating system.

The experiments with ${}^4$He in torsion oscillator give direct evidences that the He II phase below λ-point is a spin-ordered structure. This is in full agreement with Shubnikov's suggestion about close analogy between λ-transition in ${}^4$He and Curie point in ferromagnets [1]. It is evident that for all electrodynamic effects and microwave response of the He II phase below λ-transition is responsible spin subsystem of ${}^4$He.

7.4. Spin–orbital splitting and Stark effect in He II

As can be seen from Table 2 the four-spin ground state on the He–He interatomic bond is quintuply degenerated, and this degeneration must be split due to spin–orbital contribution Equation (5(5) $\begin{array}{rl}& {\hat{H}}_{\mathrm{S}\mathrm{O}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0)\\ & =-i\frac{{\mathcal{Z}}_0{g}_S{\alpha }_S^2}{4}\{\sum _s{\hat{\mathit{\sigma }}}_s[\frac{{\mathbf{\text{r}}}_s}{r_s^3}\times {\mathrm{\nabla }}_s]\\ & +\sum _s{\hat{\mathit{\sigma }}}_s[\frac{{\mathbf{\text{r}}}_s-{\mathbf{\text{R}}}_0}{|{\mathbf{\text{r}}}_s-{\mathbf{\text{R}}}_0{|}^3}\times {\mathrm{\nabla }}_s]\\ & -\frac{1}{{\mathcal{Z}}_0}\sum _s{\hat{\mathit{\sigma }}}_s\sum _{s^{\mathrm{\prime }}\ne s}[\frac{{\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}}{r_{s{s}^{\mathrm{\prime }}}^3}\times ({\mathrm{\nabla }}_s-{\mathrm{\nabla }}_{s^{\mathrm{\prime }}}\left)\right]\}\end{array}$(5) ). In view of the symmetry of the problem, we can suggest that it is a partial splitting into doubly and triply degenerated sublevels, and namely triply degenerated subgroup has a lower energy and plays the role of the renormalised ground state. A further splitting can be obtained, for example, by application of an external electric field ${\mathbf{\text{E}}}_0$ which gives the additional term to the spin-orbit Hamiltonian [43], (74) $\begin{array}{rl}& {\hat{H}}_{\mathrm{S}\mathrm{O}\mathrm{E}}^{\hat{\mathit{\sigma }}}({\mathbf{\text{r}}}_a,{\mathbf{\text{r}}}_b,{\mathbf{\text{r}}}_c,{\mathbf{\text{r}}}_d|{\mathbf{\text{R}}}_0;{\mathbf{\text{E}}}_0)\\ & =-i\frac{{\mathcal{Z}}_0{g}_S{\alpha }_S^2}{4}\left\{\sum _s{\hat{\mathit{\sigma }}}_s\right[{\mathbf{\text{E}}}_0\times {\mathrm{\nabla }}_s]+\sum _s{\hat{\mathit{\sigma }}}_s\left[\frac{{\mathbf{\text{r}}}_s}{r_s^3}\times {\mathrm{\nabla }}_s\right]\\ & +\sum _s{\hat{\mathit{\sigma }}}_s[\frac{{\mathbf{\text{r}}}_s-{\mathbf{\text{R}}}_0}{|{\mathbf{\text{r}}}_s-{\mathbf{\text{R}}}_0{|}^3}\times {\mathrm{\nabla }}_s]\\ & -\frac{1}{{\mathcal{Z}}_0}\sum _s{\hat{\mathit{\sigma }}}_s\sum _{s^{\mathrm{\prime }}\ne s}[\frac{{\mathbf{\text{r}}}_{s{s}^{\mathrm{\prime }}}}{r_{s{s}^{\mathrm{\prime }}}^3}\times ({\mathrm{\nabla }}_s-{\mathrm{\nabla }}_{s^{\mathrm{\prime }}}\left)\right]\},\end{array}$(74) and the triply degenerated ground state transforms into a central peak with two ‘wings’ shifted symmetrically relative the central maximum on the distances proportional to the magnitude of the external electric field $E_0$ (linear Stark effect). This conclusion is in the complete agreement with the direct experimental observations of Rybalko [236] (Table 4).

Table 4. Spin states within ${}^4$He–${}^4$He bond at antiferromagnetic exchange.

State	Energy, ${\mathcal{E}}_i^{\left(s\right)}/\left|J\right|$	Parity	Degeneration
1	−6	even	2
2	$-2$	odd	9
3	6	even	5

7.5. Microwave response of He II – the second Rybalko effect

Using dielectric disc resonator (DDR) technique, within 2007–2019, Rybalko discovered experimentally (see the series of works [219,236–241]) the effect of microwave resonant absorption in He II. Recently, the corresponding phenomena were interpreted within a framework of possibly response from He II phase as spin-ordered system [231,232]. The microwave adsorption in a dielectric medium implies that there exist low energy excitations (with energy of a few K) under the ground state of helium condensed phase. In a common sense, the microwave absorption is some standard phenomenon in molecular systems [242] (including such a popular matter as simple water [243]) where external electromagnetic field activates rotational and vibrational modes with corresponding low-energy eigenstates. Condensed phases of helium possess neither vibrational nor rotational intra-atomic modes, so that we have to find the necessary objects among the really existing helium degrees of freedom (electrons, spins, phonons). It is evident that in dielectric medium with small polarisability the only way for interaction with an external electromagnetic field are excitations in the spin subsystem which in fact is the only basis of the electromagnetic activity of the He II phase. The resonant character of microwave absorption follows immediately from the discrete character of the spectrum for the spin subsystem (see Section 3) of the He II phase.

Figure 25(a) illustrates the He II in DDR response for two temperatures, 1.4 and 2.1 K. It is characterised by transmission coefficient $\delta ={\delta }_b+(A_v-A_l)/A_v,$ where $A_v$ is the amplitude of the signal in empty cell, $A_l$ is the response from helium-loaded cell, and ${\delta }_b$ is the background contribution caused by intrinsic response of the measuring system. It is evident that $\delta >{\delta }_b$ (or $A_v>A_l$) means dielectric loses in the helium bath, but $\delta <{\delta }_b$ (and $A_v<A_l$) corresponds to amplification of the input signal. In the absence of flow within the measuring cell, the system demonstrates a sharp resonant absorption peak whose position on the frequency axis is temperature-dependent. Figure 25(b) shows the presence of the extremely narrow absorption line at 180.3 GHz over the relatively ‘wide’ intrinsic resonant curve of the DDR. This experiment testifies to the fact that the adsorption line has a strong atomic nature, but its manifestation depends principally on the physical state of the condensed phase where the atoms are connected through interatomic interactions. Thus the interatomic interaction should be a principal point of investigation for the problem under study.

Figure 25. (Colour online) (a) Frequency dependence of the signal amplitude retrieved from the DDR within superfluid ${}^4$He ($A_v$ is amplitude in vacuum, and $A_l$ is the signal amplitude from the resonator coupled with surrounding liquid) at two temperatures below λ-point without thermal flow [237]. (b) Response near the resonant absorption line at 180.3 GHz [219,236–238]. The frequency sampling is 2.5 kHz [236].

Figure 26(a) demonstrates the frequency positions of the absorption line as a function of temperature (black circles, see also Refs. [236,237]) in comparison with corresponding neutron diffractometry data extracted from two literature sources [244,245]. It can be seen a good agreement between the two dependences which is a direct evidence of atomic origin of the microwave absorption in the He II phase. Figure 26(b) shows the same (as on Figure 26a) temperature dependence of the absorption line position (black circles) relative to the averaged frequency response of the loaded resonator [236].

Figure 26. (Colour online) Temperature dependence of the absorption line position: comparison between our experiment and neutron data on roton gap [244,245]. (b) Temperature dependence of the absorption line position relative to the averaged frequency response (amplitude envelope) of the loaded resonator. The length of each vertical line is proportional to the width of the effective resonant curve on the level 0.707 ($-3$ dB).

The main features of the phenomenon can be summarised as follows [231,232]:

1. the position of the narrow absorption line corresponds exactly to the standard value [246,247] of the ‘roton’ gap Δ ($\mathrm{\Delta }/k_B=8.64\mathrm{K}\left[247\right]=179.36$ GHz);

2. the microwave adsorption can be detected definitely only within He II phase below λ-point (above λ-point only weak response can be detected, the absorption curve ‘spreads’ as the temperature approaches $T_{\lambda }$, and at $T>T_{\lambda }$ the absorption becomes insufficient);

3. when the temperature increases, the adsorption peak shifts to lower frequencies as it can be seen from Figures 25(a) and 26(a), so that we observe a macroscopically cooperative effect caused by interatomic interactions and destroyed by density fluctuations within condensed helium phase, and this observed behaviour is in good agreement with standard temperature dependence of the ‘roton’ gap [246];

4. the observed microwave response can be interpreted by the contribution from the spin subsystem of He II phase.

7.6. Brief summary of Section sec7

The experimentally observed microwave response of the He II phase can be clarified only through effect of the spin subsystem because namely the spin degrees of freedom can be responsible for the processes with energies of a few Kelvins, and simultaneously are able to interact effectively with an external electromagnetic field of the microwave diapason. Just the spin subsystem is responsible for electromagnetic activity of such as He II phase macroscopically electro-neutral dielectric medium with extremely low palarisability. Moreover, the regular spin-possessed microwave response is possible only at the presence of spin ordering, but spins are intrinsic property of electrons collectivised and distributed within He II valence bond [248,249]. Electrons are confined in atomic shells, so that the He II phase as an atomic system must be spatially ordered. Certainly, various effects of spin–orbit coupling are possible [250]. It is the nature of the λ-transition which was rightly compared by Shubnikov [1] with Curie transition in ferromagnets. Spin subsystem plays the paramount role for atom-atom interaction in helium, and in this connection the He II phase can be characterised undoubtedly as an evident spin ice.

8. Conclusions

The first thought comes from God, and the initial Shubnicov's idea about He II as a liquid crystal [1] seems to be the most adequate and the simplest concept to unite all the observable properties of the He II phase within a physically distinct model of the spatially ordered macroscopic system. The real background of the quantum nature for both ${}^3$He and ${}^4$He is the governing role of their spin subsystems in specific features of their observable physical properties. The above consideration makes us possible to conclude that the He II phase is a spatially ordered (and, in view of principal role of its spin subsystem, spin-ordered, just like as superconductors) atomic system in accordance with the primary suggestion of L.V. Shubnikov [1]. Shubnikov quite exactly predicted the real physical essence of the He II phase which inevitably cannot be a simple liquid and must include the spatial ordering that in Shubnikov terms was called ‘liquid crystal’ that is partially ordered (or partially disordered, it does not matter) crystal lattice. For many years researchers directed much efforts toward producing models (like ‘superfluid’ or ‘supersolid’) for explanation the observable properties of the He II phase.

At present we have a great number of experimental facts and a lot of theoretical propositions about the ${}^3$He and ${}^4$He properties, and the main problem is to put together all the pieces of the puzzle into unitary coherent physical concept. Now, it is just a moment to sink into giant material accumulated during 100 years and make some consistent conclusions for one of the most actual topics of the modern physics. It means, among them, that on this way we can outline the principles for further progress of investigations in the problems under study.

Disclosure statement

No potential conflict of interest was reported by the author.