Polarisabilities of iterated stockholder atoms

Abstract

Polarisabilities of atoms within molecules can be calculated from molecular electron densities using the density partitioning method known as Iterated Stockholder Atoms (ISA). Non-local polarisation effects are removed by optimising the ISA functional for the perturbed electron density, with the additional constraint that the atomic charges do not change. The resulting atomic polarisabilities are chemically reasonable, tend to become smaller as the atomic charge becomes more positive, and are approximately transferable between atoms in similar chemical environments. The methodology can be extended to calculate local higher-rank polarisabilities and dispersion energy coefficients.

GRAPHICAL ABSTRACT

Keywords:

• Polarisability
• atoms in molecules
• iterated stockholder atoms

1. Introduction

1.1. Background

Polarisabilities of atoms within molecules are not measurable properties, but they are important in a range of applications, including force field development [1,2], calculation of dispersion forces [3] and prediction of material properties such as Raman spectra [4].

Although molecular polarisabilities can be computed straightforwardly using quantum chemistry, calculating the separate atomic polarisabilities from first principles is a much more difficult task. Polarisation in a molecule is non local, because electron density flows between atoms when an external field is applied, but local polarisability models are preferable in applications (unless the system is an electrical conductor), since local models are generally less awkward to use and more transferable between similar atoms.

An ideal local model should be faithful, in that the atomic polarisabilities should sum to the correct molecular values, and it should also be chemically reasonable, with smaller/similar/larger atoms having smaller/similar/larger polarisabilities. It is also desirable that the polarisabilities in the model can be calculated from first principles with reasonable effort and with minimal assumptions.

Previous calculations of atomic polarisabilities have used several different approaches: two of the most successful are briefly described here. Fitting methods [5–7] use a dataset containing responses of molecules to applied electric fields and deduce the atomic polarisabilities that give the best fit to the data. The data can include molecular polarisabilities, and/or the response of the molecular electrostatic potential to perturbations, calculated at a grid of points well away from the molecule. Distributed polarisability calculations [8–13], which are more closely related to the current work, require at least a definition of atomic charges and dipoles. The response of these atomic multipoles to an applied field is calculated from first principles and is always found to include non-local charge flow, so it is necessary to make adjustments to produce a local model.

The method introduced in this work is similar to distributed polarisabilities, but the non-locality is removed as part of the first-principles calculation, not as a separate step. To achieve this, atomic charges and dipoles are defined using the Iterated Stockholder Atoms (ISA) theory [14,15], which has two main features that make it suitable for calculating local atomic properties. First, ISA are chemically reasonable, being approximately spherical, while still reproducing the overall molecular electron density, and they have shapes and charges in reasonable accord with chemical expectations, which suggests that their polarisabilities may also have chemically reasonable values. Second, ISA is defined by minimising a functional of electron density, and this minimisation can be constrained to avoid non-local effects, without introducing any further assumptions, data or approximations. The theory of ISA is briefly reviewed next, then the methodology required to calculate their polarisability is introduced, and some preliminary results are presented and discussed.

1.2. Theory

In the absence of an external field, the electron densities of iterated stockholder atoms ${\rho }_{\mathrm{A}}^{(0)}$ are defined for each atom A as a fraction of the total electron density ${\rho }^{(0)}$, using the spherically symmetrical weighting functions $W_{\mathrm{A}}^{(0)}$, where $W^{(0)}=\sum _{\mathrm{A}}{W}_{\mathrm{A}}^{(0)}$ (1) ${\rho }_{\mathrm{A}}^{(0)}=W_{\mathrm{A}}^{(0)}{\rho }^{(0)}/W^{(0)}$(1) and the weighting functions are the spherical averages of the electron densities around the centres (nuclei) of their own atoms, shown by angle brackets: (2) $W_{\mathrm{A}}^{(0)}={⟨{\rho }_{\mathrm{A}}^{(0)}⟩}_{\mathrm{A}}$(2) which implies that for all spherical shells around all nuclei, (3) ${⟨{\rho }^{(0)}/W^{(0)}⟩}_{\mathrm{A}}=1$(3) This is equivalent to minimising the functional (4) $\int W-\rho \ln (W)\mathrm{d}\mathbf{\text{r}}$(4) without an external field, subject to the condition that W is a sum of spherically symmetrical atomic contributions.

When an infinitesimal external field is applied to the molecule, the electron density changes by ${\rho }^{(1)}$, and the corresponding first-order changes in the ISA and weighting functions are given by solving (5) ${⟨-{\rho }^{(1)}/W^{(0)}+{\rho }^{(0)}{W}^{(1)}/[W^{(0)}{]}^2⟩}_{\mathrm{A}}=0$(5) for all spherical shells around all atoms, where $W^{(1)}$ is a sum of spherically symmetrical atomic contributions $W_{\mathrm{A}}^{(1)}$. However, this atomic partitioning of the polarised molecular electron density allows charge to flow between the atoms when a field is applied. To prevent the charge flow, the functional (4(4) $\int W-\rho \ln (W)\mathrm{d}\mathbf{\text{r}}$(4) ) is minimised to first order in the field, and undetermined multipliers ${\lambda }_{\mathrm{A}}$ are used to constrain the change in charge on each atom A to be zero. The change in atomic charge density ${\rho }_{\mathrm{A}}^{(1)}$ is defined analogously to (1(1) ${\rho }_{\mathrm{A}}^{(0)}=W_{\mathrm{A}}^{(0)}{\rho }^{(0)}/W^{(0)}$(1) ), and the corresponding constraints are (6) $\begin{array}{rl}\int {\rho }_{\mathrm{A}}^{(1)}\mathrm{d}\mathbf{\text{r}}& =\int \frac{W_{\mathrm{A}}^{(1)}{\rho }^{(0)}}{W^{(0)}}+\frac{W_{\mathrm{A}}^{(0)}{\rho }^{(1)}}{W^{(0)}}\\ & -\frac{W_{\mathrm{A}}^{(0)}{\rho }^{(0)}{W}^{(1)}}{[W^{(0)}{]}^2}\mathrm{d}\mathbf{\text{r}}=0\end{array}$(6) Introducing the undetermined multipliers changes (5(5) ${⟨-{\rho }^{(1)}/W^{(0)}+{\rho }^{(0)}{W}^{(1)}/[W^{(0)}{]}^2⟩}_{\mathrm{A}}=0$(5) ) to (7) $\begin{array}{rl}& {⟨-\frac{{\rho }^{(1)}}{W^{(0)}}+\frac{{\rho }^{(0)}{W}^{(1)}}{[W^{(0)}{]}^2}+{\lambda }_{\mathrm{A}}\frac{{\rho }^{(0)}}{W^{(0)}}-\sum _{\mathrm{B}}{\lambda }_{\mathrm{B}}\frac{W_{\mathrm{B}}^{(0)}{\rho }^{(0)}}{[W^{(0)}{]}^2}⟩}_{\mathrm{A}}\\ & =0\end{array}$(7) Equations (6(6) $\begin{array}{rl}\int {\rho }_{\mathrm{A}}^{(1)}\mathrm{d}\mathbf{\text{r}}& =\int \frac{W_{\mathrm{A}}^{(1)}{\rho }^{(0)}}{W^{(0)}}+\frac{W_{\mathrm{A}}^{(0)}{\rho }^{(1)}}{W^{(0)}}\\ & -\frac{W_{\mathrm{A}}^{(0)}{\rho }^{(0)}{W}^{(1)}}{[W^{(0)}{]}^2}\mathrm{d}\mathbf{\text{r}}=0\end{array}$(6) ) and (7(7) $\begin{array}{rl}& {⟨-\frac{{\rho }^{(1)}}{W^{(0)}}+\frac{{\rho }^{(0)}{W}^{(1)}}{[W^{(0)}{]}^2}+{\lambda }_{\mathrm{A}}\frac{{\rho }^{(0)}}{W^{(0)}}-\sum _{\mathrm{B}}{\lambda }_{\mathrm{B}}\frac{W_{\mathrm{B}}^{(0)}{\rho }^{(0)}}{[W^{(0)}{]}^2}⟩}_{\mathrm{A}}\\ & =0\end{array}$(7) ) define the perturbed ISA. They are solved to obtain $W^{(1)}$ and therefore ${\rho }_{\mathrm{A}}^{(1)}$, using the perturbed density ${\rho }^{(1)}$ arising from each applied field (x, y and z) in turn. The change in dipole of each atom A, and hence the atomic polarisability, is calculated by integrating ${\rho }_{\mathrm{A}}^{(1)}\mathbf{r}$.

In practice, the equations are solved by first solving (5(5) ${⟨-{\rho }^{(1)}/W^{(0)}+{\rho }^{(0)}{W}^{(1)}/[W^{(0)}{]}^2⟩}_{\mathrm{A}}=0$(5) ) to obtain $W^{(1)}[\lambda =0]$, the change in ISA weighting function in the absence of constraints. The required $W^{(1)}$, including constraints, is then expanded as (8) $W^{(1)}=W^{(1)}[\lambda =0]+\sum _{\mathrm{B}}{\lambda }_{\mathrm{B}}W[\mathrm{B}]$(8) Substituting this into (7(7) $\begin{array}{rl}& {⟨-\frac{{\rho }^{(1)}}{W^{(0)}}+\frac{{\rho }^{(0)}{W}^{(1)}}{[W^{(0)}{]}^2}+{\lambda }_{\mathrm{A}}\frac{{\rho }^{(0)}}{W^{(0)}}-\sum _{\mathrm{B}}{\lambda }_{\mathrm{B}}\frac{W_{\mathrm{B}}^{(0)}{\rho }^{(0)}}{[W^{(0)}{]}^2}⟩}_{\mathrm{A}}\\ & =0\end{array}$(7) ) eliminates the terms not involving λ, and equating the terms in ${\lambda }_{\mathrm{B}}$ gives (9) ${⟨\frac{{\rho }^{(0)}W[\mathrm{B}]}{[W^{(0)}{]}^2}+{\delta }_{\mathrm{A}\mathrm{B}}\frac{{\rho }^{(0)}}{W^{(0)}}-\frac{W_{\mathrm{B}}^{(0)}{\rho }^{(0)}}{[W^{(0)}{]}^2}⟩}_{\mathrm{A}}=0$(9) which is independent of the applied field and can be solved for each atom B separately to give the corresponding modification of the weighting function, $W[\mathrm{B}]$. Both (5(5) ${⟨-{\rho }^{(1)}/W^{(0)}+{\rho }^{(0)}{W}^{(1)}/[W^{(0)}{]}^2⟩}_{\mathrm{A}}=0$(5) ) and (9(9) ${⟨\frac{{\rho }^{(0)}W[\mathrm{B}]}{[W^{(0)}{]}^2}+{\delta }_{\mathrm{A}\mathrm{B}}\frac{{\rho }^{(0)}}{W^{(0)}}-\frac{W_{\mathrm{B}}^{(0)}{\rho }^{(0)}}{[W^{(0)}{]}^2}⟩}_{\mathrm{A}}=0$(9) ) are linear in the unknown W functions, which mean that they can be solved much more easily than the unperturbed ISA equations.

Finally, substituting (8(8) $W^{(1)}=W^{(1)}[\lambda =0]+\sum _{\mathrm{B}}{\lambda }_{\mathrm{B}}W[\mathrm{B}]$(8) ) into (6(6) $\begin{array}{rl}\int {\rho }_{\mathrm{A}}^{(1)}\mathrm{d}\mathbf{\text{r}}& =\int \frac{W_{\mathrm{A}}^{(1)}{\rho }^{(0)}}{W^{(0)}}+\frac{W_{\mathrm{A}}^{(0)}{\rho }^{(1)}}{W^{(0)}}\\ & -\frac{W_{\mathrm{A}}^{(0)}{\rho }^{(0)}{W}^{(1)}}{[W^{(0)}{]}^2}\mathrm{d}\mathbf{\text{r}}=0\end{array}$(6) ) and cancelling two terms using (5(5) ${⟨-{\rho }^{(1)}/W^{(0)}+{\rho }^{(0)}{W}^{(1)}/[W^{(0)}{]}^2⟩}_{\mathrm{A}}=0$(5) ) gives (10) $\begin{array}{rl}& \int \frac{W_{\mathrm{A}}^{(1)}[\lambda =0]{\rho }^{(0)}}{W^{(0)}}\mathrm{d}\mathbf{\text{r}}+\sum _{\mathrm{B}}{\lambda }_{\mathrm{B}}\int \frac{W_{\mathrm{A}}^{(1)}[\mathrm{B}]{\rho }^{(0)}}{W^{(0)}}\mathrm{d}\mathbf{\text{r}}\\ & -\sum _{\mathrm{B}}{\lambda }_{\mathrm{B}}\int \frac{W_{\mathrm{A}}^{(0)}{\rho }^{(0)}W[\mathrm{B}]}{[W^{(0)}{]}^2}\mathrm{d}\mathbf{\text{r}}=0\end{array}$(10) which is a matrix equation whose solution gives the multipliers ${\lambda }_{\mathrm{B}}$, and hence $W^{(1)}$ via (8(8) $W^{(1)}=W^{(1)}[\lambda =0]+\sum _{\mathrm{B}}{\lambda }_{\mathrm{B}}W[\mathrm{B}]$(8) ).

It is interesting to consider the equation that is obtained when (9(9) ${⟨\frac{{\rho }^{(0)}W[\mathrm{B}]}{[W^{(0)}{]}^2}+{\delta }_{\mathrm{A}\mathrm{B}}\frac{{\rho }^{(0)}}{W^{(0)}}-\frac{W_{\mathrm{B}}^{(0)}{\rho }^{(0)}}{[W^{(0)}{]}^2}⟩}_{\mathrm{A}}=0$(9) ) is multiplied by $W_{\mathrm{A}}^{(0)}$ (with A and B being different atoms) and integrated. (11) $\int \frac{W_{\mathrm{A}}^{(0)}{\rho }^{(0)}W[\mathrm{B}]}{[W^{(0)}{]}^2}\mathrm{d}\mathbf{\text{r}}=\int \frac{W_A^{(0)}{W}_{\mathrm{B}}^{(0)}{\rho }^{(0)}}{[W^{(0)}{]}^2}\mathrm{d}\mathbf{\text{r}}$(11) Qualitatively, the left-hand side of this equation is related to the amount of electron density on B that is redistributed to A to reinstate the unperturbed atomic charge of B, and the right-hand side is proportional to the ISA covalence of the A-B bond discussed by Wheatley and Gopal [16]. This algorithm therefore redistributes electron density preferentially through covalent bonds, especially those with higher bond order, and is conceptually similar to (but with fewer assumptions than) the charge redistribution method of Lillestolen and Wheatley [17].

2. Methods and results

A set of 43 molecules containing H, C, N, O, F, S, Cl and Br atoms is investigated. The geometry of each molecule is first optimised using the PBE density functional with a 6−31+G* basis set. The Q-Chem program [18] is used for the optimisations. The charge density, charge density response and ISA polarisability are then calculated at the Coupled Hartree–Fock level with an aug-cc-pVDZ basis set. These calculations use a program written in Nottingham. The theory of ISA polarisability is not restricted to CHF and can be applied to any calculated charge density response functions. The computational effort for the ISA and polarisability calculations, starting from the calculated responses, is independent of quantum-chemical methodology, and is generally an insignificant part of the total. ISA calculations are carried out on a grid containing approximately 180,000 points per atom, which is estimated to give a numerical uncertainty of $\approx 2\mathrm{\%}$ in the polarisabilities. No numerical problems are encountered in applying the methodology described in Section 1.2, for any of the molecules considered. Molecular geometries, ISA charges and average polarisabilities are deposited as supplementary material.

It is hypothesised that atomic polarisabilities should tend to decrease with increasing atomic charge. Atomic charges are commonly used in molecular modelling, and demonstrating a simple relationship between charge and polarisability would make the latter easier to model. The data are therefore presented as plots of average ISA polarisability versus ISA charge.

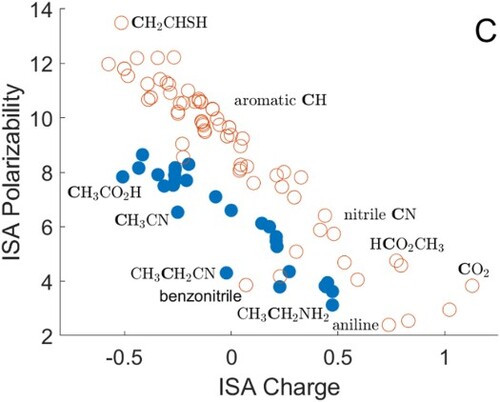
Results for carbon atoms are shown in Figure 1. The data are divided into two sets: sp and sp${}^2$ carbon atoms (open circles) tend to have higher polarisabilities than sp${}^3$ atoms (filled circles). The expected reduction of polarisability with charge is apparent, over a wide range of calculated charges and polarisabilities. The sp and sp${}^2$ atoms include carbon–carbon double bonds (top left), then a cluster of data points denoting aromatic carbons, followed by the CO molecule, nitriles, and other substituted carbon atoms. Carbon–oxygen double bonds appear at the bottom right. The most noticeable outlier from the trend is the substituted C atom in the benzonitrile ring, which has a much lower polarisability than might be expected from its charge.

Figure 1. ISA charges and polarisabilities for carbon atoms, with selected atoms shown in bold type. The substituted carbon ring atom is labelled for benzonitrile and aniline. Atoms with four covalently bonded neighbours are shown as filled circles, and other atoms as open circles. All quantities are in atomic units.

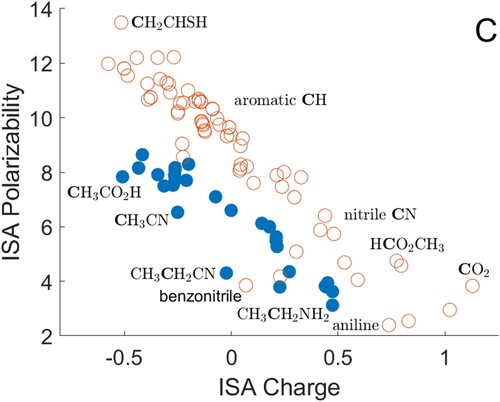
The sp${}^3$ carbon atoms show a similar decreasing trend, with carbon atoms in CH${}_3$ groups (bonded to C or H) having more negative charges and higher polarisabilities, and CH${}_2$ groups appearing at higher charge and lower polarisability. Again, a nitrile molecule (CH${}_3$CH${}_2$CN) is an outlier, with the central carbon having a lower polarisability than expected; this is also true to a lesser extent of the carbon atom adjacent to the CN group in CH${}_3$CN.

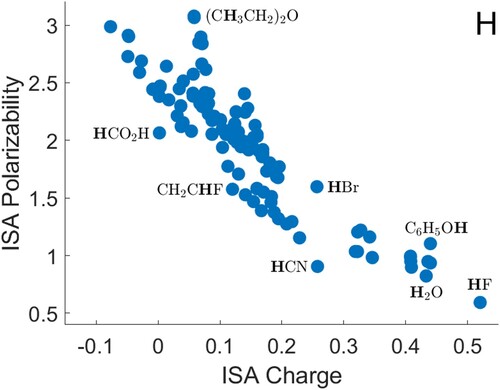
Polarisabilities of hydrogen atoms are shown in Figure 2. There is a large cluster of data towards the top left, which includes hydrogen atoms in sp${}^3$ CH${}_2$ groups, in CH${}_3$ groups, adjacent to carbon–oxygen double bonds, in aromatic molecules, and in S–H groups. There is a smaller cluster below this, around 0.16 charge and 1.4 polarisability, which consists entirely of hydrogen atoms adjacent to carbon-carbon double bonds. As observed for carbon atoms, a hydrogen atom attached to CN (in HCN) has a polarisability that is below the general trend. The remaining data, for atoms with higher charges, are generally consistent with a decreasing trend. This includes HBr, HCl, NH${}_3$, H${}_2$O and HF, and other molecules with N–H and O–H groups.

Figure 2. ISA charges and polarisabilities for hydrogen atoms, with selected atoms shown in bold type. All quantities are in atomic units.

There are fewer instances of other atoms in the data, and any trends are less clear. Data for nitrogen are presented in Figure 3. There are two separate sets of points. The sp${}^3$ atoms (filled circles), which are generally in NH${}_2$ groups, mostly have a more negative charge than N atoms in CN groups and aromatic rings (open circles). Despite the difference in charge, N atoms in the two groups have roughly similar polarisabilities. The hydride NH${}_3$ appears to be an outlier from the trend for sp${}^3$ atoms. Data for oxygen are shown in Figure 4. Here there is a decreasing trend for oxygen atoms in carbon–oxygen double bonds and the CO molecule (open circles). For other O atoms (filled circles), the two oxygen atoms in aromatic molecules give an O polarisability above this trend, whereas other O–H (left) and O–C (right) oxygen atoms generally lie below it. 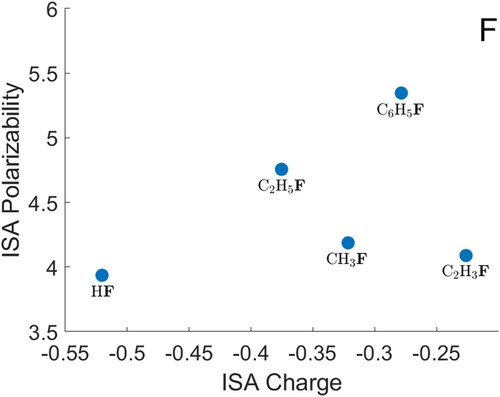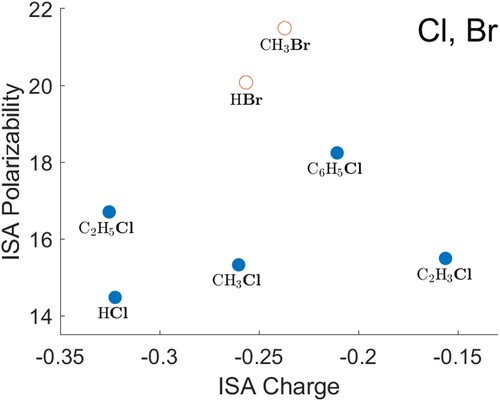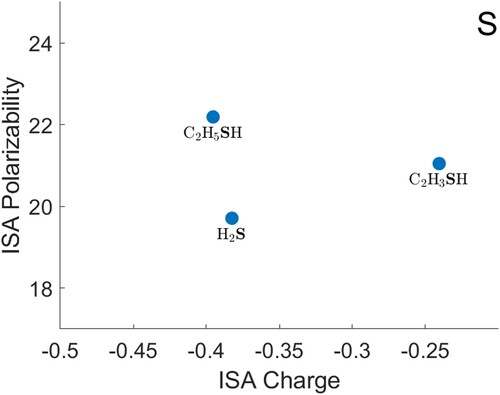As suggested for nitrogen, the hydride (H${}_2$O) gives a noticeably smaller polarisability for the heavy atom than the trend would suggest. Data for S are shown in Figure 5, F in Figure 6, Cl and Br in Figure 7. The polarisabilities of these atoms are qualitatively reasonable, when compared with each other and with H, C, N and O. The hydrides (H${}_2$S, HF, HCl and HBr) again give heavy-atom polarisabilities that are below any provisional decreasing trend in the other data. For both F and Cl, the atomic polarisability appears to be higher when the atom is bonded to an sp${}^2$ C atom, compared to an sp${}^3$ C atom.

Figure 3. ISA charges and polarisabilities for nitrogen atoms, with selected atoms shown in bold type. Atoms with three covalently bonded neighbours are shown as filled circles, and other atoms as open circles. All quantities are in atomic units.

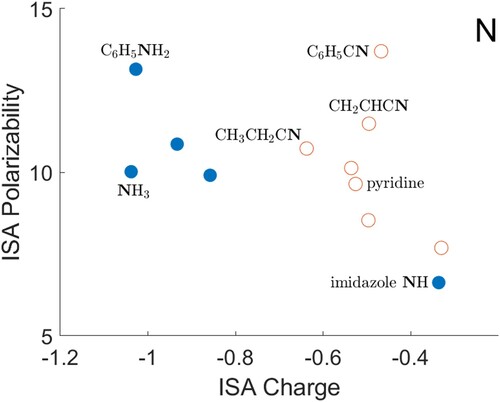
Figure 4. ISA charges and polarisabilities for oxygen atoms, with selected atoms shown in bold type. Atoms with two covalently bonded neighbours are shown as filled circles, and other atoms as open circles. All quantities are in atomic units.

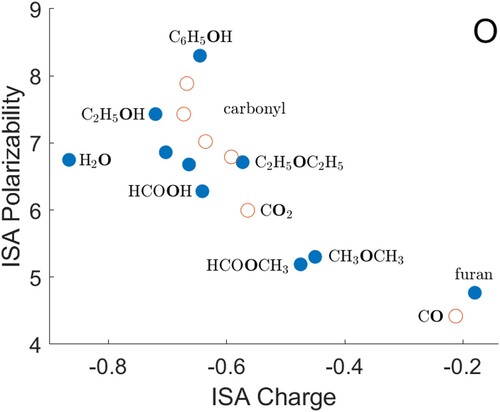
Figure 5. ISA charges and polarisabilities for sulphur atoms, shown in bold type. All quantities are in atomic units.

Figure 6. ISA charges and polarisabilities for fluorine atoms, shown in bold type. All quantities are in atomic units.

Figure 7. ISA charges and polarisabilities for atoms of chlorine (filled circles) and bromine (open circles). All quantities are in atomic units.

3. Discussion

Based on this preliminary study, the adoption of ISA polarisabilities in molecular modelling is recommended. The polarisabilities are chemically reasonable and comparable to existing datasets [7,19], and they are straightforward to calculate, using any method that produces density matrix derivatives. Unlike existing methodology, the theory presented here makes no assumptions, beyond imposing the locality constraint, and requires no supplementary data or calculations. For H and C atoms, where most data are available, there is a clear correlation between charge and polarisability, and polarisabilities are transferable between atoms in similar chemical environments. This will be essential in modelling large and/or flexible molecules where the polarisabilities cannot be calculated directly. The calculations have been carried out at a low level of theory, and obtaining more accurate results will be important for applications. However, the results presented here are expected to be semi-quantitative, and it is unlikely that any significant change in the observed trends will emerge from increasing the accuracy.

The analysis has concentrated on average polarisabilities, but the calculations give the full polarisability tensor, and can be extended to give quadrupole and higher polarisabilities if required. Furthermore, the theory is not restricted to static polarisabilities. The frequency-dependent response of a molecule can be separated into local contributions in exactly the same way, to give frequency-dependent atomic polarisabilities and atom–atom dispersion energy coefficients, which are essential in modelling intermolecular forces and performing molecular simulations.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by The University of Nottingham.