Using Ensemble-Based Methods for Directly Estimating Causal Effects: An Investigation of Tree-Based G-Computation

Abstract

Researchers are increasingly using observational or nonrandomized data to estimate causal treatment effects. Essential to the production of high-quality evidence is the ability to reduce or minimize the confounding that frequently occurs in observational studies. When using the potential outcome framework to define causal treatment effects, one requires the potential outcome under each possible treatment. However, only the outcome under the actual treatment received is observed, whereas the potential outcomes under the other treatments are considered missing data. Some authors have proposed that parametric regression models be used to estimate potential outcomes. In this study, we examined the use of ensemble-based methods (bagged regression trees, random forests, and boosted regression trees) to directly estimate average treatment effects by imputing potential outcomes. We used an extensive series of Monte Carlo simulations to estimate bias, variance, and mean squared error of treatment effects estimated using different ensemble methods. For comparative purposes, we compared the performance of these methods with inverse probability of treatment weighting using the propensity score when logistic regression or ensemble methods were used to estimate the propensity score. Using boosted regression trees of depth 3 or 4 to impute potential outcomes tended to result in estimates with bias equivalent to that of the best performing methods. Using an empirical case study, we compared inferences on the effect of in-hospital smoking cessation counseling on subsequent mortality in patients hospitalized with an acute myocardial infarction.

Introduction

There is an increasing interest in estimating causal treatment effects using observational or nonrandomized data. In observational studies, the baseline characteristics of treated or exposed subjects often differ systematically from those of untreated or unexposed subjects. Essential to the production of high-quality evidence to inform clinical and policy decisions is the ability to minimize the effect of confounding. A wide variety of methods have been proposed to minimize confounding or treatment-selection bias when estimating the effects of treatments, exposures, and interventions when using observational data. These include propensity score methods, instrumental variable analysis, and regression-based approaches.

When comparing the effects of treatments or exposures, the potential outcomes framework allows one to formally define causal treatment effects (Rubin, 1974, 2008). We briefly describe this framework in the setting in which one active or experimental treatment is compared with one control or null treatment. The two potential outcomes, Y(1) and Y(0), are the outcomes under the active and control treatments, respectively. Let Z be an indicator variable denoting the actual treatment received: Z = 1 denoting receipt of the active treatment and Z = 0 denoting receipt of the control treatment. For an individual subject, the effect of treatment is defined as Y(1) – Y(0). Three different average causal treatment effects have been proposed: the average treatment effect (ATE), the average treatment effect in the treated (ATT), and the average treatment effect in the controls (ATC). These are defined as: ATE = E[Y(1) – Y(0)], ATT = E[Y(1) – Y(0) | Z = 1], and ATC = E[Y(1) – Y(0) | Z = 0], respectively. Of these three effects, the ATE and the ATT are likely of greater interest for clinical and policy decision making. Although a distinction has been made between sample and population estimates of the different average treatment effects (Imbens, 2004), this distinction is not made in this article. Two necessary assumptions in this causal effects framework are the stable unit treatment value assumption (SUTVA) and the assumption that treatment assignment is strongly ignorable (Rubin, 2008). The first of these assumes that the potential outcomes for a given subject are affected only by the treatment that subject receives and are not influenced by the treatment received by other subjects. The second assumption is that Pr(Z|X,Y(1),Y(0)) = Pr(Z|X) and that 0 < Pr(Z = 1|X, Y(0), Y(1)) < 1 (here X denotes a vector of baseline covariates). In other words, treatment assignment, conditional on baseline covariates, is independent of the potential outcomes, and each subject has a nonzero probability of receiving either treatment.

In practice, only one of the two potential outcomes is observed: the outcome under the actual treatment received. Two regression-based approaches have been proposed to estimate potential outcomes. The first is G-computation, in which a multivariable regression model is used to regress the outcome on treatment status and baseline covariates (Snowden, Rose, & Mortimer, 2011). Using the fitted regression model, the predicted outcome is estimated for each subject as if that subject had been untreated. Then, the predicted outcome is estimated for each subject as if that subject had been treated. Thus, for each subject, the two potential outcomes can be estimated directly from the single multivariable regression model. For a given subject, the effect of treatment can be estimated as the difference between the two imputed potential outcomes. Finally, average treatment effect of interest can be estimated by averaging the subject-specific treatment effects over the entire sample (ATE), over the treated subjects (ATT), or over the untreated subjects (ATC). The second approach was proposed by Imbens (2004). Let m ₀(X) and m ₁(X) denote regression models fit in untreated and treated subjects, respectively. Each model relates the outcome to measured baseline covariates. The regression model m ₀(X) can be applied to each treated and untreated subject to predict his or her outcome had he or she been untreated. Similarly, m ₁(X) can be applied to each treated and untreated subject to predict his or her outcome had he or she been treated. Thus, for each subject, the two potential outcomes can be estimated: ₀(X _i ) and ₁(X _i ). As with G-computation, the subject-specific treatment effect can be averaged over the appropriate set of subjects to estimate the ATE, the ATT, or the ATC.

An advantage to the latter approach described earlier is that the two regression models, m ₀(X) and m ₁(X), use only baseline covariates as predictors and do not contain any variables denoting treatment status. In contrast, the first approach requires that an indicator variable denoting treatment received must be included in the regression model m(X, Z). When using conventional parametric regression models, the analyst can dictate the functional form of the regression model. However, the first approach would not be possible with a prediction method such as regression trees because the fitted regression tree may not use the treatment selection indicator. However, the second approach could easily use such methods for the regression models fit separately to untreated and treated subjects.

Regression trees frequently have been used in the medical literature. However, they often have been found to have inferior predictive ability compared with conventional regression methods (Austin, 2007; Austin, Tu, & Lee, 2010). Ensemble-based methods in which predictions are averaged across a set of regression trees have been developed in the data mining and machine learning literature. These included bootstrap aggregation (or bagging) of regression trees, random forests, and boosted regression trees. Although these methods have been developed for predicting outcomes, their utility for estimating causal treatment effects has not been well studied.

The objective of this study was to examine the utility of ensemble-based methods for estimating causal treatment effects. Our focus was on boosted regression trees, random forests, and bagged regression trees. This objective was addressed in two different ways. First, we used an extensive series of Monte Carlo simulations to compare the relative ability of different methods to estimate average treatment effects. Second, we compared estimates of the effect of in-hospital smoking cessation counseling on mortality in a sample of patients hospitalized with an acute myocardial infarction that were obtained using these ensemble-based methods. The article is structured as follows: In the first section we briefly describe the different regression methods that we consider. In the subsequent section, we describe an extensive series of Monte Carlo simulations that were used to compare the performance of these methods for estimating average treatment effects. We then present the results of an empirical case study in which we illustrate the application of each method. In the final section we summarize our findings and discuss them in the context of the existing literature.

REVIEW OF ENSEMBLE-BASED PREDICTION METHODS

In this section we briefly review bagged regression trees, random forests, and boosted regression trees. We assume that the reader is familiar with the concept of classification and regression trees and refer the interested reader elsewhere for further information and background on regression trees (Breiman, Freidman, Olshen, & Stone, 1998; Clark & Pregibon, 1993; Lemon, Roy, Clark, Friedmann, & Rakowski, 2003).

Bagging Regression Trees

Bootstrap aggregation or bagging is a generic approach that can be used with different predictive methods (Hastie, Tibshirani, & Friedman, 2001). Our focus is on bagging regression trees. Using this approach, repeated bootstrap samples are drawn from the study sample. A regression tree is grown in each of these bootstrap samples. Using each of the grown regression trees, predictions are obtained for each study subject. Finally, for each study subject, the estimated outcome is the average of the predictions obtained from the regression trees grown over the different bootstrap samples. In this study, we used the bagging function from the ipred package for the R statistical programming language to fit bagged regression trees (R Core Development Team, 2005). In our application of bagging, we used 100 bootstrap samples.

Random Forests

The Random Forests approach was developed by Breiman (2001). The Random Forests approach is similar to bagging regression trees with one important modification. When one is growing a regression tree in a particular bootstrap sample, at a given node, rather than considering all possible binary splits on all candidate variables, one only considers splits on a random sample of the candidate predictor variables. The size of the set of randomly selected predictor variables is defined prior to the process. We let the size of the set of randomly selected predictor variables be p/3 , where p denotes the total number of predictor variables and denotes the floor function (this is the default in the R implementation of Random Forests). We used the randomForest function from the RandomForests package for R to estimate random forests in our study.

Boosted Regression Trees

The AdaBoost.M1 algorithm was proposed by Freund and Schapire for use with classification trees (Freund & Schapire, 1996; Hastie et al., 2001). Boosting sequentially applies a weak classifier to series of reweighted versions of the data, thereby producing a sequence of weak classifiers. At each step of the sequence, subjects who were incorrectly classified by the previous classifier are weighted more heavily than subjects who were correctly classified. The predictions from this sequence of weak classifiers are then combined through a weighted majority vote to produce the final prediction. Generalized boosting methods adapt this algorithm for use with regression rather than with classification (Hastie et al., 2001; McCaffrey, Ridgeway, & Morral, 2004). We considered four different base regression models: regression trees of depth one, regression trees of depth two, regression trees of depth three, and regression trees of depth four. These have also been referred to as regression trees with interaction depths one through four. For each method, we considered sequences of 10,000 regression trees. R code for fitting bagged regression trees, random forests, and boosted regression trees is available online: http://works.bepress.com/peter_austin/

MONTE CARLO SIMULATIONS

We used an extensive series of Monte Carlo simulations to examine the performance of ensemble methods for estimating causal treatment effects. Our simulations used data-generating processes that were very similar to those used in two prior studies by different groups of authors to examine the utility of data mining methods to estimate propensity scores (Lee, Lessler, & Stuart, 2010; Setoguchi, Schneeweiss, Brookhart, Glynn, & Cook, 2008). Setoguchi et al. (2008) examined the ability of neural networks and recursive partitioning to estimate propensity scores for use with propensity-score matching to estimate treatment odds ratios (Setoguchi et al., 2008). Lee et al. (2010) examined the ability of regression trees, bagged regression trees, random forests, and boosted regression trees to estimate propensity scores for use with inverse probability of treatment weighting (IPTW) to estimate linear treatment effects (Lee et al., 2010).

Monte Carlo Simulations: Methods

As in Setoguchi et al. (2008) and Lee et al. (2010), we assumed that there were 10 baseline covariates (X ₁ to X ₁₀) of which 4 had standard normal distributions and 6 had Bernoulli distributions. Four of the 10 covariates affected both treatment selection and the outcome, 3 covariates affected treatment selection alone, and 3 covariates affected the outcome alone. Furthermore, there were three pairwise correlations between select pairs of baseline covariates. Setoguchi et al. and Lee et al. considered seven scenarios that differed in the nature of the true treatment-selection model (i.e., the propensity score model). We considered five of these scenarios (and use the labels of the earlier papers—we excluded scenarios B and D):

A.	Additivity and linearity (main effects only): logit(Pr(Z = 1)) = β0 + β1 X 1 + β2 X 2 + β3 X 3 + β4 X 4 + β5 X 5 + β6 X 6 + β7 X 7
B.	Moderate nonlinearity (3 quadratic terms): logit(Pr(Z = 1)) = β0 + β1 X 1 + β2 X 2 + β3 X 3 + β4 X 4 + β5 X 5 + β6 X 6 + β7 X 7 + β2 X 2 2 + β4 X 2 4 + β7 X 2 7
C.	Mild nonadditivity and nonlinearity (3 two-way interaction terms and 1 quadratic term): logit(Pr(Z = 1)) = β0 + β1 X 1 + β2 X 2 + β3 X 3 + β4 X 4 + β5 X 5 + β6 X 6 + β7 X 7 + β2 X 2 2 β1 × 0.5 × X 1 X 3 + β2 × 0.7 × X 2 X 4 + β4 × 0.5 × X 4 X 5 + β5 × 0.5 × X 5 X 6
D.	Moderate nonadditivity (10 two-way interaction terms): logit(Pr(Z = 1)) = β0 + β1 X 1 + β2 X 2 + β3 X 3 + β4 X 4 + β5 X 5 + β6 X 6 + β7 X 7 + β2 X 2 2 β1 × 0.5 × X 1 X 3 + β2 × 0.7 × X 2 X 4 + β3 × 0.5 × X 3 X 5 + β4 × 0.7 × X 4 X 6 + β5 × 0.5 × X 5 X 7 + β1 × 0.5 × X 1 X 6 + β2 × 0.7 × X 2 X 3 + β3 × 0.5 × X 3 X 4 + β4 × 0.5 × X 4 X 5 + β5 × 0.5 × X 5 X 6
E.	Moderate nonadditivity and nonlinearity (10 two-way interaction terms and 3 quadratic terms): logit(Pr(Z = 1)) = β0 + β1 X 1 + β2 X 2 + β3 X 3 + β4 X 4 + β5 X 5 + β6 X 6 + β7 X 7 + β2 X 2 2 β2 X 2 2 + β4 X 2 4 + β7 X 2 7 + β1 × 0.5 × X 1 X 3 + β2 × 0.7 × X 2 X 4 + β3 × 0.5 × X 3 X 5 + β4 × 0.7 × X 4 X 6 + β5 × 0.5 × X 5 X 7 + β1 × 0.5 × X 1 X 6 + β2 × 0.7 × X 2 X 3 + β3 × 0.5 × X 3 X 4 + β4 × 0.5 × X 4 X 5 + β5 × 0.5 × X 5 X 6

For greater details on the data-generating process, the reader is referred to the initial paper by Setoguchi et al.

We randomly generated data sets of size 1,000. For each subject we randomly generated treatment status using a logistic model based on the seven covariates that affected treatment selection (Z = 1 denoting treated and Z = 0 denoting untreated). We then randomly generated a continuous outcome and a binary outcome for each subject. For the continuous outcome, our data-generating process was a minor modification of that used by Lee et al. (2010). We randomly generated a continuous outcome from the following model:

In this model, the regression coefficients were the same as those used by Setoguchi et al. (2008) and by Lee et al.: α₀ through α₇ were equal to −3.85, 0.3, −0.36, −0.73, −0.2, 0.71, −0.19, and 0.26, respectively. As in Lee et al., the effect of treatment on the mean outcome was set as γ = −0.4. Our one deviation from Lee et al. was that the random error term was drawn from the following distribution: e_i ~ N(0,σ = 1.87). In doing so, the baseline covariates explained 13% of the variation of the outcome in the absence of treatment. Cohen has described this as a moderate effect size (Cohen, 1988).

We modified the aforementioned data-generating process to generate a binary outcome for each subject. We replaced the linear model in Formula (1) by a logistic model. We generated binary outcomes so that the probability of an event occurring if all subjects were untreated was 0.1. Furthermore, we generated data so that treatment caused an absolute risk reduction of 0.02 (equivalent to a number needed to treat [NNT] of 50). Using previously described methods, we determined that the required values for α₀ and γ were −2.44 and 0.774, respectively (Austin, 2010).

Using the aforementioned data-generating processes, we randomly generated 1,000 data sets, each of size 1,000 for each of the five scenarios. Within each simulated data set, we used boosted regression trees (interaction depth 1, interaction depth 2, interaction depth 3, and interaction depth 4), bagged regression trees, and random forests to estimate potential outcomes under treatment and lack of treatment. To do so, the simulated sample was divided into two subgroups, the first consisting of untreated subjects and the second consisting of treated subjects. The selected prediction method was developed to predict the outcome within each of the two subgroups (note: the final prediction model could differ between each of the two subsets). For each prediction method, the candidate predictor variables were the 10 randomly generated baseline covariates (the rationale for including all 10 covariates as potential predictors of the outcome, even though only 7 are predictors of the outcome, is to simulate a realistic setting in which the researcher may not know which of the measured variables are truly predictive of the outcome). Let M ₀ and M ₁ denote the prediction model developed on the treated and untreated subjects, respectively. Each prediction model, M ₀ and M ₁, was then applied to the entire sample to estimate the outcome for each subject, first assuming the subject was untreated and then assuming that the subject was treated. Let X _i denote the baseline characteristics of the ith subject. Then the two imputed potential outcomes, Ŷ(0) and Ŷ(1), were M ₀(X _i ) and M ₁(X _i ). The ATE in the kth simulated data set is then estimated as θ _k = Σ ^N _{i = 1,000} (M ₁(X _i ) – M ₀(X _i )), where N denotes the sample size (N = 1,000 in our settings). Averaging over the entire sample allows one to estimate the ATE; averaging over the treated subjects only would allow for estimation of the ATT. 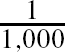If θ _k denotes the estimated treatment effect (either a difference in means or a risk difference) in the kth simulated data set, then the bias in the estimated treatment effect was estimated as Σ^1,000 _{k = 1} (θ _k – θ), where θ denotes the true treatment effect in the data-generating process. 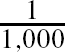The relative bias was defined as 100 × , whereas the mean squared error (MSE) of the estimated treatment effect was estimated as Σ^1,000 _{k = 1} (θ _k – θ)². We report the percent bias in the estimated average treatment effect, the standard deviation of the estimated treatment effects across the 1,000 simulated samples, and the MSE of the estimated treatment effect.

For comparative purposes, we used parametric regression models to impute the potential outcomes. This was done in two different fashions. First, using the approach described by Imbens (2004), linear (for the continuous outcome) and logistic (for the binary outcome) regression models were fit in the treated and untreated subjects separately (Imbens, 2004). Each regression model regressed the outcome on the 10 baseline covariates. The fitted regression models were then used to impute potential outcomes for each subject, assuming they were untreated and then assuming they were treated. We refer to this approach as the Imbens method. Second, we used G-computation, in which a single regression model was fit to the entire sample (linear for continuous outcome and logistic for the binary outcome). This model contained an indicator variable denoting treatment status and the 10 baseline covariates. Using the fitted regression model, we predicted outcomes for each subject assuming they had been untreated and again assuming that they had been treated. We also estimated the crude treatment effect that did not account for confounding. To do so, we estimated the difference in means or risk difference between treated and untreated subjects in the overall sample.

For comparative purposes we used inverse probability of treatment weighting (IPTW) using the propensity score to estimate the ATE in the simulated samples (Rosenbaum, 1987). The propensity score is the probability of treatment assignment conditional on observed baseline covariates (Rosenbaum & Rubin, 1983). We used the following methods to estimate the propensity score: logistic regression (including all 10 baseline covariates as main effects only), bagged regression trees, random forests, and boosted regression trees (four different sets of trees: interactions depths of 1 through 4). Let e _i denote the estimated propensity score. 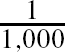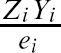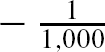Then the ATE was estimated as Σ^1,000 _{i = 1} – Σ^1,000 _{i = 1} .

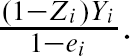The aforementioned five scenarios all assume a linear relationship between baseline covariates and the outcome (Formula (1)). In such settings, G-computation would be expected to perform very well because it is based on the multivariable regression model that corresponds to the model used to generate outcomes. Similarly, the Imbens method would be expected to perform very well. We included the aforementioned five scenarios so that our results could be compared with those from prior studies that used these data-generating processes. However, we added two additional scenarios to examine the relative performance of the different methods when the outcomes model included nonlinearities and was nonadditive. In the first of these additional scenarios, we assumed mild nonadditivity and nonlinearity in the outcome model, whereas in the second additional scenario, we assumed moderate nonadditivity and nonlinearity. To do so, the outcome model in Formula (1) was modified so as to have the functional form of the treatment-selection models (E) and (G), respectively. Furthermore, X ₅, X ₆, and X ₇ were replaced by X ₈, X ₉, and X ₁₀, respectively, whereas the regression coefficient b _i was replaced by a _i . Thus, the outcome model in Formula (1) was modified to have either mild or moderate nonadditivity and nonlinearity. However, the parametric multivariable regression models fit for G-computation and the Imbens method included only main effects and assumed linear relationships between continuous covariates and the outcome. We refer to these two scenarios as E2 and G2, respectively.

Monte Carlo Simulations: Results

We present the results for estimation of causal effects when outcomes are continuous, followed by the results when outcomes are binary.

Continuous outcomes

The percent bias for the different estimation methods is reported in Table 1. Of the different methods based on estimating potential outcomes, either G-computation or the Imbens method resulted in estimates of average treatment effect with the least bias when the outcomes model was linear and additive. Using either of these methods, the absolute percent bias was at most 1.4% across the five scenarios. Of the ensemble-based methods, boosted regression trees with interaction depths of four resulted in the least biased estimates of average treatment effects, with absolute percent bias of at most 3.3% across these five scenarios. Boosting with interaction depth of three also resulted in estimates with at most modest bias (absolute bias of at most 3.8%). Bagging and random forests resulted in absolute bias of less than 9% in all five scenarios in which the outcomes model was linear and additive. When the outcomes model was not linear and nonadditive, G-computation and the Imbens methods resulted in large biases. Boosted regression trees of depth four resulted in the least bias (20.8% and 26.9% in the two scenarios).

TABLE 1 Monte Carlo Simulations: Relative Bias (%) in Estimated Average Treatment Effect (ATE) for Continuous Outcomes Using Different Methods Across the Seven Scenarios

Estimation Method	A	C	E	F	G	E2	G2
Regression methods to directly impute potential outcomes
Crude	−44.3	−37.7	−44.1	−46.8	−38.3	−85.3	−129.4
Bagging	−7.1	−6.0	−6.9	−6.2	−5.1	−25.0	−32.3
Random forests	−8.6	−7.6	−8.0	−7.8	−6.7	−30.2	−44.0
Boosting—interaction depth 1	−10.5	−9.2	−10.0	−9.5	−8.1	−34.1	−47.8
Boosting—interaction depth 2	−5.0	−4.6	−4.5	−3.5	−2.8	−25.2	−34.1
Boosting—interaction depth 3	−3.8	−3.6	−3.3	−2.1	−1.5	−22.2	−29.2
Boosting—interaction depth 4	−3.3	−3.0	−2.9	−1.6	−1.1	−20.8	−26.9
Imbens method	−1.4	−1.3	−1.0	0.2	0.0	−50.8	−77.4
G-computation	−1.4	−1.3	−1.1	0.1	0.1	−47.0	−73.7
Inverse probability of treatment weighting
Bagging	−15.2	−13.8	−57.1	6.8	11.2	−85.6	−31.6
Random forests	−37.2	−41.4	−116.7	29.3	30.3	−143.2	−11.5
Boosting—interaction depth 1	−18.4	−8.0	−47.4	−5.7	5.0	−82.4	−51.3
Boosting—interaction depth 2	−11.9	−5.6	−48.6	1.0	10.0	−77.5	−35.4
Boosting—interaction depth 3	−11.6	−6.5	−51.8	4.7	12.0	−77.5	−27.9
Boosting—interaction depth 4	−12.9	−8.7	−55.7	7.5	13.7	−79.9	−23.6
Logistic regression	−1.4	26.0	−24.1	−24.9	−13.4	−78.7	−96.0

When using IPTW using the propensity score, none of the methods for estimating the propensity score resulted in the lowest bias across all scenarios. Boosting (interaction depth 2) had the lowest bias of the IPTW methods in two of the five scenarios in which the outcomes model was linear and additive.

In comparing bias between the IPTW methods and the methods based on directly imputing the potential outcomes, one observes that when the outcome model was linear and additive, then either G-computation or the Imbens approach resulted in the lowest bias. However, in all five scenarios directly imputing potential outcomes using boosted regression trees of depth 2, 3, or 4 resulted in bias that was negligible or very low. When the outcomes model was nonlinear and nonadditive, estimating potential outcomes using boosted regression trees of depth 3 or 4 resulted in good performance.

TABLE 2 Monte Carlo Simulations: Standard Deviation of Estimated Average Treatment Effect (ATE) for Continuous Outcomes Using Different Methods Across the Seven Scenarios

Estimation Method	A	C	E	F	G	E2	G2
Regression methods to directly impute potential outcomes
Crude	0.1262	0.1285	0.1231	0.1249	0.1290	0.1608	0.2278
Bagging	0.1316	0.1339	0.1350	0.1358	0.1387	0.1746	0.2425
Random forests	0.1276	0.1320	0.1307	0.1325	0.1344	0.1703	0.2383
Boosting—interaction depth 1	0.1265	0.1297	0.1279	0.1300	0.1312	0.1682	0.2326
Boosting—interaction depth 2	0.1287	0.1337	0.1312	0.1314	0.1344	0.1719	0.2380
Boosting—interaction depth 3	0.1298	0.1357	0.1328	0.1323	0.1360	0.1739	0.2408
Boosting—interaction depth 4	0.1304	0.1369	0.1338	0.1329	0.1372	0.1749	0.2428
Imbens method	0.1319	0.1301	0.1353	0.1361	0.1330	0.1813	0.2412
G-computation	0.1318	0.1293	0.1339	0.1357	0.1312	0.1795	0.2374
Inverse probability of treatment weighting
Bagging	0.1318	0.1435	0.1352	0.1338	0.1368	0.1686	0.2187
Random forests	0.1412	0.1447	0.1432	0.1432	0.1464	0.1642	0.1949
Boosting—interaction depth 1	0.1249	0.1282	0.1252	0.1246	0.1252	0.1622	0.2128
Boosting—interaction depth 2	0.1294	0.1334	0.1324	0.1317	0.1300	0.1692	0.2155
Boosting—interaction depth 3	0.1294	0.1360	0.1351	0.1336	0.1331	0.1712	0.2174
Boosting—interaction depth 4	0.1287	0.1367	0.1354	0.1334	0.1348	0.1706	0.2177
Logistic regression	0.1870	0.1629	0.2032	0.1982	0.1679	0.2567	0.2790

The standard deviations of the estimated treatment effects across the 1,000 simulated data sets are reported in Table 2, whereas the MSEs of the estimated average treatment effects are reported in Table 3. When restricting our attention to estimation methods based on directly imputing potential outcomes, in three of the seven scenarios, boosting (with interaction depth 2) resulted in estimates with the lowest MSE; in two of the seven scenarios, boosting (with interaction depth 4) resulted in estimates with the lowest MSE; and in the remaining two scenarios, G-computation resulted in estimates with the lowest MSE. Of important note, boosting with interaction depth of four had the lowest MSE in the two scenarios in which the outcome model was nonlinear and nonadditive. When restricting our attention to IPTW methods, using boosted regression trees (with interaction depth of one or three) resulted in estimates with the lowest MSE in four of the seven scenarios.

Binary outcomes

The percent bias for the different estimation methods are reported in Table 4. Of the methods based on directly imputing potential outcomes, G-computation resulted in estimates of average treatment effect with the least bias in two of the seven scenarios. Using G-computation, the absolute percent bias was at most 4.3% when the outcomes model was correctly specified. However, the bias was substantial when the outcomes model was incorrectly specified (47.6% and 72.6%). Bias with the Imbens method was qualitatively similar to that of G-computation in each of the seven scenarios. Of the ensemble methods, no method had uniformly superior performance. However, boosted regression trees with interaction depths of three or four tended to result in the bias that was similar to that of the best performing method in six of the seven scenarios. The use of bagged regression trees of depth 3 or 4 to impute potential outcomes resulted in bias that was either approximately equal to that of the best performing IPTW method or that was lower than that of the best performing IPTW method.

TABLE 3 Monte Carlo Simulations: MSE of Estimated Average Treatment Effect (ATE) for Continuous Outcomes Using Different Methods Across the Seven Scenarios

Estimation Method	A	C	E	F	G	E2	G2
Regression methods to directly impute potential outcomes
Crude	0.0473	0.0392	0.0462	0.0506	0.0400	0.1423	0.3199
Bagging	0.0181	0.0185	0.0190	0.0190	0.0196	0.0405	0.0755
Random forests	0.0175	0.0183	0.0181	0.0185	0.0188	0.0436	0.0878
Boosting—interaction depth 1	0.0177	0.0182	0.0180	0.0183	0.0182	0.0468	0.0906
Boosting—interaction depth 2	0.0170	0.0182	0.0175	0.0175	0.0182	0.0397	0.0752
Boosting—interaction depth 3	0.0171	0.0186	0.0178	0.0176	0.0185	0.0381	0.0715
Boosting—interaction depth 4	0.0172	0.0189	0.0180	0.0177	0.0188	0.0375	0.0705
Imbens method	0.0174	0.0169	0.0183	0.0185	0.0177	0.0742	0.1539
G-computation	0.0174	0.0167	0.0179	0.0184	0.0172	0.0675	0.1431
Inverse probability of treatment weighting
Bagging	0.0210	0.0236	0.0703	0.0186	0.0207	0.1457	0.0637
Random forests	0.0420	0.0483	0.2385	0.0342	0.0360	0.3552	0.0401
Boosting—interaction depth 1	0.0210	0.0174	0.0517	0.0160	0.0160	0.1348	0.0873
Boosting—interaction depth 2	0.0190	0.0183	0.0553	0.0174	0.0185	0.1247	0.0665
Boosting—interaction depth 3	0.0189	0.0192	0.0611	0.0182	0.0200	0.1253	0.0596
Boosting—interaction depth 4	0.0192	0.0199	0.0680	0.0187	0.0211	0.1312	0.0562
Logistic regression	0.0350	0.0373	0.0506	0.0492	0.0310	0.1649	0.2251

The standard deviations of the estimated treatment effects across the 1,000 simulated data sets are reported in Table 5, whereas the MSEs of the estimated average treatment effects are reported in Table 6. When restricting our attention to methods based on directly imputing potential outcomes, boosted regression trees with interaction depth one had the lowest MSE in four of the seven scenarios. In each of the remaining three scenarios, it had MSE very similar to the method with the lowest MSE in that scenario. Bagging and boosted regression trees with depths two, three, or four resulted in estimates with MSEs that were very similar to that of the best performing methods. When restricting our attention to IPTW methods, using bagged regression trees or random forests to estimate the propensity score tended to result in estimates with low MSE. Finally, in the five scenarios in which the outcome model was linear and additive, the use of a method based on IPTW had the lowest MSE.

TABLE 4 Monte Carlo Simulations: Relative Bias (%) in Estimated Average Treatment Effect (ATE) for Binary Outcomes Using Different Methods Across the Seven Scenarios

Estimation Method	A	C	E	F	G	E2	G2
Regression methods to directly impute potential outcomes
Crude	−129.9	−154.7	−139.7	−129.4	−153.1	−112.7	−89.3
Bagging	−4.0	2.4	−18.8	9.3	9.2	−45.7	−43.6
Random forests	−3.7	14.6	−22.1	5.3	15.9	−48.2	−29.5
Boosting—interaction depth 1	−8.8	−5.8	−16.8	−1.8	−3.1	−44.6	−56.2
Boosting—interaction depth 2	−3.6	2.4	−8.1	−0.3	1.6	−32.6	−43.8
Boosting—interaction depth 3	−4.9	3.5	−5.4	−4.1	0.0	−28.1	−42.6
Boosting—interaction depth 4	−7.1	3.0	−3.8	−8.5	−3.1	−25.7	−44.8
Imbens method	−0.6	5.2	−3.1	−0.7	2.2	−51.4	−73.3
G-computation	−0.5	4.3	−1.9	−1.3	0.6	−47.6	−72.6
Inverse probability of treatment weighting
Bagging	−32.1	−19.8	−9.3	−44.0	−35.9	−32.1	−72.9
Random forests	−77.4	−61.3	−36.5	−107.9	−94.8	−52.7	−129.7
Boosting—interaction depth 1	−165.6	−176.7	−184.4	−162.4	−171.1	−154.1	−122.5
Boosting—interaction depth 2	−175.2	−179.2	−192.7	−169.9	−170.4	−168.4	−130.9
Boosting—interaction depth 3	−174.6	−177.8	−193.1	−167.5	−166.8	−173.0	−133.1
Boosting—interaction depth 4	−171.8	−175.4	−191.3	−162.3	−162.2	−173.5	−131.4
Logistic regression	−2.2	7.2	25.3	25.2	43.3	−39.3	−53.9

CASE STUDY

We illustrate the application of the methods described earlier to estimate the effect of in-hospital smoking cessation counseling on 3-year mortality in a sample of patients discharged from the hospital with a diagnosis of acute myocardial infarction (heart attack). These data were recently used in a tutorial and case study (Austin, 2011a) that accompanied a review article on propensity score methods (Austin, 2011b). The reader is referred to this prior article for a greater description of the study sample.

TABLE 5 Monte Carlo Simulations: Standard Deviation of Estimated Average Treatment Effect (ATE) for Binary Outcomes Using Different Methods Across the Seven Scenarios

Estimation Method	A	C	E	F	G	E2	G2
Regression methods to directly impute potential outcomes
Crude	0.0176	0.0171	0.0179	0.0180	0.0174	0.0172	0.0173
Bagging	0.0195	0.0193	0.0198	0.0202	0.0189	0.0194	0.0182
Random forests	0.0206	0.0203	0.0210	0.0212	0.0201	0.0204	0.0194
Boosting—interaction depth 1	0.0191	0.0183	0.0190	0.0196	0.0183	0.0187	0.0176
Boosting—interaction depth 2	0.0197	0.0193	0.0198	0.0202	0.0190	0.0193	0.0183
Boosting—interaction depth 3	0.0200	0.0197	0.0202	0.0205	0.0194	0.0197	0.0188
Boosting—interaction depth 4	0.0202	0.0199	0.0204	0.0208	0.0197	0.0199	0.0191
Imbens method	0.0201	0.0184	0.0200	0.0207	0.0188	0.0200	0.0181
G-computation	0.0200	0.0182	0.0201	0.0204	0.0187	0.0197	0.0180
Inverse probability of treatment weighting
Bagging	0.0168	0.0165	0.0167	0.0171	0.0162	0.0159	0.0158
Random forests	0.0119	0.0113	0.0120	0.0121	0.0116	0.0115	0.0113
Boosting—interaction depth 1	0.0173	0.0163	0.0172	0.0180	0.0164	0.0166	0.0163
Boosting—interaction depth 2	0.0176	0.0165	0.0176	0.0183	0.0165	0.0169	0.0162
Boosting—interaction depth 3	0.0175	0.0164	0.0176	0.0181	0.0165	0.0169	0.0161
Boosting—interaction depth 4	0.0172	0.0162	0.0174	0.0177	0.0163	0.0166	0.0159
Logistic regression	0.0215	0.0197	0.0229	0.0257	0.0224	0.0211	0.0200

Data Sources

Detailed clinical data were obtained by retrospective chart review on a sample of patients discharged alive from 102 Ontario hospitals between April 1, 1999, and March 31, 2001. These data were collected as part of the Enhanced Feedback for Effective Cardiac Treatment (EFFECT) Study, an ongoing initiative intended to improve the quality of care for patients with cardiovascular disease in Ontario (Tu et al., 2004; Tu et al., 2009). Data on patient history, cardiac risk factors, comorbid conditions and vascular history, vital signs, and laboratory tests were collected for this sample. Patient records were linked to the Registered Persons Database using encrypted health card numbers to allow us to determine the vital status of each patient at 3 years following discharge. For this case study we restricted the sample to 2,342 subjects who were current smokers at time of hospital admission, who survived to hospital discharge, who had complete data on baseline covariates of interest, and who had evidence that smoking cessation counseling had or had not occurred. The outcome of interest was whether the patient died within 3 years of hospital discharge. The 3-year mortality rate in the study sample was 11.2%. The exposure of interest was whether or not patients received in-hospital smoking cessation counseling prior to hospital discharge.

TABLE 6 Monte Carlo Simulations: MSE of Estimated Average Treatment Effect (ATE) for Binary Outcomes Using Different Machine Learning Methods Across the Seven Scenarios

Estimation Method	A	C	E	F	G	E2	G2
Regression methods to directly impute potential outcomes
Crude	0.00099	0.00125	0.00110	0.00099	0.00124	0.00080	0.00062
Bagging	0.00038	0.00037	0.00041	0.00041	0.00036	0.00046	0.00041
Random forests	0.00042	0.00042	0.00046	0.00045	0.00041	0.00051	0.00041
Boosting—interaction depth 1	0.00037	0.00034	0.00037	0.00039	0.00033	0.00043	0.00044
Boosting—interaction depth 2	0.00039	0.00037	0.00039	0.00041	0.00036	0.00042	0.00041
Boosting—interaction depth 3	0.00040	0.00039	0.00041	0.00042	0.00038	0.00042	0.00042
Boosting—interaction depth 4	0.00041	0.00040	0.00042	0.00043	0.00039	0.00042	0.00044
Imbens method	0.00040	0.00034	0.00040	0.00043	0.00035	0.00051	0.00054
G-computation	0.00040	0.00033	0.00040	0.00041	0.00035	0.00048	0.00053
Inverse probability of treatment weighting
Bagging	0.00032	0.00029	0.00028	0.00037	0.00031	0.00029	0.00046
Random forests	0.00038	0.00028	0.00020	0.00061	0.00049	0.00024	0.00080
Boosting—interaction depth 1	0.00140	0.00152	0.00166	0.00138	0.00144	0.00122	0.00087
Boosting—interaction depth 2	0.00154	0.00156	0.00179	0.00149	0.00143	0.00142	0.00095
Boosting—interaction depth 3	0.00152	0.00153	0.00180	0.00145	0.00139	0.00148	0.00097
Boosting—interaction depth 4	0.00147	0.00149	0.00177	0.00137	0.00132	0.00148	0.00094
Logistic regression	0.00046	0.00039	0.00055	0.00068	0.00058	0.00051	0.00051

The sample consisted of 1,588 subjects who received in-patient smoking cessation counseling and 754 who did not. Baseline characteristics of patients who did and did not receive in-hospital smoking cessation counseling are described in Table 7. Patients receiving smoking cessation counseling tended to be younger, to have a lower burden of comorbid conditions, and were more likely to have received prescriptions for cardiac medications at hospital discharge compared with patients who did not receive in-patient smoking cessation counseling. There were statistically significant differences in 22 of the 33 baseline characteristics between exposed and unexposed subjects in the study sample. Twenty of the variables had absolute standardized differences that exceeded 0.10 (Austin, 2009; Flury & Riedwyl, 1986).

Methods

We considered as predictors of mortality the 33 baseline covariates listed in Table 7. The different ensemble methods were used to predict the probability of 3-year mortality in treated and untreated subjects separately. Logistic regression was also used to impute potential outcomes. With logistic regression, both classical G-computation and the Imbens approach were used. For each of the estimation methods, we estimated the ATE, the ATT, and the ATC. For each of the different estimation methods, standard errors of estimated risk reductions were estimated using bootstrap methods (Efron & Tibshirani, 1993). Two hundred bootstrap samples were drawn from the original sample. The risk reduction was estimated in each of the 200 bootstrap samples and the standard deviation of the treatment effects was estimated.

TABLE 7 Baseline Characteristics of Treated and Untreated Subjects in the Study Sample

Variable	No Smoking Cessation Counseling (N = 754)	Smoking Cessation Counseling (N = 1,588)	Overall Sample (N = 2,342)	Absolute Standardized Difference of the Mean	p Value
Demographic characteristics
Age	60.48 ± 13.26	56.24 ± 11.26	57.61 ± 12.10	0.35	< .001
Female	220 (29.2%)	397 (25.0%)	617 (26.3%)	0.09	.032
Note. Continuous variables are presented as means ± standard deviation; dichotomous variables are presented as N (%); ASA = acetylsalicylic acid.
Presenting signs and symptoms
Acute pulmonary edema	34 (4.5%)	48 (3.0%)	82 (3.5%)	0.08	.067
Vital signs on admission
Systolic blood pressure	146.99 ± 31.82	146.93 ± 29.92	146.95 ± 30.53	0.00	.966
Diastolic blood pressure	84.81 ± 18.99	85.84 ± 18.51	85.50 ± 18.67	0.06	.213
Heart rate	83.28 ± 22.75	81.10 ± 22.54	81.80 ± 22.63	0.10	.029
Respiratory rate	21.18 ± 5.75	20.18 ± 4.64	20.50 ± 5.05	0.20	< .001
Classic cardiac risk factors
Diabetes	179 (23.7%)	260 (16.4%)	439 (18.7%)	0.19	< .001
Hyperlipidemia	238 (31.6%)	539 (33.9%)	777 (33.2%)	0.05	.254
Hypertension	295 (39.1%)	541 (34.1%)	836 (35.7%)	0.11	.017
Family history of coronary artery disease	253 (33.6%)	754 (47.5%)	1,007 (43.0%)	0.28	< .001
Comorbid conditions and vascular history
Cerebrovascular accident/Transient ischemic attack	62 (8.2%)	67 (4.2%)	129 (5.5%)	0.18	<.001
Angina	198 (26.3%)	412 (25.9%)	610 (26.0%)	0.01	.871
Cancer	22 (2.9%)	20 (1.3%)	42 (1.8%)	0.13	.005
Dementia	21 (2.8%)	6 (0.4%)	27 (1.2%)	0.23	< .001
Previous myocardial infarction	161 (21.4%)	241 (15.2%)	402 (17.2%)	0.16	< .001
Asthma	40 (5.3%)	98 (6.2%)	138 (5.9%)	0.04	.406
Depression	76 (10.1%)	131 (8.2%)	207 (8.8%)	0.06	.145
Peptic ulcer disease	39 (5.2%)	111 (7.0%)	150 (6.4%)	0.07	.093
Peripheral vascular disease	77 (10.2%)	90 (5.7%)	167 (7.1%)	0.18	< .001
Previous coronary revascularization	50 (6.6%)	92 (5.8%)	142 (6.1%)	0.04	.427
Chronic congestive heart failure	24 (3.2%)	24 (1.5%)	48 (2.0%)	0.12	.008
Laboratory tests
Glucose	9.35 ± 5.63	8.57 ± 4.79	8.82 ± 5.09	0.15	< .001
White blood count	11.01 ± 4.49	10.77 ± 3.55	10.85 ± 3.88	0.06	.171
Hemoglobin	141.71 ± 19.33	145.83 ± 15.47	144.50 ± 16.92	0.24	< .001
Sodium	138.75 ± 4.54	139.40 ± 3.32	139.19 ± 3.77	0.17	< .001
Potassium	4.10 ± 0.58	4.01 ± 0.49	4.04 ± 0.52	0.16	< .001
Creatinine	99.59 ± 62.86	89.24 ± 30.24	92.57 ± 43.75	0.24	< .001
Prescriptions for cardiovascular medications at hospital discharge
Statin	193 (25.6%)	637 (40.1%)	830 (35.4%)	0.31	< .001
Beta-blocker	460 (61.0%)	1,192 (75.1%)	1,652 (70.5%)	0.31	< .001
ACE inhibitor/Angiotensin receptor blockers	344 (45.6%)	850 (53.5%)	1,194 (51.0%)	0.16	< .001
Plavix	29 (3.8%)	74 (4.7%)	103 (4.4%)	0.04	.37
ASA	544 (72.1%)	1,341 (84.4%)	1,885 (80.5%)	0.31	< .001

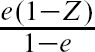For comparative purposes, we used IPTW using the propensity score to estimate the effect of provision of smoking cessation counseling on mortality. Boosting regression trees, random forests, bagging regression trees, and logistic regression were used to estimate the propensity score. Different weights were used to allow one to estimate the ATE, the ATT, and the ATC. The weights + , Z + , and 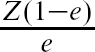+ (1 – Z) allow one to estimate the ATE, ATT, and the ATC, respectively (Morgan & Todd, 2008). As above, bootstrap methods were used to estimate standard errors of the estimated treatment effects.

Results

The estimated ATE, ATT, and ATC obtained using the different estimation methods are reported in Table 8. There existed modest variability in the estimated treatment effects across the different methods. In the Monte Carlo simulations described in the previous section, we observed that directly imputing potential outcomes using boosting (interaction depths of three or four) or random forests tended to result in minimal bias when the outcomes model was correctly specified and also resulted in the best performance when the outcomes model was nonlinear and additive. The estimated ATE using these three methods were −0.031, −0.029, and −0.028. The estimated treatment effect was qualitatively consistent across these three estimation methods. Based on our Monte Carlo simulations, we suggest that these are the most reliable estimate estimates of the effect of smoking cessation counseling on mortality.

TABLE 8 Estimated Effects of Smoking Cessation Counseling on 3-year Mortality

Regression Method	ATE	ATT	ATC
Regression methods to directly impute potential outcomes
Logistic regression (Imbens)	−0.023 (−0.05, 0.003)	−0.015 (−0.039, 0.009)	−0.042 (−0.079, −0.004)
Logistic regression (G-computation)	−0.027 (−0.054, 0)	−0.023 (−0.047, 0)	−0.034 (−f0.068, −0.001)
Bagging	−0.036 (−0.06, −0.011)	−0.028 (−0.052, −0.005)	−0.052 (−0.083, −0.02)
Boosting—interaction depth 1	−0.046 (−0.072, −0.02)	−0.04 (−0.065, −0.016)	−0.058 (−0.09, −0.026)
Boosting—interaction depth 2	−0.035 (−0.06, −0.01)	−0.027 (−0.051, −0.004)	−0.051 (−0.084, −0.018)
Boosting—interaction depth 3	−0.031 (−0.056, −0.006)	−0.023 (−0.046, 0)	−0.048 (−0.081, −0.015)
Boosting—interaction depth 4	−0.029 (−0.053, −0.004)	−0.02 (−0.043, 0.002)	−0.046 (−0.079, −0.013)
Random forests	−0.028 (−0.052, −0.003)	−0.022 (−0.045, 0.001)	−0.040 (−0.072, −0.008)
Note. ATE = average treatment effect; ATT = average treatment effect in the treated; ATC = average treatment effect in the controls.
Inverse probability of treatment weighting using the propensity score
Logistic regression	−0.025 (−0.053, 0.003)	−0.011 (−0.027, 0.005)	−0.014 (−0.028, 0.001)
Bagging:	−0.046 (−0.07, −0.023)	−0.022 (−0.036, −0.007)	−0.024 (−0.035, −0.014)
Boosting—interaction depth 1	−0.037 (−0.062, −0.012)	−0.015 (−0.031, 0)	−0.022 (−0.033, −0.011)
Boosting—interaction depth 2	−0.028 (−0.052, −0.004)	−0.007 (−0.022, 0.007)	−0.021 (−0.031, −0.01)
Boosting—interaction depth 3	−0.025 (−0.048, −0.002)	−0.003 (−0.017, 0.01)	−0.022 (−0.032, −0.011)
Boosting—interaction depth 4	−0.023 (−0.045, −0.001)	0 (−0.013, 0.013)	−0.023 (−0.034, −0.013)
Random forests	−0.007 (−0.022, 0.008)	0.045 (0.035, 0.054)	−0.052 (−0.062, −0.041)

DISCUSSION

We used an extensive series of Monte Carlo simulations to examine the relative ability of ensemble methods to estimate causal treatment effects by directly imputing potential outcomes. Although no method had uniformly superior performance for estimating linear treatment effects for continuous outcomes, the use of boosted regression trees of depth three or four to impute potential outcomes tended to have very good performance compared with competing approaches across a range of scenarios. In particular, these methods performed well even when the outcomes model was nonlinear and nonadditive. When estimating risk differences for binary outcomes, methods based on directly imputing potential outcomes tended to result in estimates with lower bias compared to IPTW estimates. As with continuous outcomes, using boosted regression trees of depth three to directly impute potential outcomes tended to have good performance, measured using bias, compared with competing approaches. In particular, the use of this method resulted in lower bias than any of the seven IPTW methods in six of the seven scenarios (in the one remaining scenario (A), the relative bias was −4.9% vs. −2.2%).

The proposed method of using ensemble-based methods to predict potential outcomes differs from classic G-computation in that it does not rely on a parametric regression model that includes an indicator variable denoting treatment status. However, Snowden et al. (2011) suggested that G-computation could be implemented using machine learning methods. Our proposed methods could be described as ensemble-based G-computation. The literature on the use of data mining and machine learning methods for estimating causal effects is limited. A handful of papers have either proposed different machine learning methods for estimating propensity scores or have compared the relative performance of different methods for estimating propensity scores on a single data set. Westreich, Lessler, and Funk (2010), when reviewing alternatives to logistic regression for estimating propensity scores, suggested that boosting and regression trees showed potential for estimating propensity scores (Westreich et al., 2010). However, they noted that extensive simulation studies were necessary to establish their utility in practice. In an empirical analysis of a single data set, Luellen, Shadish, and Clark (2005) compared inferences when using regression trees, bagged regression trees, and logistic regression to estimate propensity scores for use with stratification on the propensity score (Luellen et al., 2005). They suggested that there is a need for greater study of these methods, both through simulations and through the analysis of real data. Using an existing data set, McCaffrey et al. (2004) used IPTW to estimate treatment effects. They compared estimates of treatment effects when boosted regression trees were used to estimate the propensity score with when logistic regression was used to estimate the propensity score (McCaffrey et al., 2004). Finally, in a recent study, Hill, Weiss, and Zhai (2011) proposed that Bayesian Adaptive Regression Trees be used to directly estimate causal effects using an approach similar to that which we have outlined in the current study (Hill et al., 2011).

To the best of our knowledge, only two studies have used simulations to study the relative performance of different data mining methods to estimate propensity scores. As noted earlier, both Setoguchi et al. (2008) and Lee et al. (2010) have examined the performance of these methods for estimating propensity scores. The former paper examined the use of logistic regression, regression trees, and neural networks for estimating the propensity score when using propensity score matching to estimate treatment odds ratios. They found that data mining methods resulted in propensity scores with higher c-statistics compared to when logistic regression was used. Furthermore, the use of neural networks resulted in the least biased estimates of the competing methods. The latter paper examined the use of logistic regression, regression trees, bagged regression trees, random forests, and boosted regression trees to estimate propensity scores for use with IPTW when estimating linear treatment effects with continuous outcomes. They found that when the treatment-selection model was subject to both moderate nonadditivity and moderate nonlinearity the tree-based methods had substantially better performance compared with logistic regression. Under conditions of either nonlinearity or nonadditivity alone, all methods displayed generally acceptable performance.

There are certain limitations to the current study that suggest directions for future research. First, the majority of our statistical simulations were based on data-generating processes used in two prior studies. There is a need to repeat our analyses in other settings with different data-generating processes. In particular, one should examine the relative performance of the different methods when the number of baseline covariates is very large. Second, we compared directly estimating causal treatment effects with estimates obtained using IPTW using the propensity score. Due to space limitations, alternate propensity score methods were not considered in this paper. Matching on the propensity score allows one to estimate the ATT. In future research, the ability of propensity-score matching to estimate the ATT should be compared with directly estimating the ATT using ensemble-based G-computation.

In summary, we found that using ensemble methods to directly estimate causal treatment effects warrants consideration for application in applied analyses. In particular, the use of boosted regression trees of depth three or four to directly impute potential outcomes when outcomes are continuous or binary tended to resulted in estimates of average treatment effects with low bias.

ACKNOWLEDGMENTS

This study was supported by the Institute for Clinical Evaluative Sciences (ICES), which is funded by an annual grant from the Ontario Ministry of Health and Long-Term Care (MOHLTC). The opinions, results, and conclusions reported in this article are those of the author and are independent of the funding sources. No endorsement by ICES or the Ontario MOHLTC is intended or should be inferred. Peter C. Austin is supported in part by a Career Investigator award from the Heart and Stroke Foundation of Ontario. This study was supported in part by an operating grant from the Canadian Institutes of Health Research (CIHR; Funding number: MOP 86508). The EFFECT data used in the study was funded by a CIHR Team Grant in Cardiovascular Outcomes Research.