On the Use of Mixed Markov Models for Intensive Longitudinal Data

ABSTRACT

Markov modeling presents an attractive analytical framework for researchers who are interested in state-switching processes occurring within a person, dyad, family, group, or other system over time. Markov modeling is flexible and can be used with various types of data to study observed or latent state-switching processes, and can include subject-specific random effects to account for heterogeneity. We focus on the application of mixed Markov models to intensive longitudinal data sets in psychology, which are becoming ever more common and provide a rich description of each subject’s process. We examine how specifications of a Markov model change when continuous random effect distributions are included, and how mixed Markov models can be used in the intensive longitudinal research context. Advantages of Bayesian estimation are discussed and the approach is illustrated by two empirical applications.

KEYWORDS:

• Intensive longitudinal data
• state switching
• mixed Markov model
• latent Markov model
• time series analysis

Psychological researchers from various fields have used longitudinal research to study within-person processes that are characterized by switches between different states. Examples involve research into bipolar disorder, characterized by switches between manic and depressive states (Hamaker, Grasman, & Kamphuis, 2016); recovery and relapse as seen in addiction (Warren, Hawkins, & Sprott, 2003; Shirley, Small, Lynch, Maisto, & Oslin, 2010; Prisciandaro et al.  2012; DeSantis & Bandyopadhyay, 2011); state-dependent affect regulation (de Haan-Rietdijk, Gottman, Bergeman, & Hamaker, 2016) and various other approaches in modeling affect dynamics (Hamaker, Ceulemans, Grasman, & Tuerlinckx, 2015); catastrophe theory applied to stagewise cognitive development (Van der Maas & Molenaar, 1992); and switches in strategy use during cognitive task performance, with the speed-accuracy trade-off as a well-known example (Wagenmakers, Farrell, & Ratcliff, 2004).

One analysis approach that can be valuable and that has sometimes been used for such processes is Markov modeling, which can be used when a person alternates between discrete states. These states can be directly observed, but there are also latent Markov models (LMMs) in which a latent state variable is related to observed data. Since individual differences are to be expected in many psychological applications, a particularly promising framework is offered by the mixed Markov model, which includes continuous random effects (Altman, 2007; also see Seltman, 2002; Humphreys, 1998; Rijmen, Ip, Rapp, & Shaw, 2008a), and potentially covariates. This model is very suitable for the increasingly common intensive longitudinal data type (ILD; cf. Walls & Schafer, 2006), where 20 or more repeated measurements are obtained per individual, because such data offer a rich description of each individual process. In this paper, we focus on models with time-constant parameters and predictors, but note that ILD also lend themselves well to models involving time-varying parameters.

Markov models, including mixed Markov models, have been applied in various scientific fields, but there are relatively few examples of mixed Markov models in the psychological literature. This scarcity of applications may have to do with the models not being well-known to researchers in this field, or perhaps with perceived limitations or challenges in the implementation of mixed Markov models. We note that ILD are unique in the sense that they contain much information about each individual, so that models including individual differences in temporal dynamics not only become viable, but of prime interest. While ILD is also suitable for separate (N = 1) modeling of each individual person’s data, distinct advantages of the mixed Markov modeling approach are that we can borrow strength across persons, obtain estimates of the average population parameters, and include predictors to investigate their relationship with the individual differences. In this paper, we show how mixed Markov models can be specified and implemented with Bayesian estimation, and we illustrate the value of this approach for ILD in psychology by two empirical examples, one involving daily affect experience and the other family interactions. We also discuss the various ways that individual differences have been addressed in the Markov literature.

This paper is structured as follows: First, we present the observed and latent Markov models, and the inclusion of continuous random effects. This is followed by considerations about the implementation, particularly the reasons why Bayesian estimation seems promising in this context. Then we turn to the literature and discuss the various ways that researchers have approached between-person differences in the Markov modeling framework. After that, we analyze two empirical data sets for which Markov modeling can address unique hypotheses and complement other analysis approaches. We conclude the paper with a discussion of limitations and recommendations for researchers.

The Markov models

In this first section, we present a brief introduction of Markov models, in which we distinguish between two situations: Either researchers know the states of the system over time, or these states are assumed to underlie the data. In the first case, we can use what we call the observed Markov model (OMM), whereas in the latter, we need to use an LMM. In our discussion, we assume that the model is concerned with the states a person is in, but keep in mind that the unit of analysis could also be a dyad, family, company, group, or something else.

The observed Markov model (OMM)

When researchers know the state that a person is in at each occasion, they can use an OMM to investigate the temporal dynamics of the state-switching process. The states may correspond to the categories of a discrete observed variable, or they may be created by discretizing continuous (or multivariate) data, as our empirical application will illustrate. The OMM is also referred to as a manifest or simple Markov model or Markov chain (cf. Kaplan, 2008; Langeheine & Van De Pol, 2002).

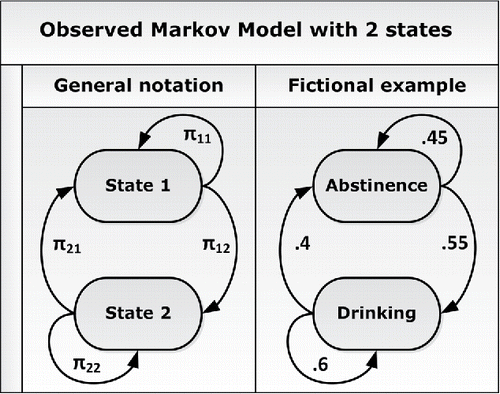
With an OMM, we analyze the observed state transitions over time and estimate the transition probabilities. Figure 1 provides a graphical representation of an OMM, with on the right-hand side, a hypothetical example based on alcohol use with two states. It can be seen that there are four possible transitions (including not switching). The transition probabilities of a Markov model are denoted as a matrix in which the element π_ij represents the probability of transitioning from state i to j between consecutive measurements (with i ∈ [1, 2, …S] and j ∈ [1, 2, …S]). We can write π_ij = p(s_tn = j|s_{(t − 1)n} = i), where s_tn represents the state of person n at occasion t. The probability of being in this state is conditioned on the state at the previous occasion. The likelihood for the data (s) from time t = 2 onwards is then given by (1) which is the product over all persons and all time points (starting at t = 2) of the categorical distribution for each individual observation, which is given by (2) Here, the expressions within square brackets evaluate to 0 or 1 when they are false or true, respectively, and ∑^S_{j = 1}π_ij = 1 for every i. Due to this logical restriction, we only need to estimate S − 1 probabilities of each row, for a total of S(S − 1) probabilities. Note that the number of probabilities to be estimated increases exponentially with the number of states.

Figure 1. Graphical representation of an OMM with two states. If a person is in a given state i at time t, the parameters next to the arrows running from that state represent the average probabilities of being in each state j at time t + 1. The right part portrays fictional parameter values concerning alcohol use.

The latent Markov model (LMM)

Sometimes the state-switching process that researchers are interested in is not directly observed, or is observed with methods that are expected to involve substantial measurement error. In these situations, researchers can use the LMM, also known as the Hidden Markov model (HMM). For quite a long time, there have been two largely separate literatures for HMMs and LMMs, originating from different disciplines, but the two names refer to the same model type (Visser, 2011; Zhang, Jones, Rijmen, & Ip, 2010).

Because an LMM is used to study a latent state-switching process, this model always needs to have a measurement (or conditional) model part, which links the unobserved states of the system to the observed outcome variable(s). We can distinguish between two broad scenarios for why and how this is done, which we will discuss in more detail below. In the first scenario, researchers have the option of applying an OMM directly to their observed categorical outcome (i.e., the state variable), but they prefer using an LMM to take measurement error into account. In contrast, in the second scenario, the LMM is the only one of the two models that can be applied to address the research questions at hand.

The first type of LMM is used when a state variable has been observed, but there is reason to expect substantial measurement error, which may cause bias in the estimated transition probabilities in an OMM (Vermunt, Langeheine, & Böckenholt, 1999). It may also be the case that multiple indicators of the state are available, in which case an OMM would have to be applied separately to each indicator. In an LMM application of this type, the number of latent states is given by the number of observed categories (per indicator), and the measurement model concerns the probabilities of correct classification versus misclassification for each true state and indicator. An example is found in Humphreys (1998), who analyzed three indicators of labor market status (employed or not employed) with a two-state LMM.

In the second type of LMM, the measurement model part does not serve merely to filter out measurement error from observed states, but instead it is used to relate the observed data to an underlying state-switching process with a different meaning. For example, Altman (2007) used a two-state LMM to study the observed lesion counts in multiple sclerosis patients during (latent) recovery and relapse states. In these kinds of LMMs, the number of latent states is chosen based on theory, or based on the fit of models with differing numbers of states. Furthermore, the exact specification of the model in these cases depends on the measurement level of the observed variable(s) and on how the states are assumed to influence them.

When it comes to differences between the interpretation of LMMs and OMMs, the study by Shirley et al. (2010) provides a nice example. As these researchers explain, applying an LMM to their alcoholism treatment trial data corresponds to a different and less rigid clinical understanding of what constitutes a “relapse” in alcoholism recovery, because the latent state in an LMM is differentiated from the observed categorical variable (drinking behavior). In contrast, an OMM would reflect the assumption that a change in the observed categories is what matters and what is relevant for clinical practice.

Apart from the fact that the number of states in an LMM does not always follow from the data, as it does in the OMM, the specification of the transition model is very similar, except that an LMM includes additional parameters π1 representing the probabilities of starting out in the different states at the first occasion. There is no fixed format for the measurement part of an LMM, because it is a flexible model that can be applied to univariate or multivariate, and continuous or discrete data. Its interpretation depends on how the underlying states and their relationship with the observed data are conceptualized.

Including random effects in Markov models

If we want to account for individual differences in dynamics, this can be done by including subject-specific random effects. Here, we follow Altman’s (2007) mixed LMM specification, modeling the logits (log-odds of the probabilities) instead of estimating the probabilities directly as described above. This makes it possible to use regression to predict the logits.

In a mixed LMM, the latent state at the first time point is still modeled using fixed probabilities. But the states from occasion t = 2 onwards are modeled, in both an OMM and LMM, using a categorical distribution where the transition probabilities depend on the individual n, so we get (3) The individual’s transition probabilities are derived from their logits α_isn, using (4) where (5) for each person n and each i, j ∈ [1, …S], such that μ_ij is the average logit for transitioning from state i to state j, and ε_ijn is person n’s deviation from that average. The random deviations have a multivariate normal distribution with a zero mean vector of length S(S − 1) and a covariance matrix Σ(ε) with S(S − 1) rows and columns. For identification, we set both μ_ij and ε_ij equal to 0 whenever i = j, making stability the reference transition for the logits.

To predict some of the individual differences in switching probabilities, we can add one or more predictor variables to Equation (5(5) ). If we have one predictor, this gives us (6) For identification purposes, we also constrain β_ij to be 0 whenever i = j. The logit specification above, which uses a reference category, can be used for ordinal and non-ordinal state variables, but for ordinal state variables, other alternatives including local, global, and continuation logit specifications, may be more parsimonious and powerful (cf. Bartolucci, Farcomeni, & Pennoni, 2013). Note that the measurement model part in an LMM can also be specified to include random effect(s). The second empirical application in this paper illustrates a mixed LMM.

Model estimation: A Bayesian approach

We now discuss the implementation of (mixed) Markov models, focusing on a few general considerations about Bayesian estimation, which is our preferred approach in this context.

Why Bayesian?

The literature contains many successful applications of Markov models implemented using classical (frequentist) estimation methods, and some of these involve LMMs with covariates, latent subgroups, or random effects to account for individual differences.¹ However, there have been conflicting opinions on the robustness of frequentist estimation for mixed LMMs, and in practice, many applications have used mixture LMMs (which will be discussed in the next section), rather than mixed LMMs. Seltman (2002) implemented a Bayesian mixed LMM with one random effect, and stated that the frequentist approach was intractable. Altman (2007) countered this claim by showing that classical estimation of several mixed LMMs, while computationally intensive, was feasible even with multiple random effects. However, she concluded that the computational burden may become prohibitive with four or more random effects. Regardless of the exact possibilities and limitations within the classical framework, we know that Bayesian estimation presents a highly flexible alternative approach.

Besides its robustness, three additional advantages of Bayesian estimation seem relevant for the use of mixed Markov models in psychology. First, it does not rely on asymptotic distributions, making it more appropriate for small samples. Importantly, in a multilevel model, the sample size at the second level is a separate issue (Hox, 2010). For instance, if there are only 30 persons in a data set, the sample size for estimating an average transition probability, a random effects variance or a covariate effect on the transition logits is small, regardless of the length of the time series. A third feature of Bayesian methods that we believe is especially valuable for psychological research is Bayesian multiple imputation, which is a state of the art technique for handling incomplete data without losing information or introducing bias (assuming, as most common approaches do, that the data points are missing at random; cf. Schafer & Graham, 2002). Fourth, we note that it is possible to extract the latent states from a fitted LMM without separate state decoding, as well as 95% credible intervals for various quantities, such as for the transition probabilities in a mixed Markov model, where the original parameters are the less easily interpretable logits.

One key characteristic of Bayesian methods is that they require the specification of prior distributions for model parameters, indicating the range of plausible values that they can take. This feature can be used to incorporate prior information (from research) or beliefs into an analysis, but it is also possible to choose vague (low informative) prior distributions so that the model estimates reflect the information in the current data and not prior beliefs (cf. Lynch, 2007). While it is sometimes desirable to conduct sensitivity analyses to compare different priors and to evaluate whether a prior is undesirably informative about the model parameters, one can also consult the literature for known characteristics of different prior distributions and base the choice of priors on expert advice. In the empirical applications in this paper, we choose priors that are recommended in the literature and that are as vague as possible.

Bayesian LMMs

While OMMs are quite straightforward to implement, there are a two points to consider about Bayesian LMMs, which could limit their usefulness in specific cases. First, there is no straightforward criterion for model fit or model selection that can be used to choose the number of latent states when that number is not known a priori. Researchers working in the frequentist framework often use the Akaike Information Criterion (AIC; Akaike, 1974) or Bayesian Information Criterion (BIC; Schwarz, 1978) for model comparison and for choosing the number of latent states (see e.g., Bauer & Curran, 2003; MacDonald & Zucchini, 2009; Nylund, Asparouhov, & Muthén, 2007; Bacci, Pandolfi, & Pennoni, 2014). In the Bayesian framework, the exact Bayes factor for model comparison is difficult to implement, and both exact and approximate Bayes Factors (such as the BIC approximation, cf. Kass & Raftery, 1995) yield results that depend on a specific prior distribution (Frühwirth-Schnatter, 2006). Another commonly used criterion is the Deviance Information Criterion (DIC; Spiegelhalter, Best, Carlin, & Van Der Linde, 2002), but there is no consensus on the right way to define the DIC for multilevel models (Celeux, Forbes, Robert, & Titterington, 2006) or for models including discrete variables (Lunn, Spiegelhalter, Thomas, & Best, 2009). A formal approach, and one that is highly consistent with Bayesian philosophy, is to estimate the number of latent states by using Reversible Jump Markov Chain Monte Carlo estimation (RJMCMC; Green, 1995; also confer Bartolucci et al., 2013). A downside of RJMCMC is that it requires custom programming and fine-tuning of algorithms.

Second, a potential issue that may arise during Bayesian estimation of LMMs (or other mixture models) is what has been referred to as label switching (Celeux, Hurn, & Robert, 2000; Frühwirth-Schnatter, 2006). Because the labels of the latent states (state “1,” “2,” and so on) are arbitrary, and because Bayesian estimation typically relies on iterative sampling from the posterior parameter distributions, it may happen that the labels are switched during the course of estimation. If this occurs, it can often (but not always) be seen from the output because the posterior distributions of the parameters will then be multimodal mixtures. For instance, if there are two states, the posterior distributions for the average transition logits μ₁₂ and μ₂₁ will each have the same two peaks, with (usually) one peak higher for one parameter and the other for the other parameter. As a result, the obtained posterior means, medians and 95% CIs of the parameters will be meaningless.² In principle, the modes that are visible in the plotted posterior densities could be used as (approximate) point estimates of the parameters (Frühwirth-Schnatter, 2006), but this only gives us a point estimate, and we typically want to have some measure of the uncertainty about the parameter value.

A common strategy to prevent label switching, in practice, is to impose order restrictions on the parameters for different states to enforce a unique labeling. (cf. Albert & Chib, 1993; Richardson & Green, 1997). However, this strategy has been criticized on various accounts (Celeux, 1998; Celeux et al., 2000; Stephens, 2000; Jasra, Holmes, & Stephens, 2005), the most important of which is that it can cause bias and inflate state differences. In fact, when the data provide little or no support for a distinction between two states, the posterior densities for those states’ parameters logically should overlap, but an order restriction will effectively obscure this “null” result by modifying the posterior and enforcing a difference between the two parameters. Thus, this approach is not recommended. It is better to allow the possibility of label switching, and if it occurs, to consider whether the cause may be overparameterization, which can result in highly similar parameters with overlapping posterior densities, or to consider whether frequentist estimation of that particular model is feasible.

In some LMM applications, label switching is unlikely to occur. Jasra et al. (2005) have argued that label switching is actually a necessary condition for model convergence, because a lack of label switching can be taken as a sign that the sampler has not covered the whole posterior distribution. However, when the parameters associated with the different latent states are clearly separated, label switching is very unlikely to occur even after many iterations, and in this case, the absence of label switching need not indicate failed convergence. In other words, only if the uncertainty about the different states’ parameters causes substantial overlap in their posterior densities, is label switching expected to happen predictably within a realistic number of sampling iterations. In practice, this means that LMMs which are used to filter out measurement error are very unlikely to present with label switching, since each latent state in such a model corresponds closely to an observed category, making for clearly distinguishable states. It is more of a risk for LMMs of the second type that we discussed, where there is no guarantee that all the latent states will be clearly separated.

Software implementations

Bayesian Markov models can be implemented in the easily accessible open-source programs OpenBUGS (Bayesian inference Using Gibbs Sampling; Lunn et al., 2009) and JAGS (Just Another Gibbs Sampler; Plummer, 2013a). Using Bayesian estimation with these programs is relatively straightforward. The user can focus on specifying the desired model and choosing the prior distributions, and the convergence of the model can be assessed using the plots and other output provided by the program. For the analyses in this paper, we use JAGS 4.0.0 in combination with R 3.2.2 (R Development Core Team, 2012) and the rjags package (Plummer, 2013b). By using this package, R can be used as the overarching program to prepare the data, run the analyses, check the convergence, and to store and further process the model results. Our JAGS model syntax is provided online as supplementary material. A detailed discussion of Bayesian methods is beyond the scope of this paper, but the interested reader is referred to the books by Kruschke (2014) and Lynch (2007).

Approaches to individual differences in the Markov literature

In this section, we will look at the ways that Markov models have been used in the literature, specifically, at the different ways that researchers have accounted for individual differences in process dynamics. In psychological research with ILD, we expect individual differences in the process parameters, and the data contains enough information to allow these differences to be modeled. Therefore, from a substantive viewpoint, it is attractive to specify a mixed Markov model, as discussed in a previous section. However, as we will see, researchers have used a number of approaches for dealing with interpersonal variation in model parameters.

The first way that researchers have dealt with between-person differences is to include one or more covariates in the model, without allowing for residual unexplained individual variation. This approach allows researchers to specify a deterministic relationship between model parameters and a covariate (which may or may not be time varying). For example, Vermunt et al. (1999) applied LMMS and OMMs to analyze educational panel data concerning pupils’ interest in physics. They included the variables sex and school grades as covariates to account for gender differences and differences between high- and low-performing pupils in the probability of starting to take an interest in physics (or losing interest). Since the model did not include person-specific random effects or unexplained interpersonal differences, it only accounted for group differences between the specified groups but not for any other sources of variation between pupils. Some other examples of LMMs that include covariates but not random effects are found in Rijmen, Vansteelandt and De Boeck (2008b), Prisciandaro et al. (2012), and Wall and Li (2009).

The second approach to taking individual variation into account is to use a mixture Markov model (sometimes also called a mixed Markov model), which tends to be computationally easier, in the frequentist framework, than the mixed Markov model. A mixture Markov model distinguishes between a number of latent classes that differ from each other with regard to the model parameters, while within each class no individual differences between persons are allowed. For instance, Crayen et al. (2012), analyzing ambulatory assessment data, identified two latent classes that differed in their mood regulation pattern during the day. This approach is also used in Maruotti (2011), who provides an illustration of a mixture LMM applied to data concerning the relationship between patent counts and research and development expenditures, and in various examples in Bartolucci et al. (2013). What may be considered a disadvantage of the mixture Markov modeling approach, is the assumption that there are a limited number of homogeneous latent classes, when many psychological differences between people are probably dimensional rather than categorical (Haslam, Holland, & Kuppens, 2012). It has been argued that mixture models need not reflect theoretical assumptions about discrete groups, but can serve as flexible non-parametric approximations of underlying continuous random effects (cf. Maruotti & Rydén, 2009; Maruotti & Rocci, 2012). Such an approach involves choosing the number of latent subgroups empirically, and in the frequentist framework, this can be done by using criteria such as the AIC or BIC (cf. Maruotti & Rocci, 2012). In the Bayesian framework, this approach would present a difficulty similar to choosing the number of latent states in an LMM, and it is not clear that a Bayesian mixture model is computationally easier than a mixed model.

The third approach, and the one that we focus on in this paper, is the inclusion of a continuous random effects distribution, by specifying a mixed Markov model as described in a previous section. We want a multilevel model that encapsulates a unique description of each person’s process, which, in the case of ILD, contains enough information that it could have been analyzed with an N = 1 model. It should be noted that a mixed Markov model with a normal distribution for the random transition logits is not the same as modeling each person’s data separately (and independently), because it involves a distributional assumption for the random effects. A normal distribution on log-odds parameters can correspond to various distributional shapes for the implied transition probabilities (due to the non-linear relationship between log-odds and probabilities), so that it is less restrictive an assumption than it may seem at first glance. Still, it is an assumption and it is worth pointing out that there are alternative, semi-parametric or non-parametric, approaches that involve less restrictive and more generalizable model specifications (cf. Maruotti & Rydén, 2009; Maruotti, 2011). Some examples of mixed LMM applications using continuous random effects are found in the studies by Altman (2007), Humphreys (1998), Rijmen et al. (2008a), DeSantis and Bandyopadhyay (2011), and Shirley et al. (2010). Of these, only Humphreys (1998) and Altman (2007) included random effects in both parts of the LMM. Rijmen and colleagues (2008) and DeSantis and Bandyopadhyay (2011) included random effects only in the measurement model. In contrast, Shirley and colleagues (2010) used random effects only in the transition model.

It is possible to allow for interpersonal variation in both parts of an LMM. Bartolucci et al. (2013), in their book about LMMs, focus only on models with random effects in either model part, and they warn readers that having random effects in both model parts would likely make the model difficult to estimate and to interpret. We do not entirely agree with this advice; the studies of Humphreys (1998) and Altman (2007) are both convincing examples where mixed LMMs with random effects in both model parts were theoretically sensible as well as practically feasible. And in some psychological applications, it makes a lot of sense to expect individual differences both in the measurement part of the model and in the latent state-switching process. Although there may be limitations on the complexity of models that can realistically be estimated for a given data set, we think researchers should not exclude a priori the possibility of including random effects in both model parts of a mixed LMM. In our application of a mixed LMM in the next section, we fit a model with random transition logits as well as a random effect in the measurement model part.

Empirical applications

In this section, we apply mixed Markov models to two empirical data sets from intensive longitudinal research, for which it makes sense to focus on the dynamics of a process, and where between-person differences in those dynamics are expected and may be linked to other person characteristics. These analyses provide an illustration of how mixed Markov models can be applied in psychology, and how they can be implemented using Bayesian estimation. We use JAGS 4.0.0 (Plummer, 2013), R 3.2.2 (R Development Core Team, 2012) and the rjags package (Plummer, 2013).

An OMM for daily negative affect

The first data set involves daily self-report measures of negative affect (NA) obtained from the older cohort (ages 50 and higher) of the Notre Dame Study of Health & Well-Being (see Bergeman & DeBoeck, 2014; Whitehead & Bergeman, 2014). We are interested in the NA subscale of the PANAS (Watson, Clark, & Tellegen, 1988), which the participants filled out on 56 consecutive days. For our analysis, we select the N = 224 persons who had at most six missing values on this composite variable (the mean of the 10 specific NA items). Specifically, we want to study the regulation of NA and how it is related to trait neuroticism, which was also measured. The daily scores on the NA scale ranged from 1 (very little or no NA) to 5 (very intense NA) in 0.1 increments, but as noted before by Wang, Hamaker, and Bergeman (2012), some persons’ scores exhibited a floor effect because they repeatedly reported experiencing no NA (i.e., for each of the NA items on the scale they chose 1, the lowest possible value with the label “very slightly or not at all”). This indicates that, at least at the level of conscious experience, NA is often absent or barely noticeable for a substantial number of people.

If we want to account for this, modeling approaches that focus on the intensity of NA as a continuous variable may not be optimal, both from a substantive and a statistical point of view. Rather than focusing immediately on questions of affect intensity, we can distinguish between the propensity to experience any NA on the one hand, and the intensity of the affect, once it is experienced, on the other. A Markov model is appropriate for this data because it can be used to investigate the frequency of transitions between episodes with and without consciously experienced NA. We will specify a mixed OMM, which allows us to investigate individual differences in the transition probabilities, and to study their relationship with neuroticism.

Model

From the original continuous NA variable, we create a dichotomous variable indicating whether or not a person experienced NA at a given time point (i.e., the state is 1 when NA was the lowest possible value of 1, and the state is 2 when the NA value was larger than 1). This dichotomous variable is then used as the data for the OMM, so that we can investigate the transitions between experiencing and not experiencing NA. There was approximately 2.2% missingness, which is dealt with automatically in JAGS through multiple imputation. This modern approach to missing data amounts to imputing many different plausible values for the missing datapoints (namely, a new value in each iteration of the estimation procedure, conditional on the model parameter estimates in that iteration), such that the model estimates for the parameters end up accounting for the uncertainty about the missing values in the data (cf. Schafer & Graham, 2002). The variable neuroticism is centered and rescaled prior to the analysis, for computational reasons discussed below. The likelihood for the observed states starting at time point t = 2 is given by Equations 3(3) , 4(4) , and 6(6) , with i, j taking on the values 1 and 2 and with neuroticism as the predictor x. Combining this all gives us the following equation: (7) where the expressions within square brackets form the exponent of the numerator and evaluate to 1 if they are true, and to 0 otherwise. The model parameters denoted by are μ₁₂, μ₂₁, β₁₂, β₂₁, and the three unique elements of the random effects covariance matrix Σ(ε).

Priors

For the intercepts μ₁₂ and μ₂₁ and for the regression coefficients β₁₂ and β₂₁, we follow the approach for logit parameters recommended by Gelman, Jakulin, Pittau and Su (2008), by specifying independent Cauchy prior distributions (or, equivalently, Student’s t distributions with one degree of freedom) with scale parameter 10 for the intercepts and 2.5 for the regression coefficients, and location parameter 0 in all cases. In accordance with this advice, we rescaled neuroticism to have a mean of 0 and a variance of 0.25.

To determine whether there are non-negligible individual differences in the transition probabilities, we needed to ensure that the prior distribution for the two random logit variances is suitably uninformative. The common choice of a multivariate prior for a covariance matrix is the Inverse-Wishart (IW) distribution with an identity matrix and degrees of freedom equal to the number of random effects, but this prior can be undesirably informative and cause overestimation when the true value of a variance is smaller than approximately 0.1 (Schuurman, Grasman, & Hamaker, 2016). Therefore, we first specified a model with separate random effects, that is, a model in which the random effects are not correlated, but come from univariate normal distributions. This way, we could follow Gelman’s (2006) recommendation for a variance term in a hierarchical model, by specifying uniform prior distributions over the interval from 0 to 100 for each of the standard deviations σ₁₂ and σ₂₁. These priors cannot bias small variance estimates upwards, so we can detect it if one of the random effects variances is very close to zero, indicating that the model is overspecified. After finding that both of the variance estimates were well over 0.1, we switched to a model specification using the IW prior for multivariate random effects, which takes into account that the random effects will be correlated to some extent. Our JAGS model syntax for the final model with the multivariate random effects is part of the supplementary material accompanying this paper.

Results

After 10,000 burnin iterations, we ran 50,000 additional iterations, using a thinning parameter of 10 so that only every 10th was stored for inference (a common approach to reduce autocorrelation in the samples without increasing the demands on computer memory). We inspected the trace plots, which showed no trend, and the density plots, which looked unimodal, both indicating adequate convergence. Most importantly, we ran a separate chain with different (randomly generated) starting values, which arrived at the same estimates. This provides a stronger reassurance about convergence, because it shows that the estimates are independent of the starting values and are unlikely to reflect only a local maximum.³ The results below are based on the 5,000 stored samples of the first chain.

Table 1 contains the estimates for the level-2 model parameters. We use the medians of the Bayesian posterior distributions as point estimates, and the SDs and 95% central credible intervals (CCIs) as indications for the uncertainty about the parameters (Lynch, 2007).

Table 1. Results for the level-2 parameters of the OMM. We use the posterior medians as point estimates, and the SD and 95% central credible intervals (CCIs) represent the uncertainty. Note that the parameters Σ(ε)₁₁ and Σ(ε)₂₂ are the variances of the random logit deviations ε₁₂ and ε₂₁, respectively, and Σ(ε)₁₂ is the covariance between these two random effects.

Empirical OMM estimates
	Median	SD	95% CCI
μ12	−0.92	0.11	[−1.13, −0.70]
Σ(ε)11	2.16	0.33	[1.63, 2.91]
β12	1.73	0.24	[1.29, 2.22]
μ21	−0.17	0.14	[−0.43, 0.11]
Σ(ε)22	3.55	0.51	[2.71, 4.71]
β21	−2.17	0.30	[−2.77, −1.61]
Σ(ε)12	−2.47	0.35	[−3.25, −1.88]

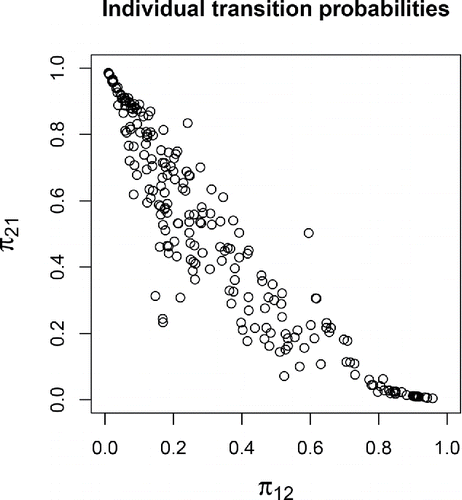
The means for the transition logits, estimated at −0.92 and −0.17, correspond to transition probabilities of 0.28 and 0.46, respectively. This implies that a person with average neuroticism has a 0.28 chance of transitioning from the non-negative to the negative state from one day to the next, and a (1 − 0.46 =) 0.54 chance of staying in the negative state. The β parameters reflect the effect of trait neuroticism on the transition logits, and because we scaled neuroticism to have an SD of 0.5, each β represents the effect of a two-SD increase in neuroticism. Since the 95% CCIs for both parameters exclude zero, we can be fairly certain that higher scores on neuroticism predict a higher chance of starting to experience NA, as well as a higher change of continuing to experience it. To gauge the relevance of these effects, we fill in different values for neuroticism (x) in Equation (4(4) ) and calculate the corresponding predicted transition probabilities. The result of this is presented in Figure 2, showing that the model implies substantial differences between more and less neurotic individuals, with more neurotic individuals having a higher propensity to experience (continued) NA. In addition, there are substantial unexplained personal differences in the transition probabilities, as indicated by the estimates for the variances of the logit deviation terms, given in Table 1. The distribution of the model-implied transition probabilities for the individual persons is presented in Figure 3, showing that π₁₂ ranges from 0.01 to 0.96 and π₂₁ ranges from 0.004 to 0.99, and that there is a negative correlation between the two probabilities. This shows that some individuals rarely started to experience NA, while others rarely stopped experiencing it. The dots in the middle of the plot represent persons who switch more frequently between episodes in which they do and do not report experiencing NA.

Figure 2. Predicted transition probabilities for individuals with varying levels of trait neuroticism ( in the sample), based on the point estimates (posterior medians) of the model parameters given in Table 1. It can be seen that individuals with higher trait neuroticism are more likely to start experiencing negative affect (i.e., their π₁₂ is larger) and, once this happens, they are also less likely to stop experiencing it (i.e., their π₂₁ is smaller).

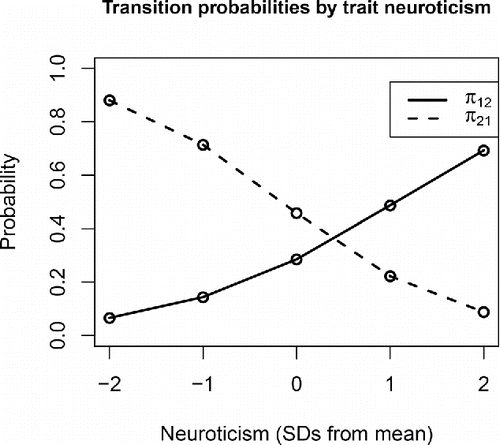
Figure 3. Scatterplot of the transition probabilities for the individual persons in the data, obtained by using Equations (4(4) ) and (6(6) ) with the estimated model parameters. The plot shows that there is substantial interpersonal variance, and that those persons with a higher probability of transitioning into the negative state (π₁₂) usually also had a lower probability of transitioning out of it (π₂₁).

Model fit

As we discussed in a previous section, the fit of a Bayesian Markov model cannot be assessed by a standard fit criterion. However, we can use posterior predictive checks to evaluate how well the model captures specific aspects of the data. Shirley et al. (2010) demonstrated several such procedures for assessing the fit of Markov models, and here we use a very similar approach. The general idea of a posterior predictive check is that the sampled parameter values can be used to simulate new data under the assumption that the model is true, and then the distribution of a certain statistic for the simulated data can be compared with the same statistic for the actual, empirical data. If the empirical data is “extreme” compared to the model-generated data sets, this indicates that the model does not adequately capture an aspect of the empirical data, or in other words, that there is misfit. A nice feature of this procedure is that uncertainty about the model parameters is taken into account, because different samples from the posterior distribution of the parameters are used to generate the simulated data.

In a first check, we assessed the model fit with regard to the proportion of days on which participants experienced NA, that is, the proportion of days spent in state 2. We used the posterior samples of the fixed parameters together with the empirical neuroticism scores and starting states (on which the model estimates are conditioned), to simulate random transition logits and “observed” time series for a new “sample” of participants in each of the 5,000 replications. For each simulated time series, we calculated the proportion of days spent in state 2, and then for each replication, we calculated the mean and standard deviation of this proportion over persons. The mean and standard deviation for the empirical dataset were then compared with the posterior predictive distributions of these statistics.

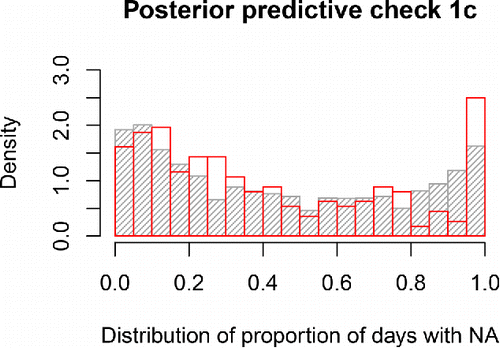
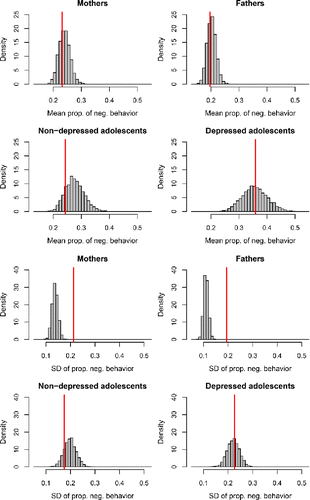
The results of the first check are illustrated in Figures 4 and 5. The predictive distribution of the mean proportion of days spent in state 2 ranges approximately from 0.35 to 0.55 and it can be seen in Figure 4 that the mean for the empirical data falls in the middle part of the distribution. Similarly, the SD of the proportion of days spent in state 2 for the empirical data falls in the middle part of the posterior predictive distribution, which ranges approximately from 0.28 to 0.36. Together these two graphs indicate that the model fit, in terms of capturing this aspect of the empirical data, is adequate, because the empirical data is not at all “extreme” under the posterior predictive distribution. Figure 5 shows the posterior predictive distribution of the proportion of days spent in state 2 for individual persons, instead of focusing on the between-persons mean or SD. This figure shows that the posterior predictive distribution closely corresponds to the observed distribution in the empirical data. The model underestimates the occurrence of (nearly) constant NA experience, but overall it captures the diversity in how often participants reported experiencing NA quite well.

Figure 4. Results of posterior predictive check 1 for the OMM. The red lines represent the empirical mean and SD of the proportion of days that participants experienced NA. The histograms represent the model predictions, which take into account the uncertainty about the estimated model parameters.

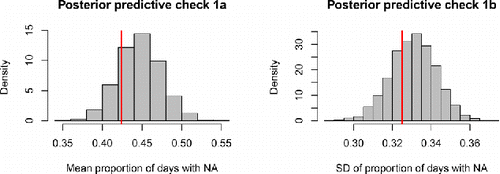
Figure 5. Distribution of the proportion of days spent in state 2 for the empirical (in red) or model-predicted (in gray) time series for the participants. The close overlap indicates adequate model fit. The model slightly underestimates the occurrence of (nearly) constant NA experience, as evidenced by the larger red bar at the extreme right of the graph.

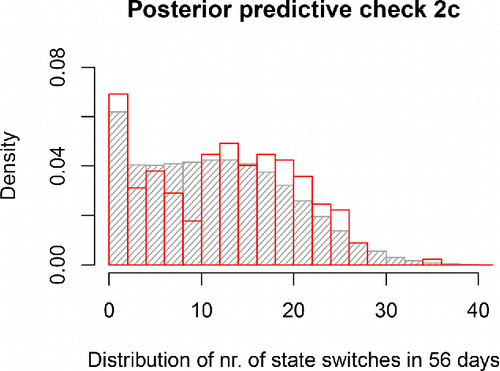
In a second check, we used the same simulated data, but we focused on the number of state switches during 56 days. As can be seen in Figures 6 and 7, the mean and SD of the empirical sample again fall near the middle of the posterior predictive distributions, and the distributions for individual persons also overlap closely between the model prediction and the empirical data. All of this indicates that the model fit is also adequate with regard to this statistic. Note that the empirical distribution has a high peak representing people who switched states 0–2 times, and the model’s posterior predictive distribution captures this closely.

Figure 6. Results of posterior predictive check 2 for the OMM. The red lines represent the empirical mean and SD of the number of state switches in 56 days. The histograms represent the model predictions, which take into account the uncertainty about the estimated model parameters.

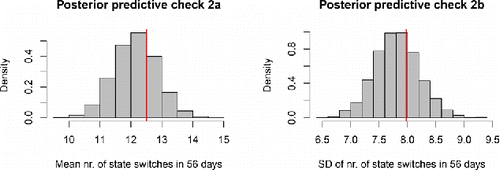
Figure 7. Distribution of the number of state switches in the empirical (in red) or model-predicted (in gray) time series for the participants. The close overlap shows that the model adequately captures the diversity among the study participants in how often they switched states.

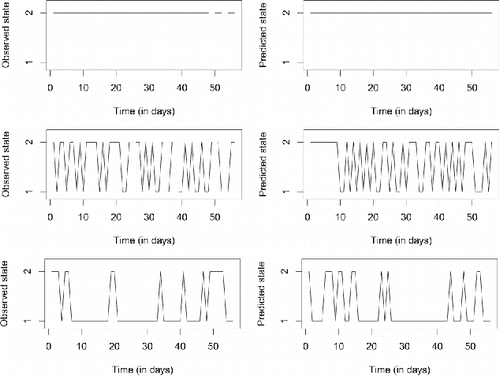
A way to illustrate (more than evaluate) the fit of the model, again following the example of Shirley and colleagues (2010), is to look at model-generated state trajectories for a few persons and compare them with their actual observed state trajectory. Figure 8 shows observed and predicted data for three persons characterized by high, low, and average state switching, respectively. The predicted time series in each case was generated using the median of the posterior samples for that person’s transition logits, together with their observed starting state and their neuroticism score. Because our model did not include time-varying predictors, a person’s predicted state at a specific day is not particularly meaningful or indicative of model fit, but rather the overall pattern of the predicted data (e.g., the switching frequency and the length of time spent in a particular state) should match that of the observed time series. If the model had included one or more time-varying predictors or if the transition logits were non-constant over time, then it would have been appropriate to check whether the predicted states matched the observed states at (roughly) the same day. From the three examples in Figure 8, it is clear that our model fits varying data patterns well: It can account for people who never switched states in the 56 days of the study, as well as for people who switched occasionally or almost constantly (or who were more likely to make one transition than the opposite one). For the first person, the model predicts that they are always in state 2 (experiencing NA) and this matches their observed data. The model predicts that the second and third person spend 59% and 25% of the days in state 2, respectively, which is close to the observed values of 57% and 27%. And the number of state switches in the predicted data for the second and third person is 34 or 17, respectively, versus 32 or 13 observed switches. We can also see that the model correctly predicts that the third person goes through long stretches of time in state 1, while rarely staying in state 2 for more than one or two days. The fact that the overall patterns in these predicted time series look similar to the observed data patterns illustrates that the model is flexible and that it fits the empirical data well.

Figure 8. Observed (left) and predicted (right) states for three persons with widely differing switching rates. In generating the predicted data, the posterior medians were used as point estimates of the transition logits. Note that the specific day at which a person is predicted to switch states is not indicative of model fit, since no time-varying predictors were used; it is the overall pattern (switching frequency, time spent in specific states) that should match between the observed and predicted data.

Conclusion

By using the OMM with a covariate and random effect, we had a simple and intuitive way of analyzing these data that accounted for the meaningful zero inflation and addressed the question of whether trait neuroticism is related to affect experience over time, as reflected in the propensity of an individual to report experiencing NA at all. As expected, we found that more neurotic persons are more likely to start experiencing NA, and less likely to stop experiencing it. The additional unexplained individual differences we found illustrate the importance of allowing for random effects in the model. Posterior predictive checks of the model fit indicated that the random effects enabled the model to adequately capture the wide range of diversity in NA experience among individual persons.

An LMM for observed family interactions

We now turn to our second data set, which comes from Kuppens, Allen and Sheeber (2010), who observed adolescents (N = 141; 94 females, 47 males; mean age = 16 years) and their parents while they participated in various 9-minute discussion tasks designed to elicit different interactions and emotions. The conversation task that we focus on here involved discussing positive and negative elements in the upbringing of the adolescent, and therefore it was expected to evoke both positive and negative interactions. The researchers used the Living in Family Environments coding system (LIFE; Hops, Biglan, Tolman, Arthur, & Longoria, 1995) to code the behavior of each individual during the conversation in realtime. The codes were then summarized in a time series variable, categorizing the behavior of each family member during each second (T = 539) as either angry, dysphoric, happy, or neutral (for more details, see Kuppens et al., 2010). We approach the resulting data set as a trivariate categorical time series, where the behavior of the mother, the father, and the adolescent are treated as indicators that reflect the family’s state at each time point. As such, in the transition model, we have at level 1 the time points, and at level 2 the family. In addition to the observational behavior data, the researchers measured whether the adolescents met criteria for clinical depression (there were 72 depressed and 69 non-depressed adolescents).

For our analysis, we used a mixed LMM that allows us to study the temporal dynamics of the family interaction and the between-family differences therein, as well as look at stable differences in observed behavior between individual adolescents, specifically between depressed and non-depressed adolescents.

Sheeber et al. (2009) and Kuppens et al. (2010) analyzed these data with a focus on the adolescents, using various specialized multilevel regression techniques to study, for example, the relationship between depression and emotional reactivity of the adolescents. However, as an alternative and supplementary approach, here we model the behavior of the family, considering the interaction between family members and analyzing them as a system; this is where the LMM comes in as a suitable model. When a family is participating in an interaction task designed to evoke some difficult emotions, it makes sense to expect that the family will switch between positive and negative (and neutral) interaction states. We expect that families differ in this regard, with some families being more prone to conflict than others, and we want to use a model that can take this into account through random effects in the transition model part. At the same time, we expect that the specific behavior of depressed adolescents may differ from that of non-depressed adolescents. A mixed LMM can incorporate both of these expectations, if it has random effects in the transition model part and random effects plus the predictor depression in the measurement model equations for the adolescent’s behavior. We would expect that depressed adolescents are more likely to behave dysphorically or angrily and less likely to behave happily, controlling for family states. In other words, we expect to find stable differences in behavior between depressed and non-depressed adolescents, that cannot be explained away by differences in family dynamics.

Some of the adolescents participated in the task with only one parent (42 participated with only their mother, and 4 with only their father). In our analyses, we only use the data for those families (N = 95) where two parents participated in the task, because it seems reasonable to expect that interactions between an adolescent and one parent may differ qualitatively from interactions between an adolescent and two parents, especially given the focus of the discussion task (namely, the upbringing of the adolescent). Furthermore, there may be differences between single-parent and two-parent families that would make it inappropriate to treat them as interchangeable “units” within the same multilevel model.⁴ The proportion of missing values for the selected families was 0.01%, 0.10%, and 0.32% for the adolescents, mothers, and fathers, respectively. These few missing values were handled in JAGS using Bayesian multiple imputation, in the same way as in the OMM discussed above.

Model

First, we compared LMMs with two and three states, in both cases with random effects in the transition model, but only fixed effects in the measurement model. As we discussed earlier, there is no straightforward statistical criterion to decide on the number of latent states in a Bayesian LMM, so we compared the estimates for the two models to determine which one offered the most useful substantive description of the data. We concluded that the three-state model made more sense, because the three states could be clearly interpreted as corresponding to positive, negative, and neutral family interactions, whereas the two-state model seemed to lump together neutral and negative interactions, making it less insightful. Hence, we focus here on the specifications and results for the three-state LMM.⁵

After deciding on the number of latent states, we added random effects in the measurement model for the adolescent’s behavior, to allow for differences in the behavior of the adolescents. These random effects are state-independent, implying that some adolescents are always more likely to act angrily than others, or that some are always more likely to act happily than others, and so on. We also included depression as a binary predictor in the measurement model for the adolescents, to reflect our hypothesis about stable differences in behavior between depressed and non-depressed adolescents.

Conditional on the latent states (s), the distribution for the observed data is given by (8) where b stands for the behavior category, and N and T are the number of families and time points, respectively. The parameters M_sb, F_sb, and A_sbn refer to the probabilities of behavior b given the current family state s; note that the probabilities A_sbn are person-specific. The expressions within square brackets evaluate to 0 or 1 depending on whether they are true. The full likelihood of the data and the latent family states together is given by (9) where the distribution of the latent states, conditional on the transition probabilities, and the starting state probabilities (π1), is specified as (10) with (11) and (12) for each family n and each i, j ∈ [1, …3], such that μ_ij is the average logit for the transition from state i to state j, and ε_ijn is family n’s deviation. For identification, we set μ_ij = ε_ijn = 0 whenever i = j, with the result that staying in the same state is always the reference transition for the logits. Thus, only 3 · 2 = 6 means and deviations need to be estimated, and the six deviations have a multivariate normal distribution with a zero mean vector of length 6, and a 6 × 6 covariance matrix Σ(ε).

In the measurement model part, the behaviors (b) 1, 2, 3, and 4 represent angry, dysphoric, happy, and neutral behavior, respectively. The probabilities A_sbn for the adolescents’ observed behavior are derived from person-specific logits, that is, (13) These logit parameters are modeled as (14) for each state s and for each behavior b, where μ_sb represents the logit intercept and β_b is the coefficient of the centered binary predictor depression, which is independent of the state, and ε_bn represents the stable (state-independent) individual deviation in the logits for behavior b. To identify the measurement model part, we specify ε_4n = μ_s4 = β₄ = 0 for each family state s, making neutral behavior the reference category for the (log) odds. The three random deviations have a multivariate normal distribution with zero means and a 3 × 3 covariance matrix Σ(beh).

Priors

An uninformative Dirichlet prior distribution with hyperparameters [1, 1, 1] was used for the initial state probabilities, and similarly, uninformative Dirichlet priors with hyperparameters [1, 1, 1, 1] were used for the mothers’ and fathers’ probabilities of exhibiting the four behaviors conditional on each latent family state. Similar to our specifications for the OMM, for the intercepts and regression coefficients (in both model parts), we specified independent Cauchy prior distributions with scale parameter (σ) 10 for the intercepts and 2.5 for the regression coefficients, and with location parameter 0 in all cases. We centered the predictor depression to have a mean of 0, but did not rescale it, in line with the advice of Gelman and colleagues (2008) concerning binary predictors. As we did in the OMM application, we first fitted a model with univariate random effects to avoid the risk of overestimating very small variances, and when we found that the variance estimates were all well over 0.1, we switched to a multivariate specification that allows the random effects within each model part to be correlated. The JAGS model syntax for the final model, that is, for the three-state mixed LMM with multivariate random effects, is provided in the Appendix.

Results

After a burnin period of 10,000 iterations, we used 50,000 additional iterations and a thinning parameter of 5 (storing every fifth value). Based on the trace plots, unimodal density plots and a second chain using different (random) starting values which arrived at a different state labeling but the same model results, we concluded that the convergence of the model was adequate. The labeling of the states appeared to remain constant over all iterations within a chain, which makes sense as the states were well separated. The results presented below are based on the 10,000 stored samples of the first chain.

To interpret the three family states, we look at the fixed parameter estimates for the measurement model part, which are given in Table 2. We see that the first state is the only one where there is a high likelihood of observing happy behavior (see the third column), so we refer to it as the positive state. The second state we interpret as the neutral state, because it is almost always characterized by neutral behavior of the parents, although the adolescents’ behavior varies a bit more. The third state has the highest probabilities of angry and dysphoric behavior of all three states, so it can be interpreted as a state of negative family interaction.

Table 2. Point estimates for the probabilities of different behavior types of each family member, conditional on the state the family is in. The probabilities for the average depressed and non-depressed adolescents are derived from the posterior medians of the average logits and the regression coefficients.

Behavior probabilities in state 1 (positive interaction)
	Angry	Dysphoric	Happy	Neutral
Average non-depressed adolescent	0.034	0.105	0.399	.462
Average depressed adolescent	0.040	0.170	0.361	.430
Mother	0.023	0.068	0.655	.255
Father	0.010	0.091	0.473	.426
Behavior probabilities in state 2 (neutral interaction)
Average non-depressed adolescent	0.028	0.165	0.097	.709
Average depressed adolescent	0.031	0.255	0.084	.629
Mother	< 0.001	< 0.001	< 0.001	.998
Father	< 0.001	0.004	< 0.001	.995
Behavior probabilities in state 3 (negative interaction)
Average non-depressed adolescent	0.045	0.219	0.080	.656
Average depressed adolescent	0.048	0.326	0.066	.560
Mother	0.114	0.530	< 0.001	.355
Father	0.072	0.452	< 0.001	.476

Looking at the average transition probabilities, given in Table 3, it can be concluded that the probabilities of staying in the same state are quite high for all three states. This makes sense when considering the short coding intervals, because family interaction states will tend to last longer than a single second. We also note that the average transition probabilities, unsurprisingly, indicate that families are unlikely to switch directly between positive and negative interactions (states 1 and 3), that is, they are more likely to make this transition by moving through a neutral interaction (state 2) first. In addition to the average transition probabilities, we have the estimated variance terms from Σ(ε) that provide a measure of how much the individual families differ in their transition probabilities. These estimates range from 0.28 (for the transition from state 2 to 3) to 1.09 (for the transition from state 3 to 2), but it is difficult to gauge the extent of the differences in probabilities between families from these logit variances. Therefore, it may be more insightful to derive the transition probabilities for the individual families, for the transitions with the smallest logit variance (the transition from state 2 to 3) and the largest logit variance (the transition from state 3 to 2). For the first one, we find that the minimum and maximum estimated probabilities for a family to make this transition (i.e., for switching from the neutral to the negative interaction state) are 0.014 and 0.102, respectively. For the second one, the smallest estimated probability of making this transition (i.e., of switching from a negative to a neutral interaction) is 0.004, while the highest probability is 0.279. These numbers give an indication of how the estimated random logit distribution translates into varying transition probabilities across families. Clearly, there are non-negligible differences in interaction dynamics between the families.

Table 3. Point estimates for the fixed effects in the transition model part. For the sake of interpretability, we present the implied probabilities, not the logits themselves. The value in row i, column j represents the probability, for an average family, of transitioning from state i to j.

Average transition probabilities
Transition to:	State 1	State 2	State 3
State 1	0.920	0.055	0.025
State 2	0.025	0.932	0.043
State 3	0.018	0.058	0.924

To address our hypothesis about depressed and non-depressed adolescents, we inspect the behavior probabilities for the average adolescent in each group (based on the parameters μ_sb and β_b of Equation 14(14) ), which are reported in Table 2. Although the differences in probabilities are modest, we see that depressed adolescents are, on average, more likely to act angrily or dysphorically than non-depressed adolescents. Another way of investigating differences between the two groups is to inspect the 95% CIs of the β regression coefficients. For example, the 95% CI for β₁ is [ − 0.32, 0.77], and since zero is included in this interval, we cannot conclude that the odds ratio of angry versus neutral behavior was different for depressed adolescents. However, the conclusion is different for the odds ratio of dysphoric versus neutral behavior, because the 95% CI for β₂ is [0.14, 0.94], indicating that depressed adolescents were more likely to exhibit dysphoria than non-depressed adolescents. The odds ratio of happy versus neutral behavior was not clearly different between the two groups, with β₃ having a 95% CI of [−0.47, 0.33]. Note that depressed adolescents were less likely to behave neutrally, based on the model-implied probabilities given in Table 2, but we cannot use a 95% CI to evaluate this difference directly, as neutral behavior was the reference category for the odds. Furthermore, we note that there was substantial variation of the behavior probabilities across adolescents, on top of the differences that were predicted by depression. The three variance parameters of the measurement model logits were 2.21, 1.55, and 0.93, and these are quite large even in comparison to the largest values contained in the 95% CIs for the three β parameters described above. Therefore, our results indicate that depression only explained a modest part of the person-specific variability in behavior of the adolescents.

Model fit

To assess the fit of the model, we used posterior predictive checks similar to the first two checks we used for the OMM. Since the latent states in an LMM cannot be directly compared to “true” states in the data (as we did for the states in the OMM in Figure 8), the posterior predictive checks here focus on the observable outcomes predicted by the LMM and known for the empirical sample: The affective behavior of family members.

We first checked whether the model adequately describes the proportion of negative behavior for mothers, fathers, and adolescents – distinguishing between depressed and non-depressed adolescents. In a similar way as we did for the OMM, we used the samples from the posterior distribution of the fixed effects and the random effects mean and covariance matrix to generate new random effects from the model, and new “observed” behavior for simulated families based on those random effects, conditional on the depression (or non-depression) of the observed adolescents. In other words, we generated data that reflects what kind of behavior we would expect to observe if the model is true and if we observed different samples of families like the ones in the empirical study.

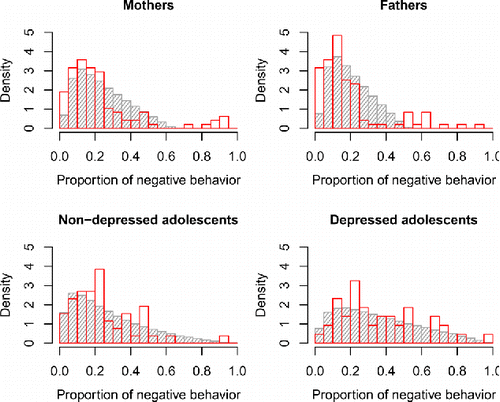
Figure 9 shows the results for the posterior check of the mean and standard deviation (over persons) of the proportion of negative behavior, for each family member separately. Note that the distributions for the two groups of adolescents are more spread out because the model estimates for either group are based on less information than the estimates concerning the parents’ behavior. As the Figure shows, the mean proportion of negative behavior for mothers, fathers, and for both groups of adolescents are captured well by the model, because in each case the statistic for the empirical data falls in the middle part of the posterior predictive distribution. When it comes to the standard deviation, the model fit is adequate for the adolescents, indicating that the random effects allow the model to capture the individual differences between adolescents in how often they showed angry or dysphoric (negative) behavior. The standard deviation for the observed mothers and fathers was larger than expected under the posterior predictive distribution, indicating that the model underestimates the diversity between individual parents in how often they behaved negatively. This indicates that additional random effects for the behavior of the parents’ might have improved the model further, but note that this would make the model very complicated and possibly empirically underidentified.

Figure 9. Results of posterior predictive check 1 for the LMM. The red lines represent the empirical mean and SD of the proportion of negative affective behavior. The histograms represent the model predictions, taking into account sampling variation as well as uncertainty about estimates.

Figure 10 shows the distribution of the proportion of negative behavior for individual people in the empirical sample (in red) and in the posterior predictive data (in gray), and this makes clear that the misfit for the mothers and fathers results from “extremes” in the empirical sample: Parents who displayed negative behavior very rarely (if at all), or very often, while the model predicts more moderate proportions of negative parent behavior. This misfit may occur because some families spent more time in negative interaction states than expected under the model, or because some individual parents deviated from the expected behavior. Overall the fit of the model is adequate, but we have to be cautious in interpreting the results given that we know the model does not describe all families equally well. In an in-depth empirical study, a result like this could be a reason to look closer at the data, and possibly other characteristics, of the individual families who are not described as well by the model as others.

Figure 10. Distribution of the proportion of negative affective behavior over persons, in the empirical data (in red) and in the model-predicted data (in gray).

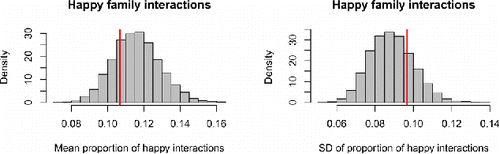
For a second posterior predictive check of the model fit, we used the same posterior predictive data, but focused on the proportion of “happy family interactions.” We define these as interactions where at least two of the three family members exhibited happy behavior. Figure 11 shows the results for the mean and SD over families of the proportion of happy interactions. It appears that neither the mean nor the SD of the empirical sample are extreme under the model prediction, indicating adequate fit with regard to this data characteristic.

Figure 11. Results of posterior predictive check 2 for the LMM. The red lines represent the empirical mean and SD of the proportion of happy family interactions (moments when at least two family members behaved happily). The histograms represent the model predictions, taking into account sampling variation as well as uncertainty about estimates.

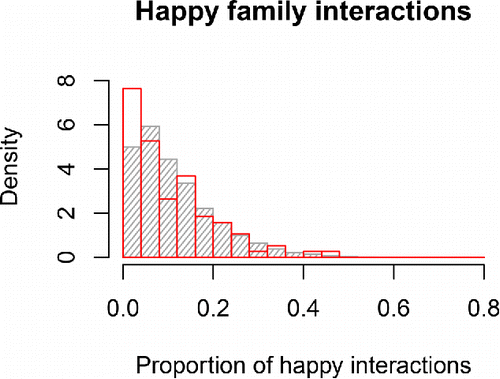
If we consider the distribution for the individual families in Figure 12, we see that there is some misfit due to an underestimation of the number of families who rarely or never displayed happy interactions according to our criterion. Similar to the first check, we can interpret these results as showing that the model does a good job of describing the average family in the sample and of capturing a large part of the inter-family differences, but it does not do a perfect job of describing the most “extreme” families in the sample. Therefore, our results should be interpreted with caution, and in an empirical study, it would make sense to further examine what other variables might be related to such differences.

Figure 12. Distribution of the proportion of happy interactions for empirical (in red) or model-predicted (in gray) families. In the empirical data, there were more families at the left end of the distribution, i.e., families where it rarely (or never) occurred that two family members behaved happily at the same time.

Conclusion

Our analysis has illustrated that by applying a mixed LMM to this problem, we can investigate inter-family and inter-individual differences in a single analysis, by allowing for random effects in the transition model and in the (adolescent’s) measurement model. In this analysis, we used a predictor variable in one part of the model, but a nice feature of the LMM is that predictors can potentially be used in both model parts, to represent diverse psychological accounts of how other characteristics relate to the process dynamics.

Substantively, our results indicated that depressed adolescents are more likely to behave angrily or dysphorically, compared with non-depressed adolescents. These differences cannot simply be attributed to possible different family dynamics, as those were to a large extent taken into account by the random effects in the transition part of our LMM. In conclusion, this example shows that an LMM can be used to address various, quite specific hypotheses using ILD, by offering the chance to study the temporal dynamics of a latent process while allowing for between-person (or between-unit) variation of several kinds. We also illustrated how posterior predictive checks can be used in the Bayesian model fitting context to investigate how well the model captures particular aspects of the empirical data, indicating where and how there is misfit of the model to the data.

Label switching was not an issue for our LMM application. The main practical challenges of the (mixed) LMM framework that we encountered in this analysis were the lack of an accessible, formal procedure for choosing the number of latent states empirically in the Bayesian context, and the computational intensity that made the analysis time consuming (i.e., taking several days), but we note that the latter issue is heavily dependent on the size of the data set and on the complexity of a given model formulation. It can be expected that further technological developments will increase computing speed so that the computational demand of Bayesian estimation of mixed LMMs will become less relevant for future applications. Furthermore, JAGS as well as other software packages that can implement (some) Bayesian models, such as Mplus (Muthén & Muthén, 1998–2015), are constantly being developed so that more efficient estimation algorithms for Markov models, or even RJMCMC implementations for determining the number of states in an LMM, are expected to become available and easily accessible.⁶ There is also ongoing research in the area of Bayesian model evaluation and comparison which leads to promising new approaches for assessing model fit from various perspectives (e.g., Vehtari, Gelman, & Gabry, 2017).

Discussion

In this paper, we set out to introduce the relatively unknown class of Markov models to psychological researchers, and to provide an introduction to how mixed Markov models may be used for the analysis of ILD. We have discussed how mixed Markov models can be specified, and have argued that while frequentist estimation has been used for these and similar models, Bayesian estimation has several advantages that are relevant in this research context. Two empirical applications demonstrated how mixed Markov models can be applied in a Bayesian framework and what kind of research questions they can address. Note that these analyses served as basic illustrations of the modeling approach, and did not involve in-depth or formal consideration of alternative models, or follow-up analyses of individual time series.

Markov models appear to be very flexible and can suit different types of data and research questions in the context of studying temporal processes. Mixed Markov models are especially promising, in our view, because they can be used to study individual differences in dynamics through the inclusion of person-specific random effects. In this paper, we discussed that the implementation of some Markov models, namely LMMs and especially mixed LMMs, can be computationally demanding and that the Bayesian approach, while advantageous in some regards, does not offer a straightforward way to choose the number of latent states empirically. Despite these limitations, this modeling framework provided useful insights for both of our empirical data sets, and we feel that it deserves more consideration in intensive longitudinal research in psychology. We hope that this paper contributes to (further) familiarizing psychological researchers with the possibilities offered by Markov modeling.

At this point, we consider a few limitations of the presented framework along with possibilities for adapting the general approach to different research situations. First, in the models that we presented, the state transition probabilities were constant over time. This assumption makes sense in the context of ILD analysis, where the focus is typically on short-term reversible variability in stationary processes, rather than on an expected pattern of growth or decline. Note, however, that it is possible to relax this model assumption in situations where the parameters describing the process are expected to change over time, or where a continuous observed variable shows a time trend above and beyond the fluctuations explained by state switching. The specification of time-varying parameters is covered in Bartolucci et al. (2013), along with other possibilities such as specifying a measurement model for ordinal observed categories, or dealing with the scenario where a specific state transition is theoretically impossible. MacDonald and Zucchini (2009) also present several variations of LMM applications. While allowing the same model parameter to be different for each person ánd each time point necessarily leads to an unidentified model, it should be possible to combine some degree of time heterogeneity, which could involve a time-varying predictor, with person-specific random effects or with discrete components as in the mixture Markov model. As a more general matter, it should be noted that the Markov models treated in this paper represent but one instance of a broad and diverse class of modeling approaches and that Markov state switching can also be combined with other models, such as autoregressive models for ILD, to allow for time-varying parameters in those models. For example, Markov-switching vector-autoregressive models are treated in detail in Fiorentini, Planas and Rossi (2016), and a Bayesian approach for such models is discussed in Harris (1997). General overviews of various Markov switching and state-space models are given in Frühwirth-Schnatter (2006) and Kim and Nelson (1999).

A second consideration is that the Markov models discussed in this paper come with the assumption of equally spaced measurements. This assumption will be violated when data is collected using the Experience Sampling Method (ESM; Larson & Csikszentmihalyi, 1983), where the time intervals between measurements have varying lengths. If a discrete-time Markov model is fitted to such a data set, it can be expected that the estimates of the transition probabilities are somewhat more noisy and that, consequently, there is less power to detect covariate effects. A better alternative for unequally spaced measurements may be to switch to a continuous-time formulation of the Markov model, where the temporal structure of the state-switching process is captured in a transition intensity matrix instead of a probability matrix (cf. Karlin & Taylor, 1975). Continuous-time Markov models can be implemented in JAGS using the inbuilt dmstate distribution (Plummer, 2013), or with classical estimation using the R package msm (Jackson, 2013), but the latter cannot (yet) handle random effects in the transition model.

An ongoing discussion in longitudinal research, more generally, focuses on how to determine an optimal time lag between measurements for modeling particular relationships (for example, Reichardt, 2011; Dorman & Griffin, 2015). When the time intervals between measurements are short, there could be relationships between measurements farther apart, and this could be investigated by using higher order models, where the current state is modeled as depending on multiple preceding states (MacDonald & Zucchini, 2009). When measurement intervals are outside an optimal range (whether too short or too long), relationships or lagged effects may be obscured or spuriously induced, so it is important to consider in the design phase of a study how quickly and how often the state switches and effects of interest are expected to occur. For instance, while mood fluctuations may take place over hours or days, behavioral observation needs to use a suitably fine scale to capture real-time interactions. In the context of the optimal lag problem, it is again relevant to note that continuous-time modeling has been proposed as a way to avoid the lag-dependency inherent in all discrete-time modeling of equally spaced data (Deboeck & Preacher, 2016).

In conclusion, although there are some unresolved questions, we believe that intensive longitudinal methods combined with Markov modeling techniques can be of great value for psychological research, as it enables us to study the dynamics of state-switching processes and to shed light on between-person differences in these dynamics. We expect that further developments in software and computing power, as well as in statistical approaches to Bayesian model evaluation, will contribute to solving current challenges in applying Bayesian mixed LMMs and facilitate easier implementation of Markov models.

Article Information

Conflict of Interest Disclosures: Each author signed a form for disclosure of potential conflicts of interest. No authors reported any financial or other conflicts of interest in relation to the work described.

Ethical Principles: The authors affirm having followed professional ethical guidelines in preparing this work. These guidelines include obtaining informed consent from human participants, maintaining ethical treatment and respect for the rights of human or animal participants, and ensuring the privacy of participants and their data, such as ensuring that individual participants cannot be identified in reported results or from publicly available original or archival data.

Funding: This work was supported by Grant VIDI 452-10-007 from the Netherlands Organization for Scientific Research, and the empirical data sets used in this study had been previously collected with the support of grants 1 R01 AG023571-A1-01 from the National Institute on Aging and NIMH R01 MH65340 from the National Institute of Mental Health.

Role of the Funders/Sponsors: None of the funders or sponsors of this research had any role in the design and conduct of the study; collection, management, analysis, and interpretation of data; preparation, review, or approval of the manuscript; or decision to submit the manuscript for publication.

Acknowledgments: The authors would like to thank the editor and the reviewers at Multivariate Behavioral Research for their comments on prior versions of this manuscript. The ideas and opinions expressed herein are those of the authors alone, and endorsement by the authors' institutions or the Netherlands Organization for Scientific Research or the National Institute on Aging or the National Institute of Mental Health is not intended and should not be inferred.

Notes

1 For an extensive discussion of classical estimation of Markov models, readers are referred to the textbooks by Bartolucci et al. (2013) and MacDonald and Zucchini (2009), and examples of LMM applications involving various types of random effects, and their computational details, can also be found in Maruotti and Rocci (2012), Altman (2007), Jackson, Albert and Zhang (2015), and Crayen, Eid, Lischetzke, Courvoisier and Vermunt (2012).

2 The reason that classical maximum likelihood estimation methods do not present this problem is that they search for a mode of the likelihood function conditional on a given labeling (Frühwirth-Schnatter, 2006).

3 Note that randomly generating all the starting values is not effective in all situations, because depending on the model complexity and on how wrong the starting values are, the sampling algorithm may get stuck and fail to converge to the posterior distribution. Convergence can be aided by choosing realistic starting values (for some parameters) based, for instance, on ML estimation of (a part of) the model, or a reasonable order of magnitude. In that case, to check that the results are independent of the starting values, one can still use different sets of starting values that reflect a range of possible values; for instance, a medium-sized positive regression effect and a medium-sized negative one both have a realistic order of magnitude, but are different enough in their interpretation.

4 Results for an analysis including all 141 families are available on request from the corresponding author. There were small differences in the results (with one behavior probability differing by 0.21, but most by less than 0.05–0.10) which could, however, simply result from sampling variation and loss of data. Overall, the conclusions from the two analyses are similar.

5 Results for the two-state model are available on request from the corresponding author.

6 Stan (Carpenter et al., 2017) is another recently developed Bayesian language that can be used with R, but it cannot fit models with discrete parameters, such as latent Markov models or other mixture models.