Bayesian PTSD-Trajectory Analysis with Informed Priors Based on a Systematic Literature Search and Expert Elicitation

ABSTRACT

There is a recent increase in interest of Bayesian analysis. However, little effort has been made thus far to directly incorporate background knowledge via the prior distribution into the analyses. This process might be especially useful in the context of latent growth mixture modeling when one or more of the latent groups are expected to be relatively small due to what we refer to as limited data. We argue that the use of Bayesian statistics has great advantages in limited data situations, but only if background knowledge can be incorporated into the analysis via prior distributions. We highlight these advantages through a data set including patients with burn injuries and analyze trajectories of posttraumatic stress symptoms using the Bayesian framework following the steps of the WAMBS-checklist. In the included example, we illustrate how to obtain background information using previous literature based on a systematic literature search and by using expert knowledge. Finally, we show how to translate this knowledge into prior distributions and we illustrate the importance of conducting a prior sensitivity analysis. Although our example is from the trauma field, the techniques we illustrate can be applied to any field.

KEYWORDS:

• Bayesian statistics
• Latent class analysis
• Mixture modeling
• Latent growth models
• PTSD

Introduction

Bayesian analyses are becoming ever more popular in many different disciplines, see the systematic reviews in the fields of organizational science (Kruschke, 2010), psychometrics (Rupp, Dey, & Zumbo, 2004), health technology (Spiegelhalter, Myles, Jones, & Abrams, 2000), epidemiology (Rietbergen, Debray, Klugkist, Janssen, & Moons, 2017), education (Köning & van de Schoot, 2017), medicine (Ashby, 2006), psychotraumatology (van de Schoot, Schalken, & Olff, 2017), and psychology (van de Schoot, Winter, Ryan, Zondervan-Zwijnenburg, & Depaoli, 2017). One reason why Bayesian statistics is increasing in popularity is because it does not require large samples (i.e., it does not rely on the central limit theorem), and hence it may produce reasonable results even with small-to-moderate sample sizes as we discuss in this paper. Many simulation studies have indeed shown that Bayesian estimation outperforms other estimation methods using small sample sizes and a wide range of statistical models (see the next section). In general, the simulation literature has concluded that small sample sizes can be aided by additional background information (via the prior) to produce accurate results. However, there are currently few articles that detail the elicitation and incorporation of such information using real background information (as opposed to hypothetical, or unrealistic examples), and this is the aim of this paper.

Note we use the term “limited data” instead of “small data” when we refer to a small sample. The reason behind this terminology is that we want to stress that the Bayesian methods we present here are especially meant for situations where gathering more data is not possible, extremely difficult, or too expensive. That is, researchers often have difficulties collecting enough data; i.e., when targeting groups that are small (e.g., children with severe burn injuries), hard to access (e.g., infants of drug-dependent mothers), or those that include prohibitive costs (e.g., measuring phonological difficulties of babies). Such obstacles to gathering data lead to a limited data set, where researchers are bound by data collection (or otherwise) circumstances and cannot collect “enough” data. The methods discussed in our paper are especially meant for such a situation and do not necessarily translate to every small sample situation.

The main goals of this paper surround the specification of priors using subjective methods to determine a plausible parameter space. Since we know that at least some degree of information is necessary to properly estimate limited data, then the next question is: Where does this information come from and what does it need to “look like” in the model? There are many different ways to specify subjective priors (e.g., using a meta-analysis, expert elicitation, previous data analysis), and none are inherently right or wrong. We dive into the realm of specifying these priors through the use of a systematic review, as well as through expert elicitation. Before delving into these issues, we describe the empirical data and the statistical model. In what follows, we first illustrate a method for extracting background information from published work for latent growth mixture modeling (LGMM; van de Schoot, Sijbrandij, Winter, Depaoli, & Vermunt, 2017) applied to extracting latent trajectories of posttraumatic stress symptoms (PTSS) after a traumatic event. The sources of background knowledge are a systematic literature search of the literature on PTSS trajectories after trauma, as well as expert opinions. This background information will then be used to determine the plausible parameter space for the parameters of the LGMM; we also provide a description for how this differs from determining exact parameter values. Next, we detail how the information can be translated into prior distributions with specific hyperparameter values that determine the shape of the prior distributions. We then present data analyses that include patients with burn injuries who are experiencing symptoms of PTSS (Van Loey, Maas, Faber, & Taal, 2003). This example follows the steps of the WAMBS-checklist (When to Worry and How to Avoid the Misuse of Bayesian Statistics; Depaoli & van de Schoot, 2017), which was used to ensure each phase of the Bayesian analysis was conducted thoroughly and correctly. We also present a strong argument that this process for defining priors should be accompanied by a sensitivity analysis to fully understand the impact of the priors on final model results.

We only briefly introduce Bayesian statistics with a special focus on the specific statistical model used to analyze our data (i.e., the LGMM). We assume a general understanding of Bayesian methods, as well as Bayesian LGMM. Readers looking to learn more about Bayesian estimation are referred to Van de Schoot, Broere, Perryck, Zondervan-Zwijnenburg, and Van Loey (2015), and those interested in Bayesian LGMM are referred to Depaoli & Boyajian (2014). We put all the relevant information needed to replicate our findings, including the systematic review data, all the R-scripts, Mplus code and, logbooks, the example data, and much more, on the Open Science Framework (OSF; see https://osf.io/vk4be).

Trajectories of PTSS, the issue of limited data, and a Bayesian solution

To illustrate how to translate background knowledge into statistical prior distributions, we use an empirical example throughout this paper. This example was selected because: (1) it carries particular challenges that can be solved using Bayesian techniques; (2) the data collection is always challenging, leading to limited data; and (3) there is enough background knowledge available to specify priors.

After traumatic events, including burns, approximately 10% of patients develop posttraumatic stress disorder (PTSD; Breslau & Davis, 1992; de Vries & Olff, 2009; Ter Smitten, de Graaf, & Van Loey, 2011). Although a substantially larger group experiences acute stress symptoms, these symptoms usually subside within the following weeks to months in many individuals (Shalev, Peri, Canetti, & Schreiber, 1996). Responses to trauma differ widely, from being resilient (Southwick, Bonanno, Masten, Panter-Brick, & Yehuda, 2014), to quickly recovering while for a subgroup of individuals, posttraumatic stress symptoms (PTSS) may persist for years (Smid, Van Der Velden, Gersons, & Kleber, 2012). From a clinical point of view, it is important to understand how PTSS develops over time and which factors are predictive for the different development patterns (Thordardottir et al., 2016). An increasing number of studies have used LGMMs to identify PTSS trajectories¹ (e.g., Bonanno et al., 2012; Mouthaan et al., 2013; Pietrzak, Van Ness, Fried, Galea, & Norris, 2013; Thormar et al., 2016; Van Loey, van de Schoot, & Faber, 2012).

Currently, most empirical evidence in trauma studies points to four distinct patterns (or LGMM trajectories) of PTSS (see our systematic review results described later). There are two relatively stable patterns, often labeled as the resilient and chronic trajectories. In addition, there are two dynamic patterns, one decreasing recovery trajectory and one increasing delayed onset trajectory. Of note, the chronic trajectory and the delayed onset trajectory are usually quite small in size (Smid, Mooren, van der Mast, Gersons, & Kleber, 2009). This increases their risk of being overlooked by researchers or overwhelmed by larger trajectories, which is particularly true for the delayed onset group. Once discharged from the hospital, individuals in this group may escape clinical attention (largely because their symptoms have a delayed onset), depriving them from treatment. The problem is that these individuals are highly clinically relevant because their symptom patterns reach a pronounced level of severity. Thus, it is imperative for clinicians to develop and test strategies to reliably detect these important but smaller groups that are in need of treatment and follow-up.

Using the conventional (non-Bayesian) LGMM estimation method, the extraction of the correct number of latent classes might be difficult to obtain. Proper latent class extraction depends on a number of factors, including: class separation (e.g., how statistically similar two latent classes appear to be), model complexity, and other properties of the model like number of classes and inclusion of covariates (Lubke & Neale, 2008). This difficulty in estimation is especially true for limited data but also when one of the latent classes (or clusters) is expected to be relatively smaller than the others. This claim has been supported by recent methodological studies, which consistently point to limitations of traditional approaches estimating LGMMs on smaller sample sizes (Bauer & Curran, 2003; Henson, Reise, & Kim, 2007; Tofighi & Enders, 2008). In particular, simulation research has shown that the relative size of the latent clusters may even have a stronger (negative) impact on parameter estimates than the total sample size of the data set (Depaoli, 2013). When two clusters differ drastically in size (e.g., when one cluster is much larger in size compared to another), then the larger cluster can overwhelm the smaller cluster, thus resulting in inaccurate estimates of cluster sizes and corresponding trajectory shapes.

When only a small number of cases represent, for example, the chronic or delayed onset group, then LGMM might struggle to identify these individuals as representing distinct latent classes (Depaoli, van de Schoot, van Loey, & Sijbrandij, 2015). There are different explanations for why some of the trajectories may not have been found in previous PTSS research. Trajectories might be based on outliers, or other random fluctuations, rather than substantive clusters (Bauer & Curran, 2003). In addition, some of the trajectories may not have been present in some of the previous data sets examined on the topic. For example, when data collection is started more than 6 months following the trauma (e.g., Pietrzak et al., 2013), a formal delayed onset trajectory cannot be detected since there is no information about an increase in symptoms from an initial lower level.² It may also be the case that this trajectory cannot be detected because the data collection ended too early (e.g., within 6 months), hence the symptoms did not have enough time to reach the increasing point or reach full-blown PTSD. Small trajectories can also be “missed” in the analysis phase if the estimation method selected does not perform well with smaller samples. Maximum likelihood (ML) estimation might have particular issues with estimating small trajectories given that it is based on large-sample theory, and this is something that the Bayesian estimation framework might be able to solve.

With limited data, ML estimates have the tendency to be unreasonably extreme (or out of bounds)—whereas Bayesian estimates are not. The reason is that the Bayesian framework can be used to “shrink” extreme estimates by incorporating information within the prior distribution (e.g., Rouder, Sun, Speckman, Lu, & Zhou, 2003). This issue has been illustrated in general (Baldwin & Fellingham, 2013), for longitudinal models (Van de Schoot et al., 2015), as well as with LGMMs (De la Cruz-Mesía, Quintana, & Marshall, 2008; Depaoli, 2013; Kohli, Hughes, Wang, Zopluoglu, & Davison, 2015; Lenk & Desarbo, 2000). Note that we do not mean to imply that noninformative priors always result in inaccurate model results. However, these types of priors carry advantages in a variety of situations. They can be used to purposefully incorporate a great deal of uncertainty in model parameter values. Likewise, noninformative priors are often used to estimate models, that would be otherwise intractable under ML, but without adding additional information into the model. In addition, when the data are limited and the degree of residual variance is also small, then one can still use noninformative priors to get stable estimates; an example of this is using Bayesian methods with noninformative priors for complex hierarchical models.

Even though Bayesian estimation does not rely on large-sample theory, it is not a fix-all cure for limited data problems. The structure and specification of the priors plays an important role regarding whether Bayes will outperform ML with limited data. In a systematic review of Bayesian papers (van de Schoot et al., 2017), it was concluded that with limited data, priors with even a minor degree of information (i.e., weakly priors) provide more accurate estimates. Optimal parameter recovery is obtained through the Bayesian approach using “accurate” priors (Depaoli, 2013); an incorrect choice of prior might bias the results dramatically (e.g., Hox, van de Schoot, & Matthijsse, 2012; Van de Schoot et al., 2015). However, we can mitigate this issue by increasing the uncertainty in the prior (through the variance hyperparameter) to mimic a weakly informed prior (Kohli et al., 2015). Therefore, we propose to use background information to specify priors that cover a plausible parameter space. A plausible parameter space captures a range of possible parameter values that is considered to be a reasonable range thereby excluding impossible values and attaining only a limited density mass to implausible values. How to specify such priors is exactly what we illustrate in the next sections to follow.

Example data

In a sample comprised of burn patients, we illustrate how Bayesian estimation might overcome the limited data issue. The data used in this study were previously described by Van Loey et al. (2003) and include a multicenter cohort of patients with burns who were admitted to a burn center between February 1997 and February 2000. Of the 321 patients who met the inclusion criteria, 301 patients (94%) consented to participate. Of the 301 patients, 231 were male (77%) and 70 were female (23%), ranging in age from 16 to 70 years (M = 38.5, SD = 13.5). Patients were assessed during hospitalization and subsequently every 8 weeks until 12 months after the burn event. Questionnaires were sent to participants by mail, including a return envelope. For more details, we refer to Van Loey et al., and the data we used for this paper can be found on the OSF (https://osf.io/vk4be/).

Measures

The Impact of Event Scale (IES; Horowitz, Wilner, & Alvarez, 1979) was used to assess PTSS. The IES is a 15-item self-report scale used to assess intrusive and avoidant symptoms associated with the experience of a particular event. The IES has been shown to effectively discriminate between individuals with posttraumatic stress disorder and noncases in a burn population (Sveen et al., 2010). Cronbach's alpha ranged between.77 and.87 in a previous study of patients of burn survivors, indicating good internal consistency (Bakker, Van der Heijden, Van Son, & Van Loey, 2013). In this study, the validated Dutch version (Brom & Kleber, 1985) was used but was scored differently on a 0 (not at all) to 100 (the worst imaginable way) visual analogue scale. Item scores were added and divided by the total item number resulting in a total score ranging from 0 to 100 instead of the original range of the IES running between 0 and 75. Van Loey et al. (2003) assumed that a cutoff point of 25 corresponded with a score of 33 on the analogue scale; both cutoffs are located at 1/3 of the total score.

The parameters in the statistical model

In this section, we introduce the statistical model used in our paper. A formal presentation of the LGMM model, including the statistical notation used throughout the paper, can be found in Appendix B, available online as supplementary material on the publisher's website. Although many of the model details are presented in online Appendix B, we also describe all of the unknown parameters here since they are linked to the prior specification described later.

To estimate trajectory membership, a conventional latent growth model is combined with a mixture component (e.g., Vermunt, 2010) to uncover unobserved subgroups of individuals developing over time (Muthén & Muthén, 2000). Within mixture modeling, it is assumed that growth parameters (i.e., intercept, slope, etc.) vary across a number of pre-specified, unobserved subpopulations. This results in separate latent growth models for each (unobserved) group, each with its unique set of growth parameters. The statistical model we used to analyze the PTSS-data (n = 301) incorporates a random intercept, a random slope parameter, and a random quadratic parameter. The first two waves of data collection were two- and three-weeks posttrauma, and another six subsequent waves were collected at eight-week intervals; these eight time points are further denoted by IES₁-IES₈. To ease the interpretation of the general trend line and the specific growth parameters, we decided to parameterize the metric of time in such a way that the intercept is actually the mean IES score at 3 months after trauma. The factor loadings of the slope parameter are specified as follows (the first column representing the factor loadings for the intercept, the second column for the slope, and the third column for the quadratic term):

Because the intercept was specified as occurring at 3 months after trauma, both the linear and quadratic slope terms had to be specified so that the 3-month-point would coincide with a value of 0 on both of these slope terms. Thus, the first measurement point, two weeks posttrauma, is now specified as occurring 11 weeks before the three months after trauma point, or –11. Squaring –11 gives us a value of 121 for the quadratic term. This method was applied to all time points and resulted in the matrix presented above.

The latent growth model was extended to include a mixture component. This indicates that the individuals follow a mixture of distributions, where each mixture component represents a latent class with (potentially) substantively different growth trajectories. The mean (but not the variance, as is default in the Mplus software) for the intercept, slope, and quadratic terms were allowed to vary across latent classes (denoted by I_k, S_k, Q_k, and σ²_I, σ_S², σ²_Q, respectively for k number of classes). This specification allows for each class to be represented by a substantively different growth trajectory. Furthermore, each individual obtains an unknown class probability of belonging to each class, and individuals are assigned to a latent class based on their highest posterior probability. All models were estimated using the software program Mplus v7.3.1 (Muthén & Muthén, 1998–2015).

The unknown parameters in our model are: class size, denoted by π₁, π₂, …, π_k for k number of classes; the means for the intercept, slope, and quadratic terms estimated for each trajectory separately (I_k, S_k, Q_k); and their variances and covariances:

Finally, the residuals for the observed IES variables were also included. More details of this model are presented in online Appendix B and the actual specification in Mplus can be found on the OSF (https://osf.io/vk4be/).

Estimation method and the WAMBS-checklist

There are three essential ingredients underlying Bayesian statistics. The first ingredient is the background knowledge of the parameters in the model being tested and is captured in the so-called prior distribution (or prior). The prior is a probability distribution reflecting the researchers' beliefs surrounding the parameter value in the population, as well as the certainty the researcher has regarding this belief. The level of informativeness of a prior is governed by hyperparameters. For example, for a normal distribution denoted by N(μ₀, σ²₀), where N denotes that the prior follows a normal distribution, the mean of the prior is given by μ₀, and σ²₀ is the prior variance. Consequently, μ₀ is based on background information, and σ²₀ can be used to specify how certain one is about the value of μ₀. The second ingredient is the information in the data itself. It is the observed evidence expressed in terms of the likelihood function of the data given the parameters. Both ingredients (i.e., the prior and the likelihood) are combined via Bayes Theorem and are summarized by the so-called posterior distribution, which is a compromise of the prior knowledge and the observed evidence. For a full introduction to Bayesian modeling, we refer the novice reader to, among many others: Kaplan (2014), Kaplan and Depaoli (2012), Kruschke (2014), or Van de Schoot et al. (2014). Likewise, a more technical introduction can be found in Gelman et al. (2004). To assess each step of the Bayesian process, we follow the 10-point checklist developed by Depaoli and van de Schoot (2017), which is summarized in Table 1.

Table 1. Summary of the 10 points of the WAMBS checklist and how each item was dealt with. See also the supplementary materials at the Open Science Framework (OSF; https://osf.io/vk4be/) for a detailed logbook, the Mplus and R files, and the relevant output files.

Item of the WAMBS Checklist	Addressing the Checklist Item
Point 1: Do you understand the priors?	The prior has the potential to have a rather large impact on final model results. As a result, it is important to report all details surrounding the prior. See the description of the priors in the section titled “Prior Specifications”
Point 2: Does the trace-plot exhibit convergence?	In order to ensure estimates can be trusted, the trace plot must be inspected for convergence (i.e., the mean—or horizontal middle of the chain—, and the variance—or height of the chain—, have stabilized). We relied on the potential scale reduction factor (PSRF; Gelman & Rubin, 1992) to assess for convergence. If this factor is near 1.0, within some preset bound, then chains are said to have converged. We initially specified that a chain had to be a minimum of 200,000 iterations (with the first half discarded as the burn-in phase). The models for both parameterizations, with the priors as specified in the previous section, converged with our original 200,000 iterations according to the PSRF.
Point 3: Does convergence remain after doubling the number of iterations?	Then an additional check of convergence is necessary, using double the amount of iterations to avoid obtaining what we call local convergence. It appeared the difference (measured through bias, see Depaoli and van de Schoot, 2015) between the original model and the model with double number of iterations was always lower than 1%. The one exception to this was for the recovering group linear slope mean (bias was 2.56% between the two chain settings), but the difference in absolute terms was deemed negligible at only 0.001.
Point 4: Does the histogram have enough information?	Visual inspection of the histogram ensures all samples pulled from the posterior adequately represent the distribution. Upon inspection of the posteriors for smoothness, no problematic issues were found. See the online supplementary materials at OSF.
Point 5: Do the chains exhibit a strong degree of autocorrelation?	Autocorrelation should be examined as a potential sign of model mis-specification. We inspected all of the autocorrelation plots and there were no problematic issues uncovered, see the online supplementary materials available at OSF.
Point 6: Does the posterior distribution make substantive sense?	It is important to check for substantive abnormalities in the posterior distribution. We inspected all of the Kernel density plots and there were no problematic issues uncovered, see the online supplementary materials available at OSF.
Point 7: Do different specifications of the multivariate variance priors influence the results?	Handling a multivariate variance prior has technical complexities that can have some severe issues if this prior is not specified properly. The multivariate priors used in this situation can be quite difficult to navigate and require detailed consideration during implementation. If the prior(s) on the covariance matrix is not well understood it is recommended to always assess an alternative setting for this prior and compare the model results to the original default setting results obtained in previous stages. However, the default settings used here were deemed sufficient during estimation and therefore not examined any further.
Point 8: Is there a notable effect of the prior when compared with noninformative priors?	When using (weakly) informative priors, it is important is to report a sensitivity analysis of priors to illustrate how robust final model results are when priors are slightly (or even greatly) modified; this provides a better understanding of the role of the prior in the analysis. This point concerns using noninformative priors for all model parameters and comparing the results with the (weakly) informed priors. We used a technique comparing estimates across the sensitivity analysis via percent bias (or percent deviation) across estimates obtained using informative priors and noninformative priors. We describe results for this point in the section titled “Comparing the informative model to the uninformative model”.
Point 9: Are the results stable from a sensitivity analysis?	When (weakly) informative priors are in place, then there might be a discrepancy between results using slightly different prior settings. A sensitivity analysis would entail adjusting hyperparameters upward and downward and re-estimating the model with these varied priors. Several different hyperparameter specifications can be made in a sensitivity analysis, and results obtained will point toward the impact of small fluctuations in hyperparameter values. We used a technique comparing estimates across the sensitivity analysis via percent bias (or percent deviation) across estimates obtained using informative priors and different derivations of these priors. We describe results for this point in the section titled “Comparing the informative model to alternative informative models”.
Point 10: Is the Bayesian way of interpreting and reporting model results used? (a) Also report on: missing data, model fit and comparison, nonresponse, generalizability, ability to replicate, etc.	Bayesian analyses have many distinct features that are not a part of traditional frequentist methods. As a result, there are different considerations when writing up results for a Bayesian model to ensure that all information has been properly conveyed and that results can be replicated or priors can be extracted and then updated in future Bayesian models. It is important to report Bayesian results with the proper interpretation of model parameters, as well as the type of results obtained (e.g., an estimated posterior distribution versus an estimated parameter value).

Background information

Incorporating background knowledge can be accomplished by modifying the priors on the unknown parameters of the LGMM or any other model—specifically, by choosing the type of prior distribution and by modifying the hyperparameters. In this section, we explain which background information we used to specify the plausible parameter space, namely a systematic literature search and an expert meeting.

Systematic literature search

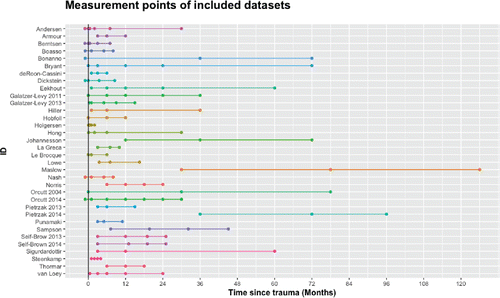
We performed a systematic search to identify longitudinal studies that applied LGMM, latent growth curve analysis, or hierarchical cluster analysis on symptoms of posttraumatic stress assessed after trauma exposure. Our search identified 11,395 papers, 34 of which satisfied the selection criteria; see Figure 1 for the PRISMA flow chart (Preferred Reporting Items for Systematic Reviews and Meta-Analyses³), and see Appendix A for details of the search and an overview of the included papers. Also, all (raw) files for the systematic search can be found on the OSF (https://osf.io/vk4be/). To compare the trajectories across papers, we created the plots in Figure 2.

Figure 1. PRISMA flow chart for our systematic search. The search for articles using LGMM to study the development of PTSD focused on four major databases: Pubmed, Embase, PsychInfo, and Scopus. After the database search and screening, we attempted to find additional relevant articles in two ways. First, we used Scopus to export the reference lists of the studies included in our qualitative analysis. Second, we used Scopus to export the articles that have cited the studies included in our qualitative analyses since their publication. All of the papers were screened in two rounds; see Appendix A for details.

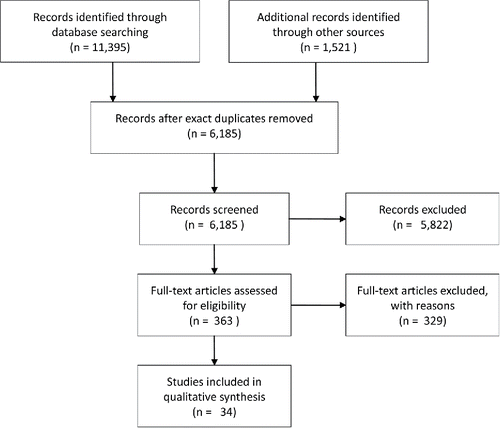
Figure 2. Visualization of the trajectories found in the 34 papers for each of the four “classical” trajectories separately. We used the following step-wise approach. First, if the observed or estimated means of each trajectory at each time point are reported in a table, then we used those numbers. Second, if the intercepts were reported, then we used those numbers for the first time-point. Finally, if no numbers were reported, then we used the graph to approximate the means at each time point. As the papers used several different PTSD scales (on different scales of measurement), we rescaled the data for each paper to adhere to a 0 to 100 point scale. As such, it is important to note that the trajectories we included are rough approximations of the trajectories found in the papers identified through the systematic review.

Expert opinions

In addition, we interviewed 22 PTSD experts, who were senior authors on many of the papers identified in our systematic search, and collected their opinions about the parameters of the LGMM model during an expert meeting held at Utrecht University, The Netherlands. This meeting was a part of the International Society for Traumatic Stress Studies (ISTSS) global meetings program. We asked the participating researchers what they expected regarding the shape of the four trajectories (see the OSF for the raw, anonymous results; https://osf.io/vk4be/). After the meeting, we sent a follow-up email with additional questions about the expected shapes of the trajectories; see Appendix C, available online as supplementary material on the publisher's website for the exact questions we asked, as well as a summary of the responses.

Plausible parameter space

We used the findings obtained from the systematic search, and especially the information from Figure 2, as well as the experts' opinions to specify a plausible parameter space. Recall that the main conclusion from the simulation studies cited above was that weakly informative priors should be specified to deal with sparse data. We interpreted this as requiring the following actions: (1) truncate parts of the parameter space that are completely impossible, due to the scale of the variables used, and (2) to specify plausible parameter space for each of the four “classical” trajectories defined by the literature and experts. These two points were completed and are reflected in Figure 3. As can be seen in this figure, there is some consensus about the general shape of the four trajectories, but there is also some disagreement about the exact shape of the trend line. However, it is important to recognize that a big proportion of the total parameter space has been removed. In the next section we use the information from Figure 3 to aid in the exact prior specification phase of data analysis.

Figure 3. Summary of the background information about the trend line for the four “classical” trajectories, thereby defining plausible parameter space.

Prior specifications

There are three sets of priors in our model:

(1)	the proportions for the latent clusters;
(2)	the estimates for the intercept, slope, and quadratic term;
(3)	the (co)variances of these parameters and the residuals of the IES variables.

We describe in two steps which priors we have used. In these steps, we also detail why and how the specific hyperparameters were defined.

Step 1. Type of prior distributions

For each of the unknown parameters in the (M) models under investigation, a Dirichlet prior distribution was chosen to incorporate knowledge about latent class sizes. In Mplus, thresholds are estimated that represent the number of cases in the kth class in relation to the last class K such that there are k = 1, …, K latent classes. The priors are specified for these thresholds [c#d] as D(α_d, α_K) where d = 1, …, K − 1, and class proportions must add to 1.0.

For the growth parameters, we used three normally distributed priors. This form of prior distribution (i.e., normal) was selected because these growth parameters may be positive or negative, but extreme positive or extreme negatives are rare. The priors were defined through the following specifications:

where the parameters with subscript 0 are specified hyperparameter values (i.e., prior mean and prior variance for the normal prior distribution), and the subscript k indicates that the hyperparameter settings may differ across latent classes (i.e., each latent class is allowed to have different prior settings for the intercept, slope, and quadratic terms).

For the covariance matrix (i.e., the variances of the growth parameters and their covariances), and the residuals of the IES variables, we relied on the default prior setting in Mplus: namely, the inverse Wishart distribution.⁴ This distribution is denoted as and contains hyperparameters  m_{0, k} and .⁵ The default settings in Mplus are m₀ = 0 and where p is the dimension of the multivariate block of latent variables (see, Muthén & Muthén, 1998–2015, p. 698), and the prior is by default set equal across classes.

Step 2. Specifying the hyperparameters for the priors

Dirichlet prior. We started with the specification of the Dirichlet prior, which is related to the number of classes and the class proportions (i.e., the size of the classes). First, the number of latent classes we specified was based on Bonanno (2004), who expected four distinct trajectories. These trajectories were classified as a resilient and a chronic trajectory, and two dynamic patterns often labeled as the recovery (decreasing) and delayed onset (increasing) trajectories. Therefore, we decided to specify k = 4. However, we were also interested in how well other latent class solutions would hold up in the data since 13 of the papers we found with our systematic review found fewer than four latent classes, see Table A2 in the Appendix A. In addition, three papers found more than four latent classes. As a result, we compared the 4-class model with two other solutions as a last step in our analysis: (1) a model with k = 3 (without the delayed onset trajectory prior specification), and (2) a model with k = 5, which would allow for an unexpected trajectory to potentially be estimated. The purpose for these additional comparisons was to fully explore the optimal number of PTSD latent classes.

Second, for the hyperparameters^{Table 2} of the Dirichlet prior, we relied on Bonanno (2004), who provided approximations of the proportion of each of the four trajectories based on a number of empirical studies. We combined these findings to define the prior distribution for latent class sizes in the current investigation. This lead to following percentages:⁶

1.	75% – resilient individuals (d1);
2.	11.25% – recovering PTSD (d2);
3.	7.5% – chronic PTSD (d3);
4.	6.25% – delayed onset PTSD (reference group).

With a total sample size of 301, the numerical hyperparameters for the Dirichlet prior (denoted by D) were (rounded to the nearest integer): where the delayed onset trajectory is the reference group denoted by the hyperparameter value of 19.

Growth Parameters. Next, we specified the priors for the mean intercept, the mean slope, and the mean quadratic trend. To decide on the specific hyperparameters, we first inspected the parameter estimates of the trend lines found in the 34 papers; see Table 2. To^{Figure 4, Figure 5Table 3}model the general shape of the trajectory, we decided to parameterize the metric of time in such a way that the intercept is actually the mean PTSD score at 3 months. This decision was made because at three months (most) experts agreed there is no significant slope (i.e., tangent) for the chronic and resilient trajectories, but that a significant slope (i.e., tangent) for the other two groups existed; see Figure 4. Since there was disagreement among the 34 papers (and among the experts) about the shape of the recovering and delayed onset trajectory (i.e., whether the quadratic effect is U-shaped or ∩-shaped), see Table 2, we decided to investigate two different parameterizations: The first was a parameterization of the trend line where the effect was U-shaped, and the second parameterization was where the trend line was ∩-shaped, see Figure 5.

Table 2. Summary of the slope parameters found in 34 papers reported on LGMM. The unexpected negative slopes for delayed onset trajectories and positive slopes in the recovering trajectories can be partially explained by very strong quadratic slopes that would still pull this estimated trajectory towards to expected direction (decrease for recovering, increase for delayed onset).

	No. of slope parameters not significant	Nr. of slope parameters significant	Direction slope if significant	If quadratic, U-shape or ∩-shape if significant	Missing info	Trajectory not present	Total times trajectory found^1
Resilient	8	15	10× negative	3 × U	11	2	34
			5× positive	5 × ∩
Chronic	8	10	2× negative	1 × U	9	7	27
			8× positive	5 × ∩
Recovering	3	20	2 × pos	5 × U	9	5	32
			18 × negative	2 × ∩
Delayed/worsening	1	8	6 × positive	3 × U	7	17	16
			2 × negative	4 × ∩

¹ Some studies include multiple variations of the same trajectory (e.g., a low stable and “true resilient” group). Some studies include multiple samples, where each sample could have its own variation of a group.

Note. U = positive Q; ∩ = negative Q.

Figure 4. Information about the tangent lines (i.e., the slope parameter of the growth process) at three months after trauma, which is used for the prior specification.

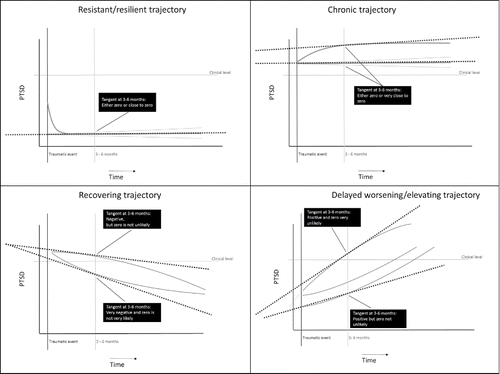
Figure 5. The bold lines represent the trend lines of the growth in PTSD symptoms based on the background information and for two different parameterizations for the recovery and delayed-onset trajectory (i.e., U-shaped or ∩-shaped). The shaded areas represent the uncertainty around the average trend lines as specified in the prior distributions.

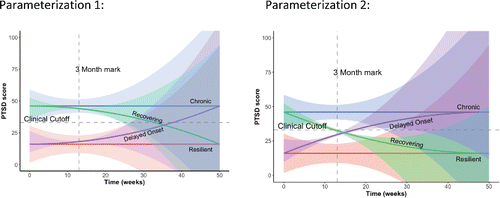
The next step was to translate the background information to actual values for the hyperparameters in such a way that the trend lines based on the prior specifications reflected the previous literature findings as well as the expert opinions. For our data, Van Loey and colleagues (2003) assumed a clinical relevant cutoff point of 33. Therefore, the mean of the intercept at T₀ (directly after the traumatic event) should be specified well below this cut-off for the resilient and delayed-onset trajectories and well above for the chronic and recovering trajectories; see Figure 3. To come up with values for the low and high intercepts (denoted by I_L and I_H, respectively) we asked the original authors of the example data for plausible values and they suggested to use I_L = 16 and I_H = 46. These values were then cross-validated by the finding of our systematic search, see Table 3. As can be seen in the Table, our chosen values fall within the range of plausible values, see also I_L and I_H in Figure 2. Note that in the sensitivity analyses presented below, we investigated how much “wiggle room” there was for these values. Stated differently, we investigated whether different specifications of these values would lead to different conclusions. The results of the sensitivity analysis allowed us to assess how much influence the exact specification has on the model results.

Table 3. Descriptive statistics of PTSD score at zero months for each trajectory based.

Trajectory	Mean (SD)	Median	Min	Max
Resilient (n = 14)	17.27 (12.67)	13.98	2.94	40.06
Delayed Onset (n = 9)	19.76 (9.43)	16.85	5.88	37.25
Recovering (n = 9)	46.42 (14.84)	40.94	27.45	66.67
Chronic (n = 7)	48.94 (12.94)	47.06	31.13	64.00

Note. Only studies with scores at zero months are included in this calculation.

Since we specified the model in such a way that the intercept is the PTSD symptom score at three months, we recalculated the intercept parameters representing the average PTSD value at three months instead of the starting point of the trend line; see Figure 6. Using the delayed onset group as an example (see the exact R-code in the online material presented on OSF; https://osf.io/vk4be/), we created a vector of numbers based on a linear model with an intercept of 16, a linear slope of 0, and a quadratic slope of 0.012 (y = 16 + 0x + 0.012x²). These specifications ensured that the trend line for the delayed onset group would start well below the clinical cutoff value (at the same level as the resilient trajectory), end up at a score of 46 after 51 weeks (the same score as the chronic trajectory), and follow a U-shaped trajectory. We then used this vector of numbers to compute the derivative (point-slope or tangent line) of the model-predicted values to inform our prior values for the linear and quadratic slopes. This procedure resulted in values for the intercept of 18.028, see in the left panel of the Figure 6, linear slope of 0.156 (i.e., a small value for the tangent at three months), and a quadratic effect of 0.012 at our chosen three-month intercept. For Parameterization 2 we followed a similar procedure and found an intercept of 29.572, a linear slope of 1.044 (i.e., a large value for the tangent at three months), and a quadratic effect of −0.012 for the delayed onset trajectory. We followed the same procedure for the other trajectories.

Figure 6. The prior distributions for the intercepts at three months (instead of directly after trauma). Black solid line represents clinical cutoff point for PTSD diagnosis. Black dashed lines represent expected average PTSD scores directly after trauma.

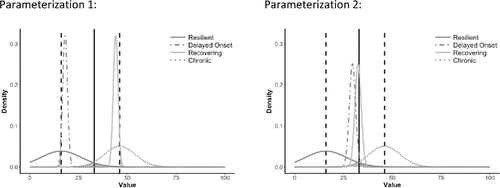
The trend lines presented in Figure 5 reflect the background knowledge found by the previous studies, as well as the information provided by the experts. However, because there was also some disagreement among the 34 papers (e.g., see the variance around the trend lines in Figure 2) and among the experts, we translated this “uncertainty” into values for the prior variances surrounding the prior mean values. We wanted the priors to reflect plausible parameter space, and we wanted to rule out those parts of the parameter space that would not make any sense based on clinical relevance. Therefore, we specified the prior variance around the intercepts for each trajectory. In Figure 6, the prior distributions for the four intercepts (i.e., average IES scores at three months after trauma for each trajectory) are given. For Parameterization 1, we hypothesized that about 5% of the prior distribution for the intercepts for the chronic and resilient trajectories at three months would cross the cutoff value of 33, indicated in Figure 6 by a solid vertical line. For the recovering and delayed onset group, we expected 5% to still score above or below the mean intercept value at three months of the chronic and resilient group, respectively; indicated in the Figure by the dashed vertical line. To find the optimal prior variances around the intercept for each trajectory, we wrote an R-function (see OSF; https://osf.io/vk4be/), which determined the optimal prior variance to reflect our expectations. Our prior expectations focused on a certain percentage of overlap between the prior distributions of two of the trajectories (e.g., resilient and chronic, or recovering and delayed onset). Thus, we estimated a large number of normal distributions, keeping the prior means of two trajectories constant, but varying the variance across a range of possible values. We then compared each of these distributions and found two that would meet our desired percentage of overlap. For Parameterization 2, we followed a similar procedure, see the right pane in Figure 6, but for the recovering and delayed onset group, we expected almost 0% to score above or below the mean intercept value at 3 months of the chronic and resilient group respectively (indicated in the Figure by the dashed vertical line).

Next,^{Figure 7Table 4}we specified prior variances around the slope parameters for each trajectory. Although we previously specified a prior mean of ±0.156 for the slopes at three months for the recovering and delayed onset trajectory in Parameterization 1, we still wanted to allow 5% of the distribution to cross the zero-point. That is, based on the information provided in Figure 3, we wanted to allow some probability mass where the recovering trajectory may have a positive slope; and for the delayed onset participants, a negative slope. We used the same function as described before, see OSF (https://osf.io/vk4be/), which resulted in a prior variance of 0.00809. For the chronic trajectory, we allowed 5% of the distribution to cross −0.156, which would allow some probability mass on a negative slope. However, the location of the probability mass would make it highly unlikely that this negative slope is steeper than the average slope of the recovering group. We did the same for the resilient group, but then vice versa; 5% of the distribution is allowed to cross 0.156. For Parameterization 2 for the recovering and delayed onset trajectory, we allowed 0% of the distribution to cross the zero-point. We did this because of the steep expected decrease/increase at three months. For the chronic trajectory, we allowed 0% of the distribution to cross −1.044 (the slope, or tangent, of the recovering trajectory at three months), which would make it impossible that the negative slope would be larger than the average slope of the recovering trajectory. We did the same for the resilient group, but then vice versa; 0% of the distribution was allowed to cross 1.044.

Then, we also needed to specify a prior variance around the quadratic effect. The Mplus default value for the prior variance results in a very large range of possible trend lines. These defaults lead to PTSD scores at 51 weeks as high as approximately 500,000,000 (see Figure 7A), which is obviously not realistic. A prior variance of 1, which seems very informative, still allows for values at 51 weeks after trauma as positive as ≈ 4,679 or as negative as ≈ −4,839 (see Figure 7B). Thus, we used the latter prior variance for the quadratic slopes of all four trajectories.

Figure 7. In this figure, the mean, the minimum, and the maximum trend lines for the resilient trajectory are provided for different prior specifications of the quadratic effect. Note the different scales of the y-axis.

In conclusion, the exact specification of the priors can be found in Table 4, but to graphically summarize the prior specification, see Figure 5. The four lines in this figure are the result of the prior means specified for the growth parameters of the model (i.e., intercept, slope, and quadratic trend). The shaded areas represent the effect of the prior variance, reflecting our uncertainty around the prior means. That is, the shaded areas are based on a fitted regression model with the 25th and 75th percentile of the intercept variance, the 25th and 75th percentile of the slope variance, and (only) the 48th and 52nd of the quadratic effect; these numbers were selected to obtain a readable graphical depiction of patterns. This graph shows that we allowed for quite some uncertainty in our^{Figure 8} prior specification, but the prior specification ruled out much of the implausible parameter space—thereby solving the limited data issue as described in the introduction section.

Table 4. Prior values used for the trend lines. The first value between brackets refers to the prior mean, while the second value refers to the prior variance.

Parameterization 1	Parameterization 2
Resistant/resilient trajectory:	Resistant/resilient trajectory:
I ∼ N(16, 106.9156)	I ∼ N(16, 106.9156)
S ∼ N(0, 0.00809)	S ∼ N(0, 0.0169)
Q ∼ N(0, 1)	Q ∼ N(0, 1)
Recovering trajectory:	Recovering trajectory:
I ∼ N(43.972, 1.5129)	I ∼ N(32.428, 2.5281)
S ∼ N(−.156, 0.00809)	S ∼ N(−1.044, 0.0169)
Q ∼ N(−.012, 1)	Q ∼ N(.012, 1)
Chronic trajectory:	Chronic trajectory:
I ∼ N(46, 62.41)	I ∼ N(46, 62.41)
S ∼ N(0, 0.00809)	S ∼ N(0, 0.0169)
Q ∼ N(0, 1)	Q ∼ N(0, 1)
Delayed onset trajectory:	Delayed onset trajectory:
I ∼ N(18.028, 1.5129)	I ∼ N(29.572, 2.5281)
S ∼ N(.156, 0.00809)	S ∼ N(1.044, 0.0169)
Q ∼ N(.012, 1)	Q ∼ N(−.012, 1)

Remaining Priors. Note that because we did not have detailed information for the variance-covariance parameters and the residuals, we relied on the default prior specifications as used in Mplus (i.e., the default IW-distribution setting).

Posterior model results

After specifying the statistical model and putting all of the priors in place, we estimated the model to inspect convergence according to the steps as described in the WAMBS-checklist, see Table 1.

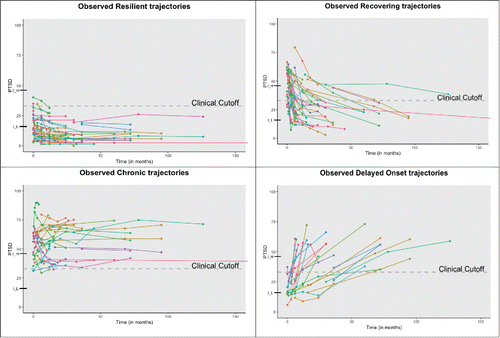
As discussed above, the theory-driven 4-class model was compared to two alternative models. Figure 8 shows the obtained trajectories for 3 to 5 class solutions with: (1) default priors (discussed in the next section dealing with the sensitivity analysis), (2) subjective priors according to Parameterization 1 where the trajectories were estimated as U-shaped, and (3) Parameterization 2 with ∩-shaped trajectories. Note that the 3-class models with subjective priors only included the priors for the resilient, recovering, and chronic groups. The 5-class model with subjective priors included priors for the original four classes plus one class with the default Mplus priors. The goal here was to assess whether a viable fifth class would emerge for this data set. Notice that Figure 8 illustrates that the five-class solution yielded some label switching issues (i.e., a single chain switched back and forth between sampling from two different classes). In this case, two of the latent classes were so similar to once another that the Markov chain bounced back and forth between the two classes during MCMC sampling. This label switching issue still occurred even with settings in place to avoid the problem (e.g., specifying a single Markov chain during sampling). The issue was likely a result of the class structure and the two classes essentially being duplicates of one another.

Figure 8. Graphical representation of the posterior results for the nine different models we fitted on the data.

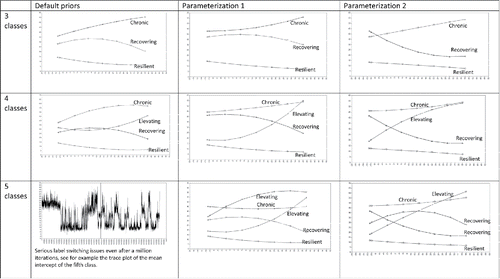
Evidence produced across all models led us to reject the three class models. Specifically, the individuals allocated to the delayed onset trajectory in the 4-class subjective-prior model were inappropriately allocated to the chronic trajectory or the recovering trajectory in the 3-class solutions. Based on substantive information gathered from the experts about the delayed onset group, we felt that these individuals clearly did not follow the classes they were assigned to and should be treated differently clinically. Adding a fifth class to either Parameterizations 1 or 2, resulted only in a variation of an already existing trajectory (and also produced label switching issues), see Figure 8. Therefore, we concluded that our final (and most reasonable) model was the 4-class solution. This is the model where, by using subjective priors, the delayed onset trajectory can be identified. Further, this model paves the way for future investigation to identify individuals at risk of delayed symptomology.

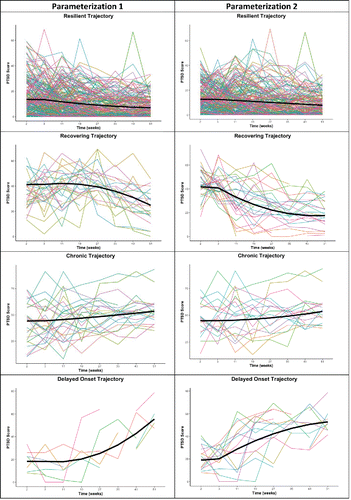
Table 5 provides the posterior estimates for both parameterizations. Figure 9 shows the observed individual trajectories per condition. It seems as though the individual trajectories of the second parameterization are more in line with the average trend lines. This especially holds for the participants classified to the recovering group (in other words, the downward trend is more clearly noticeable). Also, several individuals were classified in the delayed onset trajectory that all show a clear upward trend.

Table 5. Posterior results for both parameterizations.

	Parameterization 1			Parameterization 2
		95% Credible Interval			95% Credible Interval
Parameters	Posterior estimates (Posterior SD)	2.5%	97.5%	Posterior estimates (Posterior SD)	2.5%	97.5%
Resilient
I: mean	11.311 (0.810)	9.803	12.991	11.533 (0.891)	9.858	13.358
S: mean	−0.187 (0.036)	−0.258	−0.115	−0.099 (0.034)	−0.166	−0.033
Q: mean	0.002 (0.001)	0.000	0.004	0 (0.001)	−0.002	0.001
Chronic
I: mean	45.817 (2.307)	41.185	50.299	46.546 (3.175)	40.375	52.950
S: mean	0.163 (0.075)	0.014	0.310	0.086 (0.110)	−0.120	0.309
Q: mean	0.001 (0.002)	−0.003	0.006	0.003 (0.004)	−0.004	0.010
Recovering
I: mean	42.126 (1.231)	39.737	44.564	31.3 (1.371)	28.612	34.005
S: mean	−0.039 (0.087)	−0.212	0.128	−0.819 (0.099)	−1.022	−0.633
Q: mean	−0.011 (0.003)	−0.016	−0.004	0.012 (0.003)	0.007	0.017
Delayed onset
I: mean	18.299 (1.182)	15.975	20.615	30.739 (1.563)	27.572	33.717
S: mean	0.214 (0.085)	0.045	0.379	0.96 (0.106)	0.758	1.174
Q: mean	0.02 (0.005)	0.008	0.028	−0.01 (0.005)	−0.018	0.003
Variances
I: variance	77.697 (12.152)	58.598	106.778	95.816 (15.452)	70.430	131.036
S: variance	0.163 (0.026)	0.117	0.221	0.097 (0.024)	0.056	0.149
Q: variance	0.000 (0.000)	0.000	0.000	0.000 (0.000)	0.000	0.000

Note: in Bayesian estimation, credible intervals and the confidence interval obtained with ML-estimation may numerically be similar and might serve related inferential goals, but they are not mathematically equivalent and conceptually quite different.

Figure 9. Observed individual trajectories per type of trajectory and for both parameterizations. To classify individuals in the four trajectories, we saved the plausible values with 500 imputed data sets for class membership. The resulting file was imported into SPSS and an average class membership was estimated. For example, if an individual showed the pattern 0/0/0/100 (where 100% of the imputations assigned this person to Class 4), then this person was allocated to the delayed onset trajectory (i.e., the fourth class). If the pattern was 0.11/0.27/0.3/0.59, then the person was allocated to the delayed onset trajectory in 59% of the imputations. Most likely class membership was based on highest count.

Sensitivity analysis

To study the impact of the priors, we ran two different types of sensitivity analyses. First, we compared the model with informative priors to a model with uninformative priors (point 8 of the WAMBS-checklist), and then we compared the model with informative priors to alternative prior specifications (point 9 of the WAMBS-checklist); see Table 1. A detailed description of the analyses can be found in the online logbook available at the OSF (https://osf.io/vk4be/).

Comparing the informative model to the uninformative model

The first sensitivity analysis was to compare the theorized model (using informed priors) with a model where the priors were uninformative in order to study the impact of the informative priors. We specified our noninformative, comparison model to rely on the default prior settings of Mplus; although, there are certainly other ways to define noninformed priors, the software default settings were deemed sufficient here. The estimated trajectories with default settings can be found in Figure 8. As is evident by inspecting the graph, the results of the uninformative model are quite different from the model with informative priors. Clearly, the delayed onset trajectory was not found when specifying uninformative priors. As a result, one might conclude that these findings are not inclusive or substantively correct in capturing the individuals in the data set, provided that the delayed onset group is present.

Comparing the informative model to alternative informative models

As a second sensitivity analysis, we compared the two Parameterizations with alternative informative models that specified different prior settings. That is, we altered the prior intercept variance to be wider or narrower within the sensitivity analysis. In addition, we had three other sensitivity analysis settings, where:

1.	We shifted the prior intercept mean upward and downward per class by 10% and 20% of the original prior value (referred to as Sensitivity Analysis II);
2.	We shifted the prior linear slope mean upward and downward by 10% and 20% of the original prior value for each latent class (referred to as Sensitivity Analysis III);
3.	We altered the prior quadratic slope variance to be systematically wider or narrower, for each latent class (referred to as Sensitivity Analysis IV).

These different settings were used to systematically assess what kind of impact different prior specifications have on final model results. It is important to have a full understanding of the statistical and substantive impact that specific prior settings may have on findings before model results can be fully interpreted (Depaoli & van de Schoot, 2017; Kruschke, 2014). One important point we wish to highlight is that a sensitivity analysis should never be used as a means to change the priors based on “desirable” results obtained. In other words, original priors should be retained as the final model settings. The purpose of varying the priors in the sensitivity analysis is to better understand the robustness of results to different prior settings. If results vary (or do not vary) widely based on prior settings, then this is substantively informative regarding the impact of the priors. The sensitivity analysis is used to help aid in further understanding the impact of the priors on final model results.

All sensitivity analyses were conducted separately for our two Parameterizations. Note that for Parameterization 1, we varied the prior intercept variance for all classes simultaneously. However, for Parameterization 2, we did this on a class-by-class basis. In total, for Parameterization 1 we ran 3 × 4 × 4 × 4 + 6 = 198 alternative prior-setting conditions. In total, for Parameterization 2 we ran 4 × 4 × 4 × 4 + 6 = 256 alternative prior-setting conditions. We ran four models for each condition, each with a different seed-value. In addition, we checked for convergence by investigating the PSRF (see Table 1) for each chain. If it was below 1.05 for the last 50% of the iterations in the chain, then we concluded that the model had converged. The four seed-values always converged to the same solution for all conditions under Parameterization 2. For Parameterization 1, however, this was never the case, and there were differences in substantive interpretation of the trajectories across the different seed-values. Therefore, we concluded that Parameterization 1 was not stable (even after running 10 additional seed-values there were too many different solutions). The full set of results of the sensitivity analysis can be found in the online supplementary materials available at the OSF (https://osf.io/vk4be/).

The sensitivity analysis for Parameterization 2 shows that there is some “wiggle room” when it comes to deciding on the values for the prior mean and variance. That is, relative bias⁷ was always <5% and participants are allocated to the same classes. For Parameterization 1, however, the bias levels exceeded 5% for many conditions, and the number of individuals allocated to one of the trajectories is different. In conclusion, the prior specifications for Parameterization 2 were much more stable compared to Parameterization 1.

Conclusion: Empirical data

The results from the final model comprising the four trajectories support the leading opinion derived from the literature on PTSD trajectories and from experts in the field: In the aftermath of a traumatic event, a resilient, chronic, recovery, and delayed onset trajectory may appear. The final model was able to incorporate both the smaller and the larger sized trajectories, which is important considering their clinical relevance. Particularly the small delayed onset trajectory may be overlooked in clinical practice. In particular, after the acute phase during the first weeks, trauma-exposed individuals may not be in touch with caregivers after the hospitalization phase. The awareness that small but clinically relevant trajectories may appear, even beyond the acute phase, may help clinicians to develop efficient follow-up/screening programs and to provide these individuals with help when indicated.

From our analyses, it appears there are “degrees” of prior settings that produce viable results, rather than just one setting of priors giving “good” results. For example, one of the criticisms that may arise regarding our approach is that one could argue that the priors are doing all of the work, especially in the presence of small groups (or classes). Because of the priors resembling a plausible parameter space, we are increasing the power to detect a small group in a data set rather than completely constructing the group based on highly informative priors.

We also wanted the most stable model: A model where we were able to replicate convergence and where different seed values generated the same results. As with any informed model, a main assumption is that (accurate) background knowledge is available to incorporate during the model-building phase. This assumption is particularly relevant to informed LGMMs via the Bayesian estimation framework in that the proper specification of prior distributions based on background knowledge is an important step to ensure that theoretically sound results are obtained. However, if informative priors are used, then some bias can be introduced into model estimates; note that some level of inaccuracy in the prior is to be expected in applied contexts since we do not know the underlying “truth” of the population. However, as Depaoli (2014) shows, LGMM estimates obtained with inaccurate priors are typically still more accurate than ML or Bayesian estimation with diffuse priors. Given these simulation results, along with our illustration of implementing informative priors and identifying substantively relevant latent classes, we believe this informed LGMM approach to be an accurate and substantively rich approach to assessing growth or change over time in latent classes.

In the sensitivity analyses we compared (only) two ways of how the model was specified (i.e., the two parameterizations). As indicated by Depaoli and van de Schoot (2017) instability of the results from a sensitivity analysis indicates that the model might be mis-specified, or that the parameters are not fully identified by the data or model. In this case, researchers should consider making the necessary changes to the model to combat any identification or mis-specification issues; in our situation, we rejected Parameterization 1. Our sensitivity analysis was mainly used to study the robustness of the hyperparameters rather than explore different prior distributional forms or different model settings (besides the two types of parameterizations). Upon receiving results from the sensitivity analysis, the impact that fluctuations in the hyperparameter values had on the substantive conclusions were really minor. That is, no matter what hyperparameter values we used, we always obtained the same four “classical” trajectories. Only when we specified uninformative priors did we obtain a completely different class solution. A variation of the chronic trajectory was extracted instead of a delayed onset trajectory (see Figure 8), and this variation was not considered to be substantively meaningful. In addition, we showed a method to account for finding new trajectories not described previously by running a model with k+1 trajectories. We argue that researchers using Bayesian LGMM with informative priors should always check a model with uninformative priors placed on the k+1th trajectory to ensure the entire class-space is fully explored.

General conclusion and discussion

The main issue of Bayesian modeling is how (weakly) informed priors can be specified to determine a plausible parameter space, as well as how they can be incorporated into the estimation process. There are currently few articles that detail the elicitation of prior information from experts, how this is consolidated with background literature, and how this background information can be incorporated into exact values of the hyperparameters of prior distributions to determine a plausible parameter space to deal with limited data. We have provided a detailed step-by-step overview of this entire process for a case study on PTSD trajectories.

The main reason we implemented informed priors was to deal with a limited data issue. Our results indicated that specifying priors to cover a plausible parameter space (i.e., covering a reasonable range of values) was able to address the limited data issue. A potential criticism of a strictly informative prior is that the range of possible parameter values is not as expansive as what might be viable. Thus, the prior could force results not reflective of the data. Determining a plausible parameter space, as specified through a weakly informed prior, avoids this issue altogether. Specifically, this form of prior may not include out-of-bound parameter values, as would be the case with uninformative priors, but it is also more inclusive than a strictly informed prior.

It should be noted that we only used informed priors on a selection of the parameters in the model, while relying on uninformative priors for the variance-covariance matrix. Often, in high dimensional modeling situations, it is almost always hard to find subjective priors for all of the parameters in the model. As a result, informed priors are typically only developed for the most important (i.e., substantively relevant) parameters in the model, with the nuisance parameters being given uninformative priors (see, for a more detailed discussion: Yang & Berger, 1998). We do not claim that informative priors are always preferable. Certainly, there are good arguments for use of both informative and uninformative types of priors; see for a discussion on this topic, for example, Kaplan (2014) and Kruschke (2010).

Any time an applied researcher wishes to specify informative priors, the issue of “proper” or “accurate” elicitation arises. We believe these priors should always be assessed through a sensitivity analysis to assess the impact of the prior. It is likely that the prior has a degree of “inaccuracy” embedded within in it. Specifically, we do not likely know the exact underlying truth of the population. Instead, we rely on prior knowledge of the field to help guide our opinions and hypotheses about the population. Recognizing that our priors will undoubtedly contain some level of inaccuracy according to the unknown population, it is important to conduct a sensitivity analysis in order to assess how much of an impact different levels of the prior have on model results. If slight fluctuations in the hyperparameter make a large substantive difference in results, then this point should be noted. In this scenario, the prior has a large and instable influence on the final estimates. However, if the sensitivity analysis is showing comparable substantive results across different fluctuations of hyperparameter values, then the supposed inaccuracy of the prior does not have a large influence on substantive conclusions and the researcher can have more confidence in the stability of model results. It is important to know whether your data is supported by theory or not. If not (i.e., if there is a substantial deviation in the results during a sensitivity analysis), then this may indicate that perhaps the theory should be more closely examined and tested within the field. “Strong” theories would not produce substantively different results from slight deviations of the prior.

One natural limitation to this approach for defining priors and estimating the model is that informed LGMM will not be appropriate for every research situation (e.g., when prior knowledge is not available). However, we argue that there are many research scenarios where prior knowledge is informative to the research question and that the informed modeling process described here is beneficial for such inquiries. It is our hope that applied or clinical researchers can use the proposed method, including the sensitivity analysis process, for estimating LGMM using an informed approach in order to uncover small but real latent classes that are substantiated by theory.

Article information

Conflict of Interest disclosures: Each author signed a form for disclosure of potential conflicts of interest. No authors reported any financial or other conflicts of interest in relation to the work described.

Ethical principles: The authors affirm having followed professional ethical guidelines in preparing this work. These guidelines include obtaining informed consent from human participants, maintaining ethical treatment and respect for the rights of human or animal participants, and ensuring the privacy of participants and their data, such as ensuring that individual participants cannot be identified in reported results or from publicly available original or archival data.

Role of the Funders/Sponsors: None of the funders or sponsors of this research had any role in the design and conduct of the study; collection, management, analysis, and interpretation of data; preparation, review, or approval of the manuscript; or decision to submit the manuscript for publication.

Acknowledgments: The authors would like to thank the reviewers and Yulan Qing for their comments on prior versions of this manuscript. The ideas and opinions expressed herein are those of the authors alone, and endorsement by the authors' institutions' or the funding agency is not intended and should not be inferred.

Additional information

Funding

This work was supported by Grant NWO-VIDI-452-14-006 from the the Netherlands organization for scientific research. The empirical study was funded by the Dutch Burns Foundation.

Notes

1 The default approach of the LGMM framework starts with estimating a one cluster LGMM-model, where only a single group is presumed. Next, several additional models are estimated with an increasing number of clusters. A final model is chosen based on model comparison tools, as well as theoretical considerations (Nylund, Asparouhov, & Muthén, 2007).

2 Individuals are diagnosed with delayed onset PTSS if they fulfill criteria for PTSD and if the onset of symptoms is at least six months after trauma (APA, 2013). Recent notions of delayed onset PTSS acknowledge that delayed onset is characterized by initially mild levels of symptoms that gradually or sharply increase to full-blown PTSD over time (see Andrews et al., 2007). Some studies found that the starting point of the delayed onset trajectory is somewhat higher compared to the resilient trajectory (e.g., Bonanno, Kennedy, Galatzer-Levy, Lude, & Elfström, 2012).

3 http://www.prisma-statement.org/

4 The IW distribution is perhaps the most common prior specification for covariance matrices, but it is not without problems or controversy. There have been many comments published on the optimal specification of the (inverse) Wishart prior. Specifically, O'Malley and Zaslavsky (2008), have recommended using a scaled inverse-Wishart prior. For the scaled version, the covariance matrix is broken up into a diagonal matrix of scale parameters and an un-scaled covariance matrix. The prior is then specified on this form of the matrix. The scaled version of this prior is what we implement in the current example. However, it is important to note that the exact specification of the Wishart prior has also been found to have a large impact when variances (diagonal elements) in the covariance matrix are small (Schuurman, Grasman, & Hamaker, 2016). As a result, the (inverse) Wishart (scaled or not) may not always be the best choice of prior.

5 However, if the default IW settings in Mplus are modified to user-specified values, the prior distributions change to univariate distributions within Mplus. Specifically, in this case, inverse-gamma priors are implemented for the diagonal variance terms, and normal or uniform priors are implemented for the off-diagonal covariance terms. If this is the case, then the user must check to be sure that the sum of the parts making up the inverse Wishart prior (i.e., the inverse gamma and normal priors) creates a positive-definite matrix for the multivariate prior.

6 First, based on Smid et al. (2009), we decided that the percentage of resilient individuals should be between 60% and 80%, leaving 20% to 40% for the remaining three groups, of which 25% had to be in the delayed onset group. We chose 75% for the resilient group, and divided the remaining 25% over the remaining three groups such that the delayed onset group took up 25% of that 25% (which is 6.25%). The remaining 18.75% was split over the recovering and chronic group, with the recovering group bigger than the chronic group, based on Bonanno's (2004) findings that the majority of individuals diagnosed with PTSD recover relatively quickly.

7 The amount of relative bias for a parameter can be computed using the following formula: [(parameter estimate with initial specification) – (parameter estimate with alternative specification)/(parameter estimate with initial specification)] × 100. The relative size of this effect should be interpreted in the context of what is substantively meaningful.

Appendix A:

Details of the systematic Review

Data sources

The search for articles using LGMM to study the development of PTSD focused on four major databases: Pubmed, Embase, PsychInfo, and Scopus. To cast as wide a net as possible, we put no limits on publication year. We included all studies published until February 10, 2016. Identification of eligible papers followed the same search path for all four search-engines. The search terms were formed by including all unique combinations between five terms indicating PTSD as the topic of the article, and fourteen terms indicating LGMM as the analysis method used in the article, separated by the OR handle (see Table A1 for specific search terms used).

After the database search and screening, we attempted to find additional relevant articles in two ways. First, we used Scopus to export the reference lists of the studies included in our qualitative analysis. Second, we used Scopus to export the articles that have cited the studies included in our qualitative analyses since their publication. This additional search occurred on March 10, 2016.

Table A1. Search terms.

Topic terms	Traumatic stress, stress disorder, posttraumatic stress, posttraumatic stress, PTSD
Analysis method terms	Trajectories, latent growth, latent factors, cluster, cluster analysis, latent class analysis, latent growth mixture modeling, mixed linear models, latent profile, mixture, typologies, profile, discriminant analysis

Note. As an illustration, here is the search syntax used to find articles in Scopus: TITLE-ABS-KEY-AUTH((trajectories OR “latent growth” OR “latent factors” OR cluster OR “cluster analysis” OR “latent class analysis” OR “latent growth mixture modelling” OR “mixed linear models” OR “latent profile” OR mixture OR typologies OR profile OR “discriminant analysis”) AND (“traumatic stress” OR “posttraumatic stress” OR “posttraumatic stress” OR “stress disorder” OR PTSD))

Study selection

Following the initial identification of relevant articles, exact duplicates were excluded. After that, there were two rounds of screening for eligibility. In the first round, eligibility was decided by investigating the title and abstract of the article by one author. All relevant papers were screened for the actual application of one of the cluster techniques described in Table A1 within the context of trauma. If there was any doubt, the study was included for the second round. Note that in this stage, we were over-inclusive and during title screening, obviously irrelevant papers (N = 5,822) were removed, for example cross-sectional studies, neurobiological studies and studies from other fields such as studies examining medical procedures after physical trauma.

In the second round, the full-text articles were independently read and screened by RvdS and MS for the following inclusion criteria: (a) longitudinal studies with at least three measurement waves measuring PTSD, (b) studies that measured PTSD on a continuous scale via an interview or questionnaire, (c) and studies that used a clustering method (LGMM, LCGA, hierarchical cluster analysis), (d) traumatic stress symptoms following events that appeared to fulfill DSM-IV criterion A1 for PTSD or acute stress disorder. Any disagreements were discussed and a consensus achieved. An excel containing all decisions and reasons for exclusion is included on the Open Science Framework (see https://osf.io/vk4be/).

Data extraction

A data extraction sheet was designed in Excel to record data. From the selected articles, additional information on the design and analysis of the study was obtained, see the online supplementary materials at the OSF, Table A2 and Figure A1. The recorded variables for each article included in the review are: year published, journal, country of data collection, sample size, reported sample characteristics, type of trauma (1, 2), number of measurement waves, timing of measurement waves, measure of PTSD and subscales if reported, number of trajectories found, sample size (proportion) per trajectory, interpretation per trajectory, proportion of sample per trajectory found, whether the trajectories found in the study correspond to the four classic trajectories proposed by Bonnano et al. (2014), whether any predictors were included in the study, the final growth model estimates for the trajectories (if reported). Data were extracted by SDW and double checked by RvdS. Any disagreements were discussed with a third reviewer (MS) and a consensus was achieved.

Figure A1. Overview of the included studies including their measurement points.

Table A2. Overview of the 34 included papers.

Reference	Type of trauma	nr of trajectories	Description of trajectories (%)
Andersen, S. B., Karstoft, K. I., Bertelsen, M., & Madsen, T. (2014).	Deployment to Afghanistan	6	Six classes: Mild distress (4.1%), low-stable (78.1%), late onset (5.7%), distressed-improving (2.7%), relieved-worsening (2.0%), low-fluctuating (7.5%)
Armour, C., Shevlin, M., Elklit, A., & Mroczek, D. (2012).	Rape victims	2	Two classes: Low stable (35%), high decline (65%)
Berntsen, D., Johannessen, K. B., Thomsen, Y. D., Bertelsen, M., Hoyle, R. H., & Rubin, D. C. (2012).	6-month deployment to Afghanistan in 2009:	6	Six classes: the resilient, extremely resilient, new-onset, strong-benefit, mild-benefit, late-benefit
Boasso, A. M., Steenkamp, M. M., Nash, W. P., Larson, J. L., & Litz, B. T. (2015).	War zone deployement	5	Combined percentages over 3 subsamples: resistant/no trauma (28.3%), resilience (49.6%), recovering (8.5%), chronic (11.7%), delayed (2%)
Bonanno, G. A., Mancini, A. D., Horton, J. L., Powell, T. M., LeardMann, C. A., Boyko, E. J., … Smith, T. C. (2012).	US military personnel deployed in Afghanistan	4	Four classes: High stable (2.2%), moderate improving (8%), low stable (83.1%), worsening – chronic (6.7%)
Bryant, R. A., Nickerson, A., Creamer, M., O'Donnell, M., Forbes, D., Galatzer-Levy, I., … Silove, D. (2015).	Injury patients	5	Five classes: Chronic (4%), recovery (6%), worsening/recovery (8%), worsening (10%), resilient (73%)
deRoon-Cassini, T. A., Mancini, A. D., Rusch, M. D., & Bonanno, G. A. (2010).	Traumatic injury	4	Four classes: resilient (59%), chronic (22%), delayed (6%; started high, then had a dip, then back up high), and recovering (13%)
Dickstein, B. D., Suvak, M., Litz, B. T., & Adler, A. B. (2010).	War combat exposure	4	Four classes: resilient (84%), delayed onset (3%), unrealized expectations (9%; high pre-deployment, low postdeployment), recovery (4%)
Eekhout, I., Reijnen, A., Vermetten, E., & Geuze, E. (2016).	Deployment	3	Three classes: Resilient (85%), recovered (5%), delayed-onset (9%)
Galatzer-Levy, I. R., Ankri, Y., Freedman, S., Israeli-Shalev, Y., Roitman, P., Gilad, M., & Shalev, A. Y. (2013).	Accidents/injury (motor vehicle, terrorist, work, other)	3	Three classes: Rapid Remitting (56%), Slow Remitting (27%), Non Remitting (17%)
Galatzer-Levy, I. R., Madan, A., Neylan, T. C., Henn-Haase, C., & Marmar, C. R. (2011).	Exposure to life threatening events	3	Three classes: resilient (88%), distressed-improving (10%), distressed-worsening (2%)
Hiller, R. M., Halligan, S. L., Ariyanayagam, R., Dalgleish, T., Smith, P., Yule, W., … Meiser-Stedman, R. (2016).	Motor Vehicle Collisions	2	Two classes: Low trajectory (63.4%), high trajectory (36.6%)
Hobfoll, S. E., Mancini, A. D., Hall, B. J., Canetti, D., & Bonanno, G. A. (2011).	Political violence among Palestinians	3	Three classes: moderate-improving (73%), severe-chronic (23.2%), severe-improving (3.5%)
Holgersen, K. H., Klöckner, C. A., Jakob Boe, H., Weisæth, L., & Holen, A. (2011).	The 1980 North Sea oil rig disaster	4	Four classes: Chronic (11%), Recovering (14%), Resilient (61%), Relapsing (N = 9)
Hong, S. B., Youssef, G. J., Song, S. H., Choi, N. H., Ryu, J., McDermott, B., … Kim, B. N. (2014).	Watching the death of two mothers from classmates	4	Four classes: Chronic Dysfunction (1.8%), Recovery (19.9%), Delayed Reaction (5.6%), Resilience (72.7%)
Johannesson, K. B., Arinell, H., & Arnberg, F. K. (2015).	Tsunami	4	Four classes: resilient (72.3%), severe chronic (4.6%), moderate chronic (11.2%), recovering (11.9%)
La Greca, A. M., Lai, B. S., Llabre, M. M., Silverman, W. K., Vernberg, E. M., & Prinstein, M. J. (2013).	Natural disaster (hurricane)	3	Three classes: resilient (37%), recovering (43%), chronic (20%)
Le Brocque, R. M., Hendrikz, J., & Kenardy, J. A. (2010).	Child accidental injury; its effect on parents	3	Three classes: resilient (78%), recovery (8%), chronic subclinical (14%)
Lowe, S. R., Joshi, S., Pietrzak, R. H., Galea, S., & Cerdá, M. (2015).	Hurricane	4	Four classes: Resilient (74.9%), recovery (14.7%), chronic (5.2%), delayed (5.2%)
Maslow, C. B., Caramanica, K., Welch, A. E., Stellman, S. D., Brackbill, R. M., & Farfel, M. R. (2015).	WTC attack	5	Five classes: low-stable (53.3%), moderate- stable (28.7%), moderate-increasing (6.4%), high-decreasing (7.7%), and high-stable (4.0%).
Nash, W. P., Boasso, A. M., Steenkamp, M. M., Larson, J. L., Lubin, R. E., & Litz, B. T. (2014).	War in Afghanistan	3	Three classes: low stable (79%), new-onset PTSD (13%), pre-existing PTSD (8%)
Norris, F. H., Tracy, M., & Galea, S. (2009).	Mexico: flood USA: terrorist attack (9/11)	5 & 7	Mexico: Five classes: stable, mild (35%), stable, moderate (12%), stable severe (10%), steep decline (32%), moderate decline (11%).
			USA: Seven classes: resilient (40%), steep decline (10%), moderate decline (9%), slight increase (13%), increase after 2 years (14%), moderate increase (10%), stable severe (3%)
Orcutt, H. K., Bonanno, G. A., Hannan, S. M., & Miron, L. R. (2014).	Campus mass shooting	4	Four classes: minimal impact resilience (60.9%), high impact-recovery (29.1%), moderate impact-moderate symptoms (8.2%), chronic dysfunction (1.8%)
Orcutt, H. K., Erickson, D. J., & Wolfe, J. (2004).	War combat exposure	2	Two classes: resilient (57%), and increasing (43%)
Pietrzak, R. H., Feder, A., Singh, R., Schechter, C. B., Bromet, E. J., Katz, C. L., … Southwick, S. M. (2014).	WTC 9 –11: Police RespondersNontraditional Responders	4 & 6	Police responders: Four classes: resistant/resilient (77.8%), chronic (5.3%), recovering (8.4%), delayed-onset (8.5%).Nontraditional responders: Six classes: resistant/resilient (58.0%), severe chronic (9.5%), moderate chronic (6.2%), recovering (12.3%), subsyndromal increasing (7.3%), delayed onset (6.7%)
Pietrzak, R. H., Van Ness, P. H., Fried, T. R., Galea, S., & Norris, F. H. (2013).	Large magnitude disaster (hurricane Ike)	3	Three classes: resistant (78.7%), chronic (16.0%), delayed onset (5.3%)
Punamaki, R. L., Palosaari, E., Diab, M., Peltonen, K., & Qouta, S. R. (2014).	2008/2009 War on Gaza	3	Three classes: recovery (n = 183), resistant (29), increasing symptoms (28)
Sampson, L., Cohen, G. H., Calabrese, J. R., Fink, D. S., Tamburrino, M., Liberzon, I., … Galea, S. (2015).	Deployment	4	Four classes: Chronic Dysfunction (4.7%), constant (mild; 11.7%), resilient (42.2%), resistant (41.5%)
Self-Brown, S., Lai, B. S., Harbin, S., & Kelley, M. L. (2014).	Hurricane Katrina	3	Three classes: chronic (4%), recovering (30%), resilient (66%)
Self-Brown, S., Lai, B. S., Thompson, J. E., McGill, T., & Kelley, M. L. (2013).	Hurricane Katrina	3	Three classes: resilient (71%), recovering (25%), chronic (4%)
Sigurdardottir, S., Andelic, N., Roe, C., & Schanke, A. K. (2014).	Traumatic brain injury	4	Four classes: resilience (73.5%), delayed distress (6.8%), recovery (14.6%), chronic distress (5.1%)
Steenkamp, M. M., Dickstein, B. D., SaltersPedneault, K., Hofmann, S. G., & Litz, B. T. (2012).	Sexual assault	4	Four classes A high chronic trajectory (6.7%), a moderate chronic trajectory (16.0%), a moderate recovery trajectory (47.9%), and a marked recovery trajectory (29.4%)
Thormar, S. B., Sijbrandij, M., Gersons, B. P., Van de Schoot, R., Juen, B., Karlsson, T., & Olff, M. (2016).	WTC attack: Core and Noncore volunteers	2 & 2	Core volunteers: Two classes: Resilient (90%), chronic (10%)Non-core volunteers: Two classes: Resilent (92%), chronic (8%)
van Loey, N. E., van de Schoot, R., & Faber, A. W. (2012).	Burn victims	4	Four classes. 62.8% resilient, 17.4% recovering, 15% chronic, 4.8% delayed onset

References

• Andersen, S. B., Karstoft, K. I., Bertelsen, M., & Madsen, T. (2014). Latent trajectories of trauma symptoms and resilience: the 3-year longitudinal prospective USPER study of Danish veterans deployed in Afghanistan. The Journal of Clinical Psychiatry, 75(9), 1001–1008. https://doi.org/10.4088/JCP.13m08914.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.4088%2FJCP.13m08914 journal Latent+trajectories+of+trauma+symptoms+and+resilience%3A+the+3-year+longitudinal+prospective+USPER+study+of+Danish+veterans+deployed+in+Afghanistan author%3DS.+B.+Andersen%26author%3DK.+I.+Karstoft%26author%3DM.+Bertelsen%26author%3DT.+Madsen 2014 Andersen%2C+S.+B.%2C+Karstoft%2C+K.+I.%2C+Bertelsen%2C+M.%2C+%26+Madsen%2C+T.+%282014%29.+Latent+trajectories+of+trauma+symptoms+and+resilience%3A+the+3-year+longitudinal+prospective+USPER+study+of+Danish+veterans+deployed+in+Afghanistan.+The+Journal+of+Clinical+Psychiatry%2C+75%289%29%2C+1001%E2%80%931008.+https%3A%2F%2Fdoi.org%2F. 1001-1008 The+Journal+of+Clinical+Psychiatry 75 9 10.4088%2FJCP.13m08914 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_2_1 10.4088%252FJCP.13m08914 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.4088%252FJCP.13m08914%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DAndersen%26rft.aufirst%3DS.%2520B.%26rft.date%3D2014%26rft.atitle%3DLatent%2520trajectories%2520of%2520trauma%2520symptoms%2520and%2520resilience%253A%2520the%25203-year%2520longitudinal%2520prospective%2520USPER%2520study%2520of%2520Danish%2520veterans%2520deployed%2520in%2520Afghanistan%26rft.jtitle%3DThe%2520Journal%2520of%2520Clinical%2520Psychiatry%26rft.volume%3D75%26rft.issue%3D9%26rft.spage%3D1001%26rft.epage%3D1008 %00empty%00}-->
• Armour, C., Shevlin, M., Elklit, A., & Mroczek, D. (2012). A Latent Growth Mixture Modeling Approach to PTSD Symptoms in Rape Victims. Traumatology, 18(1), 20–28. https://doi.org/10.1177/1534765610395627.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed<!--${googleScholarLinkReplacer: 10.1177%2F1534765610395627 journal A+Latent+Growth+Mixture+Modeling+Approach+to+PTSD+Symptoms+in+Rape+Victims author%3DC.+Armour%26author%3DM.+Shevlin%26author%3DA.+Elklit%26author%3DD.+Mroczek 2012 Armour%2C+C.%2C+Shevlin%2C+M.%2C+Elklit%2C+A.%2C+%26+Mroczek%2C+D.+%282012%29.+A+Latent+Growth+Mixture+Modeling+Approach+to+PTSD+Symptoms+in+Rape+Victims.+Traumatology%2C+18%281%29%2C+20%E2%80%9328.+https%3A%2F%2Fdoi.org%2F. 20-28 Traumatology 18 1 10.1177%2F1534765610395627 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_3_1 10.1177%252F1534765610395627 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1177%252F1534765610395627%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DArmour%26rft.aufirst%3DC.%26rft.date%3D2012%26rft.atitle%3DA%2520Latent%2520Growth%2520Mixture%2520Modeling%2520Approach%2520to%2520PTSD%2520Symptoms%2520in%2520Rape%2520Victims%26rft.jtitle%3DTraumatology%26rft.volume%3D18%26rft.issue%3D1%26rft.spage%3D20%26rft.epage%3D28 %00empty%00}-->
• Berntsen, D., Johannessen, K. B., Thomsen, Y. D., Bertelsen, M., Hoyle, R. H., & Rubin, D. C. (2012). Peace and War: Trajectories of Posttraumatic Stress Disorder Symptoms Before, During, and After Military Deployment in Afghanistan. Psychological Science, 23(12), 1557–1565. https://doi.org/10.1177/0956797612457389.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1177%2F0956797612457389 journal Peace+and+War%3A+Trajectories+of+Posttraumatic+Stress+Disorder+Symptoms+Before%2C+During%2C+and+After+Military+Deployment+in+Afghanistan author%3DD.+Berntsen%26author%3DK.+B.+Johannessen%26author%3DY.+D.+Thomsen%26author%3DM.+Bertelsen%26author%3DR.+H.+Hoyle%26author%3DD.+C.+Rubin 2012 Berntsen%2C+D.%2C+Johannessen%2C+K.+B.%2C+Thomsen%2C+Y.+D.%2C+Bertelsen%2C+M.%2C+Hoyle%2C+R.+H.%2C+%26+Rubin%2C+D.+C.+%282012%29.+Peace+and+War%3A+Trajectories+of+Posttraumatic+Stress+Disorder+Symptoms+Before%2C+During%2C+and+After+Military+Deployment+in+Afghanistan.+Psychological+Science%2C+23%2812%29%2C+1557%E2%80%931565.+https%3A%2F%2Fdoi.org%2F. 1557-1565 Psychological+Science 23 12 10.1177%2F0956797612457389 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_4_1 10.1177%252F0956797612457389 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1177%252F0956797612457389%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DBerntsen%26rft.aufirst%3DD.%26rft.date%3D2012%26rft.atitle%3DPeace%2520and%2520War%253A%2520Trajectories%2520of%2520Posttraumatic%2520Stress%2520Disorder%2520Symptoms%2520Before%252C%2520During%252C%2520and%2520After%2520Military%2520Deployment%2520in%2520Afghanistan%26rft.jtitle%3DPsychological%2520Science%26rft.volume%3D23%26rft.issue%3D12%26rft.spage%3D1557%26rft.epage%3D1565 %00empty%00}-->
• Boasso, A. M., Steenkamp, M. M., Nash, W. P., Larson, J. L., & Litz, B. T. (2015). The relationship between course of PTSD symptoms in deployed U.S. Marines and degree of combat exposure. Journal of Traumatic Stress, 28(1), 73–78. https://doi.org/10.1002/jts.21988.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1002%2Fjts.21988 journal The+relationship+between+course+of+PTSD+symptoms+in+deployed+U.S.+Marines+and+degree+of+combat+exposure author%3DA.+M.+Boasso%26author%3DM.+M.+Steenkamp%26author%3DW.+P.+Nash%26author%3DJ.+L.+Larson%26author%3DB.+T.+Litz 2015 Boasso%2C+A.+M.%2C+Steenkamp%2C+M.+M.%2C+Nash%2C+W.+P.%2C+Larson%2C+J.+L.%2C+%26+Litz%2C+B.+T.+%282015%29.+The+relationship+between+course+of+PTSD+symptoms+in+deployed+U.S.+Marines+and+degree+of+combat+exposure.+Journal+of+Traumatic+Stress%2C+28%281%29%2C+73%E2%80%9378.+https%3A%2F%2Fdoi.org%2F. 73-78 Journal+of+Traumatic+Stress 28 1 10.1002%2Fjts.21988 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_5_1 10.1002%252Fjts.21988 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1002%252Fjts.21988%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DBoasso%26rft.aufirst%3DA.%2520M.%26rft.date%3D2015%26rft.atitle%3DThe%2520relationship%2520between%2520course%2520of%2520PTSD%2520symptoms%2520in%2520deployed%2520U.S.%2520Marines%2520and%2520degree%2520of%2520combat%2520exposure%26rft.jtitle%3DJournal%2520of%2520Traumatic%2520Stress%26rft.volume%3D28%26rft.issue%3D1%26rft.spage%3D73%26rft.epage%3D78 %00empty%00}-->
• Bonanno, G. A., Mancini, A. D., Horton, J. L., Powell, T. M., LeardMann, C. A., Boyko, E. J., … Smith, T. C. (2012). Trajectories of trauma symptoms and resilience in deployed US military service members: Prospective cohort study. British Journal of Psychiatry, 200(4), 317–323. https://doi.org/10.1192/bjp.bp.111.096552.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1192%2Fbjp.bp.111.096552 journal Trajectories+of+trauma+symptoms+and+resilience+in+deployed+US+military+service+members%3A+Prospective+cohort+study author%3DG.+A.+Bonanno%26author%3DA.+D.+Mancini%26author%3DJ.+L.+Horton%26author%3DT.+M.+Powell%26author%3DC.+A.+LeardMann%26author%3DE.+J.+Boyko%26author%3DT.+C.+Smith 2012 Bonanno%2C+G.+A.%2C+Mancini%2C+A.+D.%2C+Horton%2C+J.+L.%2C+Powell%2C+T.+M.%2C+LeardMann%2C+C.+A.%2C+Boyko%2C+E.+J.%2C+%E2%80%A6+Smith%2C+T.+C.+%282012%29.+Trajectories+of+trauma+symptoms+and+resilience+in+deployed+US+military+service+members%3A+Prospective+cohort+study.+British+Journal+of+Psychiatry%2C+200%284%29%2C+317%E2%80%93323.+https%3A%2F%2Fdoi.org%2F. 317-323 British+Journal+of+Psychiatry 200 4 10.1192%2Fbjp.bp.111.096552 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_6_1 10.1192%252Fbjp.bp.111.096552 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1192%252Fbjp.bp.111.096552%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DBonanno%26rft.aufirst%3DG.%2520A.%26rft.date%3D2012%26rft.atitle%3DTrajectories%2520of%2520trauma%2520symptoms%2520and%2520resilience%2520in%2520deployed%2520US%2520military%2520service%2520members%253A%2520Prospective%2520cohort%2520study%26rft.jtitle%3DBritish%2520Journal%2520of%2520Psychiatry%26rft.volume%3D200%26rft.issue%3D4%26rft.spage%3D317%26rft.epage%3D323 %00empty%00}-->
• Bryant, R. A., Nickerson, A., Creamer, M., O'Donnell, M., Forbes, D., Galatzer-Levy, I., … Silove, D. (2015). Trajectory of post-traumatic stress following traumatic injury: 6-year follow-up. The British Journal of Psychiatry, 206(5), 417–423. https://doi.org/10.1192/bjp.bp.114.145516.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1192%2Fbjp.bp.114.145516 journal Trajectory+of+post-traumatic+stress+following+traumatic+injury%3A+6-year+follow-up author%3DR.+A.+Bryant%26author%3DA.+Nickerson%26author%3DM.+Creamer%26author%3DM.+O%27Donnell%26author%3DD.+Forbes%26author%3DI.+Galatzer-Levy%26author%3DD.+Silove 2015 Bryant%2C+R.+A.%2C+Nickerson%2C+A.%2C+Creamer%2C+M.%2C+O%27Donnell%2C+M.%2C+Forbes%2C+D.%2C+Galatzer-Levy%2C+I.%2C+%E2%80%A6+Silove%2C+D.+%282015%29.+Trajectory+of+post-traumatic+stress+following+traumatic+injury%3A+6-year+follow-up.+The+British+Journal+of+Psychiatry%2C+206%285%29%2C+417%E2%80%93423.+https%3A%2F%2Fdoi.org%2F. 417-423 The+British+Journal+of+Psychiatry 206 5 10.1192%2Fbjp.bp.114.145516 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_7_1 10.1192%252Fbjp.bp.114.145516 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1192%252Fbjp.bp.114.145516%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DBryant%26rft.aufirst%3DR.%2520A.%26rft.date%3D2015%26rft.atitle%3DTrajectory%2520of%2520post-traumatic%2520stress%2520following%2520traumatic%2520injury%253A%25206-year%2520follow-up%26rft.jtitle%3DThe%2520British%2520Journal%2520of%2520Psychiatry%26rft.volume%3D206%26rft.issue%3D5%26rft.spage%3D417%26rft.epage%3D423 %00empty%00}-->
• deRoon-Cassini, T. A., Mancini, A. D., Rusch, M. D., & Bonanno, G. A. (2010). Psychopathology and Resilience Following Traumatic Injury: A Latent Growth Mixture Model Analysis. Rehabilitation Psychology, 55(1), 1–11. https://doi.org/10.1037/a0018601.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1037%2Fa0018601 journal Psychopathology+and+Resilience+Following+Traumatic+Injury%3A+A+Latent+Growth+Mixture+Model+Analysis author%3DT.+A.+deRoon-Cassini%26author%3DA.+D.+Mancini%26author%3DM.+D.+Rusch%26author%3DG.+A.+Bonanno 2010 deRoon-Cassini%2C+T.+A.%2C+Mancini%2C+A.+D.%2C+Rusch%2C+M.+D.%2C+%26+Bonanno%2C+G.+A.+%282010%29.+Psychopathology+and+Resilience+Following+Traumatic+Injury%3A+A+Latent+Growth+Mixture+Model+Analysis.+Rehabilitation+Psychology%2C+55%281%29%2C+1%E2%80%9311.+https%3A%2F%2Fdoi.org%2F. 1-11 Rehabilitation+Psychology 55 1 10.1037%2Fa0018601 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_8_1 10.1037%252Fa0018601 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1037%252Fa0018601%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DdeRoon-Cassini%26rft.aufirst%3DT.%2520A.%26rft.date%3D2010%26rft.atitle%3DPsychopathology%2520and%2520Resilience%2520Following%2520Traumatic%2520Injury%253A%2520A%2520Latent%2520Growth%2520Mixture%2520Model%2520Analysis%26rft.jtitle%3DRehabilitation%2520Psychology%26rft.volume%3D55%26rft.issue%3D1%26rft.spage%3D1%26rft.epage%3D11 %00empty%00}-->
• Dickstein, B. D., Suvak, M., Litz, B. T., & Adler, A. B. (2010). Heterogeneity in the course of posttraumatic stress disorder: Trajectories of symptomatology. Journal of Traumatic Stress, 23(3), 331–339. https://doi.org/10.1002/jts.20523.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1002%2Fjts.20523 journal Heterogeneity+in+the+course+of+posttraumatic+stress+disorder%3A+Trajectories+of+symptomatology author%3DB.+D.+Dickstein%26author%3DM.+Suvak%26author%3DB.+T.+Litz%26author%3DA.+B.+Adler 2010 Dickstein%2C+B.+D.%2C+Suvak%2C+M.%2C+Litz%2C+B.+T.%2C+%26+Adler%2C+A.+B.+%282010%29.+Heterogeneity+in+the+course+of+posttraumatic+stress+disorder%3A+Trajectories+of+symptomatology.+Journal+of+Traumatic+Stress%2C+23%283%29%2C+331%E2%80%93339.+https%3A%2F%2Fdoi.org%2F. 331-339 Journal+of+Traumatic+Stress 23 3 10.1002%2Fjts.20523 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_9_1 10.1002%252Fjts.20523 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1002%252Fjts.20523%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DDickstein%26rft.aufirst%3DB.%2520D.%26rft.date%3D2010%26rft.atitle%3DHeterogeneity%2520in%2520the%2520course%2520of%2520posttraumatic%2520stress%2520disorder%253A%2520Trajectories%2520of%2520symptomatology%26rft.jtitle%3DJournal%2520of%2520Traumatic%2520Stress%26rft.volume%3D23%26rft.issue%3D3%26rft.spage%3D331%26rft.epage%3D339 %00empty%00}-->
• Eekhout, I., Reijnen, A., Vermetten, E., & Geuze, E. (2016). Post-traumatic stress symptoms 5 years after military deployment to Afghanistan: An observational cohort study. The Lancet Psychiatry, 3(1), 58–64. https://doi.org/10.1016/S2215-0366(15)00368-5.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1016%2FS2215-0366%2815%2900368-5 journal Post-traumatic+stress+symptoms+5%C2%A0years+after+military+deployment+to+Afghanistan%3A+An+observational+cohort+study author%3DI.+Eekhout%26author%3DA.+Reijnen%26author%3DE.+Vermetten%26author%3DE.+Geuze 2016 Eekhout%2C+I.%2C+Reijnen%2C+A.%2C+Vermetten%2C+E.%2C+%26+Geuze%2C+E.+%282016%29.+Post-traumatic+stress+symptoms+5%C2%A0years+after+military+deployment+to+Afghanistan%3A+An+observational+cohort+study.+The+Lancet+Psychiatry%2C+3%281%29%2C+58%E2%80%9364.+https%3A%2F%2Fdoi.org%2F. 58-64 The+Lancet+Psychiatry 3 1 10.1016%2FS2215-0366%2815%2900368-5 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_10_1 10.1016%252FS2215-0366%252815%252900368-5 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252FS2215-0366%252815%252900368-5%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DEekhout%26rft.aufirst%3DI.%26rft.date%3D2016%26rft.atitle%3DPost-traumatic%2520stress%2520symptoms%25205%25C2%25A0years%2520after%2520military%2520deployment%2520to%2520Afghanistan%253A%2520An%2520observational%2520cohort%2520study%26rft.jtitle%3DThe%2520Lancet%2520Psychiatry%26rft.volume%3D3%26rft.issue%3D1%26rft.spage%3D58%26rft.epage%3D64 %00empty%00}-->
• Galatzer-Levy, I. R., Ankri, Y., Freedman, S., Israeli-Shalev, Y., Roitman, P., Gilad, M., & Shalev, A. Y. (2013). Early PTSD Symptom Trajectories: Persistence, Recovery, and Response to Treatment: Results from the Jerusalem Trauma Outreach and Prevention Study (J-TOPS). PLoS ONE, 8(8): e70084. https://doi.org/10.1371/journal.pone.0070084.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1371%2Fjournal.pone.0070084 journal Early+PTSD+Symptom+Trajectories%3A+Persistence%2C+Recovery%2C+and+Response+to+Treatment%3A+Results+from+the+Jerusalem+Trauma+Outreach+and+Prevention+Study+%28J-TOPS%29 author%3DI.+R.+Galatzer-Levy%26author%3DY.+Ankri%26author%3DS.+Freedman%26author%3DY.+Israeli-Shalev%26author%3DP.+Roitman%26author%3DM.+Gilad%26author%3DA.+Y.+Shalev 2013 Galatzer-Levy%2C+I.+R.%2C+Ankri%2C+Y.%2C+Freedman%2C+S.%2C+Israeli-Shalev%2C+Y.%2C+Roitman%2C+P.%2C+Gilad%2C+M.%2C+%26+Shalev%2C+A.+Y.+%282013%29.+Early+PTSD+Symptom+Trajectories%3A+Persistence%2C+Recovery%2C+and+Response+to+Treatment%3A+Results+from+the+Jerusalem+Trauma+Outreach+and+Prevention+Study+%28J-TOPS%29.+PLoS+ONE%2C+8%288%29%3A+e70084.+%2F. e70084 PLoS+ONE 8 8 10.1371%2Fjournal.pone.0070084 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_11_1 10.1371%252Fjournal.pone.0070084 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1371%252Fjournal.pone.0070084%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DGalatzer-Levy%26rft.aufirst%3DI.%2520R.%26rft.date%3D2013%26rft.atitle%3DEarly%2520PTSD%2520Symptom%2520Trajectories%253A%2520Persistence%252C%2520Recovery%252C%2520and%2520Response%2520to%2520Treatment%253A%2520Results%2520from%2520the%2520Jerusalem%2520Trauma%2520Outreach%2520and%2520Prevention%2520Study%2520%2528J-TOPS%2529%26rft.jtitle%3DPLoS%2520ONE%26rft.volume%3D8%26rft.issue%3D8%26rft.spage%3De70084 %00empty%00}-->
• Galatzer-Levy, I. R., Madan, A., Neylan, T. C., Henn-Haase, C., & Marmar, C. R. (2011). Peritraumatic and trait dissociation differentiate police officers with resilient versus symptomatic trajectories of posttraumatic stress symptoms. Journal of Traumatic Stress, 24(5), 557–565. https://doi.org/10.1002/jts.20684.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1002%2Fjts.20684 journal Peritraumatic+and+trait+dissociation+differentiate+police+officers+with+resilient+versus+symptomatic+trajectories+of+posttraumatic+stress+symptoms author%3DI.+R.+Galatzer-Levy%26author%3DA.+Madan%26author%3DT.+C.+Neylan%26author%3DC.+Henn-Haase%26author%3DC.+R.+Marmar 2011 Galatzer-Levy%2C+I.+R.%2C+Madan%2C+A.%2C+Neylan%2C+T.+C.%2C+Henn-Haase%2C+C.%2C+%26+Marmar%2C+C.+R.+%282011%29.+Peritraumatic+and+trait+dissociation+differentiate+police+officers+with+resilient+versus+symptomatic+trajectories+of+posttraumatic+stress+symptoms.+Journal+of+Traumatic+Stress%2C+24%285%29%2C+557%E2%80%93565.+https%3A%2F%2Fdoi.org%2F. 557-565 Journal+of+Traumatic+Stress 24 5 10.1002%2Fjts.20684 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_12_1 10.1002%252Fjts.20684 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1002%252Fjts.20684%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DGalatzer-Levy%26rft.aufirst%3DI.%2520R.%26rft.date%3D2011%26rft.atitle%3DPeritraumatic%2520and%2520trait%2520dissociation%2520differentiate%2520police%2520officers%2520with%2520resilient%2520versus%2520symptomatic%2520trajectories%2520of%2520posttraumatic%2520stress%2520symptoms%26rft.jtitle%3DJournal%2520of%2520Traumatic%2520Stress%26rft.volume%3D24%26rft.issue%3D5%26rft.spage%3D557%26rft.epage%3D565 %00empty%00}-->
• Gelman, A. & Rubin, D. B. (1992). Inference from Iterative Simulation Using Multiple Sequences, Statistical Science, 7, 457–472. doi:10.1214/ss/1177011136.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1214%2Fss%2F1177011136 journal %00null%00 author%3DA.+Gelman%26author%3DD.+B.+Rubin 1992 Gelman%2C+A.+%26+Rubin%2C+D.+B.+%281992%29.+Inference+from+Iterative+Simulation+Using+Multiple+Sequences%2C+Statistical+Science%2C+7%2C+457%E2%80%93472.+doi%3A. 457-472 Statistical+Science 7 %00null%00 10.1214%2Fss%2F1177011136 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_13_1 10.1214%252Fss%252F1177011136 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1214%252Fss%252F1177011136%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DGelman%26rft.aufirst%3DA.%26rft.date%3D1992%26rft.jtitle%3DStatistical%2520Science%26rft.volume%3D7%26rft.spage%3D457%26rft.epage%3D472 %00empty%00}-->
• Hiller, R. M., Halligan, S. L., Ariyanayagam, R., Dalgleish, T., Smith, P., Yule, W., … Meiser-Stedman, R. (2016). Predictors of Posttraumatic Stress Symptom Trajectories in Parents of Children Exposed to Motor Vehicle Collisions. Journal of Pediatric Psychology, 41(1), 108–116. https://doi.org/10.1093/jpepsy/jsv068.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1093%2Fjpepsy%2Fjsv068 journal Predictors+of+Posttraumatic+Stress+Symptom+Trajectories+in+Parents+of+Children+Exposed+to+Motor+Vehicle+Collisions author%3DR.+M.+Hiller%26author%3DS.+L.+Halligan%26author%3DR.+Ariyanayagam%26author%3DT.+Dalgleish%26author%3DP.+Smith%26author%3DW.+Yule%26author%3DR.+Meiser-Stedman 2016 Hiller%2C+R.+M.%2C+Halligan%2C+S.+L.%2C+Ariyanayagam%2C+R.%2C+Dalgleish%2C+T.%2C+Smith%2C+P.%2C+Yule%2C+W.%2C+%E2%80%A6+Meiser-Stedman%2C+R.+%282016%29.+Predictors+of+Posttraumatic+Stress+Symptom+Trajectories+in+Parents+of+Children+Exposed+to+Motor+Vehicle+Collisions.+Journal+of+Pediatric+Psychology%2C+41%281%29%2C+108%E2%80%93116.+https%3A%2F%2Fdoi.org%2F. 108-116 Journal+of+Pediatric+Psychology 41 1 10.1093%2Fjpepsy%2Fjsv068 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_14_1 10.1093%252Fjpepsy%252Fjsv068 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1093%252Fjpepsy%252Fjsv068%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DHiller%26rft.aufirst%3DR.%2520M.%26rft.date%3D2016%26rft.atitle%3DPredictors%2520of%2520Posttraumatic%2520Stress%2520Symptom%2520Trajectories%2520in%2520Parents%2520of%2520Children%2520Exposed%2520to%2520Motor%2520Vehicle%2520Collisions%26rft.jtitle%3DJournal%2520of%2520Pediatric%2520Psychology%26rft.volume%3D41%26rft.issue%3D1%26rft.spage%3D108%26rft.epage%3D116 %00empty%00}-->
• Hobfoll, S. E., Mancini, A. D., Hall, B. J., Canetti, D., & Bonanno, G. A. (2011). The limits of resilience: Distress following chronic political violence among Palestinians. Social Science & Medicine, 72(8), 1400–1408. https://doi.org/10.1016/j.socscimed.2011.02.022.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1016%2Fj.socscimed.2011.02.022 journal The+limits+of+resilience%3A+Distress+following+chronic+political+violence+among+Palestinians author%3DS.+E.+Hobfoll%26author%3DA.+D.+Mancini%26author%3DB.+J.+Hall%26author%3DD.+Canetti%26author%3DG.+A.+Bonanno 2011 Hobfoll%2C+S.+E.%2C+Mancini%2C+A.+D.%2C+Hall%2C+B.+J.%2C+Canetti%2C+D.%2C+%26+Bonanno%2C+G.+A.+%282011%29.+The+limits+of+resilience%3A+Distress+following+chronic+political+violence+among+Palestinians.+Social+Science+%26+Medicine%2C+72%288%29%2C+1400%E2%80%931408.+https%3A%2F%2Fdoi.org%2F. 1400-1408 Social+Science+%26+Medicine 72 8 10.1016%2Fj.socscimed.2011.02.022 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_15_1 10.1016%252Fj.socscimed.2011.02.022 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.socscimed.2011.02.022%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DHobfoll%26rft.aufirst%3DS.%2520E.%26rft.date%3D2011%26rft.atitle%3DThe%2520limits%2520of%2520resilience%253A%2520Distress%2520following%2520chronic%2520political%2520violence%2520among%2520Palestinians%26rft.jtitle%3DSocial%2520Science%2520%2526%2520Medicine%26rft.volume%3D72%26rft.issue%3D8%26rft.spage%3D1400%26rft.epage%3D1408 %00empty%00}-->
• Holgersen, K. H., Klöckner, C. A., Jakob Boe, H., Weisæth, L., & Holen, A. (2011). Disaster survivors in their third decade: Trajectories of initial stress responses and long-term course of mental health. Journal of Traumatic Stress, 24(3), 334–341. https://doi.org/10.1002/jts.20636.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1002%2Fjts.20636 journal Disaster+survivors+in+their+third+decade%3A+Trajectories+of+initial+stress+responses+and+long-term+course+of+mental+health author%3DK.+H.+Holgersen%26author%3DC.+A.+Kl%C3%B6ckner%26author%3DH.+Jakob+Boe%26author%3DL.+Weis%C3%A6th%26author%3DA.+Holen 2011 Holgersen%2C+K.+H.%2C+Kl%C3%B6ckner%2C+C.+A.%2C+Jakob+Boe%2C+H.%2C+Weis%C3%A6th%2C+L.%2C+%26+Holen%2C+A.+%282011%29.+Disaster+survivors+in+their+third+decade%3A+Trajectories+of+initial+stress+responses+and+long-term+course+of+mental+health.+Journal+of+Traumatic+Stress%2C+24%283%29%2C+334%E2%80%93341.+https%3A%2F%2Fdoi.org%2F. 334-341 Journal+of+Traumatic+Stress 24 3 10.1002%2Fjts.20636 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_16_1 10.1002%252Fjts.20636 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1002%252Fjts.20636%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DHolgersen%26rft.aufirst%3DK.%2520H.%26rft.date%3D2011%26rft.atitle%3DDisaster%2520survivors%2520in%2520their%2520third%2520decade%253A%2520Trajectories%2520of%2520initial%2520stress%2520responses%2520and%2520long-term%2520course%2520of%2520mental%2520health%26rft.jtitle%3DJournal%2520of%2520Traumatic%2520Stress%26rft.volume%3D24%26rft.issue%3D3%26rft.spage%3D334%26rft.epage%3D341 %00empty%00}-->
• Hong, S. B., Youssef, G. J., Song, S. H., Choi, N. H., Ryu, J., McDermott, B., … Kim, B. N. (2014). Different clinical courses of children exposed to a single incident of psychological trauma: A 30-month prospective follow-up study. Journal of Child Psychology and Psychiatry, 55(11), 1226–1233. https://doi.org/10.1111/jcpp.12241.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1111%2Fjcpp.12241 journal Different+clinical+courses+of+children+exposed+to+a+single+incident+of+psychological+trauma%3A+A+30-month+prospective+follow-up+study author%3DS.+B.+Hong%26author%3DG.+J.+Youssef%26author%3DS.+H.+Song%26author%3DN.+H.+Choi%26author%3DJ.+Ryu%26author%3DB.+McDermott%26author%3DB.+N.+Kim 2014 Hong%2C+S.+B.%2C+Youssef%2C+G.+J.%2C+Song%2C+S.+H.%2C+Choi%2C+N.+H.%2C+Ryu%2C+J.%2C+McDermott%2C+B.%2C+%E2%80%A6+Kim%2C+B.+N.+%282014%29.+Different+clinical+courses+of+children+exposed+to+a+single+incident+of+psychological+trauma%3A+A+30-month+prospective+follow-up+study.+Journal+of+Child+Psychology+and+Psychiatry%2C+55%2811%29%2C+1226%E2%80%931233.+https%3A%2F%2Fdoi.org%2F. 1226-1233 Journal+of+Child+Psychology+and+Psychiatry 55 11 10.1111%2Fjcpp.12241 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_17_1 10.1111%252Fjcpp.12241 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1111%252Fjcpp.12241%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DHong%26rft.aufirst%3DS.%2520B.%26rft.date%3D2014%26rft.atitle%3DDifferent%2520clinical%2520courses%2520of%2520children%2520exposed%2520to%2520a%2520single%2520incident%2520of%2520psychological%2520trauma%253A%2520A%252030-month%2520prospective%2520follow-up%2520study%26rft.jtitle%3DJournal%2520of%2520Child%2520Psychology%2520and%2520Psychiatry%26rft.volume%3D55%26rft.issue%3D11%26rft.spage%3D1226%26rft.epage%3D1233 %00empty%00}-->
• Johannesson, K. B., Arinell, H., & Arnberg, F. K. (2015). Six years after the wave. Trajectories of posttraumatic stress following a natural disaster. Journal of Anxiety Disorders, 36, 15–24. https://doi.org/10.1016/j.janxdis.2015.07.007.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1016%2Fj.janxdis.2015.07.007 journal Six+years+after+the+wave.+Trajectories+of+posttraumatic+stress+following+a+natural+disaster author%3DK.+B.+Johannesson%26author%3DH.+Arinell%26author%3DF.+K.+Arnberg 2015 Johannesson%2C+K.+B.%2C+Arinell%2C+H.%2C+%26+Arnberg%2C+F.+K.+%282015%29.+Six+years+after+the+wave.+Trajectories+of+posttraumatic+stress+following+a+natural+disaster.+Journal+of+Anxiety+Disorders%2C+36%2C+15%E2%80%9324.+https%3A%2F%2Fdoi.org%2F. 15-24 Journal+of+Anxiety+Disorders 36 %00null%00 10.1016%2Fj.janxdis.2015.07.007 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_18_1 10.1016%252Fj.janxdis.2015.07.007 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.janxdis.2015.07.007%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DJohannesson%26rft.aufirst%3DK.%2520B.%26rft.date%3D2015%26rft.atitle%3DSix%2520years%2520after%2520the%2520wave.%2520Trajectories%2520of%2520posttraumatic%2520stress%2520following%2520a%2520natural%2520disaster%26rft.jtitle%3DJournal%2520of%2520Anxiety%2520Disorders%26rft.volume%3D36%26rft.spage%3D15%26rft.epage%3D24 %00empty%00}-->
• La Greca, A. M., Lai, B. S., Llabre, M. M., Silverman, W. K., Vernberg, E. M., & Prinstein, M. J. (2013). Children's Postdisaster Trajectories of PTS Symptoms: Predicting Chronic Distress. Child and Youth Care Forum 42(4), 351–369.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs10566-013-9206-1 journal Children%27s+Postdisaster+Trajectories+of+PTS+Symptoms%3A+Predicting+Chronic+Distress author%3DA.+M.+La+Greca%26author%3DB.+S.+Lai%26author%3DM.+M.+Llabre%26author%3DW.+K.+Silverman%26author%3DE.+M.+Vernberg%26author%3DM.+J.+Prinstein 2013 La+Greca%2C+A.+M.%2C+Lai%2C+B.+S.%2C+Llabre%2C+M.+M.%2C+Silverman%2C+W.+K.%2C+Vernberg%2C+E.+M.%2C+%26+Prinstein%2C+M.+J.+%282013%29.+Children%27s+Postdisaster+Trajectories+of+PTS+Symptoms%3A+Predicting+Chronic+Distress.+Child+and+Youth+Care+Forum+42%284%29%2C+351%E2%80%93369. 351-369 Child+and+Youth+Care+Forum 42 4 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_19_1 10.1007%252Fs10566-013-9206-1 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs10566-013-9206-1%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DLa%2520Greca%26rft.aufirst%3DA.%2520M.%26rft.date%3D2013%26rft.atitle%3DChildren%2527s%2520Postdisaster%2520Trajectories%2520of%2520PTS%2520Symptoms%253A%2520Predicting%2520Chronic%2520Distress%26rft.jtitle%3DChild%2520and%2520Youth%2520Care%2520Forum%26rft.volume%3D42%26rft.issue%3D4%26rft.spage%3D351%26rft.epage%3D369 %00empty%00}-->
• Le Brocque, R. M., Hendrikz, J., & Kenardy, J. A. (2010). The course of posttraumatic stress in children: Examination of recovery trajectories following traumatic injury. Journal of Pediatric Psychology, 35(6), 637–645. https://doi.org/10.1093/jpepsy/jsp050.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1093%2Fjpepsy%2Fjsp050 journal The+course+of+posttraumatic+stress+in+children%3A+Examination+of+recovery+trajectories+following+traumatic+injury author%3DR.+M.+Le+Brocque%26author%3DJ.+Hendrikz%26author%3DJ.+A.+Kenardy 2010 Le+Brocque%2C+R.+M.%2C+Hendrikz%2C+J.%2C+%26+Kenardy%2C+J.+A.+%282010%29.+The+course+of+posttraumatic+stress+in+children%3A+Examination+of+recovery+trajectories+following+traumatic+injury.+Journal+of+Pediatric+Psychology%2C+35%286%29%2C+637%E2%80%93645.+https%3A%2F%2Fdoi.org%2F. 637-645 Journal+of+Pediatric+Psychology 35 6 10.1093%2Fjpepsy%2Fjsp050 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_20_1 10.1093%252Fjpepsy%252Fjsp050 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1093%252Fjpepsy%252Fjsp050%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DLe%2520Brocque%26rft.aufirst%3DR.%2520M.%26rft.date%3D2010%26rft.atitle%3DThe%2520course%2520of%2520posttraumatic%2520stress%2520in%2520children%253A%2520Examination%2520of%2520recovery%2520trajectories%2520following%2520traumatic%2520injury%26rft.jtitle%3DJournal%2520of%2520Pediatric%2520Psychology%26rft.volume%3D35%26rft.issue%3D6%26rft.spage%3D637%26rft.epage%3D645 %00empty%00}-->
• Lowe, S. R., Joshi, S., Pietrzak, R. H., Galea, S., & Cerdá, M. (2015). Mental health and general wellness in the aftermath of Hurricane Ike. Social Science and Medicine, 124, 162–170. https://doi.org/10.1016/j.socscimed.2014.11.032.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1016%2Fj.socscimed.2014.11.032 journal Mental+health+and+general+wellness+in+the+aftermath+of+Hurricane+Ike author%3DS.+R.+Lowe%26author%3DS.+Joshi%26author%3DR.+H.+Pietrzak%26author%3DS.+Galea%26author%3DM.+Cerd%C3%A1 2015 Lowe%2C+S.+R.%2C+Joshi%2C+S.%2C+Pietrzak%2C+R.+H.%2C+Galea%2C+S.%2C+%26+Cerd%C3%A1%2C+M.+%282015%29.+Mental+health+and+general+wellness+in+the+aftermath+of+Hurricane+Ike.+Social+Science+and+Medicine%2C+124%2C+162%E2%80%93170.+https%3A%2F%2Fdoi.org%2F10.1016%2Fj.socscimed.2014.11.032. 162-170 Social+Science+and+Medicine 124 %00null%00 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_21_1 10.1016%252Fj.socscimed.2014.11.032 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.socscimed.2014.11.032%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DLowe%26rft.aufirst%3DS.%2520R.%26rft.date%3D2015%26rft.atitle%3DMental%2520health%2520and%2520general%2520wellness%2520in%2520the%2520aftermath%2520of%2520Hurricane%2520Ike%26rft.jtitle%3DSocial%2520Science%2520and%2520Medicine%26rft.volume%3D124%26rft.spage%3D162%26rft.epage%3D170 %00empty%00}-->
• Maslow, C. B., Caramanica, K., Welch, A. E., Stellman, S. D., Brackbill, R. M., & Farfel, M. R. (2015). Trajectories of Scores on a Screening Instrument for PTSD Among World Trade Center Rescue, Recovery, and Clean-Up Workers. Journal of Traumatic Stress, 28(3), 198–205. https://doi.org/10.1002/jts.22011.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1002%2Fjts.22011 journal Trajectories+of+Scores+on+a+Screening+Instrument+for+PTSD+Among+World+Trade+Center+Rescue%2C+Recovery%2C+and+Clean-Up+Workers author%3DC.+B.+Maslow%26author%3DK.+Caramanica%26author%3DA.+E.+Welch%26author%3DS.+D.+Stellman%26author%3DR.+M.+Brackbill%26author%3DM.+R.+Farfel 2015 Maslow%2C+C.+B.%2C+Caramanica%2C+K.%2C+Welch%2C+A.+E.%2C+Stellman%2C+S.+D.%2C+Brackbill%2C+R.+M.%2C+%26+Farfel%2C+M.+R.+%282015%29.+Trajectories+of+Scores+on+a+Screening+Instrument+for+PTSD+Among+World+Trade+Center+Rescue%2C+Recovery%2C+and+Clean-Up+Workers.+Journal+of+Traumatic+Stress%2C+28%283%29%2C+198%E2%80%93205.+https%3A%2F%2Fdoi.org%2F. 198-205 Journal+of+Traumatic+Stress 28 3 10.1002%2Fjts.22011 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_22_1 10.1002%252Fjts.22011 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1002%252Fjts.22011%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DMaslow%26rft.aufirst%3DC.%2520B.%26rft.date%3D2015%26rft.atitle%3DTrajectories%2520of%2520Scores%2520on%2520a%2520Screening%2520Instrument%2520for%2520PTSD%2520Among%2520World%2520Trade%2520Center%2520Rescue%252C%2520Recovery%252C%2520and%2520Clean-Up%2520Workers%26rft.jtitle%3DJournal%2520of%2520Traumatic%2520Stress%26rft.volume%3D28%26rft.issue%3D3%26rft.spage%3D198%26rft.epage%3D205 %00empty%00}-->
• Nash, W. P., Boasso, A. M., Steenkamp, M. M., Larson, J. L., Lubin, R. E., & Litz, B. T. (2015). Posttraumatic Stress in Deployed Marines: Prospective Trajectories of Early Adaptation. Journal of Abnormal Psychology, 124(1), 155–171. https://doi.org/10.1037/abn0000020.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1037%2Fabn0000020 journal Posttraumatic+Stress+in+Deployed+Marines%3A+Prospective+Trajectories+of+Early+Adaptation author%3DW.+P.+Nash%26author%3DA.+M.+Boasso%26author%3DM.+M.+Steenkamp%26author%3DJ.+L.+Larson%26author%3DR.+E.+Lubin%26author%3DB.+T.+Litz 2015 Nash%2C+W.+P.%2C+Boasso%2C+A.+M.%2C+Steenkamp%2C+M.+M.%2C+Larson%2C+J.+L.%2C+Lubin%2C+R.+E.%2C+%26+Litz%2C+B.+T.+%282015%29.+Posttraumatic+Stress+in+Deployed+Marines%3A+Prospective+Trajectories+of+Early+Adaptation.+Journal+of+Abnormal+Psychology%2C+124%281%29%2C+155%E2%80%93171.+https%3A%2F%2Fdoi.org%2F. 155-171 Journal+of+Abnormal+Psychology 124 1 10.1037%2Fabn0000020 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_23_1 10.1037%252Fabn0000020 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1037%252Fabn0000020%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DNash%26rft.aufirst%3DW.%2520P.%26rft.date%3D2015%26rft.atitle%3DPosttraumatic%2520Stress%2520in%2520Deployed%2520Marines%253A%2520Prospective%2520Trajectories%2520of%2520Early%2520Adaptation%26rft.jtitle%3DJournal%2520of%2520Abnormal%2520Psychology%26rft.volume%3D124%26rft.issue%3D1%26rft.spage%3D155%26rft.epage%3D171 %00empty%00}-->
• Norris, F. H., Tracy, M., & Galea, S. (2009). Looking for resilience: Understanding the longitudinal trajectories of responses to stress. Social Science and Medicine, 68(12), 2190–2198. https://doi.org/10.1016/j.socscimed.2009.03.043.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1016%2Fj.socscimed.2009.03.043 journal Looking+for+resilience%3A+Understanding+the+longitudinal+trajectories+of+responses+to+stress author%3DF.+H.+Norris%26author%3DM.+Tracy%26author%3DS.+Galea 2009 Norris%2C+F.+H.%2C+Tracy%2C+M.%2C+%26+Galea%2C+S.+%282009%29.+Looking+for+resilience%3A+Understanding+the+longitudinal+trajectories+of+responses+to+stress.+Social+Science+and+Medicine%2C+68%2812%29%2C+2190%E2%80%932198.+https%3A%2F%2Fdoi.org%2F. 2190-2198 Social+Science+and+Medicine 68 12 10.1016%2Fj.socscimed.2009.03.043 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_24_1 10.1016%252Fj.socscimed.2009.03.043 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.socscimed.2009.03.043%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DNorris%26rft.aufirst%3DF.%2520H.%26rft.date%3D2009%26rft.atitle%3DLooking%2520for%2520resilience%253A%2520Understanding%2520the%2520longitudinal%2520trajectories%2520of%2520responses%2520to%2520stress%26rft.jtitle%3DSocial%2520Science%2520and%2520Medicine%26rft.volume%3D68%26rft.issue%3D12%26rft.spage%3D2190%26rft.epage%3D2198 %00empty%00}-->
• O'Malley, A. & Zaslavsky, A. (2008). Domain-level covariance analysis for survey data with structured nonresponse. Journal of the American Statistical Association, 103, 1405–1418. https://doi.org/10.1198/016214508000000724.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1198%2F016214508000000724 journal Domain-level+covariance+analysis+for+survey+data+with+structured+nonresponse author%3DA.+O%27Malley%26author%3DA.+Zaslavsky 2008 O%27Malley%2C+A.+%26+Zaslavsky%2C+A.+%282008%29.+Domain-level+covariance+analysis+for+survey+data+with+structured+nonresponse.+Journal+of+the+American+Statistical+Association%2C+103%2C+1405%E2%80%931418.+https%3A%2F%2Fdoi.org%2F10.1198%2F016214508000000724. 1405-1418 Journal+of+the+American+Statistical+Association 103 %00null%00 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_25_1 10.1198%252F016214508000000724 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1198%252F016214508000000724%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DO%2527Malley%26rft.aufirst%3DA.%26rft.date%3D2008%26rft.atitle%3DDomain-level%2520covariance%2520analysis%2520for%2520survey%2520data%2520with%2520structured%2520nonresponse%26rft.jtitle%3DJournal%2520of%2520the%2520American%2520Statistical%2520Association%26rft.volume%3D103%26rft.spage%3D1405%26rft.epage%3D1418 %00empty%00}-->
• Orcutt, H. K., Bonanno, G. A., Hannan, S. M., & Miron, L. R. (2014). Prospective trajectories of posttraumatic stress in college women following a campus mass shooting. Journal of Traumatic Stress, 27(3), 249–256. https://doi.org/10.1002/jts.21914.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1002%2Fjts.21914 journal Prospective+trajectories+of+posttraumatic+stress+in+college+women+following+a+campus+mass+shooting author%3DH.+K.+Orcutt%26author%3DG.+A.+Bonanno%26author%3DS.+M.+Hannan%26author%3DL.+R.+Miron 2014 Orcutt%2C+H.+K.%2C+Bonanno%2C+G.+A.%2C+Hannan%2C+S.+M.%2C+%26+Miron%2C+L.+R.+%282014%29.+Prospective+trajectories+of+posttraumatic+stress+in+college+women+following+a+campus+mass+shooting.+Journal+of+Traumatic+Stress%2C+27%283%29%2C+249%E2%80%93256.+https%3A%2F%2Fdoi.org%2F. 249-256 Journal+of+Traumatic+Stress 27 3 10.1002%2Fjts.21914 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_26_1 10.1002%252Fjts.21914 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1002%252Fjts.21914%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DOrcutt%26rft.aufirst%3DH.%2520K.%26rft.date%3D2014%26rft.atitle%3DProspective%2520trajectories%2520of%2520posttraumatic%2520stress%2520in%2520college%2520women%2520following%2520a%2520campus%2520mass%2520shooting%26rft.jtitle%3DJournal%2520of%2520Traumatic%2520Stress%26rft.volume%3D27%26rft.issue%3D3%26rft.spage%3D249%26rft.epage%3D256 %00empty%00}-->
• Orcutt, H. K., Erickson, D. J., & Wolfe, J. (2004). The course of PTSD symptoms among Gulf War Veterans: A growth mixture modeling approach. Journal of Traumatic Stress, 17(3), 195–202. https://doi.org/10.1023/B:JOTS.0000029262.42865.c2.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1023%2FB%3AJOTS.0000029262.42865.c2 journal The+course+of+PTSD+symptoms+among+Gulf+War+Veterans%3A+A+growth+mixture+modeling+approach author%3DH.+K.+Orcutt%26author%3DD.+J.+Erickson%26author%3DJ.+Wolfe 2004 Orcutt%2C+H.+K.%2C+Erickson%2C+D.+J.%2C+%26+Wolfe%2C+J.+%282004%29.+The+course+of+PTSD+symptoms+among+Gulf+War+Veterans%3A+A+growth+mixture+modeling+approach.+Journal+of+Traumatic+Stress%2C+17%283%29%2C+195%E2%80%93202.+https%3A%2F%2Fdoi.org%2F. 195-202 Journal+of+Traumatic+Stress 17 3 10.1023%2FB%3AJOTS.0000029262.42865.c2 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_27_1 10.1023%252FB%253AJOTS.0000029262.42865.c2 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1023%252FB%253AJOTS.0000029262.42865.c2%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DOrcutt%26rft.aufirst%3DH.%2520K.%26rft.date%3D2004%26rft.atitle%3DThe%2520course%2520of%2520PTSD%2520symptoms%2520among%2520Gulf%2520War%2520Veterans%253A%2520A%2520growth%2520mixture%2520modeling%2520approach%26rft.jtitle%3DJournal%2520of%2520Traumatic%2520Stress%26rft.volume%3D17%26rft.issue%3D3%26rft.spage%3D195%26rft.epage%3D202 %00empty%00}-->
• Pietrzak, R. H., Feder, A., Singh, R., Schechter, C. B., Bromet, E. J., Katz, C. L., … Southwick, S. M. (2014). Trajectories of PTSD risk and resilience in World Trade Center responders: An 8-year prospective cohort study. Psychological Medicine, 44(1), 205–219. https://doi.org/10.1017/S0033291713000597.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1017%2FS0033291713000597 journal Trajectories+of+PTSD+risk+and+resilience+in+World+Trade+Center+responders%3A+An+8-year+prospective+cohort+study author%3DR.+H.+Pietrzak%26author%3DA.+Feder%26author%3DR.+Singh%26author%3DC.+B.+Schechter%26author%3DE.+J.+Bromet%26author%3DC.+L.+Katz%26author%3DS.+M.+Southwick 2014 Pietrzak%2C+R.+H.%2C+Feder%2C+A.%2C+Singh%2C+R.%2C+Schechter%2C+C.+B.%2C+Bromet%2C+E.+J.%2C+Katz%2C+C.+L.%2C+%E2%80%A6+Southwick%2C+S.+M.+%282014%29.+Trajectories+of+PTSD+risk+and+resilience+in+World+Trade+Center+responders%3A+An+8-year+prospective+cohort+study.+Psychological+Medicine%2C+44%281%29%2C+205%E2%80%93219.+https%3A%2F%2Fdoi.org%2F. 205-219 Psychological+Medicine 44 1 10.1017%2FS0033291713000597 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_28_1 10.1017%252FS0033291713000597 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1017%252FS0033291713000597%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DPietrzak%26rft.aufirst%3DR.%2520H.%26rft.date%3D2014%26rft.atitle%3DTrajectories%2520of%2520PTSD%2520risk%2520and%2520resilience%2520in%2520World%2520Trade%2520Center%2520responders%253A%2520An%25208-year%2520prospective%2520cohort%2520study%26rft.jtitle%3DPsychological%2520Medicine%26rft.volume%3D44%26rft.issue%3D1%26rft.spage%3D205%26rft.epage%3D219 %00empty%00}-->
• Pietrzak, R. H., Van Ness, P. H., Fried, T. R., Galea, S., & Norris, F. H. (2013). Trajectories of posttraumatic stress symptomatology in older persons affected by a large-magnitude disaster. Journal of Psychiatric Research, 47(4), 520–526. https://doi.org/10.1016/j.jpsychires.2012.12.005.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1016%2Fj.jpsychires.2012.12.005 journal Trajectories+of+posttraumatic+stress+symptomatology+in+older+persons+affected+by+a+large-magnitude+disaster author%3DR.+H.+Pietrzak%26author%3DP.+H.+Van+Ness%26author%3DT.+R.+Fried%26author%3DS.+Galea%26author%3DF.+H.+Norris 2013 Pietrzak%2C+R.+H.%2C+Van+Ness%2C+P.+H.%2C+Fried%2C+T.+R.%2C+Galea%2C+S.%2C+%26+Norris%2C+F.+H.+%282013%29.+Trajectories+of+posttraumatic+stress+symptomatology+in+older+persons+affected+by+a+large-magnitude+disaster.+Journal+of+Psychiatric+Research%2C+47%284%29%2C+520%E2%80%93526.+https%3A%2F%2Fdoi.org%2F. 520-526 Journal+of+Psychiatric+Research 47 4 10.1016%2Fj.jpsychires.2012.12.005 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_29_1 10.1016%252Fj.jpsychires.2012.12.005 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.jpsychires.2012.12.005%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DPietrzak%26rft.aufirst%3DR.%2520H.%26rft.date%3D2013%26rft.atitle%3DTrajectories%2520of%2520posttraumatic%2520stress%2520symptomatology%2520in%2520older%2520persons%2520affected%2520by%2520a%2520large-magnitude%2520disaster%26rft.jtitle%3DJournal%2520of%2520Psychiatric%2520Research%26rft.volume%3D47%26rft.issue%3D4%26rft.spage%3D520%26rft.epage%3D526 %00empty%00}-->
• Punamaki, R. L., Palosaari, E., Diab, M., Peltonen, K., & Qouta, S. R. (2014). Trajectories of posttraumatic stress symptoms (PTSS) after major war among Palestinian children: Trauma, family- and child-related predictors. Journal of Affective Disorders, 172, 133–140. https://doi.org/10.1016/j.jad.2014.09.021.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1016%2Fj.jad.2014.09.021 journal Trajectories+of+posttraumatic+stress+symptoms+%28PTSS%29+after+major+war+among+Palestinian+children%3A+Trauma%2C+family-+and+child-related+predictors author%3DR.+L.+Punamaki%26author%3DE.+Palosaari%26author%3DM.+Diab%26author%3DK.+Peltonen%26author%3DS.+R.+Qouta 2014 Punamaki%2C+R.+L.%2C+Palosaari%2C+E.%2C+Diab%2C+M.%2C+Peltonen%2C+K.%2C+%26+Qouta%2C+S.+R.+%282014%29.+Trajectories+of+posttraumatic+stress+symptoms+%28PTSS%29+after+major+war+among+Palestinian+children%3A+Trauma%2C+family-+and+child-related+predictors.+Journal+of+Affective+Disorders%2C+172%2C+133%E2%80%93140.+https%3A%2F%2Fdoi.org%2F. 133-140 Journal+of+Affective+Disorders 172 %00null%00 10.1016%2Fj.jad.2014.09.021 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_30_1 10.1016%252Fj.jad.2014.09.021 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.jad.2014.09.021%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DPunamaki%26rft.aufirst%3DR.%2520L.%26rft.date%3D2014%26rft.atitle%3DTrajectories%2520of%2520posttraumatic%2520stress%2520symptoms%2520%2528PTSS%2529%2520after%2520major%2520war%2520among%2520Palestinian%2520children%253A%2520Trauma%252C%2520family-%2520and%2520child-related%2520predictors%26rft.jtitle%3DJournal%2520of%2520Affective%2520Disorders%26rft.volume%3D172%26rft.spage%3D133%26rft.epage%3D140 %00empty%00}-->
• Sampson, L., Cohen, G. H., Calabrese, J. R., Fink, D. S., Tamburrino, M., Liberzon, I., … Galea, S. (2015). Mental Health Over Time in a Military Sample: The Impact of Alcohol Use Disorder on Trajectories of Psychopathology After Deployment. Journal of Traumatic Stress, 28(6), 547–555. https://doi.org/10.1002/jts.22055.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1002%2Fjts.22055 journal Mental+Health+Over+Time+in+a+Military+Sample%3A+The+Impact+of+Alcohol+Use+Disorder+on+Trajectories+of+Psychopathology+After+Deployment author%3DL.+Sampson%26author%3DG.+H.+Cohen%26author%3DJ.+R.+Calabrese%26author%3DD.+S.+Fink%26author%3DM.+Tamburrino%26author%3DI.+Liberzon%26author%3DS.+Galea 2015 Sampson%2C+L.%2C+Cohen%2C+G.+H.%2C+Calabrese%2C+J.+R.%2C+Fink%2C+D.+S.%2C+Tamburrino%2C+M.%2C+Liberzon%2C+I.%2C+%E2%80%A6+Galea%2C+S.+%282015%29.+Mental+Health+Over+Time+in+a+Military+Sample%3A+The+Impact+of+Alcohol+Use+Disorder+on+Trajectories+of+Psychopathology+After+Deployment.+Journal+of+Traumatic+Stress%2C+28%286%29%2C+547%E2%80%93555.+https%3A%2F%2Fdoi.org%2F. 547-555 Journal+of+Traumatic+Stress 28 6 10.1002%2Fjts.22055 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_31_1 10.1002%252Fjts.22055 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1002%252Fjts.22055%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DSampson%26rft.aufirst%3DL.%26rft.date%3D2015%26rft.atitle%3DMental%2520Health%2520Over%2520Time%2520in%2520a%2520Military%2520Sample%253A%2520The%2520Impact%2520of%2520Alcohol%2520Use%2520Disorder%2520on%2520Trajectories%2520of%2520Psychopathology%2520After%2520Deployment%26rft.jtitle%3DJournal%2520of%2520Traumatic%2520Stress%26rft.volume%3D28%26rft.issue%3D6%26rft.spage%3D547%26rft.epage%3D555 %00empty%00}-->
• Schuurman, N. K., Grasman, R. P. P. P., & Hamaker, E. L., (2016) A Comparison of Inverse-Wishart Prior Specifications for Covariance Matrices in Multilevel Autoregressive Models. Multivariate Behavioral Research, 51(2–3), 185–206. DOI: 10.1080/00273171.2015.1065398.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1080%2F00273171.2015.1065398 journal A+Comparison+of+Inverse-Wishart+Prior+Specifications+for+Covariance+Matrices+in+Multilevel+Autoregressive+Models author%3DN.+K.+Schuurman%26author%3DR.+P.+P.+P.+Grasman%26author%3DE.+L.+Hamaker 2016 Schuurman%2C+N.+K.%2C+Grasman%2C+R.+P.+P.+P.%2C+%26+Hamaker%2C+E.+L.%2C+%282016%29+A+Comparison+of+Inverse-Wishart+Prior+Specifications+for+Covariance+Matrices+in+Multilevel+Autoregressive+Models.+Multivariate+Behavioral+Research%2C+51%282%E2%80%933%29%2C+185%E2%80%93206.+DOI%3A+. 185-206 Multivariate+Behavioral+Research 51 2%E2%80%933 10.1080%2F00273171.2015.1065398 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_32_1 10.1080%252F00273171.2015.1065398 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F00273171.2015.1065398%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DSchuurman%26rft.aufirst%3DN.%2520K.%26rft.date%3D2016%26rft.atitle%3DA%2520Comparison%2520of%2520Inverse-Wishart%2520Prior%2520Specifications%2520for%2520Covariance%2520Matrices%2520in%2520Multilevel%2520Autoregressive%2520Models%26rft.jtitle%3DMultivariate%2520Behavioral%2520Research%26rft.volume%3D51%26rft.issue%3D2%25E2%2580%25933%26rft.spage%3D185%26rft.epage%3D206 %00empty%00}-->
• Self-Brown, S., Lai, B. S., Harbin, S., & Kelley, M. L. (2014). Maternal posttraumatic stress disorder symptom trajectories following Hurricane Katrina: An initial examination of the impact of maternal trajectories on the well-being of disaster-exposed youth. International Journal of Public Health, 59(6), 957–965. https://doi.org/10.1007/s00038-014-0596-0.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs00038-014-0596-0 journal Maternal+posttraumatic+stress+disorder+symptom+trajectories+following+Hurricane+Katrina%3A+An+initial+examination+of+the+impact+of+maternal+trajectories+on+the+well-being+of+disaster-exposed+youth author%3DS.+Self-Brown%26author%3DB.+S.+Lai%26author%3DS.+Harbin%26author%3DM.+L.+Kelley 2014 Self-Brown%2C+S.%2C+Lai%2C+B.+S.%2C+Harbin%2C+S.%2C+%26+Kelley%2C+M.+L.+%282014%29.+Maternal+posttraumatic+stress+disorder+symptom+trajectories+following+Hurricane+Katrina%3A+An+initial+examination+of+the+impact+of+maternal+trajectories+on+the+well-being+of+disaster-exposed+youth.+International+Journal+of+Public+Health%2C+59%286%29%2C+957%E2%80%93965.+https%3A%2F%2Fdoi.org%2F. 957-965 International+Journal+of+Public+Health 59 6 10.1007%2Fs00038-014-0596-0 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_33_1 10.1007%252Fs00038-014-0596-0 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs00038-014-0596-0%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DSelf-Brown%26rft.aufirst%3DS.%26rft.date%3D2014%26rft.atitle%3DMaternal%2520posttraumatic%2520stress%2520disorder%2520symptom%2520trajectories%2520following%2520Hurricane%2520Katrina%253A%2520An%2520initial%2520examination%2520of%2520the%2520impact%2520of%2520maternal%2520trajectories%2520on%2520the%2520well-being%2520of%2520disaster-exposed%2520youth%26rft.jtitle%3DInternational%2520Journal%2520of%2520Public%2520Health%26rft.volume%3D59%26rft.issue%3D6%26rft.spage%3D957%26rft.epage%3D965 %00empty%00}-->
• Self-Brown, S., Lai, B. S., Thompson, J. E., McGill, T., & Kelley, M. L. (2013). Posttraumatic stress disorder symptom trajectories in Hurricane Katrina affected youth. Journal of Affective Disorders, 147(1–3), 198–204. https://doi.org/10.1016/j.jad.2012.11.002.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1016%2Fj.jad.2012.11.002 journal Posttraumatic+stress+disorder+symptom+trajectories+in+Hurricane+Katrina+affected+youth author%3DS.+Self-Brown%26author%3DB.+S.+Lai%26author%3DJ.+E.+Thompson%26author%3DT.+McGill%26author%3DM.+L.+Kelley 2013 Self-Brown%2C+S.%2C+Lai%2C+B.+S.%2C+Thompson%2C+J.+E.%2C+McGill%2C+T.%2C+%26+Kelley%2C+M.+L.+%282013%29.+Posttraumatic+stress+disorder+symptom+trajectories+in+Hurricane+Katrina+affected+youth.+Journal+of+Affective+Disorders%2C+147%281%E2%80%933%29%2C+198%E2%80%93204.+https%3A%2F%2Fdoi.org%2F. 198-204 Journal+of+Affective+Disorders 147 1%E2%80%933 10.1016%2Fj.jad.2012.11.002 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_34_1 10.1016%252Fj.jad.2012.11.002 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.jad.2012.11.002%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DSelf-Brown%26rft.aufirst%3DS.%26rft.date%3D2013%26rft.atitle%3DPosttraumatic%2520stress%2520disorder%2520symptom%2520trajectories%2520in%2520Hurricane%2520Katrina%2520affected%2520youth%26rft.jtitle%3DJournal%2520of%2520Affective%2520Disorders%26rft.volume%3D147%26rft.issue%3D1%25E2%2580%25933%26rft.spage%3D198%26rft.epage%3D204 %00empty%00}-->
• Sigurdardottir, S., Andelic, N., Roe, C., & Schanke, A. K. (2014). Identifying longitudinal trajectories of emotional distress symptoms 5 years after traumatic brain injury. Brain Injury, 28(12), 1542–1550. https://doi.org/10.3109/02699052.2014.934285.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.3109%2F02699052.2014.934285 journal Identifying+longitudinal+trajectories+of+emotional+distress+symptoms+5%C2%A0years+after+traumatic+brain+injury author%3DS.+Sigurdardottir%26author%3DN.+Andelic%26author%3DC.+Roe%26author%3DA.+K.+Schanke 2014 Sigurdardottir%2C+S.%2C+Andelic%2C+N.%2C+Roe%2C+C.%2C+%26+Schanke%2C+A.+K.+%282014%29.+Identifying+longitudinal+trajectories+of+emotional+distress+symptoms+5%C2%A0years+after+traumatic+brain+injury.+Brain+Injury%2C+28%2812%29%2C+1542%E2%80%931550.+https%3A%2F%2Fdoi.org%2F. 1542-1550 Brain+Injury 28 12 10.3109%2F02699052.2014.934285 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_35_1 10.3109%252F02699052.2014.934285 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.3109%252F02699052.2014.934285%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DSigurdardottir%26rft.aufirst%3DS.%26rft.date%3D2014%26rft.atitle%3DIdentifying%2520longitudinal%2520trajectories%2520of%2520emotional%2520distress%2520symptoms%25205%25C2%25A0years%2520after%2520traumatic%2520brain%2520injury%26rft.jtitle%3DBrain%2520Injury%26rft.volume%3D28%26rft.issue%3D12%26rft.spage%3D1542%26rft.epage%3D1550 %00empty%00}-->
• Steenkamp, M. M., Dickstein, B. D., SaltersPedneault, K., Hofmann, S. G., & Litz, B. T. (2012). Trajectories of PTSD symptoms following sexual assault: Is resilience the modal outcome? Journal of traumatic stress, 25(4), 469–474. https://doi.org/10.1002/jts.21718.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1002%2Fjts.21718 journal Trajectories+of+PTSD+symptoms+following+sexual+assault%3A+Is+resilience+the+modal+outcome%3F author%3DM.+M.+Steenkamp%26author%3DB.+D.+Dickstein%26author%3DK.+SaltersPedneault%26author%3DS.+G.+Hofmann%26author%3DB.+T.+Litz 2012 Steenkamp%2C+M.+M.%2C+Dickstein%2C+B.+D.%2C+SaltersPedneault%2C+K.%2C+Hofmann%2C+S.+G.%2C+%26+Litz%2C+B.+T.+%282012%29.+Trajectories+of+PTSD+symptoms+following+sexual+assault%3A+Is+resilience+the+modal+outcome%3F+Journal+of+traumatic+stress%2C+25%284%29%2C+469%E2%80%93474.+https%3A%2F%2Fdoi.org%2F. 469-474 Journal+of+traumatic+stress 25 4 10.1002%2Fjts.21718 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_36_1 10.1002%252Fjts.21718 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1002%252Fjts.21718%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DSteenkamp%26rft.aufirst%3DM.%2520M.%26rft.date%3D2012%26rft.atitle%3DTrajectories%2520of%2520PTSD%2520symptoms%2520following%2520sexual%2520assault%253A%2520Is%2520resilience%2520the%2520modal%2520outcome%253F%26rft.jtitle%3DJournal%2520of%2520traumatic%2520stress%26rft.volume%3D25%26rft.issue%3D4%26rft.spage%3D469%26rft.epage%3D474 %00empty%00}-->
• Thormar, S. B., Sijbrandij, M., Gersons, B. P., Van de Schoot, R., Juen, B., Karlsson, T., & Olff, M. (2016). PTSD Symptom Trajectories in Disaster Volunteers: The Role of Self-Efficacy, Social Acknowledgement, and Tasks Carried Out. Journal of Traumatic Stress, 29(1), 17–25. https://doi.org/10.1002/jts.22073.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1002%2Fjts.22073 journal PTSD+Symptom+Trajectories+in+Disaster+Volunteers%3A+The+Role+of+Self-Efficacy%2C+Social+Acknowledgement%2C+and+Tasks+Carried+Out author%3DS.+B.+Thormar%26author%3DM.+Sijbrandij%26author%3DB.+P.+Gersons%26author%3DR.+Van+de+Schoot%26author%3DB.+Juen%26author%3DT.+Karlsson%26author%3DM.+Olff 2016 Thormar%2C+S.+B.%2C+Sijbrandij%2C+M.%2C+Gersons%2C+B.+P.%2C+Van+de+Schoot%2C+R.%2C+Juen%2C+B.%2C+Karlsson%2C+T.%2C+%26+Olff%2C+M.+%282016%29.+PTSD+Symptom+Trajectories+in+Disaster+Volunteers%3A+The+Role+of+Self-Efficacy%2C+Social+Acknowledgement%2C+and+Tasks+Carried+Out.+Journal+of+Traumatic+Stress%2C+29%281%29%2C+17%E2%80%9325.+https%3A%2F%2Fdoi.org%2F. 17-25 Journal+of+Traumatic+Stress 29 1 10.1002%2Fjts.22073 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_37_1 10.1002%252Fjts.22073 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1002%252Fjts.22073%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DThormar%26rft.aufirst%3DS.%2520B.%26rft.date%3D2016%26rft.atitle%3DPTSD%2520Symptom%2520Trajectories%2520in%2520Disaster%2520Volunteers%253A%2520The%2520Role%2520of%2520Self-Efficacy%252C%2520Social%2520Acknowledgement%252C%2520and%2520Tasks%2520Carried%2520Out%26rft.jtitle%3DJournal%2520of%2520Traumatic%2520Stress%26rft.volume%3D29%26rft.issue%3D1%26rft.spage%3D17%26rft.epage%3D25 %00empty%00}-->
• van Loey, N. E., van de Schoot, R., & Faber, A. W. (2012). Posttraumatic stress symptoms after exposure to two fire disasters: Comparative study. PLoS ONE, 7(7): e41532. https://doi.org/10.1371/journal.pone.0041532.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed Web of Science ®<!--${googleScholarLinkReplacer: 10.1371%2Fjournal.pone.0041532 journal Posttraumatic+stress+symptoms+after+exposure+to+two+fire+disasters%3A+Comparative+study author%3DN.+E.+van+Loey%26author%3DR.+van+de+Schoot%26author%3DA.+W.+Faber 2012 van+Loey%2C+N.+E.%2C+van+de+Schoot%2C+R.%2C+%26+Faber%2C+A.+W.+%282012%29.+Posttraumatic+stress+symptoms+after+exposure+to+two+fire+disasters%3A+Comparative+study.+PLoS+ONE%2C+7%287%29%3A+e41532.+https%3A%2F%2Fdoi.org%2F. e41532 PLoS+ONE 7 7 10.1371%2Fjournal.pone.0041532 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_3_1_5_5_38_1 10.1371%252Fjournal.pone.0041532 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1371%252Fjournal.pone.0041532%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3Dvan%2520Loey%26rft.aufirst%3DN.%2520E.%26rft.date%3D2012%26rft.atitle%3DPosttraumatic%2520stress%2520symptoms%2520after%2520exposure%2520to%2520two%2520fire%2520disasters%253A%2520Comparative%2520study%26rft.jtitle%3DPLoS%2520ONE%26rft.volume%3D7%26rft.issue%3D7%26rft.spage%3De41532 %00empty%00}-->