Theoretical Derivation of a Unique Combination Number Hidden in the Higher-Order Neutron Correlation Factors Using the Pál-Bell Equation

Abstract

The Pál-Bell equation is a backward-type master equation that describes the probability generating function (PGF) of neutron counts in a neutron multiplication system. Thanks to the Pál-Bell equation with the two-forked and the fundamental mode approximations, an analytical solution of PGF of neutron counts in a source-driven subcritical system can be theoretically derived. This theoretical derivation clarifies that the unique combination number of double factorial (2n−3)!! does exist in the ratio of the higher-order neutron correlation factors measured in a critical state even for any kind of fissile and moderator materials. Additionally, the unique combination numbers are experimentally validated for the order 3 ≤ n ≤ 6 through reactor noise measurements in actual subcritical systems. This knowledge can be used to judge whether a target system is in a deep subcritical state or to roughly estimate the magnitude of subcriticality, based on the factorial moments of the measured reactor noise in a zero-power state.

Keywords:

• Pál-Bell equation
• probability generating function
• reactor noise
• neutron correlation factor
• double factorial

I. INTRODUCTION

We have been investigating subcriticality measurement techniques for an unknown system where detailed information about nuclide composition and geometry is not available for preliminary numerical analysis to evaluate some required parameters such as point kinetics parameters and the spatial correlation factor. As a measurement technique, we focus on reactor noise analysis methods.^1–5 The second-order neutron correlation factor $Y$ and the higher-order neutron correlation factors ${\mathcal{Y}}_n$ can be estimated by statistically analyzing the measured time-series data of neutron counts with a counting gate of width $T$. Considering that the neutron correlation is derived from the fission chain reaction, the experimental results of $Y$ and ${\mathcal{Y}}_n$ can be useful in estimating subcriticality.

Our previous study theoretically clarified that the third-order and fourth-order neutron correlation factors ${\mathcal{Y}}_3$ and ${\mathcal{Y}}_4$ can be approximated as functions of the second-order factor $Y$ (Refs. 6 and 7). Here, ${\mathcal{Y}}_3$ and ${\mathcal{Y}}_4$ represent measures of relative deviations for skewness and kurtosis from those of the Poisson distribution and are defined using the third-order and fourth-order moments shown later in Eqs. (37)(37) ${\mathcal{Y}}_3=\frac{1}{⟨\tilde{C}⟩}{\left.\frac{{\mathrm{\partial }}^{3}ln\left(\tilde{G}\right)}{\mathrm{\partial }{Z}^3}\right|}_{Z=1}=\frac{⟨\tilde{C}\left(\tilde{C}-1\right)\left(\tilde{C}-2\right)⟩-{⟨\tilde{C}⟩}^2\left(3Y+⟨\tilde{C}⟩\right)}{⟨\tilde{C}⟩},$(37) and (38(38) ${\mathcal{Y}}_4={\left.\frac{1}{⟨\tilde{C}⟩}\frac{{\mathrm{\partial }}^{4}ln\left(\tilde{G}\right)}{\mathrm{\partial }{Z}^4}\right|}_{Z=1}=\frac{⟨\tilde{C}\left(\tilde{C}-1\right)\left(\tilde{C}-2\right)\left(\tilde{C}-3\right)⟩-{⟨\tilde{C}⟩}^2\left(4{\mathcal{Y}}_3+3Y\left(Y+2⟨\tilde{C}⟩\right)+{⟨\tilde{C}⟩}^2\right)}{⟨\tilde{C}⟩},$(38) ), respectively. If the neutron-counting gate of width $T$ is sufficiently large and the subcriticality −ρ is approximately less than 10%dk/k, the saturation values ${\mathcal{Y}}_3/Y^2$ and ${\mathcal{Y}}_4/Y^3$ (hereinafter denoted as ${\mathcal{Y}}_{3,\mathrm{\infty }}/Y_{\mathrm{\infty }}^2$ and ${\mathcal{Y}}_{4,\mathrm{\infty }}/Y_{\mathrm{\infty }}^3$) are almost equal to unique numbers “3” and “15” for any subcritical system.

In order to rigorously consider three-forked and four-forked branch effects, the previous theoretical derivation was based on the first-order to fourth-order detector importance functions^6,8 and the fundamental mode approximation of the $k_{\mathrm{e}\mathrm{f}\mathrm{f}}$-eigenfunction. As the target system approaches a critical state (i.e., $-\rho \to 0$), ${\mathcal{Y}}_{3,\mathrm{\infty }}/Y_{\mathrm{\infty }}^2$ and ${\mathcal{Y}}_{4,\mathrm{\infty }}/Y_{\mathrm{\infty }}^3$ converge to “3” and “15” without depending on fissile and moderator materials. Thus, these unique numbers “3” and “15” are characteristic values in a critical state even for any kind of fissile and moderator materials. Therefore, the difference between ${\mathcal{Y}}_{3,\mathrm{\infty }}/Y_{\mathrm{\infty }}^2$ and “3” can be used to statistically determine whether the state is critical or subcritical.

In addition, this difference can be utilized to roughly estimate the absolute value of the subcriticality $-\rho$ in the absence of detailed information on the target system. Experimental validation of these unique numbers for ${\mathcal{Y}}_{3,\mathrm{\infty }}/Y_{\mathrm{\infty }}^2$ and ${\mathcal{Y}}_{4,\mathrm{\infty }}/Y_{\mathrm{\infty }}^3$ has been presented in previous studies.^6,9

Now, let us consider much higher neutron correlation factors ${\mathcal{Y}}_n$ when $n\ge 5$. Here, the physical meaning of ${\mathcal{Y}}_n$ is the strength of neutron correlation due to the detection processes for a group of $n$ neutrons (e.g., doublet, triplet, quartet, quintet, and sextet for $n=2,3,4,5,6$) belonging to the same fission chain family. As the order of $n$ increases, the theoretical derivation of ${\mathcal{Y}}_{n,\mathrm{\infty }}$ becomes more complex. Therefore, it is difficult to clarify whether the saturation value ${\mathcal{Y}}_{n,\mathrm{\infty }}$ converges a unique number in the critical state. Although we alternatively used a heuristic method for a binary tree of a fission chain having $\left(n-1\right)$ times of two-forked branches, we conjectured that ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ could be expressed as a combination number of double factorial $\left(2n-3\right)!!$ (Refs. 6 and 10).

For example, let us suppose that specific three or four neutrons (triplet or quartet) belong to the same fission chain with two or three times two-forked branches and that each neutron is detected at $t_1$, $t_2$, $t_3,$ or $t_4,$ where $t_1<t_2<t_3<t_4$. Then, by considering that one of three neutrons is detected at $t_1,$ $t_2,$ or $t_3$ just after the first branch, the total number of combinations for the specific triplet is 3. Similarly, the total number of combinations for the specific quartet is counted as 15, i.e., (4 cases: one of four neutrons is detected at $t_1$, $t_2$, $t_3$ or $t_4$ just after the first branch) × (combinations of triplet for other three neutrons) + [3 cases: two of four neutrons are detected at $\left(t_1,t_2\right)$, $\left(t_1,t_3\right),$ or $\left(t_1,t_4\right)$ just after the first branch] $=4\times 3+3=5\times 3=5!!$. Because the above-mentioned conjecture is based on a quite heuristic method, the more sophisticated theoretical derivation for ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ for any system in the critical state was an unresolved problem in our previous study.⁶ In this study, we aim to theoretically derive ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}=\left(2n-3\right)!!$ using the Pál-Bell equation to help reconfirm the historical efforts of Lénárd Pál on the neutron-detection probability theory.

The remainder of this paper proceeds as follows. Secion II describes the Pál-Bell equation,^11,12 followed by the theoretical derivation of the Pál-Mogil’ner-Zolotukhin-Bell-Babala (PMZBB) distribution-generating function.^13–18 Furthermore, we derive the theoretical value of ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ in the critical state using the theoretical formula of the PMZBB distribution-generating function. The unique combination numbers $\left(2n-3\right)!!$ for ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ are validated in Sec. III through reactor noise experiments conducted at actual subcritical cores of the Kyoto University Critical Assembly^19,20 (KUCA). Finally, Sec. IV presents the concluding remarks.

II. THEORY

II.A. Pál-Bell Equation

Let us assume that the neutron counts $C$ are detected within the counting gate of width $T$ after one neutron is born at ($\vec{r},E,\vec{\mathrm{\Omega }},t$) in the subcritical system. Note that the birth time $t\le 0$ and the counting time interval is $\left[-T,0\right]$ to give the final condition at $t=0$. If the probability of neutron counts is expressed as $P(C,T|\vec{r},E,\vec{\mathrm{\Omega }},t)$, the probability generating function (PGF) $G\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right)$ can be defined as^1,2

(1) $G\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right)\equiv \sum _{C=0}^{\mathrm{\infty }}{Z}^{C}P\left(C,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right).$(1)

By considering the balance equation for the probabilities of neutron counts between $t$ and $t+dt$ and utilizing the mathematical property that the convolution of probabilities ${\sum }_{{\sum }_{i=1}^{\nu }{c}_i=C}{\prod }_{i=1}^{\nu }P\left(c_i\right)$ can be transformed into the product of PGF ${\left(G\left(Z\right)\right)}^{\nu }$, the time-differential equation of PGF can be obtained as follows^1,8,11,12:

(2) $\begin{array}{rl}-\frac{1}{v\left(E\right)}\frac{\mathrm{\partial }G}{\mathrm{\partial }t}=& \vec{\mathrm{\Omega }}\cdot \mathrm{\nabla }G-{\mathrm{\Sigma }}_{\mathrm{t}}\left(\vec{r},E\right)G\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right)+\\ & {\int }_0^{\mathrm{\infty }}dE{ }^{\mathrm{\prime }}{\int }_{4\pi }d\mathrm{\Omega }{ }^{\mathrm{\prime }}{\mathrm{\Sigma }}_{\mathrm{s}}\left(\vec{r},E\to E{ }^{\mathrm{\prime }},\vec{\mathrm{\Omega }}\to {\vec{\mathrm{\Omega }}}^{\mathrm{\prime }}\right)\\ & G\left(Z,T|\vec{r},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\prime },t\right)+{\mathrm{\Sigma }}_{\mathrm{f}}\left(\vec{r},E\right)\sum _{\nu =0}^{{\nu }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{p}_f\left(\nu \right)\\ & {\left({\int }_0^{\mathrm{\infty }}dE{ }^{\mathrm{\prime }}{\int }_{4\pi }d\mathrm{\Omega }{ }^{\mathrm{\prime }}\frac{{\chi }_{\mathrm{f}}\left(E{ }^{\mathrm{\prime }}\right)}{4\pi }G\left(Z,T|\vec{r},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }},t\right)\right)}^{\nu }\\ & +{\mathrm{\Sigma }}_{\mathrm{c}}\left(\vec{r},E\right)+{\mathrm{\Sigma }}_{\mathrm{d}}\left(\vec{r},E\right)\left(1+\mathrm{\Delta }\left(t,T\right)\left(Z-1\right)\right)\end{array}$(2)

and

(3) $\mathrm{\Delta }\left(t,T\right)\equiv \left\{\begin{array}{cc}1& -T\le t\le 0\\ 0& t<-T,\end{array}\right.$(3)

where

$\mathrm{\Delta }\left(t,T\right)$ =	=	gate function for neutron detection
${\mathrm{\Sigma }}_{\mathrm{d}}\left(\vec{r},E\right)$ =	=	macroscopic detection cross section

and the other notations represent conventional terms in this research field. Note that the macroscopic total cross section in Eq. (2)(2) $\begin{array}{rl}-\frac{1}{v\left(E\right)}\frac{\mathrm{\partial }G}{\mathrm{\partial }t}=& \vec{\mathrm{\Omega }}\cdot \mathrm{\nabla }G-{\mathrm{\Sigma }}_{\mathrm{t}}\left(\vec{r},E\right)G\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right)+\\ & {\int }_0^{\mathrm{\infty }}dE{ }^{\mathrm{\prime }}{\int }_{4\pi }d\mathrm{\Omega }{ }^{\mathrm{\prime }}{\mathrm{\Sigma }}_{\mathrm{s}}\left(\vec{r},E\to E{ }^{\mathrm{\prime }},\vec{\mathrm{\Omega }}\to {\vec{\mathrm{\Omega }}}^{\mathrm{\prime }}\right)\\ & G\left(Z,T|\vec{r},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\prime },t\right)+{\mathrm{\Sigma }}_{\mathrm{f}}\left(\vec{r},E\right)\sum _{\nu =0}^{{\nu }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{p}_f\left(\nu \right)\\ & {\left({\int }_0^{\mathrm{\infty }}dE{ }^{\mathrm{\prime }}{\int }_{4\pi }d\mathrm{\Omega }{ }^{\mathrm{\prime }}\frac{{\chi }_{\mathrm{f}}\left(E{ }^{\mathrm{\prime }}\right)}{4\pi }G\left(Z,T|\vec{r},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }},t\right)\right)}^{\nu }\\ & +{\mathrm{\Sigma }}_{\mathrm{c}}\left(\vec{r},E\right)+{\mathrm{\Sigma }}_{\mathrm{d}}\left(\vec{r},E\right)\left(1+\mathrm{\Delta }\left(t,T\right)\left(Z-1\right)\right)\end{array}$(2) is given by ${\mathrm{\Sigma }}_{\mathrm{t}}={\mathrm{\Sigma }}_{\mathrm{s}}+{\mathrm{\Sigma }}_{\mathrm{f}}+{\mathrm{\Sigma }}_{\mathrm{c}}+{\mathrm{\Sigma }}_{\mathrm{d}}$. Considering that this study aims to clarify the nature of the neutron correlation factors at the limit of $T\to \mathrm{\infty }$, Eq. (2)(2) $\begin{array}{rl}-\frac{1}{v\left(E\right)}\frac{\mathrm{\partial }G}{\mathrm{\partial }t}=& \vec{\mathrm{\Omega }}\cdot \mathrm{\nabla }G-{\mathrm{\Sigma }}_{\mathrm{t}}\left(\vec{r},E\right)G\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right)+\\ & {\int }_0^{\mathrm{\infty }}dE{ }^{\mathrm{\prime }}{\int }_{4\pi }d\mathrm{\Omega }{ }^{\mathrm{\prime }}{\mathrm{\Sigma }}_{\mathrm{s}}\left(\vec{r},E\to E{ }^{\mathrm{\prime }},\vec{\mathrm{\Omega }}\to {\vec{\mathrm{\Omega }}}^{\mathrm{\prime }}\right)\\ & G\left(Z,T|\vec{r},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\prime },t\right)+{\mathrm{\Sigma }}_{\mathrm{f}}\left(\vec{r},E\right)\sum _{\nu =0}^{{\nu }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{p}_f\left(\nu \right)\\ & {\left({\int }_0^{\mathrm{\infty }}dE{ }^{\mathrm{\prime }}{\int }_{4\pi }d\mathrm{\Omega }{ }^{\mathrm{\prime }}\frac{{\chi }_{\mathrm{f}}\left(E{ }^{\mathrm{\prime }}\right)}{4\pi }G\left(Z,T|\vec{r},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }},t\right)\right)}^{\nu }\\ & +{\mathrm{\Sigma }}_{\mathrm{c}}\left(\vec{r},E\right)+{\mathrm{\Sigma }}_{\mathrm{d}}\left(\vec{r},E\right)\left(1+\mathrm{\Delta }\left(t,T\right)\left(Z-1\right)\right)\end{array}$(2) does not explicitly treat the difference between prompt and delayed fission neutrons. Because no neutrons are counted after the counting gate is closed at $t=0$, i.e., $P\left(0,T|\vec{r},E,\vec{\mathrm{\Omega }},0\right)=1$, PGF $G\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right)$ satisfies the following final condition:

(4) $G\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},0\right)=1.$(4)

To further transform Eq. (2(2) $\begin{array}{rl}-\frac{1}{v\left(E\right)}\frac{\mathrm{\partial }G}{\mathrm{\partial }t}=& \vec{\mathrm{\Omega }}\cdot \mathrm{\nabla }G-{\mathrm{\Sigma }}_{\mathrm{t}}\left(\vec{r},E\right)G\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right)+\\ & {\int }_0^{\mathrm{\infty }}dE{ }^{\mathrm{\prime }}{\int }_{4\pi }d\mathrm{\Omega }{ }^{\mathrm{\prime }}{\mathrm{\Sigma }}_{\mathrm{s}}\left(\vec{r},E\to E{ }^{\mathrm{\prime }},\vec{\mathrm{\Omega }}\to {\vec{\mathrm{\Omega }}}^{\mathrm{\prime }}\right)\\ & G\left(Z,T|\vec{r},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\prime },t\right)+{\mathrm{\Sigma }}_{\mathrm{f}}\left(\vec{r},E\right)\sum _{\nu =0}^{{\nu }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{p}_f\left(\nu \right)\\ & {\left({\int }_0^{\mathrm{\infty }}dE{ }^{\mathrm{\prime }}{\int }_{4\pi }d\mathrm{\Omega }{ }^{\mathrm{\prime }}\frac{{\chi }_{\mathrm{f}}\left(E{ }^{\mathrm{\prime }}\right)}{4\pi }G\left(Z,T|\vec{r},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }},t\right)\right)}^{\nu }\\ & +{\mathrm{\Sigma }}_{\mathrm{c}}\left(\vec{r},E\right)+{\mathrm{\Sigma }}_{\mathrm{d}}\left(\vec{r},E\right)\left(1+\mathrm{\Delta }\left(t,T\right)\left(Z-1\right)\right)\end{array}$(2) ), another PGF $\mathcal{G}\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right)$ is defined as

(5) $\mathcal{G}\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right)\equiv 1-G\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right).$(5)

Additionally, the following binomial expansion is utilized to transform Eq. (2)(2) $\begin{array}{rl}-\frac{1}{v\left(E\right)}\frac{\mathrm{\partial }G}{\mathrm{\partial }t}=& \vec{\mathrm{\Omega }}\cdot \mathrm{\nabla }G-{\mathrm{\Sigma }}_{\mathrm{t}}\left(\vec{r},E\right)G\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right)+\\ & {\int }_0^{\mathrm{\infty }}dE{ }^{\mathrm{\prime }}{\int }_{4\pi }d\mathrm{\Omega }{ }^{\mathrm{\prime }}{\mathrm{\Sigma }}_{\mathrm{s}}\left(\vec{r},E\to E{ }^{\mathrm{\prime }},\vec{\mathrm{\Omega }}\to {\vec{\mathrm{\Omega }}}^{\mathrm{\prime }}\right)\\ & G\left(Z,T|\vec{r},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\prime },t\right)+{\mathrm{\Sigma }}_{\mathrm{f}}\left(\vec{r},E\right)\sum _{\nu =0}^{{\nu }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{p}_f\left(\nu \right)\\ & {\left({\int }_0^{\mathrm{\infty }}dE{ }^{\mathrm{\prime }}{\int }_{4\pi }d\mathrm{\Omega }{ }^{\mathrm{\prime }}\frac{{\chi }_{\mathrm{f}}\left(E{ }^{\mathrm{\prime }}\right)}{4\pi }G\left(Z,T|\vec{r},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }},t\right)\right)}^{\nu }\\ & +{\mathrm{\Sigma }}_{\mathrm{c}}\left(\vec{r},E\right)+{\mathrm{\Sigma }}_{\mathrm{d}}\left(\vec{r},E\right)\left(1+\mathrm{\Delta }\left(t,T\right)\left(Z-1\right)\right)\end{array}$(2) into an expression using the Boltzmann operator:

(6) ${\left(1-{\bar{\mathcal{G}}}_{\mathrm{f}}\right)}^{\nu }=\sum _{i=0}^{\nu }\frac{\nu !}{\left(\nu -i\right)!\times i!}{\left(-{\bar{\mathcal{G}}}_{\mathrm{f}}\right)}^i$(6)

and

(7) ${\bar{\mathcal{G}}}_{\mathrm{f}}\left(Z,T|\vec{r},t\right)\equiv \underset{0}{\overset{\mathrm{\infty }}{\int }}dE{ }^{\mathrm{\prime }}\underset{4\pi }{\int }d\mathrm{\Omega }{ }^{\mathrm{\prime }}\frac{{\chi }_{\mathrm{f}}\left(E{ }^{\mathrm{\prime }}\right)}{4\pi }\mathcal{G}\left(Z,T|\vec{r},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }},t\right),$(7)

where ${\bar{\mathcal{G}}}_{\mathrm{f}}\left(Z,T|\vec{r},t\right)$ is the energy-averaged and angular-averaged PGF where the weighting function is the fission spectrum ${\chi }_{\mathrm{f}}\left(E\right)/4\pi$. Finally, the Pál-Bell equation, which is the adjoint Boltzmann equation for PGF $\mathcal{G}$, can be obtained as^1,11,12,21

(8) $\begin{array}{rl}-\frac{1}{v\left(E\right)}\frac{\mathrm{\partial }\mathcal{G}}{\mathrm{\partial }t}=& -{\mathbf{B}}^{†}\mathcal{G}-{\mathrm{\Sigma }}_{\mathrm{f}}\left(\vec{r},E\right)\sum _{i=2}^{\nu }⟨\frac{\nu !}{\left(\nu -i\right)!}⟩\\ & \frac{{\left(-{\bar{\mathcal{G}}}_{\mathrm{f}}\left(Z,T|\vec{r},t\right)\right)}^i}{i!}+{\mathrm{\Sigma }}_{\mathrm{d}}\left(\vec{r},E\right)\mathrm{\Delta }\left(t,T\right)\left(1-Z\right),\end{array}$(8)

where the brackets $⟨⟩$ represent the expected value and ${\mathbf{B}}^{†}$ is the adjoint Boltzmann operator given as

$\begin{array}{rl}{\mathbf{B}}^{†}\equiv & -\vec{\mathrm{\Omega }}\cdot \mathrm{\nabla }+{\mathrm{\Sigma }}_{\mathrm{t}}\left(\vec{r},E\right)\\ & -\underset{0}{\overset{\mathrm{\infty }}{\int }}dE{ }^{\mathrm{\prime }}\underset{4\pi }{\int }d\mathrm{\Omega }{ }^{\mathrm{\prime }}{\mathrm{\Sigma }}_{\mathrm{s}}\left(\vec{r},E\to E{ }^{\mathrm{\prime }},\vec{\mathrm{\Omega }}\to {\vec{\mathrm{\Omega }}}^{\mathrm{\prime }}\right)\\ & -⟨\nu ⟩{\mathrm{\Sigma }}_{\mathrm{f}}\left(\vec{r},E\right)\underset{0}{\overset{\mathrm{\infty }}{\int }}dE{ }^{\mathrm{\prime }}\underset{4\pi }{\int }d\mathrm{\Omega }{ }^{\mathrm{\prime }}\frac{{\chi }_{\mathrm{f}}\left(E{ }^{\mathrm{\prime }}\right)}{4\pi }.(9)\end{array}$

II.B. PMZBB Distribution-Generating Function

Although Eq. (8)(8) $\begin{array}{rl}-\frac{1}{v\left(E\right)}\frac{\mathrm{\partial }\mathcal{G}}{\mathrm{\partial }t}=& -{\mathbf{B}}^{†}\mathcal{G}-{\mathrm{\Sigma }}_{\mathrm{f}}\left(\vec{r},E\right)\sum _{i=2}^{\nu }⟨\frac{\nu !}{\left(\nu -i\right)!}⟩\\ & \frac{{\left(-{\bar{\mathcal{G}}}_{\mathrm{f}}\left(Z,T|\vec{r},t\right)\right)}^i}{i!}+{\mathrm{\Sigma }}_{\mathrm{d}}\left(\vec{r},E\right)\mathrm{\Delta }\left(t,T\right)\left(1-Z\right),\end{array}$(8) is the rigorous master equation for PGF $\mathcal{G}$, deriving the analytical solution is difficult owing to the nonlinear term ${\left(-{\bar{\mathcal{G}}}_{\mathrm{f}}\right)}^i$. Therefore, an analytical solution of PGF for a shallow subcritical system can be obtained by applying approximations to Eq. (8)(8) $\begin{array}{rl}-\frac{1}{v\left(E\right)}\frac{\mathrm{\partial }\mathcal{G}}{\mathrm{\partial }t}=& -{\mathbf{B}}^{†}\mathcal{G}-{\mathrm{\Sigma }}_{\mathrm{f}}\left(\vec{r},E\right)\sum _{i=2}^{\nu }⟨\frac{\nu !}{\left(\nu -i\right)!}⟩\\ & \frac{{\left(-{\bar{\mathcal{G}}}_{\mathrm{f}}\left(Z,T|\vec{r},t\right)\right)}^i}{i!}+{\mathrm{\Sigma }}_{\mathrm{d}}\left(\vec{r},E\right)\mathrm{\Delta }\left(t,T\right)\left(1-Z\right),\end{array}$(8) .

First, the two-forked approximation is utilized to neglect the higher terms ${\left(-{\bar{\mathcal{G}}}_{\mathrm{f}}\right)}^i$ for $i\ge 3$ (Ref. 12), given as

(10) $\begin{array}{rl}-\frac{1}{v\left(E\right)}\frac{\mathrm{\partial }\mathcal{G}}{\mathrm{\partial }t}\approx & -{\mathbf{B}}^{†}\mathcal{G}-\frac{⟨\nu \left(\nu -1\right)⟩}{2}{\mathrm{\Sigma }}_{\mathrm{f}}\left(\vec{r},E\right){\left({\bar{\mathcal{G}}}_{\mathrm{f}}\left(Z,T|\vec{r},t\right)\right)}^2\\ & +{\mathrm{\Sigma }}_{\mathrm{d}}\left(\vec{r},E\right)\mathrm{\Delta }\left(t,T\right)\left(1-Z\right).\end{array}$(10)

As the subcritical system approaches the critical state, the contribution of the two-forked branch to the neutron correlation factors becomes larger than that of the more-forked branches, e.g., the three-forked and four-forked terms due to $i=3$ and $4$, respectively.^5,6

Second, if the subcriticality is shallow, the fundamental mode approximation is reasonably applicable. Therefore, let us assume that PGF $\mathcal{G}$ can be expressed only by the fundamental mode of the adjoint eigenfunction ${\psi }^{†}$ (Ref. 12):

(11) $\mathcal{G}\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right)\approx g_0\left(Z,T|t\right){\psi }^{†}\left(\vec{r},E,\vec{\mathrm{\Omega }}\right)$(11)

and

(12) $\begin{array}{rl}& g_0\left(Z,T|t\right)\\ & =\frac{{\int }_{V}dV{ }^{\mathrm{\prime }}{\int }_0^{\mathrm{\infty }}dE{ }^{\mathrm{\prime }}{\int }_{4\pi }d\mathrm{\Omega }{ }^{\mathrm{\prime }}\left(\psi \left({\vec{r}}^{\mathrm{\prime }},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }}\right)\frac{1}{v\left(E{ }^{\mathrm{\prime }}\right)}\mathcal{G}\left(Z,T|{\vec{r}}^{\mathrm{\prime }},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }},t\right)\right)}{{\int }_{V}dV{ }^{\mathrm{\prime }}{\int }_0^{\mathrm{\infty }}dE{ }^{\mathrm{\prime }}{\int }_{4\pi }d\mathrm{\Omega }{ }^{\mathrm{\prime }}\left(\psi \left({\vec{r}}^{\mathrm{\prime }},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }}\right)\frac{1}{v\left(E{ }^{\mathrm{\prime }}\right)}{\psi }^{†}\left({\vec{r}}^{\mathrm{\prime }},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }}\right)\right)},\end{array}$(12)

where

$g_0\left(Z,T|t\right)$ =	=	expansion coefficient corresponding to the fundamental mode
$\psi ,$ ${\psi }^{†}$ =	=	forward and adjoint eigenfunctions for the neutron decay constant $\alpha$-eigenvalue equations, respectively, given as12,22,23

(13) $\mathbf{B}\psi =\frac{\alpha }{v\left(E\right)}\psi \left(\vec{\mathrm{r}},E,\vec{\mathrm{\Omega }}\right),$(13)

(14) ${\mathbf{B}}^{†}{\psi }^{†}=\frac{\alpha }{v\left(E\right)}{\psi }^{†}\left(\vec{r},E,\vec{\mathrm{\Omega }}\right),$(14)

and

(15) $\begin{array}{rl}\mathbf{B}\equiv & \vec{\mathrm{\Omega }}\cdot \mathrm{\nabla }+{\mathrm{\Sigma }}_{\mathrm{t}}\left(\vec{r},E\right)\\ & -\underset{0}{\overset{\mathrm{\infty }}{\int }}dE{ }^{\mathrm{\prime }}\underset{4\pi }{\int }d\mathrm{\Omega }{ }^{\mathrm{\prime }}{\mathrm{\Sigma }}_{\mathrm{s}}\left(\vec{r},E{ }^{\mathrm{\prime }}\to E,{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }}\to \vec{\mathrm{\Omega }}\right)\\ & -\frac{{\chi }_{\mathrm{f}}\left(E\right)}{4\pi }\underset{0}{\overset{\mathrm{\infty }}{\int }}dE{ }^{\mathrm{\prime }}\underset{4\pi }{\int }d\mathrm{\Omega }{ }^{\mathrm{\prime }}⟨\nu ⟩{\mathrm{\Sigma }}_{\mathrm{f}}\left(\vec{r},E{ }^{\mathrm{\prime }}\right).\end{array}$(15)

For simplicity, the forward and adjoint eigenfunctions $\psi$ and ${\psi }^{†}$ are normalized as

(16) $\underset{V}{\int }dV{ }^{\mathrm{\prime }}\underset{0}{\overset{\mathrm{\infty }}{\int }}dE{ }^{\mathrm{\prime }}\underset{4\pi }{\int }d\mathrm{\Omega }{ }^{\mathrm{\prime }}\left(\psi \left({\vec{r}}^{\mathrm{\prime }},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }}\right)\frac{1}{v\left(E{ }^{\mathrm{\prime }}\right)}{\psi }^{†}\left({\vec{r}}^{\mathrm{\prime }},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }}\right)\right)=1.$(16)

By substituting Eq. (11)(11) $\mathcal{G}\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right)\approx g_0\left(Z,T|t\right){\psi }^{†}\left(\vec{r},E,\vec{\mathrm{\Omega }}\right)$(11) into Eq. (10)(10) $\begin{array}{rl}-\frac{1}{v\left(E\right)}\frac{\mathrm{\partial }\mathcal{G}}{\mathrm{\partial }t}\approx & -{\mathbf{B}}^{†}\mathcal{G}-\frac{⟨\nu \left(\nu -1\right)⟩}{2}{\mathrm{\Sigma }}_{\mathrm{f}}\left(\vec{r},E\right){\left({\bar{\mathcal{G}}}_{\mathrm{f}}\left(Z,T|\vec{r},t\right)\right)}^2\\ & +{\mathrm{\Sigma }}_{\mathrm{d}}\left(\vec{r},E\right)\mathrm{\Delta }\left(t,T\right)\left(1-Z\right).\end{array}$(10) and utilizing the orthogonality condition of $\psi$ and ${\psi }^{†}$, the following Riccati-type differential equation for the expansion coefficient $g_0$ can be derived:

(17) $-\frac{d{g}_0}{dt}=-\alpha g_0\left(Z,T|t\right)-\frac{{\mathcal{F}}_2}{2}{\left(g_0\left(Z,T|t\right)\right)}^2+\mathcal{D}\mathrm{\Delta }\left(t,T\right)\left(1-Z\right),$(17)

(18) $\mathcal{D}\equiv \underset{V}{\int }dV\underset{0}{\overset{\mathrm{\infty }}{\int }}dE\underset{4\pi }{\int }d\mathrm{\Omega }{\mathrm{\Sigma }}_{\mathrm{d}}\left(\vec{r},E\right)\psi \left(\vec{r},E,\vec{\mathrm{\Omega }}\right),$(18)

(19) $\begin{array}{rl}{\mathcal{F}}_n\equiv & \underset{V}{\int }dV\underset{0}{\overset{\mathrm{\infty }}{\int }}dE\\ & \underset{4\pi }{\int }d\mathrm{\Omega }⟨\frac{\nu !}{\left(\nu -n\right)!}⟩{\mathrm{\Sigma }}_{\mathrm{f}}\left(\vec{r},E\right)\psi \left(\vec{r},E,\vec{\mathrm{\Omega }}\right){\left({\bar{\psi }}_{\mathrm{f}}^{†}\left(\vec{r}\right)\right)}^n,\end{array}$(19)

and

(20) ${\bar{\psi }}_{\mathrm{f}}^{†}\left(\vec{r}\right)\equiv \underset{0}{\overset{\mathrm{\infty }}{\int }}dE{ }^{\mathrm{\prime }}\underset{4\pi }{\int }d\mathrm{\Omega }{ }^{\mathrm{\prime }}\frac{{\chi }_{\mathrm{f}}\left(E{ }^{\mathrm{\prime }}\right)}{4\pi }{\psi }^{†}\left(\vec{r},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }}\right).$(20)

By solving Eq. (17)(17) $-\frac{d{g}_0}{dt}=-\alpha g_0\left(Z,T|t\right)-\frac{{\mathcal{F}}_2}{2}{\left(g_0\left(Z,T|t\right)\right)}^2+\mathcal{D}\mathrm{\Delta }\left(t,T\right)\left(1-Z\right),$(17) with the final condition of $g_0\left(Z,T|0\right)=0$ at $t=0$, the analytical solution can be obtained as

$\begin{array}{rl}& g_0\left(Z,T|t\right)\\ & =\left\{\begin{array}{cc}\frac{\alpha }{{\mathcal{F}}_2}\frac{\left({\left(z^{\ast }\right)}^2-1\right)\left(exp\left(-\alpha z^{\ast }t\right)-1\right)}{\left(z^{\ast }+1\right)exp\left(-\alpha z^{\ast }t\right)+\left(z^{\ast }-1\right)}& -T\le t\le 0\\ \frac{2\alpha }{{\mathcal{F}}_2}{\left(\frac{{\left(z^{\ast }\right)}^2+2z^{\ast }coth\left(\frac{\alpha z^{\ast }T}{2}\right)+1}{{\left(z^{\ast }\right)}^2-1}exp\left(-\alpha \left(t+T\right)\right)-1\right)}^{-1}& t<-T,\end{array}\right.\end{array}$

$(21)$

(22) $z^{\ast }\equiv \sqrt{1+2Y_{\mathrm{\infty },\mathrm{f}}\left(1-Z\right)},$(22)

and

(23) $Y_{\mathrm{\infty },\mathrm{f}}\equiv \frac{\mathcal{D}{\mathcal{F}}_2}{{\alpha }^2},$(23)

where $Y_{\mathrm{\infty },\mathrm{f}}$ corresponds to the saturation value of the second-order neutron correlation factor owing to the only fission neutron multiplicity and $z^{\ast }$ is introduced to simply express the analytical solution.

Now, let us assume that the neutron counts $C$ are detected within the counting gate of width $T$ when the external neutron source exists in the subcritical system from the infinite past. By denoting the probability as $\tilde{P}\left(C,T\right)$, PGF $\tilde{G}\left(Z,T\right)$ can be expressed in the same manner as Eq. (1)(1) $G\left(Z,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right)\equiv \sum _{C=0}^{\mathrm{\infty }}{Z}^{C}P\left(C,T|\vec{r},E,\vec{\mathrm{\Omega }},t\right).$(1) :

(24) $\tilde{G}\left(Z,T\right)\equiv \sum _{C=0}^{\mathrm{\infty }}{Z}^C\tilde{P}\left(C,T\right).$(24)

By considering the probability-balance between $P(C,T|\vec{r},E,\vec{\mathrm{\Omega }},t)$ and $\tilde{P}\left(C,T\right)$ as presented in previous studies,^8,24 the relationship between $\mathcal{G}$ and $\tilde{G}$ can be derived as

(25) $\begin{array}{rl}\mathrm{l}\mathrm{n}\left(\tilde{G}\left(Z,T\right)\right)=& \underset{V}{\int }dV\underset{-\mathrm{\infty }}{\overset{0}{\int }}dtS\left(r\right)\\ & \left(-1+\sum _{q=0}^{q_{\mathrm{m}\mathrm{a}\mathrm{x}}}{p}_{\mathrm{s}}\left(q\right){\left(1-{\bar{\mathcal{G}}}_{\mathrm{s}}\left(Z,T|\vec{r},t\right)\right)}^q\right),\end{array}$(25)

and

(26) ${\bar{\mathcal{G}}}_{\mathrm{s}}\left(Z,T|\vec{r},t\right)\equiv \underset{0}{\overset{\mathrm{\infty }}{\int }}dE{ }^{\mathrm{\prime }}\underset{4\pi }{\int }d\mathrm{\Omega }{ }^{\mathrm{\prime }}\frac{{\chi }_{\mathrm{s}}\left(E{ }^{\mathrm{\prime }}\right)}{4\pi }\mathcal{G}\left(Z,T|\vec{r},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\prime },t\right),$(26)

where

$S\left(r\right)$ =	=	source intensity for the external neutron source
$p_{\mathrm{s}}\left(q\right)$ =	=	probability that $q$ neutrons are emitted per decay of the external source
${\chi }_{\mathrm{s}}\left(E\right)$ =	=	energy spectrum of the external source
${\bar{\mathcal{G}}}_{\mathrm{s}}\left(Z,T|\vec{r},t\right)$ =	=	energy-averaged and angular-averaged PGF, where ${\chi }_{\mathrm{s}}\left(E\right)/4\pi$ is the weighting function.

By applying the two-forked and the fundamental mode approximations, Eq. (25)(25) $\begin{array}{rl}\mathrm{l}\mathrm{n}\left(\tilde{G}\left(Z,T\right)\right)=& \underset{V}{\int }dV\underset{-\mathrm{\infty }}{\overset{0}{\int }}dtS\left(r\right)\\ & \left(-1+\sum _{q=0}^{q_{\mathrm{m}\mathrm{a}\mathrm{x}}}{p}_{\mathrm{s}}\left(q\right){\left(1-{\bar{\mathcal{G}}}_{\mathrm{s}}\left(Z,T|\vec{r},t\right)\right)}^q\right),\end{array}$(25) can be further simplified as

(27) $\begin{array}{rl}\mathrm{l}\mathrm{n}\left(\tilde{G}\left(Z,T\right)\right)& \approx {\int }_{V}dV{\int }_{-\mathrm{\infty }}^{0}dtS\left(r\right)(-⟨q⟩{\bar{\mathcal{G}}}_{\mathrm{s}}\left(Z,T|\vec{r},t\right)\\ & \left.+\frac{⟨q\left(q-1\right)⟩}{2}{\left({\bar{\mathcal{G}}}_{\mathrm{s}}\left(Z,T|\vec{r},t\right)\right)}^2\right)\\ & \approx {\int }_{-\mathrm{\infty }}^0\left(-{\mathcal{S}}_1{g}_0\left(Z,T|t\right)+\frac{{\mathcal{S}}_2}{2}{\left(g_0\left(Z,T|t\right)\right)}^2\right)dt,\end{array}$(27)

(28) ${\mathcal{S}}_n\equiv \underset{V}{\int }⟨\frac{q!}{\left(q-n\right)!}⟩S\left(\vec{r}\right){\left({\bar{\psi }}_{\mathrm{s}}^{†}\left(\vec{r}\right)\right)}^{n}dV,$(28)

and

(29) ${\bar{\psi }}_{\mathrm{s}}^{†}\left(\vec{r}\right)\equiv \underset{0}{\overset{\mathrm{\infty }}{\int }}dE{ }^{\mathrm{\prime }}\underset{4\pi }{\int }d\mathrm{\Omega }{ }^{\mathrm{\prime }}\frac{{\chi }_{\mathrm{s}}\left(E{ }^{\mathrm{\prime }}\right)}{4\pi }{\psi }^{†}\left(\vec{r},E{ }^{\mathrm{\prime }},{\vec{\mathrm{\Omega }}}^{\mathrm{\prime }}\right).$(29)

By carefully solving the time integral in Eq. (27)(27) $\begin{array}{rl}\mathrm{l}\mathrm{n}\left(\tilde{G}\left(Z,T\right)\right)& \approx {\int }_{V}dV{\int }_{-\mathrm{\infty }}^{0}dtS\left(r\right)(-⟨q⟩{\bar{\mathcal{G}}}_{\mathrm{s}}\left(Z,T|\vec{r},t\right)\\ & \left.+\frac{⟨q\left(q-1\right)⟩}{2}{\left({\bar{\mathcal{G}}}_{\mathrm{s}}\left(Z,T|\vec{r},t\right)\right)}^2\right)\\ & \approx {\int }_{-\mathrm{\infty }}^0\left(-{\mathcal{S}}_1{g}_0\left(Z,T|t\right)+\frac{{\mathcal{S}}_2}{2}{\left(g_0\left(Z,T|t\right)\right)}^2\right)dt,\end{array}$(27) using the analytical solution of Eq. (21$\begin{array}{rl}& g_0\left(Z,T|t\right)\\ & =\left\{\begin{array}{cc}\frac{\alpha }{{\mathcal{F}}_2}\frac{\left({\left(z^{\ast }\right)}^2-1\right)\left(exp\left(-\alpha z^{\ast }t\right)-1\right)}{\left(z^{\ast }+1\right)exp\left(-\alpha z^{\ast }t\right)+\left(z^{\ast }-1\right)}& -T\le t\le 0\\ \frac{2\alpha }{{\mathcal{F}}_2}{\left(\frac{{\left(z^{\ast }\right)}^2+2z^{\ast }coth\left(\frac{\alpha z^{\ast }T}{2}\right)+1}{{\left(z^{\ast }\right)}^2-1}exp\left(-\alpha \left(t+T\right)\right)-1\right)}^{-1}& t<-T,\end{array}\right.\end{array}$), the analytical solution of the PMZBB distribution-generating function can be finally derived as^13–18

(30) $\begin{array}{rl}& \mathrm{l}\mathrm{n}\left(\tilde{G}\left(Z,T\right)\right)\approx -\frac{⟨\tilde{C}\left(T\right)⟩}{Y_{\mathrm{\infty },\mathrm{f}}}\\ & \left(\begin{array}{c}\left(z^{\ast }-1\right)+\frac{2}{\alpha T}ln\left(1+\frac{{\left(z^{\ast }-1\right)}^2}{4z^{\ast }}\left(1-exp\left(-\alpha z^{\ast }T\right)\right)\right)\\ +\frac{Y_{\mathrm{\infty },\mathrm{s}}}{Y_{\mathrm{\infty },\mathrm{f}}}\left(-\frac{{\left(z^{\ast }-1\right)}^2}{2}+\frac{2}{\alpha T}ln\left(1+\frac{{\left(z^{\ast }-1\right)}^2}{4z^{\ast }}\left(1-exp\left(-\alpha z^{\ast }T\right)\right)\right)\right)\end{array}\right),\end{array}$(30)

(31) $⟨\tilde{C}\left(T\right)⟩\approx \frac{\mathcal{D}{\mathcal{S}}_1}{\alpha }T\approx \frac{\mathcal{D}{\mathcal{S}}_1}{-\rho {\mathcal{F}}_1}T,$(31)

and

(32) $Y_{\mathrm{\infty },\mathrm{s}}\equiv \frac{\mathcal{D}{\mathcal{S}}_2}{\alpha {\mathcal{S}}_1}=Y_{\mathrm{\infty },\mathrm{f}}\frac{{\mathcal{S}}_2}{{\mathcal{S}}_1}\frac{\alpha }{{\mathcal{F}}_2}\approx Y_{\mathrm{\infty },\mathrm{f}}\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\frac{{\mathcal{S}}_2}{{\mathcal{S}}_1}\left(-\rho \right),$(32)

where $⟨\tilde{C}\left(T\right)⟩$ is the expected value of the neutron counts during the counting gate of width $T$, and ${\mathcal{F}}_1$ and ${\mathcal{F}}_2$ are defined by Eq. (19)(19) $\begin{array}{rl}{\mathcal{F}}_n\equiv & \underset{V}{\int }dV\underset{0}{\overset{\mathrm{\infty }}{\int }}dE\\ & \underset{4\pi }{\int }d\mathrm{\Omega }⟨\frac{\nu !}{\left(\nu -n\right)!}⟩{\mathrm{\Sigma }}_{\mathrm{f}}\left(\vec{r},E\right)\psi \left(\vec{r},E,\vec{\mathrm{\Omega }}\right){\left({\bar{\psi }}_{\mathrm{f}}^{†}\left(\vec{r}\right)\right)}^n,\end{array}$(19) when $n=1$ and 2, respectively. Note that Eqs. (31)(31) $⟨\tilde{C}\left(T\right)⟩\approx \frac{\mathcal{D}{\mathcal{S}}_1}{\alpha }T\approx \frac{\mathcal{D}{\mathcal{S}}_1}{-\rho {\mathcal{F}}_1}T,$(31) and (32(32) $Y_{\mathrm{\infty },\mathrm{s}}\equiv \frac{\mathcal{D}{\mathcal{S}}_2}{\alpha {\mathcal{S}}_1}=Y_{\mathrm{\infty },\mathrm{f}}\frac{{\mathcal{S}}_2}{{\mathcal{S}}_1}\frac{\alpha }{{\mathcal{F}}_2}\approx Y_{\mathrm{\infty },\mathrm{f}}\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\frac{{\mathcal{S}}_2}{{\mathcal{S}}_1}\left(-\rho \right),$(32) ) are approximated using the relationship between the neutron decay constant $\alpha$ and subcriticality, i.e., $\alpha \approx -\rho {\mathcal{F}}_1$ (Ref. 23).

If $T$ is sufficiently larger than the inverse of the neutron decay constant $1/\alpha$, Eq. (30)(30) $\begin{array}{rl}& \mathrm{l}\mathrm{n}\left(\tilde{G}\left(Z,T\right)\right)\approx -\frac{⟨\tilde{C}\left(T\right)⟩}{Y_{\mathrm{\infty },\mathrm{f}}}\\ & \left(\begin{array}{c}\left(z^{\ast }-1\right)+\frac{2}{\alpha T}ln\left(1+\frac{{\left(z^{\ast }-1\right)}^2}{4z^{\ast }}\left(1-exp\left(-\alpha z^{\ast }T\right)\right)\right)\\ +\frac{Y_{\mathrm{\infty },\mathrm{s}}}{Y_{\mathrm{\infty },\mathrm{f}}}\left(-\frac{{\left(z^{\ast }-1\right)}^2}{2}+\frac{2}{\alpha T}ln\left(1+\frac{{\left(z^{\ast }-1\right)}^2}{4z^{\ast }}\left(1-exp\left(-\alpha z^{\ast }T\right)\right)\right)\right)\end{array}\right),\end{array}$(30) can be further simplified, which is called the saturated PMZBB distribution-generating function $\tilde{G}\left(Z\right),$ as

(33) $\tilde{G}\left(Z\right)\approx exp\left(-\frac{⟨\tilde{C}\left(T\right)⟩}{Y_{\mathrm{\infty },\mathrm{f}}}\left(z^{\ast }-1\right)\left(1-\frac{1}{2}\frac{Y_{\mathrm{\infty },\mathrm{s}}}{Y_{\mathrm{\infty },\mathrm{f}}}\left(z^{\ast }-1\right)\right)\right).$(33)

II.C. Unique Combination Number for the Higher-Order Neutron Correlation Factor

Using the mathematical property of PGF $\tilde{G}\left(Z,T\right)$, the n’th-order neutron correlation factor ${\mathcal{Y}}_n\left(T\right)$ can be defined by the n’th-order differentiation of the natural logarithm of $\tilde{G}\left(Z,T\right)$ ($n\ge 2$) as^6,7

(34) ${\mathcal{Y}}_n\left(T\right)=\frac{1}{⟨\tilde{C}\left(T\right)⟩}{\left.\frac{{\mathrm{\partial }}^{n}ln\left(\tilde{G}\left(Z,T\right)\right)}{\mathrm{\partial }{Z}^n}\right|}_{Z=1},$(34)

and

(35) $⟨\tilde{C}\left(T\right)⟩={\left.\frac{\mathrm{\partial }ln\left(\tilde{G}\left(Z,T\right)\right)}{\mathrm{\partial }Z}\right|}_{Z=1}={\left.\left(\frac{1}{\tilde{G}\left(Z,T\right)}\frac{\mathrm{\partial }\tilde{G}\left(Z,T\right)}{\mathrm{\partial }Z}\right)\right|}_{Z=1}=\sum _{C=0}^{\mathrm{\infty }}C\tilde{P}\left(C,T\right).$(35)

For example, based on Eq. (34(34) ${\mathcal{Y}}_n\left(T\right)=\frac{1}{⟨\tilde{C}\left(T\right)⟩}{\left.\frac{{\mathrm{\partial }}^{n}ln\left(\tilde{G}\left(Z,T\right)\right)}{\mathrm{\partial }{Z}^n}\right|}_{Z=1},$(34) ), the definitions of ${\mathcal{Y}}_n\left(T\right)$ up to $n=6$ can be expressed by the following expressions using the n’th-order factorial moments of neutron counts:

(36) ${\mathcal{Y}}_2\equiv Y={\left.\frac{1}{⟨\tilde{C}⟩}\frac{{\mathrm{\partial }}^{2}ln\left(\tilde{G}\right)}{\mathrm{\partial }{Z}^2}\right|}_{Z=1}=\frac{⟨\tilde{C}\left(\tilde{C}-1\right)⟩-{⟨\tilde{C}⟩}^2}{⟨\tilde{C}⟩},$(36)

(37) ${\mathcal{Y}}_3=\frac{1}{⟨\tilde{C}⟩}{\left.\frac{{\mathrm{\partial }}^{3}ln\left(\tilde{G}\right)}{\mathrm{\partial }{Z}^3}\right|}_{Z=1}=\frac{⟨\tilde{C}\left(\tilde{C}-1\right)\left(\tilde{C}-2\right)⟩-{⟨\tilde{C}⟩}^2\left(3Y+⟨\tilde{C}⟩\right)}{⟨\tilde{C}⟩},$(37)

(38) ${\mathcal{Y}}_4={\left.\frac{1}{⟨\tilde{C}⟩}\frac{{\mathrm{\partial }}^{4}ln\left(\tilde{G}\right)}{\mathrm{\partial }{Z}^4}\right|}_{Z=1}=\frac{⟨\tilde{C}\left(\tilde{C}-1\right)\left(\tilde{C}-2\right)\left(\tilde{C}-3\right)⟩-{⟨\tilde{C}⟩}^2\left(4{\mathcal{Y}}_3+3Y\left(Y+2⟨\tilde{C}⟩\right)+{⟨\tilde{C}⟩}^2\right)}{⟨\tilde{C}⟩},$(38)

(39) ${\mathcal{Y}}_5={\left.\frac{1}{⟨\tilde{C}⟩}\frac{{\mathrm{\partial }}^{5}ln\left(\tilde{G}\right)}{\mathrm{\partial }{Z}^5}\right|}_{Z=1}=\frac{\left(\begin{array}{c}⟨\tilde{C}\left(\tilde{C}-1\right)\left(\tilde{C}-2\right)\left(\tilde{C}-3\right)\left(\tilde{C}-4\right)⟩\\ -{⟨\tilde{C}⟩}^2\left(\begin{array}{c}5{\mathcal{Y}}_4+10{\mathcal{Y}}_3\left(Y+⟨\tilde{C}⟩\right)+5Y⟨\tilde{C}⟩\left(3Y+2⟨\tilde{C}⟩\right)+{⟨\tilde{C}⟩}^3\end{array}\right)\end{array}\right)}{⟨\tilde{C}⟩},$(39)

(40) ${\mathcal{Y}}_6={\left.\frac{1}{⟨\tilde{C}⟩}\frac{{\mathrm{\partial }}^{6}ln\left(\tilde{G}\right)}{\mathrm{\partial }{Z}^6}\right|}_{Z=1}=\frac{\left(\begin{array}{c}⟨\tilde{C}\left(\tilde{C}-1\right)\left(\tilde{C}-2\right)\left(\tilde{C}-3\right)\left(\tilde{C}-4\right)\left(\tilde{C}-5\right)⟩\\ -{⟨\tilde{C}⟩}^2\left(\begin{array}{c}6{\mathcal{Y}}_5+15{\mathcal{Y}}_4\left(Y+⟨\tilde{C}⟩\right)+10{\mathcal{Y}}_3\left({\mathcal{Y}}_3+2⟨\tilde{C}⟩\left(3Y+⟨\tilde{C}⟩\right)\right)\\ +15Y⟨\tilde{C}⟩\left(Y\left(Y+3⟨\tilde{C}⟩\right)+{⟨\tilde{C}⟩}^2\right)+{⟨\tilde{C}⟩}^4\end{array}\right)\end{array}\right)}{⟨\tilde{C}⟩},$(40)

and

(41) $⟨\tilde{C}\left(\tilde{C}-1\right)\cdots \left(\tilde{C}-n+1\right)⟩={\left.\frac{{\mathrm{\partial }}^n\tilde{G}}{\mathrm{\partial }{Z}^n}\right|}_{Z=1}=\sum _{C=0}^{\mathrm{\infty }}\frac{C!}{\left(C-n\right)!}\tilde{P}\left(C,T\right),$(41)

where $⟨\tilde{C}\left(\tilde{C}-1\right)\cdots \left(\tilde{C}-n+1\right)⟩$ is the n’th-order factorial moment of neutron counts while variable $T$ is omitted to simplify the expression.

Thanks to the analytical solution of the saturated PGF $\tilde{G}\left(Z\right)$ shown in Eq. (33(33) $\tilde{G}\left(Z\right)\approx exp\left(-\frac{⟨\tilde{C}\left(T\right)⟩}{Y_{\mathrm{\infty },\mathrm{f}}}\left(z^{\ast }-1\right)\left(1-\frac{1}{2}\frac{Y_{\mathrm{\infty },\mathrm{s}}}{Y_{\mathrm{\infty },\mathrm{f}}}\left(z^{\ast }-1\right)\right)\right).$(33) ), the saturation value of $n$’th order neutron correlation factor ${\mathcal{Y}}_{n,\mathrm{\infty }}$ can be theoretically derived as

(42) ${\mathcal{Y}}_{n,\mathrm{\infty }}=\underset{T\to \mathrm{\infty }}{lim}\frac{1}{⟨\tilde{C}\left(T\right)⟩}{\left.\frac{{\mathrm{\partial }}^n}{\mathrm{\partial }{Z}^n}ln\left(\tilde{G}\left(Z,T\right)\right)\right|}_{Z=1}=\underset{T\to \mathrm{\infty }}{lim}{\left.\frac{{\mathrm{\partial }}^n}{\mathrm{\partial }{Z}^n}ln{\left(\tilde{G}\left(Z,T\right)\right)}^{1/⟨\tilde{C}\left(T\right)⟩}\right|}_{Z=1}\approx {\left.\frac{{\mathrm{\partial }}^n}{\mathrm{\partial }{Z}^n}\left(-\frac{\left(z^{\ast }-1\right)}{Y_{\mathrm{\infty },\mathrm{f}}}\left(1-\frac{1}{2}\frac{Y_{\mathrm{\infty },\mathrm{s}}}{Y_{\mathrm{\infty },\mathrm{f}}}\left(z^{\ast }-1\right)\right)\right)\right|}_{Z=1}.$(42)

For example, when $n=2$, the saturation value of the second-order correlation factor $Y_{\mathrm{\infty }}$ is given as

(43) $\begin{array}{r}{\mathcal{Y}}_{2,\mathrm{\infty }}\equiv Y_{\mathrm{\infty }}\approx Y_{\mathrm{\infty },\mathrm{f}}+Y_{\mathrm{\infty },\mathrm{s}}=Y_{\mathrm{\infty },\mathrm{f}}\left(1+\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\frac{{\mathcal{S}}_2}{{\mathcal{S}}_1}\left(-\rho \right)\right).\end{array}$(43)

Equation (43)(43) $\begin{array}{r}{\mathcal{Y}}_{2,\mathrm{\infty }}\equiv Y_{\mathrm{\infty }}\approx Y_{\mathrm{\infty },\mathrm{f}}+Y_{\mathrm{\infty },\mathrm{s}}=Y_{\mathrm{\infty },\mathrm{f}}\left(1+\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\frac{{\mathcal{S}}_2}{{\mathcal{S}}_1}\left(-\rho \right)\right).\end{array}$(43) is identical to the theoretical expression of $Y_{\mathrm{\infty }}$ derived in previous studies for multiple emission sources.^6,25

In addition, using Eqs. (33)(33) $\tilde{G}\left(Z\right)\approx exp\left(-\frac{⟨\tilde{C}\left(T\right)⟩}{Y_{\mathrm{\infty },\mathrm{f}}}\left(z^{\ast }-1\right)\left(1-\frac{1}{2}\frac{Y_{\mathrm{\infty },\mathrm{s}}}{Y_{\mathrm{\infty },\mathrm{f}}}\left(z^{\ast }-1\right)\right)\right).$(33) and (42(42) ${\mathcal{Y}}_{n,\mathrm{\infty }}=\underset{T\to \mathrm{\infty }}{lim}\frac{1}{⟨\tilde{C}\left(T\right)⟩}{\left.\frac{{\mathrm{\partial }}^n}{\mathrm{\partial }{Z}^n}ln\left(\tilde{G}\left(Z,T\right)\right)\right|}_{Z=1}=\underset{T\to \mathrm{\infty }}{lim}{\left.\frac{{\mathrm{\partial }}^n}{\mathrm{\partial }{Z}^n}ln{\left(\tilde{G}\left(Z,T\right)\right)}^{1/⟨\tilde{C}\left(T\right)⟩}\right|}_{Z=1}\approx {\left.\frac{{\mathrm{\partial }}^n}{\mathrm{\partial }{Z}^n}\left(-\frac{\left(z^{\ast }-1\right)}{Y_{\mathrm{\infty },\mathrm{f}}}\left(1-\frac{1}{2}\frac{Y_{\mathrm{\infty },\mathrm{s}}}{Y_{\mathrm{\infty },\mathrm{f}}}\left(z^{\ast }-1\right)\right)\right)\right|}_{Z=1}.$(42) ), Eq. (44)(44) $\begin{array}{rl}{\mathcal{Y}}_{n,\mathrm{\infty }}& \approx \left(2n-3\right)!!\times {\left(Y_{\mathrm{\infty },\mathrm{f}}\right)}^{n-2}\left(Y_{\mathrm{\infty },\mathrm{f}}+Y_{\mathrm{\infty },\mathrm{s}}\right)\\ & =\left(2n-3\right)!!\times {\left(Y_{\mathrm{\infty },\mathrm{f}}\right)}^{n-1}\left(1+\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\frac{{\mathcal{S}}_2}{{\mathcal{S}}_1}\left(-\rho \right)\right).\end{array}$(44) for ${\mathcal{Y}}_{n,\mathrm{\infty }}$ can be analytically solved as

(44) $\begin{array}{rl}{\mathcal{Y}}_{n,\mathrm{\infty }}& \approx \left(2n-3\right)!!\times {\left(Y_{\mathrm{\infty },\mathrm{f}}\right)}^{n-2}\left(Y_{\mathrm{\infty },\mathrm{f}}+Y_{\mathrm{\infty },\mathrm{s}}\right)\\ & =\left(2n-3\right)!!\times {\left(Y_{\mathrm{\infty },\mathrm{f}}\right)}^{n-1}\left(1+\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\frac{{\mathcal{S}}_2}{{\mathcal{S}}_1}\left(-\rho \right)\right).\end{array}$(44)

Note that Eq. (44)(44) $\begin{array}{rl}{\mathcal{Y}}_{n,\mathrm{\infty }}& \approx \left(2n-3\right)!!\times {\left(Y_{\mathrm{\infty },\mathrm{f}}\right)}^{n-2}\left(Y_{\mathrm{\infty },\mathrm{f}}+Y_{\mathrm{\infty },\mathrm{s}}\right)\\ & =\left(2n-3\right)!!\times {\left(Y_{\mathrm{\infty },\mathrm{f}}\right)}^{n-1}\left(1+\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\frac{{\mathcal{S}}_2}{{\mathcal{S}}_1}\left(-\rho \right)\right).\end{array}$(44) is derived on the two-forked branch approximation to neglect the higher-order terms owing to three-forked or more-forked branches. For example, when the three-forked branch effect is rigorously considered,⁶ the third-order neutron correlation factor ${\mathcal{Y}}_{3,\mathrm{\infty }}$ is corrected by adding the term owing to the three-forked branch, which can be expressed by a quadratic polynomial with respect to $\left(-\rho \right)$, as

(45) ${\mathcal{Y}}_{3,\mathrm{\infty }}\approx {\left(Y_{\mathrm{\infty },\mathrm{f}}\right)}^2\left(3\left(1+\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\frac{{\mathcal{S}}_2}{{\mathcal{S}}_1}\left(-\rho \right)\right)\right.+\left.\left(\frac{{\mathcal{F}}_3}{{\mathcal{F}}_2}+\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\frac{{\mathcal{S}}_3}{{\mathcal{S}}_1}\left(-\rho \right)\right)\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\left(-\rho \right)\right).$(45)

If the two-forked branch approximation is applicable because of $\left(-\rho \right)\approx 0$, the additional term $\left(\frac{{\mathcal{F}}_3}{{\mathcal{F}}_2}+\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\frac{{\mathcal{S}}_3}{{\mathcal{S}}_1}\left(-\rho \right)\right)\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\left(-\rho \right)$ is negligibly small. Similarly, the additional terms in ${\mathcal{Y}}_{n,\mathrm{\infty }}$ for $n\ge 4$ are also negligible when $\left(-\rho \right)\approx 0$. Therefore, as the subcriticality $\left(-\rho \right)$ approaches zero, the saturation value of ${\mathcal{Y}}_{n,\mathrm{\infty }}$ converges to

(46) $\underset{-\rho \to 0}{lim}{\mathcal{Y}}_{n,\mathrm{\infty }}=\left(2n-3\right)!!\times {\left(Y_{\mathrm{\infty },\mathrm{f}}\right)}^{n-1}.$(46)

Considering that the saturation value of the second-order correlation factor $Y_{\mathrm{\infty }}$ converges to $Y_{\mathrm{\infty },\mathrm{f}}$, we can finally find that the ratio of ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ is equal to the double factorial $\left(2n-3\right)!!$ for any system in the critical state:

(47) $\underset{-\rho \to 0}{lim}\frac{{\mathcal{Y}}_{n,\mathrm{\infty }}}{Y_{\mathrm{\infty }}^{n-1}}=\left(2n-3\right)!!.$(47)

Consequently, it was clarified that the unique combination number $\left(2n-3\right)!!$ can be easily derived from the saturated PMZBB distribution-generating function $\tilde{G}\left(Z\right)$ of Eq. (33).

III. EXPERIMENT

III.A. Experimental Conditions

Compared with our previous studies,^6,9 this study aims to further validate that the ratio ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ is approximately equal to the unique combination number $\left(2n-3\right)!!$ for not only the order $n=3,4$ but also the much higher order $n=5,6$ in a different subcritical system. For this purpose, we analyzed two experimental results of the reactor noise measurements carried out in the A-core at KUCA (Refs. 19 and 20). The experimental conditions are explained briefly below.

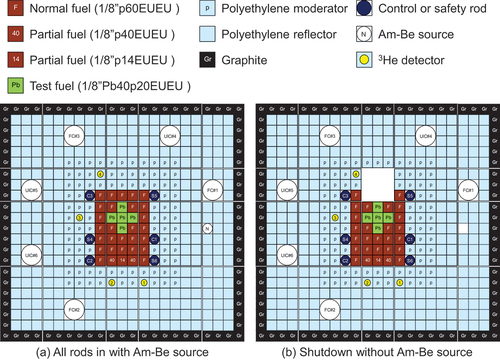
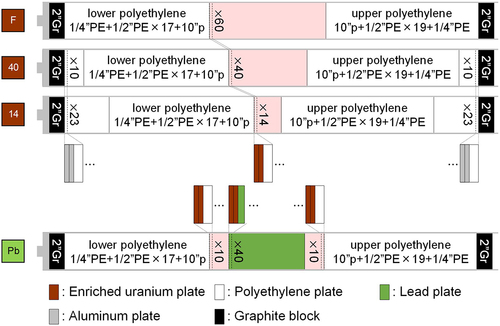
The experimental cores and loaded fuel assemblies are shown in Figs. 1 and 2, respectively. In these experiments, four types of fuel assemblies were used.²⁰ The normal fuel assembly (“F” marked element) comprised 60 unit fuel cells, which in turn comprised two 1/8-in.-thick highly enriched uranium–aluminum alloy (HEU) plates and one 1/8-in.-thick polyethylene plate. Two partial fuel assemblies (“40” and “14” marked elements) used the same unit fuel cell as the normal fuel, although the total numbers of unit fuel cells are 40 and 14, respectively, to adjust the excess reactivity. The test fuel assembly (“Pb” marked element) comprised 40 special unit cells sandwiched between 10 normal unit cells each on the top and bottom. The special unit cell comprised two 1/8-in.-thick HEU plates and one 1/8-in.-thick lead plate instead of a polyethylene plate.

Fig. 1. Top views of experimental cores.

Fig. 2. Side views of fuel assemblies.

To measure the reactor noise at zero-power states, four ³He detectors (numbers 1 through 4) were placed at the axial center positions of the ex-core reflector assemblies, which have holes of approximately 3 cm in diameter to insert detectors. A digital multichannel analyzer (MCA) (ANSeeN, HSDMCA) was used to successively measure the time-series data of the neutron-detection time. To increase detection efficiency, all time-series data employing four ³He detectors were summed up for the reactor noise analysis. As shown in Fig. 1, the reactor noise measurements were carried out for the following two cases. Case (a) is “all rods in with Am-Be neutron source”, and Case (b) is “shutdown without Am-Be neutron source”. In Case (a), all control and safety rods were fully inserted. Using the startup neutron source of Am-Be, the neutron count rate in Case (a) [$4401\pm 2$ counts per second (cps)] was maintained by subcritical neutron multiplication. Conversely, Case (b) was in the shutdown state without the Am-Be source by fully inserting all rods and withdrawing 3 × 3 fuel and reflector assemblies, in order to reduce the statistical uncertainties of neutron correlation factors by a longer reactor noise measurement in a deeper subcritical system. Because the operating time of KUCA using the Am-Be source was limited even in a deep subcritical state, the shutdown state was utilized for the longer reactor noise measurement. The lower neutron count rate in Case (b) ($91.48\pm 0.05$ cps) was maintained using only the inherent neutron source in the HEU plates, i.e., the (α,n) reactions of ²⁷Al owing to the α-decay of uranium isotopes.²⁶

The total measurement times of reactor noise for Cases (a) and (b) were 10 800 and 69 000 s, respectively. Based on Eqs. (36)(36) ${\mathcal{Y}}_2\equiv Y={\left.\frac{1}{⟨\tilde{C}⟩}\frac{{\mathrm{\partial }}^{2}ln\left(\tilde{G}\right)}{\mathrm{\partial }{Z}^2}\right|}_{Z=1}=\frac{⟨\tilde{C}\left(\tilde{C}-1\right)⟩-{⟨\tilde{C}⟩}^2}{⟨\tilde{C}⟩},$(36) through (40(40) ${\mathcal{Y}}_6={\left.\frac{1}{⟨\tilde{C}⟩}\frac{{\mathrm{\partial }}^{6}ln\left(\tilde{G}\right)}{\mathrm{\partial }{Z}^6}\right|}_{Z=1}=\frac{\left(\begin{array}{c}⟨\tilde{C}\left(\tilde{C}-1\right)\left(\tilde{C}-2\right)\left(\tilde{C}-3\right)\left(\tilde{C}-4\right)\left(\tilde{C}-5\right)⟩\\ -{⟨\tilde{C}⟩}^2\left(\begin{array}{c}6{\mathcal{Y}}_5+15{\mathcal{Y}}_4\left(Y+⟨\tilde{C}⟩\right)+10{\mathcal{Y}}_3\left({\mathcal{Y}}_3+2⟨\tilde{C}⟩\left(3Y+⟨\tilde{C}⟩\right)\right)\\ +15Y⟨\tilde{C}⟩\left(Y\left(Y+3⟨\tilde{C}⟩\right)+{⟨\tilde{C}⟩}^2\right)+{⟨\tilde{C}⟩}^4\end{array}\right)\end{array}\right)}{⟨\tilde{C}⟩},$(40) ), the variations in the n’th-order neutron correlation factors ${\mathcal{Y}}_n\left(T\right)$ with respect to the gate of width $T$ were analyzed for $2\le n\le 6$ using the measured factorial moments of neutron counts. Furthermore, using the moving block bootstrap method,^7,27,28 the ratios of ${\mathcal{Y}}_n/Y^{n-1}$ were calculated with statistical uncertainties, i.e., 95% bootstrap confidence interval and standard deviation.

III.B. Numerical Analysis

In this experiment, the subcriticality values $-\rho$ for the two experimental cores of Cases (a) and (b) were not directly measured. To estimate the subcriticality for Cases (a) and (b), a numerical analysis was carried out using the continuous energy Monte Carlo codes MCNP6.2 (Refs. 29 and 30) and Serpent 2.1.32 (Ref. 31) with ENDF/B-VIII.0 (Ref. 32). The ACE-formatted files of ENDF/B-VIII.0 were generated using the Japanese FRENDY nuclear data processing code.³³ In the numerical analysis, the nuclide composition and size of each material were quoted from Ref. 19. The total number of neutron histories was 1 billion, i.e., the neutron histories per cycle = 500 000, active cycles = 2000, and inactive cycles = 100. Along with the effective neutron multiplication factor $k_{\mathrm{e}\mathrm{f}\mathrm{f}}$, the effective delayed neutron fraction ${\beta }_{\mathrm{e}\mathrm{f}\mathrm{f}}$ and the neutron generation time $\mathrm{\Lambda }$ were also evaluated based on the iterated fission probability method³⁴ to provide supplemental information.

Table I summarizes the numerical results of $k_{\mathrm{e}\mathrm{f}\mathrm{f}}$, ${\beta }_{\mathrm{e}\mathrm{f}\mathrm{f}},$ and $\mathrm{\Lambda }$ for Cases (a) and (b). Both numerical results using MCNP6.2 and Serpent 2.1.32 were found to have agreed well with each other. The difference in $k_{\mathrm{e}\mathrm{f}\mathrm{f}}$ between MCNP6.2 and Serpent 2.1.32 were small, i.e., 0.02 and 0.03%dk/k for Cases (a) and (b), respectively. Although thorough uncertainty quantification for the numerical results of $k_{\mathrm{e}\mathrm{f}\mathrm{f}}$ is a future research topic, a posteriori nuclear data–induced uncertainties of $k_{\mathrm{e}\mathrm{f}\mathrm{f}}$ using Whisper-1.1 (Ref. 35) were estimated as 0.118 and 0.120%dk/k for Cases (a) and (b), respectively. In addition, the numerical result of $k_{\mathrm{e}\mathrm{f}\mathrm{f}}$ using MCNP6.2 with ENDF/B-VIII.0 was 0.99845 ± 0.00003 for the same core configuration in a critical state by adjusting control rods; i.e., the bias was 0.16%dk/k (Ref. 36). Therefore, the uncertainty of calculated $k_{\mathrm{e}\mathrm{f}\mathrm{f}}$ was estimated to be approximately 0.2%dk/k in this study. Consequently, the magnitudes of the subcriticality $-\rho \equiv \left(1-k_{\mathrm{e}\mathrm{f}\mathrm{f}}\right)/k_{\mathrm{e}\mathrm{f}\mathrm{f}}$ for Cases (a) and (b) were estimated as 3.6 ± 0.2 and 8.7 ± 0.2%dk/k, or 4.5 ± 0.2 $ and 10.7 ± 0.2 $, respectively.

TABLE I Summary of KUCA Numerical Results

Case	Code	$k_{\mathrm{e}\mathrm{f}\mathrm{f}}$	${\beta }_{\mathrm{e}\mathrm{f}\mathrm{f}}$ (%)	$\mathrm{\Lambda }$ (μs)
Case (a): all rods in	MCNP6.2	0.96521 ± 0.00003	0.803 ± 0.002	26.931 ± 0.011
	Serpent 2.1.32	0.96506 ± 0.00003	0.804 ± 0.002	26.894 ± 0.010
Case (b): shutdown	MCNP6.2	0.91970 ± 0.00003	0.815 ± 0.002	30.540 ± 0.014
	Serpent 2.1.32	0.91944 ± 0.00003	0.814 ± 0.002	30.342 ± 0.012

III.C. Experimental Results

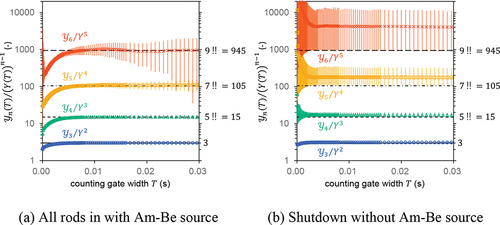
Figure 3 shows the variations in ${\mathcal{Y}}_n\left(T\right)/{\left(Y\left(T\right)\right)}^{n-1}$ in a semilogarithmic scale and the bootstrap 95% confidence intervals. The ratios of ${\mathcal{Y}}_n\left(T\right)/{\left(Y\left(T\right)\right)}^{n-1}$ saturated as the counting gate of width $T$ increased. Using the Rossi-$\alpha$ method based on the dynamic mode decomposition,^36,37 the prompt neutron decay constant $\alpha$ values for Cases (a) and (b) were preliminarily estimated as 1454 ± 4 1/s and 2645 ± 18 1/s, respectively. Therefore, when $T$ is sufficiently larger than $10/\alpha$, the ratios of ${\mathcal{Y}}_n\left(T\right)/{\left(Y\left(T\right)\right)}^{n-1}$ can be regarded as the saturation values ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$.

Fig. 3. Experimental results of ${\mathcal{Y}}_n\left(T\right)/{\left(Y\left(T\right)\right)}^{n-1}$.

The experimental results in Case (a) showed that each saturation value ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ was approximately equal to the corresponding unique combination number $\left(2n-3\right)!!.$ Considering that Eq. (47)(47) $\underset{-\rho \to 0}{lim}\frac{{\mathcal{Y}}_{n,\mathrm{\infty }}}{Y_{\mathrm{\infty }}^{n-1}}=\left(2n-3\right)!!.$(47) was reasonably applicable because the relative difference between ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ and $\left(2n-3\right)!!$ roughly corresponds to the magnitude of $-\rho ,$ the subcriticality 3.6 ± 0.2%dk/k was sufficiently smaller than 10%dk/k. Note that the statistical uncertainty of ${\mathcal{Y}}_n\left(T\right)/{\left(Y\left(T\right)\right)}^{n-1}$ increased as the order of the neutron correlation factor increased. Therefore, the experimental validation for the higher-order neutron correlation factors when $n\ge 7$ requires a longer reactor noise measurement to reduce statistical uncertainties.

In Case (b), although the order of magnitude for ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ approximately corresponded to the unique combination number $\left(2n-3\right)!!$, the measured ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ values were larger than those in Case (a). 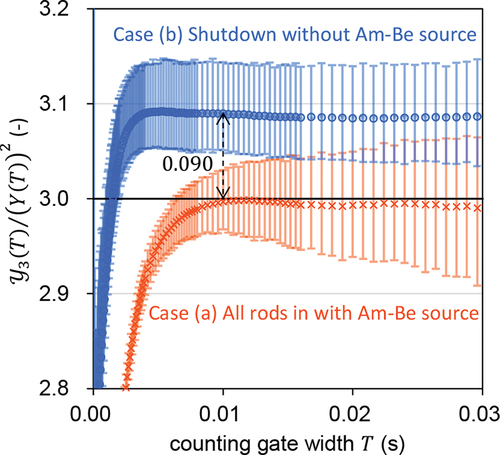Note that the differences in ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ between Cases (a) and (b) are visible for $n\ge 4$ due to the semilogarithmic graph of Fig. 3. To discuss this reason, Fig. 4 compares the two experimental results of ${\mathcal{Y}}_3\left(T\right)/{\left(Y\left(T\right)\right)}^2$ between Cases (a) and (b). Figure 4 shows the same results as the corresponding values of Fig. 3 although the vertical axis is the linear scale to enlarge the results when $n=3$. Owing to the relatively small subcriticality in Case (a), the unique combination number “3” existed within the 95% bootstrap confidence interval of ${\mathcal{Y}}_{3,\mathrm{\infty }}/Y_{\mathrm{\infty }}^2$. In other words, a longer measurement time is required to detect a difference between ${\mathcal{Y}}_{3,\mathrm{\infty }}/Y_{\mathrm{\infty }}^2$ and “3.”

Fig. 4. Comparison of ${\mathcal{Y}}_3\left(T\right)/{\left(Y\left(T\right)\right)}^2$ in different subcritical cores.

Conversely, because the subcriticality and the total measurement time of Case (b) were deeper and longer than Case (a), the statistically significant difference between ${\mathcal{Y}}_{3,\mathrm{\infty }}/Y_{\mathrm{\infty }}^2$ and “3” was detectable. Although the unique combination number “3” was theoretically derived based on the two-forked approximation, the three-forked branch effect should be rigorously considered to quantitively discuss the difference between ${\mathcal{Y}}_{3,\mathrm{\infty }}/Y_{\mathrm{\infty }}^2$ and “3.” Based on Eqs. (43)(43) $\begin{array}{r}{\mathcal{Y}}_{2,\mathrm{\infty }}\equiv Y_{\mathrm{\infty }}\approx Y_{\mathrm{\infty },\mathrm{f}}+Y_{\mathrm{\infty },\mathrm{s}}=Y_{\mathrm{\infty },\mathrm{f}}\left(1+\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\frac{{\mathcal{S}}_2}{{\mathcal{S}}_1}\left(-\rho \right)\right).\end{array}$(43) and (45(45) ${\mathcal{Y}}_{3,\mathrm{\infty }}\approx {\left(Y_{\mathrm{\infty },\mathrm{f}}\right)}^2\left(3\left(1+\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\frac{{\mathcal{S}}_2}{{\mathcal{S}}_1}\left(-\rho \right)\right)\right.+\left.\left(\frac{{\mathcal{F}}_3}{{\mathcal{F}}_2}+\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\frac{{\mathcal{S}}_3}{{\mathcal{S}}_1}\left(-\rho \right)\right)\frac{{\mathcal{F}}_1}{{\mathcal{F}}_2}\left(-\rho \right)\right).$(45) ), along with the condition of the Poisson inherent neutron source owing to the (α,n) reaction, the theoretical formula of ${\mathcal{Y}}_{3,\mathrm{\infty }}/Y_{\mathrm{\infty }}^2$ can be expressed as

(48) $\frac{{\mathcal{Y}}_{3,\mathrm{\infty }}}{Y_{\mathrm{\infty }}^2}\approx 3+\frac{{\mathcal{F}}_1{\mathcal{F}}_3}{{\left({\mathcal{F}}_2\right)}^2}\left(-\rho \right).$(48)

In Eq. (48(48) $\frac{{\mathcal{Y}}_{3,\mathrm{\infty }}}{Y_{\mathrm{\infty }}^2}\approx 3+\frac{{\mathcal{F}}_1{\mathcal{F}}_3}{{\left({\mathcal{F}}_2\right)}^2}\left(-\rho \right).$(48) ), the order of magnitude of the coefficient ${\mathcal{F}}_1{\mathcal{F}}_3/{\left({\mathcal{F}}_2\right)}^2$ is approximately estimated by ${\mathcal{F}}_1{\mathcal{F}}_3/{\left({\mathcal{F}}_2\right)}^2\approx ⟨\nu ⟩⟨\nu \left(\nu -1\right)\left(\nu -2\right)⟩/⟨\nu \left(\nu -1\right){⟩}^2.$ Based on Ref. 38, the values of $⟨\nu ⟩⟨\nu \left(\nu -1\right)\left(\nu -2\right)⟩/⟨\nu \left(\nu -1\right){⟩}^2$ for thermal neutron–induced fission are estimated as 0.760 ± 0.010, 0.766 ± 0.007, 0.793 ± 0.010, and 0.800 ± 0.008 for the major fissile nuclides ²³³U, ²³⁵U, ²³⁹Pu, and ²⁴¹Pu, respectively.

Furthermore, by quoting the energy dependency of the probabilities of fission neutrons $p_{\mathrm{f}}\left(\nu \right)$ for ²³⁵U, ²³⁸U, and ²³⁹Pu from Ref. 39, the variation of $⟨\nu ⟩⟨\nu \left(\nu -1\right)\left(\nu -2\right)⟩/⟨\nu \left(\nu -1\right){⟩}^2$ with respect to the neutron energy ($0\le E\le 10$ MeV) falls within the range of 0.76 to 0.85. Thus, the rough estimation $⟨\nu ⟩⟨\nu \left(\nu -1\right)\left(\nu -2\right)⟩/⟨\nu \left(\nu -1\right){⟩}^2\approx 0.8$ is reasonable even if detailed information of nuclide composition is not available but uranium or plutonium is the main contribution to fission reactions in a target system. Therefore, Eq. (48)(48) $\frac{{\mathcal{Y}}_{3,\mathrm{\infty }}}{Y_{\mathrm{\infty }}^2}\approx 3+\frac{{\mathcal{F}}_1{\mathcal{F}}_3}{{\left({\mathcal{F}}_2\right)}^2}\left(-\rho \right).$(48) indicates that the difference in $\left|{\mathcal{Y}}_{3,\mathrm{\infty }}/Y_{\mathrm{\infty }}^2-3\right|$ roughly corresponds to the magnitude of the subcriticality. For example, when $T=0.01$ s, the difference in $\left|{\mathcal{Y}}_3\left(T\right)/{\left(Y\left(T\right)\right)}^2-3\right|$ for Case (b) was 0.090 ± 0.024, or the 95% bootstrap confidence interval was [0.051, 0.144]. This confirmed that the difference of 9.0% ± 2.4% was approximately equal to the numerical result of subcriticality $-\rho =8.7\pm 0.2$%dk/k.

Consequently, the unique combination number hidden in ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ was validated by conducting the actual reactor noise experiment for the relatively shallow subcritical core where $-\rho =3.6\pm 0.2$%dk/k. Furthermore, this study also demonstrated that the difference in $\left|{\mathcal{Y}}_{3,\mathrm{\infty }}/Y_{\mathrm{\infty }}^2-3\right|$ can be used to determine whether a target system is in a deep subcritical state (i.e., not a near-critical state) or to roughly estimate the magnitude of the subcriticality using only factorial moments of measured neutron counts if the statistically significant difference in $\left|{\mathcal{Y}}_{3,\mathrm{\infty }}/Y_{\mathrm{\infty }}^2-3\right|$ is detectable by a sufficiently long measurement of reactor noise.

IV. CONCLUSIONS

As clarified in this study, the Pál-Bell equation with the two-forked and fundamental mode approximations enables us to theoretically derive that the ratio of neutron correlation factors ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ is equal to the double factorial moment $\left(2n-3\right)!!$ in a critical state even for any kind of fissile and moderator materials. Through actual experimental analysis of the relatively shallow subcritical core where $-\rho =3.6\pm 0.2$%dk/k, we validated that the saturation values ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ were approximately equal to the corresponding unique combination number $\left(2n-3\right)!!$ for the order $3\le n\le 6$. Furthermore, as the subcriticality $-\rho$ for a target system deepened, the difference between the measured ratios of ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ and $\left(2n-3\right)!!$ increased. Considering that the statistical uncertainty of ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ becomes larger as the order $n$ increases, the third-order ratio ${\mathcal{Y}}_{3,\mathrm{\infty }}/Y_{\mathrm{\infty }}^2$ was found to be practical. The presented knowledge can be used to determine whether the target system is in a deep subcritical state or to roughly estimate the magnitude of subcriticality, using the factorial moments of measured neutron counts. Note that although the unique combination number $\left(2n-3\right)!!$ can be theoretically derived based on the two-forked approximation, the more-forked branch effect should be rigorously considered to quantitively discuss the difference between ${\mathcal{Y}}_{n,\mathrm{\infty }}/Y_{\mathrm{\infty }}^{n-1}$ and $\left(2n-3\right)!!$.

Acknowledgments

We sincerely dedicate this study to Lénárd Pál, the pioneer of neutron-detection probability theory. This work was partly conducted under the Visiting Researcher’s Program of the Kyoto University. The authors are grateful to all the technical staff of KUCA for their assistance during the experiments.

Disclosure Statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the Japan Society for the Promotion of Science (JSPS) Grant-in-Aid for Scientific Research (C) [Grant Number 19K05328].