Source Nuclide Density First-Order and Second-Order Sensitivities in Monte Carlo Codes

Abstract

Application of perturbation capabilities for density sensitivities in Monte Carlo radiation transport codes has been limited because changing source nuclide densities or source material densities changes the intrinsic source, and in most Monte Carlo codes, the user-input source is independent of the user-input materials. The perturbation capability then has no way of accounting for changes in the intrinsic source. This paper derives the sensitivity of a response with respect to a source nuclide density in terms of a portion due to the transport operator and a portion due to the source rate density. The Monte Carlo perturbation method computes the portion due to the transport operator, and the portion due to the source rate density is computed in postprocessing using parameters from the precomputed intrinsic source calculation. This paper derives first- and second-order sensitivities. The equations require the response to be separated by contribution from each of the sources modeled. A test problem containing several (α,n) and spontaneous fission neutron sources verifies the method.

Keywords:

• Monte Carlo
• sensitivity theory
• density perturbation

I. INTRODUCTION

First-, second-, and higher-order derivatives of a response with respect to a set of input parameters are useful for uncertainty quantification, parameter estimation and other inverse problems, design optimization, and other applications. Of most relevance to this paper, materials modeled in radiation transport simulations always have some uncertainty in their densities and compositions, even if those have been measured. The sensitivities of a response with respect to nuclide and material densities can be used to propagate those uncertainties.

The Taylor series (differential operator) perturbation method,^1–3 as implemented in the Monte Carlo radiation transport codes MCNP6 (Refs. 4 and 5), MCSEN (Refs. 6 and 7), TRIPOLI-4 (Ref. 8), and MCBEND (Ref. 9) (and possibly others), can be used for first-order and (except for MCSEN) second-order sensitivity analyses in fixed-source problems. MCNP6’s and MCBEND’s second-order Taylor series terms lack the cross terms that would allow the calculation of mixed sensitivities,^10,11 but TRIPOLI-4 does compute mixed sensitivities. (The differential operator method is implemented in the MVP/GMVP Monte Carlo code,¹² but only for k_eff-eigenvalue problems.¹³)

The differential operator method in MCNP6, MCSEN, TRIPOLI-4, and MCBEND does not compute any sensitivities involving the source in a fixed-source problem. When neutrons or gamma rays are emitted from radioactive decay, the source rate density depends intrinsically on the nuclide densities in the source material. The source distribution is typically precomputed and input to the codes independent of the material inputs. When the differential operator method in MCNP6, MCSEN, TRIPOLI-4, or MCBEND is used to compute sensitivities of a response to nuclide and material densities, those sensitivities do not include the effect of the source.

This paper discusses how to compute sensitivities of a response to source nuclide densities in order to allow MCNP6, MCSEN, TRIPOLI-4, MCBEND, and other codes to compute the full sensitivity of a response to nuclide and material densities in a fixed-source problem. The listed codes have the differential operator method implemented, but any other Monte Carlo perturbation method (such as Refs. 14 and 15) will benefit from the method of this paper if the input source rate density is independent of the input materials. The conference paper¹⁶ on this topic dealt exclusively with first-order sensitivities and MCNP6, but in this paper, the application is more general and includes second-order sensitivities.

The correlated sampling method can also be used to estimate perturbed responses with Monte Carlo codes.^3,17–19 With correlated sampling, the perturbed source can be calculated and input directly into the perturbed input file. Thus, there would be no need to use the method presented here. However, correlated sampling requires one Monte Carlo transport simulation for each perturbed parameter for a one-sided finite difference estimate of a first-order sensitivity and two simulations for each perturbed parameter for a central difference, whereas the differential operator method can compute all derivatives in a single simulation without a finite difference estimate. Thus, there is an enormous advantage in using the differential operator method. (Also, because correlated sampling relies on the simulations having the same sequence of random numbers, it is not clear whether a source perturbation, which would immediately lead to a different random number sequence, can actually gain anything using correlated sampling.)

This paper is organized as follows. Notation for the transport equation and a response is presented in Sec. II. The first-order sensitivity to a nuclide density is derived in Sec. III, and the second-order sensitivity is derived in Sec. IV. Section V discusses the calculation of the derivatives involving the source. Section VI presents numerical results for an example problem. Section VII is a summary and conclusions. Appendix A derives the relationship between a second-order sensitivity and the output from the differential operator perturbation method as implemented in MCNP6. Appendix B presents an interesting observation regarding sensitivities of (α,n) sources.

II. TRANSPORT EQUATION AND RESPONSE

The transport equation for the neutral particle angular flux Ψ can be written

(1) $A\mathrm{\Psi }=Q,$(1)

where the transport operator A includes streaming, total interactions, scattering, and fission, and Q is the inhomogeneous source rate density. The response of interest R is

(2) $R=⟨{\mathrm{\Sigma }}_d\mathrm{\Psi }⟩,$(2)

where ${\mathrm{\Sigma }}_d$ is a response function and the angle brackets indicate an integral over volume, energy, and angle.

In this paper, the inhomogeneous source rate density Q is produced from radioactive decay of the nuclides in the source material. The total source rate density Q is the sum of the source rate density from each of the Z contributions to the source:

(3) $Q=\sum _{z=1}^Z{Q}_z.$(3)

Intrinsic sources from radioactive decay are computed with codes like MISC (Ref. 20) and SOURCES4C (Ref. 21) and then written to an input file for the Monte Carlo code (MCNP6, MCSEN, TRIPOLI-4, MCBEND, etc.). Contributions can be direct emissions from a decay (MCNP6 itself can generate some decay sources⁴), or they can be neutrons emitted from (α,n) reactions, in which case index z designates a particular source/target combination.²¹ The principle of superposition can be used to write the transport equation for each $Q_z$, $z=1,\dots ,Z$. The angular flux Ψ in Eq. (1)(1) $A\mathrm{\Psi }=Q,$(1) is the sum of the Z solutions ${\mathrm{\Psi }}_z$, and the response R is

(4) $R=\sum _{z=1}^Z{R}_z,$(4)

where

(5) $R_z=⟨{\mathrm{\Sigma }}_d{\mathrm{\Psi }}_z⟩,z=1,\dots ,Z.$(5)

III. FIRST-ORDER SENSITIVITY TO NUCLIDE DENSITY

The relative sensitivity $S_{R,N_i}$ of response R with respect to the density $N_i$ of nuclide $i=1,\dots ,I$ in the source material is

(6) $S_{R,N_i}=\frac{N_i}{R}\frac{\mathrm{\partial }R}{\mathrm{\partial }{N}_i}.$(6)

The relative sensitivity $S_{R_z,N_i}$ of response $R_z$ with respect to the density $N_i$ of nuclide $i=1,\dots ,I$ in the source material is

(7) $S_{R_z,N_i}=\frac{N_i}{R_z}\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{N}_i},$(7)

and because the transport operator is linear,

(8) $S_{R,N_i}=\sum _{z=1}^Z\frac{R_z}{R}{S}_{R_z,N_i}.$(8)

The angular flux and therefore the response depend on the source nuclide atom density $N_i$ through the cross sections in the transport operator A and through the parameters in the source rate density Q. Let $A_m$, $m=1,\dots ,M,$ represent the parameters in A that depend on $N_i$ (excluding $N_i$ itself). For example, we may have $A_m=\left\{{\mathrm{\Sigma }}_c,{\mathrm{\Sigma }}_f,{\mathrm{\Sigma }}_s\right\}$, where ${\mathrm{\Sigma }}_c$, ${\mathrm{\Sigma }}_f$, and ${\mathrm{\Sigma }}_s$ are the macroscopic capture, fission, and scattering cross sections in the source material. The total derivative $\mathrm{\partial }{R}_z/\mathrm{\partial }{N}_i$ is

(9) $\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{N}_i}=\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{Q}_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}.$(9)

Because the transport operator is linear and the response is zero when there is no source, we have

(10) $\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{Q}_z}=\frac{R_z}{Q_z}.$(10)

Using Eqs. (9)(9) $\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{N}_i}=\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{Q}_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}.$(9) and (10(10) $\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{Q}_z}=\frac{R_z}{Q_z}.$(10) ) in Eq. (7)(7) $S_{R_z,N_i}=\frac{N_i}{R_z}\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{N}_i},$(7) yields

(11) $S_{R_z,N_i}=\frac{N_i}{R_z}\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\frac{N_i}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}.$(11)

Define the sensitivity contributions due to the transport operator and the source separately as

(12) $S_{R_z(A),N_i}\equiv \frac{N_i}{R_z}\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}$(12)

and

(13) $S_{Q_z,N_i}\equiv \frac{N_i}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}.$(13)

Equation (11)(11) $S_{R_z,N_i}=\frac{N_i}{R_z}\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\frac{N_i}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}.$(11) becomes

(14) $S_{R_z,N_i}=S_{R_z(A),N_i}+S_{Q_z,N_i}.$(14)

Using Eq. (14)(14) $S_{R_z,N_i}=S_{R_z(A),N_i}+S_{Q_z,N_i}.$(14) in Eq. (8(8) $S_{R,N_i}=\sum _{z=1}^Z\frac{R_z}{R}{S}_{R_z,N_i}.$(8) ), the relative sensitivity $S_{R,N_i}$ of the total response R to the density of nuclide i is

(15) $S_{R,N_i}=\sum _{z=1}^Z\frac{R_z}{R}{S}_{R_z(A),N_i}+\sum _{z=1}^Z\frac{R_z}{R}{S}_{Q_z,N_i}.$(15)

It will be convenient to define the sensitivity contribution due to the transport operator on the total response R as the first term on the right side of Eq. (15)(15) $S_{R,N_i}=\sum _{z=1}^Z\frac{R_z}{R}{S}_{R_z(A),N_i}+\sum _{z=1}^Z\frac{R_z}{R}{S}_{Q_z,N_i}.$(15) :

(16) $S_{R(A),N_i}\equiv \sum _{z=1}^Z\frac{R_z}{R}{S}_{R_z(A),N_i}.$(16)

Often, the source rate density $Q_z$ due to nuclide i is proportional to the density of nuclide i. For example, the neutron source rate density due to spontaneous fission of nuclide i is²¹

(17) $Q_{s.f.,i}={\lambda }_i{N}_i{S}_i(s.f.),$(17)

where ${\lambda }_i$ is the decay constant and $S_i(s.f.)$ is the average number of spontaneous fission neutrons produced per decay of nuclide i. The derivative of $Q_{s.f.,i}$ with respect to the density $N_i$ is

(18) $\frac{\mathrm{\partial }{Q}_{s.f.,i}}{\mathrm{\partial }{N}_i}={\lambda }_i{S}_i(s.f.)=\frac{Q_{s.f.,i}}{N_i}.$(18)

Whenever the source rate density $Q_z$ due to nuclide i is proportional to the density of nuclide i, Eq. (13)(13) $S_{Q_z,N_i}\equiv \frac{N_i}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}.$(13) becomes

(19) $S_{Q_z,N_i}=1.$(19)

Unlike spontaneous fission sources, the neutron source rate density from (α,n) reactions is not proportional to any nuclide densities.^21,22 The first derivative of an (α,n) source rate density with respect to each source material nuclide density is given in Ref. 22. Suffice it to say here that every nuclide in a material contributes to the (α,n) source rate density, some because they are α particle sources, some because they are (α,n) targets, and all because they contribute to the material’s stopping power for α particles.

IV. SECOND-ORDER SENSITIVITY TO NUCLIDE DENSITY

The second-order relative sensitivity $S_{R_z,N_i,N_j}^{(2)}$ of response $R_z$ with respect to the density $N_i$ of nuclide $i=1,\dots ,I$ and $N_j$ of nuclide $j=1,\dots ,I$ in the source material is

(20) $S_{R_z,N_i,N_j}^{(2)}=\frac{N_i{N}_j}{R_z}\frac{{\mathrm{\partial }}^2{R}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.$(20)

Taking the derivative of Eq. (9)(9) $\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{N}_i}=\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{Q}_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}.$(9) with respect to $N_j$ [and using Eq. (10(10) $\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{Q}_z}=\frac{R_z}{Q_z}.$(10) )] yields

(21) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^2{R}_z}{\mathrm{\partial }{N}_j\mathrm{\partial }{N}_i}=\frac{\mathrm{\partial }}{\mathrm{\partial }{N}_j}\left(\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\frac{R_z}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}\right)\\ & =\sum _{m=1}^M\frac{\mathrm{\partial }}{\mathrm{\partial }{A}_m}\left(\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{N}_j}\right)\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{{\mathrm{\partial }}^2{A}_m}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}\\ & +\frac{1}{Q_z}\left(\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{N}_j}\right)\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}-\frac{R_z}{{Q_z}^2}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_j}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}+\frac{R_z}{Q_z}\frac{{\mathrm{\partial }}^2{Q}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.& (21)\end{array}$(21)

Using Eqs. (9)(9) $\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{N}_i}=\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{Q}_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}.$(9) and (10(10) $\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{Q}_z}=\frac{R_z}{Q_z}.$(10) ) in Eq. (21)(21) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^2{R}_z}{\mathrm{\partial }{N}_j\mathrm{\partial }{N}_i}=\frac{\mathrm{\partial }}{\mathrm{\partial }{N}_j}\left(\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\frac{R_z}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}\right)\\ & =\sum _{m=1}^M\frac{\mathrm{\partial }}{\mathrm{\partial }{A}_m}\left(\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{N}_j}\right)\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{{\mathrm{\partial }}^2{A}_m}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}\\ & +\frac{1}{Q_z}\left(\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{N}_j}\right)\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}-\frac{R_z}{{Q_z}^2}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_j}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}+\frac{R_z}{Q_z}\frac{{\mathrm{\partial }}^2{Q}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.& (21)\end{array}$(21) yields

(22) $\begin{array}{l}\frac{{\partial }^2{R}_z}{\partial N_j\partial N_i}={\displaystyle \sum _{m=1}^M\frac{\partial }{\partial A_m}}\left({\displaystyle \sum _{m^{\prime }=1}^M\frac{\partial R_z}{\partial A_{m^{\prime }}}\frac{\partial A_{m^{\prime }}}{\partial N_j}+\frac{R_z}{Q_z}\frac{\partial Q_z}{\partial N_j}}\right)\frac{\partial A_m}{\partial N_i}+\frac{1}{Q_z}\left(\sum _{m^{\prime }=1}^M\frac{\partial R_z}{\partial A_{m^{\prime }}}\frac{\partial A_{m^{\prime }}}{\partial N_j}+\frac{R_z}{Q_z}\frac{\partial Q_z}{\partial N_j}\right)\frac{\partial Q_z}{\partial N_i}\\ +{\displaystyle \sum _{m=1}^M\frac{\partial R_z}{\partial A_m}\frac{{\partial }^2{A}_m}{\partial N_i\partial N_j}}-\frac{R_z}{Q_z{}^2}\frac{\partial Q_z}{\partial N_j}\frac{\partial Q_z}{\partial N_i}+\frac{R_z}{Q_z}\frac{{\partial }^2{Q}_z}{\partial N_i\partial N_j}\\ =\sum _{m=1}^M[{\displaystyle \sum _{m^{\prime }=1}^M\frac{{\partial }^2{R}_z}{\partial A_m\partial A_{m^{\prime }}}\frac{\partial A_{m^{\prime }}}{\partial N_j}}+\sum _{m^{\prime }=1}^M\frac{\partial R_z}{\partial A_{m^{\prime }}}\frac{\partial }{\partial A_m}\left(\frac{\partial A_{m^{\prime }}}{\partial N_j}\right)\\ +\frac{1}{Q_z}\frac{\partial R_z}{\partial A_m}\frac{\partial Q_z}{\partial N_j}-\frac{R_z}{Q_z{}^2}\frac{\partial Q_z}{\partial A_m}\frac{\partial Q_z}{N_j}+\frac{R_z}{Q_z}\frac{\partial }{\partial A_m}\left(\frac{\partial Q_z}{\partial N_j}\right)]\frac{\partial A_m}{\partial N_i}+\frac{1}{Q_z}\left({\displaystyle \sum _{m^{\prime }=1}^M\frac{\partial R_z}{\partial A_{m^{\prime }}}\frac{\partial A_{m^{\prime }}}{\partial N_j}}\right)\frac{\partial Q_z}{\partial N_i}\\ +{\displaystyle \sum _{m=1}^M\frac{\partial R_z}{\partial A_m}\frac{{\partial }^2{A}_m}{\partial N_i\partial N_j}}+\frac{R_z}{Q_z}\frac{{\partial }^2{Q}_z}{\partial N_i\partial N_j}.(22)\end{array}$(22)

The source $Q_z$ has no dependence on the parameters in $A_m$, so

(23) $\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{A}_m}=\frac{\mathrm{\partial }}{\mathrm{\partial }{A}_m}\left(\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_j}\right)=0.$(23)

Also,

(24) $\frac{\mathrm{\partial }{A}_{m{ }^{\mathrm{\prime }}}}{\mathrm{\partial }{A}_m}=\left\{\begin{array}{c}1,m=m{ }^{\mathrm{\prime }}\\ 0,m\ne m{ }^{\mathrm{\prime }},\end{array}\right.$(24)

and in either case,

(25) $\frac{\mathrm{\partial }}{\mathrm{\partial }{A}_m}\left(\frac{\mathrm{\partial }{A}_{m{ }^{\mathrm{\prime }}}}{\mathrm{\partial }{N}_j}\right)=0.$(25)

Using Eqs. (23)(23) $\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{A}_m}=\frac{\mathrm{\partial }}{\mathrm{\partial }{A}_m}\left(\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_j}\right)=0.$(23) , (24(24) $\frac{\mathrm{\partial }{A}_{m{ }^{\mathrm{\prime }}}}{\mathrm{\partial }{A}_m}=\left\{\begin{array}{c}1,m=m{ }^{\mathrm{\prime }}\\ 0,m\ne m{ }^{\mathrm{\prime }},\end{array}\right.$(24) ), and (25(25) $\frac{\mathrm{\partial }}{\mathrm{\partial }{A}_m}\left(\frac{\mathrm{\partial }{A}_{m{ }^{\mathrm{\prime }}}}{\mathrm{\partial }{N}_j}\right)=0.$(25) ) in Eq. (22)(22) $\begin{array}{l}\frac{{\partial }^2{R}_z}{\partial N_j\partial N_i}={\displaystyle \sum _{m=1}^M\frac{\partial }{\partial A_m}}\left({\displaystyle \sum _{m^{\prime }=1}^M\frac{\partial R_z}{\partial A_{m^{\prime }}}\frac{\partial A_{m^{\prime }}}{\partial N_j}+\frac{R_z}{Q_z}\frac{\partial Q_z}{\partial N_j}}\right)\frac{\partial A_m}{\partial N_i}+\frac{1}{Q_z}\left(\sum _{m^{\prime }=1}^M\frac{\partial R_z}{\partial A_{m^{\prime }}}\frac{\partial A_{m^{\prime }}}{\partial N_j}+\frac{R_z}{Q_z}\frac{\partial Q_z}{\partial N_j}\right)\frac{\partial Q_z}{\partial N_i}\\ +{\displaystyle \sum _{m=1}^M\frac{\partial R_z}{\partial A_m}\frac{{\partial }^2{A}_m}{\partial N_i\partial N_j}}-\frac{R_z}{Q_z{}^2}\frac{\partial Q_z}{\partial N_j}\frac{\partial Q_z}{\partial N_i}+\frac{R_z}{Q_z}\frac{{\partial }^2{Q}_z}{\partial N_i\partial N_j}\\ =\sum _{m=1}^M[{\displaystyle \sum _{m^{\prime }=1}^M\frac{{\partial }^2{R}_z}{\partial A_m\partial A_{m^{\prime }}}\frac{\partial A_{m^{\prime }}}{\partial N_j}}+\sum _{m^{\prime }=1}^M\frac{\partial R_z}{\partial A_{m^{\prime }}}\frac{\partial }{\partial A_m}\left(\frac{\partial A_{m^{\prime }}}{\partial N_j}\right)\\ +\frac{1}{Q_z}\frac{\partial R_z}{\partial A_m}\frac{\partial Q_z}{\partial N_j}-\frac{R_z}{Q_z{}^2}\frac{\partial Q_z}{\partial A_m}\frac{\partial Q_z}{N_j}+\frac{R_z}{Q_z}\frac{\partial }{\partial A_m}\left(\frac{\partial Q_z}{\partial N_j}\right)]\frac{\partial A_m}{\partial N_i}+\frac{1}{Q_z}\left({\displaystyle \sum _{m^{\prime }=1}^M\frac{\partial R_z}{\partial A_{m^{\prime }}}\frac{\partial A_{m^{\prime }}}{\partial N_j}}\right)\frac{\partial Q_z}{\partial N_i}\\ +{\displaystyle \sum _{m=1}^M\frac{\partial R_z}{\partial A_m}\frac{{\partial }^2{A}_m}{\partial N_i\partial N_j}}+\frac{R_z}{Q_z}\frac{{\partial }^2{Q}_z}{\partial N_i\partial N_j}.(22)\end{array}$(22) yields

(26) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^2{R}_z}{\mathrm{\partial }{N}_j\mathrm{\partial }{N}_i}=\sum _{m=1}^M\left(\sum _{m^{\mathrm{\prime }}=1}^M\frac{{\mathrm{\partial }}^2{R}_z}{\mathrm{\partial }{A}_m\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}\frac{\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}{\mathrm{\partial }{N}_j}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\frac{1}{Q_z}\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_j}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}\right)+\frac{1}{Q_z}\left(\sum _{m^{\mathrm{\prime }}=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}\frac{\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}{\mathrm{\partial }{N}_j}\right)\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}\\ & +\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{{\mathrm{\partial }}^2{A}_m}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}+\frac{R_z}{Q_z}\frac{{\mathrm{\partial }}^2{Q}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.& (26)\end{array}$(26)

Using Eq. (26)(26) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^2{R}_z}{\mathrm{\partial }{N}_j\mathrm{\partial }{N}_i}=\sum _{m=1}^M\left(\sum _{m^{\mathrm{\prime }}=1}^M\frac{{\mathrm{\partial }}^2{R}_z}{\mathrm{\partial }{A}_m\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}\frac{\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}{\mathrm{\partial }{N}_j}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\frac{1}{Q_z}\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_j}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}\right)+\frac{1}{Q_z}\left(\sum _{m^{\mathrm{\prime }}=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}\frac{\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}{\mathrm{\partial }{N}_j}\right)\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}\\ & +\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{{\mathrm{\partial }}^2{A}_m}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}+\frac{R_z}{Q_z}\frac{{\mathrm{\partial }}^2{Q}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.& (26)\end{array}$(26) in Eq. (20)(20) $S_{R_z,N_i,N_j}^{(2)}=\frac{N_i{N}_j}{R_z}\frac{{\mathrm{\partial }}^2{R}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.$(20) yields

(27) $\begin{array}{rl}& S_{R_z,N_i,N_j}^{(2)}=\frac{N_i{N}_j}{R_z}\left(\sum _{m=1}^M\sum _{m^{\mathrm{\prime }}=1}^M\frac{{\mathrm{\partial }}^2{R}_z}{\mathrm{\partial }{A}_m\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}\frac{\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}{\mathrm{\partial }{N}_j}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{{\mathrm{\partial }}^2{A}_m}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}\right)+\frac{N_i}{R_z}\frac{N_j}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_j}\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}\\ & +\frac{N_j}{R_z}\frac{N_i}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_j}+\frac{N_i{N}_j}{Q_z}\frac{{\mathrm{\partial }}^2{Q}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.& (27)\end{array}$(27)

Using Eqs. (12)(12) $S_{R_z(A),N_i}\equiv \frac{N_i}{R_z}\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}$(12) and (13(13) $S_{Q_z,N_i}\equiv \frac{N_i}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}.$(13) ) in the second and third terms on the right side of Eq. (27)(27) $\begin{array}{rl}& S_{R_z,N_i,N_j}^{(2)}=\frac{N_i{N}_j}{R_z}\left(\sum _{m=1}^M\sum _{m^{\mathrm{\prime }}=1}^M\frac{{\mathrm{\partial }}^2{R}_z}{\mathrm{\partial }{A}_m\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}\frac{\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}{\mathrm{\partial }{N}_j}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{{\mathrm{\partial }}^2{A}_m}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}\right)+\frac{N_i}{R_z}\frac{N_j}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_j}\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}\\ & +\frac{N_j}{R_z}\frac{N_i}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_j}+\frac{N_i{N}_j}{Q_z}\frac{{\mathrm{\partial }}^2{Q}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.& (27)\end{array}$(27) yields

(28) $\begin{array}{rl}& S_{R_z,N_i,N_j}^{(2)}=\frac{N_i{N}_j}{R_z}\left(\sum _{m=1}^M\sum _{m^{\mathrm{\prime }}=1}^M\frac{{\mathrm{\partial }}^2{R}_z}{\mathrm{\partial }{A}_m\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}\frac{\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}{\mathrm{\partial }{N}_j}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{{\mathrm{\partial }}^2{A}_m}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}\right)+S_{Q_z,N_j}{S}_{R_z(A),N_i}\\ & +S_{Q_z,N_i}{S}_{R_z(A),N_j}+\frac{N_i{N}_j}{Q_z}\frac{{\mathrm{\partial }}^2{Q}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.& (28)\end{array}$(28)

Again, define the sensitivity contributions due purely to the transport operator and the source separately as

(29) $S_{R_z(A),N_i,N_j}^{(2)}\equiv \frac{N_i{N}_j}{R_z}\left(\sum _{m=1}^M\sum _{m{ }^{\mathrm{\prime }}=1}^M\frac{{\mathrm{\partial }}^2{R}_z}{\mathrm{\partial }{A}_m\mathrm{\partial }{A}_{m{ }^{\mathrm{\prime }}}}\frac{\mathrm{\partial }A{ }_{m^{\mathrm{\prime }}}}{\mathrm{\partial }{N}_j}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{{\mathrm{\partial }}^2{A}_m}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}\right)$(29)

and

(30) $S_{Q_z,N_i,N_j}^{(2)}\equiv \frac{N_i{N}_j}{Q_z}\frac{{\mathrm{\partial }}^2{Q}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.$(30)

Equation (28)(28) $\begin{array}{rl}& S_{R_z,N_i,N_j}^{(2)}=\frac{N_i{N}_j}{R_z}\left(\sum _{m=1}^M\sum _{m^{\mathrm{\prime }}=1}^M\frac{{\mathrm{\partial }}^2{R}_z}{\mathrm{\partial }{A}_m\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}\frac{\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}{\mathrm{\partial }{N}_j}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{{\mathrm{\partial }}^2{A}_m}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}\right)+S_{Q_z,N_j}{S}_{R_z(A),N_i}\\ & +S_{Q_z,N_i}{S}_{R_z(A),N_j}+\frac{N_i{N}_j}{Q_z}\frac{{\mathrm{\partial }}^2{Q}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.& (28)\end{array}$(28) becomes

(31) $S_{R_z,N_i,N_j}^{(2)}=S_{R_z(A),N_i,N_j}^{(2)}+S_{Q_z,N_j}{S}_{R_z(A),N_i}+S_{Q_z,N_i}{S}_{R_z(A),N_j}+S_{Q_z,N_i,N_j}^{(2)}.$(31)

The second-order relative sensitivity $S_{R,N_i,N_j}^{(2)}$ of the total response R with respect to densities $N_i$ and $N_j$ is

$\begin{array}{rl}& S_{R,N_i,N_j}^{(2)}=\frac{N_i{N}_j}{R}\frac{{\mathrm{\partial }}^{2}R}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}\\ & =\sum _{z=1}^Z{R}_z\text{overR}{S}_{R_z,N_i,N_j}^{(2)}.& (32)\end{array}$

It will be convenient to define the sensitivity contribution due to the transport operator on the total response R as

(33) $S_{R(A),N_i,N_j}^{(2)}\equiv \sum _{z=1}^Z\frac{R_z}{R}{S}_{R_z(A),N_i,N_j}^{(2)}.$(33)

Whenever the source rate density $Q_z$ due to nuclide i is proportional to the density of nuclide i only (with no dependence on nuclide j), such as for a spontaneous fission source, Eq. (30)(30) $S_{Q_z,N_i,N_j}^{(2)}\equiv \frac{N_i{N}_j}{Q_z}\frac{{\mathrm{\partial }}^2{Q}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.$(30) becomes

(34) $S_{Q_z,N_i,N_j}^{(2)}=0.$(34)

The second derivative of an (α,n) source rate density with respect to each pair of source material nuclide densities is given in Ref. 23. Unlike with spontaneous fission sources, the mixed partial derivatives in $S_{Q_z,N_i,N_j}^{(2)}$ are not zero. The second derivative of an (α,n) source rate density with respect to the material density is zero (Ref. 23).

V. COMPUTING THE SOURCE SENSITIVITY

The Taylor series perturbation capability provides a Monte Carlo estimate of $S_{R(A),N_i}$ of Eq. (16)(16) $S_{R(A),N_i}\equiv \sum _{z=1}^Z\frac{R_z}{R}{S}_{R_z(A),N_i}.$(16) and $S_{R(A),N_i,N_j}^{(2)}$ of Eq. (33(33) $S_{R(A),N_i,N_j}^{(2)}\equiv \sum _{z=1}^Z\frac{R_z}{R}{S}_{R_z(A),N_i,N_j}^{(2)}.$(33) ) (but MCNP6 and MCBEND can only compute the special case of i = j, while MCSEN has no second-order capability). The prescription for computing $S_{R(A),N_i}$ with the MCNP6 PERT capability is given in Ref. 5; the prescription for computing $S_{R(A),N_i,N_i}^{(2)}$ with the MCNP6 PERT capability is given in Appendix A. TRIPOLI-4 also requires postprocessing to compute sensitivities.²⁴ MCBEND outputs sensitivities directly.

Neither MCNP6 nor MCSEN nor TRIPOLI-4 nor MCBEND provides an estimate of $S_{Q_z,N_i}$ of Eq. (13)(13) $S_{Q_z,N_i}\equiv \frac{N_i}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}.$(13) or $S_{Q_z,N_i,N_j}^{(2)}$ of Eq. (30)(30) $S_{Q_z,N_i,N_j}^{(2)}\equiv \frac{N_i{N}_j}{Q_z}\frac{{\mathrm{\partial }}^2{Q}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.$(30) . However, Eqs. (13)(13) $S_{Q_z,N_i}\equiv \frac{N_i}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}.$(13) and (30(30) $S_{Q_z,N_i,N_j}^{(2)}\equiv \frac{N_i{N}_j}{Q_z}\frac{{\mathrm{\partial }}^2{Q}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.$(30) ) can be computed in postprocessing using data from the intrinsic source calculation, i.e., MISC, SOURCES4C, or a similar code. References 22 and 23 discuss these calculations for spontaneous fission and (α,n) neutron sources.

Equations (15)(15) $S_{R,N_i}=\sum _{z=1}^Z\frac{R_z}{R}{S}_{R_z(A),N_i}+\sum _{z=1}^Z\frac{R_z}{R}{S}_{Q_z,N_i}.$(15) and (32$\begin{array}{rl}& S_{R,N_i,N_j}^{(2)}=\frac{N_i{N}_j}{R}\frac{{\mathrm{\partial }}^{2}R}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}\\ & =\sum _{z=1}^Z{R}_z\text{overR}{S}_{R_z,N_i,N_j}^{(2)}.& (32)\end{array}$) also require source z’s relative contribution to the total response $R_z/R$. Using MCNP6 and the latest version⁷ of MCSEN, this quantity can be computed using the “special tally treatment” or FT card with the SCX keyword that “identifies the sampled index of a specified source distribution.”⁴ The way to do this is to set up a unique distribution for each of the source contributions $Q_z$, $z=1,\dots ,Z$. Let one source variable be sampled from a set of Z distributions using the “s” option on the SI card, and the probabilities on the SP card would be the total strengths of each of the Z sources. Source biasing can be specified using the SB card. Let the other source variables be dependent distributions, unless they are all the same for all Z sources. The “FT SCX” card then contains the distribution number given on the SI card. An example is given in Sec. VI.

TRIPOLI-4 can compute R_Z using the “Green’s function” feature.²⁵ MCBEND can also compute R_Z (Ref. 11).

VI. EXAMPLE PROBLEM

The example problem is a small homogeneous bare PuO₂ sphere with a radius of 4.4 cm. The composition is shown in Table I. The material mass density is 9.533052 g/cm³. (The conversion from masses to atom densities was made using nuclear data that differ slightly from those used by MCNP6, but all materials in the MCNP6 calculations were specified using atom densities.)

TABLE I Composition of PuO₂ Material

Component	Mass (g)	Atom Density (/b/cm)
^238Pu	1.982149	1.405313514E-05
^239Pu	2990.000000	2.110973593E-02
^240Pu	5.033104	3.538601590E-05
^242Pu	2.984747	2.081093907E-05
^16O	400.476171	4.225704060E-02
^17O	0.163623	1.624508343E-05
^18O	0.923840	8.662630124E-05
Total	3401.563634	6.353989800E-02

In this material, there are 12 contributions to the neutron source. Spontaneous fission and (α,n) neutron source rate densities were computed using a modified version of SOURCES4C (Ref. 21) that outputs the quantities needed to compute nuclide density derivatives in postprocessing.^22,23 The modified version also prints more digits in the output. The 12 source rate densities and the total are shown in Table II.

TABLE II Neutron Sources and Responses in the PuO₂ Material

z	Component	Qz (/cm^3/s)	Rz (/s)^a
1	^238Pu (α,n) on ^17O	6.2435E+00	3.3496E+03
2	^239Pu (α,n) on ^17O	2.6202E+01	1.4075E+04
3	^240Pu (α,n) on ^17O	1.6229E-01	8.7173E+01
4	^242Pu (α,n) on ^17O	1.3623E-03	7.3262E-01
5	^238Pu (α,n) on ^18O	7.2428E+01	3.8882E+04
6	^239Pu (α,n) on ^18O	3.1103E+02	1.6689E+05
7	^240Pu (α,n) on ^18O	1.9534E+00	1.0480E+03
8	^242Pu (α,n) on ^18O	1.6692E-02	8.9546E+00
9	^238Pu spontaneous fission	1.4447E+01	7.6624E+03
10	^239Pu spontaneous fission	1.2462E-01	6.6151E+01
11	^240Pu spontaneous fission	1.4738E+01	7.8047E+03
12	^242Pu spontaneous fission	1.4469E+01	7.6659E+03
	Total	4.6182E+02	2.4754E+05

^aThe relative uncertainty is 0.004% for all components and 0.003% for the total.

The quantity of interest was the neutron leakage from the sphere. The leakage was calculated using a version of MCNP6 that was slightly modified to print more digits in the relative uncertainty.

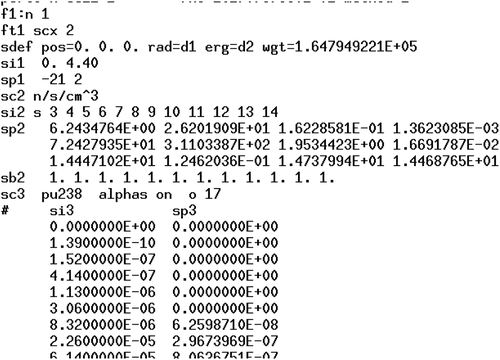
The tally contributions $R_z$, $z=1,\dots ,Z$, were computed as shown in Fig. 1. The energy ERG is given on distribution 2. The “s” option on the SI2 card means that each of the Z = 12 entries is a distribution. The probabilities on the SP2 card are the source rate densities for the 12 sources as given by SOURCES4C, copied from the tape7 file of the SOURCES4C output.²¹ (The source rate densities rather than source rates are used here because all of the sources are in the same volume.) The total source weight WGT is the sum of the source rate densities multiplied by the source volume.^a Each of the distributions 3 through 14 is the spectrum for one of the 12 sources, also copied from the tape7 file.

Fig. 1. Snippet of MCNP6 input file showing the tally and part of the source definition.

The tally, shown at the top of Fig. 1, is a current (F1) tally with an FT SCX treatment for distribution 2. The result is that the output shows the contribution from each of the 12 distributions on the SI2 card and the total. These 13 values are shown in Table II.

The relative sensitivity $S_{Q_z,N_i}$ of Eq. (13)(13) $S_{Q_z,N_i}\equiv \frac{N_i}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}.$(13) is shown for each of the I = 7 nuclides and Z = 12 sources in Table III. The relative sensitivity $S_{Q_z,N}$ of $Q_z$ to the total material density $N=\sum _{i=1}^I{N}_i$ is also shown; it is equal to 1 (Ref. 22). Also note that $S_{Q_z,N}=\sum _{i=1}^I{S}_{Q_z,N_i}$, within round-off errors.

TABLE III Source Sensitivities $S_{Q_z,N_i}$ and $S_{Q_z,N}$ (%/%) for the PuO₂ Material

z	^238Pu	^239Pu	^240Pu	^242Pu	^16O	^17O	^18O	Material
1	9.9972E-01	−6.9225E-01	−1.1604E-03	−6.8245E-04	−3.0489E-01	1.0001E+00	−6.2502E-04	1
2	−4.5975E-04	3.0939E-01	−1.1577E-03	−6.8083E-04	−3.0635E-01	9.9988E-01	−6.2801E-04	1
3	−4.5977E-04	−6.9064E-01	9.9884E-01	−6.8086E-04	−3.0632E-01	9.9988E-01	−6.2794E-04	1
4	−4.5899E-04	−6.8946E-01	−1.1557E-03	9.9932E-01	−3.0750E-01	9.9988E-01	−6.3037E-04	1
5	9.9966E-01	−6.9264E-01	−1.1611E-03	−6.8284E-04	−3.0443E-01	−1.1704E-04	9.9950E-01	1
6	−4.6019E-04	3.0879E-01	−1.1588E-03	−6.8148E-04	−3.0575E-01	−1.1754E-04	9.9943E-01	1
7	−4.6015E-04	−6.9121E-01	9.9886E-01	−6.8143E-04	−3.0576E-01	−1.1754E-04	9.9939E-01	1
8	−4.5957E-04	−6.9034E-01	−1.1572E-03	9.9934E-01	−3.0664E-01	−1.1788E-04	9.9939E-01	1
9	1	0	0	0	0	0	0	1
10	0	1	0	0	0	0	0	1
11	0	0	1	0	0	0	0	1
12	0	0	0	1	0	0	0	1

The relative sensitivities $S_{R(A),N_i}$ of Eq. (12)(12) $S_{R_z(A),N_i}\equiv \frac{N_i}{R_z}\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}$(12) are computed using the MCNP6 PERT capability according to the prescription given in Ref. 5. Sensitivities are shown in Table IV and compared with adjoint-based values computed using the multigroup discrete ordinates code^26,27 SENSMG with 30 energy groups, S₂₅₆ quadrature, and P₃ scattering. SENSMG uses PARTISN (Ref. 28) for the transport. Exact agreement is not expected because the simulation methods are different (i.e., continuous energy and continuous angle versus multigroup discrete ordinates), but the agreement achieved is excellent (there is a particularly large difference for ¹⁶O, probably because the 30-group cross sections were generated with a smooth weight function that does not account for the resonance and window behavior of ¹⁶O^b ). The 12 source spectra in the MCNP6 calculation are given in the same 30 energy groups used in the SENSMG calculation. (SENSMG, not MCNP, was used to convert masses to atom densities in Table I.)

TABLE IV Transport Sensitivities $S_{R(A),N_i}$ and $S_{R(A),N}$ (%/%)

	PERT^a	SENSMG
^238Pu	4.0703E-04 ± 1.03E-06	4.0697E-04
^239Pu	5.5362E-01 ± 6.30E-05	5.5514E-01
^240Pu	7.1056E-04 ± 1.46E-06	7.0953E-04
^242Pu	3.6284E-04 ± 1.08E-06	3.6202E-04
^16O	3.3695E-02 ± 2.03E-05	3.5749E-02
^17O	−6.2082E-07 ± 2.92E-07	−6.4448E-08
^18O	1.3482E-04 ± 1.15E-06	1.3326E-04
Material	5.8893E-01 ± 6.95E-05	5.9250E-01

^a1σ Monte Carlo uncertainties, propagated without accounting for correlations, are shown.

The relative sensitivities $S_{Q_z,N_i}$ of Eq. (13)(13) $S_{Q_z,N_i}\equiv \frac{N_i}{Q_z}\frac{\mathrm{\partial }{Q}_z}{\mathrm{\partial }{N}_i}.$(13) are computed using values from Table II and Table III. Sensitivities are shown in Table V and compared with values computed using SENSMG. The agreement achieved is excellent.

TABLE V Source Sensitivities $\sum _{z=1}^Z\frac{R_z}{R}{S}_{Q_z,N_i}$ and $\sum _{z=1}^Z\frac{R_z}{R}{S}_{Q_z,N}$ (%/%)

	This Paper, Eq. (16(16) $S_{R(A),N_i}\equiv \sum _{z=1}^Z\frac{R_z}{R}{S}_{R_z(A),N_i}.$(16) )	SENSMG
^238Pu	2.0116E-01	2.0115E-01
^239Pu	1.0469E-01	1.0468E-01
^240Pu	3.5064E-02	3.5068E-02
^242Pu	3.0389E-02	3.0392E-02
^16O	−2.7691E-01	−2.7689E-01
^17O	7.0640E-02	7.0629E-02
^18O	8.3503E-01	8.3497E-01
Material	1.0000E+00	1.0000E+00

Finally, the relative sensitivities $S_{R,N_i}$ of Eq. (6)(6) $S_{R,N_i}=\frac{N_i}{R}\frac{\mathrm{\partial }R}{\mathrm{\partial }{N}_i}.$(6) , which are the goal of this paper, are computed using the sensitivities in Table IV and Table V. Sensitivities are shown in Table VI and compared with values computed using SENSMG. The agreement achieved is excellent.

TABLE VI Total Sensitivities $S_{R,N_i}$ and $S_{R,N}$ (%/%)

	This Paper, Eq. (15)(15) $S_{R,N_i}=\sum _{z=1}^Z\frac{R_z}{R}{S}_{R_z(A),N_i}+\sum _{z=1}^Z\frac{R_z}{R}{S}_{Q_z,N_i}.$(15) ^a	SENSMG
^238Pu	2.0157E-01 ± 1.03E-06	2.0156E-01
^239Pu	6.5831E-01 ± 6.30E-05	6.5982E-01
^240Pu	3.5775E-02 ± 1.46E-06	3.5778E-02
^242Pu	3.0752E-02 ± 1.08E-06	3.0754E-02
^16O	−2.4322E-01 ± 2.03E-05	−2.4114E-01
^17O	7.0640E-02 ± 2.92E-07	7.0629E-02
^18O	8.3516E-01 ± 1.15E-06	8.3510E-01
Material	1.5889E+00 ± 6.95E-05	1.5925E+00

^a1σ Monte Carlo uncertainties, propagated without accounting for correlations, are shown.

The relative sensitivity $S_{Q_z,N_i,N_i}^{(2)}$ of Eq. (30)(30) $S_{Q_z,N_i,N_j}^{(2)}\equiv \frac{N_i{N}_j}{Q_z}\frac{{\mathrm{\partial }}^2{Q}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.$(30) is shown for each of the I = 7 nuclides and Z = 12 sources in Table VII. The relative sensitivity $S_{Q_z,N,N}^{(2)}$, where again $N=\sum _{i=1}^I{N}_i$ is the total material atom density, is also shown; it is equal to 0 (Ref. 23). Table VIII shows each of the three terms in Eq. (28)(28) $\begin{array}{rl}& S_{R_z,N_i,N_j}^{(2)}=\frac{N_i{N}_j}{R_z}\left(\sum _{m=1}^M\sum _{m^{\mathrm{\prime }}=1}^M\frac{{\mathrm{\partial }}^2{R}_z}{\mathrm{\partial }{A}_m\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}\frac{\mathrm{\partial }{A}_{m^{\mathrm{\prime }}}}{\mathrm{\partial }{N}_j}\frac{\mathrm{\partial }{A}_m}{\mathrm{\partial }{N}_i}+\sum _{m=1}^M\frac{\mathrm{\partial }{R}_z}{\mathrm{\partial }{A}_m}\frac{{\mathrm{\partial }}^2{A}_m}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}\right)+S_{Q_z,N_j}{S}_{R_z(A),N_i}\\ & +S_{Q_z,N_i}{S}_{R_z(A),N_j}+\frac{N_i{N}_j}{Q_z}\frac{{\mathrm{\partial }}^2{Q}_z}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}.& (28)\end{array}$(28) .

TABLE VII Source Sensitivities $S_{Q_z,N_i,N_i}^{(2)}$ and $S_{Q_z,N,N}^{(2)}$ (%/%) for the PuO₂ Material

z	^238Pu	^239Pu	^240Pu	^242Pu	^16O	^17O	^18O	Material
1	−9.2126E-04	9.5829E-01	2.6927E-06	9.3135E-07	1.8593E-01	−2.3439E-04	7.8135E-07	0
2	4.2276E-07	−4.2730E-01	2.6805E-06	9.2711E-07	1.8773E-01	−2.3551E-04	7.8894E-07	0
3	4.2280E-07	9.5400E-01	−2.3127E-03	9.2719E-07	1.8770E-01	−2.3549E-04	7.8879E-07	0
4	4.2135E-07	9.5074E-01	2.6715E-06	−1.3585E-03	1.8914E-01	−2.3640E-04	7.9486E-07	0
5	−9.2178E-04	9.5943E-01	2.6959E-06	9.3246E-07	1.8538E-01	2.7397E-08	−1.2474E-03	0
6	4.2353E-07	−4.2686E-01	2.6854E-06	9.2880E-07	1.8698E-01	2.7634E-08	−1.2528E-03	0
7	4.2349E-07	9.5557E-01	−2.3147E-03	9.2871E-07	1.8701E-01	2.7638E-08	−1.2528E-03	0
8	4.2242E-07	9.5315E-01	2.6783E-06	−1.3602E-03	1.8807E-01	2.7796E-08	−1.2564E-03	0
9	0	0	0	0	0	0	0	0
10	0	0	0	0	0	0	0	0
11	0	0	0	0	0	0	0	0
12	0	0	0	0	0	0	0	0

TABLE VIII Second-Order Sensitivities (%/%)

	$\sum _{z=1}^Z\frac{R_z}{R}{S}_{Q_z,N_i,N_i}^{(2)}$	$S_{R(A),N_i,N_i}^{(2)}$^a	$2\sum _{z=1}^Z\frac{R_z}{R}{S}_{Q_z,N_i}{S}_{R_z(A),N_i}$^a	This Paper, Eq. (32)$\begin{array}{rl}& S_{R,N_i,N_j}^{(2)}=\frac{N_i{N}_j}{R}\frac{{\mathrm{\partial }}^{2}R}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}\\ & =\sum _{z=1}^Z{R}_z\text{overR}{S}_{R_z,N_i,N_j}^{(2)}.& (32)\end{array}$^a	Central Difference
^238Pu	−1.5694E-04	3.3920E-07 ± 6.4E-08	1.6468E-04 ± 4.8E-07	8.0780E-06 ± 4.8E-07	7.3940E-06
^239Pu	−1.4400E-01	7.3497E-01 ± 2.4E-04	1.1600E-01 ± 4.2E-05	7.0697E-01 ± 2.4E-04	7.1424E-01
^240Pu	−8.1913E-06	9.8253E-07 ± 1.3E-07	4.6449E-05 ± 1.3E-07	3.9240E-05 ± 1.9E-07	3.9293E-05
^242Pu	7.8901E-07	1.8129E-07 ± 7.6E-08	2.0497E-05 ± 9.5E-08	2.1468E-05 ± 1.2E-07	2.1438E-05
^16O	1.6924E-01	1.7205E-03 ± 3.7E-05	−1.8524E-02 ± 1.2E-05	1.5243E-01 ± 3.9E-05	1.5373E-01
^17O	−1.6623E-05	−3.4121E-09 ± 3.4E-09	−7.3217E-08 ± 4.9E-08	−1.6700E-05 ± 4.9E-08	−1.6666E-05
^18O	−1.0458E-03	−9.7068E-08 ± 9.7E-08	2.2742E-04 ± 2.3E-06	−8.1851E-04 ± 2.3E-06	−8.2100E-04
Material	0.0000E+00	9.0333E-01 ± 3.1E-04	1.1779E+00 ± 1.4E-04	2.0812E+00 ± 3.4E-04	2.1130E+00

^a1σ Monte Carlo uncertainties, propagated without accounting for correlations, are shown.

The total second-order sensitivity for each nuclide and the material are compared in Table VIII with central-difference estimates made using SENSMG. In the first column of results, $R_z/R$ comes from Table II, and $S_{Q_z,N_i,N_i}^{(2)}$ comes from Table VII. The second column comes from an MCNP6 PERT calculation using METHOD = 3 and Eq. (A.17)(A.17) $S_{c,{\sigma }_x,{\sigma }_x}^{(2)}=\frac{2\mathrm{\Delta }{c}_2}{c_0}.$(A.17) (which assumes $p_{x,r}$ = 1) from Appendix A. In the third column, $R_z/R$ comes from Table II, $S_{Q_z,N_i}$ comes from Table III, and $S_{R_z(A),N_i}$ comes from Table IV. The fourth column of results is the sum of the first, second, and third columns. The central-difference estimate of a second derivative using first derivatives is

(35) $\begin{array}{rl}& {\left(\frac{{\mathrm{\partial }}^{2}R}{\mathrm{\partial }{N}_i^2}\right)}_{CD}=\frac{{\displaystyle {\left.\frac{\mathrm{\partial }R}{\mathrm{\partial }{N}_i}\right|}_{N_i=N_{i,0}+\mathrm{\Delta }{N}_i}-{\left.\frac{\mathrm{\partial }R}{\mathrm{\partial }{N}_i}\right|}_{N_i=N_{i,0}-\mathrm{\Delta }{N}_i}}}{(N_{i,0}+\mathrm{\Delta }{N}_i)-(N_{i,0}-\mathrm{\Delta }{N}_i)}\\ & =\frac{1}{2\mathrm{\Delta }{N}_i}\left({\left.\frac{\mathrm{\partial }R}{\mathrm{\partial }{N}_i}\right|}_{N_i=N_{i,0}+\mathrm{\Delta }{N}_i}-{\left.\frac{\mathrm{\partial }R}{\mathrm{\partial }{N}_i}\right|}_{N_i=N_{i,0}-\mathrm{\Delta }{N}_i}\right).\end{array}$(35)

The first derivatives in Eq. (35)(35) $\begin{array}{rl}& {\left(\frac{{\mathrm{\partial }}^{2}R}{\mathrm{\partial }{N}_i^2}\right)}_{CD}=\frac{{\displaystyle {\left.\frac{\mathrm{\partial }R}{\mathrm{\partial }{N}_i}\right|}_{N_i=N_{i,0}+\mathrm{\Delta }{N}_i}-{\left.\frac{\mathrm{\partial }R}{\mathrm{\partial }{N}_i}\right|}_{N_i=N_{i,0}-\mathrm{\Delta }{N}_i}}}{(N_{i,0}+\mathrm{\Delta }{N}_i)-(N_{i,0}-\mathrm{\Delta }{N}_i)}\\ & =\frac{1}{2\mathrm{\Delta }{N}_i}\left({\left.\frac{\mathrm{\partial }R}{\mathrm{\partial }{N}_i}\right|}_{N_i=N_{i,0}+\mathrm{\Delta }{N}_i}-{\left.\frac{\mathrm{\partial }R}{\mathrm{\partial }{N}_i}\right|}_{N_i=N_{i,0}-\mathrm{\Delta }{N}_i}\right).\end{array}$(35) were adjoint-based values computed using SENSMG. Density perturbations were 5% for ²³⁹Pu, ¹⁸O, and the full material; 25% for ²³⁸Pu; and 10% for all other nuclides. Exact agreement is not expected because the simulation methods are different (i.e., continuous energy and continuous angle versus multigroup discrete ordinates), but overall, the agreement achieved is excellent. There is a large difference in the second derivative for ²³⁸Pu. It is a very small value, and the difference is likely due to propagating round-off errors; in any case, it is within 2σ of the value from Eq. (32)$\begin{array}{rl}& S_{R,N_i,N_j}^{(2)}=\frac{N_i{N}_j}{R}\frac{{\mathrm{\partial }}^{2}R}{\mathrm{\partial }{N}_i\mathrm{\partial }{N}_j}\\ & =\sum _{z=1}^Z{R}_z\text{overR}{S}_{R_z,N_i,N_j}^{(2)}.& (32)\end{array}$.

To reiterate, mixed second-order derivatives of an (α,n) source rate density with respect to source material nuclide densities are not zero (Ref. 23), but no mixed second-order sensitivities are shown in this section because the MCNP6 PERT capability cannot compute them.¹⁰

Now that first- and second-order sensitivities of the leakage with respect to nuclide and material densities are known for this problem (Table VI and Table IX, respectively), it is interesting to look at them. The relative first- and second-order Taylor series terms—that is, $\mathrm{\Delta }{c}_1$ and $\mathrm{\Delta }{c}_2$, given in Appendix A, divided by the unperturbed response R—for a 1% change in the density of each nuclide and the material are shown in Table IX. For this problem, the contribution of the second-order term is minimal. In uncertainty quantification and perturbation analysis, this is often assumed, but here it is proven. Also, it may be surprising that a 1% change in the ¹⁸O density has a larger effect than a 1% change in the ²³⁹Pu density. Of course, the density of ¹⁸O cannot normally be changed independently. The effect of a 1% density change in all of the oxygen isotopes together is approximately 0.6633% (the sum of the oxygen first- and second-order terms, ignoring second-order cross terms because they were not calculated), which is almost the same as the effect of a 1% density change in ²³⁹Pu.

TABLE IX Relative Taylor Series Terms for a 1% Density Perturbation

Nuclide or Material	First Order (%)^a	Second Order (%)^a
^238Pu	0.2016 ± 0.0001	0.0000 ± 0.0000
^239Pu	0.6583 ± 0.0000	0.0035 ± 0.0000
^240Pu	0.0358 ± 0.0000	0.0000 ± 0.0000
^242Pu	0.0308 ± 0.0000	0.0000 ± 0.0000
^16O	–0.2432 ± 0.0000	0.0008 ± 0.0000
^17O	0.0706 ± 0.0000	0.0000 ± 0.0000
^18O	0.8352 ± 0.0000	0.0000 ± 0.0000
Material	1.5889 ± 0.0001	0.0104 ± 0.0000

^a1σ Monte Carlo uncertainties, propagated without accounting for correlations, are shown.

An interesting observation regarding first- and second-order sensitivities of (α,n) sources is presented in Appendix B.

VII. SUMMARY AND CONCLUSIONS

Application of the differential operator (Taylor series) perturbation capability for density sensitivities in Monte Carlo radiation transport codes has been limited because changing nuclide or material densities frequently changes the intrinsic source, and in most Monte Carlo codes, the user-input source is independent of the user-input materials. The perturbation capability has no way of accounting for changes in the intrinsic source. [MCNP6 does have an optional built-in intrinsic source generator based on the material at the sampled source point,⁴ but even when this capability is used, the differential operator perturbation method does not calculate $S_{Q_z,N_i}$ or $S_{Q_z,N_i,N_j}^{(2)}$.]

This paper derives the equations relating the precomputed intrinsic source calculation to the total first- and second-order nuclide density sensitivities. The equations require the response to be separated by contribution from each of the sources modeled. MCNP6, MCSEN, TRIPOLI-4, and MCBEND can calculate those separate responses. (MCNP6 cannot calculate the needed responses when the optional built-in intrinsic source generator is used.)

Acknowledgments

The author would like to thank Odile Petit and Andrea Zoia, Commissariat à l’Énergie Atomique-Saclay, for information about TRIPOLI-4. The author would like to thank Alan Charles, of the ANSWERS Software Service from Jacobs, for information about MCBEND, including providing a version of Ref. 1. The author would like to thank Ivan Kodeli, United Kingdom Atomic Energy Authority, for bringing MCSEN to his attention.

Disclosure Statement

No potential conflict of interest was reported by the author.

Notes

^a The source rate densities used in this calculation are from the tape6 output file. There is a slight mismatch of 0.006% between the totals in the two output files. Thus, the sum of probabilities on the SP2 card multiplied by the volume differs by 0.006% from the weight given on the SDEF card.

^b We are grateful to an anonymous referee for this explanation.

^c We are grateful to an anonymous referee for this observation.

APPENDIX A

COMPUTING THE SECOND-ORDER RELATIVE SENSITIVITY USING THE MCNP6 PERT CARD

Reference 5 derived the first-order relative sensitivity in terms of the MCNP PERT card outputs. This appendix derives the second-order relative sensitivity using the notation of Ref. 5.

A Taylor series expansion of a response c that is a function of some reaction cross section ${\sigma }_x$ is

(A.1) $c({\sigma }_x)=c({\sigma }_{x,0})+{\left.\frac{dc}{d{\sigma }_x}\right|}_{{\sigma }_{x,0}}\mathrm{\Delta }{\sigma }_x+{\left.\frac{1}{2}\frac{d^{2}c}{d{\sigma }_x^2}\right|}_{{\sigma }_{x,0}}{\left(\mathrm{\Delta }{\sigma }_x\right)}^2+\cdots ,$(A.1)

where ${\sigma }_{x,0}$ is the reference value of the cross section and

(A.2) $\mathrm{\Delta }{\sigma }_x\equiv {\sigma }_x-{\sigma }_{x,0}$(A.2)

is the perturbation. Define the first- and second-order Taylor series terms as

(A.3) $\mathrm{\Delta }{c}_1\equiv {\left.\frac{dc}{d{\sigma }_x}\right|}_{{\sigma }_{x,0}}\mathrm{\Delta }{\sigma }_x$(A.3)

and

(A.4) $\mathrm{\Delta }{c}_2\equiv {\left.\frac{1}{2}\frac{d^{2}c}{d{\sigma }_x^2}\right|}_{{\sigma }_{x,0}}{\left(\mathrm{\Delta }{\sigma }_x\right)}^2,$(A.4)

respectively. Define $p_x$ as the relative cross-section perturbation,

(A.5) $p_x\equiv \frac{\mathrm{\Delta }{\sigma }_x}{{\sigma }_{x,0}}.$(A.5)

Then, using the chain rule, the Taylor series terms can be written conveniently as

(A.6) $\mathrm{\Delta }{c}_1={\left.\frac{dc}{d{p}_x}\right|}_{p_x=0}{p}_x$(A.6)

and

(A.7) $\mathrm{\Delta }{c}_2={\left.\frac{1}{2}\frac{d^{2}c}{d{p}_x^2}\right|}_{p_x=0}{p}_x^2.$(A.7)

For notational convenience, define $c_0\equiv c({\sigma }_{x,0})$.

At present, the MCNP6 perturbation capability, invoked with the PERT card, uses a two-term Taylor expansion with no cross terms.^4,10 The perturbation feature estimates the derivatives in Eqs. (A.6)(A.6) $\mathrm{\Delta }{c}_1={\left.\frac{dc}{d{p}_x}\right|}_{p_x=0}{p}_x$(A.6) and (A.7)(A.7) $\mathrm{\Delta }{c}_2={\left.\frac{1}{2}\frac{d^{2}c}{d{p}_x^2}\right|}_{p_x=0}{p}_x^2.$(A.7) and multiplies them by the relative perturbation $p_x$ (or $p_x^2$) computed from the user input.

Define coefficients

(A.8) $c_1\equiv {\left.\frac{dc}{d{p}_x}\right|}_{p_x=0}$(A.8)

and

(A.9) $c_2\equiv {\left.\frac{1}{2}\frac{d^{2}c}{d{p}_x^2}\right|}_{p_x=0}.$(A.9)

These coefficients can be computed from any single arbitrary reference perturbation amount $p_{x,r}$ using, from Eqs. (A.6)(A.6) $\mathrm{\Delta }{c}_1={\left.\frac{dc}{d{p}_x}\right|}_{p_x=0}{p}_x$(A.6) and (A.7)(A.7) $\mathrm{\Delta }{c}_2={\left.\frac{1}{2}\frac{d^{2}c}{d{p}_x^2}\right|}_{p_x=0}{p}_x^2.$(A.7) ,

(A.10) $c_1=\frac{\mathrm{\Delta }{c}_1(p_{x,r})}{p_{x,r}}$(A.10)

and

(A.11) $c_2=\frac{\mathrm{\Delta }{c}_2(p_{x,r})}{p_{x,r}^2}.$(A.11)

The second-order relative sensitivity coefficient of a response c to some reaction cross section ${\sigma }_x$ is defined as

(A.12) $S_{c,{\sigma }_x,{\sigma }_y}^{(2)}\equiv {\left.\frac{{\sigma }_{x,0}{\sigma }_{y,0}}{c_0}\frac{d^{2}c}{d{\sigma }_{x}d{\sigma }_y}\right|}_{{\sigma }_{x,0},{\sigma }_{y,0}}.$(A.12)

Using ${\sigma }_x={\sigma }_{x,0}(1+p_x)$ in Eq. (A.12)(A.12) $S_{c,{\sigma }_x,{\sigma }_y}^{(2)}\equiv {\left.\frac{{\sigma }_{x,0}{\sigma }_{y,0}}{c_0}\frac{d^{2}c}{d{\sigma }_{x}d{\sigma }_y}\right|}_{{\sigma }_{x,0},{\sigma }_{y,0}}.$(A.12) with the chain rule yields

(A.13) $S_{c,{\sigma }_x,{\sigma }_y}^{(2)}={\left.\frac{{\sigma }_{y,0}}{c_0}\frac{d}{d{\sigma }_y}\left(\frac{dc}{d{p}_x}\right)\right|}_{{\sigma }_{y,0},p_x=0}.$(A.13)

Using ${\sigma }_y={\sigma }_{y,0}(1+p_y)$ in Eq. (A.13)(A.13) $S_{c,{\sigma }_x,{\sigma }_y}^{(2)}={\left.\frac{{\sigma }_{y,0}}{c_0}\frac{d}{d{\sigma }_y}\left(\frac{dc}{d{p}_x}\right)\right|}_{{\sigma }_{y,0},p_x=0}.$(A.13) with the chain rule yields

(A.14) $S_{c,{\sigma }_x,{\sigma }_y}^{(2)}={\left.\frac{1}{c_0}\frac{d^{2}c}{d{p}_{x}d{p}_y}\right|}_{p_x=0,p_y=0}.$(A.14)

MCNP cannot compute mixed derivatives. Setting y = x in Eq. (A.14)(A.14) $S_{c,{\sigma }_x,{\sigma }_y}^{(2)}={\left.\frac{1}{c_0}\frac{d^{2}c}{d{p}_{x}d{p}_y}\right|}_{p_x=0,p_y=0}.$(A.14) yields

(A.15) $S_{c,{\sigma }_x,{\sigma }_x}^{(2)}={\left.\frac{1}{c_0}\frac{d^{2}c}{d{p}_x^2}\right|}_{p_x=0},$(A.15)

or from Eq. (A.9)(A.9) $c_2\equiv {\left.\frac{1}{2}\frac{d^{2}c}{d{p}_x^2}\right|}_{p_x=0}.$(A.9) ,

(A.16) $S_{c,{\sigma }_x,{\sigma }_x}^{(2)}=\frac{2c_2}{c_0}.$(A.16)

The prescription to estimate the second-order sensitivity coefficient is as follows. Choose a reference perturbation $p_{x,r}$. A convenient choice is $p_{x,r}$ = 1. Set up a PERT card with the density equal to ${\sigma }_{x,r}={\sigma }_{x,0}(1+p_{x,r})$ [from Eqs. (A.2)(A.2) $\mathrm{\Delta }{\sigma }_x\equiv {\sigma }_x-{\sigma }_{x,0}$(A.2) and (A.5)(A.5) $p_x\equiv \frac{\mathrm{\Delta }{\sigma }_x}{{\sigma }_{x,0}}.$(A.5) ]. Obviously, if $p_{x,r}$ = 1, then ${\sigma }_{x,r}=2{\sigma }_{x,0}$. The PERT card uses METHOD = 3 to perform the “2nd-order perturbation calculation only and print the differential change in the unperturbed tally.”⁴ Run the problem in MCNP6. The perturbation result is $\mathrm{\Delta }{c}_2(p_{x,r})\pm s_{\mathrm{\Delta }{c}_2}$. Combining Eqs. (A.11)(A.12) $S_{c,{\sigma }_x,{\sigma }_y}^{(2)}\equiv {\left.\frac{{\sigma }_{x,0}{\sigma }_{y,0}}{c_0}\frac{d^{2}c}{d{\sigma }_{x}d{\sigma }_y}\right|}_{{\sigma }_{x,0},{\sigma }_{y,0}}.$(A.12) and (A.16)(A.16) $S_{c,{\sigma }_x,{\sigma }_x}^{(2)}=\frac{2c_2}{c_0}.$(A.16) and assuming $p_{x,r}$ = 1, the second-order sensitivity is

(A.17) $S_{c,{\sigma }_x,{\sigma }_x}^{(2)}=\frac{2\mathrm{\Delta }{c}_2}{c_0}.$(A.17)

The estimated variance of the sensitivity, assuming $c_0$ and $\mathrm{\Delta }{c}_2$ are uncorrelated (subscript unc.), is

(A.18) $s_{S_{unc.}^{(2)}}^2={\left(S_{c,{\sigma }_x,{\sigma }_x}^{(2)}\right)}^2\left[{\left(\frac{s_{c_0}}{c_0}\right)}^2+{\left(\frac{s_{\mathrm{\Delta }{c}_2}}{\mathrm{\Delta }{c}_2}\right)}^2\right],$(A.18)

where $s_{c_0}^2$ is the variance of the unperturbed tally. The quantities $s_{c_0}/c_0$ and $s_{\mathrm{\Delta }{c}_2}/\mathrm{\Delta }{c}_2$ are the usual MCNP6 outputs of the relative tally uncertainties. The exact variance of $S_{c,{\sigma }_x,{\sigma }_x}^{(2)}$ can be derived as in Ref. 5.

APPENDIX B

AN INTERESTING OBSERVATION REGARDING SENSITIVITIES OF ($\text{balpha}$,n) SOURCES

The first-order sensitivities $S_{Q_z,N_i}$ and $S_{Q_z,N}$ are given in Table III. The second-order sensitivities $S_{Q_z,N_i,N_i}^{(2)}$ and $S_{Q_z,N,N}^{(2)}$ are given in Table VII. The ratios of the second-order sensitivities to the first-order sensitivities for all (α,n) sources are shown in Table B.I. For each nuclide, they are surprisingly consistent for all (α,n) source/target combinations.^c [$S_{Q_z,N,N}^{(2)}$/$S_{Q_z,N}$ is, of course, zero for all (α,n) source/target combinations.] An analysis of this pattern—an explanation as well as its potential usefulness—is beyond the scope of this paper.

TABLE B.I $S_{Q_z,N_i,N_i}^{(2)}$/$S_{Q_z,N_i}$ for the PuO₂ Material.

z	^238Pu	^239Pu	^240Pu	^242Pu	^16O	^17O	^18O
1	−9.215E-04	−1.384E+00	−2.321E-03	−1.365E-03	−6.098E-01	−2.344E-04	−1.250E-03
2	−9.195E-04	−1.381E+00	−2.315E-03	−1.362E-03	−6.128E-01	−2.355E-04	−1.256E-03
3	−9.196E-04	−1.381E+00	−2.315E-03	−1.362E-03	−6.128E-01	−2.355E-04	−1.256E-03
4	−9.180E-04	−1.379E+00	−2.312E-03	−1.359E-03	−6.151E-01	−2.364E-04	−1.261E-03
5	−9.221E-04	−1.385E+00	−2.322E-03	−1.366E-03	−6.089E-01	−2.341E-04	−1.248E-03
6	−9.204E-04	−1.382E+00	−2.317E-03	−1.363E-03	−6.116E-01	−2.351E-04	−1.253E-03
7	−9.203E-04	−1.382E+00	−2.317E-03	−1.363E-03	−6.116E-01	−2.351E-04	−1.254E-03
8	−9.192E-04	−1.381E+00	−2.314E-03	−1.361E-03	−6.133E-01	−2.358E-04	−1.257E-03