Frequency-Dependent Discrete Implicit Monte Carlo Scheme for the Radiative Transfer Equation

Abstract

This work generalizes the discrete implicit Monte Carlo (DIMC) method for modeling the radiative transfer equation from a gray treatment to a frequency-dependent one. The classic implicit Monte Carlo (IMC) algorithm, which has been used for several decades, suffers from a well-known numerical problem, called teleportation, where the photons might propagate faster than the exact solution due to the finite size of the spatial and temporal resolution. The semi-analog Monte Carlo algorithm proposed the use of two kinds of particles, photons and material particles, that are born when a photon is absorbed. The material particle can “propagate” only by transforming into a photon due to black-body emissions. While this algorithm produces a teleportation-free result, its results are noisier compared to the IMC due to the discrete nature of the absorption-emission process.

In a previous work, Steinberg and Heizler [ApJS, Vol. 258, p. 14 (2022)] proposed a gray version of DIMC that makes use of two kinds of particles, and therefore has teleportation-free results, but also uses the continuous absorption algorithm of IMC, yielding smoother results. This work is a direct frequency-dependent (energy-dependent) generalization of the DIMC algorithm. We find in several one- and two-dimensional benchmarks that the new frequency-dependent DIMC algorithm yields teleportation-free results on one hand, and smooth results with an IMC-like noise level.

Keywords:

• Radiative transfer
• implicit Monte Carlo
• frequency-dependent approximation

I. INTRODUCTION

The radiative transfer equation (RTE) is the key equation for modeling the transport of photons that interact with matter, calculating the specific intensity of the phase-space density of photons.^1,2 Solving the RTE is crucial to understanding many astrophysical phenomena (e.g., supernova, shock breakout, etc.),^3,4 as well as the modeling of inertial confinement fusion,⁵ and in general, high energy density physics.⁶

The RTE is the Boltzmann equation for photons, where the main physical events are absorption and black-body emissions through the opacity of the material, which is usually a function of the temperature and the density of the material (under the assumption that the matter itself is in local-thermodynamic equilibrium and the electrons are distributed with the Maxwell-Boltzmann distribution with a given temperature).¹ In addition, scattering terms may be involved also, which can be elastic like the Thomson approximation or inelastic using the full Compton treatment.^1,2

The Boltzmann equation is an integrodifferential equation, where in the three dimensions the phase space contains seven independent variables: three spatial, three velocity components (usually replaced by energy and direction), and time.^1,7 A full analytic solution is rare, and can be achieved in very simplified problems. For general purposes, and specifically in higher dimensions, numerical solution are used, where the two main approaches are to solve numerically the deterministic Boltzmann equation for photons or to use statistical approaches, such as Monte Carlo techniques. The most common approximations for solving the deterministic Boltzmann equation are the spherical harmonics method (also known as the $P_N$ approximation), where the intensity is decomposed into its moments,^1,7 and the discrete ordinates method (also known as the $S_N$ method), where the intensity is solved on some discrete selected ordinates.^1,7 The statistical approaches use a particle-based Monte Carlo approach, the most common of which is the one for radiative transfer, called the implicit Monte Carlo (IMC) method, by Fleck and Cummings.^8,9

The major innovation in IMC was the implicitization of the Boltzmann equation.⁸ Since the radiation is coupled to the matter via black-body emissions, the explicit way to solve the radiation transport is to use the temperature from the beginning of the time step. In optically thin media, this assumption is reasonable, where the matter and the radiation may differ significantly. However, in optically thick media, where the radiation and matter energy may both be large but similar to each other, there is a need for very small time steps in order to keep the solution stable. Fleck and Cummings⁸ offered an implicit version of radiative Monte Carlo by finite differencing the matter energy equation and substituting it into the radiation Boltzmann equation. This enables the use of sufficiently large time steps, even in optically thick media, and enables the radiative transfer to be modeled using reasonable computer resources.

The second novelty of IMC is the use of an implicit (or continuous) absorption algorithm.^8–10 Instead of treating the mechanism of absorption as discrete statistical events, the photon deposits its energy along its track in the spatial cells. This algorithm enables significantly smoother results than the naïve explicit Monte Carlo. The IMC algorithm, with some modifications and improvements, has been used during the last five decades.^9,11–27

However, IMC suffers from a well-known numerical disadvantage, called teleportation, where the photons propagate faster than they should due to finite spatial resolution and time steps.^13,14,28 In the simplest IMC implementation, when photons reach a cold opaque cell, they are absorbed in the outer part of the cell due to the small mean free path, changing slightly the temperature of the cell. In the next time step, the photons that are emitted due to black-body emissions are sampled uniformly from the whole volume of the cell, which causes artificial propagation. Moreover, at a finite spatial resolution, this may lead to a certain “magic” time step in which the results are correct, while decreasing the time step further increases the numerical error.^28,29

One elegant way to solve this problem, called the semi-analog Monte Carlo (SMC), proposed by Ahrens and Larsen,³⁰ uses two kinds of particles, photons and matter particles. A photon propagates with the speed of light $c$ in the medium until it is absorbed, where it becomes a material particle (with zero velocity). The material particle can transform into a photon due to a black-body emission process. In this way, the creation of photons can only be from the positions where they were absorbed and the teleportation errors are avoided. Unfortunately, this scheme is explicit, and thus enforces a small time step when involving optically thick regions.

Recently, in a seminal work, Poëtte and Valentin offered an implicit version of SMC, the implicit semi-analog Monte Carlo (ISMC), that enables the use of sufficiently large time steps.²⁸ This new method offers a new implicitization technique that changes the RTE and the matter energy equation to be linear in both radiation-specific intensity and matter energy, and can be modeled via Monte Carlo techniques using photons and material particles. The method was verified against one-dimensional (1-D) gray benchmarks involving opaque media, yielding results that did not suffer from teleportation errors. Later, the ISMC method was generalized to frequency-dependent problems, yielding excellent results against many benchmarks, gray and frequency dependent, both in 1-D and two-dimensional (2-D) geometries (in both XY and RZ symmetries).²⁹

Another important work was published recently by Poëtte et al. that cancels the teleportation error within the frame of legacy (gray) IMC codes, called the no-source-sampling implicit Monte Carlo²³ (nssIMC). The work presents the very few modifications that have to be done in legacy IMC codes, where the classic source sampling is canceled, and the source events are treated as “collisions events,” thus teleportation is avoided. However, the nssIMC converges slower than the ISMC in both the spatial resolution and finite time steps (see Fig. 3 in Ref. 23). In addition, the nssIMC produces noisier results in a given resolution compared to the ISMC (see Fig. 4 in Ref. 23) and is less robust. Therefore, where the ISMC modifications are allowable, the authors recommend opting for the ISMC rather than the nssIMC.

However, both the SMC and ISMC yield noisier results compared to the IMC due to the discrete treatment of the absorption and black-body emission processes. In addition, since the total number of particles, both photons and material particles, is constant, problems that have a big difference between the heat capacities of the radiation and the material require a large statistic to converge. Recently, a new algorithm was offered, called the discrete implicit Monte Carlo³¹ (DIMC), that uses the idea of two kinds of particles on one hand, thus yielding teleportation-free results, and the algorithm of continuous (implicit) absorption on the other hand, yielding results as smooth as the IMC. This is attainable due to an algorithm that avoids the population of particles from exploding and retains the correct angular and spatial distributions.

The DIMC was derived using the IMC linearization, but this wasn’t a mandatory choice, it could have been derived via the ISMC linearization and implicitization as well. This algorithm has been tested against several gray benchmarks, both in one dimension (with or without hydrodynamics) and in two dimensions. In this work we expand the DIMC method to include frequency-dependent problems. The new frequency-dependent DIMC method is examined against all the frequency-dependent benchmarks that were tested using the ISMC in Ref. 29. We repeat the frequency-dependent benchmarks from Ref. 29, adding to each figure the comparable DIMC result.

This work is structured as follows. In Sec. II, we present the frequency-dependent version of the DIMC. In Sec. III, we present several 1-D frequency-dependent benchmarks, while in Sec. IV, we present a 2-D frequency-dependent benchmark. We finish with short conclusions in Sec. V.

II. FREQUENCY-DEPENDENT DIMC

The basic derivation is the classic derivation of the IMC implicitization and linearization. For the case of elastic (Thomson) scattering, the RTE and the coupled energy balance equation for the material energy are¹

(1a) $\begin{array}{rl}& \frac{1}{c}\frac{\mathrm{\partial }I(\mathit{r},\mathbf{\Omega },\nu ,t)}{\mathrm{\partial }t}+\mathbf{\Omega }\cdot \mathrm{\nabla }I(\mathit{r},\mathbf{\Omega },\nu ,t)=-({\sigma }_a(\nu ,T)+{\sigma }_s(\nu ,T))I(\mathit{r},\mathbf{\Omega },\nu ,t)+{\sigma }_a(\nu ,T)B(\nu ,T)\\ & +{\sigma }_s(\nu ,T){\int }_{4\pi }\frac{I_{\nu }(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }},t)}{4\pi }\mathit{d}\mathbf{\Omega }{ }^{\mathrm{\prime }}\end{array}$(1a)

and

(1b) $\frac{\mathrm{\partial }e(T)}{\mathrm{\partial }t}=c{\int }_0^{\mathrm{\infty }}\left[{\sigma }_a(\nu { }^{\mathrm{\prime }},T)\left({\int }_{4\pi }I(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }},\nu { }^{\mathrm{\prime }},t)\mathit{d}\mathbf{\Omega }{ }^{\mathrm{\prime }}-4\pi B(\nu { }^{\mathrm{\prime }},T)\right)d\nu { }^{\mathrm{\prime }}\right],$(1b)

where

$I(\mathit{r},\mathbf{\Omega },\nu ,t)$	=	= radiation-specific intensity for a unit space $\mathit{r}$, unit direction $\mathbf{\Omega }$, and unit frequency $\nu$ at time $t$
${\sigma }_a(\nu ,T)$	=	=absorption cross section (opacity), which is a function of the material temperature $T$ and the frequency
${\sigma }_s(\nu ,T)$	=	= scattering cross section
$e(T)$	=	=thermal energy per unit volume of the medium
$c$	=	= speed of light
$\begin{array}{rl}& B(\nu ,T)=\frac{2h{\nu }^3}{c^2}{\left(exp(h\nu /k_{B}T)-1\right)}^{-1}\end{array}$	=	= Planck function, where $h$ is the Planck constant and $k_B$ is the Boltzmann constant.

Note that the frequency integration over $B(\nu ,T)$ is called the frequency-integrated Planck function, which equals to $B(T)=a{T}^4/4\pi$, and $a$ is the radiation constant. We define a convenient function that is the ratio of the Planck function to the frequency integrated one $b(\nu ,T)\equiv B(\nu ,T)/B(T)=4\pi B(\nu ,T)/a{T}^4$.

The basic idea behind the IMC is to define the Fleck parameter

(2) $f=\frac{1}{1+\beta {\sigma }_{a,P}(T)c\mathrm{\Delta }t},$(2)

where $\beta \equiv \mathrm{\partial }a{T}^4/\mathrm{\partial }e$ is the ratio between the radiation and material heat capacities⁸ (which is taken at the beginning of the time step), $\mathrm{\Delta }t$ is the discretized time step, and ${\sigma }_{a,p}(T)$ is the Planck opacity ${\sigma }_{a,p}(T)\equiv {\int }_0^{\mathrm{\infty }}{\sigma }_a(\nu ,T)b_{\nu }d\nu$ (also taken at the beginning of the time step). As a matter of fact, taking the heat capacity and the opacities at the beginning of the time step prevents the classic implementation of the IMC to be a fully implicit algorithm.^16,18 Finite differencing [Eq. (1b)(1b) $\frac{\mathrm{\partial }e(T)}{\mathrm{\partial }t}=c{\int }_0^{\mathrm{\infty }}\left[{\sigma }_a(\nu { }^{\mathrm{\prime }},T)\left({\int }_{4\pi }I(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }},\nu { }^{\mathrm{\prime }},t)\mathit{d}\mathbf{\Omega }{ }^{\mathrm{\prime }}-4\pi B(\nu { }^{\mathrm{\prime }},T)\right)d\nu { }^{\mathrm{\prime }}\right],$(1b) ] and using the definition of $\beta$ yields (where the index $n$ denotes the previous time step and $n+1$ the current time step)

(3) $\begin{array}{rl}& B^{n+1}(T)=B^n(T)f+(1-f){\int }_0^{\mathrm{\infty }}{\int }_{4\pi }\frac{{\sigma }_{a,{\nu }^{\prime }}}{{\sigma }_{a,p}(T)}\frac{I(r,{\mathbf{\Omega }}^{\prime },{\nu }^{\prime },t)}{4\pi }\mathit{d}{\mathbf{\Omega }}^{\prime }d{\nu }^{\prime }\end{array}$(3)

i.e., $B^n(T)=a(T^n{)}^4/4\pi$ and $b^n(\nu ,T)\equiv B^n(\nu ,T)/B^n(T)=4\pi B^n(\nu ,T)/a(T^n{)}^4.$

Substituting Eq. (3)(3) $\begin{array}{rl}& B^{n+1}(T)=B^n(T)f+(1-f){\int }_0^{\mathrm{\infty }}{\int }_{4\pi }\frac{{\sigma }_{a,{\nu }^{\prime }}}{{\sigma }_{a,p}(T)}\frac{I(r,{\mathbf{\Omega }}^{\prime },{\nu }^{\prime },t)}{4\pi }\mathit{d}{\mathbf{\Omega }}^{\prime }d{\nu }^{\prime }\end{array}$(3) into Eqs. (1a)(1a) $\begin{array}{rl}& \frac{1}{c}\frac{\mathrm{\partial }I(\mathit{r},\mathbf{\Omega },\nu ,t)}{\mathrm{\partial }t}+\mathbf{\Omega }\cdot \mathrm{\nabla }I(\mathit{r},\mathbf{\Omega },\nu ,t)=-({\sigma }_a(\nu ,T)+{\sigma }_s(\nu ,T))I(\mathit{r},\mathbf{\Omega },\nu ,t)+{\sigma }_a(\nu ,T)B(\nu ,T)\\ & +{\sigma }_s(\nu ,T){\int }_{4\pi }\frac{I_{\nu }(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }},t)}{4\pi }\mathit{d}\mathbf{\Omega }{ }^{\mathrm{\prime }}\end{array}$(1a) and (1b)(1b) $\frac{\mathrm{\partial }e(T)}{\mathrm{\partial }t}=c{\int }_0^{\mathrm{\infty }}\left[{\sigma }_a(\nu { }^{\mathrm{\prime }},T)\left({\int }_{4\pi }I(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }},\nu { }^{\mathrm{\prime }},t)\mathit{d}\mathbf{\Omega }{ }^{\mathrm{\prime }}-4\pi B(\nu { }^{\mathrm{\prime }},T)\right)d\nu { }^{\mathrm{\prime }}\right],$(1b) yields the final frequency-dependent IMC equations

(4a) $\begin{array}{rl}& \frac{1}{c}\frac{\mathrm{\partial }I(\mathit{r},\mathbf{\Omega },\nu ,t)}{\mathrm{\partial }t}+\mathbf{\Omega }\cdot \mathrm{\nabla }I(\mathit{r},\mathbf{\Omega },\nu ,t)=-({\sigma }_a(\nu ,T)+{\sigma }_s(\nu ,T))I(\mathit{r},\mathbf{\Omega },\nu ,t)\\ & +f{\sigma }_a(\nu ,T)b^n(\nu ,T)B^n(T)+{\sigma }_s(\nu ,T){\int }_{4\pi }\frac{I_{\nu }(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }},\nu ,t)}{4\pi }\mathit{d}\mathbf{\Omega }{ }^{\mathrm{\prime }}\\ & +(1-f)\frac{{\sigma }_a(\nu ,T)b^n(\nu ,T)}{{\sigma }_{a,p}(T)}{\int }_0^{\mathrm{\infty }}{\int }_{4\pi }\frac{I(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }},\nu { }^{\mathrm{\prime }},t){\sigma }_a(\nu { }^{\mathrm{\prime }},T)}{4\pi }\mathit{d}\mathbf{\Omega }{ }^{\mathrm{\prime }}d\nu { }^{\mathrm{\prime }}\end{array}$(4a)

and

(4b) $\frac{\mathrm{\partial }e(T)}{\mathrm{\partial }t}=cf\left({\int }_0^{\mathrm{\infty }}{\int }_{4\pi }{\sigma }_a(\nu { }^{\mathrm{\prime }},T)I(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }},\nu { }^{\mathrm{\prime }},t)\mathit{d}\mathbf{\Omega }{ }^{\mathrm{\prime }}d\nu { }^{\mathrm{\prime }}-{\sigma }_{a,p}(T)a{T}^4\right).$(4b)

These are the basic frequency-dependent IMC equations, where in addition to the physical scattering term (which is proportional to the frequency-integrated specific intensity), there is an additional “effective” scattering term that is proportional to $1-f$. This effective scattering term replaces the explicit process of absorption and black-body emission, which enables the use of large time steps with $f<1$.

The implicitization and linearization of the DIMC is the same as the classic IMC, i.e., linear only in $I$ (as opposed to the ISMC, which is linear in both $I$ and $e$) (Refs. 28 and 29), and the matter energy is treated via Eq. (4b)(4b) $\frac{\mathrm{\partial }e(T)}{\mathrm{\partial }t}=cf\left({\int }_0^{\mathrm{\infty }}{\int }_{4\pi }{\sigma }_a(\nu { }^{\mathrm{\prime }},T)I(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }},\nu { }^{\mathrm{\prime }},t)\mathit{d}\mathbf{\Omega }{ }^{\mathrm{\prime }}d\nu { }^{\mathrm{\prime }}-{\sigma }_{a,p}(T)a{T}^4\right).$(4b) . The difference from the classic IMC is that the material energy is also represented by material particles, where the sum of the energy of the material particles inside a numerical cell is exactly the total energy of the matter in the cell. Photons are allowed to be created only in positions of material particles and are absorbed continuously, generating new material particles. To prevent population explosion, an algorithm of merging material particles weighted by their energy was derived, and limits at the end of the time step the number of material particles to be approximately 10 to 30 in each cell.

For a more complete description of the DIMC algorithms, the algorithm of photon creation, the single photon propagation, and the algorithm of material particle merging, see Ref. 31. The only difference in the frequency-dependent algorithm is that when a new radiation photon is emitted or when there is an effective scattering event, the photon’s new frequency is sampled in the same manner as in the emission case in the frequency-dependent IMC and ISMC. The propagation is determined via the frequency dependency of the opacity. We note that as in the classic IMC, the Monte Carlo particles that represent the photons are not photons per se, but rather “packets of energy,” that represent large numbers of photons (calculating the real number of photons is unrealistic). As a consequence, there is not a direct relation between the frequency of the energy packet and its energy, which may represent many low or (high)-energy photons.

The main substeps of each time advancement in the DIMC scheme are as follows:

1. The temperature of a cell is calculated from $e$ (which is equal to the sum of energies from all the material particles in a given cell).

2. The values for $f$ and $\beta$ are calculated using the values at the beginning of the time step.

3. A given number of new photons $N_{\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{t}\mathrm{o}\mathrm{n}}$ (packets of energy) is created (a parameter by the user), where the total energy of the photons is determined by black-body emission $V\mathrm{\Delta }tf\int {\sigma }_{a,p}(T)cB(\nu ,T)d\nu$ ($V$ is the volume of the cell), as in the classic IMC. New positions for the photons are sampled randomly from the positions of the material particles in the cell, weighted by their energy. Each packet of energy has the same energy, where its energy is then subtracted from the energy of the cell as well as from the sampled material particles. The frequency of the photon is sampled as in the IMC by randomly sampling the distribution $\int {\sigma }_a(\nu ,T)b(\nu ,T)d\nu /{\sigma }_{a,P}(T)$. Since the emission depends explicitly in the opacity ${\sigma }_a$, we build a (numerical) cumulative spectral distribution of the previous integral, sampling uniformly from the opacity-Planck-weighted integrated distribution (for more details, please see Sec. IVA in Ref. 8). For the detailed algorithm of photon creation, please see Algorithm 1 from Ref. 31 in the Appendix.

4. If there are external radiation sources/boundary conditions, new radiation photons are created with their corresponding frequency distribution.

5. Radiation photons are transported with a velocity $c$, where the distances for a collision $d_{\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}}$ moving to a neighboring cell $d_{\mathrm{m}\mathrm{e}\mathrm{s}\mathrm{h}}$ or free flight $d_{\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}}$ are calculated. The minimal distance is then taken and the reduction in the energy of the photon (a packet of energy, as explained previously) is then calculated continuously by $\mathrm{\Delta }E=E_{\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{t}\mathrm{o}\mathrm{n}}(1-exp(-f{\sigma }_a(\nu )d))$. This energy difference is then saved for when a new material particle is created.

6. If there is a collision, the photon is scattered, and with a probability of $(1-f){\sigma }_a(\nu )/((1-f){\sigma }_a(\nu )+{\sigma }_s(\nu ))$, a new frequency is sampled from the same distribution as before (i.e., only for the effective scattering).

7. Once the photon exits the cell or reaches the end of the time step, the position of a new material particle is determined by averaging the photon energy loss track (see Algorithm 2 from Ref. 31 in the Appendix). A new material particle is created at that location, and its energy is equal to the sum of the energies that were deposited by the photon. The position of a new material particle when a photon crosses the boundary between cells is not necessarily right at the boundary, but rather is determined by the track length of the photon in the old cell due to the photon’s deposition of energy inside the old cell.

8. Since each photon creates at least one material particle in each time step, material particles are merged until we reach some desired number $N_{\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}$. The merging process retains the “center of mass” (where here mass is the energy) of the material particles energy (see Algorithm 3 from Ref. 31 in the Appendix). We note again that the main difference between the DIMC and classic IMC is in the source sampling; the total energy of the cell is a global quantity. Therefore, the DIMC should be as consistent at least as the classic IMC, and is better at avoiding teleportation errors.

We note that we haven’t presented a theoretical proof that the DIMC algorithms are unbiased. However, from the numerical examples that will be shown in the upcoming sections, we see no evidence for bias. Our main concern as a source of bias was the material particle merging algorithm. We performed extensive numerical checks using different methods of merging the material particles. Our proposed algorithm had the least bias among all of the tested methods, which included in addition to our method also Russian roulette and comb sort algorithms.

III. ONE-DIMENSIONAL TESTS

In Ref. 29, we collected the well-known frequency-dependent radiative transfer benchmarks that appear in the literature and used them to test the ISMC algorithm. In this section, we use these benchmarks to test the new DIMC scheme in frequency-dependent scenarios in one dimension, which includes the frequency-dependent benchmark that have been offered lately by Olson³², and the frequency-dependent benchmark that was offered by Densmore et al.²⁷ (and was tested also by Cleveland and Gentile¹⁴).

III.A. Olson 2020 1-D Benchmark

The Olson 1-D benchmark³² that is tested here is a frequency-dependent extension setup for the optically thin source gray test, which was introduced previously in Ref. 33. The source term is a black body with a temperature of $0.5$ keV whose spatial extent is given by $Q(x)=B(0.5\mathrm{k}\mathrm{e}\mathrm{V})exp(-693\cdot x^3)$, and is turned on at time $t=0$ and turned off at time $ct=2$. The initial temperature in the domain, $0\le x\le 4.8$ (cm) is set to be $T(t=0)=0.01T_{\mathrm{k}\mathrm{e}\mathrm{V}}$ ($T_{\mathrm{k}\mathrm{e}\mathrm{V}}$ represents the temperature in the units of kilo-electron-volts), and we run the simulation until a time $ct=4$ using reflective boundary conditions at both ends.

The material is composed of carbon-hydrogen foam, whose frequency-dependent opacity (in units of $\mathrm{c}{\mathrm{m}}^2{\mathrm{g}}^{-1}$) is given by

(5) ${\kappa }_a(\nu ,T)=\left(\begin{array}{cc}\mathrm{m}\mathrm{i}\mathrm{n}{(10}^7{,10}^9{(T/T_{\mathrm{k}\mathrm{e}\mathrm{V}})}^2)& h\nu <0.008\mathrm{k}\mathrm{e}\mathrm{V}\\ \frac{{\displaystyle 3\cdot {10}^6{\left(0.008\mathrm{k}\mathrm{e}\mathrm{V}/h\nu \right)}^2}}{{\displaystyle (1+200\cdot {(T/T_{\mathrm{k}\mathrm{e}\mathrm{V}})}^{1.5})}}& 0.008\mathrm{k}\mathrm{e}\mathrm{V}<h\nu <0.3\mathrm{k}\mathrm{e}\mathrm{V}\\ \frac{3\cdot {10}^6{\left(0.008\mathrm{k}\mathrm{e}\mathrm{V}/h\nu \right)}^2\sqrt{0.3\mathrm{k}\mathrm{e}\mathrm{V}/h\nu }}{(1+200\cdot {(T/T_{\mathrm{k}\mathrm{e}\mathrm{V}})}^{1.5})}+\frac{4\cdot {10}^4{\left(0.3\mathrm{k}\mathrm{e}\mathrm{V}/h\nu \right)}^{2.5}}{1+8000(T/T_{\mathrm{k}\mathrm{e}\mathrm{V}}{)}^2}& h\nu >0.3\mathrm{k}\mathrm{e}\mathrm{V}.\end{array}\right.$(5)

The macroscopic absorption cross section is given by ${\sigma }_a(\nu ,T)=\rho {\kappa }_a(\nu ,T)$, where $\rho =0.001$ $\mathrm{g}/\mathrm{c}{\mathrm{m}}^3$. The heat capacity is given by

(6a) $\rho C_V=a{T}_{\mathrm{k}\mathrm{e}\mathrm{V}}^{3}H\left(1+\alpha +\left(T+\chi \right)\frac{\mathrm{\partial }\alpha }{\mathrm{\partial }T}\right),$(6a)

(6b) $\alpha =\frac{1}{2}{e}^{-\chi /T}\left(\sqrt{1+4e^{\chi /T}}-1\right),$(6b)

and

(6c) $\frac{\mathrm{\partial }\alpha }{\mathrm{\partial }T}=\frac{\chi }{T^2}\left(\alpha -1/\sqrt{1+4e^{\chi /T}}\right),$(6c)

where $\chi =0.1T_{\mathrm{k}\mathrm{e}\mathrm{V}}$ and $H=0.1$. For all of the schemes, we used a spatial resolution of 128 equally spaced cells and set a constant time step of $\mathrm{\Delta }t={10}^{-13}$. We tried to achieve a comparable noise level in the material temperature field between the IMC, ISMC, and DIMC. In the IMC and DIMC cases, we created 500 new photons each time step and limited the total number to be 4 × 10³, while in the ISMC case, we created 5 × 10³ new photons each time step and limited the total number of particles to be ${10}^5$. For the reference solution, we used the one calculated using a high-order $P_N$ scheme presented in Ref. 32.

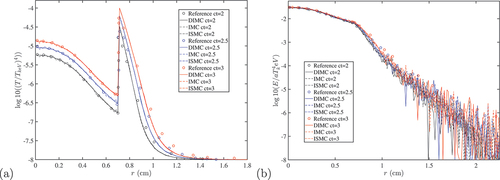
Figure 1a shows the material temperatures for different times compared with the reference solution, and the radiation energy density is shown in Fig. 1b.

Fig. 1. Low-statistic IMC and DIMC runs versus high-statistic ISMC run for (a) the material temperature at different times for the 1-D Olson³² test problem and (b) the radiation energy density at different times for the 1-D Olson³² test problem.

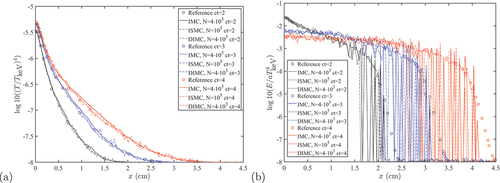
The frequency-dependent DIMC method yields the correct result and agrees well with both the IMC and ISMC solutions and the reference solution as well. As in the ISMC results, there is a difference between the discrete results of the different Monte Carlo schemes and the smooth curves of the $P_N$ near the tails of the distributions, where the radiation intensity drops by several orders of magnitude. Since all three methods converge to the same solution with an infinite number of particles, we chose for the comparison of the efficiency between the different schemes the number of particles required to achieve a similar noise level in the matter energy (since in most cases this quantity is more informative than the radiation energy). Thus, the noise level in the material temperature was almost comparable in all three methods, while in the radiation field, the noise level in the ISMC was lower than in both the IMC and DIMC, as expected. However, the total number of particles in the ISMC run was higher by two orders of magnitudes than in the other two methods. That is because both the IMC and DIMC need relatively low statistics to yield smooth material profiles, and in the ISMC, the noise levels of radiation and matter are similar. This means that for a given statistic, the ISMC is much noisier than the IMC or DIMC. To achieve similar levels of noise, the ISMC needed an overall run time that was a factor of 9.5 longer than the IMC run.

III.B. Densmore et al. 2012 1-D Benchmarks

Densmore et al.²⁷ (and also Cleveland and Gentile¹⁴) presented 1-D frequency-dependent benchmarks with varying optical depths: optically thin material, medium-level (intermediate) opacity, and optically thick material. In addition, they introduced a combination of two different materials or zones, i.e., the heat wave that initially propagates in optically thin material and “crashes” into an optically thicker “wall.” The optically thick media problems emphasize the difference between the IMC, which exhibits a teleportation error, and the ISMC and DIMC, which should be spatially converged at a lower spatial resolution with no teleportation error, even in frequency-dependent problems.

First, in the single-opacity Densmore et al. benchmark, the opacity has the form

(7) $\sigma (x,\nu ,T)=\frac{{\sigma }_0(x)}{{\left(h\nu \right)}^3\sqrt{k_{B}T}},$(7)

where ${\sigma }_0(x)=10\mathrm{k}\mathrm{e}{\mathrm{V}}^{7/2}$ is the optically thin medium, ${\sigma }_0(x)=100\mathrm{k}\mathrm{e}{\mathrm{V}}^{7/2}$ is the optically intermediate medium, and ${\sigma }_0(x)=1000\mathrm{k}\mathrm{e}{\mathrm{V}}^{7/2}$ is the optically thick medium. The heat capacity is set to be $C_V={10}^{15}\mathrm{e}\mathrm{r}\mathrm{g}/T_{\mathrm{k}\mathrm{e}\mathrm{V}}/\mathrm{c}{\mathrm{m}}^3$. The initial temperature in the domain $0\le x\le 5$ (cm) is 1 eV, the left boundary is a black-body bath source with a temperature of 1 keV, and the right boundary is a reflecting wall. The spatial resolution is taken to be small, 64 evenly spaced cells (for presenting the teleportation in opaque problems in the IMC). The test was run to a time of $t=1$ ns with a constant time step of $\mathrm{\Delta }t=0.01$ ns. For all of the runs, we created ${10}^5$ photons per time step and limited the total number of photons to be ${10}^6$. The reference solution that we compared to was taken from Densmore et al.²⁷

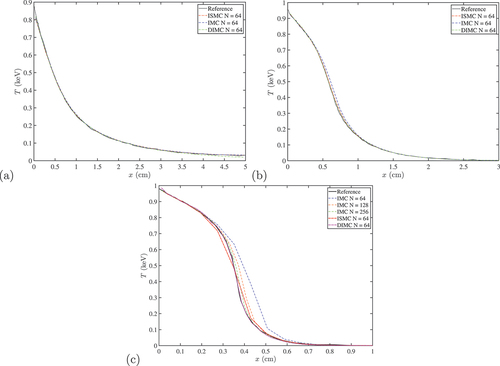
The material temperature profiles at $t=1$ ns for all three methods, along with the reference solution, are shown in Fig. 2. We can see that there is a good agreement between the three methods and the reference solution for the first two tests (optically thin and intermediate-opacity problems), while in the third test (optically thick), the IMC required a spatial resolution of 256 cells in order to avoid teleportation errors, as opposed to the ISMC or DIMC, which gave a good result even with 64 cells. As a matter of fact, the DIMC yielded even better results compared to the reference solution than the ISMC. Again, all three methods converge to the same solution with an infinite number of particles and spatial resolution. Therefore, in this problem, we chose for the comparison of the efficiency between the different schemes, the required spatial resolution for convergence. In this metric, the IMC needed four times higher resolution to achieve the same accuracy as the ISMC and DIMC.

Fig. 2. Material temperature at time $t=1$ ns for the first three Densmore et al.²⁷ benchmarks: (a) ${\sigma }_0(x)=10\mathrm{k}\mathrm{e}{\mathrm{V}}^{7/2}$/cm, (b) ${\sigma }_0(x)=100\mathrm{k}\mathrm{e}{\mathrm{V}}^{7/2}$/cm, and (c) ${\sigma }_0(x)=1000\mathrm{k}\mathrm{e}{\mathrm{V}}^{7/2}$/cm.

Next, Densmore et al. offered a two-media benchmark, testing the handling of sharp transition from an optically thin to an optically thick regime. The domain (with equally spaced cells throughout) was set to $0\le x\le 3$ (cm), and the opacity was

(8) ${\sigma }_0(x)=\left(\begin{array}{cc}10\mathrm{k}\mathrm{e}{\mathrm{V}}^{7/2}/\mathrm{c}\mathrm{m}& x<2\mathrm{c}\mathrm{m},\\ 1000\mathrm{k}\mathrm{e}{\mathrm{V}}^{7/2}/\mathrm{c}\mathrm{m}& x\ge 2\mathrm{c}\mathrm{m}.\end{array}\right.$(8)

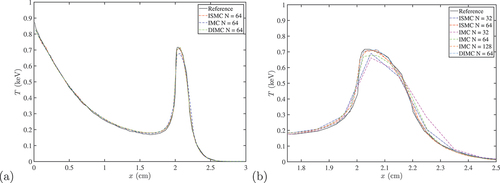
In Fig. 3, we show the material temperature for the two-media benchmark (Fig. 3b is zoomed in on the interface zone). As in the optically thick single-medium benchmark, we see that when optically thick material is present, the new DIMC algorithm (as well as the ISMC algorithm) required less spatial resolution than the IMC in order to achieve convergence due to teleportation toward the opaque material in the low spatial resolution in the IMC simulation. One again, the DIMC yielded even better accuracy with the reference solution than the ISMC.

Fig. 3. Material temperature at time $t=1$ ns for the two-media Densmore et al.²⁷ benchmark: (a) zoom out showing the entire domain and (b) zoom in showing the interface between the optically thin and optically thick materials located at $x=2$ cm.

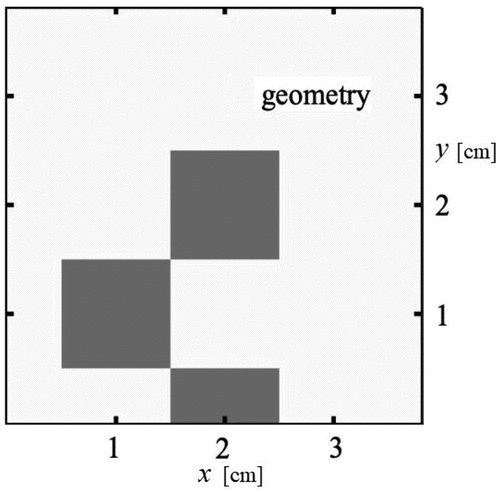
IV. OLSON 2020 2-D TEST

In this section, we present a frequency-dependent implementation of the new DIMC scheme in a full 2-D problem using the most complex 2-D problem presented in Olson.³² In this problem, a complex-geometry 3.8-cm square on each side and composed of intermediate-opaque (thus, no teleportation errors should appear in the IMC simulations) aluminum blocks surrounded by the same foam as in the previous 1-D Olson benchmark problem (see Sec. III.A). The exact setup is shown in Fig. 4. The aluminum blocks have the same density as the foam, and their heat capacity has the same functional form as the foam [Eq. (6)(6a) $\rho C_V=a{T}_{\mathrm{k}\mathrm{e}\mathrm{V}}^{3}H\left(1+\alpha +\left(T+\chi \right)\frac{\mathrm{\partial }\alpha }{\mathrm{\partial }T}\right),$(6a) ], but with $H=0.5$ and $\chi =0.3T_{\mathrm{k}\mathrm{e}\mathrm{V}}$. The opacity for the aluminum blocks is given by

(9) ${\kappa }_a(\nu ,T)=\left(\begin{array}{cc}\mathrm{m}\mathrm{i}\mathrm{n}{(10}^7{,10}^{8}T/T_{\mathrm{k}\mathrm{e}\mathrm{V}})& h\nu <0.01\mathrm{k}\mathrm{e}\mathrm{V}\\ \frac{{10}^7{\left(0.01\mathrm{k}\mathrm{e}\mathrm{V}/h\nu \right)}^2}{(1+20\cdot {(T/T_{\mathrm{k}\mathrm{e}\mathrm{V}})}^{1.5})}& 0.01\mathrm{k}\mathrm{e}\mathrm{V}<h\nu <0.1\mathrm{k}\mathrm{e}\mathrm{V}\\ \frac{{10}^7{\left(0.01\mathrm{k}\mathrm{e}\mathrm{V}/h\nu \right)}^2}{(1+20\cdot {(T/T_{\mathrm{k}\mathrm{e}\mathrm{V}})}^{1.5})}+\frac{{10}^6{\left(0.1\mathrm{k}\mathrm{e}\mathrm{V}/h\nu \right)}^2}{1+200\cdot {(T/T_{\mathrm{k}\mathrm{e}\mathrm{V}})}^2}& 0.1\mathrm{k}\mathrm{e}\mathrm{V}<h\nu <1.5\mathrm{k}\mathrm{e}\mathrm{V}\\ \frac{{10}^7{\left(0.01\mathrm{k}\mathrm{e}\mathrm{V}/h\nu \right)}^2\sqrt{1.5\mathrm{k}\mathrm{e}\mathrm{V}/h\nu }}{(1+20\cdot {(T/T_{\mathrm{k}\mathrm{e}\mathrm{V}})}^{1.5})}+\frac{{10}^5{\left(1.5\mathrm{k}\mathrm{e}\mathrm{V}/h\nu \right)}^{2.5}}{1+1000\cdot {(T/T_{\mathrm{k}\mathrm{e}\mathrm{V}})}^2}& h\nu >1.5\mathrm{k}\mathrm{e}\mathrm{V}.\end{array}\right.$(9)

Fig. 4. Geometrical setup for the 2-D frequency-dependent benchmark of Olson.³² The gray squares represent opaque regions.

The computational region is divided into 380 equally spaced cells in each axis with reflecting boundaries. A black-body source, $Q(r)=B(0.5\mathrm{k}\mathrm{e}\mathrm{V})exp(-18.7\cdot r^3)$, was turned on at time $t=0$, and remained on for the entire duration of the simulation. A constant time step of $\mathrm{\Delta }t={10}^{-13}$ s was used, 2 × 10⁶new particles were created each time step, and we limited the total number of particles to be 2.5 × 10⁷for all of the schemes.

First, in Figs. 5b, 5c, and 5d we show a colormap of the radiation energy density in the entire domain, as well as a reference from Ref. 32 (Fig. 5a). All of the Monte Carlo methods, the IMC, ISMC, and DIMC, agreed very well with each other through the computational domain and had a good qualitative agreement with the $P_N$ reference data, including all geometrical patterns.

Fig. 5. (a) Contours of the logarithm of the radiation energy density at $ct=3$ using the $P_{51}$ approximation. Figure (a) is taken from Ref. 32. The radiation energy density at $ct=3$ is shown in (b) for the IMC method, (c) for the ISMC method, and (d) for the DIMC method.

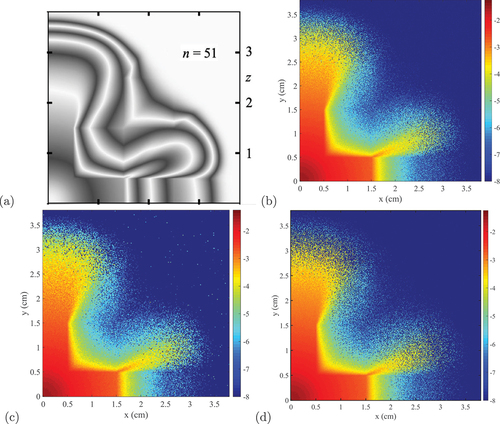
Next, slices along the diagonal are shown in Fig. 6a for the material temperature and in Fig. 6b for the radiation energy density, along with reference $P_N$ data from Ref. 32. Again, there was a good agreement between all methods in the range $0\le r\le \sqrt{0.5}$. Farther away from the origin, the sharp discontinuity in the material properties caused a small difference between the Monte Carlo methods and the reference solution.

Fig. 6. (a) Material temperatures at different times for the Olson³² 2-D test problem and (b) the radiation energy density at different times for the Olson³² 2-D test problem.

V. CONCLUSIONS

In this work, we presented a frequency-dependent (energy-dependent) generalization to the DIMC scheme that was introduced recently.³¹ The DIMC is a classic IMC implementation on one hand, but on the other hand uses the concept of two kinds of particles to avoid teleportation errors, as introduced by Ahrens and Larsen³⁰ and later by Poëtte and Valentin.²⁸ The main idea is that when a photon continuously loses its energy due to absorption, a material particle is created, which is static. The new photons that emerge due to black-body emissions are sampled only from the locations of material particles, and thus, teleportation errors are avoided.

The DIMC has been checked before in gray opacity scenarios³¹; this work completes the generalization and testing of the frequency-dependent opacity problems. We have seen in the optically thin problems, both in 1-D and the 2-D problems, that the DIMC yields good results compared to the reference solution, and yields smoother results than the ISMC, with a noise level comparable to the IMC. On the other hand, the ISMC required two orders of magnitude more particles in order to converge at the same noise level.

In the optically thick benchmarks, the DIMC yielded the best results, having no teleportation error even with a very low spatial resolution, like the ISMC results, while the IMC needed a spatial resolution four times higher in order to achieve similar results. The results of the numerical examples show no reason to think that the DIMC algorithms are biased; however, a consistent proof of unbiasedness is reserved for future work. In addition, the benchmarks were run with continuous frequency dependency, but the results should be valid also for a finite number of groups, i.e., in multigroup problems, which could be another direction for future work.

Disclosure Statement

No potential conflict of interest was reported by the author(s).

APPENDIX

FUNDAMENTAL DIMC ALGORITHMS

In this appendix, we present the fundamental algorithms of the DIMC that were presented previously in the gray DIMC paper.³¹ An outline of the photon creation process is given in Algorithm 1. The full photon propagation algorithm is shown in Algorithm 2. The merging algorithm for the material particles is presented in Algorithm 3.