Angular Adaptivity in P⁰ Space and Reduced Tolerance Solves for Boltzmann Transport

Abstract

Previously, we developed an adaptive method in angle that is based on solving in Haar wavelet space with a matrix-free multigrid for Boltzmann transport problems. This method scalably mapped to the underlying P⁰ space during every matrix-free matrix-vector product; however, the multigrid method itself was not scalable in the streaming limit. To tackle this, we recently built an iterative method based on using an Approximate Ideal Restriction multigrid with GMRES polynomials (AIRG) for Boltzmann transport that showed scalable work with uniform P⁰ angle in the streaming and scattering limits. This paper details the practical requirements of using this new iterative method with angular adaptivity. Hence, we modify our angular adaptivity to occur directly in P⁰ space rather than the Haar space. We then develop a modified stabilization term for our Finite Element Method that results in scalable growth in the number of nonzeros in the streaming operator with P⁰ adaptivity. We can therefore combine the use of this iterative method with P⁰ angular adaptivity to solve problems in both the scattering and the streaming limits, with close to fixed work and memory use.We also present a coarse-fine splitting for multigrid methods based on element agglomeration combined with angular adaptivity, which can produce a semicoarsening in the streaming limit without access to the matrix entries. The equivalence between our adapted P⁰ and Haar wavelet spaces also allows us to introduce a robust convergence test for our iterative method when using regular adaptivity. This allows the early termination of the solve in each adapt step, reducing the cost of producing an adapted angular discretization.

Keywords:

• Radiation transport
• Boltzmann
• angular adaptivity
• Haar wavelets
• AIRG

I. INTRODUCTION

In this work, we consider the monoenergetic steady-state form of the Boltzmann transport equation (BTE) written as

(1) $\begin{array}{rl}& \mathbf{\Omega }\cdot {\mathrm{\nabla }}_{\mathit{r}}\mathit{\psi }(\mathit{r},\mathbf{\Omega })+{\sigma }_t\mathit{\psi }(\mathit{r},\mathbf{\Omega })-{\int }_{\mathbf{\Omega }{\mathit{ }}^{\mathrm{\prime }}}{\sigma }_s(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }}\to \mathbf{\Omega })\\ & \mathit{\psi }(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }})\mathrm{d}\mathbf{\Omega }{ }^{\mathrm{\prime }}=S_e(\mathit{r},\mathbf{\Omega }),& (1)\end{array}$(1)

where $\mathit{\psi }(\mathit{r},\mathbf{\Omega })$ = angular flux; $\mathbf{\Omega }$ = angular direction with $\mathbf{r}$ the spatial position; ${\sigma }_t$ and ${\sigma }_s$ = macroscopic total and scattering cross sections (cm^–1), respectively, with an external source of $S_e$.

Solving Eq. (1)(1) $\begin{array}{rl}& \mathbf{\Omega }\cdot {\mathrm{\nabla }}_{\mathit{r}}\mathit{\psi }(\mathit{r},\mathbf{\Omega })+{\sigma }_t\mathit{\psi }(\mathit{r},\mathbf{\Omega })-{\int }_{\mathbf{\Omega }{\mathit{ }}^{\mathrm{\prime }}}{\sigma }_s(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }}\to \mathbf{\Omega })\\ & \mathit{\psi }(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }})\mathrm{d}\mathbf{\Omega }{ }^{\mathrm{\prime }}=S_e(\mathit{r},\mathbf{\Omega }),& (1)\end{array}$(1) can be difficult given the dimensionality of the problem. Previously, we presented methods for building adapted angular discretizations for the BTE.^[1–3] This allowed angular resolution to be focused where it is important in space/energy. Reference [1] used anisotropic adaptivity on the sphere in a Haar wavelet space, which was built on top of an underlying nested P⁰ space. The angular matrices in Haar wavelet space cannot be formed scalably because the number of nonzeros (nnzs) grows nonlinearly with angular refinement. As such, we built a matrix-free multigrid method to solve the adapted problems, which mapped the solution into the underlying P⁰ space in $\mathcal{O}(\mathit{n})$ [where $\mathit{n}$ is the number of degrees of freedom (DOFs)], and performed a matrix-vector product with the P⁰ angular matrices, which is scalable, before mapping back to Haar space.

This method resulted in a reduction in time to solve and memory use when compared to uniform discretizations. We showed that our adaptive process was scalable, enabling the use of up to 15 levels of hierarchical refinement in angle. Unfortunately, in the streaming limit, the matrix-free multigrid could not solve the linear systems with fixed work. This is due to the BTE becoming hyperbolic in the limit of no scattering, and we deliberately chose not to use Gauss-Seidel/sweep–based smoothers in an effort to build an iterative method that could scale well on unstructured grids in parallel.

Recently, we showed^[4] that by solving in P⁰ space directly, we could build an iterative method without sweeps with excellent performance in the streaming limit of the BTE. That work used uniform P⁰ discretizations in angle. The discretized streaming/removal operator was therefore block diagonal, with the same number of blocks as angular variables because there is no interangle coupling. The adaptivity used in Ref. [1] allows each octant to adapt in angle independently, and hence, the use of angular adaptivity removes the majority of the block-diagonal structure. Angles within an octant can be coupled to other angles in the same octant (at higher or lower resolution) across space when the resolution changes. The number of blocks in the streaming/removal operator is therefore always the number of octants.

Solving the linear system that results from this structure can present challenges because traditional Discontinuous Galerkin (DG) Finite Element Method (FEM)/sweep technology relies on each angle being independent. Previous work with angular adaptivity and DG FEMs typically performed block sweeps across the entirety of an octant at once (e.g., Ref. [5]), but this does not scale with angular refinement.

We designed the iterative method in Ref. [4] to be agnostic to block structure in the streaming/removal operator, and hence, we would expect to see no large difference in the performance of the method when solving either uniform or angularly adapted transport problems. As such, this work is focused on examining the performance of the iterative method in Ref. [4] when used with angular adaptivity. Rather than focus on the solution accuracy attained by adapting, as in our previous work,^[1] we deliberately chose our adaptive refinement criteria in this work to maximize the coupling between angles. This is in an attempt to test the performance of our new iterative method with the minimum number of independent blocks in the streaming/removal operator.

Furthermore, the iterative method presented in Ref. [4] requires the assembly of the discrete streaming/removal operator. This is in contrast to Ref. [1], which used matrix-free matrix-vector products on all multigrid levels. As such, we must ensure that our discretization now produces a streaming/removal operator with P⁰ adaptivity whose sparsity grows linearly with space/angle refinement. In this work we therefore introduce a modified stabilization term for our spatial discretization with controlled sparsity.

Hence, we present four contributions. The first is the sparsity-controlled adaptive P⁰ discretization for the BTE. The second is the use of an adapted P⁰ discretization with our Approximate Ideal Restriction multigrid with GMRES polynomials (AIRG)–based iterative method. The third is a method for selecting coarse (C) and fine (F) points for a multigrid hierarchy that can be combined with angular adaptivity to provide semicoarsenings without requiring matrix entries. Finally, the fourth is a convergence test for iterative methods that decreases the cost of forming an adaptive angular discretization with regular adaptivity. We therefore show that the combination of the sparsity control in our discretization and the block-agnostic iterative method from Ref. [4] results in solutions of adapted problems with close to fixed work and memory use.

II. DISCRETIZATIONS

The spatial and angular discretizations used in this work are based on what we used previously, and we describe them below.^[1,4,6–9]

II.A. Angular Discretization

We use a P⁰ DG FEM in angle, with the lowest resolution given by one P⁰ element per octant (similar to an S₂ discretization). Subsequent levels of refinement come from dividing each element into four, at the halfway points of the azimuth angle and cosine of the polar angle. All the elements at a given level of refinement therefore have constant area, and we normalize our constant basis functions, so the uniform (and hence diagonal) angular mass matrix is the identity. This P⁰ discretization is similar to an S_n product quadrature and features elements that cluster around the poles with uniform refinement. This is not a desirable feature for a uniform discretization of the BTE, but the nested nature of the refinement means that it is simple to build an adapted angular discretization and that hence refinement around the poles occurs only if it is required.

We can build a Haar wavelet discretization on top of this P⁰ space, with the hierarchy in the nested elements replaced with a hierarchy in the wavelet basis functions. These two discretizations are exactly equivalent. As in Ref. [4], in this work we solve in P⁰ space so that we can form an assembled copy of the streaming/removal matrix that has fixed sparsity with angular refinement (see Sec. II.B). The equivalence between the P⁰ and the Haar spaces is still very useful as it allows us to easily tag which angular elements require refinement/derefinement, and hence, it enables the reduced tolerance solves discussed below.

We noted in Ref. [1] that solving in P⁰ space can easily be used as part of the adaptive process that we described previously. Figure 1 shows an example of an adapted P⁰ discretization at a single node point with several levels of refinement, defined a priori in the $+\mathit{y}$ direction. We should note that the P⁰ angular discretization in Fig. 1 (and all of the pictures of angular flux in P⁰ space) are on the $\mathit{r}=1$ sphere but have been projected onto faceted polyhedra for ease of visualization, with the camera pointed in the $-\mathit{z}$ direction. In this work we show only regular adaptivity (based on achieving uniform global accuracy in the solution) given that our iterative methods are agnostic to how the adapted discretizations are formed. Regular adaptivity is not an optimal method for many problems (particularly in the streaming limit). Please see Refs. [1] and [3] for examples using a priori and goal-based adaptivity. There have also been a number of other authors who have used adaptivity in angle in Boltzmann applications. These include sparse grid methods,^[10] S_n methods,^[11–16] FEMs,^[5,17–21] and specifically finite element/wavelet methods.^[22–26]

Fig. 1. Angular domains showing angular adaptivity focused around a single important direction, namely, $\mathit{\mu }\in [0,1]$ and $\mathit{\omega }\in [1.47976,1.661832]$ in a two-dimensional simulation.

Our adaptive process starts with a uniform angular discretization (typically level 1) and performs a solve in P⁰ space. The solution is then mapped into Haar wavelet space in $\mathcal{O}(\mathit{n}),$ and an error metric is formed. Regular adaptivity results in a discretization that minimizes the global error in the problem and is simple to perform. In wavelet space, the size of the wavelet coefficients is influenced by both the size of the flux and the smoothness of the underlying function.^[27] Thresholding the wavelet coefficients with a fixed value is therefore sufficient to drive regular adaptivity. As such, we take the angular flux in Haar space and scale it by a thresholding coefficient. We also scale by the maximum of the scalar flux in an attempt to make the thresholding coefficients less problem specific.

In an adaptive simulation, this thresholding coefficient is input by the user and drives refinement as it is decreased. In general, all adaptive methods, both within and outside the radiation transport community, feature some arbritrary parameter that attempts to tell the adaptive method how much refinement to perform, with uniform refinement occuring in the limit of this parameter.

In Ref. [1], we showed how sensitive the adaptive scheme was to this thresholding coefficient. In this work, we instead try to pick a thresholding coefficient to make the adapted problems as difficult as possible in an attempt to try to test the performance of our new iterative method. As mentioned, our previous work in Ref. [4] showed this new iterative method performed well for uniform discretizations, where the sparsity of the streaming/removal operator features heavy block-diagonal structure.

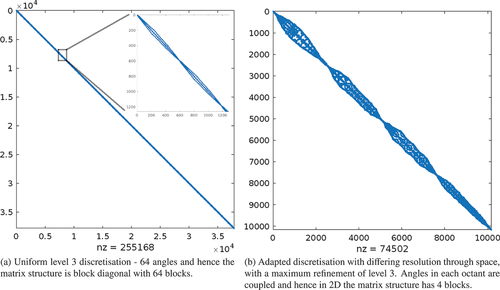
The use of angular adaptivity results in a streaming/removal operator that has less block-diagonal structure, as angles are coupled to each other due to the differing resolution throughout space. Figure 2 shows the significant difference in sparsity when comparing a uniform angular discretization to one that has adapted. This makes adapted problems hard to solve with traditional DG FEM/sweep technology as it introduces the same sort of structure to the sweep ordering that makes unstructured grids difficult to sweep.

Fig. 2. Sparsity of the streaming/removal operator with and without angular adaptivity, after three adapt steps. The solution of the adapted problem is shown in Fig. 4g with the spatial distribution of adapted angles shown in Fig. 4h.

As such, in this work, we wanted to test our new iterative method on problems where there is heavy coupling between different angles caused by the angular adaptivity. Choosing a thresholding coefficient that was large would cause no adaptivity (and hence give the uniform level 1 discretization used to initialize the adaptivity), while choosing a small thresholding coefficient would cause the adaptivity to tend toward a highly refined uniform discretization. Hence, we tried to choose a thresholding coefficient between these two extremes that results in the most change between angular resolution throughout the domain. For the streaming problem in Sec. V.A, we chose a thresholding coefficient of 0.01, and for the scattering problem in Sec. V.B, we chose 0.001.

Given the scaled wavelet coefficients, we can then set our criteria for refinement/coarsening. If each resulting wavelet coefficient is greater than 1.0, we tag it for refinement. If it is less than 0.01, we tag it for de-refinement. We therefore know which angular elements in P⁰ space to refine/de-refine, as they are given by the elements that are in the support of each wavelet; see Ref. [1]. This is performed across each spatial point separately. We then have an adapted angular discretization, and our next adapt step begins. The initial condition for the P⁰ solve on the adapted discretization can then be taken from the previous step. The hierarchical nature of the wavelets makes this simple. It is equivalent to interpolating the P⁰ solution onto the newly adapted P⁰ discretization. As mentioned, the adaptive process starts by using a uniform level 1 angular discretization; at each adapt step, the allowed level of refinement is increased by one, up to a maximum of three in this work. We then allow the adaptivity to continue until we consider the angular discretization converged for a given thresholding tolerance. We define this as the number of degrees of freedom (NDOFs) not changing by more than 10% in a subsequent adapt step.

The only difference between this adaptivity process compared with Ref. [1] is that we enforce that if a single wavelet is added, all the wavelets on the same level of refinement that share the same support (a maximum of two other wavelets) on the sphere should also be added. Similarly, the removal requires that all wavelets with the same support be below the threshold coefficient and all be removed at once. This ensures that when an angular element is refined (or de-refined), we always have four P⁰ elements present, which makes the P⁰ implementation simpler. One of the advantages of enforcing this condition is that we can always guarantee that our adaptivity is “nested,” and given the P⁰ DG FEM formulation (as opposed to a collocation scheme like S_n), this means that reflect conditions can be captured easily, even with angular adaptivity. In comparison to the matrix-free method in Ref. [1], we must also introduce further controls on the sparsity of our discretization given that we solve in P⁰ space; this is detailed below.

II.B. Spatial Discretization

Our spatial discretization is a subgrid-scale FEM, which represents the angular flux as $\mathit{\psi }=\mathit{\varphi }+\mathit{\theta }$, where $\mathit{\varphi }$ is the solution on a coarse scale and $\mathit{\theta }$ is the solution on a fine scale. We perform separate finite element expansions on both the fine and the coarse scales, with continuous linear basis functions on the coarse scale and discontinuous linear basis functions on the fine scale. We then use (constant) basis functions in angle and enforce that the coarse and fine scales have the same angular expansion on co-located nodes. Our discretized form of Eq. (1)(1) $\begin{array}{rl}& \mathbf{\Omega }\cdot {\mathrm{\nabla }}_{\mathit{r}}\mathit{\psi }(\mathit{r},\mathbf{\Omega })+{\sigma }_t\mathit{\psi }(\mathit{r},\mathbf{\Omega })-{\int }_{\mathbf{\Omega }{\mathit{ }}^{\mathrm{\prime }}}{\sigma }_s(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }}\to \mathbf{\Omega })\\ & \mathit{\psi }(\mathit{r},\mathbf{\Omega }{ }^{\mathrm{\prime }})\mathrm{d}\mathbf{\Omega }{ }^{\mathrm{\prime }}=S_e(\mathit{r},\mathbf{\Omega }),& (1)\end{array}$(1) can then be written as

(2) $\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}\right]\left[\begin{array}{c}\mathbf{\Phi }\\ \mathbf{\Theta }\end{array}\right]=\left[\begin{array}{c}{\mathbf{S}}_{\mathbf{\Phi }}\\ {\mathbf{S}}_{\mathbf{\Theta }}\end{array}\right].$(2)

The number of unknowns in the coarse scale discretized vector $\mathbf{\Phi }$ is Number of Continuous Degrees of Freedom (NCDOFS), and the number of unknowns in the fine scale discretized vector $\mathbf{\Theta }$ is Number of Discontinuous Degrees of Freedom (NDDOFs). ${\mathbf{S}}_{\mathbf{\Phi }}$ and ${\mathbf{S}}_{\mathbf{\Theta }}$ are the discretized source terms for both scales. Equation (2)(2) $\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}\right]\left[\begin{array}{c}\mathbf{\Phi }\\ \mathbf{\Theta }\end{array}\right]=\left[\begin{array}{c}{\mathbf{S}}_{\mathbf{\Phi }}\\ {\mathbf{S}}_{\mathbf{\Theta }}\end{array}\right].$(2) is built using standard FEM theory, and as such, $\mathbf{A}$ and $\mathbf{D}$ are the standard Continuous Galerkin (CG) and DG FEM matrices that result from discretizing Eq. (1).

A Schur complement of block $\mathbf{D}$ allows us to solve for the coarse scale variable $\mathbf{\Phi }$, given by

(3) $(\mathbf{A}-\mathbf{B}{\mathbf{D}}^{-1}\mathbf{C})\mathbf{\Phi }={\mathbf{S}}_{\mathbf{\Phi }}-\mathbf{B}{\mathbf{D}}^{-1}{\mathbf{S}}_{\mathbf{\Theta }},$(3)

with the fine scale solution then computed with

(4) $\mathbf{\Theta }={\mathbf{D}}^{-1}({\mathbf{S}}_{\mathbf{\Theta }}-\mathbf{C\Phi }).$(4)

The addition of the two solutions $\mathbf{\Psi }=\mathbf{\Phi }+\mathbf{\Theta }$ (where the coarse solution $\mathbf{\Phi }$ has been projected onto the fine space) then gives us our discrete solution. Solving the subgrid-scale equations as posed would be more expensive than solving with a DG FEM discretization, so we sparsify $\mathbf{D}$ (see also Refs. [1], [2], [9], [25], and [28] through [31]. We replace ${\mathbf{D}}^{-1}$ in Eqs. (3)(3) $(\mathbf{A}-\mathbf{B}{\mathbf{D}}^{-1}\mathbf{C})\mathbf{\Phi }={\mathbf{S}}_{\mathbf{\Phi }}-\mathbf{B}{\mathbf{D}}^{-1}{\mathbf{S}}_{\mathbf{\Theta }},$(3) and (4(4) $\mathbf{\Theta }={\mathbf{D}}^{-1}({\mathbf{S}}_{\mathbf{\Theta }}-\mathbf{C\Phi }).$(4) ) with ${\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}$, which is the streaming operator with removal and self-scatter, and vacuum conditions are applied on each DG element. This removes the jump terms, resulting in element blocks in $\mathbf{D}$, making the computation of ${\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}$ tractable. With a uniform P⁰ angular discretization (as in Ref. [4]), this is sufficient to ensure fixed sparsity with either spatial or angular refinement, as $\stackrel{\mathbf{ˆ}}{\mathbf{D}}$ (and hence ${\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}$) has diagonal blocks. Unfortunately, this is not sufficient when we have adapted our P⁰ angular discretization with differing angular resolution at each spatial point. If we denote the sparsity of the streaming component ${\mathbf{D}}_{\mathrm{\Omega }}$ as $S_{\mathrm{D}}\subset \{(\mathit{i},\mathit{j})|({\mathbf{D}}_{\mathrm{\Omega }}{)}_{\mathit{i},\mathit{j}}\ne 0\}$, then we enforce $({\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{)}_{\mathit{i},\mathit{j}}\in S_{\mathrm{D}}$. This is equivalent to using an ILU(0) to invert our sparsified approximation.

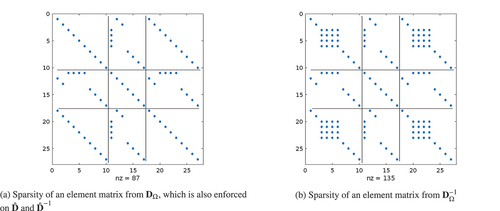
The ILU(0) is necessary only to ensure a fixed sparsity with our adapted P⁰ space. For example, if we have spatial nodes with differently adapted P⁰ discretizations, the construction of our angular discretization means that the nnzs in each of the blocks of our element matrices depends on how each adapted angle overlaps the others (i.e., the angular mass matrix is no longer diagonal). To demonstrate this, we consider three DG nodes that have 10, 7, and 10 angles present, respectively. All three nodes start with three octants at level 1 and one octant at level 2; the nodes with 10 angles have one of the level 2 patches further refined to level 3. Figure 3 shows the sparsity of this element matrix and the resulting inverse. Figure 3a shows that the element streaming operator is no longer made up of diagonal blocks. If we inverted this without the sparsity control of an incomplete LU factorization, we would significantly increase the nnzs in an adapted P⁰ space, as shown in Fig. 3b. This is in contrast to a uniform P⁰ space where the nnzs in the inverse is the same as the streaming operator.

Fig. 3. Sparsity of an element streaming matrix from $\mathbf{D}$ given adapted P0 angle in 2D.

For our adaptivity to be useful, we want the cost of our matvec to scale with the number of adapted unknowns. We can imagine a pathological case where in one dimension for example the angular resolution varies across the domain such that each (linear) spatial element has one node at the lowest resolution possible and one at the highest. The streaming operator would have the same nnzs as a uniform P⁰ discretization at the highest resolution, given the effect of overlapping angular elements in the angular matrices, described above. Thankfully, in our experience, this pathology does not occur in practice. We show this in Sec. V.

III. ITERATIVE METHOD

The iterative method that we use in this work comes from Ref. [4] and is briefly detailed here. We solve a right preconditioned version of Eq. (2)(2) $\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}\right]\left[\begin{array}{c}\mathbf{\Phi }\\ \mathbf{\Theta }\end{array}\right]=\left[\begin{array}{c}{\mathbf{S}}_{\mathbf{\Phi }}\\ {\mathbf{S}}_{\mathbf{\Theta }}\end{array}\right].$(2) given by

(5) $(\mathbf{A}-\mathbf{B}{\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}\mathbf{C}){\mathbf{M}}^{-1}\mathbf{u}={\mathbf{S}}_{\mathbf{\Phi }}-\mathbf{B}{\mathbf{D}}^{-1}{\mathbf{S}}_{\mathbf{\Theta }},\mathbf{u}=\mathbf{M}\mathit{\psi }.$(5)

We use GMRES(30) to solve this equation and a matrix-free matvec to compute the action of $(\mathbf{A}-\mathbf{B}{\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}\mathbf{C})$. The preconditioner ${\mathbf{M}}^{-1}$ uses the additive combination of a CG Diffusion Synthetic Acceleration (DSA) method and a sparsified form of our streaming/removal operator, which we denote as

(6) ${\mathbf{M}}^{-1}={\mathbf{M}}_{\mathrm{angle}}^{-1}+{\mathbf{M}}_{\mathrm{\Omega }}^{-1}.$(6)

The CG DSA preconditioner is based on a CG FEM discretization of a diffusion equation ${\mathbf{D}}_{\mathit{diff}}$ with ${\mathbf{R}}_{\mathit{angle}}$ and ${\mathbf{P}}_{\mathit{angle}}$ the restriction/prolongation of the angular flux to the constant moment and hence

(7) ${\mathbf{M}}_{\mathrm{angle}}^{-1}={\mathbf{R}}_{\mathit{angle}}{\mathbf{D}}_{\mathrm{diff}}^{-1}{\mathbf{P}}_{\mathit{angle}}.$(7)

We can rewrite Eq. (3)(3) $(\mathbf{A}-\mathbf{B}{\mathbf{D}}^{-1}\mathbf{C})\mathbf{\Phi }={\mathbf{S}}_{\mathbf{\Phi }}-\mathbf{B}{\mathbf{D}}^{-1}{\mathbf{S}}_{\mathbf{\Theta }},$(3) as the contribution from a streaming/removal component (denoted with a subscript $\mathrm{\Omega }$) and a scattering component (denoted with a subscript S), or

(8) $\left({\mathbf{A}}_{\mathrm{\Omega }}-{\mathbf{B}}_{\mathrm{\Omega }}{\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{C}}_{\mathrm{\Omega }}\right)\mathbf{\Phi }+\left(({\mathbf{A}}_S+{\mathbf{B}}_S(\mathit{y}+{\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{C}}_{\mathrm{\Omega }})+{\mathbf{B}}_{\mathrm{\Omega }}\mathit{y}\right)\mathbf{\Phi }={\mathbf{S}}_{\mathbf{\Phi }}-({\mathbf{B}}_{\mathrm{\Omega }}+{\mathbf{B}}_S){\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{S}}_{\mathbf{\Theta }},$(8)

where $\mathit{y}={\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{C}}_S$ and our fine component is $\mathbf{\Theta }={\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}({\mathbf{S}}_{\mathbf{\Theta }}-({\mathbf{C}}_{\mathrm{\Omega }}+{\mathbf{C}}_S)\mathbf{\Phi })$. In Ref. [4], we used ${\mathbf{M}}_{\mathrm{\Omega }}^{-1}=({\mathbf{A}}_{\mathrm{\Omega }}-{\mathbf{B}}_{\mathrm{\Omega }}{\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{C}}_{\mathrm{\Omega }}{)}^{-1}$, but here, our adapated P⁰ space in angle requires further sparsification. If we denote the sparsity pattern of ${\mathbf{B}}_{\mathrm{\Omega }}$ as $S_B\subset \{(\mathit{k},\mathit{l})|({\mathbf{B}}_{\mathrm{\Omega }}^e{)}_{\mathit{k},\mathit{l}}\ne 0\}$, then a sparsified streaming operator is given by

(9) $\begin{array}{rl}& {\mathbf{M}}_{\mathrm{\Omega }}^{-1}={\left({\mathbf{A}}_{\mathrm{\Omega }}-{({\mathbf{B}}_{\mathrm{\Omega }}{({\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{C}}_{\mathrm{\Omega }})}_{\mathit{i},\mathit{j}})}_{\mathit{k},\mathit{l}}\right)}^{-1},\\ & (\mathit{i},\mathit{j})\in S_D,(\mathit{k},\mathit{l})\in S_B.& (9)\end{array}$(9)

With a uniform P⁰ angle, Eq. (9)(9) $\begin{array}{rl}& {\mathbf{M}}_{\mathrm{\Omega }}^{-1}={\left({\mathbf{A}}_{\mathrm{\Omega }}-{({\mathbf{B}}_{\mathrm{\Omega }}{({\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{C}}_{\mathrm{\Omega }})}_{\mathit{i},\mathit{j}})}_{\mathit{k},\mathit{l}}\right)}^{-1},\\ & (\mathit{i},\mathit{j})\in S_D,(\mathit{k},\mathit{l})\in S_B.& (9)\end{array}$(9) is exactly ${\mathbf{A}}_{\mathrm{\Omega }}-{\mathbf{B}}_{\mathrm{\Omega }}{\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{C}}_{\mathrm{\Omega }}$; with an adapted ${\mathrm{P}}^0$ angle, it is equivalent to computing the matrix product ${\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}\mathbf{C}$ with no fill-in, and then, this result is used to compute ${\mathbf{B}}_{\mathrm{\Omega }}{\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{C}}_{\mathrm{\Omega }}$, again with no fill-in. This is necessary as again, the overlap of the adapted angular elements means that the product of the two (element) matrices with sparsity shown in Fig. 3a results in the sparsity given in Fig. 3b, which is unacceptable. When computing the action of the matrix triple product one by one as part of a matrix-free matvec for the outer GMRES, the extra nonzeros are not a concern; it is only when we wish to form an assembled version of ${\mathbf{A}}_{\mathrm{\Omega }}-{\mathbf{B}}_{\mathrm{\Omega }}{\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{C}}_{\mathrm{\Omega }}$ with which to precondition that we must take care to ensure that no extra fill-in occurs. Practically, we store an assembled copy of Eq. (9)(9) $\begin{array}{rl}& {\mathbf{M}}_{\mathrm{\Omega }}^{-1}={\left({\mathbf{A}}_{\mathrm{\Omega }}-{({\mathbf{B}}_{\mathrm{\Omega }}{({\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{C}}_{\mathrm{\Omega }})}_{\mathit{i},\mathit{j}})}_{\mathit{k},\mathit{l}}\right)}^{-1},\\ & (\mathit{i},\mathit{j})\in S_D,(\mathit{k},\mathit{l})\in S_B.& (9)\end{array}$(9) to apply the preconditioner, so we use this as a replacement for the nonsparsified ${\mathbf{A}}_{\mathrm{\Omega }}-{\mathbf{B}}_{\mathrm{\Omega }}{\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{C}}_{\mathrm{\Omega }}$ in Eq. (8)(8) $\left({\mathbf{A}}_{\mathrm{\Omega }}-{\mathbf{B}}_{\mathrm{\Omega }}{\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{C}}_{\mathrm{\Omega }}\right)\mathbf{\Phi }+\left(({\mathbf{A}}_S+{\mathbf{B}}_S(\mathit{y}+{\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{C}}_{\mathrm{\Omega }})+{\mathbf{B}}_{\mathrm{\Omega }}\mathit{y}\right)\mathbf{\Phi }={\mathbf{S}}_{\mathbf{\Phi }}-({\mathbf{B}}_{\mathrm{\Omega }}+{\mathbf{B}}_S){\stackrel{\mathbf{ˆ}}{\mathbf{D}}}^{-1}{\mathbf{S}}_{\mathbf{\Theta }},$(8) . The difference between these two approaches is simply a modified stabilization term when we have adapted.

We now require a method to apply the inverses in our preconditioner. In Ref. [4] we developed a multigrid method known as AIRG based on a reduction-style multigrid.^[32,33] We used a single V-cycle of AIRG per application of the preconditioner to apply ${\mathbf{M}}_{\mathrm{\Omega }}^{-1}$. The diffusion operator was applied with a single V-cycle of boomerAMG from hypre. We use the same approach here. If we consider a general linear system $\mathbf{Ax}=\mathbf{b},$ we can form a block system due to a coarse-fine (CF) splitting of the unknowns as

(10) $\left[\begin{array}{cc}{\mathbf{A}}_{\mathit{ff}}& {\mathbf{A}}_{\mathit{fc}}\\ {\mathbf{A}}_{\mathit{cf}}& {\mathbf{A}}_{\mathit{cc}}\end{array}\right]\left[\begin{array}{c}{\mathit{x}}_f\\ {\mathit{x}}_c\end{array}\right]=\left[\begin{array}{c}{\mathit{b}}_f\\ {\mathit{b}}_c\end{array}\right].$(10)

We discuss the CF splitting further in Sec. IV. Ideal prolongation and restriction operators are given by

(11) $\mathbf{P}=\left[\begin{array}{c}-{\stackrel{\mathbf{ˆ}}{\mathbf{A}}}_{\mathit{ff}}^{-1}{\mathbf{A}}_{\mathrm{fc}}\\ \mathbf{I}\end{array}\right],\mathbf{R}=\left[\begin{array}{cc}-{\mathbf{A}}_{\mathit{cf}}{\stackrel{\mathbf{ˆ}}{\mathbf{A}}}_{\mathit{ff}}^{-1}& \mathbf{I}\end{array}\right],$(11)

with the coarse grid matrix computed with ${\mathbf{A}}_{\mathit{coarse}}=\mathbf{RAP}$. Repeating this process on the coarse grid then builds a multigrid hierarchy. AIRG forms approximations to ${\mathbf{A}}_{ff}^{-1}$, namely, ${\stackrel{\mathbf{ˆ}}{\mathbf{A}}}_{\mathit{ff}}^{-1}$, by using fixed-order GMRES polynomials. This results in a stationary multigrid method that can be applied with just matrix-vector products (i.e., no dot products).

One key feature of AIRG is that it does not rely on any block or lower-triangular structure in our matrix. This is essential given that our spatial discretization results in a CG stencil in Eq. (3(3) $(\mathbf{A}-\mathbf{B}{\mathbf{D}}^{-1}\mathbf{C})\mathbf{\Phi }={\mathbf{S}}_{\mathbf{\Phi }}-\mathbf{B}{\mathbf{D}}^{-1}{\mathbf{S}}_{\mathbf{\Theta }},$(3) ), and hence, our linear system does not feature lower-triangular blocks in the streaming limit, unlike a traditional DG FEM. As shown in Fig. 2, if we have adapted in angle, the block-diagonal structure in our streaming/removal operator is reduced to that of blocks corresponding to each octant. We found in Ref. [4] that with a uniform angle, in both the streaming and the scattering limit, our iterative method with AIRG used is close to the fixed work in both the setup and the solve with constant memory consumption. We would hope that the structure-independent nature of AIRG gives the same performance when we have adapted in angle; we examine this in Sec. V.

IV. COARSE-FINE SPLITTING

In Ref. [4], we used the Falgout–Cleary-Luby-Jones-Plassman (CLJP) coarsening algorithm implemented in hypre to determine the CF splitting required by our AIRG multigrid method (see Ref. [34] for some general strategies related to CF splittings). In an effort to build cheaper CF splitting algorithms, in this work we also use the element agglomeration algorithms from Refs. [1] and [35]. These methods were vital to our previous work, as we needed to build and apply spatial tables on coarse elements in order to compute matrix-free matvecs on lower spatial grids. In this work we do not require the coarse elements that these methods provide, but we can still use the spatial CF points that they provide to pick which of our space/angle DOFs are fine and coarse. Given that these algorithms depend only on the spatial grid, they can be cheaper to run than algorithms that require access to the matrix entries; however, because of this, we would expect them to perform less well, given that the same spatial CF points would be applied to each angle, and hence the directionality would be ignored. For a reduction-based multigrid, the selection of good CF points results in a well-conditioned ${\mathbf{A}}_{\mathit{ff}}$; however, as we demonstrate in Sec. V, this can be ameliorated through the use of strong approximations to ${\mathbf{A}}_{ff}^{-1}$.

In this paper, when using uniform angle (i.e., for the first solve in our adapt process), our element agglomeration CF splitting has no directionality. As mentioned in Sec. II.A, however, the P⁰ angular discretization used in this work can adapt, refining in important directions. The adapt process solves a linear system with a uniformly refined angular discretization in the first step followed by angular refinement at each spatial point. From there, each subsequent adapt step continues to build anisotropically adapted angular discretizations. For the linear solves after the first step, we can use the directional information contained within the adapted angular discretizations to determine a spatially dependent coarsening direction and hence a set of CF points with directionality.

There are many ways that we could define a coarsening direction at a given spatial point. We could pick the direction of the most refined angular element, compute an average direction on the sphere across all the angular elements, compare the distribution of angles or level of refinement across the sphere, etc. For simplicity, in this work, we set the coarsening direction at each spatial node point to be the direction given by the center of the most refined angular element at that point, or if a priori angular refinement is used, the direction of that refinement is used.

We then have a set of coarsening directions at each spatial node point, and this is then used to guide our element agglomeration. The spatial coarse points are the vertices of the coarse agglomerates. If a spatial node is designated coarse, all the angular DOFs on that spatial node are also tagged as coarse. The key to this process is that it must result in a CF splitting that reflects the underlying streaming or scattering limits. One of the benefits of using element agglomeration in this fashion is that after several adapt steps, we could consider the coarsening direction to be (mostly) converged and hence freeze the element agglomeration. The spatial CF points are then frozen, and any additional angular DOFs added in subsequent adapt steps can be cheaply tagged based on the frozen spatial CF points. This could make it cheaper to form the CF splitting with many adapt steps, as we would need to perform the element agglomeration only a small number of times.

For many problems in the streaming limit, the angular adaptivity will pick out a limited number of key direction(s), and hence, the coarsening needs to occur in those directions. We should note that the coarsest level of refinement on our angular domain is given by a single basis function per octant. If we have a single important direction, for example, in Fig. 1, and our coarsening direction has been computed as, for example, $+\mathit{y}$, there will always be some angles (the unrefined elements) that are not well represented by the coarsening direction. In the limit of angular refinement, however, given the AMR-style nested refinement of our angular adaptivity, the majority of angles at that node point will be well represented by the coarsening direction.

In scattering regions, however, the angular adaptivity tends to uniform refinement, and hence, the coarsening needs to form well-shaped circular/spherical agglomerates (as there is no important direction) with agglomerates that could have a different number of fine elements compared to the streaming case, given possible differences in optimal coarsening rates. The combination of spatially dependent coarsening directions formed through angular adaptivity and scattering cross sections should therefore provide us with the information required to compute a directional element agglomeration algorithm that provides good CF splitting for the majority of unknowns in our angularly adapted problems.

There are a few related problems with this scheme. For example, both the linear system in the first adapt step and problems where uniform refinement is triggered far from the scattering limit will not have the required directional information. The first of these is not a major concern as the number of unknowns in the first adapt step is small compared to the number of unknowns at all the other adapt steps. In both cases we must return to using the directionless agglomeration algorithms described in Ref. [35]. We can also have the case where we have adapted with the angular DOFs concentrated in small regions of the spatial mesh, but the element agglomeration proceeds with a constant agglomerate size. This can result in many DOFs in those refined regions not being tagged as “coarse”; the nonuniformity of the distribution of angular DOFs across the spatial mesh therefore persists on the coarse grid. This means our multigrid may have very different operator complexity (Op Complx) when compared to uniform angle. These problems may harm the performance of our multigrid methods. We examine this further below but note that the traditional coarsening algorithms that rely on matrix entries can always be used.

IV.A. Directional Element Agglomeration Method

Previously, we presented seven different element agglomeration methods from the literature and compared their performance on scattering/absorbing problems^[35] with the matrix-free multigrid from Ref. [1]. Here, we present one of those algorithms that has been modified to use directional information. All of the algorithms mentioned in Ref. [35] can be modified (and be performed similarly).

Our element agglomeration has been modified with very simple heuristics in an attempt to roughly quantify when the solution in a given spatial region transitions from having a directional angular flux to one that is largely homogeneous in angle. The two criteria that we use are if the average scattering cross section over the agglomeration is greater than 1 cm^–1 (in this work we use the actual cross-section value on each element; ideally this would just be defined as the mean free path in an element, or an equivalent dimensionless quantity) or the number of angles on a spatial node is close to that of a uniform discretization at that level of refinement (we define “close” as having $>63\mathrm{\%}$ of the uniform angles; this is equivalent to a level 2 discretization having more than two octants refined), then agglomeration proceeds without directional information. If we do proceed with directional coarsening, the tangent vector to the face on the spatial mesh is compared with the average coarsening direction computed on that face (i.e., an average of the coarsening direction across all the spatial nodes on that face). If those two vectors are close to parallel, then agglomeration across that face is discouraged. We define close to parallel as the smallest angle between the vectors being less than $\mathit{\pi }/4$. The cleanup routine described in Ref. [35] has also been modified to use directional information. Any elements that require cleanup (e.g., unused elements, elements within completely closed agglomerates, etc.) are added to the agglomerates closest to the coarsening direction with the smallest number of elements.

Algorithm 1 uses METIS and requires setting a desired agglomerate size to control the coarsening rate. As mentioned above, typically, we would consider the ideal coarsening rate to be dependent on the cross section. Previously,^[35] we examined the ideal agglomerate size with our matrix-free multigrid applied to scattering/absorbing problems. The simple grid transfer operators that we used in that work meant that the multigrid method could be considered a geometric multigrid, and as such, we found that a very large number of elements (20 to 200 in two and three dimensions, respectively) in an agglomerate were required to keep the grid complexity low and hence maintain good performance. The same is not the case in this work, where our multigrid methods are much closer to AMG/AMGe style methods and we require high-quality interpolation/restriction for good performance across all parameter regimes. This requires much smaller numbers of elements in an agglomerate and hence higher grid complexities, although we do use the same coarsening rate in streaming and scattering problems in this work.

As in Ref. [35], once top grid agglomeration has occurred on an unstructured grid, the lower grids have fundamentally different spatial connectivity and hence come to resemble structured grids, where the agglomerate size can be easily set to a constant across levels. As such, we set the agglomerate size to 6 in two dimensions (2D)and 12 in three dimensions (3D) on the top grid, whereas on lower grids we set the agglomerate size to 2 in 2D and 4 in 3D (i.e., we perform aggressive coarsening on the top grid).

Table

Algorithm 1. METIS 5.1^[Citation36] Directional Coarsening Algorithm

1: Construct the dual-graph of the mesh

2: Construct a coarsening direction, $\mathit{a}$, at every node, by using the center of the most refined angular element

3: Compute $\mathit{s}$ to be the average scattering cross-section at every node from each of the connected elements

4: Get the number of angles on every node, $\mathit{n}$ and the number of angles with a uniform discretization, $n_{\mathit{uniform}}$

5: if $\mathit{s}>1$ or $\mathit{n}\approx n_{\mathit{uniform}}$ then

6:      Set $\mathit{a}=\mathbf{0}$ on a node

7: end if

8: Build integer area/volume weights from the dual-graph by scaling relative face areas and volumes to between 1 and 100

9: while we haven’t visited every face - denote current face as $\mathit{f}$ do

10:      Compute $a_{\mathit{avg}}$ to be the average coarsening direction on $\mathit{f}$ from each of the vertices on this face

11:      Compute $\mathit{\vartheta }$ to be the dot product between a vector parallel to $\mathit{f}$ and $a_{\mathit{avg}}$

12:      if $\mathit{\vartheta }<\mathit{\pi }/4$ and $a_{\mathit{avg}}\ne \mathbf{0}$ then

13:           Set the integer area weight on this face to be 1

14:      end if

15: end while

16: Set desired agglomerate size, $\mathit{s}$

17: Set the number of partitions as: int(number of elements/$\mathit{s}$)

18: if number of partitions $>$ 8 then

19:      Call METIS_PartGraphKway

20: else

21:      Call METIS_PartGraphRecursive

22: end if

23: Cleanup the coarsening

V. RESULTS

Outlined below are two example problems taken from Ref. [4] in the streaming and scattering limits that we use to test our P⁰ angular adaptivity. We solve our linear systems with GMRES(30) to a relative tolerance of 1 $\times$ 10^–10, with an absolute tolerance of 1 $\times$ 10^–50 (this low value ensures that the relative tolerance is always hit, and hence, we have a fair comparison of the work given different initial residuals) and use an initial guess of zero unless otherwise stated. This is the case even when we have used angular adaptivity and hence may have nonzero initial guesses from previous adapt steps. We do this to ensure fair comparisons across different material regimes at different levels of angular refinement. This is in order to show that the convergence of our method is not dependent on a good initial condition in some material regimes. In the scattering limit, the nonzero guesses from coarser angular discretizations are helpful, but in the streaming limit, ray effects mean that coarse angular discretizations often do not provide good approximations to refined angular discretizations. If using the element agglomeration CF splitting, we rerun this at each adapt step rather than freeze it after a set number of steps. All tabulations of memory used are scaled by the total NDOFs in $\mathit{\psi }$ in Eq. (2)(2) $\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}\right]\left[\begin{array}{c}\mathbf{\Phi }\\ \mathbf{\Theta }\end{array}\right]=\left[\begin{array}{c}{\mathbf{S}}_{\mathbf{\Phi }}\\ {\mathbf{S}}_{\mathbf{\Theta }}\end{array}\right].$(2) , i.e., NDOFs = NCDOFs + NDDOFs.

We use the additive preconditioners defined in Ref. [4] and all the same parameters as that work. For the application of AIRG to the streaming/removal operator, this means we use a drop tolerance on $\mathbf{A}$ of 0.0075 and $\mathbf{R}$ of 0.025. To quantify the performance of our iterative method, we use the same statistics as shown in Ref. [4], which are the following:

1. $n_{\mathit{its}}$: The number of iterations the iterative method takes to hit the required tolerance.

2. Cycle complexity (CC): The CC in the AIRG multigrid when applied to the streaming/removal operator. This counts the number of floating-point operations (FLOPs) when performing one multigrid V-cycle, scaled by the number of nonzero entries in the top grid streaming/removal operator.

3. Operator complexity (Op Complx): The Op Complx in the AIRG multigrid when applied to the streaming/removal operator. This is the sum of the nonzero entries in the operator matrix on each multigrid level, scaled by the number of nonzero entries in the top grid streaming/removal operator. If this quantity stays fixed with adaptivity, then the memory required to store the multigrid hierarchy does not grow nonlinearly as we adapt.

4. Work units (WUs): This is the number of WUs required to solve the linear system. These are simply FLOP counts scaled by the work required to compute a matrix-vector product in either streaming or scattering problems. The number of WUs is given by $n_{\mathit{its}}\times \mathrm{CC}$, plus the FLOPs required to compute the source on the righthand side of Eq. (3)(3) $(\mathbf{A}-\mathbf{B}{\mathbf{D}}^{-1}\mathbf{C})\mathbf{\Phi }={\mathbf{S}}_{\mathbf{\Phi }}-\mathbf{B}{\mathbf{D}}^{-1}{\mathbf{S}}_{\mathbf{\Theta }},$(3) and the FLOPs required to compute Eq. (4)(4) $\mathbf{\Theta }={\mathbf{D}}^{-1}({\mathbf{S}}_{\mathbf{\Theta }}-\mathbf{C\Phi }).$(4) . This quantity is then scaled by the nnzs in the streaming/removal operator (for the superscript full) in streaming problems (i.e., the FLOPs required to compute an assembled matrix-vector product) or by the FLOPs required to compute a matrix-free matrix-vector product with scattering (for the superscript mf). To enable easier comparison against DG FEMs, we also show these two quantities scaled by the FLOPs required to compute a matrix-vector product with a DG discretization (the superscript DG).

We should also note that when using angular adaptivity, the WUs listed are scaled by work required to compute a matvec in the adapted solve at each step, not the uniform solve. For example, starting with a level 1 uniform discretization, we solve the linear system, and the WUs required to do this are scaled by the FLOPs required to compute a matvec on the uniform level 1 discretization. We then perform our adapt, which uses fewer DOFs than the uniform level 2 discretization. Hence, our adapted level 2 matvec requires fewer FLOPs to compute than an equivalent uniform level 2 matvec (as we would hope with an adapted method), which means we cannot directly compare the WUs used to solve our adapted level 2 problem with the WUs used to solve a uniform level 2 problem.

The benefit of showing the WUs scaled in this fashion is that if the WUs required at each adapt step stay constant, then we have an amount of work at each adapt that scales linearly with the number of adapted DOFs. This means that we can solve problems with adaptivity in $\mathcal{O}(\mathit{n})$ FLOPs; i.e., the total work required to solve an adapted problem would therefore scale linearly in the NDOFs of all the adapt steps added together. In an attempt to show comparisons between the cost of solving a uniform problem and the total cost of solving a problem with adaptivity, we also sum the total FLOPs over all adapt steps and scale by the FLOPs required to perform a uniform matvec at the highest level of refinement that the adapt has reached; we note explicitly in the text when we have done this.

When using the Falgout-CLJP coarsening from hypre, we set a strong threshold of 0.2. The test problem in this paper is the same as in Ref. [4], namely, a 3- $\times$ 3-cm box, with a box of size 0.2 $\times$ 0.2 cm at the center of the domain, which is a source of intensity of 1 cm^–1. The same cross sections are applied across the entire domain. We apply vacuum conditions to the boundaries, and we use an unstructured triangular mesh to discretize the domain with 4464 elements and 2313 nodes in all the problems in this paper.

V.A. Pure Streaming Problem

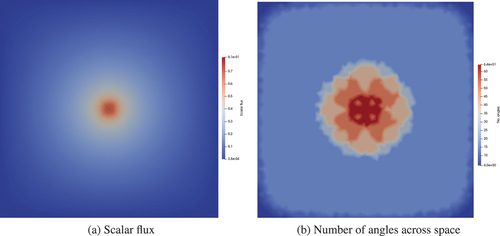
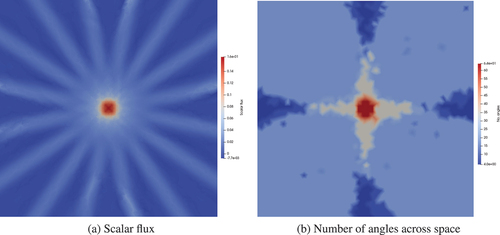
Table I shows the results from using a regular angle adapt with fixed spatial resolution (this is the third refined mesh from Ref. [4]) in the streaming limit (specifically the pure vacuum case, so the scattering and total cross sections are zero), with directional element agglomeration to compute the CF splitting. Figure 4 shows the scalar flux and the distribution of our angular resolution throughout space. We can see that our adapt process is focusing resolution in the directions away from the source and that the convergence criterion of the adaptive process (the NDOFs changing by less than 10%) has been reached after five adapt steps. We can see that for the given threshold tolerance, this results in an adapted discretization that gives the same ray effects as a uniform level 2 discretization. For example, if we kept the maximum level of refinement the same (3 in this problem) but reduced the threshold tolerance, this would cause more angles to be added to the problem (fewer than a uniform level 3 discretization would use), and we would see the same ray effects as the uniform level 3 discretization. Decreasing the tolerance further would eventually give a uniform level 3 discretization across the spatial domain.

TABLE I Results from Using AIRG on a Pure Streaming Problem with CF Splitting by Directional Element Agglomeration

CG Nodes	Adapt Step	NDOFs	$n_{\mathit{its}}$	CC	Op Complx	WUs^full	WUs^DG	Memory
2313	1	6.3 $\times$ 10^4	17	5.1	2.7	115	27.3	10.9
2313	2	9.2 $\times$ 10^4	16	5.3	2.8	112	26.9	11.3
2313	3	2.2 $\times$ 10^5	17	5.8	3.0	128	30.5	11.9
2313	4	2.8 $\times$ 10^5	16	5.2	2.8	111	26.5	11.2
2313	5	3.1 $\times$ 10^5	19	5.3	2.8	130	31.0	11.2

Fig. 4. Adapt results for a two-dimensional pure streaming problem with a small source at the center of the domain, allowing a maximum of three levels of regular angular refinement (giving a maximum number of angles as 64). The first column shows the scalar flux, and the second column shows the number of angles across space. The third column shows the resulting element agglomeration on the second spatial grid if the directional algorithm in Sec. IV.A is used (an element coloring is used to show individual agglomerates). The rows show consecutive regular adapt steps.

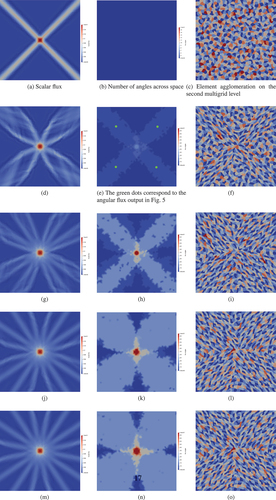
Using a regular adapt process in this problem is not necessary given that the optimal angular resolution can be easily determined a priori (refining in directions looking away from the source), but we wished to show the effect of solving our adapted discretizations at different adapt steps as there is a great degree of angular coupling as the adaptivity is converging, which helps test our iterative method as mentioned.

Figure 4 also shows that after the first adapt step, the directional element agglomeration is gluing together elements in the important direction at each spatial node, given by the refined angular flux in Fig. 5. We see that this results in an iteration count and overall work that is close to flat, with approximately 15% growth after five adapt steps. Interestingly, if we force the element agglomeration to be directionless at every adapt step, we see very similar cycle and operator complexities, with 15, 16, 17, 17, and 18 iterations. This implies that the directional element agglomeration is unnecessary. Further investigation revealed that it is the high GMRES polynomial order in AIRG ($\mathit{m}=4$, i.e., a third-order polynomial) that is compensating for the directionless CF splitting. Reducing the polynomial order to 1 with the directional CF splitting gives 17, 31, 44, 53, and 65 iterations compared with directionless at 17, 34, 40, 56, and 81 iterations. Our strong approximations to the ideal operators and F-point smoothers are compensating for the poorer CF splitting.

Fig. 5. Angular flux at four spatial points after two regular adapt steps in a pure streaming problem with a small source at the center of the domain. The four spatial points correspond to the green dots shown in Fig. 4e.

With higher spatial resolution (not pictured), the adapt can also remove the angular resolution in the regions between the rays that are added in the initial adapt steps. The coarse spatial resolution used in Fig. 4 means that numerical diffusion keeps some of the angular resolution above the removal threshold. Even with this excess resolution, we have 2.8 times and 4.8 fewer NDOFs for the adapted solves in steps 2 and 3 than in a uniform level 2 and 3 discretization in this problem. Similarly, there are 2.75 and 4.6 times fewer nnzs’s in the adapted matrices compared to the uniform. This shows that the pathology described in Sec. II.B where the nnzs grows considerably with the adapt is not seen in this problem and that the sparsity control in Sec. III is effective. The NDOFs grow 4.74 times from adapt steps 1 to 5, with the nnzs growing 4.88 times, or an increase of around 3% above the NDOFs.

Table II shows the results from using the Falgout-CLJP CF splitting instead of our directionless agglomeration algorithm, and we see a much lower iteration count with similarly flat work at each adapt step, with fixed memory use of between 10 and 11 copies of the angular flux. This shows that accounting for the directionality of all the angles (not just the important angles) can improve the convergence in the streaming limit. Both the directional element agglomeration and Falgout-CLJP CF splitting however result in close to fixed work in this streaming problem when adapting. This shows the power of combining our iterative method and P⁰ angular adaptivity and is in contrast to the results in Ref. [1], where we saw that after three angular adapt steps in a streaming problem, solving in Haar space with a matrix-free multigrid resulted in an iteration count that grew from 25 to 91.

TABLE II Results from Using AIRG on a Pure Streaming Problem with CF Splitting by Falgout-CLJP

CG Nodes	Adapt Step	NDOFs	$n_{\mathit{its}}$	CC	Op Complx	WUs^full	WUs^DG	Memory
2313	1	6.3 $\times$ 10^4	9	4.4	2.87	60	14.1	10.2
2313	2	9.2 $\times$ 10^4	11	4.7	3.2	74	17.6	10.7
2313	3	2.2 $\times$ 10^5	12	5.0	3.6	85	20.2	11.3
2313	4	2.8 $\times$ 10^5	11	4.6	3.3	73	17.5	10.7
2313	5	3.1 $\times$ 10^5	11	4.5	3.2	72	17.2	10.6

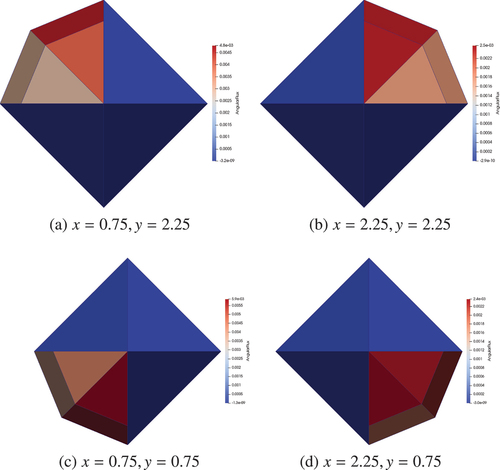
In general, with our adapted matrices, we might expect similar spectrums when compared to the uniform matrices (i.e., when comparing a uniform discretization to that of an adapt with the same maximum level of refinement), and therefore, a similar (or smaller) number of iterations would be required to converge. This is typically the case. Table II however shows that with Falgout-CLJP CF splitting, the iteration count starts at 9 given that the adapt process starts with a uniform level 1 solve; however, the second and third steps take 11 and 12 iterations.

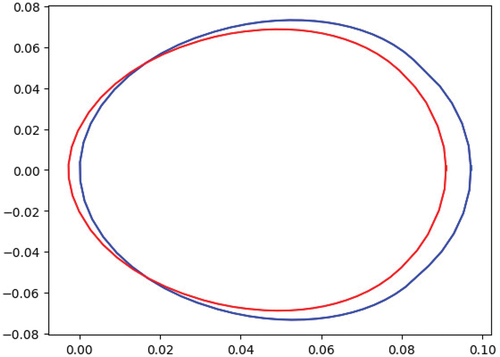
The results in Ref. [4] show that with uniform level 2 and 3 discretizations, this problem took 10 and 11 iterations to solve, respectively. The uniform level 3 matrix on this mesh has a condition number of approximately 560 compared with around 1780 for the adapted discretization in step 3 pictured in Fig. 4g, resulting in the increase in iteration count. Figure 6 shows that the field of values for the adapted discretization is closer to the origin when compared to the uniform, and the convergence of our GMRES polynomials is affected by this.^[37] As noted, the adapted discretization has fewer DOFs (and nnzs’s), so it is still much cheaper to solve than the uniform discretization, but it is worth noting that solving the matrices generated by our adapt steps is not always equivalent to solving a uniform discretization.

Fig. 6. Field of values of the streaming operators on the third spatial grid. Blue is uniform level 3 angular refinement, and red is an adapted angular discretization with a maximum level of refinement of 3.

V.B. Scattering Problem

We now examine the performance of our additively preconditioned iterative method with adaptivity in the scattering limit, where we set the total and scattering cross sections in the entire domain to be 10.0 cm^–1. The cycle and Op Complx listed are for AIRG on ${\mathbf{M}}_{\mathrm{\Omega }}$. We require only three adapt steps to converge the adaptive process in this problem.

Figure 7 shows this adapt process, and we can see that the majority of the angular resolution in the problem is focused around the source (with Fig. 8 showing the angular flux and adapted resolution at three different spatial points). Figure 7 also shows that given the high scattering cross section, the element agglomeration has proceeded uniformly, with no directional information after the first adapt step.

Fig. 7. Adapt results for a two-dimensional pure scattering problem with total and scatter cross sections of 10.0 with a small source at the center of the domain, allowing a maximum of three levels of regular angular refinement (giving a maximum number of angles as 64). The first column shows the scalar flux, and the second column shows the number of angles across space. The third column shows the resulting element agglomeration on the second spatial grid if the directional algorithm in Sec. IV.A is used (an element coloring is used to show individual agglomerates). The rows show consecutive regular adapt steps.

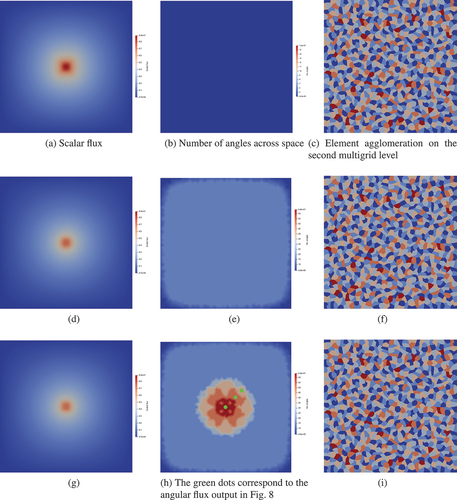
Fig. 8. Angular flux at three spatial points after three regular adapt steps in a pure scattering problem with a small source at the center of the domain. The three spatial points correspond to the green dots shown in Fig. 7h.

Table III shows that with the CF splitting by element agglomeration, we see a plateau in the iteration count and work. In contrast to the pure streaming problem in Sec. V.A, performing the CF splitting with Falgout-CLJP results in an identical iteration count (see Table IV), with slightly higher work due to the higher CC. This confirms that although the element agglomeration results in poorer CF splittings, the streaming/removal operator is easier to invert, and in problems with a large removal term, a simple CF splitting algorithm without access to the matrix entries can be sufficient to ensure scalability.

TABLE III Results from Using Additive Preconditioning on a Pure Scattering Problem with CF Splitting by Element Agglomeration

CG Nodes	Adapt Step	NDOFs	$n_{\mathit{its}}$	CC	Op Complx	WUs^mf	WUs^DG	Memory
2313	1	6.3 $\times$ 10^4	25	3.9	2.0	38	69	16.9
2313	2	2.4 $\times$ 10^5	27	3.8	2.0	39	72	16.5
2313	3	3.1 $\times$ 10^5	27	3.8	2.0	38	76	16.5

TABLE IV Results from Using Additive Preconditioning on a Pure Scattering Problem with CF Splitting by Falgout-CLJP

CG Nodes	Adapt Step	NDOFs	$n_{\mathit{its}}$	CC	Op Complx	WUs^mf	WUs^DG	Memory
2313	1	6.3 $\times$ 10^4	25	4.1	1.7	38	69	17.2
2313	2	2.4 $\times$ 10^5	27	4.0	1.4	39	73	16.5
2313	3	3.1 $\times$ 10^5	27	4.1	1.4	38	77	16.5

For both methods, the iteration count for each of the adapt steps is lower or equal to that of the uniform angular refinement shown in Ref. [4] with the work and memory use constant at around 38 WUs and 17 copies of the angular flux, respectively. The NDOF grows 4.96 times from adapt steps 1 to 3, with the growth in the nnzs of the streaming/removal operator at 5.07, giving an increase of around 2%.

V.C. Reduced Tolerance Adapts

In the previous sections, we have shown that AIRG and our additively preconditioned iterative method can solve adapted P⁰ problems in both the streaming and the scattering limit with close to fixed work with a zero initial condition used at each adapt step. In practice, however, we would like to use the solution from the previous adapt step as an initial condition to reduce the number of iterations. In streaming problems where the ray effects between different adapt steps do not align, we find this does not change the convergence. In scattering problems, however, it can help reduce the iteration count.

Furthermore, our previous work has used reduced tolerance solves^[1–3] to decrease the cost of our adaptive process, where the linear system at each adapt step, except the last, is solved to a bigger tolerance, typically 1 $\times$ 10^–3 in the 2-norm. This is not very robust and requires problem-specific tuning. However, we noted in Ref. [1] that we only need to converge sufficiently such that the error in each of our wavelets (this is also true for any hierarchical angular discretization, such as P_n or FP_n) has converged to within a relative tolerance of 0.1, so that we can determine whether the error is greater than the refinement threshold of 1.0 defined in Sec. II.A (and equivalent for de-refinement with a threshold of 0.01). The convergence criteria for the iterative method during each adapt step, except the last, can therefore be set as the infinity norm on the relative error being less than 0.1.

With goal-based adaptivity, this requires that the error metric used has a very good effectivity index, and we are forced to compute the goal-based error metric at each iteration, which may be expensive. For regular adaptivity, however, this is very simple as the error is given by a scaled version of our P⁰ solution mapped to wavelet space. As such, with our P⁰ discretization, we need to map to the equivalent wavelet space [at the cost of an $\mathcal{O}(\mathit{n})$ mapping] and compute the relative change of each wavelet coefficient. If all the wavelet coefficients have converged to a relative tolerance of 0.1, our iterative method has converged sufficiently for this adapt step, and we can exactly determine the refinement/de-refinement required by the next adapt step.

This is the weakest convergence criterion that by definition gives the exact adapted discretization that would have been achieved by solving to a tighter tolerance. Using a different convergence criterion to build up the adapted discretization would either do more iterations than necessary or risk having poorly converged wavelet coefficients that may cause incorrect refinement/de-refinement. For the last adapt step, where we wish to fully converge our solution (given the adapted discretization that we have built up), we use the same convergence criterion defined in Sec. V, namely, 1 $\times$ 10^–10 reduction in the relative residual. However, we are free to choose a different criterion for this final solve, for example, converging the scalar flux to only a given tolerance, if desired.

The use of these reduced tolerance solves in prior adapt steps is made more difficult by our subgrid-scale discretization, as the error calculation and thresholding after each adapt step uses $\mathbf{\Psi }$. This requires computing $\mathbf{\Theta }$ with Eq. (4)(4) $\mathbf{\Theta }={\mathbf{D}}^{-1}({\mathbf{S}}_{\mathbf{\Theta }}-\mathbf{C\Phi }).$(4) at every iteration when solving Eq. (3)(3) $(\mathbf{A}-\mathbf{B}{\mathbf{D}}^{-1}\mathbf{C})\mathbf{\Phi }={\mathbf{S}}_{\mathbf{\Phi }}-\mathbf{B}{\mathbf{D}}^{-1}{\mathbf{S}}_{\mathbf{\Theta }},$(3) rather than solving Eq. (3)(3) $(\mathbf{A}-\mathbf{B}{\mathbf{D}}^{-1}\mathbf{C})\mathbf{\Phi }={\mathbf{S}}_{\mathbf{\Phi }}-\mathbf{B}{\mathbf{D}}^{-1}{\mathbf{S}}_{\mathbf{\Theta }},$(3) and then computing $\mathbf{\Theta }$ afterward. This is costly given the matrix multiplications in Eq. (4)(4) $\mathbf{\Theta }={\mathbf{D}}^{-1}({\mathbf{S}}_{\mathbf{\Theta }}-\mathbf{C\Phi }).$(4) . Instead, we map the coarse variable $\mathbf{\Phi }$ to wavelet space at each iteration and check the convergence of the wavelet coefficients on the continuous mesh. This does not necessarily produce the exact adapted discretization that would otherwise have been built, but it is very close. There is typically only a handful of wavelets that would otherwise be refined/de-refined at any single adapt step and those can be picked up by subsequent steps.

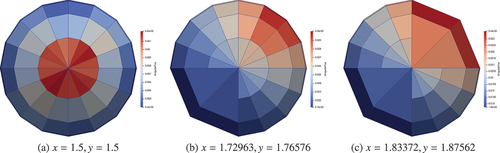
Figure 9 shows the results from using this reduced tolerance in a streaming problem, and we can see that after five adapt steps, this results in a scalar flux and adapted discretization almost identical to that without the reduced tolerance solve, shown in Figs. 4m and 4k. We can see in Fig. 9 that there is a small region at around $\mathit{x}=1.5,\mathit{y}=0$ where refinement has not been triggered in the same way, but overall, we find this is a very robust way to reduce the cost of our adaptive process.

Fig. 9. Adapt results after five regular adapt steps in a pure streaming problem with adapt steps prior to the final step solved with wavelet-based reduced tolerance to determine convergence.

Table V shows the results from using both a nonzero intial guess (which has very little effect) and the reduced tolerance solves in a streaming problem. We should note that we have included the extra cost that comes from mapping to wavelet space and computing the relative change in each wavelet coefficient at every iteration in the WUs. Compared to Table II, we can see that the cost of each of the first four adapt steps has been reduced considerably.

TABLE V Results from Using AIRG on a Pure Streaming Problem with CF Splitting by Falgout-CLJP with Adapt Steps Prior to the Final Step Solved with Wavelet-Based Reduced Tolerance to Determine Convergence

CG Nodes	Adapt Step	NDOFs	$n_{\mathit{its}}$	CC	Op Complx	WUs ^full	WUs^DG	Memory
2313	1	6.3 $\times$ 10^4	2	4.4	2.87	22	5.3	10.2
2313	2	9.2 $\times$ 10^4	6	4.7	3.3	47	11.3	10.6
2313	3	2.2 $\times$ 10^5	7	5.0	3.6	56	13.4	11.1
2313	4	2.8 $\times$ 10^5	7	4.6	3.3	53	12.6	10.6
2313	5	3.1 $\times$ 10^5	10	4.5	3.2	66	15.9	10.4

In order to compare the cost of solving a uniform discretization with the total cost of forming and solving an adapted discretization, Table VI shows the sum of FLOPs across all adapt steps, rescaled by the nnzs in a uniform level 3 streaming/removal operator. We can see that after five adapt steps, the total cost of adapting is roughly equivalent to that of solving the uniform problem, with a reduction in the NDOFs of roughly three times. The reduced tolerance solve, however, takes roughly 20% fewer FLOPs than the uniform equivalent. This cost saving only increases as the number of adapt steps is increased; previously, in Refs. [1], [2], and [3], we typically needed a higher number of adapt steps than five in order to beat a uniform discretization.

TABLE VI Total and Rescaled WUs from Using AIRG on a Pure Streaming Problem with CF Splitting by Falgout-CLJP*

CG Nodes	Maximum Angle Order	Uniform or Adapt	Adapt Steps	NDOF Final Adapt Step	Total WUs Rescaled
2313	3	Uniform	—	1 $\times$ 10^6	70
2313	3	Adapt	5	3.1 $\times$ 10^5	72
2313	3	Reduced tolerance adapt	5	3.1 $\times$ 10^5	54

*The WUs have been summed across all adapt steps and scaled by the nnzs in the uniform level 3 streaming/removal operator, so that the costs of uniform and adapted calculations can be compared.

We see similar results with scattering, with Table VII showing a substantial reduction in the number of iterations for the first two adapt steps and Fig. 10 showing that the resulting adapted discretization is almost identical to that in Fig. 7h. Table VIII compares the total cost of all three adapt steps, scaled by the FLOPs required to compute the matrix-free matvec for the uniform level 3 angular discretization. We can see that with scattering, the adapted discretization beats the uniform after only three adapt steps in this problem, with the reduced tolerance solve further reducing this cost. This gives an adapted discretization with approximately three times fewer DOFs, which can be computed at roughly 42% of the cost of an equivalent uniform discretization.

TABLE VII Results from Using Additive Preconditioning on a Pure Scattering Problem with Adapt Steps Prior to the Final Step Solved with Wavelet-Based Reduced Tolerance to Determine Convergence

CG Nodes	Adapt Step	NDOFs	$n_{\mathit{its}}$	CC	Op Complx	WUs^mf	WUs^DG	Memory
2313	1	6.3 $\times$ 10^4	2	4.1	1.7	4	7.6	17.2
2313	2	2.4 $\times$ 10^5	10	4.0	1.4	16	28.8	16.2
2313	3	3.1 $\times$ 10^5	25	4.1	1.4	36	72	16.3

TABLE VIII Total and Rescaled WUs from Using AIRG on a Pure Scattering Problem with CF Splitting by Falgout-CLJP*

CG Nodes	Maximum Angle Order	Uniform or Adapt	Adapt Steps	NDOF Final Adapt Step	Total WUs Rescaled
2313	3	Uniform	—	1 $\times$ 10^6	41
2313	3	Adapt	3	3.1 $\times$ 10^5	26
2313	3	Reduced tolerance adapt	3	3.1 $\times$ 10^5	17

*The WUs have been summed across all adapt steps and scaled by the FLOPs required to compute a uniform level 3 matvec, so that the costs of uniform and adapted calculations can be compared.

Fig. 10. Adapt results after three regular adapt steps in a pure scattering problem with adapt steps prior to the final step solved with wavelet-based reduced tolerance to determine convergence.

VI. CONCLUSIONS

In this work, we presented an adaptive angular discretization with nested hierarchical P⁰ angular elements that can be mapped to the Haar wavelet space that we presented previously.^[1] Once adapted, the angular matrices required between two nodes with different angular discretizations were no longer block diagonal, and hence, we introduced a modified stabilization term for use with our low-memory subgrid-scale FEM discretization that ensured that the nnzs in our discrete streaming/removal operator did not grow considerably with adaptivity. We found that in both pure streaming and scattering problems, this growth was 2% to 3% above that expected from the number of adapted DOFs. This meant that we could scalably assemble the discrete streaming/removal operator with angular P⁰ adaptivity and hence use AIRG and the additively preconditioned iterative method that we had developed.^[4] The results from this showed that we can solve our adapted problems in both streaming and scattering problems with very close to fixed work and memory. Our methods do not rely on Gauss-Seidel methods/sweeps, block-diagonal, lower-triangular structure, or diagonal/block scaling of our matrices and can be applied to many different (potentially adapted) discretizations.

Given that our P⁰ discretization is equivalent to a Haar wavelet discretization, with adaptivity we mapped our solution to Haar space [in $\mathcal{O}(\mathit{n})$, where $\mathit{n}$ is the number of DOFs] and hence tagged the angular elements that require angular refinement/de-refinement. As such, we introduced the ability to robustly build up our adapted discretization with regular adaptivity with reduced cost. We achieve this by mapping the coarse solution $\mathbf{\Phi }$ to Haar space and testing the relative convergence of each wavelet coefficient at each iteration of our iterative methods. This resulted in an adapted discretization very similar to that which would normally be produced and a large reduction in the iteration count of every adapt step prior to solving the final adapted discretization.

In a simple box test problem, this reduced the crossover point of when our adaptive process requires less work to compute than a uniform discretization. For more complex problems (e.g., with heterogeneous material properties), the crossover point will be different, but this work helps to show the benefit of forming a P⁰ discretization hierarchically that can be mapped to an equivalent wavelet space, even when the solve occurs in ${\mathrm{P}}^0$ space. Our refinement/de-refinement is simple, and we can use this to robustly reduce the cost of our adapt process with regular adaptivity.

We also presented a CF splitting algorithm based on element agglomeration that could use the adapted angular discretization at each spatial point to determine important directions and hence produce a semicoarsening in the streaming limit without needing the matrix entries. We found that this performed worse than typical CF splitting algorithms like Falgout-CLJP when used to invert the streaming operator, but when used with AIRG to invert the streaming/removal operator with a large total cross section, this method scaled similarly to Falgout-CLJP but with approximately twice the work in the solve. Given that it is simple to freeze the spatial element agglomeration after a few adapt steps and then simply tag any additional angular unknowns as coarse or fine, it may work out cheaper overall to use an element-agglomeration CF splitting in scattering problems with many adapt steps, but we leave examining this for future work.

Overall, the combination of Falgout-CLJP CF splitting, AIRG, and our additively preconditioned iterative method resulted in close to scalable work in the solve in both the streaming and scattering limits with angular adaptivity for the Boltzmann transport problem. In previous work,^[1] we found that in the streaming limit, the iteration count of a matrix-free multigrid method solving in Haar space tripled after only three adapt steps in angle; here, we found that the iteration count of our new method went from 9 to 12 after only three adapt steps. We believe that this makes our iterative method an attractive choice for solving adapted discretizations of the BTE. Future work will involve building an optimized version of this method in order to compare the crossover point where our P⁰ adaptivity results in a lower run time than a uniform discretization, reusing components built in prior adapt steps in order to reduce setup times and examining the performance with adaptivity in parallel with load-balancing.

Acknowledgments

The authors would like to acknowledge the support of the Engineering and Physical Sciences Research Council (EPSRC) through the funding of EPSRC grants EP/R029423/1 and EP/T000414/1.

Disclosure Statement

No potential conflict of interest was reported by the author(s).