Reasoning about Representations: Effects of an Early Math Intervention

ABSTRACT

The outcomes of a longitudinal randomized number sense intervention including pre-, post- and follow-up tests are reported. The intervention was conducted in Grade 0 when children were six years old. Using Concrete-Representational-Abstract principles, a structured explicit 10-week program focusing on numbers and collective reasoning about representations was conducted by the classroom teachers. In addition to their regular mathematics teaching, a trained control group received an equally structured and explicit intervention program but without the critical mathematics component. The children in the experimental group outperformed the children in the control group on number sense growth between the pre- and the post-test. There was also a sustained effect of the intervention nine months later when children were assessed in Grade 1.

KEYWORDS:

• Mathematics
• intervention
• number
• reasoning
• representations

School should provide an opportunity for everybody to learn mathematics. Yet, as a wealth of studies show, individuals’ possibility to succeed in school is heavily dependent on their school-entry mathematics skills (Aunola, Leskinen, Lerkkanen, & Nurmi, 2004; Bailey, Siegler, & Geary, 2014; Claessens & Engel, 2013; Claessens, Duncan, & Engel, 2009; Duncan et al., 2007; Geary, 2011; Jordan, 2007; Jordan, Glutting, & Ramineni, 2010; Koponen, Salmi, Eklund, & Aro, 2013; Laski & Yu, 2014 Morgan, Farkas, & Wu, 2009; Schneider et al., 2017). A longitudinal study by Watts, Duncan, Siegler, and Davis-Kean (2014) indicates that the development of mathematical abilities in the spectrum 4.5–7 years old seem strongly connected to mathematical knowledge through age 15.

Promising results indicate that preschool education can provide a firm foundation for later learning (e.g., Jordan, Kaplan, Ramineni, & Locuniak, 2009; Melhuish, Sylva, Sammons, Siraj-Blatchford, & Taggart, 2008; Vennberg & Norqvist, 2018). However, a review by Mononen, Aunio, Koponen, and Aro (2014) shows that few studies have focused on six-year-olds. The authors stress the importance of further intervention research to provide teachers with evidence-based practices to enhance the learning of mathematics for kindergarten children. The study reported here is one such attempt. In Sweden, Grade 0¹ is a preliminary year before formal schooling with an aim to function as a bridge between the informal learning that occurs in preschool and the more formal learning of compulsory school (National Agency for Education, 2017). Children start Grade 0 the year they turn 6 years old. This makes Grade 0 a particularly well-suited part of the school system for an early mathematics intervention. Any intervention design aimed at young children has to consider the connection between informal and formal mathematics, which is a crucial aspect of teaching and learning mathematics (Baroody, Eiland, & Thompson, 2009; Clements & Sarama, 2007; Desoete, Ceulemans, De Weerdt, & Pieters, 2012; Jordan, 2007; Purpura, Baroody, & Lonigan, 2013).

Among successful and well-researched previous interventions several follow systematic and explicit teaching, as described by Gersten et al. (2009), involving rather formalized teaching with among other things teacher think-alouds. Other important intervention examples build on learning trajectory type designs, based on developmentally sequenced activities, which help structure teacher’s assessment and intervention with individual students (Clements & Sarama, 2009; Clements, Sarama, Spitler, Lange, & Wolfe, 2011). The intervention design presented here share similarities with both those design types, but also differs in important ways. For example, teacher think-alouds are not used. Instead, to allow teachers to enhance and facilitate children’s connections between informal and formal thinking a main instructional tool is collective reasoning, that is, when the teacher orchestrates a discussion between the children, and between the children and the teacher, about the mathematical content.

To test these ideas, a 10-week math intervention was carried out intended to develop number sense among children in Grade 0 by supporting teacher use of an explicitly described mathematics instructional program that focuses on numbers, reasoning and representations. In a cluster randomized controlled trial, the effects of the program were investigated, using pre-, post-, and a delayed post-test. The main aim of the study was to examine the effect of the intervention. Since it is known that there are relationships between working memory and mathematical achievement (De Smedt et al., 2009; Li & Geary, 2017) and between working memory, language and mathematics (Kleemans, Segers, & Verschaffel, 2011; Kyttälä, Aunio, Lepola & Hautamäki, 2014), a secondary aim was to examine if visual and verbal working memory and grammatical language comprehension at the pre-test could predict mathematical skills after the intervention.

Early Numeracy Skills and Number Sense

The intervention program aims is to develop children’s number sense. Following a tradition from mathematics education research, we use the term number sense to encompass skills related to number patterns, magnitude comparisons, counting, estimating and number transformations (Jordan, 2007). In neuroscience and cognitive psychology, the term number sense typically denotes only the basic abilities related to non-symbolic numerosity that humans have in common with many animals (Dehaene, 1997). Number sense in the sense we use it is sometimes called early numeracy, early numerical skills, basic number skills, or core numerical skills and these terms refers both to non-symbolic and symbolic numerical knowledge and skills (De Smedt, Noël, Gilmore, & Ansari, 2013; Kolkman, Kroesbergen & Leseman, 2013; Xenidou-Dervou et al., 2018). Symbolic number sense involves knowledge of number words, written numerals, and an understanding that numbers represent magnitude and are used to measure quantities and that number have both a cardinal and an ordinal meaning (e.g., Aubrey, Dahl, & Godfrey, 2006; Aunola et al., 2004; Geary & vanMarie, 2016; Sarama & Clements, 2009), and that numbers are about relations and patterns (Mulligan, 2011; Nunes et al., 2007; Papic, Mulligan, & Mitchelmore, 2011).

To shed light on which sets of early numerical skills that are the crucial for children’s future mathematical development, Aunio and Räsänen (2016) reviewed longitudinal studies and based on classifying items in tests used in these studies, they produced four categories of core numerical skills: symbolic and non-symbolic number sense (basic magnitude comparison); understanding mathematical relations; counting skills; and basic skills in arithmetic.

Number sense development is not only about incorporating new skills from such categories though but relies heavily on integrating skills with each other, an insight fundamental in the theory of the central conceptual structure for whole numbers (Okamoto & Case, 1996). This theory describes two major schemas in number sense development. The global quantity schema concerns discriminations between concepts such as “more or less” or “longer or shorter”. The initial counting schema concerns counting and the question of how many. Making these structures more integrated depends on the use of symbols and operational signs as representations of numbers and number operations. Through such integration, a new conceptual structure called the mental number line emerges (Okamoto & Case, 1996). The mental number line is a construct that makes comparison of numbers, reasonable estimates and use of efficient counting strategies possible and it can serve as s a powerful tool for arithmetic reasoning (see Fosnot, 2007; Kilpatrick, Swafford, & Findell, 2001). Number estimation and the ability to use a number line is a key component in the development of children’s number sense (Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Griffin, 2007; Laski & Yu, 2014; Siegler & Booth, 2004). In the work of Griffin, the theory of Okamotó and Case have been operationalized in the form different representations of numbers like objects, dot patterns or lines, with the explicit goal to help children construct an organized knowledge network in which these ideas are interconnected by making the children experience that the same set verbal expressions for quantification and comparison translate across the different representations of number (Griffin, 2007).

Reasoning with Number Representations

Fundamental to number sense is reasoning abilities such as the ability to verbally and symbolically make connections between several representations or between a mathematical idea and another idea (Nunes, Bryant, Evans, & Barros, 2015). Such abilities seem to be typical of children who seek patterns and structure in new situations, a process that is critical to abstract thinking and generalization and can also facilitate working memory processes (Mulligan, 2011). In collaboration with teachers and peers, children develop their intuitive ideas through a more general type of reasoning (Stein, Engle, Smith, & Hughes, 2008; Yackel & Hanna, 2003), thus helping each other to refine and revise their arguments (Mueller & Maher, 2009).

When children are given the opportunity to use different forms of expression they can take advantage of one another’s thoughts and ideas and encounter different ways of thinking (Ahlberg, 2011; Mueller & Maher, 2009; Stein et al., 2008). The fact that numbers are not physical objects in their own right highlights the centrality of children’s ability to see sameness in things (representations) that look completely different and to reason about the sameness of concepts (Sfard & Lave, 2005). By the conscious act of using five fingers to represent five blocks, such sameness can be highlighted and reasoned about even before non-iconic symbols such as numerals are used. In the present intervention teacher and children use physical objects such as blocks, cubes, and fingers, though mathematical thinking is also supported by the use of signs, such as words, pictures, and drawings that include dots, lines, different icons, numerals, and number lists. Since working memory is consistently found to correlate with mathematics achievement it will also be addressed here (Kyttälä, Aunio, & Hautamäki, 2010; Li & Geary, 2017; McKenzie, Bull, & Gray, 2003; Rasmussen & Bisanz, 2005).

Early Numeracy and Working Memory

The research community has devoted considerable interest in the relation between working memory and low mathematical achievement. Bisanz, Sherman, Rasmussen, and Ho (2005) showed that visuospatial working memory is a good predictor of early numeracy skills in Kindergarten but not in Grade 1. This is also supported by several other studies, claiming that visuospatial working memory may be more important for early numeracy learning while verbal working memory skills play an important supporting role in primary school (Andersson & Lyxell, 2007; Kyttälä et al., 2010; McKenzie et al., 2003; Rasmussen & Bisanz, 2005).

Raghubar, Barnes, and Hecht (2010) claim that preschool, and elementary school children as well as adolescents use visuospatial and executive skills for the learning and applying of new skills and concepts, while they use verbal working memory after a skill has been learned. This could perhaps explain why some studies like Toll and Van Luit (2012) found that verbal, but not visuospatial, working memory correlated significantly with early numeracy skills while Kyttälä et al. (2010) found that preschool children with poor early mathematical skills performed low in both verbal and visuospatial working memory tasks.

Preschool children often seem to have difficulty solving verbal story problems even when they can solve nonverbal calculations using object representations (Dyson, Jordan, & Glutting, 2011). It may be that preschool children have difficulties accessing mental representations of quantities when explicit physical referents are not provided (Gersten, Jordan, & Flojo, 2005; Levine, Jordan, & Huttenlocher, 1992). One reason for this may be that the working memory requirement is too large (Geary, 2011; Geary et al., 2007; Krajewski & Schneider, 2009; Kyttälä et al., 2010).

It has been argued that when younger children solve number word problems they rely on an analogous mental representation of the quantities, that is, tokens that can be manipulated (Rasmussen & Bisanz, 2005). As these mental representations seem to be stored in the visuospatial working memory, they are especially useful in combination with visually presented tasks. With more formal schooling, children seem to make increasingly more use of verbally or symbolically coded representations of number combinations. This would mean that even for the same task, the working memory requirements might be more visuospatial at lower development levels and more verbal at higher development levels. However, a recently published study (Li & Geary, 2017) confirm the importance of first-to-fifth grade gains in visuospatial working memory in predicting gains in mathematics achievement through early adolescence. They did not examine for which types of mathematics the relation applies but they emphasize that instruction focusing on the use of visuospatial representations could be especially useful to support mathematical problem-solving.

The importance of symbolization and verbalization is also indicated by the longitudinal study on number sense growth of children in Grades 1 through 3 (Jordan et al., 2010). Also when controlling for age, language, spatial reasoning, and memory, they found that underlying most learning difficulties associated with mathematics are weaknesses in intermediate symbolic number sense related to counting, number relationships and basic operations. This is consistent with Purpura et al. (2013), who note that the transition from children’s informal everyday mathematical knowledge to formal school-taught mathematical knowledge is a critical juncture in number sense development. They further claim that there is no direct connection between informal and formal knowledge. Rather, it is necessary to connect informal knowledge to written symbols as these symbols provide a bridge between informal and formal skills. The ability to identify numerals is not enough to make this transition. Rather, the conceptual ability to understand the meaning of the written symbols is also necessary (Aunio & Räsänen, 2015; Baroody et al., 2009; Clements & Sarama, 2007; Desoete et al., 2012).

Early Numeracy Interventions

In light of the importance of early mathematical skills, there is an extensive interest in conducting early intervention in mathematics (e.g., Clements & Sarama, 2009; 2011; Dyson et al., 2011; Dyson, Jordan, Beliakoff, & Hassinger-Das, 2015; Griffin, 2007; Mononem & Aunio, 2016; Nunes et al., 2007; Nunes et al., 2015; Shanley et al., 2017; Toll & Van Luit, 2012), of which several have been determined to be efficient. A review of intervention studies by Gersten et al. (2005) as well as the meta-analysis of Gersten et al. (2009) suggest that the most effective instructional design for struggling learners is one that is both systematic and explicit. They provide three principles of such a design.

(1) Ensure that instructional materials are systematic and explicit. In particular, they should include numerous clear models of easy and difficult problems, with accompanying teacher think-alouds.

(2) Provide students with opportunities to solve problems in a group and communicate problem-solving strategies.

(3) Ensure that instructional materials include a cumulative review in each session (Gersten et al., 2009, p. 22).

From the wealth of intervention studies done on early numeracy, we will mention three that are particularly interesting in the context of the present study.

Clarke, Smolkowski, Baker, Fien, and Chard (2011) conducted a one-year randomized controlled study with 120, 45-minutes whole class lessons over one year including about 1300 kindergartners and 64 teachers. The mathematical content was focusing whole numbers, geometry, and measurement. The intervention followed the explicit instruction paradigm (Gersten et al., 2009). One interesting part of the design is the use of CRA-sequence (Concrete, Representational, Abstract). The CRA idea was used by Witzel, Mercer, and Miller (2003) to act as a transition between informal and formal mathematics. The instruction was delivered by the teachers, who received curricula training throughout the school year. At-risk treatment children made significantly greater gains than at-risk children in the control group and also made greater gains than peers who were not at risk, thus reducing the achievement gap.

Nunes et al. (2007) conducted an intervention that was administered to six-year-old children 40 minutes once a week over 12 weeks. Instruction, delivered in small group format by a researcher, was focused on additive composition such as the inverse relation between addition and subtraction, and solving story problems with inverse addition and subtraction using e.g., fingers, blocks, and pictures. This intervention is interesting to us because of the particular focus on reasoning. The children in the experimental group (n = 12) showed significantly higher gains than the control group (n = 14) in a test on logical competence at posttest, in a test of mathematics achievement at delayed posttest and also in an assessment of children’s achievement given by the schools.

By building on “the conceptual structure of whole numbers” (Okamoto & Case, 1996) and a focus on quantity, numbers, counting, and formal symbols, Griffin (2007) conducted a study on a program designed to create networks of relationships between different aspects of number and counting in various contexts was created. The program was positively evaluated over a 3-year period, beginning in Grade 0 and ending in Grade 2 (Griffin, 2007). Both the intervention group and the control group started far behind the normative group. By the end of Grade 2, the intervention group performed equal to the normative group.

The Present Study

The intervention design is grounded in a review of the literature. The concept of systematic and explicit teaching has formed a basis when constructing the present intervention, which we describe below. We deviate from the principles (Gersten et al., 2009) mentioned above, by not using think-alouds or any formal cumulative reviews. The present intervention can be thought of as a proof of concept for a model which is highly systematic and explicit but where the teacher’s responsibility is to ensure that every child gets to reason about the problems, the solutions and how they were represented with the other children in the group and connected to formal representations. This means that the program is also inspired by the focus on reasoning in intervention work by Nunes et al. (2007). Below we describe three fundamental design principles of the program.

A Systematic and Explicit Idea of What is to be Learned

The interventions mentioned in the previous section all build on number sense as a web of interrelated concepts that principally build on each other, but the content and order between the concepts differ based on what is perceived to be the basis for the development of number sense. We build on the theory of the central conceptual structure for whole numbers where schemas for quantity and counting are developed separately but then integrated into a new cognitive structure (Griffin, 2007; Okamoto & Case, 1996). In a similar fashion, the present intervention builds on integrating multiple representations of number relating to both continuous quantities, numerosity, and order relations as well as iconic and non-iconic symbols (Sterner & Helenius, 2015). A basic tenet in our design is that mathematical objects and, in particular, the concept of number are naturally polysemic (Winsløv, 2004), meaning that for any mathematical object, there are multiple representations and that reasoning about distinct types of representations are important in their own right, but the translation among and between them is essential (see Lesh, Post, & Behr, 1987).

A Systematic and Explicit Description of Activities Intended to Support Learning

Based on the intervention research review and an analysis of the number concept and its supporting structures presented earlier, we organized the intervention into the following themes: sorting, classifying and patterns; numbers, counting, and patterns; part-part-whole and the number line. Central aspects of the number concepts are presented repeatedly as the children move through these themes under the guidance of the teacher.

A Systematic and Explicit Instruction for Each Activity

In each theme a multitude of practical activities is conducted in cycles, each of which involves six phases. Each cycle focuses on a particular problem introduced with the help of concrete objects. The pedagogy is inspired by the concrete-representational-abstract (CRA) model (Witzel et al., 2003) used in the intervention presented by Clarke et al. (2011) and Clarke et al. (2015). Our design modifies it into a more investigative approach (Baroody, Cibulskis, Lai, & Li, 2004) that we will describe in the methods section.

Aims

A 10-week math intervention was carried out intended to develop number sense among children in Grade 0 by supporting teacher use of an explicitly described mathematics instructional program that focuses on numbers, reasoning, and representations. The aims of the study were to (1) examine the effect of the intervention at the immediate post-test and at the follow-up test one year later, and (2) to examine if visual and verbal working memory and grammatical language comprehension at the pre-test could predict mathematical skills at the immediate post-test and the follow-up test one year later.

Method

Participants

Eleven schools with 14 socially comparable Grade 0 classes in a medium-sized municipality in Western Sweden were invited to participate in the current study. Nine schools that included 12 classes accepted the invitation. Written information was provided to the children’s parents and informed consent was obtained for all children before they were assigned to an experimental or a trained control group. Two assignments were conducted. (1) The 12 Grade 0 classes were randomly assigned to an experimental group or a trained control group with six classes in each group. (2) Within each of the 12 classes, the children were randomly assigned such that all children in the experimental group participated in the training, but only half of them were subjected to testing and thus included in the study. The total sample of tested children included 124 children, of whom 62 (34 boys and 28 girls) were allocated to the experimental group and 62 (38 boys and 24 girls) to the control group. Children ranged in age from 6 years 0 months to 7 years 1 month (M = 6 years 5 months; SD = 3.3 months) at the time of the pre-test. All children spoke Swedish, but four were not native Swedish speakers. Two children in the experimental group moved before the follow-up test and thus participated only in the pre-, and post-test.

Intervention

The experimental group received 30 minutes of daily instruction using the intervention program described below over a period of 10 weeks. The control group participated in ordinary activities in mathematics. We wanted to compare the effect of the mathematics intervention with the effect of ordinary mathematics education offered by the schools. To compensate for the so-called Hawthorne effect (McCarney et al., 2007), that attention given to the experimental group in itself improves the result, the control group received 30 minutes of daily phonological awareness training for 10 weeks using a theoretically well-established program (Lundberg, Frost, & Petersen, 1988). The phonological awareness training program is widely used in Sweden (Lundberg, 2007), and was chosen because it is structurally similar to the mathematics intervention but free from all mathematical content. The classroom teachers delivered the trainings for both groups. The teachers in the experimental group ranged in instructional practice from 1 to 39 years (M = 14.5 years), and the teachers in the control group ranged in instructional practice from 2 to 27 years (M = 14.1 years). The teachers in the control group were already familiar with the phonological training program they carried out. The teachers in the experimental group participated in workshops and seminars that were conducted over a period of eight months. The teacher training started two months before the implementation of the intervention and ended when the intervention was completed. During the periods between the workshops, teachers studied the teacher’s guide, worked with the children, and kept field notes regarding their personal reflections. These field notes, along with examples of children’s drawings and other expressions of the children’s thinking and reasoning, were the basis for the joint discussions at the next teacher seminar.

The teachers in the experimental group attended seminars during the intervention period to ensure fidelity. The teachers recorded daily field notes that included brief comments on the outcomes of teaching and learning activities. Overall, program fidelity appeared high in both groups.

Before the initial randomization of classes it was made clear that the teachers who would be randomized to the control group would receive the teacher’s guide and be offered in-service training after the intervention was completed. During the intervention, the teachers in the experimental group assured that they did not discuss the intervention or the teacher’s guide with teachers in the control group.

The Mathematical Intervention Program

The intervention program consists of several cycles, each of which includes six phases (Sterner, Helenius, & Wallby, 2014). The mathematical concepts that form the basis for a particular cycle always appear again in a later cycle, but they are incarnated in a different context and linked to a different concrete representation.

Phase 1. Counting rhyme: The counting sequence coded in verbal language is an important example of a numerical tool (Wiese, 2003), and the purpose of including counting rhymes is to support children’s opportunities to learn principles and patterns in the number system. The session begins with the teacher and children gathering in a circle and counting in chorus in a way related to the concept that is the focus of the cycle, like counting forwards and backwards, in twos, fives and tens and to count by starting at different numbers in the sequence.

Phase 2. Initial activity: In this collective activity, the teacher introduces a problem, which is always presented in terms of concrete objects. As an example, in one of the cycles, the initial activity requires the teacher and children to explore all possible combinations of the number five by means of using five objects. The children take turns splitting the five objects into two groups, which are then saved so all combinations are visible and can be compared. When the children do not find any new ways to split the objects, the discussion shifts and the students are asked how they can know that they have found all possible combinations.

Phase 3. Partner work: Children work with partners on similar activity. In our example, children use cubes of two colors to build as many different combinations of five as possible. During the partner work, the teacher moves around to capture children’s thoughts and ideas and pays special attention to children who need additional support to understand the task.

Phase 4. Whole class discussion: Children and teachers engage in a joint discussion of similarities and differences among the children’s constructs. In our example, some children built the combinations somewhat haphazardly while other constructs are structured, e.g., 5 green and 0 yellow, 4 green and 1 yellow and so on. Differences and similarities among the constructs are discussed.

Phase 5. Children’s documentation: Children individually create drawings as documentations of what they have done thus far. The drawings are new representations that form the basis for further collective activities in the next phase. In the children’s individual documentations, they choose to draw pictures, dots, lines, icons, and numerals, or whatever representations that support their thinking.

Phase 6. Follow-up activity: In the last phase of the cycle children’s drawings serve as the starting point for further reasoning about the concepts on which they have worked, as well as the connections, differences, and similarities among the representations of those concepts. Children’s drawings can be considered as a part of the learning of a written symbol system (Vygotsky, 1978). In our intervention, children’s drawings represent the individual thinking and learning of the child and they also represent the collective thinking and learning that occurred (Johnsen Høines, 2000). When teachers and children discuss similarities and differences among the children’s representations, the children’s experiences can be broadened because they can conceptualize something from another child’s perspective, that is, something that he or she did not directly experience or notice (Vygotsky, 2004). Combined with our perspective of teaching and learning with respect to numbers as a matter of reasoning about multiple representations of numbers, this implies that all the children’s contributions are important to the comprehensive picture of the concept.

In collective phases 2, 4, and 6, the teacher has the explicit role to introduce and follow up with a problem and to encourage the children to share their ideas and to challenge the children’s thinking by posing questions and encouraging comparisons between different ways of reasoning or representing ideas and solutions. To support teachers and enhance their ability to pose open-ended questions that will take the discussions and the children’s thinking to the next level, examples of questions for the teacher to ask are included in teacher’s guidelines, such as: Why do you think that? What is similar and what is different between your solutions? How do we know if we have found all the solutions? What do you think Moa thought when she created this pattern? One important tool in the teaching and learning program is a puppet that is sometimes used to make statements (sometimes correct, sometimes incorrect) and ask questions that trigger the children’s desire to reason about concepts and thus expressing their own views. Using the puppet also can help the children to focus their attention on certain mathematical aspects.

In interactions with the teacher and with the puppet and peers, children tell “what they know” or rather how they have conceptualized and are able to communicate the work in the cycle that then functions as a means to learn and help others to learn. Again, the purpose of each cycle is to provide children with opportunities to present their representations, to stimulate comparisons and to challenge their thinking.

Instruments

The children’s numeracy skills and verbal and visual working memories were assessed at the pre-test. A test of receptive grammar was also included. Due to time constraints, only half of the sample participated in the receptive grammar test. The children in both the experimental and the control group were randomly assigned to participate/not participate. This resulted in 31 children from the experimental group and 31 children from the control group participating. At the immediate post-test, the children’s numeracy skills were assessed. The numeracy tests for pre- and post-tests use well-established instruments chosen for their good predictive value of future school success (see below). Nine months after the post-test, when children were in grade one, a follow-up test was conducted, and the children’s number sense, basic arithmetic skills, and reading comprehension skills were assessed. The mathematics tests for grade 1 were chosen to be appropriate for the age group and to the Swedish school curriculum.

Tasks Included Only at the Pre-test

Corsi blocks. In this visual-spatial short-term memory task, nine blocks were positioned on a board modeled after Farrell Pagulayan, Busch, Medina, Bartok, and & Krikorian’s (2007) suggestion of standardization. The task was to point to the same blocks in the same sequence as the test leader. The number of blocks was increased from two to nine, with two tasks at each difficulty level. The test was interrupted after two errors at the same level. Cronbach’s alpha reliability was .66.

Verbal working memory (Wolff, 2013). The task has the format of a dual task. The child is orally presented with a word (e.g., train), which is immediately followed by a very simple question in YES or NO format (e.g., Can dogs bark?). The task is to recall the word (i.e., train). There are 10 tasks, and the number of words to remember increases gradually (1, 1, 2, 2, 3, 3, 4, 4, 5, 5). Completely correct responses with the words in correct order yield two points; correct words in incorrect order yield one point. The maximum score is 60 points. Cronbach’s alpha reliability is .75.

Test for Reception of Grammar – Version 2 (Bishop, 2003). The test consists of 80 multiple-choice tasks aimed to investigate receptive grammatical understanding. The child is encouraged to select and point to one of four pictures that corresponds to a sentence spoken by the test- leader. The level of grammatical complexity gradually increases. The test is discontinued after one error in each of five consecutive blocks. The maximum possible score is 80 points. Cronbach’s alpha reliability is .93.

Tasks Included on the Pre- and Post-tests

The Early Numeracy Test (ENT), (Van Luit & Van de Rijt, 2005) is a task-oriented test developed for children between 4 and 7 years of age. It aims to measure the level of early mathematical competence and to identify children with delayed number sense development. The ENT test has been found to have good predictive values for number sense needed for further school success in grade 1 (Aunio & Niemivirta, 2010). The ENT consists of 40 items that address eight aspects of numerical knowledge. These aspects include the concepts of comparison, classification, correspondence, seriation (relational skills) and counting words, structured counting, resultative counting, and general knowledge of numbers (understanding and use of numbers). In addition to its single whole scale, the ENT thus provides two closely related subscales measuring slightly different aspects of children’s number sense: relational skills and the use and understanding of numbers (Aunio, Hautamäki, Sajaniemi, & Van Luit, 2010). The children are invited to answer the questions verbally or to point to the correct answer with support from the test materials provided (cubes, pictures). The test takes approximately 30 minutes to complete, with a maximum score of 40 points. Cronbach’s alpha reliability is .85 for the total test, and for the subscales “relational skills” .64 and for “understanding and use of numbers” it is .80.

Story problems. This test is adopted from the Number Sense Brief (Jordan et al., 2010). The test is comprised of addition and subtraction problems and is presented in a verbal context. For example, the test leader reads the following problem: “Jill has two pennies. Jim gives her one more penny. How many pennies does Jill have now?”. Each correct answer yields 1 point for a maximum score of 5 points. Cronbach’s alpha reliability is .67.

Tasks Included at the Follow-up Test

The Number Sense Test (NST) is adopted from Improving and Assessing the Mental Computation of School-Aged Student (McIntosh, 2004). The Number Sense Test has been further developed and adapted to the Swedish school system by McIntosh (2008). Three interrelated areas are differentiated where number sense plays a key role. These include number concepts, operations with numbers and use of numbers and operations. This test is untimed and includes 10 levels – Grades 0 through 9 (McIntosh, 2008). All items are read aloud to the children by the test leader. The total possible score is 21 points, and Cronbach’s alpha reliability is .62.

Basic arithmetic skills (Sterner, 2014). The test includes 24 symbolic addition and subtraction tasks. The items do not contain more than two terms, and the sums are below 20, e.g., 4 + 5, 14 − 3. The children are encouraged to concentrate and work on the tasks until they are told to stop and put their pencils down. The total test time is 3 minutes. The maximum score is 24 points, and the test-retest reliability was .97.

Reading comprehension (Lundberg, 2001). Short statements were presented, each with four alternative pictures. The task was to choose among the pictures and indicate which one corresponded to the statement. The distractor alternatives could, for example, illustrate a boy skating where the statement reads “The boy goes skiing”. Working time was 10 min and the total score was the number of correct answers in the given time. Test–retest reliability is .94.

Test Procedure

The pre- and post-tests were administered individually. Test time was approximately 60 minutes. The follow-up tests were group administered, and the test time was approximately 40 minutes. The children were tested in their own schools in a quiet room. The first author and three special needs education teachers administered the test. The testing was preceded by seminars where test procedures were discussed to ensure that test administrations among the test-leaders were as uniform as possible.

Data Analysis

Structural equation modeling (SEM) was used to analyze the data with the Mplus 7 program (Muthén & Muthén, 2012) under the STREAMS modeling environment (Gustafsson & Stahl, 2005). The data were longitudinal, and latent variables were used to indicate math performance on the pre-, post-, and follow-up-tests. The randomization of clusters is taken into account by using TYPE = COMPLEX in the analysis, which yields cluster-robust standard errors and a corrected chi-square statistic (Muthén & Muthén, 1998-2012). Half of the sample was randomly assigned to take one of the tests, receptive grammar (see under the heading Instruments), and thus the missing data were MCAR. Missing H1 (Muthén & Muthén, 1998-2012) and the estimator ML were applied. For the measurement models and the structural equation model, Chi-square, root mean square of approximation (RMSEA) with confidence intervals, comparative fit index (CFI), and standardized root mean square residual (SRMR) are reported. To indicate good fit, the RMSEA estimate and the upper range of its 90% confidence interval should be less than .07 (Steiger, 2007) or approximately .08 but not greater than .1 (Browne & Cudeck, 1993). The SRMR should be less than .08, and the CFI should be close to or higher than .95 (Hu & Bentler, 1999).

Results

The descriptive data for the control and the experimental groups and the measurement models with loadings of the manifest variables on the latent variables are reported, and the structural equation model is discussed. In Table 1 the descriptive data for the experimental group and the control group for all measures on the pre-, post-, and follow- up tests are presented. At the pre-test, there were significant differences on visual working memory and mathematics skills between the groups in favor of the control group.

Table 1. Means and standard deviations of the test scores on the pre-, post-, and follow-up tests for the experimental group (n = 62) and the control group (n = 61).

	Experimental group		Control group
	M	SD	M	SD
Pre-test
ENT, relational skills	16.00	2.53	16.98	2.32
ENT, counting skills	12.90	4.41	14.85	3.23
Story problems	2.70	1.65	3.35	1.40
Verbal working memory	25.71	10.24	25.67	10.11
Visual working memory	14.32	4.20	15.97	2.75
Reception of grammar	58.67	12.39	58.30	12.53
Post-test
ENT, relational skills	17.88	1.88	17.27	1.91
ENT, counting skills	15.56	3.08	15.40	2.84
Story problems	4.03	1.18	3.48	1.40
Follow-up test
Basic arithmetic, addition	9.08	3.24	10.06	2.73
Basic arithmetic, subtraction	3.02	3.01	1.58	2.68
Number sense test	18.63	2.31	17.82	2.74
Reading comprehension	11.58	6.99	13.82	7.95

Confirmatory Factor Analyses

Three oblique confirmatory factor analyses were conducted. The sums on each of the math tests were used as indicators of the latent variables at the pre-, post-, and follow-up tests. As there were only three indicators, the model was just identified yielding a trivially perfect fit. The factor loadings for the math variables on the pre-, post-, and follow-up tests are presented in Table 2.

Table 2. Factor loadings of the manifest variables on the latent variables for the pre-, post-, and follow-up tests.

	Math pre-test	Math post-test	Math follow-up
ENT, relational skills	.72	.63
ENT, counting skills	.93	.73
Story problems	.56	.70
Basic arithmetic, addition			.78
Basic arithmetic, subtraction			.59
Number sense test			.60

Structural Equation Modeling

To examine the effect of the mathematics intervention on later mathematical ability, a structural equation model was created. Autoregressive relations were applied between the latent variables that indicated mathematics skills at the pre-, post-, and follow-up tests, and the error variance from the identical indicators over time were co-varied. Reading comprehension was also included as a manifest outcome variable. The manifest variables measuring phonological working memory, visual working memory, and linguistic comprehension were freely correlated with mathematics on the pre-test. Gender differences and differences in initial mathematics skills between the experimental group and the control group were controlled for. A dichotomous variable (Group) representing the control group (coded as 0) and the experimental group (coded as 1) was related to the math variables at the post- and the follow-up tests and to reading comprehension on the follow-up test. Cross-lagged relations over time were then added to the model, the only significant cross-lagged relations were from verbal working memory at the pre-test and from math at the post-test to reading comprehension at the follow-up test. This model fit the data well (χ² = 89.286, df = 70; RMSEA = .047, CI₉₀ = .000–.074; CFI = .965; SRMR = .058). In order to check for measurement invariance the factor loadings for the same indicators at the pre- and the post-test were constrained. As the indicators for the follow-up test were not the same as for the pre- and the post-test, they were not possible to include in this examination. The constrained model had a marginally worse fit to the data (χ² = 92.458, df = 72; RMSEA = .048, CI₉₀ = .000–.074; CFI = .962; SRMR = .063), and a Chi-square difference test confirmed that the two models did not differ significantly (p = .205). In a second step, equal item intercepts were also included, and the intercept for the latent post-test variable was allowed to vary freely (χ² = 94,773, df = 73; RMSEA = .049, CI₉₀ = .008–.075; CFI = .960; SRMR = .063). Also in this model (Figure 1), a Chi-square difference test showed that the model did not differ significantly from the unconstrained model (p = .142), thus showing scalar invariance in the variables over time.

Figure 1 . A structural equation model with autoregressive relations between the latent variables indicating mathematic ability at the pre-, post-, and follow up-tests. The effects of the intervention, and phonological working memory, visual working memory and linguistic comprehension at the pre-test on mathematic ability and reading comprehension were examined, but only significant relations are visible in the model (* p ≤ .05; **p ≤ .01; ***p ≤  .001).

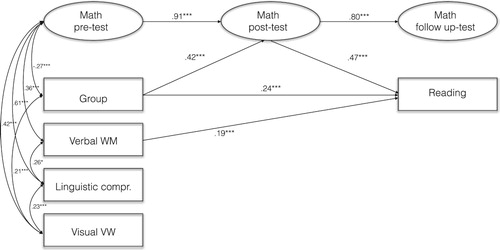
There was a significant and strong effect of the intervention on math skills at the post-test in favor of the experimental group (t = 4.261; p < .001; Effect Size (d) = .81). There was also a significant negative effect of group assignment on reading comprehension at the follow-up test, that is, in favor of the control group (t = −2.947; p < .01; d = .44). There was no direct effect of the intervention on math skills at the follow-up test. However, indirect effects were also estimated, and the total indirect effect of the intervention on mathematical ability at the follow-up test was significant (t = 3.978; p < .001; d = .69; CI₉₀ = .46–.90). The absence of direct effects at the follow-up test implies that there were no further improvement in the experimental group, as compared to the control group, after the immediate post-test. However, the indirect effects at the follow-up test through the post-test imply sustained effects of the intervention even one year after the intervention. There was also a significant negative effect of group assignment on reading comprehension at the follow-up test, that is, in favor of the control group (t = −2.947; p < .01; d = .44).

Discussion

The main aim of the study presented here was to examine the effect of a structured intervention in Grade 0 that focused on numeracy and collective reasoning regarding representations of children’s number sense improvement. The results show a significant effect on number sense growth between the pre-test and the immediate post-test. There was also a sustained effect of the intervention nine months later, when the children were in Grade 1.

At the pre-test, the control group performed better on mathematics than the experimental group. The same group also performed better on visuospatial working memory. Research on the contribution of working memory to different areas of mathematics indicates that prior to school entry children, to a great extent, rely on analogous mental representations of quantities, which are tokens that can be manipulated and stored in visuospatial working memory. This is in contrast to older school-aged children who, when introduced to verbally presented problems dealing with numbers, to a greater extent encode and solve the problems primarily verbally and thus, to a greater extent rely on verbal working memory (see Raghubar et al., 2010). This implies that visually presented problems are especially useful for children before school-entry (Rasmussen & Bisanz, 2005). Representation is an important component of mathematics. In fact, mathematicians at all levels use representations such as simplified pictures, graphs, diagrams, and equations to analyze and communicate their work (Cross, Woods, & Schweingruber, 2009). In the present study, teachers and children rely heavily on reasoning using representations such as blocks, drawings, icons, numerals, number lists, and oral and written language when solving math problems. It is assumed that this pedagogical approach may be a successful way to enhance number sense development in general when visual working memory resources are limited. The program encourages verbal reasoning while supporting visual working memory by means of acting on physical objects. In the current study, no further significant correlations between visual working memory and mathematics were found, meaning that working memory does not affect later mathematics performance beyond the effects of mathematical intervention. This strengthens the hypothesis that visual working memory is important at an early age when children’s number sense is being formed and that it is less important to older, school-aged children (Raghubar et al., 2010; Rasmussen & Bisanz, 2005).

In contrast to mathematics and visual working memory, there were no differences between the experimental group and the control group with respect to verbal working memory or linguistic skills at the pre-test. The children’s initial linguistic skills did not relate to later mathematical or reading comprehension skills, whereas verbal working memory at the pre-test predicted reading comprehension nine months later. The results indicate that children with high initial verbal working memory resources have an advantage related to reading comprehension in school-year 1, irrespective of if they were assigned to the control or the experimental group. To achieve good reading comprehension, both word decoding and interpretation of the text (comprehension) must be used simultaneously (Gough & Tunmer, 1986). Reading comprehension exerts a high load on working memory as the phonological representations must be retained while the interpretation and integration of different parts of the text are processed, i.e., the phonological loop is exposed to stress (Baddeley, 2000).

The control group received a research-based structured and explicit pedagogical program (Lundberg, 2007) focused on phonological awareness. The program was implemented by the children’s teachers with the same amount of instruction time as the experimental group received in mathematics. At the follow up-test, nine months after the intervention, the control group outperformed the experimental group on reading comprehension, a relationship between phonological awareness training and reading comprehension that has also been demonstrated in previous research (e.g., Fälth, Gustafson, Tjus, Heimann, & Svensson, 2013; Lundberg, 1985; Wolff, 2011). The fact that the control group’s performance was superior to the experimental group on reading comprehension after the training period demonstrates that the mathematical intervention did not have a global effect, but rather had a specific effect on math skills.

There was a significant effect on the children’s mathematical skills at the post-test, and a significant effect from the math post-test on reading comprehension at the follow-up test. This suggests that improvement in mathematics corresponds to an improvement in reading comprehension. The connection between reading and mathematics has not been the focus of this study, nevertheless, these results invite to some reflections. Associations between mathematics and reading have been documented in previous research (e.g., Jordan, Hanich, & Kaplan, 2003; Lie Reikerås, 2007). Gustafsson, Yang Hansen and Rosén (2013) suggest that there is theoretical and empirical research supporting the idea that the development of literacy and numeracy skills can be influenced by literacy activities. However, Duncan et al. (2007) found that preschool math was a stronger predictor of later reading achievement than early reading was of later math achievement. In a longitudinal cross-lagged study, Lerkkanen, Rasku-Puttonen, Aunola, and Nurmi (2005) found that mathematical performance during school-year one, but not school-year two, subsequently predicted reading comprehension. In line with these results, in the present study mathematical skills in Grade 0 predicted reading comprehension skills in Grade 1. In an exploratory study, Durham, Farkas, Scheffner Hammer, Tomblin, and Catts (2007) found that kindergartners’ oral language skills such as vocabulary and syntactical abilities had significant effects both on second-grade reading and third-grade mathematics. The design of the present study may contribute to explain the predictive power of mathematics on reading comprehension. The focus on reasoning and collective work means that children practice both listening comprehension and language expression ability. Notably, there were no differences between groups in linguistic abilities measured oat the pre-test in the current study.

Another important component found in Duncan et al. (2007) is that attention skills are consistently related to both reading and mathematics outcomes. One explanation they give with respect to this predictive power is that attention skills increase when children are engaged in academic endeavors and learning activities. This is consistent with the results of a longitudinal study in Grades 3 and 4 (Lundberg & Sterner, 2006) that indicate a causal relationship between task orientation, and reading comprehension and arithmetic. They assume that task orientation, to some extent, is a determinant of successful learning in school and that there is a reciprocal relationship. with respect to the similarities between the mathematical and the reading intervention program and with regard to the structure of explicit instruction, teacher scaffolding and the emphasis on the children’s active inclusion in their learning processes, it is reasonable to assume that the pedagogical approach in the present study has enhanced children’s task orientation abilities, which, in turn, may have affected mathematical abilities and reading comprehension.

Limitations

There are some limitations to the present study. One is that there is no measure of reading comprehension at the pre-test. This is because the children had not yet received any formal reading instruction, and most of them were unable to read. Instead, we included a measure of linguistic comprehension that allowed us to control for possible initial differences in comprehension between the groups.

The reliability of the follow-up measure of Number Sense was rather low. However, low alpha may result in lower correlations, never higher. Thus, if anything the results may be underestimated. Another reason the low alpha is acceptable is that the measure is used as an indicator to a latent variable, and latent variables are error-free, and the loading on the latent variable (Table 2) was highly significant.

Initially, the control group scored better on mathematics skills than the experimental group. If the higher scores were caused by measurement errors, it could result in later regression towards the mean. However, it is well known that mathematics skills and visual working memory are highly correlated in young ages (Bisanz et al., 2005; Kyttälä et al., 2010), and the fact that the control group scored higher on both these skills suggests that the significant differences reflect true scores rather than measurement errors.

In SEM analyses, large sample sizes are of course desirable, especially if the effects are subtle, and the model does not distinguish very clearly among constructs. However, in the present model the effect size is high, the constructs are clear, and the model is not very complicated, as indicated for example by SRMR and CFI. Especially the narrow confidence interval of the RMSEA estimate indicates adequate power of the model. Furthermore, it has empirically been demonstrated that in a sample size of 100, an effect size of Cohen’s d = .20 is reliably detectable, whereas in a sample of 150–500 participants, an effect size of .10 is detectable (Little, 2013). Also, the standard error reduction is slow between samples ranging from 100 to 150 participants.

Another limitation is cluster sampling. The cluster sampling was necessary because the training was implemented in groups of children by their regular Grade 0 teacher in such way that it formed a part of the daily activities. To meet this challenge, in a first step, double the amount of groups and individuals, as was finally included, was selected. In the second step, half of the children in each group were randomly allocated to be enrolled in the study. This means that children who were not enrolled in the study participated in the training, but were not subjected to any testing. To take the cluster sampling into account, the analysis type Complex was used in the Mplus program, as recommended by Muthén and Muthén (1998-2012). Finally, it may also have contributed to a deeper understanding of the results of the study if an untrained control group had been included.

Implications

This study has demonstrated that a structured intervention focused on number and collective reasoning about representations during Grade 0 has positive effects on children’s number sense and has sustained effects nine months later when the children are in Grade 1. The study is the first of its type in Sweden, and the results are promising.

In a review by Mononen et al. (2014) the authors stress the importance of further intervention research to provide teachers relevant guidance to enhance the learning of mathematics for children in Grade 0. An important focus for teaching this age group is the connection between informal and formal mathematics. The results of our study demonstrate that explicit and systematic instruction combined with structured activities and reasoning about representations and the relations between them can be a successfully way to do it.

Future research on classroom observations, teacher-children interactions, and patterns of children’s reasoning could contribute to a deeper understanding of the causal relationship between instruction and achievement. Related to this, it would be important to compare the present study’s design principles with other evident intervention designs to determine the features that are most effective on a group level, as well as on an individual level. Furthermore, in a future study, measures of task orientation could be added to the test battery, making it possible to study the development of, and interactions between, task orientation, mathematical skills, and reading comprehension.

Disclosure statement

No potential conflict of interest was reported by the authors.

Notes

1 From fall 2018 Grade 0 is an obligatory part of the Swedish school system. When the study was carried out Grade 0 was called preschool class and was voluntary but still with a participation rate of 95% (National Agency for Education, 2017).