Magnetic measurement of retained austenite in sintered steels – benefits and limitations

ABSTRACT

Measuring the magnetic saturation to quantify the retained austenite is a common method, but it is based on a relative calculation. Thus the reference, which ideally should be the same material but without retained austenite, is of extreme importance. This work focuses especially on obtaining the saturation of the reference material by using different models and applying them for determining the retained austenite content of sintered alloy steels. To verify these calculations, additional measurements of the phase fractions by X-ray diffraction were done. As a result, the contents of retained austenite vary significantly when calculating them from the saturation data using different models. Furthermore, the agreement of the results of the magnetic method and those of the X-ray measurement is not quite satisfactory. Especially when using simple approximations (reference = magnetic saturation of plain iron) the differences are very pronounced. However, it is shown that using the presented models results in markedly better agreement between the results of both methods (magnetic and X-ray diffraction) than using plain iron as a reference.

KEYWORDS:

• Magnetic saturation
• retained austenite
• X-ray measurement

1. Background

The quantification of retained austenite in heat-treated steels is of considerable industrial interest, because the properties of the material depend mainly on the volume fractions of the present phases. This leads to the point that for the adjustment of the properties of the material it is required to obtain a sufficient quantification of the retained austenite. In this case, there are several methods to achieve this task. The following work is based on the measurement of the magnetic saturation to quantify the retained austenite.

The magnetic measurement of retained austenite is a cheap and simple method, but there exist several problems when using this technique. First the method is based on an integral measurement, thus it is not possible to determine gradients of retained austenite contents. Second the determination of the mass fraction of retained austenite is usually done by(1) where is the magnetic saturation of the sample in SI unit ( and is the reference (magnetic saturation of the austenite-free sample (). As shown, the quantification is based on a relative calculation, which means that the reference is extremely important. Since there is no experimental way to obtain reference samples with exactly the same microstructure but without austenite, there exist several approaches for the reference. The most common one is to assume that the magnetic saturation of the austenite-free sample is approximately equal to the saturation of plain iron (274*10⁻⁶ [1], applied external field: 875 kA m⁻¹) [2]. But using this model very often results in overestimating the amount of retained austenite, because the presence of all the alloying elements is totally ignored. Furthermore, the heat treatment of the steel is not considered. Therefore, models were established to calculate the reference saturation from the composition (e.g. [3–5]. Exner [3] further states that for the determination of the magnetic saturation of a steel not only the alloy elements but also the heat treatment plays an important role. It must be differentiated between hardened and annealed steels.

In the present work, several models for calculating the magnetic saturation of austenite-free hardened steels (Maurer and Schroeter [4], Exner [3] and Hoselitz [5]) to determine the reference are discussed. All of these models use the following equation [6](2) where is the magnetic saturation of plain iron, A_i is the 'attenuation coefficient' of a specific element i and is the mass fraction of a specific alloying element i. It is assumed that the austenite-free sample is fully martensitic. Furthermore, the presence of alloying elements is considered by so-called attenuation coefficients. It is assumed that a specific alloying element reduces the magnetic saturation of the steel depending on its ‘attenuation coefficient’ and on the mass fraction. The total attenuation is the sum of every single attenuation caused by every single alloying element (being assumed that the effects are additive). The ‘attenuation coefficient’ of a specific alloying element depends on the chosen model. The mentioned coefficients are summarised in Table 1.

Table 1. ‘Attenuation coefficients’ for the alloying elements according to the different models (Maurer and Schroeter, Exner and Hoselitz) [6].

Alloying element	Ai–Maurer and Schroeter	Ai–Exner	Ai–Hoselitz
C	–3E–06*xc+8E–06	2E–05*xc+1E–05	15.08E–06
Cr	3.02E–06	3.70E–06	3.77E–06
Ni	2.41E–06	0.25E–06	0.94E–06
Mo	2.09E–06	1.26E–06	1.51E–06
Co	2.41E–06	2.12E–06	–
Mn	2.90E–06	2.90E–06	2.39E–06
W	1.11E–06	1.26E–06	–
Si	9.25E–06	6.04E–06	3.02E–06
Al	7.98E–06	6.92E–06	3.27E–06
V	3.53E–06	1.52E–06	–
P	–	–	3.77E–06
S	–	–	8.80E–06
Cu	–	–	2.89E–06
N	–	–	7.54E–06

The application of Equation (2) is illustrated in case of the 4100-steel (1.0% Cr, 0.7% Mn, 0.2% Mo) containing 0.6% of carbon.Maurer and Schroeter:

Exner:

Hoselitz

2. Experimental

First, sintered steel specimens Fe–Mo–C, Fe–Cr–C and Fe–Ni–C-steel with different contents of carbon were produced. Table 2 presents the powders used to produce the mentioned steels.

Table 2. Powders used for producing the sintered steel bars.

Steel	Steel powder	Carbon carrier	Lubricant
Fe–Mo–C	Astaloy85Mo	Graphite UF4	HWC
Fe–Cr–C	AstaloyCrA	Graphite UF4	HWC
Fe–Ni–C	MSP4	Graphite UF4	HWC

Astaloy85Mo: water atomised prealloyed steel powder with 0.85% Mo, Höganäs, Sweden.

AstaloyCrA: water atomised prealloyed steel powder with 1.80% Cr, Höganäs, Sweden.

MSP4: water atomised prealloyed steel powder with 4.00% Ni and 0.50% Mo, QMP (former Mannesmann, now Rio Tinto) Germany.

Graphite: UF4, Kropfmühl, Germany.

HWC: Ethylenbisstereamide, Höganäs, Sweden.

The carbon contents chosen were 0.3, 0.5, 0.7, 1.0% C_admixed (as graphite).

The calculated amounts of the powders were mixed in a tumbling mixture. Afterwards the powder mixtures were pressed at 600 MPa in a pressing tool with floating die to impact test bars ISO 5754 (55 mm × 10 mm × 6 mm). The lubricant was removed in a pusher type furnace with Kanthal heating elements and a steel muffle in flowing Ar atmosphere (2 L min⁻¹, purity: 99.999%) at 600°C, controlling the temperature with Ni–Ni/Cr-thermocouples. Subsequently, the samples were sintered in a SiC rod heated pusher type furnace and a Kanthal APM-muffle in Ar-atmosphere (2 L/min, purity: 99.999%). The sintering temperature was 1250°C, controlled optically by using a pyrometer. After sintering, the combined carbon content of the steels was measured in a C–S analyser (LECO CS 230), to determine the carbon loss during sintering.

After the sintered steel specimens had been produced, heat treatment followed. First, the sintered steels were cut in half. Then the generated pieces were austenitised at 800 and 900°C, respectively, in Ar-atmosphere (2 L min⁻¹, purity: 99.999%) for 30 min using the same furnace as for lubricant burnout, and subsequently water quenched. The quenching was done in two different ways. One-half of the samples each was just quenched by dropping them into cold water. The second half of the samples was quenched in cold water and instantly cooled in liquid N₂.

For the quantification of the retained austenite by the magnetic route it was necessary to determine the magnetic saturation of the steel samples. This was done on a ‘Foerster-Koerzimat 1.096’ using the so-called pull-method according to IEC 60404-14. The applied external field was 1.10 T (875 kA m⁻¹). Therefore the hardened steels were slowly cut into cuboids with 10 mm × 6 mm × 2 mm. The measurement was calibrated with an iron standard. The quantification of the retained austenite was done by using Equation (2), predicting the magnetic saturation of the plain martensite with the presented models (Maurer and Schroeter, Exner, and Hoselitz, see [3–5]). In addition to that, Equation (1) was also used, where the saturation of plain iron was taken as the reference. Of course, there is commercial equipment available for measuring the austenite content, e.g. [7], but calculation routines that are firmly implemented in the software would not have been useful here.

To verify the results of the magnetic method, additional measurements were done by X-ray diffraction. The XRD measurements were performed in a standard Bragg–Brentano-diffractometer in vertical -geometry using Mo- radiation. The high carbon steels (1% C-admixed) – austenitised at 800°C – were chosen for the measurements, the same samples being used as in case of the magnetic measurements. For reducing the stress in the surface the samples were polished and then etched with 1% nital-solution, to remove any deformed surface layers. The evaluation of the diffractograms was done by using ‘Highscore’ software (PANalytical). The quantification of the present phases was performed with the same software using the Rietveld method. It was not tried to determine the retained austenite by metallographic techniques. Although this is feasible in principle, it is limited to higher RA contents, which usually means higher C and/or Ni contents (e.g. [8,9]). In the present case, when specimens with widely varying and in part rather low carbon contents were studied, it did not make sense to use a method that is applicable only to part of the materials.

3. Results

In Table 3, the combined carbon content of the specimens (which is of crucial importance for the retained austenite, both experimentally and for calculations) is given.

Table 3. Carbon content of the sintered steels (C-combined).

Fe–Mo–C-steels		Fe–Cr–C-steels		Fe–Ni–C-steels
C-admixed (mass%)	C-combined (mass%)	C-admixed (mass%)	C-combined (mass%)	C-admixed (mass%)	C-combined (mass%)
0.3	0.292	0.3	0.237	0.3	0.265
0.5	0.478	0.5	0.415	0.5	0.471
0.7	0.670	0.7	0.591	0.7	0.654
1.0	0.946	1.0	0.900	1.0	0.970

As can be seen, the carbon loss is slightly higher for the Cr prealloyed steel than for the Mo and Ni-Mo alloyed grades, which is not surprising since Cr prealloyed steel contain more oxygen as-delivered, and therefore more carbon is consumed to carbothermally reduce the oxides present.

The following figures exemplify the microstructures of the hardened steels, austenitised at 800°C.

Figures 1–3 show that cooling the steel in liquid N₂ resulted in a reduction of the optically discernible retained austenite content, as expected. Not surprisingly, either, the optically visible retained austenite content is higher in the Ni–Mo-alloyed steel, due to the austenite-stabilising effect of Ni. In this case, also the effect of liquid N₂ cooling is most evident.

Figure 1. Microstructures of the hardened Fe–0.85Mo–1.0C-steels, magnification: ×500. (a) austenitised at 800°C and quenched in water. (b) austenitised at 800°, quenched in water and cooled in liquid N₂.

Figure 2. Microstructures of the hardened Fe–1.8Cr–1.0C-steels, magnification: ×500. (a) austenitised at 800°C and quenched in water. (b) austenitised at 800°, quenched in water and cooled in liquid N₂.

Figure 3. Microstructures of the hardened Fe–4.0Ni–0.5Mo–1.0C-steels, magnification: ×500. (a) austenitised at 800°C and quenched in water. (b) austenitised at 800°, quenched in water and cooled in liquid N₂.

To quantify the retained austenite content of the sintered steels investigated, both after standard water quenching and after quenching and cooling to −196°C, the magnetic saturation was measured and Equation (2) was applied. The obtained results are presented in Figures 4–9. The contents have been calculated using for the reference the models presented by Maurer and Schroeter, Exner, and Hoselitz, and also plain iron.

Figure 4. Retained austenite content in the hardened steel Fe–0.85Mo–C as a function of the carbon content (C-combined), calculated from the magnetic saturation using different models. (a) Fe–Mo–C-steels, austenitised at 800°C and quenched in water. (b) Fe–Mo–C-steels, austenitised at 800°C, quenched in water and cooled in liquid N_2.

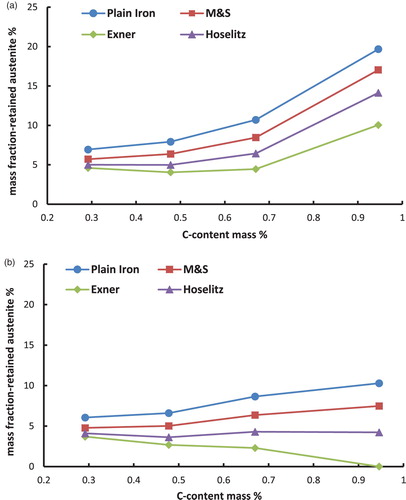
Figure 5. Retained austenite content in the hardened steel Fe–1.8Cr–C as a function of the carbon content (C-combined), calculated from the magnetic saturation using different models. (a) Fe–Cr–C-steels, austenitised at 800°C and quenched in water. (b) Fe–Cr–C-steels, austenitised at 800°C, quenched in water and cooled in liquid N_2.

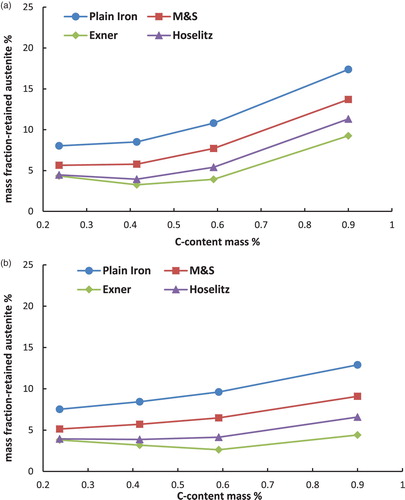
Figure 6. Retained austenite content in the hardened steel Fe–4Ni–0.5Mo–C as a function of the carbon content (C-combined), calculated from the magnetic saturation using different models. (a) Fe–Ni–C-steels, austenitised at 800°C and quenched in water. (b) Fe–Ni–C-steels, austenitised at 800°C, quenched in water and cooled in liquid N_2.

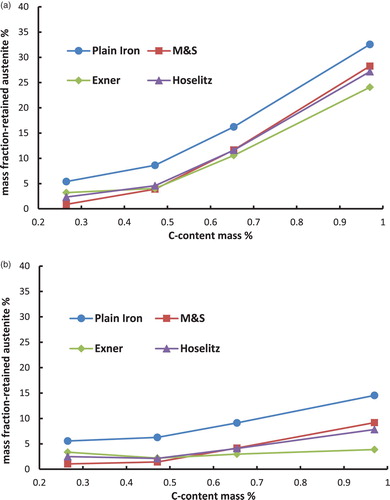
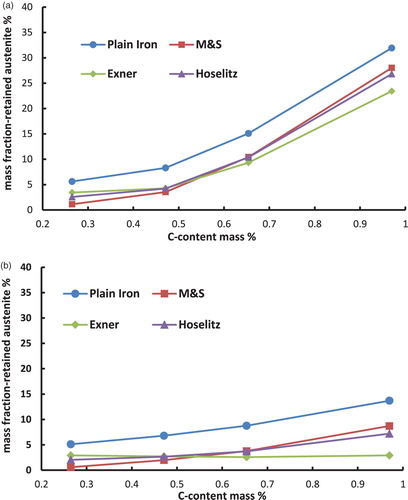
Figure 7. Retained austenite content in the hardened steel Fe–0.85Mo–C as a function of the carbon content (C-combined), calculated from the magnetic saturation using different models. (a) Fe–Mo–C-steels, austenitised at 900°C and quenched in water. (b) Fe–Mo–C-steels, austenitised at 900°C, quenched in water and cooled in liquid N_2.

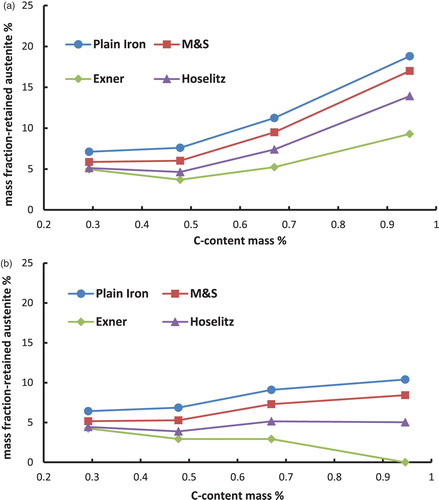
Figure 8. Retained austenite content in the hardened steel Fe–1.8Cr–C as a function of the carbon content (C-combined), calculated from the magnetic saturation using different models. (a) Fe–Cr–C-steels, austenitised at 900°C and quenched in water. (b) Fe–Cr–C-steels, austenitised at 900°C, quenched in water and cooled in liquid N_2.

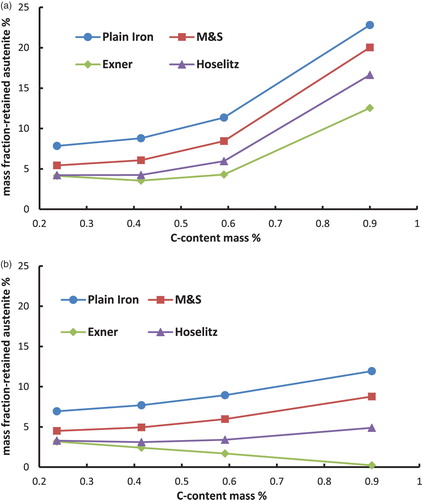
Figure 9. Retained austenite content in the hardened steel Fe–4.0Ni–0.5Mo–C-steels as a function of the carbon content (C-combined), calculated from the magnetic saturation using different models. (a) Fe–Ni–C-steels, austenitised at 900°C and quenched in water. (b) Fe–Ni–C-steels, austenitised at 900°C, quenched in water and cooled in liquid N_2.

The raw data for Figures 4–9 are represented in the appendix.

Table 4 shows the results of the XRD measurements as obtained by the Rietveld method in specimens with the highest carbon content.

Table 4. Retained austenite content measured by XRD/Rietveld.

Samples austenitised at 800°C
Samples quenched in water		Samples quenched in water and cooled in liquid N2
Steel	RA^Rietveld [mass%]	Steel	RA^Rietveld[mass%]
Fe–Mo–1.0C	17	Fe–Mo–1.0C	9
Fe–Cr–1.0C	9	Fe–Cr–1.0C	7
Fe–Ni–1.0C	29	Fe–Ni–1.0C	12

4. Discussion

Figures 4–9 first show that the total content of retained austenite depends on the chemical composition of the steel. Higher amounts of retained austenite are recorded at higher carbon content. The reason for this well-known effect [8] is the stabilisation of the austenite by carbon. Furthermore, the Fe–Ni–C-steels show higher amounts of retained austenite than the Fe–Mo–C- or the Fe–Cr–C-steels. This relationship is not surprising either and is also well known [10], because the presence of nickel in the steel, as a strong gamma stabiliser, leads to an enhanced stabilisation of the austenite.

Cooling the samples in liquid N₂ in the hardening process has reduced the amount of retained austenite, as expected. This effect is caused by increasing the driving force of the austenite–martensite-transition, which is undercooling. Not surprisingly, the effect is most pronounced with the Ni alloyed steels, esp. at higher carbon contents.

In case of the Fe–1.8Cr–1C-steels, increasing the austenitising temperature results in higher amounts of retained austenite. At 1.8% Cr and 800°C not all carbides can be dissolved, because the Cr content shifts the γ–γ + carbide boundary to higher temperatures and lower carbon contents. At the higher temperature, the steel is homogeneously austenitised. This way the austenite is higher carbon alloyed and stabilised after quenching.

Moreover, the calculated mass fraction of the retained austenite differs significantly between the used models. The (apparent) mass fraction of the -phase is considerably higher if the magnetic saturation of plain iron is used as the reference than by using the presented models to calculate the theoretical magnetic saturation of the martensite. This result obtained with plain iron as reference is induced by ignoring all the present alloying elements, which leads to an overestimation of the magnetic saturation of the reference. This is because also the drop in saturation caused by the presence of the alloy elements is – erroneously – attributed to the presence of retained austenite.

In addition to that, it is shown that according to the models for hardened steels the highest amounts of retained austenite are obtained if the model of Maurer and Schroeter is used for the calculations. On the other hand the lowest amounts of retained austenite result when the model of Exner is used. These discrepancies are caused by the different ‘attenuation coefficients’ (especially for carbon) of the models, as shown in Table 1. The model of Maurer and Schroeter presents the lowest ‘attenuation coefficient’ for the carbon and thus results in the highest reference saturation, leading to the highest amounts of retained austenite. In case of the model of Exner the opposite can be observed; in this case the attenuation coefficient is definitely set too high since with this model the retained austenite content at least after LN2 cooling decreases with higher C content (even to zero, see Figures 4(b), 7(b), 8(b)), which clearly disagrees with experimental evidence. Since the effect of carbon is particularly pronounced but is predicted quite differently by the respective models, these results show that especially in high carbon steels the calculated amounts of retained austenite differ significantly when using different models. This is particularly relevant since the topic of retained austenite – and its correct measurement – become the more critical the higher the carbon content is. Therefore it is essential to indicate the used model for the quantification of the retained austenite. Furthermore, it is important to mention that the model of Hoselitz does not consider the presence of Co as an alloying element. Therefore this model should not be used for steels containing significant amounts of Co, as in case of high-speed steels such as AISI M42.

The results of the XRD-measurements show similar relations. The calculated mass fraction of the -phase was reduced considerably by cooling the samples in liquid N₂ during the hardening process. Furthermore, the Fe–Ni–C-steels contain the highest amounts of retained austenite (see explanation above). Comparing the results of the magnetic measurements with those of the XRD measurements, presented in the appendix, shows that the agreement between both methods is not really satisfactory. The trends observed are similar, but the absolute values tend to differ in part considerably.

Especially by using simple approximations in the magnetic method (reference = magnetic saturation of plain iron) the differences are very pronounced. However, using the presented models for alloy steels tends to result in a better agreement between both methods. In any case it is important to stress that this conclusion depends on the used model to determine the theoretical (=austenite-free) magnetic saturation of the martensite.

5. Conclusion

First of all, for the quantification of retained austenite by using magnetic measurements the reference, the (usually hypothetical) austenite-free material of identical composition and microstructure, is of extreme importance. Therefore different models for hardened steels to determine the magnetic saturation of the austenite free sample are presented which have been published in the literature. The results obtained with 3 grades of sintered steels show that the calculated mass fraction of the retained austenite strongly depends on the model used to predict the magnetic saturation of the martensite (Maurer and Schroeter, Exner, and Hoselitz) since the ‘attenuation coefficients’ used to describe the effect of alloying elements vary considerably. Especially the ‘attenuation coefficient’ of carbon varies a lot, thus the differences are more pronounced in case of high carbon steels. From the results described here it is difficult to define one model as ‘the best’ or ‘the correct one’, since unless XRD is regarded as the absolute benchmark (which would be a bold claim) there is no real criterion for assessing the ‘true’ RA content. In any case, however, it is of extreme importance to indicate which model was used for the quantification of the retained austenite.

The result obtained by the magnetic method and by XRD, respectively, showed some disagreement. Especially when using simple approximations (reference = magnetic saturation of plain iron) the differences are very pronounced. Using the presented models, in contrast, tends to result in a better agreement between the results of both methods (magnetic and X-ray diffraction), although further refining of the models still seems to be necessary.

Disclosure statement

No potential conflict of interest was reported by the authors.

Notes on contributors

Kevin Ouda has been studying Technical Chemistry at TU Wien since 2011 and graduated Dipl.-Ing. in 2017. He is currently project assistant at the Institute for Chemical Technology and Analytics of TU Wien. In 2017 he also started his dissertation, which is based on powder metallurgic iron-based components.

Herbert Danninger studied Technical Chemistry at TU Wien, obtaining his PhD in 1980. Since that time he has been doing research in powder metallurgy. In 2003 he was appointed Full Professor for Chemical Technology of Inorganic Materials at TU Wien, and currently he is also Dean of the Faculty of Technical Chemistry. He has published more than 450 articles, mostly on powder metallurgy topics, and holds 3 honorary doctorates.

Christian Gierl-Mayer received the PhD degree in Technical Chemistry in 2000 from TU Wien. He is currently assistant professor for metallic sintered materials at the Institute for Chemical Technology and Analytics of TU Wien. His main research activities are in the study of the sintering mechanisms of PM steels via thermal analysis techniques.

Appendix

Table 5 Amount of retained austenite determined by the magnetic method and XRD (n.m.: not measured).

Table

Sample-nomination	[mass%]	RA^Plain Iron [mass%]	RA^Mauer&Schroeter [mass%]	RA^Exner [mass%]	RA^Hoselitz [mass%]
Samples austenitised at 800°C and quenched in water
Fe–Mo–0.3C	n.m.	7	6	5	5
Fe–Mo–0.5C	n.m.	8	6	4	5
Fe–Mo–0.7C	n.m.	11	8	4	6
Fe–Mo–1.0C	17	20	17	10	14
Fe–Cr–0.3C	n.m.	8	6	4	4
Fe–Cr–0.5C	n.m.	9	6	3	4
Fe–Cr–0.7C	n.m.	11	8	4	5
Fe–Cr–1.0C	9	17	14	9	11
Fe–Ni–0.3C	n.m.	5	1	3	2
Fe–Ni–0.5C	n.m.	9	4	5	5
Fe–Ni–0.7C	n.m.	16	12	11	12
Fe–Ni–1.0C	29	33	28	24	27
Samples austenitised at 800°C. quenched in water and cooled in liquid N2
Fe–Mo–0.3C	n.m.	6	5	4	4
Fe–Mo–0.5C	n.m.	7	5	3	4
Fe–Mo–0.7C	n.m.	9	6	2	4
Fe–Mo–1.0C	9	10	7	0	4
Fe–Cr–0.3C	n.m.	8	5	4	4
Fe–Cr–0.5C	n.m.	8	6	3	4
Fe–Cr–0.7C	n.m.	10	6	3	4
Fe–Cr–1.0C	7	13	9	4	7
Fe–Ni–0.3C	n.m.	6	1	3	2
Fe–Ni–0.5C	n.m.	6	1	2	2
Fe–Ni–0.7C	n.m.	9	4	3	4
Fe–Ni–1.0C	12	15	9	4	8
Samples austenitised at 900°C and quenched in water
Fe–Mo–0.3C	n.m.	7	6	5	5
Fe–Mo–0.5C	n.m.	8	6	4	5
Fe–Mo–0.7C	n.m.	11	9	5	7
Fe–Mo–1.0C	n.m.	19	17	9	14
Fe–Cr–0.3C	n.m.	8	5	4	4
Fe–Cr–0.5C	n.m.	9	6	4	4
Fe–Cr–0.7C	n.m.	11	8	4	6
Fe–Cr–1.0C	n.m.	23	20	13	17
Fe–Ni–0.3C	n.m.	6	1	3	3
Fe–Ni–0.5C	n.m.	8	4	4	4
Fe–Ni–0.7C	n.m.	15	10	9	10
Fe–Ni–1.0C	n.m.	32	28	23	27
Samples austenitised at 900°C. quenched in water and cooled in liquid N2
Fe–Mo–0.3C	n.m.	6	5	4	4
Fe–Mo–0.5C	n.m.	7	5	3	4
Fe–Mo–0.7C	n.m.	9	7	3	5
Fe–Mo–1.0C	n.m.	10	8	0	5
Fe–Cr–0.3C	n.m.	7	5	3	3
Fe–Cr–0.5C	n.m.	8	5	2	3
Fe–Cr–0.7C	n.m.	9	6	2	3
Fe–Cr–1.0C	n.m.	12	9	0	5
Fe–Ni–0.3C	n.m.	5	1	3	2
Fe–Ni–0.5C	n.m.	7	2	3	3
Fe–Ni–0.7C	n.m.	9	4	3	4
Fe–Ni–1.0C	n.m.	14	9	3	7