Influence of phosphate sorption on dispersion of a Ferralsol

Abstract

Soil dispersion induces soil erosion and colloidal leaching. Nutrients are lost at the same time and this causes water contamination. Phosphate is an essential element for living organisms. Because phosphate influences soil dispersion and it is an important limited resource, this influence must be evaluated well in order to diminish negative effects on soil structure. In this paper, we firstly evaluated the influence of phosphate sorption on soil dispersion by calculating repulsive potential energy between soil particles. Ferralsol, which is a typical soil in rainy tropical regions, was used as the material. The dispersion-flocculation phenomena were investigated with absorbance of soil suspension under different pH, phosphate adsorption and electrolyte concentration in an Na-NO₃-PO₄ system. The repulsive potential energy was calculated based on the diffuse double layer theory and the measured zeta potential. We indicated that the measured absorbance increased with the increase of the repulsive potential energy. The repulsive potential energy increased with increasing phosphate sorption up to about 5 to 20 mmol kg⁻¹ at all pH, and it induced the soil dispersion, because phosphate sorption increased the negative charge of the soil. After its peak, it decreased with increasing phosphate sorption because the electrolyte concentration increased and the electrolyte screened the electric field near the soil surface. The repulsive potential energy also increased with increasing pH because of the increase of the negative charge of the soil. Even at low pH, after a certain amount of phosphate sorption, the soil dispersed due to the increase of repulsive potential energy, although the soil flocculated before phosphate application. Because the soil dispersion causes soil and phosphorus loss, the influence of soil pH and phosphate sorption on the soil dispersion should be considered for good soil management.

Key words:

• Dispersion
• Ferralsol
• phosphate
• repulsive potential energy
• sorption

INTRODUCTION

When a soil is dispersive, the soil permeability decreases and it sometimes induces erosion. The dispersed soil is transported in surface runoff. Subsurface leaching also occurs. In those cases, adsorbed nutrients are also conveyed and they sometimes cause water contamination. Because phosphate is an important limited resource, it must be used effectively.

Long-term fertilizer applications have been reported to cause increases in water-stable aggregation, porosity, infiltration capacity and hydraulic conductivity, and decreases in bulk density (Haynes and Naidu 1998). A number of workers have investigated the use of phosphoric acid as an agent for promoting aggregate stability in soils (e.g. Thien 1976; Yeoh and Oades 1981) where other phosphatic fertilizers have no effect (Haynes and Naidu 1998). On the other hand, other researchers have reported that phosphate sorption induces mobilization of colloids and colloidal phosphate, and phosphate accumulation in soils increases the risk of colloid-facilitated leaching of phosphate (Siemens et al. 2004; Jianhong and Packman 2005; Scalenghe et al. 2007; Calero et al. 2008; Ilg et al. 2008). Shanmuganathan and Oades (1983), Lima et al. (2000), and Lagaly and Ziesmer (2003) have indicated that phosphate sorption increases the negative charge density of soils which affects flocculation-dispersion phenomena. Penner and Lagaly (2001) have shown that salts with multivalent anions such as sulfates and phosphates increase the critical coagulation concentration for montmorillonite and kaolinite dispersions. Teo et al. (2009) have indicated that a sufficiently high phosphate concentration completely deflocculated the clay slurries. The phosphate concentrations in soils are generally low; however, near fertilized points, phosphate concentration may reach much higher values. Celi et al. (2000) found that high phosphate addition near fertilized particles has caused a compression of the diffuse layer closer to the oxide surface, leading to an increase of phosphate sorption due to a reduction of the electrostatic repulsive forces. Therefore, understanding the influence of phosphate sorption on flocculation-dispersion under a wide range of concentrations is valuable as a fundamental study for preventing erosion and colloidal leaching with phosphate loss. In addition, because pH affects soil charge, it strongly influences the dispersion-flocculation of soils. Flocculation occurred near the point of zero charge; the aluminum (Al) oxide was flocculated at pH > 9.5 and the iron oxide was flocculated between pH 6.0 and 8.2 (Goldberg and Glaubig 1987). The soil dispersed well and the permeability decreased well at pH 9 more than those at pH 6 for the montmorillonitic and the kaolinitic soil (Suarez et al. 1984). The allophanic andisol dispersed well and the permeability decreased well at pH < 5 and pH >10 (Nakagawa and Ishiguro 1994; Ishiguro and Nakajima 2000; Ishiguro 2005). Therefore, pH is one of the most important factors when we consider the influence of dispersion-flocculation.

Electrokinetic methods are applied widely in colloid science to obtain the charge characteristics of the colloids as well as for the evaluation of colloidal stability by many authors (Celi et al. 2000; Ilg et al. 2008). Based on zeta potential, optical density and particle size, Ilg et al. (2008) concluded that the addition of phosphate caused mobilization of soil colloids when zeta potential was –20mV. Celi et al. (2000) indicated that increase of phosphate sorption on goethite made zeta potential more negative (–20 to –37mV). Colloidal dispersion can be theoretically determined by using the Derjaguin-Landau-Verwey-Overbeek (DLVO) theory in which the electric repulsive potential energy and the van der Waals attractive potential energy between the two colloidal particles are evaluated. When the electric repulsive potential energy becomes larger than the attractive potential energy as the two particles come closer, the particles disperse. By using the theory, Kobayashi et al. (2005) showed that stability of colloidal silica increases with decreasing ionic strength and increasing magnitude of particle charge. Although studies on soil dispersion influenced by phosphate sorption have been conducted, such a theoretical investigation has not been applied.

In this paper, the influence of phosphate sorption on soil dispersion was firstly evaluated by calculating repulsive potential energy. A Ferralsol, which is typical in rainy tropical regions and sorbs phosphate strongly, was used. The influence was systematically investigated under different pH and electrolyte concentration.

MATERIALS AND METHODS

Soil

Ferralsol was collected at a depth of approximately 10 cm from a rubber tree field in Nam Dong District, Thua Thien Hue Prefecture, Vietnam. The rubber trees had been planted for 15 years. All soil samples were air dried and sieved with a 2-mm sieve. The general physical and chemical properties are listed in Table 1. The organic matter content was determined by the method of Walkley and Black (1934). Exchangeable Al was extracted with 1 mol L⁻¹ potassium chloride (KCl). Total Al and iron (Fe) fractions were extracted with 0.1 mol L⁻¹ sodium pyrophosphate. The cation exchange capacity (CEC) was determined by the ammonium acetate method (Sumner and Miller 1996). The crystalline clay minerals and their composition are listed in Table 2. The crystalline clays were identified by the X-ray powder diffraction method. The elemental or oxide contents of crystalline clays were measured by the X-ray fluorescence method.

Table 1 Physical and chemical characteristics of the soil

Soil characteristics
Clay	41.16 %
Silt	29.35 %
Sand	29.49 %
pHKCl	3.99
pHH2O	4.99
CEC	8.33 ceq kg^−1
Bulk density	1.09 Mg m^−3
Density of solids	2.64 Mg m^−3
Total N	0.1 %
Organic matter	2.77 %
Exchangeable Al ^3+	0.96 ceq kg^−1
Al2O3	26.89 %
Fe2O3	13.59 %
Dithionite-extractable Al	6.3 g kg^−1
Oxalate-extractable Al	1.1 g kg^−1
Dithionite-extractable Fe	37.0 g kg^−1
Oxalate-extractable Fe	3.4 g kg^−1

Table 2 Crystalline clay fraction and composition

Clay fraction	(%)
Crystalline clay fraction
Quartz	61.0
Kaolinite	34.4
Goethite	< 4.6
Composition
Al2O3	26.89
Fe2O3	13.59
SiO2	56.77
K2O	0.82
P2O5	Not detected
CaO	0.02
TiO2	1.91

Phosphate sorption experiment

The phosphate sorption at the prescribed pH (4, 5.5, 7 and 8.5) was determined using a batch method. Phosphate was added as NaH₂PO₄ HNO₃ and NaOH were used to adjust pH. The sodium (Na) adsorption amount and that of nitrate (NO₃) at the < 10mmol L⁻¹ NaH₂PO₄ added amount were also measured.

The experimental procedure was as follows:

1. About 3 g of the soil was equilibrated with 0.025 L of a 1-mmol L⁻¹ or a 10-mmol L⁻¹ sodium nitrate (NaNO₃) solution at the prescribed pH (4, 5.5, 7, 8.5) in a centrifuge tube. It was centrifuged, and the supernatant A was stored. The weight of the centrifuge tube + the soil + the soil solution was measured after discarding the supernatant.

2. A 0.025-L phosphate solution at different concentrations (0, 0.03, 0.3, 3, 10, 30, 100 mmol L⁻¹) was added to the tube. The pH of the solution was adjusted if the pH changed. The tube was shaken for 24 h. The final equilibrium electrolyte concentration was set at 1 mmol_c L⁻¹ or 10 mmol_c L⁻¹ with NaNO₃ when the added phosphate concentration was smaller than that concentration. The final equilibrium electrolyte concentration became more than 1 mmol_c L⁻¹ or 10 mmol_c L⁻¹ when the added phosphate concentration was larger than that concentration.

3. The tube was centrifuged and the supernatant B was stored. The weight of the centrifuge tube + the soil + the soil solution was measured after discarding the supernatant.

4. 0.03 L of a 100 mmol L⁻¹ KCl solution was added to the tube. The tube was shaken for more than 1 h and then centrifuged, and we gathered the supernatant C. This was repeated 5 times.

5. The soil was oven dried and the weight was measured.

The phosphate concentrations of the supernatants (A, B, C) were measured by ascorbic acid method (Murphy and Riley 1962). Na concentrations of the supernatants (A, B, C) were measured by flame emission spectrometry. NO₃^– concentrations were measured using the calorimetric method in a continuous-flow analytical system (Traccs 800, Bran + Lubbe, Norderstedt, Germany).

The phosphate sorption was calculated by subtracting the amount in the final soil solution in Step 3 from the added amount. The Na and NO₃ adsorptions were calculated by subtracting the amount remaining in the soil solution at the end of Step 3 from the amount in the supernatant C.

Dispersion experiment

The soil and the solution under the same condition in the phosphate sorption experiment were shaken well and left to stand still for 3 h. Then, 4 cm³ of the supernatant was taken from 2 cm below the water surface. Its absorbance was measured using the light at 660 nm wavelength (UV-VIS Spectrophotometer 1240, Shimadzu Corporation, Japan).

Zeta potential measurement

The zeta potential was calculated from the measured electrophoretic mobility using the Ohshima equation (Ohshima 2004; Kobayashi 2008), because the measurement condition satisfied κa > 30, where κ is the inverse of Debye length expressed by Eq. 2, below, and a is the mean radius of the soil particles. In the mobility measurement, the mean radius of the soil particles was about 0.5 μm. The radius was measured with dynamic light scattering method. The measurement procedure was as follows:

1. The soil was prepared under the same solution condition at the end of Step 3 in the phosphate sorption experiment. It was shaken well and the suspension was taken from 2 cm below the water surface.

2. The sampled suspension was stirred by ultrasonic waves for 30 sec. One cubic centimeter of the suspension was diluted about 10,000 times by the same solution.

3. The zeta potential of the soil suspension was obtained by measuring the mobility (Model 502, Nihon Rufuto).

THEORY OF ELECTRICAL REPULSIVE POTENTIAL ENERGY

The electrical repulsive potential energy between the soil clay particles was estimated in order to evaluate the behavior of soil dispersion and flocculation affected by phosphate sorption. The energy was calculated based on the zeta potential.

In the case of low surface potentials (|ψ | < 25 mV), a potential at the distance × from the charged clay surface, ψ, can be estimated as follows:

(1)

(2)

(3)

where ψ_s is the potential of the soil surface, e = 1.602 × 10⁻¹⁹ C is the elementary charge, z_i is the charge number of ion i, n_i is expressed as the number of ions per cubic meter, ε is the dielectric constant of the medium, M_io is the concentration of ion i in equilibrium solution (mol L⁻¹) and N_A is the Avogadro constant. In this calculation, a zeta potential is used instead of ψ_s in Eq. 1 in order to get the potential distribution from the plane of the zeta potential to the bulk solution.

In the general case, the relationship between ψ and × is explained in the following equation (Eq. 4) (Hiemenz 1986):

(4)

The following approximation solution can be derived from Eq. 4:

(5)

where Δψ is the small increment of the potential after the small increment of the distance Δx.

The concentration of ion i in the midpoint between two soil particles, M_i(x), at distance × from the zeta potential plane can be calculated with the following equation:

(6)

where ψ_m(x) is the potential at the midpoint at distance × from the zeta potential plane, which is obtained from the following equation:

(7)

where ψ(x) is the potential at distance × from the zeta potential plane when the soil particle exists alone. This is obtained from Eq. 1 or Eq. 5 and the zeta potential.

The electrical repulsive force between the particles, ΔP(x), is the osmotic pressure difference between the midpoint and the bulk solution.

(8)

Therefore, the repulsive potential energy, V_ζ, when the two particles approach from far distance 2b₂ to the distance 2b₁ between each zeta potential plane, can be obtained by the following equation:

(9)

V_ζ is derived to sum up 2ΔP(x) × Δx from b₁ to b₂ as shown in Eq. 9, where b₂ is the distance from the zeta potential plane to the boundary of the bulk solution (Bresler 1970; Iwata 1995; Ishiguro et al. 2003). Colloid dispersion-flocculation is determined by the peak value of the total potential energy (repulsive-attractive) between the colloid particles. We assume that the peak value rises at the distance between the zeta potential planes of the soil particles = 1 nm (i.e. b₁ = 0.5 nm) with reference to the following publications: Israelachvili (1982), Hiemenz (1986) and The Clay Science Society of Japan (2009). We let b₂ equal 100κ⁻¹ in the calculations. The small increment of the distance Δx was equal to 0.1 κ⁻¹ in calculating Eq. 5 and Eq. 9. Because κa was larger than 30, the diffuse layer thickness was much smaller than the radii of the soil clays. Therefore, we evaluated the interaction by using this simple plate model. We used Eq. 9 because the measured conditions were not those of a z:z electrolyte. In this calculation, all ions in the solution were considered in Eq. 8; since the valences of phosphate ions in solution change with pH, they were also included. The calculations were carried out using Microsoft Excel software.

RESULTS

Flocculation and dispersion of the soil suspension evaluated by absorbance

The obtained relationship between phosphate sorption and absorbance of the soil suspension is shown in Fig. 1a. The absorbance corresponds with the dispersion. When the value is larger, the soil disperses. The largest value indicated was 4 because that was the upper limit of the absorbance for the spectrophotometer. When the value is smaller, the soil flocculates. At pH 4, the soil suspension was the most flocculative compared with other pH. However, the peak of dispersion was observed at around 20 mmol P kg⁻¹ sorption. At this pH, the increase of absorbance could be observed clearly after > 1.6 mmol P kg⁻¹ sorption at 1.1 mmol L⁻¹ equilibrium electrolyte concentration and after > 2.7 mmol P kg⁻¹ sorption at 10 mmol L⁻¹ equilibrium electrolyte concentration (Fig. 1a and d). At pH 5.5 for the initial NaNO₃ concentration of 1 mmol L⁻¹ in Step 1 in the phosphate sorption experiment, it was relatively flocculative at 0 mmol P kg⁻¹ sorption (absorbance was 0.44). It became well dispersed after phosphate sorption. At pH 5.5 for the initial NaNO₃ concentration of 10 mmol L⁻¹ in Step 1 in the phosphate sorption experiment, it dispersed well as the phosphate sorption increased; it was well dispersed at around 15 mmol P kg⁻¹ sorption. At pH 7 and pH 8.5, it dispersed well. At higher phosphate sorption, the absorbance became smaller. Increase of phosphate sorption corresponds to the increase of equilibrium electrolyte concentration at > 17 mmol P kg⁻¹ sorption because phosphate was added as NaH₂PO₄.

Figure 1 Relationship between (a) phosphate sorption, (b) phosphate concentration, (c) sodium (Na) adsorption, (d) Na concentration, and absorbance of the soil suspension.

◆ pH 4, ◆ pH 5.5, △ pH 7, ◯ pH 8.5 for initial sodium nitrate (NaNO₃) concentration of 1 mmol L^–1 at step 1 in the phosphate sorption experiment.◆ pH 4, ■ pH 5.5, ▲ pH 7, ● pH 8.5 for initial NaNO₃ concentration of 10 mmol L^–1 at step 1 in the phosphate sorption experiment.

electrolyte concentration = 1 mmol_c L^–1,

1 mmolc L^–1 < electrolyte concentration < 10 mmol_c L^–1,

electrolyte concentration = 10 mmol_c L^–1,

electrolyte concentration > 10 mmol_c L^–1.

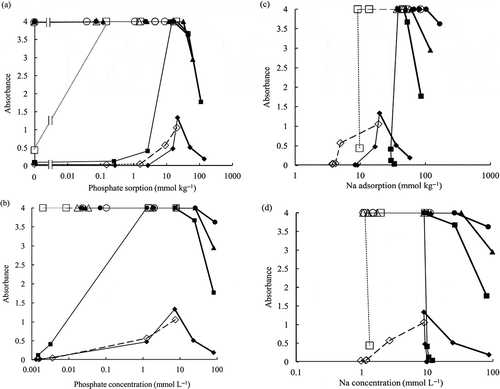
The relationship between phosphate concentration and absorbance of the soil suspension is shown in Fig. 1b. At pH 4, the peak dispersion was at 7.2–7.5 mmol P L⁻¹. At pH 5.5 for the initial NaNO₃ concentration of 10 mmol L⁻¹ in Step 1 in the phosphate sorption experiment, the influence of phosphate sorption was clear when the phosphate concentration was more than 0.001 mmol P L⁻¹. The soil also became well dispersed for the initial NaNO₃ concentration of 1 mmol L⁻¹ after phosphate sorption as mentioned above.

The relationships between Na adsorption, Na concentration and absorbance of the soil suspension are shown in Fig. 1c and d. Na concentration equals the equilibrium electrolyte concentration. At pH 5.5, the soil changed after phosphate sorption from relatively flocculative to well dispersive even at the same Na adsorption of 10 mmol Na kg⁻¹ for the initial NaNO₃ concentration of 1 mmol L⁻¹ and even at the slight increase from 30 to 38 mmol Na kg⁻¹ for the initial NaNO₃ concentration of 10 mmol L⁻¹. At these changes, the Na concentrations showed almost identical values. At pH 4 for the initial NaNO₃ concentration of 10 mmol L⁻¹, Na adsorption increased from 8 mmol Na kg⁻¹ to 20 mmol Na kg⁻¹, although the Na concentration kept almost the same value around 10 mmol L⁻¹. At higher Na concentration the absorbance became smaller. It was more flocculative at lower pH.

Zeta potential

The obtained relationship between absorbance of the soil suspension and the zeta potential is shown in Fig. 2a. The soil dispersed well when the magnitude of the zeta potential increased. It was flocculative when the zeta potential was larger than –20 mV. It was well dispersive when the zeta potential was smaller than –25 mV. However, the data at pH 5.5 and the absorbance of 1.8, and the data at pH 8.5 and the absorbance of 3.6 deviated slightly from the other data, although their trend was similar. The zeta potential for the initial NaNO₃ concentration of 1 mmol L⁻¹ and the equilibrium electrolyte concentration smaller than 10 mmol L⁻¹ was smaller than that for the initial NaNO₃ concentration of 10 mmol L⁻¹, because the potential was shielded when the electrolyte concentration was larger.

Figure 2 Relationship between (a) absorbance, (b) phosphate sorption, (c) sodium (Na) adsorption, (d) Na concentration, and zeta potential of the soil suspension.

⃟ pH 4, ◆ pH 5.5, △ pH 7, ◯ pH 8.5 for initial sodium nitrate (NaNO₃) concentration of 1 mmol L^–1 at step 1 in the phosphate sorption experiment.◆ pH 4, ■ pH 5.5, ▲ pH 7, ● pH 8.5 for initial NaNO₃ concentration of 10 mmol L^–1 at step 1 in the phosphate sorption experiment.

electrolyte concentration = 1 mmol_c L^–1,

1 mmol_c L^–1 < electrolyte concentration < 10 mmol_c L^–1,

electrolyte concentration = 10 mmol_c L^–1,

electrolyte concentration > 10 mmol_c L^–1.

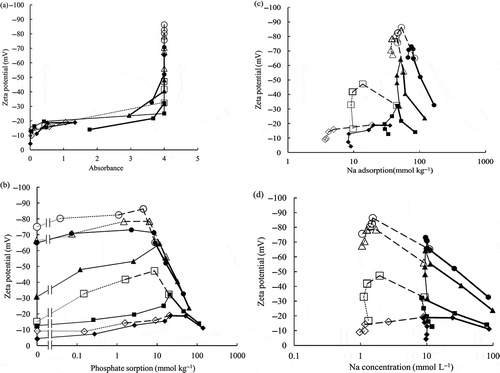
The relationship between the phosphate sorption and the zeta potential is shown in Fig. 2b. The magnitude of the zeta potential increased with the increase of the phosphate sorption until its peak value. The equilibrium electrolyte concentration increased with the increase of the phosphate sorption when the NaH₂PO₄ solution concentrations added in Step 2 of the experiment were larger than the initial NaNO₃ concentrations at Step 1. The magnitude of the zeta potential decreased with the increase of electrolyte concentration (also see in Fig. 2d) after its peak.

The relationships between the Na adsorption, the Na concentration and the zeta potential are shown in Fig. 2c and d. The Na adsorption was greater at higher pH. The magnitude of the zeta potential was larger at higher pH. Even at the similar Na adsorption and Na concentration (1 mmol L⁻¹ or 10 mmol L⁻¹ in Fig. 2) at their lower values, the magnitude of the zeta potential increased where the phosphate sorption increased as shown in Fig. 2b.

Repulsive potential energy

The obtained relationship between the absorbance of the soil suspension and the repulsive potential energy is shown in Fig. 3a. The absorbance increased with the increase of the repulsive potential energy. It flocculated well when the repulsive potential energy was less than 0.064 μJ m⁻² with absorbance < 0.05. It dispersed well when the repulsive potential energy was larger than 0.3 μJ m⁻² with absorbance = 4. A slight spread was observed among the data between 0.069 μJ m⁻² and 0.3 μJ m⁻² where the soil suspension turned to dispersion/flocculation. However, the overall correlation between the repulsive potential energy and the absorbance was good.

Figure 3 Relationship between (a) absorbance, (b) phosphate sorption, (c) sodium (Na) concentration, and repulsive potential energy.

⃟ pH 4, ◆ pH 5.5, △ pH 7, ◯ pH 8.5 for initial NaNO₃ concentration of 1 mmol L^–1 at step 1 in the phosphate sorption experiment.◆ pH 4, ■ pH 5.5, ▲ pH 7, ● pH 8.5 for initial sodium nitrate (NaNO₃) concentration of 10 mmol L^–1 at step 1 in the phosphate sorption experiment.

electrolyte concentration = 1 mmol_c L^–1,

1 mmol_c L^–1 < electrolyte concentration < 10 mmol_c L^–1,

electrolyte concentration = 10 mmol_c L^–1,

electrolyte concentration > 10 mmol_c L^–1.

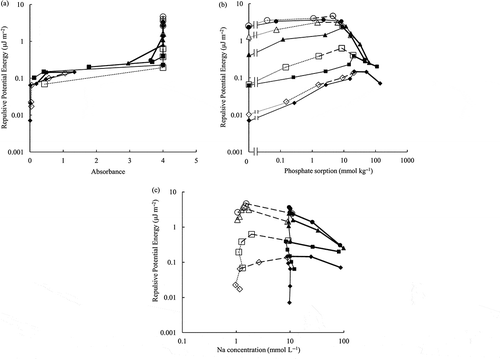
The relationship between the phosphate sorption and the repulsive potential energy is shown in Fig. 3b. The repulsive potential energy increased with the increase of pH. It increased with the increase of phosphate sorption at lower phosphate sorption (4.5 to 20 mmol P kg⁻¹). After its peak, it decreased with the increase of the phosphate sorption, which corresponded with the increase of the equilibrium electrolyte concentration; it decreased when the equilibrium electrolyte concentration was equal to or larger than 10 mmol_c L⁻¹ (the thicker lines shown in Fig. 3). The relationship between the Na concentration and the repulsive potential energy is shown in Fig. 3c. Even at the similar Na concentrations (1 mmol L⁻¹ or 10 mmol L⁻¹ in Fig. 3) at their lower values, the repulsive potential energy increased when the phosphate sorption increased as shown in Fig. 3b. The repulsive potential energy for the initial NaNO₃ concentration of 1 mmol L⁻¹ and the equilibrium electrolyte concentration lower than 10 mmol L⁻¹ was greater than that for the initial NaNO₃ concentration of 10 mmol L⁻¹, because the potential was shielded when the electrolyte concentration was greater (Fig. 3b).

NO₃ adsorption

The measured values of the NO₃ adsorption at pH 4 for the initial NaNO₃ concentration of 1 mmol L⁻¹ were 0.72 mmol NO₃ kg⁻¹ at the phosphate sorption of 0 mmol P kg⁻¹, 1.0 mmol NO₃ kg⁻¹ at the phosphate sorption of 0.15 mmol P kg⁻¹, 0.74 mmol NO₃ kg⁻¹ at the phosphate sorption of 1.6 mmol P kg⁻¹ and 0.30 mmol NO₃ kg⁻¹ at the phosphate sorption of 13 mmol P kg⁻¹. Those at pH 5.5, pH 7 and pH 8.5 were negative values ranging from –0.1 to –0.45 mmol_c NO₃ kg⁻¹.

DISCUSSION

Evaluation with repulsive potential energy

The influence of phosphate sorption on the dispersion of Ferralsol was clearly evaluated with the data of absorbance of the soil suspension (Fig. 1a). The results can be explained with the calculated repulsive potential energy between the soil particles because the absorbance and the repulsive potential energy corresponded well (Fig. 3a). When the repulsive potential energy becomes greater, the soil dispersion is stable because the soil particles cannot stick together due to the high repulsive potential energy. At lower pH, the soil was relatively flocculative because the repulsive potential energy was lower. On the other hand, the soil was dispersive at higher pH because that potential energy was greater (Fig. 3). The difference between flocculative and dispersive conditions is quite relative because it changes with time. Out of convenience, we define that the soil is well flocculative when the absorbance is less than 0.05 and the soil is well dispersive when the absorbance is 4. When the repulsive potential energy was less than 0.064 μJ m⁻², the soil was well flocculative. When it was higher than 0.3 μJ m⁻², the soil was well dispersive (Fig. 3a). Even at pH 4, the soil became rather dispersive when phosphate was sorbed; the repulsive potential energy became greater than 0.064 μJ m⁻² at 9 to 20 mmol P kg⁻¹ (Fig. 3b). At pH 5.5 for the initial NaNO₃ concentration of 1 mmol L⁻¹, the soil dispersed from lower phosphate sorption of 0.15 mmol P kg⁻¹; the repulsive potential energy was 0.19 μJ m⁻². At pH 5.5 for the initial NaNO₃ concentration of 10 mmol L⁻¹, the soil gradually dispersed with the increase of phosphate sorption and it dispersed at 15 mmol P kg⁻¹ where the repulsive potential energy was 0.23 μJ m⁻² (Fig. 3b). The influence of phosphate sorption on the soil dispersion was remarkable at pH 4 and pH 5.5 (Fig. 1a). A pH of 5.5 is also close to pH_water in the field in Table 1. Therefore, similar phenomena can occur in the real field soil. When we evaluated it from the phosphate concentration, the soil gradually became dispersive with increased concentration from about 1 mmol P L⁻¹ at pH 4 and from 0.0015 mmol P L⁻¹ at pH 5.5 for the initial NaNO₃ concentration of 10 mmol L⁻¹ (Fig. 1b). At pH 5.5 for the initial NaNO₃ concentration of 1 mmol_c L⁻¹, the soil condition changed significantly after phosphate sorption of 0.15 mmol P kg⁻¹ at 0.002 mmol P L⁻¹ from flocculative to well dispersive; the absorbance increased from 0.44 to 4 and the repulsive potential energy increased from 0.07 to 0.19 μJ m⁻² (Fig. 1b and 3a). At those lower pH values, the soil was more flocculative for the initial NaNO₃ concentration of 10 mmol L⁻¹ than that for the initial NaNO₃ concentration of 1 mmol L⁻¹ because of the shielding effect as mentioned before.

When the equilibrium electrolyte concentration was greater than 10 mmol_c L⁻¹, the soil gradually became flocculative (Fig. 1d) because the electric field near the soil particle surface was shielded by the electrolyte at high concentration, and the repulsive potential energy decreased (Fig. 3c). At pH 5.5 and pH 7, decrease of absorbance from 4 to 1.8 and 4 to 3 resulted from the decrease of repulsive potential energy from 0.41 to 0.20 μJ m⁻² and from 0.81 to 0.25 μJ m⁻² (Fig. 3a). The overall correlation between the absorbance and repulsive potential energy was good, although a slight spread was observed among the data between 0.069 μJ m⁻² and 0.3 μJ m⁻² where the soil suspension turned to dispersion/flocculation. The precise evaluation can be conducted using the DLVO theory which includes attractive Van der Waals potential energy. However, its evaluation is difficult because the repulsive potential energy is based on the measured zeta potential in this study; the distance from the soil surface to the zeta potential plane is difficult to estimate. Therefore, we evaluated using only the repulsive potential energy because the attractive Van der Waals potential energy is independent from pH and electrolyte concentration. This evaluation is similar to that which Ishiguro et al. (2003) has done in a sulfate and nitrate system. In this paper, we evaluated it concerning phosphate sorption. Kobayashi et al. (2005) successfully evaluated aggregation for a silica and Kobayashi et al. (2009) successfully did deposition for simple latex spheres using the DLVO theory. Good estimation of the distance of the slipping plane of simple latex spheres was also shown (Kobayashi 2008). The theoretical evaluation using total potential energy for the complicated soil system remains a future study.

Inspection with zeta potential and soil charge

The repulsive potential energy was smaller at lower pH and larger at higher pH (Fig. 3b) because the negative charge of the soil increased with the increase of pH. This was confirmed with the increase of the magnitude of the zeta potential with the increase of pH and Na adsorption (Fig. 2b and c); effect of pH can be detected when the data of the same equilibrium electrolyte concentration were compared among those different pHs. Na adsorption equals the negative charge of the soil. Haynes and Naidu (1998) pointed out that repulsive forces between particles dominate and lead to dispersion when the pH increases. We elucidated this using the repulsive potential energy. The repulsive potential energy was smaller at greater electrolyte concentration due to the shielding of the electric field as mentioned before (Fig. 3c). The shielding effect can be verified by the decrease of the magnitude of the zeta potential with the increase of the equilibrium electrolyte concentration; the equilibrium electrolyte concentration equals the Na concentration in this system (Fig. 2d).

The repulsive potential energy increased with the increase of phosphate sorption when the equilibrium electrolyte concentration was lower than or equal to 10 mmol_c L⁻¹ (Fig. 3b and c). This resulted from the increase of the magnitude of the zeta potential with the increase of the phosphate sorption when the equilibrium electrolyte concentration was lower than or equal to 10 mmol_c L⁻¹ (Fig. 2b). When phosphate is sorbed, the sorbed site is negatively charged in some cases. When phosphate is sorbed on an initially positively charged site, the positive charge disappears (Stoop 1983; Nanzyo 1988; Celi et al. 2000). In both cases, the net negative charge increases after phosphate sorption. It is supposed that the increased net negative charge strongly affected the electric field near the soil surface. Then the magnitude of the zeta potential increased and the repulsive potential energy increased.

The Na adsorption equals the negative charge of the soil. Although the magnitude of the zeta potential increased with increasing phosphate sorption until reaching their peak (Fig. 2b), the Na adsorption did not increase in proportion to the increase of the magnitude of the zeta potential when the phosphate sorption was lower than 3 mmol P kg⁻¹ (the smallest 3 data points of the Na adsorption for each pH and less than 10 mmol L⁻¹ concentration condition in Fig. 2c and d). The absorbance increased while the negative charge of the soil = the Na adsorption did not increase in this region (Fig. 1c). In the case that an initial positive charge was deleted and no negative charge was generated after phosphate sorption, Na was not adsorbed. Even though Na was adsorbed on a new negative charge site after phosphate sorption, the amount was smaller compared with the total Na adsorption. Therefore, Na adsorption did not correlated with the zeta potential directly under those conditions.

The particles smaller than 0.002 mm were quartz (61 %), kaolinite (34.4 %) and goethite (< 4.6 %) in the soil. The point of zero charge of quartz is about pH 0.5–3.5 (Iler 1979), that of kaolinite is about pH 4.1 (Wei et al. 2014), and that of goethite is about pH 8.2 (Wei et al. 2014), according to the literature. They and the organic materials have variable charges and the positive charge decreases or the negative charge increases with the increase of pH. The zeta potentials were all negative values in this experiment and the magnitude increased with the increase of pH. This result coincides with the expected trend of the zeta potential from the composition of the particles; the negative charge dominates at pH > 4 when the quartz predominates. Because the goethite has a positive charge when pH is lower than the point of zero charge, it might affect the soil flocculation to some extent, especially at lower pH.

Because the soil has a positive charge at lower pH, it affected the soil flocculation strongly. The positive charge was equal to NO₃ adsorption; that was about 1 mmol NO₃ kg⁻¹ at pH 4 at 1 mmol_c NaNO₃ L⁻¹ and not detected when pH was ≧ 5.5. The increase of the phosphate sorption canceled the positive charge and sometimes added a negative charge. That resulted in the increase of the magnitude of the zeta potential and the increase of repulsive potential energy, as mentioned above.

The absorbance increased with the increase of the magnitude of the zeta potential (Fig. 2a). However, the data at pH 5.5 and the absorbance of 1.8, and that at pH 8.5 and the absorbance of 3.6, deviated from the other data. Although the zeta potential itself is not a direct physical parameter of soil dispersion, it is a good indicator. Lima et al. (2000) indicated a related result, that electrophoretic mobility corresponded to the soil dispersion, and they showed phosphate-induced clay dispersion. Ilg et al. (2008) indicated that the critical value of zeta potential for phosphorus-induced dispersion was about –20 mV. Sugimoto et al. (2014) showed that zeta potential is a good indicator and a fast coagulation regime is attained by reducing its magnitude below 25 mV for a carboxyl latex. Our results also showed that the soil dispersion was observed under –20  to –25 mV, as shown in Fig. 2a. In this research, different from the other studies, we evaluated the influence of phosphate sorption on the soil dispersion by calculating the repulsive potential energy based on the zeta potential.

CONCLUSIONS

We successfully evaluated the influence of phosphate sorption on the Ferralsol dispersion by calculating repulsive potential energy based on zeta potential. The influence was systematically inspected for the Ferralsol. The soil was flocculative at lower pH. However, it became dispersive after phosphate sorption. Because soil dispersion sometimes causes soil erosion and a decrease of soil permeability, it is better to avoid the dispersive condition when applying phosphate fertilizers even if the soil is initially flocculative. Moreover, because phosphate is easily conveyed by soil particles with moving water to the water environment when the soil is dispersed after phosphate sorption, the soil must be maintained in flocculative condition in order to use phosphate effectively and prevent soil erosion and water contamination.

ACKNOWLEDGMENTS

This research was supported by Grants-in-Aid for Scientific Research (No. 25252042) from the Japan Society for the Promotion of Science.