Calibration of Stochastic Computer Simulators Using Likelihood Emulation

Abstract

We calibrate a stochastic computer simulation model of “moderate” computational expense. The simulator is an imperfect representation of reality, and we recognize this discrepancy to ensure a reliable calibration. The calibration model combines a Gaussian process emulator of the likelihood surface with importance sampling. Changing the discrepancy specification changes only the importance weights, which lets us investigate sensitivity to different discrepancy specifications at little computational cost. We present a case study of a natural history model that has been used to characterize UK bowel cancer incidence. Datasets and computer code are provided as supplementary material.

• Bayesian inference
• Computer experiments
• Gaussian process emulator
• Importance sampling
• Natural history model

INTRODUCTION

We consider the problem of calibrating a computer model of a physical process to observations from the process: finding model input values such that the model outputs match the observed data as closely as possible. Our approach is inspired by the framework for Bayesian calibration proposed by Kennedy and O’Hagan (2001) and developed in Higdon et al. (2004), Bayarri et al. (2007b), Bayarri et al. (2007a), and Higdon et al. (2008), and by Bayes’ linear history matching developed by Craig et al. (2001), Goldstein and Rougier (2006), and Vernon, Goldstein, and Bower (2010). We refer to a computer model as a “simulator” and focus on three issues: computationally expensive simulators; “discrepancy,” which is the error in a simulator prediction due to the simulator being an imperfect model of reality; and stochastic simulators, which are simulators that can return different output values from the same input values.

Any calibration method will involve running the simulator at different input values. Methods that require many simulator runs become impractical if a single simulator run at one input value takes a long time. A well-established technique for handling expensive simulators, proposed in Sacks et al. (1989), is to construct a cheap surrogate model or “emulator” of the simulator using Gaussian process regression, based on relatively few simulator runs. Variations of this method are used in the above references. We consider a simulator of ‘moderate’ computational cost, in which runs take one to two minutes, depending on input values. We argue that this changes the nature of the surrogate modeling problem. Rather than attempting to construct a very precise emulator of the simulator, we propose to use a cruder emulator to guide us to the appropriate regions of the input space, and then do direct simulator evaluations in those regions. In particular, we propose using importance sampling (see, e.g., Ripley 1987, sec, 5.2), where the emulator is used to construct the importance density.

When calibrating a simulator, it is important to account for simulator discrepancy for two reasons. First, if the inputs are physically meaningful quantities that could, in principle, be observed directly, calibrating a simulator without accounting for discrepancy may result in biased estimates with severe over-confidence, as demonstrated in Brynjarsdóttir and O’Hagan (2014). If the simulator inputs are “tuning” parameters that are not physically observable, discrepancy plays an important role when calibrating to multiple outputs, or when predicting unobserved output quantities using a calibrated simulator. Suppose that we have a physical observation for an output quantity Z₁, and wish to predict an unobserved output quantity Z₂. A simulator input value may give a poor fit to output Z₁, but a good prediction of Z₂. If we do not believe the simulator models Z₁ perfectly, we would not necessarily want to rule out such an input value and corresponding prediction of Z₂. Accounting for the simulator error in modeling Z₁ would prevent this.

As argued by Brynjarsdóttir and O’Hagan (2014), it is important to specify meaningful proper prior distributions for simulator discrepancy, but to do this may be difficult. In Vernon and Goldstein (2010), within a Bayes linear framework, the simulator expert only provided an interval for the variance of a discrepancy parameter. Strong, Oakley, and Chilcott (2012) suggested “opening the black box” and incorporating discrepancy terms within the simulator, so that the expert considers sources of simulator discrepancy explicitly, rather than attempting to make judgments about the overall discrepancy. We argue that it is desirable to be able to investigate, without too much difficulty, a range of different discrepancy distributions, within any calibration methodology. Within our proposed importance sampling framework, we suggest an initial, conservative specification of simulator discrepancy, which can then be varied with little extra computational effort via recalculation of importance weights corresponding to different discrepancy distributions.

The third issue that we consider is that of a stochastic simulator. Traditionally the interest in statistical methods for computer experiments has focused on deterministic models, but the methodology can be readily extended to stochastic models (see, e.g., Kleijnen 2007, chap. 5). In our case study, the stochasticity results from the use of discrete event simulation to simulate (among other things) transition times between cancer states. The use of simulation will typically result in at least moderate computational expense, in an attempt to eliminate or reduce simulation error. There is a broad range of examples of stochastic simulation models to which the proposed calibration method can contribute. Ghani, Monfared, and Harrison (2012) coupled virtual engineering and simulation models to efficiently minimize energy costs for a manufacturing process; here calibration can ensure that various worker and shift pattern constraints are met, allowing so-called “what-if” scenarios to be explored for further energy savings. Gillespie (2007) simulated chemical interactions of molecules over time; calibrating inputs ensures that numbers of molecules for different species match target data at given times and, given the simulation model’s structure, allows molecules’ positions and velocities at intermediate times to be understood. Simulations of fluid transport through karstic aquifiers in Jaquet et al. (2004) relied on a discrete representation of spatially variable geometric and hydraulic properties; here calibration ensures that the inputs give reliable simulations.

Studying a stochastic simulator raises the question of what it is we should try to emulate, assuming that an emulator is necessary. The simulator in our case study produces random count data. In a similar scenario, Henderson et al. (2009) constructed emulators for probabilities from which the count data were assumed to have been generated, which links to the geostatistical modeling of probabilities proposed by Diggle, Tawn, and Moyeed (1998). We propose constructing an emulator for the likelihood function given the observed data. Our simulator produces 30 count data outputs (with various dependencies between the outputs), and so emulating the likelihood reduces the computational effort to emulating a univariate output, and enables us to implement an importance sampling approach for the calibration. This is achieved by reducing the input region sequentially: ruling out inputs from regions where the likelihood is relatively low. This relates to the history matching of Vernon, Goldstein, and Bower (2010), in which parts of input space measured to have large implausibility are ruled out.

This article has the following structure. The next section introduces the natural history model that we will calibrate. Section 3 then outlines the calibration method. Section 4 presents the results of calibration for the natural history model and Section 5 offers conclusions and discussion of the calibration method.

2. MOTIVATING APPLICATION: CALIBRATING A NATURAL HISTORY MODEL OF BOWEL CANCER

We present a case study based on a natural history model (NHM). This is a stochastic computer simulation model that produces count data as output. The output stratifies UK bowel cancer incidence by age and various categories for bowel cancer type. We present only the basic set-up of the NHM; for a fuller description see Tappenden (2011). The NHM represents a birth cohort: a fixed-size sample of people followed from birth to death. A person in the cohort is deemed to have developed bowel cancer when they have reached the first cancer state, Duke’s A, having begun in a noncancer state, and progressed through three, ordered precancer states: low-, medium- and high-risk adenomas. A person may continue to progress through three more increasingly severe cancer states, Duke’s B, C and Stage D. Progression between states is governed by time. When in a given state, a progression time to the next state is simulated, together with a presentation time (the most common form of presentation being to visit a doctor), and a time until death. Out of these three actions, the one that occurs is the one with the shortest simulated time. Times are assumed to follow state-dependent Weibull distributions, the parameters of which form the majority of the NHM’s unknown parameters that we calibrate.

The NHM’s output is four sets of count data, which are calibrated against various comparable target data; Section 4.1 gives further details. The data broadly cover the distribution of cancer cases by age and by type, which are two important measures for assessing whether the NHM’s output matches reality. We can calibrate against such data because the NHM’s framework lets a person’s age be known whenever they change state. It also lets a person progress straight from birth to death (without ever contracting bowel cancer), or progress through some or all precancer and cancer states. Once a patient makes aware their symptoms, they enter the health system and receive a bowel cancer diagnosis. The age-based data that form part of the NHM’s output result from these diagnoses and the tracking of ages. Having left the health system, a person returns to a noncancer state and is still represented by the NHM, but their progression rates between states are elevated. While designed to mimic bowel cancer treatment within the health system, not all processes are necessarily well understood, or can be incorporated in the model. Simplifying assumptions used, such as times following Weilbull distributions, give examples of where discrepancy may arise.

The motivation for calibrating such a model is to support decision making. In the UK, the National Institute for Health and Care Excellence (NICE) regularly makes such healthcare resource allocation decisions on the basis of cost-effectiveness, with the decisions typically informed by simulator predictions (e.g., see Tappenden et al. 2012). Furthermore, NICE expects analysts to account for simulator input uncertainty, preferably by assigning probability distributions to the inputs and deriving the simulator output distributions (National Institute for Health and Care Excellence 2013, Section 5.8.7). The calibrated input distributions can be used for this purpose.

3. THE CALIBRATION METHOD

3.1 The Calibration Problem

We have target data Z, observed in the real world, with which we can calibrate the simulator. The data comprise observations of various binomial and multinomial random variables; for simplicity suppose that Z is a single binomial random variable, with Z|θ* ∼ Bin(N, θ*). The computer simulator encodes a function θ(x) that describes the relationship between some input parameters x and a binomial distribution probability parameter θ(x). We suppose that there is a true, observable input value X, observable in the sense that, in theory data could be obtained to estimate X directly, independently of the simulator. (To clarify, we have x as an arbitrary choice of input value, and X as the true, unknown values of the input quantities in reality.) For example, inputs 7 and 8 characterize the shape and scale of the Weibull distribution that represents transition times between cancer states Duke’s A and B. In theory, these values could be estimated directly by observing transition times in patients, but it would be unethical to allow such transitions to occur without intervening.

Relating the simulator to reality, we recognize that the simulator is not perfect, and we write θ* = θ(X) + δ, where δ represents the simulator error or discrepancy, as in Kennedy and O’Hagan (2001) and Vernon, Goldstein, and Bower (2010). Note that in Kennedy and O’Hagan (2001), the simulator had both nonrandom “control” inputs x_cont that the user could simply choose, and uncertain calibration inputs X_calib to be inferred. This would correspond to writing θ*(x_cont) = θ(x_cont, X_calib) + δ(x_cont), so that the discrepancy depends on the settings of the control inputs. In our scenario, the simulator has calibration inputs only.

3.2 Calibrating a Stochastic Computer Simulator

The computer simulator does not actually calculate θ(x) for a given input x. Instead, the simulator outputs a random variable Y(x) with Y(x)|θ(x), n(x) ∼ Bin(n(x), θ(x)). The value of n(x) is expected to increase with the patient cohort size, the original patient sample size chosen for the simulator, but is subject to some random variation. Hence, for any simulator run at input x, we will have to infer the value of θ(x) based on the observations for Y(x) and n(x). During the calibration process, we run the simulator at inputs x₁, …, x_m, to obtain simulator data D = {x_i, Y(x_i), n(x_i)}^m_{i = 1}, and use the calibration to derive the posterior distribution π(X|Z, D); we infer X given Z and D.

We can evaluate the likelihood π(Z | X = x, D) for X at the value of x via $$\begin{array}{ccc}\hfill \pi \left(Z\right|X=x,D)& =& \int \int \pi \left(Z\right|\theta \left(x\right),\delta ,x,D\left)\pi \right(\theta \left(x\right)|x,D)\hfill \\ & & \times \pi \left(\delta \right|\theta \left(x\right),x,D\left)d\theta \right(x)d\delta ,\hfill \end{array}$$which we assume can be simplified as $$\begin{array}{c}\hfill \pi \left(Z\right|X=x,D)=\int \int \pi (Z\left|\theta \right(x),\delta )\pi \left(\theta \right(x\left)\right|D\left)\pi \right(\delta \left)d\theta \right(x)d\delta .\end{array}$$We make a further simplification: we suppose that we have run the simulator at x to observe Y(x) and n(x), so that {x, Y(x), n(x)} ∈ D and then we set $$\begin{array}{c}\hfill \pi \left(\theta \right(x\left)\right|D)=\pi (\theta \left(x\right)\left|Y\right(x),n(x\left)\right),\end{array}$$so that we only use the run at x to infer the corresponding θ(x). The resulting likelihood is (1) $$\begin{array}{ccc}\hfill \pi \left(Z\right|X=x,D)& =& \int \int \pi \left(Z\right|{\theta }^{*})\pi \left({\theta }^{*}\right|Y\left(x\right),n\left(x\right))\hfill \\ & & \times \pi \left(\delta \right)d\theta \left(x\right)d\delta .\hfill \end{array}$$(1)

3.3 Incorporating Simulator Discrepancy

We need to specify a prior distribution π(δ). Assuming we are not expecting bias in any particular direction, we set E(δ) = 0. We might then specify δ ∼ N(0, τ) for some appropriate τ, but this would give an intractable likelihood (1(1) $$\begin{array}{ccc}\hfill \pi \left(Z\right|X=x,D)& =& \int \int \pi \left(Z\right|{\theta }^{*})\pi \left({\theta }^{*}\right|Y\left(x\right),n\left(x\right))\hfill \\ & & \times \pi \left(\delta \right)d\theta \left(x\right)d\delta .\hfill \end{array}$$(1) ), as would any other standard choice of distribution.

As the effect of var(δ) is to introduce extra “noise” into the system, we can instead incorporate discrepancy and obtain a closed form expression for the likelihood by inflating uncertainty about θ(x), instead of explicitly specifying π(δ). We choose a U[0, 1] prior distribution for θ(x) and suppose that $$\begin{array}{c}\hfill \theta \left(x\right)\left|Y\right(x),n(x)\sim \mathrm{Beta}(1+\lambda Y\left(x\right),1+\lambda \left(n\right(x)-Y(x\left)\right)),\end{array}$$with λ ∈ (0, 1]. In other words, the posterior for θ(x) is what we would have derived, had the simulator been run with a smaller cohort of patients. The prior distribution π(δ) is specified implicitly, with λ corresponding to var(δ); the “extra noise” is introduced via λ instead of var(δ). We now rewrite the likelihood as (2) $$\begin{array}{ccc}& & \pi \left(Z\right|X=x,D)=\int \pi (Z\left|\theta \right(x\left)\right)\pi \left(\theta \right(x\left)\right|Y\left(x\right),n\left(x\right)\left)d\theta \right(x)\hfill \\ & & =\frac{{}^N{C}_{Z}B(1+\lambda Y\left(x\right)+Z,1+\lambda (n\left(x\right)-Y\left(x\right))+N-Z)}{B(1+\lambda Y(x),1+\lambda (n\left(x\right)-Y\left(x\right)\left)\right)},\hfill \end{array}$$(2) where B(., .) is the Beta function.

Two apparent drawbacks of this approach are that prior beliefs about the discrepancy are no longer stated clearly, and that we would not be able to make posterior inferences about the discrepancy. However, we show in Section 4.2 that we can still visualize the prior discrepancy variance. It would also be possible to obtain a draw from the posterior distribution of the discrepancy π(δ|Z, D), by sampling x from the posterior π(X|Z, D), an observation error ϵ, a model output θ(x), and then calculating δ = Z − ϵ − θ(x). Though we do not actually perform this step, we present plots that compare model runs with calibration data, and hence give an impression of the posterior distribution of the discrepancy (see, e.g., Figure 4).

We discuss the choice of λ in Section 4.2 and investigate sensitivity in Section 4.8. In general, we propose an initial conservative specification. We can then obtain a sample from the posterior distribution π(X|Z, D) and use importance sampling to explore the effect of changing λ by changing the importance weights. For example, in the case where λ is multivariate, corresponding to a multiple output simulator, we can investigate scenarios where some outputs are believed to be better modeled than others. By starting with conservative values of λ we are, in effect, “broadening the search” for inputs that give simulator outputs that are close to the observed data. Without discrepancy, it is possible that no input value will give a good fit to all the output data.

3.4 Sampling from the Posterior Distribution of the Inputs

Obtaining Y(x) and n(x) is computationally expensive, so we need to be selective in where we choose to run the simulator and evaluate the likelihood. We use importance sampling, where we construct a cheap-to-evaluate importance density using a Gaussian process emulator (Sacks et al. 1989). Rasmussen (2003) used a Gaussian process approximation to a (log) posterior density function to improve the efficiency of Bayesian integration, which Fielding, Nott, and Liong (2011) extended to include parallel tempering to accommodate multimodality. Bliznyuk et al. (2008) used radial basis functions to provide a cheap-to-evaluate density function approximation. Overstall and Woods (2013) adopted similar sampling approaches to Rasmussen (2003) and Fielding, Nott, and Liong (2011), but differed by emulating multivariate simulator output directly, which reduces the dimension of the input space and allows fewer simulator runs to be used to build the emulator.

3.4.1 Emulator Construction

We build an emulator for the the log-likelihood for input vector x, x = (x⁽¹⁾, …, x^(p))^T, that is, for the function f(x), where (3) $$\begin{array}{c}\hfill f\left(x\right):=log\left\{\pi \right(z|X=x,y(x\left)\right)\}.\end{array}$$(3) Thus we model f(x) as a Gaussian process (Sacks et al. 1989), which is written $$\begin{array}{c}\hfill f\left(\right)|{\sigma }^2,\beta ,\varphi ,{\nu }^2\sim \mathrm{GP}(h^T\left(\right)\beta ,{\sigma }^{2}c(,)).\end{array}$$where h( ) and β comprise q basis functions and regression coefficients, respectively; h^T( )β is therefore, the GP mean function, σ² is its variance and c( , ) is its correlation function.

We choose the correlation function to have the Gaussian form $$\begin{array}{c}\hfill c(x_i,x_j)=\left\{\begin{array}{cc}exp\{-\sum _{d=1}^p{((x_i^{\left(d\right)}-x_j^{\left(d\right)})/{\varphi }_d)}^2\}\hfill & \text{if}{x}_i\ne x_j,\hfill \\ {(1+{\nu }^2/{\sigma }^2)}^{-1}\hfill & \text{if}{x}_i=x_j,\hfill \end{array}\right.\end{array}$$for roughness parameters φ = {φ₁, …, φ_p}, where φ_d > 0, d = 1, …, p. The parameter ν² > 0 introduces a nugget effect into the emulator, which has been shown to improve the predictive performance of Gaussian process emulators (Andrianakis and Challenor 2012; Gramacy and Lee 2012), but is imperative for a stochastic simulator. We choose a constant nugget because it is ultimately the emulator’s posterior mean that we use to sample inputs. We could let the nugget effect vary with inputs, but forms for this relationship are not obvious; while we investigated some log-linear forms, none improved upon the constant choice. We choose a Gaussian covariance function because we expect the underlying function to be smooth, and the inclusion of the nugget term is likely to make the precise choice less critical, as we are not trying to interpolate the training data exactly.

The emulator training data comprise m simulator runs. Inputs are chosen using a maximin Latin hypercube design on the emulator design region obtained having ruled out parts of the initial design region. We define input set D_X = {x₁, …, x_m}; vector of corresponding log-likelihoods f(D_X) = (f(x₁), …, f(x_m))^T; m × m matrix A with (i, j)th element c(x_i, x_j); m × q matrix H with ith row h(x_i); and t(x)^T = (c(x₁, x), …, c(x_m, x)).

Choosing hyperparameter prior π(σ², β, φ, ν²)∝σ^{− 2} gives the posterior emulator $$\begin{array}{c}\hfill f\left(\right)|D,\varphi ,{\nu }^2\sim t{P}_{n-q}(h^T\left(\right)\widehat{\beta },{\widehat{\sigma }}^2{c}^{*}(,))\end{array}$$a Student t-process on n − q degrees of freedom, where $$\begin{array}{ccc}\hfill \widehat{\beta }& =& {\left(H^T{A}^{-1}H\right)}^{-1}{H}^T{A}^{-1}f\left(D_X\right)\hfill \\ \hfill {\widehat{\sigma }}^2& =& {(m-q-2)}^{-1}{(f\left(D_X\right)-H\widehat{\beta })}^T{A}^{-1}(f\left(D_X\right)-H\widehat{\beta })\hfill \\ \hfill m^{*}\left(x\right)& =& h^T\left(x\right)\widehat{\beta }+t{\left(x\right)}^T{A}^{-1}\left(f\left(D_X\right)-H\widehat{\beta }\right)\hfill \\ & & \text{and}\hfill \\ \hfill c^{*}(x,x^{\text{'}})& =& c(x,x^{\text{'}})-t{\left(x\right)}^T{A}^{-1}t\left(x^{\text{'}}\right)+\left(h\left(x\right)-t{\left(x\right)}^T{A}^{-1}H\right)\hfill \\ & & \times {\left(H^T{A}^{-1}H\right)}^{-1}{\left(h\left(x^{\text{'}}\right)-t{\left(x^{\text{'}}\right)}^T{A}^{-1}H\right)}^T.\hfill \end{array}$$We fix (φ, ν²) at the posterior mode of π*(φ, ν²), where $$\begin{array}{c}\hfill {\pi }^{*}(\varphi ,{\nu }^2)\propto {\left({\widehat{\sigma }}^2\right)}^{-(m-q)/2}{\left|A\right|}^{-1/2}{\left|H^T{A}^{-1}H\right|}^{-1/2}\pi (\varphi ,{\nu }^2).\end{array}$$This is found using a derivative-free optimization algorithm, which is initialized using a short MCMC run with 200 iterations of a Gibbs sampler with Metropolis-Hastings updates.

3.4.2 Input Sampling Algorithm

For reliable samples from the input posterior distribution to be obtained, the emulator should represent high values of the log-likelihood fairly accurately. To achieve this we use an initial set of simulator runs to identify where the likelihood is not large, ie. where we are sure that calibrated inputs do not lie. We can repeat this procedure in waves, as in Vernon, Goldstein, and Bower (2010), until a sufficient amount of the initial input space has been ruled out to give the emulator design region. We elaborate on this preliminary step to the calibration in Section 4.4.

The calibrated inputs are obtained using importance sampling. The emulator’s posterior mean forms the importance density, and serves as an approximation to the log-likelihood. We can sample from the importance density using Gibbs sampling with Metropolis-Hastings updates. With the emulator design region identified, it may still take several attempts before the emulator forms an adequate importance density. To assess this we identify whether any parts of the input region exist where the difference between the posterior mean and the log-likelihood is large, or where, given the posterior mean is relatively large, the emulator’s uncertainty is large. The latter is measured using the pivoted Cholesky decomposition (Higham 2002). We add simulator runs in these parts to enable the emulator to provide a more accurate representation of the log-likelihood surface. The following algorithm then describes how we obtain the final sample of calibrated inputs.

1. Obtain a sample of inputs, D_S = (X₁, …, X_S), by Gibbs sampling as follows. For s = 1, …, S let X_s = (X⁽¹⁾_s, …, X^(p)_s)′ with initial state X₁. For s = 2, …, S set X_s = X_{s − 1}. For d = 1, …, p, generate X^(d)_* from univariate proposal distribution q( | X^(d)_{s − 1}) and let X_* = (X⁽¹⁾_s, …, X^{(d − 1)}_s, X_*^(d), X^{(d + 1)}_s, …, X_s^(p))′. Replace X^(d)_s with X^(d)_* with probability $min\{1,\frac{exp\left(m^{*}\left(X_{*}\right)\right)q\left(X_{s-1}^{\left(d\right)}\right|X_{*}^{\left(d\right)})}{exp\left(m^{*}\left(X_s\right)\right)q\left(X_{*}^{\left(d\right)}\right|X_{s-1}^{\left(d\right)})}\}$, where $m^{*}\left(x\right)=h^T\left(x\right)\widehat{\beta }+t{\left(x\right)}^T{A}^{-1}(f\left(D_X\right)-h^T\left(x\right)\widehat{\beta })$ and f( ) is the vector of log-likelihoods from Equation (3)(3) $$\begin{array}{c}\hfill f\left(x\right):=log\left\{\pi \right(z|X=x,y(x\left)\right)\}.\end{array}$$(3) .

2. Form the covariance matrix for the sample, ie. the S × S matrix A_S with (i, j)th element c*(X_i, X_j), for i, j = 1, …, S. Compute its Cholesky square root P with diagonal elements {p_s}^S_{s = 1}. Reorder X₁, …, X_S according to the pivot of P to give X₍₁₎, …, X_(S) and form D_piv ≔ {X₍₁₎, …, X_(u)} from the first u members, where u is the maximum number of simulator runs we are prepared to add to the training data in one iteration (which we suggest limiting to 10% of size of the input sample).

3. Define p_s to be “large” if p_s > v, for some v > 0. (Note that as A is a correlation matrix, v = 2 corresponds to a correlation below 0.05, which is a cut-off often used in geostatistics.) If no p_s are large, proceed to Step 5. Otherwise form the set D† = {X_(s) ∈ D_piv : p_s > v}, for s = 1, …, u, evaluate the simulator at each of its members and calculate their log-likelihoods, f(D†).

4. Add D† and f(D†) to the training data, rebuild the emulator, and return to Step 1.

5. Compute importance weights w_s = exp {f(X_s) − m*(X_s)} for X_s ∈ D_S. If a large proportion (we suggest more than 80%) of weights are zero, return to Step 4.

6. Obtain the calibrated inputs, D* = {X*₁, …, X_M*}, by resampling D_S with replacement according to weights w*_s = w_s/∑^S_{s = 1}w_s.

4. CALIBRATION OF A NATURAL HISTORY MODEL

4.1 Target Data, Output, and Notation

The target data and NHM output are counts that we will in general denote by Z_jk and Y_jk(x), respectively, where j = 1, …, 4 indexes the data type and k = 1, …, K_j indexes groups within types; corresponding sample sizes are denoted N_jk and n_jk(x), respectively. Here x is the input vector that we use to initialize the NHM. The data types are identified explicitly, as opposed to considering the output as a single vector, due to their inherent differences, which will emerge in the following summaries.

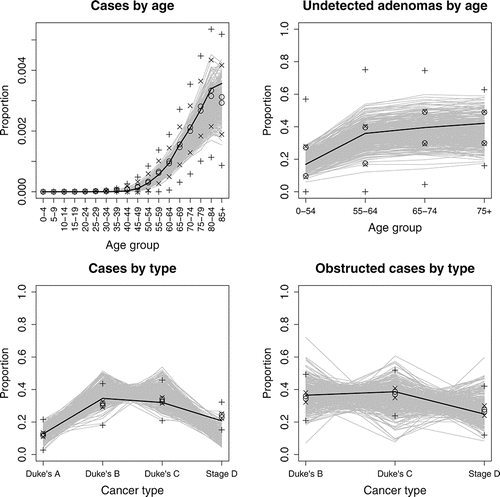
Figure 1 Variance decompositions for each target data source as described in Section 4.1. Cumulative contributions to variability (as given in equation set (4(4) $$\begin{array}{ccc}& & \text{measurement}\text{error}\pm 2\sqrt{\frac{p(1-p)}{N}},\hfill \\ & & \text{measurement}\text{error}\hfill \\ & & \text{and}\text{simulator}\text{uncertainty}\pm 2\sqrt{\frac{p(1-p)}{N}+\frac{p\left(x\right)(1-p(x\left)\right)}{n\left(x\right)}},\hfill \\ & & \text{measurement}\text{error,}\text{simulator}\text{uncertainty}\text{and}\text{simulator}\hfill \\ & & \text{discrepancy}\hfill \\ & & \pm 2\sqrt{\frac{p(1-p)}{N}+\frac{p\left(x\right)(1-p(x\left)\right)}{n\left(x\right)}+\frac{p\left(x\right)(1-p(x\left)\right)(1-\lambda )}{\lambda n\left(x\right)}}.\hfill \end{array}$$(4) )) due to target data (○), simulator uncertainty (×) and simulator discrepancy (+) are shown.

4.1.1 Cases by Age

Target data Z_1k represent a cross-sectional study and give the number of people out of N_1k in the UK developing bowel cancer in 2008, where k = 1, …, 18 indexes age groups 0–4, 5–9, …, 80–84, 85+ (Cancer Research UK 2011). The NHM’s output does not match the target data directly. Instead, it represents the cancer state and age of a birth cohort, that is, longitudinal data. To make the NHM output consistent with the target data, it is resampled by allocating each person to age group k = 1, …, 18 at random, according to probabilities determined by proportions in the UK population. Thus we take the NHM output, which corresponds to a longitudinal study, and resample it to match the target data, which corresponds to a cross-sectional study. Let r = 1, …, R index each randomization. The resulting NHM output corresponding to Z_1k is denoted Y^(r)_1k(x), with corresponding sample size n^(r)_1k(x). We assume that Z_1k and Y^(r)_1k(x) are binomially distributed with sample sizes N_1k and n^(r)_1k(x), respectively. We approximate the likelihood for this data type by averaging over randomizations, with R large.

Figure 2 Pairwise maximized log-likelihood (off-diagonal) and marginal binned maximized log-likelihoods (diagonal) for inputs 1, 2, 3, 12, and 25. (Pairwise plots are a smoothed representation of an 8 × 8 grid.)

4.1.2 Cases by Type

The number of bowel cancer cases of type k from N₂ cases is Z_2k, where k = 1, …, 4 indexes types Duke’s A, B, and C, and Stage D, respectively. The NHM output is denoted Y_2k(x) and is directly comparable to Z_2k. The total number of cases simulated is denoted n₂(x). We assume multinomial distributions for Z₂ = (Z₂₁, Z₂₂, Z₂₃, Z₂₄)′ and Y₂(x) = (Y₂₁(x), Y₂₂(x), Y₂₃(x), Y₂₄(x))′, given sample sizes N₂ and n₂(x), respectively.

4.1.3 Obstructed Cases by Type

These data also represent cases by type, but only those cases in which an obstruction (malignant large bowel) occurs and only for types Duke’s B, C and Stage D (Tekkis et al. 2004). We, therefore, define Z_3k, N₃, Y_3k(x) and n₃(x) and assume multinomial distributions similarly to the j = 2 case.

4.1.4 Undetected Adenomas by Age

The number of people out of N_4k that developed adenomas that had not been detected in their lifetime is Z_4k, where k = 1, …, 4 indexes age groups under 55, 55−64, 64−74, and over 75; these have later been detected in a necropsy study (Williams, Balasooriya, and Day 1982). NHM output Y_4k(x) and n_4k(x) are defined accordingly. We assume binomial distributions for Z_4k given N_4k and Y_4k(x) given n_4k(x).

4.2 Discrepancy Specification

Simulator discrepancy is introduced to the NHM by reducing output sample sizes and counts, n_jk(x) and Y_jk(x), which are specified as fractions, λ_j ∈ (0, 1], j = 1, …, 4. We let λ vary with data source as sample sizes in the NHM output vary by orders of magnitude. For example, the cases by age data are based only on patients that have developed cancer, whereas the undetected adenomas by age data are based on all patients in the model.

To assess calibrated output, we consider its similarity to the target data, given approximate error bounds. These bounds represent how close a simulator output should be to the target data, considering three sources of error: sampling variability in the data, stochastic variability of the simulator output, and simulator discrepancy. For brevity, we present results for binomial data, though only minor alterations are required for multinomial data.

Figure 3 Observed log-likelihoods against emulator posterior means (based on previous iteration) at iterations 1–8 for samples of size 200 and iteration 9 for a sample of size 1000. The line y = x is superimposed (- - -).

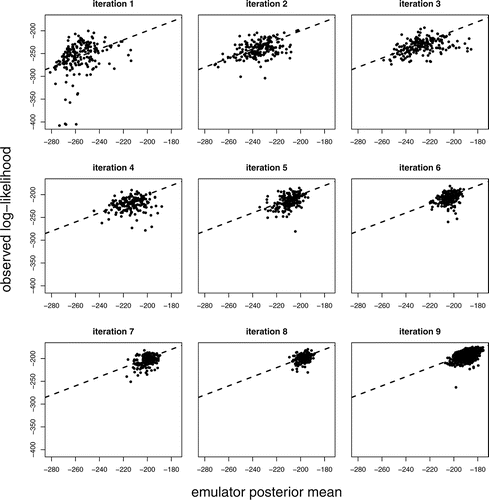
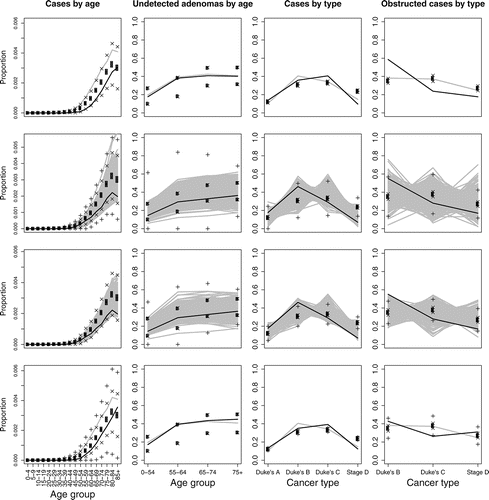
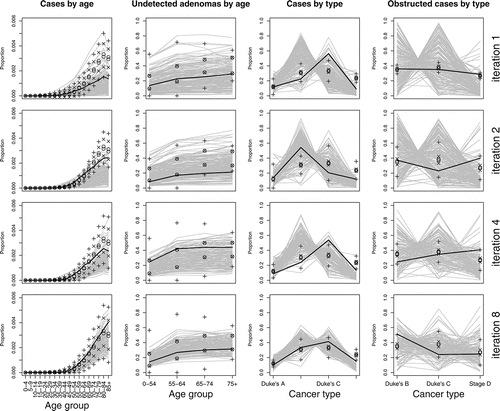
Figure 4 NHM output against target data for iterations 1, 2, 4, and 8. Uncertainty bounds are as in Figure 1. The black line highlights the run with highest likelihood.

We first consider error due to sampling variability. If Z|θ* ∼ Bin(N, θ*), then the variance of p ≔ Z/N, which is used to estimate θ*, is p(1 − p)/N. Similarly, if Y(x) ∼ Bin(n(x), θ(x)) is simulator output without discrepancy, the estimator p(x) ≔ Y(x)/n(x) has variance p(x)(1 − p(x))/n(x). The addition of simulator discrepancy, through λ ∈ (0, 1], inflates the variance to p(x)(1 − p(x))/(λn(x)), which can be partitioned as $$\begin{array}{c}\hfill \frac{p\left(x\right)(1-p(x\left)\right)}{\lambda n\left(x\right)}=\frac{p\left(x\right)(1-p(x\left)\right)}{n\left(x\right)}+\frac{p\left(x\right)(1-p(x\left)\right)(1-\lambda )}{\lambda n\left(x\right)}.\end{array}$$This decomposes the variance into contributions due to the simulator being stochastic and it being imperfect. We assess the calibrated output by considering approximate 95% intervals around the target data, which widen as we add in the different sources of error: (4) $$\begin{array}{ccc}& & \text{measurement}\text{error}\pm 2\sqrt{\frac{p(1-p)}{N}},\hfill \\ & & \text{measurement}\text{error}\hfill \\ & & \text{and}\text{simulator}\text{uncertainty}\pm 2\sqrt{\frac{p(1-p)}{N}+\frac{p\left(x\right)(1-p(x\left)\right)}{n\left(x\right)}},\hfill \\ & & \text{measurement}\text{error,}\text{simulator}\text{uncertainty}\text{and}\text{simulator}\hfill \\ & & \text{discrepancy}\hfill \\ & & \pm 2\sqrt{\frac{p(1-p)}{N}+\frac{p\left(x\right)(1-p(x\left)\right)}{n\left(x\right)}+\frac{p\left(x\right)(1-p(x\left)\right)(1-\lambda )}{\lambda n\left(x\right)}}.\hfill \end{array}$$(4) While p(x), n(x) and Y(x) vary with x, they are estimated only once, from the simulator run with highest likelihood.

Figure 1 shows variance decompositions for each data source¹. This visual representation lets us choose values of λ_j “by eye”: we choose values to give bounds around the target data that are such that, if output falls within the bounds, then we judge it and its corresponding input plausible. We perform the calibration in waves and, prior to the final calibration, can broaden the search for inputs by extending these intervals. We investigate sensitivity to different choices of λ in Section 4.8. Our method is intended to make such sensitivity analyses relatively straightforward. Ultimately we set λ₁ = 0.8, λ₂ = 0.008, λ₃ = 0.04, and λ₄ = 0.0004, which are the values represented in Figure 1. It is difficult to interpret the absolute value of the λ_j’s, due to the different corresponding sample sizes generated internally in the model. Instead Figure 1 is the main tool for understanding how much discrepancy has been incorporated, and we later inspect the calibrated model outputs to assess how well the model can fit each type of data (see Figure 5).

Figure 5 Calibrated NHM runs against target data.

Figure 6 Summaries of simulator output against target data for various discrepancy specifications: no discrepancy for any data source (row 1), discrepancy levels doubled (row 2), no discrepancy for cases by age (row 3) and no discrepancy for cases by type (row 4).

4.3 Prior Distributions for the Calibration Inputs

The prior distributions for the inputs were independent uniform, set with conservatively wide ranges. It is possible that more carefully specified priors would remove the need for some of the early waves in the history matching process (see Section 4.4). However, the elicitation problem would be hard, as the inputs do not all correspond to simple observable quantities. In that case, one might consider constructing a proper prior using the technique of “probabilistic inversion” (Du, Kurowicka, and Cooke 2006), in which experts make judgements about model outputs, from which priors for model inputs are constructed. The problem then would be that the experts may have already seen the calibration data, and may be unable/unwilling to provide judgments that do not take into account the known output data.

4.4 Likelihoods for the Cancer Data

Combining Sections 3 and 4.1 allows us to calculate the likelihood for all the NHM’s output. Notation for realizations follows from Section 4.1; for example, z_1k is the observed number of people in age group k developing bowel cancer out of N_1k and y_1k(x_i) is the corresponding NHM count out of n_1k(x_i) for input x_i, with notation for other data types defined similarly. We model the cases by age and undetected adenomas by age data as binomially distributed, and assume weak prior information for its parameters by adopting a Uniform[0,1] prior. (Note that if population age-group proportions changed considerably over time, then the cases by age data could be subject to greater-than-binomial variation.) We assume that the cases by type and obstructed cases by type data are multinomially distributed, and use a Dirichlet(1) prior to again represent weak prior knowledge. Finally the complete target data are z = (z₁, z₂, z₃, z₄) where $z_j=(z_{j1},...,z_{j{K}_j})$.

We build the emulator for the overall log-likelihood for the complete target data for an input x_i at which we have run the simulator and obtained output y(x_i), where y(x) = (y₁(x), y₂(x), y₃(x), y₄(x)) with $y_j\left(x\right)=(y_{j1}\left(x\right),...,y_{j{K}_j}\left(x\right))$. This is given by $$\begin{array}{c}\hfill f\left(x_i\right):=log\left\{\pi \left(z\right|X=x_i,y\left(x_i\right))\right\}=\sum _{j=1}^{4}log\left({\pi }_j\right),\end{array}$$where $$\begin{array}{ccc}& & {\pi }_1=\frac{1}{R}\sum _{r=1}^R\hfill \\ & & \times \left\{\prod _{k=1}^{K_1}\frac{N_{1k}!B\left(1+z_{1k}+{\lambda }_{1k}{y}_{1k}^{\left(r\right)}\left(x_i\right),1+N_{1k}-z_{1k}+{\lambda }_{1k}\{n_{1k}^{\left(r\right)}\left(x_i\right)-y_{1k}^{\left(r\right)}\left(x_i\right)\}\right)}{(N_{1k}-z_{1k})!z_{1k}!B\left(1+{\lambda }_{1k}{y}_{1k}^{\left(r\right)}\left(x_i\right),1+{\lambda }_{1k}\{n_{1k}^{\left(r\right)}\left(x_i\right)-y_{1k}^{\left(r\right)}\left(x_i\right)\}\right)}\right\}\hfill \end{array}$$with index r = 1, …, R denoting the rth randomization of the NHM output, $$\begin{array}{ccc}\hfill {\pi }_2& =& \frac{N_2!\{{\lambda }_2{n}_2\left(x_i\right)+K_2-1\}!}{\{N_2+{\lambda }_2{n}_2\left(x_i\right)+K_2-1\}!}\prod _{k=1}^{K_2}\frac{\{z_{2k}+{\lambda }_2{y}_{2k}\left(x_i\right)\}!}{z_{2k}!\left\{{\lambda }_2{y}_{2k}\left(x_i\right)\right\}!},\hfill \\ \hfill {\pi }_3& =& \frac{N_3!\{{\lambda }_3{n}_3\left(x_i\right)+K_3-1\}!}{\{N_3+{\lambda }_3{n}_3\left(x_i\right)+K_3-1\}!}\prod _{k=1}^{K_3}\frac{\{z_{3k}+{\lambda }_3{y}_{3k}\left(x_i\right)\}!}{z_{3k}!\left\{{\lambda }_3{y}_{3k}\left(x_i\right)\right\}!},\hfill \\ \hfill {\pi }_4& =& \hfill \\ & & \left\{\prod _{k=1}^{K_4}\frac{N_{4k}!B\left(1+z_{4k}+{\lambda }_{4k}{y}_{4k}\left(x_i\right),1+N_{4k}-z_{4k}+{\lambda }_{4k}\{n_{4k}\left(x_i\right)-y_{4k}\left(x_i\right)\}\right)}{(N_{4k}-z_{4k})!z_{4k}!B\left(1+{\lambda }_{4k}{y}_{4k}\left(x_i\right),1+{\lambda }_{4k}\{n_{4k}\left(x_i\right)-y_{4k}\left(x_i\right)\}\right)}\right\}.\hfill \end{array}$$

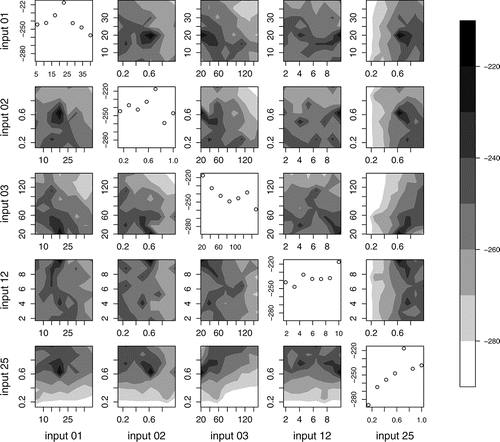
We calculate the log-likelihood for 10,000 NHM runs, each using a birth cohort of size 100,000. Figure 2 shows the log-likelihood against inputs 1, 2, 3, 12, and 25, specifically against single inputs (achieved by maximizing the likelihood over equal-sized bins) and for pairwise combinations of inputs (achieved by maximizing over grid cells). Of the 25 inputs to the NHM, these inputs tend to cause greatest change in the output, while also being relatively simple to interpret without detailed knowledge of the NHM. Input 1 represents the age at which a person can develop adenomas, input 2 the log-parameterized Weibull shape parameter for progression times between precancer states, input 3 the Weibull scale parameter for progression to the first precancer state, input 12 the change in Weibull scale parameters due to having previously been treated for cancer and input 25 the probability that a person develops adenomas in their lifetime.

Figure 2 shows that for some regions of input space the log-likelihood is much higher than for others. We use where the likelihood is relatively high to define a reduced input space, which is specified by marginal ranges and pairwise regions. Because we start with broad parameter ranges for all 25 inputs, there is large variation in the likelihood values of Figure 2, and so our criterion for ruling out parts of input space is set conservatively: we omit parts where the likelihood ratio, relative to the observed maximum, fails to exceed e^{− 40}. This reduces the input space to 0.7% of its original size. As we approximate true maximum log-likelihoods by those observed, we make conservative choices here to compensate for observed maxima being underestimates of the true maxima. This could be avoided if it were feasible to use many more simulator runs.

Three waves are used to identify the emulator design region, which is 0.0001% the size of the initial input region. Second and third waves have 10,000 NHM runs and use birth cohorts of 200,000 and 300,000 people, respectively.

4.5 Emulator Specification and Building

We use 2000 simulator runs to build the emulator and specify a constant mean function, that is, h(x) = 1. Our choice of mean function reflects that many runs have very low likelihoods, which gives a small mean for the Gaussian process and prevents inputs being sampled far away from those with high likelihoods. Polynomial terms could be added. A linear form gave unsatisfactory results, as inputs far away from those with simulator runs would be sampled if they had a high value of the linear predictor. A quadratic form with interactions might combat this, but as the NHM has 25 inputs, this was impractical. Perhaps more suitable would be (the log of) a parametric density function, though this gives a mean function that is nonlinear in its parameters.

4.6 Sampling Calibrated Inputs

For Step 1 of the calibration algorithm, outlined in Section 3.4.2, we choose S = 2000, thinning an initial sample of size 100,000 by 50. We choose u = 200 for Step 2 and v = 2 for Step 3. In the first iteration almost all p_s are large, which indicates that the emulator’s uncertainty is large for most sampled inputs. Consequently, the importance density may have insufficient support where the true log-likelihood is high. We flatten the log-likelihood to compensate for this by using αm*(x) instead of m*(x), 0 < α ⩽ 1, in Step 1; we initially choose α = 0.1. Introducing α can also combat multi-modality of the log-likelihood, as found for parallel tempering in Fielding, Nott, and Liong (2011). Log-likelihoods calculated for the simulator runs, f(x), for x ∈ D†, are compared against previous emulator posterior means, E(f(x) | D), where D are the last-used training data. This comparison is shown for iterations 1–9 in Figure 3.

From Figure 3, we see that the agreement between f(x) and E(f(x) | D) is poor for the first iteration, which means that the emulator posterior mean will not serve well as an importance density for sampling inputs from the log-likelihood. We also look at how the simulator’s output compares with the target data, given expected levels of uncertainty (as described in Section 4.2), which is shown for iterations 1, 2, 4, and 8 in Figure 4. For iteration 1, while some runs give a good match to some of the target data, most fail to provide an adequate match to all of the target data. We proceed with further iterations.

For iteration 2 we increase α to 0.2. The match between f(x) and E(f(x) | D) improves, but is still unsatisfactory; see Figure 4. Therefore, we perform further iterations, increasing α by 0.1 for each. Adequate agreement between the emulator and observed log-likelihoods is achieved by iteration 8, which is confirmed by iteration 9, the latter of which we choose to be the final emulator. There is some suggestion from Figure 4 of disagreement between the NHM output and the target data at iteration 8; however, the points used to assess this are those for which the emulator’s conditional variance is greatest, and therefore a better match between the emulator’s posterior mean and the true log-likelihoods can be expected for a random sample of inputs. Furthermore, we only need approximate agreement between the emulator posterior mean and the true log-likelihood, because those points for which agreement is poor will be downweighted during importance sampling. Further iterations could instead be performed to improve agreement, but here that was found to be less efficient than having some negligible importance weights. We, therefore, deem the emulator to be adequate for providing a proposal distribution for the importance sampler.

4.7 Calibrated Output

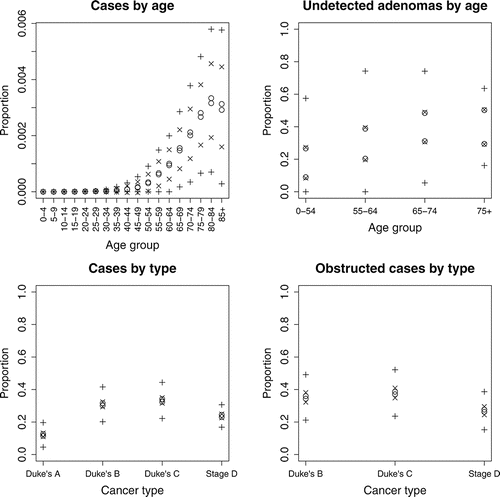
The emulator from iteration 9 is used for the final sample of calibrated inputs. We choose this sample to be of size 1000, and obtain it from an importance sample of size 2000 by sampling with replacement according to the importance weights, that is, exp {f(x) − m*(x)}. Figure 5 shows the calibrated NHM output against the target data for the four different data types. We can see the calibration to have worked well, as the calibrated output is consistent with the target data, once we account for the cumulative effect of each source of uncertainty.

4.8 Sensitivity to the Discrepancy Specification

We have calibrated the NHM using discrepancy values of λ₁ = 0.8, λ₂ = 0.008, λ₃ = 0.04, and λ₄ = 0.0004. We can investigate sensitivity to these choices by simply recalculating log-likelihoods and then importance weights for alternative discrepancy values. This requires little computational cost compared to rerunning the simulator. The calibrated output for four alternative discrepancy specifications is shown in Figure 6.

For the first alternative discrepancy scenario, we consider the case where no discrepancy is assumed, which would imply that the simulator is a perfect representation of reality at the true value of X. This results in an unsatisfactory calibration: all but two of the simulator runs have negligible importance weights, one of which is much larger than the other, and the output from neither of these runs matches the target data, given uncertainty amounts. We then consider doubling discrepancy amounts (i.e., halving the λ_j’s), relative to our preferred amounts, so that λ₁ = 0.4, λ₂ = 0.004, λ₃ = 0.02, and λ₄ = 0.0002. This results in the importance sample having a greater range, when compared to the original calibrated inputs of Section 4.7, and in turn gives more variability in the calibrated output. Altering the discrepancy specification has changed the distribution of the calibrated inputs, but the change in distribution of corresponding output is relatively small, suggesting that we do not need to be overly precise when specifying the discrepancy to achieve a reliable calibration.

We also consider assuming no discrepancy for only one data source, leaving discrepancy values for the remaining sources unchanged. With no discrepancy for the cases by age data, the calibrated output still matches the target data for the cases by age data and for the other data sources, and the sample of calibrated inputs also contains sufficiently many unique values. When we assume no discrepancy for the cases by type data, the sample of calibrated inputs again contains only two unique members (the same two as previously), and for cases by type the calibrated output fails to match the target data. In summary we find that although discrepancy amounts need some consideration, the precision that specifications require is within our capabilities, allowing the NHM to be calibrated reliably. The calibration becomes unsatisfactory when we ignore discrepancy, or specify it poorly.

5. DISCUSSION

We have presented a calibration method which, although motivated by a particular application, has features common to many calibration problems. In particular, three important issues have been addressed in the process. The first is calibrating a simulator of “moderate” computational expense, which is not practical using Monte Carlo simulation alone, but nor do we need to rely solely on a computationally cheap surrogate model, such as a Gaussian process emulator. Our calibration method combines the two: an emulator provides a preliminary, approximate calibration and is combined with simulator run data, through importance sampling, to give a final, more accurate calibration. As the simulator is of moderate computational expense, we calibrate it conservatively, especially when refining the design region and “flattening” the log-likelihood. A more expensive simulator might need us to consider optimising the calibration process to need fewer simulator runs.

Using importance sampling lets us explore a further issue: sensitivity of calibration to different discrepancy specifications, which is important to understand as discrepancy must be well quantified before calibrating any simulator (Brynjarsdóttir and O’Hagan 2014). Although we can always adjust a discrepancy specification and check the sensitivity of a calibration to adjustment, this is often impractical due to computational requirements. This becomes computationally feasible here, as we simply recalculate importance weights and obtain a new sample of calibrated inputs to assess different discrepancy specifications. The original importance sample must be suitable, with enough nonnegligible importance weights under the new discrepancy specification.

Finally we have addressed calibrating a simulator, known to be of moderate computational expense, that is stochastic and has count data output. We achieve this by using a Gaussian process prior for the log-likelihood, which is better suited to the Gaussian process assumptions than the count data. It also reduces the task of calibrating 30-dimensional output to one involving a univariate entity. Introducing a nugget effect, overcomes the simulator being stochastic, which will reflect in the log likelihood surface.

The motivation for the calibration is to support decision making. Incorporating simulator discrepancy aims to protect against over confidence. Although we have incorporated discrepancy into the four output types, the analysis is less informative for understanding the causes of simulator error, and where simulator improvements would be beneficial. Our approach to discrepancy is also less suited to capturing systematic errors, which could arise from posterior correlation in the cases by age data (Figure 5), but is not recognized in likelihood (3(3) $$\begin{array}{c}\hfill f\left(x\right):=log\left\{\pi \right(z|X=x,y(x\left)\right)\}.\end{array}$$(3) ). Such issues may be better addressed with the “internal” simulator discrepancy approach in Strong, Oakley, and Chilcott (2012). Nevertheless, the present calibrated simulator, with allowance made for discrepancy, will still have significant value in supporting decisions.

SUPPLEMENTARY MATERIAL

The compressed file LikelihoodEmulation.tar contains data from the first iteration of the calibration algorithm, R script files for sampling calibrated inputs and fuller details of the NHM’s inputs and outputs.

ACKNOWLEDGMENTS

The authors thank a reviewer and an Associate Editor for comments that have improved this article, and Paul Tappenden for providing the NHM and for guidance on its usage. This work was supported by RCUK funding for the MUCM2 project (grant EP/H007377/1).

Notes

Note that where proportions are all nonzero, representation on the logit scale might be more informative.