Fast Robust Correlation for High-Dimensional Data

Abstract

The product moment covariance matrix is a cornerstone of multivariate data analysis, from which one can derive correlations, principal components, Mahalanobis distances and many other results. Unfortunately, the product moment covariance and the corresponding Pearson correlation are very susceptible to outliers (anomalies) in the data. Several robust estimators of covariance matrices have been developed, but few are suitable for the ultrahigh-dimensional data that are becoming more prevalent nowadays. For that one needs methods whose computation scales well with the dimension, are guaranteed to yield a positive semidefinite matrix, and are sufficiently robust to outliers as well as sufficiently accurate in the statistical sense of low variability. We construct such methods using data transformations. The resulting approach is simple, fast, and widely applicable. We study its robustness by deriving influence functions and breakdown values, and computing the mean squared error on contaminated data. Using these results we select a method that performs well overall. This also allows us to construct a faster version of the DetectDeviatingCells method (Rousseeuw and Van den Bossche 2018) to detect cellwise outliers, which can deal with much higher dimensions. The approach is illustrated on genomic data with 12,600 variables and color video data with 920,000 dimensions. Supplementary materials for this article are available online.

Keywords:

• Anomaly detection
• Cellwise outliers
• Covariance matrix
• Data transformation
• Distance correlation

1 Introduction

The most widely used measure of correlation is the product-moment correlation coefficient. Its definition is quite simple. Consider a paired sample, that is $\{(x_1,y_1),\dots ,(x_n,y_n)\}$ where the two numerical variables are the column vectors $X_n={(x_1,\dots ,x_n)}^T$ and Y_n. Then the product moment of X_n and Y_n is just the inner product (1) $$\text{PM}(X_n,Y_n)=\frac{1}{n}〈X_n,Y_n〉=\frac{1}{n}{X}_n^T{Y}_n={\text{ave}}_{i=1}^n{x}_i{y}_i.$$(1)

When the (x_i, y_i) are iid observations of a stochastic vector (X, Y) the population version is the expectation $E[XY]$. The product moment (1) lies at the basis of many concepts. The empirical covariance of X_n and Y_n is the “centered” product moment (2) $$\text{cov}(X_n,Y_n)=\frac{n}{n-1}\text{PM}(X_n-\text{ave}(X_n),Y_n-\text{ave}(Y_n)),$$(2) with population version $E[(X-E[X])(Y-E[Y])]$. Therefore, (1) can be seen as a “covariance about zero.” And finally, the product-moment correlation is given by (3) $$\text{cor}(X_n,Y_n)=\frac{n}{n-1}\text{PM}(z(X_n),z(Y_n)),$$(3) where the z-scores are defined as $z(X_n)=(X_n-\text{ave}(X_n))/\text{Stdev}(X_n)$ with the standard deviation $\text{Stdev}(X_n)=\sqrt{\text{var}(X_n)}=\sqrt{\text{cov}(X_n,X_n)}$.

The product-moment quantities (1)–(3) satisfy $\text{PM}(X_n,Y_n)=\text{PM}(Y_n,X_n)$ and $\text{PM}(X_n,X_n)⩾0$. They have several nice properties. The independence property states that when X and Y are independent we have $\text{cov}(X,Y)=0$ (assuming the variances exist). Second, when our dataset ${\mathit{X}}_{n,d}$ has n rows (cases) and d columns (variables, dimensions), we can assemble all the product moments between the variables in a d × d matrix (4) $$\text{PM}({\mathit{X}}_{n,d})=\frac{1}{n}{\mathit{X}}_{n,d}^T{\mathit{X}}_{n,d}.$$(4)

The PSD property says that the matrix (4) is positive semidefinite, which is crucial. For instance, we can carry out a spectral decomposition of the covariance (or correlation) matrix, which forms the basis of principal component analysis. When d < n the covariance matrix will typically be positive definite hence invertible, which is essential for many multivariate methods such as the Mahalanobis distance and discriminant analysis. The third property is speed: the product moment, covariance, and correlation matrices can be computed very fast, even in high dimensions d.

Despite these attractive properties, it has been known for a long time that the product-moment covariance and correlation are overly sensitive to outliers in the data. For instance, adding a single far outlier can change the correlation from 0.9 to 0 or to –0.9.

Many robust alternatives to the Pearson correlation have been proposed in order to reduce the effect of outliers. The first one was probably Spearman’s (1904) correlation coefficient, in which the x_i and y_i are replaced by their ranks. Rank-based correlations do not measure a linear relation but rather a monotone one, which may or may not be preferable in a given application.

A second approach is based on the identity (5) $$\text{cor}(X,Y)=\frac{\text{var}(\tilde{X}+\tilde{Y})-\text{var}(\tilde{X}-\tilde{Y})}{\text{var}(\tilde{X}+\tilde{Y})+\text{var}(\tilde{X}-\tilde{Y})},$$(5) where $\tilde{X}=X/\sqrt{\text{var}(X)}$ and $\tilde{Y}=Y/\sqrt{\text{var}(Y)}$. Gnanadesikan and Kettenring (1972) proposed to replace the nonrobust variance by a robust scale estimator. This approach is quite popular; see, for example, Shevlyakov and Oja (2016). It does not satisfy the independence property however, and the resulting correlation matrix is not PSD so it needs to be orthogonalized, yielding the OGK method of Maronna and Zamar (2002).

Third, one can start by computing a robust covariance matrix C such as the minimum covariance determinant (MCD) method of Rousseeuw (1984). Then we can define a robust correlation measure between variables X_j and X_k by (6) $$R(X_j,X_k):=C_{jk}/\sqrt{C_{jj}{C}_{kk}}.$$(6)

In this way we do produce a PSD matrix, but we lose the independence property. In fact, here the robust correlation between two variables depends on the other variables, so adding or removing a variable changes it. Also, the computational requirements do not scale well with the dimension d, making this approach infeasible for high dimensions.

Another possibility is to start from the spatial sign covariance matrix (SSCM) of Visuri et al. (2000). This method first computes the spatial median $\widehat{\mathit{\mu }}$ of the data points ${\mathit{x}}_i$ by minimizing $\sum _i\left|\right|{\mathit{x}}_i-\mathit{\mu }\left|\right|$. It then computes the product moment of the so-called spatial signs $({\mathit{x}}_i-\widehat{\mathit{\mu }})/\left|\right|{\mathit{x}}_i-\widehat{\mathit{\mu }}\left|\right|$. Then (6) can be applied. The result is PSD but does not satisfy the independence property either.

For high-dimensional data, the product-moment technology is computationally attractive. This suggests using the idea underlying Spearman’s rank correlation, which is to transform the variables first. We do not wish to restrict ourselves to ranks however, and we want to explore how far the principle of robustness by data transformation can be pushed.

In general, we consider a transformation g applied to the individual variables, and we define the resulting g-product moment as (7) $${\text{PM}}_g(X_n,Y_n):=\text{PM}(g(X_n),g(Y_n)),$$(7) and similarly for ${\text{cov}}_g$ and ${\text{cor}}_g$. Choosing $g(x_i)=x_i$ yields the usual product moment, and setting $g(x_i)$ equal to its rank yields the Spearman correlation. The g-product moment approach satisfies all three desired properties. First of all, if we use a bounded function g the population version $E[g(X)g(Y)]$ always exists and ${\text{cov}}_g$ satisfies the independence property without any moment conditions. Second, the resulting matrices ${\text{PM}}_g({\mathit{X}}_{n,d})=\text{PM}(g(X_{.1}),\dots ,g(X_{.d}))$ always satisfy the PSD property. And finally, this method is very fast provided the transformation g can be computed quickly (which could even be done in parallel over variables).

Note that the bivariate winsorization in Khan et al. (2007) is a transformation $\tilde{g}(X_n,Y_n)$ that depends on both arguments simultaneously, unlike (7). It yields a good robust bivariate correlation but without the multivariate PSD property.

Our present goal is to find transformations g for (7) that yield covariance matrices that are sufficiently robust and at the same time sufficiently efficient in the statistical sense.

Table 1 lists some computation times (in seconds) of the robust correlation methods mentioned above for n = 1000 generated data points in various dimensions d, as well as the classical correlation matrix. (The times were measured on a laptop with Intel Core i7-5600U CPU at 2.60 GHz.) The fifth column is the g-product moment method that will be proposed in this article. Note that the MCD cannot be computed when $d\ge n$, and that the computation times of MCD and OGK become infeasible at high dimensions. The next three methods are faster, and their robustness will be compared later on.

Table 1 Computation times (in seconds) of various correlation matrices as a function of the dimension d, for n = 1000 observations.

Dimension	MCD	OGK	SSCM	Spearman	Wrapping	Classic
10	0.319	0.022	0.004	0.002	0.003	0.001
50	6.222	0.426	0.009	0.009	0.012	0.002
100	24.76	2.089	0.031	0.019	0.027	0.008
500	1599	44.78	0.678	0.226	0.281	0.171
1000	–	166.7	3.107	0.774	0.836	0.685
5000	–	4389	129.1	17.11	17.39	16.81
10,000	–	–	568.9	68.24	68.78	67.27
20,000	–	–	2448	278.4	274.9	273.6

The remainder of the article is organized as follows. In Section 2, we explore the properties of the g-product moment approach by means of influence functions, breakdown values and other robustness tools, and in Section 3 we design a new transformation g based on what we have learned. Section 4 compares these transformations in a simulation study and makes recommendations. Section 5 explains how to use the method in higher dimensions, illustrated on some real high-dimensional datasets in Section 6.

2 General Properties of g-Product Moments

The oldest type of robust g-product moments occur in rank correlations. Define a rescaled version of the sample ranks as $R_n(x_i)=(\text{Rank}(x_i)-0.5)/n$ where $\text{Rank}(x_i)$ denotes the rank of x_i in $\{x_1,\dots ,x_n\}$. The population version of $R_n(x_i)$ is the cumulative distribution function (cdf) of X. Then the following functions g define rank correlations:

• $g(x_i)=R_n(x_i)$ yields the Spearman rank correlation (Spearman 1904).

• $g(x)=\text{sign}(R_n(x_i)-0.5)$ gives the quadrant correlation.

• $g(x)={\Phi }^{-1}(R_n(x))$ (where $\Phi$ is the standard Gaussian cdf) yields the normal scores correlation.

• $g(x):={\Phi }^{-1}({[R_n(x)]}_{\alpha }^{1-\alpha })$ with the notation ${[y]}_a^b:=\text{min}(b,\text{max}(a,y))$ is the truncated normal scores function, first proposed on pages 210–211 of Hampel et al. (1986) in the context of univariate rank tests.

Kendall’s tau is of a somewhat different type as it replaces each variable X_n by a variable with $n(n-1)/2$ values, but we compare with it in Section 4.

A second type of robust g-product moments goes back to Section 8.3 in the book of Huber (1981) and is based on M-estimation. Huber transformed x_i to (8) $$g(x_i)=\psi ((x_i-\widehat{\mu })/\widehat{\sigma }),$$(8) where $\widehat{\mu }$ is an M-estimator of location defined by $\sum _i\psi ((x_i-\widehat{\mu })/\widehat{\sigma })=0$ and $\widehat{\sigma }$ is a robust scale estimator such as the MAD given by $\text{MAD}(X_n)=1.4826{\text{median}}_i|x_i-{\text{median}}_j(x_j)|$. Note that $(x_i-\widehat{\mu })/\widehat{\sigma }$ is like a z-score but based on robust analogs of the mean and standard deviation. For $\psi (z)=\text{sign}(z)$ this yields $\widehat{\mu }={\text{median}}_j(x_j)$ so we recover the quadrant correlation. Another transformation is Huber’s ψ_b function given by ${\psi }_b(z)={[z]}_{-b}^b$ for a given corner point b > 0. One can also use the sigmoid transformation $\psi (z)=\tanh (z)$. Note that the transformation (8) does not require any tie-breaking rules, unlike the rank correlations. Huber (1981) derived the asymptotic efficiency of the ψ-product moment. We go further by also computing the influence function, the breakdown value and other robustness measures. Our goal is to find a function ψ that is well-suited for correlation.

2.1 Influence Function and Efficiency

Note that the g-product moment ${\text{PM}}_g(X_j,X_k)$ between two variables X_j and X_k in a multivariate dataset does not depend on the other variables, so we can study its properties in the bivariate setting.

For analyzing the statistical properties of the ψ-product moment, we assume a simple model for the “clean” data, before outliers are added. The model says that (X, Y) follows a bivariate Gaussian distribution $F_{\rho }$ given by (9) $$F_{\rho }=N\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}1& \rho \\ \rho & 1\end{array}\right]\right)$$(9) for $-1<\rho <1$, so F₀ is just the bivariate standard Gaussian distribution. We restrict ourselves to odd functions ψ so that $E[\psi (X)]=0=E[\psi (Y)]$, and study the statistical properties of $T_n=\frac{1}{n}{\sum }_{i=1}^n\psi (x_i)\psi (y_i)$ with population version $T_{\psi }=E[\psi (X)\psi (Y)]$. Note that $T_{\psi }$ maps the bivariate distribution of (X, Y) to a real number, and is therefore called a functional. It can be seen as the limiting case of the estimator T_n for $n\to \infty$. On the other hand, a finite sample $Z_n=\{(x_1,y_1),\dots ,(x_n,y_n)\}$ yields an empirical distribution $F_n(x,y)=\frac{1}{n}{\sum }_{i=1}^{n}I(x_i\le x,y_i\le y)$ and we can define an estimator $T_n(Z_n)$ as $T_{\psi }(F_n)$, so there is a strong connection between estimators and functionals. Whereas the usual consistency of an estimator T_n requires that T_n converges to ρ in probability, there exists an analogous notion for functionals: $T_{\psi }$ is called Fisher-consistent for ρ iff $T_{\psi }(F_{\rho })=\rho$.

We will start with the influence function (IF) of $T_{\psi }$. Following Hampel et al. (1986), the raw influence function of the functional $T_{\psi }$ at $F_{\rho }$ is defined in any point (x, y) as (10) $${\text{IF}}_{\mathit{raw}}((x,y),T_{\psi },F_{\rho })=\frac{\partial }{\partial \epsilon }{T}_{\psi }((1-\epsilon )F_{\rho }+\epsilon {\Delta }_{(x,y)}){|}_{\epsilon =0},$$(10) where ${\Delta }_{(x,y)}$ is the probability distribution that puts all its mass in (x, y). Note that (10) is well-defined because $(1-\epsilon )F_{\rho }+\epsilon {\Delta }_{(x,y)}$ is a probability distribution so $T_{\psi }$ can be applied to it. The IF quantifies the effect of a small amount of contamination in (x, y) on $T_{\psi }$ and thus describes the effect of an outlier on the finite-sample estimator T_n. It is easily verified that ${\text{IF}}_{\mathit{raw}}((x,y),T_{\psi },F_0)=\psi (x)\psi (y)$.

However, we cannot compare the raw influence function (10) across different functions ψ since $T_{\psi }$ is not Fisher-consistent, that is, $T_{\psi }(F_{\rho })\ne \rho$ in general. For non-Fisher-consistent statistics T we follow the approach of Rousseeuw and Ronchetti (1981) and Hampel et al. (1986) by defining (11) $$\xi (\rho ):=T(F_{\rho })\text{and}U(F):={\xi }^{-1}(T(F)),$$(11) so U is Fisher-consistent, and putting (12) $$\text{IF}((x,y),T,F):={\text{IF}}_{\text{raw}}((x,y),U,F)=\frac{{\text{IF}}_{\text{raw}}((x,y),T,F)}{\xi \prime (\rho )}.$$(12)

Proposition 1.

When ψ is odd [i.e., $\psi (-z)=-\psi (z)$] and bounded, we have $\xi \prime (0)=E{[\psi \prime ]}^2$; hence, the influence function of $T_{\psi }$ at F₀ becomes (13) $$\text{IF}((x,y),T_{\psi },F_0)=\frac{\psi (x)\psi (y)}{E{[\psi \prime ]}^2}.$$(13)

The proof can be found in Section A.1 of the supplementary material. The influence function at $F_{\rho }$ for $\rho \ne 0$ derived in Section A.2 has the same overall shape.

Since the IF measures the effect of outliers we prefer bounded ψ, unlike the classical choice $\psi (z)=z$. Note that (13) is the raw influence function of $T^{*}=E[{\psi }^{*}(X){\psi }^{*}(Y)]$ at F₀, where ${\psi }^{*}(u)=\psi (u)/E[\psi \prime ]$. As ψ is bounded $T^{*}$ is integrable, so by the law of large numbers $T_n^{*}$ is strongly consistent for its functional value: $T_n^{*}=\frac{1}{n}{\sum }_{i=1}^n{\psi }^{*}(x_i){\psi }^{*}(y_i)\stackrel{a.s.}{\to }{T}^{*}(F_{\rho })$ for $n\to \infty$. By the central limit theorem, $T^{*}$ is then asymptotically normal under F₀: $$\sqrt{n}(T_n^{*}-0)\to N(0,V),$$ where (14) $$V=\frac{E{\left[{\psi }^2\right]}^2}{E{[\psi \prime ]}^4}={\left(\frac{E\left[{\psi }^2\right]}{E{[\psi \prime ]}^2}\right)}^2.$$(14)

From this we obtain the asymptotic efficiency $\text{eff}={(E{[\psi \prime ]}^2/E[{\psi }^2])}^2$.

Note that the influence function of $T_{\psi }$ at F₀ factorizes as the product of the influence functions of the M-estimator $L_{\psi }$ of location with the same ψ-function: (15) $$\text{IF}((x,y),T_{\psi },F_0)=\text{IF}(x,L_{\psi },\Phi )\text{IF}(y,L_{\psi },\Phi ),$$(15) because $\text{IF}(x,L_{\psi },\Phi )=\psi (x)/E[\psi \prime ]$. This explains why the efficiency of $T_{\psi }$ satisfies $\text{eff}(T_{\psi })={(\text{eff}(L_{\psi }))}^2$. We are also interested in attaining a low gross-error sensitivity ${\gamma }^{*}(T_{\psi })$, which is defined as the supremum of $|\text{IF}((x,y),T_{\psi },F_0)|$ and therefore equals ${({\gamma }^{*}(L_{\psi }))}^2$. It follows from (Rousseeuw 1981) that the quadrant correlation $\psi (z)=\text{sign}(z)$ has the lowest gross-error sensitivity among all statistics of the type $T_{\psi }=E[\psi (X)\psi (Y)]$. In fact, $\text{IF}((x,y),T_{\psi },F_0)=(\pi /2)\text{sign}(x)\text{sign}(y)$ yielding ${\gamma }_T^{*}=\pi /2$. However, the quadrant correlation is very inefficient as $\text{eff}=4/{\pi }^2=40.5\%$.

The influence functions of rank correlations are obtained by Croux and Dehon (2010) and Boudt et al. (2012). Note that for some rank correlations the function ξ of (11) is known explicitly, in fact $\xi (\rho )=\hspace{0.17em}\text{sin}\hspace{0.17em}(\rho \pi /2)$ for the quadrant correlation, $\xi (\rho )=(6/\pi )\arcsin (\rho /2)$ for Spearman and $\xi (\rho )=\rho$ for normal scores. It turns out that these IF at F₀ match the expression in Proposition 1 if ψ corresponds to the population version of the transformation g in the rank correlation, as explained in Section A.3 of the supplementary material.

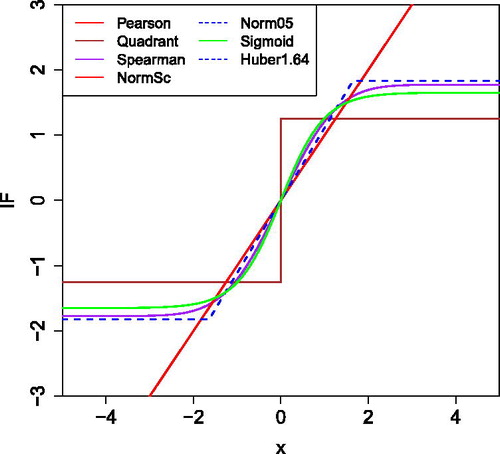
The influence functions of rank correlations at F₀ also factorize as in Equation (15)(15) $$\text{IF}((x,y),T_{\psi },F_0)=\text{IF}(x,L_{\psi },\Phi )\text{IF}(y,L_{\psi },\Phi ),$$(15) . Figure 1 plots these location influence functions for several choices of the transformation g. We see that the Pearson and normal scores correlations have the same influence function (the identity), which is unbounded. On the other hand, the IF of Huber’s ψ_b stays constant outside the corner points – b and b. The truncated normal scores (“Norm05”) has the same IF as Huber’s ψ_b provided $\alpha =\Phi (-b)$. The Spearman rank correlation and the sigmoid transformation have smooth influence functions.

Fig. 1 Location influence functions at ρ = 0 for different transformations g.

2.2 Maxbias and Breakdown Value

Whereas the IF measures the effect of one or a few outliers, we are now interested in the effect of a larger fraction ε of contamination. For the uncontaminated distribution of the bivariate (X, Y) we take the Gaussian distribution $F=F_{\rho }$ given by (9). Then we consider all contaminated distributions of the form (16) $$F_{H,\epsilon }=(1-\epsilon )F+\epsilon H,$$(16) where $\epsilon ⩾0$ and H can be any distribution. This ε-contamination model is similar to the contaminated distributions in (10) and (20), but here H is more general.

A fraction ε of contamination can induce a maximum possible upward and downward bias on $T_{\psi }=\text{cor}(\psi (X),\psi (Y))$ denoted by (17) $$\begin{array}{c}{B}^{+}(\epsilon ,T_{\psi },F)=\underset{G\in {\mathcal{F}}_{\epsilon }}{\sup }(T_{\psi }(G)-T_{\psi }(F))\text{and}\\ B^{-}(\epsilon ,T_{\psi },F)=\underset{G\in {\mathcal{F}}_{\epsilon }}{\inf }(T_{\psi }(G)-T_{\psi }(F)),\end{array}$$(17) where ${\mathcal{F}}_{\epsilon }=\{G;G=(1-\epsilon )F+\epsilon H\text{for}\text{any}\text{distribution}H\}$. The proof of the following proposition is given in Section A.4 in the supplementary material.

Proposition 2.

Let $\epsilon \in [0,1]$ be fixed and ψ be odd and bounded. Then the maximum upward bias of $T_{\psi }$ at F is given by (18) $$B^{+}(\epsilon ,T_{\psi },F)=\frac{(1-\epsilon ){\text{var}}_F(\psi (X))T_{\psi }(F)+\epsilon M^2}{(1-\epsilon ){\text{var}}_F(\psi (X))+\epsilon M^2}-T_{\psi }(F),$$(18) with $M:=\underset{x}{\sup }|\psi (x)|$, and the maximum downward bias is (19) $$B^{-}(\epsilon ,T_{\psi },F)=\frac{(1-\epsilon ){\text{var}}_F(\psi (X))T_{\psi }(F)-\epsilon M^2}{(1-\epsilon ){\text{var}}_F(\psi (X))+\epsilon M^2}-T_{\psi }(F).$$(19)

The breakdown value ${\epsilon }^{*}$ of a robust estimator is loosely defined as the smallest ε that can make the result useless. For instance, a location estimator $\widehat{\mu }$ becomes useless when its maximal bias tends to infinity. But correlation estimates stay in the bounded range $[-1,1]$ hence the bias can never exceed 2 in absolute value, so the situation is not as clear-cut and several alternative definitions could be envisaged. Here, we will follow the approach of Capéraà and Garralda (1997) who defined the breakdown value of a correlation estimator as the smallest amount of contamination needed to give perfectly correlated variables a negative correlation. More precisely:

Definition 1.

Let F be a bivariate distribution with X = Y, and R be a correlation measure. Then the breakdown value of R is defined as $${\epsilon }^{*}(R)=\inf \{\epsilon >0;\underset{G\in {\mathcal{F}}_{\epsilon }}{\inf }R(G)⩽0\}.$$

The breakdown value of $T_{\psi }$ then follows immediately from Proposition 2.

Corollary 1.

When ψ is odd and bounded the breakdown value ${\epsilon }^{*}$ of $T_{\psi }$ equals $${\epsilon }^{*}(T_{\psi })=\frac{{\text{var}}_F(\psi (X))}{{\text{var}}_F(\psi (X))+M^2}.$$

The breakdown values of rank correlations were obtained in Capéraà and Garralda (1997) and Boudt et al. (2012). They used a different contamination model, but their results still hold under ε-contamination as shown in Section A.5 in the supplementary material.

3 The Proposed Transformation

The change-of-variance curve (Hampel et al. 1981; Rousseeuw 1981) is given by (20) $$\begin{array}{c}\text{CVC}(z,T_{\psi },F)=\frac{\partial }{\partial \epsilon }[\text{log}\hspace{0.17em}V(T_{\psi },(1-\epsilon )F\\ \hspace{1em}+\epsilon ({\Delta }_z+{\Delta }_{-z})/2)]{|}_{\epsilon =0}\end{array}$$(20) and measures how stable the variance of the method is when the underlying distribution is contaminated, which may make it longer tailed. We do not want the variance to grow too much, as is measured by the change-of-variance sensitivity ${\kappa }^{*}(T_{\psi })$, which is the supremum of the CVC. (On the other hand, negative values of the CVC indicate a lower variance and are not a concern.) Since the asymptotic variance of $T_{\psi }$ satisfies $V(T_{\psi })={(V(L_{\psi }))}^2$, we obtain $\text{CVC}(z,T_{\psi },F_0)=2\text{CVC}(z,L_{\psi },\Phi )$ and ${\kappa }^{*}(T_{\psi })=2{\kappa }^{*}(L_{\psi })$. Therefore, we inherit all the results about the CVC from the location setting. For instance, the quadrant correlation [with $\psi (z)=\text{sign}(z)$] has the lowest possible ${\kappa }^{*}(T_{\psi })$.

Now suppose one wants to eliminate the effect of far outliers, say those that lie more than c robust standard deviations away. This can be done by imposing (21) $$\psi (z)=0\text{whenever}\left|z\right|>c.$$(21)

Such functions ψ can no longer be monotone, and are called redescending instead. They were first used for M-estimation of location, and performed extremely well in the seminal simulation study of Andrews et al. (1972). They have been used in M-estimation ever since. More on redescending estimators can be found in Rousseeuw and Leroy (1987) and Maronna et al. (2006).

In the context of location estimation, Hampel et al. (1981) show that the ψ-function satisfying (21) with the highest efficiency subject to a given ${\kappa }^{*}(T_{\psi })$ is of the following form: (22) $${\psi }_{b,c}(z)=\{\begin{array}{cc}z\hfill & \text{if}0⩽\left|z\right|⩽b,\hfill \\ q_1\tanh (q_2(c-\left|z\right|))\text{sign}(z)\hfill & \text{if}b⩽\left|z\right|⩽c,\hfill \\ 0\hfill & \text{if}c⩽\left|z\right|.\hfill \end{array}$$(22)

For any combination $0<b<c$ the values of q₁ and q₂ can be derived as in Section A.6 of the supplementary material. Our default choice is b = 1.5 and c = 4 as in Figure 2. As we will see in Table 2, this choice strikes a good compromise between robustness and efficiency. Note that the b in ${\psi }_{b,c}$ plays the same role as the “corner value” in the Huber ψ_b function for location estimation. In that setting, $b=1.5$ has been a popular choice from the beginning. The value c = 4 reflects that we do not trust measurements that lie more than 4 standard deviations away. The form of ${\psi }_{b,c}(z)$ for $b⩽\left|z\right|⩽c$ is the result of solving a differential equation.

Fig. 2 The proposed transformation (22) with default constants b = 1.5 and c = 4.

Table 2 Correlation measures based on transformations g with their breakdown value ${\epsilon }^{*}$, efficiency, gross-error sensitivity ${\gamma }^{*}$, rejection point ${\delta }^{*}$, and correlation between X and g(X).

${\text{cor}}_g$	${\epsilon }^{*}$(%)	eff (%)	${\gamma }^{*}$	${\delta }^{*}$	cor
Pearson	0	100	$\infty$	$\infty$	1
Quadrant	50	40.5	1.57	$\infty$	0.798
Spearman (SP)	20.6	91.2	3.14	$\infty$	0.977
Normal scores (NS)	12.4	100	$\infty$	$\infty$	1
Truncated NS, $\alpha =0.05$	16.3	95.0	3.34	$\infty$	0.987
Truncated NS, $\alpha =0.1$	20.7	88.9	2.57	$\infty$	0.971
Sigmoid	28.3	86.6	2.73	$\infty$	0.965
Huber, $b={\Phi }^{-1}(0.95)\approx 1.64$	23.5	95.0	3.34	$\infty$	0.987
Huber, $b={\Phi }^{-1}(0.9)\approx 1.28$	29.2	88.9	2.57	$\infty$	0.971
Wrapping, b = 1.5, c = 4	25.1	89.0	3.16	4.0	0.971
Wrapping, b = 1.3, c = 4	28.1	84.4	2.79	4.0	0.958

A nice property of ${\psi }_{b,c}$ is that under normality a large majority of the data values (in fact 86.6% of them for b = 1.5) are left unchanged by the transformation, and only a minority is modified. Leaving the majority of the data unchanged has the advantage that we keep much information about the distribution of a variable and the type of association between variables (e.g., linear), unlike rank transforms.

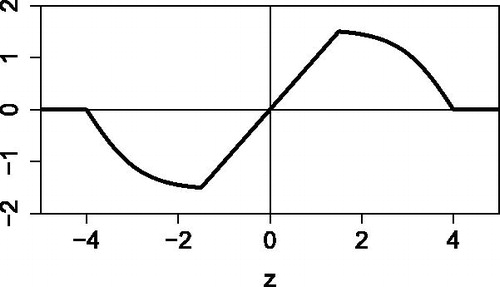
Interestingly, ${\psi }_{b,c}$ pushes values between b and c closer to the center so intermediate outliers still play some smaller role in the correlation, whereas far outliers do not count. For this reason, we refer to ${\psi }_{b,c}$ as the wrapping function, as it wraps the data around the interval $[-b,b]$. Indeed, the points on the interval are mapped to themselves, whereas the other points are wrapped around the corners, as in Figure 3.

Fig. 3 Illustration of wrapping a standardized sample $\{z_1,\dots ,z_n\}$. Values in the interval $[-b,b]$ are left unchanged, whereas values outside $[-c,c]$ are zeroed. The intermediate values are “folded” inward so they still play a role.

Another way to describe this is to say that wrapping multiplies the variable z by a weight w(z), where $w(z):=1$ when $\left|z\right|\le b$ and $w(z):={\psi }_{b,c}(z)/z$ for $\left|z\right|>b$.

The influence function (15) contains $\text{IF}(z,L_{\psi },\Phi )={\psi }_{b,c}(z)/E[\psi {\prime }_{b,c}]$, which has the shape of ${\psi }_{b,c}$ in Figure 2. The bivariate influence function $\text{IF}((x,y),T_{\psi },F_{\rho })$ is continuous and bounded, and shown in Figure 13 in Section A.6 of the supplementary material.

Table 2 lists some correlation measures based on transformations g that either use ranks or ψ-functions. For each the breakdown value ${\epsilon }^{*}$ and the efficiency and gross-error sensitivity ${\gamma }^{*}$ at ρ = 0 are listed. The rejection point ${\delta }^{*}$ says how far an outlier must lie before the IF is zero. The last column shows the product-moment correlation between a Gaussian variable X and its transformed g(X). The correlation is quite high for most transformations studied here, providing insight as to why this approach works.

In Table 2, we see that the quadrant correlation has the highest breakdown value but the lowest efficiency. The Spearman correlation reaches a much better compromise between breakdown and efficiency. Normal scores have the asymptotic efficiency and IF of Pearson but with a breakdown value of 12.4%, a nice improvement. Truncating 5% improves its robustness a bit at the small cost of 5% of efficiency, whereas truncating 10% brings its performance close to Spearman.

Both the Huber and the wrapping correlation have a parameter b, the corner point, which trades off robustness and efficiency. A lower b yields a higher breakdown value and a better gross-error sensitivity, but a lower efficiency. Note that the Huber correlation looks good in Table 2, but in the simulation study of Section 4 it performs less well than wrapping in the presence of outliers, and the same holds in the real data application in Section 6.2. The reason is that wrapping gives a lower weight $w(z):={\psi }_{b,c}(z)/z$ to outliers and even w(z) = 0 for $\left|z\right|>c$, whereas the Huber weight $w_b(z):={\psi }_b(z)/z$ is higher for outliers and always nonzero, so even far outliers still have an effect.

Note that whenever two random variables X and Y are independent the correlation between the wrapped variables $g_X(X)$ and $g_Y(Y)$ is zero, even if the original X and Y did not satisfy any moment conditions. This follows from the boundedness of ${\psi }_{b,c}$ in (22).

It is well known that the reverse is not true for the classical Pearson correlation, but that it holds when (X, Y) follow a bivariate Gaussian distribution. This is also true for the wrapped correlation.

Proposition 3.

If the variables (X, Y) follow a bivariate Gaussian distribution and the correlation between the wrapped variables $g_X(X)$ and $g_Y(Y)$ is zero, then X and Y are independent.

Another well-known property says that the Pearson correlation of a dataset $Z=\{(x_1,y_1),\dots ,(x_n,y_n)\}$ equals 1 if and only if there are constants α and β with $\beta >0$ such that (23) $$y_i=\alpha +\beta x_i$$(23) for all i (perfect linear relation). The wrapped correlation satisfies a similar result.

Proposition 4.

1. If (23) holds for all i and we transform the data to $g_X(x_i)={\psi }_{b,c}((x_i-{\widehat{\mu }}_X)/{\widehat{\sigma }}_X)$ and $g_Y(y_i)={\psi }_{b,c}((y_i-{\widehat{\mu }}_Y)/{\widehat{\sigma }}_Y)$ then $\text{cor}(g_X(x_i),g_Y(y_i))=1$.

2. If $\text{cor}(g_X(x_i),g_Y(y_i))=1$, then Equation (23)(23) $$y_i=\alpha +\beta x_i$$(23) holds for all i for which $|x_i-{\widehat{\mu }}_X|/{\widehat{\sigma }}_X\le b$ and $|y_i-{\widehat{\mu }}_Y|/{\widehat{\sigma }}_Y\le b$.

In part (ii), the linearity has to hold for all points with coordinates in the central region of their distribution, whereas far outliers may deviate from it. In that case, the points in the central region are exactly fit by a straight line. The proofs of Propositions 3 and 4 can be found in Section A.7 of the supplementary material.

Remark.

Whereas Proposition 3 requires bivariate Gaussianity, the other results in this article do not. In fact, Propositions 1, 2, and 4 as well as Corollary 1 still hold when the data are generated by a symmetric and unimodal distribution. The corresponding proofs in the supplementary material are for this more general setting.

4 Simulation Study

We now compare the correlation by transformation methods in Table 2 for finite samples. For all of these methods, the correlation between two variables does not depend on any other variable in the data, so we only need to generate bivariate data here.

For the non-rank-based methods, we first normalize each variable by a robust scale estimate, and then estimate the location by the M-estimator with the given function ψ. Next, we transform x_i to $x_i^{*}=\psi ((x_i-{\widehat{\mu }}_X)/{\widehat{\sigma }}_X)$ and y_i to $y_i^{*}=\psi ((y_i-{\widehat{\mu }}_Y)/{\widehat{\sigma }}_Y)$ and compute the plain Pearson correlation of the transformed sample $\{(x_1^{*},y_1^{*}),\dots ,(x_n^{*},y_n^{*})\}$.

4.1 Clean Data

Let us start with uncontaminated data distributed as $F=F_{\rho }$ given by (9) where the true correlation ρ ranges over $\{0,0.05,0.10,\dots ,0.95\}$. For each ρ, we generate m = 5000 bivariate datasets ${\mathit{Z}}^j$ with sample size n = 100. (We also generated data with n = 20 yielding the same qualitative conclusions.) We then estimate the bias and the mean squared error (MSE) of each correlation measure R by (24) $${\text{bias}}_{\rho }(R)={\text{ave}}_{j=1}^m\left(R({\mathit{Z}}^j)-\rho \right)\text{and}$$(24) (25) $${\text{MSE}}_{\rho }(R)={\text{ave}}_{j=1}^m{\left(R({\mathit{Z}}^j)-\rho \right)}^2.$$(25)

The bias is shown in the left part of Figure 4. The vertical axis has flipped signs because the bias was always negative, so ρ is typically underestimated. Unsurprisingly, the Pearson correlation has the smallest bias (known not to be exactly zero). The normal scores correlation and the Huber ψ with b = 1.5 are fairly close, followed by truncated normal scores, Spearman and the sigmoid. Wrapping with b = 1.5 and b = 1.3 (both with c = 4) comes next, still with a fairly small bias. The bias of the quadrant correlation is much higher. Note that we could have reduced the bias of all of these methods by applying the consistency function ${\xi }^{-1}$ of (11), which can be computed numerically. But such consistency corrections would destroy the crucial PSD property for the higher-dimensional data that motivate the present work, so we will not use them here.

Fig. 4 Bias and MSE of correlation measures based on transformation, for uncontaminated Gaussian data with sample size 100.

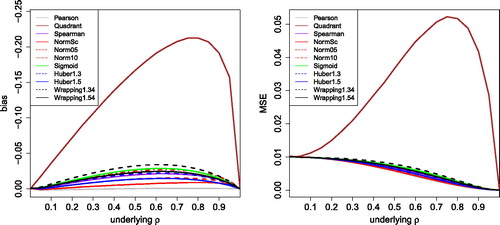
The right panel of Figure 4 shows the MSE of the same methods, with a pattern similar to that of the bias. Even for $n=20,$ the bias dominated the variance (not shown).

4.2 Contaminated Data

To compare the robustness of these correlation measures, we now add outliers to the data. Since the true correlation ρ ranges over positive values here, we will try to bring the correlation measures down. From the proof of Proposition 2 in Section A.4, we know that the outliers have the biggest downward effect when placed at points $(k,-k)$ and $(-k,k)$ for some k. Therefore, we will generate outliers from the distribution $$H=\frac{1}{2}N\left(\left[\begin{array}{c}k\\ -k\end{array}\right],{0.01}^{2}I\right)+\frac{1}{2}N\left(\left[\begin{array}{c}-k\\ k\end{array}\right],{0.01}^{2}I\right)$$ for different values of k. The simulations were carried out for 10%, 20%, and 30% of outliers, but we only show the results for 10% as the relative performance of the methods did not change much for the higher contamination levels.

The results are shown in Figure 5 for k = 3 and k = 5. For k = 3, we see that the Pearson correlation has by far the highest MSE, followed by normal scores (whose breakdown value of 12.4% is not much higher than the 10% of contamination). The 5% truncated normal scores and the Huber with b = 1.5 do better, followed by the Spearman, the sigmoid, the 10% truncated normal scores and the Huber with b = 1.3. The quadrant correlation does best among all the methods based on a monotone transformation. However, wrapping still outperforms it, because it gives the outliers a smaller weight. Even though wrapping has a slightly lower efficiency for clean data than Huber’s ψ_b with the same b, in return it delivers more resistance to outliers further away from the center.

Fig. 5 MSE of the correlation measures in Figure 4 with 10% of outliers placed at k = 3 (left) and k = 5 (right).

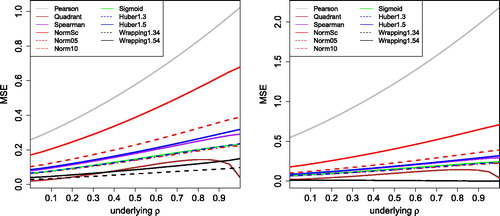
For k = 5 the pattern is the same, except that the Pearson correlation is affected even more and wrapping has given a near-zero weight to the outliers. For k = 2 (not shown) the contamination is not really outlying and all methods performed about the same, whereas for k > 5 the curves of the non-Pearson correlations remain as they are for k = 5 since all of our transformations g are constant in that region.

4.3 Comparison With Other Robust Correlation Methods

As described in the introduction, several good robust alternatives to the Pearson correlation exist that do not fall in our framework. We would like to find out how well wrapping stacks up against the most well known of them, such as Kendall’s tau. We also compare with the Gnanadesikan–Kettenring (GK) approach (5) in which we replace the variance by the square of a robust scale, in particular the MAD and the scale estimator Q_n of Rousseeuw and Croux (1993).

For the approach starting with the estimation of a robust covariance matrix, we consider the MCD method (Rousseeuw 1985) using the algorithm in (Hubert et al. 2012), and the SSCM of Visuri et al. (2000). In both cases, we compute a correlation measure between variables X₁ and X₂ from the estimated scatter matrix C by (6). For our bivariate generated data, the matrix C is only 2 × 2, but if the original data have more dimensions, the estimated correlation between X₁ and X₂ now also depends on the other variables. To illustrate this we computed the MCD and the SSCM also in d = 10 dimensions where the true covariance matrix is given by ${\Sigma }_{jk}=\rho$ for $j\ne k$ and 1 otherwise. The simulation then reports the result of (6) on the first two variables only.

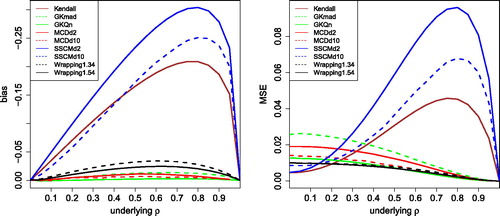
The left panel of Figure 6 shows the bias of all these methods, in the same setting as Figure 4. The two GK methods and the MCD computed in 2 and 10 dimensions have the smallest bias, followed by wrapping. The Kendall bias is substantially larger, and in fact looks similar to the bias of the quadrant correlation in Figure 6, which is not so surprising since they possess the same function $\xi (\rho )=2\arcsin (\rho )/\pi$ in (11). The bias of the SSCM is even larger, both when computed in d = 2 dimensions and in d = 10. The MSE in the right panel of Figure 6 shows a similar pattern.

Fig. 6 Bias and MSE of other robust correlation measures, for uncontaminated Gaussian data with sample size 100.

Figure 7 shows the effect of 10% of outliers, using the same generated data as in Figure 5. The left panel is for k = 3. The scale of the vertical axis indicates that the outliers have increased the MSE of all methods. The MCD in d = 2 dimensions is the least affected, whereas the GK methods, the SSCM with d = 2 and Kendall’s tau are more sensitive. Note that the data in d = 10 dimensions was only contaminated in the first 2 dimensions, and the MCD still does quite well in that setting. On the other hand, the MSE of the SSCM in d = 10 is now much higher.

Fig. 7 MSE of the correlation measures in Figure 6 with 10% of outliers placed at k = 3 (left) and k = 5 (right).

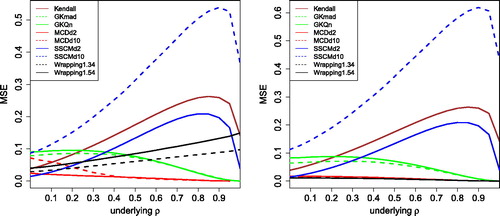
To conclude, wrapping holds its own even among well-known robust correlation measures outside our transformation approach. Wrapping was not the overall best method in our simulation, that would be the MCD, but the latter requires much more computation time which goes up a lot in high dimensions. Moreover, the highly robust quadrant transformation yields a low efficiency as it ignores much information in the data.

Therefore, wrapping seems a good choice for our purpose, which is to construct a fast robust method for fitting high-dimensional data. Some other methods like the MCD perform better in low dimensions (say, up to 20), but in high dimensions the MCD and related methods become infeasible, whereas the SSCM does not perform well any more.

5 Use in Higher Dimensions

5.1 Methodology

So far the illustrations of wrapping were in the context of bivariate correlation. In this section, we explain its use in the higher dimensional context for which it was developed. Our approach is basically to wrap the data first, carry out an existing estimation technique on the wrapped data, and then use that fit for the original data. We proceed along the following steps.

• Step 1: Estimation. For each of the (possibly many) continuous variables X_j with $j=1,\dots ,d$, we compute a robust initial scale estimate ${\widehat{\sigma }}_j$ such as the MAD. Then we compute a one-step location M-estimator ${\widehat{\mu }}_j$ with the wrapping function ${\psi }_{b,c}$ with defaults b = 1.5 and c = 4. We could take more steps or iterate to convergence, but this would lead to a higher contamination bias (Rousseeuw and Croux 1994).

• Step 2: Transformation. Next we wrap the continuous variables. That is, we transform any x_ij to

(26) $$x_{ij}^{*}=g(x_{ij})={\widehat{\mu }}_j+{\widehat{\sigma }}_j{\psi }_{b,c}\left(\frac{x_{ij}-{\widehat{\mu }}_j}{{\widehat{\sigma }}_j}\right).$$(26)

Note that ${\text{ave}}_i(x_{ij}^{*})$ is a robust estimate of μ_j and ${\text{stdev}}_i(x_{ij}^{*})$ is a robust estimate of σ_j. The wrapped variables $X_j^{*}$ do not contain outliers, and when the original X_j is Gaussian over 86% of its values remain unchanged, that is $x_{ij}^{*}=x_{ij}$. If x_ij is missing we have to assign a value to $g(x_{ij})$ in order to preserve the PSD property of product moment matrices, and $g(x_{ij})={\widehat{\mu }}_j$ is the natural choice. We do not transform discrete variables—depending on the context one may or may not leave them out of the subsequent analysis.

• Step 3: Fitting. We then fit the wrapped data $x_{ij}^{*}$ by an existing multivariate method, yielding for instance a covariance matrix or sparse loading vectors.

• Step 4: Using the fit. To evaluate the fit we will look at the deviations (e.g., Mahalanobis distances) of the wrapped cases ${\mathit{x}}_i^{*}$ as well as the original cases ${\mathit{x}}_i$.

Note that the time complexity of Steps 1 and 2 for all d variables is only O(nd). Any fitting method in Step 3 must read the data so its complexity is at least O(nd). Therefore, the total complexity is not increased by wrapping, as illustrated in Table 1.

5.2 Estimating Covariance and Precision Matrices

Covariance Matrices

The covariance matrix of the wrapped variables has the entries (27) $$\begin{array}{c}C(j,k)=\text{cov}(X_j^{*},X_k^{*})\\ ={\widehat{\sigma }}_j{\widehat{\sigma }}_k\text{cor}({\psi }_{b,c}(\frac{x_{ij}-{\widehat{\mu }}_j}{{\widehat{\sigma }}_j}),{\psi }_{b,c}(\frac{y_{ik}-{\widehat{\mu }}_k}{{\widehat{\sigma }}_k})),\end{array}$$(27) for $j,k=1,\dots ,d$. The resulting matrix is clearly PSD. We also have the independence property: if variables X_j and X_k are independent so are $X_j^{*}=g(X_j)$ and $X_k^{*}=g(X_k)$, and as these are bounded their population covariance exists and is zero.

Öllerer and Croux (2015) defined robust covariances with a formula like (27) in which the correlation on the right was a rank correlation. They showed that the explosion breakdown value of the resulting scatter matrix (i.e., the percentage of outliers required to make its largest eigenvalue arbitrarily high) is at least that of the univariate scale estimator S yielding ${\widehat{\sigma }}_j$ and ${\widehat{\sigma }}_k$, and their proof goes through without changes in our setting. Therefore, the robust covariance matrix (27) also has an explosion breakdown value of 50%.

The scatter matrix given by (27) is easy to compute, and can for instance be used for anomaly detection. In Section A.8 of the supplementary material, it is illustrated how robust Mahalanobis distances obtained from the estimated scatter matrix can detect outlying cases. The scatter matrix can also be used in other multivariate methods such as canonical correlation analysis, and serve as a fast initial estimate in the computation of other robust methods such as (Hubert et al. 2012).

Precision Matrices and Graphical Models

The precision matrix is the inverse of the covariance matrix, and allows to construct a Gaussian graphical model of the variables. Öllerer and Croux (2015) and Tarr et al. (2016) estimated the covariance matrix from rank correlations, but one could also use wrapping for this step. When the dimension d is too high the estimated covariance matrix cannot be inverted, so these authors construct a sparse precision matrix by applying GLASSO. Öllerer and Croux (2015) showed that the breakdown value of the resulting precision matrix, for both implosion and explosion, is as high as that of the univariate scale estimator. This remains true for wrapping, so the resulting robust precision matrix has breakdown value 50%.

5.3 Distance Correlation

There exist measures of dependence which do not give rise to PSD matrices but are used as test statistics for dependence, such as mutual information and the distance correlation of Székely et al. (2007), which yield a single nonnegative scalar that does not reflect the direction of the relation if there is one. The theory of distance correlation only requires the existence of first moments. The distance correlation dCor between random vectors X and Y is defined through the Pearson correlation between the doubly centered interpoint distances of X and those of Y. It always lies between 0 and 1. The population version $\text{dCor}(\mathit{X},\mathit{Y})$ can be written in terms of the characteristic functions of the joint distribution of $(\mathit{X},\mathit{Y})$ and the marginal distributions of X and Y. This allows Székely et al. (2007) to prove that $\text{dCor}(\mathit{X},\mathit{Y})=0$ implies that X and Y are independent, a property that does not hold for the plain Pearson correlation.

The population $\text{dCor}(\mathit{X},\mathit{Y})$ is estimated by its finite-sample version $\text{dCor}({\mathit{X}}_n,{\mathit{Y}}_n)$ which is used as a test statistic for dependence. For a sample of size n this would appear to require $O(n^2)$ computation time, but there exists an $O(n\hspace{0.17em}\text{log}\hspace{0.17em}(n))$ algorithm (Huo and Székely 2007) for the bivariate setting.

By itself distance correlation is not robust to outliers in the data. In fact, we illustrate in Section A.9 of the supplementary material that the distance correlation of independent variables can be made to approach 1 by a single outlier among 100,000 data points, and the distance correlation of perfectly dependent variables can be made to approach zero. On the other hand, we could first transform the data by the function g of (26) with the sigmoid $\psi (z)=\tanh (z)$, and then compute the distance covariance. This combined method does not require the first moments of the original variables to exist, and the population version is again zero if and only if the original variables are independent (since g is invertible). Figure 8 illustrates the robustness of this combined statistic.

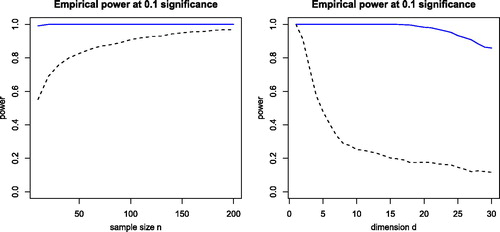
Fig. 8 Left panel: power of dCor (dashed black curve) and its robust version (blue curve) for bivariate X and Y with distribution t(1) and independence except for ${\mathit{X}}_1={\mathit{Y}}_1$ versus the sample size n. Right panel: power of dCor and its robust version for d-dimensional X and Y with distribution t(1) and n = 100, as a function of the dimension d.

The data for Figure 8 were generated following Example 1(b) in (Székely et al. 2007), where X and Y are multivariate and all their components follow t(1), the Student t-distribution with one degree of freedom. The null hypothesis states that X and Y are independent. We investigate the power of the test for dependence under the alternative that all components of X and Y are independent except for ${\mathit{X}}_1={\mathit{Y}}_1$. For this we use the permutation test implemented as dcor.test in the R package energy. As in Székely et al. (2007), we set the significance level to 0.1. The empirical power of the test is then the fraction of the 1000 replications in which the test rejects the null hypothesis.

In the left panel of Figure 8, we see the empirical power as a function of the sample size when X and Y are both bivariate. The power of the original dCor (dashed black curve) starts around 0.6 for n = 20 and approaches 1 when n = 200. This indicates that for small sample sizes the components ${\mathit{X}}_2$ and ${\mathit{Y}}_2$, even though they are independent of everything else, have added noise in the doubly centered distances. In contrast, the power of the robust method (solid blue curve) is close to 1 overall. No outliers were added to the data, but the underlying distribution t(1) is long-tailed.

The right panel of Figure 8 shows the effect of increasing the dimension d of X and Y, for fixed n = 100. At dimension d = 1, we only have the components ${\mathit{X}}_1={\mathit{Y}}_1$ and both methods have power 1. At dimension d = 2, dCor has power 0.9 and the robust version has power 1. When increasing the dimension further, the power of dCor goes down to about 0.3 around dimension d = 8, whereas the power of the robust method only starts going down around dimension d = 17 and is still reasonable at dimension d = 30. This illustrates that the transformation has tempered the effect of the d – 1 independent variables on the doubly centered distances, delaying the curse of dimensionality in this setting.

5.4 Fast Detection of Anomalous Cells

Wrapping is a coordinatewise approach which makes it especially robust against cellwise outliers, that is, anomalous cells x_ij in the data matrix. In this paradigm, a few cells in a row (case) can be anomalous whereas many other cells in the same row still contain useful information, and in such situations we would rather not remove or downweight the entire row. The cellwise framework was first proposed and studied by Alqallaf et al. (2002, 2009).

Most robust techniques developed in the literature aim to protect against rowwise outliers. Such methods tend not to work well in the presence of cellwise outliers, because even a relatively small percentage of outlying cells may affect a large percentage of the rows. For this reason, several authors have started to develop cellwise robust methods (Agostinelli et al. 2015). In the bivariate simulation of Section 4 we generated rowwise outliers, but the results for cellwise outliers are similar (see Section A.10 in the supplementary material).

Actually, detecting outlying cells in data with many dimensions is not trivial, because the correlation between the variables plays a role. The DetectDeviatingCells (DDC) method of Rousseeuw and Van den Bossche (2018) predicts the value of each cell from the columns strongly correlated with that cell’s column. The original implementation of DDC required computing all $O(d^2)$ robust correlations between the d variables, yielding total time complexity $O(n{d}^2)$ which grows fast in high dimensions.

Fortunately, the computation time can be reduced a lot by the wrapping method. This is because the product moment technology allows for nice shortcuts. Let us standardize two column vectors (i.e., variables) $X_n={(x_1,\dots ,x_n)}^T$ and Y_n to zero mean and unit standard deviation. Then it is easy to verify that their correlation satisfies (28) $$\text{cor}(X_n,Y_n)=\frac{1}{n-1}〈X_n,Y_n〉=1-\frac{\left|\right|X_n-Y_n|{|}^2}{2(n-1)},$$(28) where $\left|\right|\dots \left|\right|$ is the usual Euclidean distance. This monotone decreasing relation between correlation and distance allows us to switch from looking for high correlations in d dimensions to looking for small distances in n dimensions. When $n\ll d$, this is very helpful, and used for example in Google Correlate (Vanderkam et al. 2013).

The identity (28) can be exploited for robust correlation by wrapping the variables first. In the (ultra)high-dimensional case we can thus transpose our dataset, so it becomes d × n. If needed we can reduce its dimension even more to some $q\ll n$ by computing the main principal components and projecting on them, which preserves the Euclidean distances to a large extent.

Finding the k variables that are most correlated to a variable X_j therefore comes down to finding its k nearest neighbors in q-dimensional space. Fortunately, there exist fast approximate nearest neighbor algorithms (Arya et al. 1998) that can obtain the k nearest neighbors of all d points in q dimensions in $O(qd\hspace{0.17em}\text{log}\hspace{0.17em}(d))$ time, a big improvement over $O(n{d}^2)$. Note that we want to find both large positive and large negative correlations, so we look for the k nearest neighbors in the set of all variables and their sign-flipped versions.

Using these shortcuts we constructed the method FastDDC which takes far less time than the original DDC and can therefore, be applied to data in much higher dimensions. The detection of anomalous cells will be illustrated in the real data examples in Section 6. In both applications, finding the anomalies is the main result of the analysis.

6 Real Data Examples

6.1 Prostate Data

In a seminal article, Singh et al. (2002) investigated the prediction of two different types of prostate cancer from genomic information. The data is available as the R file Singh.rda in http://www.stats.uwo.ca/faculty/aim/2015/9850/microarrays/FitMArray/data/ and contains 12,600 genes. The training set consists of 102 patients and the test set has 34. There is also a response variable with the clinical classification, –1 for tumor and 1 for nontumor.

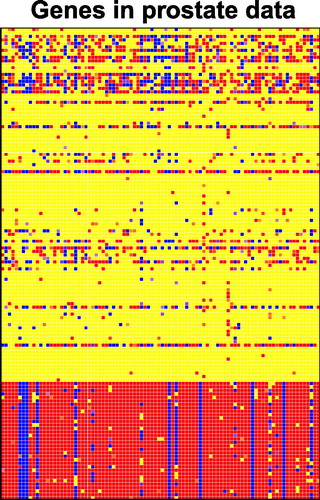
With the fast version of DDC introduced in Section 5.4, we can now analyze the entire genetic dataset with n = 136 and d = 12600, which would take very long with the original DDC algorithm. Now it takes under 1 min on a laptop. In this analysis only the genetic data is used and not the response variable, and the DDC method is not told which rows correspond to the training set. Out of the 136 rows 33 are flagged as outlying, corresponding to the test set minus one patient. The entire cellmap of size 136 × 12,600 is hard to visualize. Therefore, we select the 100 variables with the most flagged cells, yielding the cellmap in Figure 9. The flagged cells are colored red when the observed value (the gene expression level) is higher than predicted, and blue when it is lower than predicted. Unflagged cells are colored yellow.

Fig. 9 Prostate data: cellmap of the genes with the largest number of flagged cells.

The cellmap clearly shows that the bottom rows, corresponding to the test set, behave quite differently from the others. Indeed, it turns out that the test set was obtained by a different laboratory. This suggests to align the genetic data of the test set with that of the training set by some form of standardization, before applying a model fitted on the training data to predict the response variable on the test data.

6.2 Video Data

For our second example, we analyze a video of a parking lot, filmed by a static camera. The raw video can be found on http://imagelab.ing.unimore.it/visor in the category Videos for human action recognition in videosurveillance. It was originally analyzed by Ballan et al. (2009) using sophisticated computer vision technology. The video is 23 sec long and consists of 230 Red/Green/Blue (RGB) frames of 640 by 480 pixels, so each frame corresponds with 3 matrices of size 640 × 480. In the video we see two men coming from opposite directions, meeting in the center where they talk, and then running off one behind the other. Figure 10 shows 3 frames from the video. The men move through the scene, so they can be considered as outliers. Therefore, every frame (case) is contaminated, but only in a minority of pixels (cells).

Fig. 10 Frames 60, 100, and 200 of the video data.

We treat the video as a dataset X with 230 row vectors ${\mathit{x}}_i$ of length $921,600=640·480·3$, and we want to carry out a PCA based on the robust covariance matrix between the 921, 600 variables. When dealing with datasets this large one has to be careful with memory management, as a covariance matrix between these variables has nearly 10¹² entries which is far too many to store in RAM memory. Therefore, we proceed as follows:

1. Wrap the 230 data values of each RGB pixel (column) X_j which yields the wrapped data matrix ${\mathit{X}}^{*}$ and its centered version ${\mathit{Z}}^{*}={\mathit{X}}^{*}-\overline{{\mathit{x}}^{\mathit{*}}}$.

2. Compute the first k = 3 loadings of $\text{cov}({\mathit{X}}^{*})=\frac{n}{n-1}\text{PM}({\mathit{Z}}^{*})$. We cannot actually compute or store this covariance matrix, so instead we perform a truncated singular value decomposition (SVD) of ${\mathit{Z}}^{*}$ with k = 3 components, which is mathematically equivalent. For this we use the efficient function propack:svd() from the R package svd with option neig = 3, yielding the loading row vectors ${\mathit{v}}_j$ for j = 1, 2, 3.

3. Compute the three-dimensional robust scores ${\mathit{t}}_i$ by projecting the original data on the robust loadings obtained from the wrapped data, that is, ${\mathit{t}}_i=({\mathit{x}}_i-\overline{{\mathit{x}}^{\mathit{*}}})({\mathit{v}}_1^T,{\mathit{v}}_2^T,{\mathit{v}}_3^T)$.

The classical PCA result can be obtained by carrying out Steps 2 and 3 on $\mathit{Z}=\mathit{X}-\overline{\mathit{x}}$ without any wrapping.

We also want to compare with other robust methods. For the Spearman method, we first replace each column X_j by its ranks, that is, R_ij is the rank of x_ij among all x_hj with $h=1,\dots ,n$. We also compute ${\widehat{\sigma }}_j=\text{MAD}(X_j)$. Then we transform each x_ij to $(R_{ij}-{\text{ave}}_h(R_{hj})){\widehat{\sigma }}_j/{\text{stdev}}_h(R_{hj})$ yielding a matrix whose columns have mean zero and standard deviation ${\widehat{\sigma }}_j$ to which we again apply Step 2. Another method is to transform the data as in (26) but using Huber’s ψ function ${\psi }_b(z)={[z]}_{-b}^b$ with the same b = 1.5 as in wrapping.

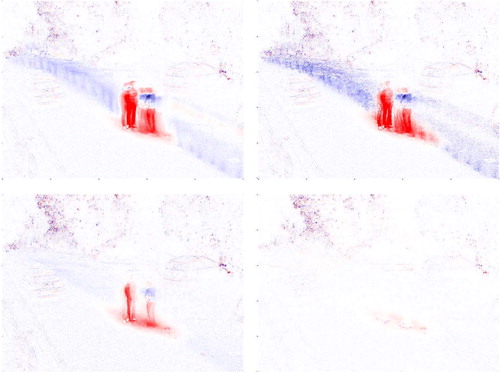
Figure 11 shows the first loading vector ${\mathit{v}}_1$ displayed as an image, for all 4 methods considered. Positive loadings are shown in red, negative ones in blue, and loadings near zero look white. For wrapping the loadings basically describe the background, whereas for classical PCA they are affected by the moving parts (mainly the men and some leaves) that are outliers in this setting. The Spearman loadings resemble those of the classical method, whereas those with Huber’s ψ are in between. Similar conclusions hold for the second and third loading vectors (not shown).

Fig. 11 First loading vector of the video data, for classical PCA (upper left), Spearman correlation (upper right), Huber’s ψ (lower left), and wrapping (lower right).

We can now compute a fit to each frame. For wrapping this is $\widehat{{\mathit{x}}_{\mathit{i}}}={\mathit{t}}_i{({\mathit{v}}_1^T,{\mathit{v}}_2^T,{\mathit{v}}_3^T)}^T+\overline{{\mathit{x}}^{\mathit{*}}}$. The residual of the frame is then ${\mathit{r}}_i={\mathit{x}}_i-\widehat{{\mathit{x}}_{\mathit{i}}}$ whose 921,600 components (pixels) we can normalize by their scales. This allows us to keep those pixels of the frame where the absolute normalized residuals exceed a threshold, and turn the other pixels gray. For wrapping, this procedure yields a new video which only contains the men. This method has thus succeeded in accurately separating the movements from the background.

The lower right panel of Figure 12 shows the result for the central part of frame 100. The corresponding computation for classical PCA is shown in the upper left panel, which has separated the men less well: many small elements of the background are marked as outlying, whereas parts of the man on the left are missing. We conclude that in this dataset wrapping is the most robust, classical PCA the least, and the other methods are in between.

Fig. 12 Residuals of the video data, for classical PCA (upper left), Spearman correlation (upper right), Huber’s ψ (lower left), and wrapping (lower right).

Note that the entire analysis of this huge dataset of size 1.6 Gb in R took about two minutes on a laptop for wrapping (the times for the other three methods were similar). This is much faster than one would expect from the computation times in Table 1, which are quadratic in the dimension since they calculate the entire covariance matrix.

Of course, in real-time situations one would estimate the robust loadings on an initial set of, say, 100 frames and then process new images while they are recorded, which is very fast as it only requires a matrix multiplication. In parallel with this the robust loadings can be updated from time to time.

7 Software Availability

The wrapping transform is implemented in the R package cellWise (Raymaekers et al. 2019) on CRAN, which now also provides the faster version of DDC used in the first example. The package contains two vignettes with examples. The video data of the second example, its analysis and the video with results can be downloaded from https://wis.kuleuven.be/stat/robust/software.

8 Conclusions

Multivariate data often contain outlying (anomalous) values, so one needs robust methods that can detect and accommodate such outliers. The underlying assumption is that the variables are roughly Gaussian for the most part, with some possible outliers that do not follow any model and could be anywhere. (If necessary some variables can be transformed first, e.g., by taking their logarithms.)

For multivariate data in low dimensions, say up to 20, there exist robust scatter matrix estimators such as the MCD method that can withstand many rowwise outliers, even those that are not visible in the marginal distributions. We recommend to use such high-breakdown methods when the dimension allows it. But in higher dimensions, these methods would require infeasible computation time to achieve the same degree of robustness, and then we need to resort to other methods.

It is not easy to construct robust methods that simultaneously satisfy the independence property, yield positive semidefinite matrices, and scale well with the dimension. We achieve this by transforming the data first, after which the usual methods based on product moments are applied.

Based on statistical properties such as the influence function, the breakdown value and efficiency we selected a particular transform called wrapping. It leaves over 86% of the data intact under normality, which preserves partial information about the data distribution, granularity, and the shape of the relation between variables. Wrapping performs remarkably well in simulation. It is especially robust against cellwise outliers, where it outperforms typical rowwise robust methods. This made it possible to construct a faster version of the DDC method. The examples show that the wrapping approach can deal with very high-dimensional data.

Supplementary Materials

These consist of a text with the proofs referenced in the article, and an R script that illustrates the approach and reproduces the examples.

Additional information

Funding

This research has been supported by projects of Internal Funds KU Leuven