Spectral Clustering on Spherical Coordinates Under the Degree-Corrected Stochastic Blockmodel

ABSTRACT

Spectral clustering is a popular method for community detection in network graphs: starting from a matrix representation of the graph, the nodes are clustered on a low-dimensional projection obtained from a truncated spectral decomposition of the matrix. Estimating correctly the number of communities and the dimension of the reduced latent space is critical for good performance of spectral clustering algorithms. Furthermore, many real-world graphs, such as enterprise computer networks studied in cyber-security applications, often display heterogeneous within-community degree distributions. Such heterogeneous degree distributions are usually not well captured by standard spectral clustering algorithms. In this article, a novel spectral clustering algorithm is proposed for community detection under the degree-corrected stochastic blockmodel. The proposed method is based on a transformation of the spectral embedding to spherical coordinates, and a novel modeling assumption in the transformed space. The method allows for simultaneous and automated selection of the number of communities and the latent dimension for spectral embeddings of graphs with uneven node degrees. Results show improved performance over competing methods in representing computer networks.

KEYWORDS:

• Degree-corrected stochastic blockmodel
• Network embeddings
• Random dot product graph
• Spectral clustering

1 Introduction

Network data are commonly observed in a variety of scientific fields, representing, for example, interactions between neurons in the brain in biology, or connections between computers in communication technologies. A fundamental problem in the statistical analysis of networks is the task of finding groups of similar nodes, known as community detection. Spectral clustering methods (Ng, Jordan, and Weiss 2001; von Luxburg 2007) provide one of the most popular approaches for the community detection task. Such techniques essentially consist of two steps: (i) spectrally embedding the graph adjacency matrix, or some transformation thereof, into a low-dimensional space, and (ii) apply a clustering algorithm, usually Gaussian mixture modeling (GMM) or k-means, in the low-dimensional space.

Spectral clustering algorithms can be used to obtain estimates of the community structure under a variety of classical network models. The traditional model for community detection is the stochastic blockmodel (SBM, Holland, Laskey, and Leinhardt 1983), each node in the network is assigned to one of K communities, and the probability of a connection between two nodes only depends on their community memberships. Asymptotic theory suggests that embeddings arising from SBMs can be modeled using Gaussian mixture models (GMMs) (Rubin-Delanchy et al. 2017). This article mainly concerns the degree-corrected stochastic blockmodel (DCSBM, Karrer and Newman 2011), which extends the SBM, allowing for heterogeneity in the within-community degree-distribution. In DCSBMs, the probability of a connection depends on the community memberships, but is adjusted by node-specific degree-correction parameters. However, unlike the SBM, spectral embeddings under the DCSBM do not adhere to a GMM, since the communities are represented by rays.

In principle, DCSBMs appear to be particularly suitable for modeling graphs arising from cyber-security applications, and in particular computer network flow data representing summaries of connections between Internet Protocol (IP) addresses, since machines within the same organization tend to have different levels of activity depending on their purpose. Furthermore, in computer networks, the need for degree-correction seems most obvious when nodes are observed for different amounts of time, so that their connection probabilities scale with their “total time on test.” For example, if a new node enters the network, it would be beneficial to identify its community, despite having very few connections.

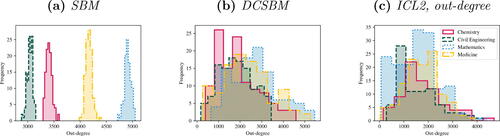
The suitability of DCSBMs for community detection in cyber-security, our application of interest, is demonstrated in Figure 1, where the within-community out-degree distributions arising from two simulated bipartite SBM (Figure 1(a)) and DCSBM (Figure 1(b)), are compared to the out-degree distribution of a real computer network (Figure 1(c)). A detailed description of the simulation is given in Section 6.2. The shape of the degree-distribution of the computer network resembles the simulated DCSBM much more closely than the SBM, suggesting that a degree-correction is required for correctly estimating the communities.

Fig. 1 Histogram of within-community degree distributions from three bipartite networks with size $439\times 60,635$, obtained from (a) a simulation of a SBM, (b) a simulation of a DCSBM, and (c) a real-world computer network (ICL2, see Section 6.2).

This article makes two main contributions. First, a novel spectral clustering algorithm for community detection under the DCSBM is proposed, based on a transformation of the embedding. Second, the proposed methodology is incorporated within a model selection framework for d, the embedding dimension, and K, the number of communities, providing a joint estimation method for those two parameters and the communities. The proposed method is shown to be competitive on simulated and real-world computer network data.

The article is structured as follows: Section 2 describes the research question and related literature, followed by a preliminary discussion of spectral embedding techniques. Our proposed model is presented in Section 3. Parameter estimation and model selection are then discussed in Section 4. The proposed model is validated in Section 5, and results on simulated and real world computer network data are presented in Section 6.

2 Background and Motivation

A network can be expressed as a graph $\mathbb{G}=(V,E)$, consisting of a set of nodes V of cardinality n, and a set of edges $E\subseteq V\times V$ representing the pairs of nodes which have interacted. The graph is summarized by its adjacency matrix $\mathbf{A}\in {\{0,1\}}^{n\times n}$, where $A_{ij}=1_E\{(i,j)\}$ for $1\le i,j\le n$, with $A_{ii}=0,1\le i\le n$. If $(i,j)\in E\iff (j,i)\in E$, the graph is undirected, implying that A is symmetric; otherwise the graph is directed.

The degree-corrected stochastic blockmodel (DCSBM, Karrer and Newman 2011) is a popular model for community detection in graphs. For K communities, the nodes are divided into blocks by random assignment of community membership indicators $\mathit{z}=(z_1,\dots ,z_n)\in {\{1,\dots ,K\}}^n$, with community probabilities $\mathit{\psi }=({\psi }_1,\dots ,{\psi }_K),{\sum }_{j=1}^K{\psi }_j=1$. Furthermore, each node is assigned a degree-correction parameter ${\rho }_i\in [0,1]$. Each entry of the adjacency matrix is then independently modeled as(1) $$A_{ij}\sim \text{Bernoulli}({\rho }_i{\rho }_j{B}_{z_i{z}_j}),$$(1) where $\mathbf{B}\in {[0,1]}^{K\times K}$ is a K × K matrix of probabilities such that $B_{k\mathcal{l}}$ is a baseline probability for a node from community k interacting with a node from community $\mathcal{l}$.

Beyond DCSBMs, random dot product graphs (RDPG, Young and Scheinerman 2007) represent a wider and more flexible class of models for network data. Each node is assigned a d-dimensional latent position ${\mathit{x}}_i\in {\mathbb{R}}^d$ such that ${\mathit{x}}_i^{⊺}{\mathit{x}}_j\in [0,1]$ for $i,j\in \{1,\dots ,n\}$. The probability of a link between i and j is then determined as $A_{ij}\sim \text{Bernoulli}({\mathit{x}}_i^{⊺}{\mathit{x}}_j).$ The latent positions can be arranged in a matrix $\mathbf{X}={[{\mathit{x}}_1,\dots ,{\mathit{x}}_n]}^{⊺}\in {\mathbb{R}}^{n\times d}$ such that $\mathbb{E}(\mathbf{A})=\mathbf{X}{\mathbf{X}}^{⊺}$. For a positive definite block connectivity probability matrix B, DCSBMs can be expressed as RDPGs. If each community is assigned an uncorrected position ${\mathit{\mu }}_k\in {\mathbb{R}}^d$, such that $B_{k\mathcal{l}}={\mathit{\mu }}_k^{⊺}{\mathit{\mu }}_{\mathcal{l}},k,\mathcal{l}\in \{1,\dots ,K\}$, the DCSBM is obtained by setting ${\mathit{x}}_i={\rho }_i{\mathit{\mu }}_{z_i},i\in V$, conditional on the communities $\mathit{z}$ and degree-correction parameters $\mathit{\rho }=({\rho }_1,\dots ,{\rho }_n)$.

This article is primarily concerned with a novel technique for estimating the underlying node communities given an adjacency matrix, under a RDPG interpretation of the DCSBM. A joint estimation method is proposed for the community structure $\mathit{z}$, the number of communities K, and the latent dimension d of the latent positions.

2.1 Related Literature, Shortcomings, and Proposed Solutions

Community detection based on DCSBMs is an active field of research. Zhao, Levina, and Zhu (2012) presented a theory for assessing consistency under the DCSBM. Amini et al. (2013) used a pseudo-likelihood approach, providing consistency results for the estimators. Peng and Carvalho (2016) frame the DCSBM in a Bayesian setting, using a logistic regression formulation with node correction terms. Chen, Li, and Xu (2018) proposed a convexified modularity maximization approach. Gao et al. (2018) obtained a minimax risk result for community detection in DCSBMs and propose a two-step clustering algorithm based on k-medians.

Spectral clustering methods have emerged as one of the most popular approaches for community detection under the DCSBM (Lei and Rinaldo 2015; Gulikers, Lelarge, and Massoulié 2017). A common technique uses k-means on the normalized rows of the embedding (Qin and Rohe 2013) obtained from the spectral decomposition of the regularized Laplacian matrix (Chaudhuri, Chung, and Tsiatas 2012). The row-normalization of the embedding is a well-established approach for spectral clustering (Ng, Jordan, and Weiss 2001) under the DCSBM, but the normalized rows live in a d – 1 dimensional manifold, so it is not fully appropriate to fit a model for d-dimensional clusters to such an embedding. Alternative methods include the SCORE algorithm of Jin (2015), which proposes to use k-means on an embedding scaled by the leading eigenvector, showing that the effect of degree heterogeneity can be largely removed.

This article proposes a novel methodology for spectral clustering under the DCSBM, interpreted as a special case of RDPG: the d-dimensional spectral embedding is reduced to a set of d – 1 directions, or angles, changing from a Cartesian coordinate system to a spherical system. This choice of transformation is carefully motivated by asymptotic theoretical properties of the embeddings arising from DCSBMs.

Additionally, many estimation methods commonly require the number of communities K to be known. Furthermore, spectral clustering methods require the specification of the embedding dimension d, and clustering is usually carried out after selecting this parameter. This sequential approach is suboptimal, since the clustering configuration and the number of communities K would ideally be estimated jointly with d. In practice, selecting d and K is a difficult task. Sanna Passino and Heard (2020) and Yang et al. (2020) independently proposed an automatic model selection framework for both the number of communities K and the dimension d of the latent node positions in SBMs, interpreted as RDPGs. In this work, the methodology is extended to DCSBMs, providing an algorithm for practitioners.

2.2 Spectral Embedding

Given a network adjacency matrix, spectral embedding methods provide estimates $\widehat{\mathbf{X}}$ of the latent positions X in RDPGs, from decompositions of the adjacency matrix or its Laplacian. This article will mainly discuss the adjacency spectral embedding, defined below.

Definition 1

(Adjacency spectral embedding). Consider a symmetric adjacency matrix $\mathbf{A}\in {\{0,1\}}^{n\times n}$ and a positive integer $d\in \{1,\dots ,n\}$. The adjacency spectral embedding (ASE) of A in ${\mathbb{R}}^d$ is $\widehat{\mathbf{X}}=\widehat{\mathbf{\Gamma }}|\widehat{\mathbf{\Lambda }}{|}^{1/2}$, where $\left|\widehat{\mathbf{\Lambda }}\right|$ is a diagonal d × d matrix containing on the main diagonal the absolute value of the top-d eigenvalues of A in magnitude, in decreasing order, and $\widehat{\mathbf{\Gamma }}$ is a n × d matrix containing corresponding orthonormal eigenvectors.

For a directed graph, the RDPG model assumes each node $i\in V$ has two latent positions ${\mathit{x}}_i,{\mathit{x}}_i^{\prime }\in {\mathbb{R}}^d$, such that $A_{ij}\sim \text{Bernoulli}({\mathit{x}}_i^{⊺}{\mathit{x}}_j^{\prime })$. The corresponding spectral embedding uses singular value decomposition. Bipartite graphs can be interpreted as a special case of directed graphs, and therefore are also spectrally embedded using the same procedure.

Definition 2

(Directed adjacency spectral embedding). Consider an adjacency matrix $\mathbf{A}\in {\{0,1\}}^{n\times n}$, not necessarily symmetric, and a positive integer $d\in \{1,\dots ,n\}$. The directed adjacency spectral embedding (DASE) of A in ${\mathbb{R}}^d$ is jointly given by $\widehat{\mathbf{X}}=\widehat{\mathbf{U}}{\widehat{\mathbf{S}}}^{1/2}$ and $\widehat{\mathbf{X}}\prime =\widehat{\mathbf{V}}{\widehat{\mathbf{S}}}^{1/2}$, where $\widehat{\mathbf{S}}$ is a diagonal d × d matrix containing on the main diagonal the top-d singular values of A in magnitude, in decreasing order, and $\widehat{\mathbf{U}}$ and $\widehat{\mathbf{V}}$ are n × d matrices containing corresponding orthonormal left and right singular vectors respectively.

2.3 Asymptotic Properties of Spectral Embedding of DCSBMs

An important result in the RDPG literature establishes the rows of the ASE as consistent estimators of the latent positions (Sussman, Tang, and Priebe 2014). Furthermore, central limit theorems (ASE-CLTs; Athreya et al. 2016; Rubin-Delanchy et al. 2017; Tang and Priebe 2018) provide strong justification for estimation of the latent positions via ASE.

When ASE is applied to DCSBMs, the asymptotic theory (see, e.g., Rubin-Delanchy et al. 2017) predicts that each community is represented as a ray from the origin in the embedding space. An example is given in Figure 2(a), which shows the two-dimensional ASE for a simulated DCSBM with n = 1000 nodes and K = 4 communities.

Fig. 2 Scatterplots of the two-dimensional ASE of a simulated DCSBM with (a) K = 4, and (b) K = 2. Figure 2(b) also highlights the true and estimated latent position for six nodes, with the corresponding 50%, 75%, and 90% contours from the ASE-CLT, and the estimated latent positions ${\widehat{\mathit{x}}}_{1,\mathcal{l}}$ for ${\mathit{x}}_1$ from simulated DCSBM adjacency matrices ${\mathbf{A}}_{\mathcal{l}},\mathcal{l}=1,\dots ,1000$.

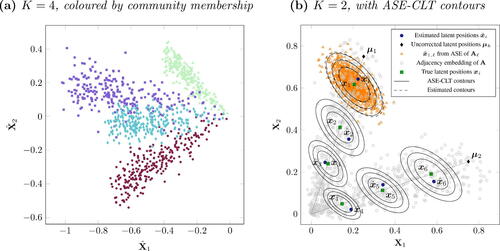
To describe each community, let $\mathit{x}=\rho {\mathit{\mu }}_k\in {\mathbb{R}}^d$ be the underlying latent position for a node in community k. Further, let ${\widehat{\mathit{x}}}^{(n)}$ be the ASE estimator of $\mathit{x}$, obtained from a graph with n nodes. For d fixed and known, the ASE-CLT (e.g., Athreya et al. 2016), applied to DCSBMs, establishes that(2) $$\underset{n\to \infty }{\lim }\mathbb{P}\left\{\sqrt{n}\left({\mathbf{Q}}^{(n)}{\widehat{\mathit{x}}}^{(n)}-\mathit{x}\right)\le \mathit{v}|\mathit{x}=\rho {\mathit{\mu }}_k\right\}\to {\Phi }_d\{\mathit{v},{\mathbf{\Sigma }}_k(\rho )\},$$(2) where $\mathit{v}\in {\mathbb{R}}^d$, ${\mathbf{Q}}^{(n)}\in {\mathbb{R}}^{d\times d}$ is an orthogonal matrix, ${\mathbf{\Sigma }}_k(\rho )$ is a d × d community-specific covariance matrix depending on ρ, and ${\Phi }_d\{·,\mathbf{\Sigma }\}$ is the CDF of a d-dimensional Gaussian distribution with zero mean and covariance $\mathbf{\Sigma }$. Jones and Rubin-Delanchy (2020) extended the result (2) to the DASE (see Definition 2). In simpler terms, (2) implies that, for n large, the estimated latent position ${\widehat{\mathit{x}}}_i$ is normally distributed about ${\rho }_i{\mathit{\mu }}_{z_i}$, after a suitable orthogonal transformation has been applied to the embedding (accounting both for the ambiguity in the choice of eigenvectors or singular vectors within the spectral embedding procedure, and the latent position identifiability in the RDPG). The theorem is exemplified by Figure 2(b), which displays the two-dimensional ASE of a simulated DCSBM with n = 1000 and K = 2 equally probable communities, with ${\mathit{\mu }}_1=[1/4,3/4]$, ${\mathit{\mu }}_2=[3/4,1/4]$, and ${\rho }_i\sim \text{Uniform}(0,1)$. For 6 nodes, the plot highlights the true and estimated latent positions, and corresponding theoretical Gaussian contours from the ASE-CLT. Additionally, the simulation of the adjacency matrix is repeated 1000 times using the same true underlying latent positions as the first simulation. Then, the ASE-estimated latent position for the first node is plotted for each simulation, along with the Gaussian contours estimated from the 1000 estimates. The empirical contours (dashed lines) remarkably correspond to the theoretical ASE-CLT contours (solid lines) around the true latent position ${\mathit{x}}_1$. Also, Figure 2(b) shows that, within the same community, the true latent positions all have the same spherical coordinates, or angle to the origin, whereas their corresponding ASE estimates are distributed around the line of the true latent positions, forming a community-specific ray. The ASE-CLT (2) also establishes that estimated latent positions tend to asymptotically concentrate increasingly tightly around the rays connecting the origin and the unnormalized latent positions ${\mathit{\mu }}_k,k\in \{1,\dots ,K\}$. Therefore, Figure 2 intuitively motivates the novel modeling choice proposed in this article: estimating the node communities from the spherical coordinates, or angles, obtained from the ASE. The use of alternative coordinate systems for network analysis has been previously shown to have beneficial properties (see, e.g., Krioukov et al. 2010; Braun and Bonfrer 2011; McCormick and Zheng 2015; Alanis-Lobato, Mier, and Andrade-Navarro 2016). Furthermore, a central limit theorem for the spherical coordinates of the latent positions is proved for d = 2 in the supplementary material, further establishing the suitable properties of such a transformation of the embedding.

One of the main characteristics of the proposed methodology will be to allow for an initial misspecification of the parameter d, choosing an m-dimensional embedding with $m\ge d$, and then recovering the correct latent dimension by proposing a discriminative model for the extended embedding. In the remainder of the article, the notation ${\widehat{\mathbf{X}}}_{:d}$ denotes the first d columns of $\widehat{\mathbf{X}}$, and ${\widehat{\mathbf{X}}}_{d:}$ denotes the m – d remaining columns. Similarly, ${\widehat{\mathit{x}}}_{i,:d}$ represents the first d components $({\widehat{x}}_1,\dots ,{\widehat{x}}_d)$ of the vector ${\widehat{\mathit{x}}}_i$, and ${\widehat{\mathit{x}}}_{i,d:}$ the last m – d components $({\widehat{x}}_{d+1},\dots ,{\widehat{x}}_m)$. Also, the row-normalized embedding is denoted as $\tilde{\mathbf{X}}={[{\tilde{\mathit{x}}}_1,\dots ,{\tilde{\mathit{x}}}_n]}^{⊺}$, where ${\tilde{\mathit{x}}}_i={\widehat{\mathit{x}}}_i/\left|\right|{\widehat{\mathit{x}}}_i\left|\right|$. Importantly, the parameter m is always assumed to be fixed.

3 Modeling a Transformation of DCSBM Embeddings

Consider an m-dimensional vector $\mathit{x}\in {\mathbb{R}}^m$. The m Cartesian coordinates $\mathit{x}=(x_1,\dots ,x_m)$ can be converted in m – 1 spherical coordinates $\mathit{\theta }=({\theta }_1,\dots ,{\theta }_{m-1})$ on the unit m-sphere using a mapping $f_m:{\mathbb{R}}^m\to {[0,2\pi )}^{m-1}$ such that $f_m:\mathit{x}\mapsto \mathit{\theta }$, where:(3) $${\theta }_1=\{\begin{array}{cc}\arccos (x_2/|\left|{\mathit{x}}_{:2}\right||)\hfill & x_1\ge 0,\hfill \\ 2\pi -\arccos (x_2/|\left|{\mathit{x}}_{:2}\right||)\hfill & x_1<0,\hfill \end{array}\mathrm{}$$(3) (4) $${\theta }_j=2\arccos (x_{j+1}/|\left|{\mathit{x}}_{:j+1}\right||),j=2,\dots ,m-1,$$(4) where $\left|\right|·\left|\right|$ is the Euclidean norm.

Consider an $(m+1)$-dimensional adjacency embedding $\widehat{\mathbf{X}}\in {\mathbb{R}}^{n\times (m+1)}$ and define its transformation $\widehat{\mathbf{\Theta }}={[{\widehat{\mathit{\theta }}}_1,\dots ,{\widehat{\mathit{\theta }}}_n]}^{⊺}\in {[0,2\pi )}^{n\times m}$, where ${\widehat{\mathit{\theta }}}_i=f_{m+1}({\widehat{\mathit{x}}}_i),i=1,\dots ,n$. The symbols ${\widehat{\mathbf{\Theta }}}_{:d}$ and ${\widehat{\mathit{\theta }}}_{i,:d}$ will denote respectively the first d columns of the matrix and d elements of the vector, and ${\widehat{\mathbf{\Theta }}}_{d:}$ and ${\widehat{\mathit{\theta }}}_{i,d:}$ will represent the remaining m – d components.

In this article, a model is proposed for the transformed embeddings $\widehat{\mathbf{\Theta }}$. Suppose a latent space dimension d, K communities, and latent community assignments $\mathit{z}=(z_1,\dots ,z_n)$. The transformed coordinates $\widehat{\mathbf{\Theta }}$ are assumed to be generated independently from community-specific m-dimensional multivariate normal distributions:(5) $${\widehat{\mathit{\theta }}}_i|d,z_i,{\mathit{\vartheta }}_{z_i},{\mathbf{\Sigma }}_{z_i},{\mathit{\sigma }}_{z_i}^2\sim {\mathbb{N}}_m\left(\left[\begin{array}{c}{\mathit{\vartheta }}_{z_i}\\ \pi {\mathbf{1}}_{m-d}\end{array}\right],\left[\begin{array}{cc}{\mathbf{\Sigma }}_{z_i}& \mathbf{0}\\ \mathbf{0}& {\mathit{\sigma }}_{z_i}^2{\mathbf{I}}_{m-d}\end{array}\right]\right).$$(5) where ${\mathit{\vartheta }}_k\in {[0,2\pi )}^d$, $k=1,\dots ,K$, represents a community-specific mean angle, ${\mathbf{1}}_m$ is a m-dimensional vector of ones, ${\mathbf{\Sigma }}_k$ is a d × d full covariance matrix, and ${\mathit{\sigma }}_k^2=({\sigma }_{k,d+1}^2,\dots ,{\sigma }_{k,m}^2)$ is a vector of positive variances. The model in (5) could be also completed in a Bayesian framework using the same prior distributions chosen in Sanna Passino and Heard (2020). For fixed d and K, consider a set of mixing proportions $\mathit{\psi }=({\psi }_1,\dots ,{\psi }_K)$ such that $\mathbb{P}(z_i=k)={\psi }_k$, where ${\psi }_k\ge 0,k=1,\dots ,K,$ and ${\sum }_{k=1}^K{\psi }_k=1$. After marginalizing out $\mathit{z}$, the likelihood function is(6) $$\begin{array}{c}L(\widehat{\mathbf{\Theta }}|d,K)\\ =\prod _{i=1}^n\left\{\sum _{j=1}^K{\psi }_j{\varphi }_d({\widehat{\mathit{\theta }}}_{i,:d};{\mathit{\vartheta }}_j,{\mathbf{\Sigma }}_j){\varphi }_{m-d}({\widehat{\mathit{\theta }}}_{i,d:};\pi {\mathbf{1}}_{m-d},{\mathit{\sigma }}_j^2{\mathbf{I}}_{m-d})\right\},\end{array}$$(6) where ${\varphi }_q(·;\mathit{\vartheta },\mathbf{\Sigma })$ is the density of a q-dimensional normal distribution with mean $\mathit{\vartheta }$ and variance $\mathbf{\Sigma }$. Note that, normally, a wrapped normal distribution would be preferred for circular data. On the other hand, in the context of DCSBMs, it is known that $\widehat{\mathbf{\Theta }}$ arises from a transformation of the embedding $\widehat{\mathbf{X}}$, and the form of the transformation can be used to inform the modeling decisions. The arccosine function is monotonically decreasing, and communities will tend to have similar values in ${\widehat{x}}_{i,j}/\left|\right|{\widehat{\mathit{x}}}_{i,:j}\left|\right|$ for $j=1,\dots ,m-1$, see (4). If two points in $\widehat{\mathbf{\Theta }}$ reach the extremes 0 and $2\pi$, then they are unlikely to belong to the same community. Therefore, wrapped distributions do not apply to this context.

The only case that could cause concern is ${\theta }_{i,1}$, where the transformation (3) is not monotonic, but has a discontinuity at 0. The first column ${\widehat{\mathbf{X}}}_1$ of the ASE corresponds to the scaled leading eigenvector of the adjacency matrix, and therefore its elements have all the same sign by the Perron–Frobenius theorem for non-negative matrices (see, e.g., Meyer 2000). The theorem makes the transformation ${\mathit{x}}_{:2}\mapsto {\theta }_1$ in (3) monotonic, since one of the two conditions in the equation for θ₁ is satisfied by all the values in ${\widehat{\mathbf{X}}}_1$.

The rationale behind the model assumptions in (5) is to use the method of normalization to the unit circle (Qin and Rohe 2013) but assume normality on the spherical coordinates, not on their Cartesian counterparts, as discussed in the comments to Figure 2(b). The transformed initial components ${\widehat{\mathit{\theta }}}_{i,:d}$ are assumed to have unconstrained mean vector ${\mathit{\vartheta }}_k\in {[0,2\pi )}^d$, and a positive-definite community-specific d × d covariance matrix ${\mathbf{\Sigma }}_k$.

In contrast to the structured model for ${\widehat{\mathbf{\Theta }}}_{:d}$, the remaining m – d dimension of the embedding are modeled as noise, using similar constraints on ${\widehat{\mathit{x}}}_{i,d:}$ to those imposed in Sanna Passino and Heard (2020) and Yang et al. (2020): the mean of the distribution is a $(m-d)$-dimensional vector centered at $2\arccos (0)=\pi$, and the covariance is a diagonal matrix ${\mathit{\sigma }}_k^2{\mathbf{I}}_{m-d}$ with positive diagonal entries. The mean value of π reflects the assumption in Sanna Passino and Heard (2020) and Yang et al. (2020) of clusters centered at zero: for j > d, $x_{i,j}$ is expected to be near 0, which makes the transformed coordinate center fluctuate around π. Importantly, the assumption of cluster-specific variances on ${\widehat{\mathbf{\Theta }}}_{d:}$ implies that d does not have the simple interpretation of being the number of dimensions relevant for clustering. This fundamentally differentiates the proposed modeling framework from traditional variable selection methods within clustering (see, e.g., Raftery and Dean 2006). The parameter d + 1 in this model represents the dimension of the latent positions that generate the network, or the rank of the block connectivity matrix B.

It must be further remarked that the model (5) concerns the distribution of the spherical coordinates of the ASE estimator of the DCSBM latent positions, and it is not a generative model for DCSBMs. If used as a generative model, paired with a distributional assumption on the degree-correction parameters, the model (5) would generate a noisy DCSBM, where the underlying latent positions are scattered around the rays, and not perfectly on the rays as a traditional DCSBM (see Figure 2(b)). Considering the ASE-CLT (2), the estimation procedure proposed in this work would still be applicable also to such a noisy DCSBM.

Finally, note that the method relies on an initial choice of the embedding dimension $m\ge d$. The parameter should be large enough to avoid potential issues with the case m < d. Choosing m is arguably easier than choosing d, and in principle one could pick m = n. As a rule of thumb, the parameter could be chosen as the third or fourth elbow based on the criterion of Zhu and Ghodsi (2006). Note that, for $m\ge d,{\widehat{\mathbf{\Theta }}}_{:d}$ is invariant to the choice of m: embeddings ${\widehat{\mathbf{\Theta }}}_{:d}$ calculated from m-dimensional and $m^{\ast }$-dimensional embeddings, with $m\ne m^{\ast }$, are identical. This is not the case for the row-normalized embedding: embeddings ${\tilde{\mathbf{X}}}_{:d}$ obtained from m-dimensional and $m^{\ast }$-dimensional embeddings are in general not equal.

4 Model Selection and Parameter Estimation

For selection of the number of communities K and latent dimension d, a classical approach of model comparison via information criteria is adopted, already used by Yang et al. (2020) in the context of simultaneous model selection in SBMs. Suppose that the maximum likelihood estimate (MLE) of the model parameters for fixed d and K is ${\{{\widehat{\mathit{\vartheta }}}_k,{\widehat{\mathbf{\Sigma }}}_k,{\widehat{\mathit{\sigma }}}_k^2,{\widehat{\psi }}_k\}}_{k=1,\dots ,K}$. The Bayesian information criterion (BIC) is defined as follows:(7) $$\begin{array}{c}\text{BIC}(d,K)\\ =-2\sum _{i=1}^n\hspace{0.17em}\text{log}\hspace{0.17em}\left\{\sum _{k=1}^K{\widehat{\psi }}_j\varphi ({\widehat{\mathit{\theta }}}_{i,:d};{\widehat{\mathit{\vartheta }}}_k,{\widehat{\mathbf{\Sigma }}}_k)\prod _{j=d+1}^m\varphi ({\widehat{\theta }}_{i,j};\pi ,{\widehat{\sigma }}_{k,j}^2)\right\}\\ \hspace{1em}+K\hspace{0.17em}\text{log}\hspace{0.17em}(n)(d^2/2+d/2+m+1).\end{array}$$(7)

The first term of the BIC (7) is the negative log-likelihood (6), whereas the second term is a penalty. The estimates of d and K will correspond to the pair that minimizes (7), obtained using grid search: $(\widehat{d},\widehat{K})={\text{argmin}}_{(d,K)}\text{BIC}(d,K)$. The latent dimension d has range $\{1,\dots ,m\}$, whereas $K\in \{1,\dots ,n\}$. In practice, it is convenient to fix a maximum number of clusters $K^{\ast }$ in the grid search procedure, such that $K\in \{1,\dots ,K^{\ast }\}$.

From (7), it follows that the MLE of the Gaussian model parameters is required for each pair (d, K). The expectation–maximization (EM, Dempster, Laird, and Rubin 1977) algorithm is typically used for problems involving likelihood maximization in model based clustering (e.g., Fraley and Raftery 2002). Finding the MLE for (6) only requires a simple modification of the standard algorithm for GMMs, adding constraints on the means and covariances of the last m – d components. Under the assumption that the model for the spherical coordinates is correctly specified, then the same framework described in Theorem 1 in Yang et al. (2020) could be used to obtain theoretical guarantees on the estimates.

Given the maximum likelihood estimates for (d, K), the communities are estimated as(8) $${\widehat{z}}_i={\text{argmax}}_{j\in \{1,\dots ,\widehat{K}\}}\left\{{\widehat{\psi }}_j{\varphi }_{\widehat{d}}\left({\widehat{\mathit{\theta }}}_{i,:\widehat{d}};{\widehat{\mathit{\vartheta }}}_j,{\widehat{\mathbf{\Sigma }}}_j\right)\right\},i=1,\dots ,n,$$(8) where a $\widehat{K}$-component GMM is fitted to the $\widehat{d}$-dimensional embedding, and the second Gaussian term in the likelihood (6), accounting for the last m – d components of the embedding, is removed to reduce the bias-variance tradeoff (Yang et al. 2020).

For a given pair (d, K), fast estimation and convergence can be achieved by initializing the EM algorithm with the MLE of a GMM fitted on the initial d components of the m-dimensional embedding. This approach for initialization will be followed in Section 6.2. The full procedure is summarized in Algorithm 1. It must be remarked that the grid search procedure for estimating (d, K) from (7) requires $m\times K^{\ast }$ EM-algorithms. This is computationally intensive, especially if the number of nodes is large, or m and $K^{\ast }$ are large. Therefore, the methodology for estimation of (d, K) is not scalable to very large graphs.

Algorithm 1:

Estimation of the latent dimension d, number of communities K, and community allocations $\mathit{z}$, given a graph adjacency matrix A.

Input: adjacency matrix $\mathbf{A}\in {\{0,1\}}^{n\times n}$, maximum number of communities $K^{\ast }$.

Result: estimated community allocations $\widehat{\mathit{z}}$ and estimated latent dimensionality $\widehat{d}$.

1 select m as the third or fourth elbow of the scree plot (Zhu and Ghodsi 2006),

2 calculate the m-dimensional ASE $\widehat{\mathbf{X}}\in {\mathbb{R}}^{n\times m}$ (or DASE for directed graphs),

3 transform the embedding $\widehat{\mathbf{X}}\in {\mathbb{R}}^{n\times m}$ into spherical coordinates $\widehat{\mathbf{\Theta }}\in {[0,2\pi )}^{n\times (m-1)}$,

4 for $d=1,2,\dots ,m$ do

5  for $K=1,\dots ,K^{\ast }$ do

6   calculate MLE ${\{{\widehat{\psi }}_j,{\widehat{\mathit{\vartheta }}}_j,{\widehat{\mathbf{\Sigma }}}_j,{\widehat{\mathit{\sigma }}}_j^2\}}_{k=1,\dots ,K}$ of model (5) using the EM algorithm,

7   calculate $\text{BIC}(d,K)$ using (7),

8  end

9 end

10 obtain the estimate $(\widehat{d},\widehat{K})={\text{argmin}}_{(d,K)}\text{BIC}(d,K)$ for the pair (d, K),

11 fit a $\widehat{K}$-component GMM to ${\widehat{\mathbf{\Theta }}}_{:\widehat{d}}$, and estimate the communities $\mathit{z}$ using (8).

5 Empirical Model Validation

In order to validate the modeling approach in (5), a simulation study has been carried out. Additional results on model validation are also reported in the supplementary material.

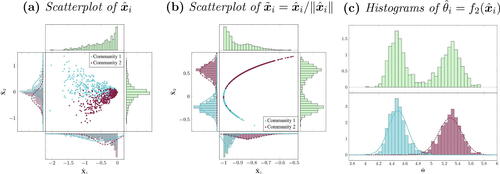
5.1 Gaussian Mixture Modeling of DCSBM Embeddings

First, a simple simulation is used to show that k-means or Gaussian mixtures are not appropriate for modeling an embedding $\widehat{\mathbf{X}}$ under the DCSBM, even when the row-normalized embedding $\tilde{\mathbf{X}}$ is used. The ASE was obtained from a simulated DCSBM with $n=1000$ nodes, K = 2 and d = 2, with an equal number of nodes allocated to each group, and $B_{11}=0.1,B_{12}=B_{21}=0.05$, and $B_{22}=0.15$, corrected by parameters ${\rho }_i\sim \text{Beta}(2,1)$. Since the community allocations $\mathit{z}$ are known a priori in the simulation, it is possible to evaluate the community-specific distributions. The results are plotted in Figure 3, which shows the scatterplot and histograms of the marginal distributions for the two-dimensional adjacency spectral embedding $\widehat{\mathbf{X}}$ and its normalized version $\tilde{\mathbf{X}}$, and for its transformation to spherical coordinates $\widehat{\mathbf{\Theta }}$, all labelled by community. From Figure 3(a), it is clear that applying k-means or Gaussian mixture modeling on $\widehat{\mathbf{X}}$ is suboptimal, since the joint distribution or cluster-specific marginal distributions are not normally distributed, as predicted by the ASE-CLT (2). Figure 3(b) shows that row-normalization is beneficial, since the marginal distributions for ${\tilde{\mathbf{X}}}_2$ are normally distributed within each community, but it is not appropriate for modeling the joint distribution and for at least one of the two marginal distributions for ${\tilde{\mathbf{X}}}_1$. On the other hand, the transformation $\widehat{\mathbf{\Theta }}$ in Figure 3(c) visually meets the assumption of normality. This visual impression is confirmed in the Supplementary Material, which describes a CLT which strongly supports the normality in $\widehat{\mathbf{\Theta }}$ for the two-dimensional case.

Fig. 3 Plots of ${\widehat{\mathit{x}}}_i,{\tilde{\mathit{x}}}_i={\widehat{\mathit{x}}}_i/\left|\right|{\widehat{\mathit{x}}}_i\left|\right|$ and ${\widehat{\theta }}_i=f_2({\widehat{\mathit{x}}}_i)$, obtained from the two-dimensional ASE of a simulated DCSBM. Joint (green) and community-specific (blue and red) marginal distributions with MLE Gaussian fit are also shown.

5.2 Structure of the Likelihood

In order to validate the conjecture on the model likelihood proposed in (5), a simulation study has been carried out. N = 1000 DCSBMs with n = 2000 nodes have been simulated, fixing K = 3, and pre-allocating the nodes to equal-sized clusters. The community-specific latent positions used in the simulation are ${\mathit{\mu }}_1=(0.7,0.4,0.1),{\mathit{\mu }}_2=(0.1,0.1,0.5)$, and ${\mathit{\mu }}_3=(0.4,0.8,-0.1)$, resulting in the block-probability matrix(9) $$\mathbf{B}=\left[\begin{array}{ccc}0.66& 0.16& 0.59\\ 0.16& 0.27& 0.07\\ 0.59& 0.07& 0.81\end{array}\right].$$(9)

The matrix is positive-definite and has full rank 3, implying that d = 2 in the embedding $\widehat{\mathbf{\Theta }}$. For each of the N simulations, the link probabilities are corrected using the degree-correction parameters ρ_i sampled from a $\text{Uniform}(0,1)$ distribution, and the adjacency matrices A are obtained using (1). For each of the simulated graphs ASE is calculated for a large value of m. The results are summarized in Figure 4.

Fig. 4 Boxplots for $N=1000$ simulations of a degree-corrected stochastic blockmodel with $n=2000$ nodes, K = 3, equal number of nodes allocated to each group, and B described in (9), corrected by parameters ρ_i sampled from a $\text{Uniform}(0,1)$ distribution.

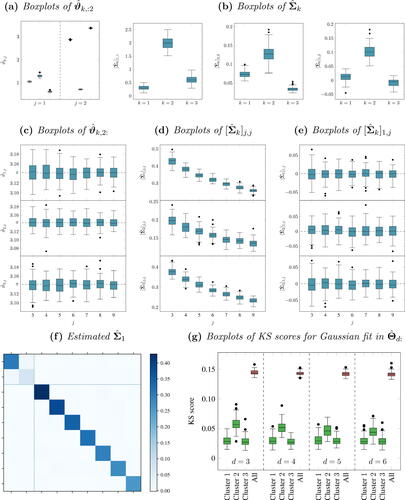
The true underlying cluster allocations are known in the simulation, and can be used to validate the model assumptions. In this section, the community-specific mean and covariance matrices obtained from the embedding $\widehat{\mathbf{\Theta }}$ of the sampled graph will be denoted as ${\widehat{\mathit{\vartheta }}}_k$ and ${\widehat{\mathbf{\Sigma }}}_k$. Figure 4(a) shows the boxplots of the community-specific estimated means for the first two components of $\widehat{\mathbf{\Theta }}$. The mean values show minimal variation across the different simulations, and are clearly different from 0 and differ between clusters. In Figure 4(b), boxplots for the community-specific estimated variances in ${\widehat{\mathbf{\Theta }}}_{:d}$ are plotted. Again, it seems that having cluster-specific variances is sensible, and at least one of the covariances is significantly different from 0, as expected from the theory. On the other hand, Figure 4(c) shows the boxplots for the community-specific estimated means in ${\widehat{\mathbf{\Theta }}}_{d:}$, which are all centered at π. Hence, the assumption on the mean structure in (5) seems to be justified.

A potentially more controversial modeling choice is the community-specific variance for the last m – d components of the embedding. Figure 4(d) shows the estimated variances for each community on different dimensions exceeding 2. It is clear that the variance is different across different communities. This consideration is reinforced by Figure 4(g), which shows the boxplots of Kolmogorov–Smirnov (KS) scores obtained from fitting community-specific Gaussian distributions on the dimensions exceeding d, compared to the KS score for a Gaussian fit on all the estimated latent positions for the corresponding dimension. Clearly, a correct modeling approach must use community-specific variances. This implies that residual cluster information is present also in the last m – d dimensions of the embedding. Finally, Figure 4(e) plots the boxplots of estimated covariances between ${\widehat{\mathbf{\Theta }}}_1$ and ${\widehat{\mathbf{\Theta }}}_{2:}$. Consistent with the model in (5), the correlations are scattered around 0, and the assumption of independence between those components seems reasonable. This is confirmed by the plot of the average estimated covariance matrix for the first community, in Figure 4(f).

5.3 Normality of the Spherical Coordinates

The most important comparison is to establish whether the embedding $\widehat{\mathbf{\Theta }}$ is better suited to GMM than the row-normalized embedding $\tilde{\mathbf{X}}$ traditionally used in the literature. To make this comparison, the p-values for the two Mardia tests for multivariate normality (Mardia 1970) have been calculated for each community-specific distribution, for each simulated graph. The tests are based on multivariate extensions of skewness and kurtosis: assume a sequence of random vectors ${\mathit{x}}_1,\dots ,{\mathit{x}}_{\mathcal{l}}\in {\mathbb{R}}^d$, and define the sample mean and sample covariance as $\overline{\mathit{x}}={\sum }_{i=1}^{\mathcal{l}}{\mathit{x}}_i/\mathcal{l}$ and $\mathbf{S}={\sum }_{i=1}^{\mathcal{l}}({\mathit{x}}_i-\overline{\mathit{x}}){({\mathit{x}}_i-\overline{\mathit{x}})}^{⊺}/\mathcal{l}$, respectively. Mardia (1970) defined two test statistics for multivariate skewness and kurtosis(10) $$T_S=\frac{1}{6\mathcal{l}}\sum _{i=1}^{\mathcal{l}}\sum _{j=1}^{\mathcal{l}}{\left[{({\mathit{x}}_i-\overline{\mathit{x}})}^{⊺}{\mathbf{S}}^{-1}({\mathit{x}}_j-\overline{\mathit{x}})\right]}^3,$$(10) (11) $$T_K=\sqrt{\frac{\mathcal{l}}{8d(d+2)}}\{\frac{1}{\mathcal{l}}\sum _{i=1}^{\mathcal{l}}{\left[{({\mathit{x}}_i-\overline{\mathit{x}})}^{⊺}{\mathbf{S}}^{-1}({\mathit{x}}_i-\overline{\mathit{x}})\right]}^2$$(11) (12) $$\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}-\frac{d(d+2)(\mathcal{l}-1)}{\mathcal{l}+1}\}.$$(12)

Under the null hypothesis of multivariate normality, $T_S\to {\chi }^2\{d(d+1)(d+2)/6\}$ and $T_K\to \mathbb{N}(0,1)$ in distribution for $\mathcal{l}\to \infty$ (Mardia 1970). Given observed values of T_S and T_K, p-values p_S and p_K can be calculated from the asymptotic distribution.

Under the same setup as the simulation in Section 5.2, p-values are calculated for the two Mardia tests applied for each community on the spherical embedding ${\widehat{\mathbf{\Theta }}}_{:2}$ and the row-normalized embedding ${\tilde{\mathbf{X}}}_{:3}$. Then, binomial sign tests for paired observations are calculated on the differences between the p-values obtained from ${\widehat{\mathbf{\Theta }}}_{:2}$, and those obtained from ${\tilde{\mathbf{X}}}_{:3}$, separately for p_S and p_K, under the null hypothesis that those are sampled from the same distribution. The alternative hypothesis is that the distribution of the p-values obtained from ${\widehat{\mathbf{\Theta }}}_{:2}$ is stochastically larger than the corresponding distribution for ${\tilde{\mathbf{X}}}_{:3}$. The p-value of the sign test is $<{10}^{-10}$ for both skewness and kurtosis, confirming the impression in Figure 3 that the transformation (4) to $\widehat{\mathbf{\Theta }}$ tends to Gaussianize the embeddings $\widehat{\mathbf{X}}$ and $\tilde{\mathbf{X}}$.

6 Applications and Results

In this section, the model selection procedure is assessed on simulated DCSBMs and real-world bipartite graphs obtained from the network flow data collected at Imperial College London. The DCSBM for bipartite graphs is a simple extension of the undirected model, and has a similar RDPG-structure to the bipartite stochastic co-blockmodel (ScBM, Rohe, Qin, and Yu 2016). In bipartite graphs, the nodes are divided into two nonoverlapping groups V and $V\prime$ such that $E\subseteq V\times V\prime$. Such networks are conveniently represented by rectangular adjacency matrices $\mathbf{A}\in {\{0,1\}}^{n\times n\prime }$, where $n=\left|V\right|$ and $n\prime =|V\prime |$. Suppose the nodes in V and $V\prime$ respectively belong to K and $K\prime$ communities, with respective community allocations $\mathit{z}\in {\{1,\dots ,K\}}^n$ and $\mathit{z}\prime \in {\{1,\dots ,K\prime \}}^{n\prime }$. Also, suppose for each of the two sets of communities there are latent positions ${\mathit{\mu }}_k\in {\mathbb{R}}^d,k\in \{1,\dots ,K\}$, and ${\mathit{\mu }}_{\mathcal{l}}^{\prime }\in {\mathbb{R}}^d,\mathcal{l}\in \{1,\dots ,K\prime \}$, such that ${\mathit{\mu }}_k^{⊺}{\mathit{\mu }}_{\mathcal{l}}^{\prime }\in [0,1]$. This gives the link probability(13) $$A_{ij}\sim \text{Bernoulli}({\rho }_i{\rho }_j^{\prime }{\mathit{\mu }}_{z_i}^{⊺}{\mathit{\mu }}_{z_j^{\prime }}^{\prime }),i\in V,j\in V\prime ,$$(13) where ${\rho }_i\in [0,1]$ and ${\rho }_j^{\prime }\in [0,1]$ are degree correction parameters for each of the nodes in V and $V\prime$. From A, it is possible to obtain embeddings $\widehat{\mathbf{X}}$ and $\widehat{\mathbf{X}}\prime$ using the DASE in Section 2.2, and cluster the two embeddings jointly or separately. In this work, the quality of the clustering is evaluated using the adjusted Rand index (ARI, Hubert and Arabie 1985). Higher values of the ARI correspond to better clustering performance, reaching a maximum of 1 for perfect agreement between the estimated clustering and the true labels.

6.1 Synthetic Networks

The performance of the model selection procedure described in Section 4 is evaluated on simulated DCSBMs. N = 250 undirected graphs with n = 1000 and $K\in \{2,3\}$ were simulated, randomly selecting B from $\text{Uniform}{(0,1)}^{K\times K}$ and sampling the degree correction parameters from $\text{Beta}(2,1)$. The nodes were allocated to communities of equal size. For each of the graphs, the models of Sanna Passino and Heard (2020) and Yang et al. (2020) are applied to the ASE $\widehat{\mathbf{X}}$ and its row-normalized version $\tilde{\mathbf{X}}$ for m = 10, selecting the estimates of d and K using BIC. The value m = 10 is usually approximately equal in the simulations to the third elbow of the scree plot using the criterion of Zhu and Ghodsi (2006), considering a total of 25 eigenvalues or singular values. Also, the model in (5) is fitted to $\widehat{\mathbf{\Theta }}$, estimating d and K using the selection procedure in Section 4, with $K^{\ast }=6$. The results of the simulations are reported in Table 1(a).

Table 1 Estimated performance for N = 250 simulated DCSBMs and bipartite DCScBMs.

(a) Undirected DCSBM
	K = 2			K = 3
	$\widehat{\mathbf{X}}$	$\tilde{\mathbf{X}}$	$\widehat{\mathbf{\Theta }}$	$\widehat{\mathbf{X}}$	$\tilde{\mathbf{X}}$	$\widehat{\mathbf{\Theta }}$
Proportion of correct d	0.788	0.796	0.972	0.740	0.736	0.748
Proportion of correct K	0.000	0.080	0.624	0.000	0.092	0.296
Average ARI	0.339	0.510	0.764	0.594	0.748	0.858
(b) Bipartite DCScBM
	K = 2			$K\prime =3$
	$\widehat{\mathbf{X}}$	$\tilde{\mathbf{X}}$	$\widehat{\mathbf{\Theta }}$	$\widehat{\mathbf{X}}\prime$	$\tilde{\mathbf{X}}\prime$	$\widehat{\mathbf{\Theta }}\prime$
Proportion of correct d	0.940	0.948	0.876	0.888	0.916	0.896
Proportion of correct K	0.000	0.056	0.580	0.000	0.096	0.540
Average ARI	0.374	0.564	0.885	0.490	0.572	0.715

A similar simulation has been repeated for bipartite DCScBMs. N = 250 graphs with n = 1000 and $n\prime$=1500 were generated, setting $K=2,K\prime =3$, communities of equal size, $\mathbf{B}\sim \text{Uniform}{(0,1)}^{K\times K\prime }$, and ${\rho }_i\sim \text{Beta}(2,1)$. The results are reported in Table 1(b).

The table shows that the transformed embedding sometimes has a slightly inferior performance when estimating the correct value of the latent dimension d (see Table 1(b)), but outperforms the alternative methodologies significantly in the ability to estimate the number of communities K. In particular, the Gaussian mixture model is not well suited to either the standard embedding $\widehat{\mathbf{X}}$ nor the row-normalized $\tilde{\mathbf{X}}$, and the distortion caused by the degree-corrections and row-normalization does not allow correct estimation of K. This problem is alleviated when the spherical coordinates estimator is used. The improvement is reflected in a significant difference in the clustering performance, demonstrated by the average ARI scores for the three different procedures. The table also shows that estimates of d based on the model of Sanna Passino and Heard (2020) and Yang et al. (2020) on $\widehat{\mathbf{X}}$ and $\widehat{\mathbf{X}}\prime$ seem to be slightly more accurate than alternative methods on the DCScBM. It might be therefore tempting to construct a hybrid model that uses ${\widehat{\mathbf{\Theta }}}_{:d}$ for the top-d embeddings and ${\widehat{\mathbf{X}}}_{d:}$ for the remaining components, and proceed to select the most appropriate d under such a joint model. Unfortunately, model comparison via BIC is not possible in that setting.

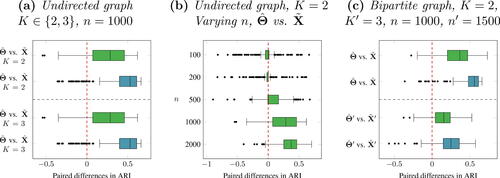
The simulation is also repeated for different values of n, evaluating the asymptotic behavior of the proposed community detection procedure. The results are plotted in Figure 5, demonstrating that the performance of the spherical coordinates estimator improves when the number of nodes in the graph increases. This is consistent with the CLT presented in the Supplementary Material. On the other hand, the results obtained from the alternative estimators degrade with n, providing further evidence that the proposed model (5) appears to be more appropriate for community detection under the DCSBM.

Fig. 5 Estimated performance for N = 250 simulated DCSBMs and DCScBMs, for $n\in \{100,200,500,1000,2000\}$. For bipartite DCScBMs, $n\prime \in \{150,300,750,1500,3000\}$.

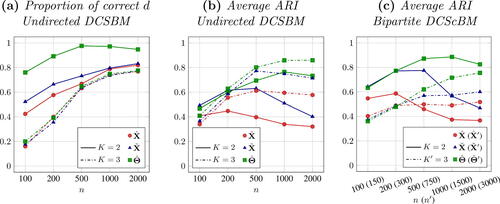
Also, the boxplots for the paired differences between ARIs are plotted in Figure 6. The clustering based on $\widehat{\mathbf{\Theta }}$ consistently outperforms $\widehat{\mathbf{X}}$ and $\tilde{\mathbf{X}}$ (see Figure 6(a) and (c)). The difference can be quantitatively evaluated using binomial sign tests for paired observations, similarly to Section 5.3. For both undirected and bipartite graphs, the p-values of the sign tests are $<{10}^{-10}$, overwhelmingly suggesting that the clustering based on $\widehat{\mathbf{\Theta }}$ is superior to the competing methodologies. Furthermore, the difference increases when the number of nodes increases (see Figure 6(b)). Overall, the simulations suggest that the proposed spectral clustering procedure for estimation of the DCSBM, based on the spherical coordinates of the ASE estimator of the latent positions, appears to outperform competing estimators, including spectral clustering on the row-normalized ASE estimator.

Fig. 6 Boxplots of differences in ARI for N = 250 simulated DCSBMs and DCScBM.

6.2 Imperial College Network Flow Data

The model proposed in this work has been specifically developed for clustering networks obtained from the network flow data collected at Imperial College London (ICL). Finding communities of machines with similar behavior is important in network monitoring and intrusion detection (Neil et al. 2013). In this application, the edges relate to all the HTTP (port 80) and HTTPS (port 443) connections observed from machines hosted in computer labs in different departments at ICL in January 2020. The source nodes V are computers hosted in college laboratories, and the destination nodes $V\prime$ are internet servers. Intuitively, computers in a laboratory tend to have a heterogeneous degree distribution of their web connections because they are not used uniformly: a computer located closed to the entrance of the laboratory might be used more than a machine at the back. Therefore, the total time of activity is different across machines in the same community, which suggests that the DCSBM is an appropriate modeling choice. This is confirmed by the within-community degree distributions in Figure 1 (Section 1), which compares one of the Imperial College networks (ICL2, see Figure 1(c)) with a simulated SBM and DCSBM (see Figure 1(a) and 1(b)). Figure 1(a) displays the within-community out-degree distribution of a simulated ScBM, see (13), with $K=K\prime =4$, equal-sized communities, and block-community matrix $\mathbf{B}/2$, with $B_{11}=0.35$, $B_{22}=0.25,B_{33}=0.15,B_{44}=0.1$, and $B_{k\mathcal{l}}=0.1$ if $k\ne \mathcal{l}$. Figure 1(b) displays the same distribution for a simulated DCScBM with block-community matrix $2\mathbf{B}$, corrected sampling ${\rho }_i,{\rho }_j^{\prime }\sim \text{Beta}(3,5)$.

Three real-world computer networks are considered here, and corresponding summary statistics are presented in Table 2, where ZG$\mathcal{l}$ denotes the position of the $\mathcal{l}$th elbow of the scree plot according to the method of Zhu and Ghodsi (2006). For the source nodes, a known underlying community structure is given by the department to which each machine belongs. ICL1 corresponds to machines hosted in the departments of Physics, Electrical Engineering, and Earth Science, whereas computers in Chemistry, Civil Engineering, Mathematics, and Medicine are considered in ICL2. For ICL3, the departments are Aeronautical Engineering, Civil Engineering, Electrical Engineering, Mathematics, and Physics. Students use the computer laboratories for tutorials and classes, and therefore some variation might be expected in the activities of different machines across different departments.

Table 2 Summary statistics for the Imperial College London computer networks.

Name	$\left|V\right|$	$|V\prime |$	$\left|E\right|$	K	ZG3	ZG4
ICL1	628	54,111	668,155	3	24	52
ICL2	439	60,635	717,912	4	24	53
ICL3	1011	84,664	1,470,074	5	27	51

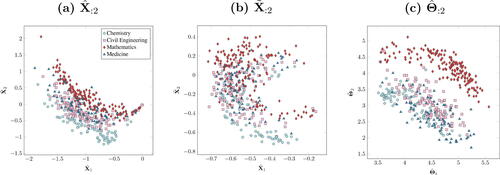
Figure 7 shows the scatterplots of the leading two dimensions of the m-dimensional embeddings $\widehat{\mathbf{X}}$, $\tilde{\mathbf{X}}$ and $\widehat{\mathbf{\Theta }}$ for m = 30 for ICL2, showing that the clustering task is particularly difficult in this network, and there is not much separation between the communities. Despite this, the transformation to spherical coordinates (see Figure 7(c)) appears to make the communities more Gaussian-shaped, as opposed to the standard and row-normalized DASE, where the within-community embeddings are curved (see Figure 7(a) and 7(b)), and therefore not amenable to Gaussian mixture modeling. This impression is quantitatively confirmed by the Mardia tests for multivariate normality on each community (see Section 5.3): the difference of the log-p-values obtained from the spherical coordinates transformation and the standard DASE is on average $\approx 42$ for the kurtosis and $\approx 82$ for the skewness, further demonstrating that the proposed transformation tends to Gaussianize the embedding.

Fig. 7 ICL2: scatterplot of the leading two dimensions for $\widehat{\mathbf{X}}$, $\tilde{\mathbf{X}}$ and $\widehat{\mathbf{\Theta }}$.

For each of the three ICL network graphs, the DASE has been calculated for m = 30 and m = 50, and the model in Sanna Passino and Heard (2020) and Yang et al. (2020) has been fitted on the source embeddings $\widehat{\mathbf{X}}$ and the row-normalized version $\tilde{\mathbf{X}}$, whereas the model (5) is used on the transformation $\widehat{\mathbf{\Theta }}$, setting $K^{\ast }=20$. The resulting estimated values of d and K, obtained using the minimum BIC, are reported in Table 3(a). In order to reduce the sensitivity to initialization, the model was fitted ten times for each pair (d, K), and the parameter estimates corresponding to the minimum BIC were retained. The choice of $m\in \{30,50\}$ corresponds to values around the third and fourth elbows in the scree plot of singular values, according to the criterion of Zhu and Ghodsi (2006) (see Table 2).

Table 3 Estimates of (d, K) and ARIs for the embeddings $\widehat{\mathbf{X}},\tilde{\mathbf{X}}$ and $\widehat{\mathbf{\Theta }}$ for $m\in \{30,50\}$ and alternative methodologies.

(a) Estimated (d, K)
	m = 30			m = 50
	$\widehat{\mathbf{X}}$	$\tilde{\mathbf{X}}$	$\widehat{\mathbf{\Theta }}$	$\widehat{\mathbf{X}}$	$\tilde{\mathbf{X}}$	$\widehat{\mathbf{\Theta }}$
ICL1	(26, 6)	(11, 6)	(11, 4)	(22, 5)	(11, 6)	(11, 4)
ICL2	(28, 5)	(8, 7)	(15, 4)	(29, 4)	(8, 7)	(15, 4)
ICL3	(24, 10)	(17, 5)	(15, 5)	(25, 6)	(13, 6)	(16, 5)
(b) ARIs for the estimated clustering
	m = 30			m = 50			Alternative methods
	$\widehat{\mathbf{X}}$	$\tilde{\mathbf{X}}$	$\widehat{\mathbf{\Theta }}$	$\widehat{\mathbf{X}}$	$\tilde{\mathbf{X}}$	$\widehat{\mathbf{\Theta }}$	Louvain	Paris	HLouvain
ICL1	0.259	0.324	0.418	0.262	0.317	0.418	0.107	0.082	0.152
ICL2	0.441	0.736	0.938	0.359	0.743	0.938	0.488	0.560	0.602
ICL3	0.246	0.342	0.409	0.269	0.265	0.364	0.079	0.032	0.157

Comparing Table 3(a) for the two different values of m, it seems that the estimates of K based on $\widehat{\mathbf{\Theta }}$ are closer to the underlying true number of communities. In particular, K = 3 for ICL1, K = 4 for ICL2, and K = 5 for ICL3, based on the number of departments.

Based on the estimates in Table 3(a), the estimated community allocations z_i were obtained using (8), and the adjusted Rand index was calculated using the department as labels. For further comparisons, the results were compared to other popular community detection methods: the Louvain algorithm (Blondel et al. 2008) adjusted for bipartite graphs (Dugué and Perez 2015), and the hierarchical Louvain (HLouvain) and Paris methods (Bonald et al. 2018), all in their default implementation for bipartite graphs in the python library scikit-network. The results are reported in Table 3(b). Clearly, clustering on the embedding $\widehat{\mathbf{\Theta }}$ outperforms the alternatives, including $\widehat{\mathbf{X}}$ and $\tilde{\mathbf{X}}$, in all the three networks. In some cases, the improvement is substantial, for example in ICL2, where the proposed method reaches the score 0.938, corresponding to only 9 misclassified nodes out of 439, particularly remarkable considering the lack of separation of the clusters in Figure 7.

The results were confirmed by binomial paired sign tests on the difference between ARI scores for N = 25 iterations of the community detection algorithms, which returned p-values $<{10}^{-4}$ in favour of the spherical coordinates estimator over the alternative methodologies.

In terms of network structure, the results could be interpreted as follows: the computers connect to a set of shared college-wide web servers (e.g., the virtual learning environment and the library services), and to services specific to the discipline carried out in each department. Furthermore, each machine has different levels of activity, which leads to heterogeneous within-community degree distributions. The SBM, corresponding to $\widehat{\mathbf{X}}$, only clusters the nodes based on their degree, whereas the DCSBM is able to uncover the departmental structure, in particular when the spherical coordinates estimator $\widehat{\mathbf{\Theta }}$ is used. Under the assumption that the networks were generated under a DCSBM, the results confirm that the estimate based on spherical coordinates proposed in this work appears to produce superior results when compared to the standard or row-normalized ASE.

7 Conclusion

In this article, a novel method for spectral clustering under the degree-corrected stochastic blockmodel has been proposed. The model is based on a transformation to spherical coordinates of the commonly used adjacency spectral embedding. Such a transformation seems more suited to Gaussian mixture modeling than the row-normalized embedding, which is widely used in the literature for spectral clustering. The proposed methodology is then incorporated within a simultaneous model selection scheme that allows the model dimension d and the number of communities K to be determined. The optimal values of d and K are chosen using the popular Bayesian information criterion. The framework also extends simply to include directed and bipartite graphs. Results on synthetic data and real-world computer networks show superior performance over competing methods.

Acknowledgments

The authors thank the editor, associate editor, and two referees for their valuable comments, that greatly improved the quality of the article. FSP acknowledges funding from EPSRC.

Supplementary Material

The supplementary material for this article describes a central limit theorem for the spherical coordinates of the latent positions for d = 2, and additional simulation studies for model validation. The first author’s Github page (https://github.com/fraspass/dcsbm) contains python code to reproduce the results and simulations presented in this article.

Additional information

Funding

The authors thank the editor, associate editor, and two referees for their valuable comments, that greatly improved the quality of the article. FSP acknowledges funding from EPSRC.