Deep Gaussian Process Emulation using Stochastic Imputation

Abstract

Deep Gaussian processes (DGPs) provide a rich class of models that can better represent functions with varying regimes or sharp changes, compared to conventional GPs. In this work, we propose a novel inference method for DGPs for computer model emulation. By stochastically imputing the latent layers, our approach transforms a DGP into a linked GP: a novel emulator developed for systems of linked computer models. This transformation permits an efficient DGP training procedure that only involves optimizations of conventional GPs. In addition, predictions from DGP emulators can be made in a fast and analytically tractable manner by naturally using the closed form predictive means and variances of linked GP emulators. We demonstrate the method in a series of synthetic examples and empirical applications, and show that it is a competitive candidate for DGP surrogate inference, combining efficiency that is comparable to doubly stochastic variational inference and uncertainty quantification that is comparable to the fully-Bayesian approach. A Python package dgpsi implementing the method is also produced and available at https://github.com/mingdeyu/DGP.

Keywords:

• Elliptical slice sampling
• Linked Gaussian processes
• Option Greeks
• Surrogate model
• Stochastic expectation maximization

1 Introduction

Gaussian Processes (GPs) are widely used in Uncertainty Quantification (UQ) applications to emulate computationally expensive computer models for fast model evaluations, reducing computational efforts required for other UQ tasks such as uncertainty propagation, sensitivity analysis, and calibration. The popularity of GP emulators is attributed to their flexibility, native uncertainty incorporation, and analytical tractability for many key properties such as the likelihood function, predictive distribution and associated derivatives. However, many standard and popular kernel functions (e.g., squared exponential and Matérn kernels) that are overwhelmingly used for GP emulation limit the expressiveness of emulators. A number of papers attempt to address this challenge. For example, Paciorek and Schervish (2003) introduce a nonstationary kernel to overcome the nonstationary assumption of GPs with standard kernel functions (hereinafter referred to as conventional GPs). Bayesian Treed Gaussian Processes (TGPs), proposed by Gramacy and Lee (2008), emulate computer models by splitting the input space into several axially-aligned partitions, over which the computer model responses can be better represented by conventional GPs. Other studies such as Montagna and Tokdar (2016) and Volodina and Williamson (2020) use augmented kernels and mixtures of conventional kernels, respectively, to improve the expressiveness of GP emulators.

Deep Gaussian Processes (DGPs) (Damianou and Lawrence 2013) model complex Input/Output (I/O) relations, by convolving conventional GPs. Compared to other approaches, DGPs provide a richer class of models with better expressiveness than conventional GPs through a feed-forward hierarchy, mirroring deep neural networks. Although DGPs offer a rich and flexible class of nonstationary models, DGP inference (i.e., training and prediction) has been proven difficult owing to the need to infer the latent layers. Efforts at meeting this challenge from within the machine learning community center around approximate inference. For example, Bui et al. (2016) use Expectation Propagation (EP) to approximate the analytically intractable objective function so that DGP fitting can be carried out by optimization, for example, Stochastic Gradient Descent (SGD). Similar to EP, Variational Inference (VI) provides the most popular approach for DGP fitting (Damianou and Lawrence 2013; Wang et al. 2016; Havasi, Hernández-Lobato, and Murillo-Fuentes 2018). Doubly Stochastic VI (DSVI) (Salimbeni and Deisenroth 2017), which has been shown to outperform EP, is the current state-of-the-art approach and has been used by Radaideh and Kozlowski (2020); Rajaram et al. (2020) for computer model emulation. It is recently also implemented in GPflux (Dutordoir et al. 2021), an actively maintained open-source library dedicated to DGP. DSVI approximates the exact posterior distribution of the latent variables of a DGP using variational distributions. However, such approximations can be unsatisfactory because the variational distributions can often be poor representations of the true posterior distributions of the latent variables, particularly in the tails. As a result, although DSVI offers computational tractability, it can come at the expense of accurate UQ for the latent posteriors, which is essential for computer model emulation.

To address this drawback, Sauer, Gramacy, and Higdon (2022) provide a Fully-Bayesian (FB) inference using elliptical slice sampling (Murray, Adams, and MacKay 2010), that accounts for the various uncertainties in the construction of DGP surrogates. However, computational tractability limits the FB framework implemented in Sauer, Gramacy, and Higdon (2022) to certain minimal DGP specifications (e.g., no more than three-layered DGPs). Additionally, the fully sampling-based inference employed by Sauer, Gramacy, and Higdon (2022) is computationally expensive and thus may not be well-suited to some UQ tasks, such as calibration or sensitivity analysis, that involve computer model emulation.

In this work, we introduce a novel inference, called Stochastic Imputation (SI) that balances the speed embraced by the optimization-based DSVI and accuracy enjoyed by the MCMC-based FB method. It is algorithmically effective and straightforward for DGP surrogate modeling with different hierarchical structures. Unlike other studies that treat DGPs simply as compositions of GPs, we see DGPs through the lenses of linked GPs (Kyzyurova, Berger, and Wolpert 2018; Ming and Guillas 2021) that enjoy a simple and fast inference procedure. By exploiting the idea that a linked GP can be viewed as a DGP with its hidden layers exposed, our approach is to convert DGPs to linked GPs by stochastically imputing the hidden layers of DGPs. As a result, the training of a DGP becomes equivalent to several simple conventional GP optimization problems, and DGP predictions can be made analytically by naturally using the closed form predictive mean and variance of linked GP under various kernel functions. It is worth noting that EP also implements DGP predictions in an analytical manner. However, linked GP provides closed form DGP predictions with a wider range of kernel choices and more general hierarchies, allowing more flexible DGP specifications and structural engineering (e.g., the input-connected structure that we demonstrate in Section 5) for computer model emulation.

Our aim is to present a novel inference approach to DGP emulation of computer models and to compare it in terms of speed and adequacy of UQ to the variational and FB approaches. Performance of DGPs in general in comparison to other nonstationary GP methods has been made elsewhere and is beyond the scope of this work. The article is organized as follows. In Section 2, we review conventional GPs, linked GPs, and DGPs. Our approach for DGP inference is then presented in Section 3, in which we detail the prediction, imputation, and training procedures for DGP. We then compare our approach to DSVI and FB, via a synthetic experiment in Section 4, and a real-world example on financial engineering in Section 5. An additional five-dimensional synthetic problem and an extra real-world application on surrogate modeling of aircraft engine simulator are presented in Sections S.1 and S.2 of the supplementary materials.

2 Review

2.1 Gaussian Processes

Let $\mathbf{X}\in {\mathbb{R}}^{M\times D}$ represent M sets of D-dimensional input to a computer model and $\mathbf{Y}(\mathbf{X})\in {\mathbb{R}}^{M\times 1}$ be the corresponding M scalar-valued outputs. Then, the GP model assumes that $\mathbf{Y}(\mathbf{X})$ follows a multivariate normal distribution $\mathbf{Y}(\mathbf{X})\sim \mathcal{N}(\mathit{\mu }(\mathbf{X}), \mathbf{\Sigma }(\mathbf{X})),$ where $\mathit{\mu }(\mathbf{X})\in {\mathbb{R}}^{M\times 1}$ is the mean vector whose ith element is often specified as a function of ${\mathbf{X}}_{i*}$, the ith row of X; $\mathbf{\Sigma }(\mathbf{X})={\sigma }^2\mathbf{R}(\mathbf{X})\in {\mathbb{R}}^{M\times M}$ is the covariance matrix with $\mathbf{R}(\mathbf{X})$ being the correlation matrix. The ijth element of $\mathbf{R}(\mathbf{X})$ is specified by $k({\mathbf{X}}_{i*}, {\mathbf{X}}_{j*})+\eta 1_{\{{\mathbf{X}}_{i*}={\mathbf{X}}_{j*}\}}$, where $k(·,·)$ is a given kernel function with η being the nugget term and $1_{\{·\}}$ being the indicator function. In this study we consider Gaussian processes with zero means, that is, $\mathit{\mu }(\mathbf{X})=\mathbf{0}$ and kernel functions with the multiplicative form: $k({\mathbf{X}}_{i*}, {\mathbf{X}}_{j*})={\prod }_{d=1}^D{k}_d(X_{id}, X_{jd}),$ where $k_d(X_{id}, X_{jd})=k_d(|X_{id}-X_{jd}|)$ is a one-dimensional isotropic kernel function (e.g., squared exponential and Matérn kernels) with range parameter γ_d, for the dth input dimension.

Assume that the GP parameters ${\sigma }^2$, η and $\mathit{\gamma }=({\gamma }_1,\dots ,{\gamma }_D)$ are known. Then, given the realizations of input $\mathbf{x}={({\mathbf{x}}_{1*}^{\top },\dots ,{\mathbf{x}}_{M*}^{\top })}^{\top }$ and output $\mathbf{y}={(y_1,\dots ,y_M)}^{\top }$, the posterior predictive distribution of output $Y_0({\mathbf{x}}_0)$ at a new input position ${\mathbf{x}}_0\in {\mathbb{R}}^{1\times D}$ follows a normal distribution with mean ${\mu }_0({\mathbf{x}}_0)$ and variance ${\sigma }_0^2({\mathbf{x}}_0)$ given by: (1) $$\begin{array}{c}{\mu }_0({\mathbf{x}}_0)=\mathbf{r}{({\mathbf{x}}_0)}^{\top }\mathbf{R}{(\mathbf{x})}^{-1}\mathbf{y}\hspace{1em}\text{and}\\ {\sigma }_0^2({\mathbf{x}}_0)={\sigma }^2\left(1+\eta -\mathbf{r}{({\mathbf{x}}_0)}^{\top }\mathbf{R}{(\mathbf{x})}^{-1}\mathbf{r}({\mathbf{x}}_0)\right),\end{array}$$(1) where $\mathbf{r}({\mathbf{x}}_0)={[k({\mathbf{x}}_0,{\mathbf{x}}_{1*}),\dots ,k({\mathbf{x}}_0,{\mathbf{x}}_{M*})]}^{\top }$. The parameters ${\sigma }^2$, η and $\mathit{\gamma }$ are typically estimated for example, using maximum likelihood or maximum a posteriori (Rasmussen and Williams 2005), though some studies use sampling to propagate their uncertainty. In the remainder of the study, we let $\mathit{\theta }=\{{\sigma }^2,\eta ,\mathit{\gamma }\}$ be the set of GP model parameters and $\widehat{\mathit{\theta }}=\{\widehat{{\sigma }^2},\widehat{\eta },\widehat{\mathit{\gamma }}\}$ be the corresponding set of estimated model parameters.

2.2 Linked Gaussian Processes

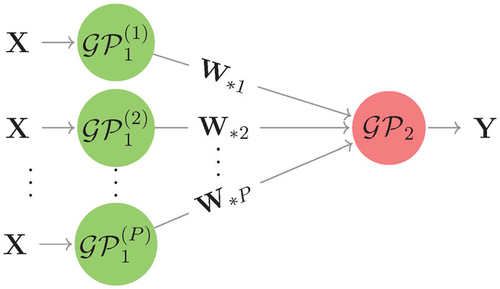
Linked GPs emulate systems of computer models, where each computer model has its own individual GP emulator. Consider a system of two computer models run with M design points, where the first model has M sets of D-dimensional input ($\mathbf{X}\in {\mathbb{R}}^{M\times D}$) and produces M sets of P-dimensional output ($\mathbf{W}\in {\mathbb{R}}^{M\times P}$) that feeds into the second computer model that produces M one-dimensional outputs ($\mathbf{Y}\in {\mathbb{R}}^{M\times 1}$). Let the GP surrogates of the two computer models be $\mathcal{G}{\mathcal{P}}_1$ and $\mathcal{G}{\mathcal{P}}_2$, respectively. Assume that the output W of the first computer model is conditionally independent across dimensions, that is, the column vectors ${\mathbf{W}}_{*p}$ of W are independent conditional on X. Then, $\mathcal{G}{\mathcal{P}}_1$ is a collection of independent GPs, ${\left\{\mathcal{G}{\mathcal{P}}_1^{(p)}\right\}}_{p=1,\dots ,P}$. Over the design, each GP corresponds to a multivariate normal distribution as in Section 2.1 with input X and output ${\mathbf{W}}_{*p}$. 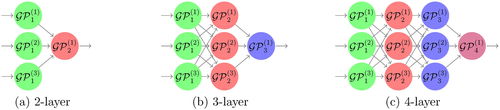The hierarchy of GPs that represents the system is shown in Figure 1.

Fig. 1 The hierarchy of GPs that represents a feed-forward system of two computer models.

Assume that, given inputs $\mathbf{X}=\mathbf{x}$ we observe realizations w and y of W and Y, and that the model parameters involved in $\mathcal{G}{\mathcal{P}}_1$ and $\mathcal{G}{\mathcal{P}}_2$ are known or estimated. Then, the posterior predictive distribution of the global output $Y_0({\mathbf{x}}_0)$ at a new global input position ${\mathbf{x}}_0$ is given by $Y_0({\mathbf{x}}_0)|\mathcal{D}\sim p(y_0|{\mathbf{x}}_0;\mathbf{y},\mathbf{w},\mathbf{x})$, where $\mathcal{D}=\{\mathbf{Y}=\mathbf{y},\mathbf{W}=\mathbf{w},\mathbf{X}=\mathbf{x}\}$ and $p(y_0|\mathbf{y},\mathbf{w},\mathbf{x})$ is the pdf of $Y_0({\mathbf{x}}_0)|\mathcal{D}$. Note that (2) $$\begin{array}{c}p(y_0|{\mathbf{x}}_0;\mathbf{y},\mathbf{w},\mathbf{x})=\int p(y_0|{\mathbf{w}}_0;\mathbf{y},\mathbf{w},\mathbf{x})p({\mathbf{w}}_0|{\mathbf{x}}_0;\mathbf{y},\mathbf{w},\mathbf{x})\mathrm{d}{\mathbf{w}}_0\\ =\int p(y_0|{\mathbf{w}}_0;\mathbf{y},\mathbf{w})\prod _{p=1}^{P}p(w_{0p}|{\mathbf{x}}_0;{\mathbf{w}}_{*p},\mathbf{x})\mathrm{d}{\mathbf{w}}_0,\end{array}$$(2) where $p(y_0|{\mathbf{w}}_0;\mathbf{y},\mathbf{w})$ and $p(w_{0p}|{\mathbf{x}}_0;{\mathbf{w}}_{*p},\mathbf{x})$ are pdf’s of the posterior predictive distributions of $\mathcal{G}{\mathcal{P}}_2$ and $\mathcal{G}{\mathcal{P}}_1^{(p)}$, respectively; and ${\mathbf{w}}_0=(w_{01},\dots ,w_{0P})$. However, $p(y_0|{\mathbf{x}}_0;\mathbf{y},\mathbf{w},\mathbf{x})$ is not analytically tractable because the integral in Equation (2)(2) $$\begin{array}{c}p(y_0|{\mathbf{x}}_0;\mathbf{y},\mathbf{w},\mathbf{x})=\int p(y_0|{\mathbf{w}}_0;\mathbf{y},\mathbf{w},\mathbf{x})p({\mathbf{w}}_0|{\mathbf{x}}_0;\mathbf{y},\mathbf{w},\mathbf{x})\mathrm{d}{\mathbf{w}}_0\\ =\int p(y_0|{\mathbf{w}}_0;\mathbf{y},\mathbf{w})\prod _{p=1}^{P}p(w_{0p}|{\mathbf{x}}_0;{\mathbf{w}}_{*p},\mathbf{x})\mathrm{d}{\mathbf{w}}_0,\end{array}$$(2) does not permit a closed form expression. It can been shown (Titsias and Lawrence 2010; Kyzyurova, Berger, and Wolpert 2018; Ming and Guillas 2021) that, given the GP specifications in Section 2.1, the mean, ${\tilde{\mu }}_0({\mathbf{x}}_0)$, and variance, ${\tilde{\sigma }}_0^2({\mathbf{x}}_0)$, of $Y_0({\mathbf{x}}_0)|\mathcal{D}$ have the following analytical expressions: (3) $${\tilde{\mu }}_0({\mathbf{x}}_0)=\mathbf{I}{({\mathbf{x}}_{\mathbf{0}})}^{\top }\mathbf{R}{(\mathbf{w})}^{-1}\mathbf{y},$$(3) (4) $$\begin{array}{c}{\tilde{\sigma }}_0^2({\mathbf{x}}_0)={\mathbf{y}}^{\top }\mathbf{R}{(\mathbf{w})}^{-1}\mathbf{J}({\mathbf{x}}_0)\mathbf{R}{(\mathbf{w})}^{-1}\mathbf{y}-{\left(\mathbf{I}{({\mathbf{x}}_0)}^{\top }\mathbf{R}{(\mathbf{w})}^{-1}\mathbf{y}\right)}^2\\ \hspace{1em}+{\sigma }^2 \left(1+\eta -\text{tr}\left\{\mathbf{R}{(\mathbf{w})}^{-1}\mathbf{J}({\mathbf{x}}_0)\right\}\right),\end{array}$$(4) where

• $\mathbf{I}({\mathbf{x}}_{\mathbf{0}})\in {\mathbb{R}}^{M\times 1}$ with its ith element $I_i={\prod }_{p=1}^P\mathbb{E}[k_p(W_{0p}({\mathbf{x}}_0),w_{ip})]$;

• $\mathbf{J}({\mathbf{x}}_0)\in {\mathbb{R}}^{M\times M}$ with its ijth element $J_{ij}={\prod }_{p=1}^P\mathbb{E}[k_p(W_{0p}({\mathbf{x}}_0), w_{ip}) k_p(W_{0p}({\mathbf{x}}_0), w_{jp})]$;

and the expectations in $\mathbf{I}({\mathbf{x}}_{\mathbf{0}})$ and $\mathbf{J}({\mathbf{x}}_0)$ have closed form expressions under the linear kernel, squared exponential kernel, and a class of Matérn kernels (Ming and Guillas 2021, Proposition 3.4). The linked GP is then defined as a normal approximation $\widehat{p}(y_0|{\mathbf{x}}_0;\mathbf{y},\mathbf{w},\mathbf{x})$ to $p(y_0|{\mathbf{x}}_0;\mathbf{y},\mathbf{w},\mathbf{x})$ with its mean and variance given by ${\tilde{\mu }}_0({\mathbf{x}}_0)$ and ${\tilde{\sigma }}_0^2({\mathbf{x}}_0)$. Moreover, the linked GP can be constructed iteratively to approximate analytically the posterior predictive distribution of global output produced by any feed-forward systems of GPs, and is shown to be a sufficient approximation in terms of minimizing Kullback–Leibler divergence (Ming and Guillas 2021).

2.3 Deep Gaussian Processes

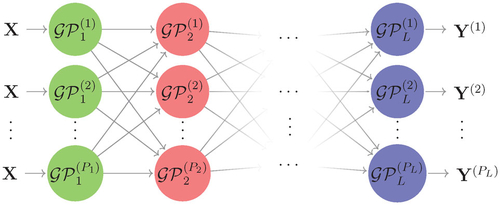
The DGP model is a feed-forward composition of conventional GPs and only differs from the linked GP model in that the internal inputs/outputs of GPs are latent. For example, the model hierarchy in Figure 1 represents a two-layered DGP when the variable W is latent. The existence of latent variables creates challenges to conduct efficient inference for DGP models. For instance, to train the two-layer DGP in Figure 1 by the maximum likelihood approach, one needs to optimize the model parameters by maximizing the likelihood function: (5) $$\mathcal{L}=p(\mathbf{y}|\mathbf{x})=\int p(\mathbf{y}|\mathbf{w})\prod _{p=1}^{P}p({\mathbf{w}}_{*p}|\mathbf{x})\mathrm{d}\mathbf{w},$$(5) where $p(\mathbf{y}|\mathbf{w})$ is the multivariate normal pdf of $\mathcal{G}{\mathcal{P}}_2$ and $p({\mathbf{w}}_{*p}|\mathbf{x})$ is the multivariate normal pdf of $\mathcal{G}{\mathcal{P}}_1^{(p)}$. However, Equation (5)(5) $$\mathcal{L}=p(\mathbf{y}|\mathbf{x})=\int p(\mathbf{y}|\mathbf{w})\prod _{p=1}^{P}p({\mathbf{w}}_{*p}|\mathbf{x})\mathrm{d}\mathbf{w},$$(5) contains an integral with respect to the latent variable w that is not analytically tractable due to the nonlinearity between y and w, and the number of such intractable integrals increases along with the depth of a DGP.

The inference challenge induced by the latent layers is tackled in the literature by DSVI that uses the variational distribution, a composition of independent (across layers) Gaussian distributions, and thus an Evidence Lower BOund (ELBO) that can be efficiently maximized. In addition to the common concern that the variational approximation may not capture important features of the posterior uncertainty, the maximization of the ELBO can be computationally challenging due to the complexity (e.g., nonconvexity and the large amount of model parameters) induced by a network of GPs. Alternatively, Sauer, Gramacy, and Higdon (2022) present a sampling-based FB inference for DGP using MCMC. The FB approach properly quantifies the uncertainties in DGP inference, but does so at the expense of computational efficiency. The approach we describe in the next section aims to blend computational efficiency of VI and accuracy of FB for DGP emulation by combining the linked GP with a sampling approach.

3 Stochastic Imputation for DGP Inference

We view the DGP as an emulator of a feed-forward system of computer models in which, each sub-model is represented by a GP and internal I/O among sub-models are nonobservable. Thus, by imputing the hidden layers and exploiting the structural dependence of the internal GP surrogates, we uncover, stochastically, the latent internal I/O from the observed global I/O. As a result, we proceed to make predictions from the DGP using the analytically tractable linked GP.

3.1 Model

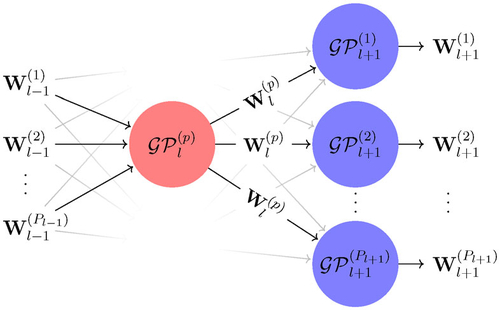
We illustrate our approach by considering the generic L-layered DGP hierarchy shown in Figure 2, where $\mathbf{X}\in {\mathbb{R}}^{M\times D}$ is the global input and ${\left\{{\mathbf{Y}}^{(p)}\right\}}_{p=1,\dots ,P_L}\in {\mathbb{R}}^{M\times 1}$ are P_L global outputs. Let $W_l^{(p)}\in {\mathbb{R}}^{M\times 1}$ be the output of $\mathcal{G}{\mathcal{P}}_l^{(p)}$ for $p=1,\dots ,P_l$ and $l=1,\dots ,L-1$ and assume that the outputs ${\left\{{\mathbf{W}}_l^{(p)}\right\}}_{p=1,\dots ,P_l}$ from GPs from the lth layer are conditionally independent given the corresponding inputs that are produced by the feeding GPs from the $(l-1)$ th layer. In the rest of the work, we use $\left\{{\mathbf{W}}_l^{(p)}\right\}$ as the shorthand of $\{{\mathbf{W}}_1^{(1)},\dots ,{\mathbf{W}}_1^{(P_1)},\dots ,{\mathbf{W}}_{L-1}^{(1)},\dots ,{\mathbf{W}}_{L-1}^{(P_{L-1})}\}$, and $\left\{{\mathit{\theta }}_l^{(p)}\right\}$ as the set of model parameters of all GPs in the DGP architecture.

Fig. 2 The generic DGP hierarchy considered to illustrate the Stochastic Imputation (SI).

3.2 Prediction

Assume that the model parameters ${\mathit{\theta }}_l^{(p)}$ of $\mathcal{G}{\mathcal{P}}_l^{(p)}$ are known and distinct for all $p=1,\dots ,P_l$ and $l=1,\dots ,L$, and that we have an observation x and $\mathbf{y}=({\mathbf{y}}^{(1)},\dots ,{\mathbf{y}}^{(P_L)})$ of the global input X and output $\mathbf{Y}=({\mathbf{Y}}^{(1)},\dots ,{\mathbf{Y}}^{(P_L)})$. To obtain the posterior predictive distribution of the pth output $Y_0^{(p)}({\mathbf{x}}_0)$ at a new input position ${\mathbf{x}}_0$, the stochastic imputation procedure fills in the latent variables $\left\{{\mathbf{W}}_l^{(p)}\right\}$ by a random realization $\left\{{\mathbf{w}}_l^{(p)}\right\}$ drawn from $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x})$, the posterior distribution of latent variables. We defer the discussion on how to draw realizations from $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x})$ to Section 3.3. After obtaining $\left\{{\mathbf{w}}_l^{(p)}\right\}$, the posterior predictive distribution $p(y_0^{(p)}|{\mathbf{x}}_0;\mathbf{y},\mathbf{x})$ of $Y_0^{(p)}({\mathbf{x}}_0)$ for all $p=1,\dots ,P_L$ can then be approximated by a linked GP with closed form mean and variance. However, a single imputation would neglect the uncertainties of the hidden layers, that is, the imputation uncertainty is not appropriately assessed. Therefore, one can draw N realizations ${\left\{{\mathbf{w}}_l^{(p)}\right\}}_1,\dots ,{\left\{{\mathbf{w}}_l^{(p)}\right\}}_N$ of $\left\{{\mathbf{W}}_l^{(p)}\right\}$ from $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x})$, and construct N linked GPs accordingly. Finally, the information contained in these N linked GPs can be combined to describe the posterior predictive distribution of $Y_0^{(p)}({\mathbf{x}}_0)$ that properly reflects the uncertainty because of the latent variables.

Note that $p(y_0^{(p)}|{\mathbf{x}}_0;\mathbf{y},\mathbf{x})$ can be approximated by a mixture of N constructed linked GPs: $$\begin{array}{c}p(y_0^{(p)}|{\mathbf{x}}_0;\mathbf{y},\mathbf{x})=\int p(y_0^{(p)}|{\mathbf{x}}_0;\mathbf{y},\{{\mathbf{w}}_l^{(p)}\},\mathbf{x}) p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x}) \mathrm{d}\{{\mathbf{w}}_l^{(p)}\}\\ ={\mathbb{E}}_{\left\{{\mathbf{W}}_l^{(p)}\right\}|\mathbf{y},\mathbf{x}}\left[p(y_0^{(p)}|{\mathbf{x}}_0;\mathbf{y},\left\{{\mathbf{W}}_l^{(p)}\right\},\mathbf{x})\right]\\ \approx \frac{1}{N}\sum _{i=1}^{N}p(y_0^{(p)}|{\mathbf{x}}_0;\mathbf{y},{\left\{{\mathbf{w}}_l^{(p)}\right\}}_i,\mathbf{x})\\ \approx \frac{1}{N}\sum _{i=1}^N\widehat{p}(y_0^{(p)}|{\mathbf{x}}_0;\mathbf{y},{\left\{{\mathbf{w}}_l^{(p)}\right\}}_i,\mathbf{x})\end{array}$$in which $\widehat{p}(y_0^{(p)}|{\mathbf{x}}_0;\mathbf{y},\left\{{\mathbf{w}}_l^{(p)}\right\},\mathbf{x})$ denotes the pdf of the linked GP. Thus, the approximate posterior predictive mean and variance of $Y_0^{(p)}({\mathbf{x}}_0)$ can be obtained by (6) $$\begin{array}{c}{\tilde{\mu }}_0^{(p)}=\frac{1}{N}\sum _{i=1}^N{\tilde{\mu }}_{0,i}^{(p)}\hspace{1em}\text{and}\\ {({\tilde{\sigma }}_0^{(p)})}^2=\frac{1}{N}\sum _{i=1}^N(({\tilde{\mu }}_{0,i}^{(p)}{)}^2+{({\tilde{\sigma }}_{0,i}^{(p)})}^2)-{({\tilde{\mu }}_0^{(p)})}^2,\end{array}$$(6) where ${\{{\tilde{\mu }}_{0,i}^{(p)},{({\tilde{\sigma }}_{0,i}^{(p)})}^2\}}_{i=1,\dots ,N}$ are closed form means and variances, the expressions of which are given in (3) and (4), of the N constructed linked GPs. The DGP prediction procedure in SI is given in Algorithm 1.

Algorithm 1

Prediction from the DGP model in Figure 2 using SI

Input: (i) Observations x and y; (ii) $\left\{\mathcal{G}{\mathcal{P}}_l^{(p)}\right\}$; (iii) a new input location ${\mathbf{x}}_0$.

Output: Mean and variance of $Y_0^{(p)}({\mathbf{x}}_0)$, for $p=1,\dots ,P_L$.

1: Impute latent variables $\left\{{\mathbf{W}}_l^{(p)}\right\}$ by N realizations ${\left\{{\mathbf{w}}_l^{(p)}\right\}}_1,\dots ,{\left\{{\mathbf{w}}_l^{(p)}\right\}}_N$ drawn from $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x})$;

2: Construct N linked GPs accordingly;

3: Compute ${\tilde{\mu }}_0^{(p)}$ and ${({\tilde{\sigma }}_0^{(p)})}^2$ of $Y_0^{(p)}({\mathbf{x}}_0)$ using (6) for all $p=1,\dots ,P_L$.

In a sampling-oriented FB inference the description of the posterior predictive distribution of $Y_0^{(p)}({\mathbf{x}}_0)$ would require N realizations of both latent variables and model parameters sampled from their posterior distributions. In addition, to obtain more precise estimates of posterior predictive mean and variance, FB also needs an adequate number of realizations of all latent variables at the prediction locations sampled through the posterior predictive distributions, for each of N sampled latent variables and model parameters. The computational cost for this prediction procedure can be expensive in tasks such as DGP-based optimization and calibration that involve a large amount of DGP predictions at different input positions. Analogously, DSVI implements predictions via sampling and thus is exposed to the same issues of the FB approach. Besides, predictions made from DSVI (as well as other VI-based approaches) lose the interpolation property (Hebbal et al. 2021) that is desired in emulating deterministic computer models. Our method combines the linked GP and an MCMC method, retaining interpolation and achieving closed form predictions (given multiple imputed latent variables) with thorough uncertainty quantification of predictions and imputations.

3.3 Imputation

Exact simulation of latent variables $\left\{{\mathbf{W}}_l^{(p)}\right\}$ from $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x})$ is difficult because of the complexity of the posterior distribution induced by the deep hierarchy of GPs. Naive application of MCMC methods (that are poorly mixing and require fine tuning with considerable human intervention) can greatly reduce the efficiency and hinder the automation of DGP inference. Elliptical Slice Sampling (ESS), a rejection-free MCMC technique, has been shown (Sauer, Gramacy, and Higdon 2022) to be a well-suited tuning-free method for latent variable simulations in three-layered DGP models. We thus use the ESS within a Gibbs sampler (ESS-within-Gibbs) to impute latent variables for the generic DGP model shown in Figure 2. In general, the ESS is designed to sample from posterior $\pi (\mathbf{w})$ over the latent variable $\mathbf{w}\in {\mathbb{R}}^{M\times 1}$ of the form: (7) $$\pi (\mathbf{w})\propto \mathcal{L}(\mathbf{w})\mathcal{N}(\mathbf{w};\mathit{\mu },\mathbf{\Sigma }),$$(7) where $\mathcal{L}(\mathbf{w})$ is a likelihood function and $\mathcal{N}(\mathbf{w};\mathit{\mu },\mathbf{\Sigma })$ is a multivariate normal prior of w with mean $\mathit{\mu }$ and covariance matrix $\mathbf{\Sigma }$. Note that $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x})$ cannot be factorized into the form of (7) and thus ESS cannot be directly applied. However, the conditional posteriors $p({\mathbf{w}}_l^{(p)}|\left\{{\mathbf{w}}_l^{(p)}\right\}\setminus {\mathbf{w}}_l^{(p)},\mathbf{y},\mathbf{x})$ of the output from $\mathcal{G}{\mathcal{P}}_l^{(p)}$ for some $p\in \{1,\dots ,P_l\}$ and $l\in \{1,\dots ,L-1\}$ can be expressed in the form of (7) as follows: (8) $$\begin{array}{c}p({\mathbf{w}}_l^{(p)}|\left\{{\mathbf{w}}_l^{(p)}\right\}\setminus {\mathbf{w}}_l^{(p)},\mathbf{y},\mathbf{x})\propto \prod _{q=1}^{P_{l+1}}p({\mathbf{w}}_{l+1}^{(q)}|{\mathbf{w}}_l^{(1)},\dots ,{\mathbf{w}}_l^{(p)},\dots ,{\mathbf{w}}_l^{(P_l)})\\ \hspace{1em}({\mathbf{w}}_l^{(p)}|{\mathbf{w}}_{l-1}^{(1)},\dots ,{\mathbf{w}}_{l-1}^{(P_{l-1})}),\end{array}$$(8) where all terms are multivariate normal; $p({\mathbf{w}}_1^{(p)}|{\mathbf{w}}_0^{(1)},\dots ,{\mathbf{w}}_0^{(P_0)})=p({\mathbf{w}}_1^{(p)}|\mathbf{x})$ when l = 1 and $$\begin{array}{c}\prod _{q=1}^{P_L}p({\mathbf{w}}_L^{(q)}|{\mathbf{w}}_{L-1}^{(1)},\dots ,{\mathbf{w}}_{L-1}^{(p)},\dots ,{\mathbf{w}}_{L-1}^{(P_{L-1})})\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}=\prod _{q=1}^{P_L}p({\mathbf{y}}^{(q)}|{\mathbf{w}}_{L-1}^{(1)},\dots ,{\mathbf{w}}_{L-1}^{(p)},\dots ,{\mathbf{w}}_{L-1}^{(P_{L-1})})\end{array}$$ when $l=L-1$. Graphically, the Gibbs sampler allows the application of ESS for each latent variable ${\mathbf{W}}_l^{(p)}$ from a two-layered elementary DGP shown in Figure 3. A single-step ESS-within-Gibbs that draws a realization from $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x})$ is given in Algorithm 2, where the algorithm for the ESS update on Line 3 is given in (Nishihara, Murray, and Adams 2014, Algorithm 1).

Fig. 3 The two-layered elementary DGP model that is targeted by ESS-within-Gibbs to sample a realization of output ${\mathbf{W}}_l^{(p)}$ from $\mathcal{G}{\mathcal{P}}_l^{(p)}$ given all other latent variables.

Algorithm 2

One-step ESS-within-Gibbs to sample from $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x})$

Input: A current sample ${\left\{{\mathbf{w}}_l^{(p)}\right\}}_i$ drawn from $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x})$.

Output: A new sample ${\left\{{\mathbf{w}}_l^{(p)}\right\}}_{i+1}$ drawn from $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x})$.

1: for $l=1,\dots ,L-1$ do

2: for $p=1,\dots ,P_l$ do

3: Draw ${\mathbf{w}}_l^{(p)}$ from $p({\mathbf{w}}_l^{(p)}|\left\{{\mathbf{w}}_l^{(p)}\right\}\setminus {\mathbf{w}}_l^{(p)},\mathbf{y},\mathbf{x})$ in the form of (8) via an ESS update;

4: end for

5: end for

3.4 Training

We have so far assumed that the model parameters ${\mathit{\theta }}_l^{(p)}$ of $\mathcal{G}{\mathcal{P}}_l^{(p)}$ are known. In this section, we detail how these parameters are optimized under SI. A naive training for the DGP model in Figure 2 might be to impute the latent variables $\left\{{\mathbf{W}}_l^{(p)}\right\}$ by sampling from the imputer $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x})$ and then to optimize the model parameters $\left\{{\mathit{\theta }}_l^{(p)}\right\}$ following the training procedure for conventional GPs. However, $\left\{{\mathit{\theta }}_l^{(p)}\right\}$ are also required by $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x})$ and thus we should update our imputer with our current best guess (in the sense of the maximum likelihood given the imputed latent variables) of the model parameters. We thus use an iterative training process, called the Stochastic Expectation-Maximization (SEM) algorithm (Celeux and Diebolt 1985), that updates model parameters at a given iteration $t\in \{1,\dots ,T-1\}$ via the following two steps:

• Imputation-step: impute the latent variables $\left\{{\mathbf{W}}_l^{(p)}\right\}$ by a single realization $$ drawn from the imputer $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x};\left\{{\widehat{\mathit{\theta }}}_l^{(p,t)}\right\})$ given estimates $\left\{{\widehat{\mathit{\theta }}}_l^{(p,t)}\right\}$ of $\left\{{\mathit{\theta }}_l^{(p)}\right\}$;

• Maximization-step: given the pseudo-complete data $\{\mathbf{y},\{{\mathbf{w}}_l^{(p)}\},\mathbf{x}\}$, update $\left\{{\widehat{\mathit{\theta }}}_l^{(p,t)}\right\}$ to $\left\{{\widehat{\mathit{\theta }}}_l^{(p,t+1)}\right\}$ by maximizing the likelihood function $\mathcal{L}(\{{\mathit{\theta }}_l^{(p)}\})=p(\mathbf{y},\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{x};\left\{{\mathit{\theta }}_l^{(p)}\right\})$, which amounts to separate optimization problems of individual GPs; update the imputer to $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x};\left\{{\widehat{\mathit{\theta }}}_l^{(p,t+1)}\right\})$ with the optimized model parameter estimates $\left\{{\widehat{\mathit{\theta }}}_l^{(p,t+1)}\right\}$.

By alternating a stochastic I-step and a deterministic M-step, SEM produces a Markov chain $\left\{{\widehat{\mathit{\theta }}}_l^{(p,1)}\right\},\dots ,\left\{{\widehat{\mathit{\theta }}}_l^{(p,T)}\right\}$ that does not converge pointwise but contains points that represent best (i.e., maximum complete-data likelihood) estimates of model parameters given a sequence of plausible values of latent variables (Ip 1994, 2002; Nielsen 2000), and one can then establish pointwise estimates $\left\{{\widehat{\mathit{\theta }}}_l^{(p)}\right\}$ of model parameters by averaging the chain after discarding burn-in periods B (Diebolt and Ip 1996): (9) $${\widehat{\mathit{\theta }}}_l^{(p)}=\frac{1}{T-B}{\displaystyle \sum _{t=B+1}^T{\widehat{\mathit{\theta }}}_l^{(p,t)}}\forall \forall p,l.$$(9)

For computational and numerical advantages of SEM over EM and other stochastic EM variants, for example, Monte Carlo EM (Wei and Tanner 1990), see Celeux, Chauveau, and Diebolt (1996) and Ip (2002).

The SEM algorithm forms a key part of our DGP inference because it has properties that make SI competitive for DGP training in comparison to FB and DSVI. FB trains the DGP by applying MCMC methods to both latent variables and model parameters. Although it captures the model uncertainty more thoroughly (in principle, albeit not always in practice due to MCMC issues on sampling model parameters), it has several computational disadvantages in comparison to SI. First, FB needs to store sampled latent variables in addition to sampled model parameters and thus can require a substantial amount of memory if the length of chain is long or the number of elementary GP nodes in the DGP is large. SI, instead, only stores updated model parameter estimates produced over iterations and is therefore more memory-efficient. The MCMC sampling in FB over the model parameters can also be computationally expensive itself (long chains of Gibbs-type draws with multiple evaluations of correlation matrix inversions at each draw). Rather than sampling, SI breaks the training problem of DGP into simpler and faster optimization problems of individual GPs and updates all model parameters in the GPs simultaneously with little human intervention. As SEM can be shown to be a stochastic perturbation of the EM dynamics (Ip 2002), the training of SI can be expected to stabilize in a comparatively small number of iterations.

DSVI trains the DGP by maximizing the ELBO, which involves a large number of model parameters including kernel hyperparameters, variational parameters and inducing point locations for each layer. Although optimization of the ELBO is computationally tractable, it embeds a simplified assumption on latent posteriors and thus can underestimate predictive uncertainties. In contrast, SI only involves optimizations of conventional GPs with respect to kernel hyperparameters using latent posteriors that are exploited thoroughly via ESS. This makes it particularly suitable for surrogate modeling for UQ, where we often have small-to-moderate data that are generated by computationally expensive simulators, and where accurate quantification of posterior uncertainties is essential.

The pseudo-code for DGP training in SI via SEM is given in Algorithm 3. It may be argued that a large C is needed in the I-step of Algorithm 3 in order to draw a realization from the stationary distribution of the imputer, and thus the training of SI can be computationally expensive to implement. However, since SEM can be seen as an example of the data augmentation method (Celeux, Chauveau, and Diebolt 1996), in practice one does not need a large C for effective inference (Ip 1994; Zhang, Chen, and Liu 2020). In our experience, C = 10 is often sufficient to obtain appropriate samples from the imputer. In addition, since in each I-step SEM only requires one realization, it is not essential to conduct convergence assessment of ESS-within-Gibbs, which is not the case for the FB approach.

Algorithm 3

Training algorithm for the DGP model in Figure 2 using SI via SEM

Input: (i) Observations x and y; (ii) initial values of model parameters $\left\{{\widehat{\mathit{\theta }}}_l^{(p,1)}\right\}$; (iii) total number of iterations T and burn-in period B for SEM; (iv) burn-in periods C for ESS.

Output: Point estimates ${\widehat{\mathit{\theta }}}_l^{(p)}$ of model parameters.

1: for $t=1,\dots ,T-1$ do

2: I-step: draw a realization $\left\{{\mathbf{w}}_l^{(p)}\right\}$ from the imputer $p(\{{\mathbf{w}}_l^{(p)}\left\}\right|\mathbf{y},\mathbf{x};\left\{{\widehat{\mathit{\theta }}}_l^{(p,t)}\right\})$ by evaluating C steps of ESS-within-Gibbs in Algorithm 2;

3: M-step: update model parameters by solving individual GP training problems: ${\widehat{\mathit{\theta }}}_l^{(p,t+1)}=\text{argmax}\hspace{0.17em}\log \hspace{0.17em}p({\mathbf{w}}_l^{(p)}|{\mathbf{w}}_{l-1}^{(1)},\dots ,{\mathbf{w}}_{l-1}^{(P_{l-1})};{\mathit{\theta }}_l^{(p)})$ for all p, l.

4: end for

5: Compute point estimates ${\widehat{\mathit{\theta }}}_l^{(p)}$ of model parameters by Equation (9)(9) $${\widehat{\mathit{\theta }}}_l^{(p)}=\frac{1}{T-B}{\displaystyle \sum _{t=B+1}^T{\widehat{\mathit{\theta }}}_l^{(p,t)}}\forall \forall p,l.$$(9) .

To deliver complete inference for the DGP model in Figure 2, one starts from Algorithm 3 to obtain estimates of model parameters for all individual GPs. Given the trained DGP (i.e., a network of trained individual GPs $\left\{\mathcal{G}{\mathcal{P}}_l^{(p)}\right\}$), one can then proceed to make predictions at new input locations using Algorithm 1, in which the multiple imputation step on Line 1 is achieved by invoking Algorithm 2 multiple (N) times.

4 Step Function

Consider a synthetic computer model with a step-wise functional form: $$f(x)=\{\begin{array}{c}1,\hspace{1em}0.5\le x<1\hfill \\ -1,\hspace{1em}0\le x<0.5\hfill \end{array}$$with input domain $[0,1]$. In this experiment, we consider a three-layered DGP, where each layer contains only one GP (i.e., $P_1=P_2=P_3=1$). Different inference approaches are compared by first measuring the predictive accuracy of the trained DGP in terms of the Normalized Root Mean Squared Error of Predictions (NRMSEPs): $$\text{NRMSEP}=\frac{\sqrt{\frac{1}{n}\sum _{i=1}^n(f(x_{0i})-{\tilde{\mu }}_{0i}{)}^2}}{\max \left\{f{(x_{0i})}_{i=1,\dots ,n}\right\}-\min \left\{f{(x_{0i})}_{i=1,\dots ,n}\right\}},$$ where $f(x_{0i})$ and ${\tilde{\mu }}_{0i}$ denotes, respectively, the true output of the computer model and mean prediction from the trained DGP evaluated at the testing input position $x_{0i}$ for $i=1,\dots ,n$. We then check if the uncertainty quantified by the trained DGP provides sensible indications of input region (i.e., the discontinuity at x = 0.5) that is deemed important by examining the produced predictive standard deviation ${\tilde{\sigma }}_{0i}$ for $i=1,\dots ,n$.

4.1 Implementation

Ten equally spaced design points were chosen over the input domain $[0,1]$, whose corresponding output are computed by evaluating the synthetic computer model. We select n = 200 testing points whose inputs are equally spaced over the input domain. For FB, we use the R package deepgp (available at https://CRAN.R-project.org/package=deepgp) by setting the total number of MCMC simulations to $10,000$ and the burn-in period to 8000 with thinning by half. These are default settings used in exercises of Sauer, Gramacy, and Higdon (2022). DSVI is implemented using the Python library GPflux (available at https://github.com/secondmind-labs/GPflux). To ensure a fair comparison to FB and SI, we switch off the sparse approximation of DSVI by setting the number of inducing points to be same as the number of training data points (i.e., 10). The ELBO is maximized using the Adam optimizer (Kingma and Ba 2015) with the learning rate of 0.01 and 1000 iterations. These are the standard settings in GPflux for ELBO optimization. With regard to SI, we implemented it using our Python package dgpsi. The total number of SEM iterations, T, is set to 500 with the first 75% (i.e., 375) of total iterations being the burn-in period B. The warm-up period C for the ESS in the I-step of SEM is set to 10. 50 imputations are conducted to make predictions at the testing input positions. These are default settings in dgpsi. Since the default DSVI implementation mimics the effects of the input-connected structure introduced in Duvenaud et al. (2014) through the use of linear mean functions (Salimbeni and Deisenroth 2017), we also explore the benefit of the input connection (IC) to SI by explicitly augmenting the input of GPs (in all layers except for those in the first layer) with the global input x. The SI with the input connection is referred to as SI-IC hereinafter. For all approaches, we use squared exponential kernels. The nugget term (the likelihood variance in the case of DSVI) is set to a small value ($\sim {10}^{-6}$) for interpolation. Unless otherwise stated, we use the same setup for different inference methods in the remainder of this study. Although the objective of the study is to introduce SI by comparing it with other inference approaches rather than comparing DGP to other GP models, in this and all remaining examples we also report results given by a conventional GP, following Salimbeni and Deisenroth (2017) and Sauer, Gramacy, and Higdon (2022), because the conventional GP can be seen as a one-layered DGP and is still the most widely used model for emulation. The conventional GP is trained by the R package RobustGaSP (Gu, Palomo, and Berger 2018).

4.2 Results

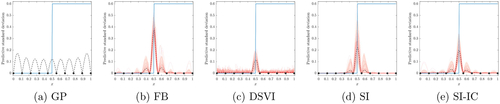
It is apparent from Figure 4 that, regardless of the inference method, the DGP model outperforms the GP model in emulating the underlying step function. The DGPs trained by FB, SI, and SI-IC provide better mean predictions than that trained by the DSVI. Both SI and FB quantify larger uncertainties than DSVI and SI-IC around the discontinuity of the step function. As addressed in Section 3.2, the DGP emulator trained by DSVI loses the interpolation property as the predictive uncertainties do not reduce to zero at some training data points. To examine the variability of such observations on predictive uncertainties under the randomness (due to latent simulations) involved in different methods, we repeat each inference approach (except for the conventional GP) 100 times and summarize predictive standard deviations across different trials in Figure 5. It is clear from Figure 5 that FB, SI, and SI-IC produce DGP emulators with better uncertainty quantification of the underlying step function than DSVI does because they highlight locations where abrupt functional transitions present with sufficiently higher predictive standard deviations.

Fig. 4 DGP emulators of the step function (the solid line) trained by different inference methods. The dashed line is the mean prediction; the shaded area is the predictive interval (i.e., two predictive standard deviations above and below the predictive mean); the filled circles are training points.

Fig. 5 Predictive standard deviations of GP and DGP emulators over the input domain. The shaded area in (b) to (e) represents the interval between the 5th and 95th percentiles (with the dash line highlighting the 50th percentile) of 100 predictive standard deviations produced by the corresponding 100 repeatedly trained DGPs; 30 out of 100 predictive standard deviations are randomly selected and drawn as the solid lines in (b) to (e). The underlying true step function and training input locations (shown as filled circles) are projected into all sub-figures.

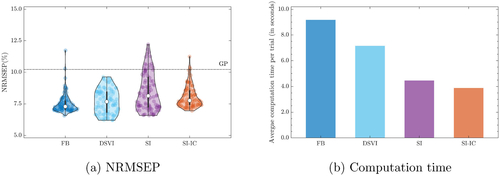
Figure 6(a) summarizes the NRMSEPs of the 100 DGP emulators produced by different approaches. We observe that DGPs trained by FB, followed by DSVI, give the best overall performance in terms of mean prediction accuracy. Although DGPs produced by SI present the least accurate mean predictions on average, their accuracy is clearly improved with SI-IC, approaching average NRMSEPs of FB and DSVI with moderate sacrifices of uncertainties (as shown in Figure 5). For practicality, we compare in Figure 6(b) the single-core computation time (including training and prediction) taken by the packages (i.e., deepgp, GPflux, and dgpsi) that implement the four inference methods on a MacBook Pro with Apple M1 Max processor and 32GB RAM. We note that SI-IC is generally faster than SI because ESS updates in SI have faster acceptances when the input connection is considered.

Fig. 6 Comparison of FB, DSVI, SI, and SI-IC across 100 repeatedly trained DGP emulators and the corresponding implementation packages’ computation time. (a): Violin plots of Normalized Root Mean Squared Error of Predictions (NRMSEPs). The dash-dot line represents the trained conventional GP. (b): Average computation time (including training and prediction) per trial.

5 Option Greeks from the Heston Model

Option Greeks are important quantities used in financial engineering to measure the sensitivity of an option’s price to features of the underlying asset such as the spot price or volatility. The Greeks are commonly used by financial engineers for risk hedging strategies and are essential elements of modern quantitative risk management. Popular Greeks include Vega that quantifies the sensitivity of an option’s price to the volatility of the underlying asset, Delta that controls the sensitivity of an option’s price to the underlying spot price, and Gamma that measures the sensitivity of an option’s Delta to the underlying spot price. However, analytical calculations of Greeks are rarely available and one often needs to solve Partial Differential Equations (PDE) with numerical approaches, such as finite-difference methods or Monte-Carlo techniques, that could be computationally expensive (Capriotti, Jiang, and Macrina 2017), especially when fast evaluations of Greeks are desired under a large number of different option scenarios. Thus, building cheap-to-evaluate surrogates of Greeks is needed.

Consider a European call option with strike price K (in $) and time-to-maturity τ (in years) whose price $C_t(S_t,K,\tau )$ at time t depends on underlying asset price S_t (in $), which follows the Heston model (Heston 1993): $$\begin{array}{c}d{S}_t=(r-q)S_{t}dt+\sqrt{V_t}{S}_{t}d{W}_t^S\\ d{V}_t=\kappa (\theta -V_t)dt+{\sigma }_V\sqrt{V_t}d{W}_t^V,\end{array}$$where r is the risk-free rate; q is the dividend yield; V_t is the asset price variance with initial level V ₀ = v₀; $\kappa >0$ is the mean reversion rate of V_t; $\theta >0$ is the long-term variance; ${\sigma }_V>0$ is the volatility of V_t; $W_t^S$ and $W_t^V$ are Wiener processes with correlation ρ. Then, the computation of Greeks at time t requires solving the Heston PDE given by (Rouah 2013): (10) $$\begin{array}{c}\frac{\partial C_t}{\partial t}+\frac{1}{2}{S}_t^2{V}_t\frac{{\partial }^2{C}_t}{\partial S_t^2}+\rho S_t{\sigma }_V{V}_t\frac{{\partial }^2{C}_t}{\partial S_t\partial V_t}+\frac{1}{2}{\sigma }_V^2{V}_t\frac{{\partial }^2{C}_t}{\partial V_t^2}\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}+(r-q)S_t\frac{\partial C_t}{\partial S_t}+\kappa (\theta -V_t)\frac{\partial C_t}{\partial V_t}=r{C}_t\end{array}$$(10) with the terminal condition $C_T=\max (0,S_T-K)$ at maturity T. Figure 7 visualizes, respectively, a slice of Vega (${\mathcal{V}}_t=\partial C_t/\partial v_0$), Delta (${\Delta }_t=\partial C_t/\partial S_t$), and Gamma (${\Gamma }_t={\partial }^2{C}_t/\partial S_t^2$) produced by (10) over $(S_t,K)\in {[10,200]}^2$ when τ is fixed to 1. It can be seen that Vega, Delta and Gamma exhibit nonstationarity because at-the-money (ATM) options (i.e., options with strike prices close to the underlying asset prices) are most sensitive to asset price changes and oscillations, and thus cause a mountain to Vega, a cliff to Delta, and a spike to Gamma over the input domain. We compare SI and SI-IC to the other two inference approaches (i.e., DSVI and FB) for DGP emulation of the relationship between Greeks and $(S_t,K,\tau )$. In the remainder of this section, we focus on ${\mathcal{V}}_t$. Results for Δ_t and Γ_t are given in Section S.3 and S.4 of the supplementary materials.

Fig. 7 Contour plots of a slice of Vega, Delta and Gamma produced by (10) over $(S_t,K)\in {[10,200]}^2$ when τ = 1.

To train DGP emulators of Vega, we generate 100 training data points by first drawing 100 input positions over $(S_t,K,\tau )\in [10,200]\times [10,200]\times [1/12,3]$ with Latin-hypercube-sampler (LHS), and then compute numerically the corresponding ${\mathcal{V}}_t$ from the Heston model using the Financial Instruments Toolbox of MATLAB. 500 testing data points are obtained in the same fashion. The model parameters $(r,q,v_0,\kappa ,\theta ,{\sigma }_V,\rho )$ in (10) are set to $(0.03,0.02,0.04,0.04,0.3,0.9,-0.5)$, following Teng, Ehrhardt, and Günther (2018). We adopt three formations (in which each individual GP has its one-dimensional kernel functions across different input dimensions sharing a common range parameter) shown in Figure 8 for DGP emulators. For each combination of formation and inference approach we conduct 40 inference trials. However, only DSVI, SI, and SI-IC are implemented for the four-layer formation because deepgp only allows DGP hierarchies up to three layers.

Fig. 8 Three different DGP formations considered to build the emulator of Vega.

5.1 Results

It can be seen from Figure 9(a) that emulators produced by SI outperform those trained by FB and DSVI under all experimental settings. Figure 9(a) also shows that with the input connection, SI could produce DGP emulators with even lower NRMSEPs. In addition, we observe that under DSVI and SI-IC, three-layered DGP emulators have systemically lower NRMSEPs than two-layered emulators. However, for both DSVI and SI-IC increasing DGP depth to four layers shows no improvement on NRMSEP.

Fig. 9 Comparison of FB, DSVI, SI, and SI-IC for 40 repeatedly trained DGP emulators (i.e., 40 inference trials) of Vega (${\mathcal{V}}_t$) from the Heston model. FB is not implemented for the 4-layer formation because deepgp only allows DGPs up to three layers. The dash-dot line represents the NRMSEP of a trained conventional GP emulator.

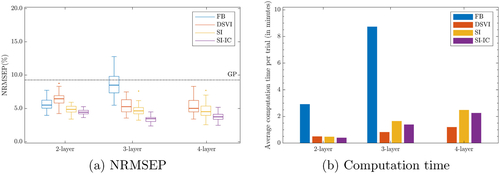
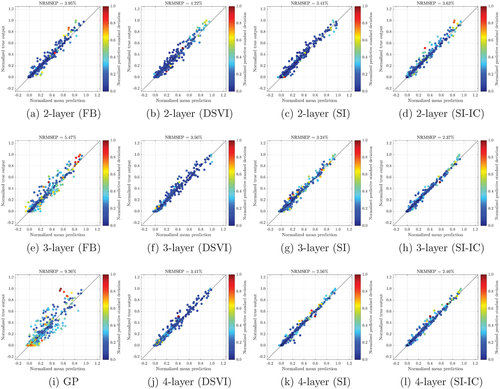
Figure 10 presents the profiles of uncertainty quantified by best DGP emulators, which are trained by different methods, from 40 inference trials. The profiles show similar uncertainty behaviors of DGPs to those in Section 4. In comparison to FB and SI (with or without the input connection), DSVI produces DGPs with lower uncertainties at locations where mean predictions are poor (e.g., dots in Figure 10(b), (f), and (j) that deviate from the diagonal lines have low predictive standard deviations) and in regions where Vega value becomes larger and exhibits more variations, across different formations. This can be problematic for tasks such as active learning in which DGP emulators trained by DSVI could unnecessarily evaluate the Heston PDE over input space where the DGP predictions are well-behaved. Although DGPs (e.g., the three-layered one in Figure 10(e)) from FB provide more distinct predictive standard deviations that better distinguish the qualities of mean predictions, the three-layered DGP (in Figure 10(h)) trained by SI-IC seems to have the overall best performance by balancing NRMSEP, uncertainty quantification, and computation (see Figure 9(b)).

Fig. 10 Plots of numerical solutions of Vega (${\mathcal{V}}_t$) (normalized by their max and min values) from the Heston model at 500 testing positions versus the mean predictions (normalized by the max and min values of numerical solutions of Vega), along with predictive standard deviations (normalized by their max and min values), made by the best emulator (with the lowest NRMSEP out of 40 inference trials) produced by FB, DSVI, SI, and SI-IC. GP represents a conventional GP emulator.

6 Conclusion

In this study, a novel inference method, called stochastic imputation, for DGP emulation is introduced. By converting DGP emulations to linked GP emulations through stochastic imputations of latent layers using ESS, we simplify the training of a DGP emulator with constructions of conventional GP emulators. As a result, predictions from a DGP emulator can be made analytically tractable by computing the closed form predictive mean and variance of the corresponding linked GP emulators. We show in both synthetic and empirical examples that our method is a competitive candidate (in terms of predictive accuracy, uncertainty, and computational cost) for DGP surrogate modeling, in comparison to other state-of-the-art inferences such as DSVI and FB. In particular, we find some evidence that it can be beneficiary to implement SI with the input connection for better emulation performance. Empirical results suggest that SI may not give significant predictive improvement on DGP emulators as the number of layers in DGP increases (up to 4), and two- or three-layered DGP emulators trained by SI with the input-connected structure can often be satisfactory in terms of predictive accuracy and computational expense.

SI is algorithmically simple and it is natural to treat inference for DGP emulators as a missing data problem in which we have missingness on internal I/O of a network of conventional GP surrogates. This simplicity and interpretability makes SI generally applicable to any DGP hierarchies formed by feed-forward connected GPs, and thus allows various potential emulation scenarios, such as multi-fidelity emulation, multi-output emulation, linked emulation and their hybrids, to be implemented and explored under the same inference framework. The Python package dgpsi we developed as a by-product of this work is generally applicable to these advanced emulation problems and publicly available on GitHub (at https://github.com/mingdeyu/DGP).

Although we only discuss the emulation of deterministic models in this work, extension to stochastic models is straightforward using SI. One could add an extra Gaussian likelihood layer to the tail of DGP hierarchy to account for either homoscedastic or heteroscedastic (Goldberg, Williams, and Bishop 1997) noise exhibited in the stochastic computer simulators. Non-Gaussian likelihoods are a natural extension and are available in dgpsi. Future work worthy of investigation include DGP emulator-based sensitivity analysis, Bayesian optimization, and calibration, taking advantage of the DGP emulators’ analytically tractable mean and variance implemented in SI. Coupling SI with sequential design (Beck and Guillas 2016; Salmanidou, Beck, and Guillas 2021) to further reinforce the predictive performance of DGP emulators with reduced computational costs is another promising research direction. Applications of sequential designs to FB-based DGP emulation are explored by Sauer, Gramacy, and Higdon (2022).

Although SI uses all data points in the dataset, this does not pose a serious computational problem to typical computer model experiments because the involved datasets are often of small-to-moderate sizes given limited computational budgets. However, when one has a big dataset, the method can become practically infeasible due to the high computational complexity associated to the storage, processing and analysis of the huge amount of data points. Therefore, it would be an interesting future work to scale the stochastic imputation method to big data, for example, via sparse approximation (Snelson and Ghahramani 2005) or GPU acceleration.

Acknowledgments

The authors would like to thank the Editor, an Associate Editor, and two referees for their insightful comments that help improve the quality of the work.

Supplementary Materials

Additional Examples and Results The file (supp˙results.pdf) contains an additional five-dimensional synthetic problem, a real-world example on aircraft engine model, and results for option Delta and Gamma of Section 5. (PDF file)

Code and Data The file (supp˙code.zip) contains codes and data used for synthetic and real-world examples in the manuscript and the supplement. It includes the version of the Python package dgpsi that produces the results in the manuscript and the supplementary materials. The latest and future versions of the package can be accessed via https://github.com/mingdeyu/DGP. (Zip file)

Disclosure Statement

The authors report that there are no competing interests to declare.