P-values, p-values everywhere!

The p-value has been an integral part of presenting and interpreting results from statistical analyses in many research domains. However, in recent decades, there has been a plethora of criticisms of the use of p-values in journal articles, editorials of journals and blogs. In an editorial in 2015, the Basic and Applied Social Psychology journal announced that use of all null hypothesis significance testing was banned, as were related procedures such as the use of CI (Trafimow and Marks 2015). This led to considerable debate and discussion on the merits of such bans and on using p-values (e.g. Ashworth 2015; Greenland et. al. 2016), and was referred to in the American Statistical Association's statement on p-values (Wasserstein and Lazar 2016). A recent issue of the Biometrical Journal (volume 59, issue 5) included a number of discussion papers on this topic in relation to medical and health research, and it was notable that all 10 contributors agreed that p-values had a role to play (Wellek 2017). Nevertheless it was generally agreed that when using p-values they should be supplemented by other measures such as CI, and consideration should be given to approaches such as Bayesian inference and a framework for simultaneously testing inferiority, equivalence, and superiority. In this editorial, we do not address the question of a total ban on p-values. Instead we suggest that p-values have a place in inferential statistics and discuss their appropriate use, in combination with CI.

In manuscripts submitted to the New Zealand Veterinary Journal, authors often include statements such as “The significance for all tests was set at 5% (p-value <0.05)” or “p-values <0.05 were considered significant”. It should be noted that p-values are associated with hypothesis testing and with defining a null and an alternative hypothesis. R.A. Fisher (1890–1962), who is widely regarded as being the father of modern statistical inference, saw the p-value as an informal index to be used as a measure of discrepancy between the data and the population (or the null hypothesis). In other words, the p-value could be thought of as a measure of strength of evidence, provided by the sample data, against the null hypothesis such that the smaller the p-value the stronger the evidence.

The dichotomisation of decision making based on the 5% level (p<0.05) has roots dating back to Neyman and Pearson (1933). They suggested a “decision-theoretic” approach where a decision is made as to whether a result is statistically significant or not. Later, Fisher stated “No scientific worker has a fixed level of significance at which, from year to year, and in all circumstances he rejects hypotheses; he rather gives his mind to each particular case in the light of his evidence and his ideas” (Fisher 1956). Moreover others argue that inference is not usually about decisions, especially using arbitrary cut-offs, and that it is a very narrow view of statistics which determines a result or effect of the parameter of interest, e.g. population mean or difference between two treatment means, being significant if p<0.05 and non-significant otherwise.

The alternative is to take the view that p-values are a continuum and provide a relative measure of strength of evidence. This leads to the guidelines of p<0.001 indicating very strong evidence, p<0.01 strong evidence, p<0.05 moderate evidence, p<0.1 weak evidence or a trend, and p≥0.1 indicating insufficient evidence. In our opinion, besides making statements along these lines, authors should provide the computed p-values (to three decimal places) so that the readers of the manuscript could interpret the results as they judge appropriate. The description of the methods used to obtain p-values must also be clearly described in the statistical analysis section of the materials and methods.

One of the main criticisms of p-values is that they do not give a direct measure for describing the strength of an effect (or effect size), but CI do. Interval estimation tries to discover values for an unknown parameter that are consistent with the sample data. In simple terms, CI attempt to answer the question: what is the size of the treatment effect or difference between two treatments? In contrast, p-values answer the question: is there evidence for a significant effect? Using 95% CI provides a range of values for the population effect that we may interpret as: we are confident that 95% of the time the method will produce an interval that contains the true population value. The narrower the CI, the higher the precision of the estimated size of the true effect. There is a connection between CI and p-values, usually associated with a two-sided alternative hypothesis. For example, if the 95% CI include the null effect, the p-value would be >0.05 and if the 95% CI exclude the null effect, the p-value would be <0.05.

A further criticism of p-values is that they are determined by both the size of the effect and the size of the sample collected. A small p-value could come from a small effect and large sample or large effect and small sample. So the main issue with relying on the size of the p-value to judge the strength of evidence for the significance of an effect is that this depends critically on the sample size. This is not unique to p-values as CI are also affected by the size of sample; the larger the sample size the narrower the interval. For example, consider the case of estimating resting pulse rates of college students. Suppose different sample sizes (n=10 or 20 or 40 or 80) gave almost identical sample means of 72.6 (SD 11.1) beats per minute. The p-values associated with testing the null hypothesis μ=68 vs. the alternative μ≠68 are 0.223, 0.079, 0.012 and<0.001, respectively, for the different sample sizes, and the 95% CI for μ are 64.7–80.5, 67.4–77.8, 69.1–76.1 and 70.1–75.1. One way to overcome this is to carry out an appropriate sample size determination process prior to carrying out a study. Most approaches to determine appropriate sample sizes depend mainly on the knowledge of variation (e.g. SD) associated with the measurement or response of interest, the anticipated detectable difference or effect size, the significance level (α) at which inferences might be based and the expected power (1−β) of the test. To take into account of the imprecise nature of the available prior knowledge with respect to the SD and effect size, we recommend using α=0.05 and 1−β=0.80 for pilot studies or initial explorations, and using α=0.01 and 1−β=0.90 for comprehensive studies.

Yet another criticism of p-values that favours use of CI is that statistical significance does not necessarily equate to practical or biological or clinical relevance, and that it is the size of the effect that determines importance. This can be illustrated as shown in Figure 1.

Figure 1. Illustration of the relationship between p-values and estimates with 95% CI (solid circles with horizontal lines) and their statistical and biological interpretation.

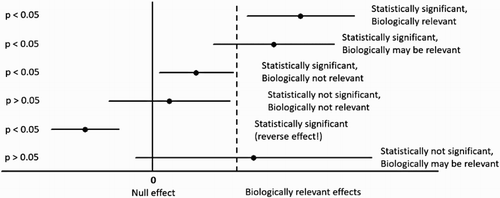
Furthermore, a common problem with p-values is that non-significance is often misinterpreted. Both authors and their audience too frequently fall into the trap of accepting the null hypothesis. For example, failing to show a difference between two treatment effects (i.e. p>0.05) is not the same as saying that they are the same. In fact, such a claim based on absence of a significant result favours a low powered experiment; the fewer the animals in the experiment the more likely that a non-significant result will be obtained. If the aim of the experiment is to show that two treatments are effectively the same, the onus of proof must change, and a bio-equivalence test is required. Similarly, a superiority test is required when the aim is to show that one treatment is superior to another, and a non-inferiority hypothesis test is required when the aim is to show that one treatment is not inferior to another (Piaggio et al. 2006). In all cases, the null hypothesis is not demonstrated by a non-significant result.

Finally, the extent to which p-values and CI provide evidence depends on how well the experiment, data collection, statistical model selection and analyses, including checking of assumptions etc., have been executed.

To summarise, the use of p-values to dichotomise results as being either significant or non-significant should be completely avoided. p-values and CI are complementary, and providing CI for the effect of interest, in addition to a p-value, has the distinct advantage of presenting imprecision on the scale of the original measurement. When there is a meaningful null hypothesis, p-values are useful to indicate the strength of evidence against the null hypothesis, but their use should not detract from the main task of determining the size of the effect of interest and the precision with which it is measured. Exact p-values should be reported to three decimal places, and p-values <0.001 should be reported as such. A p-value <0.05 does not always imply that the observed effect is biologically important, meaningful or practically relevant, and a p-value >0.05 does not provide evidence to support the null hypothesis.

Confidence intervals provide an adequately plausible range for the true value related to the point estimate of the effect of interest, and statements can be made regarding the direction of the effect as well as its strength. However CI should not be used as a surrogate means of examining significance at the conventional 5% (or a chosen) level. A justification of the level of confidence (e.g. 90%, 95% etc.) used must be given when including CI for the main results or effects of interest. Interpretation of CI should focus on the practical or biological importance of the range of values included in the interval.