 ?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
For several classes of special p-groups G, of exponent p, p > 2, we show that the near-ring, of congruence preserving functions on G is a ring if and only if G is a 1-affine complete group.
1. Introduction
Let be a finite group written additively but not necessarily abelian, with neutral element 0. As usual, we let
denote the near-ring of zero-preserving functions on G under the operations of pointwise addition and function composition. We consider subnear-rings
the near-ring of polynomial functions on G, and
the near-ring of congruence preserving functions on G. We recall
is the subnear-ring generated by the inner automorphisms of G while a function
is congruence preserving if, for each
and normal subgroup N of G, if
then
We let denote the lattice of normal subgroups of G and recall
is lattice isomorphic to the congruence lattice of G. For any subgroup H of G, the normal closure
of H is defined by
For
we let
and thus we have
if and only if
for all
We have
In this paper we continue the investigation initiated in [Citation11] as to when is a ring. Of course, if
is a ring so is
and from Chandy ([Citation3]),
is a ring if and only if G is a 2-Engel group, i.e., every element of G commutes with all of its conjugates. Since a group G of nilpotency class at most 2 is 2-Engel, in this investigation we restrict to nilpotent groups of class at most 2, and using standard results, can restrict to p-groups of class at most 2. (See [Citation11].) For finite abelian groups, A,
is a ring if and only if A is 1-affine complete, and the 1-affine complete finite abelian groups are known ([Citation11]). Recall that a group G is 1-affine complete (1-ac) means
For background material and history see [Citation10, pp 158–160].
Several necessary conditions on finite non-abelian nilpotent p-groups of class 2 for to be a ring were given in [Citation11] (see Theorem II.1 below) and in these cases for
all the groups G were 1-ac. The first examples of 1-ac non-abelian p-groups were given by Dorda ([Citation6]). These groups were p-groups, nilpotent of class 2,
In light of this example and some GAP examples, we restrict our attention to finite non-abelian p-groups, G, of class 2 and
and
is elementary abelian, that is a special p-group. Recall that a finite group G is special if G is elementary abelian or G is nilpotent of class 2,
and
is elementary abelian. (The first occurrence we have found of these groups is in Hall and Higman ([Citation9])). From group theory one finds that a non-abelian p-group, G, is special if G is nilpotent of class 2 and
(the Frattini subgroup of G). A special p-group has exponent p or p2 ([Citation7]). We focus here on non-abelian special p-groups, G,
A further reason for restricting to these special p-groups is that Verardi ([Citation13]) has shown that there exists an injective map from the class of finite groups into the class of special p-groups of exponent p. Thus information about the associated special p-group Gp may be used to obtain information about G.
In the remainder of the paper G will denote a non-abelian special p-group, of exponent p. As usual, Z(G) denotes the center of G,
the commutator subgroup, and
and
as defined above.
2. Background results: old and new
As indicated at the end of the previous section, henceforth our groups G will be non-abelian special p-groups of exponent For ease of exposition we denote this by “Let
”.
For let
denote the lattice of normal subgroups of G. Let
The pair (D, E) is called a splitting pair if for each
or
If G contains a splitting pair, we say G splits or G is split. In the case D = E, we say D is a cutting element and G is cut.
For we let
We have
and
is abelian ([Citation11, 3.3]).
For use in the sequel we collect some (mostly) known results. We note that some of these hold for any non-abelian p-group of nilpotency class 2.
Theorem II.1.
Let . If any one of the following holds:
G is split ([Citation11, 3.1]);
([Citation11, 4.7]);
G is abelian by cyclic ([Citation11, 4.6]);
There exists
such that
is cyclic ([Citation6, Hilfsatz 9]);
The derived subgroup
is cyclic ([Citation11, 4.1]);
is 2-generated, that is
then is not a ring and thus G is not 1-ac.
Proof.
For (4), Dorda ([Citation6]) constructs a function One finds that
so
is not a ring. For (6), we take
Let
and note
otherwise
is cyclic and the result follows from (4). For
if
then for
Thus Z(G) cuts G and we use (1).□
We mention two additional cases. In [Citation4], Corsi Tani proved that if G is a finite p-group of nilpotency class 2 having an automorphism with
and such that
for all
then
and G is cut. Thus these groups are not 1-ac and
is not a ring. Gorenstein ([Citation7]) calls
extra special if
and proceeds to discuss the use of extra special groups in the classification problem of finite simple groups. From Theorem II.1, extra special p-groups, G, are not 1-ac and
is not a ring.
We know if G is not cut then is a simple lattice ([Citation2, Lemma 6.1]). For
the interval I(H, K) is said to be a prime interval if
and in this case we write
From lattice theory, when
is simple then any two prime intervals are projective, hence if
and
then B/A and K/H are
isomorphic (See also [Citation1] and [Citation2]).
Lemma
II.2. Let . Let
. Then
1.
If G is not cut, then
, where
is given in part 1, and
Proof.
Let
and
Then
so
and
Since
that is
Therefore
If
then
If
then since
there exists
and
But then
so
(This also follows from ([Citation12]) since Z(G) is affine complete.)
Let
and
Then
and I(M, G) are projective so G/M and
are
isomorphic. For
we find from the first part,
so for
Thus
□
From Theorem II.1 we know if G is cut, G is not 1-ac. Thus in the sequel, when G is not cut and when attempting to show that arbitrary is also a polynomial function, without loss of generality we consider
We introduce some further notation and concepts. Let Then
and
are
-vector spaces, say
so
and
Note
is a generating set for
so without loss of generality we take
Thus each
is a linear combination of elements from B. See Cortini ([Citation5]) for this representation of
We mention that another computational approach to non-abelian special p-groups of exponent p is given by Grundhöfer and Stroppel ([Citation8]) in their investigations of Heisenberg groups. This approach is used to obtain information about automorphisms of these special p-groups.
We next introduce a directed graph in which the defining information of our groups is enclosed. Let be given by
and the linear combinations for
The vertices are the generators
and the directed edges are
For
can be determined from the graph.
Example II.3
G is full. G is isomorphic to
In this case B = T. For n = 4 we have
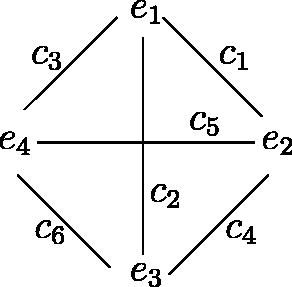
G is circular. G is isomorphic to
where we take
and other
For n = 4 we have
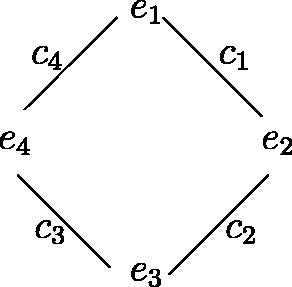
Consider G given by

where (with e5 = e1), and
Note
so
Thus G is isomorphic to
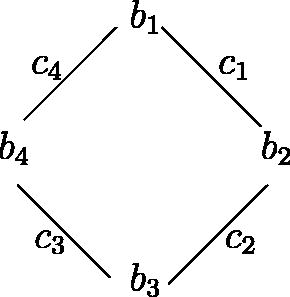 where
where Therefore G is circular.
In the next section, with the aid of this graphical representation, we determine new classes of non-abelian special p-groups of exponent p which are 1-ac and new classes which are not 1-ac. In these latter classes, is not a ring.
3. Main results
As usual,
Theorem III.1.
(Full) Let . Then G is 1-ac.
Proof.
Let As we have shown above, we may assume that
so we let
We also let
for
From
we have
for some
It follows that
So we have Furthermore,
while
From the linear independence of the cij, it follows that and hence
is forced to have the form
If we let
then
and
We put
so that
and
For
it follows similarly that
and so
Using
we get
so
and
For let
Using
we get
and
Thus we find for each
Now let
As above we find
and for
Hence
By induction, so
that is, G is 1-ac.
We may now assume For if n = 3, then
If s = 3 then from the above theorem, G is 1-ac. If s = 1 or s = 2, then from Theorem II.1,
is not a ring. For n = 2, s = 1 we are again finished using Theorem II.1. It should be mentioned that the “full” case
is the example of Dorda mentioned above.
Theorem III.2.
(Circular) Let G be circular, i.e., G is isomorphic to where we take
, and the other
. Then G is 1-ac if and only if
is a ring if and only if n is odd.
Proof.
We have where we take
where we take and identify
Let n be even, and define a function
by
and where
is arbitrary. We show
and show
is not a ring.
Now
Also,
We see that can be written as
that is,
for all
which implies
However,
from which it follows that
so
is not a ring.
Suppose now n is odd. As above we take and identify
as e1. We take
and show
Recall that we may assume without loss of generality that
for all
From we have
(identifying
), say
Next, from
we get
since
This forces
and by putting
we find that
where
Take where
and let
Now
and we show h(x) = 0 for all
that is
and G is 1-ac.
Let Then
where we take
and
which implies
But
for
so we have
We also find if
In fact, for
and
Since
for
We next show that From
and
we find that
say
But, for that is,
for some
This implies that
(1)
(1)
for all
(Note that
if at least one of k and
is zero.) The right-hand side of (1) equals the left-hand side for all
Hence,
so that
(2)
(2)
Hence, from (1), Put
and
which implies
So,
giving
(3)
(3)
From (2) and (3),
(4)
(4)
Now, put in (1). Then
since n is odd. From
we have
and hence also
By (4),
This shows that
So we now have that
We proceed by induction. Let and assume that
for any
and any
Then, without loss of generality, put
with all
Then
and
implies
We conclude that
Thus, and
□
In Theorem II.1 several sufficient conditions were stated for a group G to have not a ring. Most of these conditions lead to G being split. In Example 3.2 (2) of [Citation11], GAP was used to find a group H, not split, and a function
with
not a ring. In the next theorem we give a construction process for a large collection of groups
to construct a function
which shows
is not a ring.
First some notation. For we have a 2 × 2 determinant
For
similar to the wedge product in multilinear algebra.
Using the above definition of determinant we define a “wedge” product for by
a
-tuple.
For an abelian subgroup, A, of G, we choose a basis
for
and extend this to a basis
of
Thus without loss of generality we have
where
and
Theorem
III.3. (Wedge) Let as above with
. If there exist
such that
and
for at least one
then is not a ring.
Proof.
For suitable i.e.,
satisfying i) and ii), we will show that the function
defined by
is in
but not in
Moreover, we’ll show that, for some non-zero
which shows that
contains a non-distributive element, hence
is not a ring.
First we show that for arbitrary
Now, for suitable (those given by i) and ii)):
We show that also
This shows that By ii), there is an
such that
So
It follows that
showing that
is not a ring.□
Note that condition ii) is necessary here. Otherwise we could have chosen all and i) is still satisfied. But in this case f would be the zero function, hence distributive.
Example
III.4. Let G be given by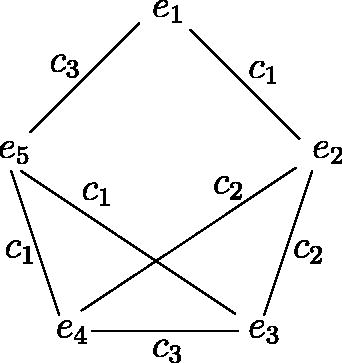
Then with
and
We have
and
Thus
is not a ring.
From Theorem II.1, if G has a maximal abelian normal subgroup A of order then
is not a ring. As an application of the wedge theorem we consider the case where a maximal abelian normal subgroup, A, has order
and G/A is not cyclic. As above we choose a basis
of
and get
For If
or
then from Theorem II.1,
is not a ring. Thus we take
for
Let
and
If
is linearly dependent over
then
and not all
So, from
we see that
is in A and
We have
and
otherwise
a contradiction. From the Wedge Theorem,
is not a ring. Thus we now take
to be linearly independent and similarly
is linearly independent. We have
Suppose say
say
not all
If
then
a contradiction to the linear independence of
We have
and
so
is not a ring. Consequently
or
is a ring.
So we have
Theorem
III.5. Let and let
, A abelian with
and
. If
then
is not a ring.□
We use the notation and definitions from the above discussion. When then
If then
or
Suppose
say
Let
and
so
hence
Let
and note
so
and
and
By using the basis,
we have
with
so when
we may take
When n = 4 we see that G is circular with n even so
is not a ring. The case for
remains open.
When and n = 4, then
since
and s = 6 is the full case. For n = 4 and s = 5 one finds via tedious calculations that G is 1-ac. The case n > 4 remains open.
In conclusion, we have identified several further classes of non-abelian p-groups, G, for which
is a ring if and only if G is 1-ac. However, the original conjecture as to whether this is true for all finite non-abelian p-groups,
remains open.
Acknowledgements
Portions of this research were done while the authors were visiting Johannes Kepler Universität, Linz, Austria. They wish to express their appreciation for the gracious hospitality and financial support provided.
Additional information
Funding
References
- Aichinger, E. (2006). The near-ring of congruence preserving functions on an expanded group. J. Pure Appl. Algebra 205(1):74–93. DOI: https://doi.org/10.1016/j.jpaa.2005.06.014.
- Aichinger, E., Lazić, M., Mudrinski, N. (2016). Finite generation of congruence preserving functions. Monatsh. Math. 181(1):35–62. DOI: https://doi.org/10.1007/s00605-015-0833-5.
- Chandy, A. J. (1971). Rings generated by the inner automorphisms of non-abelian groups. Proc. Amer. Math. Soc. 30(1):59–60. DOI: https://doi.org/10.2307/2038220.
- Tani, G. C. (1985). Automorphisms fixing every normal subgroup of a p-group. Bull. Un. Mat. Ital. B. 4:245–252.
- Cortini, R. (1998). On special p-groups. Boll. U. M. I. 8. 1-B:677–689.
- Dorda, A. (1977). Über Vollständigkeit bei endlichen Gruppen [PhD dissertation]. Wien: Tech. Universität.
- Gorenstein, D. (1968). Finite Groups. New York: Harper & Row.
- Grundhöfer, T., Stroppel, M. (2008). Automorphisms of Verardi groups; small upper triangular matrices over rings. Beiträge Algebra Geomet. 49:1–31.
- Hall, P., Higman, G. (1956). The p-length of a p-soluble group and reduction theorems for Burnside’s problem. Proc. London Math. Soc. s3-6(1):1–42. DOI: https://doi.org/10.1112/plms/s3-6.1.1.
- Kaarli, K., Pixley, A. F. (2001). Polynomial Completeness in Algebraic Systems. New York: Chapman & Hall/CRC.
- Maxson, C. J., Saxinger, F. (2018). Rings of congruence preserving functions. Monatsh. Math. 187(3):531–542. DOI: https://doi.org/10.1007/s00605-017-1105-3.
- Nöbauer, W. (1976). Über die affin vollständigen, endlich erzeugbaren. Monatsh. Math. 82(3):187–198. DOI: https://doi.org/10.1007/BF01526325.
- Verardi, L. (1997). A class of special p-groups. Arch. Math. 68(1):7–16. DOI: https://doi.org/10.1007/PL00000395.
