Completions of the Goldschmidt G₃-amalgam and alternating groups

Abstract

Here we prove that the alternating group of degree n is a faithful completion of the Goldschmidt G₃-amalgam if and only if

$n\notin \{1,2,3,4,5,7,8,9,11,12,16,17,19,23\}.$

Keywords:

• Alternating groups
• completetions
• Goldschmidt G3-amalgam

2020 Mathematics Subject Classification:

• 20D06

1 Introduction

In [3] Goldschmidt classified the primitive rank 2 amalgams of index (3, 3). These amalgams are now referred to as Goldschmidt amalgams. We recall that a rank 2 amalgam consists of groups P₁, P₂, and B together with group monomorphisms ${\phi }_1,{\phi }_2$ such that$${\phi }_1:B\to P_1\text{and}{\phi }_2:B\to P_2.$$

Suppressing the ${\phi }_i$, we refer to this amalgam as $\mathcal{A}(P_1,P_2,B)$. To say $\mathcal{A}(P_1,P_2,B)$ is primitive means that if $K\le B$ and ${\phi }_i(K)E{P}_i$ for i = 1, 2, then K = 1. If P₁ and P₂ are finite groups, then $\mathcal{A}(P_1,P_2,B)$ is called a finite amalgam whose index is $([P_1:{\phi }_1(B)],[P_2:{\phi }_2(B)])$. A group G is said to be a completion of $\mathcal{A}(P_1,P_2,B)$ if there exist group homomorphisms ${\psi }_i:P_i\to G$ i = 1, 2, for which ${\psi }_1{\phi }_1={\psi }_2{\phi }_2:B\to G$ and $G=〈im{\psi }_1,im{\psi }_2〉$. Should the ${\psi }_i,i=1,2$, be monomorphisms we then say this is a faithful completion. Here we shall only consider faithful completions, and so from now on will identify P_i with ${\psi }_i(P_i)$ and B with ${\psi }_i{\phi }_i(B)$. Hence we have $P_i\le G,i=1,2$ with $P_1\cap P_2\ge B$ and $〈P_1,P_2〉=G$ (though in all the completions we deal with we will have $P_1\cap P_2=B$). We remark that faithful completions of these Goldschmidt amalgams furnish, via their coset graphs, many examples of trivalent graphs.

The amalgams arrayed in [3] consist of fifteen amalgams, among which is the Goldschmidt G₃-amalgam. This amalgam has $P_1\cong \text{Sym}(4)\cong P_2$ and $B\cong \text{Dih}(8)$. A related Goldschmidt amalgam we shall briefly encounter is the $G_3^1$-amalgam. In this case we have $P_1\cong \text{Sym}(4)\times {\mathbb{Z}}_2\cong P_2$ with $B\cong \text{Dih}(8)\times {\mathbb{Z}}_2$. By $\text{Sym}(n)$ we mean the symmetric group of degree n and $\text{Dih}(8)$ the dihedral group of order 8. We also use $\text{Alt}(n)$ to denote the alternating group of degree n. Some small examples of faithful completions of these amalgams are ${\text{GL}}_3(2),\text{Alt}(6),$ and $\text{Sym}(6)$. Taking P₁ and P₂ to be the two standard maximal parabolic subgroups of ${\text{GL}}_3(2)$ yields a completion of the G₃-amalgam. In $\text{Sym}(6)$, letting P₁ and P₂ be, respectively, the centralizers of (1, 2) and $(1,2)(3,4)(5,6)$, we see that $\text{Sym}(6)$ is a completion of the $G_3^1$-amalgam. Intersection of P₁ and P₂ with $\text{Alt}(6)$ reveals that $\text{Alt}(6)$ is a completion of the G₃-amalgam.

It is completions of the G₃-amalgam we study here. Putting$$\mathcal{E}=\{1,2,3,4,5,7,8,9,11,12,16,17,19,23\}$$we state our main result.

Theorem 1.1.

Suppose that $n\in \mathbb{N}$. Then $\text{Alt}(n)$ is a completion of the Goldschmidt G₃-amalgam if and only if $n\notin \mathcal{E}$.

Earlier work on the Goldschmidt G₃-amalgam for alternating groups [7] verified that for all $n\le 24,\text{Alt}(n)$ is a completion precisely when $n\in \{6,10,13,14,15,18,20,21,22,24\}$. In this paper we shall demonstrate that $\text{Alt}(n)$ is a completion for all $n\ge 25$ from which Theorem 1.1 will then follow. Conder, in [2], investigated whether $G=\text{Sym}(n)$ is the automorphism group of some finite connected 5-arc transitive graph. Using the work of Lorimer [4], Conder rephrases his problem to ask whether there exists $H\cong \text{Sym}(4)\times {\mathbb{Z}}_2\le G$ and $a\in G$ such that

1. $a^2\in H$;

2. $G=〈\mathit{HaH}〉$; and

3. $[H:H\cap H^a]=3$.

If such a subgroup H and element a can be found, then $\text{Sym}(n)$ is a completion of the Goldschmidt $G_3^1$-amalgam, with $P_1=H,P_2=H^a$ and $B=H\cap H^a$, which then implies that $\text{Alt}(n)$ is a completion of the Goldschmidt G₃-amalgam (see Lemma 2.3). Now Conder’s method is to assemble various transitive representations for $\text{Sym}(4)\times {\mathbb{Z}}_2$ on $2,3,6,12,24,$ and 48 points and then taking appropriate combinations of these upon which a permutation that will fulfill the role of a is defined. This is achieved for all n of the form $n=84b+176c+177d+87$, where $b,c,d\in \mathbb{N}$. Since the Frobenius number of {84, 176, 177}- the largest integer such that it cannot be formed as $84b+176c+177d$ for $b,c,d\ge 0$ - is 2743, it means that, taking into account the additional 87, for all $n\ge 2831$, $\text{Sym}(n)$ and $\text{Alt}(n)$ are respective completions of the Goldschmidt $G_3^1$- and G₃- amalgams.

We briefly survey what else is known about completions of the Goldschmidt G₃-amalgam. Which sporadic simple groups (with the sole exception of the Monster) are completions is settled in [6] and [7]. While in [5] we have that ${\text{SL}}_3(q)$ and ${\text{PSL}}_3(q)$ are completions of the Goldschmidt G₃-amalgam if and only if $q\notin \{4,9\}$. For the unitary and orthogonal groups, ${\text{SU}}_3(q)$ and ${\text{PSU}}_3(q)$ are completions if and only if q is odd and $q\notin \{3,5\}$ and ${\text{SO}}_3(q)(\cong {\text{PSL}}_2(q))$ is a completion if and only if q or $\sqrt{q}$ is a prime and $q\equiv \pm 1(\text{mod}8)$.

This paper is arranged as follows—Section 2 begins with two elementary results concerning completions of the Goldschmidt G₃-amalgam. Then we introduce a particular type of graph, the orbit graph $\mathcal{O}(P_1,P_2,\Omega )$. Here P₁ and P₂ are subgroups of $\text{Sym}(\Omega )$, the group of permutations on Ω. This graph, courtesy of Lemma 2.6, can be used to determine whether $〈P_1,P_2〉$ is transitive on Ω or not. Definition 2.8 introduces the idea of twisting P₁ with respect to $(\Delta ,\Psi )$ where Δ and $\Psi$ are certain $(P_1\cap P_2)$-orbits of disjoint sets Ω and Γ. This idea, via Lemma 2.9, plays a central role in the recursive construction, presented in Section 3, and which underlies the proof of Theorem 1.1. We end Section 2 with Theorem 2.10, a classical result of Jordan’s.

In Section 3 we give a detailed account of a recursive construction for the case when $n\equiv 0(\text{mod}24)$. For the remaining congruences we list, in Section 4, the seed permutations which enable this construction to produce an example of $\text{Alt}(n)$ as a completion of the Goldschmidt G₃-amalgam. Further details on these seed permutations may be found in Section 3.

2 Some preliminary results

We begin with a hypothesis which lists all relevant facts about completions of the Goldschmidt $G_3^1$-amalgam which we use.

Hypothesis 2.1.

When G is a (faithful) completion of the Goldschmidt G₃-amalgam this means that G contains subgroups P₁ and P₂ such that

1. $P_1\cong \text{Sym}(4)\cong P_2$ and $B:=P_1\cap P_2\cong \text{Dih}(8)$;

2. $G=〈P_1,P_2〉$; and

3. $O_2(P_1)\cancel{=}{O}_2(P_2)$ (where $O_2(P_i)\cong {\mathbb{Z}}_2\times {\mathbb{Z}}_2$ is the largest normal 2-subgroup of P_i).

Our first result concerns involutions and completions of the Goldschmidt G₃-amalgam.

Lemma 2.2.

Suppose the group G is a completion of the Goldschmidt G₃-amalgam $\mathcal{A}(P_1,P_2,B)$. Then the involutions in $P_1\cup P_2$ are G-conjugate.

Proof.

By Hypothesis 2.1 we have $P_i\le G,i=1,2$ with $P_1\cap P_2=B\cong \text{Dih}(8)$ and $P_i\cong \text{Sym}(4)$. Now, for i = 1, 2 P_i has two conjugacy classes of involutions $C_i^{(1)}$ and $C_i^{(2)}$ with $B\cap C_i^{(1)}=O_2{(P_i)}^{♯}$. Since $O_2(P_1)\ne O_2(P_2)$ and $O_2(P_1)\cap O_2(P_2)\ne 1$, Lemma 2.2 follows. □

Next we see that a completion of the Goldschmidt $G_3^1$-amalgam, $\mathcal{A}(\text{Sym}(4)\times {\mathbb{Z}}_2,\text{Sym}(4)\times {\mathbb{Z}}_2,\text{Dih}(8)\times {\mathbb{Z}}_2)$, for $\text{Sym}(n)$ yields a completion of the Goldschmidt G₃-amalgam for $\text{Alt}(n)$.

Lemma 2.3.

If $\text{Sym}(n)$ is a completion of the Goldschmidt $G_3^1$-amalgam, then $\text{Alt}(n)$ is a completion of the Goldschmidt G₃-amalgam.

Proof.

Set $G=\text{Sym}(n)$ and $H=\text{Alt}(n)$. Let $P_1,P_2\le G$ be such that $P_i\cong \text{Sym}(4)\times {\mathbb{Z}}_2$ and $B=P_1\cap P_2\cong \text{Dih}(8)\times {\mathbb{Z}}_2$ with $〈P_1,P_2〉=G$. Also put $R_i=O^2(P_i)\cong \text{Alt}(4)$ and $Q_i=O_2(R_i)\cong {\mathbb{Z}}_2\times {\mathbb{Z}}_2$. Observe that $[B:B\cap H]=2$ for otherwise $B\le H$ and then $〈P_1,P_2〉\le H\ne G$, a contradiction. Further we must have $n\ge 5$. Note that $R_i\le H,i=1,2$ and that R₁ and R₂ normalize each other. Since $\mathcal{A}(P_1,P_2,B)$ is primitive, $Q_1\ne Q_2$. From $Q_i\le B\cap H,i=1,2$, we then see that $Q_1{Q}_2=B\cap H$. So $Q_1{Q}_2$ has order 8 and either $Q_1{Q}_2$ is abelian or $Q_1{Q}_2\cong \text{Dih}(8)$. If the former holds, then $Q_1{Q}_2=C_{P_i}(Q_i)=O_2(P_i)$ for i = 1, 2, giving the impossible $O_2(P_1)=O_2(P_2)$. Therefore, $B\cap H=Q_1{Q}_2\cong \text{Dih}(8)$. Since $[P_i:P_i\cap H]=2$ for i = 1, 2, we have $P_i\cap H\cong \text{Alt}(4)\times {\mathbb{Z}}_2$ or $\text{Sym}(4)$. The former possibility doesn’t contain a $\text{Dih}(8)$ subgroup and therefore $P_i\cap H\cong \text{Sym}(4)$. To complete the proof we must show that $H=〈P_1\cap H,P_2\cap H〉$. Now B normalizes $P_i\cap H,i=1,2$ and so$$〈P_1\cap H,P_2\cap H〉E{P}_1\cap H,P_2\cap H,B〉=G.$$

We recall that $n\ge 5$ so $\text{Alt}(n)$ is simple, whence $H=〈P_1\cap H,P_2\cap H〉$. □

In proving Theorem 1.1, for specified subgroups P₁ and P₂ of $G=\text{Alt}(n)$ we need to show that $〈P_1,P_2〉=G$. Not surprisingly, our first step is to prove that $〈P_1,P_2〉$ acts transitively on $\Omega =\{1,\dots ,n\}$. This leads us to consider a particular type of graph which we now define.

Definition 2.4.

Suppose G is a finite group acting on a finite set Ω with P₁ and P₂ being subgroups of G. Let $\{{\Delta }_1^{(1)},\dots ,{\Delta }_{\mathcal{l}}^{(1)}\}$ and $\{{\Delta }_1^{(2)},\dots ,{\Delta }_k^{(2)}\}$ be, respectively, the P₁- and P₂-orbits on Ω (and we shall regard these sets as being disjoint). The orbit graph of P₁ and P₂, $\mathcal{O}(P_1,P_2,\Omega )$, has vertex set $\{{\Delta }_1^{(1)},\dots ,{\Delta }_{\mathcal{l}}^{(1)},{\Delta }_1^{(2)},\dots ,{\Delta }_k^{(2)}\}$ with distinct vertices ${\Delta }_i^{(1)}$ and ${\Delta }_j^{(2)}$ adjacent whenever their intersection contains a $(P_1\cap P_2)$-orbit and the number of edges between them is the number of $(P_1\cap P_2)$-orbits in ${\Delta }_i^{(1)}\cap {\Delta }_j^{(2)}$.

We observe that $\mathcal{O}(P_1,P_2,\Omega )$ is a bipartite graph and that ${\Delta }_i^{(1)}$ and ${\Delta }_j^{(2)}$ being adjacent is equivalent to ${\Delta }_i^{(1)}\cap {\Delta }_j^{(2)}\ne \varnothing$ (as subsets of Ω). We next give two examples of Definition 2.4—note that in Example 2.5(ii) we have that P₁ and P₂ have the same orbit (namely Ω), but we consider them to be distinct vertices of $\mathcal{O}(P_1,P_2,\Omega )$.

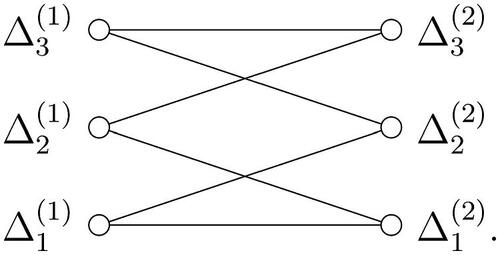
Example 2.5.

1. $\Omega =\{1,\dots ,21\},P_1=〈x,y,z〉,P_2=〈x,y,w〉$ and $B=P_1\cap P_2=〈x,y〉$ where

$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16);y:=(1,8)(2,3)(4,5)(6,7)(10,11)(13,17)(14,18)(19,20);z:=(1,11)(2,12)(5,9)(6,10)(7,8)(13,15)(14,16)(20,21)$; and$$w:=(1,17)(4,18)(5,14)(6,7)(8,13)(10,19)(11,20)(16,21).$$

Here, the B-orbits on Ω are ${\Omega }_1:=\{1,2,3,4,5,6,7,8\},{\Omega }_2:=\{9,10,11,12\},\mathrm{\backslash }\mathrm{\backslash }{\Omega }_3:=\{13,14,17,18\},{\Omega }_4:=\{15,16\},{\Omega }_5:=\{19,20\}$ and ${\Omega }_6:=\left\{21\right\}$. The P₁-orbits are ${\Delta }_1^{(1)}:={\Omega }_1\cup {\Omega }_2,{\Delta }_2^{(1)}:={\Omega }_3\cup {\Omega }_4,{\Delta }_3^{(1)}:={\Omega }_5\cup {\Omega }_6$ and the P₂-orbits are ${\Delta }_1^{(2)}:={\Omega }_1\cup {\Omega }_3,{\Delta }_2^{(2)}:={\Omega }_2\cup {\Omega }_5,{\Delta }_3^{(2)}:={\Omega }_4\cup {\Omega }_6$. So the orbit graph $\mathcal{O}(P_1,P_2,\Omega )$ is as given in Figure 1.

1. $\Omega =\{1,\dots ,24\},P_1=〈x,y,z〉,P_2=〈x,y,w〉$ and $B=P_1\cap P_2=〈x,y〉$ where$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24);$$$$y:=(1,8)(2,3)(4,5)(6,7)(9,16)(10,11)(12,13)(14,15)(17,24)(18,19)(20,21)(22,23);$$

$z:=(1,9)(2,10)(3,20)(4,19)(5,14)(6,13)(7,23)(8,24)(11,21)(12,22)(15,18)(16,17);$ and$$w:=(1,14)(2,19)(3,18)(4,10)(5,11)(6,22)(7,23)(8,15)(9,17)(12,21)(13,20)(16,24).$$

In this case, the B-orbits on Ω are $\{1,\dots ,8\},\{9,\dots ,16\}$ and $\{17,\dots ,24\}$ with both P₁ and P₂ acting transitively on Ω. Thus $\mathcal{O}(P_1,P_2,\Omega )$ is as shown in Figure 2.

Fig. 1 $\mathcal{O}(P_1,P_2,\Omega )$ for Example 2.5(i).

Fig. 2 $\mathcal{O}(P_1,P_2,\Omega )$ for Example 2.5(ii).

Example 2.5

(ii) plays a central role in proving Theorem 1.1.

Lemma 2.6.

Suppose $P_1,P_2\le \text{Sym}(\Omega )$, Ω a finite set. Then $〈P_1,P_2〉$ is transitive on Ω if and only if $\mathcal{O}(P_1,P_2,\Omega )$ is connected.

Proof.

Let $\{{\Delta }_1^{(1)},\dots ,{\Delta }_{\mathcal{l}}^{(1)}\}$ and $\{{\Delta }_1^{(2)},\dots ,{\Delta }_k^{(2)}\}$ be, respectively, the P₁- and P₂-orbits on Ω. Suppose $〈P_1,P_2〉$ acts transitively on Ω and let ${\Delta }_i^{(1)}$ and ${\Delta }_j^{(2)}$ be vertices of $\mathcal{O}(P_1,P_2,\Omega )$. Choose $\alpha \in {\Delta }_i^{(1)}$ and $\beta \in {\Delta }_j^{(2)}$. Then ${\alpha }^g=\beta$ for some $g\in 〈P_1,P_2〉$. Now $g=x_1{x}_2\dots x_m$ where $x_i\in P_1\cup P_2$, and, as $x_1\in P_1$ implies ${\Delta }_i^{(1)}{}^{x_1}={\Delta }_i^{(1)}$, we may assume $x_1\in P_2$. Put ${\alpha }^{x_1}=\gamma$ and let ${\Delta }_n^{(2)}$ be the P₂-orbit such that $\gamma \in {\Delta }_n^{(2)}$. Then $\alpha ={\gamma }^{x_1^{-1}}\in {\Delta }_i^{(1)}\cap {\Delta }_n^{(2)}$ whence ${\Delta }_i^{(1)}$ and ${\Delta }_n^{(2)}$ are adjacent in $\mathcal{O}(P_1,P_2,\Omega )$. Continuing in this fashion yields a path from ${\Delta }_i^{(1)}$ to ${\Delta }_j^{(2)}$. Therefore $\mathcal{O}(P_1,P_2,\Omega )$ is connected.

Now suppose that $\mathcal{O}(P_1,P_2,\Omega )$ is connected, and let $\alpha ,\beta \in \Omega$. Let $\alpha \in {\Delta }_{i_1}^{(1)},\beta \in {\Delta }_{i_k}^{(1)}$. We may find a sequence of P₁- and P₂-orbits in which the $\mathcal{l}$ th and $(\mathcal{l}+1)$ th orbits have non-empty intersections. This then gives $g\in 〈P_1,P_2〉$ for which ${\alpha }^g=\beta$, and so $〈P_1,P_2〉$ is transitive on Ω. □

Hypothesis 2.7.

Suppose G and H are subgroups of, respectively, $\text{Sym}(\Omega )$ and $\text{Sym}(\Gamma )$ where Ω and Γ are finite sets which are disjoint. Assume that G contains subgroups Q₁ and Q₂ with $C=Q_1\cap Q_2$ and that H contains subgroups R₁ and R₂ with $D=R_1\cap R_2$. Further assume that ${\theta }_i:Q_i\to R_i,i=1,2$, are isomorphisms for which ${\theta }_1(x)={\theta }_2(x)$ for all $x\in C$. For $x\in Q_i,i=1,2$ we regard x as a permutation on $\Omega \dot{\cup }\Gamma$ by letting x act as the identity on Γ and ${\theta }_i(x)$ as a permutation on $\Omega \dot{\cup }\Gamma$ by letting ${\theta }_i(x)$ act as the identity on Ω. Define subgroups $B,P_i,i=1,2$ of $\text{Sym}(\Omega \dot{\cup }\Gamma )$ by $P_i=\{x{\theta }_i(x)|x\in Q_i\}$ and $B=\{x{\theta }_i(x)|x\in C\}$.

We sometimes refer to $P_1,P_2,B$ as being the concatenation of $Q_1,Q_2,C$ and $R_1,R_2,D$. Note that $P_1\cong Q_1\cong R_1,P_2\cong Q_2\cong R_2$ and $B\cong C\cong D$.

Definition 2.8.

Assume Hypothesis 2.7 and let Δ and $\Psi$ be B-orbits of, respectively, Ω and Γ which are isomorphic B-sets. Now let $g=g(\Delta ,\Psi )\in \text{Sym}(\Omega \dot{\cup }\Gamma )$ be an involution in $C_{\text{Sym}(\Omega \dot{\cup }\Gamma )}(B)$ which interchanges Δ and $\Psi$ and fixes all other points of $\Omega \dot{\cup }\Gamma$. Then we refer to the conjugate $P_1^g$ as twisting P₁ (with respect to $(\Delta ,\Psi )$).

We note in Definition 2.8 that $P_1^g\cap P_2=B$.

Lemma 2.9.

Assume Hypothesis 2.7 holds, and use the notation given there. Let $g=g(\Delta ,\Psi )$ where Δ and $\Psi$ are B-orbits of Ω and Γ respectively which are isomorphic B-sets. Suppose $〈P_1,P_2〉$ is transitive on both Ω and Γ. Then $〈P_1^g,P_2〉$ is transitive on $\Omega \dot{\cup }\Gamma$ if and only if the edge in $\mathcal{O}(P_1,P_2,\Omega \dot{\cup }\Gamma )$ corresponding to Δ or the edge in $\mathcal{O}(P_1,P_2,\Omega \dot{\cup }\Gamma )$ corresponding to $\Psi$ is part of a cycle in the graph $\mathcal{O}(P_1,P_2,\Omega \dot{\cup }\Gamma )$.

Proof.

By Lemma 2.6, as $〈P_1,P_2〉$ is transitive on Ω and Γ, $\mathcal{O}(Q_1,Q_2,\Omega )$ and $\mathcal{O}(R_1,R_2,\Gamma )$ are both connected graphs. Suppose $\Delta \subseteq {\Delta }_p^{(1)}\cap {\Delta }_q^{(2)}$ and $\Psi \subseteq {\Psi }_r^{(1)}\cap {\Psi }_s^{(2)}$ where ${\Delta }_p^{(1)},{\Delta }_q^{(2)}$ are, respectively P₁- and P₂-orbits of Γ and ${\Psi }_r^{(1)},{\Psi }_s^{(2)}$ are respectively P₁- and P₂-orbits of Γ. So ${\Delta }_p^{(1)}$ and ${\Delta }_q^{(2)}$ are adjacent in $\mathcal{O}(Q_1,Q_2,\Omega )$ and ${\Psi }_r^{(1)}$ and ${\Psi }_s^{(2)}$ are adjacent in $\mathcal{O}(R_1,R_2,\Gamma )$. Since $g=g(\Delta ,\Psi )$ fixes all points in $(\Omega \dot{\cup }\Gamma )\backslash (\Delta \cup \Psi ),P_1^g$ has the same orbits on $\Omega \dot{\cup }\Gamma$ as P₁ except ${\Delta }_p^{(1)}$ and ${\Psi }_r^{(1)}$ get replaced by ${\Delta }_{p\prime }^{(1)}=({\Delta }_p^{(1)}\backslash \Delta )\cup \Psi$ and ${\Psi }_{r\prime }^{(1)}=({\Psi }_r^{(1)}\backslash \Psi )\cup \Delta$. Thus $\Delta \subseteq {\Delta }_q^{(2)}\cap {\Psi }_{r\prime }^{(1)}$ and $\Psi \subseteq {\Psi }_s^{(2)}\cap {\Delta }_{p\prime }^{(1)}$, whence ${\Delta }_q^{(2)}$ and ${\Psi }_{r\prime }^{(1)}$ are adjacent, as are ${\Psi }_s^{(2)}$ and ${\Delta }_{p\prime }^{(1)}$ in $\mathcal{O}(P_1,P_2,\Omega \dot{\cup }\Gamma )$. Since $〈P_1^g,P_2〉$ is transitive on $\Omega \dot{\cup }\Gamma$ if and only if $\mathcal{O}(P_1^g,P_2,\Omega \dot{\cup }\Gamma )$ is connected, the lemma now follows. □

The following theorem is a classical one of Jordan’s, which appears as Theorem 13.9 in [9]. This theorem suffices for our work. However, in [8], a generalization of this result is needed to deal with some of the other cases.

Theorem 2.10.

(Jordan) Let G be a primitive permutation group of degree n with a cycle of degree $p^{\lambda }>1$ where p is prime. If $n>p^{\lambda }+4$, then $G=\text{Alt}(n)$ or $G=\text{Sym}(n)$.

3 A recursive construction

Put $G=\text{Alt}(n)$ and let $\Omega =\{1,\dots ,n\}$ be the standard G-set. Bearing in mind Lemma 2.2, we are looking for G-conjugate involutions which generate appropriate $\text{Sym}(4)$ subgroups of G. Thus we seek conjugate involutions x, y, z, and w of G such that the following is satisfied.

Hypothesis 3.1.

1. ${(xy)}^2$ is conjugate to x;

2. $z\in N_G(〈x,{(xy)}^2〉)$ and zx = xz;

3. $w\in N_G(〈y,{(xy)}^2〉)$ and wy = yw;

4. zy and wx both have order 3; and

5. $G=〈x,y,z,w〉$

These conditions will ensure that for $B=〈x,y〉,P_1=〈x,y,z〉$ and $P_2=〈x,y,w〉$ we have $P_1\cap P_2=B\cong \text{Dih}(8)$ and $P_i\cong \text{Sym}(4),i=1,2$.

As indicated earlier Example 2.5(ii) will be important, one reason being given in our next result.

Lemma 3.2.

Let $x,y,z,w,P_1$, and P₂ be as in Example 2.5(ii). Then $P_i\cong \text{Sym}(4),i=1,2,P_1\cap P_2\cong \text{Dih}(8)$ and $G=〈P_1,P_2〉$. Thus (P₁, P₂) yields $\text{Alt}(24)$ as a completion of the Goldschmidt G₃-amalgam.

Proof.

It is straightforward to verify Hypothesis 3.1(i)–(iv) for $x,y,z,w$. So it remains to show that (v) holds. Since $\mathcal{O}(P_1,P_2,\Omega )$ is connected, Lemma 2.6 implies $〈P_1,P_2〉$ acts transitively on Ω. Calculation reveals that $h={[w,z]}^{x}y[w,z]$ has cycle type $5^1{.19}^1$. So $h^5\in 〈P_1,P_2〉$ is a 19-cycle. Hence, all the points of Ω in this 19-cycle either lie in the same block of a $〈P_1,P_2〉$-system of imprimitivity or they all lie in separate blocks. So any $〈P_1,P_2〉$-system of imprimitivity must either have block size at least 19 or at least 19 blocks. Since $〈P_1,P_2〉$ acts transitively on Ω and $\left|\Omega \right|=24$, we conclude that $〈P_1,P_2〉$ acts primitively on Ω. Furthermore, the presence of a 19-cycle, by Theorem 2.10, confirms $〈x,y,z,w〉=G$, so proving the lemma. □

We are now in a position to expand on the details of the recursive construction. Now Example 2.5(ii) shows $\mathcal{O}(P_1,P_2,\Omega )$ where $\Omega =\{1,\dots ,24\}$ has cycles and hence Lemma 2.9 becomes available to us. Put $G_m=\text{Alt}(m)$, acting on ${\Omega }_m=\{1,\dots ,m\}$ and suppose $Q_1^{(m)},Q_2^{(m)},C^{(m)}$ are subgroups of G_m with $Q_i^{(m)}\cong \text{Sym}(4),i=1,2$ and $Q_1^{(m)}\cap Q_2^{(m)}=C^{(m)}\cong \text{Dih}(8)$ with $〈Q_1^{(m)},Q_2^{(m)}〉=G_m$ (so G_m is a completion of the Goldschmidt G₃-amalgam). Also let $H=\text{Alt}(24)$ with H acting upon $\Gamma =\{m+1,\dots ,m+24\}$ with $R_1,R_2,D$ subgroups of H such that $(R_1,R_2,D)$ is the completion given in Example 2.5 ($R_i\cong \text{Sym}(4),R_1\cap R_2=D\cong \text{Dih}(8)$). Since the D-orbits on Γ are regular, to employ Definition 2.8 we require that $C^{(m)}$ has a regular orbit on Ω_m . So we further assume that this is the case, letting $\Delta =\{1,\dots ,8\}$ be such a regular $C^{(m)}$-orbit (we can achieve this by conjugating the $Q_i^{(m)})$. Let $x_m,y_m,z_m,w_m$ be the generators for G_m as given in Hypothesis 3.1 which give $Q_i^{(m)}$ and $C^{(m)}$. So $Q_1^{(m)}=〈x_m,y_m,z_m〉,Q_2^{(m)}=〈x_m,y_m,w_m〉$ and $C^{(m)}=〈x_m,y_m〉$. The corresponding generators for H are $x\prime ,y\prime ,z\prime ,w\prime$ where $R_1=〈x\prime ,y\prime ,z\prime 〉,R_2=〈x\prime ,y\prime ,w\prime 〉$ and $D=〈x\prime ,y\prime 〉$ and $\Psi =\{m+1,\dots ,m+8\}$ is a regular D-orbit upon which, restricted to $\Psi ,x\prime =(m+1,m+2)(m+3,m+4)(m+5,m+6)(m+7,m+8),y\prime =(m+1,m+8)(m+2,m+3)(m+4,m+5)(m+6,m+7)$.

Put $\Omega ={\Omega }_m\dot{\cup }\Gamma$. Then we may define subgroups $P_1,P_2\le \text{Sym}(\Omega )$ and $B=P_1\cap P_2$ as in Hypothesis 2.7. Thus we have $P_i=\text{Sym}(4)$ and $B\cong \text{Dih}(8)$. Now take$$g(\Delta ,\Psi )=(1,m+1)(2,m+2)(3,m+3)(4,m+4)(5,m+5)(6,m+6)(7,m+7)(8,m+8)\in \text{Sym}(\Omega )$$

Then $g(\Delta ,\Psi )$ satisfies the conditions of Definition 2.8 and so we may twist P₁ with respect to $(\Delta ,\Psi )$. Because of Lemma 2.9 we have that $〈P_1^g,P_2〉$ is a transitive subgroup of $\text{Sym}(\Omega )$ which is actually a subgroup of $\text{Alt}(\Omega )$. Theorem 1.1 is proved (constructively) by beginning with an appropriate G_m and appropriate $Q_1^{(m)},Q_2^{(m)},C^{(m)}$, and then “adding” copies of H. Thus the proof must consider twenty four cases given by the congruence of $n(\text{mod}24)$ where $n=m+24k$. For the full details we direct the reader to [8] or to the seed permutations given in Section 4 and here we will look at starting with m = 24 and repeatedly “adding” copies of H. We remark that recursive constructions of this ilk have also been employed in [1] and [6].

Definition 3.3.

If we begin with $G=\text{Alt}(m)$ and recursively add on copies of H, then any points greater than m will be denoted with numbers $\{1,\dots ,24\}$ with an appropriate subscript attached. Explicitly, the number $m+24i+j$ will be denoted $j_{i+1}$ for $j\in \{1,\dots ,24\}$. In simpler terms, this will see the ith set of 24 points to be labeled $\{1_i,\dots ,{24}_i\}$ for $1\le i\le k$. The points $\{1,\dots ,m\}$ can be considered as having the subscript 0 attached, which will be useful in writing down the cycle decomposition of z but not generally noted otherwise.

The labels j_i and $m+24(i-1)+j$ will be interchangeable depending on which is most convenient.

Theorem 3.4.

For $n\equiv 0(\text{mod}24),\text{Alt}(n)$ is a completion of the Goldschmidt G₃-amalgam.

Proof.

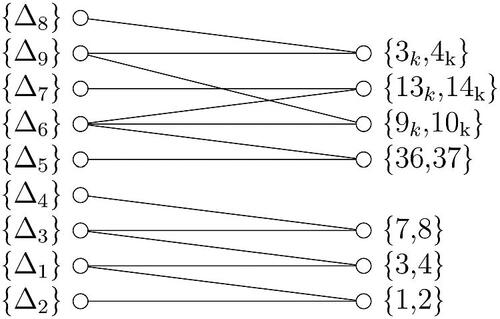
Starting at m = 48, we take the following elements for $G=\text{Alt}(48+24k)$ $$\begin{array}{c}{x}_{48+24k}:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(22,23)(24,25)(28,29)\\ (30,31)(32,33)(34,35)(36,37)(38,39)(40,41)(42,43)\\ \prod _{i=1}^k(1_i,2_i)(3_i,4_i)(5_i,6_i)(7_i,8_i)(9_i,{10}_i)({11}_i,{12}_i)({13}_i,{14}_i)({15}_i,{16}_i)({17}_i,{18}_i)\\ ({19}_i,{20}_i)({21}_i,{22}_i)({23}_i,{24}_i)\\ y_{48+24k}:=(1,8)(2,3)(4,5)(6,7)(10,11)(13,17)(14,18)(19,20)(22,24)(26,27)\\ (28,35)(29,30)(31,32)(33,34)(37,38)(40,44)(41,45)(46,47)\\ \prod _{i=1}^k(1_i,8_i)(2_i,3_i)(4_i,5_i)(6_i,7_i)(9_i,{16}_i)({10}_i,{11}_i)({12}_i,{13}_i)({14}_i,{15}_i)\\ ({17}_i,{24}_i)({18}_i,{19}_i)({20}_i,{21}_i)({22}_i,{23}_i)\\ z_{48+24k}:=(1_k,38)(2_k,39)(5_k,36)(6_k,37)(7_k,8_k)(9,10)(13,16)(14,15)(20,21)\\ (22,35)(23,34)(24,30)(25,31)(26,27)(28,29)(40,42)(41,43)(47,48)\\ \prod _{i=1}^k(1_{i-1},9_i)(2_{i-1},{10}_i)(3_{i-1},{20}_i)(4_{i-1},{19}_i)(5_{i-1},{14}_i)(6_{i-1},{13}_i)(7_{i-1},{23}_i)\\ (8_{i-1},{24}_i)({11}_i,{21}_i)({12}_i,{22}_i)({15}_i,{18}_i)({16}_i,{17}_i)\\ w_{48+24k}:=(1,17)(4,18)(5,14)(6,7)(8,13)(10,19)(11,20)(16,21)(22,26)(24,27)\\ (28,44)(31,45)(32,41)(33,34)(35,40)(37,46)(38,47)(43,48)\\ \prod _{i=1}^k(1_i,{14}_i)(2_i,{19}_i)(3_i,{18}_i)(4_i,{10}_i)(5_i,{11}_i)(6_i,{22}_i)(7_i,{23}_i)(8_i,{15}_i)(9_i,{17}_i)\\ ({12}_i,{21}_i)({13}_i,{20}_i)({16}_i,{24}_i)\end{array}$$

For convenience we will denote $x_{48+24k},y_{48+24k},z_{48+24k},w_{48+24k}$ simply as $x,y,z,w$ throughout this proof. Put $\Omega =\{1,\dots ,48+24k\}$.

We consider $H=〈{(\mathit{zyx})}^w,z,x〉\le 〈x,y,z,w〉$ and show that H fixes 19 and is transitive on $\Omega \backslash \left\{19\right\}$. Hence $〈x,y,z,w〉$ is 2-transitive on Ω. In fact, the generator x is not necessary here but it will simplify the proof. First we look at ${(\mathit{zyx})}^w$ and see that$$\begin{array}{c}{(\mathit{zyx})}^w=(19)(22)(24)(1,5,21)(2,{21}_1,{16}_1)(3,6_1,1_1)(4,8,15)(6,{12}_1,{17}_1)(7,5_1,2_1)\\ (9,12,20)(10,11,16)(13,3_1,{20}_1)(14,{24}_1,7_1)(17,8_1,{13}_1)(18,9_1,4_1)\\ (23,41,30)(25,34,40)(26,29,33)(27,44,45)(28,32,42)(31,35,48)\\ (36,{18}_k,{14}_k)(37,38,43)(39,{10}_k,{22}_k)(46,{15}_k,{11}_k)(47,{23}_k,{19}_k)\\ \prod _{i=1}^{k-1}({10}_i,9_{i+1},4_{i+1})({11}_i,{24}_{i+1},7_{i+1})({14}_i,8_{i+1},{13}_{i+1})({15}_i,3_{i+1},{20}_{i+1})\\ ({18}_i,6_{i+1},1_{i+1})({19}_i,{21}_{i+1},{16}_{i+1})({22}_i,5_{i+1},2_{i+1})({23}_i,{12}_{i+1},{17}_{i+1})\end{array}$$

The following subgraphs of $\mathcal{O}(〈{(\mathit{zyx})}^w〉,〈z〉,\Omega )$ will help to show that H is transitive on $\Omega \backslash \left\{19\right\}$, where the orbits of $〈{(\mathit{zyx})}^w〉$ are on the left hand side and orbits of $〈z〉$ are on the right. For the moment we assume $k\ge 2$, dealing with k = 0, 1 later.

Looking at Figures 3 and 4, the following are subsets of H-orbits:$${\Delta }_1:=\{1,3,5,9,10,11,12,13,16,18,20,21,1_1,3_1,4_1,6_1,9_1,{20}_1\},$$$${\Delta }_2:=\{2,6,17,8_1,{12}_1,{13}_1,{16}_1,{17}_1,{21}_1\},$$$${\Delta }_3=\{4,8,14,15,{24}_1,7_1\},$$$${\Delta }_4:=\{7,2_1,5_1\},$$$${\Delta }_5:=\{22,23,24,25,26,27,28,29,30,31,32,33,34,35,37,38,40,41,42,43,44,45,47,48,\mathrm{\backslash }\mathrm{\backslash }{1}_k,6_k,{19}_k,{23}_k\}$$$${\Delta }_6:=\{36,39,46,2_k,5_k,{10}_k,{11}_k,{12}_k,{14}_k,{15}_k,{16}_k,{17}_k,{18}_k,{21}_k,{22}_k\},$$$${\Delta }_7:=\{7_k,8_k,{13}_k,{24}_k\},$$

Fig. 3 Orbit calculations.

Fig. 4 Orbit calculations.

${\Delta }_8:=\{3_k,{20}_k\}$ and$${\Delta }_9:=\{4_k,9_k\}$$

However, when also considering orbits of $〈x〉$, we can connect these further as in Figure 5, which shows that ${\Delta }_1\cup {\Delta }_2\cup {\Delta }_3\cup {\Delta }_4$ and ${\Delta }_5\cup {\Delta }_6\cup {\Delta }_7\cup {\Delta }_8\cup {\Delta }_9$ are subsets of H-orbits, with $\{1_k,\dots ,{24}_k\}\subset {\Delta }_5\cup {\Delta }_6\cup {\Delta }_7\cup {\Delta }_8\cup {\Delta }_9$.

Fig. 5 Orbit calculations.

When $1\le i\le k-1$, Figure 6 shows that the following are subsets of H-orbits.$${\Lambda }_{i_1}:=\{1_i,6_i,{10}_i,{14}_i,4_{i+1},8_{i+1},9_{i+1},{13}_{i+1}\}$$$${\Lambda }_{i_2}:=\{8_i,{11}_i,{12}_i,{13}_i,{16}_i,{17}_i,{21}_i,{22}_i,2_{i+1},5_{i+1},7_{i+1},{24}_{i+1}\}$$$${\Lambda }_{i_3}:=\{4_i,9_i,{15}_i,{18}_i,1_{i+1},3_{i+1},6_{i+1},{20}_{i+1}\}$$$${\Lambda }_{i_4}:=\{{19}_i,{23}_i,{12}_{i+1}{16}_{i+1},{17}_{i+1},{21}_{i+1}\}$$$${\Lambda }_{i_5}:=\{7_i,{24}_i\}$$$${\Lambda }_{i_6}:=\{3_i,{20}_i\}$$$${\Lambda }_{i_7}:=\{2_i,5_i\}$$

Fig. 6 Orbit calculations.

Now, considering the orbits of $〈x〉$ we can see that ${\Lambda }_i:=\{1_i,\dots ,{24}_i,1_{i+1}\}$ is a subset of an H-orbit with the help of Figure 7. Clearly, there are more points with subscript i + 1 that we could include, but all we require is that there is at least one, hence $1_{i+1}\in {\Lambda }_i\cap {\Lambda }_{i+1}$ and therefore, ${\cup }_{i=1}^{k-1}{\Lambda }_i\subset \Gamma$, where Γ is an H-orbit. Since ${\Delta }_1\cup {\Delta }_2\cup {\Delta }_3\cup {\Delta }_4$ contains points with subscript 1- all of which are in ${\Lambda }_1\subseteq \Gamma$, so ${\Delta }_1\cup {\Delta }_2\cup {\Delta }_3\cup {\Delta }_4\subseteq \Gamma$ also. Finally, ${\Lambda }_{k-1}\cap ({\Delta }_5\cup {\Delta }_6\cup {\Delta }_7\cup {\Delta }_8\cup {\Delta }_9)=\left\{1_k\right\}$ so ${\Delta }_5\cup {\Delta }_6\cup {\Delta }_7\cup {\Delta }_8\cup {\Delta }_9\subseteq \Gamma$ and $\Gamma =\{1,\dots ,48+24k\}\backslash \left\{19\right\},\left\{19\right\}$ are H-orbits. Consequently $〈x,y,z,w〉$ is 2-transitive when $k\ge 2$.

Fig. 7 Orbit calculations.

Next we look at the case k = 0. For k = 0, consider ${(\mathit{zyx})}^{w}z\in H$,$$\begin{array}{c}{(\mathit{zyx})}^{w}z=(19)(1,36,3,17,5,20,10,11,13,15,4,7,2,48,25,23,43,6,39,18,8,14,46,\\ 16,9,12,21,38,41,24,30,34,42,29,33,27,44,45,26,28,32,40,31,22,35,\\ 47,37).\end{array}$$

This is a 47-cycle, so clearly H is transitive on $\Omega \setminus \left\{19\right\}$.

Finally we consider the case k = 1. Then

$$\begin{array}{c}{(\mathit{zyx})}^{w}z=(19)(1,62,53,39,2,59,46,66,5,20,10,11,13,51,3,37,49,68,16,9,12,21,\\ 57,52,18)(4,72,56,6,70,50,71)(7,36,63,69,65,61,17,55,15,67,48,25,23,\\ 43,54,38,41,24,30,34,42,29,33,27,44,45,26,28,32,40,31,22,35,47)(8,\\ 14)(58,60,64).\end{array}$$

Here, z contains the transpositions $(2,58),(4,67),(8,72)$ and (60, 70). These transpositions (ignoring the cycle (19)) connecting the first and fifth cycle of ${(\mathit{zyx})}^{w}z$, second and third, fourth and second and fifth and second cycles respectively. That is to say, they contain one point from each therefore proving that all of the points in both of those cycles must belong to the same H-orbit- so forming the H-orbit $\{1,\dots ,72\}\backslash \left\{19\right\}$.

Consequently for all $k\ge 0$ $〈x,y,z,w〉$ is 2-transitive.

Now we are in a position to demonstrate that $G=〈x,y,z,w〉$, using the element zw. For the moment we assume that $k\cancel{=}0$.

Observing the cycle decomposition of zw leads to us noticing that it follows patterns depending on the value of $k(\text{mod}2)$. When $k\equiv 0(\text{mod}2)$, we analyze the cycles in zw. Here, the underlined parts of the cycle are “repeated,” only with the subscript on the points in subsequent or previous repeated parts being respectively higher or lower by the same amount with each repetition;$$(2,\underset{¯}{4_1,2_2},4_3,2_4,\dots \dots ,4_{k-3},2_{k-2},\underset{¯}{4_{k-1},2_k},39,\underset{¯}{{19}_k,{10}_{k-1}},{19}_{k-2},{10}_{k-1},\dots \dots ,{19}_4,{10}_3,\underset{¯}{{19}_2,{10}_1})$$$$(4,\underset{¯}{2_1,4_2},2_3,4_4,\dots ,2_{k-3},4_{k-2},\underset{¯}{2_{k-1},4_k},\underset{¯}{{10}_k,{19}_{k-1}},{10}_{k-2},{19}_{k-3},\dots ,{10}_4,{19}_3,\underset{¯}{{10}_2,{19}_1},18)$$$$(3,{13}_1,7,\underset{¯}{7_1},7_2,\dots ,7_{k-1},\underset{¯}{7_k},{15}_k,3_k,{18}_k,8_k,\underset{¯}{{23}_k},{23}_{k-1},\dots ,{23}_2,\underset{¯}{{23}_1},6,{20}_1)$$$$(5,\underset{¯}{1_1,{17}_2,{24}_2,{15}_1,3_1,{13}_2,{22}_1,{21}_1,5_1},1_2,\dots ,1_{k-1},\underset{¯}{{17}_k,{24}_k,{15}_{k-1},3_{k-1},{13}_k,{22}_{k-1},{21}_{k-1},5_{k-1},1_k},47,43,32,41,48,38,\underset{¯}{{14}_k,}\underset{¯}{{11}_{k-1},{12}_{k-1},6_{k-1},{20}_k,{18}_{k-1},8_{k-1},{16}_k,9_k},{14}_{k-1},\dots ,{14}_2,\underset{¯}{{11}_1,{12}_1,6_1,{20}_2,{18}_1,8_1,{16}_2,9_2,{14}_1},14,15)$$

$(22,40,42,35,26,24,30,27)$, (9, 19, 10), (23, 33, 34), (25, 45, 31), (28, 29, 44),$$(36,{11}_k,{12}_k,6_k,46,37,{22}_k,{21}_k,5_k),(1,{17}_1,{24}_1,13,21,11,20,16,8,{16}_1,8,{16}_1,9_1)$$

So, by counting the lengths of these cycles, we see zw is an element of cycle type ${(18k-7)}^1.{(2k+9)}^1.{(2(1+k))}^2{.12}^1{.9}^1{.8}^1{.3}^4{.1}^1$ for which we can see the first two cycles are of odd length and the third will be divisible by 2 but not 4. Overall, this means that the only cycle of length divisible by 8 is the 8-cycle above.

When $k\equiv 1\text{mod}2$ we have the following cycles;$$(2,\underset{¯}{4_1,2_2},4_3,\dots ,4_{k-2},\underset{¯}{2_{k-1},4_k},\underset{¯}{{10}_k,{19}_{k-1}},{10}_{k-2},\dots ,{10}_3,\underset{¯}{{19}_2,{10}_1})$$$$(4,\underset{¯}{2_1,4_2},2_3,\dots ,2_{k-2},\underset{¯}{4_{k-1},2_k},39,\underset{¯}{{19}_k,{10}_{k-1}},{19}_{k-2},\dots ,{19}_3,\underset{¯}{{10}_2,{19}_1},18)$$$$(6,{20}_1,3,{13}_1,7,\underset{¯}{7_1},7_2,\dots ,7_{k-1},\underset{¯}{7_k},{15}_k,3_k,{18}_k,8_k,\underset{¯}{{23}_k},{23}_{k-1},\dots ,{23}_2,\underset{¯}{{23}_1})$$$$(5,\underset{¯}{1_1,{17}_2,{24}_2,{15}_1,3_1,{13}_2,{22}_1,{21}_1,5_1},1_2,\dots \dots ,1_{k-1},\underset{¯}{{17}_k,{24}_k,{15}_{k-1},3_{k-1},{13}_k,{22}_{k-1},{21}_{k-1},5_{k-1},1_k},47,43,32,41,48,38,\underset{¯}{{14}_k,}\underset{¯}{{11}_{k-1},{12}_{k-1},6_{k-1},{20}_k,{18}_{k-1},8_{k-1},{16}_k,9_k},{14}_{k-1},\dots ,{14}_2,\underset{¯}{{11}_1,{12}_1,6_1,{20}_2,{18}_1,8_1,{16}_2,9_2,{14}_1},14,15)$$

$(22,40,42,35,26,24,30,27)$, (9, 19, 10), (23, 33, 34), (25, 45, 31), (28, 29, 44),

$(36,{11}_k,{12}_k,6_k,46,37,{22}_k,{21}_k,5_k)$, $(1,{17}_1,{24}_1,13,21,11,20,16,8,{16}_1,8,{16}_1,9_1)$ All of this gives a cycle type of ${(18k-7)}^1.{(2k+9)}^1.{(5+2(k-1))}^1.{(3+2(k-1))}^1{.12}^1{.9}^1{.8}^1{.3}^4{.1}^1$, for which we can see that the first four cycles will all be of odd length and no others divisible by 8 other than the 8 cycle.

In both cases, for some large odd number f, ${(zw)}^{4f}=(22,26)(24,40)(27,35)(30,42)=:c$ and $c^y=(24,27)(22,44)(26,28)(29,42)$ so $c{c}^y=(22,28,26,44)(24,40,27,35)(30,29,42)$ and ${(c{c}^y)}^4$ is a 3-cycle, sufficient by Theorem 2.10 to confirm that $G=〈x,y,z,w〉$.

It remains to deal with the exceptional case k = 0. Here, $\mathit{xzw}=(1,39,17)(2,47,43,35,23,40,48,38)(3,18,4)(5,46,37,14,21,11,12,20,16)(6,36,7)(8,13,15)(10,19)(22,33,41,42,32,34,26,24,45,31,27)(25,30)(28,44)$, of cycle type ${11}^1{.9}^1{.8}^1{.3}^4{.2}^2{.1}^2$ and ${(\mathit{xzw})}^{9.8}$ is an 11-cycle, sufficient by Theorem 2.10 to confirm that $G=〈x,y,z,w〉$.

So for all $k\ge 0,G=〈x,y,z,w〉$, which completes the proof of Theorem 1.1 in the case $n\equiv 0(\text{mod}24)$. □

4 Seeds for the recursive construction

The following generators provide a starting point for the recursive method of adding 24 points for each case modulo 24. In each case $\{1,\dots ,8\}$ is a regular $〈x,y〉$-orbit with $x=(1,2)(3,4)(5,6)(7,8)$ and $y=(1,8)(2,3)(4,5)(6,7)$ on this orbit. So, we can take $\Delta =\{1,\dots ,8\}$ and $\Psi =\{m+1,\dots ,m+8\}$ as the two orbits to twist by.

When $n\equiv 0(\text{mod}24)$, we may start at m = 24 with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24)$$$$y:=(1,8)(2,3)(4,5)(6,7)(9,16)(10,11)(12,13)(14,15)(17,24)(18,19)(20,21)(22,23)$$$$z:=(1,10)(2,9)(3,20)(4,19)(5,13)(6,14)(7,23)(8,24)(11,17)(12,18)(15,22)(16,21)$$$$w:=(1,10)(2,22)(3,23)(4,14)(5,15)(6,19)(7,18)(8,11)(9,21)(12,17)(13,24)(16,20)$$

When $n\equiv 1(\text{mod}24)$, we may start at m = 25 with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)$$$$y:=(1,8)(2,3)(4,5)(6,7)(10,11)(14,15)(17,21)(18,22)(19,20)(23,24)$$$$z:=(1,12)(2,11)(3,4)(5,10)(6,9)(13,14)(17,19)(18,20)(21,22)(24,25)$$$$w:=(1,17)(2,3)(4,18)(5,22)(8,21)(10,24)(11,23)(13,16)(14,19)(15,20)$$

When $n\equiv 2(\text{mod}24)$, we may start at m = 26 with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24)$$$$y:=(1,8)(2,3)(4,5)(6,7)(9,16)(10,11)(12,13)(14,15)(18,19)(21,25)(22,26)(23,24)$$$$z:=(1,8)(2,7)(3,5)(4,6)(9,10)(11,18)(12,17)(15,20)(16,19)(21,24)(22,23)(25,26)$$$$w:=(1,25)(4,26)(5,22)(6,7)(8,21)(9,14)(10,12)(11,13)(15,16)(17,20)(18,23)(19,24)$$

When $n\equiv 3(\text{mod}24)$, we may start at m = 27 with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)$$$$y:=(1,8)(2,3)(4,5)(6,7)(10,11)(14,15)(17,21)(18,22)(23,24)(25,26)$$$$z:=(1,13)(2,14)(3,4)(5,15)(6,16)(9,10)(17,20)(18,19)(23,27)(25,26)$$$$w:=(1,18)(2,3)(4,17)(5,21)(8,22)(10,24)(11,23)(14,26)(15,25)(19,27)$$

When $n\equiv 4(\text{mod}24)$, we may start at m = 28 with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)$$$$y:=(1,8)(2,3)(4,5)(6,7)(10,11)(14,15)(17,21)(18,22)(23,24)(25,26)$$$$z:=(1,2)(3,10)(4,9)(7,12)(8,11)(15,16)(17,19)(18,20)(24,28)(26,27)$$$$w:=(1,18)(2,3)(4,17)(5,21)(8,22)(10,23)(11,24)(14,25)(15,26)(20,27)$$

When $n\equiv 5(\text{mod}24)$, we may start at m = 29 with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24)$$$$y:=(1,8)(2,3)(4,5)(6,7)(9,16)(10,11)(12,13)(14,15)(18,19)(21,25)(22,26)(27,28)$$$$z:=(1,18)(2,17)(5,20)(6,19)(7,8)(9,15)(10,16)(11,14)(12,13)(21,23)(22,24)(28,29)$$$$w:=(1,2)(3,8)(4,6)(5,7)(9,22)(10,11)(12,21)(13,25)(16,26)(18,28)(19,27)(24,29)$$

When $n\equiv 6(\text{mod}24)$, we may start at m = 30 with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(15,16)(17,18)(19,20)(21,22)(23,24)(25,26)(27,28)(29,30)$$$$y:=(1,8)(2,3)(4,5)(6,7)(9,13)(10,14)(15,22)(16,17)(18,19)(20,21)(23,30)(24,25)(26,27)(28,29)$$$$z:=(1,23)(2,24)(3,18)(4,17)(5,28)(6,27)(7,21)(8,22)(9,11)(10,12)(15,30)(16,29)(19,25)(20,26)$$$$w:=(1,13)(4,14)(5,10)(6,7)(8,9)(11,12)(15,16)(17,22)(18,20)(19,21)(23,24)(25,30)(26,28)(27,29)$$

When $n\equiv 7(\text{mod}24)$, we may start at m = 31 with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24)(25,26)(27,28)$$$$y:=(1,8)(2,3)(4,5)(6,7)(9,16)(10,11)(12,13)(14,15)(17,24)(18,19)(20,21)(22,23)(26,27)(29,30)$$$$z:=(3,25)(4,26)(5,6)(7,27)(8,28)(9,15)(10,16)(11,14)(12,13)(17,20)(18,19)(21,23)(22,24)(30,31)$$$$w:=(1,24)(2,13)(3,12)(4,20)(5,21)(6,16)(7,9)(8,17)(10,18)(11,19)(14,23)(15,22)(26,29)(27,30)$$

When $n\equiv 8(\text{mod}24)$, we may start at m = 32 with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24)(25,26)(27,28)(29,30)(31,32)$$$$y:=(1,8)(2,3)(4,5)(6,7)(9,16)(10,11)(12,13)(14,15)(17,24)(18,19)(20,21)(22,23)(25,32)(26,27)(28,29)(30,31)$$$$z:=(1,9)(2,10)(3,20)(4,19)(5,14)(6,13)(7,23)(8,24)(11,21)(12,22)(15,18)(16,17)(25,32)(26,31)(27,29)(28,30)$$$$w:=(1,2)(3,8)(4,6)(5,7)(9,22)(10,27)(11,26)(12,18)(13,19)(14,30)(15,31)(16,23)(17,25)(20,29)(21,28)(24,32)$$

When $n\equiv 9(\text{mod}24)$, we may start at m = 33 with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24)(25,26)(27,28)$$$$y:=(1,8)(2,3)(4,5)(6,7)(9,16)(10,11)(12,13)(14,15)(18,19)(22,23)(25,29)(26,30)(27,28)(31,32)$$$$z:=(1,21)(2,22)(3,4)(5,23)(6,24)(9,18)(10,17)(13,20)(14,19)(15,16)(25,28)(26,27)(29,30)(32,33)$$$$w:=(2,29)(3,25)(4,5)(6,26)(7,30)(9,11)(10,16)(12,15)(13,14)(17,20)(18,27)(19,28)(22,32)(23,31)$$

When $n\equiv 10(\text{mod}24)$, we may start at m = 34 with:

$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24)(25,26)(27,28)(29,30)(31,32)y:=(1,8)(2,3)(4,5)(6,7)(9,16)(10,11)(12,13)(14,15)(17,24)(18,19)(20,21)(22,23)(26,27)(29,33)(30,34)(31,32)z:=(1,3)(2,4)(5,8)(6,7)(9,26)(10,25)(13,28)(14,27)(15,16)(17,23)(18,24)(19,22)(20,21)(29,32)(30,31)(33,34)w:=(1,14)(2,19)(3,18)(4,10)(5,11)(6,22)(7,23)(8,15)(9,17)(12,21)(13,20)(16,24)(25,28)(26,31)(27,32)(30,34)$ When $n\equiv 11(\text{mod}24)$, we may start at $m=35$ with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24)(25,26)(27,28)$$$$y:=(1,8)(2,3)(4,5)(6,7)(9,16)(10,11)(12,13)(14,15)(18,19)(22,23)(25,29)(26,30)(31,32)(33,34)$$$$z:=(1,23)(2,24)(5,21)(6,22)(7,8)(9,19)(10,20)(13,17)(14,18)(15,16)(25,28)(26,27)(31,32)(34,35)$$$$w:=(1,2)(3,8)(4,6)(5,7)(9,16)(10,25)(11,29)(14,30)(15,26)(18,32)(19,31)(22,34)(23,33)(27,35)$$

When $n\equiv 12(\text{mod}24)$, we may start at $m=36$ with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24)(25,26)(27,28)$$$$y:=(1,8)(2,3)(4,5)(6,7)(9,16)(10,11)(12,13)(14,15)(18,19)(21,29)(22,30)(23,31)(24,32)(33,34)$$$$z:=(1,8)(2,7)(3,5)(4,6)(11,20)(12,19)(13,14)(15,18)(16,17)(21,26)(22,25)(23,27)(24,28)(33,35)$$$$w:=(1,32)(4,31)(5,23)(6,7)(8,24)(9,30)(12,29)(13,21)(14,15)(16,22)(18,34)(19,33)(26,36)(27,35)$$

When $n\equiv 13(\text{mod}24)$, we may start at $m=37$ with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24)(25,26)(27,28)(29,30)(31,32)$$$$y:=(1,8)(2,3)(4,5)(6,7)(9,16)(10,11)(12,13)(14,15)(17,24)(18,19)(20,21)(22,23)(26,27)(30,31)(33,34)(35,36)$$$$z:=(1,26)(2,25)(5,28)(6,27)(7,8)(9,12)(10,11)(13,15)(14,16)(17,29)(18,30)(19,20)(21,31)(22,32)(33,37)(35,36)$$$$w:=(1,14)(2,19)(3,18)(4,10)(5,11)(6,22)(7,23)(8,15)(9,17)(12,21)(13,20)(16,24)(26,33)(27,34)(30,35)(31,36)$$

When $n\equiv 14(\text{mod}24)$, we may start at $m=14$ with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)$$$$y:=(1,8)(2,3)(4,5)(6,7)(9,13)(10,14)$$$$z:=(1,8)(2,7)(3,5)(4,6)(9,11)(10,12)$$$$w:=(1,13)(4,14)(5,10)(6,7)(8,9)(11,12)$$

When $n\equiv 15(\text{mod}24)$, we may start at $m=15$ with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)$$$$y:=(1,8)(2,3)(4,5)(6,7)(10,11)(13,14)$$$$z:=(1,2)(3,10)(4,9)(7,12)(8,11)(14,15)$$$$w:=(1,6)(2,4)(3,5)(7,8)(10,13)(11,14)$$

When $n\equiv 16(\text{mod}24)$, we may start at $m=40$ with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24)(25,26)(27,28)(29,30)(31,32)(33,34)(35,36)(37,38)(39,40)$$$$y:=(1,8)(2,3)(4,5)(6,7)(9,16)(10,11)(12,13)(14,15)(17,24)(18,19)(20,21)(22,23)(25,32)(26,27)(28,29)(30,31)(33,40)(34,35)(36,37)(38,39)$$$$z:=(1,3)(2,4)(5,8)(6,7)(9,25)(10,26)(11,21)(12,22)(13,30)(14,29)(15,18)(16,17)(19,28)(20,27)(23,31)(24,32)(33,35)(34,36)(37,40)(38,39)$$$$w:=(1,38)(2,19)(3,18)(4,34)(5,35)(6,22)(7,23)(8,39)(9,10)(11,16)(12,14)(13,15)(17,33)(20,37)(21,36)(24,40)(25,26)(27,32)(28,30)(29,31)$$

When $n\equiv 17(\text{mod}24)$, we may start at $m=41$ with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(21,22)(23,24)(25,26)(27,28)(29,30)(31,32)(33,34)(35,36)$$$$y:=(1,8)(2,3)(4,5)(6,7)(10,11)(13,17)(14,18)(19,20)(21,28)(22,23)(24,25)(26,27)(30,31)(33,37)(34,38)(39,40)$$$$z:=(1,31)(2,32)(5,29)(6,30)(7,8)(9,24)(10,23)(11,28)(12,27)(13,15)(14,16)(19,20)(21,22)(33,35)(34,36)(40,41)$$$$w:=(1,14)(2,3)(4,13)(5,17)(8,18)(10,19)(11,20)(15,16)(21,37)(24,38)(25,34)(26,27)(28,33)(30,39)(31,40)(36,41)$$

When $n\equiv 18(\text{mod}24)$, we may start at $m=18$ with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)$$$$y:=(1,8)(2,3)(4,5)(6,7)(10,11)(13,17)(14,18)(15,16)$$$$z:=(1,8)(2,7)(3,5)(4,6)(9,10)(13,15)(14,16)(17,18)$$$$w:=(1,17)(4,18)(5,14)(6,7)(8,13)(9,12)(10,15)(11,16)$$

When $n\equiv 19(\text{mod}24)$, we may start at $m=43$ with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(23,24)(25,26)(27,28)(29,30)(31,32)(33,34)(35,36)(37,38)$$$$y:=(1,8)(2,3)(4,5)(6,7)(10,11)(15,17)(16,18)(19,20)(23,30)(24,25)(26,27)(28,29)(32,33)(35,39)(36,40)(41,42)$$$$z:=(1,33)(2,34)(5,31)(6,32)(7,8)(9,27)(10,28)(11,23)(12,24)(13,16)(14,15)(20,21)(29,30)(35,37)(36,38)(42,43)$$$$w:=(2,17)(3,15)(4,5)(6,16)(7,18)(10,19)(11,20)(14,22)(23,39)(26,40)(27,36)(28,29)(30,35)(32,41)(33,42)(38,43)$$

When $n\equiv 20(\text{mod}24)$, we may start at $m=20$ with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)$$$$y:=(1,8)(2,3)(4,5)(6,7)(10,11)(13,17)(14,18)(19,20)$$$$z:=(1,2)(3,10)(4,9)(7,12)(8,11)(13,15)(14,16)(19,20)$$$$w:=(1,14)(2,3)(4,13)(5,17)(8,18)(10,19)(11,20)(15,16)$$

When $n\equiv 21(\text{mod}24)$, we may start at $m=21$ with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)$$$$y:=(1,8)(2,3)(4,5)(6,7)(10,11)(15,17)(16,18)(19,20)$$$$z:=(1,12)(2,11)(3,4)(5,10)(6,9)(13,16)(14,15)(19,21)$$$$w:=(1,3)(2,8)(4,7)(5,6)(10,20)(11,19)(14,21)(16,18)$$

When $n\equiv 22(\text{mod}24)$, we may start at $m=22$ with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)$$$$y:=(1,8)(2,3)(4,5)(6,7)(10,11)(13,17)(14,18)(19,20)$$$$z:=(1,11)(2,12)(5,9)(6,10)(7,8)(13,16)(14,15)(20,21)$$$$w:=(1,8)(2,14)(3,18)(6,17)(7,13)(10,20)(11,19)(15,22)$$

When $n\equiv 23(\text{mod}24)$, we may start at $m=47$ with:$$x:=(1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24)(25,26)(27,28)(29,30)(31,32)(33,34)(35,36)(37,38)(39,40)(41,42)(43,44)$$$$y:=(1,8)(2,3)(4,5)(6,7)(9,16)(10,11)(12,13)(14,15)(17,24)(18,19)(20,21)(22,23)(25,32)(26,27)(28,29)(30,31)(33,40)(34,35)(36,37)(38,39)(42,43)(45,46)$$$$z:=(1,9)(2,10)(3,20)(4,19)(5,14)(6,13)(7,23)(8,24)(11,21)(12,22)(15,18)(16,17)(25,43)(26,44)(29,41)(30,42)(31,32)(33,35)(34,36)(37,40)(38,39)(45,47)$$$$w:=(1,2)(3,8)(4,6)(5,7)(9,10)(11,16)(12,14)(13,15)(17,30)(18,35)(19,34)(20,26)(21,27)(22,38)(23,39)(24,31)(25,33)(28,37)(29,36)(32,40)(42,45)(43,46)$$