On the tropical two-sided discrete logarithm and a key exchange protocol based on the tropical algebra of pairs

Abstract

Since the existing tropical cryptographic protocols are either susceptible to the Kotov-Ushakov attack and its generalization, or to attacks based on tropical matrix periodicity and predictive behavior, several attempts have been made to propose protocols that resist such attacks. Despite these attempts, many of the proposed protocols remain vulnerable to attacks targeting the underlying hidden problems, one of which we call the tropical two-sided discrete logarithm with shift. An illustrative case is the tropical Stickel protocol, which, when formulated with a single monomial instead of a polynomial, becomes susceptible to attacks based on solutions of the above mentioned tropical version of discrete logarithm. In this paper we will formally introduce the tropical two-sided discrete logarithm with shift, discuss how it is solved, and subsequently demonstrate an attack on a key exchange protocol based on the tropical semiring of pairs. This particular protocol is compromised due to the existence of efficient (albeit heuristic) solution of the tropical two-sided logarithm problem, and this highlights the ongoing challenges in search of a “good” key exchange protocol in tropical cryptography.

Keywords:

• Cryptographic attack
• key exchange protocol
• public key cryptography
• tropical cryptography
• tropical matrix powers

2020 Mathematics Subject Classification:

• 94A60
• 15A80

1 Introduction

Tropical cryptography is a new and promising area that seeks to transform the traditional public key exchange methods in cryptography using tropical mathematics. Grigoriev and Shpilrain [5] pioneered the use of tropical algebra as an alternative framework for cryptographic protocols. In particular, they developed a tropical version of Stickel’s key exchange protocol [18], the original version of which had been previously compromised by Shpilrain [16] using a linear algebra attack. We also note here that Stickel’s protocol appears to be a special case of a more general protocol studied by Sidel’nikov, Cherepnev, and Yashchenko [17] in early 1990s.

One of the motivations for the development of tropical cryptography came from the non-invertible nature of matrices in tropical algebra. The scarcity of invertible matrices makes the tropical implementation resistant to attacks resembling the ones faced by the original Stickel protocol (such as described in [16]). However, the tropical implementation of Stickel’s protocol has been attacked by Kotov and Ushakov [8]. The Kotov-Ushakov attack was further generalized in [11] where it was shown how to apply the same idea to other implementations of Stickel protocol based on matrix commutativity. This has prompted the exploration of alternative ideas beyond matrix commutativity in Stickel protocols to implement tropical cryptographic protocols.

In response, Grigoriev and Shpilrain [6] proposed two protocols based on tropical semi-direct product, but one of them was shown to be invalid by Isaac and Kahrobaei [7] and the other was successfully attacked by the same authors as well as by [14] and [12]. The underlying problem that was solved and led to compromising the protocol was the tropical one-sided discrete logarithm. Subsequently, several alternative tropical protocols have been proposed that do not rely on this problem or matrix commutativity. Notably, one such protocol is based on the tropical algebra of pairs, as presented by Ahmed, Pal, and Mohan [1].

The main ideas of the present paper are to formulate the problem which we call the “tropical two-sided discrete logarithm with shift” and present some heuristic methods of solving it, and then, based on a reduction of the matrix algebra over the tropical semiring of pairs to the usual tropical matrix algebra, develop some attacks on the above mentioned protocol of Ahmed, Pal, and Mohan [1] and demonstrate their efficiency and success rate. More specifically, the paper is organized as follows. In Section 2 we start with some preliminaries and basic definitions, particularly those related to tropical matrix periodicity. In Section 3 we present the tropical two-sided discrete log with shift problem and two heuristic algorithms to solve it, showing their efficiency and success rate. In Section 4 we recall the tropical semiring of pairs and the implementation of Stickel protocol suggested in [1]. In Section 5 we cryptanalyze this implementation using the solution of the tropical two-sided discrete log with shift problem, and present some numerical experiments showing the efficiency and performance of the attacks. Our codes have been uploaded to GitHub.¹

2 Preliminaries

In this section, we present some of the standard definitions in tropical matrix algebra, for most of this part closely following Butkovič [3]. Note that we use the standard notation $[m]=\{1,\dots ,m\}$ and $[n]=\{1,\dots ,n\}$ for most common index sets.

Definition 2.1

(Tropical Semiring and Tropical Matrix Algebra). We define the tropical/max-plus semiring as ${\mathbb{R}}_{\mathrm{\text{max}}}=(\mathbb{R}\cup \{-\infty \},\oplus ,\otimes ),$ where traditional addition + and multiplication × are replaced by tropical addition ⊕ and tropical multiplication ⊗, respectively. These new arithmetical operations are defined by $x\oplus y=\mathrm{\text{max}}\{x,y\}$ and $x\otimes y=x+y$ for all $x,y\in {\mathbb{R}}_{\mathrm{\text{max}}}$.

The tropical arithmetic operations are naturally extended to include matrices and vectors. In particular, the operation $A\otimes \alpha =\alpha \otimes A,\hspace{1em}$ where $\alpha \in {\mathbb{R}}_{\mathrm{\text{max}}},A\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{m\times n}}$ and ${(A)}_{\mathit{\text{ij}}}=a_{\mathit{\text{ij}}}$ for $i\in [m]$ and $j\in [n]$, is defined by $${(A\otimes \alpha )}_{\mathit{\text{ij}}}={(\alpha \otimes A)}_{\mathit{\text{ij}}}=\alpha \otimes a_{\mathit{\text{ij}}}\hspace{1em}\forall i\in \left[m\right]\text{ and }\forall j\in \left[n\right].$$

The tropical addition $A\oplus B$ of two matrices $A\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{\text{mxn}}}$ and $B\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{m\times n}}$, where ${(A)}_{\mathit{\text{ij}}}=a_{\mathit{\text{ij}}}$ and ${(B)}_{\mathit{\text{ij}}}=b_{\mathit{\text{ij}}}$ for $i\in [m]$ and $j\in [n]$, is defined by $$j\in \left[n\right]$$

The tropical multiplication of two matrices is also similar to the “traditional” algebra. Namely, we define $A\otimes B$ for two matrices, where $A\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{\mathit{\text{mxp}}}}$ and $B\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{p\times n}}$, as follows: $${(A\otimes B)}_{\mathit{\text{ij}}}={\oplus }_{k=1}^p{a}_{\mathit{\text{ik}}}\otimes b_{\mathit{\text{kj}}}=\left(a_{i1}\otimes b_{1j}\oplus a_{i2}\otimes b_{2j}\oplus \cdots \oplus a_{\mathit{\text{in}}}\otimes b_{\mathit{\text{nj}}}\right)\hspace{1em}\forall i\in \left[m\right]\text{ and }\forall j\in \left[n\right].$$

Note that, despite introducing this tropical arithmetic, we will also quite often utilize the usual arithmetical operations to introduce concepts and explain arguments.

Definition 2.2

(Tropical Matrix Powers). For $M\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{n\times n}}$, the n-th tropical power of M is denoted by $M^{\otimes n}$, and is equal to $$M^{\otimes n}=\underset{n\text{ times }}{\underbrace{M\otimes M\otimes \cdots \otimes M}}$$

We now introduce elements of graph theory to define the upcoming concepts. We begin by defining the directed graph (or digraph) associated with A and recalling the definitions of cycles, strongly connected components and other related concepts.

Definition 2.3

(Digraphs, Walks and Cycles). The digraph associated with $A\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{n\times n}}$, where ${(A)}_{\mathit{\text{ij}}}=a_{\mathit{\text{ij}}}$ for $i,j\in [n]$, is the pair $G(A)=(N_A,E_A)$, where $N_A=[n]$ is called the set of nodes of G(A) and $E_A=\{(i,j):a_{\mathit{\text{ij}}}\ne -\infty \}$ is called the set of arcs of G(A).

A walk on G_A can be defined as a sequence of nodes $(i_1,\dots ,i_m)$ where each $(i_l,i_{l+1})$ for $l=1,\dots ,m-1$ is an arc. A closed walk is a walk that starts and finishes at the same node, and a cycle is any closed walk that does not contain any repeated nodes, except for the beginning node and the end node.

The tropical analogue of irreducible matrix can be now defined (closely following its classical prototype).

Definition 2.4

(Irreducibility). A matrix $A\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{n\times n}}$ is called irreducible if G_A is strongly connected, i.e., if for each $i,j\in [n]$ there exists a walk on G_A whose starting node is i and end node is j. A is called reducible if it is not irreducible.

We now introduce the concept of a maximum cycle mean, which is the value of the cycle that has the greatest average weight. We then also introduce a special subgraph of G(A) called the critical digraph of A. Formal definitions are given below.

Definition 2.5

(Maximum Cycle Mean and Critical Digraph). For $A\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{n\times n}}$, the maximum cycle mean $\lambda (A)$ is defined in the usual notation as $$\lambda (A)={\mathrm{\text{max}}}_k{\mathrm{\text{max}}}_{i_1,\dots ,i_k\in \left[n\right]}\frac{a_{i_1{i}_2}+\cdots +a_{i_k{i}_1}}{k},$$which is the same as $$\lambda (A)=\underset{k}{\oplus }\underset{i_1,\dots ,i_k\in \left[n\right]}{\oplus }\sqrt[\otimes k]{a_{i_1{i}_2}\otimes \cdots \otimes a_{i_k{i}_1}}$$ in the tropical notation.

By definition, a cycle that attains the maximum cycle mean is a critical cycle. The critical graph of A, denoted by $G_A^c=(N_A^c,E_A^c)$ is the subgraph of G_A which consists of all nodes and arcs of G_A that belong to the critical cycles. The nodes belonging to $N_A^c$ and the arcs belonging to $E_A^c$ are also called critical.

The matrix inverses in tropical algebra can be defined only for a limited class of matrices, but the analogue of ${(I-A)}^{-1}$ is more convenient to define.

Definition 2.6

(Kleene Star and Tropical Identity Matrix). Let $M\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{n\times n}}$ have $\lambda (M)\le 0$. The Kleene star of M is defined by $$M^{*}=I\oplus M\oplus M^{\otimes 2}\oplus \cdots \oplus M^{\otimes (n-1)},$$where I is the tropical identity matrix, whose all diagonal entries are equal to 0 and all off-diagonal entries are equal to $-\infty$.

One of the key ideas of solving the discrete logarithm problems (or, more specifically, Problems 1–4 formulated below) is to use the ultimate periodicity properties of tropical matrix powers. Strictly speaking, 1) the ultimate periodicity (in the sense of Theorem 2.1) occurs with a certain shift, that is, instead of repeating themselves the powers get multiplied in the tropical sense by some scalar, 2) the ultimate periodicity does not occur for general square matrix A, but is guaranteed only under certain conditions which (at their best) only slightly generalize the irreducibility property. For simplicity, the ultimate periodicity theorem is stated below only for the irreducible case, close to the original formulation in Cohen et al. [4].

Theorem 2.1

(Ultimate Periodicity of Tropical Matrix Powers [4]). Let $A\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{n\times n}}$ be irreducible and let $\lambda =\lambda (A)$ be the maximum cycle mean of A. Then for some natural numbers T_A and γ we have (1) $$A^{\otimes (t+\gamma )}={\lambda }^{\otimes \gamma }\otimes A^{\otimes t}=\gamma ·\lambda +A^{\otimes t}\hspace{1em}\forall t\ge T_A$$(1)

Below we will also use the more particular ultimate periodicity of the ith columns and the ith rows: (2) $$A_{·i}^{\otimes (t+\gamma )}={\lambda }^{\otimes \gamma }\otimes A_{·i}^{\otimes t}=\gamma ·\lambda +A_{·i}^{\otimes t}\hspace{1em}\forall t\ge {(T_A)}^i,$$(2) (3) $$A_{i·}^{\otimes (t+\gamma )}={\lambda }^{\otimes \gamma }\otimes A_{i·}^{\otimes t}=\gamma ·\lambda +A_{i·}^{\otimes t}\hspace{1em}\forall t\ge {(T_A)}_i,$$(3)

The ultimate periodicity gives rise to a number of important concepts, of which we will define the following one.

Definition 2.7

(Periodicity Transients). The smallest integer T_A for which (1) holds or, respectively, the smallest integers ${(T_A)}^i$ and ${(T_A)}_i$ for which (2) and (3) hold, is called the periodicity transient of (the tropical matrix powers of) A or, respectively, the periodicity transient of the ith column and the ith row of those powers.

Obviously, the periodicity transients of ith row and ith column can be much smaller than the periodicity transient of A, and this is particularly relevant in the case where $i\in N_A^c$ (i.e., when i is a critical node of A). It is also known that, for $i\in N_A^c$, the properties (2) and (3) take place also for general reducible matrices A. Below we will recall a particularly useful result due to Nachtigall [13].

Theorem 2.2

(Ultimate Periodicity of Critical Rows and Columns [13]). Let $A\in {\mathbb{R}}^{n\times n}$ and k be a critical node on a critical cycle Z of length l_Z. Then ${(T_A)}_k\le (n-1)·l_Z$ and ${(T_A)}^k\le (n-1)·l_Z$.

To explain how to compute the critical rows and columns in the ultimately periodic regime, let us also present the following result, which is a variation of the weak CSR theorems of [9] and can be seen as a slight simplification of [12], Proposition 2.5.

Theorem 2.3

(Weak CSR Expansion [9]). Let $A\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{n\times n}}$ have $\lambda =\lambda (A)\ne -\infty$, and let Z be a critical cycle of A with length l_Z. Then for some integer T_weak we have $$\begin{array}{cc}{A}^{\otimes t}\hfill & ={\lambda }^{\otimes t}\otimes \left(C_Z\otimes S_Z^{\otimes t}\otimes R_Z\right)\oplus B_Z^{\otimes t}\hspace{1em}\forall t\ge T_{\mathit{\text{weak}}}\hfill \\ \hfill & ={\lambda }^{\otimes t}\otimes \left(C_Z\otimes S_Z^{\otimes t\left(\text{rem}{l}_Z\right)}\otimes R_Z\right)\oplus B_Z^{\otimes t}\hspace{1em}\forall t\ge T_{\mathit{\text{weak}}}.\hfill \end{array}$$where $t(\text{rem}{l}_Z)$ is the remainder when t is divided by l_Z and $C_Z,S_Z,R_Z$, and B_Z are defined by $$\begin{array}{cc}{\left(C_Z\right)}_{\mathit{\text{ij}}}\hfill & =\{\begin{array}{c}{\left(U_Z\right)}_{\mathit{\text{ij}}}\text{ if }j\text{ is in }Z\hfill \\ -\infty \text{ otherwise }\hfill \end{array}\hfill \\ {\left(R_Z\right)}_{\mathit{\text{ij}}}\hfill & =\{\begin{array}{c}{\left(U_Z\right)}_{\mathit{\text{ij}}}\text{ if }i\text{ is in }Z\hfill \\ -\infty \text{ otherwise }\hfill \end{array}\hfill \\ {\left(S_Z\right)}_{\mathit{\text{ij}}}\hfill & =\{\begin{array}{c}\left(a_{\mathit{\text{ij}}}\otimes {\lambda }^{-1}\right)\text{ if }(i,j)\text{ is in }Z\hfill \\ -\infty \text{ otherwise }\hfill \end{array}\hfill \\ {\left(B_Z\right)}_{\mathit{\text{ij}}}\hfill & =\{\begin{array}{c}-\infty \text{ if }i\in Z\text{ or }j\in Z\hfill \\ a_{\mathit{\text{ij}}}\text{ otherwise }\hfill \end{array}\hfill \end{array}$$ where $U_Z={({(A\otimes {\lambda }^{-1})}^{\otimes {\text{ l/}}_Z})}^{*}$ (i.e., the Kleene star of $({(A\otimes {\lambda }^{-1})}^{\otimes {\text{ l/}}_Z})$).

Combining Theorem 2.2 with Theorem 2.3 as well as with [15] Corollary 3.7, we obtain the following result, which we will be using below in some algorithms:

Theorem 2.4

(CSR Formula for Critical Rows and Columns). Let $A\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{n\times n}}$ have $\lambda =\lambda (A)\ne -\infty$, and let Z be a critical cycle of A with length l_Z. Then for any $i\in Z$ we have $$A_{i·}^{\otimes t}={\lambda }^{\otimes t}\otimes {(S_Z^{\otimes t\left(\text{rem}{l}_Z\right)}\otimes R_Z)}_{i·},A_{·i}^{\otimes t}={\lambda }^{\otimes t}\otimes {(C_Z\otimes S_Z^{\otimes t\left(\text{rem}{l}_Z\right)})}_{·i},\forall t\ge (n-1)l_Z.$$

This theorem can be utilized to solve the different forms of tropical discrete logarithm problems, which are summarized below.

Problem 1.

Given $U,M,D\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{n\times n}}$ such that $U=M\otimes D^{\otimes t}$ for some $t\in \mathbb{N}$, find this t.

Problem 2.

Given $U,M,D\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{n\times n}}$, such that $U=\alpha \otimes M\otimes D^{\otimes t}$ for some $t\in \mathbb{N}$ and $\alpha \in {\mathbb{R}}_{\mathrm{\text{max}}}$, find τ and $t\prime$ such that $U=\tau \otimes M\otimes D^{\otimes t\prime }$.

Solution to Problem 1 was discussed in [12] and further in [10], and Problem 2 can be solved by similar methods. However, since it involves a scalar, Problem 2 typically has an infinite number of solutions, unlike Problem 1, whose solution is typically unique. Also note that one can pose a version of Problem 1, respectively Problem 2, with $D^{\otimes t}\otimes M$ instead of $M\otimes D^{\otimes t}$, which can be regarded as a transposition of Problem 1, respectively Problem 2, and can be solved similarly.

Let us now pose two other problems, which will be referred to as tropical two-sided discrete logarithm problems.

Problem 3.

Given $D_1,D_2,M,U\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{n\times n}}$ such that $U=D_1^{\otimes t_1}\otimes M\otimes D_2^{\otimes t_2}$ for some $t_1,t_2\in \mathbb{N}$. Find $t_1^{\prime },t_2^{\prime }$ such that $U=D_1^{\otimes t_1^{\prime }}\otimes M\otimes D_2^{\otimes t_2^{\prime }}$.

Problem 4.

Given $D_1,D_2,M,U\in {\mathbb{R}}_{{\mathrm{\text{max}}}^{n\times n}}$ such that $U=\alpha \otimes D_1^{\otimes t_1}\otimes M\otimes D_2^{\otimes t_2}$ for some $t_1,t_2\in \mathbb{N}$ and $\alpha \in \mathbb{R}$. Find $t_1^{\prime },t_2^{\prime }$ such that $U=\tau \otimes D_1^{\otimes t_1^{\prime }}\otimes M\otimes D_2^{\otimes t_2^{\prime }}$, where $\tau \in {\mathbb{R}}_{\mathrm{\text{max}}}$.

An attempt to solve Problem 3 can be found in [10], where it is observed, in particular, that the solution to this problem is in general non-unique. However, the number of solutions to this problem (unlike the number of solutions to Problem 4 is typically finite).

It is natural to solve the problems listed above by exploiting the ultimate periodicity properties of the tropical matrix powers or, in particular, by using the more precise information about those powers in the ultimate periodic regime as given, e.g., by the CSR decomposition. Let us note, however, that this approach has some limitations. Firstly, tropical matrix powers are not ultimately periodic in general (see, e.g., [3]), and both Alice and Bob can opt to use matrices whose powers are not ultimately periodic, which offers them some protection against attacks based on ultimate periodicity of entire tropical matrix powers. Secondly, the periodicity transient of tropical matrix powers depends on the matrix entries and it can be quite high.

In view of the above observations it looks more reasonable to exploit the ultimate periodicity of those columns and rows of tropical matrix powers whose indices correspond to the critical nodes. These columns and rows are ultimately periodic for any matrix and some of the known bounds on their periodicity transients are quadratic or even linear, if such columns and rows belong to a critical cycle of a known length.

This was the approach adopted in [12] and [10] and the same approach will be developed in the next section, see Algorithms 2, and 4. The more “naive” approach, based on the assumption that the tropical matrix powers are ultimately periodic, is more relevant to Algorithms 1 and 3.

3 Heuristic attacks on the tropical two-sided discrete logarithm with shift

In this section, we will discuss two approaches to how Problem 4 can be solved. Let us first note that this problem differs from the tropical two-sided discrete logarithm problem (Problem 3) since it includes a coefficient. The introduction of this coefficient enhances the solvability of the problem since it becomes sufficient to find a pair of exponents $t_1^{\prime },t_2^{\prime }$ that makes U a shifted version of $D_1^{\otimes t_1^{\prime }}\otimes M\otimes D_2^{\otimes t_2^{\prime }}$. For this reason, if there is a pair $(t_1^{\prime },t_2^{\prime })$ satisfying this equation, where $t_1^{\prime }$, respectively $t_2^{\prime }$, are above the ultimate periodicity thresholds for D₁, respectively D₂, then there are infinitely many such pairs. The first algorithm, which we are going to propose, will utilize this property, since we are relying on the intuition that the smallest pair of exponents $t_1^{\prime }$ and $t_2^{\prime }$ satisfying the equation is small enough, which is true if the sequences of matrix powers of D₁ and D₂ are ultimately periodic in the sense of Theorem 2.1 and if the threshold of their ultimate periodicity is small enough.

Algorithm 1

Solving the tropical two-sided discrete logarithm with shift using the non-uniqueness of exponents

Input: $U,D_1,M,D_2,{\mathrm{\text{max}}}_t$

Output: $t_1^{\prime },t_2^{\prime },\tau$

1: for $t_1=0 \text{to} {\mathrm{\text{max}}}_t$ do

2: for $t_2=0 \text{to} {\mathrm{\text{max}}}_t$ do

3: if ${(U-D_1^{\otimes t_1}\otimes M\otimes D_2^{\otimes t_2})}_{\mathit{\text{ij}}}=\beta \forall i,j\in [n]$ for some $\beta \in \mathbb{R}$ then

4: $t_1^{\prime }=t_1,t_2^{\prime }=t_2$, $\tau =\beta$.

5: end if

6: end for

7: end for

Algorithm 1 has a perfect success rate in solving Problem 4 when ${\mathrm{\text{max}}}_t$ is equal to the maximum exponent that could be used in the problem, but it is also expected to have a high success rate for lower values of ${\mathrm{\text{max}}}_t$ for the reasons outlined above.

For the second algorithm, we apply Theorem 2.4 for the powers of D₁ and D₂ to solve Problem 4. Note that here we can find $t_1^{\prime },t_2^{\prime }$ by only searching in a search space of a size equal to the product of the two critical cycle lengths of the two matrices D₁ and D₂, while the previous algorithm has a maximum search space equal to the product of the maximum exponents that could be used in the problem (or, to be more precise, our estimates of such maximum exponents).

Note that this algorithm is heuristic in nature in particular since the CSR formulas of Theorem 2.4 are only guaranteed to hold when the exponent is larger than $(n-1)·\mathrm{\text{max}}(l_Z,l_W)$ where l_Z and, respectively, l_W are the lengths of the critical cycle Z of D₁ and, respectively, the critical cycle W of D₂. The algorithm might not solve the problem if the original exponents t₁, t₂ are lower than this bound. One might add to the algorithm some parts where the exponents lower than this bound are also checked, similarly to the algorithms in [12] and [10].

To justify and explain the second algorithm we observe that we can use the CSR formulas of Theorem 2.4 for the rows of powers of D₁ with indices in Z and for the columns of powers of D₂ with indices in W, and then focus on the submatrix of U extracted from the rows with indices in Z and columns with indices in W. We then obtain the following equation $$\begin{array}{cc}\hfill & {(U)}_{\mathit{\text{ij}}}=(\alpha \otimes {\lambda }_1^{\otimes t_1}\otimes {\lambda }_2^{\otimes t_2}\otimes {\left(S_Z^{\otimes t_1\text{rem}\left(l_Z\right)}\otimes R_Z\otimes M\otimes C_W\otimes S_W^{\otimes t_2\text{rem}\left(l_W\right)}\right)}_{\mathit{\text{ij}}}\hfill \\ \hfill & \forall (i,j)\text{ where }i\in Z\text{ and }j\in W\text{ and }\forall t_1\ge (n-1)l_Z\text{ and }\forall t_2\ge (n-1)l_W,\hfill \end{array}$$where λ₁,λ₂ denote the maximum cycle means of the two matrices.

Then we want to solve the problem of finding $(t_1^{\prime },t_2^{\prime },\tau )$ for some $t_1^{\prime },t_2^{\prime }\in \mathbb{N}$ and $\tau \in \mathbb{R}$ such that $$\begin{array}{cc}\hfill & {(U)}_{\mathit{\text{ij}}}=(\tau \otimes {\lambda }_1^{\otimes t_1^{\prime }}\otimes {\lambda }_2^{\otimes t_2^{\prime }}\otimes {\left(S_Z^{\otimes t_1^{\prime }\text{rem}\left(l_Z\right)}\otimes R_Z\otimes M\otimes C_W\otimes S_W^{\otimes t_2^{\prime }\text{rem}\left(l_W\right)}\right)}_{\mathit{\text{ij}}}\hfill \\ \hfill & \forall (i,j)\text{ where }i\in Z\text{ and }j\in W\text{ and }\forall t_1^{\prime }\ge (n-1)l_Z\text{ and }\forall t_2^{\prime }\ge (n-1)l_W,\hfill \end{array}$$and this is achieved by firstly finding a pair of exponents $(t_1^{\prime }\text{rem}(l_Z),t_2^{\prime }\text{rem}(l_W))$ among $l_Z·l_W$ possibilities such that it will make the above described submatrix of U and the same submatrix of $S_Z^{\otimes t_1^{\prime }\text{rem}(l_Z)}\otimes R_Z\otimes M\otimes C_W\otimes S_W^{\otimes t_2^{\prime }\text{rem}(l_W)}$ “in phase”.

We will denote $t_1^{\prime }\text{rem}(l_Z),t_2^{\prime }\text{rem}(l_W)$ by ${\overline{t}}_1,{\overline{t}}_2$ respectively. In particular, we begin by finding ${\overline{t}}_1\in \{1,2,\dots ,l_Z\}$ and ${\overline{t}}_2\in \{1,2,\dots ,l_W\}$ that makes the submatrix of U extracted from the rows with indices in Z and the columns with indices in W a shifted version of the same submatrix of ${(S_Z^{\otimes {\overline{t}}_1}\otimes R_Z\otimes M\otimes C_W\otimes S_W^{\otimes {\overline{t}}_2})}_{\mathit{\text{ij}}}$. Then we try to find $(t_1^{\prime },t_2^{\prime },\tau )$ by solving the following equation (4) $$\begin{array}{cc}\beta \hfill & =\tau +t_1^{\prime }·{\lambda }_1+t_2^{\prime }·{\lambda }_2,\text{ where}\hfill \\ \beta \hfill & ={\left(U-S_Z^{\otimes {\overline{t}}_1}\otimes R_Z\otimes M\otimes C_W\otimes S_W^{\otimes {\overline{t}}_2}\right)}_{\mathit{\text{ij}}}\hspace{1em}\forall (i,j):i\in Z,j\in W.\hfill \end{array}$$(4)

As it follows from numerical experiments, it is also reasonable to impose some lower bounds on $t_1^{\prime }$ and $t_2^{\prime }$ which guarantee that the submatrix of U with rows in Z and columns in W is in the ultimately periodic regime.

We now formulate (4) (with the above mentioned lower bounds on $t_1^{\prime }$ and $t_2^{\prime }$) in a more precise way as a mixed-integer linear programming problem. Recall that ${\overline{t}}_1$ and ${\overline{t}}_2$ denote the remainders when $t_1^{\prime }$, respectively $t_2^{\prime }$ are divided by l_Z and, respectively, l_W. Thus $t_1^{\prime }=l_Z·x+{\overline{t}}_1$ and $t_2^{\prime }=l_W·y+{\overline{t}}_2$ where $x,y\in \mathbb{N}$. We obtain $$\beta =\tau +(l_Z·x+{\overline{t}}_1)·{\lambda }_1+(l_W·y+{\overline{t}}_2)·{\lambda }_2,$$

which can be rearranged to give $$\beta -\tau -{\lambda }_1·{\overline{t}}_1-{\lambda }_2·{\overline{t}}_2={\lambda }_1·l_Z·x+{\lambda }_2·l_W·y$$

We also impose the lower bounds $t_1^{\prime }\ge (n-1)l_Z\text{ and }{t}_2^{\prime }\ge (n-1)l_W$ since we are counting on the critical rows and columns reaching the ultimate periodic regime, which may not be the case if these inequalities do not hold. We then have $$t_1^{\prime }=l_Z·x+{\overline{t}}_1\ge (n-1)l_Z\hspace{1em}\text{ and }\hspace{1em}{t}_2^{\prime }=l_W·y+{\overline{t}}_2\ge (n-1)l_W,$$which we can rearrange to obtain $$x\ge \frac{(n-1)l_Z-{\overline{t}}_1}{l_Z}\hspace{1em}\text{ and }\hspace{1em}y\ge \frac{(n-1)l_W-{\overline{t}}_2}{l_W}$$

Then we can find solutions $(t_1^{\prime },t_2^{\prime },\tau )$ by solving (5) $$\{\begin{array}{c}\beta -\tau -{\lambda }_1·{\overline{t}}_1-{\lambda }_2·{\overline{t}}_2=({\lambda }_1·l_Z)x+({\lambda }_2·l_W)y\hfill \\ x\ge \frac{(n-1)l_Z-{\overline{t}}_1}{l_Z}\hfill \\ y\ge \frac{(n-1)l_W-{\overline{t}}_2}{l_W}\hfill \end{array}$$(5) for $(x,y)\in {\mathbb{N}}^2$ and $\tau \in \mathbb{R}$. Note that this is a mixed integer linear programming problem with unknowns $x,y,\tau$. We are now ready to formulate the solution method, see Algorithm 2.

Algorithm 2

Solving the tropical two-sided discrete logarithm with shift using CSR

Input: $U,D_1,M,D_2$

Output: $t_1^{\prime },t_2^{\prime },\tau$

1: Calculate $\lambda (D_1)={\lambda }_1,\lambda (D_2)={\lambda }_2$

2: Find a critical cycle Z from D₁, and W from D₂, let their lengths be l_Z and l_W, respectively.

3: Calculate S_Z, R_Z, C_W and S_W as in Theorem 2.3

4: for ${\overline{t}}_1=0 \text{to} l_Z$ do

5: for ${\overline{t}}_2=0 \text{to} l_W$ do

6: if $(U-{(S_Z^{\otimes {\overline{t}}_1}\otimes R_Z\otimes M\otimes C_W\otimes S_W^{{\overline{t}}_2})}_{\mathit{\text{ij}}}=\beta$ for some $\beta \in \mathbb{R}$ and for all i, j where $i\in Z$ and $j\in W$ then

7: Check if (5) is solvable. If it is, then return $(t_1^{\prime },t_2^{\prime },\tau )$ where $t_1^{\prime }=l_Z·x+{\overline{t}}_1$ and $t_2^{\prime }=l_W·y+{\overline{t}}_2$.

8: end if

9: end for

10: end for

The following numerical experiments show the success rate and time consumption for Algorithm 1 and Algorithm 2 as a function of matrix dimension. For all experiments, the entries of the matrices are random integers in $[-1000,1000]$, and 100 trials were performed for each dimension. All numerical experiments are implemented on MATLAB R2023b running on Windows 11 64-bit, equipped with an Intel(R) Core(TM) i7-9750H CPU @ 2.60GHz and 16.0 GB RAM.

Success rate for Algorithm 1 is shown in Figure 1. The exponents t₁, t₂ in Problem 4 are randomly chosen among integers in $[1,n^5]$, and the scalar value α is in $[1,1000]$. Algorithm 1 parameter ${\mathrm{\text{max}}}_t$ is n⁵ for the left hand side of the figure and n³ for the right hand side of the figure.

Fig. 1 Algorithm 1 success rate with ${\mathrm{\text{max}}}_t=n^5$ (left) and ${\mathrm{\text{max}}}_t=n^3$ (right).

We notice that Algorithm 1 never fails when the maximum searchable exponent ${\mathrm{\text{max}}}_t$ is the same as the one used in Problem 4 since the algorithm searches for all possible matrix exponents that make U in phase or equal to $D_1^{\otimes t_1^{\prime }}\otimes M\otimes D_2^{\otimes t_2^{\prime }}$. The guaranteed success results from testing all potential exponent combinations. The efficiency and quickness of the algorithm in finding appropriate exponents depends on the cyclicity pattern of the matrices D₁ and D₂. When we limit ${\mathrm{\text{max}}}_t$ to a lower exponent, we lose the guaranteed success rate, but we still achieve a high success rate with a faster time.

Success rate for Algorithm 2 is shown in Figure 2. The exponents t₁, t₂ in Problem 4 are allowed to be less than $(n-1)l_Z$ and $(n-1)l_W$ for the left hand side, and are required to be larger than $(n-1)l_Z$ and $(n-1)l_W$ for the right hand side, and the scalar value α is in the interval $[1,1000]$.

Fig. 2 Algorithm 2 success rate when $t_1<(n-1)l_Z$ and $t_2<(n-1)l_W$ (left), and when $t_1\ge (n-1)l_Z$ and $t_2\ge (n-1)l_W$ (right).

We notice that Algorithm 2 has a high success rate when the exponents used in Problem 4 are larger than $(n-1)l_Z$ and $(n-1)l_W$ for t₁ and t₂ respectively since the critical entries are guaranteed to enter the ultimately periodic regime after such bounds. The attack however does not perform so well when the used exponents are lower than this threshold which is expected since the CSR formulas do not necessarily hold for such exponent values (i.e., entries in the critical rows or columns have not necessarily entered the ultimate periodicity).

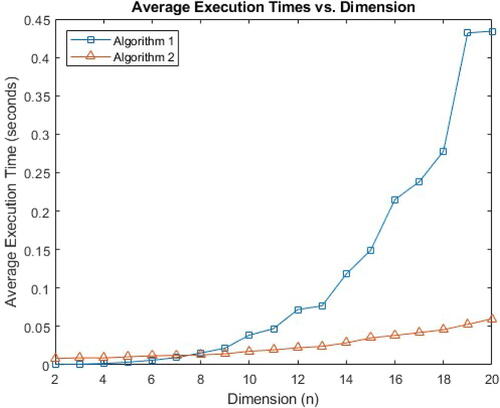
The time consumption for the two algorithms is quite different, as shown in Figure 3. Here, the exponents t₁, t₂ in Problem 4 are random integers larger than $(n-1)l_Z$ and $(n-1)l_W$, respectively, and the scalar value α is in the interval $[1,1000]$.

Fig. 3 Time taken for Algorithms 1 and 2.

We notice that Algorithm 2 is faster than Algorithm 1 since it limits its search to a finite set of values equal to the product of the critical cycle sizes of the two matrices D₁, D₂. However, for lower values of n, we note that Algorithm 1 is faster since the search space is small and Algorithm 2 requires more steps such as computing the CSR terms and maximum cycle means.

Note that one can combine the two algorithms to get better overall performance in terms of success rate and execution time. One possible combination is to apply Algorithm 1 for t₁ until $(n-1)l_Z$ and t₂ until a big enough number, then for t₂ until $(n-1)l_W$ and for t₁ until a big enough number, and then to perform Algorithm 2 for larger exponents.

4 The tropical semiring of pairs and the key exchange protocol

In this section, we examine a key exchange protocol proposed in [1]. The protocol employs a modified tropical structure and is claimed to resist the known attacks on conventional tropical key exchange protocols. We will begin by introducing the modified tropical structure, followed by presenting the associated protocol and outlining its construction.

4.1 The tropical semiring of pairs

Let ${\mathbb{R}}_{\mathrm{\text{max}}}$ be the tropical semiring defined in 2.1, then we have the following definition.

Definition 4.1.

(Tropical Algebra of Pairs [1, 2]). We define the tropical algebra of pairs ${\mathbb{R}}_{\mathrm{\text{max}}}^2$ as $${\mathbb{R}}_{\mathrm{\text{max}}}^2=\left({\mathbb{R}}_{\mathrm{\text{max}}}\times {\mathbb{R}}_{\mathrm{\text{max}}},{\oplus }^{\prime },{\otimes }^{\prime }\right)$$with elements of the shape $(a^{(1)},a^{(2)})$ such that $a^{(k)}\in {\mathbb{R}}_{\mathrm{\text{max}}}$ for $k\in \{1,2\}$ denotes the first and second element of a two-dimensional vector in ${\mathbb{R}}_{\mathrm{\text{max}}}^2$ with the operations $(\oplus \prime ,\otimes \prime )$ defined as $$\begin{array}{c}(a^{(1)},a^{(2)}){\oplus }^{\prime }(b^{(1)},b^{(2)})=(a^{(1)}\oplus b^{(1)},a^{(2)}\oplus b^{(2)})\\ (a^{(1)},a^{(2)}){\otimes }^{\prime }(b^{(1)},b^{(2)})=((a^{(1)}\otimes b^{(1)})\oplus (a^{(2)}\otimes b^{(2)}),(a^{(1)}\otimes b^{(2)})\oplus (a^{(2)}\otimes b^{(1)}))\\ \text{such that}\hspace{1em}({\mathrm{a}}^{(1)},{\mathrm{a}}^{(2)}),({\mathrm{b}}^{(1)},{\mathrm{b}}^{(2)})\in {\mathbb{R}}_{\mathrm{\text{max}}}^2\hspace{1em}\text{and}\hspace{1em}{\mathrm{a}}^{(1)},{\mathrm{a}}^{(2)},{\mathrm{b}}^{(1)},{\mathrm{b}}^{(2)}\in {\mathbb{R}}_{\mathrm{\text{max}}}\end{array}$$

The following example illustrates these operations.

Example 4.1.

Let $(1,3),(2,5)\in {\mathbb{R}}_{\mathrm{\text{max}}}^2$ then $$\begin{array}{c}(1,3){\oplus }^{\prime }(2,5)=(1\oplus 2,3\oplus 5)=(2,5)\\ (1,3){\otimes }^{\prime }(2,5)=((1\otimes 2)\oplus (3\otimes 5),(1\otimes 5)\oplus (3\otimes 2))=(8,6)\end{array}$$

The operations of this semiring can also be extended to include matrices following the same manner as the conventional tropical matrix operations in Definition 2.1 but with replacing the elements of ${\mathbb{R}}_{\mathrm{\text{max}}}$ by the elements of ${\mathbb{R}}_{\mathrm{\text{max}}}^2$ and $(\oplus ,\otimes )$ by $(\oplus \prime ,\otimes \prime )$. Thus, we will denote the semiring of matrices over ${\mathbb{R}}_{\mathrm{\text{max}}}^2$ by ${({\mathbb{R}}^2)}_{\mathrm{\text{max}}}^{n\times n}$.

4.2 Key exchange protocol based on the semiring of pairs

We now present the key exchange protocol proposed by the authors in [1] which is based on the tropical algebra of pairs ${({\mathbb{R}}^2)}_{\mathrm{\text{max}}}^{n\times n}$. Note that the authors in this protocol altered the second operation of ${\mathbb{R}}_{\mathrm{\text{max}}}^2$ to be $(x,y){\otimes }_c(z,w)=((c\otimes x\otimes z)\oplus (c\otimes y\otimes w),(c\otimes x\otimes w)\oplus (c\otimes y\otimes z))$ where $0\ne c\in \mathbb{Z}$. This modification constructs a new semiring ${\mathbb{R}}_{{\mathrm{\text{max}}}_c}^2$ with multiplicative identity $(-c,-\infty )$.

Protocol 1 (Key Exchange Protocol based on the Semiring of Pairs).

1. Alice and Bob agree upon two public matrices $X,Y\in {({\mathbb{R}}^2)}_{\mathrm{\text{max}}}^{n\times n}$.

2. Alice chooses a semiring ${\mathbb{R}}_{{\mathrm{\text{max}}}_c}^2=({\mathbb{R}}_{\mathrm{\text{max}}}\times {\mathbb{R}}_{\mathrm{\text{max}}},{\oplus }_c,{\otimes }_c)$ where

   $\begin{array}{c}(a^{(1)},a^{(2)}){\oplus }_c(b^{(1)},b^{(2)})=(a^{(1)}\oplus b^{(1)},a^{(2)}\oplus b^{(2)})\\ (a^{(1)},a^{(2)}){\otimes }_c(b^{(1)},b^{(2)})=((c\otimes a^{(1)}\otimes b^{(1)})\oplus (c\otimes a^{(2)}\otimes b^{(2)}),(c\otimes a^{(1)}\otimes b^{(2)})\oplus (c\otimes a^{(2)}\otimes b^{(1)}))\end{array}$

   Here, $c\in \mathbb{Z}$ is her fixed private parameter. Bob also picks ${\mathbb{R}}_{{\mathrm{\text{max}}}_d}^2=({\mathbb{R}}_{\mathrm{\text{max}}}\times {\mathbb{R}}_{\mathrm{\text{max}}},{\oplus }_d,{\otimes }_d)$ where

   $\begin{array}{c}(a^{(1)},a^{(2)}){\oplus }_d(b^{(1)},b^{(2)})=(a^{(1)}\oplus b^{(1)},a^{(2)}\oplus b^{(2)})\\ (a^{(1)},a^{(2)}){\otimes }_d(b^{(1)},b^{(2)})=((d\otimes a^{(1)}\otimes b^{(1)})\oplus (d\otimes a^{(2)}\otimes b^{(2)}),(d\otimes a^{(1)}\otimes b^{(2)})\oplus (d\otimes a^{(2)}\otimes b^{(1)}))\end{array}$

   and $d\in \mathbb{Z}$ is his fixed private parameter.

3. Alice picks two private natural numbers k, l and calculates $A=X^{{\otimes }_{c}k}\otimes Y^{{\otimes }_{c}l}$. She then chooses another private integer p and sends $A_{(p)}$ to Bob, where $A_{(p)}$ is $p\otimes A$.

4. Bob also picks his private natural numbers r, s, calculates $B=X^{{\otimes }_{d}r}\otimes Y^{{\otimes }_{d}s}$ and sends $B_{(q)}$ to Alice, where $B_{(q)}$ is $q\otimes B$ and $q\in \mathbb{Z}$ is Bob’s private parameter.

5. Alice computes her key $K_{\mathit{\text{Alice}}}={(X^{{\otimes }_{c}k})}_{(p)}\otimes B_{(q)}\otimes Y^{{\otimes }_{c}l}$ and Bob’s key is $K_{\mathit{\text{Bob}}}={(X^{{\otimes }_{d}r})}_{(q)}\otimes A_{(p)}\otimes Y^{{\otimes }_{d}s}$.

The two parties end up with the same key K_Alice = K_Bob as proved in [1].

The following example illustrates the above key exchange protocol.

Example 4.2.

Alice and Bob agree on the public matrices X and Y: $$X=\left[\begin{array}{cc}(9,6)& (1,-2)\\ (8,-4)& (4,1)\end{array}\right]\text{ and }Y=\left[\begin{array}{cc}(-2,0)& (8,-2)\\ (6,10)& (8,-5)\end{array}\right]$$and they choose the private parameters $c=3,k=27,l=18,p=-2$ for Alice, and $d=4,r=17,s=23,q=5$ for Bob.

Alice calculates $A=X^{{\otimes }_{3}27}\otimes Y^{{\otimes }_{3}18}=\left[\begin{array}{cc}(532,534)& (532,530)\\ (531,533)& (531,529)\end{array}\right]$ and sends

$A_{(-2)}=\left[\begin{array}{cc}(530,532)& (530,528)\\ (529,531)& (529,527)\end{array}\right]$ to Bob.

Bob calculates $B=X^{{\otimes }_{4}17}\otimes Y^{{\otimes }_{4}23}=\left[\begin{array}{cc}(509,511)& (509,511)\\ (508,510)& (508,510)\end{array}\right]$ and sends

$B_{(5)}=\left[\begin{array}{cc}(514,516)& (514,516)\\ (513,515)& (513,515)\end{array}\right]$ to Alice.

Then Alice and Bob compute their keys using those received transmissions: $$\begin{array}{c}{K}_{\mathit{\text{Alice}}}={\left(X^{{\otimes }_{3}27}\right)}_{(-2)}\otimes B_{(5)}\otimes Y^{{\otimes }_{3}18}=\left[\begin{array}{cc}(1048,1046)\hfill & (1048,1046)\hfill \\ (1047,1045)\hfill & (1047,1045)\hfill \end{array}\right]\\ K_{\mathit{\text{Bob}}}={\left(X^{{\otimes }_{4}17}\right)}_{(5)}\otimes A_{(-2)}\otimes Y^{{\otimes }_{4}23}=\left[\begin{array}{cc}(1048,1046)\hfill & (1048,1046)\hfill \\ (1047,1045)\hfill & (1047,1045)\hfill \end{array}\right]\end{array}$$

Thus they end up with the same shared key.

5 Cryptanalysis of the protocol

In this section, we introduce our attacks on the proposed protocol. It is claimed that it is more resilient than its conventional tropical counterparts since it doesn’t reveal a cyclicity pattern for high powers, but we will show otherwise. We begin by presenting an alternative representation of matrices in ${({\mathbb{R}}^2)}_{\mathrm{\text{max}}}^{n\times n}$, providing a foundation for constructing our attacks which are based on solving Problem 4. Subsequently, we implement our attacks showing their efficiency and success rate.

5.1 Representing matrices in ${({\mathbb{R}}^2)}_{\mathrm{\text{max}}}^{n\times n}$ as matrices in ${\mathbb{R}}_{\mathrm{\text{max}}}^{2n\times 2n}$

Observe that a matrix with entries in the tropical semiring of pairs can be associated with a conventional tropical matrix in ${\mathbb{R}}_{\mathrm{\text{max}}}^{2n\times 2n}$ by replacing each entry of the matrix over that semiring with a 2 × 2 square matrix. More formally this representation is defined as follows.

Definition 5.1.

Suppose $A\in {({\mathbb{R}}^2)}_{\mathrm{\text{max}}}^{n\times n}$ is given by $$A=\left[\begin{array}{cccc}(a_{11}^{(1)},a_{11}^{(2)})& (a_{12}^{(1)},a_{12}^{(2)})& \dots & (a_{1n}^{(1)},a_{1n}^{(2)})\\ (a_{21}^{(1)},a_{21}^{(2)})& (a_{22}^{(1)},a_{22}^{(2)})& \dots & (a_{2n}^{(1)},a_{2n}^{(2)})\\ ⋮& ⋮& \ddots & ⋮\\ (a_{n1}^{(1)},a_{n1}^{(2)})& (a_{n2}^{(1)},a_{n2}^{(2)})& \dots & (a_{\mathit{\text{nn}}}^{(1)},a_{\mathit{\text{nn}}}^{(2)})\end{array}\right],$$then we define $\tilde{A}\in {\mathbb{R}}_{\mathrm{\text{max}}}^{2n\times 2n}$ as follows: $$\tilde{A}=\left[\begin{array}{ccccccc}{a}_{11}^{(1)}& a_{11}^{(2)}& a_{12}^{(1)}& a_{12}^{(2)}& \dots & a_{1n}^{(1)}& a_{1n}^{(2)}\\ a_{11}^{(2)}& a_{11}^{(1)}& a_{12}^{(2)}& a_{12}^{(1)}& \dots & a_{1n}^{(2)}& a_{1n}^{(1)}\\ a_{21}^{(1)}& a_{21}^{(2)}& a_{22}^{(1)}& a_{22}^{(2)}& \dots & a_{2n}^{(1)}& a_{2n}^{(2)}\\ a_{21}^{(2)}& a_{21}^{(1)}& a_{22}^{(2)}& a_{22}^{(1)}& \dots & a_{2n}^{(2)}& a_{2n}^{(1)}\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ a_{n1}^{(1)}& a_{n1}^{(2)}& a_{n2}^{(1)}& a_{n2}^{(2)}& \dots & a_{\mathit{\text{nn}}}^{(1)}& a_{\mathit{\text{nn}}}^{(2)}\\ a_{n1}^{(2)}& a_{n1}^{(1)}& a_{n2}^{(2)}& a_{n2}^{(1)}& \dots & a_{\mathit{\text{nn}}}^{(2)}& a_{\mathit{\text{nn}}}^{(1)}\end{array}\right].$$

We now observe that this representation gives rise to an injective homomorphism from the matrix algebra ${({\mathbb{R}}^2)}_{\mathrm{\text{max}}}^{n\times n}$ to the matrix algebra ${\mathbb{R}}_{\mathrm{\text{max}}}^{2n\times 2n}$. In other words, each matrix in ${({\mathbb{R}}^2)}_{\mathrm{\text{max}}}^{n\times n}$ is uniquely represented by a matrix in ${\mathbb{R}}_{\mathrm{\text{max}}}^{2n\times 2n}$ and this representation respects the matrix addition (obviously), and also the matrix multiplication, due to the following proposition.

Proposition 5.1.

Let $A,B\in {({\mathbb{R}}^2)}_{\mathrm{\text{max}}}^{n\times n}$, then $\tilde{A}\otimes \tilde{B}=\widetilde{A\otimes B}$ where $\tilde{A},\tilde{B},\widetilde{(A\otimes B)}\in {\mathbb{R}}_{\mathrm{\text{max}}}^{2n\times 2n}$.

Proof.

We infer from the definition of the multiplication over ${\mathbb{R}}_{\mathrm{\text{max}}}^2$ (Definition 4.1) that if $$A=\left[\begin{array}{ccc}(a_{11}^{(1)},a_{11}^{(2)})& \dots & (a_{1n}^{(1)},a_{1n}^{(2)})\\ ⋮& \ddots & ⋮\\ (a_{n1}^{(1)},a_{n1}^{(2)})& \dots & (a_{\mathit{\text{nn}}}^{(1)},a_{\mathit{\text{nn}}}^{(2)})\end{array}\right]$$and $$B=\left[\begin{array}{ccc}(b_{11}^{(1)},b_{11}^{(2)})& \dots & (b_{1n}^{(1)},b_{1n}^{(2)})\\ ⋮& \ddots & ⋮\\ (b_{n1}^{(1)},b_{n1}^{(2)})& \dots & (b_{\mathit{\text{nn}}}^{(1)},b_{\mathit{\text{nn}}}^{(2)})\end{array}\right]$$

Then we have $$\begin{array}{c}{(A\otimes B)}_{\mathit{\text{pq}}}=\left({\oplus }_{k=1}^n{a}_{\mathit{\text{pk}}}^{(1)}\otimes b_{\mathit{\text{kq}}}^{(1)}\oplus a_{\mathit{\text{pk}}}^{(2)}\otimes b_{\mathit{\text{kq}}}^{(2)},{\oplus }_{k=1}^n{a}_{\mathit{\text{pk}}}^{(1)}\otimes b_{\mathit{\text{kq}}}^{(2)}\oplus a_{\mathit{\text{pk}}}^{(2)}\otimes b_{\mathit{\text{kq}}}^{(1)}\right)\\ {(A\otimes B)}_{\mathit{\text{pq}}}=(z_{\mathit{\text{pq}}}^{(1)},z_{\mathit{\text{pq}}}^{(2)})\hspace{1em}\forall p,q\in \left[n\right]\end{array}$$where $z_{\mathit{\text{pq}}}^{(1)}={\oplus }_{k=1}^n{a}_{\mathit{\text{pk}}}^{(1)}\otimes b_{\mathit{\text{kq}}}^{(1)}\oplus a_{\mathit{\text{pk}}}^{(2)}\otimes b_{\mathit{\text{kq}}}^{(2)}$ and $z_{\mathit{\text{pq}}}^{(2)}={\oplus }_{k=1}^n{a}_{\mathit{\text{pk}}}^{(1)}\otimes b_{\mathit{\text{kq}}}^{(2)}\oplus a_{\mathit{\text{pk}}}^{(2)}\otimes b_{\mathit{\text{kq}}}^{(1)}$. Using Definition 5.1 to obtain matrices $\tilde{A},\tilde{B}$ and $\widetilde{(A\otimes B)}\in {\mathbb{R}}_{\mathrm{\text{max}}}^{2n\times 2n}$, we have that $$\begin{array}{c}\begin{array}{c}\tilde{A}=\left[\begin{array}{ccccc}{a}_{11}^{(1)}& a_{11}^{(2)}& \dots & a_{1n}^{(1)}& a_{1n}^{(2)}\\ a_{11}^{(2)}& a_{11}^{(1)}& \dots & a_{1n}^{(2)}& a_{1n}^{(1)}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ a_{n1}^{(1)}& a_{n1}^{(2)}& \dots & a_{\mathit{\text{nn}}}^{(1)}& a_{\mathit{\text{nn}}}^{(2)}\\ a_{n1}^{(2)}& a_{n1}^{(1)}& \dots & a_{\mathit{\text{nn}}}^{(2)}& a_{\mathit{\text{nn}}}^{(1)}\end{array}\right]\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\tilde{B}=\left[\begin{array}{ccccc}{b}_{11}^{(1)}& b_{11}^{(2)}& \dots & b_{1n}^{(1)}& b_{1n}^{(2)}\\ b_{11}^{(2)}& b_{11}^{(1)}& \dots & b_{1n}^{(2)}& b_{1n}^{(1)}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ b_{n1}^{(1)}& b_{n1}^{(2)}& \dots & b_{\mathit{\text{nn}}}^{(1)}& b_{\mathit{\text{nn}}}^{(2)}\\ b_{n1}^{(2)}& b_{n1}^{(1)}& \dots & b_{\mathit{\text{nn}}}^{(2)}& b_{\mathit{\text{nn}}}^{(1)}\end{array}\right]\hfill \end{array}\\ \widetilde{(A\otimes B)}=\left[\begin{array}{ccccc}{z}_{11}^{(1)}& z_{11}^{(2)}& \dots & z_{1n}^{(1)}& z_{1n}^{(2)}\\ z_{11}^{(2)}& z_{11}^{(1)}& \dots & z_{1n}^{(2)}& z_{1n}^{(1)}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ z_{n1}^{(1)}& z_{n1}^{(2)}& \dots & z_{\mathit{\text{nn}}}^{(1)}& z_{\mathit{\text{nn}}}^{(2)}\\ z_{n1}^{(2)}& z_{n1}^{(1)}& \dots & z_{\mathit{\text{nn}}}^{(2)}& z_{\mathit{\text{nn}}}^{(1)}\end{array}\right]\end{array}$$

Then it is clear that we have a 2 × 2 sub-matrix in $(\tilde{A}\otimes \tilde{B})$ for each pair $(p,q)\in [n]\times [n]$, which has $${\oplus }_{k=1}^n{a}_{\mathit{\text{pk}}}^{(1)}\otimes b_{\mathit{\text{kq}}}^{(1)}\oplus a_{\mathit{\text{pk}}}^{(2)}\otimes b_{\mathit{\text{kq}}}^{(2)}=z_{\mathit{\text{pq}}}^{(1)}\hspace{1em}\text{for the two diagonal elements}$$and $${\oplus }_{k=1}^n{a}_{\mathit{\text{pk}}}^{(1)}\otimes b_{\mathit{\text{kq}}}^{(2)}\oplus a_{\mathit{\text{pk}}}^{(2)}\otimes b_{\mathit{\text{kq}}}^{(1)}=z_{\mathit{\text{pq}}}^{(2)}\hspace{1em}\text{for the two non‐diagonal elements}$$

Therefore $$\tilde{A}\otimes \tilde{B}=\left[\begin{array}{ccccc}{z}_{11}^{(1)}& z_{11}^{(2)}& \dots & z_{1n}^{(1)}& z_{1n}^{(2)}\\ z_{11}^{(2)}& z_{11}^{(1)}& \dots & z_{1n}^{(2)}& z_{1n}^{(1)}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ z_{n1}^{(1)}& z_{n1}^{(2)}& \dots & z_{\mathit{\text{nn}}}^{(1)}& z_{\mathit{\text{nn}}}^{(2)}\\ z_{n1}^{(2)}& z_{n1}^{(1)}& \dots & z_{\mathit{\text{nn}}}^{(2)}& z_{\mathit{\text{nn}}}^{(1)}\end{array}\right]=\widetilde{(A\otimes B)}.$$

□

Example 5.1.

Suppose we have $$A=\left[\begin{array}{cc}(-7,-1)& (6,2)\\ (-4,9)& (4,-8)\end{array}\right]\text{ and }B=\left[\begin{array}{cc}(2,2)& (-6,7)\\ (1,10)& (3,-2)\end{array}\right]$$

Then $$A\otimes B=\left[\begin{array}{cc}(-7,-1)& (6,2)\\ (-4,9)& (4,-8)\end{array}\right]\otimes \left[\begin{array}{cc}(2,2)& (-6,7)\\ (1,10)& (3,-2)\end{array}\right]=\left[\begin{array}{cc}(12,16)\hfill & (9,5)\hfill \\ (11,14)\hfill & (16,3)\hfill \end{array}\right]$$

The above operation can be equivalently calculated using the conventional tropical matrix algebra, as we have $$\begin{array}{c}\tilde{A}=\left[\begin{array}{cccc}-7& -1& 6& 2\\ -1& -7& 2& 6\\ -4& 9& 4& -8\\ 9& -4& -8& 4\end{array}\right],\hspace{1em}\tilde{B}=\left[\begin{array}{cccc}2& 2& -6& 7\\ 2& 2& 7& -6\\ 1& 10& 3& -2\\ 10& 1& -2& 3\end{array}\right]\\ \tilde{A}\otimes \tilde{B}=\left[\begin{array}{cccc}-7& -1& 6& 2\\ -1& -7& 2& 6\\ -4& 9& 4& -8\\ 9& -4& -8& 4\end{array}\right]\otimes \left[\begin{array}{cccc}2& 2& -6& 7\\ 2& 2& 7& -6\\ 1& 10& 3& -2\\ 10& 1& -2& 3\end{array}\right]\\ =\left[\begin{array}{cccc}12& 16& 9& 5\\ 16& 12& 5& 9\\ 11& 14& 16& 3\\ 14& 11& 3& 16\end{array}\right]=\widetilde{(A\otimes B)}\end{array}$$

Notice that the odd numbered rows of $\tilde{A}\otimes \tilde{B}$ are identical to the rows of $A\otimes B$. We will exploit this observation to attack Protocol 1.

5.2 Attacks on Protocol 1 based on solving the tropical two-sided discrete logarithm

After the suggested matrix transformation, we observe that the problem of attacking the proposed protocol is essentially reduced to solving Problem 4. Thus, to attack the protocol, it is sufficient to find a pair of exponents $(k\prime ,l\prime )$ that makes the tropical product of the public matrices $X^{\otimes k^{\prime }}\otimes Y^{\otimes l^{\prime }}$ in phase with the transmitted matrix $A_{(p)}$, and not necessarily the exact exponents that generated the instance. In particular, we know from the definition of the proposed protocol that $$\begin{array}{c}A=X^{{\otimes }_{c}k}\otimes Y^{{\otimes }_{c}l}\\ =(k-1)c\otimes X^{\otimes k}\otimes (l-1)c\otimes Y^{\otimes l}\end{array}$$

Then when the two sides are multiplied by p, we get $$A_{(p)}=p\otimes (k-1)c\otimes X^{\otimes k}\otimes (l-1)c\otimes Y^{\otimes l}.$$

This $A_{(p)}$ can be intercepted by the attacker, and he can transform it to ${\tilde{A}}_{(p)}\in {\mathbb{R}}_{\mathrm{\text{max}}}^{2n\times 2n}$ using Definition 5.1. Similarly, the attacker also transforms public matrices X and Y to $\tilde{X}$ and $\tilde{Y}$. The attacker can then utilize the following equality, which holds by Proposition 5.1 (6) $${\tilde{A}}_{(p)}=p\otimes (k+l-2)c\otimes {\tilde{X}}^{\otimes k}\otimes {\tilde{Y}}^{\otimes l}$$(6)

This equation resembles Problem 4 which can be solved by finding a pair of exponents $k\prime ,l\prime$ such that ${\tilde{A}}_{(p)}$ is a shifted version of ${\tilde{X}}^{\otimes k\prime }\otimes {\tilde{Y}}^{\otimes l\prime }$ by a fixed integer τ which equals to the scalar part of the above equation ($\tau =p^{\prime }+(k^{\prime }+l^{\prime }-2)c^{\prime }$). In other words, all entries of ${\tilde{A}}_{(p)}$ differ by the same amount from the corresponding entry of ${\tilde{X}}^{\otimes k\prime }\otimes {\tilde{Y}}^{\otimes l\prime }$. There are highly likely infinite number of solutions due to the ultimate periodicity of tropical matrices. Note that the attacker can find the private parameters $p^{\prime },c^{\prime }$ by solving the equation $\tau =p^{\prime }+(k\prime +l\prime -2)c^{\prime }$ for $p^{\prime },c^{\prime }$. However, these parameters are not required to construct the shared key as it suffices to use τ.

The shared key can then be computed using the found exponents $(k\prime ,l\prime )$ and τ and the other intercepted massage $B_{(q)}$ as (7) $$\begin{array}{cc}{K}_{\text{Attack }}\hfill & =\tau \otimes \left(X^{\otimes k^{\prime }}\otimes B_{(q)}\otimes Y^{\otimes l^{\prime }}\right)\hfill \\ \hfill & =(p\prime +(k\prime +l\prime -2)c\prime +q+(r+s-2)d)\otimes \left(X^{\otimes k^{\prime }}\otimes X^{\otimes r}\otimes Y^{\otimes s}\otimes Y^{\otimes l^{\prime }}\right)\hfill \\ \hfill & =(p\prime +(k\prime +l\prime -2)c\prime +q+(r+s-2)d)\otimes \left(X^{\otimes r}\otimes X^{\otimes k^{\prime }}\otimes Y^{\otimes l^{\prime }}\otimes Y^{\otimes s}\right)\hfill \\ \hfill & =(p+(k+l-2)c+q+(r+s-2)d)\otimes \left(X^{\otimes k}\otimes X^{\otimes r}\otimes Y^{\otimes s}\otimes Y^{\otimes l}\right)\hfill \\ \hfill & =K_{\text{Alice }}=K_{\text{Bob }}\hfill \end{array}$$(7)

The attack is described in Algorithm 3. We also present an example illustrating this attack.

Algorithm 3

Attacking Protocol 1 by using Algorithm 1

Input: $X,Y,A_{(p)},B_{(q)},{\mathrm{\text{max}}}_t$

Output: Key

1: Transform $X,Y,A_{(p)}$ to $\tilde{X},\tilde{Y},{\tilde{A}}_{(p)}$ using Definition 5.1

2: Perform Algorithm 1 with Input:${\tilde{A}}_{(p)},\tilde{X},I,\tilde{Y},{\mathrm{\text{max}}}_t$, then we get the output $k\prime ,l\prime ,\tau$

3: $$\mathit{\text{Key}}=\tau \otimes \left(X^{\otimes k\prime }\otimes B_{(q)}\otimes Y^{\otimes l\prime }\right)$$

Example 5.2.

Suppose that Alice and Bob agree on the public matrices X and Y that are shown in Example 4.2, with the private parameters being $c=3,k=27,l=18,p=-2$ for Alice and $d=4,r=17,s=23,q=5$ for Bob. The attacker intercepts $A_{(p)}$ and transforms it to a conventional tropical matrix ${\tilde{A}}_{(p)}$ in ${\mathbb{R}}_{\mathrm{\text{max}}}^{2n\times 2n}$. He also transforms the public matrices X and Y to $\tilde{X}$ and $\tilde{Y}$, respectively. Let the results of this transformation be $${\tilde{A}}_{(p)}=\left[\begin{array}{cccc}530& 532& 530& 528\\ 532& 530& 528& 530\\ 529& 531& 529& 527\\ 531& 529& 527& 529\end{array}\right],\hspace{1em}\tilde{X}=\left[\begin{array}{cccc}9& 6& 1& -2\\ 6& 9& -2& 1\\ 8& -4& 4& 1\\ -4& 8& 1& 4\end{array}\right]\hspace{1em}\tilde{Y}=\left[\begin{array}{cccc}-2& 0& 8& -2\\ 0& -2& -2& 8\\ 6& 10& 8& -5\\ 10& 6& -5& 8\end{array}\right]$$

The attacker then searches for a pair of exponents $k\prime$ and $l\prime$ that satisfies the following equation $${\left({\tilde{A}}_{(p)}-{\tilde{X}}^{\otimes k\prime }\otimes {\tilde{Y}}^{\otimes l\prime }\right)}_{\mathit{\text{ij}}}=\tau \text{ for some }\tau \in \mathbb{R}\hspace{1em}\forall \mathrm{i},\mathrm{j}\in \left[\text{2n}\right]$$

The attacker notices that any pair from $k\prime \in \{2,3,4,\dots \}$ and $l\prime \in \{10,14,18,\dots \}$ satisfies the above equality. Suppose the attacker picks k = 2 and l = 10 $${\left({\tilde{A}}_{(p)}-{\tilde{X}}^{\otimes 2}\otimes {\tilde{Y}}^{\otimes 10}\right)}_{\mathit{\text{ij}}}=424\hspace{1em}\forall i,j\in \left[2n\right]$$

Then, the shared key can be computed as: $$\begin{array}{c}{\tilde{K}}_{\text{Attack }}=\tau \otimes \left({\tilde{X}}^{\otimes 2}\otimes {\tilde{B}}_{(q)}\otimes {\tilde{Y}}^{\otimes 10}\right)\\ =424\otimes \left[\begin{array}{cccc}624& 622& 624& 622\\ 622& 624& 622& 624\\ 623& 621& 623& 621\\ 621& 623& 621& 623\end{array}\right]=\left[\begin{array}{cccc}1048& 1046& 1048& 1046\\ 1046& 1048& 1046& 1048\\ 1047& 1045& 1047& 1045\\ 1045& 1047& 1045& 1047\end{array}\right]\end{array}$$

which represents $$\begin{array}{cc}\left[\begin{array}{cc}(1048,1046)& (1048,1046)\\ (1047,1045)& (1047,1045)\end{array}\right]\hfill & =K_{\text{Alice}}=K_{\text{Bob}}\hfill \end{array}$$

We notice that the attacker successfully recovered the secret key using smaller exponents than those that generated the protocol instance.

We now describe the attack based on the CSR solution to the two-sided discrete logarithm problem. Starting from (6) we focus on the submatrix extracted from the rows with indices in a critical cycle Z of $\tilde{X}$ and the columns with indices in a critical cycle W of $\tilde{Y}$, for which we obtain $$\begin{array}{c}{\left({\tilde{A}}_{(p)}=\tau \otimes {\lambda }_1^{\otimes k}\otimes {\lambda }_2^{\otimes l}\otimes S_Z^{\otimes k\text{rem}\left(l_Z\right)}\otimes R_Z\otimes C_W\otimes S_W^{\otimes l\text{rem}\left(l_W\right)}\right)}_{\mathit{\text{ij}}}\forall i\in Z,j\in W\\ k\ge (2n-1)l_Z,\hspace{1em}l\ge (2n-1)l_W.\end{array}$$

Here l_Z, l_W denote the lengths of Z and W, and $\tau =p\otimes (k+l-2)c$. Then, we want to find a pair of exponents $k\prime ,l\prime$ such that ${({\tilde{A}}_{(p)})}_{\mathit{\text{ij}}}$ is a shifted version of ${(S_Z^{\otimes k\prime \text{rem}(l_Z)}\otimes R_Z\otimes C_W\otimes S_W^{\otimes l\prime \text{rem}(l_W)})}_{\mathit{\text{ij}}}$ by a fixed integer β which equals to the scalar part ($\beta =\tau \otimes {\lambda }_1^{\otimes k\prime }\otimes {\lambda }_2^{\otimes l\prime }$). To achieve that, we firstly need to find $\overline{k}=k\prime \text{rem}(l_Z)$ and $\overline{l}=l\prime \text{rem}(l_W)\in \{1,2,\dots ,l_Z\}\times \{1,2,\dots ,l_W\}$ that satisfies this shift requirement, and then find $(k\prime ,l\prime ,\tau )$ by solving the following mixed integer linear programming problem (8) $$\{\begin{array}{c}\beta -\tau -{\lambda }_1·\overline{k}-{\lambda }_2·\overline{l}=({\lambda }_1·l_Z)x+({\lambda }_2·l_W)y\hfill \\ x\ge \frac{(2n-1)l_Z-\overline{k}}{l_Z}\hfill \\ y\ge \frac{(2n-1)l_W-\overline{l}}{l_W}\hfill \end{array}$$(8) with unknowns $\tau ,x$ and y. Then we obtain $k\prime =x·l_Z+\overline{k}$ and $l\prime =y·l_W+\overline{l}$. If it happens that (6) holds for the pair of exponents thus found, then this method also yields a common key, by applying the same argument as in (7). The attack is formally written as Algorithm 4.

Algorithm 4

Attacking Protocol 1 by Using Algorithm 2

Input: $X,Y,A_{(p)},B_{(q)}$

Output: Key

1: Transform $X,Y,A_{(p)}$ to $\tilde{X},\tilde{Y},{\tilde{A}}_{(p)}$ using Definition 5.1

2: Calculate $\lambda (\tilde{X})={\lambda }_1,\lambda (\tilde{Y})={\lambda }_2$

3: Find a critical cycle Z from $\tilde{X}$, and W from $\tilde{Y}$, let their lengths be l_Z and l_W, respectively.

4: Calculate S_Z, R_Z, C_W and S_W as in Theorem 2.3

5: Perform Algorithm 2 with Input:${\tilde{A}}_{(p)},\tilde{X},I,\tilde{Y}$, then we get the output $k\prime ,l\prime ,\tau$

6: $\mathit{\text{Key}}=\tau \otimes (X^{\otimes k\prime }\otimes B_{(q)}\otimes Y^{\otimes l\prime })$

5.3 Numerical experiments

Both of the suggested attacks on Protocol 1 have been tested numerically. Specifically, we looked at the success rate for each attack as a function of matrix dimension. Additionally, we analyzed the time required for the attacker to construct the secret shared key. This analysis serves as a basis for comparison with the process of original secret key generation. For all experiments, the protocol parameters $p,q,c,d$ and the matrix entries are random integers in $[-1000,1000]$, and 100 trials are performed for each dimension.

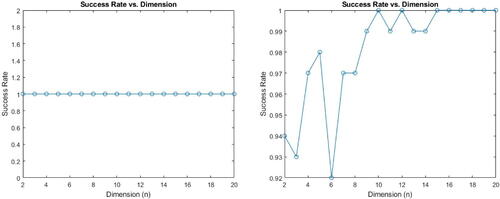
Success rate for Algorithm 3 is presented on Figure 4. Here, the private exponents $k,l,r,s$ in the protocol are random integers in $[1,n^5]$, where n is the dimension of the matrices, and the parameter ${\mathrm{\text{max}}}_t$ is n⁵ (on the left) and n³ (on the right).

Fig. 4 Attack 3 success rate with ${\mathrm{\text{max}}}_t=n^5$ and ${\mathrm{\text{max}}}_t=n^3$.

Since Algorithm 3 uses Algorithm 1, it never fails when the maximum searchable exponent ${\mathrm{\text{max}}}_t$ is the same as the one used in the protocol since the algorithm searches for all possible matrix exponents that make $A_{(P)}$ in phase or equal to $X^{\otimes k}\otimes Y^{\otimes l}$. The guaranteed success results from testing all potential exponent combinations. The efficiency and quickness of the algorithm in finding appropriate exponents depends on the ultimate periodicity threshold of the public matrices X and Y.

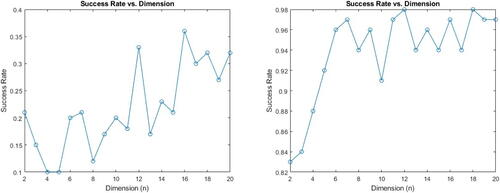
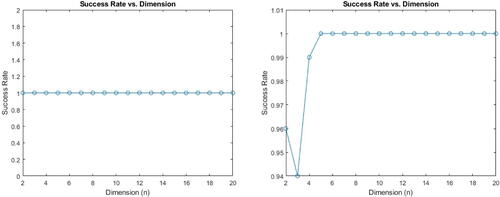
Success Rate for Algorithm 4 is shown in Figure 5. The private exponents k, r are random integers less that $(n-1)l_Z$, in $[(n-1)l_Z,(2n-1)l_Z]$, larger than $(2n-1)l_Z$ for the left, middle and right figure, respectively. The same follows for l, s but with l_W as the critical cycle length. For easier notations, we will denote both l_Z, l_W as l_Z in what follows.

Fig. 5 Attack 4 success rate with protocol’s exponents less than $(n-1)l_Z$, in $[(n-1)l_Z,(2n-1)l_Z]$ and larger than $(2n-1)l_Z$ respectively.

We notice that it is sufficient for Attack 4 to perform almost optimally when the original protocol’s exponents are larger than $(n-1)l_Z$ and not necessarily larger than $(2n-1)l_Z$, which is the guaranteed threshold for the CSR formulas of Theorem 2.4 to hold. This might indicate that after transforming the matrices from ${({\mathbb{R}}^2)}_{\mathrm{\text{max}}}^{n\times n}$ to ${\mathbb{R}}_{\mathrm{\text{max}}}^{2n\times 2n}$, the periodicity behavior is still maintained. The small number of failures are probably due the critical graph of 1 or more of the public matrices having multiple strongly connected components. We also notice that Algorithm 4 does not perform as well when the used exponents are lower than $(n-1)l_Z$ which is expected since the CSR decomposition does not necessarily hold for such exponent values (i.e., entries in the critical rows or columns haven’t necessarily converged yet to ultimate periodicity).

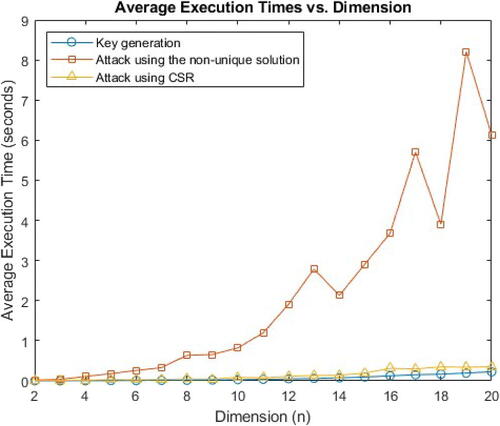
The time consumption comparison between the protocol and the two attacks is presented on Figure 6. The private exponents $k,l,r,s$ in the protocol are random integers larger than $(2n-1)l_Z$.

Fig. 6 Time taken to attack and to generate Protocol 1.

We notice that recovering the key with Algorithm 4 is faster than Algorithm 3 since it limits its search to a finite set of values equal to the product of the critical cycle sizes of the two public matrices. We see that there is no significant difference between the attacker’s time and the users’ time in generating the secret key.

5.4 An attack based on absolute values of tropical pairs

In this section, we describe another attack that does not require the attacker to double the matrices sizes, which makes it more efficient than the previous ones. However, while performing this attack we lose some information and this worsens the success rate. We firstly present the following definition, inspired by the symmetrized semiring introduced in [2].

Definition 5.2

(Absolute Value). Let $(a^{(1)},a^{(2)})\in {\mathbb{R}}_{{\mathrm{\text{max}}}^2}$. Then the absolute value of this pair is defined by $|(a^{(1)},a^{(2)})|=a^{(1)}\oplus a^{(2)}$.

For two pairs $(a^{(1)},a^{(2)}),(b^{(1)},b^{(2)})\in {\mathbb{R}}_{{\mathrm{\text{max}}}^2}$ the following properties hold: $$\begin{array}{cc}|(a^{(1)},a^{(2)})\oplus (b^{(1)},b^{(2)})|\hfill & =|(a^{(1)}\oplus b^{(1)},a^{(2)}\oplus b^{(2)})|\hfill \\ \hfill & =a^{(1)}\oplus a^{(2)}\oplus b^{(1)}\oplus b^{(2)}=|(a^{(1)},a^{(2)})|\oplus |(b^{(1)},b^{(2)})|\hfill \end{array}$$and $$\begin{array}{cc}|(a^{(1)},a^{(2)})\otimes (b^{(1)},b^{(2)})|\hfill & =|(a^{(1)}\otimes b^{(1)}\oplus a^{(2)}\otimes b^{(2)}),(a^{(1)}\otimes b^{(2)}\oplus a^{(2)}\otimes b^{(1)})|\hfill \\ \hfill & =(a^{(1)}\otimes b^{(1)}\oplus a^{(2)}\otimes b^{(2)})\oplus (a^{(1)}\otimes b^{(2)}\oplus a^{(2)}\otimes b^{(1)})\hfill \\ \hfill & =(a^{(1)}\oplus a^{(2)})\otimes (b^{(1)}\oplus b^{(2)})=|(a^{(1)},a^{(2)})|\otimes |(b^{(1)},b^{(2)})|\hfill \end{array}$$

The first of them is rather unusual, since we only have $|a+b|\le \left|a\right|+\left|b\right|$ in the usual algebra.

These properties can be also extended to matrices over tropical pairs, as we have $$\left|{(A\oplus B)}_{\mathit{\text{ij}}}\right|=|A{|}_{\mathit{\text{ij}}}\oplus |B{|}_{\mathit{\text{ij}}},$$

which directly follows from the above definition, and $$\begin{array}{cc}\left|{(A\otimes B)}_{\mathit{\text{ij}}}\right|=\left|{\oplus }_{k=1}^n{a}_{\mathit{\text{ik}}}\otimes b_{\mathit{\text{kj}}}\right|\hfill & =\underset{k=1}{\overset{n}{\oplus }}\left|a_{\mathit{\text{ik}}}\otimes b_{\mathit{\text{kj}}}\right|\hfill \\ \hfill & ={\oplus }_{k=1}^n\left|a_{\mathit{\text{ik}}}\right|\otimes \left|b_{\mathit{\text{kj}}}\right|={(|A|\otimes |B|)}_{\mathit{\text{ij}}}\hfill \end{array}$$

Here A, $B\in {({\mathbb{R}}^2)}_{\mathrm{\text{max}}}^{n\times n}$ and $a_{\mathit{\text{ij}}},b_{\mathit{\text{ij}}}\in {\mathbb{R}}_{\mathrm{\text{max}}}^2\forall i,j\in [n]$.

We can use the above operations to perform the ${({\mathbb{R}}^2)}_{\mathrm{\text{max}}}^{n\times n}$ matrix addition and multiplication, and we will get a half sized conventional ${\mathbb{R}}_{\mathrm{\text{max}}}^{n\times n}$ matrix. These operations with half sized result are often sufficient to attack the proposed protocol. The attack is very similar to Attack 4, but they only differ in the type of matrix transformation. It is formally presented below as Algorithm 5.

Algorithm 5

Attacking Protocol 1 using the absolute values

Input: $X,Y,A_{(p)},B_{(q)}$

Output: Key

1: Transform $X,Y,A_{(p)}$ to $\left|X\right|,\left|Y\right|,\left|A_{(p)}\right|$ using Definition 5.2

2: Calculate $\lambda (|X|)={\lambda }_1,\lambda (|Y|)={\lambda }_2$

3: Find a critical cycle Z from $\left|X\right|$, and W from $\left|Y\right|$, let their lengths be l_Z and l_W, respectively.

4: Calculate S_Z, R_Z, C_W, and S_W as in Theorem 2.3

5: Perform Algorithm 2 with Input:$\left|A_{(p)}\right|,\left|X\right|,I,\left|Y\right|$, then we get the output $k\prime ,l\prime ,\tau$

6: $$\mathit{\text{Key}}=\tau \otimes \left(X^{\otimes k\prime }\otimes B_{(q)}\otimes Y^{\otimes l\prime }\right)$$

We expect this attack to have a lower success rate than the previous ones due to the observation that $\alpha \otimes |X{|}^{\otimes t_1}\otimes |Y{|}^{\otimes t_2}=\left|U\right|$ does not always imply that $\alpha \otimes X^{\otimes t_1}\otimes Y^{\otimes t_2}=U$. Hence, the attack in this case will not successfully recover the secret key since the found exponents do not really solve the original tropical two-sided discrete log with shift problem over the tropical pairs. However, it is going to be faster since it does not require doubling the matrix size which expedites the process of computing the CSR terms and finding the exponents through solving the tropical two-sided discrete logarithm with shift. We performed a numerical experiment in which we observed that the algorithm had approximately 50–60% success rate but roughly twice the speed of Algorithm 4.

6 Conclusion

In this paper, we presented the tropical two-sided discrete logarithm with shift problem and its solution. We showed that two algorithms solve the problem with a high success rate. The first algorithm relies on the non-uniqueness of the exponents that can satisfy the problem’s equation, and it showed a perfect success rate but potentially slower convergence. The other algorithm heuristically solves the problem using the CSR decomposition, demonstrating a high success rate and a much faster execution time. We then presented a key exchange protocol that is based on the tropical semiring of pairs. We firstly showed that the matrix operations over the tropical semiring of pairs can be equivalently calculated using the conventional tropical semiring by doubling the matrices’ size. After the transformation to the conventional tropical semiring, the problem was reduced to the tropical two-sided discrete logarithm with shift, which can be solved using the two proposed algorithms. Lastly, we introduced an even faster approach that does not require the attacker to double the matrix size, showing roughly twice the speed of the previous heuristic attack, but it has a lower success rate.

We also note that the proposed protocol remains vulnerable to the known tropical cryptographic attacks even if the parties use matrix polynomials over the semiring of pairs. If Alice and Bob use matrix polynomials over the semiring of pairs, then the problem will not reduce to the tropical two-sided logarithm with shift, but in this case it may be possible to apply a modified version of the Kotov-Ushakov attack [8] (which, however, shows an exponential blow up in the number of operations as the maximal degree of the polynomials increases). The main reason for insecurity of the protocols using the matrix algebra over the tropical semiring of pairs is the existence of injective homomorphism from this matrix algebra to the ordinary tropical matrix algebra.

Acknowledgments

The authors are grateful to Sergeĭ’s M.Sci. student Sarah Elt who gave them the idea to try using also the absolute value of pairs and its extension to matrices. We are also grateful to our anonymous referee for careful reading and comments which helped to improve our paper.

Notes

1 https://github.com/suliman1n/Two-sided-Discrete-Logarithm-