The maximal Tori of finite exceptional groups of Lie type

Abstract

Let G(q) be a twisted or untwisted finite exceptional group of Lie type over $\text{GF}(q)$, either adjoint or simply connected, and let W be the Weyl group of G(q). This paper compiles an extensive data set on the maximal tori of G(q). A systematic labeling is given, via the corresponding conjugacy classes of W, together with a complete list of the structures of the maximal tori in terms of their torsion coefficient decomposition. Additionally the associated admissible graphs and the structure or shape of centralizers of elements in W are given as well as compatible computer files. Also various apparent inconsistencies in the current literature on simply connected groups are discussed and resolved.

Keywords:

• Exceptional groups of Lie type
• Maximal tori
• torsion coefficient decomposition
• Weyl groups

2020 Mathematics Subject Classification:

• 20D06

1 Introduction

Maximal tori of finite groups of Lie type frequently play a role in many facets of these groups. For example, they feature in the representation theory of groups of Lie type, and, indeed, are very much centre stage in Kazhdan-Lusztig theory (see [10]). Also, they arise in investigations into group structure as every semisimple element of a group of Lie type lies inside some maximal torus. An important fact, first observed in [1, E.II.1.2], is the one-to-one correspondence between conjugacy (twisted conjugacy) classes of the Weyl group and conjugacy classes of maximal tori. In [7], Carter presents a unified approach to the conjugacy classes of Weyl groups making it feasible to systematically describe maximal tori. Further, Carter introduced the admissible graph associated with a given (untwisted) conjugacy class and showed that this graph determines the characteristic polynomial on the standard vector space of the class representative. In [8, 9], he described the maximal tori for finite classical groups (see also Buturlakin and Grechkoseeva [6]).

The aim of the present paper is to present an extensive, and comprehensive, collection of data on the maximal tori for the untwisted and twisted finite exceptional groups of Lie type. Most of this information is gathered in tables appearing in Sections 4 and 5. These tables rest on a systematic labeling of the conjugacy classes of the Weyl groups which we use to christen the corresponding conjugacy class of maximal tori. We take a leaf from the Atlas [11] in the naming and ordering of conjugacy classes. So for conjugacy class representatives w₁ and w₂ of the Weyl group W, $w_1^W$ precedes $w_2^W$ in the labeling if w₁ and w₂ have the same order and $|C_W(w_1)|>|C_W(w_2)|$. We resolve the conundrum of what to do when $|C_W(w_1)|=|C_W(w_2)|$ with recourse to specific Coxeter group properties of the two conjugacy classes. Section 3 covers these issues in detail. We now give an overview of what appears in the tables. The compact tabular data in Sections 4 and 5 give, for a particular Weyl group W, a W-(twisted) conjugacy class representative w decomposed into a product of involutions, its name, the associated admissible graph Γ_w (only in the untwisted case), the structure or shape of both $C_W(w)$ ($C_{W,\sigma }(w)$ when twisted) and the corresponding maximal torus in its torsion coefficient decomposition. Describing a maximal torus in this manner not only exposes its torsion coefficients, it also gives it in an invariant form. Moreover, the data in Tables 6, 7, and 14 has been verified to hold for both the adjoint and simply connected groups of type ${\mathrm{E}}_6,{}^2{\mathrm{E}}_6$ and ${\mathrm{E}}_7$. That is, the torus structures are the same for the adjoint and simply connected groups of these types. This cannot be guaranteed for a general group of Lie type - the files of [25] contain counterexamples in types $\mathrm{B}$ and $\mathrm{C}$.

Table 6 The maximal tori of ${\mathrm{E}}_6(q)$.

w	Class	Min	$T_w(q)$	Γw	Shape of $C_W(w)$	Structure of $T_w(q)$
Id	1A	(0,1)	1	$\varnothing$	$W({\mathrm{E}}_6)\sim {\text{Sp}}_4(3):2$	${(q-1)}^6$
[1]	2A	(1,6)	2	${\mathrm{A}}_1$	$2\times \text{Sym}(6)$	${(q-1)}^4\times (q^2-1)$
[1,4,6,69] $\sim w_0$	2B	(12,1)	8	$4{\mathrm{A}}_1$	$W({\mathrm{F}}_4)\sim 2_{+}^{1+4}:\text{Sym}{(3)}^2$	${(q+1)}^2\times {(q^2-1)}^2$
[1,2]	2C	(2,10)	3	$2{\mathrm{A}}_1$	$\text{Dih}(8)\times \text{Sym}(4)$	${(q-1)}^2\times {(q^2-1)}^2$
[1,4,6]	2D	(3,5)	5	$3{\mathrm{A}}_1$	$2^2\times \text{Sym}(4)$	${(q^2-1)}^3$
[1,2,5][3,6,69]	3A	(24,80)	21	$3{\mathrm{A}}_2$	$3_{+}^{1+2}:{\text{SL}}_2(3)$	${(q^2+q+1)}^3$
[1][3]	3B	(2,10)	4	${\mathrm{A}}_2$	$3\times (\text{Sym}(3)\mathrm{\wr }2)$	${(q-1)}^3\times (q^3-1)$
[1,5][3,6]	3C	(4,4)	10	$2{\mathrm{A}}_2$	$3\times \text{Sym}{(3)}^2$	Table 9
[2,3][4,18]	4A	(6,12)	14	${\mathrm{D}}_4(a_1)$	${\text{GU}}_2(3)\sim 4\cdot \text{Sym}(4)$	${(q^3-q^2+q-1)}^2$
[1,69,4,6][5]	4B	(13,16)	16	$2{\mathrm{A}}_1+{\mathrm{A}}_3$	$4\times \text{Sym}(4)$	${(q+1)}^2\times (q^4-1)$
[1,4][3]	4C	(3,20)	7	${\mathrm{A}}_3$	$4\times \text{Dih}(8)$	${(q-1)}^2\times (q^4-1)$
[1,4,6][5]	4D	(4,16)	11	${\mathrm{A}}_1+{\mathrm{A}}_3$	$2^2\times 4$	$(q^2-1)\times (q^4-1)$
[1,4][3,5]	5A	(4,32)	12	${\mathrm{A}}_4$	10	$(q-1)\times (q^5-1)$
[1,18,4][2,3,48]	6A	(12,144)	25	${\mathrm{E}}_6(a_2)$	$3\times {\text{SL}}_2(3)$	$(q^2-q+1)\times (q^4+q^2+1)$
[1,4][5]	6B	(3,20)	6	${\mathrm{A}}_1+{\mathrm{A}}_2$	$6\times \text{Sym}(3)$	${(q-1)}^2\times (q^4+q^3-q-1)$
[3,2,5][4]	6C	(4,8)	13	${\mathrm{D}}_4$		$(q^2-1)\times (q^4-q^3+q-1)$
[1,2,5][3,6]	6D	(5,4)	15	${\mathrm{A}}_1+2{\mathrm{A}}_2$		$(q^2+q+1)\times (q^4+q^3-q-1)$
[1,4,6,69][3,2]	6E	(14,48)	22	${\mathrm{A}}_1+{\mathrm{A}}_5,{\mathrm{A}}_6$		$(q+1)\times (q^5+q^4+q^3+q^2+q+1)$
[1,2,5][6]	6F	(4,10)	9	$2{\mathrm{A}}_1+{\mathrm{A}}_2$	$3\times \text{Dih}(8)$	$(q^2-1)\times (q^4+q^3-q-1)$
[1,4,6][3,5]	6G	(5,16)	18	${\mathrm{A}}_5$	$2^2\times 3$	Table 9
[1,4][3,2,5]	8A	(5,32)	19	${\mathrm{D}}_5$	8	$q^6-q^4+q^2-1$
[1,4,18][2,3,6]	9A	(8,80)	24	${\mathrm{E}}_6(a_1)$	9	$q^6+q^3+1$
[1,2,5][4,6]	10A	(5,16)	17	${\mathrm{A}}_1+{\mathrm{A}}_4$	10	$q^6+q^5-q-1$
[1,4,6][3,2,5]	12A	(6,32)	23	${\mathrm{E}}_6$	12	$q^6+q^5-q^3+q+1$
[2,3][4,18,1]	12B	(7,64)	20	${\mathrm{D}}_5(a_1)$	12	$q^6-q^5+q^4-q^2+q-1$

Table 7 The maximal tori of ${\mathrm{E}}_7(q)$.

w		Min	$T_w(q)$	Γw	Shape of $C_W(w)$	Structure of $T_w(q)$
Id	1A	(0,1)	$1\prime$	$\varnothing$	$W({\mathrm{E}}_7)\sim 2.{\text{Sp}}_6(2)$	${(q-1)}^7$
w0	2A	(63,1)	$-1\prime$	$7{\mathrm{A}}_1$		${(q+1)}^7$
[1]	2B	(1,7)	$2\prime$	${\mathrm{A}}_1$	$2^6:\text{Sym}(6)$	${(q-1)}^5\times (q^2-1)$
[3,2,5,7,97,61]	2C	(30,1)	$-2\prime$	$6{\mathrm{A}}_1$		${(q+1)}^5\times (q^2-1)$
[4,17,97]	2D	(3,1)	–8	$3{\mathrm{A}}_1$	$(2_{+}^{1+4}:(2\times 2^2)).\text{Sym}{(3)}^2$	Table 9
[1,4,6,69]	2E	(12,1)	8	$4{\mathrm{A}}_1$		Table 9
[1,2]	2F	(2,15)	$3\prime$	$2{\mathrm{A}}_1$	$2^5:(2^2\times \text{Sym}(4))$	${(q-1)}^3\times {(q^2-1)}^2$
[97,3,2,5,7]	2G	(13,1)	$-3\prime$	$5{\mathrm{A}}_1$		${(q+1)}^3\times {(q^2-1)}^2$
[1,4,6]	2H	(3,10)	$5\prime$	$3{\mathrm{A}}_1$	$2^7:\text{Sym}(3)$	$(q-1)\times {(q^2-1)}^3$
[2,3,5,7]	2I	(4,2)	$-5\prime$	$4{\mathrm{A}}_1$		$(q+1)\times {(q^2-1)}^3$
[1][3]	3A	(2,12)	$4\prime$	${\mathrm{A}}_2$	$6\times \text{Sym}(6)$	${(q-1)}^4\times (q^3-1)$
[1,2,5][3,6,69]	3B	(24,80)	21	$3{\mathrm{A}}_2$	$2\times (3_{+}^{1+2}:{\text{SL}}_2(3))$	${(q^2+q+1)}^2\times (q^3-1)$
[1,5][3,6]	3C	(4,16)	10	$2{\mathrm{A}}_2$	$6\times \text{Sym}{(3)}^2$	$(q-1)\times {(q^3-1)}^2$
[2,3][4,18]	4A	(6,12)	$14\prime$	${\mathrm{D}}_4(a_1)$	$2^3\times (4°\text{Dih}(8)).\text{Sym}(3)$	$(q-1)\times {(q^3-q^2+q-1)}^2$
[97,3,5,7][1,6,2]	4B	(33,360)	$-14\prime$	${\mathrm{A}}_1+2{\mathrm{A}}_3$		$(q+1)\times {(q^3+q^2+q+1)}^2$
[1,4][3]	4C	(3,24)	$7\prime$	${\mathrm{A}}_3$	$\text{Sym}(4)\times 2^2\times 4$	${(q-1)}^3\times (q^4-1)$
[2,5,7][4]	4D	(4,8)	$-16$	${\mathrm{A}}_1+{\mathrm{A}}_3$		Table 9
[1,69,4,6][5]	4E	(13,16)	16	$2{\mathrm{A}}_1+{\mathrm{A}}_3$		Table 9
[97,3,2,5,7][6]	4F	(14,8)	$-7\prime$	$3{\mathrm{A}}_1+{\mathrm{A}}_3$		${(q+1)}^3\times (q^4-1)$
[2,3][4,18,7]	4G	(7,12)	28	${\mathrm{A}}_1+{\mathrm{D}}_4(a_1)$	$(2^3\times \text{Dih}(8)):4$	Table 9
[97,3,5,7][1,6]	4H	(16,60)	–28	$2{\mathrm{A}}_3,{\mathrm{A}}_2+{\mathrm{D}}_4(a_1)$		Table 9
[1,4,6][5]	4I	(4,36)	11	${\mathrm{A}}_1+{\mathrm{A}}_3$	$2^4\times 4$	$(q-1)\times (q^2-1)\times (q^4-1)$
[1,7,2,5][4]	4J	(5,12)	$-11$	$2{\mathrm{A}}_1+{\mathrm{A}}_3$		$(q+1)\times (q^2-1)\times (q^4-1)$
[1,4][3,5]	5A	(4,40)	$12\prime$	${\mathrm{A}}_4$	$10\times \text{Sym}(3)$	${(q-1)}^2\times (q^5-1)$
[97,3,2,5,7,61][4]	6A	(31,32)	$-4\prime$	$3{\mathrm{A}}_1+{\mathrm{D}}_4$	$6\times \text{Sym}(6)$	${(q+1)}^4\times (q^3+1)$
[1,4,18,82][2,3,48]	6B	(21,800)	$-21$	${\mathrm{E}}_7(a_4)$	$2\times (3_{+}^{1+2}:{\text{SL}}_2(3))$	${(q^2-q+1)}^2\times (q^3+1)$
[1,4][5]	6C	(3,36)	$18\prime$	${\mathrm{A}}_1+{\mathrm{A}}_2$	$2\times 6\times \text{Sym}(4)$	${(q-1)}^3\times (q^4+q^3-q-1)$
[3,2,5][4]	6D	(4,8)	$13\prime$	${\mathrm{D}}_4$		$(q-1)\times (q^2-1)\times (q^4-q^3+q-1)$
[97,3,2,6][7]	6E	(5,2)	$-13\prime$	$3{\mathrm{A}}_1+{\mathrm{A}}_2$		$(q+1)\times (q^2-1)\times (q^4+q^3-q-1)$
[97,3,2,5,7][4]	6F	(14,16)	$-18\prime$	$2{\mathrm{A}}_1+{\mathrm{D}}_4$		${(q+1)}^3\times (q^4-q^3+q-1)$
[1,4,18,82][2,3,7]	6G	(23,708)	$-10$	${\mathrm{A}}_1+{\mathrm{D}}_6(a_2)$	$6\times \text{Sym}{(3)}^2$	$(q+1)\times {(q^3+1)}^2$
[1,18,4][2,3,48]	6H	(12,144)	25	${\mathrm{E}}_6(a_2)$	$6\times {\text{SL}}_2(3)$	$(q^2-q+1)\times (q^5-q^4+q^3-q^2+q-1)$
[97,2,5,7][1,4,6]	6I	(25,420)	$-25$	${\mathrm{A}}_2+{\mathrm{A}}_5$		$(q^2+q+1)\times (q^5+q^4+q^3+q^2+q+1)$
[1,2,5][6]	6J	(4,24)	$9\prime$	$2{\mathrm{A}}_1+{\mathrm{A}}_2$	$2\times 6\times \text{Dih}(8)$	$(q-1)\times (q^2-1)\times (q^4+q^3-q-1)$
[3,2,5][4,7]	6K	(5,8)	$-9\prime$	${\mathrm{A}}_1+{\mathrm{D}}_4$		$(q+1)\times (q^2-1)\times (q^4-q^3+q-1)$
[1,2,5][3,6]	6L	(5,12)	15	${\mathrm{A}}_1+2{\mathrm{A}}_2$	$2\times 6\times \text{Sym}(3)$	$(q^3-1)\times (q^4+q^3-q-1)$
[2,5,7][4,6]	6M	(5,16)	$-22$	${\mathrm{A}}_5$		Table 9
[1,4,18,82][2,3]	6N	(10,112)	$-15$	${\mathrm{D}}_6(a_2)$		$(q^3+1)\times (q^4-q^3+q-1)$
[1,4,6,69][3,2]	6O	(14,48)	22	${\mathrm{A}}_1+{\mathrm{A}}_5$		Table 9
[1,4,6][3,5]	6P	(5,32)	18	${\mathrm{A}}_5$	$2^2\times 6$	$(q-1)\times (q^6-1)$
[1,2,5,7][4,6]	6Q	(6,16)	$-18$	${\mathrm{A}}_1+{\mathrm{A}}_5$		$(q+1)\times (q^6-1)$
[1,4,6][3,5,7]	7A	(6,32)	29	${\mathrm{A}}_6$	14	$q^7-1$
[1,4][3,2,5]	8A	(5,32)	19	${\mathrm{D}}_5$	$2^2\times 8$	$(q-1)\times (q^6-q^4+q^2-1)$
[1,4][3,2,5,7]	8B	(6,16)	$-19$	${\mathrm{A}}_1+{\mathrm{D}}_5$		$(q+1)\times (q^6-q^4+q^2-1)$
[2,3,97][1,4,18]	8C	(8,64)	30	${\mathrm{D}}_6(a_1)$		Table 9
[97,3,5,7][1,4,6]	8D	(17,316)	$-30$	${\mathrm{A}}_7$		Table 9
[1,4,18][2,3,6]	9A	(8,80)	24	${\mathrm{E}}_6(a_1)$	18	$q^7-q^6+q^4-q^3+q-1$
[2,3,5,7][4,6,97]	10A	(15,96)	$-12\prime$	${\mathrm{A}}_1+{\mathrm{D}}_6$	$10\times \text{Sym}(3)$	${(q+1)}^2\times (q^5+1)$
[1,2,5][4,6]	10B	(5,40)	17	${\mathrm{A}}_1+{\mathrm{A}}_4$	2 × 10	$(q-1)\times (q^6+q^5-q-1)$
[2,3,5,7][4,6]	10C	(6,32)	$-17$	${\mathrm{D}}_6$		$(q+1)\times (q^6-q^5+q-1)$
[1,5,7][3,6]	12A	(5,24)	26	${\mathrm{A}}_2+{\mathrm{A}}_3$	$2^2\times 12$	$(q-1)\times (q^6+q^5+q^4-q^2-q-1)$
[1,2,5][97,3,6]	12B	(6,8)	$-{20}^{\prime }$	${\mathrm{A}}_1+{\mathrm{A}}_2+{\mathrm{A}}_3$		$(q+1)\times (q^6+q^5+q^4-q^2-q-1)$
[2,3][4,18,1]	12C	(7,64)	$20\prime$	${\mathrm{D}}_5(a_1)$		$(q-1)\times (q^6-q^5+q^4-q^2+q-1)$
[2,3][4,18,1,7]	12D	(8,32)	$-26$	${\mathrm{A}}_1+{\mathrm{D}}_5(a_1)$		$(q+1)\times (q^6-q^5+q^4-q^2+q-1)$
[1,4,6][3,2,5]	12E	(6,32)	23	${\mathrm{E}}_6$	2 × 12	$q^7-q^5-q^4+q^3+q^2-1$
[1,4,18,82][2,3,6]	12F	(11,280)	$-23$	${\mathrm{E}}_7(a_2),{\mathrm{E}}_7(b_2)$		$q^7-q^5+q^4+q^3-q^2+1$
[1,4,18,7][3,2,6]	14A	(9,160)	$-29$	${\mathrm{E}}_7(a_1)$	14	$q^7+1$
[97,4,6][1,5,7]	15A	(6,16)	27	${\mathrm{A}}_2+{\mathrm{A}}_4$	30	$q^7+q^6+q^5-q^2-q-1$
[1,4,6][3,2,5,7]	18A	(7,64)	$-24$	${\mathrm{E}}_7$	18	$q^7+q^6-q^4-q^3+q+1$
[1,4,18][2,3,48,97]	30A	(13,366)	$-27$	${\mathrm{E}}_7(a_3)$	30	$q^7-q^6+q^5+q^2-q+1$

Table 14 The maximal tori of ${}^2{\mathrm{E}}_6(q)$.

w	σ-class of w	Min	$T_w(q)$	Shape of $C_{W,\sigma }(w)$	Structure of $T_w(q)$
w0	$2{\mathrm{B}}_1$	(36,1)	1	$W({\mathrm{E}}_6)\sim {\text{Sp}}_4(3):2$	${(q+1)}^6$
$[5,4,5,69,3,4,5]$	$2{\mathrm{D}}_{12}4{\mathrm{B}}_{24}$	(15,1)	2	$2\times \text{Sym}(6)$	$(q^2-1)\times {(q+1)}^4$
${\text{Id}}_W$	$1{\mathrm{A}}_{1}2{\mathrm{C}}_{12}3{\mathrm{C}}_{32}$	(0,1)	8	$W({\mathrm{F}}_4)\sim 2_{+}^{1+4}:\text{Sym}{(3)}^2$	${(q-1)}^2\times {(q^2-1)}^2$
$[18,6,48,5]$	$6{\mathrm{A}}_{16}{\mathrm{C}}_{64}$	(12,80)	21	$3_{+}^{1+2}:{\text{SL}}_2(3)$	${(q^2-q+1)}^3$
$[5,2,4,69,3,18]$	$6{\mathrm{C}}_{32}{\mathrm{E}}_{64}{\mathrm{F}}_{144}$	(16,20)	4	$3\times (\text{Sym}(3)\mathrm{\wr }2)$	${(q+1)}^3\times (q^3+1)$
$[69,4]$	$2{\mathrm{B}}_{12}{\mathrm{C}}_{18}4{\mathrm{D}}_{144}6{\mathrm{E}}_{96}$	(6,1)	3	$\text{Dih}(8)\times \text{Sym}(4)$	${(q+1)}^2\times {(q^2-1)}^2$
$[2,1,3,48]$	$2{\mathrm{B}}_{32}4{\mathrm{D}}_{288}6{\mathrm{A}}_{128}{\mathrm{E}}_{32}$	(14,146)	10	$3\times \text{Sym}{(3)}^2$	Table 15
$[1]$	$2{\mathrm{A}}_{24}4{\mathrm{C}}_{36}6{\mathrm{B}}_{192}{\mathrm{G}}_{288}$	(1,4)	16	$4\times \text{Sym}(4)$	${(q-1)}^2\times (q^4-1)$
$[6,2,4,69]$	$4{\mathrm{A}}_{12}{\mathrm{D}}_{144}12{\mathrm{A}}_{384}$	(18,120)	14	${\text{GU}}_2(3)\sim 4\cdot \text{Sym}(4)$	${(q^3+q^2+q+1)}^2$
$[69]$	$2{\mathrm{A}}_{12}{\mathrm{D}}_{72}4{\mathrm{C}}_{72}6{\mathrm{D}}_{96}{\mathrm{G}}_{288}$	(1,2)	5	$2^2\times \text{Sym}(4)$	${(q^2-1)}^3$
$[5,6,2,69]$	$3{\mathrm{A}}_{16}{\mathrm{C}}_{128}6{\mathrm{F}}_{192}9{\mathrm{A}}_{384}$	(16,180)	25	$3\times {\text{SL}}_2(3)$	$(q^2+q+1)\times (q^4+q^2+1)$
$[4,2]$	$3{\mathrm{A}}_{64}{\mathrm{B}}_{32}6{\mathrm{C}}_{288}{\mathrm{F}}_{96}9{\mathrm{A}}_{384}12{\mathrm{A}}_{576}$	(2,2)	13	$6\times \text{Sym}(3)$	$(q^2-1)\times (q^4+q^3-q-1)$
$[6,5]$	$2{\mathrm{C}}_{96}3{\mathrm{B}}_{64}{\mathrm{C}}_{32}4{\mathrm{D}}_{288}5{\mathrm{A}}_{576}9{\mathrm{A}}_{384}$	(2,6)	22		$(q-1)\times (q^5-q^4+q^3-q^2+q-1)$
$[3,18,6]$	$2{\mathrm{D}}_{96}4{\mathrm{C}}_{288}6{\mathrm{G}}_{96}8{\mathrm{A}}_{576}12{\mathrm{B}}_{384}$	(5,22)	15		$(q^2-q+1)\times (q^4-q^3+q-1)$
$[69,4,3]$	$4{\mathrm{B}}_{192}6{\mathrm{B}}_{288}{\mathrm{G}}_{192}10{\mathrm{A}}_{576}12{\mathrm{B}}_{192}$	(7,8)	6		${(q+1)}^2\times (q^4-q^3+q-1)$
$[2,69,4]$	$2{\mathrm{D}}_{72}4{\mathrm{B}}_{36}{\mathrm{C}}_{72}6{\mathrm{D}}_{288}8{\mathrm{A}}_{576}10{\mathrm{A}}_{576}$	(7,6)	7	$4\times \text{Dih}(8)$	${(q+1)}^2\times (q^4-1)$
$[3,4]$	$3{\mathrm{B}}_{144}4{\mathrm{D}}_{576}5{\mathrm{A}}_{576}6{\mathrm{A}}_{192}{\mathrm{C}}_{96}12{\mathrm{A}}_{576}$	(2,4)	9	$3\times \text{Dih}(8)$	$(q^2-1)\times (q^4-q^3+q-1)$
$[6,4]$	$2{\mathrm{C}}_{144}3{\mathrm{C}}_{288}4{\mathrm{A}}_{144}{\mathrm{D}}_{72}5{\mathrm{A}}_{576}6{\mathrm{E}}_{288}{\mathrm{F}}_{576}9{\mathrm{A}}_{1152}$	(2,6)	11	$2^2\times 4$	$(q^2-1)\times (q^4-1)$
$[6,2,3]$	$2{\mathrm{D}}_{288}4{\mathrm{B}}_{288}6{\mathrm{B}}_{192}{\mathrm{D}}_{96}{\mathrm{G}}_{1152}8{\mathrm{A}}_{576}10{\mathrm{A}}_{576}12{\mathrm{B}}_{1152}$	(3,6)	18	$2^2\times 3$	Table 15
$[6,2,4]$	$6{\mathrm{B}}_{192}{\mathrm{D}}_{384}{\mathrm{G}}_{1152}8{\mathrm{A}}_{1152}10{\mathrm{A}}_{1152}12{\mathrm{B}}_{288}$	(3,4)	20	12	$q^6+q^5+q^4-q^2-q-1$
$[4,18,48,5]$	$4{\mathrm{A}}_{384}5{\mathrm{A}}_{1152}6{\mathrm{C}}_{576}{\mathrm{F}}_{576}9{\mathrm{A}}_{1152}12{\mathrm{A}}_{480}$	(6,56)	23		$q^6-q^5+q^3-q+1$
$[5,4,1]$	$4{\mathrm{C}}_{576}6{\mathrm{B}}_{576}{\mathrm{G}}_{576}8{\mathrm{A}}_{1152}10{\mathrm{A}}_{1152}12{\mathrm{B}}_{1152}$	(3,12)	17	10	$q^6-q^5+q-1$
$[2,69,3,18]$	$4{\mathrm{D}}_{576}5{\mathrm{A}}_{1152}6{\mathrm{E}}_{576}{\mathrm{F}}_{576}9{\mathrm{A}}_{1152}12{\mathrm{A}}_{1152}$	(8,40)	12		$(q+1)\times (q^5+1)$
$[2,18,6,3]$	$4{\mathrm{D}}_{1152}5{\mathrm{A}}_{1152}6{\mathrm{A}}_{384}{\mathrm{C}}_{384}{\mathrm{E}}_{384}9{\mathrm{A}}_{1152}12{\mathrm{A}}_{1152}$	(4,24)	24	9	$q^6-q^3+1$
$[5,2,4]$	$4{\mathrm{C}}_{576}6{\mathrm{D}}_{576}{\mathrm{G}}_{576}8{\mathrm{A}}_{2448}10{\mathrm{A}}_{1152}12{\mathrm{B}}_{1152}$	(3,8)	19	8	$q^6-q^4+q^2-1$

Incomplete lists of maximal tori for untwisted simply connected exceptional groups of Lie type are available in Deriziotis and Fakiolas [12], while Galt and Staroletov [17–20] give lists which are, in some cases, partial for ${\mathrm{G}}_2(q),{}^2{\mathrm{G}}_2(q),{}^3{\mathrm{D}}_4(q),{\mathrm{F}}_4(q),{\mathrm{E}}_6(q),{\mathrm{E}}_7(q)$ and ${\mathrm{E}}_8(q)$. Various lists are also to be found in Deriziotis and Michler [13], Fleischmann and Janiszczak [14], [15], Gager [16], Haller [21], Lawther [23], Shinoda [26], and Shoji [27]. Partial lists of admissible graphs may also be found in [12] (for ${\mathrm{E}}_6,{\mathrm{E}}_7,{\mathrm{E}}_8$) and [16]. We remark that in [16], complete lists of both maximal tori (in the twisted and untwisted case) and admissible graphs are given for both ${\mathrm{G}}_2(q)$ and ${\mathrm{F}}_4(q)$. Moreover, lists of admissible graphs and corresponding tori structures are given for ${\mathrm{E}}_6,{\mathrm{E}}_7$ and ${\mathrm{E}}_8$, but only for the semi-Coxeter and Coxeter classes of W. Carter [7] gives complete lists of admissible graphs, however, these are not directly linked to maximal tori like they are here. Also, related work on the spectra of exceptional groups of Lie type is given in Buturlakin [3–5]. To enable backward compatibility, where appropriate, our tables have a column giving the corresponding label for the maximal tori in [12] (see Section 3 for how we label those not appearing in [12]).

All decompositions exhibited in Tables 4–15 have been computed by hand, and, sometimes, agree with the output from the Magma [2] function TwistedTorusOrder or the lists of [16], [26] and [12]. The ambiguity here lies in the fact that there are many ways to describe a finite abelian group as a direct product of cyclic groups. To address this confusion in general, we tabulate the torsion coefficient decompositions of the maximal tori in groups of exceptional type. By this, we mean that we express each torus $T_w(q)$ as a direct product ${\lambda }_1(q)\times {\lambda }_2(q)\times \cdots {\lambda }_n(q)$, with ${\lambda }_1(q)|{\lambda }_2(q)|\cdots |{\lambda }_n(q)$ where ${\lambda }_i(q)$ denotes a cyclic group of order ${\lambda }_i(q)$. In the case of [16], [26] and [12], torus structures are obtained by diagonalizing relation matrices. These papers present many torus structures corresponding to diagonal matrices which are not in the canonical form, as detailed in 8. The function TwistedTorusOrder obtains torus structures at all prime powers $q\le 20$ and produces a collection of polynomials in q which yield the cyclic factors of the maximal tori for groups over the field of q elements, on substitution of any $q\le 20$. The polynomials produced by this algorithm are not necessarily presented in the torsion coefficient decomposition, and there is no reason they should yield the cyclic factors for the maximal tori of groups over the field of q > 20 elements, although using Tables 4–15 we present authors have verified the validity of the output of TwistedTorusOrder in the untwisted exceptional cases. A more detailed discussion of how TwistedTorusOrder works is included in Section 6. In [25] we include a function which takes a fixed q as an argument and is hence guaranteed to produce accurate torus structures, in torsion coefficient decomposition, for all Lie types. Additionally, our function accepts twisted root data, and can therefore be used to compute maximal torus structures in a wider range of groups than was previously possible.

Table 4 The maximal tori of ${\mathrm{G}}_2(q)$.

w	Class	Min	Γw	Shape of $C_W(w)$	Structure of $T_w(q)$
Id	1A	(0,1)	$\varnothing$	$\text{Dih}(12)$	${(q-1)}^2$
[1,6] = w0	2A	(6,1)	${\mathrm{A}}_1+{\tilde{\mathrm{A}}}_1$		${(q+1)}^2$
[2]	2B	(1,1)	${\mathrm{A}}_1$	2^2	$q^2-1$
[1]	2C	(1,1)	${\tilde{\mathrm{A}}}_1$		$q^2-1$
[2][6]	3A	(4,2)	${\mathrm{A}}_2$	6	$q^2+q+1$
[1][2]	6A	(2,2)	${\mathrm{G}}_2$		$q^2-q+1$

Table 5 The maximal tori of ${\mathrm{F}}_4(q)$.

w	Class	Min	Γw	Shape of $C_W(w)$	Structure of $T_w(q)$
Id	1A	(0,1)	$\varnothing$	$W({\mathrm{F}}_4)\sim 2_{+}^{1+4}:\text{Sym}{(3)}^2$	${(q-1)}^4$
[1,14,20,22] $\sim w_0$	2A	(24,1)	$4{\mathrm{A}}_1,4{\tilde{\mathrm{A}}}_1,2{\mathrm{A}}_1+2{\tilde{\mathrm{A}}}_1$		${(q+1)}^4$
[3]	2B	(1,2)	${\tilde{\mathrm{A}}}_1$	$2^2\times \text{Sym}(4)$	${(q-1)}^2\times (q^2-1)$
[1]	2C	(1,2)	${\mathrm{A}}_1$		${(q-1)}^2\times (q^2-1)$
[3,14,21]	2D	(9,1)	$3{\mathrm{A}}_1,2{\tilde{\mathrm{A}}}_1+{\mathrm{A}}_1$		${(q+1)}^2\times (q^2-1)$
[1,3,14]	2E	(9,1)	$3{\tilde{\mathrm{A}}}_1,2{\mathrm{A}}_1+{\tilde{\mathrm{A}}}_1$		${(q+1)}^2\times (q^2-1)$
[1,20]	2F	(4,1)	$2{\mathrm{A}}_1,2{\tilde{\mathrm{A}}}_1$	$\text{Dih}{(8)}^2$	Table 9
[1,3]	2G	(2,3)	${\mathrm{A}}_1+{\tilde{\mathrm{A}}}_1$	2^4	${(q^2-1)}^2$
[1,21,2][4]	3A	(16,16)	${\mathrm{A}}_2+{\tilde{\mathrm{A}}}_2$	$3\times {\text{SL}}_2(3)$	${(q^2+q+1)}^2$
[3][4]	3B	(2,2)	${\tilde{\mathrm{A}}}_2$	$6\times \text{Sym}(3)$	$(q-1)\times (q^3-1)$
[1][2]	3C	(2,2)	${\mathrm{A}}_2$		$(q-1)\times (q^3-1)$
[1,4][13,14]	4A	(12,12)	$2{\mathrm{B}}_2,{\mathrm{D}}_4(a_1)$	${\text{GU}}_2(3)\sim 4\cdot \text{Sym}(4)$	${(q^2+1)}^2$
[2][3]	4B	(2,2)	${\mathrm{B}}_2$	$4\times \text{Dih}(8)$	$(q-1)\times (q^3-q^2+q-1)$
[1,14][2,21]	4C	(14,16)	${\mathrm{A}}_3+{\tilde{\mathrm{A}}}_1,{\mathrm{B}}_2+2{\mathrm{A}}_1$		$(q+1)\times (q^3+q^2+q+1)$
[6,21][13]	4D	(5,4)	${\tilde{\mathrm{A}}}_3,{\mathrm{A}}_1+{\mathrm{B}}_2$	$2^2\times 4$	Table 9
[14,20][2]	4E	(5,4)	${\mathrm{A}}_3,{\tilde{\mathrm{A}}}_1+{\mathrm{B}}_2$		Table 9
[2,4][3,14]	6A	(8,16)	${\mathrm{F}}_4(a_1)$	$3\times {\text{SL}}_2(3)$	${(q^2-q+1)}^2$
[1,14,20][2]	6B	(10,8)	${\mathrm{D}}_4,{\mathrm{B}}_3+{\tilde{\mathrm{A}}}_1$	$6\times \text{Sym}(3)$	$(q+1)\times (q^3+1)$
[3,6,21][13]	6C	(10,8)	${\tilde{\mathrm{D}}}_4,{\mathrm{C}}_3+{\mathrm{A}}_1$		$(q+1)\times (q^3+1)$
[2,21][4]	6D	(3,2)	${\mathrm{A}}_1+{\tilde{\mathrm{A}}}_2$	$2^2\times 3$	$q^4+q^3-q-1$
[2][14,21]	6E	(3,2)	${\tilde{\mathrm{A}}}_1+{\mathrm{A}}_2$		$q^4+q^3-q-1$
[4][3,14]	6F	(3,4)	${\mathrm{C}}_3$		$q^4-q^3+q-1$
[2,4][14]	6G	(3,4)	${\mathrm{B}}_3$		$q^4-q^3+q-1$
[1,14][2,4]	8A	(6,14)	${\mathrm{B}}_4,{\mathrm{C}}_4$	8	$q^4+1$
[1,3][2,4]	12A	(4,8)	${\mathrm{F}}_4$	12	$q^4-q^2+1$

Table 8 The maximal tori of ${\mathrm{E}}_8(q)$.

w	Class	Min	$T_w(q)$	Γw	Shape of $C_W(w)$	Structure of $T_w(q)$
Id	1A	(0,1)	$1″$	$\varnothing$	$W({\mathrm{E}}_8)\sim 2\mathrm{ }·\mathrm{ }{\Omega }_8^{+}(2).2$	${(q-1)}^8$
w0	2A	(120,1)	$-1″$	$8{\mathrm{A}}_1$		${(q+1)}^8$
[1]	2B	(1,8)	$2″$	${\mathrm{A}}_1$	$2^2\times {\text{Sp}}_6(2)$	${(q-1)}^6\times (q^2-1)$
[97,3,2,5,7,120,61]	2C	(63,1)	$-2″$	$7{\mathrm{A}}_1$		${(q+1)}^6\times (q^2-1)$
[1,4,6,69]	2D	(12,1)	$8\prime$	$4{\mathrm{A}}_1$	$2^2·(2^8:\text{Sym}{(3)}^3)$	Table 9
[1,2]	2E	(2,21)	$3″$	$2{\mathrm{A}}_1$	$2^6·(2^2\times \text{Sym}(6))$	${(q-1)}^4\times {(q^2-1)}^2$
[97,3,2,5,7,120]	2F	(30,1)	$-3″$	$6{\mathrm{A}}_1$		${(q+1)}^4\times {(q^2-1)}^2$
[1,4,6]	2G	(3,21)	$5″$	$3{\mathrm{A}}_1$	$2^5·(2^4:\text{Sym}{(3)}^2)$	${(q-1)}^2\times {(q^2-1)}^3$
[97,3,2,5,7]	2H	(13,2)	$-5″$	$5{\mathrm{A}}_1$		${(q+1)}^2\times {(q^2-1)}^3$
[2,3,5,7]	2I	(4,7)	31	$4{\mathrm{A}}_1$	$2^6·(\text{Sym}(4)\times 2^2)$	${(q^2-1)}^4$
[1][3]	3A	(2,14)	$4″$	${\mathrm{A}}_2$	$(6\times {\text{Sp}}_4(3)):2$	${(q-1)}^5\times (q^3-1)$
[1,2,5,8][3,69,6,120]	3B	(80,4480)	56	$4{\mathrm{A}}_2$	$3\times 2^{·}{\mathrm{U}}_4(2)$	${(q^2+q+1)}^4$
[1,2,5][3,6,69]	3C	(24,80)	$21\prime$	$3{\mathrm{A}}_2$	$(\text{Dih}(12)\times 6)·{\text{ASL}}_2(3)$	Table 9
[1,5][3,6]	3D	(4,32)	$10\prime$	$2{\mathrm{A}}_2$	$(2\times 3\times \text{Sym}{(3)}^3):2$	${(q-1)}^2\times {(q^3-1)}^2$
[2,3,7,120][4,18,8,74]	4A	(60,15120)	59	$2{\mathrm{D}}_4(a_1)$	$(4°2_{+}^{1+4}).\text{Alt}(6).2$	${(q^2+1)}^4$
[2,3][4,18]	4B	(6,12)	$14″$	${\mathrm{D}}_4(a_1)$	$(2^3:\text{Sym}(4)):{\text{GU}}_2(3)$	${(q-1)}^2\times {(q^3-q^2+q-1)}^2$
[97,3,5,7,2,120][1,6]	4C	(66,1260)	$-14″$	$2{\mathrm{A}}_1+2{\mathrm{A}}_3$		${(q+1)}^2\times {(q^3+q^2+q+1)}^2$
[1,4][3]	4D	(3,28)	$7″$	${\mathrm{A}}_3$	$2^5:(4\times \text{Sym}(5))$ $\sim 2^5:{\text{CO}}_3(5)$	${(q-1)}^4\times (q^4-1)$
[97,3,2,5,7,120][1]	4E	(31,12)	$-7″$	$4{\mathrm{A}}_1+{\mathrm{A}}_3$		${(q+1)}^4\times (q^4-1)$
[1,69,4,6][5]	4F	(13,16)	$16\prime$	$2{\mathrm{A}}_1+{\mathrm{A}}_3$	$(2\times 4\times \text{Alt}(4)\times \text{Sym}(4)):2$	Table 9
[2,3][4,18,7]	4G	(7,24)	28	${\mathrm{A}}_1+{\mathrm{D}}_4(a_1)$	$2^3:(2\times {\text{GU}}_2(3))$	Table 9
[97,3,5,7][1,6,2]	4H	(33,360)	$-28$	${\mathrm{A}}_1+2{\mathrm{A}}_3$		Table 9
[97,3,5,7][1,6]	4I	(16,60)	37	$2{\mathrm{A}}_3$	$(2^4\times \text{Dih}(8))\mathrm{ }·(2\times 4)$	Table 9
[1,4,6][5]	4J	(4,80)	$11\prime$	${\mathrm{A}}_1+{\mathrm{A}}_3$	$\text{Sym}(4)\times 2^3\times 4$	${(q-1)}^2\times (q^2-1)\times (q^4-1)$
[97,3,2,5,7][6]	4K	(14,24)	$-11\prime$	$3{\mathrm{A}}_1+{\mathrm{A}}_3$		${(q+1)}^2\times (q^2-1)\times (q^4-1)$
[2,3,7,120][4,18,8]	4L	(21,384)	49	${\mathrm{A}}_3+{\mathrm{D}}_4(a_1)$	$(2\times 4^3):\text{Sym}(3)$	${(q^2+1)}^2\times (q^4-1)$
[1,7,2,5][4]	4M	(5,40)	33	$2{\mathrm{A}}_1+{\mathrm{A}}_3$	$(\text{Dih}(8)\times 2^3)·2^2$	${(q^2-1)}^2\times (q^4-1)$
[3,5,7,120][4,8]	4N	(6,32)	36	$2{\mathrm{A}}_3$	$(2\times 4)\mathrm{\wr }2$	${(q^4-1)}^2$
[1,4][3,5]	5A	(4,48)	$12″$	${\mathrm{A}}_4$	$10\times \text{Sym}(5)$	${(q-1)}^3\times (q^5-1)$
[1,4,69,8][3,5,7,120]	5B	(48,7952)	57	$2{\mathrm{A}}_4$	$5\times {\text{SL}}_2(5)$	${(q^4+q^3+q^2+q+1)}^2$
[97,3,2,5,7,61][4,120]	6A	(64,56)	$-4″$	$4{\mathrm{A}}_1+{\mathrm{D}}_4$	$(6\times {\text{Sp}}_4(3)):2$	${(q+1)}^5\times (q^3+1)$
[1,4,18,82][2,3,48,56]	6B	(40,4480)	$-56$	${\mathrm{E}}_8(a_8)$	$3\times 2^{·}{\mathrm{U}}_4(2)$	${(q^2-q+1)}^4$
[1,4][5]	6C	(3,56)	$6″$	${\mathrm{A}}_1+{\mathrm{A}}_2$	$2\times 6\times \text{Sym}(6)$	${(q-1)}^4\times (q^4+q^3-q-1)$
[97,3,2,5,7,61][4]	6D	(31,32)	$-6″$	$3{\mathrm{A}}_1+{\mathrm{D}}_4$		${(q+1)}^4\times (q^4-q^3+q-1)$
[1,4,18,82][2,3,48,120]	6E	(42,11592)	$-21\prime$	${\mathrm{A}}_1+{\mathrm{E}}_7(a_4)$	$(2\times {\text{SU}}_3(2)\times \text{Sym}(3)):3$	Table 9
[3,2,5][4]	6F	(4,8)	$13″$	${\mathrm{D}}_4$	$(2^2\times 3){.2}^4.\text{Sym}{(3)}^2$	${(q-1)}^2\times (q^2-1)\times (q^4-q^3+q-1)$
[1,2,5,7,120][3]	6G	(14,2)	$-13″$	$4{\mathrm{A}}_1+{\mathrm{A}}_2$		${(q+1)}^2\times (q^2-1)\times (q^4+q^3-q-1)$
[1,4,18,82][2,3,48]	6H	(21,800)	$-43$	${\mathrm{E}}_7(a_4)$	$(2^2\times {\text{SU}}_3(2)):3$	${(q^2-q+1)}^2\times (q^4-q^3+q-1)$
[1,5,8][3,6,120,2]	6I	(25,80)	43	${\mathrm{A}}_1+3{\mathrm{A}}_2$		${(q^2+q+1)}^2\times (q^4+q^3-q-1)$
[1,4,18,82][2,3,7,120]	6J	(44,4070)	$-10\prime$	$2{\mathrm{A}}_1+{\mathrm{D}}_6(a_2)$	$(2\times 3\times \text{Sym}{(3)}^3):2$	${(q+1)}^2\times {(q^3+1)}^2$
[1,18,4,120][2,3,48,8]	6K	(44,16374)	63	${\mathrm{A}}_2+{\mathrm{E}}_6(a_2)$	$3\times {\text{SL}}_2{(3)}^2$	${(q^4+q^2+1)}^2$
[1,2,5][6]	6L	(4,56)	$9″$	$2{\mathrm{A}}_1+{\mathrm{A}}_2$	$2\times 3\times \text{Dih}(8)\times \text{Sym}(4)$	${(q-1)}^2\times (q^2-1)\times (q^4+q^3-q-1)$
[97,3,2,5,7][4]	6M	(14,16)	$-9″$	$2{\mathrm{A}}_1+{\mathrm{D}}_4$		${(q+1)}^2\times (q^2-1)\times (q^4-q^3+q-1)$
[1,18,4][2,3,48]	6N	(12,144)	$25\prime$	${\mathrm{E}}_6(a_2)$	$2\times 3\times \text{Sym}(3)\times {\text{SL}}_2(3)$	$(q^3-2q^2+2q-1)\times (q^5-q^4+q^3-q^2+q-1)$
[1,2,5,7,120][3,6,8]	6O	(46,3752)	$-25\prime$	${\mathrm{A}}_1+{\mathrm{A}}_2+{\mathrm{A}}_5$		$(q^3+2q^2+2q+1)\times (q^5+q^4+q^3+q^2+q+1)$
[3,2,5][4,7]	6P	(5,16)	$-32$	${\mathrm{A}}_1+{\mathrm{D}}_4$	$2^2\times 6\times \text{Sym}(4)$	${(q^2-1)}^2\times (q^4-q^3+q-1)$
[97,3,2,6][7]	6Q	(5,16)	32	$3{\mathrm{A}}_1+{\mathrm{A}}_2$		${(q^2-1)}^2\times (q^4+q^3-q-1)$
[1,2,5][3,6]	6R	(5,32)	$15\prime$	${\mathrm{A}}_1+2{\mathrm{A}}_2$	$2\times 6\times \text{Sym}{(3)}^2$	$(q-1)\times (q^3-1)\times (q^4+q^3-q-1)$
[1,4,6,69][3,2]	6S	(14,48)	$22\prime$	${\mathrm{A}}_1+{\mathrm{A}}_5$		Table 9
[1,4,18,82][2,3,120]	6T	(23,708)	$-15\prime$	${\mathrm{A}}_1+{\mathrm{D}}_6(a_2)$		$(q+1)\times (q^3+1)\times (q^4-q^3+q-1)$
[1,2,5,8][3,6]	6U	(6,8)	34	$2{\mathrm{A}}_1+2{\mathrm{A}}_2$	$(2^2\times 6\times \text{Sym}(3)):2$	${(q^4+q^3-q-1)}^2$
[1,4,18,82][2,3]	6V	(10,112)	$-34$	${\mathrm{D}}_6(a_2)$		${(q^4-q^3+q-1)}^2$
[1,18,4][2,3,48,8]	6W	(13,114)	54	${\mathrm{A}}_1+{\mathrm{E}}_6(a_2)$	$2\times 6\times {\text{SL}}_2(3)$	Table 9
[97,2,5,7][1,4,6]	6X	(25,420)	$-54$	${\mathrm{A}}_2+{\mathrm{A}}_5$		Table 9
[2,3,5,7][4,8]	6Y	(6,16)	40	${\mathrm{A}}_2+{\mathrm{D}}_4$	$6^2\times \text{Sym}(3)$	$(q^2-1)\times (q^6-1)$
[1,4,6][3,5]	6Z	(5,64)	$18\prime$	${\mathrm{A}}_5$	$2^2\times 6\times \text{Sym}(3)$	${(q-1)}^2\times (q^6-1)$
[1,4,82,120,6][2,8]	6AA	(15,48)	$-18\prime$	$2{\mathrm{A}}_1+{\mathrm{A}}_5$		${(q+1)}^2\times (q^6-1)$
[1,2,5,7][4,6]	6BB	(6,48)	39	${\mathrm{A}}_1+{\mathrm{A}}_5$	$2^3\times 6$	$(q^2-1)\times (q^6-1)$
[1,4,6][3,5,7]	7A	(6,96)	29	${\mathrm{A}}_6$	2 × 14	$(q-1)\times (q^7-1)$
[1,4][3,2,5]	8A	(5,32)	$19\prime$	${\mathrm{D}}_5$	$2:(8\times \text{Sym}(4))$	${(q-1)}^2\times (q^6-q^4+q^2-1)$
[1,4,6,8][7,82,120]	8B	(15,32)	$-19\prime$	$2{\mathrm{A}}_1+{\mathrm{D}}_5$		${(q+1)}^2\times (q^6-q^4+q^2-1)$
[1,4,18,82][2,3,8,74]	8C	(30,7748)	61	${\mathrm{D}}_8(a_3)$	${\text{CU}}_2(3)\sim 8^{·}\text{Sym}(4)$	${(q^4+1)}^2$
[2,3,97][1,4,18]	8D	(8,64)	30	${\mathrm{D}}_6(a_1)$	$8\times (2^2:4)$	Table 9
[1,4,6,8][3,7,82,120]	8E	(34,2080)	$-30$	${\mathrm{A}}_3+{\mathrm{D}}_5$		Table 9
[1,4][3,2,5,7]	8F	(6,48)	42	${\mathrm{A}}_1+{\mathrm{D}}_5$	$2^3\times 8$	$(q^2-1)\times (q^6-q^4+q^2-1)$
[97,3,5,7][1,4,6]	8G	(17,316)	48	${\mathrm{A}}_7$		Table 9
[1,4,6,8][3,5,7]	8H	(7,64)	47	${\mathrm{A}}_7$	2 × 8	$q^8-1$
[1,4,18][2,3,6]	9A	(8,80)	$24\prime$	${\mathrm{E}}_6(a_1)$	$18\times \text{Sym}(3)$	$(q-1)\times (q^7-q^6+q^4-q^3+q-1)$
[1,4,6,8][3,5,7,120]	9B	(28,2816)	58	${\mathrm{A}}_8$	3 × 18	Table 9
[2,3,5,7][4,6,97,120]	10A	(32,256)	$-12″$	$2{\mathrm{A}}_1+{\mathrm{D}}_6$	$10\times \text{Sym}(5)$	${(q+1)}^3\times (q^5+1)$
[1,4,18,118][2,3,48,97]	10B	(24,3370)	$-57$	${\mathrm{E}}_8(a_6)$	$5\times {\text{SL}}_2(5)$	${(q^4-q^3+q^2-q+1)}^2$
[1,2,5][4,6]	10C	(5,96)	$17\prime$	${\mathrm{A}}_1+{\mathrm{A}}_4$	$2\times 10\times \text{Sym}(3)$	${(q-1)}^2\times (q^6+q^5-q-1)$
[2,3,5,7][4,6,97]	10D	(15,96)	$-17\prime$	${\mathrm{A}}_1+{\mathrm{D}}_6$		${(q+1)}^2\times (q^6-q^5+q-1)$
[2,3,5,7][4,6]	10E	(6,32)	$-38$	${\mathrm{D}}_6$	$10\times \text{Dih}(8)$	$(q^2-1)\times (q^6-q^5+q-1)$
[1,4,6,8][7,120]	10F	(6,32)	38	$2{\mathrm{A}}_1+{\mathrm{A}}_4$		$(q^2-1)\times (q^6+q^5-q-1)$
[2,3][4,18,1]	12A	(7,64)	$20″$	${\mathrm{D}}_5(a_1)$	$4\times 6\times \text{Sym}(4)$	${(q-1)}^2\times (q^6-q^5+q^4-q^2+q-1)$
[2,3,7][4,18,8]	12B	(8,24)	41	${\mathrm{A}}_2+{\mathrm{D}}_4(a_1)$	$2\times 3\times {\text{GU}}_2(3)$	$(q^3-q^2+q-1)\times (q^5+q^3-q^2-1)$
[97,3,5,2,120][1,6]	12C	(15,16)	$-20″$	$2{\mathrm{A}}_1+{\mathrm{A}}_2+{\mathrm{A}}_3$	$4\times 6\times \text{Sym}(4)$	${(q+1)}^2\times (q^6+q^5+q^4-q^2-q-1)$
[2,3,120,7,61][4,18,8]	12D	(46,15134)	$-41$	${\mathrm{D}}_4+{\mathrm{D}}_4(a_1)$	$2\times 3\times {\text{GU}}_2(3)$	$(q^3+q^2+q+1)\times (q^5+q^3+q^2+1)$
[1,4,18,82][2,3,6,29]	12E	(20,2696)	67	${\mathrm{E}}_8(a_3),{\mathrm{E}}_8(b_3)$	$3\times {\text{GU}}_2(3)$	${(q^4-q^2+1)}^2$
[1,4,18,82][2,3,48,8]	12F	(22,2360)	$-62$	${\mathrm{E}}_8(a_7)$	$12\times {\text{SL}}_2(3)$	$(q^2-q+1)\times (q^6-q^5+q^3-q+1)$
[1,4,6,8][3,2,5,120]	12G	(26,840)	62	${\mathrm{A}}_2+{\mathrm{E}}_6$		$(q^2+q+1)\times (q^6+q^5-q^3+q+1)$
[1,5,7][3,6]	12H	(5,80)	26	${\mathrm{A}}_2+{\mathrm{A}}_3$	$2\times 12\times \text{Dih}(8)$	${(q-1)}^2\times (q^6+q^5+q^4-q^2-q-1)$
[1,4,7,82,120][3,8]	12I	(17,168)	$-26$	${\mathrm{A}}_3+{\mathrm{D}}_4$		${(q+1)}^2\times (q^6-q^5+q^4-q^2+q-1)$
[1,4,6][3,2,5]	12J	(6,32)	$23\prime$	${\mathrm{E}}_6$	$2\times 12\times \text{Sym}(3)$	$(q-1)\times (q^7-q^5-q^4+q^3+q^2-1)$
[1,4,18,82][2,3,6,120]	12K	(24,1758)	$-23\prime$	${\mathrm{A}}_1+{\mathrm{E}}_7(a_2)$		$(q+1)\times (q^7-q^5+q^4+q^3-q^2+1)$
[1,2,6,8][4,7]	12L	(6,32)	35	${\mathrm{A}}_1+{\mathrm{A}}_2+{\mathrm{A}}_3$	$2^3\times 12$	$(q^2-1)\times (q^6+q^5+q^4-q^2-q-1)$
[2,3][4,18,1,7]	12M	(8,96)	$-35$	${\mathrm{A}}_1+{\mathrm{D}}_5(a_1)$		$(q^2-1)\times (q^6-q^5+q^4-q^2+q-1)$
[2,3,7][4,18,1,8]	12N	(9,64)	51	${\mathrm{A}}_2+{\mathrm{D}}_5(a_1)$	6 × 12	$q^8+q^6-q^2-1$
[2,3,97,7][4,18,1,8]	12O	(22,2040)	60	${\mathrm{D}}_8(a_1)$	$12\times \text{Sym}(3)$	$(q^2+1)\times (q^6+1)$
[1,4,6][3,2,5,120]	12P	(7,32)	52	${\mathrm{A}}_1+{\mathrm{E}}_6$	$2^2\times 12$	$q^8+q^7-q^6-2q^5+2q^3+q^2-q-1$
[1,4,18,82][2,3,6]	12Q	(11,280)	$-52$	${\mathrm{E}}_7(a_2)$		$q^8-q^7-q^6+2q^5-2q^3+q^2+q-1$
[2,3,5,7][4,6,8]	12R	(7,64)	55	${\mathrm{D}}_7$	2 × 12	$q^8-q^6+q^2-1$
[1,4,6,8][5,7,120]	14A	(7,32)	46	${\mathrm{A}}_1+{\mathrm{A}}_6$	2 × 14	$q^8+q^7-q-1$
[1,4,18,7][3,2,6]	14B	(9,160)	$-46$	${\mathrm{E}}_7(a_1)$		$q^8-q^7+q-1$
[2,3,5,7,120][4,6,8]	14C	(18,852)	$-29$	${\mathrm{D}}_8$		$(q+1)\times (q^7+1)$
[97,4,6][1,5,7]	15A	(6,64)	27	${\mathrm{A}}_2+{\mathrm{A}}_4$	2 × 30	$(q-1)\times (q^7+q^6+q^5-q^2-q-1)$
[1,4,18,7][2,3,48,29]	15B	(16,1516)	$-64$	${\mathrm{E}}_8(a_5),{\mathrm{E}}_8(b_5)$	30	$q^8-q^7+q^5-q^4+q^3-q+1$
[1,4,6][3,2,5,7,120]	18A	(16,192)	$-24\prime$	${\mathrm{A}}_1+{\mathrm{E}}_7$	$18\times \text{Sym}(3)$	$(q+1)\times (q^7+q^6-q^4-q^3+q+1)$
[1,4,18,8][2,3,48,97]	18B	(14,732)	$-58$	${\mathrm{E}}_8(a_4)$	3 × 18	Table 9
[1,4,6][3,2,5,7]	18C	(7,64)	$-53$	${\mathrm{E}}_7$	2 × 18	$q^8-q^6-q^5+q^3+q^2-1$
[1,4,18][2,3,6,8]	18D	(9,80)	53	${\mathrm{A}}_1+{\mathrm{E}}_6(a_1)$		$q^8-q^6+q^5-q^3+q^2-1$
[1,4,6,8][3,7,120]	20A	(7,32)	45	${\mathrm{A}}_3+{\mathrm{A}}_4$	2 × 20	$q^8+q^7+q^6+q^5-q^3-q^2-q-1$
[2,3,97][4,18,1,8]	20B	(9,128)	$-45$	${\mathrm{D}}_7(a_1)$		$q^8-q^7+q^6-q^5+q^3-q^2+q-1$
[1,4,18,7][3,2,6,29]	20C	(12,624)	66	${\mathrm{E}}_8(a_2)$	20	$q^8-q^6+q^4-q^2+1$
[1,4,7][3,2,5,8]	24A	(7,32)	50	${\mathrm{A}}_2+{\mathrm{D}}_5$	2 × 24	$q^8+q^7-q^5+q^3-q-1$
[1,4,18,82][2,3,8]	24B	(11,256)	$-50$	${\mathrm{D}}_7(a_2)$		$q^8-q^7+q^5-q^3+q-1$
[1,4,18,7][3,2,6,8]	24C	(10,320)	65	${\mathrm{E}}_8(a_1)$	24	$q^8-q^4+1$
[1,2,6,8][4,7,120]	30A	(7,16)	44	${\mathrm{A}}_1+{\mathrm{A}}_2+{\mathrm{A}}_4$	2 × 30	$q^8+2q^7+2q^6+q^5-q^3-2q^2-2q-1$
[1,4,18][2,3,48,97]	30B	(13,366)	$-44$	${\mathrm{E}}_7(a_3)$		$q^8-2q^7+2q^6-q^5+q^3-2q^2+2q-1$
[1,4,18][2,3,48,97,120]	30C	(26,4996)	$-27$	${\mathrm{A}}_1+{\mathrm{E}}_7(a_3)$		$(q+1)\times (q^7-q^6+q^5+q^2-q+1)$
[1,4,6,8][3,2,5,7]	30D	(8,128)	64	${\mathrm{E}}_8$	30	$q^8+q^7-q^5-q^4-q^3+q+1$

Table 9 The torsion coefficient decomposition of various maximal tori of ${\mathrm{F}}_4(q),{\mathrm{E}}_6(q),{\mathrm{E}}_7(q)$, and ${\mathrm{E}}_8(q)$.

G(q)	Class	Torsion coefficient decomposition	Uniform structure
${\mathrm{F}}_4(q)$	$2\mathrm{F}$	$\{\begin{array}{cc}{(q^2-1)}^2,\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times \frac{(q^2-1)}{2}\times (q^2-1),\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q-1)\times (q+1)\times (q^2-1)$
	$4\mathrm{D}$	$\{\begin{array}{cc}{q}^4-1,\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times \frac{(q^4-1)}{2},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q^2-1)\times (q^2+1)$
	$4\mathrm{E}$	$\{\begin{array}{cc}{q}^4-1,\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times \frac{(q^4-1)}{2},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q^2-1)\times (q^2+1)$
${\mathrm{E}}_6(q)$	$3\mathrm{C}$	$\{\begin{array}{cc}3\times \frac{(q^3-1)}{3}\times (q^3-1),\hfill & q\equiv 1\mathrm{ }\text{mod}\mathrm{ }3\hfill \\ {(q^3-1)}^2,\hfill & q\equiv 0,2\mathrm{ }\text{mod}\mathrm{ }3\hfill \end{array}$	$(q-1)\times (q^2+q+1)\times (q^3-1)$
	$6\mathrm{G}$	$\{\begin{array}{cc}3\times \frac{(q^6-1)}{3},\hfill & q\equiv 1\mathrm{ }\text{mod}\mathrm{ }3\hfill \\ (q^6-1),\hfill & q\equiv 0,2\mathrm{ }\text{mod}\mathrm{ }3\hfill \end{array}$	$(q^2+q+1)\times (q^4-q^3+q-1)$
${\mathrm{E}}_7(q)$	$2\mathrm{D}$	$\{\begin{array}{cc}(q-1)\times {(q^2-1)}^3,\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times (q-1)\times \frac{(q^2-1)}{2}\times {(q^2-1)}^2,\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q+1)\times {(q-1)}^2\times {(q^2-1)}^2$
	$2\mathrm{E}$	$\{\begin{array}{cc}(q+1)\times {(q^2-1)}^3,\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times (q+1)\times \frac{(q^2-1)}{2}\times {(q^2-1)}^2,\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q-1)\times {(q+1)}^2\times {(q^2-1)}^2$
	$4\mathrm{D}$	$\{\begin{array}{cc}(q-1)\times (q^2-1)\times (q^4-1),\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times (q-1)\times \frac{(q^2-1)}{2}\times (q^4-1),\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q+1)\times {(q-1)}^2\times (q^4-1)$
	$4\mathrm{E}$	$\{\begin{array}{cc}(q+1)\times (q^2-1)\times (q^4-1),\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times (q+1)\times \frac{(q^2-1)}{2}\times (q^4-1),\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q-1)\times {(q+1)}^2\times (q^4-1)$
	$4\mathrm{G}$	$\{\begin{array}{cc}(q^3-q^2+q-1)\times (q^4-1),\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times (q^3-q^2+q-1)\times \frac{(q^4-1)}{2},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q^2-1)\times (q^2+1)\times (q^3-q^2+q-1)$
	$4\mathrm{H}$	$\{\begin{array}{cc}(q^3+q^2+q+1)\times (q^4-1),\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times (q^3+q^2+q+1)\times \frac{(q^4-1)}{2},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q^2-1)\times (q^2+1)\times (q^3+q^2+q+1)$
	$6\mathrm{M}$	$\{\begin{array}{cc}(q-1)\times (q^6-1),\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times (q-1)\times \frac{(q^6-1)}{2},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q-1)\times (q^3-1)\times (q^3+1)$
	$6\mathrm{O}$	$\{\begin{array}{cc}(q+1)\times (q^6-1),\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times (q+1)\times \frac{(q^6-1)}{2},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q+1)\times (q^3-1)\times (q^3+1)$
	$8\mathrm{C}$	$\{\begin{array}{cc}(q^7-q^6+q^5-q^4+q^3-q^2+q-1),\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times \frac{(q^7-q^6+q^5-q^4+q^3-q^2+q-1)}{2},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q^2+1)\times (q^5-q^4+q-1)$
	$8\mathrm{D}$	$\{\begin{array}{cc}(q^7+q^6+q^5+q^4+q^3+q^2+q+1),\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times \frac{(q^7+q^6+q^5+q^4+q^3+q^2+q+1)}{2},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q^2+1)\times (q^5+q^4+q+1)$
${\mathrm{E}}_8(q)$	$2\mathrm{D}$	$\{\begin{array}{cc}{(q^2-1)}^4,\hfill & q\mathrm{ }\text{even}\hfill \\ 2^2\times {(\frac{(q^2-1)}{2})}^2\times {(q^2-1)}^2,\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	${(q-1)}^2\times {(q+1)}^2\times {(q^2-1)}^2$
	$3\mathrm{C}$	$\{\begin{array}{cc}3\times (q^2+q+1)\times \frac{(q^3-1)}{3}\times (q^3-1),\hfill & q\equiv 1\mathrm{ }\text{mod}\mathrm{ }3\hfill \\ (q^2+q+1)\times {(q^3-1)}^2,\hfill & q\equiv 0,2\mathrm{ }\text{mod}\mathrm{ }3\hfill \end{array}$	$(q-1)\times {(q^2+q+1)}^2\times (q^3-1)$
	$4\mathrm{F}$	$\{\begin{array}{cc}{(q^2-1)}^2\times (q^4-1),\hfill & q\mathrm{ }\text{even}\hfill \\ 2^2\times {(\frac{(q^2-1)}{2})}^2\times (q^4-1),\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	${(q-1)}^2\times {(q+1)}^2\times (q^4-1)$
	$4\mathrm{G}$	$\{\begin{array}{cc}(q-1)\times (q^3-q^2+q-1)\times (q^4-1),\hfill & q\mathrm{ }\text{even}\hfill \\ (2q-2)\times (q^3-q^2+q-1)\times \frac{(q^4-1)}{2},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q^2-1)\times {(q^3-q^2+q-1)}^2$
	$4\mathrm{H}$	$\{\begin{array}{cc}(q+1)\times (q^3+q^2+q+1)\times (q^4-1),\hfill & q\mathrm{ }\text{even}\hfill \\ (2q+2)\times (q^3+q^2+q+1)\times \frac{(q^4-1)}{2},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q^2-1)\times {(q^3+q^2+q+1)}^2$
	$4\mathrm{I}$	$\{\begin{array}{cc}{(q^4-1)}^2,\hfill & q\mathrm{ }\text{even}\hfill \\ 2^2\times {(\frac{(q^4-1)}{2})}^2,\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	${(q^2-1)}^2\times {(q^2+1)}^2$
	$6\mathrm{E}$	$\{\begin{array}{cc}3\times (q^2-q+1)\times \frac{(q^3+1)}{3}\times (q^3+1),\hfill & q\equiv 2\mathrm{ }\text{mod}\mathrm{ }3\hfill \\ (q^2-q+1)\times {(q^3+1)}^2,\hfill & q\equiv 0,1\mathrm{ }\text{mod}\mathrm{ }3\hfill \end{array}$	$(q+1)\times {(q^2-q+1)}^2\times (q^3+1)$
	$6\mathrm{S}$	$\{\begin{array}{cc}(q^2-1)\times (q^6-1),\hfill & q\mathrm{ }\text{even}\hfill \\ 2^2\times \frac{(q^2-1)}{2}\times \frac{(q^6-1)}{2},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q-1)\times (q+1)\times (q^3-1)\times (q^3+1)$
	$6\mathrm{W}$	$\{\begin{array}{cc}3\times (q^2-q+1)\times \frac{(q^6-1)}{3},\hfill & q\equiv 2\mathrm{ }\text{mod}\mathrm{ }3\hfill \\ (q^2-q+1)\times (q^6-1),\hfill & q\equiv 0,1\mathrm{ }\text{mod}\mathrm{ }3\hfill \end{array}$	${(q^2-q+1)}^2\times (q^4+q^3-q-1)$
	$6\mathrm{X}$	$\{\begin{array}{cc}3\times (q^2+q+1)\times \frac{(q^6-1)}{3},\hfill & q\equiv 1\mathrm{ }\text{mod}\mathrm{ }3\hfill \\ (q^2+q+1)\times (q^6-1),\hfill & q\equiv 0,2\mathrm{ }\text{mod}\mathrm{ }3\hfill \end{array}$	${(q^2+q+1)}^2\times (q^4-q^3+q-1)$
	$8\mathrm{D}$	$\{\begin{array}{cc}(q-1)\times (q^7-q^6+q^5-q^4+q^3-q^2+q-1),\hfill & q\mathrm{ }\text{even}\hfill \\ (2q-2)\times \frac{(q^7-q^6+q^5-q^4+q^3-q^2+q-1)}{2},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q^3-q^2+q-1)\times (q^5-q^4+q-1)$
	$8\mathrm{E}$	$\{\begin{array}{cc}(q+1)\times (q^7+q^6+q^5+q^4+q^3+q^2+q+1),\hfill & q\mathrm{ }\text{even}\hfill \\ (2q+2)\times \frac{(q^7+q^6+q^5+q^4+q^3+q^2+q+1)}{2},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q^3+q^2+q+1)\times (q^5+q^4+q+1)$
	$8\mathrm{G}$	$\{\begin{array}{cc}(q^8-1),\hfill & q\mathrm{ }\text{even}\hfill \\ 2^2\times \frac{(q^8-1)}{4},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q^2-1)\times (q^2+1)\times (q^4+1)$
	$9\mathrm{B}$	$\{\begin{array}{cc}(q^8+q^7+q^6+q^5+q^4+q^3+q^2+q+1),\hfill & q\mathrm{ }\text{even}\hfill \\ 3\times \frac{(q^8+q^7+q^6+q^5+q^4+q^3+q^2+q+1)}{3},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q^2+q+1)\times (q^6+q^3+1)$
	$18\mathrm{B}$	$\{\begin{array}{cc}(q^8-q^7+q^6-q^5+q^4-q^3+q^2-q+1),\hfill & q\mathrm{ }\text{even}\hfill \\ 3\times \frac{(q^8-q^7+q^6-q^5+q^4-q^3+q^2-q+1)}{3},\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$	$(q^2-q+1)\times (q^6-q^3+1)$

Table 10 The maximal tori of ${}^2{\mathrm{B}}_2(q)$.

w	σ-class of w	Min	Shape of $C_{W,\sigma }(w)$	Structure of $T_w(q)$
[1]	$2{\mathrm{B}}_1{\mathrm{C}}_1$	(1,2)	4	$q-\sqrt{2q}+1$
[1,2,1]	$2{\mathrm{B}}_1{\mathrm{C}}_1$	(3,2)		$q+\sqrt{2q}+1$
${\text{Id}}_W$	$1{\mathrm{A}}_{1}2{\mathrm{A}}_{1}4{\mathrm{A}}_2$	(0,1)	2	q–1

Table 11 The maximal tori of ${}^2{\mathrm{G}}_2(q)$.

w	σ-class of w	Min	Shape of $C_{W,\sigma }(w)$	Structure of $T_w(q)$
[1]	$2{\mathrm{B}}_1{\mathrm{C}}_1$	(1,2)	6	$q-\sqrt{3q}+1$
[6,2,1]	$2{\mathrm{B}}_1{\mathrm{C}}_1$	(3,2)		$2\times \frac{(q+1)}{2}$
[6]	$2{\mathrm{B}}_1{\mathrm{C}}_1$	(5,2)		$q+\sqrt{3q}+1$
${\text{Id}}_W$	$1{\mathrm{A}}_{1}2{\mathrm{A}}_{1}3{\mathrm{A}}_{2}6{\mathrm{A}}_2$	(0,1)	2	q–1

Table 12 The maximal tori of ${}^3{\mathrm{D}}_4(q)$.

w	σ-class of w	Min	Shape of $C_{W,\sigma }(w)$	Structure of $T_w(q)$
$[1,4,3,2]$	$3{\mathrm{A}}_{6}6{\mathrm{A}}_2$	(4,8)	$\text{SL}(2,3)$	${(q^2-q+1)}^2$
$[1,4,3,2,1,4,3,2]$	$3{\mathrm{A}}_{2}6{\mathrm{A}}_6$	(8,8)		${(q^2+q+1)}^2$
${\text{Id}}_W$	$1{\mathrm{A}}_{1}2{\mathrm{B}}_3{\mathrm{C}}_3{\mathrm{D}}_{3}4{\mathrm{A}}_6$	(0,1)	$\text{Dih}(12)$	$(q-1)\times (q^3-1)$
$[1,4,2,3,4,2]$	$2{\mathrm{A}}_1{\mathrm{B}}_3{\mathrm{C}}_3{\mathrm{D}}_{3}4{\mathrm{A}}_6$	(6,9)		$(q+1)\times (q^3+1)$
[2]	$2{\mathrm{E}}_9{\mathrm{F}}_{3}4{\mathrm{B}}_{12}{\mathrm{C}}_{12}{\mathrm{D}}_{12}$	(1,1)	2^2	$q^4+q^3-q-1$
[1]	$2{\mathrm{E}}_3{\mathrm{F}}_{9}4{\mathrm{B}}_{12}{\mathrm{C}}_{12}{\mathrm{D}}_{12}$	(1,3)		$q^4-q^3+q-1$
[1,2]	$3{\mathrm{A}}_{24}6{\mathrm{A}}_{24}$	(2,6)	4	$q^4-q^2+1$

Table 13 The maximal tori of ${}^2{\mathrm{F}}_4(q)$.

w	σ-class of w	Min	Shape of $C_{W,\sigma }(w)$	Structure of $T_w(q)$
[14,1,2,3]	$2{\mathrm{F}}_2{\mathrm{G}}_{4}8{\mathrm{A}}_{2}12{\mathrm{A}}_4$	(6,12)	${\text{GU}}_2(3)\sim 4\cdot \text{Sym}(4)$	${(q-\sqrt{2q}+1)}^2$
[21,2,3,2]	$2{\mathrm{F}}_2{\mathrm{G}}_{4}8{\mathrm{A}}_{2}12{\mathrm{A}}_4$	(18,12)		${(q+\sqrt{2q}+1)}^2$
[14,20]	$2{\mathrm{F}}_2{\mathrm{G}}_{4}4{\mathrm{A}}_{2}8{\mathrm{A}}_{8}12{\mathrm{A}}_8$	(12,24)	${\text{GL}}_2(3)$	${(q+1)}^2$
[20,1]	$2{\mathrm{F}}_8{\mathrm{G}}_{8}3{\mathrm{A}}_{4}4{\mathrm{A}}_4{\mathrm{B}}_4{\mathrm{C}}_{4}6{\mathrm{A}}_{4}8{\mathrm{A}}_{20}12{\mathrm{A}}_{16}$	(8,22)	4^2	$q^2+1$
${\text{Id}}_W$	$1{\mathrm{A}}_{1}2{\mathrm{A}}_1{\mathrm{F}}_4{\mathrm{G}}_{4}3{\mathrm{A}}_{4}4{\mathrm{A}}_6{\mathrm{B}}_8{\mathrm{C}}_{8}6{\mathrm{A}}_{4}8{\mathrm{A}}_{16}12{\mathrm{A}}_{16}$	(0,1)	$\text{Dih}(16)$	${(q-1)}^2$
[3,1]	$2{\mathrm{G}}_{16}3{\mathrm{B}}_8{\mathrm{C}}_{8}4{\mathrm{B}}_4{\mathrm{C}}_{4}6{\mathrm{B}}_8{\mathrm{C}}_{8}8{\mathrm{A}}_{24}12{\mathrm{A}}_{16}$	(2,6)	12	$q^2-\sqrt{2q^3}+q-\sqrt{2q}+1$
[21,1]	$2{\mathrm{G}}_{16}3{\mathrm{B}}_8{\mathrm{C}}_{8}4{\mathrm{B}}_4{\mathrm{C}}_{4}6{\mathrm{B}}_8{\mathrm{C}}_{8}8{\mathrm{A}}_{24}12{\mathrm{A}}_{16}$	(10,16)		$q^2+\sqrt{2q^3}+q+\sqrt{2q}+1$
[2]	$2{\mathrm{B}}_4{\mathrm{C}}_4{\mathrm{D}}_4{\mathrm{E}}_{4}4{\mathrm{D}}_{16}{\mathrm{E}}_{16}$ $6{\mathrm{D}}_{24}{\mathrm{E}}_{24}{\mathrm{F}}_{24}{\mathrm{G}}_{24}$	(1,2)	2 × 4	$q^2-q\sqrt{2q}+\sqrt{2q}-1$
[21]	$2{\mathrm{B}}_4{\mathrm{C}}_4{\mathrm{D}}_4{\mathrm{E}}_{4}4{\mathrm{D}}_{16}{\mathrm{E}}_{16}$ $6{\mathrm{D}}_{24}{\mathrm{E}}_{24}{\mathrm{F}}_{24}{\mathrm{G}}_{24}$	(3,2)		$q^2+q\sqrt{2q}-\sqrt{2q}-1$
[2,20]	$2{\mathrm{G}}_{16}3{\mathrm{A}}_8{\mathrm{B}}_{16}{\mathrm{C}}_{16}4{\mathrm{B}}_{16}{\mathrm{C}}_{16}6{\mathrm{A}}_8{\mathrm{B}}_{16}{\mathrm{C}}_{16}8{\mathrm{A}}_{48}12{\mathrm{A}}_{16}$	(4,10)	6	$q^2-q+1$
[1]	$2{\mathrm{B}}_4{\mathrm{C}}_4{\mathrm{D}}_4{\mathrm{E}}_{4}4{\mathrm{D}}_{40}{\mathrm{E}}_{40}6{\mathrm{D}}_{48}{\mathrm{E}}_{48}{\mathrm{F}}_{48}{\mathrm{G}}_{48}$	(1,2)	2^2	$q^2-1$

Table 15 The structure of various maximal tori in in ${}^2{\mathrm{E}}_6(q)$.

Class	Torsion coefficient decomposition	Uniform structure
$2{\mathrm{B}}_{32}4{\mathrm{D}}_{288}6{\mathrm{A}}_{128}{\mathrm{E}}_{32}$	$\{\begin{array}{cc}3\times \frac{(q^3+1)}{3}\times (q^3+1),\hfill & q\equiv 2\mathrm{ }\text{mod}\mathrm{ }3\hfill \\ {(q^3+1)}^2,\hfill & q\equiv 0,1\mathrm{ }\text{mod}\mathrm{ }3\hfill \end{array}$	$(q+1)\times (q^2-q+1)\times (q^3+1)$
$2{\mathrm{D}}_{288}4{\mathrm{B}}_{288}6{\mathrm{B}}_{192}{\mathrm{D}}_{96}{\mathrm{G}}_{1152}$	$\{\begin{array}{cc}3\times \frac{(q^6-1)}{3},\hfill & q\equiv 2\mathrm{ }\text{mod}\mathrm{ }3\hfill \\ (q^6-1),\hfill & q\equiv 0,1\mathrm{ }\text{mod}\mathrm{ }3\hfill \end{array}$	$(q^2-q+1)\times (q^4+q^3-q-1)$
$8{\mathrm{A}}_{576}10{\mathrm{A}}_{576}12{\mathrm{B}}_{1152}$

In the literature reviewed above there are many maximal torus structures which seem at first glance to be in disagreement. These apparent infelicities are mostly to be observed in the cases covered by Tables 9 and 15. We now give an overview of these apparent disparities. Using the labeling system described in Section 3, the structures of tori with labels 3C, 6G (${\mathrm{E}}_6$), 2D, 2E, 4D, 4E, 4G, 4H, 6M, 6O (${\mathrm{E}}_7$), and 2D, 3C, 4F, 4G, 4H, 4I, 6E, 6S, 6W, 6X, 8D, 8E, 8G, 9B, 18B (${\mathrm{E}}_8$) agree with both those outputted by Magma and those given in [12]. However, in all these cases neither Magma nor [12] gives the torsion coefficient decomposition like we do here. Additionally, there are a number of structures in [12], again not given in torsion decomposition form, for which it is not clear that they yield isomorphic groups to those presented here. These are listed in Table 1.

Table 1 Discrepancies.

G(q)		$T_w(q)$	Structure given here	Structure in [12]
$E_6(q)$	6B	6	${(q-1)}^2\times (q^4+q^3-q-1)$	$(q-1)\times (q^2-1)\times (q^3-1)$
$E_7(q)$	6C	$18\prime$	${(q-1)}^3\times (q^4+q^3-q-1)$	$(q-1)\times (q^2+q+1)\times (q^4-q^3+q-1)$
	6F	$-18\prime$	${(q+1)}^3\times (q^4-q^3+q-1)$	$(q+1)\times (q^2-q+1)\times (q^4+q^3-q-1)$
	8C	30	$(q^2+1)\times (q^5-q^4+q-1)$	$(q^3-q^2+q-1)\times (q^4+1)$
	8D	–30	$(q^2+1)\times (q^5+q^4+q+1)$	$(q^3+q^2+q+1)\times (q^4+1)$
	12A	26	$(q-1)\times (q^6+q^5+q^4-q^2-q-1)$	$(q^3-1)\times (q^4-1)$
	12B	–26	$(q+1)\times (q^6-q^5+q^4-q^2+q-1)$	$(q^3+1)\times (q^4-1)$
$E_8(q)$	6C	$6^{″}$	${(q-1)}^4\times (q^4+q^3-q-1)$	${(q-1)}^3\times (q^2-1)\times (q^3-1)$
	6D	$-6^{″}$	${(q+1)}^4\times (q^4-q^3+q-1)$	${(q+1)}^3\times (q^2-1)\times (q^3+1)$
	6K	63	${(q^4+q^2+1)}^2$	$(q^2-q+1)\times (q^2+q+1)\times (q^4+q^2+1)$
	6N	$25\prime$	$(q^3-2q^2+2q-1)\times (q^5-q^4+q^3-q^2+q-1)$	$(q-1)\times (q^2-q+1)\times (q^5-q^4+q^3-q^2+q-1)$
	6O	$-25\prime$	$(q^3+2q^2+2q+1)\times (q^5+q^4+q^3+q^2+q+1)$	$(q+1)\times (q^2+q+1)\times (q^5+q^4+q^3+q^2+q+1)$
	12H	26	${(q-1)}^2\times (q^6+q^5+q^4-q^2-q-1)$	$(q-1)\times (q^3-1)\times (q^4-1)$
	12I	–26	${(q+1)}^2\times (q^6-q^5+q^4-q^2+q-1)$	$(q+1)\times (q^3+1)\times (q^4-1)$
	12L	35	$(q^2-1)\times (q^6+q^5+q^4-q^2-q-1)$	$(q^4-1)\times (q^4+q^3-q-1)$
	12M	–35	$(q^2-1)\times (q^6-q^5+q^4-q^2+q-1)$	$(q^4-1)\times (q^4-q^3+q-1)$

The motivation for including the structure or shape of $C_W(w)$ is as follows. Let G(q) be one of our finite groups of Lie type, W its Weyl group and $w\in W$. Then for the corresponding maximal torus, $T_w(q)$, the group $N_{G(q)}(T_w(q))/T_w(q)$ contains a subgroup isomorphic to $C_W(w)$. For more on this consult Proposition 3.3.6 of [10]. A final remark on the tables is that the list of conjugacy class representatives is linked to compatible computer files in [25].

We now outline the contents of this paper. Section 2 gives sufficient background on the finite exceptional groups of Lie type, followed by details concerning the root systems of the relevant Weyl group. At the end of this section we explain the notation used in describing group structures. The theme of notational conventions continues in Section 3 where we discuss at length the labeling of Weyl group conjugacy classes. Then, as already mentioned, Sections 4 and 5 display the various tables of maximal tori data. Our final section gives some sample calculations and also contains a discussion of the algorithm for maximal tori used in Magma.

2 Background

Suppose q is a power of a prime p and let G(q) be a finite group of exceptional Lie type, either twisted or untwisted. Then there exists some algebraic group G of the corresponding untwisted type over $\overline{\text{GF}(q^a)}$ for some $a\in \{1,2,3\}$, and a Steinberg endomorphism σ on G under which $G(q)=G_{\sigma }=\{g\in G|\sigma (g)=g\}$. Let $W=W(G)$ be the Weyl group of G. Choose some σ-stable maximal torus T of G and let X(T) be the character group thereof. As in [24, Proposition 22.2], σ acts on $X(T)\otimes ℝ$ as ${\sigma }_q\varphi$, where $\varphi$ induces a permutation on the positive roots of the root system $\Phi$ of W and also σ induces an automorphism of W. Either $\varphi$ is trivial and ${\sigma }_q=F_q$ is the standard Frobenius morphism, or G has type ${\mathrm{G}}_2$ and p = 3, ${\mathrm{B}}_2$ or ${\mathrm{F}}_4$ and p = 2, ${\mathrm{D}}_4$, or ${\mathrm{E}}_6$. In these cases an additional ‘twisted’ possibility for σ with $\varphi$ nontrivial yields the finite exceptional groups of type ${}^2{\mathrm{B}}_2,{}^2{\mathrm{G}}_2,{}^3{\mathrm{D}}_4,{}^2{\mathrm{F}}_4$, and ${}^2{\mathrm{E}}_6$ as $G_{\sigma }$.

Following [24, 25.1], there is a well-known one-to-one correspondence between the G(q)-conjugacy classes of σ-stable maximal tori of G and the $\varphi$-classes, often referred to as twisted conjugacy classes, of the Weyl group W. We recall that $x,y\in W$ belong to the same $\varphi$-class if and only if there is some $g\in W$ with $y=\varphi (g)x{g}^{-1}$. Note that when $\varphi$ is trivial the $\varphi$-classes are nothing but the conjugacy classes of W. The twisted centralizer of $w\in W$ is defined to be $$C_{W,\sigma }(w)=\{x\in W|\sigma (x)w{x}^{-1}=w\}.$$

Let $T_w(q)=T_{\sigma }=\{g\in T|\sigma (g)=g\}$ for some σ-stable maximal torus T of G whose G-conjugate maximal tori correspond to the $\varphi$-class of $w\in W$. Then by [24, Proposition 25.2] we have that $$|T_w(q)|=|{\text{det}}_{X(T)\otimes ℝ}(\sigma w-I)|.$$

In particular, whenever $\sigma =F_q$, the order $|T_w(q)|$ can be obtained by evaluating the characteristic polynomial of w at q. Moreover, by [16, Proposition 1.4], the action of $\sigma w-I$ on $X(T)\otimes ℝ$ gives the relation matrix for the torus $T_w(q)$, so that we may use w to compute the structure of $T_w(q)$. We remark that the results above hold regardless of the isogeny type of G(q), and can therefore be used to obtain torus structures for groups of both adjoint and simply connected type.

For convenience, we often refer to the maximal torus of G(q) corresponding to the Weyl group element w, rather than to the conjugacy (twisted conjugacy) class of each. We shall denote by w₀ the longest Weyl group element throughout.

In [16] and [12], a method of determining the cyclic structure of maximal tori is presented. In [16] q is considered as an indeterminant and then the polynomial matrix $q.w-I$ is a relation matrix for the corresponding maximal torus $T_w(q)$. Diagonalizing this relation matrix over $\mathbb{Z}[q]$ then reveals the cyclic structure of the maximal torus, as the cyclic parts of $T_w(q)$ may be read off the diagonal. However, $\mathbb{Z}[q]$ is not a principal ideal domain, and so not every relation matrix we encounter is diagonalizable. More detail and examples of how we deal with this are given in Section 6. Using this approach we find the torsion coefficient decomposition for all maximal tori of the finite groups of exceptional Lie type. That is, the unique decomposition into a direct product of cyclic groups ${\lambda }_1(q)\times {\lambda }_2(q)\times \cdots \times {\lambda }_n(q)$ where ${\lambda }_i(q)$ divides ${\lambda }_{i+1}(q)$ for $1\le i<n$. We remark yet again that the structures given in [12] are not necessarily in this unique form, and were verified only for groups of simply connected type.

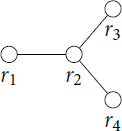
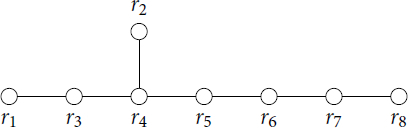
Each $w\in W$ can be expressed as a product of involutions $w=w_1{w}_2$ where $w_1=w_{i_1}···w_{i_m},w_2=w_{j_1}···w_{j_n}$ are products of reflections corresponding to mutually orthogonal roots. This decomposition is minimal, in that $L(w)=m+n$, where L(w) denotes the reflection length of w. For each such decomposition of w, we define a graph Γ_w consisting of L(w) nodes corresponding to the roots $r_1,\dots ,r_{m+n}$ where two distinct roots r_i and r_j are joined by an edge of weight $n_{ij}{n}_{ji}$ where $$n_{ij}=\frac{2(r_i,r_j)}{(r_i,r_i)}\in \mathbb{Z}.$$

In Sections 2.2, 2.4, and 2.5, we define roots that allow us to express every class representative w in the above decomposition. See Section 3 for a detailed explanation of the notation we use to denote this decomposition in the later tables.

If w has graph Γ_w , then any conjugate of w also has graph Γ_w . We say such a graph is admissible if the nodes correspond to a set of linearly independent roots and each subgraph, which is a cycle, contains an even number of nodes. We define a subgraph to be a subset of the nodes and all edges joining such nodes. A cycle is a graph in which each node is joined to exactly two other nodes by edges of weight greater than zero. As remarked in [7], each conjugacy class of W has a corresponding admissible graph. However, this correspondence is not one-to-one; distinct classes may be associated with the same graph and an individual class may have more than one admissible graph. The graph Γ_w determines the characteristic polynomial of the action of w on $X(T)\otimes ℝ$ (see [7]). Consequently, by the results of [24], the admissible graph Γ_w determines the order $|T_w(q)|$.

Next we review the root systems we will encounter. In the Dynkin diagrams and graphs, in Section 2.6, a black node denotes that the root is long, whilst a white node denotes that the root is short. The arrows all point from a long root to a short root. In a root system of type ${\mathrm{E}}_n$, all roots are of equal length; hence we use a white node for all roots.

2.1 Roots for ${\mathrm{B}}_2$

Let $\{r_1,r_2\}$ be the simple roots of a root system of type ${\mathrm{B}}_2$.

2.2 Roots for ${\mathrm{G}}_2$

Let $\{r_1,r_2\}$ be the simple roots of a root system of type ${\mathrm{G}}_2$, and define $r_6=3r_1+2r_2$.

2.3 Roots for ${\mathrm{D}}_4$

Let $\{r_1,r_2,r_3,r_4\}$ be the simple roots of a root system of type ${\mathrm{D}}_4$ with Dynkin diagram

2.4 Roots for ${\mathrm{F}}_4$

Let $\{r_1,r_2,r_3,r_4\}$ be the simple roots of a root system of type ${\mathrm{F}}_4$ with Dynkin diagram

Now define

Table

$r_6=r_2+r_3$	$r_{13}=r_2+2r_3+r_4$	$r_{14}=r_1+2r_2+2r_3$
$r_{20}=r_{14}+2r_4$	$r_{21}=r_{20}+r_3$	$r_{22}=r_{20}+2r_3$

2.5 Roots for ${\mathrm{E}}_6,{\mathrm{E}}_7$, and ${\mathrm{E}}_8$

Let G be a simple algebraic group of type ${\mathrm{E}}_6,{\mathrm{E}}_7$, or ${\mathrm{E}}_8$ over the algebraic closure $\overline{\text{GF}(q)}$ with Weyl group $W=W(G)$. Let $\Phi$ be the root system of G. If G is of type ${\mathrm{E}}_8$, we consider $\Phi$ to be embedded in ${ℝ}^8$ with orthonormal basis $\left\{{\mathrm{ϵ}}_i\right|1\le i\le 8\}$. Then $\Phi$ is generated by the simple roots $\left\{r_i\right|1\le i\le 8\}$. If G is of type ${\mathrm{E}}_6$ (respectively ${\mathrm{E}}_7$) then we consider $\Phi$ to be generated by the simple roots $\left\{r_i\right|1\le i\le 6\}$ (respectively $\left\{r_i\right|1\le i\le 7\}$). Root labels are chosen with respect to the following Dynkin diagram.

Now define

Table

$r_{17}=r_2+r_3+r_4$	$r_{18}=r_2+r_4+r_5$	$r_{29}=r_5+r_6+r_7+r_8$
$r_{48}=r_{17}+r_4+2r_5+r_6$	$r_{56}=r_4+r_{17}+r_{29}$	$r_{61}=r_{48}+r_6+r_7$
$r_{69}=r_1+r_{17}+r_{48}$	$r_{74}=r_{48}+r_6+2r_7+r_8$	$r_{82}=r_1+r_3+r_4+r_5+r_{61}$
$r_{97}=r_{17}+r_{82}$	$r_{118}=r_8+r_{61}+r_{97}$	$r_{120}=r_7+r_8+r_{118}$

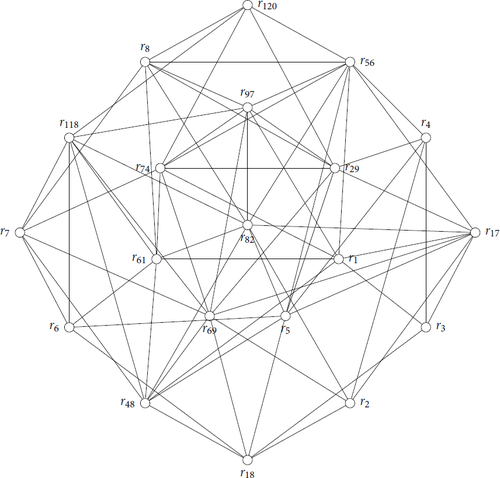
We note that the roots r₆₉, r₉₇, and r₁₂₀ are the longest roots in ${\mathrm{E}}_6,{\mathrm{E}}_7$, and ${\mathrm{E}}_8$, respectively.

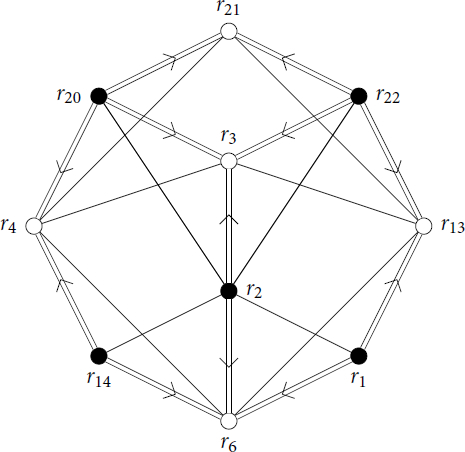
2.6 Root graphs

Figures 1 and 2 illustrate the graphs described earlier in this section when considering the roots described in Sections 2.5 and 2.4 as vertices, respectively. In particular, these graphs both contain all the admissible graphs listed in Tables 5–8 as subgraphs.

Figure 1 The graph of the roots for ${\mathrm{E}}_n$ (n = 6,7,8) defined in Section 2.5

Figure 2 The graph of the roots for ${\mathrm{F}}_4$ defined in Section 2.4.

Finally we discuss the notation used to describe group structures. Broadly speaking we follow the Atlas [11] conventions and notation. The exceptions or additions are $\text{Sym}(n)$ and $\text{Alt}(n)$ which denote, respectively, the symmetric and alternating groups of degree n. While $\text{Dih}(n)$ denotes the dihedral group of order n and ${\text{ASL}}_n(q)$ the n-dimensional affine special linear group over $\text{GF}(q)$. Further, we use the prefix $\mathrm{C}$ to denote the conformal version of a classical group.

3 Notational conventions

First we consider the situation when G(q) is untwisted. Let W denote the Weyl group of G(q). The tables for Weyl groups of the untwisted groups are in Section 4 and are arranged as follows.

The first column gives a representative w for each conjugacy class of W, using [$i_1,i_2,\dots i_m$][$j_1,j_2,\dots j_n$] to denote the decomposition w = uv into a product of involutions where $u=w_{i_1}{w}_{i_2}\dots w_{i_m}$ and $v=w_{j_1}{w}_{j_2}\dots w_{j_n}$ in W. We use w_i to denote the reflection in the hyperplane orthogonal to the positive root r_i . In all cases, the set $\{i_1,i_2,\dots i_m,j_1,j_2,\dots j_n\}$ corresponds to a linearly independent set of roots that constitute the nodes of the associated admissible graph defined in the column headed Γ_w . The roots we use in such decompositions are listed in 2.2, 2.4, and 2.5. So for the Weyl groups of type, respectively, ${\mathrm{E}}_6,{\mathrm{E}}_7$, and ${\mathrm{E}}_8$ we have $w_0=r_{69},w_0=r_{97}$ and $w_0=r_{120}$. If the root system $\Phi$ has roots of different lengths, then admissible graphs may also contain roots of different lengths. As in [16], we use a tilde to denote graphs consisting of only short roots. For example, the graph ${\tilde{\mathrm{A}}}_3$ denotes the graph ${\mathrm{A}}_3$ consisting of only short roots, whilst we simply write ${\mathrm{A}}_3$ for the graph consisting of only long roots. See [7] and [16] for a detailed explanation of the notation used to describe the graphs Γ_w .

We give a short example illustrating the above notation. Consider the class 10E in $W({\mathrm{E}}_8)$. This has admissible graph ${\mathrm{D}}_6$, which can be realized as a subgraph of the ${\mathrm{E}}_8$ (and indeed the ${\mathrm{E}}_7$) Dynkin diagram, by considering the following roots:

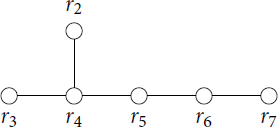
From this we can form two sets of mutually orthogonal roots, namely $[r_2,r_3,r_5,r_7]$ and $[r_4,r_6]$. Being a subset of the fundamental roots, we see that this set of roots is linearly independent. Then, the class representative $w\in W({\mathrm{E}}_8)$ of class 10E can be written as $w=w_1{w}_2$ where $w_1=w_2{w}_3{w}_5{w}_7$ and $w_2=w_4{w}_6$. This element can be explicitly constructed in Magma, in a permutation representation, using the command w:=makew("E8",R,[2,3,5,7,4,6],"perm") where R: = RootDatum("E8") and the function makew may be found in the accompanying computer file [25]. A matrix representation can also be achieved here, by replacing "perm" with "mat". A structure of the corresponding torus $T_w(q)$ may then be determined using the in-built Magma function TwistedTorusOrder(R,w) or by using the function TorusStructure(R,0,w,q) from [25] (note that TwistedTorusOrder takes w as a permutation and TorusStructure takes w as a matrix). We remark that, as this graph may also be realised in ${\mathrm{E}}_7$, there is a conjugacy class of $W({\mathrm{E}}_7)$ (namely 10C), that has admissible graph ${\mathrm{D}}_6$ and representative given by the same product of reflections defined above.

In general, one must specify an isogeny type when calling RootDatum(). We note that, of the types considered in this paper, isogeny need only be considered for ${\mathrm{E}}_6,{}^2{\mathrm{E}}_6$, and ${\mathrm{E}}_7$, see [7, 1.19].

Now moving back to the arrangement of the tables. The second column is the name of the conjugacy class. As mentioned in Section 1, in our tables we follow in the footsteps of the amazing Atlas. Thus, those W-conjugacy classes having order n elements are labeled nA, nB, $\dots$ as in [11]. On one occasion we run out of alphabet letters for ${\mathrm{E}}_8(q)$ (see Table 8). There are 28 classes of elements of order 6 in W. So we use 6AA and 6BB. If for two such classes X₁ and X₂ we have $\left|X_1\right|=\left|X_2\right|$, we fall back on Coxeter group related properties to decide which class has precedence. The properties we use are related to the minimal Coxeter length elements of the classes. For X a W-conjugacy class, set min(X) = min $\{\ell (x)|x\in X\}$ and $X_{\min }=\{x\in X|\ell (x)=\min (X)\}$. Here $\ell (x)$ is the Coxeter length of x. The third column, headed Min, gives an ordered pair (min(X), $\left|X_{\min }\right|$) where X is a conjugacy class of W. Returning to X₁ and X₂ with $\left|X_1\right|=\left|X_2\right|$, if min(X₁) ¡ min(X₂) or if min(X₁) = min(X₂) and $\left|X_{1\min }\right|<\left|X_{2\min }\right|$, then X₁ precedes X₂. These rules serve to order almost all the classes. How we deal with those for which $\left|X_1\right|=\left|X_2\right|$, min(X₁) = min(X₂) and $\left|X_{1\min }\right|=\left|X_{2\min }\right|$ will be explained shortly after an example. In the ${\mathrm{E}}_7(q)$ table, the names 6L and 6M are given as 6L precedes 6M because the Min column tells us that min(6L) = 5 = min(6M) and $\left|{6\mathrm{L}}_{\min }\right|=12<16=\left|{6\mathrm{M}}_{\min }\right|$. All classes in $W({\mathrm{E}}_6)$ and $W({\mathrm{E}}_7)$ can be sorted in this way. We defer discussing $W({\mathrm{G}}_2)$ and $W({\mathrm{F}}_4)$ for the moment.

We now explain how we order the remainder of the classes in $W=W({\mathrm{E}}_8)$. For $w\in W$, the excess of w (see [22]), e(w), is defined as $$e(w)=\min \{\ell (w)-\ell (x)-\ell (y)|w=xy,x^2=y^2=1\}.$$

For X a W-conjugacy class, set $$X_{\min }^0=\{x\in X|x\in X_{\min },e(x)=0\}.$$

The remaining unordered classes of W are dealt with by considering $\left|X_{\min }^0\right|$. Let X₁ and X₂ be two W-conjugacy classes such that $\left|X_1\right|=\left|X_2\right|$, min(X₁) = min(X₂) and $\left|X_{1\min }\right|=\left|X_{2\min }\right|$. Then, X₁ precedes X₂ in the tables if $\left|X_{1\min }^0\right|<\left|X_{2\min }^0\right|$. For such classes, the cardinality $\left|X_{\min }^0\right|$ is given in Table 2.

Table 2 Values of $\left|X_{\min }^0\right|$ for various classes X of $W({\mathrm{E}}_8)$.

w	X	Min	$\left|X_{\min }^0\right|$
[3,2,5][4,7]	6P	(5,16)	4
[97,3,2,6][7]	6Q	(5,16)	16
[2,3,5,7][4,6]	10E	(6,32)	2
[1,4,6,8][7,120]	10F	(6,32)	8

The idea of choosing minimal sized sets (such as $\left|X_{\min }\right|$ and $\left|X_{\min }^0\right|$) to indicate pre-eminence follows the spirit of the Atlas which, in effect, uses the minimal size of conjugacy classes to decide the order of conjugacy classes whose elements have the same order.

The tables for ${\mathrm{E}}_6(q),{\mathrm{E}}_7(q)$, and ${\mathrm{E}}_8(q)$ have an extra column labeled $T_w(q).$ In this column, we list numbers i corresponding to the torus T_i as given in [12]. When $w_0\in Z(W)$, multiplication by w₀ sends a W-conjugacy class X to $w_{0}X$, also a W-conjugacy class. Hence in [12], when $X\ne w_{0}X$, only one of the corresponding maximal tori is listed. Assume X corresponds to T_i in [12] and $X\ne w_{0}X$. Then, as we wish to list all maximal tori, here we use–i to denote the maximal torus associated to $w_{0}X$. In other words, if T_i is $T_w(q)$ for some $w\in W$ here, then $T_{-i}$ corresponds to $T_{w_{0}w}(q)$. The use of the negative sign is prompted by the fact that when $w_0\in Z(W)$, it is minus the identity matrix in the reflection representation.

Next we explain the occurrence of primes which decorate the entries of the fourth column in the ${\mathrm{E}}_7(q)$ and ${\mathrm{E}}_8(q)$ tables. Let $w\in W({\mathrm{E}}_6)$ (respectively $W({\mathrm{E}}_7)$) be such that the admissible graph of w is determined by roots orthogonal to r₇ (respectively r₈). Then, the torus with label i of ${\mathrm{E}}_6(q)$ (respectively ${\mathrm{E}}_7(q))$ gives rise to a torus which we label $i\prime$ of ${\mathrm{E}}_7(q)$ (respectively ${\mathrm{E}}_8(q)$). The structure of the torus with label $i\prime$ is given by $(q-1)\times T_w(q)$ where $T_w(q)$ is the torus with label i. A double prime in Table 8 indicates that the structure of the torus with label $i^{″}$ may be determined from the structure of the torus with label i in Table 6 by multiplying by ${(q-1)}^2$.

We demonstrate this with an example. Consider the class 4C in $W({\mathrm{E}}_6)$, with admissible graph ${\mathrm{A}}_3$

that can be realised as a subgraph of the Dynkin diagram of ${\mathrm{E}}_6$. As before, a representative of the corresponding class is given by w = uv where $u=w_1{w}_4$ and v = w₃. The structure of $T_w(q)$ can be obtained using the methods shown in the previous example. This admissible graph can be realized as a subgraph of both the ${\mathrm{E}}_7$ and ${\mathrm{E}}_8$ Dynkin diagrams. Moreover, as roots r₁, r₃, and r₄ are all orthogonal to both r₇ and r₈, we have that the maximal torus $T_w(q)$ extends to a maximal torus $T_w(q)\prime ,T_w{(q)}^{″}$ of both ${\mathrm{E}}_7$ and ${\mathrm{E}}_8$, by multiplying $T_w(q)$ by cyclic factors $(q-1)$ and ${(q-1)}^2$, respectively. Indeed, we see that classes 4C and 4D in ${\mathrm{E}}_7$ and ${\mathrm{E}}_8$ have torus $T_w(q)\prime ,T_w{(q)}^{″}$ respectively. The admissible graph for these classes is identical to the original graph ${\mathrm{A}}_3$ in ${\mathrm{E}}_6$ and thus all three of these classes have representative given by the same product of reflections. Note that when multiplying by a cyclic factor of $(q-1)$, the torsion coefficient decomposition of $T_w(q)$ may not be preserved. An example of this, and how we deal with it, is given in Section 6.

We must also consider the Weyl groups with unequal root lengths as these cannot be completely sorted in the same way. We note that in both $W({\mathrm{G}}_2)$ and $W({\mathrm{F}}_4)$, if two W(G)-conjugacy classes X₁ and X₂ both contain elements of the same order and $\left|X_1\right|=\left|X_2\right|$, then more often than not, we have min(X₁) = min(X₂), $\left|X_{1\min }\right|=\left|X_{2\min }\right|$ and $\left|X_{1\min }^0\right|=\left|X_{2\min }^0\right|$. Hence we use a different method to order such classes. Let Λ denote the set of short roots and let $N^{\Lambda }(w)=N(w)\cap \Lambda$, where N(w) is the set of positive roots sent negative by w. For a class X, we define $N_{\min }^{\Lambda }(X)$ to be $$N_{\min }^{\Lambda }(X)=\min \left\{\right|N^{\Lambda }(w)\left|\right|w\in X\}.$$

Then for two W-conjugacy classes X₁ and X₂ with min(X₁) = min(X₂), $\left|X_{1\min }\right|=\left|X_{2\min }\right|$ and $\left|X_{1\min }^0\right|=\left|X_{2\min }^0\right|$, we have X₁ preceding X₂ if $|N_{\min }^{\Lambda }(X_1)|<|N_{\min }^{\Lambda }(X_2)|$. Such classes X and the corresponding values $|N_{\min }^{\Lambda }(X)|$ can be found in Table 3. This is sufficient to resolve all of the remaining classes.

Table 3 Values of $|N_{\min }^{\Lambda }(X)|$ for the remaining unsorted classes in $W({\mathrm{G}}_2)$ and $W({\mathrm{F}}_4)$.

W	w	X	Min	$|N_{\min }^{\Lambda }(X)|$
$W({\mathrm{G}}_2)$	[2]	2B	(1,1)	0
	[1]	2C	(1,1)	1
$W({\mathrm{F}}_4)$	[3]	2B	(1,2)	0
	[1]	2C	(1,2)	1
	[3,14,21]	2D	(9,1)	3
	[1,3,14]	2E	(9,1)	6
	[3][4]	3B	(2,2)	0
	[1][2]	3C	(2,2)	2
	[6,21][13]	4D	(5,4)	2
	[14,20][2]	4E	(5,4)	3
	[1,14,20][2]	6B	(10,8)	4
	[3,6,21][13]	6C	(10,8)	6
	[2,21][4]	6D	(3,2)	1
	[2][14,21]	6E	(3,2)	2
	[4][3,14]	6F	(3,4)	1
	[2,4][14]	6G	(3,4)	2

We remark that, as shown in [16], if τ is an automorphism of ${\mathrm{F}}_4(q)$ which acts on the root system by interchanging long and short roots, and we have two conjugacy classes of W represented by w and $w\prime$ such that ${\Gamma }_w={({\Gamma }_{w\prime })}^{\tau }$, then $T_w(q)\cong T_{w\prime }(q)$. In particular, if ${\Gamma }_1,{\Gamma }_2$ are admissible graphs associated with two distinct conjugacy classes and ${\Gamma }_2$ can be obtained from ${\Gamma }_1$ by interchanging long and short roots, then the maximal tori corresponding to both classes are isomorphic.

We now turn to the twisted cases.

The tables for the twisted groups are in Section 5 and follow a similar structure to the tables in the untwisted case. In the second column, we describe each $\varphi$-class of a Weyl group W by its makeup in terms of the standard conjugacy classes of W. For example, in Table 11 the $\varphi$-class containing the Weyl group identity is labeled $1{\mathrm{A}}_{1}2{\mathrm{A}}_1$ $3{\mathrm{A}}_2$ $6{\mathrm{A}}_2$ to indicate that it contains one element of the $W({\mathrm{G}}_2)$-conjugacy classes $1\mathrm{A}$ and $2\mathrm{A}$, and two elements of $W({\mathrm{G}}_2)$-conjugacy classes $3\mathrm{A}$ and $6\mathrm{A}$. Our labeling for the standard conjugacy classes of W is as given in Section 4. The ordering of the maximal tori in the twisted case is done in a similar way to the untwisted case. As before, the column headed Min gives the ordered pair (min(X), $\left|X_{\min }\right|$) where X is the twisted conjugacy class. The twisted classes are then sorted by the same conditions as in the untwisted case. We remark that considering the ordered pair (min(X), $\left|X_{\min }\right|$) is sufficient to order all classes in the twisted case.

4 Maximal Tori in untwisted G(q)

5 Maximal Tori of twisted G(q)

Recall that, in order to compress the description of the σ-classes in Tables 10–14, we have the convention that, for example, $2{\mathrm{A}}_{12}{\mathrm{D}}_{72}4{\mathrm{C}}_{72}6{\mathrm{D}}_{96}{\mathrm{G}}_{288}$ ($w=[69]$ in Table 14) means $2{\mathrm{A}}_{12}2{\mathrm{D}}_{72}4{\mathrm{C}}_{72}6{\mathrm{D}}_{96}6{\mathrm{G}}_{288}$.

Since ${\mathrm{D}}_4(q)$ does not appear in this paper, we have no fixed labeling of the standard conjugacy classes of the related Weyl group. This only impacts upon the labeling of the σ-classes represented by $[2]$ and $[1]$ in Table 12. We remark that the σ-class of $[1]$ contains the simple reflections corresponding to $[3]$ and $[4]$, which is enough to differentiate it from that of $[2]$.

Table 14, giving the maximal tori for ${}^2{\mathrm{E}}_6(q)$, has an additional column. This column gives the corresponding $T_w(q)$ number in the ${\mathrm{E}}_6(q)$ Table 6, so illuminating the one-to-one correspondence between the maximal tori of ${\mathrm{E}}_6(q)$ and ${}^2{\mathrm{E}}_6(q)$.

6 Examples

As indicated in Section 2, the matrix $\sigma w-I$ need not always be diagonalizable in a uniform manner. That is, there may not exist a single collection of matrix operations which give a diagonal output at every prime power q. This is a consequence of the fact that, treating q as a variable, the polynomial ring $\mathbb{Z}[q]$ is not a principal ideal domain and hence there may not exist a Smith normal form for $\sigma w-\mathrm{I}$. An example in [12] is given of the torus corresponding to class $6\mathrm{G}$ of $W({\mathrm{E}}_6)$ (class name as in Table 6), where the operations performed to diagonalize $\sigma w-\mathrm{I}$ differ depending on the value of q modulo 3. Deriziotis and Fakiolas conclude by working backwards to write the torus structure as a direct product of cyclic groups in such a way that a single set of polynomials in q describe the torus structure uniformly.

Consider the maximal torus in the adjoint group ${\mathrm{E}}_7(q)$ corresponding to the class $6\mathrm{M}$ in $W({\mathrm{E}}_7)$. We can obtain a class representative w from $[2,5,7][4,6]$ in Table 7 by taking the product of the reflection matrices corresponding to roots $2,4,5,6,7$ in the given order. The matrix $\sigma w-I=q.w-1$ is then as follows. $$\left(\begin{array}{ccccccc}q-1& 0& 0& 0& 0& 0& 0\\ 0& -q-1& 0& -q& 0& 0& 0\\ 0& 0& q-1& q& 0& 0& 0\\ 0& q& 0& q-1& q& q& 0\\ 0& 0& 0& -q& -q-1& -q& 0\\ 0& 0& 0& q& q& q-1& q\\ 0& 0& 0& 0& 0& -q& -q-1\end{array}\right)$$

We start diagonalizing by applying the operations: $C_2\mapsto C_2-C_4,C_4\mapsto C_4-q{C}_2,R_3\mapsto R_3-q{R}_2,R_4\mapsto R_4+R_2,R_5\mapsto R_5+q{R}_2,R_6\mapsto R_6-q{R}_2,R_3\mapsto R_3+R_5,R_6\mapsto R_6+R_5,C_5\mapsto C_5+q{C}_4,C_6\mapsto C_6+q{C}_4,R_5\mapsto R_5-(q^q+q)R_4,C_5\mapsto C_5-C_6,R_7\mapsto R_7+q{R}_5,C_6\mapsto C_6-(q^3+q^2+q)C_5,C_7\mapsto C_7+q{C}_6,R_7\mapsto R_7-(q^4+q^3+q^2+q)R_6,R_3\mapsto R_3+(q^q+q)R_6,R_3\mapsto R_3-R_5,C_7\mapsto C_7-(q^3+2q^2+2q+2)C_3,R_3\leftrightarrow R_6,C_3\leftrightarrow C_6$. We are left with the matrix $$\left(\begin{array}{ccccccc}q-1& 0& 0& 0& 0& 0& 0\\ 0& -1& 0& 0& 0& 0& 0\\ 0& 0& -1& 0& 0& 0& 0\\ 0& 0& 0& -1& 0& 0& 0\\ 0& 0& 0& 0& -1& 0& 0\\ 0& 0& 0& 0& 0& q-1& 2\\ 0& 0& 0& 0& 0& 0& -q^5-q^4-q^3-q^2-q-1\end{array}\right).$$

Now, if q is even we apply the operations $C_6\to C_6-\frac{q}{2}{C}_7,C_7\to C_7+2C_6$ and $R_7\to R_7+\frac{(q^6+q^5+q^4+q^3+q^2+q)}{2}{R}_6$. If q is odd we apply operations $C_6\to C_6-\frac{(q-1)}{2}{C}_7,R_7\mapsto R_7+\frac{(q^5+q^4+q^3+q^2+q+1)}{2}{R}_6,R_6\leftrightarrow R_7$. So a diagonal form of $q.w-I$ is $$\{\begin{array}{cc}\text{diag}(q-1,-1,-1,-1,-1,-1,q^6-1),\hfill & q\mathrm{ }\text{even}\hfill \\ \text{diag}(q-1,-1,-1,-1,-1,2,(q^6-1)/2),\hfill & q\mathrm{ }\text{odd}\hfill \end{array}$$ and we can rearrange diagonal entries so that these matrices constitute a Smith normal form.

Now for the simply connected case. We obtain a class representative in the same way as before, however now we must specify the simply connected isogeny type. To do this, we call RootDatum("E7":Isogeny:="SC") and this will be the second argument in our function makew. The matrix $\sigma w-I=q.w-1$ is then $$\left(\begin{array}{ccccccc}q-1& 0& 0& 0& 0& 0& 0\\ 0& -1& q& -q& q& 0& 0\\ 0& 0& q-1& 0& 0& 0& 0\\ 0& q& q& -q-1& q& 0& 0\\ 0& q& q& -q& q-1& -q& q\\ 0& 0& 0& 0& q& -q-1& q\\ 0& 0& 0& 0& q& -q& -1\end{array}\right).$$

Now we apply the operations: $R_4\to R_4+q{R}_2,R_5\to R_5+q{R}_2,C_3\to C_3+q{C}_2,C_4\to C_4-q{C}_2,C_5\to C_5+q{C}_2,C_6\to C_6-q{C}_7,C_5\to C_5+q{C}_7,R_6\to R_6+q{R}_7,R_5\to R_5+q{R}_7,R_4\to R_4-R_5,R_5\to R_5-(q^2+q)R_4,C_5\to C_5-(q^2-1)C_4,C_6\to C_6+(q^2+q)C_4,C_6\to C_6+C_5,C_5\to C_5+(q^2+q)C_6,R_5\to R_5-(q^3+q^2+q+1)R_6,R_5\to R_5-(q+2)R_3,R_5\leftrightarrow R_7,C_5\leftrightarrow C_7,C_3\leftrightarrow C_6,R_3\leftrightarrow R_6$. We are left with the matrix $$\left(\begin{array}{ccccccc}q-1& 0& 0& 0& 0& 0& 0\\ 0& -1& 0& 0& 0& 0& 0\\ 0& 0& -1& 0& 0& 0& 0\\ 0& 0& 0& -1& 0& 0& 0\\ 0& 0& 0& 0& -1& 0& 0\\ 0& 0& 0& 0& 0& q-1& 0\\ 0& 0& 0& 0& 0& 2& -q^5-q^4-q^3-q^2-q-1\end{array}\right)$$ which we see is the transpose of the matrix we had earlier. Hence by interchanging rows with columns and vice versa in the operations for cases q even and q odd from before, we arrive at the same diagonal matrices. Consequently, the torus structure is the same in both the adjoint and simply connected cases.

According to the Magma handbook, the function TwistedTorusOrder can be used to obtain the structures of the maximal tori in groups of Lie type. The function takes as arguments a root datum R and an element w of the Weyl group corresponding to R, and produces a list of polynomials in q which, upon evaluation, yield the orders of the cyclic factors of the maximal torus corresponding to w. The function was written by Haller, based on work from their thesis [21]. We note that for groups of type ${\mathrm{E}}_6,{\mathrm{E}}_7$, and ${\mathrm{E}}_8$, the output of TwistedTorusOrder does not always coincide with the cyclic factors given in [12].

We further illustrate the methods used to obtain the structures in Table 9 with another example. To reduce listing all column operations, we now signpost our calculations with the phrase kill row j. By kill row j we mean a_jj is the only non-zero entry in column j and divides all the entries in row j, so appropriate column operations will result in a_jj being the only non-zero entry in row j and not disturbing the rest of the matrix. Consider our representative w corresponding to the class 6W in $W({\mathrm{E}}_8)$. The matrix $q.w-I$ is $$\left(\begin{array}{cccccccc}-q-1& -q& -2q& -2q& -2q& -q& 0& 0\\ 0& -q-1& q& 2q& q& q& 0& 0\\ q& q& 2q-1& 2q& q& 0& 0& 0\\ 0& -q& -q& -q-1& 0& 0& 0& 0\\ 0& q& 0& 0& -1& 0& 0& 0\\ 0& -q& 0& -q& -q& -1& 0& 0\\ 0& q& q& 2q& 2q& q& q-1& q\\ 0& 0& 0& 0& 0& 0& 0& -q-1\end{array}\right)$$

As [12] remarks, this matrix is not diagonalizable over $\mathbb{Z}[q]$. Now we perform the following elementary row and column operations: $R_1\mapsto R_1+R_3,R_3\mapsto R_3+q{R}_1,C_3\mapsto C_3-C_1,C_5\mapsto C_5-q{C}_1,C_6\mapsto C_6-q{C}_1,R_2\mapsto R_2-R_3,R_2\leftrightarrow R_1,C_2\leftrightarrow C_1,R_3\mapsto R_3+q{R}_1,R_4\mapsto R_4-q{R}_1,R_5\mapsto R_5+q{R}_1,R_6\mapsto R_6-q{R}_1,R_7\mapsto R_7+q{R}_1,C_3\mapsto C_3+C_1,C_5\mapsto C_5+q^2{C}_1,C_6\mapsto C_6+(q^2+q)C_1,C_3\mapsto C_3-C_4,R_3\leftrightarrow R_1,C_3\leftrightarrow C_1,R_4\mapsto R_4+(-q+1)R_1,R_5\mapsto R_5+q{R}_1,C_4\mapsto C_4+2q{C}_1,C_5\mapsto C_5+(q^3-q^2+q)C_1,C_6\mapsto C_6+q^3{C}_1,R_4\mapsto R_4+R_5,R_4\mapsto R_4+R_6,R_4\leftrightarrow R_1,C_4\leftrightarrow C_1,R_5\mapsto R_5+2q^2{R}_1,R_6\mapsto R_6-q{R}_1,R_7\mapsto R_7+2q{R}_1,C_5\mapsto C_5+(-q^2-1)C_1,C_6\mapsto C_6+(-q^2-1)C_1,R_7\mapsto R_7+R_8,R_7\leftrightarrow R_1,C_8\leftrightarrow C_1,R_8\mapsto R_8+(-q-1)R_1,C_5\mapsto C_5-q^3{C}_1,C_6\mapsto C_6+(-q^3+q^2-q)C_1,R_8\mapsto R_8+(-q-1)R_1,C_5\mapsto C_5-q^3{C}_1,C_6\mapsto C_6+(-q^3+q^2-q)C_1,C_7\mapsto C_7+(q-1)C_1,R_5\mapsto R_5-q^2{R}_6,R_8\mapsto R_8-(-q^2-q)R_6,C_5\mapsto C_5-(-q^2-q-1)C_7,C_5\leftrightarrow C_8,R_6\leftrightarrow R_7,R_5\leftrightarrow R_6.$ We now have the matrix: (1) $$\left(\begin{array}{cccccccc}-1& 0& 0& 0& 0& 0& 0& 0\\ 0& -1& 0& 0& 0& 0& 0& 0\\ 0& 0& -1& 0& 0& 0& 0& 0\\ 0& 0& 0& -1& 0& 0& 0& 0\\ 0& 0& 0& 0& -1& 0& 0& 0\\ 0& 0& 0& 0& 0& -q^2+q-1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& -q^4-q^2-1\\ 0& 0& 0& 0& 0& 0& -q^2+1& q+1\end{array}\right)$$(1)

If $q\equiv 0$ mod 3 then we may apply $R_8\mapsto R_8+\frac{q}{3}{R}_7$ and $R_7\mapsto R_7+3R_8$. We may then kill row 8 to obtain the matrix $\text{diag}(-1,-1,-1,-1,-1,-q^2+q-1,-q^6+1,1)$.

If $q\equiv 1$ mod 3 then we may apply $R_8\mapsto R_8+\frac{q+2}{3}{R}_7$ and $R_7\mapsto R_7-3R_8$. We may then kill row 8 to obtain $\text{diag}(-1,-1,-1,-1,-1,-q^2+q-1,-q^6+1,1)$ once again.

If $q\equiv 2$ mod 3, then we apply $R_8\mapsto R_8+\frac{q+1}{3}{R}_7,C_7\mapsto C_7-(q^5-q^4+q^3-q^2+q-1)C_8$ and $C_7\leftrightarrow C_8$ to obtain $\text{diag}(-1,-1,-1,-1,-1,-q^2+q-1,-3,-q^6+1)$.

Hence we see that the maximal torus corresponding to class 6W in $W({\mathrm{E}}_8)$ has structure $$T_w(q)\cong \{\begin{array}{cc}3\times (q^2-q+1)\times \frac{(q^6-1)}{3}\hfill & q\equiv 2\mathrm{ }\text{mod}\mathrm{ }3\hfill \\ (q^2-q+1)\times (q^6-1)\hfill & q\equiv 0,1\mathrm{ }\text{mod}\mathrm{ }3\hfill \end{array}$$ and from this we can read off the torsion coefficients.

We now have a further example involving a maximal torus of ${\mathrm{E}}_8$ that is an extension (by a cyclic factor of q–1) of a maximal torus from ${\mathrm{E}}_7$. As we shall see, when adding on this additional cyclic factor, the resulting matrix may no longer be in Smith normal form. Thus, in these cases, there is additional work to be done in order to give the torsion coefficient decomposition of the corresponding torus.

Consider the class 6S in $W({\mathrm{E}}_8)$ with corresponding torus index $22\prime$. We remark that the admissible graph for this class, namely ${\mathrm{A}}_1+{\mathrm{A}}_5$, can consist of roots that are orthogonal to r₈ as one would expect. The matrix $q.w-I$ is $$\left(\begin{array}{cccccccc}-q-1& 0& -q& 0& 0& 0& 0& 0\\ -q& -q-1& -q& -2q& -2q& -q& 0& 0\\ q& q& q-1& q& 0& 0& 0& 0\\ 0& -q& -q& -q-1& 0& 0& 0& 0\\ 0& q& q& q& q-1& q& 0& 0\\ 0& 0& 0& 0& 0& -q-1& 0& 0\\ q& q& 2q& 3q& 2q& 2q& q-1& 0\\ 0& 0& 0& 0& 0& 0& 0& q-1\end{array}\right)$$

This matrix can be decomposed into a 7 × 7 matrix that can be extended to an 8 × 8 matrix by adding an additional row and column consisting of all 0 entries apart from q–1 in the new diagonal entry. This 7 × 7 sub-matrix corresponds to the matrix $q.w-I$ where w is a representative of class 6O in $W({\mathrm{E}}_7)$ (the class with torus index 22). We omit the details for the diagonalization of this 7 × 7 sub-matrix, but from Table 9 we see that $$T_w(q)\cong \{\begin{array}{cc}(q+1)\times (q^6-1),\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times (q+1)\times \frac{(q^6-1)}{2},\hfill & q\mathrm{ }\text{odd}.\hfill \end{array}$$

The operations used to diagonalize this sub-matrix are independent of the last row and column, hence in ${\mathrm{E}}_8$ we have that $$T_w(q)\cong \{\begin{array}{cc}(q-1)\times (q+1)\times (q^6-1),\hfill & q\mathrm{ }\text{even}\hfill \\ 2\times (q-1)\times (q+1)\times \frac{(q^6-1)}{2},\hfill & q\mathrm{ }\text{odd}.\hfill \end{array}$$

However, these structures are not in Smith normal form. When q is even, q–1 and q + 1 are coprime. Indeed, let d be a common divisor. Then d divides $(q+1)-(q-1)=2$. Hence d = 1 or 2. As q–1 and q + 1 are both odd, we cannot have d = 2 and so d = 1 as required. Hence, using the fact ${\mathbb{Z}}_n\times {\mathbb{Z}}_m\cong {\mathbb{Z}}_{nm}$ when n, m are coprime, we get that $T_w(q)\cong (q^2-1)\times (q^6-1)$ for q even.

Now suppose q is odd. By our previous remarks, we know that we may diagonalize $q.w-I$ to obtain the diagonal matrix (2) $$\left(\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 2& 0& 0& 0\\ 0& 0& 0& 0& 0& q+1& 0& 0\\ 0& 0& 0& 0& 0& 0& \frac{(q^6-1)}{2}& 0\\ 0& 0& 0& 0& 0& 0& 0& q-1\end{array}\right)$$(2)

Consider the 3 × 3 diagonal sub-matrix of (2) given by $$\left(\begin{array}{ccc}q+1& 0& 0\\ 0& \frac{(q^6-1)}{2}& 0\\ 0& 0& q-1\end{array}\right)$$

To this matrix, we may apply the following row and column operations to obtain the Smith normal form: $R_3\mapsto R_3+R_1,C_3\mapsto C_3-C_1,R_1\mapsto R_1-\frac{q+1}{2}{R}_3,C_1\mapsto C_1+\frac{q+1}{2}{C}_3$. This results in the matrix $$\left(\begin{array}{ccc}2& 0& 0\\ 0& \frac{(q^2-1)}{2}& 0\\ 0& 0& \frac{(q^6-1)}{2}\end{array}\right)$$ and hence we have arrived at the result shown in Table 9.

The methods demonstrated here can be applied to all the conjugacy and twisted conjugacy classes in this paper, including those in ${\mathrm{G}}_2$ and ${\mathrm{F}}_4$.

We return to say one more thing about the MAGMA function TwistedTorusOrder(R,w) which takes as arguments an untwisted root datum R and Weyl group element w and, according to the handbook [2], produces a list of cyclic direct factor orders (as polynomials in q) for the maximal torus corresponding to w in a group with root datum R. As noted earlier, the function was written by Haller, whose thesis [21] explains that the torus structure can be obtained from the Smith normal form of qw–I computed over the ring $\mathbb{Q}[q]/(q^{\left|w\right|}-1)$, but gives no details on how. Upon inspection of the Magma code, the function first computes the Smith normal form of qw–I over $\mathbb{Q}[q]/(q^{\left|w\right|}-1)$ and compares the torsion coefficients of the abelian group corresponding to this Smith normal form and the additive groups of the eigenspaces of qw–I, at every prime power q < 20. If the torsion coefficients agree, then the function returns a list of the diagonal entries of the Smith normal form. Otherwise, the components of the Smith normal form are successively factored until the torsion coefficients of the corresponding abelian group agree with those from the eigenspaces at each q < 20. While we authors have been unable to find an example where TwistedTorusOrder returns an inaccurate torus structure, there is no guarantee that one can be sure the structure is accurate at every q by checking only against prime powers less than 20.

We close this paper with a remark on something to be observed in the tables shown in Section 4. Suppose w₁ and w₂ are representatives from two distinct conjugacy classes of $W(E_n)$ (n = 6,7,8) such that ${\Gamma }_{w_1}$ = ${\Gamma }_{w_2}$. Then $T_{w_1}(q)\cong T_{w_2}(q)$ when q is even.

Acknowledgments

Attempts to understand the maximal tori of ${\mathrm{E}}_8(3)$ during a Focussed Research Workshop funded by the Heilbronn Institute, then grew and grew into the present paper. The second and fourth authors were funded by EPSRC PhD studentships. As is clear, Roger Carter’s work in [7] is pivotal in probing the maximal tori of groups of Lie type. A further debt is owed by the third author who received much encouragement from Roger early in his academic career.