CUBICALLY REGULARIZED STOKESLETS FOR FAST PARTICLE SIMULATIONS OF LOW-REYNOLDS-NUMBER DROP FLOWS

Abstract

Swarms of Stokeslets have previously been shown to be effective for simulating three-dimensional, free-surface, buoyancy-driven drop flows at unit viscosity ratio, including interfacial rupture and pass-through phenomena. This article presents an efficient marker-and-cell/fast Fourier transform (MAC-FFT) algorithm that yields N log N scaling of the operations, thereby enabling accurate simulations involving millions of particles. The formerly separate steps of regularization of the Green's function (commonly used in vortex blob methods for inviscid flow) and discretization are unified by regularizing the Stokeslet over the cubical cells that form the underlying grid—as opposed to the spherical blobs used in the past. A piecewise-constant drop phase function, obtained by simple binning of the particles, thereby yields second-order quadrature of the Green's function to obtain the velocity field. An iterative cascade algorithm (adapted from Daubechies wavelets) allows the Stokes “cubelet” field to be calculated very efficiently. A similar cubelet approach is used for the cohesive forces that mimic interfacial tension. A user-friendly library of Fortran 95 subroutines ( DropLib , www.droplib.org) has been developed to carry out the simulations and visualize drop shape evolutions in three dimensions.

Keywords:

• Creeping flow
• Discrete convolution
• Drop dynamics
• Fast convolution
• Fast Fourier transform
• Green's function
• Marker-and-cell
• Regularization
• Stokeslet

Introduction

This contribution culminates a series of previous articles (Machu et al., 2001; Nitsche and Schaflinger, 2001; Nitsche et al., 2004a,b) that developed the numerical approach of simulating creeping, free-surface flows of liquid drops—thus far at unit viscosity ratio—with swarms of Stokeslets. For extremely large numbers of Stokeslets, we present here a marker-and-cell/fast Fourier transform (MAC-FFT) scheme whereby the particle positions at each time step are mapped onto a regular grid of cubical cells to extract a piecewise constant density profile. By regularizing the Stokeslet over the cubical cell (as opposed to a spherical blob), second-order accuracy is obtained for the grid integration. A cubical distribution is also used for the (non-singular) cohesive kernel that mimics the effect of interfacial tension. Discrete convolutions for the cell-cell interaction kernels are reduced to O(N log N) operations using the FFT. Particle velocities are then trilinearly interpolated from the grid to update the positions in a fourth-order Runge-Kutta integration of the dynamical system. Owing to 1/r decay of the Stokeslet and fixed radius of cohesion relative to the (small) cell dimension δ, the near-cell hydrodynamic and cohesive interactions are of order δ² and δ³, respectively. Thus, near-field contributions are sufficiently resolved by the regularized kernels in our pure particle-mesh method, without the need for particle-particle terms from the P³M approach of Hockney and Eastwood (1988).

A main purpose of this article is to present efficient methods for calculating the cubically smeared-out kernels. For the Stokes cubelet, we combine the analytical far-field formula with an iterative recursion scheme that is reminiscent of the cascade algorithm for calculating Daubechies wavelets (Daubechies, 1988; Debnath, 2002). For the cohesive cubelet we obtain an asymptotic formula.

In contrast to the literature on low-Reynolds-number flows, the literature on inviscid flows records a long history of particle-based numerical approaches to the Euler equations. These methods use either singular point vortices (PVM) or regularized vortex blobs (VBM) that get advected by the flow that they themselves generate by superposition (Chorin, 1973; Beale and Majda, 1982; Anderson and Greengard, 1985; Leonard, 1985; Beale, 1986; Hou and Lowengrub, 1993; Hou et al., 1993; Haroldsen and Meiron, 1998; Winckelmans et al., 2005). In this application, the summation of vortices represents a particular discretization for implementing the Biot-Savart law, by which a convolution integral of the Green's function for Poisson's equation against the curl of the vorticity yields the velocity field.

An analogous point dipole method (PDM) was used more recently to simulate two-dimensional non-Newtonian flow in a journal bearing (Phillips, 2003). An integral constitutive equation yielded the (history-dependent) viscoelastic stresses from which the dipole strengths were obtained. These point dipoles were then summed against the relevant propagator (gradient of the Stokeslet) to yield the velocity field by which the dipole positions could be updated.

A multitude of exact and approximate solutions have been obtained for creeping flow in various geometries by distributing the Stokeslet and/or its derivatives over curves and surfaces (Blake, 1971; Dabroś, 1985; Nitsche and Brenner, 1990; Claugue and Phillips, 1996, 1997). Both slender body theory (Batchelor, 1970; Cox, 1970; Tillett, 1970) and the boundary-integral method (Rallison and Acrivos, 1978; Rallison, 1981; Stone and Leal, 1989; Manga and Stone, 1993; Pozrikidis, 1990, 1992, 2001, 2002; Loewenberg and Hinch, 1996; Cristini et al., 1998, 2001; Davis, 1999; Zinchenko and Davis, 2006; Griggs et al., 2007, 2008) represent versions of the general singularity approach that are particularly amenable to systematic and highly sophisticated discretization schemes. It therefore seems odd that volumetric distributions of freely advected Stokeslets have received much less attention than their counterparts in inviscid flow.

Because the unbounded singular solutions induce unphysically large mutual velocity disturbances at nearby points, they are usually regularized by mathematically smearing out the distribution of force/vorticity/stretching over a small volume—typically in a spherically symmetric fashion using a radial cutoff function. Estimates of quadrature error and considerations of numerical stability speak in favor of choosing the cutoff diameter to exceed the interparticle spacing, so that these “fuzzy Stokeslets”/“vortex blobs”/“dipole blobs” overlap as they move according to the local velocity field (Hou et al., 1993; Lowengrub et al., 1993; Phillips, 2003; Baker and Beale, 2004; Nitsche et al., 2004a); see also Hockney and Eastwood (1988, p. 270). Our cubically regularized interaction kernels do not advect or overlap: rather, they stack contiguously together to form a fixed grid. Thus, we have unified the formerly separate steps of regularization and discretization.

In vortex-based numerics, grids are used in two different contexts. One (Lagrangian) usage refers simply to the initial placement of the vortex particles in a regular lattice. This lattice enables the spatial quadrature for the Biot-Savart law, but may also be used to calculate the vorticity by a finite-difference approximation (Beale and Majda, 1982; Hou and Lowengrub, 1990).

Two uses of Eulerian grids are standard in inviscid flow numerics for accelerating the particle summations (Winckelmans et al., 2005). The tree codes of fast multipole methods (FMM) use a binary hierarchy of cells, each half as large as those of the preceeding level, to organize the particles into nearby versus distant clusters. Local multipole expansions are tuned to the cell sizes and distances of interaction (Chew et al., 2000; Greengard, 1994; Greengard and Rokhlin, 1987; Carrier et al., 1988; Rokhlin, 1985; Sangani and Mo, 1996; Phillips, 2003). For a fixed level of accuracy, the summations can be reduced to O(N) operations. For our purposes fixed error is not entirely realistic as a criterion, because the motivation for adding more particles within the same drop volume is to diminish the discretization error in the convolution integrals. In enforcing the aforementioned O(N ^−1/2 log N) error scaling, one might expect FMM to come in around O(N log N) operations.

Eulerian grids are also used in multigrid and other fast Poisson solvers, as an alternative to the Biot-Savart convolution integral of the Green's function to obtain the velocity field from the grid-mapped vorticity (Hockney and Eastwood, 1988; Liu and Doorly, 2000; Liu, 2001; Winckelmans et al., 2005).

Once the particles are binned into the piecewise-constant density profile, we apply the FFT to carry out the discrete convolution sums for cohesive and hydrodynamic cell-cell interactions in O(N log N) operations (Press et al., 1992). Spatial periodicity inherent in the Fourier transform does not imply periodic boundary conditions in our simulations, because the grid on which we carry out the FFT is doubled in each dimension relative to the original simulation grid. To fill the FFT grid, the particle density and force arrays are padded out with zeros, and the kernel arrays are extended to twice the original range of interaction. Thus, the implied periodic extension of the Stokeslet on the doubled FFT grid is not equivalent to the periodic Stokeslet of Hasimoto (1959): indeed, it preserves the convolution sum for the free-space Stokeslet on the original grid.

Particle-mesh Ewald techniques use the FFT to accelerate a reciprocal-space convolution sum, which accompanies an additional short-range, physical-space sum of O(N) operations to represent the grid-mapped interaction of particles via a periodic kernel of electrostatic (Darden et al., 1993; Essmann et al., 1995) or hydrodynamic (Sierou and Brady, 2001, 2002; Saintillan et al., 2005) origin.

Our MAC-FFT method is appealingly simple yet sufficiently versatile to track exceedingly complicated shape evolutions of drops. Before proceeding with further details, it is appropriate to establish the mathematical formulation.

Boundary Integral Formulation

For unit viscosity ratio, the inertialess flow field set in motion by gravity and interfacial tension for any drop configuration—volume 𝒱 bounded by surface(s) 𝒮—can be represented by a suitable spatial distribution of the (dimensionless) Green's function for Stokes flow, or Stokeslet:

The velocity at each point is given by

with e _g the unit vector pointing in the direction of gravity, H the local surface mean curvature, and n the local, outward pointing unit normal vector on the surface. In terms of the undeformed drop radius a, interfacial tension σ, and density difference Δρ, the (dimensionless) Bond number B is given by

This represents the strength of viscous deforming forces relative to the restoring force of interfacial tension.

The boundary integral formulation applies the divergence theorem to transfer the body force from the volume to the surface:

The advantage of discretizing in two dimensions rather than three is offset by the difficulty of tracking interfaces when these become substantially distended, roll up, pinch off, or coalesce (Cristini et al., 1998, 2001). Equation (4) will be integrated numerically in order to validate the MAC-FFT velocity field for spheroidal drops.

Volumetric Cohesion as a Model of Interfacial Tension

Volumetric approaches can deal with exceedingly complicated drop shapes; these include front tracking (Unverdi and Tryggvason, 1992; Tryggvason et al., 2001; Olgac et al., 2006) level-set methods (Chang et al., 1996; Osher and Fedkiw, 2002; Bassano, 2004; Tanguy and Berlemont, 2005; Deshpande and Zimmerman, 2006; Xu et al., 2006), the volume-of-fluid method (Gueyffier et al., 1999; Scardovelli and Zaleski, 1999; Li et al., 2000; Renardy and Renardy, 2002), diffuse interface methods (Anderson et al., 1998; Yue et al., 2004), and our Stokeslet method (Machu et al., 2001; Nitsche and Schaflinger, 2001; Nitsche et al., 2004a,b). When viewed in volumetric terms, forces due to interfacial tension are effectively concentrated into a surface delta function; see Equation (2). For numerical purposes, this singular spike must be distributed over a thin but finite zone straddling the interface—at some loss of accuracy. Current volumetric approaches to interfacial tension require spatial derivatives of the normal vector, which itself is calculated from the gradient of the phase function or level-set function (Brackbill et al., 1992; Lafaurie et al., 1994; Coward et al., 1997; Gueyffier et al., 1999; Scardovelli and Zaleski, 1999; Morris, 2000). Interfacial tension is actually equivalent to a cohesive force acting only between those drop material points that lie at (or within a thin layer covering) the surface; see Nitsche et al. (2004a).

Two previous articles (Nitsche and Schaflinger, 2001; Nitsche et al., 2004a) have developed an alternative volumetric approach that entirely avoids the surface normal vector. A radially symmetric cohesive potential φ, acting volumetrically between all drop material points within some cutoff radius ε (i.e., not just between material points on the surface), was shown to lead to the same velocity field as in Equation (4), within O(ε²) corrections.

Defining ℬ( r ;ε) to be a ball of radius ε centered at point r , we have

Radial moments of the dimensionless cohesive potential φ are defined as follows:

There is considerable latitude with regard to the functional form φ(ρ). It may, but need not, mimic an actual intermolecular potential. Aside from continuous differentiability and compact support (φ = 0 for ρ > 1), the potential must have a net energetic effect: I ₂ ≠ 0.

The cohesive potential does not actually produce tensile forces at the interface, but it does extract an asymptotic approximation of the local mean curvature when it is evaluated exactly on the interface (Rowlinson and Widom, 1989; Nitsche et al., 2004a).

The volumetrically forced velocity field (5) results from neglecting the ord(ε²) correction term. Formally then, one would therefore require the radius of cohesion ε to be asymptotically small compared to the smallest radius of curvature on the interface (which does not mean that the drops being modeled are confined to small deformations). In numerical practice the forgiving nature of the asymptotic expansion (8) allows this formal restriction to be relaxed considerably. For example, Nitsche et al. (2004a) bounded the coefficient A for a prolate spheroid of minor/major axis ratio R and a typical functional form for the dimensionless radial potential φ:

The influence of ε on a simulated evolution of drop shapes will be seen in Figure 4.

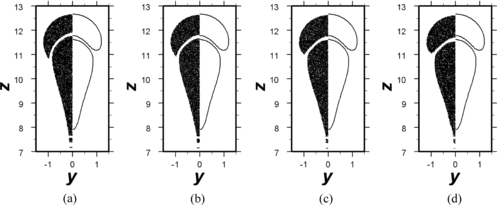
Figure 4 Validation of the volumetric MAC-FFT simulations (sectional view of points on the left) against the boundary-integral method (interfacial outlines on the right; see Davis, 1999) for two buoyant drops at Bond number B = 5 and unit viscosity ratio. The initially spherical drops are both of unit radius with a gap of 0.1, and the configurations depicted correspond to t = 25. The overall shape evolution is well captured even when the radius of cohesion is as large as the undeformed drop radius (ε = 1). Higher-curvature details are more accurately obtained with smaller values of ε. The trail of particles is due to (i) extreme curvature at the lower tip of the trailing drop, which is poorly resolved by the cohesive potential, and (ii) neglect of particles that pass outside the drop-following grid. (a) ε = 1.0, (b) ε = 0.8, (c) ε = 0.63, (d) ε = 0.5.

The cohesive pressure field corresponding to the velocity field (5) differs from that due to interfacial tension, but this has no consequence for tracking drop shapes. The actual pressure field could be reconstructed on a post facto basis from its gradient, as given by the Laplacian of the numerically calculated velocity according to the Stokes equations.

We represent each drop with a swarm of particles distributed with statistically uniform number density over its interior. The volume attributed to each particle is denoted by δV. The interface is defined at length scales larger than the mean interparticle spacing (δV)^1/3, as a jagged zone of transition between the particle-laden and particle-free regions. Summing the cohesive and Stokeslet kernels over the particle positions is equivalent to a discretized, Monte Carlo approximation of the convolution integrals (5) and (6).

In numerical practice, the Stokeslet kernel G( r ) would be replaced by a regularized version—see Equation (30), below—with a cutoff radius at least as large as (δV)^1/3 in order that neighboring Stokeslet blobs overlap their diffuse clouds of force. Because these regularized kernels do not blow up at r = 0, the self-interaction term would not be omitted from the summation in Equation (10). As written, the dynamical system (10), (11) would require order N ² operations to calculate the mutual cohesive and viscous interactions between all particles. Such a direct procedure becomes computationally intractable for tens or hundreds of thousands of particles—hence the need for fast summation techniques.

Toward more efficient summations, we first define a phase (or color) function

that allows both Equations (5) and (6) to be written in convolution form:

with

Cubically Distributed Kernels and Second-Order Quadrature

For numerical evaluation of the convolution integral (13), we combine the (usually separate) steps of discretization and regularization into a single operation. By averaging the Stokeslet over a cubical cell 𝒞(δ) of side length δ in the Eulerian grid:

we obtain second-order quadrature errors upon multiplying by the cubewise-constant force density.

where the cubical averages are taken over the argument q . For example,

An analogous argument applies to the cohesion integral (14).

with

Defining the cubical average of the cohesive potential

we note the relation

which will prove useful for evaluating .

In tracking liquid drops with sharp interfaces, one should not expect better than a second-order quadrature error when c( r ) and f  ( r ) have jump discontinuities. Thus, simple binning of the particles for the MAC lumping is sufficient to extract and . Higher order volume interpolation (Hockney and Eastwood, 1988; Liu and Doorly, 2000; Liu, 2001; Walther and Morgenthal, 2002) would be superfluous.

Based upon the binned cell concentrations , we evaluate the forces at the centers of all of the cells via the discrete convolution sum corresponding to Equation (14).

with

The forces at the individual particles are interpolated trilinearly between the cell-center values f _i,j,k and subsequently binned to obtain the cell-averaged forces . These forces in turn figure in the discrete convolution sum for the velocities.

with

Since the convolution sums over all cells can readily be accelerated with the FFT (Press et al., 1992), what remains to consider is an efficient approach for calculating discrete tabulations of the cubically regularized Stokeslet kernel and of the cubically distributed cohesive kernel . Note that the kernel tables need be calculated only once and then stored for repeated use at each time step of a simulation.

The Stokes Cubelet

Suitable scaling of the cubically regularized Stokeslet for δ = 1 yields for arbitrary side length δ:

For large distances ∥ r ∥ one can approximate by substituting a Taylor expansion of the Stokeslet (1) into Equation (18) and integrating term-by-term in the dummy argument q over the unit cube. All terms of odd order vanish immediately by symmetry. Even terms are isotropic, whereby the successive gradients reduce to iterates of the Laplacian: ∇⁴ G and higher derivatives vanish due to the Stokes equations. Thus we obtain the far-field formula

For the near field one could use a numerical quadrature, but sufficiently fine discretizations for extremely accurate results would be needlessly slow to compute. Instead, we propose an iteration scheme that is reminiscent of the cascade algorithm for calculating Daubechies wavelets (Daubechies, 1988; Debnath, 2002).

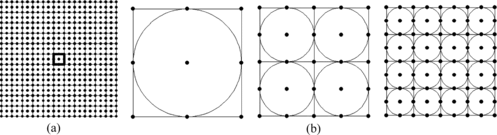
We begin by observing that the unit Stokes cubelet field is exactly equivalent to the sum of eight half-size cubelets.

To launch the iteration scheme one can use any solution of the inhomogeneous Stokes equations that localizes unit total force entirely within the unit cube 𝒞(1); see Equation (16). In order to distribute the force density as uniformly as possible at the outset, we use a spherically regularized Stokeslet

inscribed in the unit cube (i.e., radius a = 1/2), as illustrated in Figure 1(b). This formula is equivalent to the Hadamard-Rybczynski solution for unit viscosity ratio (Happel and Brenner, 1983; Kim and Karrila, 1991), and would represent a very crude approximation of the Stokes cubelet field .

Figure 1 Efficient evaluation of the Stokes cubelet . (a) The applicable subroutine retrieves stored values for the unit cubelet (outlined in bold) at the discrete points shown, and applies the far-field formula (28) at more distant points. (b) First three stages of the iteration scheme.

We evaluate the initial field (30) at the discrete half-cell positions

and store the resulting tensorial values of 𝒢 for |I|, |J|, |K| ≤ 11 in a five-dimensional array (3 × 3 × 23 × 23 × 23). A cubelet subroutine returns the (current) stored values of when |I|, |J|, |K| ≤ 11, and applies the far-field formula (28) otherwise; see Figure 1(a). This subroutine is now applied to the iteration Equation (29) to update the array for all |I|, |J|, |K| ≤ 11. Two observations are in order. First, the half-cell array (34)—as opposed to just the cell-center array in Equation (26)—is necessary in order that the half-cell values of the half-size cubelets on the right-hand side of Equation (29) cover the discrete array positions needed for the full-size cubelet on the left-hand side; see Figure 1(b). Second, the points for 7 ≤ |I|, |J|, |K| ≤ 11 lie beyond the array for all eight half-size cubelets on the right-hand side of Equation (29), which is precisely why the far-field formula is necessary. Figure 1(b) shows how successive updates of the array values are equivalent to increasingly uniform distributions of force density over the unit cube. In other words, n iterations are equivalent to a spatial resolution of 2⁻ⁿ . We obtained 11-digit accuracy for the cube center with 18 iterations, which required about 3 s of computation time on a Dell Latitude D830 notebook PC running the gfortran compiler (http://gcc.gnu.org/fortran/).

The Cohesive Cubelet

A judicious choice for the cohesive potential (Figure 2)

allows the cubical average (21) to be integrated easily in closed form for positions r such that , because then all points q in the cube 𝒞(δ) lie safely within the cutoff radius:

Similarly, must vanish for , because then all points in the cube 𝒞(δ) lie beyond the cutoff radius. To facilitate integration for the intervening regime, we consider points r lying along the x axis. For the asymptotic limit of a cube that is small compared to the radius of cohesion (δ << ε) we can replace the spherical cutoff surface with a plane

Accordingly the transitional values of x become ε ± δ/2 instead of . The resulting integral

is again easily evaluated. Thus we obtain the asymptotic formula

with

For ε = 0.8 and δ = 0.4, Figure 2 compares this asymptotic curve with a Monte Carlo integration of Equation (21), with distance ∥ r ∥ being taken along the ray θ = π/6, φ = π/3 in polar coordinates—i.e., specifically not along the x axis, as was used to derive Equation (40). This shows that radial symmetry in Equation (39) is actually a very good approximation.

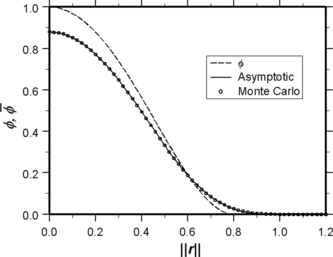
Figure 2 Radial dependence of the cohesive cubelet field for ε = 0.8 and cube side δ = 0.4, evaluated by two alternative methods: (i) asymptotic formulas (39) and (40), and (ii) Monte Carlo evaluation of Equation (21). Also shown is the original potential φ, Equation (35), before taking the cubical average.

Differentiating Equation (40) with respect to ρ yields , according to Equation (22).

with

Implementation and Validation of the Numerical Scheme

As is described in the Appendix, a library of Fortran 95 routines (DropLib, www.droplib.org) was written to implement the numerical scheme outlined above. For all calculations we used the cell size δ = 0.08 with a nominal number density of 64 particles per cell. Thus each drop (of unit undeformed radius) was represented by a statistically uniform swarm of about 523,600 randomly placed particles. The drop configurations were rendered as three-dimensional images by the following procedure. At each time step the particles associated with each drop (regarded as a separate phase) were binned to yield a number density attributed to the center of each cell. In order to damp out local statistical fluctuations, the discrete array of densities was first smoothed by two successive passes of weighted averaging with the 26 immediately neighboring cells. For each drop the phase function c( r ) analogous to Equation (12) was obtained by interpolating trilinearly between the corresponding smoothed density array. The interface was then rendered as the c = 0.5 level surface (including shadows and reflections) with a ray-tracing module (www.quickie3d.org) called by the particle simulation code. All computations were carried out on a Dell Latitude D830 notebook PC running the gfortran compiler (http://gcc.gnu.org/fortran/). For the two-drop system with cohesion (Figure 5), calculation of all particle velocities from their positions required about 70 s.

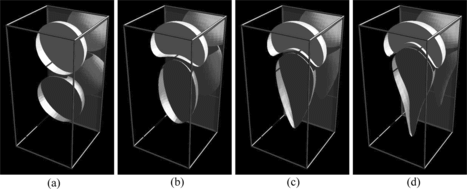
Figure 5 Shape evolution of two buoyant drops for B = 5. Both initially spherical drops are of unit radius, and the radius of cohesion is ϵ = 0.63. (a) t = 0, (b) t = 10, (c) t = 20, (d) t = 30.

For a sufficiently small radius of cohesion ε, the cohesive potential Φ( r ;ε) defined in Equation (6) extracts the local surface mean curvature H( r ) when the point r lies exactly on the interface; see Equation (8). In exchange for an asymptotically small error, we have extended throughout three-dimensional space what was originally defined as purely a surface quantity. In order to test the accuracy of Equation (8) in numerical practice, consider a spheroidal drop (semi-axes a and b) and the associated deformation D:

Note that D is positive/negative for prolate/oblate spheroids. In order to match the volume of the unit sphere with D = 0.3, we take a = 1.5109 and b = 0.8136. Standard formulas from differential geometry (Gray, 1998) applied to the surface parametrization

yield the surface mean curvature:

For various radii of cohesion ε, Figure 3(a) employs this exact formula to test the volumetric-cohesive model (6), (8), and (35), as implemented with our MAC-FFT scheme. The progression ε = 0.5, 0.63, 0.8, 1.0 is chosen to yield roughly a twofold increase in volume (proportional to the number of particles involved in the local cohesive summation) between successive values of ε. As ε is decreased, the high curvatures at the poles (θ = 0, π) are resolved more accurately. The smallest sum (ε = 0.5) is seen to be the most susceptible to local statistical fluctuations; this effect would be mitigated by refining the particulate and grid discretizations.

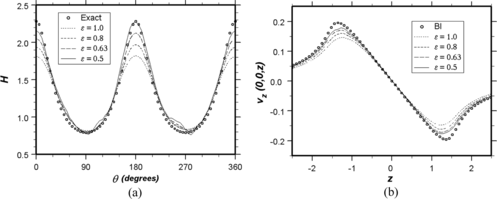
Figure 3 Validation of the MAC-FFT scheme using four different radii of cohesion (ε = 0.5, 0.63, 0.8, 1.0) for a prolate, spheroidal drop with deformation D = 0.3. (a) Mean curvature as a function of polar position. Equation (8) is compared with the exact result (45). (b) Velocity field. Traversing along the axis of revolution, the numerically calculated axial velocity v _z (0, 0, z) is compared with the boundary-integral formula (46).

The interfacial-tension contribution to the boundary-integral velocity field (4) can be written out explicitly as a double integral over the surface variables θ and φ:

with G being evaluated according to Equation (1). The integral (46) is then approximated numerically via Simpson's rule, using a step size of π/100 in both θ and φ. For a traverse along the z axis, Figure 3(b) compares the theoretical versus numerical velocity components v _z (0, 0, z) for several values of the cohesive radius ε. Again, accuracy increases with decreasing ε.

The MAC-FFT simulation of the axisymmetric shape evolution of two trailing drops was tested against a boundary-integral code (generously provided by Professor Robert H. Davis, University of Colorado at Boulder), as illustrated in Figure 4. The overall shape evolution is well captured even when the radius of cohesion is as large as the undeformed drop radius (ε = 1). Higher-curvature details are more accurately obtained with smaller values of ε. High mean curvature (and correspondingly large tensile forces) form at the lower tip of the trailing drop to balance strong local viscous stretching forces. This fine structure is not well resolved with our radii of cohesion, ε ≥ 0.5. Thus, the resultant cohesive force is insufficient to hold together the particles at the tip, and they are left behind in an accumulating tail. Particles that trail too far behind do not get counted in the drop-following grid and therefore do not contribute to the velocity field. The cumulative loss of particles does not significantly degrade accuracy of the overall simulation, and could be diminished by reducing the radius of cohesion (which would require a finer mesh to resolve accurately). A direct comparison of our CPU times with the boundary-integral code is not meaningful because the latter (which finished in seconds) is confined to the axysymmetric case and requires the interfacial curves to remain unbroken.

With regard to the cohesive forces, distinct drops are regarded as belonging to different species even though they have the same viscosity. Particles representing a given drop cohere to each other, but not to particles in any other drop. This provision is necessary to suppress unphysical coalescence between nearby drops, which would otherwise occur in the simulations.

Distribution of Particles

Our random initial distribution of markers was obtained by choosing a box large enough to contain all drops, then populating the box with a suitable number of Cartesian coordinates from a uniformly distributed random number generator, and finally retaining only those points lying inside the drops. For an instantaneous drop configuration thus randomly discretized, the resulting Monte Carlo integration (Press et al., 1992, §7.6) of the Green's function according to Equation (13) yields a better scaling of the quadrature error (N ^−1/2 log N; see Machu et al., 2001) than would a periodic lattice of markers (N ^−1/3) as is typically used in vortex methods (Beale, 1986; Goodman et al., 1990; Cottet et al., 1991; Hou and Lowengrub, 1990). Quadrature errors in the velocity field are addressed by Figure 3(b); see also Adachi et al. (1978) and Ekiel-Jezewska et al. (2006).

Particle redistribution schemes or adaptive creation of new particles is sometimes necessary in order to prevent anisotropic clustering or local depletion of particles in the course of a simulation, which can degrade accuracy; see, e.g., Liu and Doorly (2000) and Winckelmans et al. (2005) in connection with inviscid flow. A dipole regeneration scheme was also used by Phillips (2003) for non-Newtonian flows. For Stokeslet-based simulations of liquid drops without interfacial tension, a random initial particle distribution without redistribution is sufficient for tracking the bell-mushroom-ring transition and the subsequent cascade of bifurcations (Machu et al., 2001). Cohesive forces can engender some spurious clustering effects for coarser swarms (Nitsche and Schaflinger, 2001; Nitsche et al., 2004a), but these have been largely obviated by our MAC-FFT approach—because the enhanced computational efficiency allows much finer spatial discretization and smaller time steps. For the durations of the cohesive simulations presented below (Figures 4 and 5), nonuniformity of the particle distribution was not a significant issue.

We regularize/distribute the interaction kernels over the same fixed, cubical grid cells used to represent the phase function—as opposed to using particle-attached cutoff functions (Chorin, 1973; Anderson and Greengard, 1985; Hou et al., 1993; Phillips, 2003). Because our particles act only as markers for the local presence of the drop phase, and because each cell contains a large number of particles, we do not anticipate any significant dynamical effects associated with local statistical fluctuations in the particle number density.

Even in sedimentation of suspension drops (where the particles and their statistical distribution have more tangible physical significance), substructural effects beyond the Stokes hydrodynamics become asymptotically negligible as the particulate discretization is refined (Nitsche and Batchelor, 1997; Schaflinger and Machu, 1999; Machu et al., 2001; Ekiel-Jezewska et al., 2006). For example, in tracking the statistics of a spherical swarm of 4978 sedimenting Stokeslets through a distance of 150 drop radii, Machu et al. (2001) found that the thin trail of exiting particles did not cause a significant statistical redistribution of particles in the drop.

Results and Conclusions

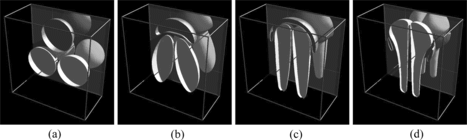
The buoyancy-driven motions and shape evolutions for immiscible (B = 5) versus miscible (B → ∞ ) trailing drops are shown in Figures 5 versus 6, respectively. A cutaway view reveals internal structures, and the reflection from the back wall of the simulation box shows the external structure. Penetration of the leading drop by the trailing drop has occurred by dimensionless time t = 30 in the miscible case; see Machu et al. (2001). Interfacial tension (represented here by cohesion) is seen to reduce the deformation and prevent penetration (Davis, 1999). Finally, a non-axisymmetric shape evolution involving three drops appears in Figure 7.

Figure 6 Shape evolution of two buoyant drops for B → ∞. Both initially spherical drops are of unit radius. (a) t = 0, (b) t = 10, (c) t = 20, (d) t = 30.

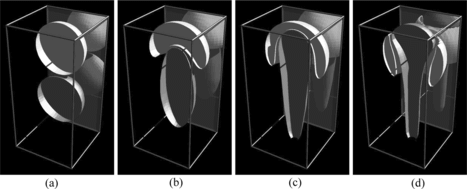
Figure 7 Shape evolution of three buoyant drops for B → ∞. All three initially spherical drops are of unit radius. (a) t = 0, (b) t = 10, (c) t = 20, (d) t = 30.

In our volumetric MAC method, an “interface” is represented by—and visually interpreted as—the abrupt zone of transition between the (ideally, uniform) particulate number density within the drop(s) and zero number density outside. Although the interfacial location and shape are defined only within a distance on the order of the mean interparticle spacing, the “fuzzy” interface itself exists as a meaningful entity independent of the individual identities of the particles that collectively represent the macroscopic shape of a drop at any instant. Because the interfacial zone is automatically renewed with particles from the interior as the free-surface flow proceeds, rupture, penetration, or evolving topology of this thin zone poses no special difficulty for the MAC approach, in contrast to methods that track the interface with markers or other elements of surface discretization (Rallison and Acrivos, 1978; Rallison, 1981; Stone and Leal, 1989; Manga and Stone, 1993; Pozrikidis, 1990, 1992, 2001, 2002; Loewenberg and Hinch, 1996; Cristini et al., 1998, 2001; Davis, 1999; Zinchenko and Davis, 2006; Griggs et al., 2007, 2008). For example, we can track the pass-through mechanism described by Rother et al. (2001); see also Machu et al. (2001).

The MAC-FFT method presented here affords computational efficiency for extremely large numbers of particles. Future work is contemplated in three main directions. First, perturbation and iteration techniques hold promise for generalizing the Stokeslet method to unequal viscosities of the drop phase and surrounding liquid. Second, short-range interspecies potentials will be investigated as a means of modeling coalescence with the retarding effect of film drainage; see Chi and Leal (1989), Yiantsios and Davis (1991), Manga and Stone (1993), and Rother et al. (1997). Finally, the rheology of emulsions (Loewenberg and Hinch, 1996; Zinchenko and Davis, 2002) could be modeled by superposing an ambient shear flow field inside the unit cell of a spatially periodic array of drops and using the particle mesh Ewald analog (Sierou and Brady, 2001, 2002; Saintillan et al., 2005) of our FFT approach to accelerate convolution sums of Hasimoto's (1959) periodic Stokeslet. The effective viscosity of the emulsion could then be extracted from the imposed shear rate and either the resultant viscous dissipation or the total forces on opposing sides of the unit cell.

Acknowledgments

The authors are grateful for the boundary-integral code that was generously provided by Professor Robert H. Davis, University of Colorado, Boulder. This enabled the comparison shown in Figure 4.

Notes

Respectfully dedicated to Professor Howard Brenner on the occasion of his 80th birthday.

Appendix: DropLib Simulation Package

A user-friendly Fortran 95 subroutine library called DropLib was developed to carry out the simulations that are presented in this article. For several Fortran compilers (Silverfrost FTN95, Portland Group PGI Fortran, gfortran) the website www.droplib.org provides precompiled link libraries that may be freely downloaded for use with various computer platforms: Windows/Vista (.dll files), Mac OS X (.dylib files), and Linux (.so files). Linked to the DropLib package, the following short program automatically generates as bitmap images (.bmp files) the three-dimensional renderings appearing in Figure 5, above.

program drop_run

integer :: i

double precision :: radius1, deform1, buoyancy1, cohesion1

double precision :: radius2, deform2, buoyancy2, cohesion2

double precision, dimension(3) :: center1, center2

call unlock (‘2008:af#8-g4fd-&khj:f4s2-k2hj-t4k2:k*(f-hjk&-j2#3’)

buoyancy1 = 1.0d0 ; cohesion1 = 0.2d0 ; deform1 = 0.0d0 ; radius1 = 1.0d0

buoyancy2 = 1.0d0 ; cohesion2 = 0.2d0 ; deform2 = 0.0d0 ; radius2 = 1.0d0

center1 = (/ 0.0d0, 0.0d0, 0.0d0 /)

center2 = (/ 0.0d0, 0.0d0, 2.1d0 /)

call drop3d_param (0.63d0,0.08d0,64,200,0.05d0,‘top’)

call drop3d_spher (3,deform1,radius1,center1,buoyancy1,cohesion1,‘red’)

call drop3d_spher (3,deform2,radius2,center2,buoyancy2,cohesion2,‘green’)

call drop3d_start

call drop3d_image (600)

do i = 1, 3

   call drop3d_tstep (2.5d0,10.0d0)

   call drop3d_image (600)

end do

end program drop_run