A Framework for the Analysis of Thermal Losses in Reciprocating Compressors and Expanders

Abstract

This article presents a framework that describes formally the underlying unsteady and conjugate heat transfer processes that are undergone in thermodynamic systems, along with results from its application to the characterization of thermodynamic losses due to irreversible heat transfer during reciprocating compression and expansion processes in a gas spring. Specifically, a heat transfer model is proposed that solves the one-dimensional unsteady heat conduction equation in the solid simultaneously with the first law in the gas phase, with an imposed heat transfer coefficient taken from suitable experiments in gas springs. Even at low volumetric compression ratios (of 2.5), notable effects of unsteady heat transfer to the solid walls are revealed, with thermally induced thermodynamic cycle (work) losses of up to 14% (relative to the work input/output in equivalent adiabatic and reversible compression/expansion processes) at intermediate Péclet numbers (i.e., normalized frequencies) when unfavorable solid and gas materials are selected, and closer to 10–12% for more common material choices. The contribution of the solid toward these values, through the conjugate variations attributed to the thickness of the cylinder wall, is about 8% and 2% points, respectively, showing a maximum at intermediate thicknesses. At higher compression ratios (of 6) a 19% worst-case loss is reported for common materials. These results suggest strongly that in designing high-efficiency reciprocating machines the full conjugate and unsteady problem must be considered and that the role of the solid in determining performance cannot, in general, be neglected.

INTRODUCTION

Unsteady and Conjugate Heat Transfer

Numerous engines, thermal-fluid devices, and other systems are capable of utilizing clean and renewable energy sources such as solar, geothermal, and waste heat, which is expected to render them increasingly relevant in domestic as well as industrial settings. A common feature of these systems concerns their interaction (externally) with inherently time-varying fluid and heat streams (e.g., flow rates, pressures, temperatures), and/or the occurrence (internally) of naturally time-varying thermodynamic processes during operation, even when the external conditions are steady. These interactions can readily give rise to unsteady and conjugate heat exchange, in which heat transfer occurs simultaneously by convection between the fluid streams and the internal surfaces of the relevant components and by conduction through the solid walls.

In many cases the unsteady (i.e., time-varying) heat transfer can take place simultaneously with pressure and density variations in the fluid, for example, in thermoacoustic engines [1–3], dry free-liquid-piston (Fluidyne) engines [4–6] or two-phase thermofluidic oscillator equivalents [7–9], free-piston Stirling engines [10–12], and pulse tubes [13–15], as well as in stand-alone compressors and expanders or when these units appear as components within larger systems. In some cases the conditions can give rise to conjugate heat transfer in the presence of the time-varying variations of pressure, density, and temperature. This is the subject of the present paper.

Rankine Cycle Expanders

Among others, compressors and expanders can be employed in Rankine cycle engines, including organic (ORC) equivalents [16], for power generation. In fact, an efficient and low-cost expander is a crucial component of any economically efficient ORC system. Typical breakdowns of the thermodynamic exergy destruction in the case of a basic and a regenerative ORC system reveal that after the evaporator(s), the expander is the component associated with the largest performance penalty, with an exergetic loss of about 20% [17].

Various expanders are available and these are usually categorized as belonging to two main classes of machines:

1.	Positive-displacement machines (also known as “volume” type, such as pneumatic converters, or screw, scroll or reciprocating piston expanders).
2.	Turbomachines (also “velocity” or “dynamic” type, such as axial or axial-flow turbine expanders).

Positive-displacement expanders are further classified according to the mechanism used for fluid flow (motion), into (i) rotary expanders (including multivane or rotating piston expanders [18], screw or helical expanders [19], and scroll expanders [19–22]), and, (ii) reciprocating (or reciprocal) piston expanders [23]. Turbomachines include axial- and radial-flow (or centrifugal) turbine expanders (or turbo-expanders) [24].

Operational and specification data from expansion devices employed in more than 2,000 Rankine engines were collected by Curran [25]. These data, which span power outputs from 0.1 to 1,120 kWe, reveal that low-speed expansion devices (<5,000 rpm) tend to be predominantly positive-displacement (e.g., reciprocating) machines producing power outputs of up to 10 kWe, while turbomachines on the other hand are adopted at higher speeds (>5,000 rpm) for meeting greater demands, with output shaft powers in excess of 10 kWe.

A second compilation of specification and performance information was employed by Balje [26] in order to identify the optimal geometries and maximum obtainable design efficiencies for different types of expander. The resulting compilation of performance characteristics indicates that at low speeds positive-displacement expanders offer superior performance (i.e., exhibit greater efficiencies) when compared to single-stage turbomachines. Rotary positive-displacement expanders achieve isentropic efficiencies η_is similar to those of single-stage turbines at specific diameters (and consequently sizes) that are only 1/4 to 1/3 of those required for single-stage turbo-expanders, while reciprocating positive-displacement expanders can achieve similar efficiencies at even lower speeds [26].

Piston Compressors and Expanders

As discussed earlier, positive-displacement machines offer the potential of higher efficiencies compared to turbomachines, especially in smaller scale applications. In theoretical studies of reciprocating Joule/Brayton cycles [27, 28], compression and expansion efficiencies in excess of 98% have been employed. Moss et al. [27] used isentropic efficiency values η_is of 97.5% for compression and 99.3% for expansion in the context of a reciprocating Joule/Brayton combined heat and power (CHP) plant, while White [28] based his study on theoretical values of 98% and 99% for the polytropic efficiency of reciprocating compressors and expanders as part of a reverse Joule/Brayton cycle heat pump for domestic applications. In both cases the authors concede that these figures are only estimates of minimum losses and are not based upon direct measurement [28]. Where measurements do exist (see later discussion) they suggest lower efficiencies, but in such cases it is likely that leakage flow and valve pressure losses (both of which have scope for reduction) are to a significant extent detrimentally affecting performance.

Nonetheless, for low-cost small-scale machines with medium to large leakage gaps manufactured with low precision, Table 1 (compiled from data found in Ref. [29]) suggests that reciprocating and rotary piston compressors and expanders also significantly outperform their scroll counterparts. Specifically, piston machines have indicated η_ind efficiencies in the range 85–91% for compression and 78–87% for expansion, and isentropic η_is in the range 72–76% for compression and 63–72% for expansion. In Ref. [29] it is also suggested that for even smaller leakage gap sizes of 5 μm, η_ind and η_is reach ∼95% and ∼90% for both compression and expansion, respectively. Clearly, reciprocating and rotary piston compressors and expanders are of interest in the applications just mentioned. The present study focuses on reciprocating piston machines; however, the results are transferable to rotary piston equivalents, as well as related engines and devices (e.g., [1–15]).

Table 1 Positive-displacement compressor and expander indicated and isentropic efficiencies for leakage gap sizes of 10–15 μm, taken from reference [29]

Machine	Type	ηind	ηis
Compressor	Reciprocating piston	0.85–0.91	0.72–0.76
	Rotary piston	0.85–0.90	0.72–0.75
	Scroll	0.39–0.64	0.36–0.56
Expander	Reciprocating piston	0.81–0.87	0.66–0.72
	Rotary piston	0.78–0.84	0.63–0.69
	Scroll	0.47–0.75	0.32–0.69

Irreversible Heat Transfer Losses

Performance losses in reciprocating engines, compressors, and expanders arise from mechanical irreversibilities (i.e., mechanical friction, pressure drops through the intake and exhaust valves), but also from thermal irreversibilities (i.e., heat transfer between the fluid and walls of the device). In order to improve their efficiency it becomes essential to minimize all loss mechanisms. Valve losses may be minimized by a combination of careful valve timing, rapid opening, and large open areas. Once mechanical losses have been minimized, thermal losses become the dominant loss mechanism. The present investigation focuses on this aspect of performance.

A performance loss in reciprocating systems arising as a consequence of unsteady heat transfer occurs even if the overall process is globally adiabatic (i.e., for zero time-mean heat transfer), since any heat exchange due to a finite temperature difference between the gas and the cylinder walls is an inherently irreversible process. The exergetic loss due to the (zero-mean) heat transfer fluctuations arises as a consequence of the fact that heat from the fluid (gas, liquid, or vapor) at a high temperature is temporarily stored in the solid walls, which are at a lower temperature, and then returned (in its entirety) to the fluid at an even lower temperature. Although the net fluctuating heat loss is zero, a finite exergetic penalty is paid.

For this reason, beyond the steady (time-averaged) heat losses, it is important to be able to account for, characterize, and predict accurately the time-varying heat exchange fluctuations between the fluid and solid. A further characteristic of interest concerns the timing (phase difference) of the heat transfer relative to the temperature fluctuations; in some systems the heat is lost and gained by the fluid at the wrong time in the cycle, thus adversely affecting performance and efficiency.

Heat Transfer in Reciprocating Systems

Unsteady heat transfer in reciprocating systems (engines, compressors, expanders, etc.) has been the subject of various investigations [30–36]. These have shown that it is not possible to describe the convective heat transfer process with a single, constant heat transfer coefficient (HTC). In fact, the employment of such a “steady flow” HTC in the quantitative description of the unsteady thermal interaction between a solid and fluid, although a simple and powerful approach, can be seriously inadequate in many cases. Yet many theoretical and modelling approaches assume a constant value for the HTC taken from steady flows in order to quantify the unsteady convective heat exchange. In other studies attempts are made to modify the Nusselt number correlations generated in steady flows, through the definition of suitable Reynolds numbers, and they have shown that this goes some way toward offering a correction, but that important deviations between measured and the predicted heat transfer rates from correlations remain [37].

Studies that do account for the unsteady heat transfer process often continue to neglect the full, conjugate problem by assuming either a constant temperature or a constant heat flux boundary condition at the (internal) solid–fluid interface. Consequently, computational results are often in considerable disagreement with experiments. The assumption of a constant wall temperature may be adequate when dealing with gases, but this is not always the case (as we show later) and becomes tenuous at best in the case of high HTCs (or equivalently, phase change) or under certain geometrical conditions [38, 39].

In this paper a simple, one-dimensional framework is presented that has been developed for the quantitative description of unsteady and conjugate heat transfer in the presence of displacement work. This framework applies the approach presented in Refs. [38–40] to a generalized model of a reciprocating compression and/or expansion process. Specifically we use the solution to the one-dimensional (1D) thermal conduction in a solid investigated in Mathie and Markides [40] as a boundary condition to the compression space. The work in Mathie and Markides [38] extended upon that work and showed how to evaluate the unsteady heat transfer as the result of a fluctuating heat transfer coefficient in the fluid while imposing a conjugate solid boundary with the use of a thermal impedance representing the solid domain. Finally, Mathie et al. [39] validated this framework by applying it to a number of experimental results. The specific process examined here is that of a gas spring, in which a fixed mass undergoes sequential compression and expansion within the same closed space (volume) [30, 32, 33, 36].

METHODS

Problem Formulation

The full problem treated here deals with the thermodynamic process undergone by a fixed mass of gas trapped in a reciprocating piston-in-cylinder configuration in the presence of finite heat transfer from/to the gas, with a fixed temperature imposed on the external (rather than the internal) wall of the cylinder. The latter has been done in order to estimate the effects of conjugate heat transfer. This is also an approximation, but one that allows assessment of the thermal properties of the wall. The model that is developed is valid for operation at low volumetric compression ratios (C _R < 6), due to the description used for the convective heat transfer coefficient in the fluid [32,33]; however, this can be easily extended to higher compression ratios C _R. Radiative heat transfer, mechanical, and fluid viscous losses are not considered in the present work.

Figure 1 Schematic of the gas spring problem.

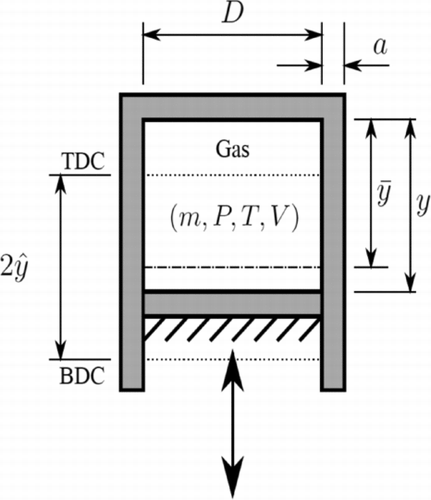
Consider the sinusoidal compression and expansion with frequency ω₁ of a mass of gas m enclosed by the cylinder and the reciprocating piston shown in Figure 1. The geometry features a piston of diameter D following an imposed reciprocating motion (e.g., by connection via a mechanism to a motor rotating at constant angular speed ω₁), with amplitude about a mean position described by,

During a cycle the piston makes one full movement from bottom dead center (BDC) to top dead center (TDC) and back again. As the piston progresses from BDC to TDC the volume enclosed by the piston V(t)=Ay(t) decreases, which results in a corresponding increase in the pressure P(t) and temperature T _f(t) of the enclosed gas. Here, A=πD ²/4 is the cross-sectional area of the cylinder. Conversely, as the piston travels back to BDC the pressure P and temperature of the gas T _f will decrease.

It is assumed, for convenience, that the mass of gas enclosed by the spring m is fixed, that is, that there is no leakage between the piston and the cylinder, and that the gas is ideal. These assumptions should isolate the effect of the unsteady heat transfer loss mechanism in the gas spring system from other effects. Consider for a moment a real system in which the assumption of an ideal gas may not hold true, such as a reciprocating compressor in a cryogenic refrigeration unit. In this case, the working fluid may be operating close to its vapor point (i.e., low temperature and high pressures). The use of the ideal gas model in such a situation should lead to a significant underestimation of the heat transfer, as the real gas densities (e.g., hydrogen at low temperature [41]) and also the heat transfer coefficients (and their fluctuations thereof) would be higher. It can thus be deduced that by using the ideal gas model in situations where the working fluid comes close to the dew point, the loss due to cyclic heat transfer will be underpredicted. Similarly, gas leakage from around the piston seal when work is done on the gas would result in an additional exergetic loss. In this case, work would effectively be lost with the gas as it escapes from the cylinder during compression. This would also add the additional complication that the mass of gas in the compression space would decrease over time. However, the application of a real gas model and the accounting of gas leakage will not be considered here, as they will add little to our overall understanding of the loss mechanism due to unsteady (and possibly conjugate) heat transfer, which is the main objective of this work.

The fluctuations in the fluid temperature T _f(t) during the cycle give rise to time-varying heat transfer between the fluid and the walls of the cylinder , and consequently also through the cylinder walls to the environment, which is assumed to be isothermal at a constant (external) temperature T ₀. In general, the solid wall temperature T _w(t) will be fluctuating in response to the time-varying heat transfer rate .

Following Lee [30], Kornhauser and Smith [32, 33], and others, cyclic convective heat transfer in a gas spring may be described by a modified Newton's law of cooling while employing complex temperatures, heat fluxes, and heat transfer coefficients (or equivalently, Nusselt numbers ). This results in a complex formulation of Newton's law,

Note that in Eq. (2), is a flux, that is, the heat transfer rate per unit time-varying surface area available to heat transfer S(t), which includes the sides of the cylinder, as well as its base and the face of piston, such that S(t)=πDy(t)+πD ²/2. In addition, and contrary to convention, note that is defined as positive when leaving the gas (see also Eqs. (9) and (21)).

The imaginary part of the complex Nusselt number formulation in Eq. (2) arises physically from a turning point in the temperature profile through the gas [42]. This turning point is caused by the work done by/on the gas, which acts to introduce a phase difference between the heat flux at the wall and the bulk temperature difference across the gas T _f−T _w.

At low Péclet numbers (or, normalized frequencies ω), that is, < 100, the flow inside the compression space will be predominantly laminar and the heat transfer across it can be solved analytically, as done by Lee [30]. The Nusselt number (or, normalized HTC h) can be found by solving the energy equation in the gas after simplification [30],

which is a function of the Péclet number ,

and where . Here, α_f,0 is the thermal diffusivity of the working fluid when the piston is in the mean (central) position (i.e., when ), and ω=ω₁ is the oscillation frequency of the piston in rad s⁻¹.

At higher Péclet numbers, > 100, there is greater mixing in the compression space due to flow instabilities and eventually turbulence. In this case the heat transfer cannot be solved analytically but instead must be characterized empirically. The Nusselt number for the present study was taken from an empirical correlation derived by Kornhauser and Smith [33],

Combining the two complex Nusselt number correlations in Eqs. (4) and (5), that is, at both low and high Péclet numbers , allows for a Nusselt number relationship that covers an extended Péclet number range, as shown in Figure 2.

Figure 2 Complex Nusselt number

relations imposed in the present study as a function of Péclet number

, together with the real and imaginary components of the Nusselt number from the studies of Lee [30] and Kornhauser and Smith [32, 33].

The heat flux through the wall can be found as the cyclic convolution (operation denoted by *) of the solid's thermal response to fluctuations in the wall temperature [38, 39],

where Z is a representation of the thermal impedance in the time domain, that is, the thermal impulse response. The thermal response or “impedance” of the solid for an isothermal outer boundary condition can be represented in the frequency domain, at a given frequency ω _n , as Z_n =Z(ω _n ) and can be found by solving the one-dimensional unsteady heat diffusion equation in the solid to obtain [38, 39],

This solution contains two lengths: the thickness of the cylinder wall a, and a thermal diffusion length scale in the solid, δ_s,n , sometimes referred to as the “thermal penetration depth,”

where k _s, ρ_s, and c _s are the thermal conductivity, density, and specific heat capacity of the solid.

Equations (2) and (6) can be solved for T_w , since the heat fluxes must match at the inner wall, , while integrating the energy equation (i.e., Eq. (9)) to obtain the evolution of the bulk fluid temperature T _f(t) over the cycle,

Performing dimensional analysis on the preceding equations it can be seen that the system can be described by nine independent variables. The set of chosen variables is given as:

where ρ_f,0 and α_f,0 are the density and thermal diffusivity of the gas phase when the piston is in the mean (central) position, . The variables include: (i) ratios of geometric parameters, and of fluid and solid thermophysical properties; (ii) the Péclet number ; and (iii) a dimensionless external (environment) temperature T*₀, with T ₀ constant.

The dimensionless geometric parameters that describe the geometry of the gas spring are found by normalizing against each variable's mean value, giving the displacement (y*), area (A*), volume (V*), and density (ρ*) variables given here:

where t*=ω₁ t is the dimensionless time and ω*=1 the dimensionless harmonic frequency.

Normalizing all temperatures by (ω₁ D)²/2c_v , which is a measure of the amount of energy given to the system scaled as a temperature, results in the dimensionless temperature,

and the dimensionless pressure,

Accordingly, the real part of the heat flux in Eq. (2) becomes,

and Eq. (6) is rewritten as,

where Z* is the dimensionless thermal impedance of the solid at a given dimensionless frequency Ω* _n , such that,

whereby the dimensionless frequency is defined as Ω* _n =ω _n /ω₁=n. Furthermore,

in Eq. (19) is the solid to fluid thermal diffusivity ratio, with the former evaluated at the fundamental frequency ω₁ and the latter evaluated when the piston is in the central position .

Finally, Eq. (9) that describes the energy balance in the gas domain becomes,

On examination of Eq. (21) it can be observed that for low Péclet numbers the majority of the work done by the gas will be exchanged in the form of heat with the solid walls, and the system will effectively undergo isothermal compression and expansion. On the other hand, at high Péclet numbers the heat exchanged will be minimal, and the system will experience adiabatic compression and expansion.

Consequently, we would expect that at intermediate Péclet numbers the work will result from interplay between both the internal energy of the gas and the heat transfer to the solid and, by extension, the environment. A phase lag between the temperature of the fluid T*_f and the heat transfer will result in a net loss of work around the cycle.

A useful metric to gauge the relative importance of the fluid and solid domains in the heat transfer solution is the Biot number, which can be interpreted as a ratio of temperature changes in the fluid to temperature changes across the solid,

By definition the solution to the gas spring problem will deviate from the isothermal boundary condition imposed in all previous studies on the internal walls of the cylinder when the Biot number Bi is large. In this condition the temperature of the wall will begin to fluctuate. Due to the relationship of to the Péclet number , the Biot number Bi will become large when the Péclet number is either much less than 1, 1, or much greater than 1, 1. Two additional parameters of importance in determining the Biot number Bi are the thermal effusivity ratio ϵ_r=κ_rρ_r,0 c _rγ between the solid and the fluid, and the ratio b _s of the wall thickness to the thermal diffusion length in the solid. Both small effusivity ratios ϵ_r and/or large length-scale ratios b _s lead to large Biot numbers Bi.

In a similar manner the governing equation for the gas spring system can be derived when subject to a sinusoidal oscillation in the pressure,

instead of the volumetric variation previously discussed. In this instance it is convenient to consider the enthalpy of the system, H=U+PV, in place of its internal energy, which leads to the equation,

Using the same normalization scheme on Eq. (24) as that used on Eq. (9) we obtain,

This formulation is similar to that of studies of Lee [30] and Kornhauser and Smith [32, 33].

For compressors with a fixed stroke length it is more convenient to use the volumetric formulation that we derived earlier, in Eq. (21). This is because the pressure ratio of the gas spring for a fixed volume ratio will change depending upon whether it is operating in an isothermal or adiabatic condition, as we show later.

Numerical Method

The solution to the gas spring problem was calculated numerically. Firstly the temperature of the working fluid, T*_f, and wall, T*_w, were discretized in the time domain. An initial guess was made for the wall temperature T*_w throughout the cycle at each time instance, and the initial fluid bulk temperature. The corresponding wall heat flux, , was then calculated using Eq. (18) by taking the wall temperature into the frequency domain with a fast Fourier transform (FFT) and applying the wall transfer function, Z*. The ordinary differential equation (ODE) in Eq. (21) was then integrated numerically to find the evolution of the fluid temperature throughout the cycle subject to the imposed fluctuation in V*. The wall heat flux could then be evaluated using the complex Nusselt formulation in Eq. (17). The individual values of T*_w and T*_w(0)could then be solved for such that and T*_w(0)=T*_w(2π). Any suitable algorithm could be used to solve for T*_w, such as the Newton–Raphson method. For the simulations the number discretization points was kept at 100 after experimentation showed that at this value the total relative error for the model was low, of the order 10⁻⁸, and had little variation down to 30 points.

RESULTS AND DISCUSSION

Cyclic Heat Flux and Temperature Differences in the Fluid

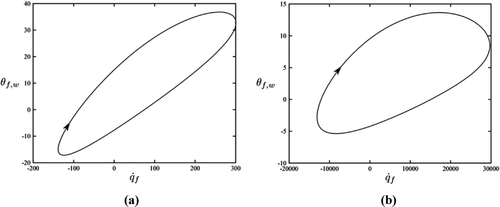
Figure 3 shows typical temperature difference–heat flux (θ-) plots for two gas spring cases: (a) = 17 and a/δ_s,1 = 3.2 × 10⁻¹; and (b) = 1000 and a/δ_s,1 = 1.9. The temperature difference refers to the difference between the fluid and the internal surface of the solid wall,

In a (quasi-)steady heat transfer scenario one would expect to see straight lines passing through the origin, with a gradient that is not dependent on the direction of the process (i.e., heating vs. cooling). The closed area inscribed by the resulting curves is an indicator of the (imposed, through Eqs. (2) to (5)) phase difference between θ and . Moreover, the positive asymmetry of this plot with respect to the vertical axis at = 0 suggests a net heat flow from the gas to the solid, and hence also from the solid to the surroundings, which can only come from a net work input to the gas spring cycle. This work input is a pure loss, with the ideal gas spring requiring exactly the same amount of work to compress the gas as is gained by its subsequent expansion.

Figure 3 Modeled heat flux

and temperature difference across the gas θ around the cycle for a gas spring with κ_r = 1, ρ_r,0 = 1, and C _R = 1 for: (a)

= 17 and a/δ_s,1 = 3.2 × 10⁻¹; (b)

= 1 ×10⁵ and a/δ_s,1 = 3.2 × 10⁻¹.

Time-Varying Heat Transfer Coefficient

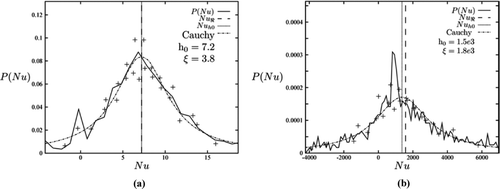
It is useful to be able to evaluate the expected value of the heat transfer coefficient in thermodynamic processes such as the one presented in this paper so as to evaluate the heat transfer performance. However, the heat transfer coefficient, , is a ratio of two variables that fluctuate about zero, namely, the heat flux and the temperature difference across the fluid θ. This will result in a heat transfer coefficient h that has a probability distribution that can be approximated by a Cauchy distribution function,

where h ₀ is the location parameter, or expected value of h, describing the location of the peak probability density, and ξ is the scale, or width, of the distribution. Such a distribution will arise, for example, if the two independent variables (heat flux and temperature difference θ) are normally distributed. In Figure 4 the probability distribution of the modeled heat transfer coefficient throughout the cycle is displayed. Here the heat fluxes are calculated using the complex Nusselt formulation from Eq. (2), and subsequently the instantaneous Nusselt number calculated using the relation . It can be seen that the Cauchy distribution fits the probability distribution of the modeled Nusselt number remarkably well, providing a level of confidence in this choice of distribution function.

Figure 4 Distribution of the instantaneous Nusselt number

and Cauchy approximations

: (a) distribution of

for

= 17 and a/δ_s,1 = 3.2 1 0⁻¹, showing a Cauchy approximation with expected value

= 7.2 and ξ = 3.8; (b) distribution of

for

= 1 × 10⁵ and a/δ_s,1 = 3.2 × 10⁻¹, showing a Cauchy approximation with expected value

= 1.5 × 10³ and ξ = 1.8 × 10³. Note: (i) The “+” marks indicate the sampled

on a particular simulation run; (ii) the vertical lines indicating

and

in the left-most figure are overlapping.

A Cauchy distribution poses a problem, however, as it has no mean value, or higher moments. Additionally, when using numerical methods or experimental data the mean is evaluated using a sample mean estimator, which for a Cauchy distribution is itself a Cauchy distribution. Furthermore, even if expressions for and θ are known analytically, the mean value cannot be calculated as the integral to find the expected value of h will not converge. Therefore, the mean value of the Nusselt number (and consequently also, of ) cannot be used to estimate the expected value, and a sample mean will give unpredictable results.

It is important to note that for a Cauchy distribution, despite this limitation, the parameters h ₀ and ξ can be estimated by maximizing the log likelihood estimator,

This estimation is performed herein in order to provide a value for the expected values of the heat transfer coefficient h ₀ and a corresponding value for the Nusselt number .

Study of Different Gas Spring Cases

In the following section we look at the response of the gas spring in four different cases. In each case the three key material property ratios, κ_r, ρ_r,0, C _R, are set to specific values, and the effect of changing the Péclet number and wall thickness is investigated:

•	Case 1 investigates the response when the property ratios are set to unity.
•	Case 2 selects property ratios that lead to interesting results but that correspond to conventional materials—that is, a plastic-coated cylinder liner filled with hydrogen as the working fluid, to a pressure 50 bar at 300 K.
•	Case 3 sets the parameters to achieve the worst case (highest loss) with realistic cylinder materials and pressures.
•	Case 4 considers the effect of increased pressure ratio on the gas spring response.

Case 1: Unity Material Property Ratios

We now proceed to investigate the gas spring case with the three key material property ratios set to unity, that is, with κ_r = 1, ρ_r,0 = 1, and C _R = 1. The main results are shown in Figure 5. The thermal loss parameter ψ in Figure 5a is defined as,

in accordance with the earlier discussion concerning this parasitic (net) work input to the thermodynamic cycle. Note that although the correlations from Kornhauser and Smith [32, 33] account for any turbulence or viscous effects in the fluid in terms of rate of heat transfer from the compression space, the present model takes no account of losses due to the mechanical/fluid dynamic irreversibilities present in the fluid domain as a result of any viscous or turbulent dissipation.

Figure 5 Response of a gas spring with the material ratios κ_r = 1, ρ_r,0 = 1, and C _R = 1 as a function of Péclet number

and for different a/δ_s,1 from 0.010 to 10: (a) thermal cycle loss ψ in percentage points, from Eq. (29); (b) pressure ratio P_r =min{P}/max{P}; (c) expected Nusselt number

.

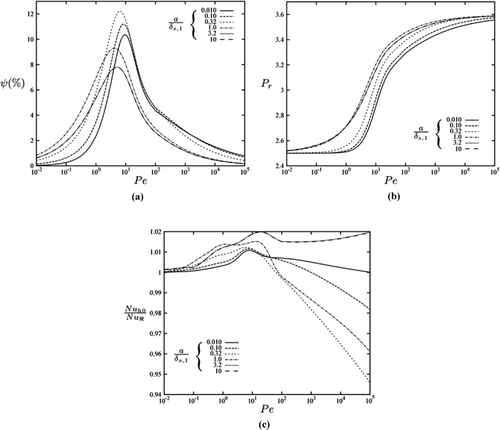
Considering the case when the wall thickness is small, that is, a/δ_s,1 = 0.01 in Figure 5a, the thinness of the wall gives rise to a strong coupling of the internal surface of the solid wall to the external (isothermal) boundary condition T ₀, which in turn results in the internal wall–fluid boundary condition being effectively isothermal. This is the condition that has been solved by Lee [30], and by almost all other similar studies.

At low Péclet numbers the frequency is low enough to allow heat transfer to take place between the fluid contained within the spring and the solid walls of the cylinder and piston, thus allowing the fluid to remain at (or near) thermal equilibrium with the solid. As such, the gas effectively experiences isothermal compression and expansion. In this condition all of the work done on the gas is transferred as heat to the walls but across a very small temperature difference, resulting in a low cycle loss. Similarly, at high Péclet numbers the process is fast, so there is not sufficient time to allow for heat exchange. In effect, at high Péclet numbers the system is undergoing adiabatic compression and expansion, with the majority of the work being exchanged with the internal energy of the gas. The thermal cycle loss is again low. This can also be seen in Figure 5b, whereby the pressure ratio at high or low Péclet numbers is consistent (for the fixed volumetric compression ratio) with an adiabatic process or isothermal processes, respectively.

When the Péclet number is at an intermediate value, however, heat is exchanged out of phase with the (finite) temperature difference θ across the gas resulting in an exergetic cycle loss. From Figure 5a, the peak thermal loss with an isothermal external wall boundary condition is about 10% and occurs at a Péclet number of around 10. Looking at Figure 5b it can be seen that this peak in thermal loss coincides with the transition between the isothermal and adiabatic process. This compares well to the result from Lee [30], though the loss here appears shifted to a slightly higher due to the fact that in the present work a fixed volumetric variation is imposed on the gas (Eq. (1)), whereas in Lee [30] (and elsewhere) a pressure variation is imposed with a given pressure ratio. This is associated with higher pressure ratios at higher , as demonstrated in Figure 5b, where it shown that as the system moves from isothermal (low ) to adiabatic (high ) operation the pressure ratio for the same volumetric time variation increases.

In the case of having a thick wall with a/δ_s,1 = 10 it is observed that the internal wall condition is only weakly coupled to (insulated from) the external boundary condition, so the temperature at the interface between the wall T _w and fluid temperatures T _f are free to fluctuate. At high Péclet numbers the effect of the thicker cylinder wall is to make the system more adiabatic and to reduce the thermal losses. Nevertheless, at lower the effects of the finite fluctuations in wall temperature T _w act so as to move the cycle away from the ideal isothermal process, leading to higher thermal losses. This is somewhat counterintuitive: One would expect the addition of material to have an insulating effect and to reduce the thermal loss, through an increase in the thermal resistance due to conduction. In fact, the peak thermal loss has reduced, and the peak has migrated to a lower value of .

When the wall thickness is chosen to be of order unity, or , the magnitude of the thermal loss is greater than that observed at both low and high a/δ_s,1. This arises from a thermal interaction in the solid (in the unsteady conduction) between the internal and external walls and leads to a modification of the phase of the heat flux out of the fluid . Thus, even though the magnitude of the heat flux is reduced, the phase at which it occurs relative to the temperature across the fluid θ gives rise to a greater cycle loss.

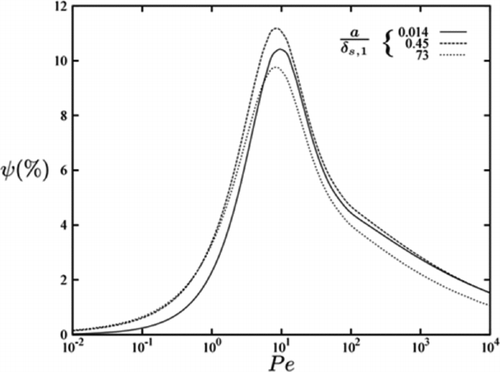
Case 2: Conventional Material Properties

The ratios of material properties in conventional systems do not typically equal unity, with the solid walls of the piston and cylinder likely to be considerably denser than the gas. The thermal conductivity of the solid is also likely to be higher, though the specific heat capacities of many gases tend to be higher than that of common solids. We consider a set of more typical values for our selected solid and gas properties by imagining that the walls of the cylinder are coated in a plastic such as polytetrafluoroethylene (PTFE) or acrylic, and that the spring is filled (when extended to BDC) with hydrogen at 50 bar at 300 K. The material ratios become κ_r = 1.06, ρ_r,0 = 145.1, and C _R = 0.15.

In this case the effect of the wall (see Figure 6) is very much reduced compared to our earlier results in Figure 5. Nevertheless, the exergetic loss exhibits similar characteristics to those observed previously, according to which produces the maximum loss and thicker walls make the fluid boundary condition less isothermal, increasing the cycle losses at low Péclet numbers and reducing them at high ones.

Figure 6 Thermal cycle loss ψ in a gas spring (in percentage points) as a function of Péclet number,

, with the material property ratios set to κ_r = 1.06, ρ_r,0 = 145.1, and C _R = 0.15, and over a range of wall thicknesses a/δ_s,1.

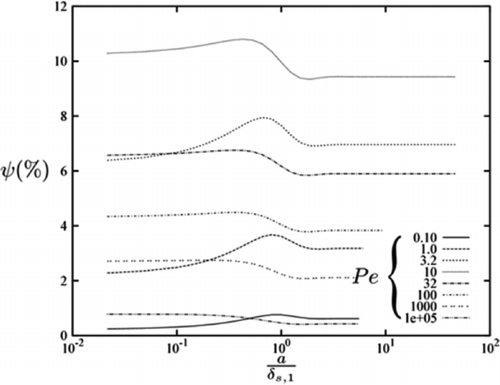
Figure 7 shows more clearly the dependence of the irreversible thermal loss on the dimensionless wall thickness a/δ_s,1. A wall thickness exists for which the maximum loss arises for a given Péclet number . The shape of these plots leads to a nontrivial conclusion with significant implications. Starting from a thin wall, it is interesting to observe that increasing the thickness of the wall, or insulation, is expected to lead to higher cycle losses, after which the losses decrease again. At low the loss when the wall is thin, is lower than when the wall is thick, . Conversely at higher Péclet numbers, that is, 5, the loss of a thick wall is lower than when the wall is thin.

Figure 7 Thermal cycle loss ψ in a gas spring (in percentage points) as a function of dimensionless wall thickness a/δ_s,1, with the material property ratios set to κ_r = 1.06, ρ_r,0 = 145.1, and C _R = 0.15, and over a range of Péclet numbers

.

By comparing the wall heat flux from Eqs. (17) and (18) it can be seen that,

where θ _j,k =T* _j −T* _k is the temperature difference across the solid or fluid domain. Due to the way in which Z* scales with a/δ_s in Eq. (19), and specifically given that tanh{x}∼x for x≪ 1, Eq. (30) leads to a scaling for the ratio of the temperature difference across the fluid to the temperature difference across the solid domain, θ_w,0/θ_f,w, of the form,

when a/δ_s is less than 1. Equation (31) also applies to the steady-state (mean temperature difference) part of the solution, since the steady-state problem is associated with an a/δ_s of 0. When a/δ_s is greater than 1 the ratio of the fluctuations in the temperature differences across the domains will still scale with Bi, but with a modification due to tanh{x}∼ 1 for x≫ 1,

where is an “unsteady” Biot number.

Figure 8 Response of a gas spring with the material ratios κ_r = 0.033, ρ_r,0 = 10, and C _R = 0.07, for a fixed (volumetric) compression ratio C _R as a function of Péclet number

and for different a/δ_s,1 from 0.010 to 10: (a) thermal cycle loss ψ in percentage points, from Eq. (29); (b) pressure ratio P_r =min{P}/max{P}.

Expressions (31) and (32) show the relative importance of the solid to the fluid domain on the solution, and are essentially a function of the Péclet number and the material thermal effusivity ratio ϵ_r (since the Nusselt number is also a function of the Péclet number ). When the Biot Bi or unsteady Biot numbers are less than 1 the fluctuations of the wall temperature T*_ware minimal and the problem is equivalent to having an isothermal wall temperature. Conversely when the Bi or numbers are greater than 1 the wall temperature T*_w will fluctuate significantly, thus affecting the solution. It can be seen therefore that the solid walls of the gas spring cylinder do affect the cycle undertaken by the gas when the effusivity ratio ϵ_r between the solid and the gas is low. In Figure 6 the effusivity ratio was ϵ_r = 32.3, whereas in Figure 5 this was ϵ_r = 1.40. As expected, at lower ratios ϵ_r the walls of the cylinder have a greater effect on the cycle losses.

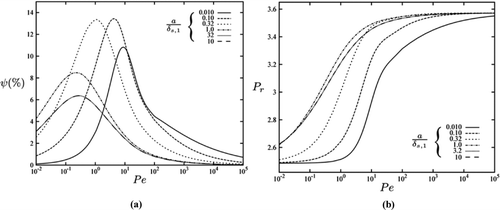
Case 3: Materials With Unfavorable Properties

The gas spring can exhibit more extreme effects due to the solid wall when the effusivity ratio ϵ_r is lowered below unity. To obtain a low effusivity the heat capacity, thermal conductivity and density of the gas must be high relative to the solid. Hydrogen has the highest specific heat capacity c_v and thermal conductivity k _f of any gas. Gases with higher atomic weights have higher densities ρ_f for the same pressure; however, this is outweighed by their lower heat capacities c_v and lower thermal conductivities k _f, thus leading to lower thermal effusivities ϵ. In addition, if turbulence is introduced into the gas spring chamber, such as would be expected when operating with a gas intake and exhaust through suitable valves, Cantelmi [34] showed that this can be modeled by a modified “turbulent” thermal conductivity for the gas, which can be up to 30 times larger than for the nonturbulent (molecular) case. Finally, if the cylinder walls are made of a low-density material, such as a foam, the thermal conductivity k _s, heat capacity c_s , and density ρ_s of the solid side are also significantly reduced.

Using hydrogen gas at high pressure, specifically ∼100 bar, an equivalent turbulent thermal conductivity multiplier guided by and with a foam layer insulating the inside of the cylinder as in Cantelmi [34] and a cylinder and piston faces with internal surfaces insulated by a foam (this can be fitted within a metal outer section for structural strength), it is feasible to obtain material ratios of κ_r = 0.033, ρ_r,0 = 10, and C _R = 0.07, which correspond to a thermal effusivity ratio of ϵ_r = 0.032. The results obtained from the gas spring described in the preceding paragraphs are shown in Figure 8. Clearly the losses are more pronounced, reaching a maximum value of more than 14% at intermediate dimensionless wall thickness a/δ_s,1 and Péclet numbers values.

A further interesting feature can be seen in Figure 8b, whereby, for a given Péclet number , the pressure ratio P_r is higher at intermediate wall thicknesses compared to when the wall is significantly thinner or thicker than the diffusion length δ_s,1. This is most likely the result of the increased cycle loss, which tends to occur at intermediate wall thicknesses (see Figure 8a), which would result in higher gas temperatures and so will give rise to a larger pressure ratio P_r to drive the same volumetric compression of the gas.

Figure 9 Loss ψ and pressure ratio P_r at a higher volumetric compression ratio in a gas spring as a function of Péclet number

, with the material property ratios set to κ_r = 1.06, ρ_r,0 = 145.1, and C _R = 0.15, and over a range of wall thicknesses a/δ_s,1: (a) thermal cycle loss in percentage points; (b) pressure ratio P_r .

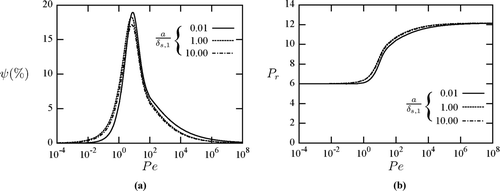
Case 4: High Compression Ratios

It has already been established that an increase in the gas density results in exacerbated heat transfer effects as the Biot number is lowered. This also implies that the cycle losses in the gas spring should also increase with pressure ratio P_r . The maximum volumetric compression ratio for which the models for the Nusselt number in Eqs. (3) and (5) can be considered as remaining reasonably valid is approximately C _R = 6. In this final part of the investigation we consider the case of high compression ratio conditions: specifically, with C _R = 6. The corresponding pressure ratio in perfectly isothermal conditions (in the low limit) is P_r = 6, and the corresponding pressure ratio in perfectly adiabatic conditions (in the high limit) is P_r = 12.3.

The losses incurred for these high pressure ratio conditions, with a typical selection of materials (to match the “Case 2” results in Figure 6, where C _R = 2.5), are shown in Figure 9a. In this figure it can be seen that the losses attained are as high as 19%, almost twice as high as the lower pressure ratio conditions of the earlier “Case 2” investigation with the same materials (see Figure 6). Finally, Figure 9b shows that, as expected, the pressure ratio varies between P_r = 6 and P_r = 12, as the system moves between the isothermal and adiabatic ideals, at the low and high extremes, respectively.

CONCLUSIONS

A conjugate model that solves the one-dimensional unsteady heat conduction equation in the solid simultaneously with the first law in the gas phase has been applied to the study of gas springs. An imposed heat transfer coefficient has been used, which was taken from relevant experimental studies in the literature. Beyond the explicit inclusion of conjugate heat transfer, the model extends upon previous investigations by considering the case of imposed volumetric compression, instead of an imposed pressure ratio, and thus allows the gas pressure to vary accordingly. The solution used for the 1D unsteady heat condition equation in this study was for planar conduction, so is only valid for axial geometries when a≪D. However, the conduction solution for axial geometries could easily be integrated into the model if required.

Notable effects of unsteady heat transfer to the solid walls of the gas spring are uncovered, with cycle losses of up to 14% for cases in which unfavorable materials (solid/gas) are selected, and losses closer to 10–12% for more common material choices, when compression ratios of 2.5 are investigated. The losses are maximized at intermediate Péclet numbers. The contribution of the solid toward these values, through the conjugate variations attributed to the thickness of the cylinder wall, amounts to about 8% and 2% points, respectively, with a maximum contribution at intermediate thicknesses. At higher compression ratios (of 6) the losses become even worse, reaching values of up to 19% when using common materials. Generally, the cycle losses due to these heat transfer effects are maximized when (i) the effective thermal conductivity of the gas is high, such as when dealing with light gasses or turbulent flows; (ii) the heat capacity and density of the gas is high, which occurs when operating at high pressures or low temperatures ranges; and (iii) at intermediate Péclet numbers (operational frequencies) and cylinder wall thicknesses. It was seen that the maximum thermal losses coincided with the transition between isothermal and adiabatic process in the gas spring.

These losses are not limited to gas springs; other reciprocating compression and expansion devices will be affected by similar thermal cycle loss mechanisms. The effects that have been investigated here will be of particular interest when the gas is at a low temperature and/or high pressure, such as in Stirling cryo-coolers, or when the heat transfer in the gas is enhanced by turbulence or phase change. The results suggest that in designing high-efficiency machines, the full conjugate and unsteady problem must be considered.

FUNDING

This work was supported by the Engineering and Physical Sciences Research Council (EPSRC) (grant number EP/J006041/1). RM gratefully acknowledges the DTA studentship awarded to him by the Department of Chemical Engineering, Imperial College London and EPSRC, without which he would not have been able to embark on this research.

NOMENCLATURE

a	=	piston/cylinder cross-sectional area
A*	=	dimensionless heat transfer area
a	=	piston/cylinder wall thickness
Bi	=	Biot number
b s	=	dimensionless piston/cylinder wall thickness
C R	=	volumetric compression ratio
c	=	specific heat capacity
c p	=	isobaric specific heat capacity
C R	=	specific heat capacity ratio
cv	=	isochoric specific heat capacity
D	=	piston/cylinder diameter
h	=	heat transfer coefficient
	=	mean heat transfer coefficient
h 0	=	heat transfer coefficient location parameter/expected value
k	=	thermal conductivity
m	=	total mass of gas
	=	Nusselt number
	=	mean Nusselt number
	=	expected Nusselt number
	=	imaginary part of the Nusselt number
	=	real part of the Nusselt number
P	=	gas pressure
Pr	=	pressure ratio
P C	=	Cauchy distribution function
	=	Péclet number
	=	heat transfer from the gas to the piston/cylinder walls
	=	heat flux from the gas to the piston/cylinder walls
	=	heat flux out of the gas
	=	heat flux into the cylinder walls
R	=	gas constant
R SB	=	stroke-to-bore ratio
S	=	total surface area available to heat transfer
T	=	temperature
T*	=	dimensionless temperature
T 0	=	constant external temperature
T f	=	gas temperature
T w	=	piston/cylinder inner wall temperature
T	=	time
V	=	gas/cylinder volume
y	=	piston position
y a	=	dimensionless piston displacement amplitude
	=	mean piston position
	=	piston displacement amplitude
Z	=	thermal impedance of the solid

Greek Symbols

α	=	thermal diffusivity
γ	=	ratio of specific heat capacities
δ	=	thermal diffusion length scale
ϵ	=	thermal effusivity
ϵr	=	thermal effusivity ratio
ηind	=	indicated efficiency
ηis	=	isentropic efficiency
θf,w	=	temperature difference between the (bulk) fluid and the inside piston/cylinder wall
θw,0	=	temperature difference between the inside piston/ cylinder wall and the external wall
κr	=	thermal conductivity ratio
ρ	=	density
ρr	=	density ratio
ξ	=	Cauchy distribution function scale/width
ψ	=	thermal loss
ω	=	angular speed
Ω*	=	dimensionless frequency

Subscripts

0	=	external
1	=	fundamental, or first harmonic
f	=	fluid
n	=	nth harmonic
s	=	solid
w	=	inner piston/cylinder wall

Superscript

*

=

dimensionless