So, How Deep Is the Mariana Trench?

Abstract

HMS Challenger made the first sounding of Challenger Deep in 1875 of 8184 m. Many have since claimed depths deeper than Challenger's 8184 m, but few have provided details of how the determination was made. In 2010, the Mariana Trench was mapped with a Kongsberg Maritime EM122 multibeam echosounder and recorded the deepest sounding of 10,984 ± 25 m (95%) at 11.329903°N/142.199305°E. The depth was determined with an update of the HGM uncertainty model combined with the Lomb-Scargle periodogram technique and a modal estimate of depth. Position uncertainty was determined from multiple DGPS receivers and a POS/MV motion sensor.

Keywords:

• multibeam bathymetry
• Challenger Deep
• Mariana Trench

Introduction

The quest to determine the deepest depth of Earth's oceans has been ongoing since 1521 when Ferdinand Magellan made the first attempt with a few hundred meters of sounding line (Theberge 2008). Although the area Magellan measured is much deeper than a few hundred meters, Magellan concluded that the lack of feeling the bottom with the sounding line was evidence that he had located the deepest depth of the ocean. Three and a half centuries later, HMS Challenger sounded the Mariana Trench in an area that they initially called Swire Deep and determined on March 23, 1875, that the deepest depth was 8184 m (Murray 1895). Since then, efforts to determine the deepest depth of the oceans have been a focus of numerous cruises. All of the other late 19th and early 20th century claims of locating the deepest depth in the oceans were in other trenches in the Pacific but not in the Mariana Trench. As it turned out, none of the claims were as deep as Challenger Deep's 8184 m. The early history of the various cruises that attempted to locate and claim the ocean's deepest depth is colorfully described by Richie (2003).

Over time, the scientific consensus eventually converged on the Mariana Trench (Figure 1) as containing the deepest point of the Earth's oceans. Determining the position of this deepest depth is, however, more challenging. Plotting the actual location of the two 1875 sounding is impossible because of the 19th century kilometer-scale navigation uncertainties. Pinpointing the locations of many of the mid-20th century claims of “the deepest sounding” in Challenger Deep is impossible because the claims either neglected to publish the coordinates for their deepest depth or provided positions only to the nearest minute of arc, again with no discussion of position uncertainty. These attempts can be split into three main groups: early single-beam echosounders, early multibeam echosounders, and modern (i.e., post-GPS, high-resolution) multibeam echosounders. Figure 2 is a summary of all available locations of each claim for the deepest depth of Challenger Deep.

Figure 1 General location of the Mariana Trench. Data from Smith and Sandwell (1997) 1-arcminute grid. White arrow points the area of the Challenger Basin.

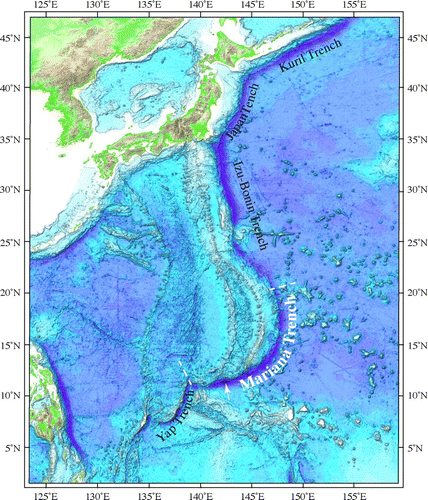
Figure 2 Locations of all published reports of the deepest depth at Challenger Deep with ship in square brackets; (1) Murray 1895 [HMS Challenger], (2) Gaskell et al. 1953 [Challenger II], (3) Richie 1992 [Challenger I in 195I], (4) Taira et al. 2004 [Vityaz in 1957] and JHOD 1984 [Takuyo], (5) Dean 1965 [Bathyscape Trieste in 1960], (5a) Mantyla and Reid 1978 [R/V Thomas Washington in 1976], (6) Todo et al. 2005 [ROV Kaiko in 1995], (7) Fryer et al. 2003 [MR1 in 1997], (8) Fujioka et al. 2002 [Kairei], (9) Bowen et al. 2009 [ROV Nereus], (10) this study [USNS Sumner]. The isobath, shown as white polygon, is at 10,000 m.

The vast improvements in multibeam echosounder technology and navigation in the 21st century provided the impetus to revisit Earth's deepest depth. A U.S. Extended Continental Shelf cruise to the Mariana Trench provided the opportunity to collect a new dataset from the trench. A preliminary determination of the deepest depth of 10,994 ± 40 m (at 95%) from the multibeam data was reported by Gardner and Armstrong (2011) at the American Geophysical Union 2011 fall meeting. The purpose of the present report is to provide details of the data collection from that cruise and present a thorough statistical determination of the deepest depth.

Early Echosounder Measurements

The two 20th century world wars caused a hiatus in the quest for the deepest depth, but after World War II the expansion of marine sciences included renewed interest in surveying the deep bathymetry of the Pacific trenches. The British ship HMS Challenger II therefore returned to the Challenger Deep in 1952. Using explosives and a hand-held stopwatch and using a wire-line sounding machine with a 40-lb weight and an echosounder, a maximum depth of 5960 fm (10,900 m) was recorded at 11°19′N/142°15′E, but the scientific team reluctantly reduced the reported maximum depth by 20 fm (37 m) for a record depth of 5940 fm (10,863 m) (Carruthers and Lawford 1952). Carruthers and Lawford describe the corrections made to the various systems measurements, but only approximate corrections were used to determine the final depth. Fisher (1954) described various techniques and error sources in early explosive charge oscilloscope echosounders and concluded that at depths of 5814 fm (10,632 m) the uncertainty is ±15 fm (27 m).

One of the most ubiquitous claims of the deepest depth of the Challenger Deep (11,034 m) comes from references to a cruise of the Soviet ship Vityaz during the 1957 International Geophysical Year. A Russian website (Anonymous 2011) reports that the deepest sounding in the Challenger Deep by Vityaz was collected with an echosounder set with a constant sound speed of 1500 m/s. A statement is made that the sounding was at the limit of the echosounder's range. After collecting the echosounder data, the ship hove-to and thermometer and water bottle casts were collected in the vicinity of the deepest depth. Temperature and salinity values from these casts were used to generate a sound-speed profile to correct the echosounder depth, although no details of the sound-speed calculations can be found. Regardless, the initial deepest depth was subsequently increased to 11,034 m using a corrected sound speed (Anonymous 2011). Only two English language references state the location of this sounding (Taira et al. 2004 and Nakanishi and Hashimoto 2011), both of which give the same location and cite a Russian language article by Hanson et al. (1959) that is not available on the web or in U.S. research libraries. Most textbooks, many peer-reviewed articles and ubiquitous websites declare that the maximum depth in the Challenger Deep is 11,034 m and cite this Vityaz cruise as the source.

The manned bathyscaph Trieste dove to the bottom at Challenger Deep in 1960 at a reported maximum “calibrated” depth of 10,911 m (Piccard and Dietz 1961). The depth was determined by a pressure sensor aboard Trieste. The area of the trench was too deep for the escort ship's PDR echosounder, so timed TNT charges were used to position over the deepest spot (Fisher and Hess 1963; Fisher 2009). The surface ship recorded a maximum depth of 10,915 ± 20 m, but the only position for the deepest depth is the location of the surface ship drifting above the Trieste.

Sixteen years lapsed before the next attempts were reported to determine the maximum depth at Challenger Deep. In 1976, Mantyla and Reid (1978) measured a 10,933 m depth in the Mariana Deep by echosounder. They corrected the sounding by both Matthews Tables (Matthews 1939) and by measurements of temperature from free-vehicle hydrocasts and stated that the corrections were accurate to ∼±50 m.

Multibeam Echosounder Measurements

It was eight more years before the Mariana Trench was surveyed with a newly available narrow-beam multibeam echosounder (MBES). These systems decrease the sounding uncertainties compared with the relatively wide-angle single-beam echosounders (SBES) that had been previously used. The MBES systems also have the advantage of covering a broad across-track area with many soundings, each with a relatively small footprint (e.g., for a MBES with a 1° beamwidth, a 137 m diameter footprint at 11,000 m water depth at 45° off nadir) when compared with a SBES, which records a single sounding from a broad circular footprint on the seafloor (e.g., for a 10° beamwidth, a 1.9 km diameter footprint at 11,000 m water depth). The location of each MBES sounding on the seafloor can be accurately determined because of the narrow angular resolution of each receive aperture and by using integrated vehicle motion sensors with differential GPS navigation and accurately measured sound-speed profiles. This compares to SBES that have a relatively wide receive aperture, typically >10°, no angular resolution, frequently use a sound-speed constant to convert travel time to depth and make sound-speed corrections from Matthews (1939) or Carter (1980) tables.

Mapping by Japan

The earliest MBES measurement of the claimed maximum depth of the Challenger Deep was made with the S/V Takuyo of the Hydrographic Department of the Japan Maritime Safety Agency in 1984 (Yashima unpublished; cited in Fujioka et al. 2002, 10-2). The deepest depth is given as 10,920±10 m at 11°22.4’N, 142°35.5’E. In 1998, a Japanese R/V Kairei cruise mapped a 140-km² area of Challenger Deep, recorded a maximum depth of 10,920 m with a claimed uncertainty of ±10 m, and it was declared that “at this point, the competition to find the ocean's greatest depth seems to be over …” (Fujioka et al., 10–2). Both cruises used a conductivity-temperature-depth (CTD) system to measure water temperature and salinity profiles of the water column, calculated sound-speed profiles from these measurements to generate corrected depths and used ray tracing to locate each sounding on the seafloor. The reported navigational accuracy provided by the R/V Kairei navigation system claims the location to the nearest arc second (∼25 m in this area) of latitude and longitude, although there is no mention of what navigation system was used during the cruise.

The University of Toyko's Ocean Research Institute returned to the Challenger Deep in 1992 with the S/V Hakuho-Maru equipped with an updated multibeam system but did not collect sound-speed profiles to correct the soundings. Instead, they calculated depth from travel time by using a constant speed of 1500 m/s and corrected the multibeam soundings with the Carter (1980) tables, reporting a “corrected” maximum depth of the Challenger Deep of 10,933 m at 11°22.4′N 142°35.5′E but with no uncertainty estimate (Fujimoto et al. 1993). Data from surveys of the Challenger Deep in 1998, 1999 and 2002 by the Japan Agency for Marine-Earth Science and Technology's R/V Kairei with an updated 12-kHz 2°x2° MBES were used to claim a 10,920 ± 5 m depth for the deepest point from center-beam data. The details of the processing steps used to reduce the soundings to depths are detailed in Nakanishi and Hashimoto (2011). Importantly, multiple sound-speed profiles were obtained by CTD and XBT in the area but a malfunction of the CTD on the 2002 cruise required two-year-old sound-speed profiles to be used (Nakanishi and Hashimoto 2011).

The Japanese Agency for Marine Earth Science and Technology deployed the KAIKO remotely operated vehicle (ROV) to the Challenger Deep in 2002. The ROV recorded a maximum depth of 10,896 m at 11°20.093′N 142°11.083′E using a pressure sensor. However, they made no claim of establishing the deepest depth of Challenger Deep.

University of Hawaii Mapping

In 2008, the University of Hawaii's R/V Kilo Moana supported field trials of a hybrid underwater robotic vehicle (Nereus) in Challenger Deep and reported a depth of 10,903 m at 11°22.1′N, 142°35.4′E (Bowen et al. 2009). The ship was equipped with a Kongsberg Maritime EM120 MBES. If properly calibrated and with a proximal sound-speed profile, this system is capable of collecting accurate and well-navigated bathymetric soundings with a minimum uncertainty of between 0.2% and 0.5% of water depth, depending on the signal-to-noise ratio (a function of the impedance of the bottom sediment) and the pulse length. However, as of this writing, the multibeam bathymetry data have yet to be publicly released, so the data are not available for comparisons with other soundings.

University of New Hampshire Mapping

In 2010, the entire Mariana Trench, which comprises the southern section of the Izu-Bonin-Mariana Trench (Figure 1), was mapped using a 1° × 1° 12-kHz Kongsberg Maritime EM122, the latest generation of their multibeam echosounder system (MBES), mounted on the USNS Sumner. The EM122 MBES can produce a maximum of 432 soundings from each ping over a maximum swath of 150°. The EM122 also has a multi-ping mode that provides two pings per sounding cycle, thereby greatly increasing the along-track sounding density. The actual number of soundings used and the swath width are both functions of initial runtime parameters of the MBES, of the signal-to-noise ratio of the received signal (a function of attenuation, spherical spreading, acoustical impedance of the seafloor and ambient noise), and of perceived artifacts that are edited out of the recorded soundings. The manufacturer's uncertainty of each sounding (not including systematic effects due to the survey system or common-mode effects such as vertical correctors or shared sound-speed profiles as described later) ranges from 0.2% of water depth at nadir to 0.6% of water depth at 70° from nadir.

Two one-month cruises of the University of New Hampshire's U.S. Extended Continental Shelf Bathymetry Mapping Project (Gardner et al. 2006; Gardner 2010; Armstrong 2011) were devoted to mapping the trench. The runtime parameters for the EM122 for these cruises were configured for full transmit power, a swath width of ±75°, 432 soundings/ping and dual-ping mode. Eight survey lines were collected in the Challenger Basin at a speed of 5.1 m/s (10 knts); the ambient noise level was consistently below 50 dB, as determined by built-in self tests of the MBES system while underway. Sound-speed in the water column was calculated at least every six hours using Sippican Deep Blue Expendable Bathythermographs (XBTs), designed for high-speed deployments, that were calibrated to a Seabird CTD (conductivity, temperature, depth) cast during both cruises. XBT casts on both legs were also compared to U.S. Naval Oceanographic Office salinity and temperature databases for additional verification. Sound speed as a function of depth was calculated from each XBT cast and immediately input into the MBES system. At any time when the calculated sound speed at the transducer depth differed by more than 0.5 m/s from a measured sound speed at the transducer, a new XBT cast was made. Positions were determined by an Applanix POS/MV (model 320 v. 4) interfaced to two Force 5 differential global positioning (DGPS) receivers and a Starfire NavCOM model SF-2050R satellite-based augmentation system for differential correctors. Together, these navigation systems provided 1-Hz position fixes with an accuracy of ∼±0.5 m (at the sonar transducer) as calculated by the POS/MV. The MBES subsystems were calibrated for alignments by a full patch test on the first cruise and by cross-track analyses conducted throughout both cruises. A preliminary determination of the deepest depth from this cruise was reported at the 2011 American Geophysical Union Fall meeting as 10,994 ± 40 m (at 95%), located at 11.326344°N/142.187248°E (Gardner and Armstrong 2011). Subsequently, in order to verify the preliminary deepest depth, a full statistical analysis was undertaken.

Determining the Deepest Depth

Uncertainty in Depth Estimation

Estimating the depth from multibeam echosounder (MBES) data is confounded by a number of factors. In deep water, major issues are (1) echosounder measurement uncertainty, (2) lack of knowledge of the sound-speed variability in the water column with which to correct for refractions effects, and (3) modeling or data processing methods, because inappropriate methods can significantly skew the depth estimates.

The uncertainty of MBES systems has received some attention in the literature (Hare et al. 1995; Hare 1995, 2001; Lurton 2000; Lurton and Augustin 2010), and there is a range of theoretical, semi-empirical and empirical models that predict to a greater or lesser extent the likely measurement uncertainty. Measurement uncertainty is only a part of the total uncertainty, however, and it is a common oversight to assume that the echosounder exists in isolation rather than as part of a larger survey system. A reasonable estimate of the total system uncertainty must include the effects of the motion sensor, positioning system, integration of the disparate parts of the systems, calibration constants, etc., and the Hare-Godin-Mayer (HGM) model (Hare et al. 1995; Hare 1995) is the most commonly used method for providing this integrated total uncertainty (the MBES- and refraction-specific components of the original model have been superseded by the work of other authors as outlined above). For this present study, an updated version of the HGM model (Hare 2001) has been utilized, except that empirical models have been substituted for the sounder and refraction uncertainties.

As with many aspects of the ocean environment, sound speed as a function of depth is a fully four-dimensional field in which very high accuracy measurements at any datum can be obtained, but in which the ability to generate synoptic measurements of the entire field is limited. While conducting an underway survey, a choice must be made of either stopping the ship for a significant length of time in order to conduct a high-resolution, high-accuracy CTD profile of the water column or using an expendable underway system such as an expendable bathythermograph (XBT), which is less accurate than a CTD. (The possibility of undulating sensors such as moving vessel profilers that typically only survey the topmost layer of the ocean has been purposely ignored.) In either case, the measurement is continuous only in depth and fixed in space and time, so that the field is still under-sampled except with respect to depth. When the data are used to correct for refraction, they are (almost) always in the wrong place at the wrong time. The question is how out-of-date, or how far off, are the measurements, and what effect these factors might have on the uncertainty of the position and depth of the resolved depth sounding using the data. Approaches to this problem have varied, mainly depending on the availability of auxiliary data (Marks and Smith 2008). Here, the approach of Beaudoin et al. (2009) has been used, which considers the potential uncertainty within the ensemble of known measurements (typically XBT observations for deep-water surveys) and estimates the magnitude of the effect as a function of angle and depth via Monte Carlo resampling and a current generation refraction model.

Probably the most variable uncertainty effect in the estimation of depth in the deep ocean comes from the different approaches to data processing along with their associated modeling assumptions. For a grid-based estimate of depth, however, unless the resolution of the grid is carefully matched to the spatial scale of the local bathymetry, such estimates may be significantly skewed (and may lead to under-estimates of associated uncertainty).

The data-processing task typically involves three goals: elimination (or avoidance) of doubtful soundings, reduction of measurement uncertainty and interpolation in areas where there is no data. Although in shallow-water applications these are typically tackled as three separate problems, it is common in deeper water applications to look for a system that might achieve all three simultaneously (Nakanishi and Hashimoto 2011). However, unless care is taken, the assumptions of continuity or smoothness implicit in such methods can skew the depth estimates because some components of structural change in the data are partitioned into the assumed random component of the model rather than being maintained in the deterministic portion (Cressie 1993, section 3.1). Typical examples include averaging over an area where the surface has significant deterministic energy or enforcing more regularity than the data warrant by inappropriate choice of tension in a spline-based interpolation scheme.

The approach in the present study takes each measurement of depth as at best an estimate, limited by stochastic effects that have not been measured (e.g., acoustic inter- face roughness, electrical noise) and a lack of knowledge (e.g., unobserved sound speed variability). Therefore, an average over some appropriate neighborhood of soundings must be made to determine a best estimate of depth, and an implicit model of zero^th order continuity within the analysis region is assumed, so long as the size of the region is appropriately chosen. In addition, a pre-analysis of the power spectrum of the data was preformed to suggest an appropriate scale of analysis and to reduce the number of operations conducted on the data. Fundamentally, an assumption has been made that the focus should be solely on the problem of estimating point depths, plus the associated question of their uncertainty, rather than trying to explicitly eliminate doubtful depths or interpolate over gaps in the data. A method that embodies this approach, which in addition avoids the question of doubtful soundings, is outlined as follows.

Depth and Observation Uncertainty Estimation

After deterministic corrections, each sounding is resolved to a point , but to simplify computations over the small area of interest, consider the data projected into a locally Euclidean coordinate system giving points . Let be the closed ball radius r about so that for the neighbors, radius r, of an arbitrary position are . The goal is to estimate the most likely depth at a point given the neighbors , and the associated uncertainty.

For arbitrary analysis location and neighborhood radius, the kernel density estimate of the depth distribution may be computed as

where is the depth of the sounding, is the depth predicted and

is a generic kernel of center location z₀ and bandwidth u (the kernel bandwidth u is chosen as the optimal value with respect to AMISE (Asymptotic Mean Integrated Square Error) under the assumption that the distribution is Gaussian (see Scott 1992, section 6.2). The first and second differences of the density function may then be computed to determine the location of all (local) modes. Let be the set of the depths associated with the modes. There are always an odd number of zeros in the first derivative of the distribution, and if the approximation of the domain of the distribution is computed as , then a partition can be made for the domain between the modes at the concave up zeros of the first derivative function. Let be the portion of the domain associated with mode z_i so that

The variability of each mode may then be defined as the second central moment about the modal location,

on |D(z_i )|−1 degrees of freedom, and the most likely mode may be selected simply as

Bias Estimation and Compensation

The sample estimate of variance can overestimate the actual variance of the data where there are biases; in the current context this can occur because of correctors applied in common to different lines in the survey. Although a bias in a single line cannot be determined without independent measurements, an estimate can be made of the bias between two lines. Considering soundings in the coordinate frame of the MBES (so that absolute positioning uncertainty can be neglected), a plausible model for vertical biases in soundings as a function of beam number n is:

where is the bias in depth, z ₀ is the true depth, θ _i is the mean beam angle relative to the swath at the analysis site, is the vector of sound speeds in the water column, θ _n is the beam angle associated with the soundings and ϵ(z ₀, θ _n )∼N(0, σ²(z ₀, θ _n )) is the stochastic component representing measurement uncertainty of the sonar.

Consider the simplest but common case where the mode of the data consists of soundings from two separate lines in unequal proportions so that the distribution of the depths is a weighted mixture distribution, P(z)=w ₁ p ₁(z)+w ₂ p ₂(z) (with w ₁+w ₂=1). The expected depth of the sample is just the weighted expectation of the depths from each line,

where with corresponding variance

so that the weighted blend of variance, and a truncated version of the bias, is estimated though the sample variance. Because in this case the source line of each sounding is known, it is clear that (where is the sample mean of the N_i soundings from line i associated with the mode in question) and that the weights are . Therefore, it is possible to estimate the third term of the variance in (9), using this to correct the sample variance estimate (at least partially) for the effects of uncompensated static bias between the lines.

Finally, the uncertainty associated with the depth estimate may be computed by including in the adjusted observed variance of the mode a component to represent the effects of the unobserved portion of refraction, and a component to represent the effects of the measurement uncertainty of the other sensors that make up the survey system. The former is estimated by the method of Beaudoin et al. (2009) based on the CTD and XBT data collected during the cruise; the latter may be estimated using the HGM model calibrated according to the configuration of the survey system, with modifications to exclude the model's components of measurement uncertainty from the MBES itself, and from refraction. For simplicity, the assumption is made that the effects are independent and that the variance of the three terms may therefore be simply summed before computing the expanded uncertainty (Dieck 2007).

Analysis of Challenger Deep Bathymetry

The raw data in the vicinity of Challenger Deep consist of 2,051,371 soundings from eight survey lines; the data were converted from raw format in CARIS HIPS, clipped to an approximate bounding box of 11.2606°N to 11.4453°N × 141.9761°E to 142.8753°E and output as ASCII text for further processing, maintaining position, depth, source line, ping and beam information. The data were then projected into Universal Transverse Mercator projection using the WGS-84-based ellipsoid and datum and zone 54N before the estimation took place. Analyses were conducted in MATLAB with custom scripts.

A coarse search of the data within the Challenger Deep basin was conducted using a regular grid spacing of 500 m and neighborhood radius 500 m to identify the most likely areas of the deepest depths for closer scrutiny. This process identified the deepest point somewhere in the rectangle at approximately 11.356760°N/142.133747°E to 11.303109°N/142.280569°E. The Lomb-Scargle periodogram (Scargle 1982; Press et al. 2007, section 13.8) was used to compute the (spatial) spectral density around the most likely location for the deepest depth constructed from the coarse search. The periodogram suggested that there was minimal significant energy at wavelengths shorter than ∼500 m; therefore, the focused area was re-analyzed at 100 m intervals using a neighborhood radius of 250 m.

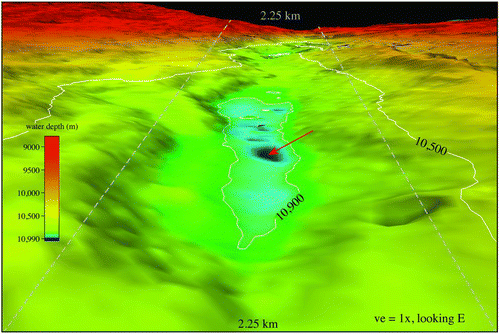
This technique identified a deepest estimate of depth at approximately (623,875.0, 1,252,789.5) m UTM zone 54 N, or 11.329903°N/142.199305°E, with a depth of 10,984 ± 25 m (95%) on 9 degrees of freedom (d.f.); Figure 3 provides a surface plot of the bathymetry. The estimate of uncertainty here includes a survey system component of 4.2 m (95%), estimated at the beam angle that corresponds to the most probable beam in the neighborhood, and a refraction component of 3.1 m (95%) based on the same beam angle. The horizontal uncertainty of the position of this depth is approximately 20–25 m (2drms), including the effect of refraction, because the centroid of sounding positions was computed to locate the depth.

Figure 3 Perspective view of Challenger Deep looking east. The 10,500 and 10,900 m isobaths are shown in white. Vertical exaggeration is 1x. The gray dashed lines are 2.25 km apart to give a measure of horizontal distance. The red arrow points to the location of the deepest depth determined in this work.

Conclusions

So, how deep is the Mariana Trench, and where is the deepest location? With the best of 2010 multibeam technologies, determining a depth in 11 km of water still has a calculated depth uncertainty of ±25 m (95%) on 9 d.f. (and we believe that the user should be cautious of the interpretation of uncertainties from multibeam echosounder estimates of depth in this region that are significantly smaller than this value). The depth uncertainty is a composite of measured uncertainties in the spatial variations in sound-speed through the water volume, the ray-tracing and bottom-detection algorithms of the multibeam system, the accuracies and calibration of the motion sensor and navigation systems, estimates of spherical spreading, attenuation throughout the water volume, and so forth. The location of the deepest depth recorded in the 2010 mapping (10,984 ± 25 m) is 11.329903°N/142.199305°E. These analyses give a position accuracy of 20 to 25 m (2drms).

Acknowledgements

We thank the officers and crew of the U.S. Naval Oceanographic Office USNS Sumner (T-AGS 61) and the U.S. Naval Oceanographic Office science parties for their cooperation during the cruise. This work was supported by NOAA grants NA05NOS4001153 and NA10NOS4000073 and ship time was funded by NOAA. Russian translations were provided by Y. Rzhanov and V. Schmidt provided some preliminary statistical analyses of the soundings. We thank L. Mayer and D. Monahan for constructive reviews of earlier versions of the manuscript.