A comparison of Olympic and Paralympic performances

Abstract

In 2012, Oscar Pistorius created history as the first amputee sprinter to compete in the Olympics. Other athletes achieved amazing feats long before the Paralympics were introduced, including gymnast George Eyser who won six medals at the 1904 Olympics with a wooden leg, and others who competed in both Games. An exciting challenge of considerable interest is to compare performances of Olympic and Paralympic athletes, so contributing to improving integration of the two competitions. We generalise the recent dynamic shrinkage method for class handicapping and apply it to competition results from equestrian individual dressage at the London 2012 Summer Games and cross country skiing at the Sochi 2014 Winter Games. Our analysis generates promising results and surprising revelations. It also offers a fair method for comparing performances by athletes from other diverse groups, with potential benefits of extra incentive and reward systems for motivating unified sporting participation in general settings.

Keywords:

• Sports
• practice of OR
• decision support systems
• recreation
• decision analysis

1. Introduction

The history of multi-sport competitions is rich and can be traced back thousands of years. Major international multi-sport competitions began with the modern Olympic Games, with summer events starting in 1896 and winter events starting in 1924. Olympic Games are open to all competitors, though there are now many other international multi-sport competitions aimed at specific communities. Perhaps surprisingly, the Deaflympic Games for deaf athletes began in the summer of 1924 and the winter of 1949, whereas the hugely popular Paralympic Games for athletes with physical disabilities began in the summer of 1960 and the winter of 1976. Another important competition is the Special Olympics World Games for athletes with intellectual disabilities, which began in the summer of 1968 and the winter of 1977. Other major international multi-sport competitions include the Commonwealth, Asian, Pan-American, All-Africa, Pacific, European, Youth Olympic, and Invictus Games.

There are some remarkable stories of disabled athletes who participated in open competition at Olympic Games. Among the most notable of these are gymnast George Eyser (USA) who won three gold medals in 1904 despite a wooden leg, deaf-mute boxer Carlo Orlandi (Italy) who won a gold in 1928, lower-leg amputee Oliver Halassy (Hungary) who won golds for water polo in 1932 and 1936, Károly Takács (Hungary) who won golds for shooting in 1948 and 1952 with a badly injured hand, hammer thrower Harold Connolly (USA) who had Erbs Palsy yet won a gold in 1956, deaf fencer Ildikó Újlaky-Rejtő (Hungary) who won two golds in 1964, deaf swimmer Jeffrey Float (USA) who won a gold in 1984 and blind archer Im Dong-Hyun (South Korea) who won golds in 2004 and 2008.

Speaking before the London 2012 Olympic and Paralympic Games, the Chair of the Organising Committee, Lord Coe, said: “We want to change public attitudes towards disability, celebrate the excellence of Paralympic sport and to enshrine from the very outset that the two Games are an integrated whole”. This objective was achieved with overwhelming success in London and subsequently at the Rio de Janeiro Games in 2016. Meanwhile, the operational research community has shown considerable interest in performance measurement for multi-sport competitions.

The predominant technique that has been used for analysing the success of nations at the Olympic Games is data envelopment analysis (Churilov & Flitman, 2006; Gomes & Lins, 2008; Li, Lei, Dai, & Liang, 2015; Li, Liang, Chen, & Morita, 2008; Lozano, Villa, Guerrero, & Cortés, 2002; *YLL2008, 2015; Zhang, Li, Meng, & Liu, 2009). This procedure is inherently nonparametric, which makes it robust against model misspecification at the cost of reduced power and clarity. Another recent and relevant method, which is more parametric in nature, is multiple attribute decision making (Ball$\iota$ & Korukoǧlu, 2014; Li, Kou, Lin, Xu, & Liao, 2015; Rezaei, 2015). Both approaches offer ways for combining observations of several different attributes to compare individual units. The main differences between those formulations and the developments in this paper are that we focus on comparing a single measure across units that belong to natural or contrived clusters. In this respect, we add to the literature by tacklingthe specific problem of comparing disparate groups of competitors. The resulting methodology offers potential benefits for applications in many diverse situations.

In this paper, we consider how, and to what extent, we might compare the performances of Olympic and Paralympic athletes in order to offer enhanced integration of the two competitions. The next section reviews a suitable methodology for making such comparisons and then we generalise this theory to enable its application to a much wider variety of sports. After this abstract development, we present some empirical analyses based on data collected from sports competitions at the London 2012 Summer Games and the Sochi 2014 Winter Games. Then we extend these ideas to consider applications of the generalised shrinkage method to compare diverse categories. Finally, we conclude the paper by discussing these results, suggesting how Olympic and Paralympic Games might develop in future, and considering whether other population subgroups could or should be integrated in a similar manner.

2. Shrinkage method for class handicapping

The International Paralympic Committee invests considerable effort in allocating athletes to disability classes, in order to ensure that all athletes in any particular class have similar physical and mental capacities, so resulting in fair competition. However, athletes from different classes in individual Paralympic sports often compete for the same medals to ensure fair rewards for effort when there are many classes or few competitors.

For some events, simple handicaps can be applied to render all competitors equally able. Examples include the use of eyeshades in goalball and upper bounds for each team’s aggregate physical ability in wheelchair basketball. Most events involve scaling the performance measure, racing time perhaps, by a factor that relates to the athlete’s disability class. For example, if the average racing time in a specific class is 50% greater than that of the average racing time in the best performing class, then we scale the times of individual athletes in the specific class by a factor of 2/3 to enable fair comparisons.

Current practice is that each of these sports has a committee to assign base factors to classes and to adjust these factors following major sporting competitions. However, this approach has some disadvantages: the system lacks transparency and is complicated; base factors require frequent committee adjustments; historical factors ignore the effects of current racing conditions; changes in classifications and technology are difficult to incorporate; the system does not fully allow for different class sizes.

In order to combat these problems, Percy (2011) proposed a shrinkage method for class handicapping, which uses data from only the current competition that is in progress. This method is based on ideas developed by Efron and Morris (1975), Efron and Morris (1977) that relate to James-Stein estimators. Copas (1983) provides a comprehensive description of these estimation procedures and Wang, Huwang, and Yu (2015) present a recent application of them in the context of quality control charts. A subsequent paper by Percy (2013) presents a mathematical justification for this shrinkage method based on an objective Bayesian analysis of a suitable probability model.

The shrinkage method for class handicapping can be applied interactively, either immediately after events where athletes compete together and results are observed simultaneously, or dynamically during events where athletes compete sequentially and results are not observed simultaneously. There are two purposes of the present paper: firstly to generalise this approach for application to a considerably broader range of sports; secondly to investigate how we might use it to compare the performances of Olympic and Paralympic athletes. To facilitate this analysis, we start with a brief review of the shrinkage method.

Suppose that we observe racing times $r_{\mathit{ij}}$ for $i=1,\cdots ,m$ and $j=1,\cdots ,n_i$ corresponding to athlete j in class i. Define ${\tilde{r}}_{i·}$ to be the sample median racing time of class i and ${\tilde{r}}_{··}$ to be the overall sample median racing time. The purpose of using medians rather than means is for robustness and to avoid outliers; see Huber and Ronchetti (2009). Next define a weighted geometric mean of these measures(1) $$\begin{array}{c}\hfill {\tilde{r}}_{i·}^{\prime }={\left({\tilde{r}}_{i·}^{n_i}{\tilde{r}}_{··}\right)}^{1/(n_i+1)}\end{array}$$(1)

to represent a shrinkage of ${\tilde{r}}_{i·}$ towards ${\tilde{r}}_{··}$ by an amount that is inversely correlated with the number of athletes in class i. Geometric means are used rather than arithmetic means here because racing times are positive, so multiplicative models are more appropriate than additive models.

This shrinkage towards the overall average is necessary as the precision of sample class medians as estimators of corresponding population medians increases with sample size. Estimators based on small samples are unreliable and empirical evidence alone cannot distinguish between the abilities of individuals and their classes. By regressing class medians towards the global average in relation to their sample sizes, shrinkage reduces the mean squared errors when estimating the average racing times. Hence, it allows for varying class sizes and enables fair comparisons among groups with different numbers of competitors; see Everson (2007).

The scaling factor for class i is then defined by the ratio(2) $$\begin{array}{c}\hfill x_i=\frac{{min}_i\left({\tilde{r}}_{i·}^{\prime }\right)}{{\tilde{r}}_{i·}^{\prime }}\end{array}$$(2)

and finally the scoring time corresponding to athlete j in class i is given by(3) $$\begin{array}{c}\hfill s_{\mathit{ij}}=x_i{r}_{\mathit{ij}}\end{array}$$(3)

for $i=1,\cdots ,m$ and $j=1,\cdots ,n_i$. These scoring times are then compared across athletes and classes to determine the winners and rank order of competitors.

3. Generalised shrinkage method for class handicapping

The shrinkage method described above is useful for performance measures that are constrained to be positive and for which the aim is to achieve small values. Such measures are common and typically represent times that arise in sports such as running, swimming, cycling and skiing. It adapts easily to deal with the situation where there is a non-zero lower bound, by subtracting the bound from each athlete’s result prior to calculations. However, we now generalise the shrinkage method in two ways.

Firstly, we consider performance measures that are again constrained to be positive but for which the aim is to achieve large values. Such measures typically represent laps, distances, heights or weights that arise in sports such as sailing, discus, high jump and weightlifting. The extension to allow for maximisation simply involves redefining the best class. This requires us to replace the scaling factor in Equation (2(2) $$\begin{array}{c}\hfill x_i=\frac{{min}_i\left({\tilde{r}}_{i·}^{\prime }\right)}{{\tilde{r}}_{i·}^{\prime }}\end{array}$$(2) ) with(4) $$\begin{array}{c}\hfill x_i=\frac{{max}_i\left({\tilde{r}}_{i·}^{\prime }\right)}{{\tilde{r}}_{i·}^{\prime }}\end{array}$$(4)

and then calculate the scoring times from Equation (3(3) $$\begin{array}{c}\hfill s_{\mathit{ij}}=x_i{r}_{\mathit{ij}}\end{array}$$(3) ) as before.

Secondly, we consider performance measures that more generally take values from any real interval, which is an appropriate assumption for all sports and includes values taken from a countable subset of a real interval. This extension includes unbounded measures, such as displacement in sports like tug-of-war, and bounded measures, such as points and ratings in sports like archery, gymnastics, diving and figure skating. Rather than develop separate algorithms for each of these situations, we propose a unified algorithm for class handicapping. We refer to this as the generalised shrinkage method, as it models all these cases and includes the existing methods as special cases.

Our proposal involves transforming the performance measure onto the set of real numbers and then applying an additive version of the theory presented above. This procedure is reminiscent of generalised linear models (Nelder & Wedderburn, 1972) and we shall see that it corresponds to the existing analysis for performance measures that are constrained to be positive. We need to consider just four possibilities: proper and bounded [a, b]; left-bounded and right-unbounded $[a,\infty )$; left-unbounded and right-bounded $(-\infty ,b]$; unbounded at both ends $(-\infty ,\infty )=\mathbb{R}$. We define a transformation $t_{\mathit{ij}}=f(r_{\mathit{ij}})$ according to the support of the performance measure, which takes one of the forms(5) $$\begin{array}{c}\hfill t=f(r)=\left\{\begin{array}{cc}ln\left(\frac{r-a}{b-r}\right)\hfill & \mathrm{i}fr\in [a,b]\hfill \\ ln(r-a)\hfill & \mathrm{i}fr\in [a,\infty )\hfill \\ -ln(b-r)\hfill & \mathrm{i}fr\in (-\infty ,b]\hfill \\ r\hfill & \mathrm{i}fr\in (-\infty ,\infty )\hfill \end{array}\right.\end{array}$$(5)

for simplicity and consistency. These forms ensure that $t_{\mathit{ij}}\in \mathbb{R}$ and retain the direction of achievement, whereby small or large values represent the best results. Although finite bounds map onto infinity for these transformations, this does not present a problem in practice. Appendix 1 presents a theoretical justification for the choice of transformations in Equation (5(5) $$\begin{array}{c}\hfill t=f(r)=\left\{\begin{array}{cc}ln\left(\frac{r-a}{b-r}\right)\hfill & \mathrm{i}fr\in [a,b]\hfill \\ ln(r-a)\hfill & \mathrm{i}fr\in [a,\infty )\hfill \\ -ln(b-r)\hfill & \mathrm{i}fr\in (-\infty ,b]\hfill \\ r\hfill & \mathrm{i}fr\in (-\infty ,\infty )\hfill \end{array}\right.\end{array}$$(5) ).

As we use medians rather than means and the above transformations are strictly increasing functions, it follows that the medians of the transformed performance measures equal the transformed medians of the performance measures. This implies that we can save on computational effort by calculating class and overall medians before transformation, rather than transforming all the data before calculating the medians. Hence, ${\tilde{t}}_{i·}=f({\tilde{r}}_{i·})$ for $i=1,\cdots ,m$ and ${\tilde{t}}_{··}=f({\tilde{r}}_{··})$ from Equation (5(5) $$\begin{array}{c}\hfill t=f(r)=\left\{\begin{array}{cc}ln\left(\frac{r-a}{b-r}\right)\hfill & \mathrm{i}fr\in [a,b]\hfill \\ ln(r-a)\hfill & \mathrm{i}fr\in [a,\infty )\hfill \\ -ln(b-r)\hfill & \mathrm{i}fr\in (-\infty ,b]\hfill \\ r\hfill & \mathrm{i}fr\in (-\infty ,\infty )\hfill \end{array}\right.\end{array}$$(5) ).

Having transformed the class and overall medians onto the set of real numbers, we now use additive models, rather than multiplicative models, when evaluating the scoring results. In this case, we replace Equation (1(1) $$\begin{array}{c}\hfill {\tilde{r}}_{i·}^{\prime }={\left({\tilde{r}}_{i·}^{n_i}{\tilde{r}}_{··}\right)}^{1/(n_i+1)}\end{array}$$(1) ) with the weighted arithmetic mean(6) $$\begin{array}{c}\hfill {\tilde{t}}_{i·}^{\prime }=\frac{n_i{\tilde{t}}_{i·}+{\tilde{t}}_{··}}{n_i+1}\end{array}$$(6)

and then determine the arithmetic adjustment or difference for class i. This replaces Equation (2(2) $$\begin{array}{c}\hfill x_i=\frac{{min}_i\left({\tilde{r}}_{i·}^{\prime }\right)}{{\tilde{r}}_{i·}^{\prime }}\end{array}$$(2) ) and is defined by(7) $$\begin{array}{c}\hfill y_i=\underset{i}{min}\left({\tilde{t}}_{i·}^{\prime }\right)-{\tilde{t}}_{i·}^{\prime }\end{array}$$(7)

if scoring results close to the lower bound of r are desirable, or(8) $$\begin{array}{c}\hfill y_i=\underset{i}{max}\left({\tilde{t}}_{i·}^{\prime }\right)-{\tilde{t}}_{i·}^{\prime }\end{array}$$(8)

if scoring results close to the upper bound of r are desirable. In both cases, the transformed scoring result for athlete j in class i is given by(9) $$\begin{array}{c}\hfill u_{\mathit{ij}}=y_i+t_{\mathit{ij}}\end{array}$$(9)

and this enables us to determine the corresponding untransformed scoring result for this athlete. This is given by(10) $$\begin{array}{c}\hfill s_{\mathit{ij}}=f^{-1}\left(u_{\mathit{ij}}\right)\end{array}$$(10)

where(11) $$\begin{array}{c}\hfill s=f^{-1}(u)=\left\{\begin{array}{cc}\frac{a+b{e}^u}{1+e^u}\hfill & \mathrm{f}ors\in [a,b]\hfill \\ a+e^u\hfill & \mathrm{f}ors\in [a,\infty )\hfill \\ b-e^{-u}\hfill & \mathrm{f}ors\in (-\infty ,b]\hfill \\ u\hfill & \mathrm{f}ors\in (-\infty ,\infty )\hfill \end{array}\right.\end{array}$$(11)

from Equation (5(5) $$\begin{array}{c}\hfill t=f(r)=\left\{\begin{array}{cc}ln\left(\frac{r-a}{b-r}\right)\hfill & \mathrm{i}fr\in [a,b]\hfill \\ ln(r-a)\hfill & \mathrm{i}fr\in [a,\infty )\hfill \\ -ln(b-r)\hfill & \mathrm{i}fr\in (-\infty ,b]\hfill \\ r\hfill & \mathrm{i}fr\in (-\infty ,\infty )\hfill \end{array}\right.\end{array}$$(5) ), which replaces Equation (3(3) $$\begin{array}{c}\hfill s_{\mathit{ij}}=x_i{r}_{\mathit{ij}}\end{array}$$(3) ). It is easy to prove that this generalised shrinkage method reduces to the existing shrinkage method for minimising racing times that satisfy $r_{\mathit{ij}}\in [0,\infty )$.

Before proceeding, we note that exceptional athletes can achieve perfect scores in some sports, particularly those with bounded ranges such as diving or figure skating. However, this does not pose a problem as the arithmetic adjustments within generalised shrinkage do not require transformations of individual scoring times, merely of class and overall medians. Although transformations of individual scoring times are included within Equations (9(9) $$\begin{array}{c}\hfill u_{\mathit{ij}}=y_i+t_{\mathit{ij}}\end{array}$$(9) ) and (10(10) $$\begin{array}{c}\hfill s_{\mathit{ij}}=f^{-1}\left(u_{\mathit{ij}}\right)\end{array}$$(10) ), the net effect of transforming, adjusting and back-transforming a perfect score is the same perfect score, so the analysis will rightly recommend the gold medal for such an athlete.

We also note that small class sizes can be included in the analysis, though this leads to the possibility of collusion. However, the use of medians, rather than means, provides security against this and pooling very small classes would also help to avoid collusion. In theory, it would even be possible to introduce a continuum disability scale, which effectively assigns a different class to each athlete. However, this scheme would be very difficult to implement in practice. The main problem is that the classification of each athlete would be very subjective and susceptible to bribery and corruption, so rendering this analysis unworkable.

4. Comparing Olympic and Paralympic athletes

Percy (2011) applied the shrinkage method to compare the performances of athletes in different Paralympic classes. We now investigate whether the method is able to compare such performances with those of Olympic athletes, effectively regarding the latter as belonging to a different disability class. The purposes are not to remove open competition, but rather to enable fair comparisons of athletes with different abilities.

We define the adjective “fair” in this context as ranking competitors from the classes under consideration in order of their departures from corresponding class averages, such that exceptional relative performances are rated best. In particular, though somewhat tautologically, the rankings are determined by the values of the transformed scoring results $u_{\mathit{ij}}$ of Equation (9(9) $$\begin{array}{c}\hfill u_{\mathit{ij}}=y_i+t_{\mathit{ij}}\end{array}$$(9) ).

The transformation and shrinkage that are applied to the observed results are designed to map the data onto the set of real numbers, such that the differences between classes merely represent additive disparities and the variances of different classes are roughly equal. This is a common assumption in generalised linear modelling, specifically the analysis of variance, which is much related to the methodology considered here. The transformed scoring results are then compared directly to identify athletes that performed exceptionally well relative to other competitors in their particular classes.

Although Olympic and Paralympic Games are held at the same venues at about the same times, there is still little true integration as a result of which Paralympic sports remain marginalised. The shared competitions proposed in this paper are certainly not replacements for the separate games. Rather, they are intended to generate supplementary rewards that encourage further cooperation. These might take the form of an extra layer of medal awards that appeals to sponsors and competitors, so offering incentives for tournament organisers to integrate the sports. Sponsors, including broadcast media and sports manufacturers, benefit through extra publicity and marketing opportunities. Competitors, both Olympic and Paralympic, benefit by higher profiles and improved unification of the two games.

Some sports are offered in only one of these two types of games, in which case comparisons of this nature are inappropriate. Even so, it is still possible to unite Olympics and Paralympics further by merging events and ceremonies and by introducing more unified sports. Extracting results data from the websites www.olympic.org and www.paralympic.org, we now consider two sports where such comparisons are possible.

4.1. London 2012 Summer Games

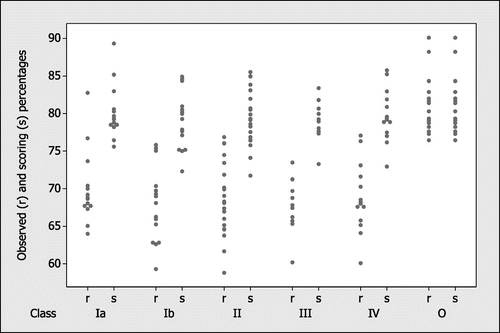
The summer sport that we consider here is mixed-sex equestrian individual dressage, where the best performance corresponds to the largest percentage score achieved of the form $r_{\mathit{ij}}\in [0,100]$. Corresponding to this event, medals were awarded for open competition in the Olympic Games and for each of five functional classes in the Paralympic Games:

(I)	riders with impaired limb function, or poor balance and good upper limb function (subdivided into classes Ia and Ib);
(II)	riders with locomotion impairment;
(III)	blind riders with moderate locomotion impairment;
(IV)	riders with some visual impairment or impaired function in one or two limbs.

Figure 1 contains a plot of grouped individual values that displays the observed and scoring percentages, the latter transformed using generalised shrinkage, for each Paralympic functional class and for the Olympic open class. As expected, the last of these classes performed best and so its observed and scoring results are equal. The rankings of individual athletes within each class are unchanged by transformation.

Figure 1. Observed and scoring percentages for London 2012.

The tables in Appendix 2 present the numerical values of the observed and scoring percentages for each functional class, along with overall rankings based on the transformed results using generalised shrinkage. Our method would allocate the gold and bronze medals to Olympic athletes from Class O, Charlotte Dujardin (GBR) and Adelinde Cornelissen (NED) respectively, and the silver medal to a Paralympic athlete from Class Ia, Sophie Christiansen (GBR). Interestingly, Sophie Christiansen graduated with a master’s degree in mathematics from Royal Holloway, University of London, which hosted the Operational Research Society’s 2014 conference where the author first presented this research. The reasons for these combined medal allocations are clear from Figure 1 and Appendix 2. These three winning athletes achieved considerably larger observed percentages than those of other competitors in their respective classes.

4.2. Sochi 2014 Winter Games

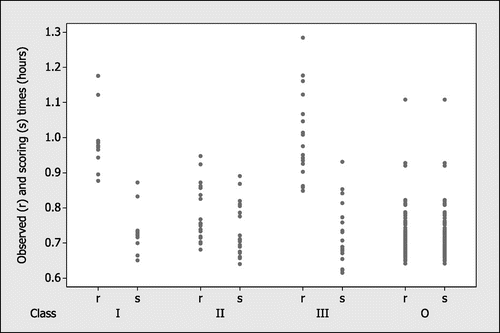
The winter sport that we consider here is men’s cross country skiing, where the best performance minimises a time of the form $r_{\mathit{ij}}\in [0,\infty )$. Corresponding to this event, medals were awarded for open competition over 15km in the Olympic Games and for each of three functional classes in the Paralympic Games:

(I)	20km classical technique visually impaired;
(II)	15km sitting;
(III)	20km classical technique standing.

The race distances vary among these classes for historical reasons, though they are reasonably similar. Consequently, the loglinear transformation of Equation (5(5) $$\begin{array}{c}\hfill t=f(r)=\left\{\begin{array}{cc}ln\left(\frac{r-a}{b-r}\right)\hfill & \mathrm{i}fr\in [a,b]\hfill \\ ln(r-a)\hfill & \mathrm{i}fr\in [a,\infty )\hfill \\ -ln(b-r)\hfill & \mathrm{i}fr\in (-\infty ,b]\hfill \\ r\hfill & \mathrm{i}fr\in (-\infty ,\infty )\hfill \end{array}\right.\end{array}$$(5) ), which generalised shrinkage applies in this setting, ensures that the classes are comparable. Figure 2 contains a plot of grouped individual values that displays the observed and scoring times (hours), the latter transformed using generalised shrinkage, for each Paralympic functional class and for the Olympic open class. As expected, the last of these classes performed best in terms of the observed values and so its observed and scoring results are equal. The rankings of individual athletes within each class is unchanged by transformation.

Figure 2. Observed and scoring times (hours) for Sochi 2014.

The tables in Appendix 3 present the numerical values of the observed and scoring times (hours, minutes and seconds) for each functional class, along with overall rankings based on the transformed results using generalised shrinkage. Our method would allocate all three medals to Paralympic athletes from Class III, Rushan Minnegulov (RUS), Ilkka Tuomisto (FIN) and Vladislav Lekomtcev (RUS) respectively.

The reasons for these combined medal allocations are clear from Figure 2 and Appendix 3. These three winning athletes achieved considerably smaller observed racing times than those of other competitors in their class, whereas the best results in other classes were less distinct from those of other competitors in their respective classes. Note that although there are considerably more athletes in the open Olympic class than in any of the Paralympic classes for this event, the generalised shrinkage method allows for differing class sizes and treats competitors in large classes fairly.

4.3. General observations

Before proceeding, it is important to reflect on the feasibility of the assumptions behind the shrinkage method. In particular, the theoretical justifications given by Percy (2013) relate to comparisons between Paralympic classes within a single sport. By extending the analysis to include Olympic classes, our investigations seem to present no problems and the analysis works well as intended. Here, Paralympic and Olympic classes merely represent different levels of physical or mental ability.

However, our analysis of the Sochi Winter games reveals an interesting variation, as the actual race distances differ among the Olympic and Paralympic classes. Following transformations as described earlier in this paper, the generalised shrinkage method implicitly assumes similar locations, dispersions and skewnesses for all classes, in order that all competitors have equal opportunities to excel from their class packs. Hence, we must question whether this assumption is still valid for this scenario.

Although the race distances vary for cross-country skiing, a glance at Figure 2 is sufficient to show that the locations and dispersions of observed racing times are comparable across all Olympic and Paralympic classes. Moreover, the skewnesses of observed racing times in the different classes are all positive. Consequently, the assumptions underlying this method are reasonable for this analysis and suggest that comparisons of Olympic and Paralympic performances might generally be fair within any particular sport.

5. Comparing diverse categories

As the generalised shrinkage method appears to compare results fairly among differing classes of ability, it is natural to ask what other comparisons are feasible. Perhaps the most exciting prospect in this regard would be to compare the performances of male and female athletes, so that occasional competitions might enable them to compete fairly for an overall prize. However, other opportunities with significant benefits would arise by facilitating comparisons among youth, adult and senior competitors. And why not even compare different events after standardising the corresponding results?

In order to compare different events, we first need to standardise the results to allow for different distributions. As this algorithm already transforms the observed results onto the set of real numbers for intermediate calculations, we use the transformed results $t_{\mathit{ij}}$ from Equation (5(5) $$\begin{array}{c}\hfill t=f(r)=\left\{\begin{array}{cc}ln\left(\frac{r-a}{b-r}\right)\hfill & \mathrm{i}fr\in [a,b]\hfill \\ ln(r-a)\hfill & \mathrm{i}fr\in [a,\infty )\hfill \\ -ln(b-r)\hfill & \mathrm{i}fr\in (-\infty ,b]\hfill \\ r\hfill & \mathrm{i}fr\in (-\infty ,\infty )\hfill \end{array}\right.\end{array}$$(5) ) as the basis of this standardisation. Specifically, we propose that the $t_{\mathit{ij}}$ should be mapped linearly for each event, via translation and scaling, so that the mean and standard deviation of all transformed results for each event are 0 and 1, respectively, and so that better performances correspond to positive scores rather than negative scores.

This use of mean and standard deviation is appropriate as the transformed results are real numbers, and the values 0 and 1 arbitrarily but conveniently correspond to the additive and multiplicative identities for the complete ordered field of real numbers. Denoting the mean and standard deviation of the transformed results by $\mu$ and $\sigma$ respectively, the appropriate linear transformation is(12) $$\begin{array}{c}\hfill z_{\mathit{ij}}=\pm \left(\frac{t_{\mathit{ij}}-\mu }{\sigma }\right)\end{array}$$(12)

where the plus sign is used if the aim is to maximise the original performance measure and the minus sign is used if the aim is to minimise the original performance measure. Pleasingly, this is also the linear equation that is used to standardise the normal probability distribution.

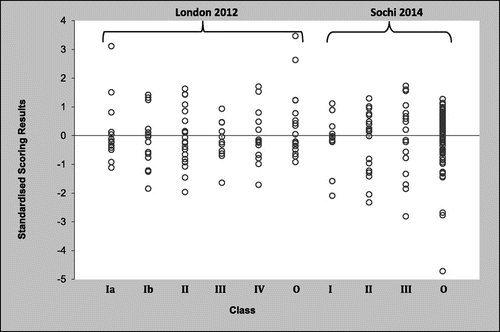
Figure 3 displays the standardised scores resulting from both events considered earlier, mixed-sex equestrian individual dressage at London 2012 and men’s cross country skiing at Sochi 2014. The best rated performances are those with the largest values. As the standardisation formula in Equation (12(12) $$\begin{array}{c}\hfill z_{\mathit{ij}}=\pm \left(\frac{t_{\mathit{ij}}-\mu }{\sigma }\right)\end{array}$$(12) ) involves a linear mapping, the performances across all classes within each event are ranked exactly as for the separate analyses presented in the previous section. However, it is very clear that performances across all classes are now comparable between these otherwise unrelated events. This offers a remarkable prospect for enhancing the appeal of competitive sports, across different categories and activities.

Figure 3. Standardised scoring results for London 2012 and Sochi 2014.

Actual comparisons between these two events lead to the conclusion that the gold, silver and bronze medallists would be the three respective equestrian winners identified previously, when generalised shrinkage was used to compare classes. This is slightly disappointing, as it leads us to question whether skiers are treated unfairly by this standardisation approach, particularly as there were more skiers than equestrians. Glancing back at Figures 1 and 2, it is tempting to suggest that the skewness of results explains why equestrians perform better than skiers in this combined analysis. Specifically, the equestrian results in this study tend to cluster around an average with a few exceptionally good performances, whereas the skiing results in this study tend to cluster around an average with a few relatively bad performances.

However, these differences in skewness are less important than they seem, as our standardisation algorithm applies to the transformed results $t_{\mathit{ij}}$ of Equation (5(5) $$\begin{array}{c}\hfill t=f(r)=\left\{\begin{array}{cc}ln\left(\frac{r-a}{b-r}\right)\hfill & \mathrm{i}fr\in [a,b]\hfill \\ ln(r-a)\hfill & \mathrm{i}fr\in [a,\infty )\hfill \\ -ln(b-r)\hfill & \mathrm{i}fr\in (-\infty ,b]\hfill \\ r\hfill & \mathrm{i}fr\in (-\infty ,\infty )\hfill \end{array}\right.\end{array}$$(5) ) rather than the observed results $r_{\mathit{ij}}$. Moreover, six skiers finished in the top twenty places of the combined analysis. These include the three winning skiers in Class III, who finished in fourth, seventh and eighth positions. Regardless of skewness directed towards good or bad performances, it is entirely reasonable that the declared winners are those athletes who registered performances that were considerably better than those of the other elite athletes in their sport, which is what occurred here. Nevertheless, these observations suggest that caution should be exercised when comparing performances from different sports if the class skewness varies substantially.

6. Discussion

This article generalises the shrinkage method for class handicapping that was proposed by Percy (2011, 2013), by extending it to allow for maximisation of performance measures and to allow for bounded and unbounded performance measures. It applies this new generalised shrinkage method in a novel way, to compare the performances of Paralympic athletes with those of Olympic athletes. It uses sets of data from two representative sports, mixed-sex equestrian individual dressage (London 2012) and men’s cross country skiing (Sochi 2014), to illustrate these comparisons. Our results demonstrate that such comparisons among athletes of mixed abilities are fair, according to the definition presented in this article, and enable new layers of incentives and rewards further to integrate Olympic and Paralympic Games.

We do not advocate the removal of any existing medal structure, but merely hope to enhance diversity and inclusivity in sport. This could supplement other methods that are currently used to achieve improved cooperation between Olympic and Paralympic competitions, including the merging of events and ceremonies, and the introduction of more unified sports. In a distinct section, we even consider the application of generalised shrinkage to compare the results arising from the two distinct events considered previously, with interesting and pleasing conclusions. However, the possibilities seem to be considerably more varied than this.

First, this method is generic and might be used to compare results arising from different competitions, perhaps to determine the best performing golfer or tennis player in any given year (Bozóki, Csató, & Temesi, 2016), the greatest hockey or football team of all time (Baker & McHale, 2015), or the best all-time athlete in any particular sport relative to peer competitors. For example, it might provide an alternative method for comparing the boxing achievements of former and current heavyweight champions Muhammad Ali and Manuel Charr, or determining who is the greatest football player of all time from among the likes of Pele, Maradonna, Ronaldo and Messi. An early application of shrinkage in a similar sporting context (American football) was presented by Everson (2007).

Second, and perhaps most remarkably, generalised shrinkage could be applied to compare results arising from different sports, as demonstrated above. This could potentially offer a further level of reward for achievement in multi-sport competitions, such as determining an overall best achieving athlete or gymnast, primarily for entertainment purposes. At least, such inter-sport rewards would encourage cooperation and collaboration that might lead to shared knowledge and resources. This methodology could potentially also lead to fairer scoring systems for multi-event competitions such as triathlon, heptathlon, decathlon and modern pentathlon. In the heptathlon and decathlon, for example, the final event is a middle distance race that is widely considered to be the hardest in which to achieve a good points score. Perhaps generalised shrinkage could help address such issues. The use of operational research in contexts like this offers an opportunity to illustrate the potential of our field to a wide audience in an interesting and easily digestible way.

Third, there is tremendous potential for this method fairly to compare different categories of competitor in any particular sport. Examples for which this could offer substantial benefits include comparisons of professionals and amateurs, classes that employ different forms of technology, male and female athletes, and various age groups such as youth, adult and senior. Such combined results would enhance existing competitions by encouraging between-category activity. Indeed, many amateur sports involve distinct open and handicapped tournaments, and these comparisons could offer considerable benefits for the latter by reducing the amount of subjective handicapping required, so avoiding accidental and intentional bias.

Fourth, it is possible to broaden the scope of this algorithm substantially by applying it to non-sporting competitions. For example, consider students’ marks for several modules on a degree programme (Dalziel, 1998). The assessments might be of different standards and need not involve exactly the same students. Generalised shrinkage could be used, as an alternative to existing approaches, to standardise the marks for accurate ranking. Also in the context of higher education, this approach could be used by governing authorities to determine whether universities discriminate in their admission of undergraduate students or whether employers discriminate in their recruitment of graduates. Such possibilities clearly offer many opportunities for future applications of operational research.

Acknowledgements

The author is grateful to Bruce Warner and Hugh Daniel, for helpful discussions about the role of class handicapping in Paralympic sports.

Notes

No potential conflict of interest was reported by the authors.

Appendix 1

Justification of transformations in Equation (5(5) $$\begin{array}{c}\hfill t=f(r)=\left\{\begin{array}{cc}ln\left(\frac{r-a}{b-r}\right)\hfill & \mathrm{i}fr\in [a,b]\hfill \\ ln(r-a)\hfill & \mathrm{i}fr\in [a,\infty )\hfill \\ -ln(b-r)\hfill & \mathrm{i}fr\in (-\infty ,b]\hfill \\ r\hfill & \mathrm{i}fr\in (-\infty ,\infty )\hfill \end{array}\right.\end{array}$$(5) )

Our challenge is to determine a convenient, coherent mapping of all possible results ranges onto the set of real numbers, in order to apply an additive version of the shrinkage method for class handicapping.

Theorem:

The transformations in Equation (5(5) $$\begin{array}{c}\hfill t=f(r)=\left\{\begin{array}{cc}ln\left(\frac{r-a}{b-r}\right)\hfill & \mathrm{i}fr\in [a,b]\hfill \\ ln(r-a)\hfill & \mathrm{i}fr\in [a,\infty )\hfill \\ -ln(b-r)\hfill & \mathrm{i}fr\in (-\infty ,b]\hfill \\ r\hfill & \mathrm{i}fr\in (-\infty ,\infty )\hfill \end{array}\right.\end{array}$$(5) ) uniquely comprise the simplest bijective function $r\mapsto f(r)$ that maps $[a,b]\to \mathbb{R}$ and is consistent as $a\to -\infty$, $b\to \infty$ or both.

Proof Nelder and Wedderburn (1972) show that the canonical link function for mapping $[0,1]\to \mathbb{R}$ in generalised linear modelling is the logit link defined by $r\mapsto ln\{r/(1-r)\}$. Accordingly, this is the natural bijective function to use as a default basis for constructing appropriate maps that apply to other ranges.

For $r\in [a,b]$ a linear transformation of r extends this logit link to give(A1) $$\begin{array}{c}\hfill r\mapsto ln\left(\frac{r-a}{b-r}\right).\end{array}$$(A1)

However, $ln\{(r-a)/(b-r)\}\to \pm \infty$ as $a\to -\infty$ or $b\to \infty$, so we scale the argument in Relation (A1(A1) $$\begin{array}{c}\hfill r\mapsto ln\left(\frac{r-a}{b-r}\right).\end{array}$$(A1) ) by a constant ratio of linear terms involving a and b to ensure that the function does not diverge as either limit becomes infinite. This gives(A2) $$\begin{array}{c}\hfill r\mapsto ln\left\{\frac{(b-c)(r-a)}{(c-a)(b-r)}\right\}\end{array}$$(A2)

in terms of an unspecified constant $c\in (a,b)$. As these limits separately become infinite, the function of r defined by Relation (A2(A2) $$\begin{array}{c}\hfill r\mapsto ln\left\{\frac{(b-c)(r-a)}{(c-a)(b-r)}\right\}\end{array}$$(A2) ) satisfies(A3) $$\begin{array}{c}\hfill \underset{a\to -\infty }{lim}ln\left\{\frac{(b-c)(r-a)}{(c-a)(b-r)}\right\}=ln\left(\frac{b-c}{b-r}\right)\end{array}$$(A3)

and(A4) $$\begin{array}{c}\hfill \underset{b\to \infty }{lim}ln\left\{\frac{(b-c)(r-a)}{(c-a)(b-r)}\right\}=ln\left(\frac{r-a}{c-a}\right)\end{array}$$(A4)

both of which remain finite.

Unfortunately, these expressions show that $r\mapsto 0$ for all r as both $a\to -\infty$ and $b\to \infty$, which is inconsistent with the required generality to encompass the unbounded results range $r\in \mathbb{R}$. To avoid this problem, consider the Mercator series expansion $ln(1+x)=x-x^2/2+x^3/3-\cdots$ for $-1<x\le 1$. Fixing r and allowing b to vary in the mapping of Equation (A3(A3) $$\begin{array}{c}\hfill \underset{a\to -\infty }{lim}ln\left\{\frac{(b-c)(r-a)}{(c-a)(b-r)}\right\}=ln\left(\frac{b-c}{b-r}\right)\end{array}$$(A3) ) gives(A5) $$\begin{array}{c}\hfill ln\left(\frac{b-c}{b-r}\right)=-ln\left(1-\frac{r-c}{b-c}\right)=\frac{r-c}{b-c}+O\left(b^{-2}\right)\end{array}$$(A5)

for $c<(b+r)/2$ so that $|(r-c)/(b-c)|<1$. Fixing r and allowing a to vary in the mapping of Equation (A4(A4) $$\begin{array}{c}\hfill \underset{b\to \infty }{lim}ln\left\{\frac{(b-c)(r-a)}{(c-a)(b-r)}\right\}=ln\left(\frac{r-a}{c-a}\right)\end{array}$$(A4) ) gives(A6) $$\begin{array}{c}\hfill ln\left(\frac{r-a}{c-a}\right)=ln\left(1-\frac{c-r}{c-a}\right)=\frac{r-c}{c-a}+O\left(a^{-2}\right)\end{array}$$(A6)

for $c>(a+r)/2$ so that $|(c-r)/(c-a)|<1$. Hence, we can avoid this asymptotic mapping to zero for all r as both $a\to -\infty$ and $b\to \infty$ by scaling the function in Equation (A2(A2) $$\begin{array}{c}\hfill r\mapsto ln\left\{\frac{(b-c)(r-a)}{(c-a)(b-r)}\right\}\end{array}$$(A2) ) by a factor $(b-c)(c-a)$, which is the product of the principal denominators in Equations (A5(A5) $$\begin{array}{c}\hfill ln\left(\frac{b-c}{b-r}\right)=-ln\left(1-\frac{r-c}{b-c}\right)=\frac{r-c}{b-c}+O\left(b^{-2}\right)\end{array}$$(A5) ) and (A6(A6) $$\begin{array}{c}\hfill ln\left(\frac{r-a}{c-a}\right)=ln\left(1-\frac{c-r}{c-a}\right)=\frac{r-c}{c-a}+O\left(a^{-2}\right)\end{array}$$(A6) ). In order to ensure that our mapping remains strictly increasing and finite as either limit becomes infinite, we divide this product by the simplest factor that guarantees this property, which is $(b-a)$.

Collating all these results leads to the general functional forms(A7) $$\begin{array}{c}\hfill f(r)=\left\{\begin{array}{cc}\frac{(b-c)(c-a)}{(b-a)}ln\left\{\frac{(b-c)(r-a)}{(c-a)(b-r)}\right\}\hfill & \mathrm{i}fr\in [a,b]\hfill \\ (c-a)ln\left(\frac{r-a}{c-a}\right)\hfill & \mathrm{i}fr\in [a,\infty )\hfill \\ (b-c)ln\left(\frac{b-c}{b-r}\right)\hfill & \mathrm{i}fr\in (-\infty ,b]\hfill \\ r-c\hfill & \mathrm{i}fr\in (-\infty ,\infty )\hfill \end{array}\right.\end{array}$$(A7)

where in each case the constant c lies inside the corresponding range of r values. Although we imposed further constraints on c in order to analyse variable bounds, these can now be relaxed as the results ranges are fixed for all sporting competitions. These functions are consistent with one another and offer a simple bijective mapping from any real interval onto the set of real numbers $\mathbb{R}$. Moreover, any strictly increasing linear transformations of these functions yield identical results in practice, as users see only the back-transformed scoring results s as determined by Equation (11(11) $$\begin{array}{c}\hfill s=f^{-1}(u)=\left\{\begin{array}{cc}\frac{a+b{e}^u}{1+e^u}\hfill & \mathrm{f}ors\in [a,b]\hfill \\ a+e^u\hfill & \mathrm{f}ors\in [a,\infty )\hfill \\ b-e^{-u}\hfill & \mathrm{f}ors\in (-\infty ,b]\hfill \\ u\hfill & \mathrm{f}ors\in (-\infty ,\infty )\hfill \end{array}\right.\end{array}$$(11) ).

Finally, we simplify the formulae in Equation (A7(A7) $$\begin{array}{c}\hfill f(r)=\left\{\begin{array}{cc}\frac{(b-c)(c-a)}{(b-a)}ln\left\{\frac{(b-c)(r-a)}{(c-a)(b-r)}\right\}\hfill & \mathrm{i}fr\in [a,b]\hfill \\ (c-a)ln\left(\frac{r-a}{c-a}\right)\hfill & \mathrm{i}fr\in [a,\infty )\hfill \\ (b-c)ln\left(\frac{b-c}{b-r}\right)\hfill & \mathrm{i}fr\in (-\infty ,b]\hfill \\ r-c\hfill & \mathrm{i}fr\in (-\infty ,\infty )\hfill \end{array}\right.\end{array}$$(A7) ) for practical applications by specifying suitable values for the constant c in these four situations. These values may differ as every implementation of this method involves only one results range with fixed bounds. The simplest expressions arise by setting c to be $(a+b)/2$, $a+1$, $b-1$ and 0, respectively. We then scale the first term by a constant factor of $4/(b-a)$ for convenience as justified in the previous paragraph, which then uniquely generates the functional forms in Equation (5(5) $$\begin{array}{c}\hfill t=f(r)=\left\{\begin{array}{cc}ln\left(\frac{r-a}{b-r}\right)\hfill & \mathrm{i}fr\in [a,b]\hfill \\ ln(r-a)\hfill & \mathrm{i}fr\in [a,\infty )\hfill \\ -ln(b-r)\hfill & \mathrm{i}fr\in (-\infty ,b]\hfill \\ r\hfill & \mathrm{i}fr\in (-\infty ,\infty )\hfill \end{array}\right.\end{array}$$(5) ).

Appendix 2

Mixed-sex equestrian individual dressage (London, 2012)

Table

Observed	Scoring	Rank
(%)	(%)	(medallist)
Class Ia
82.75	89.32	2 (SC)
76.70	85.16	7
73.65	82.97	18
70.40	80.56	33
70.00	80.26	37
69.20	79.66	42
68.80	79.35	44
68.65	79.24	50
68.05	78.78	59
67.70	78.51	62
67.70	78.51	62
67.30	78.20	66
65.05	76.44	81
64.00	75.60	85
Class Ib
75.83	84.90	10
75.39	84.59	11
75.04	84.35	12
70.35	80.96	28
69.74	80.51	35
69.30	80.18	38
69.00	79.95	40
68.09	79.27	49
66.26	77.87	68
65.96	77.64	70
65.26	77.10	76
62.83	75.18	86
62.83	75.18	86
62.61	75.00	88
59.30	72.31	92
Class II
76.86	85.52	5
76.05	84.95	8
76.00	84.92	9
74.48	83.84	15
73.43	83.09	17
71.86	81.95	22
70.14	80.68	30
70.10	80.65	31
69.91	80.51	34
69.05	79.87	41
68.29	79.29	47
68.10	79.14	53
67.38	78.60	61
66.95	78.27	64
66.00	77.54	72
65.14	76.87	78
64.62	76.46	79
64.57	76.42	82
63.76	75.78	84
61.67	74.10	89
58.81	71.74	93
Class III
73.47	83.38	16
71.27	81.80	24
71.23	81.77	25
69.70	80.65	32
68.77	79.95	39
67.80	79.23	51
67.43	78.95	56
66.23	78.04	67
65.73	77.65	69
65.33	77.35	74
60.20	73.26	90
Class IV
77.07	85.74	4
76.32	85.23	6
73.10	82.94	19
71.61	81.87	23
70.26	80.87	29
68.52	79.57	43
68.23	79.35	45
68.00	79.18	52
67.58	78.86	57
67.58	78.86	57
65.77	77.47	73
65.16	77.00	77
64.10	76.16	83
60.10	72.94	91
Class O
90.09	90.09	1 (CD)
88.20	88.20	3 (AC)
84.34	84.34	13
84.30	84.30	14
82.86	82.86	20
82.00	82.00	21
81.66	81.66	26
81.38	81.38	27
80.29	80.29	36
79.32	79.32	46
79.29	79.29	48
79.09	79.09	54
79.05	79.05	55
78.73	78.73	60
78.21	78.21	65
77.61	77.61	71
77.29	77.29	75
76.45	76.45	80

Appendix 3

Men’s cross country skiing (Sochi, 2014)

Table

Observed	Scoring	Rank
(h:m:s)	(h:m:s)	(medallist)
Class I
0:52:37	0:39:02	7
0:53:43	0:39:51	21
0:56:35	0:41:59	59
0:57:56	0:42:59	79
0:58:23	0:43:19	83
0:58:37	0:43:30	86
0:59:06	0:43:51	93
0:59:22	0:44:02	96
0:59:28	0:44:07	99
1:07:19	0:49:56	128
1:10:32	0:52:20	132
Class II
0:40:52	0:38:25	4
0:41:55	0:39:24	11
0:42:09	0:39:37	14
0:42:09	0:39:37	15
0:42:54	0:40:19	32
0:43:07	0:40:32	36
0:44:00	0:41:21	53
0:44:19	0:41:40	55
0:44:58	0:42:16	61
0:44:59	0:42:17	63
0:45:13	0:42:30	68
0:45:21	0:42:37	69
0:45:22	0:42:39	71
0:46:03	0:43:17	82
0:49:31	0:46:33	114
0:50:12	0:47:11	117
0:51:24	0:48:19	119
0:51:43	0:48:37	122
0:52:20	0:49:11	125
0:55:25	0:52:06	131
0:56:51	0:53:26	133
Class III
0:50:55	0:36:55	1 (RM)
0:51:32	0:37:21	2 (IT)
0:51:45	0:37:30	3 (VL)
0:54:10	0:39:16	10
0:55:31	0:40:14	27
0:56:06	0:40:40	39
0:56:32	0:40:58	43
0:57:02	0:41:21	52
0:58:31	0:42:25	65
1:00:30	0:43:51	94
1:00:51	0:44:06	98
1:02:47	0:45:31	107
1:04:00	0:46:24	112
1:04:02	0:46:25	113
1:07:21	0:48:49	124
1:09:39	0:50:29	129
1:10:37	0:51:11	130
1:17:04	0:55:52	136
Class O
0:38:30	0:38:30	5
0:38:58	0:38:58	6
0:39:08	0:39:08	8
0:39:09	0:39:09	9
0:39:29	0:39:29	12
0:39:31	0:39:31	13
0:39:38	0:39:38	16
0:39:42	0:39:42	17
0:39:43	0:39:43	18
0:39:47	0:39:47	19
0:39:50	0:39:50	20
0:40:03	0:40:03	22
0:40:07	0:40:07	23
0:40:08	0:40:08	24
0:40:09	0:40:09	25
0:40:11	0:40:11	26
0:40:14	0:40:14	28
0:40:15	0:40:15	29
0:40:15	0:40:15	30
0:40:18	0:40:18	31
0:40:23	0:40:23	33
0:40:28	0:40:28	34
0:40:28	0:40:28	35
0:40:33	0:40:33	37
0:40:37	0:40:37	38
0:40:41	0:40:41	40
0:40:42	0:40:42	41
0:40:53	0:40:53	42
0:40:59	0:40:59	44
0:41:01	0:41:01	45
0:41:03	0:41:03	46
0:41:12	0:41:12	47
0:41:14	0:41:14	48
0:41:16	0:41:16	49
0:41:17	0:41:17	50
0:41:20	0:41:20	51
0:41:30	0:41:30	54
0:41:45	0:41:45	56
0:41:49	0:41:49	57
0:41:50	0:41:50	58
0:42:06	0:42:06	60
0:42:16	0:42:16	62
0:42:22	0:42:22	64
0:42:26	0:42:26	66
0:42:28	0:42:28	67
0:42:39	0:42:39	70
0:42:42	0:42:42	72
0:42:42	0:42:42	73
0:42:45	0:42:45	74
0:42:45	0:42:45	75
0:42:50	0:42:50	76
0:42:55	0:42:55	77
0:42:55	0:42:55	78
0:43:02	0:43:02	80
0:43:07	0:43:07	81
0:43:22	0:43:22	84
0:43:23	0:43:23	85
0:43:30	0:43:30	87
0:43:36	0:43:36	88
0:43:39	0:43:39	89
0:43:39	0:43:39	90
0:43:39	0:43:39	91
0:43:44	0:43:44	92
0:43:52	0:43:52	95
0:44:05	0:44:05	97
0:44:07	0:44:07	100
0:44:15	0:44:15	101
0:44:35	0:44:35	102
0:44:35	0:44:35	103
0:45:08	0:45:08	104
0:45:16	0:45:16	105
0:45:28	0:45:28	106
0:45:36	0:45:36	108
0:45:44	0:45:44	109
0:45:47	0:45:47	110
0:46:16	0:46:16	111
0:46:42	0:46:42	115
0:47:01	0:47:01	116
0:47:16	0:47:16	118
0:48:30	0:48:30	120
0:48:35	0:48:35	121
0:48:45	0:48:45	123
0:49:11	0:49:11	126
0:49:20	0:49:20	127
0:55:13	0:55:13	134
0:55:39	0:55:39	135
1:06:29	1:06:29	137