Capacity management of migrant accommodation centers using approximate dynamic programming

Abstract

Irregular migration has become a major macro-economic and political challenge. Due to rising political conflicts and income inequality across the world, the number of migrants is expected to increase exponentially over the coming decade. Thus, it is of critical importance to effectively use the limited resources allocated to humanitarian operations for irregular migration. In this paper we model the problem of capacity management and migrant transfers within a network of migrant accommodation centres with stochastic dynamic programming. Our study extends the literature on stochastic modelling and humanitarian operations by applying Approximate Dynamic Programming (ADP) into a new context. The model is translatable in other similar migratory routes and locations around the world where governments need to deal with uncertain numbers of irregular migrants. We test our approach on five Greek islands which have been the main migrant arrival points during the European Migrant Crisis. The results show that ADP provides a better computational performance than a simple myopic heuristic. The sensitivity analysis gives insights to the decision-makers about the impact of parameter values on the policies.

Keywords:

• Humanitarian operations
• Sustainable Development Goals
• Strategic planning
• Stochastic Programming
• Dynamic Programming

1. Introduction

Of the 70 million people worldwide who have been forced to flee from their homes due to armed conflict or prosecution, 25 million are estimated to be refugees, crossing borders to seek safety (United Nations High Commissioner for Refugees, 2020). There are high-level discussions between countries both directly and via international organizations, such as the United Nations (UN), to address irregular migration¹. While it is imperative to continue the this communication between countries to stabilize social and economic volatility in migrants’ home countries in the long-term, there is an urgent need of improving life-threatening conditions for those who have already crossed borders. Considering the lack of access to the receiving countries’ national health systems, hygiene products, as well as safety and security conditions in general, migrants are at high risk of facing serious health problems, including contracting diseases, such as the recent coronavirus (COVID-19) pandemic (Hargreaves et al., 2020; Raju & Ayeb-Karlsson, 2020). Thus, it is of critical importance to effectively use the limited resources allocated to humanitarian operations. Focusing on the most frequently used route to enter Europe, that of the Eastern Mediterranean (between Turkey and Greece), we create a stochastic model aiming to optimize the capacity planning and operational management of migrant arrivals in five Greek islands.

This research contributes to the Sustainable Development Goals set by the UN (UNSDGs), by developing a stochastic approach for the management of humanitarian operations for irregular migration. Our research is directly aligned with UNSD Goal 10, Target 10.7 that aims to facilitate orderly, safe, and responsible migration and mobility of people, including through implementation of planned and well-managed migration policies. This is further reinforced by the recent addition (March 2020) of a new indicator (number 89) on the recommendation to track numbers of people displaced across national borders as a result of conflict, natural disasters, or other causes. By reducing the complexity of government decisions on irregular migration, our stochastic modelling approach aims to relieve tensions within local island populations, and thereby reducing the risk of regional instabilities. Furthermore, our approach also can be applied to other UNSDGs connected to global migrant crises such as: Goal 1 (ending poverty in all its forms) and Goal 3 (improving health and well-being).

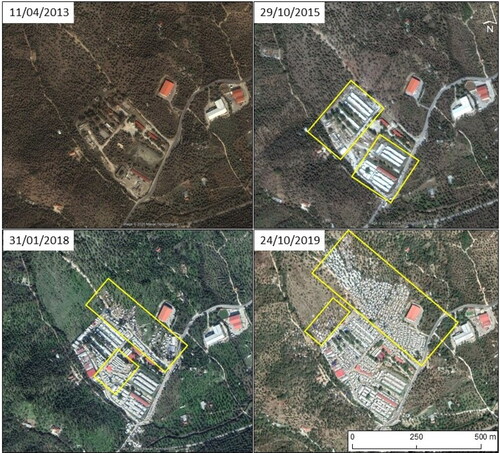
Reaching a peak of approximately 860000 arrivals in 2015, the Eastern Mediterranean remains the most used route by the migrants entering the EU (United Nations High Commissioner for Refugees, 2020). With on-going conflicts in the Middle East such as the Syrian civil war, as well as the increase in frequency of natural disasters due to climate change, a similar irregular migration scenario to that of 2015 is highly anticipated. At present, the five Greek islands (Lesvos, Chios, Samos, Kos, and Leros) account for more than 93% of total arrivals in the country (United Nations High Commissioner for Refugees, 2020). These migrants are hosted in irregular accommodation which is posing numerous health and safety challenges for themselves as well as the local Greek population. Currently, the largest irregular accommodation is Moria in Lesvos which was initially designed for hosting 3000 people. Nevertheless, due to large numbers of arrivals during the last five years, Moria has chaotically expanded to host 12000 people. In Figure 1 we illustrate the irregular expansion of the Moria accommodation.

Figure 1. Expansion of Moria irregular accommodation (Lesvos). The yellow boxes illustrate structural expansions between each year. The Greek government has announced the closure of this structure which will be replaced by a new one capable of hosting 5000 people initially. The satellite imagery belongs to Maxar technologies and was acquired through Google Earth.

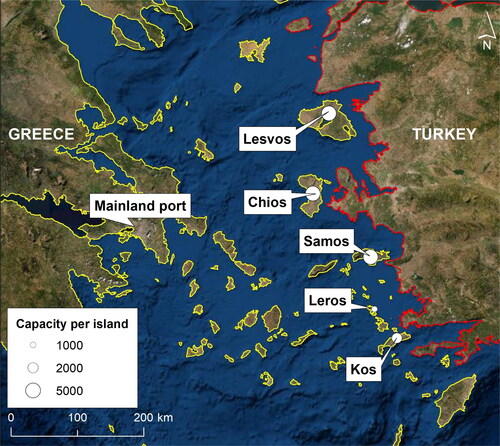
Several incidents such as a deadly fire taking place in 2019 (BBC, 2019) and the difficulty for migrants to self-isolate during the COVID-19 pandemic (Raju & Ayeb-Karlsson, 2020) have led to increased health, safety, and security risks for the migrant population and the local Greek community. Improper management of migrant crisis translates to losses in the tourism sector (Deutsche, 2020). In order to better manage the current and future flows and minimise the impacts from the aforementioned risks, the Greek government has announced that it plans to replace the existing irregular structures in five islands with new accommodation centres. In Figure 2, we provide a map of the islands and their future accommodation capacities. (Please note that suggested capacities are taken as an example (real numebrs as of March 2020), these might change due to updated planning from the Greek government.)

Figure 2. Potential locations of migrant accommodation centres and suggested capacities per island. The basemap used is ESRI World imagery. The Greek and Turkish administrative boundaries used are from the Regional IM Working Group - Europe.

Our model aims to support the decision-making of the Greek government during the Presidency of the Council of Europe which focuses on mitigating the risks for a) irregular migrants arriving in the Greek islands, b) the five Greek islands facing the challenge of hosting increased irregular migrant flows, and c) the Greek government for a better management of the increasing numbers of asylum seekers who enter and reside in the country. To deal with the peak of arrivals, the government can either (i) expand the island’s capacities further, and/or (ii) move some of the migrants to the mainland accommodation centres which have lower restrictions in terms of the capacity expansion. However, the authorities hold a limited budget for these operations. We develop a stochastic dynamic programming model to find the optimum capacity expansion and migrant carriage decisions over a fixed planning period in five Greek islands, considering uncertain migrant arrivals. Due to the large state and action spaces, we use an Approximate Dynamic Programming (ADP) method to obtain approximately optimum policies. The contributions of the paper can be summarized as:

1. Modelling a significant humanitarian operational problem with stochastic dynamic programming,

2. Developing a computationally efficient solution algorithm for the model based on the ADP,

3. Conducting computational experiments to investigate the influence of potential scenarios on the decisions taken by the authorities.

The paper is organized as follows. Next section presents a brief review of the related literature. Section 3 provides the problem description and underlying assumptions along with the optimization model. Section 4 presents the suggested solution approach based on ADP. In Section 5, we introduce the design of experiments and results. Finally, Section 6 summarizes the results of our model and provides future research directions.

2. Literature review

OR methods have been frequently used in humanitarian operations (Besiou et al., 2018; Boonmee et al., 2017; Wassenhove, 2006), particularly focusing on natural disasters such as flooding (Salmerón & Apte, 2010), earthquakes (Khare et al., 2020), and hurricanes (Consuelos et al., 2012; Lodree, 2011; Taskin & Lodree, 2011). These methods have been proven to enhance efficiency in humanitarian operations including resource allocation (Salmerón & Apte, 2010), warehouse and facility location (Jahre et al., 2016; Johansen et al., 2014), and transportation planning (Barbarosoǧlu & Arda, 2004).

Through many applications, such as planning of energy resources (Powell et al., 2012; Sedighizadeh et al., 2019), trading (Abbaszadeh et al., 2018) and pharmaceuticals (Gökalp & Branke, 2020), ADP has proved to be useful in dealing with complex stochastic and dynamic problems, which makes it suitable for the problem considered in this paper. Although, the OR literature on humanitarian operations is well developed, as mentioned above, studies tend to rely on traditional techniques such as integer programming. In this study we present the application of the ADP, for the first time, in the context of irregular migration.

2.1. Approximate dynamic programming and humanitarian operations

The stochastic dynamic programming models lead to very large problem sizes due to rapidly exploiding sizes of state and/or action spaces: this phenomenon is labeled as ‘curse of dimensionality’ (Bertsekas, 2012). To overcome this issue, various methods are proposed under the umbrella terms ADP or reinforcement learning as commonly used in the computer science field (Powell, 2007). These methods utilise simulation to predict an approximation to the true value of states defined as value function. They mostly differ on how the simulation is utilized for the approximation. A class of algorithms use selected features from the state variables, called basis functions, to approximate the value function. The algorithms using basis function approximation can be divided as parametric and non-parametric. Among the non-parametric algorithms, neuro-dynamic programming (Bertsekas & Tsitsiklis, 1995) refers to using neural networks to find the best basis function approximation to the observed (simulated) state values. To update the value function approximation with the new simulation observations, a recursive algorithm such as least squares method can be used (Forootani et al., 2019).

More recently, particularly since the start of the European migrant crisis in 2015, OR literature was extended with humanitarian operations efforts dealing with better managing these crises. For example, Pérez-Galarce et al. (2017) develop a static, mixed-integer linear model to decide on to which locations the victims of a disaster should be sent. The model was then solved with a commercial mixed-integer solver for the Chilean case. In another study, Drakaki et al. (2018) develop a model to find the best location for refugee sites. They use multi-criteria decision-making and fuzzy methods to rank each site. In the most relevant paper to ours, Günay et al. (2019) aim to find the optimal number and location of facilities for refugee humanitarian aid. They assume that the refugee locations are given beforehand, while the size of aid in each facility is assumed to be uncertain.

While the studies cited above have focused on problems such as migrant accommodation siting and emergency supplies for migrant populations (Drakaki et al., 2018; Günay et al., 2019; Pérez-Galarce et al., 2017), they have not dealt with the transportation of migrants between different sites in addition to the capacity expansion decisions. Our study extends this body of research by incorporating real data to optimize humanitarian operations for migrants arriving to the Greek Islands by sea. Additionally, the models developed in these papers do not consider a long-term of decision planning, i.e. they are not dynamic models, and thus do not suffer from large problem size as in our paper. To overcome this ‘curse of dimensionality’, we have developed an ADP algorithm that allows to obtain approximately good solutions within reasonable computation times for large size stochastic and dynamic models (Powell, 2009).

3. Dynamic capacity management model for migrant accommodation centres

3.1. Problem description

We consider the capacity management for migrant accommodation centres (labelled as MACs thereafter) in five Greek islands and the mainland during a finite period. Meanwhile, a number of migrants arrive to the MACs at each time period, i.e. one week. Overcrowding, i.e. when the migrant population is larger than a MAC’s capacity, incurs a cost linearly dependent on the difference between the capacity and the migrant population. To reduce overcrowding, the migrants can be moved to the mainland with a certain cost. The authorities need to decide on the operating capacities of several MACs in Greece and the number of migrants to move to the mainland from the MACs during a finite period. We assume that the operating capacities cannot be expanded immediately. Besides, the capacity expansions require a one-time cost and there is a fixed budget.

The main uncertainty in the problem is the number of migrant arrivals. The objective is to minimize the total cost incurred during the planning period which consists of (i) cost of capacity expansion in all MACs, (ii) cost of moving migrants to the mainland, and (iii) cost due to overcrowding. We assume that the MACs’ capacities are only expanded, not reduced. This is because historical data show that the migrant population in the MACs has been steadily increasing (United Nations High Commissioner for Refugees, 2020).

3.2. Problem formulation

The problem summarized above is a stochastic and dynamic problem that is modeled with a Markov Decision Process (MDP) framework. The MAC capacities are measured in terms of population size that can be provided with reasonable living conditions. We model the problem for a finite planning horizon, T, with time periods $t=1,\dots ,T.$

Assumptions:

• We assume that the MAC capacities can only be expanded in fixed increments and up to a limit. The basis of this assumption is that the new MAC materials are bought in bulk (based on our interviews with MAC staff). For example, if the increment unit is 350 and the maximum limit is 700, then a MAC capacity can be increased by 350 or 700 in one time period.

• Each MAC receives a fixed percentage of overall migrant arrivals. In other words, when there is a surge of arrivals, each island is affected in a similar way. This assumption is validated mostly through the historical migrant data. Additionally, we only model the sea arrivals of migrants, and thus the mainland only receives the transported migrants from the islands.

• The number of migrants that can be moved are in the magnitudes of fixed percentages. For example, only 5%, 10% or 15% of the migrants in a MAC can be moved to the mainland in a time period. In addition to the computational concerns (i.e. an extremely large action space otherwise), the basis of this assumption is that usually a limited number of migrants is eligible to move to the mainland due to the time-consuming asylum-seeking process (The Guardian, 2019). Also, we assume that there is a fixed capacity of the boats moving migrants.

• The time lag between a capacity expansion decision and its realization (labeled as delay duration in the rest of the paper) is the same for all MACs. Also, the delay is assumed to be independent on the unit of capacity expansion. This is because in migrant crisis management, significant delays are usually linked to bureaucracy (Fee, 2019; Soederberg, 2019; Werker, 2007). The impact of these two assumptions are investigated in Section 5.3.

A summary of the model notation is provided in Table 1.

Table 1. Model notation.

Notation	Description
	Indices
j	MACs $j=1,\dots ,J,$ where j = 1 is the mainland.
t	Time periods $t=1,\dots ,T.$
	Parameters
$\overline{t}$	Delay for capacity expansion.
$C_j$	Fixed cost of capacity expansion in MAC j.
$\varphi$	Cost of moving one migrant to the mainland.
Τ	Cost of one extra migrant.
λj	% of arrivals received by MAC j.
B	The fixed capacity expansion limit (in terms of units) per time period.
Y	Unit of capacity expansion.
Ρ	Unit percentage of migrants moved from a MAC.
δ	Maximum capacity increment that can be done in a MAC.
Z	Maximum number of migrants that can be moved from the MACs to the mainland.
$\widetilde{R_t}$	Total arrivals to the islands at period t.
${\tilde{r}}_{j,t}$	Arrivals to MAC j at period t.
	Variables (Decisions)
${\Delta }_{j,t}$	Units of capacity increase in MAC j at period t.
$z_{j,t}$	Magnitudes of ρ% of migrants to be moved to the mainland from MAC j at period t.
$y_{j,t}$	Operating capacity of MAC j at period t.
$w_{j,t}$	Number of migrants in MAC j at period t.
$p_{j,t}$	Capacity increase that MAC j is waiting for at period t.
${ϵ}_{j,t}$	Periods passed since the capacity expansion decision is taken for MAC j at period t.

Uncertainties: The main uncertainty is the net migrant arrivals in period t, denoted with ${\tilde{R}}_t.$ We assume that this uncertainty can be modelled with a probability density function, denoted with $P({\tilde{R}}_t=R_t)$ that does not follow a known distribution, i.e. a custom distribution. The details of this distribution are provided in the computational experiments section. The arrivals to MAC j, denoted with $r_{j,t}$ is then equal to ${\lambda }_j{R}_t,$ where λ_j is the fixed percentage of the arrivals received by the corresponding MAC. For the sake of computational efficiency, we assume that ${\tilde{R}}_t$ can take only a finite number of values, denoted with $\overline{R}.$ For example, $\overline{R}=3$ corresponds to only 3 arrival scenarios at each time period: low, normal, and high migrant arrivals.

State: The state at period t is denoted by ${\mathbf{S}}_t=\{{\mathbf{y}}_t,{\mathbf{w}}_t,{\mathbf{p}}_t,{\mathit{ϵ}}_t,{\tilde{R}}_t\}.$ The first two variables in the state represent the capacities and migrant populations in the MACs in period t. In addition to those, we denote the capacity increase that a MAC is waiting for and periods passed since the last capacity expansion decision with $p_{j,t}\in \{0,1,\dots ,\delta \}$ and ${ϵ}_{j,t}\in \{0,1,\dots ,\overline{t}\},$ respectively, where the maximum capacity increase and maximum delay is represented with δ and $\overline{t},$ respectively.

Action: The action taken at period t is denoted with ${\mathit{a}}_t=\{{\mathbf{\Delta }}_t,{\mathbf{z}}_t\},$ which consists of the capacity expansion and migrant carriage decisions. Note that ${\Delta }_{j,t}\in \{0,1,\dots ,\delta \}$ represent the units of capacity expansion that will be made in MAC j. Similarly, $z_{j,t}\in \{0,1,\dots ,\overline{\rho }\}$ represent whether $z_{j,t}\rho$ % of migrants in MAC j are moved to the mainland or not (0). The feasible action space, denoted by ${\mathcal{A}}_t$ is determined by the current state ${\mathbf{S}}_t:$ if $z_{j,t}<w_{j,t}$ i.e. there is no migrant in MAC j, then there would be no migrant to move. Also, the capacity expansions and transported migrant population are limited with fixed capacities: $\sum _j{\Delta }_{j,t}Y\le B$ and $\sum _j{z}_{j,t}{w}_{j,t}\rho \le Z.$ Finally, if a MAC is already waiting for an expansion: $p_{j,t}>0,$ then another capacity expansion decision cannot be made: ${\Delta }_{j,t}=0.$ Note that no migrant is carried from the mainland: $z_{1,t}=0$ for all t. A policy, $\pi \in \Pi$ corresponds to a certain sequence of actions: $\pi =\{{\mathit{a}}_1,\dots ,{\mathit{a}}_{T-1}\},$ where ${\mathit{a}}_t\in {\mathcal{A}}_t$ and Π is the set of feasible policies.

Stage cost: At a time period, the cost incurred due to the action ${\mathit{a}}_t$ consists of the costs of (i) capacity expansions, (ii) carriage of migrants from islands to the mainland, (iii) overcrowding, and can be formulated as: (1) $$\phi ({\mathit{a}}_t,{\mathit{S}}_t)=\sum _j({\Delta }_{j,t}Y{C}_j+\varphi z_{j,t}{w}_{j,t}\rho +\tau |w_{j,t}-y_{j,t}{|}^{+}),$$(1) where C_j, $\varphi$ and τ represent the unit costs of capacity expansion in site j, moving one migrant to the mainland and one extra migrant (in overcrowding), respectively. There is no cost at the end of the planning period.

State update: The state at period t + 1, ${\mathit{S}}_{t+1},$ depends on the state at period t, the actions taken in the current time period, and the realized migrant arrivals $R_{t+1},$ i.e. ${\mathit{S}}_{t+1}({\mathit{S}}_t,{\mathit{a}}_{\mathit{t}}|R_{t+1}).$ Note that the probability of moving to ${\mathit{S}}_{t+1}$ is then equal to $P({\tilde{R}}_{t+1}=R_{t+1}).$

The update on the rest of the state variables can be formulated as follows: $$\begin{array}{c}{y}_{j,t+1}=\{\begin{array}{cc}{y}_{j,t}+p_{j,t}Y,\hfill & \text{if}{ϵ}_{j,t}=\overline{t},\hfill \\ y_{j,t},\hfill & \mathrm{o}.\mathrm{w}.\hfill \end{array}\\ w_{j,t+1}=\{\begin{array}{cc}{w}_{j,t}+{\tilde{r}}_{j,t}-\rho z_{j,t}{w}_{j,t},\hfill & j=2,\dots ,J,\hfill \\ w_{j,t}+\sum _j\rho z_{j,t}{w}_{j,t},\hfill & j=1.\hfill \end{array}\\ {ϵ}_{j,t+1}=\{\begin{array}{cc}1,\hfill & \text{if}\mathrm{ }{\Delta }_{j,t}\ge 1,\hfill \\ {ϵ}_{j,t}+1,\hfill & \text{else}\mathrm{ }\text{if}\mathrm{ }\overline{t}>{ϵ}_{j,t}>0,\hfill \\ 0,\hfill & \mathrm{o}.\mathrm{w}.\hfill \end{array}\\ p_{j,t+1}=\{\begin{array}{ccc}1,\hfill & \text{if}\mathrm{ }{\Delta }_{j,t}\ge 1,\hfill & \hfill \\ p_{j,t},\hfill & \text{else}\mathrm{ }\text{if}\mathrm{ }{p}_{j,t}>0\mathrm{\&}\hfill & {ϵ}_{j,t}<\overline{t},\hfill \\ 0,\hfill & \mathrm{o}.\mathrm{w}.\hfill & \hfill \end{array}\end{array}$$

Each state, ${\mathit{S}}_t$ has a value defined by the value function denoted with $V({\mathit{S}}_t)$ that depends on the value of the possible future states and can be formulated as follows: (2) $$V({\mathit{S}}_t)=\underset{{}_{\pi \in \Pi }}{\max }E\{V_T({\mathit{S}}_T)-\sum _{t\prime =t}^{T-1}\phi ({\mathit{a}}_{t\prime },{\mathit{S}}_{t\prime })\},\forall {\mathit{S}}_t,t=1,\dots ,T-1,$$(2) where $\pi =\{{\mathit{a}}_1,\dots ,{\mathit{a}}_{T-1}\}.$ This value function gives the optimum policy that maximizes the subtraction of the action costs from the expected final (state) value. The expectation requires to take the probabilities of moving into the future states, i.e. $P({\tilde{R}}_{t+1}=R_{t+1}).$ The values of the states in the final periods are assumed to be zero: $V_T({\mathit{S}}_T)=0.$

4. Solution approach: approximate dynamic programming

The mathematical formulation outlined in the previous section is computationally expensive to solve due to the large state space. Several state variables, such as capacities, migrant arrivals and migrant populations, can take a large range of integer values. Assuming that these integer variables can take 5 different values, for 20 time periods and maximum 5 periods of delay for capacity expansions, total number of states can be as large as $5^5\times 5^5\times 5^5\times 3\times 20.$ On the other hand, due to few possible actions and the feasibility conditions, the action space is relatively smaller. Therefore, we use enumeration to find the optimal action at each decision point.

ADP is very suitable to solve large stochastic dynamic programming problems (Powell, 2009). Therefore, we develop a lookup table based, value iteration ADP algorithm to solve the problem. A linear programming based ADP is not applied since the value function (2) is complex (Powell, 2009). Also, the value iteration is preferred over policy iteration because of the large state space and a comparatively small action set (Sun & Li, 2013).

In each iteration of the algorithm, a simulation model simulates the uncertainties in each time period of the planning period; i.e. moves forward in time at each iteration. However, the costs incurred in the later time periods should be transferred to the previous time periods. To overcome this problem, a double pass is suggested (Powell, 2007) which employs an additional backward pass updating the value function estimations by moving backwards in time in the simulated trajectory in each iteration.

To visit more states during the algorithm, a random feasible action is chosen in the first half of the iterations with probability Γ. In the case of multiple optima, the action is chosen randomly among them. The inputs to the algorithm are the initial state ${\mathbf{S}}^0,$ and the probability distributions for migrant arrivals. The initial state is the same in each iteration, and its value $\overline{V}({\mathbf{S}}_{n=1}^0)$ is initialized as zero in the first iteration. The algorithm can be performed in two main stages after initialization: forward and backward passes. In the forward pass, migrant arrivals are simulated for each time period and an action is chosen based on value function (2)(2) $$V({\mathit{S}}_t)=\underset{{}_{\pi \in \Pi }}{\max }E\{V_T({\mathit{S}}_T)-\sum _{t\prime =t}^{T-1}\phi ({\mathit{a}}_{t\prime },{\mathit{S}}_{t\prime })\},\forall {\mathit{S}}_t,t=1,\dots ,T-1,$$(2) or randomly based on the probability Γ in the first half of the run. Each visited state, its estimated value and the selected action are entered to a table, called as a lookup table. Algorithm 1 shows the pseudo-code of the ADP algorithm with value iteration, lookup table and double pass.

There are two main value-function related variables: the value function approximations (stored in a lookup table), ${\overline{V}}_t^n,$ and computed state values (during the algorithm), $v_t^n.$ In each iteration $n=1,\dots ,N,$ after the forward pass, the algorithm goes backward in time and recursively adds the values of the future states (in the sample path) into $v_t^n$ for $t=T-1,\dots ,1.$ If a state ${\mathbf{S}}_t^n$ is visited for the first time by the algorithm, then its computed value $v_t^n$ is directly added to the lookup table, i.e. ${\overline{V}}_t^n({\mathbf{S}}_t^n)=v_t^n({\mathbf{S}}_t^n).$ Otherwise, ${\overline{V}}_t^n({\mathbf{S}}_t^n)$ is equal to the weighted sum of $v_t^n({\mathbf{S}}_t^n)$ and ${\overline{V}}_t^{n-1}({\mathbf{S}}_t^n),$ the most recent value of the state (in the lookup table): ${\overline{V}}_t^n({\mathbf{S}}_t^n)={\alpha }_n{\overline{V}}_t^{n-1}({\mathbf{S}}_t^n)+(1-{\alpha }_n)v_t^n({\mathbf{S}}_t^n),$ where α_n is a smoothing parameter. Since the state values are expected to approach their exact values through iterations, α_n is formulated as a linearly increasing function of the iteration counter n: ${\alpha }_n=a+b{\alpha }_n$ where a and b are the parameters, estimated by trial-and-error. The linear form is selected because of its simplicity and also convergence (Powell, 2007). Finally, the values stored in the lookup table for all states visited until iteration n are carried over to the next iteration; ${\overline{V}}_t^{n+1}({\mathbf{S}}_t^k)={\overline{V}}_t^n({\mathbf{S}}_t^k)$ for $k=1,\dots ,n$ and $t=1,\dots ,T.$ Once the maximum number of iterations has been reached, the algorithm returns the lookup table.

Basis function approximation: The ADP algorithm presented above provides an action for the states generated by the simulation. In other words, it does not guarantee to find the right action for each possible state, but for most of them. Therefore, we also implement a basis function approach which approximates the state values using a linear weighted formulation of few state variables (Powell, 2007) based on the value estimations from the lookup table. As explained earlier, alternative approaches such as neural networks or stochastic gradients methods can be utilized to obtain the best approximation structure (Powell, 2009). We used a simple linear regression to find the best weights of the basis functions fitting to the value estimations for this finite horizon problem.

After trying several formulations, the best fit for the state-value pairs in the lookup table (with R² of 0.88) is achieved by: $$\overline{V}(S_t)=w_1{c}_j{y}_{jt}+w_2\tau |w_{jt}-y_{jt}{|}^{+},$$ where w₁ and w₂ represent the weights of the basis functions. For each problem instance, first the lookup table is obtained and then the linear regression is applied to find the best weight values.

Algorithm 1.

Pseudo-code of the ADP algorithm

Set maximum number of iterations N, Γ and n = 1. Initialize the value of the initial state ${\overline{V}}_1^0({\mathbf{S}}_1^k)$ as 0 for $k=1,\dots ,n-1,n=1,\dots ,N.$ for $n=1,2,\dots ,N,$ do

For $k=1,\dots ,n$ and $t=1,\dots ,T,$ set ${\overline{V}}_t^n({\mathbf{S}}_t^k)={\overline{V}}_t^{n-1}({\mathbf{S}}_t^k).$

Forward Pass:  for $t=1,2,\dots ,T-1,$ do

 – Generate ${\mathit{R}}_t^n.$

 – Generate a random number ω,  if $n\le N/2$ and $\omega \le \Gamma$ then

  Randomly select ${\mathit{a}}_t^n$ among the feasible action set ${\mathcal{A}}_t,$ and compute $v_t^n({\mathbf{S}}_t^n)$ by using (2)(2) $$V({\mathit{S}}_t)=\underset{{}_{\pi \in \Pi }}{\max }E\{V_T({\mathit{S}}_T)-\sum _{t\prime =t}^{T-1}\phi ({\mathit{a}}_{t\prime },{\mathit{S}}_{t\prime })\},\forall {\mathit{S}}_t,t=1,\dots ,T-1,$$(2) . else

  – Find the action ${\mathit{a}}_t^n$ and $v_t^n({\mathbf{S}}_t^n)$ by solving (2)(2) $$V({\mathit{S}}_t)=\underset{{}_{\pi \in \Pi }}{\max }E\{V_T({\mathit{S}}_T)-\sum _{t\prime =t}^{T-1}\phi ({\mathit{a}}_{t\prime },{\mathit{S}}_{t\prime })\},\forall {\mathit{S}}_t,t=1,\dots ,T-1,$$(2) based on the state values stored in the lookup table. – If a state value does not exist in the lookup table, then its value is assumed to be computed based on (1)(1) $$\phi ({\mathit{a}}_t,{\mathit{S}}_t)=\sum _j({\Delta }_{j,t}Y{C}_j+\varphi z_{j,t}{w}_{j,t}\rho +\tau |w_{j,t}-y_{j,t}{|}^{+}),$$(1) but without the cost of capacity expansion or migrant transfer. end if

 – Update state variables based on the action ${\mathit{a}}_t^n$ and ${\mathit{S}}_t^n:$ ${\mathbf{S}}_{t+1}^n={\mathbf{S}}_{t+1}({\mathbf{S}}_t^n,{\mathit{a}}_t^n).$ end for

Backward Pass:   for $t=T-1,\dots ,1$ do

 – Compute $v_t^n({\mathbf{S}}_t^n)=v_{t+1}^n({\mathbf{S}}_{t+1}^n)-\phi ({\mathbf{a}}_t^n,{\mathbf{S}}_t^n),$ where $\phi ({\mathbf{a}}_t^n,{\mathbf{S}}_t^n)$ is defined as in (1)(1) $$\phi ({\mathit{a}}_t,{\mathit{S}}_t)=\sum _j({\Delta }_{j,t}Y{C}_j+\varphi z_{j,t}{w}_{j,t}\rho +\tau |w_{j,t}-y_{j,t}{|}^{+}),$$(1) . if state ${\mathbf{S}}_t^n$ exists in the lookup table, then

  – Update ${\overline{V}}_t^n({\mathbf{S}}_t^n)=({\alpha }^{n-1}){\overline{V}}_t^{n-1}({\mathbf{S}}_t^n)+(1-{\alpha }^{n-1})v_t^n({\mathbf{S}}_t^n),$ else

   – Set ${\overline{V}}_t^n({\mathbf{S}}_t^n)=v_t^n({\mathbf{S}}_t^n).$    end if   end for

Return all value function approximations $({\overline{V}}_t^N,$ i.e. lookup table) for $t=1,\dots ,T.$

5. Computational experiments

This section aims to (i) analyse the performance of the solution method and (ii) provide policy suggestions to the decision-makers. First, we present the input data used for the experiments. All the experiments are conducted in Intel Core i7-6700K CPU @ 4.00 Ghz with 32 GB memory and x64 based processor. The ADP algorithm is coded in Matlab 2018 b. The parameters used for the ADP algorithm are chosen as $\Gamma =0.5,$ a = 0.05 and $b=0.95/n$ based on the results of some preliminary experiments. The algorithm converges to stable state values after 1000 iterations.

5.1. Input Data

We consider the capacity management of the five Greek island MACs as well as the mainland (assumed to be one MAC) for almost a year. The duration of each time period is 3 weeks while the planning horizon consists of 20 time periods, i.e. 60 weeks. The net migrant arrivals to the islands are retrieved from the database provided by United Nations High Commissioner for Refugees (2020). Based on these data, we then computed low, medium, and high migrant arrival scenarios for each time period with respective probabilities. The percentage of overall arrivals to each island is also estimated based on the historical data. The cost for migrant transport is estimated based on the most recent migrant transportation contract (of 1560 migrants from the islands to the mainland) provided by the Greek government (Greek Ministry of Migration & Asylum, 2020). The rest of the data are collected through informal interviews with staff working in the MACs. Table 2 shows the dataset used for the experiments.

Table 2 Input data used for the experiments.

MAC Site	Mainland	Lesvos	Chios	Samos	Kos	Leros
Initial migrant populations	62000	4843	2130	2562	1830	685
Initial capacities of MACs	64000	5000	5000	5000	2000	1000
Unit of capacity expansion for a MAC	350
Unit % of migrants transported to the mainland (ρ)	5%
Delay time for capacity expansion	9 weeks
Carriage cost of one migrant to the mainland	250€
Maximum migrant move (Z) and capacity expansion (B)	500 & 1500
Maximum % of migrants that can be moved from a MAC	20%
% of migrant arrivals to each island	0	47	14	20	11	8
Migrant arrival scenarios in each month (probability)	Low (0.2)	Medium (0.7)	High (0.1)
1	263.375	384.5	8498.75
2	236.625	376.5	7306.625
3	368.125	633	4112.625
4	305.75	748.5	2209.875
5	413.375	536	2588.875
6	418.125	673	4291.625
7	489.625	798.5	7378.125
8	727.75	1220	14303.63
9	843.625	1382.5	19446.25
10	802.375	1366.5	27351.25
11	518.875	780.5	19659.13
12	445.875	563	14162.38

The cost of capacity expansion in the islands is assumed to be five times of that in the mainland. Note that the costs of capacity expansion and overcrowding involve societal and humanitarian concerns and can vary depending on the socioeconomic factors. Therefore, we model these cost parameters as multiples of the cost of migrant transportation: $C_j={\alpha }_1\varphi ,$ for $j=2,\dots ,J,$ and $\tau ={\alpha }_2\varphi .$ We conduct the experiments for plausible ranges of α₁ and α₂.

5.2. Results

This section presents (i) the computational analysis of the proposed solution method and (ii) the insights generated from the ADP policy.

Computational Performance of ADP: The computational time required to obtain the approximate policy with the ADP is around 2.5 h for 1000 iterations. Considering that the policy is generated for a planning period of more than a year, the computation time is acceptable. However, we should also note that the computation time is highly dependent on the size of the feasible action space and the number of iterations. For example, if the feasible actions for migrant transfer is doubled, the computation time increases by 8-fold. On the other hand, if a shorter computation time is needed, then the resolution of the model should be reduced by increasing the duration of a period or using a higher percentage unit for migrant transfer, such as 10% instead of 5%. In other words, the parameter levels or the action space can be modified based on the preferred computation time and the modeling resolution.

To investigate the performance of the ADP algorithm, we compare it with a myopic heuristic as a benchmark solution method. The myopic heuristic only considers one time cost in equation (1)(1) $$\phi ({\mathit{a}}_t,{\mathit{S}}_t)=\sum _j({\Delta }_{j,t}Y{C}_j+\varphi z_{j,t}{w}_{j,t}\rho +\tau |w_{j,t}-y_{j,t}{|}^{+}),$$(1) assuming that the capacity expansions are realized immediately, i.e. the overcapacity migrant population is computed based on these expansions. Our discussions with authorities confirmed that the heuristic is very close to governmental agencies’ current practices for managing capacities. Next, we generate 1000 scenarios and apply ADP policy and the myopic heuristic to each. The costs by two policies are then compared. The results show that the ADP generates 40% lower cost compared to the myopic heuristic. Specifically, the myopic heuristic usually suggests the capacity expansion decisions rather than moving the refugees to the mainland due to the negligence of expansion delays. This at the end results in a much higher number of refugees left outside camps: around 12% more than the ADP solution. Another disadvantage of the myopic approach is that the future events cannot be predicted well, which results in reacting to the situation rather than planning for the future. As a result, total capacity increase over the planning period is slightly lower in the myopic heuristic compared to the ADP.

Therefore, we can conclude that ADP produces a better policy than a simple heuristic within a reasonable computational time.

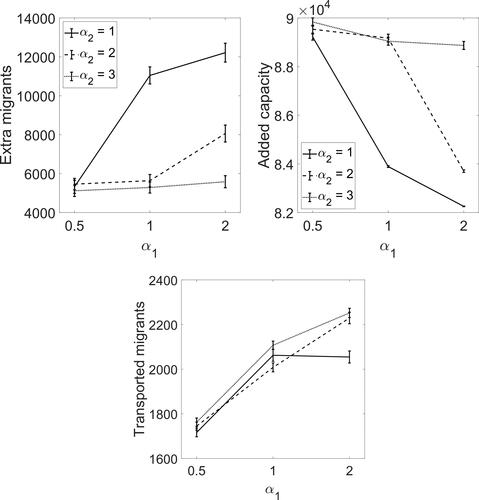
Analysis of ADP Policy: Figure 3 shows the mean and 95% CI of (i) total number of migrants left outside the MAC capacities (extra migrants), (ii) total capacity added to the MACs (added capacity), and (iii) total number of migrants moved to the mainland (transported migrants) during the planning horizon over 1000 scenarios, for three possible values of two cost coefficients.

Figure 3. Outputs obtained by ADP for various cost coefficients.

As expected, when the overcrowding is more costly (a higher α₂), the MACs’ capacities are increased. However, α₂ has a lower impact when the capacity expansion is cheaper (${\alpha }_1=0.5$) at which the capacity expansion is already fully exploited and there is not a significant trade-off between capacity expansion and overcrowding costs.

When overcrowding is very costly (${\alpha }_2=3$), the policy exploits expansion of the island MACs as well as the mainland and then transports the migrants to the mainland. If it is less costly (${\alpha }_2=2$), the policy still exploits the expansion of the mainland and transporting the migrants there (cheaper), but prefers less expansion in the islands. Therefore, in terms of the migrants transported, we do not see a significant difference when ${\alpha }_2>1$ since the mainland capacity is expanded with similar amounts.

In short, the government needs to expand the capacity of islands or the mainland significantly during the planning horizon. Even with those capacity expansions, there may be overcrowding depending on the objective weights. This may indicate that the budget for capacity expansions, or the migrant transportation should be increased to prevent overcrowding.

Table 3 shows the policy computed by ADP for a randomly chosen scenario when ${\alpha }_1=2$ and ${\alpha }_2=3,$ i.e. capacity expansion is cheaper than overcrowding. The multipliers for decisions are shown with “x”. For example, in period 12, the capacities of Samos and Kos are increased by one unit while that of Leros is increased by 2 units and 10% of migrants in Kos are transported to the mainland. In general, the capacities of the mainland and Lesvos, that has the largest arrivals, are increased more frequently. Transporting the migrants to the mainland is the preferred option for other islands, especially for Leros, which has the smallest migrant population but a significant influx of migrants. This policy may be utilized by the decision-makers as follows: the transportation route from Leros to the mainland may be strengthened and Lesvos may be prepared for more capacity expansion with increased physical infrastructure.

Table 3. Policy for a randomly chosen scenario.

Time	Scen.	Capacity increase	Transport migrants from
1	Low		Lesvos
2	High
3	Low	Lesvos x3, Chios	Leros
4	Mid	Mainland, Samos x3	Kos
5	Mid
6	Mid	Lesvos x3, Chios	Leros
7	Mid	Mainland, Samos x3	Kos
8	High	Kos x3, Leros
9	High	Lesvos x3, Chios x2	Leros
10	Medium		Kos
11	Medium	Lesvos, Chios x3	Chios
12	Low	Samos, Kos, Lerosx2	Kos x2
13	Low		Leros
14	Medium		Leros
15	High	Lesvos x3	Leros
16	Low	Lesvos x3
17	Medium		Kos x2
18	Medium		Kos, Leros
19	Medium	Lesvos x3, Kos	Lesvos
20	Low		Leros x2

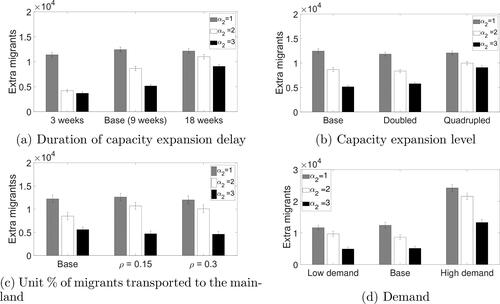
5.3. Sensitivity analysis

In this section, we investigate the impact of several model parameters on the results, especially the overcrowding in the MACs. Throughout the experiments, one of the cost coefficients is always fixed at ${\alpha }_1=2.$

Impact of Expansion Delay: An important challenge in MAC expansions is the logistic related delays. This experiment investigates the impact of a longer (18 weeks) and a shorter (3 weeks) delay with respect to the base case. Figure 4(a) shows the extra migrants for different cost coefficients and delay.

Figure 4. Extra migrants for various costs of overcrowding in the sensitivity tests.

When the delay is prolonged, overcrowding is higher, as expected. However, the impact of delay is negligible when overcrowding is not costly (${\alpha }_2=1$). In that case, capacity expansion may be more expensive than overcrowding. Another observation is that overcrowding can be reduced significantly if the delay is decreased to 3 weeks.

Impact of Fixed Expansion Capacity Unit: In this test, we investigate the impact of fixed expansion unit on the outputs. Figure 4(b) shows the overcrowding levels for base (350), doubled (700) and quadrupled (1400) incremental units for capacity expansion decision. In other words, when the capacity is expanded by one unit in a MAC, its capacity is increased by 700 in the ‘doubled’ case. When the expansion unit is doubled, the delay in expansion (3 weeks in the base case) is also doubled accordingly to investigate the impact of these parameter, too.

We only see a significant effect of this parameter on the results when the cost of overcrowding is very high and the expansion unit is quadrupled. This is possibly because in this case, only one of the MAC’s capacity can be expanded (due to the budget limit) and the delay is too long.

Impact of Transported Migrant Percentage: This test investigates the impact of transported migrant percentage, ρ, on the results. Figure 4 shows the number of extra migrants for base (5%), 15% and 30%. The maximum % of migrants that can be carried from a MAC is also changed accordingly. In other words, either 0%, 15%, 30% or 45% of the migrants can be moved from a MAC in the second case.

When ${\alpha }_2=2,$ the mainland’s capacity is expanded significantly and the migrants are transported there, instead of expanding the capacity of islands. With a higher number of migrants moved, the mainland is then overcrowded, whereas the islands are underutilized. It shows that above 15% is higher than the optimum for ${\alpha }_2=2.$ When a lower ratio of migrants are moved, the balance between the islands and the mainland is better. We do not observe this issue when ${\alpha }_2=3,$ because in this case, the island’s capacities, in addition to the mainland, are also expanded.

Impact of Demand Change: This test examines the cases where the demand is higher and lower than the base case. Specifically, these cases are designed as (i) the probabilities of high and medium demand scenarios are 0.1 higher and lower than their base values, respectively, and (ii) the probabilities of low and medium demand scenarios are 0.1 higher and lower than their base values, respectively. Figure 4(d) shows the extra migrants for these two cases as well as the base case for different α₂ values.

The impact of increase in high demand is highly significant, in all α₂ levels. On the other hand, the increase in the low demand scenario is not significant. This shows that the model is able to optimize the policy in the base demand case such that no more gains could be achieved in terms of minimizing extra migrants. Therefore, a further decrease in the demand does not affect the extra migrants.

Summary of Sensitivity Analysis:

• For ${\alpha }_2=1,3,$ there is less trade-off between different actions; either nothing is done or full expansion strategy is implemented.

• A reduction in the expansion delay can cause a significant decrease in the overcrowding.

• Increasing the incremental unit of capacity expansion does not improve the situation for most cases.

• The fixed percentage for migrant transportation does not have a linear effect on overcrowding. A high percentage does not necessarily mean better outcomes.

6. Conclusions

While ADP has been used in numerous areas of humanitarian operations, the focus was never given on managing MAC capacities. By using a wide range of datasets derived from multiple sources (e.g. government, UNHCR, asylum services), we have extended the ADP framework to the migrant crisis management problem. To the best of our knowledge, this is the first study in stochastic optimisation for humanitarian operations which deals with the transportation of migrants between different centres in addition to the capacity expansion decisions. The experiments with a benchmark heuristic showed that ADP is suitable for finding an approximately optimum policy. The results in other experiments show the significant reduction in overcrowding with a shorter delay for capacity expansion. They also indicate that the incremental unit of capacity expansion does not have a significant impact.

There are numerous avenues for future research. The model can be expanded to the rest of the European Union in order to provide policies for migration management in a larger scale. For example, our model solely focuses on decisions which affect migrants from the time of arrival to an island up to their asylum allocation. Future research can extend the model by incorporating processes for migrant integration to society. Additionally, our model is designed to make decisions once migrants have arrived to the islands, which creates a delay between migrant arrivals and the effects of each decision. The model can be extended by incorporating the factors affecting migrant decisions for date of travel. This will help decision makers to take necessary measures ahead and thus improve the management of humanitarian operations. Finally, the proposed ADP method can be combined with integer programming to reduce the computation time for larger instances.

Disclosure statement

No potential conflict of interest was provided by the author(s).

Notes

1 We use irregular migration to take into account both migrants and refugees. While the term refugee refers to people fleeing armed conflict or persecution, the term migrant refers to people who move to other countries to improve their living conditions.