On Multiple Symmetric Fixed Points in GOST

Abstract

In this article the author revisits the oldest attack on GOST known, the Kara Reflection attack, and another totally unrelated truncated differential attack by Courtois and Misztal. It is hard to imagine that there could be any relationship between two so remote attacks which have nothing in common. However, there is one: Very surprisingly, both properties can be combined and lead the fastest attack on GOST ever found, which is nearly feasible to execute in practice.

Keywords:

• black-box reductions
• block ciphers
• differential cryptanalysis
• Feistel schemes
• fixed points
• GOST
• ISO 18033
• key scheduling
• low-data complexity
• multiple-key attacks
• reflection attacks
• self-similarity

1. Background

The Russian encryption standard GOST 28147–89 is a former top secret encryption algorithm. In 1989, it became an official standard for confidential information, but the specification of the cipher remained confidential [23]. In 1994, shortly after the dissolution of the Soviet Union, the standard was declassified, published, and also translated to English [23]. GOST is a block cipher with a simple Feistel structure, 64-bit block size, 256-bit keys, and 32 rounds. Each round contains a key addition modulo 2³², a set of eight bijective S-boxes on four bits, and a simple rotation by 11 positions. It is widely known that the structure of GOST is in itself quite weak, and in particular the diffusion is quite poor; however, this is expected to be compensated by a large number of rounds. Thus, until 2011, there was no significant attack on this algorithm from the point of view of communications confidentiality: an attack which would allow decryption or key recovery in a realistic scenario where GOST is used for encryption with various random keys. This is in the sense of pure mathematical attacks. In real life, GOST would be broken routinely by a side channel attack (see for example [18]).

The turning point in the security of GOST was the discovery of the so-called “reflection” property [14]. Initially, at Indocrypt 2008, only a weak-key attack with time complexity of 2¹⁹² was proposed, with large proportion of 2⁻³² of weak keys. In 2011, several attacks on regular GOST keys were discovered, and more than half of these new attacks use this reflection property [12], sometimes two, three, or four times [5]. Most of these attacks can be described as attacks with a “complexity reduction” [5, 6], where from some data for the full 32 rounds GOST, we obtain a certain number of pairs for eight or less rounds of GOST. The quantity of data available after reduction is very small, for example, two, three, or four pairs for a reduced cipher. In this aritcle, we will look at some of the simplest of these attacks and avoid the highly complex ones.

A basic assessment of the security of GOST against linear and differential cryptanalysis was conducted in 2000 by Shorin, Jelezniakov, and Gabidulin see [25]. The results were quite impressive: At the prescribed security of level of 2²⁵⁶, five rounds are sufficient to protect GOST against linear cryptanalysis. Differential cryptanalysis [1] of GOST seems comparatively easier and has attracted more attention. In [25] the authors also estimated that seven rounds should be sufficient to protect GOST against differential cryptanalysis. The authors also claimed that “breaking the GOST with five or more rounds is very hard” [p. 5]. In addition, two Japanese researchers [24], explained that the straightforward classical differential attack with one single differential characteristic is unlikely to work at all for a large number of rounds. In the same article [24], more advanced differential attacks on GOST were described. They are advanced truncated differential attacks, cf. [16]. The first advanced multiple differential attack proposed in [24] allows to break about 13 rounds of GOST. Numerous recent works have tried to understand, evaluate, and improve the resistance of GOST against differential cryptanalysis, in view of the standardization of GOST [1, 17, 22]. At the same time, in 2011–2012, many improved differential attacks on GOST were found, allowing finally to break full 32-round GOST faster than by brute force, see [7, ⁹¹⁰¹¹]. We also exploit these properties in this article.

In this article we do not study GOST in much depth. We just revisit the oldest attack on GOST known, the Kara Reflection attack, and ask ourselves a simple question: Do multiple symmetric fixed points exist? We can safely consider that eight rounds of GOST are a black box and that it has a simple truncated differential property, which has been discovered recently. These two properties seem totally unrelated. However, their combination leads to an extremely simple and powerful attack on GOST.

2. The Reflection Property of GOST

We write GOST as the following functional decomposition (to be read from right to left), which has been proposed at Indocrypt 2008 [14]:

(1)

where ℰ is exactly the first eight rounds which exploits the whole 256-bit key, 𝒮 is a swap function which exchanges the left and right hand sides and does not depend on the key, and 𝒟 is the corresponding decryption function with .

Fact 1 (Internal Reflection Property). Consider the last 16 rounds of GOST 𝒟○𝒮○ℰ for one fixed GOST key. This function has an exceptionally large number of fixed points: applied to X gives the same value X with probability 2⁻³² over the choice of X, instead of 2⁻⁶⁴ for a random permutation.

Justification: Our permutation 𝒟 ○ 𝒮 ○ ℰ has a well-known “conjugated” structure of type Q⁻¹ ○ P ○ Q. Consequently, it has the same cycle structure as the swap function S and 2³² fixed points. The state of the cipher after the first eight rounds ℰ is symmetric with probability 2⁻³², and 𝒟 ○ ℰ = Id.

Note: This theorem about Q⁻¹○P ○ Q and P has played a very important role in the cryptanalysis of important government and military ciphers, in particular many rotor machines. It was first used by Marian Rejewski in the cryptanalysis of Enigma in the early 1930s, and it is sometimes called “the theorem which won World War 2,” see [13, 20, 21].

3. Attacks with Symmetric Fixed Points

At Indocrypt 2008, Kara described a weak-key attack on full 32-round GOST. It has time complexity of 2¹⁹² and works for a large proportion of 2⁻³² of weak keys. It uses a very interesting new “reflection” property [14]. At first sight, this attack has only limited interest. However, a large number of very good attacks have been discovered, and more than half of them use this reflection property [12], sometimes two, three, or four times [7].

In late 2012, another weak key attack was proposd by Kara and Karakoç, cf. [15]. The paper was presented at CANS 2012, in Darmstadt, Germany, on 12–14 December 2012. This attack is quite interesting because it uses pairs of symmetric fixed points. This article is about showing that such pairs exist with a probability which is larger than expected and that triple and quadruple symmetric fixed points also exist with surprisingly high probabilities. In one sense, we revisit this attack from [15], and propose very important variants which are based on highly non-trivial facts that are somewhat impossible to expect from [15]. We are going to deduce them from other major results on GOST [7, ⁹¹⁰¹¹, 24], even though it is safe to say that nobody would expect that these attacks could be related in any way.

3.1. Recent Weak Key Attacks from CANS 2012

The new weak key attack on GOST [15] is based on the assumption that there are two symmetric fixed points in the first 16 rounds of GOST. Such symmetric fixed points happen only for weak keys and can happen for two distinct reasons. It is possible to see that the attack from [15] can be split into two independent weak key attacks, which the authors describe as one single attack with a distinction of two distinct events (Event1 and Event2, see [15]). We recall briefly the attack from [15]. Let ℰ be the first eight rounds of GOST. In Event1, the assumption is that there exists two symmetric A ≠ B such that ℰ(A) = B and ℰ(B) = A, which is a swap. In Event2, we assume that there exists two symmetric fixed points A ≠ B (i.e., ℰ(A) = A and ℰ(B) = B). Both events lead to two symmetric fixed points for the full 32-round GOST. Each of these events occurs only for a proportion of d = 2⁻⁶⁵ of keys, or at least it seemed so to the authors. In fact, the main point in this article is that such a probability can be much higher than expected, especially for multiple symmetric fixed points.

In this article, we only look at Event2; however, similar observations could also be made about Event1, and this can also lead to some non-trivial attacks and their generalizations and special cases, see [5]. We can observe that Event2 is particularly simple: It is just twice the event which is used in the oldest reflection attack on GOST [16]. This gives the following very simple attack from [15]:

Fact 2 (Event2 Attack From [15]). For every key such that Event2 happens (i.e., there are at least two symmetric fixed points for the first eight rounds of GOST), given 2³² CP (chosen plaintexts), we can obtain two P/C pairs for eight rounds of GOST correct with probability close to 1. Then, in time of about 2¹²⁷ GOST encryptions, one can enumerate and check 2¹²⁸ candidates for the GOST key and identify the correct key.

Remark

The original paper [15] used the final step presented by Dinur, Dunkelman, and Shamir at FSE 2012 with time complexity of 2¹²⁸ GOST encryptions [12]. However, this can be reduced to an expected average of 2¹²⁷ GOST encryptions and still 2¹²⁸ in the worst case, at the price of more memory, see [5].

3.2. Technical Analysis of CANS 2012 Attack

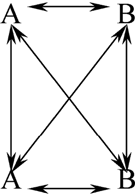
In this attack, the attacker observes that IF we have two symmetric fixed points, THEN we have the whole situation depicted in Figure 1, then the two symmetric fixed points also work for the whole GOST, and therefore they are visible to the attacker. However, symmetric fixed points of Enc_k() are not very likely to ever occur by accident, and in this attack we already study a property which occurs for a proportion of 2⁻⁶⁵ of all GOST keys. With the same probability, two symmetric fixed could have occurred also for the whole GOST, purely by accident, as they would occur for a random permutation. For this reason, the authors of [15] analyse the success probability of their attack in a very detailed way, though they are assuming that eight rounds of GOST behave as a random permutation, even though the present article will show that it does not behave as a random permutation. With this assumption, they arrive at a conclusion that if the whole 32-round GOST has two symmetric points, the Event 2 would occur with probability about 1/5 (and the other event which we ignore in this article with another 1/5).

Figure 1 Two symmetric fixed points, a.k.a. Event2 in [15].

In this article, we will show that most likely, and at least for the default sets of GOST S-boxes [23], the basic event occurs with higher probability than expected for both eight and 32 rounds of GOST. Therefore, the analysis of [15] is not at all what happens when their attack is implemented. Moreover, the nature of many events such as Event2 is to occur with two points A, B which are closely correlated in the sense that they have many shared bits. This is a very serious problem: Actually, it is trivial to see that if we have 2KP for eight rounds of GOST, neither the FSE 2012 attack [12] will work, nor any of numerous weaker and stronger variants known from [6] can work at all. Each key bit is only used once in the first eight rounds of GOST, and the diffusion is very poor. If the two data points share many bits, then in the first few rounds, states of many S-boxes will be identical, and we just do not have enough information about these key bits from the information theoretical point of view. Substantially larger number of solutions means that the overall time complexity is going to be substantially larger.

It may seem that our observations totally “ruin” the attack from [15], and it should be possible to show that the attack from [15] does not work at all with probability close to 1 (i.e., it almost never works as described). However, our observations do not ruin the attack; it is still expected to work as predicted for roughly the same number of weak GOST keys. There will be many additional cases for which the attack fails or is much slower than expected which have not been anticipated by the authors.

More importantly, we are going to present a way to turn to our advantage these internal correlations inside GOST and high frequency of pairs and larger sets of points, as well as the fact that data in these points are strongly correlated.

It remains to study the frequency of double symmetric fixed points in GOST and then analyse all the consequences of these quite unexpected facts. Before that, we recall a seemingly unrelated differential property of GOST.

4. Truncated Differential Cryptanalysis of GOST

We consider the following standard situation that has been introduced [11] and further studied in [7, ⁹¹⁰¹¹]. Let Δ = 0x80700700 which mask has seven active bits out of 32. We denote by (Δ, Δ) a set of 2¹⁴ − 1 non-zero differences on 64 bits with up to 14 active bits. Then, following [9, 10], we have the following fact (Fact 3). We should note that in this article, it does matter a lot that this event is symmetric.

Fact 3. For a random permutation, there are 2⁷⁷ pairs with the input difference (Δ, Δ), and for a proportion of 2⁻⁵⁰ or an average of 2⁷⁷⁻⁵⁰ = 2²⁷ pairs, the output difference is also in the set (Δ, Δ). For eight rounds of GOST, we have about 2⁵² pairs which satisfy these differences (Δ, Δ) at both ends, cf. Figure 2.

Figure 2 Standard symmetric event with 14 active bits for eight rounds.

5. On Frequency of Symmetric Fixed Points in GOST

Fact 4 (Symmetric Fixed Points in GOST). For eight rounds of GOST and a random key, the probability that there is a symmetric fixed point is about 2⁻³³ and is expected to be the same for a random permutation. However, for the default set of GOST S-boxes, the probability that there are two symmetric fixed points sharing as many as 50 bits which will be the inactive bits in mask (Δ, Δ) (such events are depicted in Figure 3) is at least 2⁻⁶⁰ instead of about 2^{−2−64−50} for a random permutation. Consequently, at least for the default set of GOST S-boxes, Event2 of Figure 1 occurs with key density of at least approximately d ≥ 2⁻⁶⁰ over GOST keys.

Figure 3 Two related fixed points for eight rounds (each pair has the same 50 bits).

Justification: We provide a method to estimate this probability. Let A′ = ℰ(A) and B′ = ℰ(B). Following [10], eight rounds of GOST, there are 2⁷⁷ pairs with the input difference of type (Δ, Δ), and for a proportion of 2⁻²⁵ of them, which is 2⁵² pairs A, B on average, the output difference is also in (Δ, Δ). This for the default set of GOST S-boxes.

Our computer simulations show that when the propagation occurs, the entropy of A ⊕ B is low, and the probability that A ⊕ B = A′ ⊕ B′ is only about 2⁻⁹. Furthermore, A = A′ with probability 2⁻⁶⁴, which also implies B = B′. Furthermore, A is symmetric with probability 2⁻³². Since their difference lies within (Δ, Δ), which is symmetric, B is symmetric with probability at most 2⁻⁷. Overall, for a proportion of d = 2^{52−9−64−32−7} = 2⁻⁶⁰ of GOST keys, we have two symmetric fixed points A, B sharing the same 50 bits.

Remark 1

This is higher than what we would get for having just two symmetric fixed points without any extra condition, which is roughly about 2⁻²⁻⁶⁴ for a random permutation. This is because two fixed points would occur with probability of (1 − 2/e) ≈ 0.26, and each would be symmetric with probability 2⁻³². We refer to [2, 19] for related research and fundamental facts on fixed points in random permutations.

Remark 2

So far, this reduction in probability was only demonstrated for the default set of GOST S-boxes. However, this is a conservative estimate with just one mask (Δ, Δ). These probabilities must be added for different masks, and in real life, this probability should be even higher (!). We also expect very similar results for other sets of S-boxes.

6. CANS 2012 Attack in the Multiple Key Scenario

In order to grasp all the implications of Fact 4, we must consider not only the attack from [15], but also a particular adaptation of this attack which we have personally suggested to the authors, and which is already described very briefly inside the paper [15]. However, it is safe to say that nobody has realized all the implications of this variant and its extensions.

Fact 5 (Event2 Attack in the Multiple Key Scenario). If we have a diverse population of at least 2⁶⁵ different 256-bit GOST keys generated at random, with access to 2³² CP per key, one can recover one of these 256-bit keys in total overall time of at least 2¹³¹ GOST encryptions for the default set of GOST S-boxes. For other S-boxes, the complexity is expected to be lower, about 2¹²⁹ GOST encryptions.

Justification: This attack requires that some 2⁶⁵ devices with random keys exist. It is possible to see that for a proportion of about 2⁻⁶⁵ keys, the first eight rounds are expected to have two symmetric fixed points in the same way a random permutation would have one. This is strictly following the calculations of [15], and because this event occurs at random, A, B are not expected to share many bits. Therefore, the final step on 2 KP is likely to work as predicted with the running time of 2¹²⁸ or maybe even 2¹²⁷ GOST computations [5, 12].

However, a truly remarkable thing happens with keys which are not weak. Such cases are basically “visible” to the attacker. He can reject them at a very low cost. There is no need to run the whole attack in 2¹²⁷ for a majority of the keys. This is true because for a random permutation, the probability that Enc_k() has two symmetric fixed points A, B is low, even though it is not as low as we initially thought. There is no need to run the attack 2⁶⁴ times. We only must to run the attack about 2⁶⁴⁻⁶⁰ times, only for the 2⁻⁶⁰ of cases predicted by Fact 5.

For all except a proportion of about 2⁶⁴⁻⁶⁰ GOST keys, we can reject them right away. We have 2⁶⁴ different keys, and we check them for two symmetric fixed points in time of about 2³² each, which will be very small compared to the dominant term in the attack. With 2⁶⁴ different keys, two symmetric fixed points will occur only a few times (2⁶⁴⁻⁶⁰ is expected). Therefore, the complexity of the whole attack is at least 2^127+64−60 = 2¹³¹ GOST computations to recover one key, and possibly more (this is if the probability in Fact 4 is even higher). Later in this article, we will show how to benefit from the fact that GOST has more symmetric fixed points than expected, which is a problem in this attack.

For other sets than the default set of GOST S-boxes, we are not aware of a similar reduction in probability of having two symmetric fixed points; it is expected to be the same as for a random permutation. Then, the analysis of [15] applies. We expect that Enc_k() has two symmetric fixed points with frequency about five times bigger than the frequency that Event2 occurs, and we expect to run our attack maybe five times and get the complexity of at least 2¹²⁷⁺² = 2¹²⁹ GOST computations.

7. Approximate Fixed Point Bicliques

In this section, we introduce a new concept which is essentially an invariant affine space common for many encryptions at both sides and also an approximate invariant property:

Definition 7.0.1. (An approximate fixed point biclique)

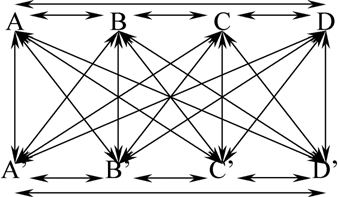
An approximate fixed point biclique with k points and dimension D and for r = 8 rounds of GOST is defined as a set of k + k values A, B,… and A′, B′, … , such that A′ is the encryption of A after eight rounds and so on (Figure 4), and such that all these k + k values lie in the same affine space of dimension D.

Figure 4 An approximate fixed point biclique with k = 4.

This is different from bicliques studied in cryptanalysis of AES [4], as our bicliques occur for one single key, and multiple connections on the graph mean that each pair is similar in the sense it shares a common substring of 50 bits.

We have discovered a new form of approximate self-similarity of GOST which happens to occur in the real life. For example, for one set, we can have four input points (k = 4) and four output points which share some fixed set of 50 bits, so that D = 14, and that for every arrow in Figure 4, the 50 bits in question are the same. This can be seen as a higher order truncated differential property. Surprisingly, this occurs for GOST and 256-bit keys generated at random with a non-negligible probability. The key observation is that (as we will see later) the number of such events with three or four points is not much lower than the number of events with two points.

7.1. Approximate Fixed Point Bicliques for Eight Rounds

We can remark that we are looking at a relatively strong property, and sets of points which satisfy it are unlikely to exist for many more rounds of GOST or for a random permutation. However, the internal structure and poor diffusion inside GOST allows many sets which satisfy the Definition 7.0.1 for some k.

Fact 6 (A 2/3/4-point approximate fixed point biclique for eight rounds of GOST and D = 14). For a typical GOST key, we have on average 2² possibilities for the set of four points A, B, A′, B′, such that A′, B′ are the encryption of A, B after eight rounds, AND which have differences with up to 14 bits and all the points A, B, A′, B′ share the same set of 50 bits, following the pattern using the mask (Δ, Δ). For the default set of GOST S-boxes [23], for a proportion of at least 2⁻⁸ of GOST keys, there exists a set of 50 bits and a set of six points A, B, C and A′, B′, C′, such that A′ is the encryption of A after eight rounds and so on, and which have differences with up to 14 bits and share the same set of 50 bits. For another proportion of at least about 2⁻⁹ of GOST keys, there exists a set of 50 bits and a suitable set of eight points A, B, C, D and A′, B′, C′, D′, which again pairwise correspond to each other and after 8 rounds all share 50 bits as depicted in Figure 4.

Justification: We consider the affine space of D = 14 defined by the popular mask (Δ, Δ), cf. [7, ⁹¹⁰¹¹]. It is possible to observe that for one encryption A, A′ for eight rounds of GOST, if A ⊕ B ∈ (Δ, Δ), then if A′ ⊕ B′ ∈ (Δ, Δ) with probability 2^−25.0, cf [7, 9, 10]. There is about 2⁶⁴⁺¹⁴/2! ≈ 2⁷⁷ couples A, B with suitable input differences, then with probability 2⁻²⁵ for one pair we have the correct output difference A′ ⊕ B′. Furthermore, then common 50 bits are the same for the input and for the output with probability 2⁻⁵⁰. Thus, we expect that there are on average about 2^77−25−50 ≈ 2² pairs which share a fixed 50 common bits.

For k > 2, the existence of such configurations can be seen as a simultaneous higher-order truncated differential attack with three or four points, respectively. As above, if A ⊕ B ∈ (Δ, Δ), then if A′ ⊕ B′ ∈ (Δ, Δ) with probability 2^−25.0, cf. [7, 9, 10]. Then if A, A′ and B, B′ are the suitable pairs for eight rounds, it is easier to find more such pairs C, C′. Our computer simulation shows that now if C ⊕ A ∈ (Δ, Δ), then C′ ⊕ A′ ∈ (Δ, Δ) with probability of only about 2⁻²² instead of 2^−25.0. In the same way, there will be a fourth pair D, D′ with even better probability of about 2⁻¹³.

There are about 2^64+14+14/3! ≈ 2^89.4 triples A, B, C with suitable input differences, then with probability 2⁻²⁵ for one pair we have the correct output difference A′ ⊕ B′, and then the third point also has the same 50 bits with probability of only about 2⁻²². Thus, we expect that there are on average about 2^{89−25−22−50} ≈ 2⁻⁸ triple points which share a fixed 50 common bits.

In the same way, there are about 2^64+14+14+14/4! ≈ 2^101.4 quadruples A, B, C, D with suitable input differences, with probability 2⁻²⁵ for one pair we have the correct output difference A′ ⊕ B′, and then the third point is correct with probability of only about 2⁻²², this multiplied by 2⁻¹³ for the fourth point and finally by 2⁻⁵⁰ for the 50 bits on both sides being equal. Thus, we expect on average about 2^{101−25−22−13−50} ≈ 2⁻⁹ quadruple points which share a fixed 50 common bits and have differences with up to 14 bits as depicted in Figure 4.

7.2. Real Life Events

It is difficult to guarantee that the events which we study really happen as predicted. For example, it is very surprising to see that events with four points will occur more or less as frequently as events with three points. To validate this, we have tried 2³⁹ encryptions for eight rounds with random keys an initial random difference with 14 active key bits within (Δ, Δ), and if after the eight rounds the final difference was also within (Δ, Δ), then we count how many other plaintexts with the same 50 bits also produce the same 50 bits as the two cases. In our simulation, we have seen exactly 21 events with four points and also exactly 21 events with four points with random keys and random 50 bits.

Example: We exhibit one event with four points from our simulation. This event was generated strictly at random and has no special properties other than those which might occur naturally at random for such events. The data are self-explanatory.

8 rounds 4 points 50 inactive bits 8070070080700700key = C4EEEC4D9FC4A3C55DB81B7BEE470567396682007AE8D9B59E3FD9A3225BC7B4 P = 6492F05231436EBF E4D2F152317368BF 64D2F452B14368BF E492F552B1736EBF C = 89C3449606C28E22 09C3409606C28F22 89C3409686A28822 09C3449686A28922

8. On Triple and Quadruple Symmetric Fixed Points in GOST

We have established that multiple approximate fixed points occur with probabilities higher than expected. In this section, we look at a special case: triple and quadruple symmetric fixed points.

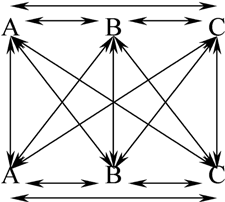
Fact 7 (Frequency of Triple and Quadruple Symmetric Fixed Points). For the default set of GOST S-boxes [26] the probability that for eight rounds there are two symmetric fixed points sharing as many as 50 bits, as shown in Figure 5, is at least 2⁻⁶⁰ instead of about 2^{−2−64−50} for a random permutation.

Figure 5 Triple fixed point (each pair is related and shares the same 50 bits).

The probability that there are three symmetric fixed points sharing the same set of 50 bits is at least 2⁻⁷⁰ instead of roughly about 2^{−4−96−50} for a random permutation. For four symmetric fixed points sharing the same set of 50 bits, it is at least 2⁻⁷⁹ instead of roughly about 2^{−6−128−50} for a random permutation.

Justification: Let A′ = ℰ(A) and B′ = ℰ(B) and C′ = ℰ(C) for eight rounds of GOST. Following Fact 6 for a proportion of at least 2⁻⁸ of GOST keys, there exists A, B, C such that all the six points share the same set of 50 bits following the mask 0x8070070080700700. The probability that A is symmetric is 2⁻³². Then, the probability that A = A′ is 2⁻¹⁴. Then, the probability that A ⊕ B = A′ ⊕ B′ and simultaneously A ⊕ C = A′ ⊕ C′ is maybe about 2⁻¹⁶ due to low entropy of these differences, which we have experimentally tested. Overall, for a proportion of at least d = 2^{−8−32−14−16} = 2⁻⁷⁰ of GOST keys, we have three symmetric fixed points A, B, C sharing the same 50 bits.

In the same way, for a proportion of maybe d = 2^{−9−32−14−24} = 2⁻⁷⁹ of GOST keys, we have four symmetric fixed points A, B, C, D sharing the same 50 bits. These are rough estimations, and they require further research.

Remark 1

This is much higher than what would get for having just 3/4 symmetric fixed points without any extra condition, which is roughly about 2⁻⁴⁻⁹⁶ or respectively 2⁻⁶⁻¹²⁸ for a random permutation.

Remark 2

Again, this reduction in probability was only demonstrated for the default set of GOST S-boxes. However, this is a conservative estimate with just one mask 0x8070070080700700, and these probabilities get higher if we take into account other masks. We expect similar results for other sets of S-boxes.

Remark 3

Again, symmetric fixed points for eight rounds also symmetric fixed points for the full 32-round GOST [14, 15], and in what follows, we will use them to propose a remarkably efficient attack on full GOST. We skip a triple symmetric fixed point attack and go directly for the quadruple point attack.

8.1. Quadruple Symmetric Fixed Point Attack

We call this attack Family 8.4 attack in order to honor the numbering of various weak key classes from [5].

Fact 8 (Weak Keys Family 8.4 Attack). We define the Weak Keys Family 8.4 by keys such that there exists four symmetric fixed points A, B, C, D for the eight rounds ℰ(). With the default GOST S-boxes, this occurs with probability of at least d = 2⁻⁷⁹ over the GOST keys. For every such key given 2³² CP, we can obtain four P/C pairs for eight rounds of GOST, correct with probability close to 1, and we can recover the key given 2³² CP, with running time of 2⁹⁹ GOST encryptions and with negligible memory.

Justification: We get d = 2⁻⁷⁹ by applying Fact 7. The four pairs are then ℰ(A) = A, ℰ(B) = B, ℰ(C) = C, and ℰ(D) = D. We cannot just apply one of the attacks from the recent Cryptologia 2013 article [8] in 2⁹⁴ GOST computations. This is due to the fact that our four points are closely related, and the attacks from [9] are not expected to work. However, it is possible to show that a variant of this attack in 2⁹⁹ GOST computations will work and that the system does NOT have too many solutions which would prevent the attack from working as in Section 3.2. The detailed description of the dedicated attack in 2⁹⁹ can be found in the Appendix of [5].

Again, we have a conversion step with early rejection of non-weak keys:

Fact 9 (Family 8.4 Attack for a Population of 2⁷⁹ Random Keys). If we have a diverse population of at least 2⁷⁹ different 256-bit GOST keys generated at random, with access to 2³² CP per key, one can recover one of these 256-bit keys in total overall time of about 2¹⁰¹ GOST encryptions.

Justification: We have an attack where given 2³² CP per device, namely the encryption of all symmetric plaintexts, the weak key becomes immediately “visible” for the attacker. The probability that a random 64-bit permutation has four symmetric fixed points is about 2⁻¹³⁴. Thus, for all except the correct device out of 2⁷⁹, we can reject this device right away after checking 2³² plaintexts in time of 2⁷⁹⁺³² CPU clocks, which is about 2¹⁰¹ GOST encryptions.

For the remaining one case, which we expect to be really our weak key with correct additional differences, we apply Fact 8 above, which gives about 2⁹⁹ GOST encryptions and negligible memory. Overall, we expect to recover one key in time of about 2¹⁰¹ GOST encryptions.

9. Conclusion

Symmetric fixed points for GOST and advanced differential attacks on GOST have been invented independently for very different purposes. One recent attack presented at CANS 2012 does not work as exactly predicted. This is due to the fact that pairs of fixed points in GOST exist with a probability lower than anybody would have imagined, and this is a problem in this attack.

In this article, We show that something even more remarkable happens with multiple symmetric fixed points: They exist for eight rounds of GOST with probability not slightly but very substantially bigger than for a random permutation. We get a very strong property and very robust internal correlations between these points, which are “visible” to the attacker. This leads to a remarkable new attack on GOST, which requires a totally unrealistic quantity of encrypted data. However, it would be feasible for an intelligence agency to execute such an attack in the near future if not today. Further analysis of this attack should show that the complexity can be even lower.

Additional information

Notes on contributors

Nicolas Courtois

Nicolas T. Courtois is a cryptologist and a Senior Lecturer at University College London. He was born in Poland, received his PhD from the Paris 6 University, and then he worked as a cryptographic engineer for the French smart card industry. He is a highly influential code-breaker with more than 100 regular publications and more than 6000 citations. He has pioneered and/or achieved significant results in all of the following areas of cryptography: Design and analysis of new public key cryptosystems (Sflash, Quartz, HFE), generalized linear cryptanalysis of block ciphers (Crypto 2004), cryptanalysis of LFSR-based stream ciphers with and without additional memory (Eurocrypt 2003, Crypto 2004, ICISC 2004), efficient algorithms for solving systems of multivariate equations (Eurocrypt 2000), innovative attacks on block ciphers (Asiacrypt 2001, AES'4), alternatives to Grobner bases algorithms (Asiacrypt 2001, FSE 2012), low-data complexity cryptanalysis of block ciphers with SAT Solvers (IMA 2007), self-similarity attacks on block ciphers with black-box reductions (FSE 2008, Cryptologia 2012), advanced differential attacks (SECRYPT 2009), and importantly, in security analysis of major industrial standards and real life cryptographic algorithms used by hundreds of millions of people every day (E0 cipher in Bluetooth, automobile cipher KeeLoq, MiFare Classic Crypto-1 in contactless smart cards).