On latin squares, invariant differentials, random permutations and historical Enigma rotors

Abstract

In this article we study the quality of permutations in historical cipher machines from Germany, Spain, Italy, Norway, Switzerland, Japan, Hungary, Croatia, Poland, Czechoslovakia, Russia and the United States. We show that numerous real-life rotors have been made in order to imitate or tend to a certain ideal property related to latin squares. Rotors from the same source and the same period have consistent properties deeply rooted in classical cryptography of polyalphabetical ciphers. We demonstrate this based on probabilities: random occurrence of permutations having such features is unlikely, or would amount to winning in a lottery several times in row. We put all this in the context of known historical sources on how cipher machines and cryptanalysis have developed on both German and Allied sides. We also exhibit strong linear and differential properties. The same occurs in Fialka cipher machines. Finally, a stronger property holds for the historical block cipher T-310.

Keywords:

• Enigma
• Fialka
• impossible differentials
• latin squares
• linear approximations
• permuted alphabets
• quasigroups
• rotor wiring
• weak keys
• T-310

1. Introduction

All works on cryptanalysis of Enigma known to the authors, from the 1930s until now, have assumed that rotors are just permutations and do not exhibit any particular weakness or internal structure. This was also what Hebern recommended explicitly in the 1920s. However, very clearly most rotors are NOT random permutations as we are going to show in this article. The main question we study here, is a form of reverse engineering of Enigma, which was previously studied very carefully by Rejewski in the 1930s and by Turing, cf. page 16 in Turing (1940). However we are asking questions deeper than recovering the connections of the rotors. We would like to know how a permutation inside a rotor was made or decided. A broader question is the design criteria for cryptographic components: how a long term cryptographic setup is generated, selected and approved for official use. In contemporary cryptology considerable attention is paid to the design criteria for block cipher functional components. Permutations implemented by the Enigma rotors represent a natural equivalent of these blocks, however we are not aware of any contemporary study of their selection process and security.

For block ciphers, this problem was carefully studied ever since the 1970s. For the Cold War T-310 block cipher there was a question of a “long-term key” cf. (Courtois, Drobick, and Schmeh 2018) and (Courtois et al. 2017) for more details. Likewise the question was studied for DES (cf. Courtois et al. 2003; Meyer and Vaudenay 2017) and later for AES etc. This question is however inevitably older. In this article we will show that many historical cipher machines already had carefully chosen components which do satisfy some properties, which make them systematically, substantially different than a random permutation. What is more, the difference is actually visible and detectable.

It is important to see that our problem is not quite the same as with block ciphers. We have abundant literature about how permutations in block ciphers (S-boxes) can be weak or strong. For example, some well chosen permutations such as the inverse S-box (Courtois 2005) were chosen to resist basic attacks on block ciphers, which is how the AES S-box has been chosen and standardised. More recently, a topic of non-linear invariant attacks have been popular among researchers, and the corresponding notion of anti-invariant resistance for bijective S-boxes was proposed by Calderini (2015, 2018). However the invariant resistance notions for permutations is natural and relative to the vector space structure of $I{F}_2^n,$ and the key in the block ciphers is about transforming affine spaces into other affine spaces. In rotor machines the key is applied by rotation of the rotor, which corresponds to +1 mod 26 without a rich multi-dimensional vector space structure. We therefore need to work in a different way.

The main research question, already studied in classical cryptanalysis literature in the first half of 20th century, was about encryption with multiple “permuted alphabets” cf. Section 7.1 in Bauer (2006). The main question we study here is what happens when you derive several encryption alphabets for different encryption keys. Then an ideal situation, is when different keys lead to totally distinct encryption letter, and we have a latin square. In this article we show that most Enigma rotors, for an unknown reason which almost certainly lies in classical cryptanalysis, were chosen to approximate this ideal situation (which itself is hard to achieve cf. Section 8.3). In addition, we show that some rotors have substantially stronger properties and rotors which come from the same source and the same period are similar.

This article is organised as follows. In Section 2, we study how engineering and later code breaking have shaped the devleopement of cipher machines in the early XXth century. In Section 3, we look in more detail at the development of cipher machines in Germany. In Section 4, we examine the history of various rotors used in known Enigma cipher machines. In Section 5 rodding attack, and in Section 6 we study how it works. In Section 7 we study one extremely strange old historical rotor. Then in Section 8 we show that most Enigma rotors ever made are concerned by a broader question of latin squares, and we discuss how we can measure the distance from the ideal situation and report some statistics computed for random permutations. In Section 9 we look at another famous rotor machine, Fialka. Finally, in Section 10, we will show that quite strangely a similar property was mandated, again, for a block cipher machine T-310, which was in widespread use in Eastern Germany in the 1980s.

2. Historical background on development of rotor machines

The history of electro-mechanical cipher machines starts towards the end of World War One. Earliest rotor ciphering machines have been proposed during and immediately after the end of WWI by several inventors working independently from each other. The first known attempt to construct a ciphering machine was undertaken in or around 1915, by two officers of the Royal Dutch Navy, Hengelo and Spengler (cf. Leeuw 2003). Although their nominal experience was focussed around the construction of the naval mines and torpedoes, their engineering skills proved to be sufficient for the construction of the ciphering machine. Initially, constructors cared primarily about reliable operation: speeding up the encryption tasks and making them less error prone, rather than about security. In parallel to their efforts, an American, Edward Hebern, started patenting a series of ciphering machines of growing complexity. Hebern’s initial idea back in 1912–1914 with US patent US1912682933A, was connecting two electrical typewrites with the mesh of reconfigurable wires. This yielded a simple monoalphabetic substitution, a cipher whose methods of breaking was known for about a thousand years (AlKindi frequency analysis). His next step - a single moving rotor between the keyboard and the printhead – improved the situation only slightly in 1921, with US Patent 1510441A. His machine was generating a polyalphabetic substitution cipher with a constant period equal to the length of the alphabet. The ultimate design of Hebern was US Patent 1683072A of 1923 granted in 1928. A machine with five rotors moving regularly in an odometer fashion. It increased the length of the period drastically. Compared to Enigma in Hebern cipher machines, the current was flowing just once and in one direction through all the rotors. Inside this patent, Hebern makes numerous claims about randomness and security of his machine. It allows complex movement with levers moving other wheel after full revolution, and several wheels could move simultaneously. Moreover he explicitly states that “each code wheel is wired at random and differently,” which is not quite what actually happened later when cipher machines achieved wider adoption, as we will discover in this article.

2.1. Engineering meets cryptography - United States

Hebern’s professional background was rather distant from cryptology: he was basically a carpenter who became a construction contractor. Hebern attempted to sell his machine both to the US Army and the US Navy, succeeding only marginally and in an indirect way. In 1922 Hebern built for his company a monumental two-storey Gothic building in Oakland, California. Yet for a few more years the company didn’t sell a single cipher machine. Hebern’s commercial offer was rejected by the US Army when its chief cryptologist, William Friedman, unknowingly to Hebern, cryptanalysed his cipher machine around 1922, (Simpson 2020), and this without knowing the wiring of the rotors. Maybe Hebern started too early: extremely few customers ever bought his cipher machines. Eventually the building was repossessed due to unpaid debt, and his glorious pioneering Electric Code Company business collapsed.

In parallel with business and engineering development of the rotor ciphering machines, these cryptographic innovations have attracted the attention of professional cryptographers of the time. Experts started to study the initial designs concentrating on security, rather than on commercial or engineering questions. Hebern did not know that the US military had decided, starting 1926, to re-develop his inventions (cf. Mucklow 2015). The goal was strengthening their security, however without his participation, and without paying him any royalties. It was only in the 1950s that his family managed to obtain, as a compensation for obvious violations of Hebern’s patent rights, a rather ridiculous or simply inadequate sum of 30 thousand US dollars.

2.2. Engineering meets code breakers

We see that cipher machines were developed by engineers and business people, and initially none of them had any direct or earlier contact with cryptology. Therefore, it is not surprising that some of their ideas were a bit naive, from the contemporary perspective. The commercial offer by Hebern was also rejected by the US Navy. Here again the (same) cipher was broken by Agnes Meyer Driscoll, one of the Navy’s leading code breakers of this era (Johnson 2015). Her success resulted in Hebern’s decision to employ Driscoll as a cryptologic consultant at his company, cf. Friedman 1973.

We should not under-estimate the importance of these early years of machine crypto history in 1920-1939. This is a period before designers have managed to complicate machines’ construction, or before the market would allow more complex and more costly machines to be developed, introducing complex irregular rotor movement (e.g. SIGABA) and additional wired substitutions in a form of a plugboard etc. We claim that only in this period certain fine questions about cipher design would be studied because code breakers had specific historical attacks in mind, and worked initially with ciphers which were not too complex and were breakable by manual methods. According to Driscoll (1889), for an extensive period of time from 1924 until approximately 1940 Agnes Driscoll worked on various Japanese codes and ciphers which were very important for the U.S. Navy. In October 1940, Agnes Driscoll was transferred to a team working on German naval Enigma. Here, according to Encyclopedia Britannica, she worked for two years in old fashioned ways, without mathematics, without machine support and without any success. Reportedly she refused help on Enigma from Bletchley Park code breakers, who travelled to US to advise her. It would be, in these early days of Hebern and Friedman, where ciphers were not yet very complex, an important line of defense, would a very careful selection of the permutations defining rotor’s wiring. That question represented a problem well known among the cryptologists of this period, as it appeared in a very similar form in the design of the classical (manual) polyalphabetic ciphers. A well known reference is the French de Viaris Attack cf. Section 14 in Bauer (2006) which was later studied and improved by Friedman. Marquis Gaëtan Henri Léon de Viaris was, after Babbage, the first scholar to use mathematics in cryptology as early as 1888 (cf. Bauer 2006).

2.3. Not random rotors after all

In this article we will discover that designers of German Enigma started to pay attention to the proper selection of the rotors’ substitutions also very early. Conscious of the existence of the letter frequency attack on the monoalphabetic substitution cipher, designers of the polyalphabetic ciphers attempted to achieve the possibly uniform letter frequency distribution in the ciphertext. One of the ways leading to that goal, was ensuring that the table of different encryption alphabets (corresponding to a polyalphabetic substitution) would represent a Latin square. This approach is directly applicable to the design of the rotor wiring. However a perfect latin square can hardly be achieved, as we will see later in Section 8.3. What remains is to approximate a latin square. In this article we will see that numerous historical Enigma rotors have such properties. We will also see that this is closely related to the so called “rodding” attack, which is how “everybody” has broken early rotor machines according to Batey (2008). We will see that Germany had serious crypto expertise, they were also breaking Enigma of other nations, and were well aware of its weak points. This is why they made their military Enigma a lot more complex than other countries (with a stecker) as early as 1930.

3. Machine cipher and crypto engineering in Germany

In 1918, a German engineer, Arthur Scherbius, filed a patent application for the device which was later to turn into the most famous cipher machine in history - the Enigma. Scherbius specialised in several disciplines of mechanical and electrical engineering, such as technical ceramics or control of water and steam turbines, and before patenting his invention he had no direct contact with cryptology. His apprentice and successor was Willi Korn. Initially Scherbius and Korn they worked at Gewerkschaft Securitas of Berlin, the original company of Arthur Scherbius. In some countries, patents were filed by the German Securitas, (later Chiffriermaschinen AG 1) whilst the same patent was filed in other countries by the Dutch Securitas branch. This was probably done to avoid claims that, after WWI, Germany wasn’t allowed to develop and produce certain high-tech equipment as part of the Treaty of Versailles. After the unexplained death of Scherbius in 1929, cf. page 114 in Bauer (2006), this company was officially dissolved and was taken over by another company known as Chiffriermaschinen Gessellschaft Heimsoeth und Rinke.

The development of Enigma rotor machines started with Hebern and commercial Enigma in the 1920s. Our brief review of known information about the inventors of the earliest rotor machines suggests that we should look at their creations primarily from an engineering point of view. They were concentrating on speed, reliability, portability and ease of use. Their complexity was not very high. We then see that the systematic study of these machines by cryptologists went a long away, with progressive development of powerful attacks. At no moment in the history of cryptology it is business as usual, and we have rarely run out of new disturbing discoveries. Even today, we are discovering new, weak points of Enigma cipher machines, as we will see below.

3.1. Engineering meets cryptanalysis again in Germany

In Germany, the development of Enigma cipher machines is attributed to Willi Korn, cf. page 114 in Bauer (2006). His name is very rarely mentioned by other German cryptologists, and the main source of information about his work and ideas are the numerous patents on cipher machines he filed in his name in 1926-1930. We also have the final product: numerous versions of Enigma machines themselves, see Section 4 below. Numerous documents state very clearly that Korn had for a very long time collaborated with Wilhelm Fenner cf. (Alvarez 2007) and (“Further interrogation of” 2017). Fenner had worked in decryption of foreign communications since 1922 and was later director of cryptanalysis section of the Signal Intelligence Agency of the Supreme Command German Armed forces, commonly known as OKW/Chi (Alvarez 2007). He reported to Rudolph Schmidt, major of the general staff.

Willi Korn was the chief engineer at Heimsoeth&Rinke, based in Berlin, and continued working there until at least 1942. Design decisions made by Korn in early periods of Enigma development have had serious adverse consequences. Korn is responsible for the invention and introduction into Enigma construction of the reflector (Umkehrwalze). A reflector is a brilliant way to use the permutations of the rotors twice and therefore we could (very naively) believe that Korn’s Engima with one reflector and three rotors has as much (apparent) complexity as a Hebern-type machine with seven rotors. Reciprocity between encryption and decryption also somewhat simplified the machine’s use. However this comes at the price of two fundamental cryptographic weaknesses: permutations generated belong to a substantially smaller set of self-reciprocal permutations (a.k.a. involutions), and the fact that a letter does not encrypt to itself. Thus, every single of multiple alphabets generated by an Enigma machine is an involution without fixed points. For some years prior to 1939, Fenner operated a small section with Fritz Menzer, where the security of their own Enigmas was studied (Army Security Agency 1946). Fenner said that Menzer indicated the possibility of a solution and made suggestions for the necessary improvement on Engima cipher machines (Armed Forces Security Agency 1950).

3.2. Short history of German Enigma with a stecker

A crucial question is one of adoption of Enigma with a stecker for military use. Starting from 1925 the German Reichsmarine started experimenting with Enigma C, without a stecker (Figure 1). Then it seems that Germany decided to make these machines more complex and more secure. In the Reichswehr, another model, Enigma G, was introduced in July 1928 by Major Rudolf Shmidt. It had a relatively complex rotor movement for that time (with multiple rotor turn-overs) but it did not have a stecker. Even though according to cryptomuseum.com there existed historically one version of Enigma G with a stecker, there is no evidence that such machines were actually used. One version of Enigma G, also without a stecker, is now commonly known as the Abwehr Enigma.

Figure 1. A military Enigma with a stecker.

On 1 June 1930, the German army introduced another different Enigma machine, with simpler odometer-like rotor movement (a.k.a. cyclometric method) and with a stecker. This machine is known under the name of Enigma I of the Heer, Wehrmacht Enigma, German military Enigma or Service Enigma. It is also known under later names of M1, M2 and M3 which were in fact successive compatible versions produced in large quantities. In 1934 the Reichswehr also finally agreed to accept this same Enigma as a common version, as it was necessary for different armed forces to communicate with each other. In August 1935, the same Enigma was also adopted by the Luftwaffe (Bauer 2006).

4. Short history of enigma rotors

From available sources, we assume that work on the exact wiring of Enigma rotors was done by the main historical Enigma developer and serial inventor Willi Korn, known from numerous patents on Enigma cryptography from 1926 to 1930. Some important information can be found in post-war TICOM interrogations of two German cryptologists Dr. Huettenhein and Dr. Fricke which occurred on 25 August 1945 and declassified in 2017 (cf. “Further interrogation of” 2017). The crucial question of who made the wiring of various Enigma rotors, was then asked explicitly, on behalf of Mr. Friedman of the NSA himself, who as we know was involved in development of rotor machines since the very beginning. Dr. Huettenhein responded that Willi Korn was the principal person who developed the machines, in collaboration with Fenner, and that they were based in Berlin in Uhlanstrasse. The wheels for the army and air were made by Konsky&Krüger, in Chausseestrasse, Berlin, a small firm which probably made only Enigma machines. The naval machines were made by Ertel in Munich. Some other non-specified machines were also made by Olympia typewriter company in Erfurt, which later also made variable-notch rotors (Lueckenfuellerwalze).

In early 1930s the army released for use by Enigma operators only three rotors I, II, and III. On 15 December 1938, two more rotors were added, IV and V. In 1938, the Heer (German navy) added three more rotors, VI, VII and VIII. The British recovered rotors VI and VII from the crew of U-33 in February 1940, while rotor VIII was captured in August 1940 (cf. Erskine and Enigma 1988). Two more new wheels known as Beta and Gamma, were introduced for the naval Enigma M4 model only, on 1 July 1943, see page 4 in Bletchley Park (1944). Then, maybe surprisingly, all these rotors remained in active use until 1945: probably because it would have been too costly to replace them, and also because the machine was overall considered to be very secure. In fact, Germany was very careful as to make Enigma substantially stronger with a stecker, which most other countries did not have, not even in 1945. The complexity of a stecker is very high, equivalent to as many as 47 bits of entropy. This led to a high cost of decrypting Enigma communications by Britain during WW2, which was without any doubt enormous.

4.1. Recovering the Enigma rotor wiring by code breakers

One rotor in Enigma could be a permutation chosen uniformly at random. There are 26! possible wirings for one rotor, therefore the entropy of one rotor is about 88 bits. For this reason recovering the unknown rotors was a big challenge. These rotors could have been obtained from some sort of “pinch” on German military equipment, or provided by a spy or a traitor. However, as far as we know, this did not happen. We know that the French had a spy in the German Armed Forces’ Cipher Office, Hans Thilo-Schmidt, and who was the brother of Rudolf Schmidt mentioned earlier. This spy provided operation manuals, genuine examples of plaintext, ciphertext, and some keys used in realistic circumstances. He also provided countless other documents not directly relevant here, including documents about 14 French diplomatic codes broken by German code breakers. A total of 285 or maybe 303 documents depending on the source (Dumas 1997). Out of these, exactly 10 are technical documents on Enigma cipher machines (cf. Bouchaudy 2021). However, he NEVER transmitted to any allied intelligence service, the actual connections of any of the Enigma rotors. It is therefore logical to believe that Hans Thilo-Schmidt was a spy trying to do only limited harm, and it is difficult to agree with the title of Kahn (2009) if we limit ourselves to Enigma. The information transmitted (sold for large sums of money) was without doubt valuable and had serious short term benefits (learning about the machine such as decryption with known keys). However he did not do everything which was in his power to help the foreign intelligence services to defeat Enigma (which are supposed to be strong even it falls into enemy hands according to famous Kerckhoffs’ principle). From this information, a Polish mathematician Marian Rejewski was able to reverse engineer Enigma rotors by mathematical techniques (Lawrence 2005) in the early 1930s. It is also possible that the fact that only 10 documents were about Enigma, simply means that the French intelligence have under-estimated the importance of Enigma cipher machines back in early 1930s, and simply did not ask their agent to provide more information about them.

The methodology to recover unknown rotors was through study of mathematical theory of permutations, and specifically, through solving the set of so called Rejewski equations which have later been studied by Lawrence (2005). The fact that this task was actually possible to do, was much later called by David Kahn “the greatest breakthrough in cryptanalysis in a thousand years.” In Kahn (2009), David Kahn wrote: “Poland had greater cryptanalytic ability […] only one of the three to employ mathematicians […] and only mathematics could make it possible to reconstruct the Enigma rotor’s internal wirings.” This information and some actual rotors and actual complete working clones of military Enigma cipher machines produced by a secret factory at a company known as AVA in Poland, was then shared with the French and the British intelligence services. It is worth noticing that Alan Turing has also studied in depth the question of recovering the rotors of Enigma. This precise question occupies very substantial space in his book (Turing 1940) starting from page 16. Alan Turing worked with the so called “boxes” formed by showing the cyclical structure when composing two involutions without cycles. In page 17, Turing says that both involutions can be recovered from “boxes,” or in effect that such permutations can be uniquely factored. Turing does not say where this fact comes from. In fact it is a well-known theorem of Rejewski, cf. Section 13.8 in (Courtois 2011), Section 3 in (Rejewski 1940), and pages 9–10 in (Pommerening 2008). A recent paper shows that it is an imperfect method with some difficulties (Kuhl 2007).

4.2. Rewiring and peripheral smaller scale or late adoption

Copies of commercial Enigma were sold or donated to a number of countries such as Switzerland, Hungary and Japan, many of which made a seemingly reasonable decision to rewire their rotors before use. Intelligence service of Norway, which have been using seised military Enigmas for some time after the end of WWII, made a similar decision. we discovered, however; that cryptologists of these countries typically understood their security at a lower level than their original designers. Our research below shows that these rewired machines such as in Norway Enigma represent lower quality substitutions than the rotors selected for German military use, see our later Table 1. German cryptographer Buggisch testified that Germany equipped Hungary, Finland, Romania, Italy and Japan with a more secure military Enigma (cf. TICOM/I-9292 1945). He also clearly says that they deliberately supplied less secure machines without a stecker to Croatia, fearing they would be selling information to the British. Rotors for the Croatian Enigma were made by Konsky& Krueger in Berlin. From here German code breakers were able to know their connections from the start, and they decrypted Croatian army communications extremely easily (cf. Christos 2017). Buggisch said very clearly that breaking Croat Enigma was “not an outstanding cryptanalytic achievement.”

Table 1. Collisions and entropy of one column for selected historical rotors.

Rotor name	Nb.	Code	Dates	Ims	Ent
Army I	1	EKM	1930	17	3.95
Army II	2	AJD	1930	19	4.16
Army III	3	BDF	1930	20	4.21
Army IV-VIII	4–8		1938-39	23/24	$\ge$4.47
Railway I-III	12–14		1941	23/24	$\ge$4.47
Japan/Tirpitz	37–44		1944	23–25	$\ge$4.47
Mil Amt KD I-III	34–36		1944	24	4.55
Zagreb 16081 I-V	62–66		1943	22–25	$\ge$4.36
Hungary G-111 I, II, V	67–69		193X	23–24	$\ge$4.44
11 Spanish rotors from [Fuensanta, López-Brea Espiau, and Weierud 2010]	51–61		194X	21–24	$\ge$4.32
Norway I,I,III,V	20–22,24		1945	13–16	$\ge$3.46
Swiss Airforce I-III	17–19		1938	16/17	$\approx$3.85
U.S. SIGABA rotors 1-10			1941	15–18	$\approx$3.9

4.3. Weak German rotors and mystery questions

In addition, it is impossible to claim that all German Enigma rotors are OK. The first three from early 1930s are clearly not OK. In this article we show that the old rotor III in the original, military Enigma model I (common with the Kriegsmarine’s models M-3 and later M-4) is very special and clearly weak. Isolated nature of this phenomenon prevents us from drawing solid conclusions from our findings. It seems unlikely that the particular structure of this rotor’s wiring alone translates directly into a serious weakness. All our findings are simply and primarily a reflection of the cryptographic expertise which existed at the time. It seems that almost nobody (except for Swiss and Norwegian Enigma and U.S. Sigaba cipher machines) followed the recommendation of Hebern about using rotors chosen at random.

This question remains very important until today in modern cryptography: for example when AES/Rijndael was designed in late 1990s, many authors suggested using a random permutation on 8 bits, which is not at all what the designers did. There exist numerous contemporary works which examine the choice of cipher components à posteriori, looking for hidden properties (cf. Courtois et al. 2003; Courtois et al. 2015). We discover that there exist, permanently and since the 1920s, two schools of thought in cipher design: random permutations and relying on complexity of the cipher, since Hebern, or a more refined study of properties of small components (rotors, S-boxes, Boolean functions) and specific (strong) choices which are very far from being random. This dichotomy was very clearly visible in the AES cipher competition in 1997–2000. In many cases, no one can say if some weakness can or can not be compensated by more rounds in a block cipher, or by more rotors in a rotor machine. For example the Russian Fialka machine has as many as 10 rotors, yet the rotors are certainly not random permutations, see Section 9. Can a combination of 2,3,…10 such special rotors be distinguished from a random permutation? Can such a combination be factored in order to recover individual rotors? New attacks are found in cryptography on a regular basis and these questions need yet to be studied.

4.4. A permutation impossible to recover unless… it is trivial

A major difficulty is to simply obtain some secret permutation used inside an enemy encryption system. We need to realise how difficult this question can be, well in theory. One famous permutation which code breakers at Bletchley Park did not have was the famous QUERTZU question, which Turing called the diagonal and the question of recovering it is also studied in Turing (1940). Initially, not knowing how keyboard was connected to the machine, Dilly Knox was effectively discouraged to ever try to break German military Enigma, and initially has studied this question as a theoretical one. Until 1937, Britain was essentially not trying to intercept and collect encrypted messages actually transmitted by the German army (Batey 2008). A serious obstacle, which was completely impossible to just guess, there are 26! possibilities, which is an extremely large number, about 2${}^{88}.$ Dilly was shocked when Polish code breakers told him in Pyry in 1939 that this initial super secret permutation was actually that A was connected to A, B to B etc.

If we study this question from the point of view of one rotor, the question of the initial permutation does not seem very interesting, it amounts to renaming a metallic contact called Q to be now called A, etc. In this article we show some surprising facts: Enigma rotors have NOT been generated at random and they are NOT agnostic w.r.t. the order in which contacts are named. One old German military Enigma rotor reveals a hidden property when we name contacts in the alphabetic order, a property which could be overlooked if we name the contacts differently, and was probably overlooked, as we are the first to show this property. First however, we need to study a well known old attack on Enigma.

5. Rodding attack or undoing the effect of the fast rotor

Officially, the rodding attack was known and studied in Bletchley Park around 1935, and is typically and attributed to Dilly Knox. However, this attack is almost certainly older. According to Batey (2008) who worked for and under direction of Dilly, “everybody who tried cryptanalysis of the commercial Enigma machine arrived at the rod solution.” This attack was basically known to many other intelligence services worldwide, including France and probably the US. It actually had a French name, Les Bâtons and few other names such as Strips or Isomorphs. Since 1935 French and British intelligence services had collaborated very closely on monitoring and decryption of Italian Enigma traffic in the Spanish Civil War. Another name for this attack is the Method of Isomorphs and it was made public in 1946 by a New York-based cryptography lecturer Rosario Candela (cf. Bauer 2006). However, strangely the attack was not known to Rejewski in Poland in 1939, Good & Deavours 1981. We are also nearly certain that this attack was known in Germany. According to page 281 in Bauer (2006) knowledge of this attack was the MAIN reason for the introduction as early as 1930, of the stecker in military Enigma machines.

An interesting question is that the rodding attack is relatively simple and it can be implemented in many different ways, with sticks, paper strips, or 26 × 26 squares known as rod square and inverse rod square in Alan Turing Prof’s Book (Turing 1940). From available sources (Foss 2001), we learn that even though Dilly Knox purchased a commercial Enigma in 1925, and Foss had in 1929 already understood that it was breakable with a crib, Foss has later admitted that his earlier methods were “cumbersome” and Foss attributes the invention of a more practical method, the rodding method, to Dilly (Batey 2008). Here, the date of this invention is very far from being clear: it could be at any moment between Foss’ report from 1929 and April 1937 when Knox was already able to break into Italian-Spanish Enigma traffic (Batey 2008). This was not without an additional difficulty: the rotor connections were also to be recovered in the process. Overall, reading Batey we are inclined to believe that the date when Dilly Knox would discover the rodding attack is closer to 1935 than to 1929. Some sources claim that Foss invented this attack as early as 1927 (Bauer 2006), maybe in some early form. Trying to reconcile these conflicting sources with what we discover in this article, we are in fact inclined to believe that this attack could be known in Germany as early as 1930, and possibly before it was known in England or in France. If Germany did not study this very major weakness in Enigma, why would they have made the stecker mandatory as early as 1930? The answer could be because the attack was known, which is also claimed in page 281 of Bauer (2006).

5.1. Germany against Engima type K without a stecker

Another serious argument to support this claim is that according to various sources, both Germany and the United States were able to break into Swiss WW2 Enigma traffic, reading it, pretty much throughout the war and until 1945. Swiss Enigma was of type K without a stecker and operating procedures were not very strong (cf. Jennings 2018). The same applied to Germany reading the messages encrypted with the Croatian¹ Enigma which was also of type K without a stecker cf. Section 4.3. This was reportedly extremely simple and done by hand, with “wiring charts” and with short cribs (TICOM/I-9292 1945; Christos 2017).

Initially, at Bletchley Park, colonel Tiltman was able to read Swiss diplomatic traffic starting from September 1939 (cf. Hamer, Sullivan, and Weierud 1998). One source of information on solving Swiss Enigma in Germany is Army Security Agency (1946) where we read that a certain Lt. Kunze was Chief of Swiss substection at OKW/Chi in charge of decrypting Swiss traffic which “was regularly read” in Germany. Then, in 1942, machine was modified and later the Swiss traffic remained unsolved (cf. TICOM/I-200200 1946), at least at OKW/Chi. In fact, following a recent book by Jennings there was another specialist of Swiss Enigma traffic, Dr. Bruno Kröger, expert at Forschungsamt, a rival agency, who “worked hard to break the secrets of the Swiss Enigma” (Jennings 2018) apparently without any coordination with OKW/Chi. It is clear the Swiss did not use the machine correctly: initially large numbers of messages were encrypted with the same key (cf. Jennings 2018). According to Jennings, Swiss trafic was read longer, until early 1944 by Kröger and his team at Forschungsamt. They gave up on it after Swiss Enigma operators have updated their operational procedures to use a random key and change the order of wheels for each message, which made decryption too costly.

All the attacks mentioned above are expected to be close cousins of the rodding attack and took place in the 1940s. In this article however we hypothesise that this type of attack was studied already in early 1930s. We will argue that, while historical documents are scarce, certain claims are highly plausible based on probabilities, with a reference being a random permutation. This will be reinforced by observing that rotors which come from the same source behave in the same consistent way.

6. Rodding – various variants of the same attack

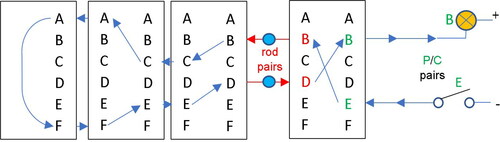
An important question is one of how the rodding attack can exist in many different conceptual forms with incompatible implementations (Figure 2). A certain pattern which will be visible in our implementation of the rodding attack, cf. Figure 3, will not be apparent in another implementation.

Figure 2. Rodding attack on Enigma without a stecker, a.k.a. “the method of isomorphs.”

Figure 3. A strange order of letters with old wartime rotor III, see Courtois 2020.

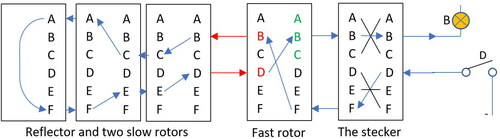
Our implementation of the rodding attack is simplified, and the same as the Method of Isomorphs using the so called “rotated Enigma alphabets,” cf. page 253 in Bauer (2006). It was initially designed as a student exercise during and after our annual Bletchley Park trip (Courtois, 2020) and our table is actually the same as displayed in page 126 in Bauer (2006), except that we do it for a different rotor. Rodding is about pairs of letters which occur at the border between the fast rotor and two slow rotors inside an Enigma machine, which following Dilly Knox and Alan Turing, we call “Rod Pairs.” cf. Def. 6.2 below.

We also work with “Rod Pairs,” however our version of the attack is actually greatly simplified and different from how this attack was traditionally² studied and implemented in Britain, which may seem more complicated. We will stick to the basic “mathematical” version³ of how the rodding attack works. It consists of creating some fixed tables, which allows us to then decrypt the plaintext and ciphertext letters one round backwards, to obtain possible rod letters. This partial decryption is attempted several times for each position of the fast rotor. In order to implement this we use a 26 × 26 table⁴ to represent all the possible ways in which the fast rotor can be decrypted 1 step forward from a plaintext letter or one step in the backwards direction after a ciphertext letter.

In each case, the attacker produces an ephemeral table of rod pairs for this encryption. In this table, assuming that the fast rotor is not moving, the same letters should give consistent answers. This process is further enhanced by using the fact this transformation is expected to be an involution. From here the attacker will typically obtain a contradiction very quickly after examining just a few letters and without recovering the whole mapping. A contradiction indicates that his initial guess about the position of the fast and rightmost rotor was incorrect. One short example of how this can be done can be found in Section 14.5.2 in Bauer (2006), another in Exercise 2 in Courtois (2020).

6.1. Rod letters, letter, number and rotor encoding conventions

We define, for the purpose of this paper:

Definition 6.2

(Rod Letter). We call a “Rod Letter” a letter corresponding to a wire active at the border between the fast rotor and 2 slow rotors inside an Enigma machine.

Remark.

This letter corresponds to a set 26 physical contacts inside a machine, where the current leaves one rotor and goes into another rotor. The same rod letter can have different names, for example the rotor contact we call A would be called Q in Prof’s book by Turing (1940). The situation is a bit simpler with numbers. Alan Turing has a convention to code letter Q with 1, the same letter which we call A will be denoted 0 in this paper: this is because we make extensive use of arithmetic modulo 26. In general if Alan Turing uses number k we should use k – 1 modulo 26. In reality however we end up using the same number, k, as Turing starts numbering relative to a different starting column, as explained below. Therefore at the end many numbers we use would be entirely compatible with work of Turing, except that we will not use number 26, it is replaced by 0 as we work modulo 26.

For rotor specification, we do in this paper use the same conventions as in 100% of modern works on Enigma known to us, cf. cryptomuseum.com, (Fuensanta, López-Brea Espiau, and Weierud 2010), etc. An interesting observation is that the original position where a wheel is assumed to start or not move (a base position or neutral position with i = 0 in this paper) is then bound to differ by 1 step compared with the work of Turing. In page 6 of Turing (1940) the description of the actual wiring of rotor start with a mapping of Q to Z or 1 to 6 for a Railway rotor. We recall the Enigma simulators such as https://cryptii.com/pipes/enigma-machine take into account the fact that in a real-life Enigma machine, the fast rotor rotates by one position and only then the first ciphertext letter is produced. This means that if an Enigma simulator shows AAZ in the window, and if the ringstellung is in a neutral position which is AAA, then the actual position of rotors used in encryption is AAA. If we compare how the Enigma rotor is typically described in modern sources, the Railway rotor is described by: $$\begin{array}{c}\text{ABCDEFGHIJKLMNOPQRSTUVWXYZ}\cdot \\ \text{JGDQOXUSCAMIFRVTPNEWKBLZYH}\cdot \end{array}$$

Which in our coding is 9,6,3,16 corresponding to output letters JGDQ, for input letters ABCD and in Turing coding the same rotor is encoded by 6,3,16, where the first number 9 will be shifted to the very end and this corresponds to output letters ZEJ for input letters QWE.

6.3. Notation and rotated alphabets

In this paper we denote by ρ a function which rotates the letters by one position, A becomes B etc. We identify 26 letters with numbers A = 0, B = 1, C = 2, etc. Then we also have ρ a function which adds 1 modulo 26. Now let R be a permutation of one rotor: $$R:Z{Z}_{26}\to Z{Z}_{26} \text{and} \mathrm{R}:\{\mathrm{A},\dots ,\mathrm{Z}\}\to \{\mathrm{A},\dots ,\mathrm{Z}\}$$ then at step i the transformation of this rotor will be (which needs to be read form right to left): $${\rho }^{-i}°R°{\rho }^i.$$

6.4. A first glimpse at rotor III

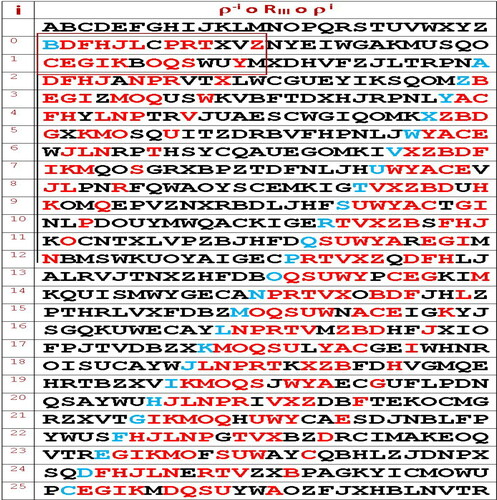
In this article, we show that a very strange order governs the connections of wartime Rotor III. A peculiar order seems to dominate in one corner of our table, and in particular for the first half of inputs A to M, i.e. $x=0\dots 12.$

There is certainly something not right here. This is an extremely strong property. The full pattern will be shown here below in Figure 4.

Figure 4. A proportion of 10/26 letters in colour is concerned by our property.

6.5. Permuted letter variants

An interesting question is why this property was not discovered before. A plausible explanation on why this property would not be by discovered by Turing, is that in his book, letters in an Enigma rotor were named not ABC like in the present article, but using an older QWERTZU ordering. The exact same Enigma metallic contact will the have a different name, Q not A, W not B etc. This is what Alan Turing advocates explicitly, as naming contacts the “Cryptographer’s” way. In addition, our table is very different than the “Rod Square” and the “Inverse Rod Square” tables studied by Turing and presumably defined earlier by Knox. Our table is more basic: all it does is to represent a list of rotated alphabets: effectively each line simply represents the wiring of our rotor, when it is moved to a different position. Therefore, it is possible that this extremely strong pattern we see here was simply not noticed at Bletchley Park during the war, because the columns would be permuted, or that rodding was primarily studied for a different set of rotors (e.g. Spanish/Italian rotors).

7. The full table of permuted alphabets for the original rotor III

In the table below, we write, in the first line the permutation of the military Enigma Rotor III. Then, below we write the permutation obtained where this rotor moves one step forward (which is anti-clockwise if we look at an Enigma machine from the right hind side). Likewise, for any $i=0..25,$ we display the same permutation when our rotor moves by one position. This is the same table as in page 185 in Ulbricht (2005) which computed the table for many different rotors, and in page 126 in Bauer (2006) where it was done only for Rotor I.

We recall that ρ is a function which rotates the letters by one position, with A = 0 mapped to B = 1 etc. We observe that the following affine approximation holds for all entries in colour:

Fact 7.1 (Linear Approximation). $${\rho }^{-i}°R_{\mathit{III}}°{\rho }^i(j)\stackrel{?}{=}i+2j+1={\rho }^{i+1}(2j \text{mod} 26) \text{with\hspace{0.5em}A}=0,\mathrm{B}=1,\hspace{0.5em}\text{etc}.\text{\hspace{0.5em}with} Pr=\frac{10}{26}$$

7.2. On linear cryptanalysis of Enigma

This is nothing else than a linear approximation, which is linear modulo 26, of an old Enigma rotor, presumably from 1930. Who says that linear cryptanalysis was invented in 1990s and was not known to the designers of DES? In fact linear approximations of non-linear cipher components were already studied in 1970s for the block ciphers SKS V/1 and T-310 (cf. Courtois, Oprisanu, and Schmeh 2018) and possibly it is even older. However we do not think that the way this property could or should be used in cryptanalysis will have a lot to do with linear cryptanalysis of block ciphers. This is because other components of our cipher do not have good linear approximations.

7.3. An important observation

It is easy to see linear approximation for our table will behave in a way which is a bit counter-intuitive. Indeed it holds for a large proportion of 26${}^2$ values not 26, for any i, j. How is this possible? Should not the probability be negligible for so many values? We have the following result:

Theorem 7.4

(Conjugation Property). Let a, b be two fixed integers. We fix i and we consider the probability (over all $x\in Z_{26}$) that we have: $${\rho }^{-i}°R_{\mathit{III}}°{\rho }^i(x)\stackrel{?}{=}(a-1)i+ax+b.$$

This probability is the same for every i, and for every j. Consequently, the number of coloured letters is the same in every line in our square, and also in every column, cf. Figure 4. This probability is also the same for every letter y where $y={\rho }^{-i}°R_{\mathit{III}}°{\rho }^i(x)$ is the letter displayed. Consequently, the number of coloured letters is the same for every letter.

Proof.

We prove the first result by induction on i, modulo 26 we can start from any point. We assume that ${\rho }^{-i}°R_{\mathit{III}}°{\rho }^i(x)\stackrel{?}{=}(a-1)i+ax+b$ for some i. We apply ρ on both sides and we replace x by $z-1={\rho }^{-1}(z)$ modulo 26, which is a bijective transformation: $${\rho }^{-i+1}°R_{\mathit{III}}°{\rho }^i({\rho }^{-1}(z))\stackrel{?}{=}(a-1)i+a(z-1)+b+1=(a-1)(i-1)+az+b$$ which gives us the same probability over $z\in Z_{26}$ for i − 1: $${\rho }^{-(i-1)}°R_{\mathit{III}}°{\rho }^{(i-1)}(z)\stackrel{?}{=}(a-1)(i-1)+az+b$$

We see that if we have k solutions x for one i, we can produce also k solutions z for i − 1. Moreover after 26 steps we can back to the same place so the number of solutions in this process cannot increase, it must stay constant for every i.

For the second column-wise invariance result we fix i and vary x. It is easy to see that ${\rho }^{-i}°R_{\mathit{III}}°{\rho }^i(x)=y$ is equivalent to ${\rho }^{-(i-1)}°R_{\mathit{III}}°{\rho }^{i-1}(x+1)=y+1.$ In each case where $y=(a-1)i+ax+b={\rho }^{(a-1)i+b}(ax)$ we have also $y+1=(a-1)i+ax+b+1=(a-1)i+a(x+1)-a+b+1=(a-1)(i-1)+a(x+1)+b$ which is exactly what we expect. Finally the last result, is due y rotating though all possible values in 2nd result, letter y being in coloured in column x was transformed into y + 1 also in colour in column x + 1. □

8. On ideal encryption alphabets or latin squares

8.1. Theory of permuted alphabets in classical cryptography

The classical cryptographic theory of encryption in the first half of 20th century was about multiple “permuted alphabets” cf. Section 7.1 in Bauer (2006) and (Eyraud 1953). It was about how multiple variations of one alphabet could be systematically derived from basic building blocks such as iterating certain permutations and transforming them by cyclical shifts. In Section 7.2.5 in Bauer (2006) the cardinality of the set of different rotated versions of the same rotors ${\rho }^{-i}°R°{\rho }^i$ is discussed, and it is observed that in small sizes, such as with $N\le 4$ elements, there are many events where some of these permutations could be identical. However, this type of event coincidences occur with a negligible probability for permutations with N = 26 letters.

8.2. Latin squares

We would like to propose a plausible explanation why the Rotor III has letters in order ABCDEFG in the first column. There is a very famous requirement in classical cryptography (Bauer 2006), which is that if we have a collection of 26 encryption alphabets, no character should repeat twice in each column. This property is also known as a latin square, or under the French name of “alphabets réellement non-parallèles.” In mathematics it is equivalent to the notion of a quasi-group, a topic which is studied extensively until this day.

According to Bauer (2006) latin squares were studied in cryptography since the 18th century (Bauer 2006). A definition of a latin square appears in the official Bletchley Park dictionary of cryptographic terms from 1944 (cf. Cryptographic Co-ordination and Records Section G.C. & C.S 1944). It also appears in page 51 in East german crypto dictionnary of 1971 (cf. Zentrales Chiffrierorgan der DDR 1971). They play an important role in optimising the diffusion P-box in DES, cf. page 58 in Brown (1991), and it has been a popular recreational mathematics topic ever since Euler. A few years ago during an international congress of mathematics the community discovered that in fact latin squares are yet older. A confucian scholar and Korean mathematician, Seok-Jeong Choi, published in year 1700 a work known as Gusuryak where he studied magic squares, and presents the first known orthogonal latin square of order 9 (cf. Sangwook 2014). This was at least 67 years before Euler has made this topic popular with European mathematicians.

It is easy to see that Enigma Rotor III does not satisfy this requirement, for example in the first column the letter K occurs three times for i = 9, i = 11 and i = 14. Moreover we also have an equivalent of Thm: 7.4 if we shift our values by 1, the probability distribution obtained is the same in each column in Figure 4, and if one column was a latin square, another would be. Given the state of cryptographic knowledge at the beginning of the 20th century, and the popularity of latin squares over the centuries, this fact alone should also be considered as a weakness in the spirit of classical poly-alphabetic cryptanalysis methods, cf. de Viaris Attack in Section 14 in Bauer (2006) later improved by Friedman.

Therefore cryptologists should in principle design a rotor such that this table is a latin square.

8.3. Can Table 4 for rotor III be a latin square?

This question is not obvious at all. In fact the requirement of obtaining a latin square for all permuted alphabets for a given rotor, seems an extremely difficult one. We have examined some 70 different historical rotors and also vast numbers of their combinations. We have never obtained a latin square in our table, not even in one case. This fact was already observed for Rotor I in page 138 of Bauer (2006) and the author also says clearly that we should not expect this to happen for other rotors either. Latin squares are hard to make, and there is a famous example of an almost perfect latin square by Mauborgne cf. Table 3 page 137 in Bauer (2006) which has three exceptions only and can be fixed by permuting three letters.

Table 3. Results for selected historical rotors.

Rotor name	Nb.	Code	Dates	Ims	Ent(R)	Imk	Possible differentials $k\to k$
Army I	1	EKM	1930	17	3.95	10	2,3,6,7,9,11,12,13
Army II	2	AJD	1930	19	4.16	17	8,9,10,11
Army III	3	BDF	1930	20	4.21	14	2,3,5,8,10,13
Army IV	4	ESO	1938	23	4.47	19	5,8,12
Army V	5	VZB	1938	24	4.55	23	5
Army VI	6	JPG	1938	24	4.55	22	6,13
Army VII	7	NZJ	1938	23	4.47	19	3,5,8
Army VIII	8	FKQ	1939	24	4.55	21	4,7
Hungary G-111 I	12	JGD	193X	24	4.55	22	2,13
Hungary G-111 II	13	NTZ	193X	24	4.55	21	6,7
Hungary G-111 III	14	JVI	193X	23	4.47	21	1,12
Naval Beta	15	LEY	1942	21	4.32	16	2,6,10,11,13
Naval Gamma	16	FSO	1942	20	4.24	19	6,9,11
G-310 Abwehr/G 316.58 I	28	DMT	193X	21	4.32	17	5,6,7,8
G-310 Abwehr/G 316.58 II	29	HQZ	193X	24	4.55	22	8,13
G-310 Abwehr/G 316.58 III	30	UQN	193X	24	4.55	21	5,10
G-260 Abwehr/NSA Mus. I	31	RCS	194X	23	4.47	21	4,7
G-260 Abwehr/NSA Mus. II	32	WCM	194X	23	4.55	23	6
G-260 Abwehr/NSA Mus. III	33	FVD	194X	23	4.55	21	6,10
Japan/Tirpitz I	37	KPT	1944	23	4.47	21	7,10
Japan/Tirpitz II	38	UPH	1944	23	4.47	19	5,6,11
Japan/Tirpitz III	39	QUD	1944	23	4.47	19	1,3,5
Japan/Tirpitz IV	40	CIW	1944	24	4.55	21	2,4
Japan/Tirpitz V	41	UAX	1944	24	4.55	22	10,13
Japan/Tirpitz VI	42	XFU	1944	24	4.55	22	6,13
Japan/Tirpitz VII	43	BJV	1944	25	4.62	24	13
Japan/Tirpitz VIII	44	YMT	1944	24	4.55	21	4,7
Zagreb 16081 I	62	CVF	1943	24	4.55	21	4,12
Zagreb 16081 II	63	XJG	1943	22	4.36	17	5,6,9,11
Zagreb 16081 III	64	SYI	1943	24	4.55	21	4,8
Zagreb 16081 IV	65	HKT	1943	24	4.55	21	4,6
Zagreb 16081 V	66	WMG	1943	25	4.62	23	9
Norway I	20	WTO	1945	13	3.46	5	1,3,4,6,7,8,9,10,11,12
Norway II	21	GJL	1945	16	3.80	6	2,3,4,5,7,8,9,10,12,13
Norway III	22	JWF	1945	15	3.66	6	2,3,5,6,7,9,10,11,12,13
Norway V	23	HEJ	1945	15	3.80	8	2,4,5,6,7,9,10,12,13
Swiss Airforce I	17	PEZ	1938	17	3.90	5	2,3,5,6,7,8,9,10,11,12
Swiss Airforce II	18	ZOU	1938	16	3.83	10	2,4,5,6,7,8,9,13
Swiss Airforce III	19	EHR	1938	16	3.83	11	2,4,5,6,8,10,12

Table 4. Selected values in probability distribution of Imk for random permutations.

Random permutation
0	2	4	8	12	16	18	19	20	21	22	23	24	25
$2^{-7.8}$	$2^{-5.8}$	$2^{-4.5}$	$2^{-3.6}$	$2^{-4.2}$	$2^{-7.0}$	$2^{-9.5}$	$2^{-9.7}$	$2^{-13.2}$	$2^{-13.9}$	$2^{-19}$	$2^{-20}$	$2^{-26}$	$0$

Latin squares are very hard to make if all lines in our table need to be obtained from one single rotor. We estimate the probability that we obtain a latin square for a rotor chosen at random to be approximately equal to the probability that there is no repeated characters in the first column, then we compute the first line, and again if we are lucky, there should be no repeated characters. Assuming that both events are approximately independent, this probability will be about: $${(26!/{26}^{26})}^2\approx 2^{-67.6}.$$

This argument does not explain how to find a suitable rotor. Until recently it was not clear if there exist efficient algorithm for generating a rotor for Enigma, and in a way such that we obtain a latin square for the set of rotated alphabets.

We have built a software tool based on formal coding and a SAT solver and our software returned UNSAT. Therefore we claim that this problem has no solution for n = 26. An ideal rotor does not exist for N = 26 contacts. More generally, in a companion paper (Courtois, Grajek and Rams 2020) we settle this problem once and for all with a mathematical theorem: it turns out that our problem has a solution if and only if N is odd. For example a solution exists for N = 13, one example is LAIFHBKEJDCGM. In fact for odd N, a working solution can be obtained generated in a prescriptive way, with a simple closed formula using modular arithmetic see our Thm. 8.7 below. However such prescriptive solutions would not satisfy the secrecy requirements in cryptography: the attacker should not be able to guess what the rotor connections are.

8.4. On invariance of collisions

In the same way as in Thm. 7.4, we have a property which occurs in the same way for every input of a given rotor, or in every column of our table:

Theorem 8.5

(Rotor Collision Invariance). We consider a rotor such that a collision occurs in one column in our table of rotated alphabets, i.e. there exist two integers (or two lines) $i\ne i\prime$ and one input letter (column) x such that $${\rho }^{-i}°R_{\mathit{III}}°{\rho }^i(x)={\rho }^{-i\prime }°R_{\mathit{III}}°{\rho }^{i\prime }(x)$$

Then for each column in our table x we obtain the same number of collisions.

Proof.

We can simply translate our property by c steps for every c, and these translations are one to one: $${\rho }^{-(i-c)}°R_{\mathit{III}}°{\rho }^{i-c}(x+c)={\rho }^{-(i\prime -c)}°R_{\mathit{III}}°{\rho }^{i\prime -c}(x+c).$$

Example.

For example in Figure 4, in each column we have four letters concerned by events of this type, with K repeated 3 times at i = 9, 11, 14, N repeated twice for i = 10, 12, P repeated twice with i = 15, 25 and S repeated twice for i = 16, 24. Then in fact in each column we also have four letters concerned by events of this type which are L,O,Q,T in the next column and so on.

8.6. A feasibility result

Theorem 8.7

(On Existence of Quasi-groups Derived From one Single Permutation). For every odd N there exists a rotor with N contacts so that the corresponding table of permutated alphabets (expanding it in the same way as we did in Figure 4) generates a quasi group and we get a perfect latin square.

Proof.

For an odd N it is easy to check that the rotor $R(x)=2*x+1$ mod N always works for any odd $N\ge 1.$ In line i we have then $x\mapsto i+2*x+1$ mod N which is always a permutation, and each column x we have $i\mapsto i+2*x+1$ mod N which is also always a permutation.

Remark 1.

With our rotor R_III we also had $i+2*x+1$ albeit with probability $\frac{10}{26}.$ This strongly suggests that the designers of Enigma in 1930 have studied latin squares and knew how to solve our problem for an odd N. The formula was still somewhat applied.

Remark 2.

Simple prescriptive solutions of this type are not recommended in cryptography. They do not satisfy the secrecy requirements in cryptography: the attacker should not be able to guess what the rotor connections are and it should be possible to keep them secret.

8.8. Historical rotors vs. random permutations

We denote by Ims the size of the image in one column. This corresponds to the number of possible encryptions of one fixed input letter, for example A, by this rotor R, for any rotor position i. This number Ims is the same for every input letter and we have a latin square if and only if Ims = 26. We denote by Ent(R) the entropy of this output which would be a maximum of ${\hspace{0.17em}\text{log}\hspace{0.17em}}_2(26)=4.7$ bits if we had a uniform distribution which is only possible if we had a latin square which is impossible and is never the case in practice, cf. Thm 8.7. In table below we compare our Rotor III to some other rotors. Some further results are also displayed in Table 3.

We observe that rotors from the same source are very similar. We have examined some 63 different real-life historical Enigma rotors. On average, the entropy is 4.39 while it is 3.87 for a rotor chosen as a random permutation. We are almost always far from what Hebern would recommend. We also examined 6 different original rotors by Hebern and found that Ims is between 13 and 18 as we would expect for random rotors. Only Swiss and Norwegian Enigma rotors have Ims being close to 16 and were possibly generated at random, except for one Norwegian rotor. We omitted Norwegian rotor IV, which was not rewired towards the end of the war like others, instead the same exact original German rotor IV was kept. Almost all other rotors from all known sources are clearly not random as their Ims is very high.

We also examined 10 rotors from the US cipher machine SIGABA from Wing On Chan (2007) and the results seem to perfectly confirm the idea that these rotors were generated at random.

8.9. More details and comparison to random permutations

Random permutation statistics play an important role in cryptanalysis of block ciphers (cf. Bard, Ault, and Courtois 2012). For smaller permutations results can be obtained more easily by computer simulations. We observe that middle values such as Ims = 12 can happen for a random permutation with probability of about $2^{-7.4}.$ What is not likely to happen accidentally is when Ims is very low or very high.

We recall that when Ims = 26 we would have a latin square. It seems that German army rotors behave very much as approximating a latin square with high Ims close to 26, rather than behaving like random permutations. The probability that we have Ims = 23 of 24 for a random permutation is about $2^{-15}$ and $2^{-20}$ respectively. It is even more exceptional to have Ims = 25, like with one of Japanese Enigma rotors. Here the probability is less than $2^{-26}.$ The case with Ims = 26 and obtaining actual latin square was never observed so far, and we estimated this probability of it to be less than $2^{-60}.$ However we frequently observe values close to 26. Small numbers $\mathit{Ims}\le 18$ are quite rare as shown in Table 1, and potentially these rotors and only those were actually generated at random. In fact our table contains all known rotors such that $\mathit{Ims}\le 18.$ We do not list rotors with $\mathit{Ims}\ge 23$ because most of known rotors are such and accordingly most rotors are such that they could very hardly be generated at random (Table 2).

Table 2. Probability distribution of Ims for random permutations.

Random permutation
7	8	9	10	12	14	16	18	20	22	23	24	25	26
$2^{-27.1}$	$2^{-22.4}$	$2^{-17.5}$	$2^{-13.6}$	$2^{-7.4}$	$2^{-3.7}$	$2^{-2.1}$	$2^{-2.7}$	$2^{-5.6}$	$2^{-11.1}$	$2^{-14.8}$	$2^{-20.0}$	$2^{-26.4}$	$0$

For all real-life historical Enigma rotors known to us, we found that on average Ims is 22.2 which is a very high value. In contrast if a rotor chosen as a random permutation the average value is 16 and values higher than 22 occur with low probability of less than $2^{-14.8}.$

High values of Ims in the range 23–25 show that German army and many other Enigma rotors were certainly not chosen at random and this already in 1938, before the war started. Rather, they were chosen with some specific properties or design criteria in mind. These original criteria are currently unknown to researchers.

This is a repeated game and the chances of what we see in Table 1 happening accidentally are extremely small. For example with all 8 Japanese Tirpitz rotors, the probability that they all have $\mathit{Ims}\ge 23$ is less than $2^{-6·14.8}\approx 2^{-89}.$ For the five German military rotors IV-VIII we get $2^{-74}.$ This is like winning in a lottery four or five times in a row.

8.10. Combination of rotors

An important question is, if we combine just two rotors with high Ims, does the combination behave as a random permutation? In other words, is there a long-term effect for Enigma when we combine several rotors? Unhappily the value of Ims will not be abnormal anymore. We observed that a combination of just two rotors with Ims = 25 gives a rotor with Ims close to 16 which is also what we expect for a random permutation.

8.11. Related research: impossible invariant differentials

In a companion paper we study another very closely related question of the existence of invariant differentials of type $${\Delta }^i=k\to {\Delta }^o=k$$ where differences are taken modulo 26. The study of Imk is another metric which allows one to show that most known rotors are far from being random permutations (and allows to distinguish them from such). We have the following definition:

Definition 8.12

(Imk). We call Imk the number of horizontal offsets k which are impossible in any column of our table or rotated alphabets (such as in Figure 4) when we have a collision in this column. In other terms we look at values of $k=k_1-k_2$ such that for no value x we have: $${\rho }^{-k_1}°R°{\rho }^{k_1}(x)={\rho }^{-k_2}°R°{\rho }^{k_2}(x)$$

It also easy to see that the number Imk is equal to the number of impossible invariant differentials for this rotor R of type $k\to k$ where $k=k_1-k_2.$ It is also easy to see that this set of impossible offsets k is in fact the same in every column in Figure 4 and in general. We observe that for most Enigma rotors not only Ims is large but Imk is also typically quite large and both are closely related. The maximum value of Imk is 25 because $0\to 0$ is always possible and we have 25 if and only if we have a latin square.

Examples of Imk values for different rotors are shown in Table 3.

8.13. On relationship of Imk and Ims

We observe that for most Enigma rotors not only Ims is large but Imk is also typically quite large and both are closely related. If one is close to maximum, the other is also close to maximum. We note that Ims is always bigger typically and in line with the maximum allowed values: we have $\mathit{Ims}\le 25$ and $\mathit{Imk}\le 24.$ A strong relationship between Ims and Imk values does not hold anymore for smaller values.

The resistance of real-life Enigma rotors to invariant differentials of type $k\to k$ is frequently unusually high and very few k are possible. We have Imk equal to 17.97 when averaged over all real-life Enigma rotors known to us. For example for German Army Rotor V we have Imk = 23 and only $k=\pm 5$ is at all possible. Yes, the set of invariant differentials has exactly one element, this is quite incredible. In fact this happens frequently for many different real-life rotors, some examples are given in Table 3.

For rotors chosen uniformly at random, the average value of Imk is substantially lower, about 9.1, and we obtain numerous invariant differentials $k\to k$ which are possible. For example for Norway Rotor V which seems to be generated at random and has no special properties known to us, the following k are possible: $2,4,5,6,7,9,10,12,13$ and also $-2,-4$ etc. We observe that there is a huge, roughly between 5x and tenfold difference, between what happens with random rotors and most real-life Enigma rotors. This is shown in Table 3.

8.14. On anti-latin squares

An important observation is that on the other side of the spectrum, low values of Imk are not forbidden and can occur for random rotors.

Definition 8.15

(Anti-Latin Square Property). We call a rotor an anti-latin square if for every $k\in \{0,\dots ,25\}$ the differential $${\Delta }^i=k\to {\Delta }^o=k$$ has a non-zero probability. This is equivalent to Imk = 0.

The probability that Imk = 0 is about $2^{-7.8}$ for a random permutation on 26 letters. We do not know any real-life rotors with Imk = 0.

Interesting Observation: In all known cases where Imk = 0 the very special differential $13\to 13$ for the basic rotor itself propagates with a quite high probability at least 8/26 and typically rather 12/26. Therefore potentially the cases of Imk = 0 could be cryptographically significant.

8.16. On Imk in random permutations (Table 4)

9. Comparison to Fialka

Fialka is a very complex Russian cipher machine with as many 10 rotors. Known rotors are listed in CryptoMuseum.com (2020). Each rotor has 30 contacts instead of 26 which makes that the numbers we obtain are a bit higher than for Enigma but it is overall very similar. In Table 5, we compare the average parameters obtained for each known set of ten Fialka rotors, compared to what we obtain on average for a random permutation.

Table 5. Parameters of totors in Fialka cipher machines.

Version	Code	Ims	Entropy	Imk
Poland	3 K	27.1	4.71	23.6
Czechoslovakia	5 K	27.2	4.72	24.3
Hungary	6 K	26.5	4.67	23.1
USSR	68	26.8	4.69	23.1
Random		18.96	4.08	10.54

A quick computer simulation shows that the probability that $\mathit{Ims}\ge 27$ for a random permutation is as low as about $2^{-18}$ and such events have occurred for about half of 40 rotors we examined. This cannot happen by accident and we see that all rotors without exception ever used in Fialka cipher machines have been very carefully chosen to approximate a latin square as with Enigma rotors, and they never behave like random permutations. The reason for this is again the lessons learned from classical cryptography about making the distribution of letters as uniform as possible when the key varies and this already for one single rotor.

10. Comparison to T-310 block cipher and local injectivity

It might come as a surprise, but similar properties exist for other ciphers, for example in modern block ciphers, which tend to behave rather like latin squares and not at all like random permutations. This is when the number of iterations (rounds) is limited. For a larger number of rounds we expect to obtain a random permutation.

10.1. Local injectivity in T-310

For example in the 1970s a substantial effort went into the design of the T-310 cipher which later was the main government encryption system used in Eastern Germany with some 3,800 cipher machines in active service in the 1980s (cf. Courtois, Drobick, and Schmeh 2018). Our property says that if we fix the input letter of one rotor and vary the key [which is accomplished by rotating the rotor] then the number of possible encryptions Ims is surprisingly large (e.g. 24) for the majority of historical rotors without ever reaching the maximum of 26. We can do the same in a block cipher and keep the input constant and vary the key.

It turns out that a similar and stricter property of this type was mandated in the 1970s for any “good quality” long term keys in T-310, cf. page 49 in Referat 11 (1980) and Section 11 in Courtois et al. (2017). This old historical result proves that this sort of questions have been studied also in Germany after the war. This makes our interpretation that this property is intentional, and a product of careful cryptographic engineering, also with Enigma cipher machines, more plausible. More precisely, the designers of T-310 have mandated in the 1970s the following very strict property:

Fact 10.2 (Local injectivity result for T-310). For 1,2,3 and 4 rounds of T-310, if we fix the block round input u on 36 bits, and vary the 12 bits of the key and IV bits, we obtain 2${}^{12}$ pairwise distinct $\varphi (u)$ values on 36 bits.

In contrast for 5 rounds, and for some weaker keys, this property is in rare cases violated, leading to the so called “related key collision attacks.” Specific examples of such attacks can be found in Section 5 of Courtois, Scarlata, and Georgiou (2019) and these events remain extremely rare for just 5 rounds. Now we are going to show that, very much like the majority of Enigma rotors, T-310 also imitates a latin square in a substantial way. We need a more detailed quantitative assessment: how large is the analogue of Ims for T-310 when the number of rounds grows. We call $\mathit{Ims}\prime$ the analogue of Ims when the key space is no longer the same as the input space. It is defined as the size of the output space when key varies and the input is fixed.

A direct estimation of $\mathit{Ims}\prime$ for T-310 requires about 8 Gbytes of memory and substantial running time. A practical and reportedly accurate method to estimate $\mathit{Ims}\prime$ from the frequency of collisions was described in Section 18.4 of Courtois et al. (2017). It is using the inverted Ramanujan formula and we expect that: $$\mathit{Ims}\prime \approx \frac{2{(3Eck-2)}^2}{9\pi }$$ where Eck is the average expected number of keys which need to be tried in order to find a collision for a randomly chosen fixed cipher input. We can now answer the question whether real-life government keys for T-310 behave like latin squares also for more than four rounds.

The answer is yes, and we observe that for all real-life keys, such as those used to encrypt government communications during the Cold War, and for 12 rounds of T-310 we get results of type $\mathit{Ims}\prime =2^{23.9}$ different images. We have not observed in practice any significant deviation from 2${}^{24}.$ The injectivity holds far beyond what is expected (from 4 to 12 rounds!). In contrast some other keys are substantially weaker. A nice proof of concept is the KT1 key 716 specified in Section 5 of Courtois, Scarlata, and Geougiou (2019). Here the size of the output space is only $2^{19.2}.$ We conjecture that testing if $\mathit{Ims}\prime =2^{24}$ for 12 rounds could be considered as a practical method to evaluate the quality of long-term keys in T-310 which follows closely to the actual ideas⁵ and intentions of the designers of T-310. Our key 716 is the weakest KT1 key currently known and in Section 5.6 of Courtois, Scarlata, and Geougiou (2019) we read that this sort of collisions with two different keys are rare for say 5 or 12 rounds but eventually become almost inevitable at 16 rounds approximately, this including real-life historical keys. We conclude that the designers of T-310 have avoided this type of collisions with different keys as hard as they could, leading to T-310 imitating a latin square through partial injectivity⁶ for up to 16 rounds.

10.3. Other block ciphers – local injectivity vs. birthday bound

We would like to compare different ciphers, those like T-310 which in 8 rounds use a very short key, and most other with very long keys. Let n be the block size in bits. It is easy to see that all results with Eck above the birthday bound of $2^{n/2}$ are representative of local injectivity we study. We tested this property for GOST block cipher, where key size is 256 bits (cf. Courtois 2012). For 2 rounds of GOST we obtain $\mathit{Eck}\gg 2^{n/2},$ far above the birthday bound. We see that GOST also satisfies a property similar to Fact 10.2 and therefore it also somewhat vaguely imitates a latin square. This reveals the fact that most Feistel ciphers have properties which go beyond what happens with one key, yet great majority of researchers only study what happens in one single key scenario. In specialist terms, they are expected to be not only good permutations but also good permutation generators (the attacker is allowed to compare different permutations for different keys). For 3 rounds GOST behaves already more like a random function with $\mathit{Eck}\approx 2^{n/2}.$

11. Conclusion

All known attacks on Enigma, for more than 90 years, have worked under assumption that the permutations of the rotors do not have special properties. In this paper we show that most Enigma rotors ever made have not been chosen at random. Instead, they have been chosen to imitate a certain ideal property about permuted encryption alphabets. There are only a handful of exceptions with the Swiss and Norwegian rotors and in US rotor machines such as original Hebern rotors and also with US Army SIGABA rotors.

Our property is closely related to latin squares and it also translates into having an unusually large number of impossible invariant differentials. In addition certain rotors have unusually strong linear approximations. It is clear that in some cases rotors can be implemented in software cheaper than random rotors. This can be used to speed up (modern) implementations of the Turing-Welchman bombe attack and modern ciphertext-only attacks on Enigma (cf. Gillogly 1995; Ostwald and Weierud 2017). In general we observe that the differential properties of most Enigma rotors are quite peculiar. From here, an open question is, if it would be possible to reject a certain rotor order, through a sophisticated statistical distinguisher, without running the attack in full and without cribs. This could possibly save precious bombe time. After 90 years of study of Enigma we are just discovering that some rotors are special and not all rotor orders are the same.

The question of latin squares goes back to the 17th century and was studied in Korea long before it became a topic of interest among European mathematicians and cryptologists. Our discovery is simply an indirect proof that designers of various cipher machines in the XXth century have studied earlier classical cryptanalytic attacks. This opens a major research question about what is a balanced set of design criteria for rotors leading to an optimal resistance against known attacks. A satisfactory answer is unlikely to be determined from old sources alone. We need in fact be sceptical, and question the idea that individual rotors need to be as strong as observed. It is clear that our property affects the security of early Hebern cipher machines combining very few rotors without a reflector. For later cipher machines with a reflector and with a larger number of active rotors, there is no evidence that such properties will make the full ciphers weaker overall. For example we show that 100% of known Fialka rotors have been carefully chosen. However, Fialka combines as many as 10 such permutations and the chances of distinguishing such complex permutations from random are probably quite slim. Future research will show how many rotors are actually needed to obtain a decent level of security.

A natural extension of our property is to study local injectivity: we fix the input and vary the key for some part of the cipher and see if collisions are possible. This can apply potentially to any cipher ever made from 1920s until today, including all modern block ciphers. We expect that to some extent, injectivity is strong in any reduced-round cipher. We show that a very strong property of this type has been mandated in the 1970s for four rounds of the T-310 block cipher and it remains true in approximation for up to 16 rounds. Long term keys in T-310 need to be tested for this property and even inside the very narrow KT1 class of keys which was mandated for official use, there exist some substantially weaker keys in this respect.

About the Authors

Nicolas Courtois is a Crypto Research Engineer at Qualcomm, Sophia Antipolis, France. In 2006–2021 he was a lecturer at University College London, UK where he taught about applied cryptography and cryptanalysis. Prior to 2006, he worked a crypto research engineer at Thales/Gemalto, the worlds largest manufacturer of secure hardware. He has filed more than ten patents on practical applications of cryptography. His research focuses on cryptographic engineering with particular focus on cryptographic primitives used by millions of people every day in government, military, telecommunication and financial sectors, inside mobile phones, smart cards, crypto currency, etc. His Google Scholar profile lists more than 200 papers with 10,200 citations in cryptography. He is well known for his research on algebraic cryptanalysis using Boolean polynomials. He has contributed 20 research papers in the post-quantum cryptography spectrum with digital signature schemes such as HFE, Quartz, Sflash or CFS variant of McEliece. More recently he has co-authored several research papers on cryptocurrency with particular focus on questions of bitcoin mining, key management, password cracking, payment anonymity and cryptocurrency crime. His H-index is 42. A university team lead by Nicolas Courtois was given the UK University Cipher Champion in March 2013. He is a founding member of the group Code-Breakers at LinkedIn and a member of the editorial board of Cryptologia. His blog is blog.bettercrypto.com.

Marek Grajek – consultant, journalist, and historian. Spent a major part of his professional career in the IT, the other part in the financial services, combining finally both in his portfolio of consulting projects (digital identity, trust services). Author or editor of more than 10 books on the history of cryptology. His book “Enigma. Bliżej prawdy” was nominated the “History Book of the Year 2008” in Poland. An English translation is expected to appear soon. His book “Not Only Enigma. The Fish That Talked” was nominated the “Popular Science Book of the Year 2014” in Poland. One of the initiators of the monument in memory of Marian Rejewski, Jerzy Różycki and Henryk Zygalski in Poznań and more recently author and contributor at Enigma Cipher Center interactive museum in Poznań.

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Notes

1 Later below we study the so called Zagreb Enigma which also comes from TICOM and was used German military attaché in Zagreb. We expect however that it is not the same as Croatian army Enigma decrypted by Germany (cf. Christos 2017).

2 We refer to Turing (1940) and to “Dermot Turing” (2018) for a very brief summary and the definitions of Rod Square and the Inverse Rod Square which are actually not needed in this article.

3 In a basic version of this attack we assume that the crib is fixed. More generally it can be enriched with a “linguistic” or crib guessing dimension, if the attacker is not sure what the crib is, or for example he wants to deduce a longer crib from a shorter one.

4 An example of this is our later Figure 4.

5 Reportedly the original software used for testing T-310 long-term keys for faults was lost.

6 This also means that roughly up to 16 rounds of T-310 can be distinguished from a random permutation generator by simply studying the frequency of collisions with the same input and different key.