Unifying Amplitude and Phase Analysis: A Compositional Data Approach to Functional Multivariate Mixed-Effects Modeling of Mandarin Chinese

Abstract

Mandarin Chinese is characterized by being a tonal language; the pitch (or F₀) of its utterances carries considerable linguistic information. However, speech samples from different individuals are subject to changes in amplitude and phase, which must be accounted for in any analysis that attempts to provide a linguistically meaningful description of the language. A joint model for amplitude, phase, and duration is presented, which combines elements from functional data analysis, compositional data analysis, and linear mixed effects models. By decomposing functions via a functional principal component analysis, and connecting registration functions to compositional data analysis, a joint multivariate mixed effect model can be formulated, which gives insights into the relationship between the different modes of variation as well as their dependence on linguistic and nonlinguistic covariates. The model is applied to the COSPRO-1 dataset, a comprehensive database of spoken Taiwanese Mandarin, containing approximately 50,000 phonetically diverse sample F₀ contours (syllables), and reveals that phonetic information is jointly carried by both amplitude and phase variation. Supplementary materials for this article are available online.

• Functional data analysis
• Linguistics
• Multivariate linear mixed models
• Phonetic analysis
• Registration

INTRODUCTION

Mandarin Chinese is one of the world’s major languages (Central Intelligence Agency 2012) and is spoken as a first language by approximately 900 million people, with considerably more being able to understand it as a secondary language. Spoken Mandarin Chinese, in contrast to most European languages, is a tonal language (Su and Wang 2005). The modulation of the pitch of the sound is an integral part of the lexical identity of a word. Thus, any statistical approach of Mandarin pitch attempting to provide a pitch typology of the language, must incorporate the dynamic nature of the pitch contours into the analysis (Gu, Hirose, and Fujisaki 2006; Prom-On, Xu, and Thipakorn 2009).

Pitch contours, and individual human utterances generally, contain variations in both the amplitude and phase of the response, due to effects such as speaker physiology and semantic context. Therefore, to understand the speech synthesis process and analyze the influence that linguistic (e.g., context) and nonlinguistic effects (e.g., speaker) have, we need to account for variations of both types. Traditionally, in many phonetic analyses, pitch curves have been linearly time normalized, removing effects such as speaker speed or vowel length, and these time normalized curves are subsequently analyzed as if they were the original data (Xu and Wang 2001; Aston, Chiou, and Evans 2010). However, this has a major drawback: potentially interesting information contained in the phase is discarded as pitch patterns are treated as purely amplitude variational phenomena.

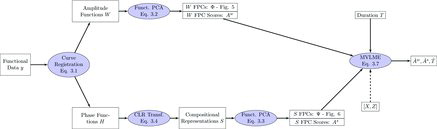
In a philosophically similar way to Kneip and Ramsay (2008), we model both phase and amplitude information jointly and propose a framework for phonetic analysis based on functional data analysis (FDA; Ramsay and Silverman 2005) and multivariate linear mixed-effects (LME) models (Laird and Ware 1982). Using a single multivariate model that concurrently models amplitude, phase, and duration, we are able to provide a phonetic typology of the language in terms of a large number of possible linguistic and nonlinguistic effects, giving rise to estimates that conform directly to observed data. We focus on the dynamics of F₀; F₀ is the major component of what a human listener identifies as speaker pitch (Jurafsky and Martin 2009) and relates to how fast the vocal folds of the speaker vibrate. We use two interlinked sets of curves; one set consisting of time normalized F₀ amplitude curves and a second set containing their corresponding time-registration/warping functions registering the original curves to a universal time-scale. Using methodological results from the compositional data literature (Aitchison 1982), a principal component analysis of the centered log ratio of the time-registration functions is performed. The principal component scores from the amplitude curves and the time warping functions along with the duration of the syllable are then jointly modeled through a multivariate LME framework.

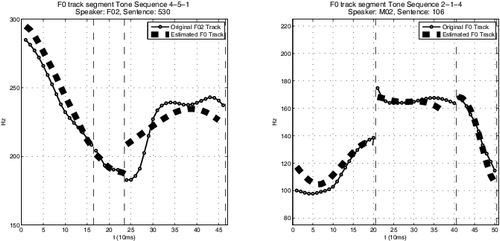
Figure 1 An example of triplet trajectories from speakers F02 and M02 over natural time. F(emale)02 tonal sequence: 4-5-1, M(ale)02 tonal sequence: 2-1-4; Mandarin Chinese rhyme sequences [oŋ-@-iou] and [ien-in-$$], respectively. See supplementary material for full contextual covariate information.

One aspect of note in our modeling approach is that it is based on a compositional representation of the warping functions. This representation is motivated by viewing the registration functions on normalized time domains as cumulative distribution functions, with derivatives that are density functions, which in turn can be approximated by histograms arbitrarily closely in the L² norm. We may then take advantage of the well-known connection between histograms and compositional data (Leonard 1973; Pawlowsky-Glahn and Egozcue 2006).

The proposed model is applied to a large linguistic corpus of Mandarin Chinese consisting of approximately 50,000 individual syllables in a wide variety of linguistic and nonlinguistic contexts. Due to the large number of curves, computational considerations are of critical importance to the analysis. The dataset is prohibitively large to analyze with usual multilevel computational implementations (Hadfield 2010; Bates et al. 2013), so a specific computational approach for the analysis of large multivariate LME models is developed. Using the proposed model, we are able to identify a joint model for Mandarin Chinese that serves as a typography for spoken Mandarin. This study thus provides a robust and flexible statistical framework describing intonation properties of the language.

The article proceeds as follows. In Section 2, a short review of the linguistic properties of Mandarin will be given. General statistical methodology for the joint modeling of phase and amplitude functions will then be outlined in Section 3, including its relation to compositional data analysis and other methods of modeling phase and amplitude. Section 4 contains the analysis of the Mandarin corpus where it will be seen that the model not only provides a method for determining the role of linguistic covariates in the synthesis of Mandarin, but also allows comparisons between the estimated and the observed curves. Finally, the last section contains a short discussion of the future prospects of FDA in linguistics. Further details of the analysis implemented are given in the supplementary material.

2. PHONETIC ANALYSIS OF MANDARIN CHINESE

We focus our attention on modeling fundamental frequency (F₀) curves. The amplitude of F₀, usually measured in Hz, quantifies the rate/frequency of the speaker’s vocal folds’ vibration and is an objective measure of how high or low the speaker’s voice is. In this study, the observation units of investigation are brief syllables: F₀ segments that typically span between 120 and 210 msec (Figure 1) and are assumed to be smooth and continuous throughout their trajectories. Linguistically our modeling approach of F₀ curves is motivated by the intonation model proposed by Fujisaki (2004) where linguistic, paralinguistic, and nonlinguistic features are assumed to affect speaker F₀ contours. Another motivation for our rationale of combining phase and amplitude variation comes from the successful usage of hidden Markov models (HMM; Rabiner 1989; Yoshioka et al. 2012) in speech recognition and synthesis modeling. However, unlike the HMM approach, we aim to maintain a linear modeling framework favored by linguists for its explanatory value (Baayen, Davidson, and Bates 2008; Evans et al. 2010) and suitability for statistical modeling.

Table 1 Covariates examined in relation to F₀ production in Taiwanese Mandarin. Tone variables in a 5-point scale representing tonal characterization, 5 indicating a toneless syllable, with 0 representing the fact that no rhyme precedes the current one (such as at the sentence start). Reference tone trajectories are shown in the supplementary material section: Linguistic Covariate Information

Effects	Values	Meaning	Notation mark
Fixed effects
Previous tone	0:5	Tone of previous syllable, 0 no previous tone present	tnprevious
Current tone	1:5	Tone of syllable	tncurrent
Following tone	0:5	Tone of following syllable, 0 no following tone present	tnnext
Previous consonant	0:3	0 is voiceless, 1 is voiced, 2 not present, 3 sil/short pause	cnprevious
Next consonant	0:3	0 is voiceless, 1 is voiced, 2 not present, 3 sil/short pause	cnnext
B2	linear	Position of the B2 index break in sentence	B2
B3	linear	Position of the B3 index break in sentence	B3
B4	linear	Position of the B4 index break in sentence	B4
B5	linear	Position of the B5 index break in sentence	B5
Sex	0:1	1 for male, 0 for female	Sex
Duration	linear	10 sec of msec	Duration
Rhyme type	1:37	Rhyme of syllable	rhymet
Random effects
Speaker	N(0, σ^2speaker)	Speaker effect	SpkrID
Sentence	N(0,σ^2sentence)	Sentence effect	Sentence

Usual approaches segment the analysis of acoustic data. First one applies a “standard” dynamic time warping (DTW) treatment to the sample using templates (Sakoe 1979), registers the data in this new universal time scale, and then continues with the analysis of the variational patterns in the synchronized speech utterances (Latsch and Netto 2011). In contrast, we apply functional principal component analysis (FPCA; Castro, Lawton, and Sylvestre 1986) to the “warped” F₀ curves and also to their corresponding warping functions, the latter being produced during the curve registration step. These functional principal component scores then serve as input for using a multivariate LME model, allowing a joint modeling of both the phase and amplitude variations.

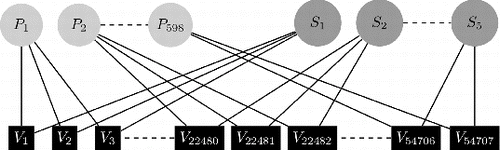
We analyze a comprehensive speech corpus of Mandarin Chinese. The Sinica Continuous Speech Prosody Corpora (COSPRO; Tseng, Cheng, and Chang 2005) was collected at the Phonetics Lab of the Institute of Linguistics in Academia Sinica and consists of nine sets of speech corpora. We focus our attention on the COSPRO-1 corpus; the phonetically balanced speech database. COSPRO-1 was designed to specifically include all possible syllable combinations in Mandarin based on the most frequently used 2- to 4-syllable lexical words. Additionally, it incorporates all the possible tonal combinations and concatenations. It therefore offers a high quality speech corpus that, in theory at least, encapsulates all the prosodic effects that might be of acoustic interest. Specifically, we analyze 54,707 fully annotated “raw” syllabic F₀ curves that were uttered by a total of five native Taiwanese Mandarin speakers (two males and three females). Each speaker uttered the same 598 predetermined sentences having a median length of 20 syllables; each syllable had on average 16 readings.

In total, aside from Speaker and Sentence information, associated with each F₀ curve are covariates of break index (within word (B2), intermediate (B3), intonational (B4), and utterance (B5) segments), its adjacent consonants, its tone, and rhyme type (Table 1). In our work, all of these variables serve as potential scalar covariates and with the exception of break counts, the fixed covariates are of categorical form. The break (or pause) counts, representing the number of syllables between successive breaks of a particular type, are initialized at the beginning of the sentence and are subsequently reset every time a corresponding or higher order break occurs. They represent the perceived degree of disjunction between any two words, as defined in the ToBi annotations (Beckman, Hirschberg, and Shattuck-Hufnagel 2006). Break counts are very significant as physiologically a break has a resetting effect on the vocal folds’ vibrations; a qualitative description of the break counts is provided in Table S.1 of the supplementary material.

3. STATISTICAL METHODOLOGY

3.1 A Joint Model

The application of functional data analysis (FDA) in the field of Phonetics, while not wide-spread, is not unprecedented; previous functional data analyses included lip-motion (Ramsay et al. 1996), analysis of prosodic effects (Lee, Byrd, and Krivokapic 2006), speech production (Koening, Lucero, and Perlman 2008) as well as basic language investigation based solely on amplitude analysis (Aston, Chiou, and Evans 2010). FDA is, by design, well suited as a modeling framework for phonetic samples as F₀ curves are expected to be smooth. Concurrent phase and amplitude variation is expected in linguistic data and as phonetic datasets feature “dense” measurements with high signal-to-noise ratios (Ramsay and Silverman 2005), FDA naturally emerges as a statistical framework for F₀ modeling. Nevertheless in all phonetic studies mentioned above, the focus of the phonetic analysis has been almost exclusively the amplitude variations (the size of the features on a function’s trajectory) rather than the phase variation (the location of the features on a function’s trajectory) or the interplay between the two domains.

To alleviate the limitation of only considering amplitude, we use the formulation presented by Tang and Müller (2009) and introduce two types of functions, w_i and h_i associated with our observed curve y_i, i = 1, …, N, where y_i is the ith curve in the sample of N curves. For a given F₀ curve y_i, w_i is the amplitude variation function on the domain [0, 1] while h_i is the monotonically increasing phase variation function on the domain [0, 1], such that h_i(0) = 0 and h_i(1) = 1. For generic random phase variation or warping functions h and time domains [0, T], T also being random, we consider time transformations $u=h^{-1}\left(\frac{t}{T}\right)$ from [0, T] to [0, 1] with inverse transformations t = Th(u). Then, the measured curve y_i over the interval t ∈ [0, T_i] is assumed to be of the form $$\begin{array}{ccc}\hfill y_i\left(t\right)& =& w_i\left(h_i^{-1}\left(\frac{t}{T_i}\right)\right)\iff \hfill \\ \hfill w_i\left(u\right)& =& y_i\left(T_i{h}_i\left(u\right)\right),i=1,...,N,\hfill \end{array}$$where u ∈ [0, 1] and T_i is the duration of the ith curve. A curve y_i is viewed as a realization of the amplitude variation function w_i evaluated over u, with the mapping h^{− 1}_i( · ) transforming the scaled real time t onto the universal/sample-wide time-scale u. In addition, each curve can depend on a set of covariates, fixed effects X_i, such as the tone being said, and random effects Z_i, where such random effects correspond to additional speaker and context characteristics. While each individual curve has its own length T_i, which is directly observed, the lengths entering the functional data analysis are normalized and the T_i are subsequently included in the modeling as part of the multivariate linear mixed effects framework.

In our application, the curves y_i are associated with various covariates, for example, tone, speaker, and sentence position. These are incorporated into the model via the principal component scores that result from adopting a common principal component approach (Flury 1984; Benko, Härdle, and Kneip 2009), where we assume common principal components (across covariates) for the amplitude functions and another common set (across covariates) for phase functions (but these two sets can differ). We use a common PCA framework with common mean and eigenfunctions so that all the variation in both phase and amplitude is reflected in the respective FPC scores. These ideas have been previously used in a regression setting (although not in the context of registration) (Benko, Härdle, and Kneip 2009; Aston, Chiou, and Evans 2010; Chen and Müller 2014). As will be discussed in Section 4.2, this is not a strong assumption in this application. Of the covariates likely present in the model, tone is known to affect the shape of the curves (indeed it is in the phonetic textual representation of the syllable), and therefore the identification of warping functions is carried out within tone classes as opposed to across the classes, as otherwise very strong (artifactual) warpings will be introduced.

As a direct consequence of our generative model (Equation 1$$\begin{array}{ccc}\hfill y_i\left(t\right)& =& w_i\left(h_i^{-1}\left(\frac{t}{T_i}\right)\right)\iff \hfill \\ \hfill w_i\left(u\right)& =& y_i\left(T_i{h}_i\left(u\right)\right),i=1,...,N,\hfill \end{array}$$), w_i dictates the size of a given feature and h^{− 1}_i dictates the location of that feature for a particular curve i. We assume that w_i and h_i are both elements of L²[0, 1]. The w_i can be expressed in terms of a basis expansion: $$\begin{array}{c}\hfill w_i\left(u\right)={\mu }^w\left(u\right)+\sum _{j=1}^{\infty }{A}_{i,j}^w{\phi }_j\left(u\right),\end{array}$$where μ^w(u) = E{w(u)}, φ_j is the jth basis function, and A^w_{i, j} is the coefficient for the ith amplitude curve associated with the jth basis function. The h_i are a sample of random distribution functions that are square integrable but are not naturally representable in a basis expansion in the Hilbert space L²[0, 1], since the space of distribution functions is not closed under linear operations. A common approach to circumvent this difficulty is to observe that $log\left(\frac{d}{du}h\left(u\right)\right)$ is not restricted and can be modeled as a basis expansion in L²[0, 1]. A restriction however is that the densities h_i have to integrate to 1, therefore the functions $s_i\left(u\right)=log\left(\frac{d}{du}{h}_i\left(u\right)\right))$ are modeled with the unrestricted basis expansion: $$\begin{array}{cc}\hfill s_i\left(u\right)& {\displaystyle ={\mu }^s\left(u\right)+\sum _{j=1}^{\infty }{A}_{i,j}^s{\psi }_j\left(u\right),}\end{array}$$where μ^s(u), ψ_k, and A^s_{i, j} are defined analogously to μ^w(u), φ_k, and A^w_{i, j}, respectively, but for the warping rather than amplitude functions. A transformation step is then introduced to satisfy the integration condition, which yields the representation: $$\begin{array}{cc}\hfill h_i\left(u\right)& {\displaystyle =\frac{{\int }_0^u{e}^{s_i\left(u^{\text{'}}\right)}d{u}^{\text{'}}}{{\int }_0^1{e}^{s_i\left(u^{\text{'}}\right)}d{u}^{\text{'}}}}\end{array}$$for the warping function h_i. Clearly different choices of bases will give rise to different coefficients A, which then can be used for further analysis. A number of different parametric basis functions can be used as basis; for example, Grabe et al. advocated the use of Legendre polynomials (Grabe, Kochanski, and Coleman 2007) for the modeling of amplitude. We advocate the use of a principal component basis for both w_i and s_i in Equations 2.3$$\begin{array}{c}\hfill w_i\left(u\right)={\mu }^w\left(u\right)+\sum _{j=1}^{\infty }{A}_{i,j}^w{\phi }_j\left(u\right),\end{array}$$ and 3.3$$\begin{array}{cc}\hfill s_i\left(u\right)& {\displaystyle ={\mu }^s\left(u\right)+\sum _{j=1}^{\infty }{A}_{i,j}^s{\psi }_j\left(u\right),}\end{array}$$, as will be discussed in the next sections, although any basis can be used in the generic framework detailed here. However, a principal components basis does provide the most parsimonious basis in terms of a residual sum of squares like criterion (Ramsay and Silverman 2005). We note that to ensure statistical identifiability of the model (Equation 3.1$$\begin{array}{ccc}\hfill y_i\left(t\right)& =& w_i\left(h_i^{-1}\left(\frac{t}{T_i}\right)\right)\iff \hfill \\ \hfill w_i\left(u\right)& =& y_i\left(T_i{h}_i\left(u\right)\right),i=1,...,N,\hfill \end{array}$$), several regularity assumptions were introduced in Tang and Müller (2008, 2009), including the exclusion of essentially flat amplitude functions w_i for which time-warping cannot be reasonably identified, and more importantly, assuming that the time-variation component that is reflected by the random variation in h_i and s_i asymptotically dominates the total variation. In practical terms, we will always obtain well-defined estimates for the component representations in Equations 3.2$$\begin{array}{c}\hfill w_i\left(u\right)={\mu }^w\left(u\right)+\sum _{j=1}^{\infty }{A}_{i,j}^w{\phi }_j\left(u\right),\end{array}$$ and 3.3$$\begin{array}{cc}\hfill s_i\left(u\right)& {\displaystyle ={\mu }^s\left(u\right)+\sum _{j=1}^{\infty }{A}_{i,j}^s{\psi }_j\left(u\right),}\end{array}$$, and their usefulness hinges critically on their interpretability; see Section 5.

For our statistical analysis, we explicitly assume that each covariate X_i influences, to different degrees, all of the syllable’s components/modes as well as influencing the syllable’s duration T_i. Additionally, as mentioned above in accordance with the Fujisaki model, we assume that each syllable component includes speaker-specific and sentence-specific variational patterns; we incorporate this information in the covariates Z_i. Then the general form of our model for a given sample curve y_i of duration T_i with two sets of scalar covariates X_i and Z_i is $$\begin{array}{c}\hfill E\left\{w_i\left(u\right)\right|X_i,Z_i\}={\mu }^w\left(u\right)+\sum _{j=1}^{\infty }E\left\{A_{i,j}^w\right|X_i,Z_i\}{\phi }_j\left(u\right),\end{array}$$and $$\begin{array}{c}\hfill E\left\{s_i\left(u\right)\right|X_i,Z_i\}={\mu }^s\left(u\right)+\sum _{j=1}^{\infty }E\left\{A_{i,j}^s\right|X_i,Z_i\}{\psi }_j\left(u\right).\end{array}$$Truncating expansions (3.5)$$\begin{array}{c}\hfill E\left\{w_i\left(u\right)\right|X_i,Z_i\}={\mu }^w\left(u\right)+\sum _{j=1}^{\infty }E\left\{A_{i,j}^w\right|X_i,Z_i\}{\phi }_j\left(u\right),\end{array}$$ and (3.6)$$\begin{array}{c}\hfill E\left\{s_i\left(u\right)\right|X_i,Z_i\}={\mu }^s\left(u\right)+\sum _{j=1}^{\infty }E\left\{A_{i,j}^s\right|X_i,Z_i\}{\psi }_j\left(u\right).\end{array}$$, to M_w and M_s components, respectively, is a computational necessity and simplifies the implementation. Curves are then reduced to finitely many scores A^w_ij, A^s_ij and these score vectors then act as surrogate data for curves w_i and s_i. The final joint model for amplitude, phase, and syllable duration is then formulated as $$\begin{array}{c}\hfill E\left\{[A_i^w,A_i^s,T_i]\right|X_i,Z_i\}=X_{i}B+Z_i\Gamma ,\Gamma \sim N(0,{\Sigma }_{\Gamma }),\end{array}$$where A^w_i and A^s_i are the vectors of component coefficients for the ith sample. Here, B (a k × p matrix, where k is the number of fixed effects in the model and p is the number of multivariate components in the mixed effects model, p = M_w + M_s + 1, where the “1” arises from the additional duration component in the model) is the parameter matrix of the fixed effects and Γ (a l × p matrix, where l is the number of random effects in the model) contains the coefficients of the random effects and is assumed to have mean zero, while ${\Sigma }_{\Gamma }$ is the covariance matrix of the amplitude, phase, and duration components with respect to the random effects.

The process as a whole is summarized in Figure 2.

Figure 2 Summary of the overall estimation procedure resulting in the estimates of the functional principal components and scores via the covariates in the linear mixed effect model.

3.2 Amplitude Modeling

In our study, amplitude analysis is conducted through a functional principal component analysis of the amplitude variation functions. Qualitatively, the random amplitude functions w_i are the time-registered versions of the original F₀ samples. Using FPCA, we determine the eigenfunctions that correspond to the principal modes of amplitude variation in the sample and then use a finite number of eigenfunctions corresponding to the largest eigenvalues as a truncated basis, so that representations in this basis will explain a large fraction of the total variation. Specifically, we define the kernel C^w of the covariance operator as $$C^w(u,u^{*})=E\left\{(w\left(u\right)-{\mu }^w\left(u\right))(w\left(u^{*}\right)-{\mu }^w\left(u^{*}\right))\right\}$$and by Mercer’s theorem (Mercer 1909), the spectral decomposition of the symmetric amplitude covariance function C^w can be written as $$\begin{array}{c}\hfill C^w(u,u^{*})=\sum _{p_w=1}^{\infty }{\lambda }_{p_w}{\phi }_{p_w}\left(u\right){\phi }_{p_w}\left(u^{*}\right),\end{array}$$where the eigenvalues ${\lambda }_{p_w}$ are ordered by declining size and the corresponding eigenfunction is ${\phi }_{p_w}$. Additionally, the eigenvalues ${\lambda }_{p_w}$ allow the determination of the total percentage of variation exhibited by the sample along the pth principal component and whether the examined component is relevant for further analysis. As will be seen later, the choice of the number of components is based on acoustic criteria (Black and Hunt 1996; Kochanski 2006) with direct interpretation for the data, such that components that are not audible are not considered. Having fixed M_w as the number of φ modes/eigenfunctions to retain, we use φ to compute $A_{i,p_w}^w$, the amplitude projections scores associated with the ith sample and its p_wth corresponding component (Equation (3.10)$$\begin{array}{c}\hfill A_{i,p_w}^w=\int \{w_i\left(u\right)-{\mu }^w\left(u\right)\}{\phi }_{p_w}\left(u\right)dt,\\ \hfill \text{where}\text{as}\text{before}{\mu }^w\left(u\right)=E\left\{w\left(u\right)\right\},\end{array}$$) as $$\begin{array}{c}\hfill A_{i,p_w}^w=\int \{w_i\left(u\right)-{\mu }^w\left(u\right)\}{\phi }_{p_w}\left(u\right)dt,\\ \hfill \text{where}\text{as}\text{before}{\mu }^w\left(u\right)=E\left\{w\left(u\right)\right\},\end{array}$$where a suitable numerical approximation to the integral is used for practical analysis.

3.3 Phase Modeling

When examining the warping functions it is important to note that we expect the mean of the random warping function to correspond to the identity (i.e., the case of no warping). Therefore, assuming their domains are all normalized to [0,1], with t = Th(u), this assumption is $$\begin{array}{c}\hfill u=E\left\{h\right(u\left)\right\},\end{array}$$and this allows one to interpret deviations of h from the identity function as phase distortion. This clearly also applies conceptually when working with the function s(u). As with the amplitude analysis, phase analysis is carried out using a principal component analysis approach. Using the eigenfunctions of the random warping functions s_i, we identify the principal modes of variation of the sample and use those modes as a basis to project our data to a finite subspace. Directly analogous to the decomposition of C^w, the spectral decomposition of the phase covariance function C^s is $$\begin{array}{c}\hfill C^s(u,u^{*})=\sum _{p_s=1}^{\infty }{\lambda }_{p_s}{\psi }_{p_s}\left(u\right){\psi }_{p_s}\left(u^{*}\right),\end{array}$$where the ${\psi }_{p_s}$ are the eigenfunctions and the ${\lambda }_{p_s}$ are the eigenvalues, ordered in declining order. The variance decomposition through eigencomponents is analogous to that for the amplitude functions. As before we will base our selection processes not on an arbitrary threshold based on percentages but on an acoustic perceptual criteria (Quene 2007; Jacewicz, Fox, and Wei 2010) for perceivable speed changes. If one retains M_s eigencomponents in the expansion (3.6)$$\begin{array}{c}\hfill E\left\{s_i\left(u\right)\right|X_i,Z_i\}={\mu }^s\left(u\right)+\sum _{j=1}^{\infty }E\left\{A_{i,j}^s\right|X_i,Z_i\}{\psi }_j\left(u\right).\end{array}$$, the corresponding functional principal component scores for the ith warping or phase variation function w_i are obtained as (3.13)$$\begin{array}{c}\hfill A_{i,p_s}^s=\int \{s_i\left(u\right)-{\mu }^s\left(u\right)\}{\psi }_{p_s}\left(u\right)dt,\\ \hfill \text{where}\text{as}\text{before}{\mu }^s\left(u\right)=E\left\{s\left(u\right)\right\}.\end{array}$$: $$\begin{array}{c}\hfill A_{i,p_s}^s=\int \{s_i\left(u\right)-{\mu }^s\left(u\right)\}{\psi }_{p_s}\left(u\right)dt,\\ \hfill \text{where}\text{as}\text{before}{\mu }^s\left(u\right)=E\left\{s\left(u\right)\right\}.\end{array}$$

It is worth stressing that our choice of the number of components to retain will be dictated by an external criterion that is specific to the phonetic application, rather than being determined by a purely statistical criterion such as fraction of total variance explained. Purely data-driven approaches have been developed (Minka 2001) as well as a number of different heuristics (Cangelosi and Goriely 2007) for less structured applications, where no natural and interpretable choice is available.

3.4 Sample Time-Registration

The estimation of the phase variation/warping functions is as in Tang and Müller (2008), as implemented in the routine WFPCA in PACE (Tang and Müller 2009). There, one defines the pairwise warping function $g_{i^{\text{'}},i}\left(t\right)=h_{i^{\text{'}}}\left(h_i^{-1}\left(t\right)\right)$ as the 1-to-1 mapping from the ith curve’s time-scale to that of the i′th by minimizing a distance (usually selected as L² distance) by warping the time-scale of the ith curve as closely as possible to that of the i′th curve. The inverse of the average $g_{i^{\text{'}},i}(·)$ (Equation (3.15)$$\begin{array}{c}\hfill {\widehat{h}}_i^{-1}\left(t\right)=\frac{1}{N^{*}}\sum _{i^{\text{'}}=1}^{N^{*}}{\widehat{g}}_{i^{\text{'}},i}\left(t\right),N^{*}\le N,\end{array}$$) for a curve i then can be shown to yield a consistent estimate of the time-warping function h_i that is specific for curve y_i and corresponds to a map between individual-specific warped time to absolute time (Tang and Müller 2008).

The $g_{i^{\text{'}},i}(·)$, being time-scale mappings, have a number of obvious restrictions on their structure. First, $g_{i^{\text{'}},i}\left(0\right)=0$ and $g_{i^{\text{'}},i}\left(1\right)=1$. Second, they should be monotonic, that is, $g_{i^{\text{'}},i}\left(t_j\right)⩽g_{i^{\text{'}},i}\left(t_{j+1}\right)$, 0 ⩽ t_j < t_{j + 1} ⩽ 1. Finally, $E\left[g_{i^{\text{'}},i}\left(t\right)\right]=t$. This final condition is necessary for representing the warping function h_i through its inverse h^{− 1}_i: $$\begin{array}{cc}\hfill h_i^{-1}\left(t\right)& =E\left[g_{i^{\text{'}},i}\left(t\right)\right|h_i\left(t\right)]\end{array}$$with sample version: $$\begin{array}{c}\hfill {\widehat{h}}_i^{-1}\left(t\right)=\frac{1}{N^{*}}\sum _{i^{\text{'}}=1}^{N^{*}}{\widehat{g}}_{i^{\text{'}},i}\left(t\right),N^{*}\le N,\end{array}$$where N* is the number of sample pairwise registrations used to obtain the estimate. In small datasets, all the curves can be used for the pairwise comparisons that lead to (3.15)$$\begin{array}{c}\hfill {\widehat{h}}_i^{-1}\left(t\right)=\frac{1}{N^{*}}\sum _{i^{\text{'}}=1}^{N^{*}}{\widehat{g}}_{i^{\text{'}},i}\left(t\right),N^{*}\le N,\end{array}$$, but in a much larger dataset such as the one in our phonetic application, only a random subsample of curves of size N* is used to obtain the estimates for computational reasons.

Aside from the pairwise alignment framework we employ (Tang and Müller 2008), we have identified at least two alternative approaches based on different metrics, the square-root velocity function metric (Kurtek et al. 2012) or area under the curve normalization metric (Zhang and Müller 2011), which can be used interchangeably, depending on the properties of the warping that are considered most important in specific application settings. Indeed it has been seen that considering warping and amplitude functions together, based on the square-root velocity metric, can be useful for classification problems (Tucker, Wu, and Srivastava 2013). However, we need to stress that each method makes some explicit assumptions to overcome the nonidentifiability between the h_i and w_i (Equation (3.1)$$\begin{array}{ccc}\hfill y_i\left(t\right)& =& w_i\left(h_i^{-1}\left(\frac{t}{T_i}\right)\right)\iff \hfill \\ \hfill w_i\left(u\right)& =& y_i\left(T_i{h}_i\left(u\right)\right),i=1,...,N,\hfill \end{array}$$) and this can lead to significantly different final estimates.

3.5 Compositional Representation of Warping Functions

To apply the methods to obtain the time warping functions in Section 3.4 and their functional principal component representations in Section 3.3, we still need a suitable representation of individual warping functions that ensures that these functions have the same properties as distribution functions. For this purpose, we adopt step function approximations of the warping functions h_i, which are relatively simple yet can approximate any distribution function arbitrarily closely in the L² or sup norms by choosing the number of steps large enough. A natural choice for the steps is the grid of the data recordings, as the phonetic data are available on a grid. The differences in levels between adjacent steps then give rise to a histogram that represents the discretized warping functions.

This is where a novel connection to the proposed compositional decompositions arises. Based on standard compositional data methodology (centered log-ratio transform) (Aitchison 1982), the first difference Δh_{i, j} = h_i(t_{j + 1}) − h_i(t_j) of a discretized instance of h_i over an (m + 1)-dimensional grid is used to evaluate s_i as $$\begin{array}{c}\hfill s_{i,j}=log\frac{\Delta h_{i,j}}{{\left(\Delta h_{i,1}·\Delta h_{i,2}...\Delta h_{i,m}\right)}^{\frac{1}{m}}}j=\{1,\cdots ,m\}\end{array}$$the reverse transformation being: $$\begin{array}{c}\hfill h_{i,j+1}=\frac{e^{s_{i,j}}}{{\sum }_j{e}^{s_{i,j}}},h_{i,1}=0.\end{array}$$This ensures that monotonicity (h_{i, j} < h_{i, j + 1}), and boundary requirements (h_{i, 1} = 0, h_{i, m + 1} = 1) are fulfilled as required in the pairwise warping step; this compositional approach guarantees that an evaluation will always remain in the space of warping functions. The sum of the first differences of all discretized h_i warping functions is equal to a common C, and thus Δh_i is an instance of compositional data (Aitchison 1982).

We can then employ the centered log-ratio transform for the analysis of the compositional data, essentially dividing the components by their geometric means and then taking their logarithms. The centered log-ratio transform has been the established method of choice for the variational analysis of compositional data; alternative methods such as the additive log-ratio (Aitchison 1982) or the isometric log-ratio (Egozcue et al. 2003) are also popular choices. In particular, the centered log-ratio, as it sums the transformed components to zero by definition, presents itself as directly interpretable in terms of “time-distortion,” negative values reflecting deceleration and positive values acceleration in the relative phase dynamics. Clearly, this summation constraint imposes a certain degree of collinearity in our transformed sample (Filzmoser, Hron, and Reimann 2009); nevertheless it is the most popular choice of compositional data transformation (Aitchison 1983; Aitchison and Greenacre 2002) and allows direct interpretation as mentioned above.

Figure 3 The multivariate mixed effects model presented exhibits a crossed (nonbalanced) random structure. The vowel-rhyme curves (V) examined are cross-classified by their linguistic (Sentence—P_i) and their nonlinguistic characterization (Speaker—S_i).

3.6 Further Details on Mixed Effects Modeling

Given an amplitude-variation function w_i, its corresponding phase-variation function s_i, and the original F₀ curve duration T_i, each sample curve is decomposed into two mean functions (one for amplitude and one for warping) and an M_w + M_s + 1 ≔ p vector space of partially dependent measurements arising from the scores associated with the eigenfunctions along with the duration. Here, M_w is the number of eigencomponents encapsulating amplitude variations, M_s is the number of eigencomponents carrying phase information, and the 1 refers to the curves’ duration. The final linear mixed effect model for a given sample curve y_i of duration T_i and sets of scalar covariates X_i and Z_i is $$\begin{array}{c}\hfill [A_{i,k}^w,A_{i,m}^s,T_i]=X_{i}B+Z_i\Gamma +E_i,\\ \hfill \Gamma \sim N(0,{\Sigma }_{\Gamma }),E\sim N(0,{\Sigma }_E),\end{array}$$Σ_E being the diagonal matrix of measurement error variances (Equation S.2). The covariance structures ${\Sigma }_{\Gamma }$ and Σ_E are of particular forms; while Σ_E (Equation S.2) assumes independent measurement errors, the random effects covariance (Equation S.1) allows a more complex covariance pattern (see supplementary material for relevant equations).

As observed in previous work (Hadjipantelis, Aston, and Evans 2012), the functional principal components for the amplitude process are uncorrelated among themselves and so are those for the phase process. However, between phase and amplitude they are expected to be correlated, and will also be correlated with time T. Therefore, the choice of an unstructured covariance for the random effects is necessary; we have found no theoretical or empirical evidence to believe any particular structure such as a compound symmetric covariance structure, for example, is present within the eigenfunctions and/or duration. Nevertheless our framework would still be directly applicable if we choose another restricted covariance (e.g., compound symmetry) structure and if anything it will become computationally easier to investigate as the number of parameters would decrease.

Our sample curves are concurrently included in two nested structures: one based on “speaker” (nonlinguistic) and one based on “sentence” (linguistic) (Figure 3). We therefore have a crossed design with respect to the random-effects structure of the sample (Brumback and Rice 1998; Aston, Chiou, and Evans 2010), which suggests the inclusion of random effects: $$\begin{array}{cc}\hfill A_{n\times p}& =X_{N\times k}{B}_{k\times p}+Z_{N\times l}{\Gamma }_{l\times p}+E_{N\times p},\end{array}$$where p is the multivariate dimension, k is the number of fixed effects, and l is the number of random effects, as before. This generalization allows the formulation of the conditional estimates as $$\begin{array}{cc}\hfill A& |\Gamma \sim N(XB+Z\Gamma ,{\Sigma }_E)\end{array}$$or unconditionally and in vector form for $\overrightarrow{A}$ as $$\begin{array}{ccc}& & {\overrightarrow{A}}_{Np\times 1}\sim N((I_p\otimes X){\overrightarrow{B}}_{Np\times 1},{\Lambda }_{Np\times Np}),\hfill \\ & & \Lambda =(I_p\otimes Z)({\Sigma }_{\Gamma }\otimes I_l){(I_p\otimes Z)}^T+({\Sigma }_E\otimes I_N),\hfill \end{array}$$where X is the matrix of fixed effects covariates, B is the matrix of fixed effects coefficients, Z is the matrix of random effects covariates, Γ is the matrix of random effects coefficients (a sample realization dictated by N(0, Σ_Γ)), Σ_Γ = $D_{\Gamma }^{\frac{1}{2}}$ $P_{\Gamma }$ ${D_{\Gamma }^{\frac{1}{2}}}^T$, the random effects covariance matrix, D_Γ is the diagonal matrix holding the individual variances of random effects, P_Γ is the correlation matrix of the random effects between the series in columns i, j, and Σ_E is the diagonal measurement errors covariance matrix. Kronecker products (⊗) are used to generate the full covariance matrix Λ of $\overrightarrow{A}$ as the sum of the block covariance matrix for the random effects and the measurement errors.

3.7 Estimation

Estimation is required in two stages: obtaining the warping functions and multivariate mixed effects regression estimation. Requirements for the estimation of pairwise warping functions g_{k, i} were discussed in Section 3.4. In practical terms, these requirements mean that: (i) g_{k, i}( · ) needs to span the whole domain, (ii) we cannot go “back in time,” that is, the function must be monotonic, and (iii) the time-scale of the sample is the average time-scale followed by the sample curves. With these restrictions in place, we can empirically estimate the pairwise (not absolute) warping functions by targeting the minimizing time transformation function g_{k, i}( · ) as ${\widehat{g}}_{k,i}\left(t\right)={\text{argmin}}_{g}D(y_k,y_i,g),$ where the “discrepancy” cost function D is defined as $$\begin{array}{ccc}\hfill D_{\lambda }(y_k,y_i,g)& =& E\left\{{\int }_0^1{(y_k(g\left(t\right);T_k)-y_i(t;T_i))}^2\right.\hfill \\ \hfill & & \left.+\lambda {(g\left(t\right)-t)}^{2}dt|y_k,y_i,T_k,T_i\phantom{\{{\int }_0^1\left(y_k\right(g\left(t\right)}\right\},\hfill \end{array}$$

λ being an empirically evaluated nonnegative regularization constant, chosen in a similar way to Tang and Müller (2008); see also Ramsay and Li (1998); T_i and T_k being used to normalize the curve lengths. Intuitively the optimal g_{k, i}( · ) minimize the differences between the reference curve y_i and the “warped” version of y_k subject to the amount of time-scale distortion produced on the original time-scale t by g_{k, i}( · ). Having a sufficiently large sample of N* pairwise warping functions g_{k, i}( · ) for a given reference curve y_i, the empirical internal time-scale for y_i is given by Equation (3.15)$$\begin{array}{c}\hfill {\widehat{h}}_i^{-1}\left(t\right)=\frac{1}{N^{*}}\sum _{i^{\text{'}}=1}^{N^{*}}{\widehat{g}}_{i^{\text{'}},i}\left(t\right),N^{*}\le N,\end{array}$$, the global warping function h_i being easily obtainable by simple inversion of h^{− 1}_i. It is worth noting that in Mandarin, each tone has its own distinct shape; their features are not similar and therefore should not be aligned. For this reason, the curves were warped separately per tone, that is, realizations of Tone1 curves where warped against other realizations of Tone1 only, the same being applied to all other four tones. In order for the minimization in (3.22)$$\begin{array}{ccc}\hfill D_{\lambda }(y_k,y_i,g)& =& E\left\{{\int }_0^1{(y_k(g\left(t\right);T_k)-y_i(t;T_i))}^2\right.\hfill \\ \hfill & & \left.+\lambda {(g\left(t\right)-t)}^{2}dt|y_k,y_i,T_k,T_i\phantom{\{{\int }_0^1\left(y_k\right(g\left(t\right)}\right\},\hfill \end{array}$$ to be well defined, it is essential to have a finite-dimensional representation for the time transformation/warping functions g. Such a representation is provided by the compositional centered log transform and this makes it possible to implement the minimization.

Finally to estimate the mixed model via the model’s likelihood, we observe that usual maximum likelihood (ML) estimation underestimates the model’s variance components (Patterson and Thomson 1971). We therefore use restricted maximum likelihood (REML); this is essentially equivalent to taking the ML estimates for our mixed model after accounting for the fixed effects X. The restricted maximum (log)likelihood estimates are given by maximizing the following formula: $$\begin{array}{ccc}\hfill L_{\mathrm{REML}}\left(\theta \right)& =& -\frac{1}{2}[p(N-k)log\left(2\pi \right)\hfill \\ & & +log\left(\right|\Psi \left|\right)+{\overrightarrow{\Omega }}^T{\Psi }^{-1}\overrightarrow{\Omega }],\hfill \end{array}$$where Ψ = K^TΛK and Ω = K^TA; with K being the “whitener” matrix such that 0 = K^T(I_p⊗X) (Searle, Casella, and McCulloch 2006). Based on this, we concurrently estimate the random effect covariances while taking into account the possible nondiagonal correlation structure between them. Nevertheless because we “remove” the influence of the fixed effects to compare models with different fixed effects structures we would need to use ML rather REML estimates. Standard mixed-effects software such as lme4 (Bates et al. 2013), nlme (Pinheiro et al. 2013), and MCMCglmm (Hadfield 2010) either do not allow the kinds of restrictions on the random effects covariance structures that we require, as they are not designed to model multivariate mixed effects models, or computationally are not efficient enough to model a dataset of this size and complexity; we were therefore required to write our own implementation for the evaluation of REML/ML. Exact details about the optimization procedure used to do this are given in the supplementary material section: Computational aspects of multivariate mixed effects regression.

4. DATA ANALYSIS AND RESULTS

4.1 Sample Preprocessing

It is important as a first step to ensure F₀ curves are “smooth,” that is, they possess “one or more derivatives” (Ramsay and Silverman 2005). In line with Chiou, Müller, and Wang (2003), we use a locally weighted least squares smoother to fit local linear polynomials to the data and produce smooth data-curves interpolated upon a common time-grid on a dimensionless interval [0, 1]. Guo (2002) presented a smoothing framework producing comparable results by employing smoothing splines. The form of the kernel smoother used is as in Chiou, Müller, and Wang (2003) with fixed parameter bandwidth estimated using cross-validation (Izenman 2008) and Gaussian kernel function.

The curves in the COSPRO sample have an average of 16 readings per case, hence the number of grid points chosen was 16. The smoother bandwidth was set to 5% of the relative curve length. As is common in a dataset of this size, occasional missing values have occurred and curves having 5% or more of the F₀ readings missing were excluded from further analysis. These missing values usually occurred at the beginning or the end of a syllable’s recording and are most probably due to the delayed start or premature stopping of the recording. During the smoothing procedure, we note each curve’s original time duration (T_i) so it can be used within the modeling. At this point, the F₀ curve sample is not yet time-registered but has been smoothed and interpolated to lie on a common grid.

4.2 Model Presentation and Fitting

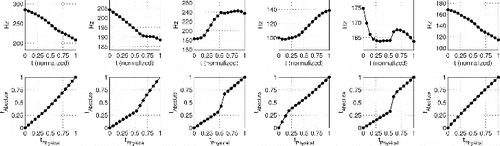
As mentioned in Section 2, the data consisted of approximately 50,000 sample curves. However, as can be seen in Figure S.2, in noncontextual situations, the tones have simple and distinct shapes. Therefore, registration was not performed on the dataset in its entirety but rather using each tone class as its own registration set. This raises an interesting discussion as to whether the curves are now one common sample, or rather a group of five separate samples. However, if we assume that the five tone groups all have common means and principal components (Benko, Härdle, and Kneip 2009) for both amplitude and phase variations, then this alleviates any issues with the use of separate registrations. This assumption substantially simplifies the model and is not particularly restrictive in that the ability of the vocal folds to produce very different pitch contours is limited, and as such it is likely that common component contours are present in each group.

Figure 4 Corresponding amplitude variation functions w (top row) and phase variation functions h (bottom row) functions for the triples shown in Figure 1.

Figure 5 Functional estimates (continuous curves) are shown superimposed of the corresponding original discretized speaker data over the physical time domain t.

Figure 6 W (amplitude) eigenfunctions Φ: mean function ([0.05, 0.95] percentiles shown in gray) and first, second, third, fourth, fifth, and sixth functional principal components (FPCs) of amplitude.

It is possible to develop many different linguistic models for this data. However, the following model is proposed, as it accounts for all the linguistic effects that might be present in a dataset of this form (Hadjipantelis, Aston, and Evans 2012), which is a particular case of (3.18)$$\begin{array}{c}\hfill [A_{i,k}^w,A_{i,m}^s,T_i]=X_{i}B+Z_i\Gamma +E_i,\\ \hfill \Gamma \sim N(0,{\Sigma }_{\Gamma }),E\sim N(0,{\Sigma }_E),\end{array}$$ where the covariates are now specified: $$\begin{array}{ccc}\hfill [A_{i,k}^w,A_{i,m}^s,T_i]& =& \{[t{n}_{\mathrm{previous}}*t{n}_{\mathrm{current}}*t{n}_{\mathrm{next}}]\hfill \\ & & +[c{n}_{\mathrm{previous}}*t{n}_{\mathrm{current}}*c{n}_{\mathrm{next}}]\hfill \\ & & +[\left(B2\right)+{\left(B2\right)}^2+{\left(B2\right)}^3+\left(B3\right)+{\left(B3\right)}^2\hfill \\ & & +{\left(B3\right)}^3+\left(B4\right)+{\left(B4\right)}^2+{\left(B4\right)}^3+\left(B5\right)\hfill \\ & & +{\left(B5\right)}^2+{\left(B5\right)}^3{]*Sex+\left[{\mathrm{rhyme}}_t\right]\}}_{i}B\hfill \\ & & +{\{\left[\text{Sentence}\right]+\left[\text{SpkrID}\right]\}}_i\Gamma +E_i.\hfill \end{array}$$Standard Wilkinson notation (Wilkinson and Rogers 1973) is used here for simplicity regarding the interaction effects; [K*L] represents a short-hand notation for [K + L + K:L] where the colon specifies the interaction of the covariates to its left and right (Baayen 2008). First, examining the fixed effects structure, we incorporate the presence of tone-triplets and of consonant:tone:consonant interactions. Both types of three-way interactions are known to be present in Mandarin Chinese and to significantly dictate tonal patterns (Xu 1999; Torgerson 2005). We also look at break counts, our only covariate that is not categorical. A break’s duration and strength significantly affects the shape of the F₀ contour and not just within a rhyme but also across phrases. Break counts are allowed to exhibit squared and cubic patterns as cubic downdrift has been previously observed in Mandarin studies (Aston, Chiou, and Evans 2010; Hadjipantelis, Aston, and Evans 2012). We also model breaks as interacting with the speaker’s sex as we want to provide the flexibility of having different curvature declination patterns among male and female speakers. This partially alleviates the need to incorporate a random slope as well as a random intercept in our mixed model’s random structure. The final fixed effect we examine is the type of rhyme uttered. Each syllable consists of an initial consonant or ∅ followed by a rhyme. The rhyme contains a vowel followed by -∅/ -n/ -ŋ. The rhyme is the longer and more sonorous part of the syllable during which the tone is audible. Rhyme types are the single most linguistically relevant predictors for the shape of F₀’s curve as when combined together they form words, with words carrying semantic meaning.

Examining the random effects structure we incorporate speaker and sentence. The inclusion of speaker as a random effect is justified as factors of age, health, neck physiology, and emotional condition affect a speaker’s utterance and are mostly immeasurable but still rather “subject-specific.” Additionally, we incorporate Sentence as a random effect since it is known that pitch variation is associated with the utterance context (e.g., commands have a different F₀ trajectory than questions). We need to note that we do not test for the statistical significance of our random effects; we assume they are “given” as any linguistically relevant model has to include them. Nevertheless if one wished to access the statistical relevance of their inclusion, the χ² mixtures framework used by Lindquist et al. (2012) provides an accessible approach to such a high-dimensional problem, as resampling approaches (bootstrapping) are computationally too expensive in a dataset of the size considered here. Fixed effects comparisons are more straightforward; assuming a given random-effects structure, Akaike information criterion (AIC)-based methodology can be directly applied (Greven and Kneib 2010). Fitting the models entails maximizing REML of the model (Equation (3.23)$$\begin{array}{ccc}\hfill L_{\mathrm{REML}}\left(\theta \right)& =& -\frac{1}{2}[p(N-k)log\left(2\pi \right)\hfill \\ & & +log\left(\right|\Psi \left|\right)+{\overrightarrow{\Omega }}^T{\Psi }^{-1}\overrightarrow{\Omega }],\hfill \end{array}$$).

Our findings can be grouped into three main categories, those from the amplitude analysis, those from the phase, and those from the joint part of the model. Some examples of the curves produced by the curve registration step are given in Figure 4. However, overall, as can be seen in Figure 5, there is a good correspondence between the model estimates and the observed data when the complete modeling setup is considered. Small differences in the estimates can be ignored due to the just noticeable difference (JND) criteria (see below). The only noticeable departure between the estimates and the observed data is in the third segment of Figure 5 (left). The sinusoidal difference in the measured data that is not in the estimate can be directly attributed to the exclusion of amplitude PC’s five and six, as these were below the JND criteria. The continuity difference in the observed curves is not enforced by the model and is hence not as prominent in the estimates. The general shape is the same but the continuity yields a sharper change in the observed data than is expected. It would be of great interest in future research to extend the ideas of registration to models where both amplitude and warping functions are included as bivariate dependent random functions.

Empirical findings from the amplitude FPCA: The first question one asks when applying any form of dimensionality reduction is how many dimensions to retain, or more specifically in the case of FPCA how many components to use. We take a perceptual approach. Instead of using an arbitrary percentage of variation, we calculate the minimum variation in Hz each FPC can actually exhibit (Tables 2 and 3). Based on the notion of JND (Buser and Imbert 1992), we use for further analysis only eigenfunctions that reflect variation that is actually detectable by a standard speaker (F₀ JND: ≈10 Hz; M_w = 4). The empirical wFPCs (Figure 6) correspond morphologically to known Mandarin tonal structures (Figure S.2) increasing our confidence in the model. Looking into the analogy between components and reference tones with more details, wFPC1 corresponds closely to Tone 1, wFPC2 can be easily associated with the shape of Tones 2 and 4 and wFPC3 corresponds to the U-shaped structure shown in Tone 3. wFPC4 appears to exhibit a sinusoid pattern that can be justified as necessary to move between different tones in certain tonal configurations (Hadjipantelis, Aston, and Evans 2012).

Empirical findings from the phase FPCA: Again the first question is how many components to retain. Based on existing JND in tempo studies (Quene 2007; Jacewicz, Fox, and Wei 2010), we choose to follow their methodology for choosing the number of “relevant” components (tempo JND: ≈ 5% relative distortion; M_s = 4). We focus on percentage changes on the transformed domain over the original phase domain as it is preferable to conduct principal component analysis (Aitchison 1983); sFPCs also corresponding to “standard patterns” (Figure 7). sFPC1 and sFPC2 exhibit a typical variation one would expect for slow starts and/or trailing syllable utterances where a decelerated start leads to an accelerated ending of the word—a catch-up effect—and vice versa. sFPC3 and sFPC4, on the other hand, show more complex variation patterns that are most probably rhyme specific (e.g., /-ia/) or associated with uncommon sequences (e.g., silent pause followed by a Tone 3) and do not have an obvious universal interpretation. While the curves in Figure 7 are not particularly smooth due to the discretized nature of the modeling, as can be seen in Figure S.1 in the supplementary material, the resulting warping functions after transformation are smooth.

Table 2 Percentage of variances reflected from each respective FPC (first 9 shown). Cumulative variance in parenthesis

	Amplitude/(w)	Phase/(s)
FPC1	88.67 (88.67)	49.40 (49.40)
FPC2	10.16 (98.82)	19.25 (68.65)
FPC3	0.75 (99.57)	9.02 (77.68)
FPC4	0.22 (99.80)	6.53 (84.19)
FPC5	0.10 (99.90)	4.34 (88.53)
FPC6	0.05 (99.94)	2.98 (91.51)
FPC7	0.02 (99.97)	2.32 (93.83)
FPC8	0.01 (99.98)	1.96 (95.79)
FPC9	0.01 (99.99)	1.29 (97.08)

Table 3 Actual deviations in Hz from each respective FPC (first 9 shown). Cumulative deviance in parenthesis. (Human speech auditory sensitivity threshold ≈ 10 Hz)

	Amplitude/(w)
FPC1	121.16(121.16)
FPC2	66.52 (187.68)
FPC3	31.22 (218.90)
FPC4	17.50 (236.40)
FPC5	9.00 (245.39)
FPC6	4.86 (250.26)
FPC7	3.64 (253.90)
FPC8	2.71 (256.61)
FPC9	1.96 (258.56)

Figure 7 (Phase) eigenfunctions Ψ: mean function ([0.05, 0.95] percentiles shown in gray) and first, second, third, fourth, fifth, and sixth functional principal components (FPCs) of phase. Roughness is due to differentiation and finite grid; the corresponding warping functions in their original domain are given in Figure S.1 in the supplementary material.

Empirical findings from the Multi-Variate Linear Mixed Effects (MVLME) analysis: The most important joint findings are the correlation patterns presented in the covariance structures of the random effects as well as their variance amplitudes. A striking phenomenon is the small, in comparison with the residual amplitude, amplitudes of the Sentence effects (Table 4). This goes to show that pitch as a whole is much more speaker dependent than context dependent. It also emphasizes why certain pitch modeling algorithms focus on the simulations of “neck physiology”(Taylor 2000; Fujisaki 2004; Louw and Barnard 2004).

Table 4 Random effects std. deviations

Estimate	$w{\text{FPC}}_1$	$w{\text{FPC}}_2$	$w{\text{FPC}}_3$	$w{\text{FPC}}_4$	Duration	${\text{sFPC}}_1$	$s{\text{FPC}}_2$	$s{\text{FPC}}_3$	$s{\text{FPC}}_4$
Speaker	89.245	6.326	3.655	1.330	2.806	0.289	0.023	0.022	0.030
Sentence	38.674	4.059	0.045	0.102	0.043	0.049	0.043	0.042	0.043
Residual	114.062	44.386	15.399	10.072	4.481	0.959	0.591	0.431	0.370

In addition to that we see some linguistically relevant correlation patterns in Figure 8 (also see S.25–S.26 in the supplementary material). For example, wFPC2 and duration are highly correlated both in the context of Speaker and Sentence-related variation. The shape of the second wFPC is mostly associated with linguistic properties (Hadjipantelis, Aston, and Evans 2012) and a syllable’s duration is a linguistically relevant property itself. As wFPC2 is mostly associated with the slope of syllable’s F₀ trajectory, it is unsurprising that changes in the slope affect the duration. Moreover, looking at the signs we see that while the Speaker influence is negative, in the case of Sentence, it is positive. That means that there is a balance on how variable the length of an utterance can be to remain comprehensible (so, e.g., when a speaker tends to talk more slowly than normal, the effect of the Sentence will be to “accelerate” the pronunciation of the words in this case). (See supplementary material for ${\Sigma }_{R_i}$’s definitions.) In relation to that, in the speaker random effect, $s{\text{FPC}}_1$ is also correlated with duration as well as $w{\text{FPC}}_2$; yielding a triplet of associated variables. Looking specifically to another phase component, $s{\text{FPC}}_2$ indicating mid syllable acceleration or deceleration that allow for changes in the overall pitch patterns, is associated with a syllable’s duration, this being easily interpreted by the face that such changes are modulated by alterations in the duration of the syllable itself. Complementary to these phenomena is the relation between the syllable duration and $w{\text{FPC}}_1$ sentence-related variation. This correlation does not appear in the speaker effects and thus is likely due to more linguistic rather than physiological changes in the sample. As mentioned previously, wFPC1 can be thought of as dictating pitch-level placement, and the correlation implies that higher-pitched utterances tend to last longer. This is not contrary to the previous finding; higher F₀ placements are necessary for a speaker to utter a more pronounced slope differential and obviously need more time to be manifested.

Figure 8 Random effects correlation matrices. The estimated correlation between the variables of the original multivariate model (Equation (3.19)$$\begin{array}{cc}\hfill A_{n\times p}& =X_{N\times k}{B}_{k\times p}+Z_{N\times l}{\Gamma }_{l\times p}+E_{N\times p},\end{array}$$) is calculated by rescaling the variance-covariance submatrices ${\Sigma }_{R_1}$ and ${\Sigma }_{R_2}$² of ${\Sigma }_{\Gamma }$ to unit variances. Each cell i, j shows the correlation between the variance of component in row i that of column j; row/columns 1–4: wFPC1-4, row/columns 5–8: sFPC1-4, row/columns 9: Duration.

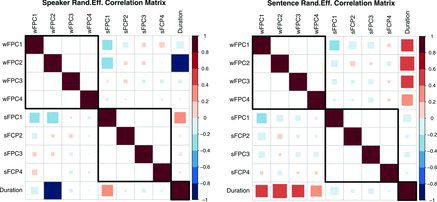
Interestingly, a number of lower magnitude correlation effects appear to associate $w{\text{FPC}}_1$ and sFPCs. This is something that needs careful interpretation. $w{\text{FPC}}_1$ is essentially “flat” (Figure 6, upper middle panel), and as such cannot be easily interpreted when combined with registration functions. Nevertheless this shows the value in our joint modeling approach for these data. We concurrently account for all these correlations during model estimation and, as such, our estimates are less influenced by artifacts in individual univariate FPCs.

Examining the influence of fixed effects, the presence of adjacent consonants was an important feature for almost every component in the model. Additionally, certain “domain-specific” fixed effects emerged also. The syllable’s rhyme type appeared to significantly affect duration; the break-point information to influence the amplitude of the F₀ curve and specific consonant-vowel-consonant (C-V-C) triplets to play a major role for phase. Phase also appeared to be related to the rhyme types but to a lesser extent (table of $\widehat{B}$ and associated standard errors available in https://tinyurl.com/COSPRO-Betas).

More specifically regarding duration of the F₀ curve, certain rhyme types (e.g., /-oŋ/, /-i$E$n/) gave prominent elongation effects while others (e.g., /-u/, /-$$/) were associated with shorter curves. These are high vowels, meaning that the jaw is more closed and the tongue is nearer to the top of the mouth than for low vowels. It is to be expected that some rhymes are shorter than others and that high vowels with no following nasal consonant would indeed be the shorter ones. The same pattern of variability in the duration was associated with the adjacent consonants information; when a vowel was followed by a consonant, the F₀ curve was usually longer while when the consonant preceded a vowel, the F₀ curve was shorter. Amplitude-related components are significantly affected by the utterances’ break-type information; particularly B2 and B3 break types. This is not a surprising finding; a pitch trajectory, to exhibit the well-established presence of “down-drift” effects (Fujisaki 2004), needs to be associated with such variables. As in the case of duration, the presence of adjacent consonants affects the amplitude dynamics. Irrespective of its type (voiced or unvoiced), the presence of consonant before or after a rhyme led to an “overall lowering” of the F₀ trajectory. Tone type and the sex of the speaker also influenced the dynamics of amplitude but to a lesser degree. Finally examining phase, it is interesting that most phase variation was mainly due to the adjacent consonants and the rhyme type of the syllable; these also being the covariates affecting duration. This confirms the intuition that as both duration and phase reflect temporal information, they would likely be affected by the same covariates. More specifically a short or a silent pause at the edge of rhyme caused that edge to appear decelerated while the presence of a consonant caused that edge to be accelerated. As before, certain rhymes (e.g., /-a/, /-ai/) gave more pronounced deceleration–acceleration effects. Tone types, while very important in the case of univariate models for amplitude (Hadjipantelis, Aston, and Evans 2012), did not appear significant in this analysis individually; they were usually significant when examined as interactions. However, this again illustrates the importance of considering joint models versus marginal models, as it allows a more comprehensive understanding of the nature of covariate effects.

In addition, we have reimplemented the main part of the analysis using the area under the curve methodology of Zhang and Müller (2011) that had previously been considered in Liu and Müller (2004) (results shown in supplementary material, Section S.6) and while the registration functions obtained are different, the analysis resulted in almost identical insights for the linguistic roles of w_i and s_i, again emphasizing the need to consider a joint model.

5. DISCUSSION

Linguistically our work establishes the fact that when trying to give a description of a language’s pitch, one needs to take care of amplitude and phase covariance patterns while correcting for linguistic (Sentence) and nonlinguistic (Speaker) effects. This need was prominently demonstrated by the strong correlation patterns observed (Figure 8). Clearly we do not have independent components in our model and therefore a joint model is appropriate. This has an obvious theoretical advantage in comparison to standard linguistic modeling approaches such as MOMEL (Hirst and Espesser 1993) or the Fujisaki model (Mixdorff 2000; Fujisaki 2004) where despite the use of splines to model amplitude variation, phase variation is ignored.

Focusing on the interpretation of our results, it is evident that the covariance between phase and amplitude is mostly due to nonlinguistic (Speaker-related) rather than linguistic features (Sentence-related). This is also reflected in the dynamics of duration, where the influence is also greater (than the Sentence-related). Our work as a whole presents a first coherent statistical analysis of pitch incorporating phase, duration, and amplitude modeling into a single overall approach.

One major statistical issue with the interpretation of our results is due to the inherent identifiability problem of curve registration. It is not possible, without extra assumptions, to determine two functions (amplitude and phase) from one sampled curve. While this is a problem in general, especially for the relatively simply structured pitch functions that we consider here, nonidentifiability of the decomposition of total variation into warping and amplitude variation is a well-known issue. This is in contrast with situations where functions have distinct structures such as well-defined peaks (Kneip and Gasser 1992). In any case, identifiability usually needs to be enforced by model assumptions or algorithmically. We use pairwise registration, for which identifiability conditions have been given in Tang and Müller (2008). In practice, we enforce a unique decomposition algorithmically by first obtaining the warping functions through the pairwise comparisons, and then attributing the remaining variation to amplitude variation that is quantified in a second step. However, as outlined in Kneip and Ramsay (2008), while there are many registration procedures that will give rise to consistent registrations, the most meaningful criterion to determine whether observed variation is due to registration or amplitude variation is interpretability in the context of specific applications, which in our application is intrinsically linked to the nature of the relationship between the linguistic covariates and the functional principal component scores of both amplitude and warping functions. Emphasizing the linguistically important JND criteria, the eigenfunctions associated with the largest four eigenvalues in both the amplitude and phase bases could all be detected by the human ear, and as such, would affect the sound being perceived. Further, because we consider an LME model for the joint score vector associated with the amplitude and warping functions, we are able to capture correlations between the two sets of functions. This joint modeling helps alleviate some of the concerns regarding overall identifiability, as it is the joint rather than marginal results that are of interest. The fact that the scores and FPCs were all linguistically interpretable also gives further credence to the approach. Additionally, applying a different registration method (Zhang and Müller 2011) led to similar linguistic interpretations (see supplementary material, Section S.6).

In addition to the issue of identifiability, the obvious technical caveats with this work stem from three main areas: the discretization procedure, the time-registration procedure, and the multivariate mixed effects regression. Focusing on the discretization, the choice of basis is of fundamental importance. While we used principal components for the reason mentioned above, there have been questions as to whether a residual sum of squares optimality is most appropriate. It is certainly an open question when it comes to application specific cases (Bruns 2004). Aside from the case of parametric bases, nonparametric basis function generation procedures such as ICA (Hyvärinen and Oja 2000) have become recently increasingly more prominent. These bases could be used in the analysis, although the subsequent modeling of the scores would become inherently more complex due to the lack of certain orthogonality assumptions.

Regarding time-registration, there are a number of open questions regarding the choice of the framework to be used. However, we have examined two different frameworks and both these resulted in similar overall conclusions. The choice of the time-registration framework ultimately relies on the theoretical assumptions one is willing to make and on the application and the samples to be registered. For the linguistic application, we are concerned with, it is not unreasonable to assume that the pairwise alignment corresponds well to the intuitive belief that intrinsically humans have a “reference” utterance onto which they “map” what they hear to comprehend it (Benesty, Sondhi, and Huang 2008).

Finally, multivariate mixed effects regression is itself an area with many possibilities. Optimization for such models is not always trivial and as the model and/or the sample size increases, estimation of the model tends to get computationally expensive. In our case, we used a hybrid optimization procedure that changes between a simplex algorithm (Nelder-Mead) and a quasi-Newton approach (Broyden-Fletcher-Goldfarb-Shanno; BFGS) (Kelley 1999) (see supplementary material for more information); in recent years research regarding the optimization tasks in an LME model has tended to focus on derivative free procedures. In a related issue, the choice of covariance structure is of importance. While we chose a very flexible covariance structure, the choice of covariance can convey important experimental insights. A final note specific to our problem was the presence of only five speakers. Speaker effect is prominent in many components and appears influential despite the small number of speakers available; nevertheless we recognize that including more speakers would have certainly been beneficial if they had been available. Given that the Speaker effect was the most important random-effect factor of this study, the inclusion of random slopes might also have been of interest (Schielzeth and Forstmeier 2009; Barr et al. 2013). Nevertheless, the inclusion of generic linear, quadratic, and cubic gender-specific down-drift effects presented through the break components allows substantial model flexibility to avoid potential design-driven misspecification of the random effects.

In conclusion, we have proposed a comprehensive modeling framework for the analysis of phonetic information in its original domain of collection, via the joint analysis of phase, amplitude, and duration information. The models are interpretable due to the LME structure, and estimable in a standard Euclidean domain via the compositional transform of the warping functions. The resulting model provides estimates and ultimately a typography of the shape, distortion and duration of tonal patterns, and effects in one of the world’s major languages.

SUPPLEMENTARY MATERIAL

Additional supplementary information is provided in the following files:

• Supplementary Material Additional figures, information about covariance structures, and implementation details concerning the multivariate linear mixed effect analysis.

• Supplementary Code Code and example analysis for multivariate linear mixed effect model.

Additional information

Notes on contributors

P. Z. Hadjipantelis

P. Z. Hadjipantelis is PhD, Centre for Research in Statistical Methodology; Centre for Complexity Science, University of Warwick, Coventry CV4 7AL, UK (E-mail: [email protected]).

J. A. D. Aston

J. A. D. Aston is Professor, Centre for Research in Statistical Methodology, University of Warwick, Coventry CV4 7AL, UK and Department of Pure Maths and Mathematical Statistics, Statistical Laboratory, University of Cambridge, Cambridge, UK (E-mail: [email protected]).

H. G. Müller

H. G. Müller is Professor, Department of Statistics, University of California, Davis, CA 95616 (E-mail: [email protected]).

J. P. Evans

J. P. Evans is PhD, Institute of Linguistics, Academia Sinica, Taipei, Taiwan (E-mail: [email protected])