Generalized Additive Models for Gigadata: Modeling the U.K. Black Smoke Network Daily Data

Abstract

We develop scalable methods for fitting penalized regression spline based generalized additive models with of the order of 10⁴ coefficients to up to 10⁸ data. Computational feasibility rests on: (i) a new iteration scheme for estimation of model coefficients and smoothing parameters, avoiding poorly scaling matrix operations; (ii) parallelization of the iteration’s pivoted block Cholesky and basic matrix operations; (iii) the marginal discretization of model covariates to reduce memory footprint, with efficient scalable methods for computing required crossproducts directly from the discrete representation. Marginal discretization enables much finer discretization than joint discretization would permit. We were motivated by the need to model four decades worth of daily particulate data from the U.K. Black Smoke and Sulphur Dioxide Monitoring Network. Although reduced in size recently, over 2000 stations have at some time been part of the network, resulting in some 10 million measurements. Modeling at a daily scale is desirable for accurate trend estimation and mapping, and to provide daily exposure estimates for epidemiological cohort studies. Because of the dataset size, previous work has focused on modeling time or space averaged pollution levels, but this is unsatisfactory from a health perspective, since it is often acute exposure locally and on the time scale of days that is of most importance in driving adverse health outcomes. If computed by conventional means our black smoke model would require a half terabyte of storage just for the model matrix, whereas we are able to compute with it on a desktop workstation. The best previously available reduced memory footprint method would have required three orders of magnitude more computing time than our new method. Supplementary materials for this article are available online.

Keywords:

• Air pollution
• Big data
• Parallel computing
• Regression
• Smoothing

1. Introduction

This article proposes a method for estimating generalized additive models (a particular class of Gaussian latent process models) for much larger datasets and models than has hitherto been possible. For our application we achieve a three order of magnitude speed up relative to previous big data GAM methods (e.g., Wood, Goude, and Shaw 2015). Our new method rests on three innovations: (i) an efficient new fitting iteration, employing a minimal number of matrix operations all of which scale reasonably well, (ii) OpenMP based parallelization of these matrix operations, and (iii) a novel marginal covariate discretization scheme, enabling compact model representation and efficient computation of key matrix crossproducts. These three elements work together, and dropping any one of them leads to an increase in fitting time of an order of magnitude or more.

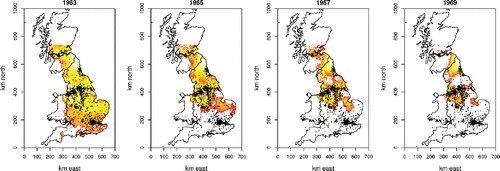
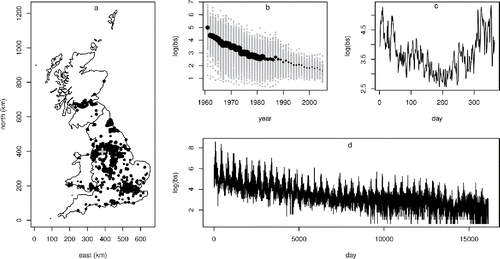
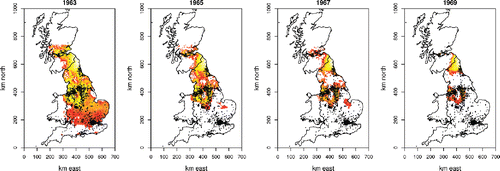
We are motivated by a practical problem in spatial epidemiology: the local estimation of short-term exposure to air pollution, based on monitoring network data. Specifically we focus on the United Kingdom Black Smoke (BS) monitoring network, which collected daily data on $\mu \text{g}{\text{m}}^{-3}$ (micrograms per cubic meter) of BS particulates (largely from coal and Diesel combustion) from 1961 to 2005. The U.K. BS network fluctuated in size with different stations being added and removed over time, peaking at 1269 stations in 1967 but declining to 73 stations by 2005. Figure 1(a) shows the network in 1967, indicating the average log BS measurements in that year. The other panels in Figure 1 illustrate the temporal patterns in the data, and in the network size. In total the data comprise 9,451,232 daily measurements from 2862 monitoring sites.

Figure 1. (a) The U.K. Black Smoke Network monitoring network at its largest in 1967. Symbol sizes are proportional to annual average log black smoke. (b) Annual average log black smoke against year. Black dots are averages over space, with dot size proportional to network size. Gray dots are station averages. (c) Daily averages for 1967, across all stations shown in (a). (d) All daily measurements for the longest running site, shown as a gray “+” in (a).

Because of the data volume, previous attempts to model spatiotemporal patterns in the BS data have focused on annual averages (e.g., Shaddick and Zidek 2014). This is not entirely satisfactory from an epidemiological perspective, since acute respiratory disease is usually sensitive to exposure to high levels of pollution over short time periods, and such exposure can be completely hidden in an annual average. Retrospective cohort studies, for example, really require estimates of exposure at the daily level, rather than annual averages, if they are to successfully uncover acute effects. This difference between acute and long-term exposure is also reflected in the health guidelines, with EU regulations currently stipulating that annual average exposure should not exceed $68\mu \text{g}{\text{m}}^{-3}$ while daily peak exposure should not exceed $213\mu \text{g}{\text{m}}^{-3}$.

Given the data volume, an obvious option is not to model, but simply to estimate daily exposure directly from the raw measurement, but this is a poor option for several reasons. First, the network design is not random but shows a type of preferential sampling (Shaddick and Zidek 2014), so that a design based approach to exposure estimation will result in bias, which is only avoidable by taking a model-based approach. Second, the reduced number of stations later in the data make spatial predictions difficult without a model that is able to share information across years. Third, there are strong covariate effects.

We will end up using a model structure (1) $$\begin{array}{ccc}& & log\left({\mathtt{bs}}_i\right)\hfill \\ & & =f_1\left({\mathtt{y}}_i\right)+f_2\left({\mathtt{doy}}_i\right)+f_3\left({\mathtt{dow}}_i\right)+f_4({\mathtt{y}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_5({\mathtt{y}}_i,{\mathtt{dow}}_i)+f_6({\mathtt{doy}}_i,{\mathtt{dow}}_i)\hfill \\ & & +f_7({\mathtt{n}}_i,{\mathtt{e}}_i)+f_8({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{y}}_i)+f_9({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_{10}({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{dow}}_i)+f_{11}\left({\mathtt{h}}_i\right)+f_{12}({\mathtt{T}}_i^0,{\mathtt{T}}_i^1)\hfill \\ & & +f_{13}({\overline{\mathtt{T}\mathtt{1}}}_i,{\overline{\mathtt{T}\mathtt{2}}}_i)\hfill \\ & & +f_{14}\left({\mathtt{r}}_i\right)+{\alpha }_{k\left(i\right)}+b_{\text{id}\left(i\right)}+e_i\hfill \end{array}$$(1) where $\mathtt{y}$, $\mathtt{doy}$ and $\mathtt{dow}$ denote, year, day of year, and day of week; $\mathtt{n}$ and $\mathtt{e}$ denote location as kilometers north and east; $\mathtt{h}$ and $\mathtt{r}$ are height (elevation of station) and cube root transformed rainfall (unfortunately only available as monthly average); ${\mathtt{T}}^0$ and ${\mathtt{T}}^1$ are daily minimum and maximum temperature, while $\overline{\mathtt{T}\mathtt{1}}$ and $\overline{\mathtt{T}\mathtt{2}}$ are daily mean temperature on and two days previously; α_k(i) is a fixed effect for the site type k of the $i\text{th}$ observation (type is one of R (rural), A (industrial), B (residential), C (commercial), D (city/town center), X (mixed), or M (missing)); $b_{\text{id}\left(i\right)}$ is a random effect for the $\text{id}\text{th}$ station, while e_i is a Gaussian error term following an AR process at each site.

Using reduced rank spline basis expansions for the terms in (1(1) $$\begin{array}{ccc}& & log\left({\mathtt{bs}}_i\right)\hfill \\ & & =f_1\left({\mathtt{y}}_i\right)+f_2\left({\mathtt{doy}}_i\right)+f_3\left({\mathtt{dow}}_i\right)+f_4({\mathtt{y}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_5({\mathtt{y}}_i,{\mathtt{dow}}_i)+f_6({\mathtt{doy}}_i,{\mathtt{dow}}_i)\hfill \\ & & +f_7({\mathtt{n}}_i,{\mathtt{e}}_i)+f_8({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{y}}_i)+f_9({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_{10}({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{dow}}_i)+f_{11}\left({\mathtt{h}}_i\right)+f_{12}({\mathtt{T}}_i^0,{\mathtt{T}}_i^1)\hfill \\ & & +f_{13}({\overline{\mathtt{T}\mathtt{1}}}_i,{\overline{\mathtt{T}\mathtt{2}}}_i)\hfill \\ & & +f_{14}\left({\mathtt{r}}_i\right)+{\alpha }_{k\left(i\right)}+b_{\text{id}\left(i\right)}+e_i\hfill \end{array}$$(1) ) requires around 8000 model coefficients. So estimating the model as a penalized GLM in the manner of Wood (2011) would require half a terabyte of storage just for the model matrix and is clearly infeasible. Our original intention was to use the method of Wood, Goude, and Shaw (2015) (available in R package mgcv) or to follow Shaddick and Zidek (2014) in using the method of Rue, Martino, and Chopin (2009) (via the INLA package), however this proved not to be feasible. Even if the computational load had been acceptable in terms of execution time, our experiments with smaller models and datasets suggested that INLA would require more than the 128Gb of memory that we had available. The Wood, Goude, and Shaw (2015) method would have been possible in terms of memory footprint, but we estimated that fitting would have taken in excess of a month of computing time (12 core Xeon E5-2670 2.3 GHz CPU), even using an enhanced efficiency version of the method employing some of the ideas from the current article for REML smoothing parameter selection. Using just the published method would have required approximately five times as long.

After reviewing model representation in Section 2, we develop a practical fitting method in Sections 3 and 4, which reduces the fitting time for model (1(1) $$\begin{array}{ccc}& & log\left({\mathtt{bs}}_i\right)\hfill \\ & & =f_1\left({\mathtt{y}}_i\right)+f_2\left({\mathtt{doy}}_i\right)+f_3\left({\mathtt{dow}}_i\right)+f_4({\mathtt{y}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_5({\mathtt{y}}_i,{\mathtt{dow}}_i)+f_6({\mathtt{doy}}_i,{\mathtt{dow}}_i)\hfill \\ & & +f_7({\mathtt{n}}_i,{\mathtt{e}}_i)+f_8({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{y}}_i)+f_9({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_{10}({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{dow}}_i)+f_{11}\left({\mathtt{h}}_i\right)+f_{12}({\mathtt{T}}_i^0,{\mathtt{T}}_i^1)\hfill \\ & & +f_{13}({\overline{\mathtt{T}\mathtt{1}}}_i,{\overline{\mathtt{T}\mathtt{2}}}_i)\hfill \\ & & +f_{14}\left({\mathtt{r}}_i\right)+{\alpha }_{k\left(i\right)}+b_{\text{id}\left(i\right)}+e_i\hfill \end{array}$$(1) ) to under an hour. The novel developments that allow this are covered in Section 4 and appendix A. Sections 5 and 5.1 then discuss the black smoke modeling in more detail.

2. Model Class and Representation

We first review the class of generalized additive models (GAM) introduced by Hastie and Tibshirani (1986, 1990) (see also Wahba 1990), relating a univariate response, y_i to predictors x_ji (which may be vector). A GAM has the structure (2) $$\begin{array}{c}\hfill y_i\sim \text{EF}({\mu }_i,\varphi )\text{where}g\left({\mu }_i\right)=\mathbf{A}(i,:)\mathit{}\mathbf{\theta }+\sum _j{f}_j\left(x_{ji}\right),\end{array}$$(2) μ_i = E(y_i), EF denotes an exponential family distribution with known or unknown scale parameter φ, g is a known smooth monotonic link function, A(i, : ) the $i\text{th}$ row of any parametric model matrix, and $\mathit{}\mathbf{\theta }$ the corresponding parameter vector. The f_j are unknown smooth functions to be estimated (and must usually be subjected to sum-to-zero identifiability constraints).

For estimation purposes we adopt the widely used approach of representing the unknown functions using reduced rank smoothing splines. Full smoothing splines arise from solving variational problems. For example, the cubic spline problem seeks f, from some reproducing kernel Hilbert (or appropriate Sobolov) space, to minimize ∑ⁿ_{i = 1}{y_i − f(x_i)}² + λ∫f′′(x)²dx (λ is a smoothing parameter). The result can be represented in terms of an explicit n-dimensional basis, while the spline penalty becomes a quadratic penalty on the basis coefficients. However, since, at latest, Wahba (1980) and Parker and Rice (1985), it has been recognized that an n-dimensional basis representation is computationally wasteful for negligible statistical gain and use of a k ≪ n dimensional basis is often preferable. Theoretical work by Gu and Kim (2002), Hall and Opsomer (2005), Li and Ruppert (2008), Kauermann, Krivobokova, and Fahrmeir (2009), Claeskens, Krivobokova, and Opsomer (2009) and Wang, Shen, and Ruppert (2011) show that the reduced rank approach is well founded, with k needing to grow only rather slowly with sample size (e.g., k = O(n^1/5) for a cubic spline under REML smoothness estimation).

A rich variety of reduced rank model terms are available in addition to cubic splines. Examples are the P-splines of Eilers and Marx (1996); Marx and Eilers (1998); Ruppert, Wand, and Carroll (2003), and adaptive variants (e.g., Wood 2011), as well as the isotropic thin plate and other Duchon splines (Duchon 1977), for which rank reduction is conveniently performed by the eigen method of Wood (2003). Reduced rank tensor product splines (e.g., Eilers and Marx 2003; Wood 2006) are important for representing smooth interactions, splines on the sphere (Wahba 1981) and Gaussian process smoothers (Kammann and Wand 2003; Handcock, Meier, and Nychka 1994) are useful in some spatial applications. In all cases if ${\mathbf{f}}_j={[f_j\left(x_{j1}\right),f_j\left(x_{j2}\right),\dots ]}^{\mathsf{T}}$ we can write ${\mathbf{f}}_j={\mathbf{X}}_j{\mathit{}\mathbf{\beta }}_j$ where X_j is an n × p_j model matrix for the smooth, containing its basis functions evaluated at the observed x_j values. ${\mathit{}\mathbf{\beta }}_j$ is the corresponding coefficient vector. The smoothing penalty for f_j can then be written ${\mathit{}\mathbf{\beta }}_j^{\mathsf{T}}{\mathit{}\mathcal{S}}_j{\mathit{}\mathbf{\beta }}_j$, where ${\mathit{}\mathcal{S}}_j$ contains known coefficients. Since the individual f_j in (2(2) $$\begin{array}{c}\hfill y_i\sim \text{EF}({\mu }_i,\varphi )\text{where}g\left({\mu }_i\right)=\mathbf{A}(i,:)\mathit{}\mathbf{\theta }+\sum _j{f}_j\left(x_{ji}\right),\end{array}$$(2) ) are only estimable to within an intercept term, identifiability constraints need to be applied. As discussed in Wood, Scheipl, and Faraway (2013) the sum-to-zero constraints, ∑_if_j(x_ji) = 0 have the advantage of leading to narrow confidence intervals on the constrained f_j, and it is easy to reparameterize to incorporate the constraints directly into X_j and ${\mathit{}\mathcal{S}}_j$ (which, respectively, lose a column, and a row and column in the process).

It is then straightforward to create a single n × p model matrix X = (A, X₁, X₂, …) with corresponding combined parameter vector $\mathit{}\mathbf{\beta }$. Given some smoothing parameters $\mathit{}\mathbf{\lambda }$ a combined smoothing penalty could then be written as ${\sum }_j{\lambda }_j{\mathit{}\mathbf{\beta }}_j^{\mathsf{T}}{\mathit{}\mathcal{S}}_j{\mathit{}\mathbf{\beta }}_j={\sum }_j{\lambda }_j{\mathit{}\mathbf{\beta }}^{\mathsf{T}}{\mathbf{S}}_j\mathit{}\mathbf{\beta }={\mathit{}\mathbf{\beta }}^{\mathsf{T}}{\mathbf{S}}_{\lambda }\mathit{}\mathbf{\beta }$, where S_j is simply a zero padded version of ${\mathit{}\mathcal{S}}_j$ and S_λ = ∑_jλ_jS_j. Hence, we have an overparameterized GLM structure, $g\left(\mathit{}\mathbf{\mu }\right)=\mathbf{X}\mathit{}\mathbf{\beta }$. Given smoothing parameters it is estimated via (3) $$\begin{array}{c}\hfill \widehat{\mathit{}\mathbf{\beta }}=\underset{\beta }{\text{argmax}}l\left(\mathit{}\mathbf{\beta }\right)-{\mathit{}\mathbf{\beta }}^{\mathsf{T}}{\mathbf{S}}_{\lambda }\mathit{}\mathbf{\beta }/2.\end{array}$$(3) This penalized likelihood approach (e.g., Green and Silverman 1994) can be viewed as a reasonable approach in its own right. An alternative is to view penalization as the expression of a belief that “smooth is more probable than wiggly” and to express this using the (improper) prior $$\mathit{}\mathbf{\beta }\sim N(\mathbf{0},{\mathbf{S}}_{\lambda }^{-}),$$where S⁻_λ is a Moore-Penrose pseudoinverse (S_λ being rank deficient because the penalties leave some space of functions unpenalized, and in any case do not penalize the fixed effects). In that case $\widehat{\mathit{}\mathbf{\beta }}$ is the MAP estimator of $\mathit{}\mathbf{\beta }$, and it is clear that we can view the GAM as a Gaussian latent random field model (see Kimeldorf and Wahba 1970; Wahba 1983; Silverman 1985; Fahrmeir and Lang 2001; Ruppert, Wand, and Carroll 2003, etc.). The smoothing parameters, $\mathit{}\mathbf{\lambda }$, can be estimated by generalized cross-validation or similar (e.g., Craven and Wahba 1979), but Reiss and Ogden (2009) showed that a (restricted) marginal likelihood approach (e.g., Wood 2011) offers practical reliability advantages, in being less prone to multiple local optima and consequent undersmoothing.

3. The Fitting Iteration

The purpose of this article is to allow the rich existing modeling framework, described in Section 2, to be used with much larger models and datasets than has hitherto been possible, by providing substantially new scalable fitting methods. The new methods are based on the performance iteration (Gu 1992) or PQL (Breslow and Clayton 1993) approach to model fitting, modified to obtain reasonable scalability. Before introducing the modifications, we motivate the basic approach and provide an alternative justification for its use, suited to penalized regression.

It is readily shown that maximization of (3(3) $$\begin{array}{c}\hfill \widehat{\mathit{}\mathbf{\beta }}=\underset{\beta }{\text{argmax}}l\left(\mathit{}\mathbf{\beta }\right)-{\mathit{}\mathbf{\beta }}^{\mathsf{T}}{\mathbf{S}}_{\lambda }\mathit{}\mathbf{\beta }/2.\end{array}$$(3) ) by Fisher scoring is equivalent to the following penalized iteratively reweighted least squares (PIRLS) scheme. Initialize ${\widehat{\mu }}_i=y_i+{\delta }_i$ and ${\widehat{\eta }}_i=g\left({\widehat{\mu }}_i\right)$ where δ_i is a small constant (often zero) chosen to ensure $g\left({\widehat{\mu }}_i\right)$ exists. Then iterate the following to convergence

1.

Form “pseudodata” $z_i=g^{\text{'}}\left({\widehat{\mu }}_i\right)(y_i-{\widehat{\mu }}_i)+{\widehat{\eta }}_i$ and weight matrix $\mathbf{W}=\text{diag}\left(w_i\right)$ where $w_i^{-1}=V\left({\widehat{\mu }}_i\right)g^{\text{'}}{\left({\widehat{\mu }}_i\right)}^2$.

2.

By penalized least squares, estimate $\mathit{}\mathbf{\beta }$ for the working model $$\begin{array}{ccc}\hfill \mathbf{z}& =& \mathbf{X}\mathit{}\mathbf{\beta }+\mathit{}\mathbf{ϵ},\text{where}\mathit{}\mathbf{\beta }\sim N(\mathbf{0},{\mathbf{S}}_{\lambda }^{-}),\hfill \\ \hfill E\left(\mathit{}\mathbf{ϵ}\right)& =& \mathbf{0}\text{and}E\left(\mathit{}\mathbf{ϵ}{\mathit{}\mathbf{ϵ}}^{\mathsf{T}}\right)=\varphi {\mathbf{W}}^{-1}.\hfill \end{array}$$

The key idea of performance iteration/PQL is to estimate $\mathit{}\mathbf{\lambda }$ and φ at each iteration from the working model. Consider using restricted marginal likelihood (REML) for this purpose. First suppose that we were to make the clearly false assumption that $\mathit{}\mathbf{ϵ}\sim N(\mathbf{0},{\mathbf{W}}^{-1}\varphi )$. If ${\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }={\text{argmin}}_{\beta }{\parallel \mathbf{z}-\mathbf{X}\mathit{}\mathbf{\beta }\parallel }_w^2/\varphi +{\mathit{}\mathbf{\beta }}^{\mathsf{T}}{\mathbf{S}}_{\lambda }\mathit{}\mathbf{\beta }$, where ${\parallel \mathbf{x}\parallel }_w^2={\mathbf{x}}^{\mathsf{T}}\mathbf{Wx}$ and M is the dimension of the null space of S_λ, then the twice negative log REML (e.g. Wood 2011) is (4) $$\begin{array}{ccc}\hfill \mathcal{V}\left(\mathit{}\mathbf{\lambda }\right)& =& \parallel \mathbf{z}-\mathbf{X}{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }{\parallel }_w^2/\varphi +{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }^{\mathsf{T}}{\mathbf{S}}_{\lambda }{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }+log|{\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\varphi +{\mathbf{S}}_{\lambda }|\hfill \\ & & -log|{\mathbf{S}}_{\lambda }{|}_{+}+nlog\left(\varphi \right)+(n-M)log\left(2\pi \right).\hfill \end{array}$$(4) Differentiating $\mathcal{V}$ with respect to φ and equating to zero, we find that the REML estimate of φ must satisfy (5) $$\begin{array}{c}\hfill \widehat{\varphi }=\frac{\parallel \mathbf{z}-\mathbf{X}{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }{\parallel }_w^2}{n-\tau },\end{array}$$(5) where $\tau =\text{tr}\{{({\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\widehat{\varphi }+{\mathbf{S}}_{\lambda })}^{-1}{\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\widehat{\varphi }\}$ is the “effective degrees of freedom” of the model. So $\widehat{\varphi }$ is simply the “Pearson estimator” of the scale parameter, which is a reasonable estimator without any REML justification, and without assuming normality of z (see, e.g., Wahba 1983; McCullagh and Nelder 1989; Hastie and Tibshirani 1990).

Now let us eliminate the false assumption of normality of z, replacing it with central limit theorem justification. Consider the QR decomposition $\sqrt{\mathbf{W}}\mathbf{X}=\mathit{}\mathcal{Q}\mathbf{R}$, where $\mathit{}\mathcal{Q}$ has orthogonal columns and $\mathit{}\mathcal{R}$ is upper triangular (this decomposition is purely a theoretical device, nowhere in the new methods below do we actually need to compute a QR decomposition). Define $\mathbf{f}={\mathbf{Q}}^{\mathsf{T}}\sqrt{\mathbf{W}}\mathbf{z}$, r = ‖z‖²_w − ‖f‖². In that case ${\mathbf{X}}^{\mathsf{T}}\mathbf{WX}={\mathit{}\mathcal{R}}^{\mathsf{T}}\mathit{}\mathcal{R}$, $\parallel \mathbf{z}-\mathbf{X}{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }{\parallel }_w^2={\parallel \mathbf{f}-\mathit{}\mathcal{R}\mathit{}\mathbf{\beta }\parallel }^2+r$, and we have the alternative working model (6) $$\begin{array}{c}\hfill \mathbf{f}=\mathit{}\mathcal{R}\mathit{}\mathbf{\beta }+\mathbf{e},\mathit{}\mathbf{\beta }\sim N(\mathbf{0},{\mathbf{S}}_{\lambda }^{-})\text{and}\mathbf{e}\sim N(\mathbf{0},\mathbf{I}\varphi ),\end{array}$$(6) where the multivariate central limit theorem justifies e ∼ N(0, Iφ) as an n/p → ∞ approximation. The twice negative log restricted marginal likelihood for this model is $$\begin{array}{ccc}\hfill {\mathcal{V}}_r\left(\mathit{}\mathbf{\lambda }\right)& =& \parallel \mathbf{f}-\mathit{}\mathcal{R}{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }{\parallel }^2/\varphi +{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }^{\mathsf{T}}{\mathbf{S}}_{\lambda }{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }+log|{\mathit{}\mathcal{R}}^{\mathsf{T}}\mathit{}\mathcal{R}/\varphi +{\mathbf{S}}_{\lambda }|\hfill \\ & & -log|{\mathbf{S}}_{\lambda }{|}_{+}+plog\varphi +(p-M)log\left(2\pi \right).\hfill \end{array}$$For a given φ, $\mathcal{V}$ and ${\mathcal{V}}_r$ differ only by an additive constant, and therefore result in identical inference about $\mathit{}\mathbf{\lambda }$ and $\mathit{}\mathbf{\beta }$. Inference about φ would of course differ, since r carries information about φ, but if we plug the Pearson estimate (5(5) $$\begin{array}{c}\hfill \widehat{\varphi }=\frac{\parallel \mathbf{z}-\mathbf{X}{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }{\parallel }_w^2}{n-\tau },\end{array}$$(5) ) into ${\mathcal{V}}_r$ then we obtain identical inference to that obtained by simply using $\mathcal{V}$ for φ and $\mathit{}\mathbf{\lambda }$. This justifies use of (4(4) $$\begin{array}{ccc}\hfill \mathcal{V}\left(\mathit{}\mathbf{\lambda }\right)& =& \parallel \mathbf{z}-\mathbf{X}{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }{\parallel }_w^2/\varphi +{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }^{\mathsf{T}}{\mathbf{S}}_{\lambda }{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }+log|{\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\varphi +{\mathbf{S}}_{\lambda }|\hfill \\ & & -log|{\mathbf{S}}_{\lambda }{|}_{+}+nlog\left(\varphi \right)+(n-M)log\left(2\pi \right).\hfill \end{array}$$(4) ) for $\mathit{}\mathbf{\lambda },\varphi$ estimation.

Note that once the coefficients and smoothing parameters are estimated, further inference can be based on the large sample Bayesian result, (7) $$\begin{array}{c}\hfill \mathit{}\mathbf{\beta }\sim N(\widehat{\mathit{}\mathbf{\beta }},{({\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\varphi +{\mathbf{S}}_{\lambda })}^{-1}),\end{array}$$(7) which turns out to provide well calibrated frequentist inference (Wahba 1983; Silverman 1985; Nychka 1988; Marra and Wood 2012; Wood 2013).

4. A Practical Fitting Method

Implementation of the fitting iteration of Section 3 is limited by several practical considerations.

1.	For the target datasets and models, it is impractical to explicitly form X whole.
2.	The log determinant terms in $\mathcal{V}$ are potentially numerically unstable. Because having some λj → ∞ is legitimate in GAM estimation, Sλ can become so badly scaled that the computation of log determinants involves taking the logs of terms that are numerically zero.
3.	For maximal efficiency it is not sensible to optimize $\mathcal{V}$ at each iteration step, when it will anyway be modified at the next step.
4.	The update step for $\mathcal{V}$ should involve computations that scale well to multi-core computation.

Wood, Goude, and Shaw (2015) addressed 1 by iteratively updating the QR factorization of X, and then applying the method of Wood (2011) to (6(6) $$\begin{array}{c}\hfill \mathbf{f}=\mathit{}\mathcal{R}\mathit{}\mathbf{\beta }+\mathbf{e},\mathit{}\mathbf{\beta }\sim N(\mathbf{0},{\mathbf{S}}_{\lambda }^{-})\text{and}\mathbf{e}\sim N(\mathbf{0},\mathbf{I}\varphi ),\end{array}$$(6) ). This approach ignored 3, requires pivoted QR decomposition and addressed 2 by stabilizing reparameterizations involving p × p symmetric eigen decomposition: the QR and eigen decompositions do not scale well. For example the state of the art block pivoted QR decomposition of Quintana-Ortí, Sun, and Bischof (1998), only has around half the floating point operations as matrix-matrix computations. In consequence the Wood, Goude, and Shaw (2015) was computationally impractical for the black smoke model. See appendix C for a discussion of the issues around multicore computing.

Our proposal here addresses 3 by taking a single Newton step to update $\mathit{}\mathbf{\rho }=log\left(\mathit{}\mathbf{\lambda }\right)$ at each cycle of the iteration (rather than fully optimizing $\mathcal{V}$ at each cycle). We propose to avoid the stabilizing reparameterization step by avoiding evaluation of the log determinants altogether (hence, addressing 2). This is based on the observation that the Newton step, $\mathit{}\mathbf{\Delta }$, only involves the derivative of $\mathcal{V}$, and the derivatives of the log determinants are less numerically problematic. Evaluation of $\mathcal{V}$ is usually required to ensure that the Newton step results in an improvement of $\mathcal{V}$. We cannot skip such a check, but we can substitute the alternative check that ${\mathit{}\mathbf{\Delta }}^{\mathsf{T}}\nabla \mathcal{V}(\mathit{}\mathbf{\rho }+\mathit{}\mathbf{\Delta })\le 0$, that is, that $\mathcal{V}$ is nonincreasing in the direction of $\mathit{}\mathbf{\Delta }$ at the end of the Newton step (see, e.g., Wood, 2015, sec. 5.1.1).

Adopting this approach we find that the derivatives of $\mathcal{V}$ can be obtained using simple matrix operations and a pivoted Cholesky decomposition of ${\mathbf{X}}^{\mathsf{T}}\mathbf{WX}$, which can be accumulated blockwise, thereby dealing with 1. Lucas (2004) provides a block oriented pivoted Cholesky decomposition readily parallelized using openMP (OpenMP Architecture Review Board, 2008), which deals with point 4. The resulting method has the further advantage that, with some further work, it turns out to be possible to produce further substantial efficiency savings by discretization of the model covariates (see Section 4.5).

4.1. The Modified Fitting Iteration

Based on the above considerations, the proposed fitting iteration is as follows. Its convergence properties are discussed in Appendix B.

• Perform the term by term reparameterization described in Section 4.3.

• Initialize ${\mathit{}\mathbf{\rho }}_0$, ${\mathit{}\mathbf{\Delta }}_0=\mathbf{0}$, ${\widehat{\mu }}_i=y_i+{\delta }_i$ and ${\widehat{\eta }}_i=g\left({\widehat{\mu }}_i\right)$. δ_i is 0 or a small value chosen to ensure that ${\widehat{\eta }}_i$ exists.

• Repeat...

1.	Accumulate ${\mathbf{X}}^{\mathsf{T}}\mathbf{WX}$, $\mathbf{f}={\mathbf{X}}^{\mathsf{T}}\mathbf{W}\mathbf{z}$ and penalized deviance, D. $z_i=g^{\text{'}}\left({\widehat{\mu }}_i\right)(y_i-{\widehat{\mu }}_i)+{\widehat{\eta }}_i$ and W is diagonal with entries $w_i={\left\{V\left({\widehat{\mu }}_i\right)g^{\text{'}}{\left({\widehat{\mu }}_i\right)}^2\right\}}^{-1}$.
2.	Test for convergence, terminate if achieved.
3.	Except at iteration one, if $D^{*}/\varphi +{\mathit{}\mathbf{\beta }}^{*\mathsf{T}}{\mathbf{S}}_{\rho }{\mathit{}\mathbf{\beta }}^{*}<D/\varphi +{\widehat{\mathit{}\mathbf{\beta }}}^{\mathsf{T}}{\mathbf{S}}_{\rho }\widehat{\mathit{}\mathbf{\beta }}$ set $\widehat{\mathit{}\mathbf{\beta }}\leftarrow ({\mathit{}\mathbf{\beta }}^{*}+\widehat{\mathit{}\mathbf{\beta }})/2$ and return to 1.
4.	${\mathit{}\mathbf{\beta }}^{*}\leftarrow \widehat{\mathit{}\mathbf{\beta }}$.
5.	$\mathit{}\mathbf{\rho }={\mathit{}\mathbf{\rho }}_0+{\mathit{}\mathbf{\Delta }}_0$..
6.	Given ${\mathbf{X}}^{\mathsf{T}}\mathbf{WX}$, f and $\mathit{}\mathbf{\rho }$, obtain $\mathit{}\mathbf{\Delta }$, the Newton step for the working model, $\nabla \mathcal{V}$ the gradient of the working REML and $\widehat{\mathit{}\mathbf{\beta }}$.
7.	If $\nabla {\mathcal{V}}^{\mathsf{T}}{\mathit{}\mathbf{\Delta }}_0>ϵD$ then ${\mathit{}\mathbf{\Delta }}_0\leftarrow {\mathit{}\mathbf{\Delta }}_0/2$ and return to 5.
8.	${\mathit{}\mathbf{\Delta }}_0\leftarrow \mathit{}\mathbf{\Delta }$, ${\mathit{}\mathbf{\rho }}_0\leftarrow \mathit{}\mathbf{\rho }$, D* ← D. Form $\widehat{\mathit{}\mathbf{\eta }}=\mathbf{X}\widehat{\mathit{}\mathbf{\beta }}$ and ${\widehat{\mu }}_i=g^{-1}\left({\widehat{\eta }}_i\right)$.

Note that Step 1 does not require the explicit formation of the whole matrix X. Step 3 reduces the $\mathit{}\mathbf{\beta }$ step taken if the Newton step was too long, in that it increased the penalized deviance at the $\mathit{}\mathbf{\rho }$ value at which it was computed. Step 5 reduces the $\mathit{}\mathbf{\rho }$ step if it was so long that the REML score was increasing at the end of the step. When log φ is unknown it can be included as an extra element of $\mathit{}\mathbf{\rho }$.

Step 6 consists of estimating the ${\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }$ implied by the proposed $\mathit{}\mathbf{\rho }$ and the current W and z. Further more the marginal likelihood of the working penalized linear model is uses as a smoothing parameter estimation criterion, and the gradient vector of this criterion along with the first Newton step for optimizing it are also computed. The next sections detail how Step 6 is accomplished.

4.2. The REML Update

Now consider the calculation of the Newton step, $\mathit{}\mathbf{\Delta }$, to improve (4(4) $$\begin{array}{ccc}\hfill \mathcal{V}\left(\mathit{}\mathbf{\lambda }\right)& =& \parallel \mathbf{z}-\mathbf{X}{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }{\parallel }_w^2/\varphi +{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }^{\mathsf{T}}{\mathbf{S}}_{\lambda }{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }+log|{\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\varphi +{\mathbf{S}}_{\lambda }|\hfill \\ & & -log|{\mathbf{S}}_{\lambda }{|}_{+}+nlog\left(\varphi \right)+(n-M)log\left(2\pi \right).\hfill \end{array}$$(4) ). We have that ${\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }$ is the solution of $({\mathbf{X}}^{\mathsf{T}}\mathbf{WX}+\varphi {\mathbf{S}}_{\lambda }){\mathit{}\mathbf{\beta }}_{\lambda }={\mathbf{X}}^{\mathsf{T}}\mathbf{Wz}$. The actual computation proceeds by taking a Cholesky decomposition ${\mathbf{R}}^{\mathsf{T}}\mathbf{R}={\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\varphi +{\mathbf{S}}_{\lambda }$ using a parallel version of Lucas (2004). This is usually done with pivoting, in which case the rank of R is then estimated and unidentifiable parameters set to zero and dropped from subsequent computations. We then compute ${\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }={\mathbf{R}}^{-1}{\mathbf{R}}^{-\mathsf{T}}{\mathbf{X}}^{\mathsf{T}}\mathbf{Wz}/\varphi$ (by backward and forwards substitution). In what follows “pivoting” and “unpivoting” refer to the application of the Cholesky pivoting order and its reversal.

The Newton step is $\mathit{}\mathbf{\Delta }=-{({\mathrm{d}}^2\mathcal{V}/\mathrm{d}\mathit{}\mathbf{\rho }\mathrm{d}{\mathit{}\mathbf{\rho }}^{\mathsf{T}})}^{-1}\mathrm{d}\mathcal{V}/\mathrm{d}\mathit{}\mathbf{\rho }$, where ${\mathrm{d}}^2\mathcal{V}/\mathrm{d}\mathit{}\mathbf{\rho }\mathrm{d}{\mathit{}\mathbf{\rho }}^{\mathsf{T}}$ will have been perturbed if necessary to ensure definiteness (see Nocedal and Wright 2006). Recalling that ${\left.\mathrm{d}(\parallel \mathbf{z}-\mathbf{X}\mathit{}\mathbf{\beta }{\parallel }_w^2/\varphi +{\mathit{}\mathbf{\beta }}^{\mathsf{T}}{\mathbf{S}}_{\lambda }\mathit{}\mathbf{\beta })/\mathrm{d}\mathit{}\mathbf{\beta }\right|}_{{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }}=\mathbf{0}$, we have (8) $$\begin{array}{c}\hfill \frac{\mathrm{d}\mathcal{V}}{\mathrm{d}{\rho }_j}={\lambda }_j{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }^{\mathsf{T}}{\mathbf{S}}_j{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }+\frac{\mathrm{d}log|{\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\varphi +{\mathbf{S}}_{\lambda }|}{\mathrm{d}{\rho }_j}-\frac{\mathrm{d}log|{\mathbf{S}}_{\lambda }{|}_{+}}{\mathrm{d}{\rho }_j}\end{array}$$(8) and, defining δ^j_k = 1 if k = j and 0 otherwise, $$\begin{array}{ccc}\hfill \frac{{\mathrm{d}}^2\mathcal{V}}{\mathrm{d}{\rho }_j\mathrm{d}{\rho }_k}& =& 2\frac{\mathrm{d}{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }^{\mathsf{T}}}{\mathrm{d}{\rho }_k}({\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\varphi +{\mathbf{S}}_{\lambda })\frac{\mathrm{d}{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }}{\mathrm{d}{\rho }_j}\hfill \\ & & +2{\lambda }_j{\mathit{}\mathbf{\beta }}_{\lambda }^{\mathsf{T}}{\mathbf{S}}_j\frac{\mathrm{d}{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }}{\mathrm{d}{\rho }_k}+2{\lambda }_k{\mathit{}\mathbf{\beta }}_{\lambda }^{\mathsf{T}}{\mathbf{S}}_k\frac{\mathrm{d}{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }}{\mathrm{d}{\rho }_j}+{\delta }_k^j{\lambda }_j{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }^{\mathsf{T}}{\mathbf{S}}_j{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }\hfill \\ & & +\frac{{\mathrm{d}}^{2}log|{\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\varphi +{\mathbf{S}}_{\lambda }|}{\mathrm{d}{\rho }_j\mathrm{d}{\rho }_k}-\frac{{\mathrm{d}}^{2}log{\left|\mathbf{S}\right|}_{+}}{\mathrm{d}{\rho }_j\mathrm{d}{\rho }_k}.\hfill \end{array}$$Implicit differentiation implies that $$\frac{\mathrm{d}{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }}{\mathrm{d}{\rho }_j}=-{\lambda }_j{\mathbf{R}}^{-1}{\mathbf{R}}^{-\mathsf{T}}{\mathbf{S}}_j{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }.$$This latter computation is most efficient if ${\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }$ is first unpivoted, ${\mathbf{S}}_j{\widehat{\mathit{}\mathbf{\beta }}}_{\lambda }$ is formed and this is then repivoted: the block structure of S_j (see next section) can then be be exploited. The next two sections cover computation of the derivatives of the log determinants.

4.3. Computing The Derivatives Of log |S_λ|₊

S_λ has block diagonal structure that can be exploited. For example, denoting zero blocks by ‘.’, $$\begin{array}{c}\hfill {\mathbf{S}}_{\lambda }=\left(\begin{array}{ccccc}\hfill {\lambda }_1{\mathbf{S}}_1& \hfill .& \hfill .& .& .\\ \hfill .& \hfill {\lambda }_2{\mathbf{S}}_2& \hfill .& .& .\\ \hfill .& \hfill .& \hfill \sum _j{\lambda }_j{\mathbf{S}}_j& .& .\\ \hfill .& \hfill .& \hfill .& .& .\\ \hfill .& \hfill .& \hfill .& .& .\end{array}\right).\end{array}$$

That is there are some blocks with single smoothing parameters, and others with a more complicated additive structure. There are usually also some zero blocks on the diagonal. The block structure means that the generalized determinant and its derivatives w.r.t. ρ_k = log λ_k can be computed blockwise. Note in particular that, for the above example, $$\begin{array}{ccc}\hfill log|{\mathbf{S}}_{\lambda }{|}_{+}& =& \mathrm{rank}\left({\mathbf{S}}_1\right)log\left({\lambda }_1\right)+log{\left|{\mathbf{S}}_1\right|}_{+}+\mathrm{rank}\left({\mathbf{S}}_2\right)log\left({\lambda }_2\right)\hfill \\ & & +log|{\mathbf{S}}_2{|}_{+}+log{\left|\sum _j{\lambda }_j{\mathbf{S}}_j\right|}_{+}+\cdots \hfill \end{array}$$For any ρ_k relating to a single parameter block we have $$\frac{{\mathrm{d}log\left|\mathbf{S}\right|}_{+}}{\mathrm{d}{\rho }_k}=\text{rank}\left({\mathbf{S}}_k\right)$$and zero second derivatives. For multi-λ blocks there will generally be first and second derivatives to compute. There are no second derivatives “between-blocks.” To facilitate computations some prefit reparameterization is undertaken, according to the type of block.

1.	Single parameter diagonal blocks. These can be reparameterized so that all nonzero elements are one, and the rank precomputed.
2.	Single parameter dense blocks. These can be reparameterized to look like the previous type, by similarity transform, again computing rank.
3.	Multi-λ blocks are transformed so that ∑jλjSj has full rank in the new parameterization. Again a similarity transform is used. Typically the Sj are of smaller dimension in the reparameterization and consequently an extra zero block is introduced on the diagonal of Sj.

The generalized determinant of type 3 blocks becomes an ordinary determinant of ∑_jλ_jS_j after reparameterization. Hence, its derivatives follow from the standard result $$\frac{\mathrm{d}log\left|\mathbf{S}\right|}{\mathrm{d}\rho }=\text{tr}\left({\mathbf{S}}^{-1}\frac{\partial \mathbf{S}}{\partial \rho }\right).$$

4.4. Computing The Derivatives of $log|{\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\varphi +{\mathbf{S}}_{\lambda }|$

The following computations build on the Cholesky decomposition of the previous sections

1.	Form P = R− 1, and unpivot the rows of P. Then form ${\mathbf{PP}}^{\mathsf{T}}$. These steps are O(p3), but can be parallelized.
2.	Form the matrices containing the nonzero rows of ${\mathbf{S}}_k{\mathbf{PP}}^{\mathsf{T}}$ (∀k). This step is cheap for all but type 3 blocks.
3.	Compute the required derivatives using $$\frac{\mathrm{d}log|{\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\varphi +{\mathbf{S}}_{\lambda }|}{\mathrm{d}{\rho }_k}={\lambda }_k\text{tr}\left({\mathbf{S}}_k{\mathbf{PP}}^{\mathsf{T}}\right)$$and $$\begin{array}{ccc}& & \frac{{\mathrm{d}}^{2}log|{\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\varphi +{\mathbf{S}}_{\lambda }|}{\mathrm{d}{\rho }_k\mathrm{d}{\rho }_j}\hfill \\ & & ={\delta }_k^j{\lambda }_k\text{tr}\left({\mathbf{S}}_k{\mathbf{PP}}^{\mathsf{T}}\right)-{\lambda }_j{\lambda }_k\text{tr}\left({\mathbf{S}}_k{\mathbf{PP}}^{\mathsf{T}}{\mathbf{S}}_j{\mathbf{PP}}^{\mathsf{T}}\right).\hfill \end{array}$$

Note that ${\mathbf{PP}}^{\mathsf{T}}={({\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\varphi +{\mathbf{S}}_{\lambda })}^{-1}$, the Bayesian covariance matrix.

The trace computations in step 3 are very efficient, given the block structure of the S_k, if we employ the following tricks. In general $\text{tr}\left(\mathbf{AB}\right)={\sum }_{kj}{A}_{kj}{B}_{jk}$. Now let A have nonzero rows only between k₁ and k₂, while B has nonzero rows only between j₁ and j₂. $$\text{tr}\left(\mathbf{A}\right)=\sum _{k=k_1}^{k_2}{A}_{kk}\text{and}\text{tr}\left(\mathbf{AB}\right)=\sum _{k=k_1}^{k_2}\sum _{j=j_1}^{j_2}{A}_{kj}{B}_{jk}.$$Of course normally the initial zero rows would not actually be stored in which case we have $$\text{tr}\left(\mathbf{A}\right)=\sum _{k=k_1}^{k_2}{A}_{k-k_1,k}\text{and}\text{tr}\left(\mathbf{AB}\right)=\sum _{k=k_1}^{k_2}\sum _{j=j_1}^{j_2}{A}_{k-k_1,j}{B}_{j-j_1,k}.$$

4.5. The Model Matrix: Efficient Storage and Computation

We are interested in computing with models in which it is impractical to store the whole model matrix, and in which computing the required matrix cross product may be prohibitively expensive. For this reason we discretize the model covariates so that the columns of the model matrix corresponding to a single smooth term can be stored in compact form. Specifically, suppose that the covariate for the jth term is discretized into m discrete values, then the model matrix columns for that term can be written as $${\mathbf{X}}_j(i,j)={\bar{\mathbf{X}}}_j(k\left(i\right),j),$$where ${\bar{\mathbf{X}}}_j$ has only m rows and k is an index vector. Storing ${\bar{\mathbf{X}}}_j$ and k uses much less memory than storing X_j directly. This idea is introduced in Lang et al. (2014) to obtain efficient storage and computation for large datasets. However, in that article they employ smooths of one covariate and only require terms of the form ${\mathbf{X}}_j^{\mathsf{T}}\mathbf{W}{\mathbf{X}}_j$, but not ${\mathbf{X}}_j^{\mathsf{T}}\mathbf{W}{\mathbf{X}}_k$. For smoothing parameter estimation we require these “off diagonal” product terms as well. In addition we require tensor product smooths of multiple covariates. Discretizing multiple covariates onto multidimensional grids requires either substantial storage or substantial approximation error, and in the tensor product context it makes sense to instead discretize each component marginal model matrix separately, constructing the full tensor product model matrix “on the fly.”

Appendix A develops the identities and algorithms required to compute with X and its products when the submatrices of X corresponding to individual terms are stored compactly, and when tensor product terms are computed “on-the-fly” from compactly stored marginal model matrices. With the correct structuring each matrix inner product is a factor of p faster than it would be under direct computation, where p is the number of columns in the largest marginal model matrix involved in the product and for nontensor product smooths their only model matrix is their single model matrix. The crucial advance over Lang et al. (2014) is the ability to deal with tensor product smooths efficiently, and to compute the off diagonal crossproducts efficiently (between single smooths, tensor product smooths or a mixture of the two). Our method has the major advantage over alternative discretization approaches (e.g., Helwig and Ma 2016) of discretizing covariates independently (marginally), rather than discretizing jointly so that the unique combinations of discretized covariates are stored (or the basis functions evaluated at those unique combinations). The joint approach typically requires more storage, and/or coarser discretization than our fully marginal approach.

An obvious question is how fine a discretization is necessary? Suppose we discretize n observations of covariate x onto a regular grid of m values (just covering the x range). In the large m limit an upper bound on the resulting approximation error is 0.5m^{− 1}max |g′(x)| where g is the true function we are trying to recover. The sampling error on the estimate of g is at best O(n^{− 1/2}), implying that m = O(n^1/2) is more than adequate. For any finite sample analysis the approximation error bound can be evaluated to check the adequacy of m. Note however, that for the black smoke network data, many covariates are already discrete: for example, there are only a finite number of site locations, site labels and elevations, temperature is only recorded to within 0.1°C, etc.

5. Black Smoke Model Development

Following^{Figure 1, Figure 2}the industrial revolution, problems associated with air pollution worsened in many countries. During the first half of the 20th century major pollution episodes occurred in London, notably in 1952 an episode of fog, in which levels of black smoke exceeded 4500 μg m^{− 3}, was associated with 4000 excess deaths (Ministry of Health 1954). Other early episodes, which were caused by a combination of industrial pollution sources and adverse weather conditions, and resulted in large numbers of deaths among the surrounding populations, include those in the Meuse valley (Firket 1936) and the United States (Ciocco and Thompson 1961). Attempts to measure levels of air pollution in a regular and systematic way arose as a result of these episodes. In 1961 the world's first coordinated national air pollution monitoring network was established in the United Kingdom, to monitor black smoke and sulphur dioxide at around 1000 sites (Clifton 1964). Since then all European countries have established monitoring networks, some of them run at the national level, others by local authorities or municipalities, with the initial focus on black smoke (soot) and sulfur dioxide, initially largely from coal burning but shifting more recently to other pollutants. Monitoring has increased in the wake of national and international legislation and the issuing of air quality guidelines, but most monitoring networks share features of the U.K. BS network that challenge the interpretation of the data for epidemiological and policy purposes: (i) monitoring is expensive and so monitoring networks are typically sparse and change over time, (ii) concentrations may vary greatly over small distances, especially in urban areas and (iii) networks designed to monitor compliance with standards, may not give a good representation of levels over an area. Modeling offers the possibility to alleviate these problems, at least partially, and our approach to the U.K. black smoke data should be applicable to other monitoring networks.

In addition to the Black smoke data (Loader 2002), we obtained daily temperature and monthly rainfall data for the United Kingdom (Perry and Hollis 2005b, 2005a) to use as covariates, alongside site elevation (of Terrain-50 2015). Given the volume of data, our initial exploratory model development concentrated first on modeling space without time, and then time without space. In this way we were able to develop candidate temporal decompositions (in terms of year, day of year, and day of week), and candidate models for covariates and space, which were then combined while allowing space and time effects to interact.

Our basic approach was first to decompose the black smoke signal into components dependent on different temporal scales: year (y) for the long term changes, day of year (doy) for the annual cycle and day of week (dow) for the working week related cycle. These are represented by f₁ − f₃ in model (1(1) $$\begin{array}{ccc}& & log\left({\mathtt{bs}}_i\right)\hfill \\ & & =f_1\left({\mathtt{y}}_i\right)+f_2\left({\mathtt{doy}}_i\right)+f_3\left({\mathtt{dow}}_i\right)+f_4({\mathtt{y}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_5({\mathtt{y}}_i,{\mathtt{dow}}_i)+f_6({\mathtt{doy}}_i,{\mathtt{dow}}_i)\hfill \\ & & +f_7({\mathtt{n}}_i,{\mathtt{e}}_i)+f_8({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{y}}_i)+f_9({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_{10}({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{dow}}_i)+f_{11}\left({\mathtt{h}}_i\right)+f_{12}({\mathtt{T}}_i^0,{\mathtt{T}}_i^1)\hfill \\ & & +f_{13}({\overline{\mathtt{T}\mathtt{1}}}_i,{\overline{\mathtt{T}\mathtt{2}}}_i)\hfill \\ & & +f_{14}\left({\mathtt{r}}_i\right)+{\alpha }_{k\left(i\right)}+b_{\text{id}\left(i\right)}+e_i\hfill \end{array}$$(1) ). These effects were all allowed to interact: for example, the weekly pattern could change with time of year, and over longer timescales. These interactions are f₄ − f₆ in model (1(1) $$\begin{array}{ccc}& & log\left({\mathtt{bs}}_i\right)\hfill \\ & & =f_1\left({\mathtt{y}}_i\right)+f_2\left({\mathtt{doy}}_i\right)+f_3\left({\mathtt{dow}}_i\right)+f_4({\mathtt{y}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_5({\mathtt{y}}_i,{\mathtt{dow}}_i)+f_6({\mathtt{doy}}_i,{\mathtt{dow}}_i)\hfill \\ & & +f_7({\mathtt{n}}_i,{\mathtt{e}}_i)+f_8({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{y}}_i)+f_9({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_{10}({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{dow}}_i)+f_{11}\left({\mathtt{h}}_i\right)+f_{12}({\mathtt{T}}_i^0,{\mathtt{T}}_i^1)\hfill \\ & & +f_{13}({\overline{\mathtt{T}\mathtt{1}}}_i,{\overline{\mathtt{T}\mathtt{2}}}_i)\hfill \\ & & +f_{14}\left({\mathtt{r}}_i\right)+{\alpha }_{k\left(i\right)}+b_{\text{id}\left(i\right)}+e_i\hfill \end{array}$$(1) ). We then allowed the effects of year, time of year and day of the week to vary spatially (terms f₈ − f₁₀), as well as allowing a “main effect” of space, f₇. Elevation and rainfall effects f₁₁ and f₁₄ were also included alongside effects for site type and a site specific random effect. Residual analysis for a model including only these effects suggested strong temperature dependence, with an interaction of daily minimum and maximum temperatures (f₁₂). Including this latter term still left a correlation with mean temperatures at lags of one and two days, resulting in f₁₃.

Main effects of time were represented using cubic regression splines for y and cyclic cubic regression splines for doy and dow. Tensor product smooths (e.g., Wood 2006) were used for the interactions. In cases in which smooth main effects and interactions were present, then the interaction smooths were constructed to exclude the main effects, by the simple expedient of applying sum-to-zero constraints to the marginal bases of the tensor product smooth, prior to construction of the tensor product basis. Space time interaction terms follow Augustin et al. (2009), that is tensor product smoothers with isotropic smoothers used for the spatial marginal smooth and cubic splines for the temporal margin.

Due to the marked reduction in the size of the network in its last decade, and the uneven spatial coverage, some care is required in the specification of the two-dimensional spatial smoothers of n and e, to avoid extrapolation artifacts in later years. We chose to use Duchon splines (see Duchon 1977; Miller and Wood 2014), using first derivative penalties with Duchon’s s parameter therefore set to 1/2. The use of first derivative penalties means that such smoothers are smoothing toward the constant function, which is a reasonable modeling assumption for black smoke data in sparsely observed regions. Duchon splines are the general class of splines introduced in Duchon (1977) of which the popular thin plate spline is a special case: see Miller and Wood (2014) for an accessible introduction. For comparison we also tried Gaussian process smoothers with a Matérn covariance function following Kammann and Wand (2003) and Handcock, Meier, and Nychka (1994), as well as thin plate splines, but in both cases basic model checking revealed artifacts in model predictions toward the end of the data. The online supplementary material includes an animation of predicted log black smoke, clearly illustrating such artifacts for the thin plate spline based model (the equivalent animation for the Duchon spline based model is also included).

Given our interest in using the model for prediction away from the stations, we aimed to keep the station specific random effects structure of the model as simple as possible, however it proved impossible to achieve an adequate fit without any random effects at all, and the model therefore includes a single random intercept term per station, reflecting the individual idiosyncrasies of station locations not captured by the available covariates.

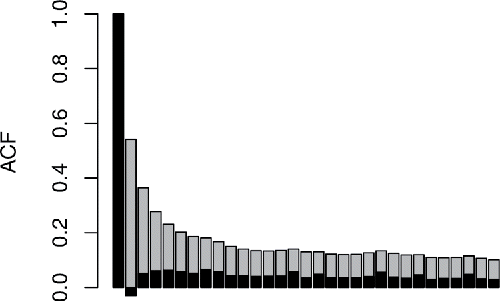
Model^{Figure 4}adequacy was checked using standard residual plots, as well as autocorrelation function plots and semivariogram plots to check for unmodeled spatial and temporal correlation. Figures 2 and 3 show such plots for model 1(1) $$\begin{array}{ccc}& & log\left({\mathtt{bs}}_i\right)\hfill \\ & & =f_1\left({\mathtt{y}}_i\right)+f_2\left({\mathtt{doy}}_i\right)+f_3\left({\mathtt{dow}}_i\right)+f_4({\mathtt{y}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_5({\mathtt{y}}_i,{\mathtt{dow}}_i)+f_6({\mathtt{doy}}_i,{\mathtt{dow}}_i)\hfill \\ & & +f_7({\mathtt{n}}_i,{\mathtt{e}}_i)+f_8({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{y}}_i)+f_9({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_{10}({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{dow}}_i)+f_{11}\left({\mathtt{h}}_i\right)+f_{12}({\mathtt{T}}_i^0,{\mathtt{T}}_i^1)\hfill \\ & & +f_{13}({\overline{\mathtt{T}\mathtt{1}}}_i,{\overline{\mathtt{T}\mathtt{2}}}_i)\hfill \\ & & +f_{14}\left({\mathtt{r}}_i\right)+{\alpha }_{k\left(i\right)}+b_{\text{id}\left(i\right)}+e_i\hfill \end{array}$$(1) , showing that the model does a reasonable job of capturing spatial and temporal correlation, in the data. Further plots are shown in the online supplementary material. To illustrate the importance of the weather variables and site-specific random effects, models were fitted without these leading to AIC increases of 1.6 × 10⁶ and 2.4 × 10⁶ for models without weather variables and the random effect, respectively (the corresponding r² reductions were approximately 2% and 1%).

Figure 2. Semivariograms for the 40th (top row) and 200th (bottom row) days of years 1966, 76, 86, and 96, checking for residual spatial autocorrelation. Each plot shows the empirical semivariogram for the log black smoke measurements as black dots, with the corresponding reference bands under zero autocorrelation as black lines. The white dots and dotted lines show the equivalent for the residuals of model (1(1) $$\begin{array}{ccc}& & log\left({\mathtt{bs}}_i\right)\hfill \\ & & =f_1\left({\mathtt{y}}_i\right)+f_2\left({\mathtt{doy}}_i\right)+f_3\left({\mathtt{dow}}_i\right)+f_4({\mathtt{y}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_5({\mathtt{y}}_i,{\mathtt{dow}}_i)+f_6({\mathtt{doy}}_i,{\mathtt{dow}}_i)\hfill \\ & & +f_7({\mathtt{n}}_i,{\mathtt{e}}_i)+f_8({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{y}}_i)+f_9({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_{10}({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{dow}}_i)+f_{11}\left({\mathtt{h}}_i\right)+f_{12}({\mathtt{T}}_i^0,{\mathtt{T}}_i^1)\hfill \\ & & +f_{13}({\overline{\mathtt{T}\mathtt{1}}}_i,{\overline{\mathtt{T}\mathtt{2}}}_i)\hfill \\ & & +f_{14}\left({\mathtt{r}}_i\right)+{\alpha }_{k\left(i\right)}+b_{\text{id}\left(i\right)}+e_i\hfill \end{array}$$(1) ). The reduction of the network in later years leads to wide reference bands, but in all plots the model appears to offer a reasonable representation of the spatial pattern.

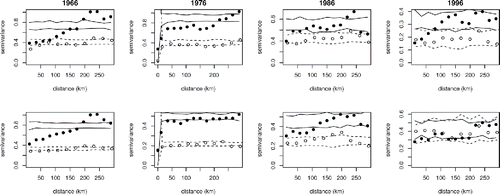
Figure 3. Aggregate ACF for model (1(1) $$\begin{array}{ccc}& & log\left({\mathtt{bs}}_i\right)\hfill \\ & & =f_1\left({\mathtt{y}}_i\right)+f_2\left({\mathtt{doy}}_i\right)+f_3\left({\mathtt{dow}}_i\right)+f_4({\mathtt{y}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_5({\mathtt{y}}_i,{\mathtt{dow}}_i)+f_6({\mathtt{doy}}_i,{\mathtt{dow}}_i)\hfill \\ & & +f_7({\mathtt{n}}_i,{\mathtt{e}}_i)+f_8({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{y}}_i)+f_9({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_{10}({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{dow}}_i)+f_{11}\left({\mathtt{h}}_i\right)+f_{12}({\mathtt{T}}_i^0,{\mathtt{T}}_i^1)\hfill \\ & & +f_{13}({\overline{\mathtt{T}\mathtt{1}}}_i,{\overline{\mathtt{T}\mathtt{2}}}_i)\hfill \\ & & +f_{14}\left({\mathtt{r}}_i\right)+{\alpha }_{k\left(i\right)}+b_{\text{id}\left(i\right)}+e_i\hfill \end{array}$$(1) ) residuals assuming independent residuals in gray, with the equivalent for the standardized residuals assuming AR1 residuals, overlaid in black. While not perfect, the AR1 model greatly reduces the unmodeled temporal autocorrelation.

A concern with these data is that they show evidence of a type of preferential sampling (Shaddick and Zidek 2014): as the network was reduced over time, monitors in areas of low concentrations were more likely to be dropped than those in high pollution areas (note that this is different in nature to preferential sampling considered by Diggle, Menezes, and Su (2010), for example). If we had a perfect model without penalties (smoothing priors) then this preferential sampling might reduce efficiency but would not introduce bias. However, when using penalties there is a danger that the reduction of the network so reduces the coverage over some space-time regions that the model predictions for these regions are dominated by the influence of the penalty. If the network reduction is subject to preferential sampling, then it is possible that these space-time regions are systematically those in which pollution is actually lowest, and that the reliance on the penalty/prior then introduces systematic positive bias.

To investigate the potential for such effects, we fitted a reduced model (1(1) $$\begin{array}{ccc}& & log\left({\mathtt{bs}}_i\right)\hfill \\ & & =f_1\left({\mathtt{y}}_i\right)+f_2\left({\mathtt{doy}}_i\right)+f_3\left({\mathtt{dow}}_i\right)+f_4({\mathtt{y}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_5({\mathtt{y}}_i,{\mathtt{dow}}_i)+f_6({\mathtt{doy}}_i,{\mathtt{dow}}_i)\hfill \\ & & +f_7({\mathtt{n}}_i,{\mathtt{e}}_i)+f_8({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{y}}_i)+f_9({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_{10}({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{dow}}_i)+f_{11}\left({\mathtt{h}}_i\right)+f_{12}({\mathtt{T}}_i^0,{\mathtt{T}}_i^1)\hfill \\ & & +f_{13}({\overline{\mathtt{T}\mathtt{1}}}_i,{\overline{\mathtt{T}\mathtt{2}}}_i)\hfill \\ & & +f_{14}\left({\mathtt{r}}_i\right)+{\alpha }_{k\left(i\right)}+b_{\text{id}\left(i\right)}+e_i\hfill \end{array}$$(1) ) to the data from the year with the most complete spatial coverage, 1967, dropping all terms involving long-term effects of time. We also dropped the temperature and rainfall effects, to force the spatial effects to do as much of the explanatory work as possible. Using the actual network design (i.e., with stations added and dropped over time), we then simulated from a model in which the 1967 fitted model spatiotemporal pollution fields were repeated each year, but with a long-term decay matching the full dataset. Station-specific random effects were added with standard deviations as estimated from our fit of (1(1) $$\begin{array}{ccc}& & log\left({\mathtt{bs}}_i\right)\hfill \\ & & =f_1\left({\mathtt{y}}_i\right)+f_2\left({\mathtt{doy}}_i\right)+f_3\left({\mathtt{dow}}_i\right)+f_4({\mathtt{y}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_5({\mathtt{y}}_i,{\mathtt{dow}}_i)+f_6({\mathtt{doy}}_i,{\mathtt{dow}}_i)\hfill \\ & & +f_7({\mathtt{n}}_i,{\mathtt{e}}_i)+f_8({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{y}}_i)+f_9({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_{10}({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{dow}}_i)+f_{11}\left({\mathtt{h}}_i\right)+f_{12}({\mathtt{T}}_i^0,{\mathtt{T}}_i^1)\hfill \\ & & +f_{13}({\overline{\mathtt{T}\mathtt{1}}}_i,{\overline{\mathtt{T}\mathtt{2}}}_i)\hfill \\ & & +f_{14}\left({\mathtt{r}}_i\right)+{\alpha }_{k\left(i\right)}+b_{\text{id}\left(i\right)}+e_i\hfill \end{array}$$(1) ) to the full dataset. Further details are given in the online supplementary material. So our simulated data comes from a “truth” that maintains a degree of spatiotemporal complexity driven by the most “spatially complete” year throughout the simulated dataset, and in which the sampling is given by the real network evolution and, therefore, preferentially drops stations from low pollution regions of the simulation. We then fitted the complete model (1(1) $$\begin{array}{ccc}& & log\left({\mathtt{bs}}_i\right)\hfill \\ & & =f_1\left({\mathtt{y}}_i\right)+f_2\left({\mathtt{doy}}_i\right)+f_3\left({\mathtt{dow}}_i\right)+f_4({\mathtt{y}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_5({\mathtt{y}}_i,{\mathtt{dow}}_i)+f_6({\mathtt{doy}}_i,{\mathtt{dow}}_i)\hfill \\ & & +f_7({\mathtt{n}}_i,{\mathtt{e}}_i)+f_8({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{y}}_i)+f_9({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_{10}({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{dow}}_i)+f_{11}\left({\mathtt{h}}_i\right)+f_{12}({\mathtt{T}}_i^0,{\mathtt{T}}_i^1)\hfill \\ & & +f_{13}({\overline{\mathtt{T}\mathtt{1}}}_i,{\overline{\mathtt{T}\mathtt{2}}}_i)\hfill \\ & & +f_{14}\left({\mathtt{r}}_i\right)+{\alpha }_{k\left(i\right)}+b_{\text{id}\left(i\right)}+e_i\hfill \end{array}$$(1) ) to the simulated data, and examined its ability to reconstruct the simulated “true” pollution field at each of the locations of stations present in 1967, throughout the whole modeling period (i.e., without any drop out). If our model is sensitive to the preferential sampling evident in the network evolution, then we should be able to detect a positive bias in the full model predictions, which would be likely to grow over time. In fact we can only detect a very small constant bias of about 0.006 on the log scale (corresponding to a 0.6% bias on the original scale). There is no evidence for a trend in the bias: the online supplementary material includes a plot illustrating this and a fuller discussion.

5.1. Results and Predictions

The model (1(1) $$\begin{array}{ccc}& & log\left({\mathtt{bs}}_i\right)\hfill \\ & & =f_1\left({\mathtt{y}}_i\right)+f_2\left({\mathtt{doy}}_i\right)+f_3\left({\mathtt{dow}}_i\right)+f_4({\mathtt{y}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_5({\mathtt{y}}_i,{\mathtt{dow}}_i)+f_6({\mathtt{doy}}_i,{\mathtt{dow}}_i)\hfill \\ & & +f_7({\mathtt{n}}_i,{\mathtt{e}}_i)+f_8({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{y}}_i)+f_9({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{doy}}_i)\hfill \\ & & +f_{10}({\mathtt{n}}_i,{\mathtt{e}}_i,{\mathtt{dow}}_i)+f_{11}\left({\mathtt{h}}_i\right)+f_{12}({\mathtt{T}}_i^0,{\mathtt{T}}_i^1)\hfill \\ & & +f_{13}({\overline{\mathtt{T}\mathtt{1}}}_i,{\overline{\mathtt{T}\mathtt{2}}}_i)\hfill \\ & & +f_{14}\left({\mathtt{r}}_i\right)+{\alpha }_{k\left(i\right)}+b_{\text{id}\left(i\right)}+e_i\hfill \end{array}$$(1) ) has a conditional r² of 0.79 (i.e., treating the AR process as induced by a random field), and a marginal r² of 0.7 (i.e., ignoring the auto-regressive structure of the residuals). The online supplementary material includes an animation showing the evolution of the predicted spatial pollution field over time. Careful examination shows some artifacts in the fields, usually in coastal regions away from observation stations, but otherwise the results appear reasonable, predicting high pollution levels in the industrial centers especially in the first decade or so, generally showing cleaner air in wetter regions, and tending to show an annual cycle reflecting higher fossil fuel use in the winter.

In this^{Figure 5}section we illustrate the model results with two sets of plots examining how the chance of exceeding current daily recommended limits (213 $\mu \text{g}{\text{m}}^{-3}$) has changed over time. Figure 4 shows the log of the number of days for which levels are predicted to exceed the daily limit, for a town center location, for several years in the 1960s. These figures are obtained by simply counting up predicted exceedance days by 5 km².

Figure 4. Image plots of log predicted number of days exceeding the EU daily exposure threshold for town center locations for several years in the 1960s. By 1975 there were essentially no exceedance days predicted.

An alternative is to compute the average posterior probability of the mean exceeding the recommended level using the predicted level and its standard deviation, based on (7(7) $$\begin{array}{c}\hfill \mathit{}\mathbf{\beta }\sim N(\widehat{\mathit{}\mathbf{\beta }},{({\mathbf{X}}^{\mathsf{T}}\mathbf{WX}/\varphi +{\mathbf{S}}_{\lambda })}^{-1}),\end{array}$$(7) ). Figure 5 shows such a plot. Broadly both figures show the same pattern, with the situation improving rapidly in London in the wake of the U.K. Clean Air Acts, but taking much longer to improve in the cold northern industrial conurbations.

Figure 5. Image plots of log average probability of exceeding the EU daily exposure threshold for town center locations for several years in the 1960s. Red is -6 corresponding to less than one exceedance day expected per year, while the top of the scale is 0.

6. Discussion

Our development of scalable additive model fitting methods rests on three innovations: (i) the development of a fitting method which required only basic easily parallelized matrix computations and a pivoted Cholesky decompostion; (ii) the use of a scalable parallel block pivoted Cholesky algorithm; and (iii) an efficient approach to model matrix storage and computations with the model matrix, using discretized covariates. The approach allows much larger additive/latent Gaussian process models of much larger datasets than has hitherto been feasible, and is general enough for routine use (see R package mgcv). For the black smoke modeling, fitting is three orders of magnitude faster than we could have achieved otherwise.

The three method innovations are interlinked so that cleanly attributing elements of the speed up to each separately is not really possible. However, model fitting time increases from around 55 min to over 7.5 hr if we use a single core, instead of 12 (CPU turbo modes disabled to aid comparability). Using the new method, profiling reveals that the time spent on the matrix crossproduct is approximately equal to the time spent on the other method steps, for the black smoke model. From the operations counts in Appendix A the crossproduct is around a factor of 10² less floating point intensive using the new discrete methods relative to direct crossproduct formation, while the subleading order cost of basis function evaluation is up to 10⁴ times less costly. Similarly the leading order costs of each smoothing parameter update can be compared. The Wood, Goude, and Shaw (2015) method requires approximately 40 times the floating point operations per smoothing parameter update, due to O(p³) costs per smoothing parameter, coupled with a symmetric eigen decompositon and several QR steps. Hence, all three components of the new method are required to achieve the observed efficiency gains.

For discretization we chose to generalize the approach of Lang et al. (2014), rather than attempt to use the grid-based approach of Currie, Durban, and Eilers (2006). This is largely as a result of the very irregular nature of our “grids”: for example, the approach here avoids having to compute anything that will then be given zero weight as a result of data being missing at a grid node. However, our smoothing parameter selection method should be directly applicable to models fit using the Currie, Durban, and Eilers (2006) approach (unlike, e.g., the approach of Wood (2011)).

The Black smoke model presented here is the first successful attempt to model these data on a daily basis over several decades, and offers a basis for estimating daily exposures for use in retrospective cohort studies, for example. While a major advance, we do not believe that this model is definitive. For example, the only meteorological variables available to us on a daily basis were temperature, and the fact that we are forced to use monthly rainfall data offers an obvious area for improvement. The model as it stands shows some artifacts in coastal areas that we are working to improve. Another obvious deficiency is the lack of any pollution source data. One might expect substantial improvements if fine scale data on coal and diesel use were available as predictors.

The method is implemented in the bam function of R package mgcv from version 1.8-9, and is invoked via bam arguments discrete and nthreads. The black smoke data are available from the first author’s web page (http://www.maths.bris.ac.uk/∼sw15190/).

Supplementary Materials

The supplementary material contains further information on the data, model checking and preferential sampling. In addition, gigam2-AppBC.pdf contains appendices B and C of the paper, on covergence properties and parallel computing issues. Finally files tps.mp4 and duchon.mp4 contain movies showing the fitted model predictions for the whole UK.

Acknowledgments

We are grateful to the editor and anonymous referees for comments which substantially improved the article, to Electricité de France for funding background investigation of parallel computing methods, and to Yannig Goude for discussion of GAM scalable computing issues.

Funding

This work was funded by EPSRC grant EP/K005251/1 and a University of Bath studentship to ZL.

A. Methods for Discretized Covariates

This section describes the algorithms required to compute efficiently with marginally gridded covariates in detail. The idea is that we have a model matrix X = (X₀: X₁: ⋅⋅⋅). Each X_j represents either a single smooth, or a tensor product smooth (e.g. Wood 2006). In the case of a single smooth (9) $$\begin{array}{c}\hfill X_j(i,l)={\bar{X}}_j(k_j\left(i\right),l),\end{array}$$(9) where ${\bar{\mathbf{X}}}_j$ is an m_j × p_j matrix evaluating the smooth at the corresponding gridded values. For a tensor product $${\mathbf{X}}_j={\mathbf{M}}_0^j\odot {\mathbf{M}}_1^j\odot \cdots {\mathbf{M}}_{d_j-1}^j{\mathbf{Q}}^j,$$where M^j_k are marginal model matrices and Q^j is a constraint matrix, usually imposing a sum to zero constraint over a representative subset of the data. ⊙ denotes the Kronecker product (⊗) applied row-wise (i.e., one row at a time). In this case the marginal model matrices are stored in compact form: $$M_l^j(i,m)={\bar{M}}_l^j(k_l^j\left(i\right),m).$$The following algorithms are most efficient if tensor product terms are always arranged so that the marginal model matrix with the most columns is last, but this can be achieved by automatic rearrangement.

Note that in principle covariates could be discretized jointly onto a multidimensional grid, so that we store the unique combinations of covariates, rather than storing the unique covariate values independently. With the joint scheme the cross product ${\mathbf{X}}^{\mathsf{T}}\mathbf{WX}$ is easy to compute. If $\bar{\mathbf{X}}$ and $\bar{\mathbf{W}}$ contain the unique model matrix rows and corresponding unique weights, respectively, while $\bar{\mathbf{N}}$ is the diagonal matrix containing the number of occurrences of each now of $\bar{\mathbf{X}}$ in X then ${\mathbf{X}}^{\mathsf{T}}\mathbf{WX}={\bar{\mathbf{X}}}^{\mathsf{T}}\bar{\mathbf{N}}\bar{\mathbf{W}}\bar{\mathbf{X}}$. The problem is that the number of unique combinations of covariates, and hence number of rows of $\bar{\mathbf{X}}$ can be very large, unless very coarse discretisation is used. Hence the requirement for the methods of this appendix.

A variant of the scheme is required when the model contains terms of the form ${\sum }_k{f}_j\left(z_{ik}\right)L_{ik}={\mathit{}\mathbf{\Sigma }}_j\{f_j\left(\text{vec}\left(\mathbf{z}\right)\right)\odot \text{vec}\left(\mathbf{L}\right)\}={\mathit{}\mathbf{\Sigma }}_j\{\tilde{\mathbf{X}}\odot \text{vec}\left(\mathbf{L}\right)\}\mathit{}\mathbf{\beta }$, where $${\mathit{}\mathbf{\Sigma }}_j=\left(\begin{array}{cccccccccc}\hfill 1& \hfill 0& \hfill .& .& .& 0& 1& 0& .& .\\ \hfill 0& \hfill 1& \hfill 0& .& .& .& 0& 1& 0& .\\ \hfill .& \hfill .& \hfill .& .& .& .& .& .& .& .\end{array}\right).$$If z is n × m, then ${\mathit{}\mathbf{\Sigma }}_j$ is n × nm, and the index vectors must be of length nm, which is also the number of rows in $\tilde{\mathbf{X}}$ (the model matrix for $f_j\left(\text{vec}\left(\mathbf{z}\right)\right)$). The regular case corresponds to ${\mathit{}\mathbf{\Sigma }}_j=\mathbf{I}$. Note that an L term can be treated as an extra single column tensor product marginal. A1, A2, A5 and A6, below, simply require ${\mathit{}\mathbf{\Sigma }}_j$ to be applied as the final step, while A3 and A4 require the extra work detailed.

The matrix products required in fitting require the following basic algorithms.

A1	Extraction of a single column of a single term Xj uses (9(9) $$\begin{array}{c}\hfill X_j(i,l)={\bar{X}}_j(k_j\left(i\right),l),\end{array}$$(9) ) at O(n) cost.
A2	Extraction of a single column of a tensor product term Xj. Let pk denote the number of columns of Mjk, and qk = ∏dj − 1i = k + 1pi, with $q_{d_j-1}=1$. Then $$X_j(i,l)=\prod _{m=0}^{d_j-1}{\bar{M}}_m^j(k_m\left(i\right),j_m)$$where the jm are defined by the following recursion. q− 1 = ∏dj − 1i = 0pj, j′− 1 = j, then iterate from i = 0: qi = qi − 1/pi, ji = ⌊j′i − 1/qi⌋, $j_i^{\text{'}}=j_{i-1}^{\text{'}}mod{q}_i$. The cost of the whole column is O(ndj).
A3	Single term ${\mathbf{X}}_j^{\mathsf{T}}\mathbf{y}$. $$X_j^{\mathsf{T}}y={\bar{X}}_j^{\mathsf{T}}\bar{y}\text{where}{\bar{y}}_l=\sum _{k_j\left(i\right)=l}{y}_i,$$which has cost O(n) + O(mjpj). If ${\mathit{}\mathbf{\Sigma }}_j\ne \mathbf{I}$ then $${\bar{y}}_l=\sum _{k_j\left(i\right)=l}{\left({\mathit{}\mathbf{\Sigma }}_j^{\mathsf{T}}\mathbf{y}\right)}_i,$$where the latter is readily computable without explicit formation of ${\mathit{}\mathbf{\Sigma }}^{\mathsf{T}}\mathbf{y}$.
A4	Tensor product term $\mathbf{v}={\mathbf{X}}_j^{\mathsf{T}}\mathbf{y}$ at cost $O\left(n\bar{p}\right)+O\left(m_{d_j-1}{p}_j\right)$. Let pk be as in A2 and $\bar{p}={\prod }_{i=0}^{d_j-2}{p}_i$. Then repeat the following for $l=0\dots \bar{p}-1$. 1. Extract column l of $\mathbf{A}={\mathbf{M}}_0^j\odot {\mathbf{M}}_1^j\odot \cdots {\mathbf{M}}_{d_j-2}^j\odot \mathbf{y}$ using A2 (without ${\mathit{}\mathbf{\Sigma }}_j$). 2. Form $v(l{p}_{d_j}:(l{p}_{d_j}+p_{d_j}-1))={\mathbf{M}}_{d_j-1}^{\mathsf{T}}\mathbf{A}(:,l)$ using A3 (with ${\mathit{}\mathbf{\Sigma }}_j$, if present). 3. Set $\mathbf{v}\leftarrow {\mathbf{Q}}_j^{\mathsf{T}}\mathbf{v}$
A5	${\mathbf{X}}_j\mathit{}\mathbf{\beta }$ for single term. $\left({\mathbf{X}}_j\mathit{}\mathbf{\beta }\right)\left(i\right)=\left({\bar{\mathbf{X}}}_j\mathit{}\mathbf{\beta }\right)\left(k_j\left(i\right)\right)$. Cost O(mjpj) + O(n).
A6	$\mathbf{f}={\mathbf{X}}_j\mathit{}\mathbf{\beta }$ for tensor product term. Notation as A4. Let B be $p_{d_j}\times \bar{p}$ such that $\text{vec}\left(\mathbf{B}\right)={\mathbf{Q}}_j\mathit{}\mathbf{\beta }$. Let $\mathbf{C}={\bar{\mathbf{M}}}_{d_j-1}\mathbf{B}$, and $\mathbf{A}={\mathbf{M}}_0^j\odot {\mathbf{M}}_1^j\odot \cdots {\mathbf{M}}_{d_j-2}^j$. Then repeat the following for $l=0\dots \bar{p}-1$. 1. Extract column j of A using A2 (without ${\mathit{}\mathbf{\Sigma }}_j$). 2. For i = 0…n − 1 $f\left(i\right)\leftarrow f\left(i\right)+C(k_{d_j-1}\left(i\right),j)A(i,j)$.

The formation of ${\mathbf{X}}_j^{\mathsf{T}}{\mathbf{WX}}_k$ then uses these basic algorithms as follows. First, if the final marginal of k has more columns than the final marginal of j then form ${\mathbf{X}}_k^{\mathsf{T}}{\mathbf{WX}}_j$ and transpose (a single smooth is its own marginal, of course). This maximizes efficiency, since the factor saved relative to direct formation is the dimension of the largest final marginal. The algorithm is then as follows.

1.	For i = 0, …, pk − 1… (a) Extract Xk(:, i) using A1 or A2 as appropriate. (b) Form WXk(:, i). (c) Form ${\mathbf{X}}_j^{\mathsf{T}}\mathbf{W}{X}_k(:,i)$ using A3 or A4 as appropriate.
2.	If the Xk is a tensor product then we may need to update $${\mathbf{X}}_j^{\mathsf{T}}{\mathbf{WX}}_k\leftarrow {\mathbf{X}}_j^{\mathsf{T}}{\mathbf{WX}}_k{\mathbf{Q}}_k$$

Q is usually implemented as a single Householder matrix, so that multiplication by Q is an efficient rank one update. Step one is easily parallelized using openMP (OpenMP Architecture Review Board 2008). Finally note that it is easy to substitute W with a banded matrix, such as the tri-diagonal precision matrix implied by an AR1 residual error model.

Prediction from the fitted model can use A5 and A6, but the computation of prediction variances also requires that we compute $\text{diag}\left({\mathbf{XVX}}^{\mathsf{T}}\right)$ where V is a covariance matrix. This computation can also be built from A5 and A6 using the fact that $$\begin{array}{c}\hfill \text{diag}\left({\mathbf{XVX}}^{\mathsf{T}}\right)=\sum _i\mathbf{XV}(:,i)\odot \mathbf{X}(:,i).\end{array}$$