Oracle Estimation of a Change Point in High-Dimensional Quantile Regression

ABSTRACT

In this article, we consider a high-dimensional quantile regression model where the sparsity structure may differ between two sub-populations. We develop ℓ₁-penalized estimators of both regression coefficients and the threshold parameter. Our penalized estimators not only select covariates but also discriminate between a model with homogenous sparsity and a model with a change point. As a result, it is not necessary to know or pretest whether the change point is present, or where it occurs. Our estimator of the change point achieves an oracle property in the sense that its asymptotic distribution is the same as if the unknown active sets of regression coefficients were known. Importantly, we establish this oracle property without a perfect covariate selection, thereby avoiding the need for the minimum level condition on the signals of active covariates. Dealing with high-dimensional quantile regression with an unknown change point calls for a new proof technique since the quantile loss function is nonsmooth and furthermore the corresponding objective function is nonconvex with respect to the change point. The technique developed in this article is applicable to a general M-estimation framework with a change point, which may be of independent interest. The proposed methods are then illustrated via Monte Carlo experiments and an application to tipping in the dynamics of racial segregation. Supplementary materials for this article are available online.

KEYWORDS:

• High-dimensional M-estimation
• LASSO
• SCAD
• Sparsity
• Variable selection

1. Introduction

In this article, we consider a high-dimensional quantile regression model where the sparsity structure (e.g., identities and effects of contributing regressors) may differ between two sub-populations, thereby allowing for a possible change point in the model. Let $Y\in \mathbb{R}$ be a response variable, $Q\in \mathbb{R}$ be a scalar random variable that determines a possible change point, and $X\in {\mathbb{R}}^p$ be a p-dimensional vector of covariates. Here, Q can be a component of X, and p is potentially much larger than the sample size n. Specifically, high-dimensional quantile regression with a change point is modeled as follows: (1.1) $$\begin{array}{cc}\hfill Y& =X^T{\beta }_0+X^T{\delta }_{0}1\{Q>{\tau }_0\}+U,\hfill \end{array}$$(1.1) where (β^T₀, δ₀^T, τ₀) is a vector of unknown parameters and the regression error U satisfies $\mathbb{P}(U\le 0|X,Q)=\gamma$ for some known γ ∈ (0, 1). Unlike mean regression, quantile regression analyzes the effects of active regressors on different parts of the conditional distribution of a response variable. Therefore, it allows the sparsity patterns to differ at different quantiles and also handles heterogeneity due to either heteroscedastic variance or other forms of nonlocation-scale covariate effects. By taking into account a possible change point in the model, we provide a more realistic picture of the sparsity patterns. For instance, when analyzing high-dimensional gene expression data, the identities of contributing genes may depend on the environmental or demographical variables (e.g., exposed temperature, age, or weights).

Our article is closely related to the literature on models with unknown change points (e.g., Tong 1990; Chan 1993; Hansen 1996, 2000; Pons 2003; Kosorok and Song 2007; Seijo and Sen 2011a, 2011b; Li and Ling 2012, among many others). Recent articles on change points under high-dimensional setups include Enikeeva and Harchaoui (2013), Chan, Yau, and Zhang (2014), Frick, Munk, and Sieling (2014), Cho and Fryzlewicz (2015), Chan et al. (2017), Callot et al. (2017), and Lee, Seo, and Shin (2016) among others; however, none of these articles consider a change point in high-dimensional quantile regression. The literature on high-dimensional quantile regression includes Belloni and Chernozhukov (2011), Bradic, Fan, and Wang (2011), Wang, Wu, and Li (2012), Wang (2013), and Fan, Fan, and Barut (2014) among others. All the aforementioned articles on quantile regression are under the homogenous sparsity framework (equivalently, assuming that δ₀ = 0 in (1.1(1.1) $$\begin{array}{cc}\hfill Y& =X^T{\beta }_0+X^T{\delta }_{0}1\{Q>{\tau }_0\}+U,\hfill \end{array}$$(1.1) )). Ciuperca (2013) considered penalized estimation of a quantile regression model with breaks, but the corresponding analysis is restricted to the case when p is small.

In this article, we consider estimating regression coefficients α₀ ≡ (β^T₀, δ^T₀)^T as well as the threshold parameter τ₀ and selecting the contributing regressors based on ℓ₁-penalized estimators. One of the strengths of our proposed procedure is that it does not require to know or pretest whether δ₀ = 0 or not, that is, whether the population’s sparsity structure and covariate effects are invariant or not. In other words, we do not need to know whether the threshold τ₀ is present in the model.

For a sparse vector $v\in {\mathbb{R}}^p$, we denote the active set of v as J(v) ≡ {j: v_j ≠ 0}. One of the main contributions of this article is that our proposed estimator of τ₀ achieves an oracle property in the sense that its asymptotic distribution is the same as if the unknown active sets J(β₀) and J(δ₀) were known. Importantly, we establish this oracle property without assuming a perfect covariate selection, thereby avoiding the need for the minimum level condition on the signals of active covariates.

The proposed estimation method in this article consists of three main steps: in the first step, we obtain the initial estimators of α₀ and τ₀, whose rates of convergence may be suboptimal; in the second step, we reestimate τ₀ to obtain an improved estimator of τ₀ that converges at the rate of O_P(n^{− 1}) and achieves the oracle property mentioned above; in the third step, using the second step estimator of τ₀, we update the estimator of α₀. In particular, we propose two alternative estimators of α₀, depending on the purpose of estimation (prediction vs. variable selection).

The most closely related work is Lee, Seo, and Shin (2016). However, there are several important differences: first, Lee, Seo, and Shin (2016) considered a high-dimensional mean regression model with a homoscedastic normal error and with deterministic covariates; second, their method consists of one-step least-square estimation with an ℓ₁ penalty; third, they derive nonasymptotic oracle inequalities similar to those in Bickel, Ritov, and Tsybakov (2009) but do not provide any distributional result on the estimator of the change point. Compared to Lee, Seo, and Shin (2016), dealing with high-dimensional quantile regression with an unknown change point calls for a new proof technique since the quantile loss function is different from the least-square objective function and is nonsmooth. In addition, we allow for heteroscedastic and nonnormal regression errors and stochastic covariates. These changes coupled with the fact that the quantile regression objective function is nonconvex with respect to the threshold parameter τ₀ raise new challenges. It requires careful derivation and multiple estimation steps to establish the oracle property for the estimator of τ₀ and also to obtain desirable properties of the estimator of α₀. The technique developed in this article is applicable to a general M-estimation framework with a change point, which may be of independent interest.

One particular application of (1.1(1.1) $$\begin{array}{cc}\hfill Y& =X^T{\beta }_0+X^T{\delta }_{0}1\{Q>{\tau }_0\}+U,\hfill \end{array}$$(1.1) ) comes from tipping in the racial segregation in social sciences (see, e.g., Card, Mas, and Rothstein 2008). The empirical question addressed in Card, Mas, and Rothstein (2008) is whether and the extent to which the neighborhood’s white population decreases substantially when the minority share in the area exceeds a tipping point (or change point). In Section 5, we use the US Census tract dataset constructed by Card, Mas, and Rothstein (2008) and confirm that the tipping exists in the neighborhoods of Chicago.

The remainder of the article is organized as follows. Section 2 provides an informal description of our estimation methodology. In Section 3.1, we derive the consistency of the estimators in terms of the excess risk. Further asymptotic properties of the proposed estimators are given in Sections 3.2 and 3.3. Section 4 gives a summary of our extensive simulation results. Section 5 illustrates the usefulness of our method by applying it to tipping in the racial segregation and Section 6 concludes. In Appendix A, we provide a set of regularity assumptions to derive asymptotic properties of the proposed estimators in Section 3. Online supplements are comprised of six appendices for all the proofs as well as additional theoretical and numerical results that are left out for the brevity of the article.

Notation. Throughout the article, we use |v|_q for the ℓ_q norm for a vector v with q = 0, 1, 2. We use |v|_∞ to denote the sup norm. For two sequences of positive real numbers a_n and b_n, we write a_n ≪ b_n and equivalently b_n ≫ a_n if a_n = o(b_n). If there exists a positive finite constant c such that a_n = c · b_n, then we write a_n∝b_n. Let λ_min(A) denote the minimum eigenvalue of a matrix A. We use w.p.a.1 to mean “with probability approaching one.” We write θ₀ ≡ β₀ + δ₀. For a 2p dimensional vector α, let α_J and ${\alpha }_{J^c}$ denote its subvectors formed by indices in J(α₀) and {1, …, 2p}∖J(α₀), respectively. Likewise, let X_J(τ) denote the subvector of X(τ) ≡ (X^T, X^T1{Q > τ})^T whose indices are in J(α₀). The true parameter vectors β₀, δ₀, and θ₀ (except τ₀) are implicitly indexed by the sample size n, and we allow that the dimensions of J(β₀), J(δ₀), and J(θ₀) can go to infinity as n → ∞. For simplicity, we omit their dependence on n in our notation. We also use the terms “change point” and “threshold” interchangeably throughout the article.

2. Estimators

2.1. Definitions

In this section, we describe our estimation method. We take the check function approach of Koenker and Bassett (1978). Let ρ(t₁, t₂) ≡ (t₁ − t₂)(γ − 1{t₁ − t₂ ⩽ 0}) denote the loss function for quantile regression. Let $\mathcal{A}$ and $\mathcal{T}$ denote the parameter spaces for α₀ ≡ (β^T₀, δ^T₀)^T and τ₀, respectively. For each $\alpha \equiv (\beta ,\delta )\in \mathcal{A}$ and $\tau \in \mathcal{T}$, we write X^Tβ + X^Tδ1{Q > τ} = X(τ)^Tα with the shorthand notation that X(τ) ≡ (X^T, X^T1{Q > τ})^T. We suppose that the vector of true parameters is defined as the minimizer of the expected loss: (2.1) $$({\alpha }_0,{\tau }_0)=\underset{\alpha \in \mathcal{A},\tau \in \mathcal{T}}{argmin}\mathbb{E}\left[\rho (Y,X{\left(\tau \right)}^T\alpha )\right].$$(2.1) By construction, τ₀ is not unique when δ₀ = 0. However, if δ₀ = 0, then the model reduces to the linear quantile regression model in which β₀ is identifiable under the standard assumptions. In Online Appendix C.1, we provide sufficient conditions under which α₀ and τ₀ are identified when δ₀ ≠ 0.

Suppose we observe independent and identically distributed samples {Y_i, X_i, Q_i}_{i ⩽ n}. Let X_i(τ) and X_ij(τ) denote the ith realization of X(τ) and jth element of X_i(τ), respectively, i = 1, …, n and j = 1, …, 2p, so that X_ij(τ) ≡ X_ij if j ⩽ p and X_ij(τ) ≡ X_{i, j − p}1{Q_i > τ} otherwise. Define $$\begin{array}{ccc}\hfill R_n(\alpha ,\tau )& \equiv & \frac{1}{n}\sum _{i=1}^n\rho (Y_i,X_i{\left(\tau \right)}^T\alpha )\hfill \\ & =& \frac{1}{n}\sum _{i=1}^n\rho (Y_i,X_i^T\beta +X_i^T\delta 1\{Q_i>\tau \}).\hfill \end{array}$$In addition, let D_j(τ) ≡ {n^{− 1}∑ⁿ_{i = 1}X_ij(τ)²}^1/2, j = 1, …, 2p.

We describe the main steps of our ℓ₁-penalized estimation method. For some tuning parameter κ_n, define: (2.2) $$\begin{array}{ccc}\hfill \mathit{Step}\mathit{1}:(\breve{\alpha },\breve{\tau })& =& {\text{argmin}}_{\alpha \in \mathcal{A},\tau \in \mathcal{T}}{R}_n(\alpha ,\tau )+{\kappa }_n\sum _{j=1}^{2p}{D}_j\left(\tau \right)\left|{\alpha }_j\right|,\hfill \end{array}$$(2.2) where α_j is the jth element of α. This step produces an initial estimator $(\breve{\alpha },\breve{\tau })$. The tuning parameter κ_n is required to satisfy (2.3) $${\kappa }_n\propto (logp)(logn)\sqrt{\frac{logp}{n}}.$$(2.3) Note that we take κ_n that converges to zero at a rate slower than the standard (log p/n)^1/2 rate in the literature. This modified rate of κ_n is useful in our context to deal with an unknown τ₀. A data-dependent method of choosing κ_n is discussed in Section 2.3.

Remark 1.

Define $d_j\equiv {\left(\frac{1}{n}{\sum }_{i=1}^n{X}_{ij}^2\right)}^{1/2}$ and $d_j\left(\tau \right)\equiv {\left(\frac{1}{n}{\sum }_{i=1}^n{X}_{ij}^{2}1\{Q_i>\tau \}\right)}^{1/2}$. Note that ∑^2p_{j = 1}D_j(τ)|α_j| = ∑^p_{j = 1}d_j|β_j| + ∑^p_{j = 1}d_j(τ)|δ_j|, so that the weight D_j(τ) adequately balances the regressors; the weight d_j regarding |β_j| does not depend on τ, while the weight d_j(τ) with respect to |δ_j| does, which takes into account the effect of the threshold τ on the parameter change δ.

Remark 2.

The computational cost in Step 1 is the multiple of grid points to the computational time of estimating the linear quantile model with an ℓ₁ penalty, which is solvable in polynomial time (see, e.g., Belloni and Chernozhukov 2011; Koenker and Mizera 2014 among others). In other words, the computation cost increases linearly in terms of the number of grid points. In practice, one may choose the grid to be $\{Q_i:i=1,\dots ,n\}\cap \mathcal{T}$.

The main purpose of the first step is to obtain an initial estimator of α₀. The achieved convergence rates of this step might be suboptimal due to the uniform control of the score functions over the space $\mathcal{T}$ of the unknown τ₀.

In the second step, we introduce our improved estimator of the change point τ₀. It does not use a penalty term, while using the first-step estimator of α₀. Define: (2.4) $$\begin{array}{cc}\hfill \mathit{Step}\mathit{2}:\widehat{\tau }& =\underset{\tau \in \mathcal{T}}{argmin}{R}_n(\breve{\alpha },\tau ),\hfill \end{array}$$(2.4) where $\breve{\alpha }$ is the first-step estimator of α₀ in (2.2(2.2) $$\begin{array}{ccc}\hfill \mathit{Step}\mathit{1}:(\breve{\alpha },\breve{\tau })& =& {\text{argmin}}_{\alpha \in \mathcal{A},\tau \in \mathcal{T}}{R}_n(\alpha ,\tau )+{\kappa }_n\sum _{j=1}^{2p}{D}_j\left(\tau \right)\left|{\alpha }_j\right|,\hfill \end{array}$$(2.2) ). In Section 3.2, we show that when τ₀ is identifiable, $\widehat{\tau }$ is consistent for τ₀ at a rate of n^{− 1}. Furthermore, we obtain the limiting distribution of $n(\widehat{\tau }-{\tau }_0)$, and establish conditions under which its asymptotic distribution is the same as if the true α₀ were known, without a perfect model selection on α₀, nor assuming the minimum signal condition on the nonzero elements of α₀.

In the third step, we update the Lasso estimator of α₀ using a different value of the penalization tuning parameter and the second step estimator of τ₀. In particular, we recommend two different estimators of α₀ : one for the prediction and the other for the variable selection, serving for different purposes of practitioners. For two different tuning parameters ω_n and μ_n whose rates will be specified later by (2.7(2.7) $$\begin{array}{c}\hfill {\omega }_n\propto \sqrt{\frac{log(p\vee n)}{n}},\end{array}$$(2.7) ) and (3.2(3.2) $${\omega }_n+s\sqrt{\frac{logs}{n}}\ll {\mu }_n\ll \underset{j\in J\left({\alpha }_0\right)}{min}\left|{\alpha }_{0J}^{\left(j\right)}\right|.$$(3.2) ), define: (2.5) $$\begin{array}{cc}\hfill \mathit{Step}\mathit{3}\mathit{a}& \left(\mathit{for}\mathit{prediction}\right):\hfill \\ \hfill \widehat{\alpha }& ={\text{argmin}}_{\alpha \in \mathcal{A}}{R}_n(\alpha ,\widehat{\tau })+{\omega }_n\sum _{j=1}^{2p}{D}_j\left(\widehat{\tau }\right)\left|{\alpha }_j\right|,\hfill \end{array}$$(2.5) (2.6) $$\begin{array}{cc}\hfill \mathit{Step}\mathit{3}\mathit{b}& \left(\mathit{for}\mathit{variable}\mathit{selection}\right):\hfill \\ \hfill \tilde{\alpha }& ={\text{argmin}}_{\alpha \in \mathcal{A}}{R}_n(\alpha ,\widehat{\tau })+{\mu }_n\sum _{j=1}^{2p}{w}_j{D}_j\left(\widehat{\tau }\right)\left|{\alpha }_j\right|,\hfill \end{array}$$(2.6) where $\widehat{\tau }$ is the second step estimator of τ₀ in (2.4(2.4) $$\begin{array}{cc}\hfill \mathit{Step}\mathit{2}:\widehat{\tau }& =\underset{\tau \in \mathcal{T}}{argmin}{R}_n(\breve{\alpha },\tau ),\hfill \end{array}$$(2.4) ), and the “signal-adaptive” weight w_j in (2.6(2.6) $$\begin{array}{cc}\hfill \mathit{Step}\mathit{3}\mathit{b}& \left(\mathit{for}\mathit{variable}\mathit{selection}\right):\hfill \\ \hfill \tilde{\alpha }& ={\text{argmin}}_{\alpha \in \mathcal{A}}{R}_n(\alpha ,\widehat{\tau })+{\mu }_n\sum _{j=1}^{2p}{w}_j{D}_j\left(\widehat{\tau }\right)\left|{\alpha }_j\right|,\hfill \end{array}$$(2.6) ), motivated by the local linear approximation of the SCAD penalties (Fan and Li 2001; Zou and Li 2008), is calculated based on the Step 3a estimator $\widehat{\alpha }$ from (2.5(2.5) $$\begin{array}{cc}\hfill \mathit{Step}\mathit{3}\mathit{a}& \left(\mathit{for}\mathit{prediction}\right):\hfill \\ \hfill \widehat{\alpha }& ={\text{argmin}}_{\alpha \in \mathcal{A}}{R}_n(\alpha ,\widehat{\tau })+{\omega }_n\sum _{j=1}^{2p}{D}_j\left(\widehat{\tau }\right)\left|{\alpha }_j\right|,\hfill \end{array}$$(2.5) ): $$w_j\equiv \left\{\begin{array}{cc}\hfill 1,& \hfill |{\widehat{\alpha }}_j|<{\mu }_n\\ \hfill 0,& \hfill |{\widehat{\alpha }}_j|>a{\mu }_n\\ \hfill \frac{a{\mu }_n-\left|{\widehat{\alpha }}_j\right|}{{\mu }_n(a-1)}& \hfill {\mu }_n\le \left|{\widehat{\alpha }}_j\right|\le a{\mu }_n.\end{array}\right.$$Here, a > 1 is some prescribed constant, and a = 3.7 is often used in the literature. We take this as our choice of a.

Remark 3.

For $\widehat{\alpha }$ in (2.5(2.5) $$\begin{array}{cc}\hfill \mathit{Step}\mathit{3}\mathit{a}& \left(\mathit{for}\mathit{prediction}\right):\hfill \\ \hfill \widehat{\alpha }& ={\text{argmin}}_{\alpha \in \mathcal{A}}{R}_n(\alpha ,\widehat{\tau })+{\omega }_n\sum _{j=1}^{2p}{D}_j\left(\widehat{\tau }\right)\left|{\alpha }_j\right|,\hfill \end{array}$$(2.5) ), we set ω_n to converge to zero at a rate of (log (p∨n)/n)^1/2: (2.7) $$\begin{array}{c}\hfill {\omega }_n\propto \sqrt{\frac{log(p\vee n)}{n}},\end{array}$$(2.7) which is a more standard rate compared to κ_n in (2.3(2.3) $${\kappa }_n\propto (logp)(logn)\sqrt{\frac{logp}{n}}.$$(2.3) ). Therefore, the estimator $\widehat{\alpha }$ converges in probability to α₀ faster than $\breve{\alpha }$. In addition, μ_n in (2.6(2.6) $$\begin{array}{cc}\hfill \mathit{Step}\mathit{3}\mathit{b}& \left(\mathit{for}\mathit{variable}\mathit{selection}\right):\hfill \\ \hfill \tilde{\alpha }& ={\text{argmin}}_{\alpha \in \mathcal{A}}{R}_n(\alpha ,\widehat{\tau })+{\mu }_n\sum _{j=1}^{2p}{w}_j{D}_j\left(\widehat{\tau }\right)\left|{\alpha }_j\right|,\hfill \end{array}$$(2.6) ) is chosen to be slightly larger than ω_n for the purpose of the variable selection. A data-dependent method of choosing ω_n as well as μ_n is discussed in Section 2.3. In Sections 3.2 and 3.3, we establish conditions under which $\widehat{\alpha }$ achieves the (minimax) optimal rate of convergence in probability for α₀ regardless of the identifiability of τ₀.

Remark 4.

Step 2 can be repeated using the updated estimator of α₀ in Step 3. Analogously, Step 3 can be iterated after that. This would give asymptotically equivalent estimators but might improve the finite-sample performance especially when p is very large. Repeating Step 2 might be useful especially when $\breve{\delta }=0$ in the first step. In this case, there is no unique $\widehat{\tau }$ in Step 2. So, we skip the second step by setting $\widehat{\tau }=\breve{\tau }$ and move to the third step directly. If a preferred estimator of δ₀ in the third step (either $\widehat{\delta }$ or $\tilde{\delta }$), depending on the estimation purpose, is different from zero, we could go back to Step 2 and reestimate τ₀. If the third step estimator of δ₀ is also zero, then we conclude that there is no change point and disregard the first-step estimator $\breve{\tau }$ since τ₀ is not identifiable in this case.

2.2. Comparison of Estimators in Step 3

Step 3 defines two estimators for α₀. In this subsection, we briefly explain their major differences and purposes. Step 3b is particularly useful when the variable selection consistency is the main objective, yet it often requires the minimum signal condition (${min}_{{\alpha }_{0j}\ne 0}\left|{\alpha }_{0j}\right|$ is well separated from zero). In contrast, Step 3a does not require the minimum signal condition, and is recommended for predictionpurposes. More specifically:

1.	If the minimum signal condition (3.3(3.3) $${\mu }_n=o\left(\underset{j\in J\left({\alpha }_0\right)}{min}\left|{\alpha }_{0J}^{\left(j\right)}\right|\right),$$(3.3) ) indeed holds, a perfect variable selection (variable selection consistency) is possible. The Step 3b estimator achieves the variable selection consistency. In contrast, Step 3a does not use signal-adaptive weights. To achieve the variable selection consistency, it has to rely on much stronger conditions on the design matrix (i.e., the irrepresentable condition by Zhao and Yu 2006) so as to “balance out” the effects of shrinkage biases, and is less adaptive to correlated designs.
2.	In the presence of the minimum signal condition, not only does Step 3b achieve the variable selection consistency, it also has a better rate of convergence than Step 3a (Theorem 6). The faster rate of convergence is built on the variable selection consistency, and is still a consequence of the signal-adaptive weights. Intuitively, nonzero elements of α0 are easier to identify and estimate when the signal is strong.
3.	In the absence of the minimum signal condition, neither method can achieve variable selection consistency. However, it is not a requirement for the prediction purpose. In this case, we recommend the estimator of Step 3a, because it achieves a fast (minimax) rate of convergence (Theorem 5), which is useful for predictions.

2.3. Tuning Parameter Selection

In this subsection, we provide details on how to choose tuning parameters in applications. Recall that our procedure involves three tuning parameters in the penalization: (1) κ_n in Step 1 ought to dominate the score function uniformly over the range of τ, and hence should be slightly larger than the others; (2) ω_n is used in Step 3a for the prediction, and (3) μ_n in Step 3b for the variable selection should be larger than ω_n. Note that the tuning parameters in both Steps 3a and 3b are similar to those of the existing literature since the change point $\widehat{\tau }$ has been estimated.

We build on the data-dependent selection method by Belloni and Chernozhukov (2011). Define (2.8) $$\begin{array}{c}\hfill \Lambda \left(\tau \right):=\underset{1\le j\le 2p}{max}\left|\frac{1}{n}\sum _{i=1}^n\frac{X_{ij}\left(\tau \right)(\gamma -1\{U_i\le \gamma \})}{D_j\left(\tau \right)}\right|,\end{array}$$(2.8) where U_i is simulated from the iid uniform distribution on the interval [0, 1]; γ is the quantile of interest (e.g., γ = 0.5 for median regression). Note that Λ(τ) is a stochastic process indexed by τ. Let ${\bar{\Lambda }}_{1-{ϵ}^{*}}$ be the (1 − ε*)-quantile of ${sup}_{\tau \in \mathcal{T}}\Lambda \left(\tau \right)$, where ε* is a small positive constant that will be selected by a user. Then, we select the tuning parameter in Step 1 by ${\kappa }_n=c_1·{\bar{\Lambda }}_{1-{ϵ}^{*}}.$ Similarly, let ${\Lambda }_{1-{ϵ}^{*}}\left(\widehat{\tau }\right)$ be the (1 − ε*)-quantile of $\Lambda \left(\widehat{\tau }\right)$, where $\widehat{\tau }$ is chosen in Step 2. We select ω_n and μ_n in Step 3 by ${\omega }_n=c_1·{\Lambda }_{1-{ϵ}^{*}}\left(\widehat{\tau }\right)$ and μ_n = c₂ · ω_n. It is also necessary to choose $\mathcal{T}$ in applications. In our Monte Carlo experiments in online Appendix F, we take $\mathcal{T}$ to be the interval from the 15th percentile to the 85th percentile of the empirical distribution of the threshold variable Q_i. For example, Hansen (1996) employed the same range in his application to U.S. GNP dynamics. In practice, it is important to have a sufficient number of observations lying outside $\mathcal{T}$.

Based on the suggestions by Belloni and Chernozhukov (2011) and some preliminary simulations, we choose to set c₁ = 1.1, c₂ = log log n, and ε* = 0.1. In addition, recall that we set a = 3.7 when calculating the SCAD weights w_j in Step 3b following the convention in the literature (e.g., Fan and Li 2001; Loh and Wainwright 2013). In Step 1, we first solve the lasso problem for α given each grid point of $\tau \in \mathcal{T}$. Then, we choose $\breve{\tau }$ and the corresponding $\breve{\alpha }\left(\breve{\tau }\right)$ that minimize the objective function. Step 2 can be solved simply by the grid search. Step 3 is a standard lasso quantile regression estimation given $\widehat{\tau }$, whose numerical implementation is well established. We use the rq() function of the R “quantreg” package with the method = ”lasso” in each implementation of the standard lasso quantile regression estimation (Koenker 2016).

3. Asymptotic Properties

Throughout the article, we let s ≡ |J(α₀)|₀, namely, the cardinality of J(α₀). We allow that s → ∞ as n → ∞ and will give precise regularity conditions regarding its growth rates. In Appendix A, we list a set of assumptions that are needed to derive these properties.

3.1. Risk Consistency

Given the loss function ρ(t₁, t₂) ≡ (t₁ − t₂)(γ − 1{t₁ − t₂ ⩽ 0}) for the quantile regression model, define the excess risk to be (3.1) $$\begin{array}{c}\hfill R(\alpha ,\tau )\equiv \mathbb{E}\rho (Y,X{\left(\tau \right)}^T\alpha )-\mathbb{E}\rho (Y,X{\left({\tau }_0\right)}^T{\alpha }_0).\end{array}$$(3.1) By the definition of (α₀, τ₀) in (2.1(2.1) $$({\alpha }_0,{\tau }_0)=\underset{\alpha \in \mathcal{A},\tau \in \mathcal{T}}{argmin}\mathbb{E}\left[\rho (Y,X{\left(\tau \right)}^T\alpha )\right].$$(2.1) ), we have that R(α, τ) ⩾ 0 for any $\alpha \in \mathcal{A}$ and $\tau \in \mathcal{T}$. What we mean by the “risk consistency” here is that the excess risk converges in probability to zero for the proposed estimators.

The following theorem is concerned about the convergence of $R(\breve{\alpha },\breve{\tau })$ with the first-step estimator.

Theorem 1 (Risk Consistency).

Let Assumption A.1 hold. Suppose that the tuning parameter κ_n satisfies (2.3(2.3) $${\kappa }_n\propto (logp)(logn)\sqrt{\frac{logp}{n}}.$$(2.3) ). Then, $R(\breve{\alpha },\breve{\tau })=O_P\left({\kappa }_{n}s\right).$

Note that Theorem 1 holds regardless of the identifiability of τ₀ (i.e., whether δ₀ = 0 or not). In addition, the rate O_P(κ_ns) is achieved regardless of whether κ_ns converges, and we have the risk consistency if κ_ns → 0 as n → ∞. The restriction on s is slightly stronger than that of the standard result $s=o\left(\sqrt{n/logp}\right)$ in the literature for the M-estimation (see, e.g., van de Geer 2008 and chap. 6.6 of Bühlmann and van de Geer 2011) since the objective function ρ(Y, X(τ)^Tα) is nonconvex in τ, due to the unknown change point.

Remark 5.

The extra logarithmic factor (log p)(log n) in the definition of κ_n (see (2.3(2.3) $${\kappa }_n\propto (logp)(logn)\sqrt{\frac{logp}{n}}.$$(2.3) )) is due to the existence of the unknown and possibly nonidentifiable threshold parameter τ₀. In fact, an inspection of the proof of Theorem 1 reveals that it suffices to assume that κ_n satisfies κ_n ≫ log ₂(p/s)[log (np)/n]^1/2. The term log ₂(p/s) and the additional (log n)^1/2 term inside the brackets are needed to establish the stochastic equicontinuity of the empirical process $${\nu }_n\left(\alpha ,\tau \right)\equiv \frac{1}{n}\sum _{i=1}^n[\rho (Y_i,X_i{\left(\tau \right)}^T\alpha )-\mathbb{E}\rho (Y,X{\left(\tau \right)}^T\alpha )]$$uniformly over $(\alpha ,\tau )\in \mathcal{A}\times \mathcal{T}$.

In Appendix C.2, we show that an improved rate of convergence, O_P(ω_ns), is possible for the excess risk by taking the second and third steps of estimation.

3.2. Asymptotic Properties: Case I. δ₀ ≠ 0

We first establish the consistency of $\breve{\tau }$ for τ₀.

Theorem 2 (Consistency of $\breve{\tau }$).

Let Assumptions A.1, A.2, A.5, and A.6 hold. Furthermore, assume that κ_ns = o(1). Then, $\breve{\tau }\stackrel{P}{⟶}{\tau }_0$.

The following theorem presents the rates of convergence for the first-step estimators of α₀ and τ₀. Recall that κ_n is the first-step penalization tuning parameter that satisfies (2.3(2.3) $${\kappa }_n\propto (logp)(logn)\sqrt{\frac{logp}{n}}.$$(2.3) ).

Theorem 3 (Rates of Convergence When δ₀ ≠ 0).

Suppose that κ_ns²log p = o(1). Then under Assumptions A.1–A.6, we have $$\begin{array}{ccc}\hfill |\breve{\alpha }-{\alpha }_0{|}_1& =& O_P\left({\kappa }_{n}s\right),R(\breve{\alpha },\breve{\tau })=O_P\left({\kappa }_n^{2}s\right),\text{and}|\breve{\tau }-{\tau }_0|\hfill \\ & =& O_P\left({\kappa }_n^{2}s\right).\hfill \end{array}$$

In Theorem 1, we have that $R(\breve{\alpha },\breve{\tau })=O_P\left({\kappa }_{n}s\right).$ The improved rate of convergence for $R(\breve{\alpha },\breve{\tau })$ in Theorem 3 is due to additional assumptions (in particular, compatibility conditions in Assumption A.3 among others). It is worth noting that $\breve{\tau }$ converges to τ₀ faster than the standard parametric rate of n^{− 1/2}, as long as s²(log p)⁶(log n)⁴ = o(n). The main reason for such super-consistency is that the objective function behaves locally linearly around τ₀ with a kink at τ₀, unlike in the regular estimation problem where the objective function behaves locally quadratically around the true parameter value. Moreover, the achieved convergence rate for $\breve{\alpha }$ is nearly minimax optimal, with an additional factor (log p)(log n) compared to the rate of regular Lasso estimation (e.g., Bickel, Ritov, and Tsybakov 2009; Raskutti, Wainwright, and Yu 2011). This factor arises due to the unknown change point τ₀. We will improve the rates of convergence for both τ₀ and α₀ further by taking the second and third steps of estimation.

Recall that the second-step estimator of τ₀ is defined as $$\begin{array}{cc}\hfill \widehat{\tau }& =\underset{\tau \in \mathcal{T}}{argmin}{R}_n(\breve{\alpha },\tau ),\hfill \end{array}$$where $\breve{\alpha }$ is the first-step estimator of α₀ in (2.2(2.2) $$\begin{array}{ccc}\hfill \mathit{Step}\mathit{1}:(\breve{\alpha },\breve{\tau })& =& {\text{argmin}}_{\alpha \in \mathcal{A},\tau \in \mathcal{T}}{R}_n(\alpha ,\tau )+{\kappa }_n\sum _{j=1}^{2p}{D}_j\left(\tau \right)\left|{\alpha }_j\right|,\hfill \end{array}$$(2.2) ). Consider an oracle case for which α in R_n(α, τ) is fixed at α₀. Let R*_n(τ) = R_n(α₀, τ) and $$\tilde{\tau }=\underset{\tau \in \mathcal{T}}{argmin}{R}_n^{*}\left(\tau \right).$$

We now give one of the main results of this article.

Theorem 4 (Oracle Estimation of τ₀).

Let Assumptions A.1–A.6 hold. Furthermore, suppose that κ_ns²log p = o(1). Then, we have that $$\widehat{\tau }-\tilde{\tau }=o_P\left(n^{-1}\right).$$Furthermore, $n(\widehat{\tau }-{\tau }_0)$ converges in distribution to the smallest minimizer of a compound Poisson process, which is given by $$M\left(h\right)\equiv \sum _{i=1}^{N_1(-h)}{\rho }_{1i}1\{h<0\}+\sum _{i=1}^{N_2\left(h\right)}{\rho }_{2i}1\{h\ge 0\},$$where N₁ and N₂ are Poisson processes with the same jump rate f_Q(τ₀), and {ρ_1i} and {ρ_2i} are two sequences of independent and identically distributed random variables. The distributions of ρ_1i and ρ_2i, respectively, are identical to the conditional distributions of $\dot{\rho }(U_i-X_i^T{\delta }_0)-\dot{\rho }\left(U_i\right)$ and $\dot{\rho }(U_i+X_i^T{\delta }_0)-\dot{\rho }\left(U_i\right)$ given Q_i = τ₀, where $\dot{\rho }\left(t\right)\equiv t(\gamma -1\{t\le 0\})$ and U_i ≡ Y_i − X^T_iβ₀ − X^T_iδ₀1{Q_i > τ₀} for each i = 1, …, n. Here, N₁, N₂, {ρ_1i}, and {ρ_2i} are mutually independent.

The first conclusion of Theorem 4 establishes that the second-step estimator of τ₀ is an oracle estimator in the sense that it is asymptotically equivalent to the infeasible, oracle estimator $\tilde{\tau }$. As emphasized in the introduction, the oracle property is obtained without relying on the perfect model selection in the first step nor on the existence of the minimum signal condition on active covariates. The second conclusion of Theorem 4 follows from combining well-known weak convergence results in the literature (see, e.g., Pons 2003; Kosorok and Song 2007; Lee and Seo 2008) with the argmax continuous mapping theorem by Seijo and Sen (2011b).

Remark 6.

Li and Ling (2012) proposed a numerical approach for constructing a confidence interval by simulating a compound Poisson process in the context of least-square estimation. We adopt their approach to simulate the compound Poisson process for quantile regression. See Online Appendix B for a detailed description of how to construct a confidence interval for τ₀.

We now consider the Step 3a estimator of α₀ defined in (2.5(2.5) $$\begin{array}{cc}\hfill \mathit{Step}\mathit{3}\mathit{a}& \left(\mathit{for}\mathit{prediction}\right):\hfill \\ \hfill \widehat{\alpha }& ={\text{argmin}}_{\alpha \in \mathcal{A}}{R}_n(\alpha ,\widehat{\tau })+{\omega }_n\sum _{j=1}^{2p}{D}_j\left(\widehat{\tau }\right)\left|{\alpha }_j\right|,\hfill \end{array}$$(2.5) ). Recall that ω_n is the Step 3a penalization tuning parameter that satisfies (2.7(2.7) $$\begin{array}{c}\hfill {\omega }_n\propto \sqrt{\frac{log(p\vee n)}{n}},\end{array}$$(2.7) ).

Theorem 5 (Improved Rates of Convergence When δ₀ ≠ 0).

Suppose that κ_ns²log p = o(1). Then under Assumptions A.1–A.6, $$|\widehat{\alpha }-{\alpha }_0{|}_1=O_P\left({\omega }_{n}s\right)\text{and}R(\widehat{\alpha },\widehat{\tau })=O_P\left({\omega }_n^{2}s\right).$$

Theorem 5 shows that the estimator $\widehat{\alpha }$ defined in Step 3a achieves the optimal rate of convergence in terms of prediction and estimation. In other words, when ω_n is proportional to {log (p∨n)/n}^1/2 in Equation (2.7(2.7) $$\begin{array}{c}\hfill {\omega }_n\propto \sqrt{\frac{log(p\vee n)}{n}},\end{array}$$(2.7) ) and p is larger than n, it obtains the minimax rates as in, for example, Raskutti, Wainwright, and Yu (2011).

As we mentioned in Section 2, the Step 3b estimator of α₀ has the purpose of the variable selection. The nonzero components of $\tilde{\alpha }$ are expected to identify contributing regressors. Partition $\tilde{\alpha }=({\tilde{\alpha }}_J,{\tilde{\alpha }}_{J^c})$ such that ${\tilde{\alpha }}_J=({\tilde{\alpha }}_j:j\in J\left({\alpha }_0\right))$ and ${\tilde{\alpha }}_{J^c}=({\tilde{\alpha }}_j:j\notin J\left({\alpha }_0\right))$. Note that ${\tilde{\alpha }}_J$ consists of the estimators of β_0J and δ_0J, whereas ${\tilde{\alpha }}_{J^c}$ consists of the estimators of all the zero components of β₀ and δ₀. Let α^(j)_0J denote the jth element of α_0J.

We now establish conditions under which the estimator $\tilde{\alpha }$ defined in Step 3b has the change-point-oracle properties, meaning that it achieves the variable selection consistency and has the limiting distributions as though the identities of the important regressors and the location of the change point were known.

Theorem 6 (Variable Selection When δ₀ ≠ 0).

Suppose that κ_ns²log p = o(1), s⁴log s = o(n), and (3.2) $${\omega }_n+s\sqrt{\frac{logs}{n}}\ll {\mu }_n\ll \underset{j\in J\left({\alpha }_0\right)}{min}\left|{\alpha }_{0J}^{\left(j\right)}\right|.$$(3.2) Then under Assumptions A.1–A.6, we have: (i) $${\left|{\tilde{\alpha }}_J-{\alpha }_{0J}\right|}_2=O_P\left(\sqrt{\frac{slogs}{n}}\right),{\left|{\tilde{\alpha }}_J-{\alpha }_{0J}\right|}_1=O_P\left(s\sqrt{\frac{logs}{n}}\right),$$(ii) $$P({\tilde{\alpha }}_{J^c}=0)\to 1,$$and (iii) $$\begin{array}{c}\hfill R(\tilde{\alpha },\widehat{\tau })=O_P\left({\mu }_{n}s\sqrt{\frac{logs}{n}}\right).\end{array}$$

We see that (3.2(3.2) $${\omega }_n+s\sqrt{\frac{logs}{n}}\ll {\mu }_n\ll \underset{j\in J\left({\alpha }_0\right)}{min}\left|{\alpha }_{0J}^{\left(j\right)}\right|.$$(3.2) ) provides a condition on the strength of the signal via ${min}_{j\in J\left({\alpha }_0\right)}\left|{\alpha }_{0J}^{\left(j\right)}\right|$, and the tuning parameter in Step 3b should satisfy ω_n ≪ μ_n and s²log s/n ≪ μ²_n. Hence, the variable selection consistency demands a larger tuning parameter than in Step 3a.

To conduct statistical inference, we now discuss the asymptotic distribution of ${\tilde{\alpha }}_J$. Define ${\widehat{\alpha }}_J^{*}\equiv {argmin}_{{\alpha }_J}{R}_n^{*}({\alpha }_J,{\tau }_0)$. Note that the asymptotic distribution for ${\widehat{\alpha }}_J^{*}$ corresponds to an oracle case that we know τ₀ as well as the true active set J(α₀) a priori. The limiting distribution of ${\tilde{\alpha }}_J$ is the same as that of ${\widehat{\alpha }}_J^{*}$. Hence, we call this result the change-point-oracle property of the Step 3b estimator and the following theorem establishes this property.

Theorem 7 (Change-Point-Oracle Properties).

Suppose that all the conditions imposed in Theorem 6 are satisfied. Furthermore, assume that $\frac{\partial }{\partial \alpha }E\left[\rho (Y,X^T\alpha )\right|Q=t]$ exists for all t in a neighborhood of τ₀ and all its elements are continuous and bounded, and that s³(log s)(log n) = o(n). Then, we have that ${\tilde{\alpha }}_J={\widehat{\alpha }}_J^{*}+o_P\left(n^{-1/2}\right).$

Since the sparsity index (s) grows at a rate slower than the sample size (n), it is straightforward to establish the asymptotic normality of a linear transformation of ${\tilde{\alpha }}_J,$ that is, $\mathbf{L}{\tilde{\alpha }}_J,$ where $\mathbf{L}:{\mathbb{R}}^s\to \mathbb{R}$ with |L|₂ = 1, by combing the existing results on quantile regression with parameters of increasing dimension (see, e.g., He and Shao 2000) with Theorem 7.

Remark 7.

Without the condition on the strength of minimal signals, it may not be possible to achieve the variable selection consistency or establish change-point-oracle properties. However, the following theorem shows that the SCAD-weighted penalized estimation can still achieve a satisfactory rate of convergence in estimation of α₀ without the condition that ${\mu }_n\ll {min}_{j\in J\left({\alpha }_0\right)}\left|{\alpha }_{0J}^{\left(j\right)}\right|$. Yet, the rates of convergence are slower than those of Theorem 6.

Theorem 8 (Satisfactory Rates Without Minimum Signal Condition).

Assume that Assumptions A.1–A.6 hold. Suppose that κ_ns²log p = o(1) and ω_n ≪ μ_n. Then, without the lower bound requirement on ${min}_{j\in J\left({\alpha }_0\right)}\left|{\alpha }_{0J}^{\left(j\right)}\right|$, we have that $|\tilde{\alpha }-{\alpha }_0{|}_1=O_P\left({\mu }_{n}s\right).$ In addition, $R(\tilde{\alpha },\widehat{\tau })=O_P\left({\mu }_n^{2}s\right).$

3.3. Asymptotic Properties: Case II. δ₀ = 0

In this section, we show that our estimators have desirable results even if there is no change point in the true model. The case of δ₀ = 0 corresponds to the high-dimensional linear quantile regression model. Since X^Tβ₀ + X^Tδ₀1{Q > τ₀} = X^Tβ₀, τ₀ is nonidentifiable, and there is no structural change on the coefficient. But a new analysis different from that of the standard high-dimensional model is still required because in practice we do not know whether δ₀ = 0 or not. Thus, the proposed estimation method still estimates τ₀ to account for possible structural changes. The following results show that in this case, the first-step estimator of α₀ will asymptotically behave as if δ₀ = 0 were a priori known.

Theorem 9 (Rates of Convergence When δ₀ = 0).

Suppose that κ_ns = o(1). Then under Assumptions A.1–A.4, we have that $$|\breve{\alpha }-{\alpha }_0{|}_1=O_P\left({\kappa }_{n}s\right)\text{and}R(\breve{\alpha },\breve{\tau })=O_P\left({\kappa }_n^{2}s\right).$$

The results obtained in Theorem 9 combined with those obtained in Theorem 3 imply that the first-step estimator performs equally well in terms of rates of convergence for both the ℓ₁ loss for $\breve{\alpha }$ and the excess risk regardless of the existence of the threshold effect. It is straightforward to obtain an improved rate result for the Step 3a estimator, equivalent to Theorem 5 under Assumptions A.1–A.4. We omit the details for brevity.

We now give a result that is similar to Theorem 6 and Theorem 8.

Theorem 10 (Variable Selection When δ₀ = 0).

Suppose that κ_ns = o(1), s⁴log s = o(n), ${\omega }_n+s\sqrt{\frac{logs}{n}}\ll {\mu }_n$, and Assumptions A.1–A.4 hold. We have:

(i)

If the minimum signal condition holds: (3.3) $${\mu }_n=o\left(\underset{j\in J\left({\alpha }_0\right)}{min}\left|{\alpha }_{0J}^{\left(j\right)}\right|\right),$$(3.3) then $$\begin{array}{ccc}\hfill |{\tilde{\beta }}_J-{\beta }_{0J}{|}_2& =& O_P\left(\sqrt{\frac{slogs}{n}}\right),\hfill \\ \hfill |{\tilde{\beta }}_J-{\beta }_{0J}{|}_1& =& O_P\left(s\sqrt{\frac{logs}{n}}\right),\hfill \\ \hfill P({\tilde{\beta }}_{J^c}& =& 0)\to 1,P(\tilde{\delta }=0)\to 1,\text{and}\hfill \\ \hfill R(\tilde{\alpha },\widehat{\tau })& =& O_P\left({\mu }_{n}s\sqrt{\frac{logs}{n}}\right).\hfill \end{array}$$

(ii)

WithoutTable 1the minimum signal condition (3.3(3.3) $${\mu }_n=o\left(\underset{j\in J\left({\alpha }_0\right)}{min}\left|{\alpha }_{0J}^{\left(j\right)}\right|\right),$$(3.3) ), we have $$\begin{array}{c}\hfill R(\tilde{\alpha },\widehat{\tau })=O_P\left({\mu }_n^{2}s\right),{|\tilde{\alpha }-{\alpha }_0|}_1=O_P\left(s{\mu }_n\right).\end{array}$$

Theorem 10 demonstrates that when there is in fact no change point, our estimator for δ₀ is exactly zero with a high probability. Therefore, the estimator can also be used as a diagnostic tool to check whether there exists any change point. Results similar to Theorems 7 can be established straightforwardly as well; however, their details are omitted for brevity.

4. Summary of Monte Carlo Experiments

We have carried out extensive Monte Carlo experiments to examine the finite sample performance of our proposed estimators. To save space, we provide a summary of simulation results and show full results in online Appendix F.

1.	The proposed estimator (Step 3b) selected different nonzero coefficients at different quantile levels. The mean regression estimator in Lee, Seo, and Shin (2016) cannot detect these heterogenous models.
2.	The coverage probabilities of the confidence interval for τ0 were good and the root mean squared error of $\widehat{\tau }$ decreased quickly. The latter confirms the super-consistency result of $\widehat{\tau }$.
3.	The median regression estimator showed better performances than the mean regression estimator for heteroscedastic designs and for the fat-tail error distributions.
4.	The performanceFigure 1of our proposed estimators was satisfactory when δ0 = 0.
5.	When the model contains low minimal signals in δ, the Step 3b estimator performed worse than the step 3a estimator.
6.	The main qualitative results were not sensitive to different simulation designs on τ0 and Qi as well as to some variation on tuning parameter values.

Overall, the simulation results confirm the asymptotic theory developed in the previous sections and show the advantage of quantile regression models over the existing mean regression models with a change point.

5. Estimating a Change Point in Racial Segregation

As an empirical illustration, we investigate the existence of tipping in the dynamics of racial segregation using the dataset constructed by Card, Mas, and Rothstein (2008). They showed that the neighborhood’s white population decreases substantially when the minority share in the area exceeds a tipping point (or threshold point), using U.S. Census tract-level data. Lee, Seo, and Shin (2011) developed a test for the existence of threshold effects and applied their test to this dataset. Different from these existing studies, we consider a high-dimensional setup by allowing both possibly highly nonlinear effects of the main covariate (minority share in the neighborhood) and possibly higher-order interactions between additional covariates.

We build on the specifications used by Card, Mas, and Rothstein (2008) and Lee, Seo, and Shin (2011) to choose the following median regression with a constant shift due to the tipping effect: (5.1) $$\begin{array}{c}\hfill Y_i=g_0\left(Q_i\right)+{\delta }_{0}1\{Q_i>{\tau }_0\}+X_i^{\text{'}}{\beta }_0+U_i,\end{array}$$(5.1) where for census tract i, the dependent variable Y_i is the 10 year change in the neighborhood’s white population, Q_i is the base-year minority share in the neighborhood, and X_i is a vector of six tract-level control variables and their various interactions depending on the model specification. Both Y_i and Q_i are in percentage terms. The basic six variables in X_i include the unemployment rate, the log of mean family income, the fractions of single-unit, vacant, and renter-occupied housing units, and the fraction of workers who use public transport to travel to work. The function g( · ) is approximated by the cubic b-splines with 15 knots over equi-quantile locations, so the degrees of freedom are 19 including an intercept term. In our empirical illustration, we use the census-tract-level sample of Chicago whose base year is 1980.

In the first set of models, we consider possible interactions among the six tract-level control variables up to six-way interactions. Specifically, the vector X in the six-way interactions will be composed of the following 63 regressors, $$\begin{array}{ccc}& & \{X^{\left(1\right)},\dots ,X^{\left(6\right)},X^{\left(1\right)}{X}^{\left(2\right)},\dots ,X^{\left(5\right)}{X}^{\left(6\right)},\dots ,\hfill \\ & & X^{\left(1\right)}{X}^{\left(2\right)}{X}^{\left(3\right)}{X}^{\left(4\right)}{X}^{\left(5\right)}{X}^{\left(6\right)}\},\hfill \end{array}$$where X^(j) is the jth element among those tract-level control variables. Note that the lower order interaction vector (e.g., two-way or three-way) is nested by the higher order interaction vector (e.g., three-way or four-way). The total number of regressors varies from 26 (19 from b-splines, 6 from X_i and 1{Q_i > τ}) when there is no interaction to 83 when there are full six-way interactions. In the next set of models, we add the square of each tract-level control variable and generate similar interactions up to six. In this case the total number of regressors varies from 32 to 2529. For example, the number of regressors in the largest model consists of $\#\left(\text{b-spline}\text{basis}\right)+\#\left(\text{indicator}\text{function}\right)+\#$ (interactions up to six-way out of $12)=19+1+{\sum }_{k=1}^6\left(\genfrac{}{}{0pt}{}{12}{k}\right)=2529$. This number is much larger than the sample size (n = 1813).

Table 1 summarizes the estimation results at the 0.25, 0.5, and 0.75 quantiles, respectively. We report the total number of regressors in each model and the number of selected regressors in Step 3b. The change point τ is estimated by the grid search over 591 equi-spaced points in [1, 60]. The lower bound value 1% corresponds to the 1.6 sample percentile of Q_i and the upper bound value 60%, which is about the upper sample quartile of Q_i, is the same as one used by Card, Mas, and Rothstein (2008). In this empirical example, we report the estimates of τ₀ and the confidence intervals updated after Step 3b (i.e., τ is reestimated using the estimates of α₀ in Step 3b). If this estimate is different from the previous one in Step 2, then we repeat Step 3b and Step 2 until it converges.

Table 1. Estimation results from quantile regression.

	No. of reg.	No. of selected reg. in step 3b	$\widehat{\tau }$	CI for τ0	$\widehat{\delta }$
γ = 0.25
6 control variables
No interaction	26	17	5.65	[4.75, 6.17]	−4.07
Two-way interaction	41	20	2.35	[1.00, 4.44]	−1.82
Three-way interaction	61	24	2.35	[1.00, 4.15]	−2.19
Four-way interaction	76	21	5.65	[4.69, 6.08]	−5.50
Five-way interaction	82	22	2.45	[1.00, 4.93]	−1.55
Six-way interaction	83	22	2.45	[1.00, 4.75]	−1.55
12 control variables
No interaction	32	17	5.65	[4.75, 6.17]	−4.07
Two-way interaction	98	18	5.25	[3.55, 6.09]	−3.40
Three-way interaction	318	22	5.25	[3.63, 5.94]	−3.61
Four-way interaction	813	26	5.25	[3.79, 5.97]	−3.53
Five-way interaction	1605	27	5.25	[4.57, 5.65]	−5.37
Six-way interaction	2529	28	5.65	[4.96, 6.06]	−5.50
γ = 0.50
6 control variables
No interaction	26	15	5.65	[1.67, 11.85]	−2.24
Two-way interaction	41	17	5.05	[2.25, 7.46]	−2.63
Three-way interaction	61	20	5.25	[4.22, 6.38]	−4.15
Four-way interaction	76	19	5.05	[3.60, 7.00]	−3.14
Five-way interaction	82	20	5.05	[1.23, 9.16]	−1.90
Six-way interaction	83	20	5.05	[1.33, 9.39]	−1.90
12 control variables
No interaction	32	16	1.95	[0.77, 4.61]	−3.69
Two-way interaction	98	21	6.75	[1.00, 45.57]	0.48
Three-way interaction	318	25	4.05	[1.00, 13.15]	−0.97
Four-way interaction	813	27	3.65	[1.00, 15.91]	−0.56
Five-way interaction	1605	29	3.25	[1.00, 13.16]	−0.68
Six-way interaction	2529	28	3.25	[1.00, 11.67]	−0.74
γ = 0.75
6 control variables
No interaction	26	15	10.05	[9.37, 11.29]	−10.62
Two-way interaction	41	14	NA	NA	0.00
Three-way interaction	61	21	NA	NA	0.00
Four-way interaction	76	18	NA	NA	0.00
Five-way interaction	82	18	NA	NA	0.00
Six-way interaction	83	18	NA	NA	0.00
12 control variables
No interaction	32	14	10.05	[8.44, 11.94]	−7.14
Two-way interaction	98	20	NA	NA	0.00
Three-way interaction	318	21	NA	NA	0.00
Four-way interaction	813	25	NA	NA	0.00
Five-way interaction	1605	28	NA	NA	0.00
Six-way interaction	2529	24	NA	NA	0.00

NOTES: The sample size is n = 1813. The parameter τ₀ is estimated by the grid search on the 591 equi-spaced points over [1, 60]. Both $\widehat{\tau }$ and the 95% confidence interval are based on reestimation after Step 3b: that is, τ is estimated again using $({\tilde{U}}_i,\tilde{\alpha })$ from Step 3b.

The estimation results suggest several interesting points. First, at each quantile, the proposed method selects sparse representations in all model specifications even when the number of regressors is relatively large. Furthermore, the number of selected regressors does not grow rapidly when we increase the number of possible covariates. It seems that the set of selected covariates overlaps across different dictionaries at each quantile. See Appendix G for details on selected regressors. Second, the estimation results are different across different quantiles, indicating that there may exist heterogeneity in this application. The confidence intervals for τ₀ at the 0.25 quantile are quite tight in all cases and they provide convincing evidence of the tipping effect. If we look at the case of six-way interactions with 12 control variables, the estimated tipping point is 5.65% and the estimated jump size is − 5.50%. However, this strong tipping effect becomes weaker at the 0.50 and 0.75 quantiles as shown either by wider confidence intervals or by the zero jump size, that is, $\widehat{\delta }=0$.

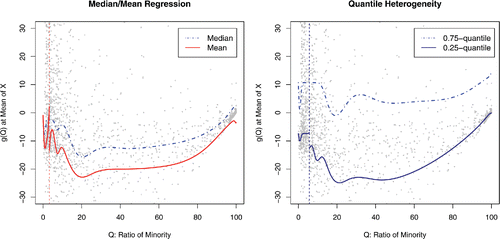
Figure 1 shows the fitted values over Q_i at the sample mean of the six basic covariates. They are from the model of six-way interactions with 12 control variables and the vertical line indicates the location of a tipping point. The left panel of Figure 1 compares the results between the mean and median regression results and the right panel shows the interquartile range of the conditional distribution of Y_i as a function of Q_i given other regressors. It can be seen that the mean regression estimates are much more volatile around the tipping point than the median regression estimates, although the estimated tipping point is the same. Looking at the right panel of Figure 1, we can see that the 25 percentile of the conditional distribution drops at the tipping point of 5.65% but no such change at the 75% quantile. This shows that the quantile regression estimates can provide insights into distributional threshold effects in racial segregation.

Figure 1. Estimation results: 12 control variables and six-way interaction.

6. Conclusions

In this article, we have developed ℓ₁-penalized estimators of a high-dimensional quantile regression model with an unknown change point due to a covariate threshold. We have shown among other things that our estimator of the change point achieves an oracle property without relying on a perfect covariate selection, thereby avoiding the need for the minimum level condition on the signals of active covariates. We have illustrated the usefulness of our estimation methods via Monte Carlo experiments and an application to tipping in the racial segregation.

One of the important remaining questions is how to extend our approach to a high-dimensional quantile regression model with multiple change points. A computationally attractive approach is to use the binary segmentation algorithm (see, e.g., Fryzlewicz 2014; Cho and Fryzlewicz 2015 among others). In a recent working article, Leonardi and Bühlmann (2016) considered a high-dimensional mean regression model with multiple change points whose number may grow as the sample size increases. They have proposed a binary segmentation algorithm to choose the number and locations of change points. It is an important future research topic to develop a computationally efficient algorithm to detect multiple changes for high-dimensional quantile regression models.

Supplementary Materials

Online supplements are comprised of 6 appendices. In Appendix B, we provide the al- gorithm of constructing the confidence interval for τ₀. In Appendix C, we provide sufficient conditions for the identification and show that an improved rate of convergence is possible for the excess risk by taking the second and third steps of estimation. To prove the theoretical results in the main text, we consider a general M-estimation framework that includes quantile regression as a special case. We provide high-level regularity conditions on the loss function in Appendix D. Under these conditions, we derive asymptotic properties and then we verify all the high level assumptions for the quantile regression model in Appendix E. Hence, our general results are of independent interest and can be applicable to other models, for example logistic regression models. In Section F, we present the results of extensive Monte Carlo experiments, and Appendix G gives additional results for the empirical example.

Acknowledgment

The authors thank Bernd Fitzenberger, an editor, an associate editor, and three anonymous referees for helpful comments.

Additional information

Funding

This work was supported in part by Promising-Pioneering Researcher Program through Seoul National University, by the European Research Council (ERC-2014-CoG-646917-ROMIA), by the Research and Scholarship Award grant of University of Maryland, and by the Australian Research Council (DP170100987).

Appendix A: Assumptions for Asymptotic Properties

In this section, we list a set of assumptions that will be useful to derive asymptotic properties of the proposed estimators. The first two assumptions are standard.

Assumption A.1 (Setting).

(i)	The data {(Yi, Xi, Qi)}ni = 1 are independent and identically distributed. Furthermore, for all j and every integer m ⩾ 1, there is a constant K1 < ∞ such that $\mathbb{E}|X_{ij}{|}^m\le \frac{m!}{2}{K}_1^{m-2}$, where Xij denotes the jth element of Xi.
(ii)	$\mathbb{P}({\tau }_1<Q\le {\tau }_2)\le K_2({\tau }_2-{\tau }_1)$ for any τ1 < τ2 and some constant K2 < ∞.
(iii)	${\alpha }_0\in \mathcal{A}\equiv {\{\alpha :|\alpha |}_{\infty }\le M_1\}$ for some constant M1 < ∞, and ${\tau }_0\in \mathcal{T}\equiv [\underset{\_}{\tau },\bar{\tau }]$. Furthermore, the probability of $\{Q<\underset{\_}{\tau }\}$ and that of $\{Q>\bar{\tau }\}$ are strictly positive, and $$\begin{array}{c}\hfill \underset{j\le p}{sup}\underset{\tau \in \mathcal{T}}{sup}\mathbb{E}\left[X_{ij}^2\right|Q=\tau ]<\infty .\end{array}$$
(iv)	There exist universal constants $\underset{\_}{D}>0$ and $\bar{D}>0$ such that w.p.a.1, $$0<\underset{\_}{D}\le \underset{j\le 2p}{min}\underset{\tau \in \mathcal{T}}{inf}{D}_j\left(\tau \right)\le \underset{j\le 2p}{max}\underset{\tau \in \mathcal{T}}{sup}{D}_j\left(\tau \right)\le \bar{D}<\infty .$$
(v)	$\mathbb{E}\left[{\left(X^T{\delta }_0\right)}^2\right|Q=\tau ]\le M_2{\left|{\delta }_0\right|}_2^2$ for all $\tau \in \mathcal{T}$ and for some constant M2 satisfying 0 < M2 < ∞.

A simple sufficient condition for condition (v) is that the eigenvalues of $\mathbb{E}\left[X_{J\left({\delta }_0\right)}{X}_{J\left({\delta }_0\right)}^T\right|Q=\tau ]$ are bounded uniformly in τ, where $X_{J\left({\delta }_0\right)}$ denotes the subvector of X corresponding to the nonzero components of δ₀.

Assumption A.2 (Underlying Distribution).

(i)	The conditional distribution Y|X, Q has a continuously differentiable density function fY|X, Q(y|x, q) with respect to y, whose derivative is denoted by ${\tilde{f}}_{Y|X,Q}\left(y\right|x,q)$.
(ii)	There are constants C1, C2 > 0 such that for all (y, x, q) in the support of (Y, X, Q), $$\begin{array}{c}\hfill |{\tilde{f}}_{Y|X,Q}\left(y\right|x,q)|\le C_1,f_{Y|X,Q}\left(x{\left({\tau }_0\right)}^T{\alpha }_0\right|x,q)\ge C_2.\end{array}$$
(iii)	When δ0 ≠ 0, Γ(τ, α0) is positive definite uniformly in a neighborhood of τ0, where $$\begin{array}{ccc}\hfill \Gamma (\tau ,{\alpha }_0)& \equiv & \frac{{\partial }^2\mathbb{E}\left[\rho (Y,X_J{\left(\tau \right)}^T{\alpha }_{0J})\right]}{\partial {\alpha }_J\partial {\alpha }_J^T}\hfill \\ & =& \mathbb{E}\left[X_J\left(\tau \right)X_J{\left(\tau \right)}^T{f}_{Y|X,Q}\left(X{\left(\tau \right)}^T{\alpha }_0\right|X,Q)\right].\hfill \end{array}$$When δ0 = 0, the matrix $\mathbb{E}\left[X_{J\left({\beta }_0\right)}{X}_{J\left({\beta }_0\right)}^T{f}_{Y|X,Q}\left(X_{J\left({\beta }_0\right)}^T{\beta }_{0J\left({\beta }_0\right)}\right|X,Q)\right]$ is positive definite.

A.1. Compatibility Conditions

We now make an assumption that is an extension of the well-known compatibility condition (see Bühlmann and van de Geer 2011, chap. 6). In particular, the following condition is a uniform-in-τ version of the compatibility condition. Recall that for a 2p dimensional vector α, we use α_J and ${\alpha }_{J^c}$ to denote its subvectors formed by indices in J(α₀) and {1, …, 2p}∖J(α₀), respectively.

Assumption A.3 (Compatibility Condition).

(i)	When δ0 ≠ 0, there is a neighborhood ${\mathcal{T}}_0\subset \mathcal{T}$ of τ0, and a constant φ > 0 such that for all $\tau \in {\mathcal{T}}_0$ and all $\alpha \in {\mathbb{R}}^{2p}$ satisfying $|{\alpha }_{J^c}{|}_1\le 5{\left|{\alpha }_J\right|}_1$, (A.1) $$\varphi |{\alpha }_J{|}_1^2\le s{\alpha }^T\mathbb{E}\left[X\left(\tau \right)X{\left(\tau \right)}^T\right]\alpha .$$(A.1)
(ii)	When δ0 = 0, there is a constant φ > 0 such that for all $\tau \in \mathcal{T}$ and all $\alpha \in {\mathbb{R}}^{2p}$ satisfying $|{\alpha }_{J^c}{|}_1\le 4{\left|{\alpha }_J\right|}_1$, (A.2) $$\varphi |{\alpha }_J{|}_1^2\le s{\alpha }^T\mathbb{E}\left[X\left(\tau \right)X{\left(\tau \right)}^T\right]\alpha .$$(A.2)

Assumption A.3 requires that the compatibility condition holds uniformly in τ over a neighborhood of τ₀ when δ₀ ≠ 0 and over the entire parameter space $\mathcal{T}$ when δ₀ = 0. Note that this assumption is imposed on the population covariance matrix $\mathbb{E}\left[X\left(\tau \right)X{\left(\tau \right)}^T\right]$; thus, a simple sufficient condition of Assumption A.3 is that the smallest eigenvalue of $\mathbb{E}\left[X\left(\tau \right)X{\left(\tau \right)}^T\right]$ is bounded away from zero uniformly in τ. Even if p > n, the population covariance can still be strictly positive definite while the sample covariance is not.

A.2. Restricted Nonlinearity Conditions

In this subsection, we make an assumption called a restricted nonlinear condition to deal with the quantile loss function. We extend condition D.4 in Belloni and Chernozhukov (2011) to accommodate the possible existence of the unknown threshold in our model (specifically, a uniform-in-τ version of the restricted nonlinear condition as in the compatibility condition).

We define the “prediction balls” with radius r and corresponding centers as follows: (A.3) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{B}({\beta }_0,r)& =\{\beta \in \mathcal{B}\subset {\mathbb{R}}^p:\mathbb{E}\left[{\left(X^T(\beta -{\beta }_0)\right)}^{2}1\{Q\le {\tau }_0\}\right]\le r^2\},\hfill \\ \hfill \mathcal{G}({\theta }_0,r)& =\{\theta \in \mathcal{G}\subset {\mathbb{R}}^p:\mathbb{E}\left[{\left(X^T(\theta -{\theta }_0)\right)}^{2}1\{Q>{\tau }_0\}\right]\le r^2\},\hfill \end{array}\end{array}$$(A.3) where $\mathcal{B}$ and $\mathcal{G}$ are parameter spaces for β₀ and θ₀, respectively. To deal with the case that δ₀ = 0, we also define (A.4) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \tilde{\mathcal{B}}({\beta }_0,r,\tau )& =\{\beta \in \mathcal{B}\subset {\mathbb{R}}^p:\mathbb{E}\left[{\left(X^T(\beta -{\beta }_0)\right)}^{2}1\left\{Q\le \tau \right\}\right]\le r^2\},\hfill \\ \hfill \tilde{\mathcal{G}}({\beta }_0,r,\tau )& =\{\theta \in \mathcal{G}\subset {\mathbb{R}}^p:\mathbb{E}\left[{\left(X^T(\theta -{\beta }_0)\right)}^{2}1\left\{Q>\tau \right\}\right]\le r^2\}.\hfill \end{array}\end{array}$$(A.4)

Assumption A.4 (Restricted Nonlinearity).

The following holds for the constants C₁ and C₂ defined in Assumption A.2 (ii).

(i)

When δ0 ≠ 0, there exists a constant r*QR > 0 such that (A.5) $$\begin{array}{c}\hfill \underset{\beta \in \mathcal{B}({\beta }_0,r_{QR}^{*}),\beta \ne {\beta }_0}{inf}\frac{\mathbb{E}\left[\right|X^T(\beta -{\beta }_0){{|}^{2}1\{Q\le {\tau }_0\}]}^{3/2}}{\mathbb{E}\left[\right|X^T(\beta -{\beta }_0){|}^{3}1\{Q\le {\tau }_0\}]}\ge r_{QR}^{*}\frac{2C_1}{3C_2}>0\end{array}$$(A.5) and that (A.6) $$\begin{array}{c}\hfill \underset{\theta \in \mathcal{G}({\theta }_0,r_{QR}^{*}),\theta \ne {\theta }_0}{inf}\frac{\mathbb{E}\left[\right|X^T(\theta -{\theta }_0){{|}^{2}1\{Q>{\tau }_0\}]}^{3/2}}{\mathbb{E}\left[\right|X^T(\theta -{\theta }_0){|}^{3}1\{Q>{\tau }_0\}]}\ge r_{QR}^{*}\frac{2C_1}{3C_2}>0.\end{array}$$(A.6)

(ii)

When δ0 = 0, there exists a constant r*QR > 0 such that (A.7) $$\begin{array}{c}\hfill \underset{\tau \in \mathcal{T}}{inf}\underset{\beta \in \tilde{\mathcal{B}}({\beta }_0,r_{QR}^{*},\tau ),\beta \ne {\beta }_0}{inf}\frac{\mathbb{E}\left[\right|X^T(\beta -{\beta }_0){{|}^{2}1\{Q\le \tau \}]}^{3/2}}{\mathbb{E}\left[\right|X^T(\beta -{\beta }_0){|}^{3}1\{Q\le \tau \}]}\ge r_{QR}^{*}\frac{2C_1}{3C_2}>0\end{array}$$(A.7) and that (A.8) $$\begin{array}{c}\hfill \underset{\tau \in \mathcal{T}}{inf}\underset{\theta \in \tilde{\mathcal{G}}({\beta }_0,r_{QR}^{*},\tau ),\beta \ne {\beta }_0}{inf}\frac{\mathbb{E}\left[\right|X^T(\theta -{\theta }_0){{|}^{2}1\{Q>\tau \}]}^{3/2}}{\mathbb{E}\left[\right|X^T(\theta -{\theta }_0){|}^{3}1\{Q>\tau \}]}\ge r_{QR}^{*}\frac{2C_1}{3C_2}>0.\end{array}$$(A.8)

Remark A.1.

As pointed out by Belloni and Chernozhukov (2011), if X^Tc follows a logconcave distribution conditional on Q for any nonzero c (e.g., if the distribution of X is multivariate normal), then Theorem 5.22 of Lovász and Vempala (2007) and the Hölder inequality imply that for all $\alpha \in \mathcal{A}$, $$\begin{array}{c}\hfill \mathbb{E}\left[\right|X{\left({\tau }_0\right)}^T(\alpha -{\alpha }_0){|}^3\left|Q\right]\le 6{\left\{\mathbb{E}\left[{\left\{X{\left({\tau }_0\right)}^T(\alpha -{\alpha }_0)\right\}}^2\right|Q]\right\}}^{3/2},\end{array}$$which provides a sufficient condition for Assumption A.4. On the other hand, this assumption can hold more generally since Equations (A.5(A.5) $$\begin{array}{c}\hfill \underset{\beta \in \mathcal{B}({\beta }_0,r_{QR}^{*}),\beta \ne {\beta }_0}{inf}\frac{\mathbb{E}\left[\right|X^T(\beta -{\beta }_0){{|}^{2}1\{Q\le {\tau }_0\}]}^{3/2}}{\mathbb{E}\left[\right|X^T(\beta -{\beta }_0){|}^{3}1\{Q\le {\tau }_0\}]}\ge r_{QR}^{*}\frac{2C_1}{3C_2}>0\end{array}$$(A.5) )–(A.8(A.8) $$\begin{array}{c}\hfill \underset{\tau \in \mathcal{T}}{inf}\underset{\theta \in \tilde{\mathcal{G}}({\beta }_0,r_{QR}^{*},\tau ),\beta \ne {\beta }_0}{inf}\frac{\mathbb{E}\left[\right|X^T(\theta -{\theta }_0){{|}^{2}1\{Q>\tau \}]}^{3/2}}{\mathbb{E}\left[\right|X^T(\theta -{\theta }_0){|}^{3}1\{Q>\tau \}]}\ge r_{QR}^{*}\frac{2C_1}{3C_2}>0.\end{array}$$(A.8) ) in Assumption A.4 need to hold only locally around true parameters α₀.

A.3. Additional Assumptions When δ₀ ≠ 0

Assumption A.5 (Additional Conditions on the Distribution of (X, Q)).

Assume δ₀ ≠ 0. In addition, there exists a neighborhood ${\mathcal{T}}_0\subset \mathcal{T}$ of τ₀ that satisfies the following.

(i)	Q has a density function fQ( · ) that is continuous and bounded away from zero on ${\mathcal{T}}_0$.
(ii)	Let $\tilde{X}$ denote all the components of X excluding Q in case that Q is an element of X. The conditional distribution of Q given $\tilde{X}$ has a density function $f_{Q|\tilde{X}}\left(q\right|\tilde{x})$ that is bounded uniformly in both $q\in {\mathcal{T}}_0$ and $\tilde{x}$.
(iii)	There exists M3 > 0 such that $M_3^{-1}\le \mathbb{E}\left[{\left(X^T{\delta }_0\right)}^2\right|Q=\tau ]\le M_3$ for all $\tau \in {\mathcal{T}}_0$.

When τ₀ is identified, we require δ₀ to be considerably different from zero. This requirement is given in condition (iii). Note that this condition is concerned with $\mathbb{E}\left[{\left(X^T{\delta }_0\right)}^2\right|Q=\tau ]$, which is an important quantity to develop asymptotic results when δ₀ ≠ 0. Note that condition (iii) is a local condition with respect to τ in the sense that it has to hold only locally in a neighborhood of τ₀.

Assumption A.6 (Moment Bounds).

(i)

There exist finite positive constants $\tilde{C}$ and r such that for all $\beta \in \mathcal{B}({\beta }_0,r)$ and for any $\theta \in \mathcal{G}({\theta }_0,r)$, $$\begin{array}{cc}\hfill \mathbb{E}\left[\right|X^T(\beta -{\beta }_0)\left|1\{Q>{\tau }_0\}\right]& \le \tilde{C}\mathbb{E}\left[\right|X^T(\beta -{\beta }_0)\left|1\{Q\le {\tau }_0\}\right],\hfill \\ \hfill \mathbb{E}\left[\right|X^T(\theta -{\theta }_0)\left|1\{Q\le {\tau }_0\}\right]& \le \tilde{C}\mathbb{E}\left[\right|X^T(\theta -{\theta }_0)\left|1\{Q>{\tau }_0\}\right].\hfill \end{array}$$

(ii)

There exist finite positive constants M, r and the neighborhood ${\mathcal{T}}_0$ of τ0 such that $$\begin{array}{ccc}& & \mathbb{E}\left[{\left(X^T[(\theta -\beta )-({\theta }_0-{\beta }_0)]\right)}^2|Q=\tau \right]\le M,\hfill \\ & & \mathbb{E}\left[\right|X^T(\beta -{\beta }_0)\left|\right|Q=\tau ]\le M,\hfill \\ & & \mathbb{E}\left[\right|X^T(\theta -{\theta }_0)\left|\right|Q=\tau ]\le M,\hfill \\ & & \underset{\tau \in {\mathcal{T}}_0:\tau >{\tau }_0}{sup}\mathbb{E}\left[|X^T(\beta -{\beta }_0)|\frac{1\{{\tau }_0<Q\le \tau \}}{(\tau -{\tau }_0)}\right]\hfill \\ & & \le M\mathbb{E}\left[\right|X^T(\beta -{\beta }_0)\left|1\{Q\le {\tau }_0\}\right],\hfill \\ & & \underset{\tau \in {\mathcal{T}}_0:\tau <{\tau }_0}{sup}\mathbb{E}\left[|X^T(\theta -{\theta }_0)|\frac{1\{\tau <Q\le {\tau }_0\}}{({\tau }_0-\tau )}\right]\hfill \\ & & \le M\mathbb{E}\left[\right|X^T(\theta -{\theta }_0)\left|1\{Q>{\tau }_0\}\right],\hfill \end{array}$$uniformly in $\beta \in \mathcal{B}({\beta }_0,r)$, $\theta \in \mathcal{G}({\theta }_0,r),$ and $\tau \in {\mathcal{T}}_0$.

Remark A.2.

Condition (i) requires that Q have nonnegligible support on both sides of τ₀. This condition can be viewed as a rank condition for identification of α₀. In the standard threshold model with a fixed dimension, our condition is trivially satisfied by the rank condition such that both $\mathbb{E}\left[X{X}^{T}1\{Q\le {\tau }_0\}\right]$ and $\mathbb{E}\left[X{X}^{T}1\{Q>{\tau }_0\}\right]$ are positive definite (see, e.g., Chan 1993 or Hansen 2000). If the rank condition fails, the regression coefficient may not be identified and thus affecting the identification of the change point. In the high-dimensional setup, it is undesirable to impose the same rank condition due to the high-dimensionality. Instead, we replace it with condition (i). Condition (ii) requires the boundedness and certain smoothness of the conditional expectation functions $\mathbb{E}\left[{\left(X^T[(\theta -\beta )-({\theta }_0-{\beta }_0)]\right)}^2\right|Q=\tau ]$, $\mathbb{E}\left[\right|X^T(\beta -{\beta }_0)\left|\right|Q=\tau ]$, and $\mathbb{E}\left[\right|X^T(\theta -{\theta }_0)\left|\right|Q=\tau ]$, and prohibits degeneracy in one regime. The last two inequalities in condition (ii) are satisfied if $$\frac{\mathbb{E}\left[\left|X^T\beta \right||Q=\tau \right]}{\mathbb{E}\left[\left|X^T\beta \right|\right]}\le M$$for all $\tau \in {\mathcal{T}}_0$ and for all β satisfying $0<\mathbb{E}|X^T\beta |\le c$ for some small c > 0.