Batch Effects Correction with Unknown Subtypes

ABSTRACT

High-throughput experimental data are accumulating exponentially in public databases. Unfortunately, however, mining valid scientific discoveries from these abundant resources is hampered by technical artifacts and inherent biological heterogeneity. The former are usually termed “batch effects,” and the latter is often modeled by subtypes. Existing methods either tackle batch effects provided that subtypes are known or cluster subtypes assuming that batch effects are absent. Consequently, there is a lack of research on the correction of batch effects with the presence of unknown subtypes. Here, we combine a location-and-scale adjustment model and model-based clustering into a novel hybrid one, the batch-effects-correction-with-unknown-subtypes model (BUS). BUS is capable of (a) correcting batch effects explicitly, (b) grouping samples that share similar characteristics into subtypes, (c) identifying features that distinguish subtypes, (d) allowing the number of subtypes to vary from batch to batch, (e) integrating batches from different platforms, and (f) enjoying a linear-order computation complexity. We prove the identifiability of BUS and provide conditions for study designs under which batch effects can be corrected. BUS is evaluated by simulation studies and a real breast cancer dataset combined from three batches measured on two platforms. Results from the breast cancer dataset offer much better biological insights than existing methods. We implement BUS as a free Bioconductor package BUScorrect. Supplementary materials for this article are available online.

KEYWORDS:

• Disease subtype discovery
• High-throughput experiments
• Integrative analysis
• Interlaboratory comparisons
• Model-based clustering

1. Introduction

To date, more than 1.7 million samples have been deposited into the Gene Expression Omnibus (Edgar et al. 2002), which provides unprecedented opportunities to decipher the gene regulation machinery (Pickrell et al. 2010), understand disease mechanisms (Chahrour et al. 2008), and develop personalized treatments (Suárez-Fariñas et al. 2010). Nevertheless, digging in this gold mine is a daunting task. On the one hand, raw data from high-throughput experiments suffer from various types of technical artifacts. On the other hand, biological samples are inherently heterogenous. How to tease out meaningful biological variations from technical artifacts is the major complication in fully using the abundant data sources available for downstream analysis.

Researchers have long been aware that samples generated on different days are not directly comparable. Samples processed at the same time are usually referred to as coming from the same “batch.” Even when the same biological conditions are measured, data from different batches can present very different patterns. The variation among different batches may be due to changes in laboratory conditions, preparation time, reagent lots, and experimenters (Leek et al. 2010). The effects caused by these systematic factors are called “batch effects.” Batch effects are prevalent among all types of high-throughput technologies, ranging from microarray (Irizarry et al. 2005) and next-generation sequencing (Taub et al. 2010) to single-cell sequencing experiments (Hicks et al. 2015).

Various “batch effects” correction methods have been proposed when the subtype information for each sample is known. Here, we adopt a “broad” definition for “subtype.” “Subtype” is defined as a set of samples that share the same underlying genomic profile, in other words biological variability, when measured with no technical artifacts. For instance, groupings such as “case” and “control” can be viewed as two subtypes. Given subtypes that are known, Johnson et al. (2007) adjusted batch effects for microarray data in a model-based location-and-scale (L/S) scheme via an empirical Bayesian approach called ComBat. Their model also allows the incorporation of known confounding factors such as age and gender. However, in many experiments, researchers have no measurements of these confounding factors. To adjust for “unmodeled factors,” Leek and Storey (2007) introduced surrogate variable analysis (SVA) for microarray data. Although unmodeled factors cannot be reconstructed exactly, the surrogate variables, whose expanded linear space is the same as that of unmodeled factors, can be learned directly from the data. Accordingly, introducing surrogate variables into the model sidesteps spurious variation due to unmodeled factors and provides accurate estimation of the association between disease status and gene expression. Later, Leek (2014) extends SVA to deal with batch effects in next generation sequencing datasets.

Unfortunately, both ComBat and SVA require the subtype information for each sample and are infeasible when the subtypes are unknown. The frozen robust multi-array analysis (fRMA; McCall et al. 2010) was developed to normalize microarray samples individually so that samples from different batches are comparable after normalization. fRMA relies on training a large database of samples from the same microarray platform. As a result, fRMA is only available for a very limited number of array platforms and cannot handle batches measured on different platforms. The single-channel array normalization (SCAN) proposed by Piccolo et al. (2012) can normalize microarray samples measured by different platforms. SCAN fits a two-component normal mixture to the probes of a single sample, one component for background noise and the other for signals. However, SCAN only looks at one sample at a time and thus fails to identify systematic biases associated with the batch. To borrow information and estimate the correlation of measurements from different platforms, Franks et al. (2015) proposed a hierarchical model and applied it to quantify the coordination between transcription and translation level in yeast. Nevertheless, the model assumes a single biological condition without subtype heterogeneity. Therefore, to the best of our knowledge, the general problem of batch effects correction in the presence of unknown subtypes remains an open problem.

Meanwhile, assuming the absence of batch effects, there is extensive research on subtype discovery. Pan and Shen (2007) proposed a model-based clustering algorithm using penalized Expectation Maximization (EM). The approach appends a Lasso penalty (Tibshirani 1996) to the Q function in the EM algorithm (Dempster et al. 1977). The missing data formulation in the EM algorithm clusters samples into subtypes. The penalty term helps to distinguish the genes whose expression levels remain the same across all subtypes from those genes with varying means among different subtypes. This latter set of genes characterizing distinct subtypes is called the intrinsic gene set (Huo et al. 2016). Wang and Zhu (2008) improved the penalized approach by replacing the Lasso penalty with an L_∞-norm penalty or a hierarchical penalty. Consequently, parameters belonging to one gene are treated as a single group and penalized together, thus reducing the number of falsely included noninformative genes. Intrinsic gene selection for subtype discovery is also discussed in sparse K-means (Witten and Tibshirani 2012). Note that the traditional K-means can be viewed as maximizing Between Cluster Sum of Squares (BCSS), which can be further partitioned into the summation of gene-specific BCSS. Sparse K-means give nonnegative weights to each gene-specific BCSS term and then optimize the weighted BCSS under L₁ and L₂ constraints on weights. Finally, genes with nonzero weights remain in the intrinsic gene set, and clustering is achieved simultaneously. However, none of the aforementioned methods consider batch effects. As a result, direct application of the above methods to data combined from several batches will lead to problematic scientific conclusions. However, clustering subtypes within each batch separately suffers from small sample size and fails to use shared information among the different batches. Therefore, methods for removing batch effects from datasets with unknown subtypes are important and in urgent demand.

Recently, building upon sparse K-means, Huo et al. (2016) proposed MetaSparseKmeans to discover subtypes using samples from multiple batches. MetaSparseKmeans designs a pattern-matching reward function to encourage the matching of the same subtype across batches. Nevertheless, MetaSparseKmeans requires each batch to contain all subtypes, which is not feasible for many experimental designs. Moreover, the computational complexity of calculating the pattern-matching reward function is O((K!)^{B − 1}) for K subtypes and B batches. As admitted by the authors, even when K = 5 and B = 5, an accurate exhaustive search is prohibitive for 207.36 million comparisons. Furthermore, most importantly, MetaSparseKmeans does not explicitly characterize and correct for batch effects. Consequently, it is only limited to the clustering problem and cannot benefit other analyses such as differential gene expression detection and gene regulatory network construction.

In this article, we integrate the L/S model with model-based clustering and propose the batch-effects-correction-with-unknown-Subtypes (BUS) approach. BUS simultaneously corrects batch effects, discovers subtypes, and selects features that discriminate different subtypes. After correcting the batch effects with BUS, the corrected value can be used for other analysis as if all samples are measured in a single batch. BUS can integrate batches measured from different platforms and allow subtypes to be measured in some but not all of the batches. We prove the identifiability of BUS. Based on the theoretical results, we provide conditions for experimental designs under which batch effects can be corrected.

We conduct statistical inference under the Bayesian framework and develop a Gibbs sampler to draw samples from the posterior distribution. BUS can compute efficiently with the computational complexity growing linearly as subtype number K and batch number B increase. Our simulation studies demonstrate that BUS accurately estimates batch effects and subtype effects, clusters subtypes, as well as selects intrinsic genes. Finally, BUS is applied to three batches of breast cancer microarray data with five subtypes measured on two different platforms (Huo et al. 2016). Although we focus on gene expression microarray data here, the same framework can be adapted to DNA methylation microarrays, RNA-seq data, and single-cell sequencing data.

2. Model Formulation

2.1. Location-and-Scale Adjustments

In this subsection, we review the classic location-and-scale adjustment model (L/S) for batch effects correction when the subtypes are known (Johnson et al. 2007). The L/S model characterizes two types of batch effects, the additive effects influencing the means and the multiplicative effects affecting the variances of gene expression. Specifically, let us denote the gene expression level of gene g for the sample j in the batch b by Y_bjg, then the L/S model is formulated as follows: (2.1) $$Y_{bjg}={\alpha }_g+{\mathbf{X}}_{bj}{\mu }_g+{\gamma }_{bg}+{\delta }_{bg}{\epsilon }_{bjg}.$$(2.1) Here, X_bj encodes the study design, that is, which subtype each sample comes from. Suppose there are K subtypes in the dataset, then X_bj is a K-dimensional binary vector with its kth element being one and the others being zeros if sample j in the batch b belongs to subtype k. Consequently, ${\mu }_g=({\mu }_{g1},\dots ,{\mu }_{g_K})$ records the subtype effects for gene g. To make the model identifiable, in the following analysis, we set μ_g1 = 0. Subsequently, α_g represents the mean gene expression level of gene g in subtype one.

In terms of batch effects, the “location” term γ_bg captures the shift in the mean due to additive effects, and the “scale” term δ_bg quantifies the variability of the gene expression caused by the multiplicative batch effects. For model identifiability, without loss of generality, we always refer to batch one as the “reference batch,” where the location batch effects and the scale batch effects are assumed to be absent. In other words, γ_1g = 0 and δ_1g = 1 for all 1 ⩽ g ⩽ G. Finally, the noise term ϵ_bjg is assumed to follow a normal distribution N(0, σ²_0g) with mean zero and variance σ²_0g.

For the convenience of future discussion, we absorb δ_bgϵ_bjg into ε_bjg and arrive at the equivalent model: (2.2) $$Y_{bjg}={\alpha }_g+{\mathbf{X}}_{bj}{\mu }_g+{\gamma }_{bg}+{ϵ}_{bjg},$$(2.2) where ε_bjg follows N(0, σ²_bg), and note that the ratio of σ²_bg to σ²_1g (= δ²_bg) is the squared multiplicative batch effect.

2.2. The BUS Model

Nevertheless, the L/S model assumes that the subtype information is known to the investigator. To handle the case in which subtype information is unknown, we propose the following Batch-effects-correction-with-Unknown-Subtypes (BUS) model built upon the L/S model. The main challenge is that the subtype indicators X_bj in Equation (2.2(2.2) $$Y_{bjg}={\alpha }_g+{\mathbf{X}}_{bj}{\mu }_g+{\gamma }_{bg}+{ϵ}_{bjg},$$(2.2) ) now become missing data, and hence, we need to infer the subtype information for each sample as well. Here, we employ ideas from the literature on model-based clustering (Banfield and Raftery 1993; Yeung et al. 2001; Fraley and Raftery 2002; McLachlan and Peel 2004).

Let us first assume that all of the samples come from K subtypes and are measured in a single batch. Therefore, we temporarily drop the subscript b for batch indicators and collect all of the gene expression values for sample j into Y_j = (Y_j1, …, Y_jG). If sample j belongs to subtype k, then we assume Y_j follows a multivariate Gaussian distribution N(m_k, Σ) with a subtype mean m_k = (m_1k, …, m_Gk) and a common diagonal covariance matrix $\Sigma =\text{diag}({\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_G^2)$ across the subtypes (Fraley and Raftery 2002; McLachlan and Peel 2004; Bickel and Levina 2004). The resulting model is a Gaussian mixture: (2.3) $$\begin{array}{ccc}\hfill {\mathbf{Y}}_j& \sim & {\pi }_1\mathbf{N}({\mathbf{m}}_1,\Sigma )+{\pi }_2\mathbf{N}({\mathbf{m}}_2,\Sigma )+\cdots \hfill \\ & & +{\pi }_K\mathbf{N}({\mathbf{m}}_K,\Sigma ),\text{iid}j=1,\dots ,n,\hfill \end{array}$$(2.3) where “iid” stands for “independent and identically distributed,” and π_k indicates the proportion of subtype k in the samples, satisfying π_k ⩾ 0, ∑^K_{k = 1}π_k = 1. Bringing in a subtype indicator Z_j for each sample j, in which Z_j = k if sample j comes from subtype k, an equivalent model can be formulated as follows: for 1 ⩽ j ⩽ n and 1 ⩽ g ⩽ G (2.4) $$\begin{array}{ccc}& & Z_j\sim \text{Multinomial}(1;{\pi }_1,\dots ,{\pi }_K);\hfill \\ & & Y_{jg}\sim N(m_{gk},{\sigma }_g^2\left)\right|Z_j=k.\hfill \end{array}$$(2.4) To align with model 2.2, Z_j = k can be mapped to X_j with its kth element equal to one and all of the others being zero and vice versa.

Going one step further, we now consider the multi-batch case in which heterogenous samples from multiple subtypes are measured in multiple batches. We assume that there are in total B batches and K subtypes, and batch b contains n_b samples. For each sample, gene expression levels in all G genes are measured. As in Section 2.1, we denote the gene expression level of gene g for the sample j in the batch b by Y_bjg. We allow the proportion of subtypes to vary from one batch to another. Therefore, we use π_bk to denote the proportion of subtype k in the batch b; thus, ∑^K_{k = 1}π_bk = 1. Consequently, the integration of Model 2.2 and Model 2.3 gives rise to: for 1 ⩽ b ⩽ B, 1 ⩽ j ⩽ n_b, 1 ⩽ g ⩽ G (2.5) $$\begin{array}{ccc}& & Z_{bj}\sim \text{Multinomial}(1;{\pi }_{b1},\dots ,{\pi }_{bK});\hfill \\ & & Y_{bjg}\sim N(m_{bgk},{\sigma }_{bg}^2\left)\right|Z_{bj}=k;\hfill \\ & & m_{bgk}={\alpha }_g+{\mathbf{X}}_{bj}{\mu }_g+{\gamma }_{bg}={\alpha }_g+{\mu }_{gk}+{\gamma }_{bg}|Z_{bj}=k.\hfill \end{array}$$(2.5) Accordingly, the complete likelihood function for the observed data $\mathbf{Y}={\left\{Y_{bjg}\right\}}_{b=1,\dots ,B;j=1,\dots ,n_b}^{g=1\dots ,G}$ and missing data $\mathbf{Z}={\left\{Z_{bj}\right\}}_{b=1,\dots ,B;j=1,\dots ,n_b}$ becomes: $$\begin{array}{ccc}& & L_c\left(\Theta \right|\mathbf{Y},\mathbf{Z})=\prod _{b=1}^B\prod _{j=1}^{n_b}\prod _{k=1}^K\hfill \\ & & {\left[{\pi }_{bk}\prod _{g=1}^G\frac{1}{\sqrt{2\pi }{\sigma }_{bg}}\times \text{exp}\left\{-\frac{{(y_{bjg}-{\alpha }_g-{\mu }_{gk}-{\gamma }_{bg})}^2}{2{\sigma }_{bg}^2}\right\}\right]}^{I(Z_{bj}=k)},\hfill \end{array}$$where Θ is composed of all unknown parameters {π_bk: 1 ⩽ b ⩽ B, 1 ⩽ k ⩽ K}, {α_g: 1 ⩽ g ⩽ G}, {μ_gk: 1 ⩽ g ⩽ G, 2 ⩽ k ⩽ K}, {γ_bg: 2 ⩽ b ⩽ B, 1 ⩽ g ⩽ G}, and {σ²_bg: 1 ⩽ b ⩽ B, 1 ⩽ g ⩽ G}. Recall that μ_g1 and γ_1g (1 ⩽ g ⩽ G) are constrained to zero for identifiability.

As a side note, BUS can also handle known confounding factors such as age, gender, and BMI by modifying m_gk to ${\alpha }_g+{\mu }_{gk}+{\mathbf{U}}_{bj}{\beta }_g+{\gamma }_{bg}$, where U_bj corresponds to the confounding variables.

3. Identifiability

In this section, we first prove that BUS is identifiable when every subtype presents on every batch. Next, we extend the results to more general study design and provide guidelines on the experimental design so that batch effects can be corrected.

3.1. With Complete Subtypes

We first investigate the scenario as proposed by MetaSparseKmeans (Huo et al. 2016) in which all subtypes are required to occur in all the batches. We refer to this setting as the “complete subtypes” case. In BUS model, the likelihood function for the observed data is $$\begin{array}{ccc}& & L_o\left(\Theta \right|\mathbf{Y})=\prod _{b=1}^B\prod _{j=1}^{n_b}\hfill \\ & & \left[\sum _{k=1}^K{\pi }_{bk}\prod _{g=1}^G\frac{1}{\sqrt{2\pi }{\sigma }_{bg}}\times \text{exp}\left\{-\frac{{(y_{bjg}-{\alpha }_g-{\mu }_{gk}-{\gamma }_{bg})}^2}{2{\sigma }_{bg}^2}\right\}\right],\hfill \end{array}$$where Θ consists of all unknown parameters $\Theta =\{\pi ,\alpha ,{\mu }_2,\dots ,{\mu }_K,{\gamma }_2,\dots ,{\gamma }_B,{\sigma }_1,\dots ,{\sigma }_B\}$ with $\pi =\{{\pi }_{bk}\ge 0:1\le b\le B,1\le k\le K\}$, $\alpha =\{{\alpha }_g:1\le g\le G\}$, ${\mu }_k=\{{\mu }_{gk}:1\le g\le G\},{\gamma }_b=\{{\gamma }_{bg}:1\le g\le G\}$, and ${\sigma }_b=\{{\sigma }_{bg}:1\le g\le G\}$. Recall that ${\mu }_1=\mathbf{0}$, ${\gamma }_1=\mathbf{0}$.

Theorem 1.

If ${\mu }_{k_1}-{\mu }_{k_2}\ne {\mu }_{k_3}-{\mu }_{k_4}$ for any (k₁, k₂) ≠ (k₃, k₄) (Assumption I) and π_bk > 0 for every b and k, then BUS is identifiable (up to label switching) in the sense that L_o(Θ|Y) = L_o(Θ*|Y) for any Y implies that π_bk = π*_bρ(k), $\alpha +{\mu }_k={\alpha }^{*}+{\mu }_{\rho \left(k\right)}^{*}$, ${\gamma }_b={\gamma }_b^{*}$, and ${\sigma }_b={\sigma }_b^{*}$, where ρ is a permutation of {1, 2, …, K}.

The condition on π_bk > 0 corresponds to the “complete subtypes” experimental design. Assumption I is a very mild one. It actually only asks for the existence of one gene g whose mean expression differences between subtypes satisfy ${\mu }_{g{k}_1}-{\mu }_{g{k}_2}\ne {\mu }_{g{k}_3}-{\mu }_{g{k}_4}$ for any (k₁, k₂) ≠ (k₃, k₄), which is always easily met for high-throughput biology data.

3.2. With Missing Subtypes

Next, we investigate the scenario in which subtypes are measured in some but not all of the batches, which is the general study design usually encountered in real life. We call this setting as “with missing subtypes.” In other words, we allow π_bk = 0 for some b and k. In the following, we use C_b to denote the subtypes that are present in batch b and D_b to denote all of the data measured on batch b. We provide two types of experimental design that guarantee the identifiability of BUS.

Theorem 2.

Given (A) ${\bigcup }_{b=1}^B{C}_b=\{1,2,\dots ,K\}$, (B) K_b = |C_b|, the cardinality of C_b, K_b ⩾ 2 for every batch b, (C) C₁ = {1, 2, …, K} and Assumption I is satisfied, then BUS is identifiable (up to label switching).

Condition (C) assumes that there exist a reference batch, without loss of generality taken as batch one, that contains samples from all subtypes. In practice, this assumption often holds if we have a large database built upon previous experiments. In a new experiment consisting of batches two to B (B ⩾ 2), if for each batch b (2 ⩽ b ⩽ B) we collect samples that are from at least two subtypes present in batch one, then Theorem 2 holds. Therefore, we can apply BUS to the dataset {D_b: b = 1, …, B} to separate the confounding batch effects from the true biological variations in the new experiment.

Theorem 3.

Given (A) ${\bigcup }_{b=1}^B{C}_b=\{1,2,\dots ,K\}$, (B) K_b = |C_b|, the cardinality of C_b, K_b ⩾ 2 for every batch b, (D) $|C_b\cap C_{b-1}|\ge 2$ for every b ⩾ 2 and Assumption I is satisfied, then BUS is identifiable (up to label switching).

Theorem 3 tells us how to design a valid study when we do not have a large database that contains every subtype. In detail, we can begin with batch one whose samples are known to be taken from at least two subtypes. When preparing samples for batch two, we recommend collecting samples that are from at least two known subtypes in batch one. Based on Theorem 3, we can then apply BUS to {D_b: b = 1, 2} to learn the subtype for each sample in batch two. In the same spirit, we require the samples for batch three to be from at least two learned subtypes in batch two, and we then apply BUS to {D_b: b = 1, 2, 3} and so on and so forth. This chain-type experimental design satisfies the conditions of Theorem 3, so batch effects are estimable.

In a nutshell, both the conditions for Theorems 2 and 3 can be executed and implemented in planning real multi-batch experiments. Therefore, from the perspective of practitioners, these conditions help to guide experimental designs which can simultaneously filter out batch effects and keep true biological variations.

4. Statistical Inference

4.1. Prior Specification

We adopt a full Bayesian approach to conduct statistical inference (Hein et al. 2005; Gelman et al. 2014). We assign independent conjugate priors to each component of Θ as follows: ${\pi }_b=({\pi }_{b1},\dots ,{\pi }_{bK})\sim Dir(\alpha ,\dots ,\alpha ),1\le b\le B$; α_g ∼ N(m, τ²_m), 1 ⩽ g ⩽ G; γ_bg ∼ N(0, τ²_γ), 2 ⩽ b ⩽ B, 1 ⩽ g ⩽ G; ${\sigma }_{bg}^2\sim Inv\Gamma (\tilde{a},\tilde{b}),1\le b\le B,1\le g\le G$ with hyper-parameters $(\alpha ,m,{\tau }_m^2,{\tau }_{\gamma }^2,\tilde{a},\tilde{b})$.

Regarding the subtype effect μ_gk, we assign a spike-and-slab prior (George and McCulloch 1993) using a normal mixture. Specifically, one component of the mixture concentrates near zero with a small variance, and the other is more dispersed with a larger variance. To represent the mixture distribution, we introduce the latent variable L_gk to indicate which component of the mixture distribution μ_gk comes from. When L_gk = 0, gene g is believed to have the same expression level in subtype k and subtype one. Therefore, μ_gk is assumed to be close to zero, following the normal component with a small variance. When L_gk = 1, gene g is differentially expressed (DE) between subtype k and subtype one. Consequently, μ_gk tends to largely deviate from zero, following the normal component with a large variance. As a result, the expression of gene g does not hold constant across subtypes if and only if D_g≐∑^K_{k = 2}L_gk > 0. We call such genes intrinsic genes following Huo et al. (2016) and name D_gs intrinsic gene indicators. Scientifically, L_gks identify the set of genes that define and differentiate subtypes. Denoting the proportion of L_gks being one by p, the relationship between μ_gk and L_gk for g = 1, …, G; k = 2, …, K is as follows: $$\begin{array}{ccc}& & L_{gk}\sim \text{Bernoulli}\left(p\right);\hfill \\ & & {\mu }_{gk}\sim N(0,{\tau }_{\mu 1}^2)|L_{gk}=1;\hfill \\ & & {\mu }_{gk}\sim N(0,{\tau }_{\mu 0}^2)|L_{gk}=0.\hfill \end{array}$$τ²_μ1 is set to a large number, and τ²_μ0 follows an inverse-gamma prior InvΓ(a_τ, b_τ) with a small prior mean. Meanwhile, p has the conjugate prior $\text{Beta}(a_p,b_p)$.

With all the priors, the full posterior distribution f(Θ, Z, L|Y) is proportional to $$\begin{array}{ccc}& & \prod _{b=1}^B\prod _{j=1}^{n_b}\prod _{k=1}^K\hfill \\ & & {\left[{\pi }_{bk}\prod _{g=1}^G\frac{1}{\sqrt{2\pi }{\sigma }_{bg}}\text{exp}\left\{-\frac{{(y_{bjg}-{\alpha }_g-{\mu }_{gk}-{\gamma }_{bg})}^2}{2{\sigma }_{bg}^2}\right\}\right]}^{I(Z_{bj}=k)}\hfill \\ & & ·\prod _{b=1}^{B}Dir({\pi }_b;\mathit{\alpha })\prod _{g=1}^{G}N({\alpha }_g;m,{\tau }_m^2)\hfill \\ & & ·\prod _{b=2}^B\prod _{g=1}^{G}N({\gamma }_{bg};0,{\tau }_{\gamma }^2)\prod _{b=1}^B\prod _{g=1}^G\mathrm{Inv}\Gamma ({\sigma }_{bg}^2;\tilde{a},\tilde{b})\hfill \\ & & ·\prod _{g=1}^G\prod _{k=2}^K\left[N\right({\mu }_{gk};0,{\tau }_{\mu 1}^2)·L_{gk}+N({\mu }_{gk};0,{\tau }_{\mu 0}^2)·(1-L_{gk})]\hfill \\ & & ·\prod _{g=1}^G\prod _{k=2}^K{p}^{L_{gk}}{(1-p)}^{1-L_{gk}}·\text{Beta}(p;a_p,b_p)·\mathrm{Inv}\Gamma ({\tau }_{\mu 0}^2;a_{\tau },b_{\tau }).\hfill \end{array}$$

4.2. Posterior Inference

To explore the posterior distribution, we develop a Gibbs sampler algorithm to draw samples (Geman and Geman 1984; Robert and Casella 2013). At iteration t:

1.	Update the inclusion probability p[t] for Lgks from $$\text{Beta}\left(\sum _{g=1}^G\sum _{k=2}^K{L}_{gk}^{[t-1]}+a_p,G(K-1)-\sum _{g=1}^G\sum _{k=2}^K{L}_{gk}^{[t-1]}+b_p\right).$$
2.	Sample the variance of the spike component of the spike-and-slab prior (τ[t]μ0)2 from $$\begin{array}{c}\hfill \mathrm{Inv}\Gamma (a_{\tau }+\frac{1}{2}\#\left\{(g,k):L_{gk}^{[t-1]}=0,2\le k\le K\right\},\\ \hfill b_{\tau }+\frac{1}{2}\sum _{\{(g,k):L_{gk}=0\}}\left({\mu }_{gk}^{[t-1]}{)}^2\right).\end{array}$$
3.	For each gene g and for 2 ⩽ k ⩽ K, update indicator L[t]gk from $$\begin{array}{ccc}& & \text{Bernoulli}\hfill \\ & & \left(\frac{p^{\left[t\right]}·N({\mu }_{gk}^{[t-1]};0,{\tau }_{\mu 1}^2)}{p^{\left[t\right]}·N({\mu }_{gk}^{[t-1]};0,{\tau }_{\mu 1}^2)+(1-p^{\left[t\right]})·N({\mu }_{gk}^{[t-1]};0,({\tau }_{\mu 0}^{\left[t\right]}{)}^2)}\right).\hfill \end{array}$$
4.	For each batch b, sample subtype proportions ${\pi }_b^{\left[t\right]}$ from the Dirichlet distribution
5.	For each sample j in every batch b, update its subtype indicator according to $$\begin{array}{ccc}& & p\left(Z_{bj}^{\left[t\right]}=k|-\right)\hfill \\ & & \propto {\pi }_{bk}^{\left[t\right]}\text{exp}\left\{-\sum _{g=1}^G\frac{(y_{bjg}-{\alpha }_g^{[t-1]}-{\mu }_{gk}^{[t-1]}-{\gamma }_{bg}^{[t-1]}{)}^2}{2({\sigma }_{bg}^{[t-1]}{)}^2}\right\},\hfill \end{array}$$where “-” indicates the rest of variables.
6.	For each gene g, sample its baseline expression level α[t]g from $$\begin{array}{ccc}& & N\left(\frac{{\tau }_m^2{\sum }_{b=1}^B{\sum }_{j=1}^{n_b}\left[\right(y_{bjg}-{\mu }_{g{Z}_{bj}^{\left[t\right]}}^{[t-1]}-{\gamma }_{bg}^{[t-1]}\left)\frac{1}{({\sigma }_{bg}^{[t-1]}{)}^2}\right]+m}{{\tau }_m^2{\sum }_{b=1}^B\frac{n_b}{({\sigma }_{bg}^{[t-1]}{)}^2}+1},\right.\hfill \\ & & \left.\frac{{\tau }_m^2}{{\tau }_m^2{\sum }_{b=1}^B\frac{n_b}{({\sigma }_{bg}^{[t-1]}{)}^2}+1}\phantom{\frac{{\tau }_m^2{\sum }_{b=1}^B{\sum }_{j=1}^{n_b}\left[\right(y_{bjg}-{\mu }_{g{Z}_{bj}^{\left[t\right]}}^{[t-1]}-{\gamma }_{bg}^{[t-1]}\left)\frac{1}{({\sigma }_{bg}^{[t-1]}{)}^2}\right]+m}{{\tau }_m^2{\sum }_{b=1}^B\frac{n_b}{({\sigma }_{bg}^{[t-1]}{)}^2}+1}}\right).\hfill \end{array}$$
7.	For each gene g in subtype two to K, sample its subtype effect μ[t]gk from $$\begin{array}{ccc}& & \mathrm{if}{L}_{gk}^{\left[t\right]}=1,\hfill \\ & & N\left(\frac{{\tau }_{\mu 1}^2{\sum }_{b=1}^B{\sum }_{j\in \{1\le j\le n_b:Z_{bj}^{\left[t\right]}=k\}}(y_{bjg}-{\alpha }_g^{\left[t\right]}-{\gamma }_{bg}^{[t-1]})\frac{1}{({\sigma }_{bg}^{[t-1]}{)}^2}}{{\tau }_{\mu 1}^2{\sum }_{b=1}^B\#\{j:Z_{bj}^{\left[t\right]}=k\}·\frac{1}{({\sigma }_{bg}^{[t-1]}{)}^2}+1},\right.\hfill \\ & & \left.\frac{{\tau }_{\mu 1}^2}{{\tau }_{\mu 1}^2{\sum }_{b=1}^B\#\{j:Z_{bj}^{\left[t\right]}=k\}·\frac{1}{({\sigma }_{bg}^{[t-1]}{)}^2}+1}\right);\hfill \\ & & \mathrm{if}{L}_{gk}^{\left[t\right]}=0,\hfill \\ & & N\left(\frac{{\tau }_{\mu 0}^{\left[t\right]2}{\sum }_{b=1}^B{\sum }_{j\in \{1\le j\le n_b:Z_{bj}^{\left[t\right]}=k\}}(y_{bjg}-{\alpha }_g^{\left[t\right]}-{\gamma }_{bg}^{[t-1]})\frac{1}{({\sigma }_{bg}^{[t-1]}{)}^2}}{{\tau }_{\mu 0}^{\left[t\right]2}{\sum }_{b=1}^B\#\{j:Z_{bj}^{\left[t\right]}=k\}·\frac{1}{({\sigma }_{bg}^{[t-1]}{)}^2}+1},\right.\hfill \\ & & \left.\frac{{\tau }_{\mu 0}^{\left[t\right]2}}{{\tau }_{\mu 0}^{\left[t\right]2}{\sum }_{b=1}^B\#\{j:Z_{bj}^{\left[t\right]}=k\}·\frac{1}{({\sigma }_{bg}^{[t-1]}{)}^2}+1}\right).\hfill \end{array}$$
8.	For each gene in batch two to B, sample the additive “location” batch effects γ[t]bg from $$N\left(\frac{{\tau }_{\gamma }^2{\sum }_{j=1}^{n_b}(y_{bjg}-{\alpha }_g^{\left[t\right]}-{\mu }_{g{Z}_{bj}^{\left[t\right]}}^{\left[t\right]})\frac{1}{({\sigma }_{bg}^{[t-1]}{)}^2}}{{\tau }_{\gamma }^2\frac{n_b}{({\sigma }_{bg}^{[t-1]}{)}^2}+1},\frac{{\tau }_{\gamma }^2}{{\tau }_{\gamma }^2\frac{n_b}{({\sigma }_{bg}^{[t-1]}{)}^2}+1}\right).$$
9.	Sample the multiplicative “scale” batch effects from the inverse-Gamma distribution for each gene in each batch.

To determine the number of iterations for the Gibbs sampler, we adopt the estimated potential scale reduction (EPSR) factors criterion (Gelman et al. 2014) (see supplementary materials Section S1). Based on the collected samples from the Gibbs sampler, we conduct posterior inferences. For the underlying subtype effects (μ_gks), location batch effects (α_bgs), and scale batch effects (σ²_bgs), which take continuous values, we use the means of their posterior samples for estimation, since the posterior mean minimizes the Bayes risk (Casella and Berger 2002). Regarding clustering, we take the posterior mode of samples for Z_bj as the subtype for sample j in batch b.

Compared to single-batch-based methods, BUS can borrow information across all batches and all genes. For example, in step 7 of the Gibbs sampler, updating subtype effects μ^[t]_gk depends on data related to gene g and subtype k in all of the batches, which offers more robust and accurate estimation. On the other hand, in step 5, the subtype determination for a given sample uses information across the genes. The two-way information sharing across genes and batches improves the statistical power of BUS.

Recall that gene g is an intrinsic gene if L_gk = 1 for some k (2 ⩽ k ⩽ K). To reduce the errors in inferring L_gk’s, we control the Bayesian false discovery rate (FDR; Newton et al. 2004; Peterson et al. 2015). We denote by ${\text{PPI}}_{gk}$ the posterior marginal probability for gene g to be DE in subtype k compared to subtype one and let ${\xi }_{gk}=1-{\text{PPI}}_{gk}$; then according to Newton et al. (2004) and Peterson et al. (2015), the expected Bayesian FDR for inferring DE indicators becomes (4.1) $$\text{FDR}\left(\kappa \right)=\frac{{\sum }_{g=1}^G{\sum }_{k=2}^K{\xi }_{gk}I({\xi }_{gk}\le \kappa )}{{\sum }_{g=1}^G{\sum }_{k=2}^{K}I({\xi }_{gk}\le \kappa )}.$$(4.1) From the posterior samples of L_gk, $\{L_{gk}^{\left(t\right)}:t=N_{\text{burn-in}}+1,\dots ,N_{\text{total}}\}$, we can estimate ${\text{PPI}}_{gk}=P(L_{gk}=1|\mathbf{X})\approx \frac{1}{N_{\text{total}}-N_{\text{burn-in}}}{\sum }_{t=N_{\text{burn-in}}+1}^{N_{\text{total}}}{L}_{gk}^{\left(t\right)}$ and further approximate $\text{FDR}\left(\kappa \right)$. If we want to control the FDR at a prespecified threshold α, such as 0.1, we can select κ₀ such that estimated $\text{FDR}\left({\kappa }_0\right)\le \alpha$. In other words, if the estimated ${\text{PPI}}_{gk}\ge 1-{\kappa }_0$, we claim L_gk as one and zero otherwise.

So far, we have focused on the case where investigators have prior knowledge of the number of subtypes. When K is unknown, the Bayesian information criterion (BIC; Schwarz et al. 1978) can be used to select the optimal number of subtypes. The Bayesian information criterion (BIC) formula for BUS is (4.2) $$-2·\left[\sum _{b=1}^B\sum _{j=1}^{n_b}\text{log}\left(\sum _{k=1}^K{\widehat{\pi }}_{bk}\prod _{g=1}^{G}N(y_{bjg};{\widehat{\alpha }}_g+{\widehat{\mu }}_{gk}+{\widehat{\gamma }}_{bg},{\widehat{\sigma }}_{bg}^2)\right)\right]$$(4.2) (4.3) $$+\left(KG+(2B-1)G\right)·\text{log}\left(\sum _{b=1}^B{n}_b·G\right),$$(4.3) where the first term (4.2(4.2) $$-2·\left[\sum _{b=1}^B\sum _{j=1}^{n_b}\text{log}\left(\sum _{k=1}^K{\widehat{\pi }}_{bk}\prod _{g=1}^{G}N(y_{bjg};{\widehat{\alpha }}_g+{\widehat{\mu }}_{gk}+{\widehat{\gamma }}_{bg},{\widehat{\sigma }}_{bg}^2)\right)\right]$$(4.2) ) approximates two times the negative observed-data log likelihood and the second term (4.3(4.3) $$+\left(KG+(2B-1)G\right)·\text{log}\left(\sum _{b=1}^B{n}_b·G\right),$$(4.3) ) is the product of the parameter number and the logarithm of the observation number. ${\widehat{\pi }}_{bk}$, ${\widehat{\alpha }}_g$, ${\widehat{\mu }}_{gk}$, ${\widehat{\gamma }}_{bg}$, and ${\widehat{\sigma }}_{bg}^2$ are the posterior mean estimates. We choose the subtype number K such that BIC attains its minimum. Once the optimal number of K is determined, all of the aforementioned analyses follow.

Compared to MetaSparseKmeans (Huo et al. 2016), BUS has two advantages for clustering. First, BUS allows only some of the total K subtypes to appear in each batch. In contrast, MetaSparseKmeans requires all subtypes to be measured on every batch, which imposes very strong constraints on the datasets that can be used for meta-analysis and is often infeasible for many experimental designs. Second, BUS avoids the combinatorial matching encountered by MetaSparseKmeans. The computation complexity of BUS for every round of updates is only O(∑^B_{b = 1}n_b · GK), both linear in the number of batches B and in the number of subtypes K, thus significantly outperforming the computational complexity of MetaSparseKmeans O((K!)^{B − 1}), which grows exponentially in the number of batches B and factorially in the number of subtypes K.

4.3. Downstream Analysis

In addition to clustering, BUS also provides an explicit characterization of batch effects and enables correction of the raw input data. To correct batch effects, we can follow a similar approach as the L/S model (Johnson et al. 2007). As batch one is always taken as the reference batch, no correction is needed. For batches two to B, the corrected gene expression value ${\widehat{y}}_{bjg}$ after removing the “location” and “scale” batch effects can be calculated as (4.4) $${\widehat{y}}_{bjg}={\widehat{\alpha }}_g+{\widehat{\mu }}_{g{\widehat{Z}}_{bj}}+\frac{y_{bjg}-{\widehat{\alpha }}_g-{\widehat{\mu }}_{g{\widehat{Z}}_{bj}}-{\widehat{\gamma }}_{bg}}{{\widehat{\sigma }}_{bg}/{\widehat{\sigma }}_{1g}}.$$(4.4)

The corrected expression values will be free from nonbiological effects and serve as valid data sources for downstream analysis such as differential gene expression detection and gene regulatory network construction.

5. Simulation

In this section, we evaluate the performance of BUS in correcting batch effects, clustering subtypes as well as selecting intrinsic genes via simulation studies. We compare BUS to MetaSpaseKmeans (Huo et al. 2016) and a two-stage approach coupling ComBat (Johnson et al. 2007) with SparseKmeans (Witten and Tibshirani 2012).

5.1. With Complete Subtypes

Following the^{Figure 1}terminology in Section 3, we first investigate the “complete subtypes” case. In Simulation I, we simulate expression level for G = 10, 000 genes from K = 3 subtypes measured in B = 3 batches. The sample sizes for each batch are (n₁, n₂, n₃) = (100, 110, 120). The subtype proportions for each batch are ${\pi }_1=(0.2,0.2,0.6)$, ${\pi }_2=(0.1,0.8,0.1),$ and ${\pi }_3=(0.6,0.1,0.3)$, respectively. For each batch b, we assume the first π_b1 · 100% of simulated samples are from subtype one, the second π_b2 · 100% of simulated samples from subtype two, and the rest of the samples from subtype three.

We then specify the underlying mean gene expression level. α_g is set to two for all of the genes. Recall that subtype effect μ_g1 is constrained to zero for all genes in subtype one. The top 500 genes are chosen to be DE in subtype two compared to subtype one with a mean shift of two: μ_g2 = 2, g = 1…, 500. Similarly, genes 501–1000 are up-regulated in subtype three with a mean difference of two: μ_g3 = 2, g = 501…, 1000. Other than that, none of the remaining genes are DE. In other words, μ_g2 = 0, g = 501…, 1000; μ_g3 = 0, g = 1…, 500; and μ_gk = 0, k = 2, 3 for the rest of the genes. Figure 1(a) shows the underlying true gene expression level α_g + μ_gk for each gene in each subtype.

Figure 1. Patterns for Simulation I. (a) True subtype mean. Each row represents a gene, and each column corresponds to a subtype. There are in total 10,000 genes and three subtypes. (b) True batch effects. Each row represents a gene and each column corresponds to a batch. There are three batches in total. (c) Observed gene expression. Each row represents a gene and each column is a sample. There are 330 samples. (d) BIC plot. (e) Estimated subtype mean. (f) Estimated batch effects. (g) Corrected gene expression grouped by batches. The samples are first ordered by batch (the top bar) and then ordered by subtype (the bottom bar). (h) Corrected gene expression grouped by subtypes. The samples are first ordered by subtype (the bottom bar) and then ordered by batch (the top bar).

Now, we determine the batch effects. For the additive batch effects in batch 2, as illustrated in Figure 1(b), we set γ_2g = 3 for genes 1–2000; γ_2g = 2 for genes 2001–4000; γ_2g = 1 for genes 4001–6000; γ_2g = 2 for genes 6001–8000; and γ_2g = 3 for genes 8001–10,000. If we abbreviate such pattern for 2000 consecutive genes as (3,2,1,2,3), then γ_3g are specified to (1,2,3,2,1) in the same fashion for batch three. The multiplicative batch effects are σ²_1g = 0.1, σ²_2g = 0.2, and σ²_3g = 0.15 for all genes.

Finally, we generate all of the raw gene expression values from Model 2.5(2.5) $$\begin{array}{ccc}& & Z_{bj}\sim \text{Multinomial}(1;{\pi }_{b1},\dots ,{\pi }_{bK});\hfill \\ & & Y_{bjg}\sim N(m_{bgk},{\sigma }_{bg}^2\left)\right|Z_{bj}=k;\hfill \\ & & m_{bgk}={\alpha }_g+{\mathbf{X}}_{bj}{\mu }_g+{\gamma }_{bg}={\alpha }_g+{\mu }_{gk}+{\gamma }_{bg}|Z_{bj}=k.\hfill \end{array}$$(2.5) . Figure 1(c) displays the observed data. Obviously, a naive application of traditional clustering methods to the raw data without considering batch effects would fail to identify the true subtypes.

For the prior distributions discussed in Section 4.1, we set the hyper-parameters as follows: m = 1, ${\tau }_m=\sqrt{5}$, ${\tau }_{\gamma }=\sqrt{5}$, α = 2, $\tilde{a}=2$, $\tilde{b}=1$, a_τ = 2, b_τ = 0.005, (a_p, b_p) = (1, 3), and τ_μ1 = 10. We conduct analysis for K from 2 to 10. BIC correctly chooses K = 3 (Figure 1(d)). The Markov chain produced by the Gibbs sampler converges very quickly according to the EPSR factors (see supplementary materials Section S1 for details and supplementary Figure S1 for trace plots). After 150 iterations of the burn-in period, we collect 150 iterations for posterior inference. Figure 1(e) and 1(f) shows the posterior means for subtype means and additive batch effects. Comparing to Figure 1(a) and 1(b), BUS accurately estimates the true parameters. Figure 1(g) and 1(h) is the heatmaps for batch-effects-corrected ${\widehat{y}}_{bjg}$, and it can be seen that the corrected gene expression values now no longer suffer from technical noise and reveal their true biological variation.

Besides correcting batch effects, BUS can cluster all samples automatically with the posterior modes of their subtype indicators $\widehat{\mathbf{Z}}=\{{\widehat{Z}}_{bj}:1\le b\le B,1\le j\le n_b\}$. Samples with the same value of ${\widehat{Z}}_{bj}$ are grouped together. To measure how close the estimates $\widehat{\mathbf{Z}}$ are to the underlying truth Z, we adopt the adjusted Rand index (ARI; Hubert and Arabie 1985). The ARI is bounded above by one, and the higher the value is, the more consistent the two categorical vectors are. The ARI between $\widehat{\mathbf{Z}}$ and Z is exactly one, showing that BUS perfectly recovers the underlying true subtypes for all samples.

Next, we study the performance of BUS in identifying intrinsic genes that reflect the difference among subtypes. The intrinsic gene indicator D_g is estimated as ${\sum }_{k=2}^K{\widehat{L}}_{gk}$, where $\{{\widehat{L}}_{gk}:1\le g\le G,2\le k\le K\}$ are estimated by setting κ = 0.5 to control FDR in Equation (4.1(4.1) $$\text{FDR}\left(\kappa \right)=\frac{{\sum }_{g=1}^G{\sum }_{k=2}^K{\xi }_{gk}I({\xi }_{gk}\le \kappa )}{{\sum }_{g=1}^G{\sum }_{k=2}^{K}I({\xi }_{gk}\le \kappa )}.$$(4.1) ) below 0.1. Genes with ${\widehat{D}}_g>0$ are regarded as intrinsic genes. BUS claims all of the 1000 assumed intrinsic genes correctly with only one false discovery.

In comparison, for this small-scale dataset, MetaSparseKmeans also has an ARI = 1 and identifies all of the intrinsic genes correctly. Both MetaSparseKmeans and BUS have comparably fast computation time here around 2 min. Nevertheless, noteworthy, the samples from the Markov chain Monte Carlo (MCMC) method (Robert and Casella 2013) obtained by BUS can provide the full posterior distribution for all of the parameters, especially quantifying the uncertainties in parameter estimations.

We also test a two-stage approach that we abbreviate as “ComSpa.” ComSpa first applies ComBat to the three batches, then treats the corrected values from all of the batches as a single batch and uses SparseKmeans to cluster samples. However, even after the correction by ComBat, the expression profiles of the same subtype show very distinct patterns in different batches. For example, in supplementary Figure S2, subtype two (colored by blue in the lower color bar) samples on batch one show significantly higher expression values than subtype two samples on batch two for the top 500 intrinsic genes. The issue is that ComBat requires known subtype information or homogenous biological samples to tease out batch effects. When multiple unknown subtypes exist within each batch, ComBat can easily over-correct the biological variations as artificial noise. The problematic batch effects correction in the first-stage leads to the poor clustering performance of ComSpa with a low ARI of 0.546.

5.1.1. Sensitivity Analysis

We conduct sensitivity analysis to check the influence of prior distributions and find that the choices of hyper-parameters have little effect on the posterior inference (see supplementary materials Section S2.1 and supplementary Figure S3), so we fix the same set of hyperparameters as in Simulation I throughout the article.

In addition to the choices of hyper-parameters, we investigate the effects of sample misclassification on batch effects estimation (see supplementary materials Section S2.2). According to supplementary Figure S4, the batch effects estimations are not sensitive to sample misclassification for intrinsic genes and are always accurate for nonintrinsic genes. Therefore, even in cases where some subtypes are wrongly claimed, Equation (4.4(4.4) $${\widehat{y}}_{bjg}={\widehat{\alpha }}_g+{\widehat{\mu }}_{g{\widehat{Z}}_{bj}}+\frac{y_{bjg}-{\widehat{\alpha }}_g-{\widehat{\mu }}_{g{\widehat{Z}}_{bj}}-{\widehat{\gamma }}_{bg}}{{\widehat{\sigma }}_{bg}/{\widehat{\sigma }}_{1g}}.$$(4.4) ) still provides robust corrected expression values.

5.1.2. Varied Signal Strengths

We further test the robustness of BUS under different signal strengths. Notice that there are two ways to vary signals: (a) keep the sample size fixed and change the strengths of the subtype effects and (b) fix the strengths of the subtype effects and vary the sample size.

For scenario a, we fix the sample size as (100, 110, 120) for the three batches, respectively. For each gene g, we set σ²_g1 = 0.1 on batch one, σ²_g2 = 0.2 on batch two, and σ²_g3 = 0.15 on batch three. We represent the signal matrix that encodes the subtype effects as Each column of S(v) corresponds to a subtype, and each row refers to a gene. Specifically, the kth column of S(v), S(v)_k = (μ_1k, …, μ_Gk)^T, represents the subtype effects of all of the genes for subtype k. Consequently, v indicates the signal strength of the subtype effects: the lower the v is, the weaker the signals are. We vary v from 0 to 3 taking values at {0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5, 1, 1.5, 2, 2.5, 3}. For each setting, we apply BUS and calculate the corresponding ARI (see supplementary Figure S5(a)). When v < 0.15, the signals are overwhelmed by noise. However, as long as v ⩾ 0.4 which is about the size of ${max}_b{\sigma }_{gb}=\sqrt{0.2}\approx 0.45$, BUS can precisely cluster all of the samples and infer the underlying parameters.

For scenario b, keeping the subtype effect strength v = 2 and the other settings the same as above, we reduce the sample size from (100, 110, 120) to (100, 110, 120) · ω for ω = 0.1, 0.2, …, 0.8, 0.9, 1. For each generated dataset, we apply BUS and calculate the corresponding ARI (see supplementary Figure S5(b)). As long as ω ⩾ 0.2, even with a small-sample size (20, 22, 24) for ω = 0.2, BUS is able to correctly cluster all of the samples and estimate the parameters precisely.

5.1.3. Model Misspecification

BUS assumes that given a subtype the expression levels of different genes are independent, which leads to a diagonal covariance matrix $\Sigma$ in Equation (2.3(2.3) $$\begin{array}{ccc}\hfill {\mathbf{Y}}_j& \sim & {\pi }_1\mathbf{N}({\mathbf{m}}_1,\Sigma )+{\pi }_2\mathbf{N}({\mathbf{m}}_2,\Sigma )+\cdots \hfill \\ & & +{\pi }_K\mathbf{N}({\mathbf{m}}_K,\Sigma ),\text{iid}j=1,\dots ,n,\hfill \end{array}$$(2.3) ). However, as is often the case, the expression levels of many genes are correlated, so $\Sigma$ is no longer diagonal. We incorporate correlation structures into gene expression following a similar simulation setting of Huo et al. (2016), assuming that the expression values for every 20 consecutive intrinsic genes follow a multivariate normal distribution with the covariance matrix sampled from an inverse Wishart distribution W^{− 1}(Φ, 60), where Φ = 0.5I_{20 × 20} + 0.51_{20 × 1}1^T_{20 × 1}. The expressions for the remaining genes, that is, the nonintrinsic genes, are independent. We apply BUS to this model-misspecified setting, and it turns out that BUS successfully identifies the true subtypes for all of the samples ($\text{ARI}=1$) and estimates subtype effects and location batch effects very well (see supplementary materials Section S3.1 and supplementary Figure S6).

In real-world datasets, some samples might be purely noise or outliers and cannot be grouped into any cluster, which are defined as “scattered samples” (Tseng and Wong 2005; Maitra and Ramler 2009). Although Tseng and Wong (2005) proposed an algorithm under the K-means framework, in principle their resampling ideas are generalizable to detection of scattered samples for other clustering methods. We adapt algorithm A of Tseng and Wong (2005) to BUS and propose an algorithm to detect scattered samples with a given cluster number (see supplementary materials Section S3.2). To illustrate, we add one scattered sample to each batch in Simulation I. In batch b, the expression level of gene g in the scattered sample is drawn from N(4 + γ_gb, σ²_gb). We then carry out the “scattered sample-finding” algorithm. As shown in supplementary Figure S7(a)– S7(c), the scattered sample is successfully identified for each batch.

All in all, BUS is robust to the choices of hyper-parameters, sample misclassification, noise levels, correlation structures, and scattered samples.

For the “complete subtypes” setting, we also test a large-scale dataset, Simulation II, which consists of 10 batches and 5 subtypes. The performance of BUS remains the same, taking 1.32 hr on a 2.6GHz processor (the same processor used across the article) and resulting in zero FDR (κ = 0.5) and an ARI of one, whereas the original MetaSparseKmeans algorithm fails to work using its exhaustive version. Therefore, we run an approximate version MetaSparseMeans using simulated annealing (MetaSparseMeans-SA), which takes 1.73 hr and also has an ARI of one. Thus, MetaSparseMeans-SA has performance comparable to BUS on Simulation II. Nevertheless, as discussed above, BUS can provide the full posterior distribution for all of the parameters. Please see supplementary materials Section S4 and supplementary Table S1 for the details of Simulation II.

5.2. With Missing Subtypes

Now we move on to the scenario “with missing subtypes” as defined in Section 3. We consider a large-scale case, Simulation III, in which there are 10 batches. The sample sizes of the 10 batches are set to (300, 110, 220, 100, 180, 110, 100, 180, 150, 110), respectively. The total number of subtypes across all samples, K, is set to be 5. However, let K_b denote the number of subtypes in batch b, then K_b ⩽ K changes across batches. For illustration, subtype one appears only in batch one and batch eight; subtype five is present only in batch one and two. Supplementary Table S2 shows the values of all of the parameters, and Figure 2(a)–(c) depicts the assumed subtype means, batch effects as well as the observed data, respectively.

Figure 2. Patterns for Simulation III. (a) True subtype mean. Each row represents a gene, and each column corresponds to a subtype. There are in total 10,000 genes and five subtypes. (b) True batch effects. Each row represents a gene and each column corresponds to a batch. There are 10 batches in total. (c) Observed gene expression. Each row represents a gene and each column is a sample. There are 1560 samples. (d) BIC plot. (e) Estimated subtype mean. (f) Estimated batch effects. (g) Corrected gene expression grouped by batches. The samples are first ordered by batch (the top bar) and then ordered by subtype (the bottom bar). (h) Corrected gene expression grouped by subtypes. The samples are first ordered by subtype (the bottom bar) and then ordered by batch (the top bar).

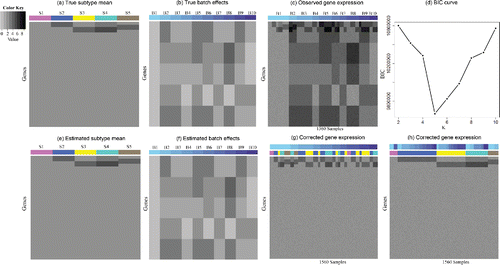
BIC values (Figure 2(d)) are calculated for K = 2, 3, …, 10, respectively, and the optimal subtype number is five, in accord with the underlying truth. We conduct the same posterior inference as before, run 3000 MCMC iterations which achieve convergence based on EPSR factors, and collect samples from the last 1500 iterations. The Gibbs Sampler cost 1.73 hr.

Subtype means (Figure 2(e)) and batch effects (Figure 2(f)) are correctly recovered once again. The corrected expression data are free from technical artifacts and demonstrate their underlying true biological variability (Figure 2(g) and 2(h)). The ARI between the results produced by BUS and the underlying truth is one again, which indicates the perfect sample clustering of BUS. BUS also finds all the intrinsic genes with no false discovery (κ = 0.5 in Equation (4.1(4.1) $$\text{FDR}\left(\kappa \right)=\frac{{\sum }_{g=1}^G{\sum }_{k=2}^K{\xi }_{gk}I({\xi }_{gk}\le \kappa )}{{\sum }_{g=1}^G{\sum }_{k=2}^{K}I({\xi }_{gk}\le \kappa )}.$$(4.1) )).

In comparison, we run MetaSparseKmeans-SA, SparseKemans, and ComSpa with the prespecified total cluster number set to 5. MetaSparseKmeans-SA and ComSpa are applied to the whole dataset combined from 10 batches, and SparseKmeans is applied to each single batch separately. Finally, we calculate their ARIs with the underlying truth. Across all samples from all batches, the MetaSparseKmeans-SA’s ARI is 0.289 and cost 2.43 hr; ComSpa has an ARI of 0.43 and takes 13.3 hr; and the SparseKmeans consumes less than 1 hr but its ARI is 0.193. All of them have ARIs much lower than BUS’ ARI of one. The main issues are: (a) MetaSparseKmeans and SparseKmeans force all of the K subtypes to be present in all of the batches, as a result, they ignore the fact that K_b’s can be less than K in each individual batch and vary across batches; (b) ComBat, the first stage of ComSpa, cannot filter out batch effects correctly when there are unknown biological variations.

6. Application

In this section, we apply BUS to a breast cancer dataset that is preprocessed by Huo et al. (2016) and used to apply the MetaSparseKmeans model. The study design of the dataset is summarized in Table 1. In total, B = 3 batches are analyzed and they come from two different platforms. The batch generated by The Cancer Genome Atlas (TCGA) (Cancer Genome Atlas Network 2012) was measured using the Agilent platform, and consequently, the measurement unit is log ratio intensity. The two batches generated by Wang et al. (2005) and Desmedt et al. (2007) used the Affymetrix array, and hence, the measurement unit is log intensity. From Table 1, we can see that the expression values from the two platforms are of very different ranges and medians. Figure 3(a) is the heatmap of the raw gene expression combined directly from the three batches. Not only do the batches measured on different platform (batch 1 vs. batches 2 and 3) show distinct patterns due to artifacts, but also the batches measured on the same platform (batch 2 vs. 3) demonstrate strong batch effects. The subtype differences are completely overwhelmed by the batch effects.

Figure 3. Heatmaps for breast cancer datasets. (a) Observed gene expression, where rows represent 11,058 genes and columns represent 533 (TCGA)+260 (Wang et al.)+164 (Desmedt et al.) = 957 samples; (b) Corrected gene expression by BUS.

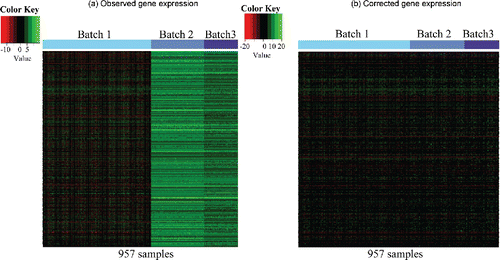
Table 1. Breast cancer datasets information. Part of the table is reproduced from Table 1 of Huo et al. (2016).

Study name	TCGA	Wang et al.	Desmedt et al.
Platform	Agilent	Affymetrix	Affymetrix
Unit	Log ratio intensity	Log intensity	log intensity
Number of samples	533	260	164
Range of intensity	[−13.816, 14.207]	[3.085,14.389]	[2.104,14.160]
Median intensity	0.023	6.745	5.379

According to BIC (see supplementary Figure S8), BUS identifies four subtypes, which is consistent with conclusions from existing biomedical literature (Carey et al. 2006; Onitilo et al. 2009) that there are four main breast cancer subtypes: basal-like, HER2+/ER-, luminal A, and luminal B. However, to have a direct comparison with MetaSparseKmeans (Huo et al. 2016) which specifies five subtypes for the same dataset, we deliberately fix K at five instead of using the BIC. After carrying out Gibbs sampling for 4000 iterations which meets the convergence criterion by the EPSR factors (see supplementary materials Section S1), we treat the first 2000 iterations as burn-in and keep the last 2000 iterations. It takes in total 1.81 hr. Figure 4(a)–(c) plots the three heatmaps for the gene expression values of each batch with samples ordered by learned subtypes, respectively. Figure 3(b) corresponds to the corrected expression values by BUS, and the heatmap illustrates that the corrected values can be viewed as being measured in the same batch.

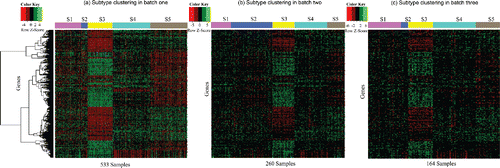
Figure 4. Heatmaps for intrinsic genes selected by BUS from the breast cancer dataset. (a) Row-scaled gene expression values from TCGA. The rows are clustered by hierarchical clustering, and the columns are clustered based on the BUS model. (b) Row-scaled gene expression values from Wang et al. The row order is the same as that in (a), and columns are clustered based on the BUS model; (c) Row-scaled gene expression values from Desmedt et al. The row order is the same as that in (a), and columns are clustered based on the BUS model.

Now, for each subtype k and each gene g, we calculate ${\widehat{L}}_{gk}$ by controlling the Bayesian FDR in Equation (4.1(4.1) $$\text{FDR}\left(\kappa \right)=\frac{{\sum }_{g=1}^G{\sum }_{k=2}^K{\xi }_{gk}I({\xi }_{gk}\le \kappa )}{{\sum }_{g=1}^G{\sum }_{k=2}^{K}I({\xi }_{gk}\le \kappa )}.$$(4.1) ) at 0.1, which leads to κ = 0.4, and estimate ${\widehat{D}}_g$ accordingly. Subsequently, 391 genes are selected as the intrinsic genes, which potentially explain the differences among breast cancer subtypes. From the heatmaps for the intrinsic genes (Figure 4), the subtype patterns are observable for each batch.

In contrast, 203 intrinsic genes are obtained using MetaSparseKmeans (Huo et al. 2016). We note that BUS associates each intrinsic gene g with the intrinsic gene indicator D_g ≔ ∑^K_{k = 2}L_gk > 0. Thus, genes with the highest D_g’s show the strongest signals to be intrinsic genes. Therefore, to select the same number of intrinsic genes as that identified by MetaSparseKmeans, we order the intrinsic genes by D_g’s and choose the top 203 intrinsic genes to conduct pathway analysis on the same website http://software.broadinstitute.org/gsea/msigdb/annotate.jsp using the same BioCarta database. The top 203 intrinsic genes produced by BUS lead to 21 significant (q-value less than 0.05) BIOCARTA pathways (see the column “BUS 203” in Table 2). In contrast, the intrinsic gene set on the same dataset selected by MetaSparseKmeans gives seven significant BIOCARTA pathways. Only three enriched BIOCARTA pathways, BIOCARTA_RANMS_PATHWAY, BIOCARTA_MCM_PATHWAY, and BIOCARTA_G1_PATHWAY, overlap between these two intrinsic gene sets. However, the rest of the pathways enriched in BUS analysis are closely related to breast cancer. Especially, the highest-ranked-enriched pathway from BUS analysis is the BIOCARTA_HER2_PATHWAY. Her2 is one of the most important biomarkers in breast cancer (Slamon et al. 1987). Actually, overexpression of Her2 is strongly associated with increased disease recurrence and a poor prognosis (Xia et al. 2004). Subtype-specific therapy, trastuzumab, targets Her2 and is only effective in Her2-positive patients (Piccart-Gebhart et al. 2005). The efficacy of trastuzumab is a classic example of subtype-specific diagnosis and treatment. However, this very important breast cancer pathway—BIOCARTA_HER2_PATHWAY—is completely mis-sed by MetaSparseKmeans. Moreover, IGF-1 (Wolf et al. 2008), MTA-3 (Fujita et al. 2003), and STATHMIN (Alli et al. 2007) are all key pathways for breast cancer. They are significant for BUS but missed by MetaSparseKmeans. These facts strongly support that the intrinsic gene set from BUS offers scientifically meaningful subtyping.

Table 2. Significant (q-value less than 0.05) BIOCARTA pathways identified by different studies. Results from joint analyses of three batches by BUS are compared to that from MetaSparseKmeans on three batches and sparse K-means on each batch separately. “BUS 391” indicates that we use all of the 391 intrinsic genes identified by BUS to carry out pathway analysis. “BUS 203” corresponds to using the top 203 genes with the highest intrinsic gene indicators learned by BUS. “-” represents that the corresponding BIOCARTA pathway is not significant for the corresponding method. The numbers displayed in the table are q-values.

Pathway name	BUS 391	BUS 203	MetaSparseKmeans	TCGA	Wang	Desmedt
HER2	1.74 × 10^− 3	3.32 × 10^− 4	—	—	0.0078	—
LONGEVITY	1.04 × 10^− 3	2.39 × 10^− 3	—	—	—	—
RANMS	2.54 × 10^− 3	0.0168	0.0229	—	—	—
BAD	0.029	4.94 × 10^− 3	—	—	—	—
IL7	9.17 × 10^− 3	—	—	—	—	—
CARDIACEGF	1.04 × 10^− 3	2.39 × 10^− 3	—	—	—	—
TEL	1.04 × 10^− 3	2.39 × 10^− 3	—	—	—	—
COMP	—	0.0403	—	—	—	—
MTA3	0.0116	2.42 × 10^− 3	—	—	—	—
IGF1	0.0143	2.89 × 10^− 3	—	—	—	—
CELLCYCLE	1.04 × 10^− 3	3.32 × 10^− 4	—	—	—	—
SRCRPTP	—	—	0.0255	—	—	—
MCM	—	0.0403	6.47 × 10^− 6	—	—	—
G1	0.0265	5.56 × 10^− 3	0.0427	—	—	—
G2	—	—	0.0367	—	—	—
P27	—	—	0.0472	—	—	—
PTC1	—	—	0.0287	—	—	—
ERK	2.79 × 10^− 3	—	—	—	—	—
P53	8.55 × 10^− 3	2.39 × 10^− 3	—	—	—	—
CTCF	0.0172	—	—	—	—	—
KERATINOCYTE	—	0.0203	—	—	—	—
HSP27	—	0.0328	—	—	—	—
BCELLSURVIVAL	—	0.0347	—	—	—	—
STATHMIN	—	0.0403	—	—	—	—
IGF1MTOR	—	0.0419	—	—	—	—
MIOCHONDRIA	—	0.0419	—	—	—	—
TFF	—	0.0419	—	—	—	—
IL6	—	0.0437	—	—	—	—

It is noteworthy that the two-stage approach ComSpa learn more than 4000 intrinsic genes for the same dataset. Such a large number of intrinsic genes tends to include many false discoveries, and it exceeds the largest number of genes allowed for the pathway analysis on http://software.broadinstitute.org/gsea/msigdb/annotate.jsp.

We also use the original 391 intrinsic genes called by BUS to conduct pathway analyses on the BioCarta (see the column “BUS 391” in Table 2), KEGG and GO biological processes, respectively (see supplementary Tables S3 to S5). For the KEGG database, there are 58 significant pathways including the KEGG_ERBB_SIGNALING_PATHWAY (q-value: 6.02 × 10^{− 3}), which plays a crucial role in the development of breast cancer, KEGG_MAPK_SIGNALING_PATHWAY (q-value: 5.76 × 10^{− 5}), and KEGG_PHOSPHATIDYLINOSITOL_SIGNALING_SYSTEM (q-value: 0.0181), which are activated by most ErbBs receptors, and the KEGG_PATHWAYS_IN_CANCER (q-value: 1.33 × 10^{− 11}). Meanwhile, more than 100 GO biological processes are significantly enriched. Most of them pertain to the cell cycle, cell proliferation, cell death, cell differentiation, cell communication, all of which are potential factors related to the induction of breast cancer.

The pathway analyses very convincingly show that BUS provides biologically and clinically valid subtyping and outperforms MetaSparseKmeans, let alone sparse K-means applied to individual batch separately.

7. Discussion

To the best of our knowledge, BUS is the first method to explicitly model batch effects and discover underlying subtypes at the same time. Scientifically, BUS is able to integrate batches measured from different platforms in which subtypes can be present on some but not all batches. Statistically, BUS leverages information across batches to estimate subtype effects and borrows strength across genes to cluster subtypes, thus providing robust and legitimate inferences. Computationally, BUS overcomes the factorial growth of computation time, and its computational complexity only grows linearly with the batch number and subtype number. Moreover, BUS models the additive and multiplicative batch effects explicitly. Consequently, we can easily filter the two types of batch effects directly from the raw input data. The corrected data are robust to sample misclassification and can be used for downstream analysis as if they originate from a single batch.

Theoretically, we prove that BUS is identifiable when all subtypes are measured on each batch. In addition, we offer two very convenient experimental designs where subtypes are allowed to be measured on a subset of batches, and we prove the model identifiability under each scenario. We hope these results will provide researchers more freedom and flexibility in designing valid studies that can be protected from batch effects.

During the review period for this article, Jacob et al. (2016) proposed approaches to remove unwanted factors with unknown information of batches or biological phenotypes. However, their approaches require control genes whose expressions are known to be irrelevant to the factors of interest and/or control samples that have replicates in all batches, and their methods can work only when the control genes or control samples are available. Practically, incorporating control genes or control samples can be challenging. In contrast, BUS does not require any control genes, and the experimental designs suggested by Theorems 2 and 3 are more flexible than those that use control samples. BUS only asks for batch information. In real datasets, batch information can often be obtained directly or indirectly such as by tracking series numbers of the assayed arrays or sequencing experiments. Therefore, the requirement of known batch information is not very restrictive. In addition, as mentioned above, BUS explicitly models the batch effects and offers the capability of sample clustering.

BUS serves as a general framework for batch effects correction when unknown subtypes are present. It can be further tailored to adapt to the distributions from other types of high-throughput datasets such as DNA methylation microarrays, next-generation bulk sequencing data, and single-cell sequencing data. In BUS, we assume that given a batch the gene expression profile for a sample follows a mixture of multivariate normal distributions (see Equation (2.3(2.3) $$\begin{array}{ccc}\hfill {\mathbf{Y}}_j& \sim & {\pi }_1\mathbf{N}({\mathbf{m}}_1,\Sigma )+{\pi }_2\mathbf{N}({\mathbf{m}}_2,\Sigma )+\cdots \hfill \\ & & +{\pi }_K\mathbf{N}({\mathbf{m}}_K,\Sigma ),\text{iid}j=1,\dots ,n,\hfill \end{array}$$(2.3) )). In the same spirit, we can adopt a mixture of beta distributions (Ji et al. 2005) to model the DNA methylation values that are between zero and one, a mixture of multivariate Poisson distributions (Karlis and Meligkotsidou 2007) to fit RNA-seq count data, and a mixture of zero-inflated Poisson distributions to account for dropout events in the single-cell RNA-seq experiments. Nevertheless, the exact implementations of BUS for each of the above data types, such as computation with nonconjugate priors, are beyond the scope of this article, and they will be our future research directions. For now, to apply the current version of BUS to RNA-seq data and DNA methylation data for convenience, we can first transform the data and then apply BUS to the transformed values. We provide an example of RNA-seq data as a proof of principle in the supplementary materials Section S5.

Given the statistical power and computation efficiency of BUS, we believe that BUS will become a powerful tool. On the one hand, its ability to correct batch effects will substantially facilitate preprocessing of the enormous amount of noisy, heterogenous data in public databases and thus speed up mining of such rich data resources for valid scientific discoveries. On the other hand, its capability to identify subtypes will also help identify subgroups of patients. We provide BUS as a user-friendly free Bioconductor package BUScorrect, and we envision it will be widely adopted in the era of personalized medicine.

Supplementary Materials

The supplementary materials provide technical details and figures referred in the article as well as the datasets used in simulation studies and real application.

Appendix: Proofs

A1. Theorem 1

Proof.

Writing $\mathbf{Y}=\{{\mathbf{Y}}_b,1\le b\le B\}$, then the marginal distribution of $f\left({\mathbf{Y}}_b\right|\Theta )$ reduces to a Gaussian mixture model on batch b. Therefore, the BUS model can be viewed as a combination of B Gaussian mixture models sharing common parameters $\alpha ,{\mu }_1,\dots ,{\mu }_K$ (${\mu }_1=\mathbf{0}$). In other words, we can consider it as B Gaussian mixture models each with parameter sets $\{{\alpha }^{\left(b\right)},{\mu }_2^{\left(b\right)},\dots ,{\mu }_K^{\left(b\right)},{\gamma }_b,{\sigma }_b\}$ under the constraint that ${\mu }_k^{\left(1\right)}=\cdots ={\mu }_k^{\left(B\right)}={\mu }_k$ for each k and ${\alpha }^{\left(1\right)}=\cdots ={\alpha }^{\left(B\right)}=\alpha$.

Within Gaussian mixture model b, it is identifiable (up to label switching) (Yakowitz and Spragins 1968; Ritter 2014), so there exists a permutation of {1, 2, …, K}, ρ^(b), such that ${\pi }_{bk}={\pi }_{b{\rho }^{\left(b\right)}\left(k\right)}^{*},{\sigma }_b={\sigma }_b^{*},$${\alpha }^{\left(b\right)}+{\mu }_k^{\left(b\right)}+{\gamma }_b={\alpha }^{*\left(b\right)}+{\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*\left(b\right)}+{\gamma }_b^{*}.$ Because ${\alpha }^{\left(b\right)}=\alpha ,{\alpha }^{*\left(b\right)}={\alpha }^{*},{\mu }_k^{\left(b\right)}={\mu }_k,$ and ${\mu }_k^{*\left(b\right)}={\mu }_k^{*}$, we have (A.1) $$\alpha +{\mu }_k+{\gamma }_b={\alpha }^{*}+{\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}+{\gamma }_b^{*}.$$(A.1) Recall that ${\mu }_1=\mathbf{0}$, let k = 1 in Equation (A.1(A.1) $$\alpha +{\mu }_k+{\gamma }_b={\alpha }^{*}+{\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}+{\gamma }_b^{*}.$$(A.1) ), then we have (A.2) $$\alpha +{\gamma }_b={\alpha }^{*}+{\mu }_{{\rho }^{\left(b\right)}\left(1\right)}^{*}+{\gamma }_b^{*},$$(A.2) Combining Equation (A.1(A.1) $$\alpha +{\mu }_k+{\gamma }_b={\alpha }^{*}+{\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}+{\gamma }_b^{*}.$$(A.1) ) and Equation (A.2(A.2) $$\alpha +{\gamma }_b={\alpha }^{*}+{\mu }_{{\rho }^{\left(b\right)}\left(1\right)}^{*}+{\gamma }_b^{*},$$(A.2) ) leads to ${\mu }_k={\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}-{\mu }_{{\rho }^{\left(b\right)}\left(1\right)}^{*}$ for every b, k. Specifically, ${\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}-{\mu }_{{\rho }^{\left(b\right)}\left(1\right)}^{*}={\mu }_{{\rho }^{\left(1\right)}\left(k\right)}^{*}-{\mu }_{{\rho }^{\left(1\right)}\left(1\right)}^{*}$ for every b and k. By Assumption I, ρ^(b) = ρ⁽¹⁾ for each b. Now denote ρ = ρ⁽¹⁾ = ⋅⋅⋅ = ρ^(B), we have π_bk = π*_bρ(k), and $\alpha +{\mu }_k+{\gamma }_b={\alpha }^{*}+{\mu }_{\rho \left(k\right)}^{*}+{\gamma }_b^{*}$ for each b, k. In Equation (A.1(A.1) $$\alpha +{\mu }_k+{\gamma }_b={\alpha }^{*}+{\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}+{\gamma }_b^{*}.$$(A.1) ), let (k, b) = (1, 1) and k = 1, respectively, then $$\begin{array}{ccc}\hfill \alpha & =& {\alpha }^{*}+{\mu }_{\rho \left(1\right)}^{*},\hfill \\ \hfill \alpha +{\gamma }_b& =& {\alpha }^{*}+{\mu }_{\rho \left(1\right)}^{*}+{\gamma }_b^{*}.\hfill \end{array}$$Consequently, we have ${\gamma }_b={\gamma }_b^{*}$. Therefore, BUS is identifiable (up to label switching).

A2. Theorem 2

Proof.

We just need to prove that ρ^(b)(k) = ρ⁽¹⁾(k) for each k ∈ C_b (b ⩾ 2). Note that Equation (A.1(A.1) $$\alpha +{\mu }_k+{\gamma }_b={\alpha }^{*}+{\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}+{\gamma }_b^{*}.$$(A.1) ) still holds for k ∈ C_b. In Equation (A.1(A.1) $$\alpha +{\mu }_k+{\gamma }_b={\alpha }^{*}+{\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}+{\gamma }_b^{*}.$$(A.1) ), let b = 1 and since ${\gamma }_1=\mathbf{0}$, then (A.3) $$\alpha +{\mu }_k={\alpha }^{*}+{\mu }_{{\rho }^{\left(1\right)}\left(k\right)}^{*},\forall k\in C_b.$$(A.3) Equation (A.1(A.1) $$\alpha +{\mu }_k+{\gamma }_b={\alpha }^{*}+{\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}+{\gamma }_b^{*}.$$(A.1) ) minus Equation (A.3(A.3) $$\alpha +{\mu }_k={\alpha }^{*}+{\mu }_{{\rho }^{\left(1\right)}\left(k\right)}^{*},\forall k\in C_b.$$(A.3) ) gives ${\gamma }_b={\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}-{\mu }_{{\rho }^{\left(1\right)}\left(k\right)}^{*}+{\gamma }_b^{*}$ for every k ∈ C_b. Therefore, for any distinct k₁, k₂ ∈ C_b, we have ${\mu }_{{\rho }^{\left(b\right)}\left(k_2\right)}^{*}-{\mu }_{{\rho }^{\left(b\right)}\left(k_1\right)}^{*}={\mu }_{{\rho }^{\left(1\right)}\left(k_2\right)}^{*}-{\mu }_{{\rho }^{\left(1\right)}\left(k_1\right)}^{*}$, which implies that ρ^(b)(k) = ρ⁽¹⁾(k) for each k ∈ C_b by Assumption I.

A3. Theorem 3

Proof.

Our goal is to prove that, given a batch b, for each $k\in {\bigcup }_{i\ne b}\left(C_b\cap C_i\right)$, assuming k also belongs to $C_{\tilde{b}}$, the equation ${\rho }^{\left(b\right)}\left(k\right)={\rho }^{\left(\tilde{b}\right)}\left(k\right)$ always holds. We separate the proof into two steps.

We first prove ρ^(b)(k) = ρ^{(b − 1)}(k) for each $k\in C_b\cap C_{b-1}$. Note that (A.4) $$\alpha +{\mu }_k+{\gamma }_b={\alpha }^{*}+{\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}+{\gamma }_b^{*}k\in C_b,$$(A.4) (A.5) $$\alpha +{\mu }_k+{\gamma }_{b-1}={\alpha }^{*}+{\mu }_{{\rho }^{(b-1)}\left(k\right)}^{*}+{\gamma }_{b-1}^{*}k\in C_{b-1}.$$(A.5) Let Equation (A.4(A.4) $$\alpha +{\mu }_k+{\gamma }_b={\alpha }^{*}+{\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}+{\gamma }_b^{*}k\in C_b,$$(A.4) ) minus (A.5(A.5) $$\alpha +{\mu }_k+{\gamma }_{b-1}={\alpha }^{*}+{\mu }_{{\rho }^{(b-1)}\left(k\right)}^{*}+{\gamma }_{b-1}^{*}k\in C_{b-1}.$$(A.5) ) for $k\in C_b\cap C_{b-1}$, and then we have (A.6) $${\gamma }_b-{\gamma }_{b-1}={\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}-{\mu }_{{\rho }^{(b-1)}\left(k\right)}^{*}+{\gamma }_b^{*}-{\gamma }_{b-1}^{*}.$$(A.6) For each distinct $k_1,k_2\in C_b\cap C_{b-1}$, Equation (A.6(A.6) $${\gamma }_b-{\gamma }_{b-1}={\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}-{\mu }_{{\rho }^{(b-1)}\left(k\right)}^{*}+{\gamma }_b^{*}-{\gamma }_{b-1}^{*}.$$(A.6) ) implies that ${\mu }_{{\rho }^{\left(b\right)}\left(k_2\right)}^{*}-{\mu }_{{\rho }^{\left(b\right)}\left(k_1\right)}^{*}={\mu }_{{\rho }^{(b-1)}\left(k_2\right)}^{*}-{\mu }_{{\rho }^{(b-1)}\left(k_1\right)}^{*}$. By Assumption I, we proved ρ^(b)(k) = ρ^{(b − 1)}(k) provided that $k\in C_b\cap C_{b-1}$.

Second, for any $k\in {\bigcup }_{i\ne b}\left(C_b\cap C_i\right)$, there exists a $\tilde{b}\ne b$ such that $k\in C_{\tilde{b}}$. Without loss of generality, we assume $\tilde{b}<b$. From the two equations $$\begin{array}{ccc}& & \alpha +{\mu }_k+{\gamma }_{\tilde{b}}={\alpha }^{*}+{\mu }_{{\rho }^{\left(\tilde{b}\right)}\left(k\right)}^{*}+{\gamma }_{\tilde{b}}^{*},\hfill \\ & & \alpha +{\mu }_k+{\gamma }_b={\alpha }^{*}+{\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}+{\gamma }_b^{*},\hfill \end{array}$$we have that (A.7) $${\gamma }_b-{\gamma }_{\tilde{b}}={\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}-{\mu }_{{\rho }^{\left(\tilde{b}\right)}\left(k\right)}^{*}+{\gamma }_b^{*}-{\gamma }_{\tilde{b}}^{*}.$$(A.7) Meanwhile, ρ^(b)(k) = ρ^{(b − 1)}(k) for $k\in C_b\cap C_{b-1}$ proven in the first step turns Equation (A.6(A.6) $${\gamma }_b-{\gamma }_{b-1}={\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}-{\mu }_{{\rho }^{(b-1)}\left(k\right)}^{*}+{\gamma }_b^{*}-{\gamma }_{b-1}^{*}.$$(A.6) ) into $${\gamma }_b-{\gamma }_{b-1}={\gamma }_b^{*}-{\gamma }_{b-1}^{*},$$for each b ⩾ 2. As a result, ${\gamma }_b-{\gamma }_{\tilde{b}}={\sum }_{i=\tilde{b}}^{b-1}({\gamma }_{i+1}-{\gamma }_i)={\sum }_{i=\tilde{b}}^{b-1}({\gamma }_{i+1}^{*}-{\gamma }_i^{*})={\gamma }_b^{*}-{\gamma }_{\tilde{b}}^{*}$. Consequently, ${\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}-{\mu }_{{\rho }^{\left(\tilde{b}\right)}\left(k\right)}^{*}=0$ according to Equation (A.7(A.7) $${\gamma }_b-{\gamma }_{\tilde{b}}={\mu }_{{\rho }^{\left(b\right)}\left(k\right)}^{*}-{\mu }_{{\rho }^{\left(\tilde{b}\right)}\left(k\right)}^{*}+{\gamma }_b^{*}-{\gamma }_{\tilde{b}}^{*}.$$(A.7) ). By Assumption I, ${\rho }^{\left(b\right)}\left(k\right)={\rho }^{\left(\tilde{b}\right)}\left(k\right)$. Thus, we have proved the identifiability in Theorem 3.