A Particle Method for Solving Fredholm Equations of the First Kind

Abstract

Fredholm integral equations of the first kind are the prototypical example of ill-posed linear inverse problems. They model, among other things, reconstruction of distorted noisy observations and indirect density estimation and also appear in instrumental variable regression. However, their numerical solution remains a challenging problem. Many techniques currently available require a preliminary discretization of the domain of the solution and make strong assumptions about its regularity. For example, the popular expectation maximization smoothing (EMS) scheme requires the assumption of piecewise constant solutions which is inappropriate for most applications. We propose here a novel particle method that circumvents these two issues. This algorithm can be thought of as a Monte Carlo approximation of the EMS scheme which not only performs an adaptive stochastic discretization of the domain but also results in smooth approximate solutions. We analyze the theoretical properties of the EMS iteration and of the corresponding particle algorithm. Compared to standard EMS, we show experimentally that our novel particle method provides state-of-the-art performance for realistic systems, including motion deblurring and reconstruction of cross-section images of the brain from positron emission tomography.

Keywords:

• Expectation maximization
• Indirect density estimation
• Inverse problems
• Monte Carlo methods
• Positron emission tomography

1 Introduction

We consider Fredholm equations of the first kind of the form(1) $$h(y)={\int }_{\mathbb{X}}f(x)g(y|x)\mathrm{d}x\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\forall y\in \mathbb{Y},$$(1) with f(x) and h(y) probability densities on $\mathbb{X}$ and $\mathbb{Y}$, respectively, and $g(y|x)$ the density of a Markov kernel from $\mathbb{X}$ to $\mathbb{Y}$. Given g and (some characterization of) h, we aim to estimate f. Our particular interest is the setting in which we have access to a collection of samples from h, rather than the function itself.

This class of equations has numerous applications in statistics and applied mathematics. For example, h might correspond to a mixture model for which we wish to estimate its mixing distribution, f, from samples from h. This problem is known as density deconvolution or indirect density estimation (Delaigle, 2008; Ma, 2011; Pensky et al., 2017; Yang et al., 2020). In epidemiology, (1) links the incidence curve of a disease to the observed number of cases (Goldstein et al., 2009; Gostic et al., 2020; Marschner, 2020). In instrumental variable regression and causal inference, Fredholm equations can be used to estimate a nonlinear regression function or identify causal effects in the presence of confounders (Hall et al., 2005; Miao et al., 2018). Since the seminal work of Vardi et al. (1985); Vardi and Lee (1993), Fredholm equations have also been widely used in positron emission tomography. In this and similar contexts, f corresponds to an image which needs to be inferred from noisy measurements (Aster et al., 2018; Clason et al., 2019; Snyder et al., 1992; Zhang et al., 2019).

In most interesting cases, Fredholm integral equations of the first kind are ill-posed and it is necessary to introduce a regularizer to obtain a unique solution. Solving the regularized problem remains computationally very challenging. For certain subclasses of this problem, such as density deconvolution (Delaigle, 2008) good methods exist and can achieve optimal convergence rates as the number of observations increases (Carroll and Hall, 1988). However, generally applicable approaches which do not assume a particular form of g typically require discretization of the domain, $\mathbb{X}$, which restricts their applications to low-dimensional scenarios, and often assume a piecewise-constant solution (Burger et al., 2019; Koenker and Mizera, 2014; Ma, 2011; Tanana et al., 2016; Yang et al., 2020). This is the case for the popular Expectation Maximization Smoothing (EMS) scheme (Silverman et al., 1990), a smoothed version of the infinite dimensional expectation maximization algorithm of Kondor (1983).

In this paper, our contributions are three-fold. First, we provide novel theoretical results for the EMS scheme on continuous spaces, establishing that it admits a fixed point under weak assumptions. Second, we propose a novel particle version of EMS which does not suffer from the limitations of the original scheme. This Monte Carlo algorithm provides an adaptive stochastic discretization of the domain and outputs a sample approximation of f through which a smooth approximation can be obtained via a natural kernel density estimation procedure. Although this algorithm is related to sequential Monte Carlo (SMC) methods which have been widely used to perform inference for complex Bayesian models (Chopin and Papaspiliopoulos, 2020; Del Moral, 2013; Douc et al., 2014; Doucet and Johansen, 2011; Liu and Chen, 1998; Liu, 2001), standard SMC convergence results do not apply to this scheme so we also provide an original theoretical analysis of the algorithm. Third, we demonstrate this algorithm on both illustrative examples and realistic image processing applications.

The rest of this paper is organized as follows. In Section 2, we review Fredholm integral equations of the first kind and the EMS algorithm, and establish existence of a fixed point for the continuous version. In Section 3, we introduce a particle approximation of the EMS recursion and provide convergence results for this scheme. We demonstrate the application of the algorithm in Section 4 and then briefly conclude.

2 Fredholm equations and EMS

2.1 Fredholm integral equations of the first kind

We recall that we consider equations of the form (1). We concern ourselves in particular with the case in which

(A0) $\mathbb{X}\subset {\mathbb{R}}^{d_{\mathbb{X}}}$ and $\mathbb{Y}\subset {\mathbb{R}}^{d_{\mathbb{Y}}}$ are compact subsets of Euclidean spaces, g can be evaluated pointwise and a sample, Y, from h is available.

In most applications the space $\mathbb{H}=\mathbb{X}\times \mathbb{Y}\subset {\mathbb{R}}^{d_{\mathbb{X}}\times d_{\mathbb{Y}}}$ is closed and bounded and (A0) is satisfied. For instance, in image processing both $\mathbb{X}$ and $\mathbb{Y}$ are typically of the form $[-a,a]\times [-b,b]$ for $a,b>0$, f and h are continuous densities on $\mathbb{X}$ and $\mathbb{Y}$, respectively. In applications the analytic form of h is often unknown, and the available data arise from discretization of h over $\mathbb{Y}$, as in, e.g., Vardi and Lee (1993), or from sampling, as in, e.g. Ma (2011). In the image processing context, the available data are usually either the values of h over the discretization of $\mathbb{Y}$ induced by the pixels of the image (e.g. an image with 10 × 10 pixels induces a discretization on $\mathbb{Y}$ in which the intervals $[-a,a]$ and $[-b,b]$ are each divided into 10 bins) or samples from h. We focus here on the sampling case.

Considering (1) in the context of probability densities is not too restrictive. A wider class of integral equations can be recast in this framework by appropriate normalizations and translations, provided that f and h are bounded below (Chae et al., 2018, Section 6).

As the set of probability densities on $\mathbb{X}$ is not finite, if the kernel g is not degenerate then the resulting integral equation is in general ill-posed (Kress, 2014, Theorem 15.4). Fredholm’s alternative (see, e.g., (Kress, 2014, Corollary 4.18)) gives a criterion to assess the existence of solutions of (1); however, the lack of continuous dependence on h causes the solutions to be unstable and regularization techniques are needed (Kress, 2014; Groetsch, 2007). Common methods are Tikhonov regularization (Tikhonov, 1963) and iterative methods (Landweber, 1951; Kondor, 1983). See Yuan and Zhang (2019) for a recent review.

2.2 Expectation Maximization and Related Algorithms

2.2.1 Expectation Maximization

From a statistical point of view, (1) describes an indirect density estimation problem: the mixing density f has to be recovered from the mixture h. This can in principle be achieved by maximizing an incomplete data likelihood for f through the Expectation Maximization (EM) algorithm (Dempster et al., 1977). Nevertheless, the maximum likelihood estimator is not consistent, as the parameter to be estimated (i.e. f) is infinite dimensional (Laird, 1978); a problem aggravated by the ill-posedness of (1) (Silverman et al., 1990).

We briefly review a number of iterative schemes based on the EM algorithm which aim to find approximate solutions of (1) through regularization. The starting point is the iterative method of Kondor (1983), an infinite dimensional EM algorithm,(2) $$f_{n+1}(x)=f_n(x)\int \frac{g(y|x)}{\int f_n(z)g(y|z)\mathrm{d}z}h(y)\mathrm{d}y,$$(2) which minimizes the Kullback–Leibler divergence,(3) $$\text{KL}\left(h,{\int }_{\mathbb{X}}f(x)g(·|x)\mathrm{d}x\right)={\int }_{\mathbb{Y}}h(y)\hspace{0.17em}\text{log}\hspace{0.17em}\left(\frac{h(y)}{{\int }_{\mathbb{X}}f(x)g(y|x)\mathrm{d}x}\right)\mathrm{d}y,$$(3) with respect to f over the set of probability densities on $\mathbb{X}$ (Mülthei et al., 1989). Minimizing (3) is equivalent to maximizing$$\Lambda (f):={\int }_{\mathbb{Y}}h(y)\hspace{0.17em}\text{log}\hspace{0.17em}{\int }_{\mathbb{X}}f(x)g(y|x)\mathrm{d}x\mathrm{d}y,$$ a continuous version of the incomplete data log-likelihood for the function f (Mülthei et al., 1989). This scheme has several good properties, iterating (2) monotonically decreases (3) (Mülthei et al., 1987, Theorem 7) and if the iterative formula converges, then the limit is a minimizer of (3) (Mülthei et al., 1987, Theorem 8) — but the minimizer need not be unique. Convergence of the EM iteration (2) to a fixed point has been proved under the existence of a sequence ${(f_s^{\star })}_{s\ge 1}$ with $h_s^{\star }(y)={\int }_{\mathbb{X}}{f}_s^{\star }(x)g(y|x)\mathrm{d}x$, such that $\text{KL}(h,h_s^{\star })$ converges to the infimum of (3) and additional integrability conditions (Chae et al., 2018).

In general, implementing the recursive formula (2) analytically is not possible and discretization schemes are needed. Under the assumption of piecewise constant densities f, h and g, with the discretization grid fixed in advance, the EM recursion (2) reduces to the EM algorithm for Poisson data (Vardi and Lee, 1993), known as the Richardson–Lucy (RL) algorithm in the image processing field (Richardson, 1972; Lucy, 1974), where the intensities of pixels are modeled as Poisson counts,(4) $$f_b^{(n+1)}=f_b^{(n)}\sum _{d=1}^D\left(\frac{h_d{g}_{bd}}{\sum _{k=1}^B{f}_k^{(n)}{g}_{kd}}\right),$$(4) here f_b for $b=1,\dots ,B$ and h_d for $d=1,\dots ,D$ are the constant values over the deterministic discretization of the space for f and h respectively.

The Iterative Bayes (IB) algorithm of Ma (2011) considers the case in which only samples from h are available. These samples are used to build a kernel density estimator (KDE) for h, which is then plugged into the discretized EM iteration (4).

As discussed earlier, despite being popular and easy to implement, the EM algorithm (4) has a number of drawbacks: after a certain number of iterations the EM approximations deteriorate resulting in unstable estimates that lack smoothness and give spiky estimates of f (Silverman et al., 1990; Nychka, 1990); in fact minimizing (3) does not deal with the ill-posedness of the problem and regularization is needed (Byrne and Eggermont, 2015).

A natural way to introduce regularization is via maximum penalized likelihood estimation (MPLE; see, e.g. Green (1990)), maximizing, for some penalty term, P:$$\Lambda \prime (f):={\int }_{\mathbb{Y}}h(y)\hspace{0.17em}\text{log}\hspace{0.17em}{\int }_{\mathbb{X}}f(x)g(y|x)\mathrm{d}x\mathrm{d}y-P(f).$$

In most cases, an updating formula like (4) cannot be obtained straightforwardly for MPLE because the derivative of P(f) usually involves several derivatives of f. A possible solution is to update the estimate of f from iteration f_n to $f_{n+1}$ evaluating the penalty term at f_n , rather than at the new value $f_{n+1}$. This is known as the one-step late (OSL) algorithm (Green, 1990). The resulting update formula is usually easier to compute but there is no guarantee that each iteration will increase the penalized log-likelihood. However, if convergence occurs, the OSL algorithm converges more quickly than the corresponding EM for the penalized likelihood.

2.2.2 Expectation Maximization Smoothing

An easy-to-implement regularized version of the EM recursion (4) is the EMS algorithm of Silverman et al. (1990), an EM-like algorithm in which a smoothing matrix $\mathrm{K}$ is applied to the EM estimates at each iteration(5) $$f_b^{(n+1)}=\sum _{\kappa =1}^B{\mathrm{K}}_{b\kappa }{f}_{\kappa }^{(n)}\sum _{d=1}^D\left(\frac{h_d{g}_{\kappa d}}{\sum _{k=1}^B{f}_k^{(n)}{g}_{kd}}\right).$$(5)

The EMS algorithm has long been attractive from a practical point of view as the addition of the smoothing step to the EM recursion (4) gives good empirical results, with convergence occurring empirically in a relatively small number of iterations (e.g. Silverman et al. (1990); Li et al. (2017); Becker et al. (1991)).

Under mild conditions on the smoothing matrix the discretized EMS recursion (5) has a fixed point (Latham and Anderssen, 1992). In addition, with a particular choice of smoothing matrix, the fixed point of (5) minimizes a penalized likelihood with a particular roughness penalty (Nychka, 1990). With this choice of penalty, the OSL and the EMS recursion have the same fixed point (Green, 1990). Fan et al. (2011) establish convergence of (5) to local-EM, an EM algorithm for maximum local-likelihood estimation, when the smoothing kernel is a symmetric positive convolution kernel with positive bandwidth and bounded support. If the space on which the EMS mapping is defined is bounded, the discrete EMS mapping is globally convergent for sufficiently large bandwidth.

The focus of this work is a continuous version of the EMS recursion, in which we do not discretize the space and use smoothing convolutions $Kf(·):={\int }_{\mathbb{X}}K(u,·)f(u)\mathrm{d}u$ in place of smoothing matrices, i.e.(6) $$f_{n+1}(x)={\int }_{\mathbb{X}}K(x\prime ,x)f_n(x\prime ){\int }_{\mathbb{Y}}\frac{g(y|x\prime )h(y)}{{\int }_{\mathbb{X}}{f}_n(z)g(y|z)\mathrm{d}z}\mathrm{d}y\mathrm{d}x\prime .$$(6)

2.3 Properties of the Continuous EMS Recursion

Contrary to the discrete EMS map (5), relatively little is known about the continuous EMS mapping. We prove, under the following assumptions, that it also admits a fixed point in the space of probability distributions:

(A1)The density of the kernel $g(y|x)$ is continuous and bounded away from 0 and $\infty$:$$\exists m_g>0\mathrm{ }\text{such}\mathrm{ }\text{that}0<m_g^{-1}\le g(y|x)\le m_g<\infty \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\forall (x,y)\in \mathbb{X}\times \mathbb{Y}.$$

(A2)The smoothing kernel is specified via a continuous bounded density, T, over ${\mathbb{R}}^{d_{\mathbb{X}}}$, such that $\underset{v\in \mathbb{X}}{\inf }{\int }_{\mathbb{X}}T(u-v)\mathrm{d}u>0$ as:$$K(v,u)=\frac{T(u-v){\mathbb{I}}_{\mathbb{X}}(u)}{{\int }_{\mathbb{X}}T(u\prime -v)\mathrm{d}u\prime }.$$

Assumption (A1) is common in the literature on Fredholm integral equations as continuity of g rules out degenerate integral equations which require special treatment (Kress, 2014, Chapter 5). The boundedness condition on g ensures the existence of a minimizer of (3) (Mülthei, 1992, Theorem 1). Assumption (A2) on T is mild and is satisfied by most commonly used kernels for density estimation (Silverman, 1986) and implies that $K(v,·)$ is a density over $\mathbb{X}$ for any fixed v. We can draw samples from $K(v,·)$, e.g. by rejection sampling whenever T is proportional to a density from which sampling is feasible.

The EMS map describes one iteration of this algorithm, for a probability density f,$${\mathrm{F}}_{\mathit{EMS}}:f\mapsto {\mathrm{F}}_{\mathit{EMS}}f:={\int }_{\mathbb{X}}f(x\prime )K(x\prime ,·){\int }_{\mathbb{Y}}\frac{g(y|x\prime )h(y)}{{\int }_{\mathbb{X}}f(z)g(y|z)\mathrm{d}z}\mathrm{d}y\mathrm{d}x\prime .$$

It is the composition of linear smoothing by the kernel K defined in (A2) and the non-linear map corresponding to the EM iteration, ${\mathrm{F}}_{EM}$,(7) $${\mathrm{F}}_{EM}(f)(x)=\frac{{\overline{G}}_f(x)f(x)}{f({\overline{G}}_f)}\text{where}{\overline{G}}_f(·):={\int }_{\mathbb{Y}}\frac{g(y|·)h(y)}{{\int }_{\mathbb{X}}f(z)g(y|z)\mathrm{d}z}\mathrm{d}y$$(7) and we introduce the normalizing constant $f({\overline{G}}_f)\equiv 1$ to highlight the connection with the particle methods introduced in Section 3 (here and elsewhere we adopt the convention that for any suitable integrable function, $\phi$, and probability or density, f, $f(\phi )=\int f(x)\phi (x)\mathrm{d}x$). That is, ${\mathrm{F}}_{EM}$ corresponds to a simple reweighting of a probability, with the weight being given by ${\overline{G}}_f$.

The existence of the fixed point of ${\mathrm{F}}_{\mathit{EMS}}$ is established in the supplementary material using results from non-linear functional analysis. This result is obtained taking h to be any probability distribution over $\mathbb{Y}$, and shows that a fixed point exists both in the case in which h admits a density and that in which h is the empirical distribution of a sample Y — the latter is common in applications, and is the setting we are concerned with.

Proposition 1.

Under (A0), (A1)and (A2), the EMS map, ${\mathrm{F}}_{\mathit{EMS}}$, has a fixed point in the space of probability distributions over $\mathbb{X}$.

3 Particle implementation of the EMS Recursion

In order to make use of the continuous EMS recursion in practice, it is necessary to approximate the integrals which it contains. To do so, we develop a particle method specialized to our context via a stochastic interpretation of the recursion.

3.1 Particle methods

Particle methods also known as Sequential Monte Carlo (SMC) methods are a class of Monte Carlo methods that sequentially approximate a sequence of target probability densities ${\{{\eta }_n(z_{1:n})\}}_{n\ge 1}$ defined on the product spaces ${\mathbb{H}}^n$ of increasing dimension, whose evolution is described by Markov transition kernels M_n and positive potential functions G_n (Del Moral, 2013)(8) $${\eta }_{n+1}(z_{1:n+1})\propto {\eta }_n(z_{1:n})G_n(z_n)M_{n+1}(z_{n+1}|z_n).$$(8)

These sequences naturally arise in state space models (e.g. Liu and Chen (1998); Doucet and Johansen (2011); Li et al. (2016)) and many inferential problems can be described by (8) (see, e.g., Liu (2001); Chopin and Papaspiliopoulos (2020), and references therein).

The approximations of η_n for $n\ge 1$ are obtained through a population of Monte Carlo samples, called particles. The population consists of a set of N weighted particles ${\{Z_n^i,W_n^i\}}_{i=1}^N$ which evolve in time according to the dynamic in (8). Given the equally weighted population at time n – 1, ${\{{\tilde{Z}}_{n-1}^i,\frac{1}{N}\}}_{i=1}^N$, new particle locations $Z_n^i$ are sampled from $M_n(·|{\tilde{Z}}_{n-1}^i)$ to obtain the equally weighted population at time n, ${\{Z_n^i,\frac{1}{N}\}}_{i=1}^N$. Then, the fitness of the new particles is measured through $G_n$, which gives the weights $W_n^i$. The new particles are then replicated or discarded using a resampling mechanism, giving the equally weighted population at time n, ${\{{\tilde{Z}}_n^i,\frac{1}{N}\}}_{i=1}^N$. Several resampling mechanisms have been considered in the literature ((Douc et al., 2014, page 336), Gerber et al. (2019)) the simplest of which consists of sampling the number of copies of each particle from a multinomial distribution with weights ${\left\{W_n^i\right\}}_{i=1}^N$ (Gordon et al., 1993).

At each n, the empirical distribution of the particle population provides an approximation of the marginal distribution of Z_n under ${\eta }_n$ via ${\eta }_n^N=N^{-1}{\sum }_{i=1}^N{\delta }_{Z_n^i}.$ Throughout, in the interests of brevity, we will abuse notation slightly and treat ${\eta }_n^N$ as a density, allowing ${\delta }_{x_0}(x)\mathrm{d}x$ to denote a probability concentrated at x₀. These approximations possess various convergence properties (e.g. Del Moral (2013)), in particular ${\mathbb{L}}_p$ error estimates and a strong law of large numbers for the expectations ${\eta }_n^N(\phi ):={\int }_{\mathbb{H}}{\eta }_n^N(u)\phi (u)\mathrm{d}u=N^{-1}{\sum }_{i=1}^N\phi (Z_n^i)$ of sufficiently regular test functions $\phi$ (Crisan and Doucet, 2002; Míguez et al., 2013).

3.2 A stochastic interpretation of EMS

The EMS recursion (6) can be modeled as a sequence of densities satisfying (8) by considering an extended state space. Denote by ${\eta }_n$ the joint density at $(x,y)\in \mathbb{H}$ defined by ${\eta }_n(x,y)=f_n(x)h(y)$ so that $f_n(x)={\eta }_n{|}_{\mathbb{X}}(x)={\int }_{\mathbb{Y}}{\eta }_n(x,y)\mathrm{d}y$. This density satisfies a recursion similar to that in (6)(9) $${\eta }_{n+1}(x,y)={\int }_{\mathbb{X}}{\int }_{\mathbb{Y}}{\eta }_n(x\prime ,y\prime )K(x\prime ,x)h(y)\frac{g(y\prime |x\prime )}{{\int }_{\mathbb{X}}{f}_n(z)g(y\prime |z)\mathrm{d}z}\mathrm{d}y\prime \mathrm{d}x\prime .$$(9)

With a slight abuse of notation, we denote by η_n the joint density of $(x_{1:n},y_{1:n})\in {\mathbb{H}}^n$ obtained by iterative application of (9) with the integrals removed.

Proposition 2.

The sequence of densities ${\left\{{\eta }_n\right\}}_{n\ge 1}$ defined over the product spaces ${\mathbb{H}}^n={(\mathbb{X}\times \mathbb{Y})}^n$ by (8) with $z_n:=(x_n,y_n)$,(10) $$M_{n+1}\left((x_{n+1},y_{n+1})|(x_n,y_n)\right)=K(x_n,x_{n+1})h(y_{n+1})$$(10) and(11) $$G_n(x_n,y_n)=\frac{g(y_n|x_n)}{{\int }_{\mathbb{X}}{\eta }_n{|}_{\mathbb{X}}(z)g(y_n|z)\mathrm{d}z}$$(11) satisfies, marginally, recursion (9). In particular, the marginal distribution over x_n of ${\eta }_n$,(12) $${\eta }_n{|}_{\mathbb{X}}(x_n)={\int }_{\mathbb{Y}}{\int }_{{\mathbb{H}}^{n-1}}{\eta }_n\left(x_{1:n},y_{1:n}\right)\mathrm{d}{x}_{1:n-1}\mathrm{d}{y}_{1:n}={\int }_{\mathbb{Y}}{\eta }_n\left(x_n,y_n\right)\mathrm{d}{y}_n$$(12) satisfies recursion (6) with the identification $f_n(x)={\eta }_n{|}_{\mathbb{X}}(x)$.

Proof.

Starting from (8) with $M_{n+1}$ and $G_n$ as in (10)-(11)(13) $${\eta }_{n+1}(x_{1:n+1},y_{1:n+1})=\frac{{\eta }_n(x_{1:n},y_{1:n})G_n(x_n,y_n)}{{\eta }_n(G_n)}{M}_{n+1}\left((x_{n+1},y_{n+1})|(x_n,y_n)\right),$$(13) where ${\eta }_n(G_n):={\int }_{\mathbb{H}}{\eta }_n(x_n,y_n)G_n(x_n,y_n)\mathrm{d}{x}_n\mathrm{d}{y}_n=1$, and integrating out $(x_{1:n},y_{1:n})$ $$\begin{array}{c}\begin{array}{l}{\eta }_{n+1}(x_{n+1},y_{n+1})\\ =\underset{{\mathbb{H}}^n}{{\displaystyle \int }}\frac{{\eta }_n(x_{1:n},y_{1:n})G_n(x_n,y_n)}{{\eta }_n(G_n)}{M}_{n+1}((x_{n+1},y_{n+1})|(x_n,y_n))\text{d}{x}_{1:n}\text{d}{y}_{1:n}\\ =\underset{\mathbb{H}}{{\displaystyle \int }}\{\underset{{\mathbb{H}}^{n-1}}{{\displaystyle \int }}{\eta }_n(x_{1:n},y_{1:n})\text{d}{x}_{1:n-1}\text{d}{y}_{1:n-1}\\ \times \frac{g(y_n|x_n)}{{{\displaystyle \int }}^{\text{}}{\eta }_n{|}_{\mathbb{X}}(z)g(y_n|z)\text{d}z}K(x_n,x_{n+1})h(y_{n+1})\}\text{d}{x}_n\text{d}{y}_n\\ =\underset{\mathbb{H}}{{\displaystyle \int }}\{{\eta }_n(x_n,y_n)\frac{g(y_n|x_n)}{{{\displaystyle \int }}^{\text{}}{\eta }_n{|}_{\mathbb{X}}(z)g(y_n|z)\text{d}z}\\ \times K(x_n,x_{n+1})h(y_{n+1})\}\text{d}{x}_n\text{d}{y}_n.\end{array}\end{array}$$

We can then compute the marginal over $\mathbb{X},{\eta }_{n+1}{|}_{\mathbb{X}}$ $$\begin{array}{c}{\eta }_{n+1}{|}_{\mathbb{X}}(x_{n+1})={\int }_{\mathbb{Y}}{\eta }_{n+1}(x_{n+1},y_{n+1})\mathrm{d}{y}_{n+1}\\ ={\int }_{\mathbb{Y}}h(y_{n+1})\mathrm{d}{y}_{n+1}{\int }_{\mathbb{H}}{\eta }_n(x_n,y_n)\frac{g(y_n|x_n)}{\int {\eta }_n{|}_{\mathbb{X}}(z)g(y_n|z)\mathrm{d}z}K(x_n,x_{n+1})\mathrm{d}{x}_n\mathrm{d}{y}_n\\ ={\int }_{\mathbb{X}}{\eta }_n{|}_{\mathbb{X}}(x_n)K(x_n,x_{n+1}){\int }_{\mathbb{Y}}h(y_n)\frac{g(y_n|x_n)}{\int {\eta }_n{|}_{\mathbb{X}}(z)g(y_n|z)\mathrm{d}z}\mathrm{d}{y}_n\mathrm{d}{x}_n\end{array}$$which, with the given identifications, satisfies the EMS recursion (6). □

To facilitate the theoretical analysis we separate the contribution of the mutation kernels (10) and of the potential functions (11), in particular, we denote the weighted distribution obtained from η_n by ${\Psi }_{G_n}({\eta }_n)(x_n,y_n):={\eta }_n(x_n,y_n)G_n(x_n,y_n)/{\eta }_n(G_n)$.

3.3 A particle method for EMS

Having shown that the EMS recursion describes a sequence of densities satisfying (8), it is possible to use SMC techniques to approximate this recursion. This involves replacing the true density at each step with a sample approximation obtained at the previous iteration, giving rise to Algorithm 1, which describes the case in which only a fixed number of samples from h are available and in line 1-2 we draw $Y_n^i$ from their empirical distribution; when sampling freely from h is feasible one could instead draw these samples from it.

The resulting SMC scheme is not a standard particle approximation of (8), because of the definition of the potential (11). Indeed, $G_n$ cannot be computed exactly, because ${\eta }_n{|}_{\mathbb{X}}$ is not known. The SMC scheme provides an approximation for ${\eta }_n{|}_{\mathbb{X}}$ at time n. Let us denote by ${\eta }_n^N{|}_{\mathbb{X}}$ the particle approximation of the marginal ${\eta }_n{|}_{\mathbb{X}}$ in (12)$${\eta }_n^N{|}_{\mathbb{X}}:={\int }_{\mathbb{Y}}{\eta }_n^N\left(·,y_n\right)\mathrm{d}{y}_n=\frac{1}{N}\sum _{i=1}^N{\delta }_{X_n^i}.$$

We can approximate$$G_n(x_n,y_n)=\frac{g(y_n|x_n)}{h_n(y_n)}=\frac{g(y_n|x_n)}{{\int }_{\mathbb{X}}{\eta }_n{|}_{\mathbb{X}}(z)g(y_n|z)\mathrm{d}z}$$using the particle approximation of the denominator $h_n(y_n):={\int }_{\mathbb{X}}{f}_n(z)g(y|z)\mathrm{d}z$,(14) $$h_n^N(y_n):=\frac{1}{N}\sum _{i=1}^{N}g(y_n|X_n^i)={\eta }_n^N{|}_{\mathbb{X}}\left(g(y_n|·)\right),$$(14) to obtain the approximate potentials(15) $$G_n^N(x_n,y_n):=\frac{g(y_n|x_n)}{h_n^N(y_n)}.$$(15)

Algorithm 1: Particle Method for Fredholm Equations of the First Kind

At time n = 1

1 Sample ${\tilde{X}}_1^i\sim f_1,{\tilde{Y}}_1^i$ uniformly from Y for $i=1,\dots ,N$ and set $W_1^i=\frac{1}{N}$

At time n > 1

2 Sample $X_n^i\sim K({\tilde{X}}_{n-1}^i,·)$ and $Y_n^i$ uniformly from Y for $i=1,\dots ,N$

3 Compute the approximated potentials $G_n^N(X_n^i,Y_n^i)$ in (15) and obtain the normalized weights $W_n^i=G_n^N(X_n^i,Y_n^i)/{\sum }_{j=1}^N{G}_n^N(X_n^j,Y_n^j)$

4 (Re)Sample $\left\{(X_n^i,Y_n^i),W_n^i\right\}$ to get $\left\{({\tilde{X}}_n^i,{\tilde{Y}}_n^i),\frac{1}{N}\right\}$ for $i=1,\dots ,N$

5 Estimate $f_{n+1}(x)$ as in (17)

The use of $G_n^N$ within the importance weighting step corresponds to an additional approximation which is not found in standard SMC algorithms. In particular, (15) are biased estimators of the true potentials (11). As a consequence, it is not possible to use arguments based on extensions of the state space (as in particle filters using unbiased estimates of the potentials (Liu and Chen, 1998; Del Moral et al., 2006; Fearnhead et al., 2008)) to provide theoretical guarantees for this SMC scheme. If $G_n$ itself were available then it would be preferable to make use of it; in practice this will never be the case but the idealized algorithm which employs such a strategy is of use for theoretical analysis.

At time n + 1, we estimate $f_{n+1}(x)$ by computing a kernel density estimate (KDE) of the weighted particle approximation$${\Psi }_{G_n^N}({\eta }_n^N){|}_{\mathbb{X}}:=\sum _{i=1}^N\frac{G_n^N(X_n^i,Y_n^i)}{\sum _{j=1}^N{G}_n^N(X_n^j,Y_n^j)}{\delta }_{X_n^i},$$and then applying the EMS smoothing kernel K. This approach may seem counter-intuitive but the KDE kernel and the EMS kernel are fulfilling different roles. The KDE gives a good smooth approximation of the density associated with the EMS recursion at a point in that recursion which we expect to be under-smoothed and is driven by the usual considerations of KDE when obtaining a smooth density approximation from an empirical distribution; going on to apply the EMS smoothing kernel is simply part of the EMS regularization procedure. One could instead apply kernel density estimation after step 2 of the subsequent iteration of the algorithm but this would simply introduce additional Monte Carlo variance, with the described approach corresponding to a Rao-Blackwellisation of that slightly simpler strategy. Using the kernel of Fredholm equations of the second kind to extract smooth approximations of their solution from Monte Carlo samples has also been found empirically to perform well (Doucet et al., 2010). Depending on the intended use of the approximation, the KDE step can be omitted entirely; the empirical distribution provides a good (in the sense of Proposition 4) approximation to that given by the EMS recursion but one which does not admit a density.

We consider standard $d_{\mathbb{X}}$-dimensional kernels for KDE, $u\mapsto s_N{}^{-d_{\mathbb{X}}}|\Sigma {|}^{-1/2}S({(s_N{}^2\Sigma )}^{-1/2}u)$, where $s_N$ is the smoothing bandwidth and S is a continuous bounded symmetric density (Silverman, 1986). To account for the dependence between samples, when computing the bandwidth, $s_N$, instead of N we use the effective sample size (Kong et al., 1994)(16) $$\text{ESS}={\left(\sum _{i=1}^N{G}_n^N{(X_n^i,Y_n^i)}^2\right)}^{-1}{\left(\sum _{j=1}^N{G}_n^N(X_n^j,Y_n^j)\right)}^2.$$(16)

The resulting estimator,(17) $$f_{n+1}^N(x)={\int }_{\mathbb{X}}K(x\prime ,x)\sum _{i=1}^N\frac{G_n^N(X_n^i,Y_n^i)}{\sum _{j=1}^N{G}_n^N(X_n^j,Y_n^j)}{s}_N{}^{-d_{\mathbb{X}}}|\Sigma {|}^{-1/2}S\left({\left(s_N{}^2\Sigma \right)}^{-1/2}(X_n^i-x\prime )\right)\mathrm{d}x\prime ,$$(17) satisfies the standard KDE convergence results in ${\mathbb{L}}_1$ and in ${\mathbb{L}}_2$ (see Section 3.4.2).

As the EMS recursion (6) aims at finding a fixed point, after a certain number of iterations the approximation of f provided by the SMC scheme stabilizes. We could therefore average over approximations obtained at different iterations to get more stable reconstructions. When the storage cost is prohibitive, a thinned set of iterations could be used.

In principle, one could reduce the variance of associated estimators by using a different proposal distribution within Algorithm 1 just as in standard particle methods (see, e.g., (Doucet and Johansen, 2011, Section 25.4.1)) but this proved unnecessary in all of the examples which we explored as we obtained good performances with this simple generic scheme (the effective sample size was above 70% in all the examples considered). Another strategy to reduce the variance of the estimators would be to implement the quasi-Monte Carlo version of SMC (Gerber and Chopin, 2015) which is particularly efficient in the relatively low-dimensional settings typically found in the context of Fredholm equations.

3.3.1 Algorithmic Setting

Algorithm 1 requires specification of a number of parameters. The initial density, f₁, must be specified but we did not find performance to be sensitive to this choice (see Section E.1 in the supplementary material). We advocate choosing f₁ to be a diffuse distribution with support intended to include that of f because the resampling step allows SMC to more quickly forget overly diffuse initializations than overly concentrated ones. For problems with bounded domains, choosing f₁ to be uniform over $\mathbb{X}$ is a sensible default choice.

We propose to stop the iteration in Algorithm 1 when the difference between successive approximations, measured through the ${\mathbb{L}}_2$ norm of the reconstruction of h obtained by convolution of $f_n^N$ with g, ${\widehat{h}}_n^N(y):={\int }_{\mathbb{X}}{f}_n^N(x)g(y|x)\mathrm{d}x$, is smaller than the variability due to the Monte Carlo approximation of (6)(18) $${\int }_{\mathbb{Y}}{\left|{\widehat{h}}_{n+1}^N(y)-{\widehat{h}}_n^N(y)\right|}^2\mathrm{d}y<\text{var}\left(\zeta (f_k^N);k=n+1-m,\dots n+1\right),$$(18) where ζ is some function of the estimator $f_{n+1}^N$ and we consider its variance over the last m iterations. The term on the left-hand side is an indicator of whether the EMS recursion (6) has reached a fixed point, while the variance takes into account the error introduced by approximating (6) through Monte Carlo. For given N there is a point at which further increasing n does not improve the estimate because Monte Carlo variability dominates. We employ this stopping rule in the PET example in Section 4.2.

The amount of regularization introduced by the smoothing step is controlled by the smoothing kernel K. In principle, any density T can be used to specify K as in (A2); we opted for isotropic Gaussian kernels since in this case the integral in (17) can be computed analytically with an appropriate choice of S. In this case, the amount of smoothing is controlled by the variance ${\epsilon }^2$. If the expected smoothness of the fixed point of the EMS recursion (6) is known, ε should be chosen so that (17) matches this knowledge. If no information is known on the expected smoothness, the level of smoothing introduced could be picked by cross validation, comparing, e.g., the reconstruction accuracy or smoothness. In addition, one could allow extra flexibility by letting K change at each iteration: e.g., allowing larger moves in early iterations can be beneficial in standard SMC settings to improve stability and ergodicity; alternatively one could choose the smoothing parameter adaptively using information on the smoothness of the current estimate.

We end this section by identifying a further degree of freedom which can be exploited to improve performance: a variance reduction can be achieved by averaging over several $Y_n^i$ when computing the approximated potentials $G_n^N$. At time n, draw M samples $Y_n^{ij},j=1,\dots ,M$ without replacement for each particle $i=1,\dots ,N$ and compute the approximated potentials by averaging over the M replicates$$G_n^{N,M}(X_n^i,Y_n^i)=\frac{1}{M}\sum _{j=1}^M\frac{g(Y_n^{ij}|X_n^i)}{h_n^N(Y_n^{ij})}.$$

This incurs an O(MN) computational cost and can be justified by further extending the state space to $\mathbb{X}\times {\mathbb{Y}}^M$. Unfortunately, the results on the optimal choice of M obtained for pseudo-marginal methods (e.g. Pitt et al. (2012)) cannot be applied here, as the estimates of $G_n$ given by (15) are not unbiased. In the examples shown in Section 4 we resample without replacement M samples from Y where M is the smallest between N and the size of Y, but smaller values of M could be considered (see Section E.1 in the supplement).

3.3.2 Comparison with EMS

The discretized EMS (5) and Algorithm 1 both approximate the EMS recursion (6). There are two main aspects under which the SMC implementation of EMS is an improvement with respect to the one obtained by brute-force discretization: the information on h which is needed to run the algorithm and the scaling with the dimensionality of the domain of f.

The discretized EMS (5) requires the value of h on each of the D bins of the space discretization of $\mathbb{Y}$, when we only have a sample Y from h, as it is the case in most applications (Delaigle, 2008; Miao et al., 2018; Goldstein et al., 2009; Gostic et al., 2020; Marschner, 2020; Hall et al., 2005), h should then be approximated through a histogram or a kernel density estimator as in the Iterative Bayes algorithm (Ma, 2011). On the contrary, Algorithm 1 does not require this additional approximation and naturally deals with samples from h. In Section 4.1 we show on a one dimensional example that the brute-force discretization (5) struggles at recovering the shape of a bimodal distribution while the SMC implementation achieves much better performances in terms of accuracy. In addition, increasing the number of bins for EMS has a milder effect on the accuracy than increasing the number of particles in the SMC implementation.

Similar considerations apply when $\mathbb{X},\mathbb{Y}$ are higher dimensional (i.e. $d_{\mathbb{X}}\ge 2$). The number of bins B in the EMS recursion (5) necessary to achieve reasonable accuracy increases exponentially with $d_{\mathbb{X}}$, resulting in higher runtime which quickly exceed those needed to run Algorithm 1. On the contrary the convergence rate for SMC remains $N^{-1/2}$, and although the associated constants may grow with $d_{\mathbb{X}}$, its performance is shown empirically to scale better with dimension than EMS in the supplementary material.

3.4 Convergence properties

As the potentials (11) cannot be computed exactly but need to be estimated, the convergence results for standard SMC (e.g., Del Moral (2013)) do not hold. We present here a strong law of large numbers (SLLN) and ${\mathbb{L}}_p$ error estimates for our particle approximation of the EMS and also provide theoretical guarantees for the estimator (17).

3.4.1 Strong law of large numbers

For simplicity, we only consider multinomial resampling (Gordon et al., 1993). Lower variance resampling schemes can be employed but considerably complicate the theoretical analysis ((Douc et al., 2014, page 336), Gerber et al. (2019)). Compared to the SLLN proof for standard SMC methods, we need to analyze here the contribution of the additional approximation introduced by using $G_n^N$ instead of $G_n$ and then combine the results with existing arguments for standard SMC; see, e.g., Míguez et al. (2013).

The SSLN is stated in Corollary 1. This result follows from the ${\mathbb{L}}_p$ inequality in Proposition 3, the proof of which is given in the supplementary material and follows the inductive argument of Crisan and Doucet (2002); Míguez et al. (2013). Both results are proved for bounded measurable test functions $\phi$, a set we denote ${\mathcal{B}}_b(\mathbb{H})$.

As a consequence of (A1), the potentials $G_n$ and $G_n^N$ are bounded and bounded away from 0 (see Lemma 1 in the supplement), a strong mixing condition that is common in the SMC literature and is satisfied in most of the applications which we have considered.

Proposition 3

(${\mathbb{L}}_p$-inequality). Under (A0), (A1)and (A2), for every $n\ge 1$ and every $p\ge 1$ there exist finite constants ${\widehat{C}}_{p,n},{\tilde{C}}_{p,n}$ such that(19) $$\mathbb{E}{\left[|{\Psi }_{G_n^N}({\eta }_n^N)(\phi )-{\Psi }_{G_n}({\eta }_n)(\phi ){|}^p\right]}^{1/p}\le {\widehat{C}}_{p,n}\frac{\Vert \phi \Vert }{\infty }\sqrt{N}$$(19) (20) $$\text{and}\mathbb{E}{\left[|{\eta }_n^N(\phi )-{\eta }_n(\phi ){|}^p\right]}^{1/p}\le {\tilde{C}}_{p,n}\frac{\Vert \phi \Vert \infty }{\sqrt{N}},$$(20) for every bounded measurable function $\phi \in {\mathcal{B}}_b(\mathbb{H})$, where the expectations are taken with respect to the law of all random variables generated within the SMC algorithm.

The SLLN follows from the ${\mathbb{L}}_p$-inequality using a standard Borel-Cantelli argument (see, e.g. (Boustati et al., 2020, Appendix D) for a reference in the context of SMC):

Corollary 1 (Strong law of large numbers). Under (A0), (A1)and (A2), for all $n\ge 1$ and for every $\phi \in {\mathcal{B}}_b(\mathbb{H})$, we have almost surely as $N\to \infty$:$${\Psi }_{G_n^N}({\eta }_n^N)(\phi )\to {\Psi }_{G_n}({\eta }_n)(\phi )\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\text{and}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\eta }_n^N(\phi )\to {\eta }_n(\phi ).$$

A standard approach detailed in the supplementary material yields convergence of the sequence ${\left\{{\eta }_n^N\right\}}_{n\ge 1}$ itself, showing that the particle approximations of the distributions converge to the sequence in (13), whose marginal over x satisfies the EMS recursion (6).

Proposition 4.

Under (A0), (A1)and (A2), for all $n\ge 1,{\eta }_n^N$ converges weakly to ${\eta }_n$ with probability 1.

3.4.2 Convergence of kernel density estimator

Under standard assumptions on the bandwidth $s_N$ we can show that the estimator $f_{n+1}^N(x)$ converges in ${\mathbb{L}}_1$ to $f_{n+1}(x)$ and its mean integrated square error (MISE) goes to 0 as N goes to infinity as shown in the supplementary material:

Proposition 5.

Under (A0), (A1)and (A2), if $s_N\to 0$ as $N\to \infty ,f_{n+1}^N$ converges almost surely to $f_{n+1}$ in ${\mathbb{L}}_1$ for every $n\ge 1$:(21) $$\underset{N\to \infty }{\lim }{\int }_{\mathbb{X}}|f_{n+1}^N(x)-f_{n+1}(x)|\mathrm{d}x\stackrel{\mathrm{a}.\mathrm{s}.}{=}0;$$(21)

and the MISE satisfies(22) $$\underset{N\to \infty }{\lim }\text{MISE}(f_{n+1}^N)\equiv \underset{N\to \infty }{\lim }\mathbb{E}\left[{\int }_{\mathbb{X}}|f_{n+1}^N(x)-f_{n+1}(x){|}^2\mathrm{d}x\right]=0.$$(22)

4 Examples

This section shows the results obtained using the SMC implementation of the recursive formula (6) on some common examples. Two additional examples are investigated in the supplementary material. We consider a simple density estimation problem and a realistic example of image restoration in positron emission tomography (Webb, 2017). In the first example, the analytic form of h is known and is used to implement the discretized EM and EMS. IB and SMC are implemented using a fixed sample Y drawn from h. For image restoration problems we consider the observed distorted image as the empirical distribution of a sample Y from h and resample from it at each iteration of line 2 in Algorithm 1.

The initial distribution f₁ is uniform over $\mathbb{X}$ and the number of iterations is either fixed to n = 100 (we observed that convergence occurs in a smaller number of steps for all algorithms; see Section E.1 in the supplement) or determined using the stopping criterion (18). For the smoothing kernel K, we use isotropic Gaussian kernels with marginal variance ${\epsilon }^2$. The bandwidth $s_N$ is the plug-in optimal bandwidth for Gaussian distributions where the effective sample size (16) is used instead of the sample size N (Silverman, 1986, page 45).

The deterministic discretization of EM and EMS ((4) and (5) respectively) is obtained by considering B equally spaced bins for $\mathbb{X}$ and D for $\mathbb{Y}$. The number of bins, and the number of particles, N, for SMC vary between examples. In the first example, the choice of D, B and N is motivated by a comparison of error and runtime. For the image restoration problems, D, B are the number of pixels in each image, while the number of particles N is chosen to achieve a good trade-off between reconstruction accuracy and runtime.

For the SMC implementation, we use the adaptive multinomial resampling scheme described by (Liu, 2001, page 35). At each iteration the effective sample size (16) is evaluated and multinomial resampling is performed if $\text{ESS}<N/2$. This choice is motivated by the fact that up to adaptivity (which we anticipate could be addressed by the approach of Del Moral et al. (2012)) this is the setting considered in the theoretical analysis of Section 3.4 and we observed only modest improvements when using lower variance resampling schemes (e.g. residual resampling, see Liu (2001)) instead of multinomial resampling. The accuracy of the reconstructions is measured through the integrated square error(23) $$\text{ISE}(f_{n+1}^N)={\int }_{\mathbb{X}}{\left(f(x)-f_{n+1}^N(x)\right)}^2\mathrm{d}x.$$(23)

Although the density estimation example of Section 4.1 does not satisfy conditions (A0) or (A1) under which our theoretical guarantees hold; we nonetheless observe good results in terms of reconstruction accuracy and smoothness, demonstrating that assumption (A1) is not necessary and could be relaxed (see also Section G in the supplementary material). The other examples do satisfy all of our theoretical assumptions.

4.1 Indirect density estimation

The first example is the Gaussian mixture model used in Ma (2011) to compare the Iterative Bayes (IB) algorithm with EM. Take $\mathbb{X}=\mathbb{Y}=\mathbb{R}$ (although note that $|1-{\int }_0^{1}f(x)\mathrm{d}x|<{10}^{-30}$ and restricting out attention to $[0,1]$ would not significantly alter the results) and$$\begin{array}{c}f(x)=\frac{1}{3}\mathcal{N}(0.3,{0.015}^2)+\frac{2}{3}\mathcal{N}(0.5,{0.043}^2),\\ g(y|x)=\mathcal{N}(x,{0.045}^2),\\ h(y)=\frac{1}{3}\mathcal{N}(0.3,{0.045}^2+{0.015}^2)+\frac{2}{3}\mathcal{N}(0.5,{0.045}^2+{0.043}^2).\end{array}$$

The initial distribution f₁ is Uniform on $[0,1]$ and the bins for the discretized EMS are B equally spaced intervals in $[0,1]$, noting that discretization schemes essentially require known compact support and this interval contains almost all of the probability mass. We run Algorithm 1 assuming that we have a sample Y of size 10³ from h from which we re-sample $M=\min (N,{10}^3)$ times without replacement at each iteration of line 2. We analyze the influence of the number of bins B and of the number of particles N on the integrated square error and on the runtime for the deterministic discretization of EMS (5) and for the SMC implementation of EMS (Figure 1). We compare the two implementations of EMS with a class of estimators for deconvolution problems, deconvolution kernel density estimators with cross validated bandwidth (DKDE-cv; Stefanski and Carroll (1990)) and plug-in bandwidth (DKDE-pi; Delaigle and Gijbels (2004))¹. These estimators take as input a sample from h of size N and output a kernel density estimator for f.

Fig. 1 Average $\text{ISE}(f_{n+1}^N)$ and runtime for 1,000 repetitions of discretized EMS, SMC and DKDE. The number of bins and of particles/samples N ranges between 10² and 10⁴.

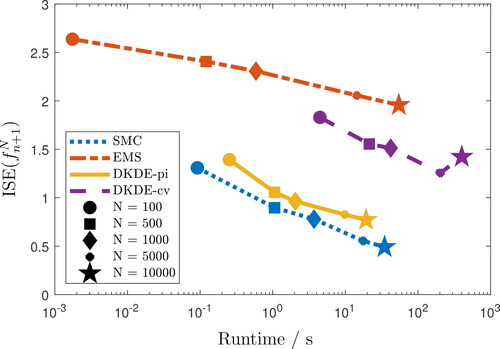
The discretized EMS has the lowest runtime for fixed N, however $\text{ISE}(f_{n+1}^N)$ is the highest and finer discretizations for EMS do not significantly improve accuracy. The runtime of DKDE are closer to those of the SMC implementation, however, the SMC implementation gives better results in terms of $\text{ISE}(f_{n+1}^N)$ for any particle size and, indeed, for given computational cost. We set $\epsilon ={10}^{-3}$, for both EMS and SMC, somewhat arbitrarily, based on the support of the target in this example; where that is not possible cross validation could be used — and might be expected to provide better reconstructions — at the expense of some additional computational cost. We did not find solutions overly sensitive to the precise value of ε (see Appendix E.1 in the supplementary material). A significant portion of the runtime of DKDE-cv is needed to obtain the bandwidth through cross validation and in this sense the comparison may not be quite fair, but the use of the much cheaper plug-in estimates of bandwidth within DKDE-pi also led to poorer estimates at given cost than those provided by the SMC-EMS algorithm.

Secondly, we compare the reconstructions provided by the proposed SMC scheme with those given by deterministic discretization of the EM iteration (4) with exact h and when only samples are available (IB) and deterministic discretization of the EMS iteration (5).

Having observed a small decrease in $\text{ISE}(f_{n+1}^N)$ for large B, we fix the number of bins $B=D=100$. For the SMC scheme, we compare N = 500, N = 1, 000 and N = 5, 000. We discard N = 10, 000, as it shows little improvement in $\text{ISE}(f_{n+1}^N)$ with respect to N = 5, 000, and N = 100, because of the higher $\text{ISE}(f_{n+1}^N)$. We draw a sample Y from h of size 10³ and we use this sample to get a kernel density estimator for the IB algorithm, compute the DKDE and (re)sample points at line 2 of Algorithm 1.

We set $\epsilon ={10}^{-3}$ and compare the smoothing matrix obtained by discretization of the Gaussian kernel (EMS ($\mathrm{K}$)) with the three-point smoothing proposed in (Silverman et al., 1990, Section 3.2.2), where the value $f_b^{(n+1)}$ is obtained by a weighted average over the values $f_{\kappa }^{(n)}$ of the two nearest neighbors (the third point is $f_b^{(n)}$), with weights proportional to the distance $|\kappa -b|$ $${\mathrm{K}}_{b\kappa }=2^{-2}\left(\begin{array}{c}3-1\\ \kappa -b+(3-1)/2\end{array}\right).$$

The reconstruction process is repeated 1,000 times and the reconstructions are compared by computing their means and variances, the integrated squared error (23) and the Kullback–Leibler divergence between h and the reconstruction of h obtained by convolution of $f_{n+1}^N$ with g, ${\int }_{\mathbb{X}}{f}_{n+1}^N(x)g(y|x)\mathrm{d}x$, (Table 1). To characterize the roughness of $f_{n+1}^N$, we evaluate both $f_{n+1}^N$ and f at the 100 bin centers x_c and for each bin center we approximate (with 1,000 replicates) the mean squared error (MSE)(24) $$\text{MSE}(x_c)=\mathbb{E}\left[{\left(f(x_c)-f_{n+1}^N(x_c)\right)}^2\right].$$(24)

Table 1 Estimates of mean, variance, ISE, 95th-percentile of MSE, KL-divergence and runtime for 1,000 repetitions of EM, EMS, IB, SMC and DKDE for the Gaussian mixture example. The mean of f is 0.43333, the variance is 0.010196. Bold indicates best values.

	Mean	Variance	$\text{ISE}(f_{n+1}^N)$	$\text{MSE}(x_c)$	KL	${\hspace{0.17em}\text{log}\hspace{0.17em}}_{10}$
				(95th)		Runtime / s
EM	0.36667	0.010	3.26	16.32	2299	-6.01
EMS (K)	0.36646	0.012	2.41	8.20	2355	−5.90
EMS (3-point)	0.3668	0.011	1.58	13.04	2303	−5.88
IB	0.43304	0.011	1.71	10.17	2489	−5.29
SMC (500)	0.43303	0.011	0.90	3.42	2484	0.63
SMC (1000)	0.43302	0.011	0.78	3.33	2483	1.87
SMC (5000)	0.43302	0.011	0.55	2.17	2485	3.47
DKDE-pi	0.43288	0.012	0.96	3.38	2483	0.81
DKDE-cv	0.43287	0.014	1.5	4.76	2503	4.15

Table 1 shows the 95th percentile w.r.t. the 100 bin centers x_c .

The discretized EM (4) gives the best results in terms of Kullback–Leibler divergence (restricting to the $[0,1]$ interval and computing by numerical integration). This is not surprising, as IB is an approximation of EM when the analytic form of h is not known, and the EMS algorithms (both those with the deterministic discretization (5) and those with the stochastic one given by the SMC scheme) do not seek to minimize the $\text{KL}$ divergence, but to provide a more regular solution. The solutions recovered by EM and IB have considerably higher $\text{ISE}$ than that given by the other algorithms and are considerably worse than the other algorithms at recovering the smoothness of the solution.

SMC is generally better at recovering the global shape of the solution (ISE is at least two times smaller than EM and EMS (K) and about half than EMS (3-point) and IB) and the smoothness of the solution (the 95th-percentile for $\text{MSE}(x_c)$ is at least two times smaller). For the discretized EMS (5) and the SMC implementation the estimates of the variance are higher than those of EM, this is a consequence of the addition of the smoothing step and can be controlled by selecting smaller values of ε. DKDEs behave similarly to SMC, however their reconstruction accuracy and smoothness are slightly worse than those of SMC (even when both algorithms use the same sample size N = 1, 000). In particular, DKDE-cv has runtime of the same order of that of SMC but achieves considerably worse results. IB, SMC and DKDE give similar values for the KL divergence. The slight increase observed for the SMC scheme with N = 5, 000 is apparently due to the sensitivity of this divergence to tail behaviors; taking a bandwidth independent of N eliminated this effect (results not shown).

4.2 Positron emission tomography

Positron Emission Tomography (PET) is a medical diagnosis technique used to analyze internal biological processes from radial projections to detect medical conditions such as schizophrenia, cancer, Alzheimer’s disease and coronary artery disease (Phelps, 2000).

The data distribution of the radial projections $h(\varphi ,\xi )$ is defined on $\mathbb{Y}=[0,2\pi ]\times [-R,R]$ for R > 0 and is linked to the cross-section image of the organ of interest f(x, y) defined on the 2D square $\mathbb{X}={[-r,r]}^2$ for r > 0 through the kernel g describing the geometry of the PET scanner. The Markov kernel $g(\varphi ,\xi |x,y)$ gives the probability that the projection onto $(\varphi ,\xi )$ corresponds to point (x, y) (Vardi et al., 1985) and is modeled as a zero-mean Gaussian distribution with small variance (we use ${\sigma }^2={0.02}^2$) to mimic the alignment between projections and recovered emissions (see the supplementary material). As g is defined on $\mathbb{X}\times \mathbb{Y}$ where $\mathbb{X}={[-r,r]}^2$ and $\mathbb{Y}=[0,2\pi ]\times [-R,R]$, assumption (A1) is satisfied.

The data used in this work are obtained from the reference image in the final panel of Figure 2, a simplified imitation of the brain’s metabolic activity (e.g. Vardi and Lee (1993)). The collected data are the values of h at 128 evenly spaced projections over ${360}^{°}$ and 185 values of ξ in $[-92,92]$ to which Poisson noise is added. Figure 2 shows the reconstructions obtained with the SMC scheme with smoothing parameter $\epsilon ={10}^{-3}$ and number of particles is N = 20, 000. Convergence to a fixed point occurs in less than 100 iterations, in fact the criterion (18) with $\zeta (f_n^N)={\int }_{\mathbb{X}}|f_n^N(x){|}^2\mathrm{d}x$ and m = 15 stops the iteration at n = 15. The $\text{ISE}$ between the original image and the reconstructions stabilizes around 0.08. Additional results and model details are given in the supplementary material.

Fig. 2 Reconstruction of the Shepp–Logan phantom with N = 20, 000 particles and $\epsilon =0.001$. The stopping criterion (18) is satisfied at iteration 15.

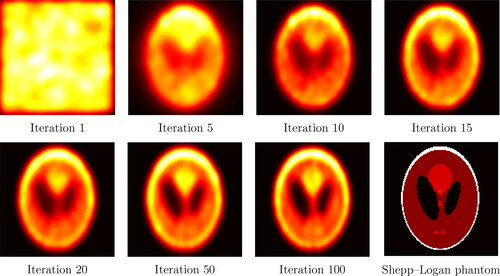
The results above show that the SMC implementation of the EMS recursion achieves convergence in a small number of steps ($\approx$ 12 minutes on a standard laptop) and that, contrary to EM (Silverman et al., 1990, Section 4.2), these reconstructions are smooth and do not deteriorate with the number of iterations. In addition, contrary to standard reconstruction methods, e.g. filtered back-projection, ordered-subset EM, Tikhonov regularization (see, e.g., Tong et al. (2010)) the SMC implementation does not require that a discretization grid is fixed in advance.

5 Conclusion

We have proposed a novel particle algorithm to solve a wide class of Fredholm equations of the first kind. This algorithm has been obtained by identifying a close connection between the continuous EMS recursion and the dynamics (8). It performs a stochastic discretization of the EMS recursion and can be naturally implemented when only samples from the distorted signal h are available. Additionally, it does not require the assumption of piecewise constant solutions common to deterministic discretization schemes.

Having established that the continuous EMS recursion admits a fixed point, we have studied the asymptotic properties of the proposed particle scheme, showing that the empirical measures obtained by this scheme converge almost surely in the weak topology to those given by the EMS recursion as the number of particles N goes to infinity. This result is a consequence of the ${\mathbb{L}}_p$ convergence of expectations and the strong law of large numbers which we extended to the particle scheme under study. We have also provided theoretical guarantees on the proposed estimator for the solution f of the Fredholm integral equation. This algorithm outperforms the state of the art in this area in several examples.

Supplementary Material

The supplementary material contains the analysis of the EMS map, proofs of all results and additional examples. MATLAB code to reproduce all examples is available online at https://github.com/FrancescaCrucinio/smcems.

Additional information

Funding

This work was supported by funding from the EPSRC and MRC OXWASP Centre for Doctoral Training EP/L016710/1, EPSRC grants EP/R034710/1 and EP/T004134/1, and the Lloyd’s Register Foundation Programme on Data-Centric Engineering at the Alan Turing Institute.

Notes

1 MATLAB code is available on the authors’ web page: https://researchers.ms.unimelb.edu.au/∼aurored/links.html\#Code