Empirical Bayes Mean Estimation With Nonparametric Errors Via Order Statistic Regression on Replicated Data

Abstract

We study empirical Bayes estimation of the effect sizes of N units from K noisy observations on each unit. We show that it is possible to achieve near-Bayes optimal mean squared error, without any assumptions or knowledge about the effect size distribution or the noise. The noise distribution can be heteroscedastic and vary arbitrarily from unit to unit. Our proposal, which we call Aurora, leverages the replication inherent in the K observations per unit and recasts the effect size estimation problem as a general regression problem. Aurora with linear regression provably matches the performance of a wide array of estimators including the sample mean, the trimmed mean, the sample median, as well as James-Stein shrunk versions thereof. Aurora automates effect size estimation for Internet-scale datasets, as we demonstrate on data from a large technology firm.

Keywords:

• Asymptotic optimality
• Empirical Bayes
• Linear regression
• L-statistics
• Nonparametric regression

1 Introduction

Empirical Bayes (EB) (Efron 2012; Robbins 1956, 1964) and related shrinkage methods are the de facto standard for estimating effect sizes in many disciplines. In genomics, EB is used to detect differentially expressed genes when the number of samples is small (Smyth 2004; Love, Huber, and Anders 2014). In survey sampling, EB improves noisy estimates of quantities, like the average income, for small communities (Rao and Molina 2015). The key insight of EB is that one can often estimate unit-level quantities better by sharing information across units, rather than analyzing each unit separately.

Formally, EB models the observed data $\mathit{Z}=(Z_1,\dots ,Z_N)$ as arising from the following generative process:(1) $${\mu }_i\sim G,Z_i|{\mu }_i\sim F(·|{\mu }_i),i=1,\dots ,N.$$(1)

The goal here is to estimate the mean parameters, ${\mu }_i:={\mathbb{E}}_F\left[Z_i|{\mu }_i\right]$ for $i=1,\dots ,N$, from the observed data $\mathit{Z}$. If G and F are fully specified, then the optimal estimator (in the sense of mean squared error) is the posterior mean ${\mathbb{E}}_{G,F}\left[{\mu }_i | Z_i\right]$, which achieves the Bayes risk. EB deals with the case where F or G is unknown, so the Bayes rule cannot be calculated. Most modern EB methods (Jiang and Zhang 2009; Brown and Greenshtein 2009; Muralidharan 2012; Saha and Guntuboyina 2020) assume that F is known (say, $F(· | {\mu }_i)=\mathcal{N}({\mu }_i,1)$) and construct estimators ${\widehat{\mu }}_i$ that asymptotically match the risk of the unknown Bayes rule, without making any assumptions about the unknown prior G.

We examine the same problem of estimating the μ_i s when the likelihood F is also unknown. Indeed, knowledge of F is an assumption that requires substantial domain expertise. For example, it took many years for the genomics community to agree on an EB model for detecting differences in gene expression based on microarray data (Baldi and Long 2001; Lönnstedt and Speed 2002; Smyth 2004). Then, once this technology was superseded by bulk RNA-Seq, the community had to devise a new model from scratch, eventually settling on the negative binomial likelihood (Love, Huber, and Anders 2014; Gierliński et al. 2015).

Unfortunately, there is no way to avoid making such strong assumptions when there is no information besides the one Z_i per μ_i . If F is even slightly underspecified, then it becomes hopeless to disentangle F from G. To appreciate the problem, consider the Normal–Normal model:(2) $$G=\mathcal{N}(0,A)F(·|{\mu }_i)=\mathcal{N}({\mu }_i,{\sigma }^2).$$(2)

Here, Z_i is marginally distributed as $\mathcal{N}(0,A+{\sigma }^2)$, and the observations Z_i only provide information about $A+{\sigma }^2$. Now, when ${\sigma }^2$ is known, A can be estimated by first estimating the marginal variance and subtracting ${\sigma }^2$. Indeed, Efron and Morris (1973) showed that by plugging in a particular estimate of A into the Bayes rule ${\mathbb{E}}_{G,F}\left[{\mu }_i | Z_i\right]=(1-\frac{{\sigma }^2}{{\sigma }^2+A})Z_i$, one recovers the celebrated James-Stein estimator (James and Stein 1961). Yet, as soon as ${\sigma }^2$ is unknown, then A (and hence, G) is unidentified, and there is no hope of approximating the unknown Bayes rule.

However, as any student of random effects knows, the Normal–Normal model (2) becomes identifiable if we simply have independent replicates Z_ij for each unit i. The driving force behind this work is an analogous observation in the context of empirical Bayes estimation: replication makes it possible to estimate μ_i with essentially no assumptions on F or G. The method we propose, described in the next section, performs well in practice and nearly matches the risk of the Bayes rule, which depends on the unknown F and G.

2 The Aurora Method

First, we formally specify the EB model when replicates $Z_{ij}\in \mathbb{R}$ are available.(3) $$\begin{array}{c}({\mu }_i,{\alpha }_i) \stackrel{\text{iid}}{\sim } G,i=1,\dots ,N\\ Z_{ij}|({\mu }_i,{\alpha }_i) \stackrel{\text{iid}}{\sim } F(·|{\mu }_i,{\alpha }_i)j=1,\dots ,K.\end{array}$$(3)

Again, the quantity of interest is the mean parameter ${\mu }_i:={\mathbb{E}}_F\left[Z_{ij}|{\mu }_i,{\alpha }_i\right]$. The additional parameter α_i is a nuisance parameter that allows for heterogeneity across the units, while preserving exchangeability (Galvao and Kato 2014; Okui and Yanagi 2020). For example, α_i is commonly taken to be the conditional variance ${\sigma }_i^2:={\text{var}}_F\left[Z_{ij}|{\mu }_i,{\alpha }_i\right]$ to allow for heteroscedasticity. However, α_i could even be infinite-dimensional—for instance, a random element from a space of distributions. The α_i have no impact on our estimation strategy and are purely a technical device.

Given data from model (3), one approach would be to collapse the replicates into a single observation per unit—say, by taking their mean—which would bring us back to the setting of model (1). We could appeal to the central limit theorem to justify knowing that the likelihood is Normal. An important message of this paper is that we can do better by using the replicates.

2.1 Proposed Method

Since we have replicates, we can split the Z_ij into two groups for each i. First, consider the case of K = 2 replicates so that we can write (X_i , Y _i ) for $(Z_{i1},Z_{i2})$. Now, X_i and Y_i are conditionally independent given $({\mu }_i,{\alpha }_i)$. Figure 1 illustrates the relationship between X_i and Y_i under two different settings. The key insight is that the conditional mean ${\mathbb{E}}_{G,F}\left[Y_i | X_i\right]$ is (almost surely) identical to the posterior mean ${\mathbb{E}}_{G,F}\left[{\mu }_i | X_i\right]$, by the following calculation (Krutchkoff 1967). (For convenience, we suppress the dependence of the expected values on G, F.)(4) $$\begin{array}{c}\mathbb{E}\left[Y_i | X_i\right]=\mathbb{E}\left[\mathbb{E}\left[Y_i | {\mu }_i,{\alpha }_i,X_i\right] | X_i\right]\\ =\mathbb{E}\left[\mathbb{E}\left[Y_i | {\mu }_i,{\alpha }_i\right] | X_i\right]=\mathbb{E}\left[{\mu }_i | X_i\right].\end{array}$$(4)

Fig. 1 EB with replicates: Two simulations with N = 1000 and K = 2. First, we draw ${\mu }_i\sim G$, where $G=\mathcal{N}(0.5,4)$ in the left panel and G is the uniform distribution on the discrete set $\left\{-3,0,3\right\}$ in the right panel. Then, for each i, we draw $X_i,Y_i | {\mu }_i \stackrel{\text{iid}}{\sim } \mathcal{N}({\mu }_i,1)$ and plot the points (X_i , Y _i ). The line shows the posterior mean $\mathbb{E}\left[{\mu }_i | X_i\right]$, which in light of (4), is identical to the conditional mean $\mathbb{E}\left[Y_i | X_i\right]$.

This suggests that we can estimate the Bayes rule based on X_i (i.e., the posterior mean $\mathbb{E}[{\mu }_i | X_i]$) by simply regressing Y_i on X_i using any black-box predictive model, such as a local averaging smoother. Let $\widehat{m}(·)$ be the fitted regression function; our estimate of each μ_i is then just ${\widehat{\mu }}_i=\widehat{m}(X_i)$.

To extend this method to K > 2, we can again split the replicates ${\mathit{Z}}_i$ into two parts:(5) $$\begin{array}{c}{\mathit{X}}_i:={\mathit{X}}_i(j):=(Z_{i1},\dots ,Z_{i(j-1)},Z_{i(j+1)},\dots ,Z_{iK})\\ Y_i:=Y_i(j):=Z_{ij},\end{array}$$(5) where $j\in \left\{1,\dots ,K\right\}$ is an arbitrary fixed index for now. (We suppress j in the notation below.) Now, one approach is to summarize the vector ${\mathit{X}}_i$ by the mean of its values ${\overline{X}}_i$ and regress Y_i on ${\overline{X}}_i$ to learn $\mathbb{E}\left[{\mu }_i | {\overline{X}}_i\right]$ (Coey and Cunningham 2019). This works for essentially the same reason as the K = 2 case. However, if ${\overline{X}}_i$ is not sufficient for $({\mu }_i,{\alpha }_i)$ in model (3) with K – 1 replicates, then $\mathbb{E}\left[{\mu }_i | {\overline{X}}_i\right]$ may be different from and suboptimal to $\mathbb{E}\left[{\mu }_i | {\mathit{X}}_i\right]$.

Instead, we propose learning $\mathbb{E}\left[{\mu }_i | {\mathit{X}}_i\right]$ directly. The rationale is contained in the following result.

Proposition 1.

Let Z_ij be generated according to Equation (3)(3) $$\begin{array}{c}({\mu }_i,{\alpha }_i) \stackrel{\text{iid}}{\sim } G,i=1,\dots ,N\\ Z_{ij}|({\mu }_i,{\alpha }_i) \stackrel{\text{iid}}{\sim } F(·|{\mu }_i,{\alpha }_i)j=1,\dots ,K.\end{array}$$(3) and assume that $\mathbb{E}[\left|{\mu }_i\right|]<\infty ,\mathbb{E}[\left|Z_{ij}\right|]<\infty$. Define ${\mathit{X}}_i$ and Y_i as in Equation (5)(5) $$\begin{array}{c}{\mathit{X}}_i:={\mathit{X}}_i(j):=(Z_{i1},\dots ,Z_{i(j-1)},Z_{i(j+1)},\dots ,Z_{iK})\\ Y_i:=Y_i(j):=Z_{ij},\end{array}$$(5) . Let ${\mathit{X}}_i^{(·)}$ be the vector of order statistics of ${\mathit{X}}_i$:$${\mathit{X}}_i^{(·)}:=\left(X_i^{(1)},\dots ,X_i^{(K-1)}\right),X_i^{(1)}\le \dots \le X_i^{(K-1)}.$$

That is, ${\mathit{X}}_i^{(·)}$ is simply a sorted version of ${\mathit{X}}_i$. Then, almost surely(6) $$\mathbb{E}\left[Y_i|{\mathit{X}}_i^{(·)}\right]=\mathbb{E}\left[{\mu }_i|{\mathit{X}}_i\right].$$(6)

Proof.

The same argument as Equation (4)(4) $$\begin{array}{c}\mathbb{E}\left[Y_i | X_i\right]=\mathbb{E}\left[\mathbb{E}\left[Y_i | {\mu }_i,{\alpha }_i,X_i\right] | X_i\right]\\ =\mathbb{E}\left[\mathbb{E}\left[Y_i | {\mu }_i,{\alpha }_i\right] | X_i\right]=\mathbb{E}\left[{\mu }_i | X_i\right].\end{array}$$(4) shows that $\mathbb{E}[Y_i|{\mathit{X}}_i^{(·)}]=\mathbb{E}[{\mu }_i|{\mathit{X}}_i^{(·)}]$ almost surely. Now, under exchangeable sampling, the order statistics ${\mathit{X}}_i^{(·)}$ are sufficient for $({\mu }_i,{\alpha }_i)$ and therefore it follows that $\mathbb{E}[{\mu }_i|{\mathit{X}}_i^{(·)}]=\mathbb{E}[{\mu }_i|{\mathit{X}}_i]$ almost surely, with no assumptions on F. □

Equation (6)(6) $$\mathbb{E}\left[Y_i|{\mathit{X}}_i^{(·)}\right]=\mathbb{E}\left[{\mu }_i|{\mathit{X}}_i\right].$$(6) suggests that we should regress Y_i on the order statistics ${\mathit{X}}_i^{(·)}$ to learn a function $\widehat{m}(·):{\mathbb{R}}^{K-1}\to \mathbb{R}$ that approximates the posterior mean. The fitted values $\widehat{m}({\mathit{X}}_i^{(·)})$ can be used to estimate μ_i . There is one more detail worth mentioning. The estimate $\widehat{m}({\mathit{X}}_i^{(·)})$ depends on the arbitrary choice of j in Equation (5)(5) $$\begin{array}{c}{\mathit{X}}_i:={\mathit{X}}_i(j):=(Z_{i1},\dots ,Z_{i(j-1)},Z_{i(j+1)},\dots ,Z_{iK})\\ Y_i:=Y_i(j):=Z_{ij},\end{array}$$(5) . To reduce the variance of the estimate, we average over all choices of $j\in \left\{1,\dots ,K\right\}$. This method, summarized in Table 1, is called Aurora, which stands for “Averages of Units by Regressing on Ordered Replicates Adaptively.”

Table 1 A summary of Aurora, which is the proposed method for estimating the means μ_i when the data come from model (3).

Aurora: “Averages of Units by Regressing on Ordered Replicates Adaptively.”
For $j\in \left\{1,\dots ,K\right\}$
1. Split the replicates for each unit, ${\mathit{Z}}_i$, into ${\mathit{X}}_i:=(Z_{i1},\dots ,Z_{i(j-1)},Z_{i(j+1)},\dots ,Z_{iK})$ and $Y_i:=Z_{ij}$, as in (5).
2. For each ${\mathbf{X}}_i$, order the values to obtain ${\mathit{X}}_i^{(·)}$.
3. Regress Yi on ${\mathit{X}}_i^{(·)}$ using any black-box predictive model. Let ${\widehat{m}}_j$ be the fitted regression function.
4. Let ${\widehat{\mu }}_{i,j}^{\text{Aur}}:={\widehat{m}}_j({\mathit{X}}_i^{(·)})$.
end
Estimate each μi by ${\widehat{\mu }}_i^{\text{Aur}}:=\frac{1}{K}{\sum }_{j=1}^K{\widehat{\mu }}_{i,j}^{\text{Aur}}$.

3 Related Work

The Aurora method is closely related to the extensive literature on empirical Bayes, which we cite throughout this paper. One work that is worth emphasizing is Stigler (1990), who motivated empirical Bayes estimators such as James-Stein, through the lens of regression to the mean; for us, regression is not just a motivation but the estimation strategy itself. We were surprised to find a similar idea to Aurora in a forgotten manuscript, uncited to date, that Johns (1986) contributed to a symposium for Herbert Robbins (Van Ryzin 1986). Although Johns (1986) used a fairly complex predictive model (projection pursuit regression, Friedman and Stuetzle 1981), we show theoretically (Sections 4 and 5) and empirically (Sections 6 and 7) that the order statistics encode enough structure that linear regression and k-nearest neighbor regression can be used as the predictive model.

Models similar to Equation (3)(3) $$\begin{array}{c}({\mu }_i,{\alpha }_i) \stackrel{\text{iid}}{\sim } G,i=1,\dots ,N\\ Z_{ij}|({\mu }_i,{\alpha }_i) \stackrel{\text{iid}}{\sim } F(·|{\mu }_i,{\alpha }_i)j=1,\dots ,K.\end{array}$$(3) with replicated noisy measurements of unobservable random quantities have been studied in the context of deconvolution and error-in-variables regression (Devanarayan and Stefanski 2002; Schennach 2004). In econometrics, panel data with random effects are often modelled as in Equation (3)(3) $$\begin{array}{c}({\mu }_i,{\alpha }_i) \stackrel{\text{iid}}{\sim } G,i=1,\dots ,N\\ Z_{ij}|({\mu }_i,{\alpha }_i) \stackrel{\text{iid}}{\sim } F(·|{\mu }_i,{\alpha }_i)j=1,\dots ,K.\end{array}$$(3) with the additional potential complication of time dependence, that is, $j=1,\dots ,K$ indexes time, while $i=1,\dots ,N$ may correspond to different geographic regions (Horowitz and Markatou 1996; Hall and Yao 2003; Neumann 2007; Jochmans and Weidner 2018). Fithian and Ting (2017) used observations from model (3) to learn a low-dimensional smooth parametric model that describes the data well. However, their goal was testing, whereas our goal is mean estimation.

The Aurora method is also related to a recent line of research that leverages black-box prediction methods to solve statistical tasks that are not predictive in nature. For example, Chernozhukov et al. (2018) considered inference for low dimensional causal quantities when high dimensional nuisance components are estimated by machine learning. Boca and Leek (2018) reinterpreted the multiple testing problem in the presence of informative covariates as a regression problem and estimated the proportion of null hypotheses conditionally on the covariates. The estimated conditional proportion of null hypotheses may then be used for downstream multiple testing methods (Ignatiadis and Huber 2021). Black-box regression models can also be used to improve empirical Bayes point estimates in the presence of side-information (Ignatiadis and Wager 2019).

Finally, a crucial ingredient in Aurora is data splitting, which is a classical idea in statistics (Cox 1975), typically used to ensure honest inference for low-dimensional parameters. In the context of simultaneous inference, Rubin, Dudoit, and Van der Laan (2006) and Habiger and Peña (2014) used data-splitting to improve power in multiple testing.

4 Properties of the Aurora Estimator

We provide theoretical guarantees for the general Aurora estimator described in Section 2. Throughout this section, we split ${\mathit{Z}}_i$ into ${\mathit{X}}_i(j)$ and $Y_i(j)$ as in Equation (5)(5) $$\begin{array}{c}{\mathit{X}}_i:={\mathit{X}}_i(j):=(Z_{i1},\dots ,Z_{i(j-1)},Z_{i(j+1)},\dots ,Z_{iK})\\ Y_i:=Y_i(j):=Z_{ij},\end{array}$$(5) , and we write ${\mathit{X}}_i^{(·)}(j)$ for the order statistics of ${\mathit{X}}_i(j)$. We also write $\mathit{Z}$ and ${\mathit{X}}^{(·)}(j)$ for the concatenation of all the ${\mathit{Z}}_i$ and ${\mathit{X}}_i^{(·)}(j)$, respectively. As before, we omit j whenever a definition does not depend on the specific choice of j.

4.1 Three Oracle Benchmarks

In this section, we define three benchmarks for assessing the quality of a mean estimator in model (3) (in terms of mean squared error). These benchmarks provide the required context to interpret the theoretical guarantees of Aurora that we establish in Section 4.2.

First, it is impossible to improve on the Bayes rule, so the Bayes risk serves as an oracle. We denote the Bayes risk (based on all K replicates) by(7) $$\begin{array}{c}{\mathcal{R}}_K^{*}(G,F):={\mathbb{E}}_{G,F}\left[{({\mu }_i-{\mathbb{E}}_{G,F}[{\mu }_i | {\mathit{Z}}_i])}^2\right]\\ ={\mathbb{E}}_{G,F}\left[{({\mu }_i-{\mathbb{E}}_{G,F}[{\mu }_i | {\mathit{X}}_i^{(·)},Y_i])}^2\right].\end{array}$$(7)

As explained in Proposition 1, the function we seek to mimic (for each j in the loop of the Aurora algorithm in Table 1) is the oracle Bayes rule based on the order statistics of K – 1 replicates,(8) $$m^{*}({\mathit{X}}_i^{(·)}):={\mathbb{E}}_{G,F}\left[{\mu }_i | {\mathit{X}}_i^{(·)}\right].$$(8)

The risk of $m^{*}(·)$ is the Bayes risk based on $K-1$ replicates,(9) $$\begin{array}{c}{\mathcal{R}}_{K-1}^{*}(G,F):={\mathbb{E}}_{G,F}\left[{({\mu }_i-{\mathbb{E}}_{G,F}[{\mu }_i | {\mathit{X}}_i^{(·)}])}^2\right]\\ ={\mathbb{E}}_{G,F}\left[{({\mu }_i-m^{*}({\mathit{X}}_i^{(·)}))}^2\right].\end{array}$$(9)

In the Aurora algorithm, we average over the choice of held-out replicate j. Thus, we also define an oracle rule that averages $m^{*}({\mathit{X}}_i^{(·)}(j))$ over all j. We use the following notation for this oracle and its risk:(10) $$\begin{array}{c}{\overline{m}}^{*}({\mathit{Z}}_i):=\frac{1}{K}\sum _{j=1}^K{m}^{*}\left({\mathit{X}}_i^{(·)}(j)\right),\\ {\overline{\mathcal{R}}}_{K-1}^{*}(G,F):={\mathbb{E}}_{G,F}\left[{\left({\mu }_i-{\overline{m}}^{*}({\mathit{Z}}_i)\right)}^2\right].\end{array}$$(10)

It is immediate that ${\mathcal{R}}_K^{*}(G,F)\le {\overline{\mathcal{R}}}_{K-1}^{*}(G,F)$. Also, by the definition of ${\overline{m}}^{*}$ in Equation (10)(10) $$\begin{array}{c}{\overline{m}}^{*}({\mathit{Z}}_i):=\frac{1}{K}\sum _{j=1}^K{m}^{*}\left({\mathit{X}}_i^{(·)}(j)\right),\\ {\overline{\mathcal{R}}}_{K-1}^{*}(G,F):={\mathbb{E}}_{G,F}\left[{\left({\mu }_i-{\overline{m}}^{*}({\mathit{Z}}_i)\right)}^2\right].\end{array}$$(10) and by Jensen’s inequality, it holds that,$$\begin{array}{c}{\mathbb{E}}_{G,F}\left[{\left({\mu }_i-{\overline{m}}^{*}({\mathit{Z}}_i)\right)}^2\right]\hfill \\ \hspace{1em}= {\mathbb{E}}_{G,F}\left[{\left\{\frac{1}{K}\sum _{j=1}^K\left({\mu }_i-m^{*}\left({\mathit{X}}_i^{(·)}(j)\right)\right)\right\}}^2\right]\hfill \\ \hspace{1em}\le \frac{1}{K}\sum _{j=1}^K{\mathbb{E}}_{G,F}\left[{\left({\mu }_i-m^{*}\left({\mathit{X}}_i^{(·)}(j)\right)\right)}^2\right],\hfill \end{array}$$so ${\overline{\mathcal{R}}}_{K-1}^{*}(G,F)\le {\mathcal{R}}_{K-1}^{*}(G,F)$. This bound can be improved through the following insight: $m^{*}({\mathit{X}}_i^{(·)}(j)), j=1,\dots ,K$ are jackknife estimates of the posterior mean $\mathbb{E}\left[{\mu }_i|{\mathit{Z}}_i\right]$ and ${\overline{m}}^{*}({\mathit{Z}}_i)$ is their average. By a fundamental result for the jackknife (Efron and Stein 1981, theor. 2), it holds that¹ $\text{var}[{\overline{m}}^{*}({\mathit{Z}}_i)|{\mu }_i,{\alpha }_i]\le \text{var}[m^{*}({\mathit{X}}_i^{(·)})|{\mu }_i,{\alpha }_i]·(K-1)/K$. Armed with this insight, in Supplement A.1 we prove the following Proposition.

Proposition 2.

Under model (3) with $\mathbb{E}\left[{\mu }_i^2\right]<\infty ,\mathbb{E}\left[Z_{ij}^2\right]<\infty$, it holds that(11) $$\begin{array}{c}{\mathcal{R}}_K^{*}(G,F)\le {\overline{\mathcal{R}}}_{K-1}^{*}(G,F)\le {\mathcal{R}}_{K-1}^{*}(G,F)\\ \hspace{1em}-\mathbb{E}\left[\text{var}[m^{*}({\mathbf{X}}_i^{(·)})|{\mu }_i,{\alpha }_i]\right]/K.\end{array}$$(11)

Remark 1.

For sufficiently “regular” problems, ${\mathcal{R}}_K^{*}(G,F)$ will typically be of order $O(1/K)$, while ${\mathcal{R}}_{K-1}^{*}(G,F)-{\mathcal{R}}_K^{*}(G,F)$ will be of order $O(1/K^2)$; we make this argument rigorous for location families in Section 5.2 and Supplement E. The correction term on the right-hand side of Equation (11)(11) $$\begin{array}{c}{\mathcal{R}}_K^{*}(G,F)\le {\overline{\mathcal{R}}}_{K-1}^{*}(G,F)\le {\mathcal{R}}_{K-1}^{*}(G,F)\\ \hspace{1em}-\mathbb{E}\left[\text{var}[m^{*}({\mathbf{X}}_i^{(·)})|{\mu }_i,{\alpha }_i]\right]/K.\end{array}$$(11) will also be of order $O(1/K^2)$ in such problems. In our next example, we demonstrate the importance of this additional term.

Example 1

(Normal likelihood with Normal prior). We consider the Normal–Normal model (2) from the introduction with prior variance A and noise variance ${\sigma }^2=1$, and with replicates $Z_{ij},j=1,\dots ,K$ as in Equation (3)(3) $$\begin{array}{c}({\mu }_i,{\alpha }_i) \stackrel{\text{iid}}{\sim } G,i=1,\dots ,N\\ Z_{ij}|({\mu }_i,{\alpha }_i) \stackrel{\text{iid}}{\sim } F(·|{\mu }_i,{\alpha }_i)j=1,\dots ,K.\end{array}$$(3) . In this case,² we can analytically compute that ${\mathcal{R}}_K^{*}(G,F)=A/(KA+1)$, and so it follows that ${\mathcal{R}}_{K-1}^{*}(G,F)-{\mathcal{R}}_K^{*}(G,F)=\Theta (1/K^2)$. The right-most inequality in (11) is an equality and ${\overline{\mathcal{R}}}_{K-1}^{*}(G,F)-{\mathcal{R}}_K^{*}(G,F)=\Theta (1/K^4)$. We conclude that, in the Normal-Normal model, the averaged oracle ${\overline{m}}^{*}$ has risk closer to the full Bayes estimator than to the Bayes estimator based on K – 1 replicates.

4.2 Regret Bound for Aurora

In this section, we derive our main regret bound for Aurora. The basic idea is that the in-sample error of the regression method $\widehat{m}$ directly translates to bounds on the estimation error for the effect sizes μ_i , and thus, Aurora can leverage black-box predictive models. To this end, we define the in-sample prediction error for estimating the averaged oracle ${\overline{m}}^{*}$,(12) $$\overline{\text{Err}}\left(m^{*},\widehat{m}\right):=\frac{1}{N}\sum _{i=1}^N{\mathbb{E}}_{G,F}\left[{\left\{{\overline{m}}^{*}({\mathit{Z}}_i)-\frac{1}{K}\sum _{j=1}^K{\widehat{m}}_j\left({\mathit{X}}_i^{(·)}(j)\right)\right\}}^2\right].$$(12)

When the predictive mechanism of the Aurora algorithm (Table 1) is the same for all j,³ then Jensen’s inequality provides the following convenient upper bound on Equation (12)(12) $$\overline{\text{Err}}\left(m^{*},\widehat{m}\right):=\frac{1}{N}\sum _{i=1}^N{\mathbb{E}}_{G,F}\left[{\left\{{\overline{m}}^{*}({\mathit{Z}}_i)-\frac{1}{K}\sum _{j=1}^K{\widehat{m}}_j\left({\mathit{X}}_i^{(·)}(j)\right)\right\}}^2\right].$$(12) :(13) $$\begin{array}{c}\overline{\text{Err}}\left(m^{*},\widehat{m}\right)\le \text{Err}\left(m^{*},\widehat{m}\right)\\ \hspace{1em}:=\frac{1}{N}\sum _{i=1}^N{\mathbb{E}}_{G,F}\left[{\left\{m^{*}\left({\mathit{X}}_i^{(·)}\right)-\widehat{m}\left({\mathit{X}}_i^{(·)}\right)\right\}}^2\right].\end{array}$$(13)

$\text{Err}(m^{*},\widehat{m})$ is the in-sample error from approximating $m^{*}$ by $\widehat{m}$. We are ready to state our main result:

Theorem 3.

The mean squared error of the Aurora estimator ${\widehat{\mu }}_i^{\text{Aur}}$ (described in Table 1) satisfies the following regret bound under model (3) with $\mathbb{E}\left[{\mu }_i^2\right]<\infty ,\mathbb{E}\left[Z_{ij}^2\right]<\infty$:$$\begin{array}{cc}\frac{1}{N}\sum _{i=1}^N{\mathbb{E}}_{G,F}\left[{\left({\mu }_i-{\widehat{\mu }}_i^{\text{Aur}}\right)}^2\right]& \\ \hspace{1em}\le {\mathcal{R}}_K^{*}(G,F)\hspace{1em}& \mathrm{(}\text{Irreducible}\mathrm{ }\text{Bayes}\mathrm{ }\text{error}\mathrm{)}\\ \hspace{1em}+2\left({\overline{\mathcal{R}}}_{K-1}^{*}(G,F)-{\mathcal{R}}_K^{*}(G,F)\right)& \mathrm{(}\text{Error}\mathrm{ }\text{due}\mathrm{ }\text{to}\mathrm{ }\text{data}\mathrm{ }\text{splitting}\mathrm{)}\\ \hspace{1em}+2\overline{\text{Err}}\left(m^{*},\widehat{m}\right)& \mathrm{(}\text{Estimation}\mathrm{ }\text{error}\mathrm{)}\end{array}$$

${\widehat{\mu }}_{i,j}^{\text{Aur}}$ (i.e., the Aurora estimator based on a single held-out response replicate) satisfies the above regret bound with ${\overline{\mathcal{R}}}_{K-1}^{*}(G,F), \overline{\text{Err}}(m^{*},\widehat{m})$ replaced by ${\mathcal{R}}_{K-1}^{*}(G,F), \text{Err}(m^{*},\widehat{m})$.

As elaborated in Remark 1, the second error term in the above decomposition will typically be negligible compared to ${\mathcal{R}}_K^{*}(G,F)$; this is the price we pay for making no assumptions about F and G. Hence, beyond the irreducible Bayes error, the main source of error depends on how well we can estimate $m^{*}(·)$. Crucially, this error is the in-sample estimation error of $\widehat{m}$, which is often easier to analyze and smaller in magnitude than out-of-sample estimation error (Hastie, Tibshirani, and Friedman 2009; Chatterjee 2013; Rosset and Tibshirani 2020).

4.3 Aurora With k-Nearest-Neighbors is Universally Consistent

Theorem 3 d

emonstrated that a regression model with small in-sample error translates, through Aurora, to mean estimates with small mean squared error. Now, we combine this result with results from nonparametric regression to prove that under model (3), it is possible to asymptotically (in N) match the oracle risk (10) and in view of Proposition 2, to outperform the Bayes risk based on K – 1 replicates.

Theorem 4

(Universal consistency with k-Nearest-Neighbor (kNN) estimator). Consider model (3) with $\mathbb{E}[{\mu }_i^2]<\infty ,\mathbb{E}[Z_{ij}^2]<\infty$. We estimate μ_i with the Aurora algorithm where $\widehat{m}(·)$ is the k-Nearest-Neighbor (kNN) estimator with $k=k_N\in \mathbb{N}$, that is, the nonparametric regression estimator which predicts⁴ $$\begin{array}{c}\widehat{m}(\mathit{x})=\frac{1}{k}\sum _{i\in {\mathcal{S}}_k(\mathit{x})}{Y}_i,\hspace{1em}\text{where}\mathrm{ }\\ \hspace{1em}{\mathcal{S}}_k(\mathit{x})=\left\{i\in \left\{1,\dots ,N\right\}:\sum _{j\ne i}\mathbf{1}\left({\Vert {\mathit{X}}_i^{(·)}-\mathit{x}\Vert }_2>{\Vert {\mathit{X}}_j^{(·)}-\mathit{x}\Vert }_2\right)<k\right\},\end{array}$$

and ${\Vert ·\Vert }_2$ is the Euclidean norm. If $k=k_N$ satisfies $k\to \infty ,k/N\to 0$ as $N\to \infty$, then$$\underset{N\to \infty }{\lim \sup }\frac{1}{N}\sum _{i=1}^N\mathbb{E}\left[{\left({\mu }_i-{\widehat{\mu }}_i^{\text{Aur}}\right)}^2\right]={\overline{\mathcal{R}}}_{K-1}^{*}(G,F)\le {\mathcal{R}}_{K-1}^{*}(G,F).$$

This result is a consequence of universal consistency in nonparametric regression (Stone 1977; Györfi et al. 2002). It demonstrates that Aurora can asymptotically nearly match the Bayes risk with substantial generality,⁵ and suggests the power and expressivity of the Aurora algorithm.

To apply Aurora with kNN, a data-driven choice of k is required. In Supplement B.2 we describe a procedure that chooses the number of nearest neighbors k_j per held-out response replicate j through leave-one-out (LOO) cross-validation on the units, and we study its performance empirically in the simulations of Section 6. Nevertheless, Aurora-kNN tuned by LOO, is computationally involved. This motivates our next section; there we study a procedure that is interpretable, easy to implement and that scales well to large datasets.

5 Aurora With Linear Regression

In this section, we analyze the Aurora algorithm when linear regression is used as the predictive model. That is, $\widehat{m}$ is a linear function of the order statistics(14) $$\widehat{m}({\mathbf{X}}_i^{(·)})={\widehat{\beta }}_0+\sum _{j^{\prime }=1}^{K-1}{\widehat{\beta }}_{j^{\prime }}{X}_i^{(j^{\prime })},$$(14) where $\widehat{\beta }$ are the ordinary least squares coefficients of the linear regression $Y\sim {\mathit{X}}^{(·)}$. We call the method Auroral, with the final “l” signifying “linear” and write ${\widehat{\mu }}_i^{\text{AurL}}$ for the resulting estimates of μ_i . Our main result is that Auroral matches the performance of the best estimator that is linear in the order statistics based on K – 1 replicates. To state this result formally, we first define the minimum risk among estimators in class $\mathcal{C}$:(15) $${\mathcal{R}}_{K-1}^{\mathcal{C}}(G,F):=\underset{m\in \mathcal{C}}{\inf }\left\{\frac{1}{N}\sum _{i=1}^N{\mathbb{E}}_{G,F}\left[{\left({\mu }_i-m\left({\mathit{X}}_i^{(·)}\right)\right)}^2\right]\right\}.$$(15)

The class of interest to us specifically is the class of estimators linear in the order statistics(16) $$\text{Lin}:=\text{Lin}\left({\mathbb{R}}^{K-1}\right):=\left\{m:m(x)={\beta }_0+\sum _{j\prime =1}^{K-1}{\beta }_{j\prime }{x}^{(j\prime )}\right\}.$$(16)

This is a broad class that includes all estimators of μ_i based on ${\mathit{X}}_i^{(·)}$ that proceed through the following two steps: (i) summarization, where an appropriate summary statistic of the likelihood F is used, that is linear in the order statistics, and (ii) linear shrinkage, where the summary statistic is linearly shrunk toward a fixed location. Schematically$$\begin{array}{c}\text{Step}\mathrm{ }1\mathrm{ }\mathrm{(}\text{Summarization}\mathrm{)}:\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\mathit{X}}_i\mapsto T\left({\mathit{X}}_i\right)\in \mathbb{R},\hfill \\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\text{where}\hspace{1em}T(·)\in \{\begin{array}{c}\text{Sample}\mathrm{ }\text{mean}\hfill \\ \text{Sample}\mathrm{ }\text{median}\hfill \\ \text{Trimmed}\mathrm{ }\text{mean}\hfill \\ ⋮\hfill \end{array}\hfill \\ \text{Step}\mathrm{ }2\mathrm{ }\mathrm{(}\text{Linear}\mathrm{ }\text{shrinkage}\mathrm{)}:\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}T\left({\mathit{X}}_i\right)\mapsto \alpha T\left({\mathit{X}}_i\right)+\gamma ,\hfill \\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}(\mathrm{e}.\mathrm{g}.,\text{James}-\text{Steinshrinkage})\hfill \end{array}$$

The summarization step can apply nonlinear functions of the original data, such as the median and the trimmed mean, because the input to the linear model are the order statistics, rather than the original data. Such linear combinations of the order statistics are known as L-statistics, which is a class so large that it includes efficient estimators of the mean in any smooth, symmetric location family, see Van der Vaart (2000) and Section 5.2.

We now show that Auroral matches ${\mathcal{R}}_{K-1}^{\text{Lin}}(G,F)$ asymptotically in N in the setting of Theorem 3.

Theorem 5

(Regret over linear estimators).

1. Assume there exists C_N > 0 such that $\mathbb{E}\left[{\max }_{i=1,\dots ,N}\text{var}[Y_i | {\mathit{X}}_i^{(·)}]\right]\le C_N$,⁶ then:$$\frac{1}{N}\sum _{i=1}^N\mathbb{E}\left[{\left({\mu }_i-{\widehat{\mu }}_i^{\text{AurL}}\right)}^2\right]\le {\mathcal{R}}_{K-1}^{\text{Lin}}(G,F)+C_N\frac{K}{N}.$$

2. Assume there exists $\Gamma >0$, such that $\mathbb{E}\left[Y_i^4\right]\le {\Gamma }^2$, then:$$\frac{1}{N}\sum _{i=1}^N\mathbb{E}\left[{\left({\mu }_i-{\widehat{\mu }}_i^{\text{AurL}}\right)}^2\right]\le {\mathcal{R}}_{K-1}^{\text{Lin}}(G,F)+\Gamma \sqrt{\frac{K}{N}}.$$

If $m^{*}\in \text{Lin}({\mathbb{R}}^{K-1})$, then the conclusion of Theorem 3 holds for ${\widehat{\mu }}^{\text{AurL}}$ with the term $\overline{\text{Err}}(m^{*},\widehat{m})$ bounded by $C_{N}K/N$ (under Assumption (1)), resp. $\Gamma \sqrt{K/N}$ (under (2)).

In datasets, we often encounter $K\ll N$. Then, Theorem 5 implies that Auroral will almost match the risk ${\mathcal{R}}_{K-1}^{\text{Lin}}(G)$ of the best L-statistic based on K – 1 replicates. This result is in the spirit of restricted empirical Bayes (Griffin and Krutchkoff 1971; Maritz 1974; Norberg 1980; Robbins 1983), which seeks to find the best estimator among estimators in a given class, such as the best Bayes linear estimators of Hartigan (1969). In these works, linearity typically refers to linearity in ${\mathit{X}}_i$ and not ${\mathit{X}}_i^{(·)}$; Lwin (1976), however, used empirical Bayes to learn the best L-statistic from the class $\text{Lin}$, when the likelihood takes the form of a known location-scale family.

5.1 Examples of Auroral Estimation

In this section, we give three examples in which Auroral satisfies strong risk guarantees.

Example 2

(Point mass prior). Suppose the prior on μ is a point mass at $\overline{\mu }$; that is, ${\mathbb{P}}_G\left[{\mu }_i=\overline{\mu }\right]=1$. Then, the Bayes rule based on the order statistics, $m^{*}({\mathit{X}}_i^{(·)})\equiv \overline{\mu }$, has risk 0 and is trivially a member of $\text{Lin}({\mathbb{R}}^{K-1})$, so ${\mathcal{R}}_{K-1}^{\text{Lin}}(G,F)=0$. Therefore, by Theorem 5, provided that ${\sigma }_i^2\le C$ almost surely (${\sigma }_i^2=\text{var}\left[Z_{ij}|{\mu }_i,{\alpha }_i\right]$), the risk of the Auroral estimator satisfies

$$\frac{1}{N}\sum _{i=1}^N\mathbb{E}\left[{\left({\mu }_i-{\widehat{\mu }}_i^{\text{AurL}}\right)}^2\right]\le C\frac{K}{N}.$$

Example 3

(Normal likelihood with Normal prior). We revisit Example 1,⁷ wherein we argued that the averaged oracle ${\overline{m}}^{*}({\mathbf{Z}}_i)$ (10) has risk equal to the Bayes risk ${\mathcal{R}}_K^{*}(G,F)$ plus $O(1/K^4)$. Auroral attains this risk, plus the ordinary least squares estimation error that decays as $O(K/N)$.

In addition to Auroral, we consider two estimators, that take advantage of the fact that ${\overline{Z}}_i:=\frac{1}{K}{\sum }_{j=1}^K{Z}_{ij}$ is sufficient for μ_i in the Normal model with K replicates:

• Coey and Cunningham (2019) (CC-L): We proceed similarly to the Auroral algorithm with one modification. For the jth held-out replicate, we regress $Y_i(j)$ on ${\overline{X}}_i(j)=\frac{1}{K-1}\sum _{j\prime \ne j}{Z}_{ij\prime }$ using ordinary least squares to obtain ${\widehat{m}}_j^{\text{CC}-\mathrm{L}}$ and ${\widehat{\mu }}_{ij}^{\text{CC}-\mathrm{L}}:={\widehat{m}}_j^{\text{CC}-\mathrm{L}}({\overline{X}}_i(j))$. Finally we estimate μ_i by ${\widehat{\mu }}_i^{\text{CC}-\mathrm{L}}:=\frac{1}{K}{\sum }_{j=1}^K{\widehat{\mu }}_{ij}^{\text{CC}-\mathrm{L}}$.

• James and Stein (1961) (JS): We estimate μ_i by ${\widehat{\mu }}_i^{\text{JS}}=(1-\frac{(N-2)/K}{{\sum }_{i=1}^N{\overline{Z}}_i{}^2}){\overline{Z}}_i$.

CC-L implicitly uses the assumption of Normal likelihood by reducing the replicates to their mean, which is the sufficient statistic. Similar to Auroral, its risk is equal to ${\mathcal{R}}_K^{*}(G,F)$ plus $O(1/K^4)$ and the least-square estimation error, which in this case is $O(1/N)$ (only the slope and intercept need to be estimated for each held-out replicate). James-Stein makes full use of the model assumptions (Normal prior, Normal likelihood, and known variance) and is expected to perform best. JS achieves the Bayes risk based on K observations, ${\mathcal{R}}_K^{*}(G,F)$ plus an error term that decays as $O(1/(N{K}^2))$. The price Auroral pays compared to CC-L and JS for using no assumptions whatsoever, when reduction to the mean was possible, is modest.

Example 4

(Exponential families with conjugate priors). Let ν be a σ-finite measure on the Borel sets of $\mathbb{R}$ and $\mathfrak{X}$ be the interior of the convex hull of the support of ν. Let $M(\theta )=\hspace{0.17em}\text{log}\hspace{0.17em}(\int \hspace{0.17em}\text{exp}\hspace{0.17em}(z·\theta )d\nu (z))$. Suppose $\Theta =\left\{\theta \in \mathbb{R}:M(\theta )<\infty \right\}$ is open, that both $\mathfrak{X},\Theta$ are nonempty and that $M(·)$ is differentiable for $\theta \in \Theta$ with strictly increasing derivative $\theta \mapsto M\prime (\theta )$.

Now, suppose ${\mu }_i,Z_{ij}$ are generated from model (3) as follows (with G, F implicitly defined). First, θ_i is drawn from a prior with Lebesgue density proportional to $\text{exp}\hspace{0.17em}(K_0(z_0·\theta -M(\theta )))$ on Θ for some $K_0>0$ and $z_0\in \mathfrak{X}$. Next, ${\mu }_i=M\prime ({\theta }_i)$ and $Z_{ij} | {\mu }_i$ is drawn from the distribution with ν-density equal to $\text{exp}\hspace{0.17em}(z·{\theta }_i-M({\theta }_i))$, where ${\theta }_i={(M\prime )}^{-1}({\mu }_i)$. Diaconis and Ylvisaker (1979, theor. 2) then prove that,$$m^{*}({\mathit{X}}_i^{(·)})=\mathbb{E}\left[{\mu }_i | {\mathit{X}}_i^{(·)}\right]=\frac{K_0{z}_0+(K-1){\overline{X}}_i}{K_0+K-1}.$$

Thus, $m^{*}\in \text{Lin}({\mathbb{R}}^{K-1})$ and Auroral matches the risk of $m^{*}$ up to the error term in Theorem 5.

5.2 Auroral Estimation in Location Families

In this section, we provide another example of Auroral estimation. In contrast to the rest of this article, which treats K as fixed, we consider an asymptotic regime in which both K and N tend to $\infty$ (with K growing substantially slower than N). In doing so, we hope to provide the following conceptual insights: first, we provide a concrete setting in which Auroral dominates any method that first summarizes ${\mathit{Z}}_i$ as ${\overline{Z}}_i$. Second, we elaborate on the expressivity of the class $\text{Lin}({\mathbb{R}}^{K-1})$ (16).

We consider model (3) with ${\mu }_i\sim G$ for a smooth prior G and $Z_{ij} \stackrel{\text{iid}}{\sim } F(·|{\mu }_i)$, where $F(·|{\mu }_i)$ has density $f(·-{\mu }_i)$ with respect to the Lebesgue measure and $f(·)$ is a density that is symmetric around 0.

We proceed with a heuristic discussion, that we will make rigorous in the formal statements below. Suppose for now that $f(·)$ is sufficiently regular with Fisher Information,⁸ (18) $$\mathcal{I}(f)=\int \frac{f\prime {(x)}^2}{f(x)}\mathbf{1}(f(x)>0)dx <\infty .$$(18)

Then, by classical parametric theory, we expect that $K·{\mathcal{R}}_K^{*}(G,F)\to \mathcal{I}{(f)}^{-1}$ as $K\to \infty$⁹. On the other hand, another classical result in the theory of robust statistics (Bennett 1952; Jung 1956; Chernoff, Gastwirth, and Johns 1967; Van der Vaart 2000) states that for smooth location families, there exists an L-statistic (i.e., a linear combination of the order statistics) that is asymptotically efficient. By Theorem 5, we thus anticipate that the risk of Auroral is equal to $(1+o(1))\mathcal{I}{(f)}^{-1}/K$.

In contrast, if we first summarize ${\mathit{Z}}_i$ by ${\overline{Z}}_i$, then the best estimator we can possibly use is the posterior mean, $\mathbb{E}\left[{\mu }_i|{\overline{Z}}_i\right]$. However, for K large (so that the likelihood swamps the prior), $\mathbb{E}\left[{\mu }_i|{\overline{Z}}_i\right]\approx {\overline{Z}}_i$, and so the risk will behave roughly as ${\sigma }^2/K$, where ${\sigma }^2=\int f^2(x)dx$. We summarize our findings in the Corollary below, and provide the formal proofs in Supplement E.

Corollary 6 (Smooth location families). Suppose that G satisfies regularity Assumption 1 and $f(·)$ satisfies regularity Assumption 2 (where both assumptions are stated in Supplement E.1). Then, in an asymptotic regime with $K,N\to \infty ,K^2/N\to 0$, it holds that,$$\begin{array}{c}\frac{1}{N}\sum _{i=1}^N\mathbb{E}\left[{\left({\mu }_i-{\widehat{\mu }}_i^{\text{AurL}}\right)}^2\right]/\frac{\mathcal{I}{(f)}^{-1}}{K}\to 1,\\ \frac{1}{N}\sum _{i=1}^N\mathbb{E}\left[{\left({\mu }_i-{\widehat{\mu }}_i^{\text{Avg}}\right)}^2\right]/\frac{{\sigma }^2}{K}\to 1\mathrm{ }\text{as}\mathrm{ }N\to \infty ,\end{array}$$where ${\widehat{\mu }}_i^{\text{Avg}}$ can be either the CC-L estimator ${\widehat{\mu }}_i^{\text{CC}-\mathrm{L}}$ or the Bayes estimator $\mathbb{E}\left[{\mu }_i|{\overline{Z}}_i\right]$.

Recalling that $\mathcal{I}{(f)}^{-1}\le {\sigma }^2$ with equality when $f(·)$ is the Gaussian density, we see that Auroral adapts¹⁰ to the unknown density $f(·)$ and outperforms any estimator that first averages ${\mathit{Z}}_i$.

What about location families that are not regular? Below we give an example, namely the Rectangular location family with $f(·)=U[-B,B]$, B > 0 in which a similar conclusion to Corollary 6 holds. The advantage of Auroral is even more pronounced in this case ($O(K^{-2})$ risk for Auroral, versus $O(K^{-1})$ for any method that first averages ${\mathit{Z}}_i$).

Corollary 7 (Rectangular location family). Suppose $f(·)$ is the uniform density on $[-B,B]$ for a B > 0, that G satisfies regularity Assumption 1 in Supplement E.1 and that $K,N\to \infty , K^3/N\to 0$. Then,$$\begin{array}{c}\underset{N\to \infty }{\lim \sup }\{K·(\frac{1}{N}\sum _{i=1}^N\mathbb{E}\left[{\left({\mu }_i-{\widehat{\mu }}_i^{\text{AurL}}\right)}^2\right]/\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\frac{1}{N}\sum _{i=1}^N\mathbb{E}\left[{\left({\mu }_i-{\widehat{\mu }}_i^{\text{Avg}}\right)}^2\right])\}\le 6.\end{array}$$

6 Empirical Performance in Simulations

In this section, we study the empirical performance of Aurora and competing empirical Bayes algorithms in three scenarios: homoscedastic location families (Section 6.1), heteroscedastic location families (Section 6.2) and a heavy-tailed likelihood (Section 6.3).

6.1 Homoscedastic Location Families

We start by empirically studying the location family problem from Section 5.2 for K = 10 replicates and $N={10}^4$ units. We first generate the means μ_i from one of two possible priors G, parameterized by a simulation parameter A: the Normal prior $\mathcal{N}(0.5,A)$ and the three-point discrete prior that assigns equal probabilities to $\left\{-\sqrt{3A/2}, 0, \sqrt{3A/2}\right\}$. Both prior distributions have variance A.

We then generate the replicates Z_ij around each mean μ_i from one of three location families: Normal, Laplace, or Rectangular. The parameters of these distributions are chosen so that the noise variance is ${\sigma }^2=\text{var}\left[Z_{ij}|{\mu }_i\right]=4$.

We compare eight estimators of μ_i :

• Aurora-type methods: Auroral, Aurora-kNN (Aur-kNN) with k chosen by leave-one-out cross-validation from the set $\left\{1,\dots ,1000\right\}$ (as described in Supplement B.2) and CC-L (described in Example 3).

• Standard estimators of location: The mean ${\overline{Z}}_i$, the median and the midrange (that is, ${\widehat{\mu }}_i=({\max }_j\left\{Z_{ij}\right\}+{\min }_j\left\{Z_{ij}\right\})/2$).

• Standard empirical Bayes estimators applied to the averages ${\overline{Z}}_i$: James-Stein (positive-part) shrinking toward ${\sum }_{i=1}^N{\overline{Z}}_i/N$ (which we provide with oracle knowledge of ${\sigma }^2=4$) and the nonparametric maximum likelihood estimator (NPMLE) of Koenker and Mizera (2014) (as implemented in the REBayes package [Koenker and Gu 2017] in the function “GLmix”), which is a convex programming formulation of the estimation scheme of Kiefer and Wolfowitz (1956) and Jiang and Zhang (2009). For the NPMLE we estimate the standard deviation for each unit by the sample standard deviation ${\widehat{\sigma }}_i^2$ over its replicates and use the working approximation ${\overline{Z}}_i|{\mu }_i\stackrel{·}{\sim }\mathcal{N}({\mu }_i,{\widehat{\sigma }}_i^2/K)$.

The results¹¹ are shown in Figure 2. The standard location estimators have constant mean squared error (MSE) in all panels, since they do not make use of the prior.

Fig. 2 Homoscedastic location families: The MSE of the 8 estimators, as a function of the prior standard deviation. Each column represents a different prior distribution: Normal (left) and a three-point distribution (right). Each row represents a different location family for the likelihood (Normal, Laplace, Rectangular).

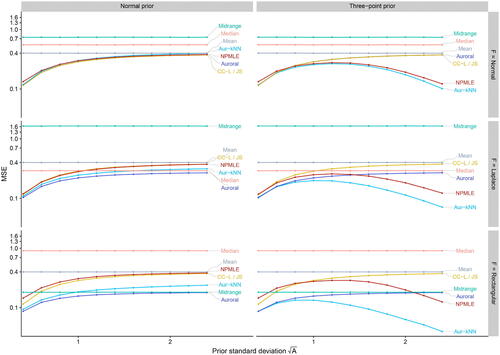
We discuss the case of a Normal prior first: here the MSE of all methods is non-decreasing in A. Auroral closely matches the best estimator for every A and likelihood. In the case of Normal likelihood, James-Stein (with oracle knowledge of ${\sigma }^2$), CC-L and Auroral perform best,¹² followed closely by Aurora-kNN and the NPMLE. The standard location estimators are competitive when the prior is relatively uninformative (i.e., A is large). Among these, the mean performs best for the Normal likelihood, the median for the Laplace likelihood and the midrange for the Rectangular likelihood.

The three component prior highlights a case in which nonlinear empirical Bayes shrinkage can be helpful. Here, Aurora-kNN performs best across all settings, closely followed by the NPMLE in the case of the Normal likelihood¹³. The NPMLE is also the second most competitive method for the Laplace likelihood with large prior variance A. The behavior of all other methods tracks closely with their behavior under a Normal prior.

One may at this point wonder: How do the Auroral weights (coefficients) $\widehat{\beta }$ in Equation (14)(14) $$\widehat{m}({\mathbf{X}}_i^{(·)})={\widehat{\beta }}_0+\sum _{j^{\prime }=1}^{K-1}{\widehat{\beta }}_{j^{\prime }}{X}_i^{(j^{\prime })},$$(14) look like? In Figure 3, we show these weights from a single replication (with $N=2·{10}^5$ and K = 10) for each of the three likelihoods considered above and for two Normal priors. First, we focus on the points in blue, which correspond to an uninformative prior ($G=\mathcal{N}(0.5,400)$). When the likelihood F is Normal, the Auroral weights are roughly constant and equal to 1/9. In other words, ${\widehat{\mu }}_{i,j}^{\text{AurL}}$, that is the Auroral estimate with held-out replicate j, is (approximately) the sample mean ${\overline{X}}_i(j)$ of ${\mathit{X}}_i^{(·)}(j)$. When the likelihood F is Laplace, the Auroral weights pick out the median $X_i^{(5)}(j)$ and a few order statistics around it. When the likelihood F is Rectangular, Auroral assigns approximately 1/2 weight each to the minimum and the maximum and 0 weight to all of the other order statistics. In other words, ${\widehat{\mu }}_{i,j}^{\text{AurL}}$ is (approximately) the midrange of ${\mathit{X}}_i^{(·)}(j)$. Notice that Auroral did not know the likelihood F in any of these examples. Rather, it adaptively learned an appropriate summary from the data.

Fig. 3 The coefficients of the intercept and the order statistics in the linear regression model for $\widehat{m}$ in Auroral: The colors represent different choices of prior G (defined in the legend), while the panels represent different choices of likelihood F. The coefficients shown have been averaged over the held-out replicate j of the Auroral algorithm (Table 1).

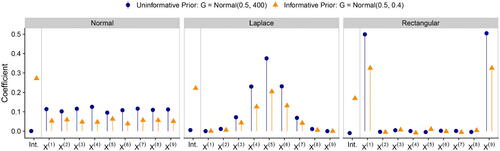
Next, we examine the difference between using informative versus uninformative priors G. When the prior is informative ($G=\mathcal{N}(0.5,0.4)$, orange in Figure 3), Auroral automatically learns a nonzero intercept, which is determined by the prior mean, and the remaining weights are shrunk toward zero.

6.2 Heteroscedastic Location Families

In our second simulation setting, we study location families where ${\sigma }_i^2$ is also random and so we find ourselves in the heteroscedastic location family problem. Again we benchmark Auroral, Aurora-kNN (k chosen by leave-one-out cross-validation from the set $\left\{1,\dots ,1000\right\}$), CC-L, the Gaussian NPMLE and the sample mean. We also consider two estimators which have been proposed specifically for the heteroscedastic Normal problem, the SURE (Stein’s Unbiased Risk Estimate) method of Xie, Kou, and Brown (2012) that shrinks toward the grand mean and the GL (Group-linear) estimator of Weinstein et al. (2018). We apply these estimators to the averages ${\overline{Z}}_i$. Both of these estimators have been developed under the assumption that the analyst has exact knowledge of ${\sigma }_i^2$; so we provide them with this oracle knowledge (SURE (or.) and GL (or.)—the other methods are not provided this information). Furthermore, we apply the Group-linear method that uses the sample variance ${\widehat{\sigma }}_i^2$ calculated based on the replicates.

We use three simulations, inspired by simulation settings (a), (c) and (f) of Weinstein et al. (2018): in all three simulations we let $N=10,000,K=10$. First we draw ${\overline{\sigma }}_i^2\sim U[0.1,{\overline{\sigma }}_{\text{max}}^2]$, where ${\overline{\sigma }}_{\text{max}}^2$ is a simulation parameter that we vary. Then for the first setting we draw ${\mu }_i\sim \mathcal{N}(0,0.5)$, while for the last two settings we let ${\mu }_i={\overline{\sigma }}_i^2$. Weinstein et al. (2018) used the latter as a model of strong mean–variance dependence. The methods that have access to ${\overline{\sigma }}_i^2$ can in principle predict perfectly (i.e., the Bayes risk is equal to 0). Finally we draw $Z_{ij}|{\mu }_i,{\sigma }_i^2\sim F(·|{\mu }_i,{\sigma }_i^2)$ where ${\sigma }_i^2={\overline{\sigma }}_i^2·K$ and F is either the Normal location-scale family (first two settings) or the Rectangular location-scale family (last setting).

Results from the simulations are shown in Figure 4. The oracle SURE and oracle Group-linear estimators perform best in the first panel and oracle Group-linear strongly outperforms all other methods in the last two panels. This is not surprising, since oracle Group-linear has oracle access to ${\sigma }_i^2$ and the method was developed for precisely such settings with strong mean-variance relationship. Among the other methods, Auroral and Aurora-kNN remain competitive. In the first panel, they match CC-L, while in the last two panels they outperform Group-linear with estimated variances. We point out that Auroral outperforms CC-L in the second panel, despite the Normal likelihood. This is possible, because the mean is no longer sufficient in the heteroscedastic problem.

Fig. 4 Heteroscedastic location families: Data are generated as follows: First ${\overline{\sigma }}_i^2\sim U[0.1,{\overline{\sigma }}_{\text{max}}^2]$, with ${\overline{\sigma }}_{\text{max}}^2$ varying on the x-axis. Then ${\mu }_i\sim \mathcal{N}(0,0.5)$ (in the left panel) or ${\mu }_i={\overline{\sigma }}_i^2$. Finally $Z_{ij}|{\mu }_i,{\sigma }_i^2\sim F(·|{\mu }_i,{\sigma }_i^2)$, $j=1,\dots ,K$ where K = 10, ${\sigma }_i^2={\overline{{\sigma }_i}}^{2}K$ and $F(·|{\mu }_i,{\sigma }_i^2)$ is a Normal location-scale family (first two panels) or Rectangular (last panel). The y-axis shows the mean squared error of the estimation methods.

6.3 A Pareto Example

For our third example, we consider a Pareto likelihood, which is heavy tailed and non-symmetric. Concretely, we let ${\mu }_i\sim G=U[2,{\mu }_{\text{max}}]$ (with ${\mu }_{\text{max}}$ a varying simulation parameter) and $F(·|{\mu }_i)$ is the Pareto distribution with tail index α = 3 and mean μ_i . We compare Auroral, Aurora-kNN (Aur-kNN) with k chosen by leave-one-out cross-validation from the set $\left\{1,\dots ,100\right\}$ (as described in Supplement B.2), CC-L, the sample mean and median, as well as the maximum likelihood estimator for the Pareto distribution (assuming the tail index is unknown). For this example we also vary $(K,N)=(20,{10}^4),(100,{10}^4),(100,{10}^5)$. The results are shown in Figure 5. Throughout all settings, Auroral performs best, followed by Aurora-kNN. All methods improve as K increases. Auroral and Aurora-kNN also improve as N increases.

Fig. 5 Pareto distribution example: Data are generated as ${\mu }_i\sim U[2,{\mu }_{\text{max}}]$, with ${\mu }_{\text{max}}$ varying on the x-axis and $Z_{ij}|{\mu }_i\sim F(·|{\mu }_i)$, where $F(·|{\mu }_i)$ is the Pareto distribution with mean μ_i and tail index α = 3. The panels correspond to different choices for K and N. The y-axis shows the mean squared error of the estimation methods.

7 Application: Predicting Treatment Effects at Google

In this section, we apply Auroral to a problem encountered at Google and other technology companies—estimating treatment effects at a fine-grained level. All major technology firms run large randomized controlled experiments, often called A/B tests, to study interventions and to evaluate policies (Tang et al. 2010; Kohavi et al. 2013; Kohavi and Longbotham 2017; Athey and Luca 2019). Estimation of the average treatment effect from such an experiment (e.g., comparing a metric between treated users and control users) is a well-understood statistical task (Wager et al. 2016; Athey and Imbens 2017). In the application we consider below, instead, interest lies in estimating treatment effects on fine-grained groups – a separate treatment effect for each of thousands of different online advertisers. In this setting, EB techniques, such as Auroral, can stabilize estimates by sharing information across advertisers.

To apply Auroral for the task of fine-grained estimation of treatment effects, we require replicates. Interestingly, the data from the technology firm we work with is routinely organized and analyzed using “streaming buckets,” that is, the experiment data is divided into K chunks of approximately equal size that are called streaming buckets. The buckets correspond to (approximately) disjoint subsets of users, partitioned at random, and so data across different buckets are independent to sufficient approximation. We refer to Chamandy et al. (2012) for a detailed description of the motivation for using streaming buckets to deal with the data’s scale and structure, as well as statistical and computational issues involved in the analysis of streaming bucket data. For the purpose of our application, each streaming bucket corresponds to a replicate in Equation (3)(3) $$\begin{array}{c}({\mu }_i,{\alpha }_i) \stackrel{\text{iid}}{\sim } G,i=1,\dots ,N\\ Z_{ij}|({\mu }_i,{\alpha }_i) \stackrel{\text{iid}}{\sim } F(·|{\mu }_i,{\alpha }_i)j=1,\dots ,K.\end{array}$$(3) .

We model the statistical problem of our application as follows. The metric of interest is the cost-per-click (CPC), which is the price a specific advertiser pays for an ad clicked by a user. The goal of the experiment is to estimate the change in CPC before and after treatment. We have data for each of N advertisers and two treatment arms: control (w = 0) and treated (w = 1). The data are further divided into K buckets. For each advertiser $i=1,\dots ,N$, bucket $j=1,\dots ,K$, and treatment arm w = 0, 1, we record the total number of clicks $N_{\mathit{ijw}}\in {\mathbb{N}}_{>0}$ and the total cost of the clicks A_ijw . We define ${\text{CPC}}_{\mathit{ijw}}:=A_{\mathit{ijw}}/N_{\mathit{ijw}}$, the empirical cost-per-click for advertiser i in bucket j and treatment arm w.

In this application, the advertisers are the units and the buckets are the replicates. Each observation is $Z_{ij}={\text{CPC}}_{ij1}-{\text{CPC}}_{ij0}$, and the goal is to estimate the treatment effect(19) $${\mu }_i:=\mathbb{E}\left[{\text{CPC}}_{ij1}-{\text{CPC}}_{ij0} | {\mu }_i,{\alpha }_i\right].$$(19)

${\mu }_i,{\alpha }_i$ from model (3) capture advertiser-level idiosyncrasies. We consider the following estimation strategies:

1. The aggregate estimate: we pool the data in all buckets and then compute the difference in CPCs, that is, ${\widehat{\mu }}_i={\sum }_{j=1}^K{A}_{ij1}/{\sum }_{j=1}^K{N}_{ij1}-{\sum }_{j=1}^K{A}_{ij0}/{\sum }_{j=1}^K{N}_{ij0}$.

2. The mean of the Z_ij , that is, ${\widehat{\mu }}_i=\frac{1}{K}{\sum }_{j=1}^K{Z}_{ij}$.

3. The CC-L estimator, wherein for each j we use ordinary least squares to regress $Y_i(j)$ onto the aggregate estimate in the other K – 1 buckets, that is, onto $\sum _{j\prime \ne j}{A}_{ij\prime 1}/\sum _{j\prime \ne j}{N}_{ij\prime 1}-\sum _{j\prime \ne j}{A}_{ij\prime 0}/\sum _{j\prime \ne j}{N}_{ij\prime 0}$.

4. The CC-L estimator, wherein for each j we use ordinary least squares to regress $Y_i(j)$ onto the mean of the other K – 1 buckets, that is, onto $\frac{1}{K-1}\sum _{j\prime \ne j}{Z}_{ij\prime }$

5. The Auroral estimator that (for each j) regresses $Y_i(j)$ on the order statistics ${\mathit{X}}_i^{(·)}(j)$.

We empirically evaluate the methods as follows: we use data from an experiment running at Google for one week, retaining only the top advertisers based on number of clicks, resulting in $N >$50,000. The number of replicates is equal to K = 4. As ground truth, we use the aggregate estimate based on experiment data from the 3 preceding and 3 succeeding weeks. Then, we compute the mean squared error of the estimates (calculated from the one week data) against the ground truth and report the percent change compared to the aggregate estimate.

The results are shown in Table 2. The table also shows the results of the same analysis applied to a second metric, the change in click-through rate (CTR), which is the proportion of times that an ad by a given advertiser which is shown to a user is actually clicked. We observe that the improvement in estimation error through Auroral is substantial. Furthermore, Auroral outperforms both variants of CC-L, which in turn outperform estimators that do not share information across advertisers (i.e., the aggregate estimate and the mean of the Z_ij ).

Table 2 Empirical performance on the advertiser-level estimation problem: Percent change in mean squared error for estimating change in cost-per-click ($\Delta \text{CPC}$) and change in click-through rate ($\Delta \text{CTR}$) compared to the aggregate estimate (± standard errors).

	$\%\mathrm{ }\text{change}\mathrm{ }\text{in}\mathrm{ }\text{MSE}$
Estimator	$\Delta \text{CPC}$	$\Delta \text{CTR}$
Aggregate	Baseline	Baseline
Mean	$-8.1\%(\pm 9.8\%)$	$-1.0\%\mathrm{ }(\pm 1.2\%)$
CC-L with Aggregate	$-49.7\%(\pm 5.8\%)$	$-34.0\%(\pm 0.9\%)$
CC-L with Mean	$-48.1\%(\pm 6.0\%)$	$-33.7\%(\pm 0.9\%)$
Auroral	$-\mathbf{6}\mathbf{3}.\mathbf{7}\%(\pm 4.2\%)$	$-\mathbf{3}\mathbf{7}.\mathbf{1}\%(\pm 0.9\%)$

8 Conclusion

We have presented a general framework for constructing empirical Bayes estimators from K noisy replicates of N units. The basic idea of our method, which we term Aurora, is to leave one replicate out and regress this held-out replicate on the remaining $K-1$ replicates. We then repeat this process over all choices of held-out replicate and average the results. We have shown that if the $K-1$ replicates are first sorted, then even linear regression produces results that are competitive with the best methods, which usually make parametric assumptions, while our method is fully nonparametric.

We conclude by mentioning some direct extensions of Aurora that are suggested by its connection to regression.

8.1 More Powerful Regression Methods

In this article, we have used linear regression and k-Nearest Neighbor regression to learn $\widehat{m}(·)$. But we can go further; for example, we could use isotonic regression [Guntuboyina and Sen 2018] based on a partial order on ${\mathit{X}}_i^{(·)}$. Or we could combine linear and isotonic regression by considering single index models with nondecreasing link function (Balabdaoui, Durot, and Jankowski 2019), that is, predictors of the form $\widehat{m}(x^{(·)})=t({\alpha }^{\top }{x}^{(·)})$, where ${\Vert \alpha \Vert }_2=1$ and t is an unknown non-decreasing function. Other possibilities include recursive partitioning (Breiman et al. 1984; Zeileis, Hothorn, and Hornik 2008), in which linear regression is fit on the leaves of a tree, or even random forests aggregated from such trees (Friedberg et al. 2021; Künzel et al. 2019).

8.2 More General Targets

We have only considered estimation of ${\mu }_i=\mathbb{E}[Z_{ij} | {\mu }_i,{\alpha }_i]$ in Equation (3)(3) $$\begin{array}{c}({\mu }_i,{\alpha }_i) \stackrel{\text{iid}}{\sim } G,i=1,\dots ,N\\ Z_{ij}|({\mu }_i,{\alpha }_i) \stackrel{\text{iid}}{\sim } F(·|{\mu }_i,{\alpha }_i)j=1,\dots ,K.\end{array}$$(3) . As pointed out in Johns (1957, 1986) this naturally extends to parameters ${\theta }_i=\mathbb{E}[h(Z_{ij}) | {\mu }_i,{\alpha }_i]$ where h is a known function. The only modification needed to estimate θ_i is that we fit a regression model to learn $\mathbb{E}[h(Y_i) | {\mathit{X}}_i^{(·)}]$ instead. We may further extend Vernon Johns’ observation to arbitrary U-statistics. Concretely, given $r<K,r\in \mathbb{N}$ and a fixed function $h:{\mathbb{R}}^r\to \mathbb{R}$, we can use Aurora to estimate ${\theta }_i=\mathbb{E}\left[h(Z_{i1},Z_{i2},\dots ,Z_{ir}) | {\mu }_i,{\alpha }_i\right]$. In this case we need to hold out r replicates to form the response. For example, with r = 2 and $h(z_1,z_2)={(z_1-z_2)}^2/2$, we can estimate the conditional variance ${\sigma }_i^2=\text{var}\left[Z_{ij} | {\mu }_i,{\alpha }_i\right]$. Denoising the variance with empirical Bayes is an important problem that proved to be essential for the analysis of genomic data (Smyth 2004; Lu and Stephens 2016). However, these articles assumed a parametric form of the likelihood, while Aurora would permit fully nonparametric estimation of the variance parameter.

8.3 External Covariates

Model (3) posits a priori exchangeability of the N units. However, in many applications, domain experts also have access to side-information ζ_i about each unit. Hence, multiple authors (Fay and Herriot 1979; Tan 2016; Kou and Yang 2017; Banerjee, Mukherjee, and Sun 2020; Coey and Cunningham 2019; Ignatiadis and Wager 2019) have developed methods that improve mean estimation by utilizing information in the ζ_i . Aurora can be directly extended to accommodate such side information. Instead of regressing Y_i on ${\mathit{X}}_i^{(·)}$, one regresses Y_i on both ${\mathit{X}}_i^{(·)}$ and ζ_i .

9 Software

We provide reproducible code for our simulation results in the following Github repository: https://github.com/nignatiadis/AuroraPaper. A package implementing the method is available at https://github.com/nignatiadis/Aurora.jl. The package has been implemented in the Julia programming language (Bezanson et al. 2017).

Acknowledgments

We are grateful to Niall Cardin, Michael Sklar, and Stefan Wager for helpful discussions and comments on the article. We would also like to thank the associate editor and the anonymous reviewers for their insightful and helpful suggestions.

Supplementary Material

The supplementary materials contain details and proofs for theoretical claims made in the article and a description of the implementation of Aurora with k-Nearest-Neighbors.

Notes

¹ Here we use the fact that the entries of ${\mathit{Z}}_i$ are independent conditionally on ${\mu }_i,{\alpha }_i$. This inequality is also known in the theory of U-statistics (Hoeffding 1948, theor. 5.2).

² The details are given in Supplement D.

³ That is, the map ${({\mathit{X}}_i^{(·)}(j),Y_i(j))}_{i=1,\dots ,N}\mapsto {\widehat{m}}_j$ is the same for all j. This does not imply that ${\widehat{m}}_j={\widehat{m}}_{j\prime }$ for $j\ne j\prime$, since the training data changes.

⁴ The definition below assumes no ties. In the proof we explain how to randomize to deal with ties.

⁵ Vernon Johns (1957) established a result similar to Theorem 4. We find this remarkable, since Johns (1957) anticipated later developments in nonparametric regression, independently proving universal consistency for partition-based regression estimators as an intermediate step.

⁶ By the law of total variance, almost surely, it holds that(17) $$\begin{array}{c}\text{var}\left[Y_i | {\mathit{X}}_i^{(·)}\right]=\text{var}\left[\mathbb{E}\left[Y_i | {\mu }_i,{\alpha }_i,{\mathit{X}}_i^{(·)}\right] | {\mathit{X}}_i^{(·)}\right]+\mathbb{E}\left[\text{var}\left[Y_i | {\mu }_i,{\alpha }_i,{\mathit{X}}_i^{(·)}\right] | {\mathit{X}}_i^{(·)}\right]\\ =\text{var}\left[{\mu }_i | {\mathit{X}}_i^{(·)}\right]+\mathbb{E}\left[{\sigma }_i^2 | {\mathit{X}}_i^{(·)}\right].\end{array}$$(17)

Thus, for example, when ${\mu }_i,{\sigma }_i^2$ have bounded support, there exists C > 0 such that $\text{var}\left[Y_i | {\mathit{X}}_i^{(·)}\right]\le C$ almost surely and so, the stated assumption holds with $C_N=C$.

⁷ See Supplement D for details regarding the regret bounds we discuss here.

⁸ In location families, the Fisher information is constant as a function of the location parameter μ_i.

⁹ Since $K\to \infty$, the likelihood swamps the prior. Furthermore, we will place regularity assumptions on the prior to rule out the possibility of superefficiency.

¹⁰ This adaptivity is perhaps expected, in light of existing theory on semiparametric efficiency in location families. For example, it is known that even for N = 1 one can asymptotically (as $K\to \infty$) match the variance of the parametric maximum likelihood estimator in symmetric location families, even without precise knowledge of F (Stein 1956; Bickel et al. 1998). However, the simulations of Section 6.1 demonstrate that Auroral adapts to the unknown likelihood already for K = 10, while semiparametric efficiency results are truly asymptotic in K, requiring an initial nonparametric density estimate.

¹¹ Throughout this section, we calculate the mean squared error by averaging over 100 Monte Carlo replicates.

¹² CC-L and James-Stein perform so similarly in the simulations of this subsection that they are indistinguishable in all panels of Figure 2 with the difference of their MSEs smaller than ${10}^{-3}$ in all cases. In the first panel (Normal likelihood), Auroral is also indistinguishable from CC-L and James-Stein.

¹³ Even for the Normal likelihood, the assumptions of the implemented NPMLE are not fully satisfied, since we use estimated standard deviations ${\widehat{\sigma }}_i^2$ for each unit.