Toward Causal Inference for Spatio-Temporal Data: Conflict and Forest Loss in Colombia

Abstract

How does armed conflict influence tropical forest loss? For Colombia, both enhancing and reducing effect estimates have been reported. However, a lack of causal methodology has prevented establishing clear causal links between these two variables. In this work, we propose a class of causal models for spatio-temporal stochastic processes which allows us to formally define and quantify the causal effect of a vector of covariates X on a real-valued response Y. We introduce a procedure for estimating causal effects and a nonparametric hypothesis test for these effects being zero. Our application is based on geospatial information on conflict events and remote-sensing-based data on forest loss between 2000 and 2018 in Colombia. Across the entire country, we estimate the effect to be slightly negative (conflict reduces forest loss) but insignificant (P = 0.578), while at the provincial level, we find both positive effects (e.g., La Guajira, P = 0.047) and negative effects (e.g., Magdalena, P = 0.004). The proposed methods do not make strong distributional assumptions, and allow for arbitrarily many latent confounders, given that these confounders do not vary across time. Our theoretical findings are supported by simulations, and code is available online.

Keywords:

• Covariate adjustment
• Causal model
• Latent confounding
• Permutation test
• Treatment effect

1 Introduction

1.1 Spatio-Temporal Data Analysis

In principle, all data are spatio-temporal data: Any observation of any phenomenon occurs at a particular point in space and time. If information on the spatio-temporal origin of data is available, this information can be exploited for statistical modeling in various ways; this is the study of spatio-temporal statistics (e.g., Cressie and Wikle 2015; Wikle, Zammit-Mangion, and Cressie 2019). Spatio-temporal statistical models find their application in many environmental and sustainability sciences, and have been used, for example, for the analysis of biological growth patterns (Chaplain, Singh, and McLachlan 1999), to model meteorological fields (Bertolacci et al. 2019), or to assess the development of land-use change (Liu, Huang, and Zhang 2017) and sea level rise (Zammit-Mangion et al. 2015). They are used in epidemiology for prevalence mapping of infectious diseases (Giorgi et al. 2018), and play a key role in socio-economic research, for example, for the modeling of housing prices (Holly, Pesaran, and Yamagata 2010), or for election forecasting (Pavía, Larraz, and Montero 2008). In almost all of these domains, the abundance of spatio-temporal data has increased rapidly over the last decades. Several advances aim to improve the accessibility of such datasets, for example, via “data cube” approaches (e.g., Nativi, Mazzetti, and Craglia 2017; Mahecha et al. 2020).

Most spatio-temporal statistical models are models for the observational distribution, that is, they model processes that are passively observed. By allowing for spatio-temporal trends and dependence structures, such models can be accurate descriptions of complex processes, and have proven to be effective tools for spatio-temporal prediction, inference and forecasting (e.g., Wikle, Zammit-Mangion, and Cressie 2019). However, to answer interventional questions such as “How does a certain policy change affect land-use patterns?”, we require a model for the intervention distribution, that is, for data generated under a change in the data generating mechanism—we require a causal model for the data-generating process.

1.2 Causality

Causal models can be used to quantify causal relations between random variables, (e.g., by analyzing the change in expected value of Y when intervening on X). However, existing causal models do not apply well to our setting, since they are either restricted to independent and identically distributed (iid) or time series data, or they rely on various assumptions which cannot be expected to hold in our application (see Appendix A for a review of existing work). In this article, we introduce a novel class of causal models for multivariate spatio-temporal stochastic processes. A spatio-temporal dataset may then be viewed as a single realization from such a model, observed at discrete points in space and time. The full causal structure among all variables of a spatio-temporal process can hardly be fully specified. In practice, however, a full causal specification may also not be necessary: we are often interested in quantifying only certain causal relationships, while being indifferent to other parts of the causal structure. The causal models introduced in this article are well adapted to such settings. They allow us to model a causal influence of a vector of covariates X on a target variable Y while leaving other parts of the causal structure unspecified. In particular, the models accommodate largely unspecified autocorrelation patterns in the response variable, which are a common phenomena in spatio-temporal data.

The introduced framework allows us to formally talk about causality in a spatio-temporal context and can be used to construct well-defined targets of inference. As an example, we define the intervention effect (“causal effect”) of X on Y. We show that this effect can be estimated from observational spatio-temporal data and introduce a corresponding estimator. We prove consistency and verify this finding by a simulation experiment. We furthermore construct a nonparametric hypothesis test for the causal effect being zero. Our methods do not rely on any distributional assumptions on the data-generating process. They furthermore allow for the influence of arbitrarily many latent confounders if these confounders do not vary across time. In principle, our method also allows to analyze problems where temporal and spatial dimensions are interchanged, meaning that confounders may vary in time but remain static across space.

Our work has been motivated by the following application.

1.3 Conflict and Forest Loss in Colombia

Tropical forests are rich in biodiversity (Kreft and Jetz 2007), store large amounts of carbon (Avitabile et al. 2016), play an important role in climate-regulation, and provide livelihoods to millions of people (Lambin and P. Meyfroidt 2011). Yet, tropical forests continue to be under pressure due to agricultural expansion (Angelsen and Kaimowitz 1999), mining (Sonter et al. 2017), timber harvest (Pearson, Brown, and Casarim 2014), or urban expansion (DeFries et al. 2010). A problem that is still only partly understood is the interaction between forest loss and armed conflicts (Baumann and Kuemmerle 2016), which are frequent events in tropical areas (Pettersson and Wallensteen 2015). Armed conflict may have both positive and negative impacts on forest loss. On the one hand, conflict can lead to increasing pressure on forests, as timber may finance warfare activities Harrison (2015). Also, reduced law enforcement in conflict regions may lead to plundering of natural resources leading to increasing forest loss (Butsic et al. 2015). On the other hand, the outbreak of armed conflicts can reduce pressure on forest resources, for example, when economic and political insecurity interrupt large-scale mining activities, or when economic sanctions stop international timber trade (Le Billon 2000). Investors may furthermore be hesitant to invest in agricultural activities (Collier et al. 2000), thereby reducing the pressure on forest areas compared to peace times (Gorsevski et al. 2012).

Here, we focus on the specific case of Colombia, where an armed conflict has been present for over 50 years, causing more than 200,000 fatalities, until a peace agreement was reached in 2016. There is evidence that increased forest loss can be, at least regionally, attributed to the armed conflict (Castro-Nunez et al. 2017; Landholm, Pradhan, and Kropp 2019). At the same time, there are also arguments suggesting that the pressure on forests was partially reduced when armed conflict prevented logging (Dávalos, Sanchez, and Armenteras 2016). Most articles report evidence that both positive and negative impacts of conflict on forest loss may happen in parallel, depending on the local conditions (e.g., Sánchez-Cuervo and Aide 2013; Castro-Nunez et al. 2017). We believe that a purely data-driven approach can be a useful addition to this debate.

In our analysis, we use a dataset containing the following variables.

• $X_s^t:$ binary conflict indicator for location s at year t.

• $Y_s^t:$ absolute forest loss in location s from year t – 1 to year t, measured in ${\text{km}}^2$.

• $W_s^t:$ distance from location s to the closest road, measured in $\text{km}$.

Data are annually aggregated, covering the years from 2000 to 2018, and spatially explicit at a $10\text{km}\times 10\text{km}$-resolution. We provide a detailed description of the data processing in Section 4.

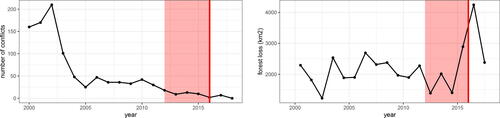
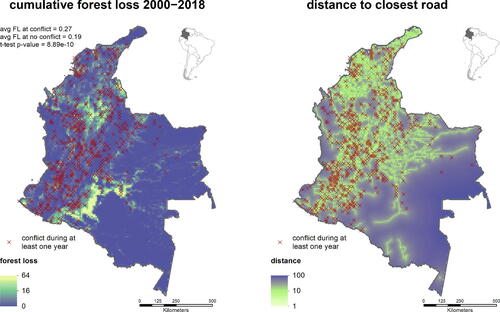
A summary of the dataset can be seen in Figure 1. Visually, there is a strong positive dependence between the occurrence of a conflict and the loss of forest canopy. This observation is supported by simple summary statistics: the average forest loss across measurements classified as conflict events significantly exceeds that from non-conflict events by almost 50% (Figure 1, left), conforming previous findings (e.g., Landholm, Pradhan, and Kropp 2019). When seeking a causal explanation for the observed data, however, we regard such an analysis as flawed in two ways. First, both conflicts and forest loss predominantly occur in areas with high accessibility (Figure 1, right), indicating that the potential causal effect of X on Y is confounded by W. In fact, we expect the existence of several other confounders (e.g., population density, market infrastructure, etc.), many of which may be unobserved. Failing to account for confounding variables leads to biased estimates of the causal effect. Second, strong spatial dependencies in X and Y reduce the effective sample size, and a standard t-test thus exaggerates the significance of the observed difference in sample averages. To test hypotheses about X and Y, we need statistical tests which are adapted to the spatio-temporal nature of data.

Fig. 1 Temporally aggregated summary of the dataset described in Section 1.3. Conflicts are predictive of exceedances in forest loss (left), but this dependence is partly induced by a common dependence on accessibility, which we measure by the mean distance to a road (right). Failing to account for this variable and other confounders biases our estimate of the causal influence of conflict on forest loss.

1.4 Contributions and Structure of the Article

Apart from the case study, this article contains three main theoretical contributions: the definition of a causal model for spatio-temporal data, a method for estimating causal effects (both Section 2), and a hypothesis test for the overall existence of such effects (Section 3). Section 4 applies our methodology to the above example. All data used for our analysis are publicly available. A description of how it can be obtained, along with an implementation of our method and reproducing scripts for all our figures and results, can be found at github.com/runesen/spatio_temporal_causality. All proofs are contained in Appendix H.

2 Quantifying Causal Effects for Spatio-Temporal Data

A spatio-temporal dataset may be viewed as a single realization of a spatio-temporal stochastic process, observed at discrete points in space-time. In this section, we provide a formal framework to quantify causal relations among the components of a multivariate spatio-temporal process, and show how to estimate causal effects from observational data.

2.1 Causal Models for Spatio-Temporal Processes

Throughout this section, let $(\Omega ,\mathcal{A},P)$ be some background probability space. A p-dimensional spatio-temporal process Z is a random variable taking values in the sample space ${\mathcal{Z}}_p$ of all $(\mathcal{B}({\mathbb{R}}^2\times \mathbb{N}),\mathcal{B}({\mathbb{R}}^p))$-measurable functions, where $\mathcal{B}(·)$ denotes the Borel σ-algebra. We equip ${\mathcal{Z}}_p$ with the σ-algebra ${\mathcal{F}}_p$, defined as the smallest σ-algebra such that for all $B\in \mathcal{B}({\mathbb{R}}^p)$, the mapping ${\mathcal{Z}}_p\ni z\mapsto {\int }_{B}z(x)dx$ is $({\mathcal{F}}_p,\mathcal{B}(\mathbb{R}))$-measurable. The induced probability measure $\mathbb{P}$ on the measurable space $({\mathcal{Z}}_p,{\mathcal{F}}_p)$, for every $F\in {\mathcal{F}}_p$ defined by $\mathbb{P}(F):=P({\mathbf{Z}}^{-1}(F))$, is said to be the distribution of Z . Throughout this article, we use the notation $Z_s^t$ to denote the random vector obtained from marginalizing Z at location s and time point t. We use ${\mathbf{Z}}_s$ for the time series ${(Z_s^t)}_{t\in \mathbb{N}},{\mathbf{Z}}^t$ for the spatial process ${(Z_s^t)}_{s\in {\mathbb{R}}^2}$, and ${\mathbf{Z}}^{(S)}$ for the spatio-temporal process corresponding to the coordinates in $S\subseteq \{1,\dots ,p\}$. We call a spatio-temporal process weakly stationary if the marginal distribution of $Z_s^t$ is the same for all $(s,t)\in {\mathbb{R}}^2\times \mathbb{N}$, and time-invariant if $\mathbb{P}({\mathbf{Z}}^1={\mathbf{Z}}^2=\cdots )=1$.

Multivariate spatio-temporal processes are used for the joint modeling of different phenomena, each of which corresponds to a coordinate process. Let us consider a decomposition of these coordinate processes into disjoint ‘bundles’. We are interested in specifying causal relations among these bundles while leaving the causal structure among variables within each bundle unspecified. Similarly to a graphical model (Lauritzen 1996), our approach relies on a factorization of the joint distribution of Z into a number of components, each of which models the conditional distribution for one bundle given several others. This approach induces a graphical relation among the different bundles. We will equip these relations with a causal interpretation by additionally specifying the distribution of Z under certain interventions on the data-generating process.

Definition 1

(Causal graphical models for spatio-temporal processes). A causal graphical model for a p-dimensional spatio-temporal process Z is a triplet $(\mathcal{S},\mathcal{G},\mathcal{P})$ consisting of

• a family $\mathcal{S}={(S_j)}_{j=1}^k$ of nonempty, disjoint sets $S_1,\dots ,S_k\subseteq \{1,\dots ,p\}$ with ${\cup }_{j=1}^k{S}_j=\{1,\dots ,p\}$,

• a directed acyclic graph $\mathcal{G}$ with vertices $S_1,\dots ,S_k$, and

• a family $\mathcal{P}={({\mathcal{P}}^j)}_{j=1}^k$ of collections ${\mathcal{P}}^j={\left\{{\mathbb{P}}_z^j\right\}}_{z\in {\mathcal{Z}}_{\left|P{A}_j\right|}}$ of distributions on $({\mathcal{Z}}_{\left|S_j\right|},{\mathcal{F}}_{\left|S_j\right|})$, where for every j, $P{A}_j:=\underset{i:S_i\to S_j\in \mathcal{G}}{\cup }{S}_i$. Whenever $P{A}_j=\varnothing ,{\mathcal{P}}^j$ consists only of a single distribution which we denote by ${\mathbb{P}}^j$.

Since $\mathcal{G}$ is acyclic, we can without loss of generality assume that $S_1,\dots ,S_k$ are indexed such that $S_i\cancel{\to }{S}_j$ in $\mathcal{G}$ whenever i > j. The above components induce a unique joint distribution $\mathbb{P}$ over Z. For every $F={\times }_{j=1}^k{F}_j$, it is defined by(1) $$\mathbb{P}(F)={\int }_{F_1}\cdots {\int }_{F_k}{\mathbb{P}}_{z^{(P{A}_k)}}^k(d{z}^{(S_k)})\cdots {\mathbb{P}}^1(d{z}^{(S_1)}).$$(1)

We call $\mathbb{P}$ the observational distribution. For each $j\in \{1,\dots ,k\}$, the conditional distribution of ${\mathbf{Z}}^{(S_j)}$ given ${\mathbf{Z}}^{(P{A}_j)}$ as induced by $\mathbb{P}$ equals ${\mathcal{P}}^j$. We define an intervention on ${\mathbf{Z}}^{(S_j)}$ as replacing ${\mathcal{P}}^j$ by another model ${\tilde{\mathcal{P}}}^j$. This operation results in a new graphical model $(\mathcal{S},\mathcal{G},\tilde{\mathcal{P}})$ for Z which induces, via (1)(1) $$\mathbb{P}(F)={\int }_{F_1}\cdots {\int }_{F_k}{\mathbb{P}}_{z^{(P{A}_k)}}^k(d{z}^{(S_k)})\cdots {\mathbb{P}}^1(d{z}^{(S_1)}).$$(1) , a new distribution $\tilde{\mathbb{P}}$, the interventional distribution.

Assume that we perform an intervention on ${\mathbf{Z}}^{(S_i)}$. By definition, the resulting interventional distribution differs from the observational distribution only in the way in which ${\mathbf{Z}}^{(S_i)}$ depends on ${\mathbf{Z}}^{({\text{PA}}_i)}$, while all other conditional distributions ${\mathbf{Z}}^{(S_j)} | {\mathbf{Z}}^{({\text{PA}}_j)},j\cancel{=}i$, remain the same. This property is analogous to the modularity property of structural causal models (Haavelmo 1944; Pearl 2009; Peters, Janzing, and Schölkopf 2017) and justifies a causal interpretation of the conditionals in $\mathcal{P}$. We refer to the graph $\mathcal{G}$ as the causal structure of Z, and sometimes write $\mathbf{Z}=[{\mathbf{Z}}^{(S_k)} | {\mathbf{Z}}^{({\text{PA}}_k)}]\cdots [{\mathbf{Z}}^{(S_1)}]$ to emphasize this structure.

2.2 Latent Spatial Confounder Model

Motivated by the example introduced in Section 1.3, we are particularly interested in scenarios where a target variable Y is causally influenced by a vector of covariates X, and where (X, Y) are additionally affected by some latent variables H. In general, inferring causal effects under arbitrary influences of latent confounders is impossible, and we therefore need to impose additional restrictions on the variables in H. We here make the fundamental assumption that they do not vary across time (alternatively, one can assume that the hidden variables are invariant over space, see Appendix B.3).

Definition 2

(Latent spatial confounder model). Consider a spatio-temporal process $(\mathbf{X},\mathbf{Y},\mathbf{H})={(X_s^t,Y_s^t,H_s^t)}_{(s,t)\in {\mathbb{R}}^2\times \mathbb{N}}$ over a real-valued response Y, a vector of covariates $X\in {\mathbb{R}}^d$ and a vector of latent variables $H\in {\mathbb{R}}^{\mathcal{l}}$. We call a causal graphical model over $(\mathbf{X},\mathbf{Y},\mathbf{H})$ with causal structure $[\mathbf{Y} | \mathbf{X},\mathbf{H}][\mathbf{X} | \mathbf{H}][\mathbf{H}]$ a latent spatial confounder model (LSCM) if both of the following conditions hold true for the observational distribution.

• The latent process H is weakly stationary and time-invariant.

• There exists a measurable function $f:{\mathbb{R}}^{d+\mathcal{l}+1}\to \mathbb{R}$ and an iid sequence ${\mathit{\epsilon }}^1,{\mathit{\epsilon }}^2,\dots$ of weakly stationary spatial error processes, independent of $(\mathbf{X},\mathbf{H})$, such that(2) $$Y_s^t=f(X_s^t,H_s^t,{\epsilon }_s^t)\text{for}\mathrm{ }\text{all}\mathrm{ }(s,t)\in {\mathbb{R}}^2\times \mathbb{N}.$$(2)

We require that for all $x\in {\mathbb{R}}^d,f(x,H_0^1,{\epsilon }_0^1)$ has finite expectation.

Throughout this section, we assume that $(\mathbf{X},\mathbf{Y},\mathbf{H})$ come from an LSCM. The above definition says that for every s, t, $Y_s^t$ depends on $(\mathbf{X},\mathbf{H})$ only via $(X_s^t,H_s^t)$, and that this dependence remains the same for all points in space-time. Together with the weak stationarity of H and $\mathit{\epsilon }$, this assumption ensures that the average causal effect of $X_s^t$ on $Y_s^t$ (which we introduce below) remains the same for all s, t. Our model class imposes no restrictions on the marginal distribution of X. The spatial dependence structure of the error process $\mathit{\epsilon }$ must have the same marginal distributions everywhere, but is otherwise unspecified (in particular, $\mathit{\epsilon }$ is not required to be stationary). The temporal independence assumption on $\mathit{\epsilon }$ is necessary for our construction of resampling tests, see Section 3. We now formally define our inferential target.

Definition 3

(Average causal effect). The average causal effect of X on Y is defined as the function $f_{\text{AVE}(X\to Y)}:{\mathbb{R}}^d\to \mathbb{R}$, for every $x\in {\mathbb{R}}^d$ given by(3) $$f_{\text{AVE}(X\to Y)}(x):=\mathbb{E}[f(x,H_0^1,{\epsilon }_0^1)].$$(3)

Here, the causal effect is an average effect in that it takes the expectation over both the noise variable (as opposed to making counterfactual statements (Rubin 1974)) and the hidden variables. Alternatively, one may define the inferential target in terms of the single realization of H which manifested itself in the data, see Appendix C. ¹ The following proposition justifies $f_{\text{AVE}(X\to Y)}$ as a quantification of the causal influence of X on Y.

Proposition 1

(Causal interpretation). Let $(s,t)\in {\mathbb{R}}^2\times \mathbb{N}$ and $x\in {\mathbb{R}}^d$ be fixed, and consider any intervention on X such that $X_s^t=x$ holds almost surely in the induced interventional distribution ${\mathbb{P}}_x$. We then have that ${\mathbb{E}}_{{\mathbb{P}}_x}[Y_s^t]=f_{\text{AVE}(X\to Y)}(x).$ That is, $f_{\text{AVE}(X\to Y)}(x)$ is the expected value of $Y_s^t$ under any intervention that enforces $X_s^t=x$.

In many applications, we do not have explicit knowledge of, or data from, the interventional distributions ${\mathbb{P}}_x$. If we have access to the causal graph, however, we can sometimes compute intervention effects from the observational distribution. In the iid setting, depending on which variables are observed, this can be done by covariate adjustment or G-computation (Pearl 2009; Rubin 1974; Shpitser, VanderWeele, and Robins 2010), for example. The following proposition shows a similar result in the case of an LSCM. It follows directly from Fubini’s theorem.

Proposition 2

(Covariate adjustment). Let $f_{Y|(X,H)}$ denote the regression function $(x,h)\mapsto \mathbb{E}[Y_s^t | X_s^t=x,H_s^t=h]$ (by definition of an LSCM, this function is the same for all s, t). For all $x\in {\mathbb{R}}^d$, it holds that(4) $$f_{\text{AVE}(X\to Y)}(x)=\mathbb{E}[f_{Y|(X,H)}(x,H_0^1)].$$(4)

Proposition 2 shows that $f_{\text{AVE}(X\to Y)}$ is identified from the full observational distribution over $(\mathbf{X},\mathbf{Y},\mathbf{H})$ (given that the LSCM structure is known). Since H is unobserved, the main challenge is to estimate (4)(4) $$f_{\text{AVE}(X\to Y)}(x)=\mathbb{E}[f_{Y|(X,H)}(x,H_0^1)].$$(4) merely based on data from $(\mathbf{X},\mathbf{Y})$, see Section 2.3. (We discuss in Appendix B.1 how to furthermore include observable time-varying covariates.)

2.3 Estimation of the Average Causal Effect

2.3.1 Definition and Consistency

In practice, we only observe the process $(\mathbf{X},\mathbf{Y})$ at a finite number of points in space and time. We assume that at every temporal instance, we observe the process at the same spatial locations $s_1,\dots ,s_n\in {\mathbb{R}}^2$ (these locations need not lie on a regular grid). To simplify notation, we furthermore assume that the observed time points are $t=1,2,\dots ,m$, that is, we have access to a dataset $({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)={(X_s^t,Y_s^t)}_{(s,t)\in \{s_1,\dots ,s_n\}\times \{1,\dots ,m\}}$. The proposed method is based on the following key idea: for every $s\in \{s_1,\dots ,s_n\}$, we observe several time instances $(X_s^t,Y_s^t),t\in \{1,\dots ,m\}$, all with the same conditionals $Y_s^t | (X_s^t,H_s^t)$. Since H is time-invariant, we can, for every s, estimate $f_{Y|(X,H)}(·,h_s)$ for the (unobserved) realization h_s of $H_s^1$ using the data $(X_s^t,Y_s^t),t\in \{1,\dots ,m\}$. The expectation in (4)(4) $$f_{\text{AVE}(X\to Y)}(x)=\mathbb{E}[f_{Y|(X,H)}(x,H_0^1)].$$(4) is then approximated by averaging estimates obtained from different spatial locations. This idea is visualized in Figure 2. More formally, our method requires as input a model class for the regressions $f_{Y|(X,H)}(·,h),h\in {\mathbb{R}}^{\mathcal{l}}$, alongside with a suitable estimator ${\widehat{f}}_{Y|X}={({\widehat{f}}_{Y|X}^m)}_{m\in \mathbb{N}}$, and returns(5) $${\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)(x):=\frac{1}{n}\sum _{i=1}^n{\widehat{f}}_{Y|X}^m({\mathbf{X}}_{s_i}^m,{\mathbf{Y}}_{s_i}^m)(x),$$(5) an estimator of the average causal effect (3) within the given model class. In Section 3, we furthermore provide a statistical test for the overall existence of a causal effect. Our approach may be seen as summarizing the output of a spatially varying regression model (e.g., Gelfand et al. 2003) that is allowed to change arbitrarily from one location to the other (within the model class dictated by ${\widehat{f}}_{Y|X}$). By permitting such flexibility, our method does not rely on observing data from a continuous or spatially connected domain, and accommodates complex influences of the latent variables. An implementation can be found in our code package, see Section 1.4.

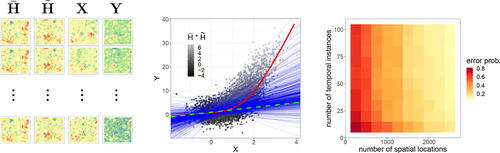
Fig. 2 Conceptual idea for estimating the average causal effect (green line) defined in (3)(3) $$f_{\text{AVE}(X\to Y)}(x):=\mathbb{E}[f(x,H_0^1,{\epsilon }_0^1)].$$(3) . In both the left and right panel, we do not display time and space. The middle figure shows the data at different locations, that is, every small plot corresponds to a single time series. The dashed curve illustrates the latent spatial confounder $H_s^t$ (for visual purposes, we here consider one-dimensional space). Due to $H_s^t$, regressing $Y_s^t$ on $X_s^t$ (red line in left plot) leads to a biased estimator. Our estimator (blue line in right plot) removes this bias. The procedure is shown in the middle figure: for all s, we observe several instances $(X_s^t,Y_s^t),t=1,\dots ,m$, with the same conditionals $Y_s^t | (X_s^t,H_s^t)$ and the same (unobserved) value of $H_s^t$. For each realization h_s of $H_s^1$, we can thus estimate the regression $f_{Y|(X,H)}(·,h_s)$ only using the data $({\mathbf{X}}_s^m,{\mathbf{Y}}_s^m)$ (blue lines in middle figure). A final estimate of the average causal effect (blue line in right plot) is obtained by approximating the expectation in (5)(5) $${\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)(x):=\frac{1}{n}\sum _{i=1}^n{\widehat{f}}_{Y|X}^m({\mathbf{X}}_{s_i}^m,{\mathbf{Y}}_{s_i}^m)(x),$$(5) by a sample average over all spatial locations, see Section 2.3.

To prove consistency of our estimator, we let the number of observable points in space-time increase. Let therefore ${(s_n)}_{n\in \mathbb{N}}\subseteq {\mathbb{R}}^2$ be a sequence of spatial coordinates, and consider the array of data ${({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)}_{n,m\ge 1}$, where for every $n,m\in \mathbb{N},({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)={(X_s^t,Y_s^t)}_{(s,t)\in \{s_1,\dots ,s_n\}\times \{1,\dots ,m\}}$. We want to prove that the corresponding sequence of estimators (5)(5) $${\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)(x):=\frac{1}{n}\sum _{i=1}^n{\widehat{f}}_{Y|X}^m({\mathbf{X}}_{s_i}^m,{\mathbf{Y}}_{s_i}^m)(x),$$(5) consistently estimates (3)(3) $$f_{\text{AVE}(X\to Y)}(x):=\mathbb{E}[f(x,H_0^1,{\epsilon }_0^1)].$$(3) . To obtain such a result, we need two central assumptions.

Assumption 1

(LLN for the latent process). For all measurable functions $\phi :{\mathbb{R}}^{\mathcal{l}}\to \mathbb{R}$ with $\mathbb{E}[|\phi (H_0^1)|]<\infty$ it holds that $\frac{1}{n}{\sum }_{i=1}^n\phi (H_{s_i}^1)\to \mathbb{E}[\phi (H_0^1)]$ in probability as $n\to \infty$.

Assumption 1 ensures that, for an increasing number of spatial locations at which data are observed, the spatial average in (5)(5) $${\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)(x):=\frac{1}{n}\sum _{i=1}^n{\widehat{f}}_{Y|X}^m({\mathbf{X}}_{s_i}^m,{\mathbf{Y}}_{s_i}^m)(x),$$(5) approximates the expectation in (3)(3) $$f_{\text{AVE}(X\to Y)}(x):=\mathbb{E}[f(x,H_0^1,{\epsilon }_0^1)].$$(3) . The assumption is satisfied, for example, for a stationary Gaussian process ${\mathbf{H}}^1$ that is sampled regularly across an increasing spatial domain, see Proposition 1 in Appendix D. As the number of observed time points tends to infinity, we furthermore require the estimators ${\widehat{f}}_{Y|X}^m$ to converge to the integrand in (3)(3) $$f_{\text{AVE}(X\to Y)}(x):=\mathbb{E}[f(x,H_0^1,{\epsilon }_0^1)].$$(3) , at least in some area $\mathcal{X}\subseteq {\mathbb{R}}^d$.

Assumption 2

(Consistent estimators of the conditional expectations). There exists $\mathcal{X}\subseteq {\mathbb{R}}^d$ such that for all $x\in \mathcal{X}$ and $s\in {\mathbb{R}}^2$, it holds that ${\widehat{f}}_{Y|X}^m({\mathbf{X}}_s^m,{\mathbf{Y}}_s^m)(x)-f_{Y|(X,H)}(x,H_s^1)\to 0$, in probability as $m\to \infty$.

A slightly stronger, but maybe more intuitive formulation is to require the above consistency to hold conditionally on H, that is, assuming that for all $x\in \mathcal{X},s\in {\mathbb{R}}^2$ and almost all h, ${\widehat{f}}_{Y|X}^m({\mathbf{X}}_s^m,{\mathbf{Y}}_s^m)(x)\to f_{Y|(X,H)}(x,h_s^1)$ as $m\to \infty$, in probability under $\mathbb{P}(· | \mathbf{H}=\mathbf{h})$. It follows from the dominated convergence theorem that this assumption implies Assumption 2. Under Assumptions 1 and 2, we obtain the following consistency result.

Theorem 1

(Consistent estimator of the average causal effect). Let $(\mathbf{X},\mathbf{Y},\mathbf{H})$ come from an LSCM as defined in Definition 2. Let ${(s_n)}_{n\in \mathbb{N}}$ be a sequence of spatial coordinates such that the marginalized process ${(H_{s_n}^1)}_{n\in \mathbb{N}}$ satisfies Assumption 1, and assume that for all $x\in \mathcal{X},\mathbb{E}[|f_{Y|(X,H)}(x,H_0^1)|]<\infty$. Let furthermore ${\widehat{f}}_{Y|X}={({\widehat{f}}_{Y|X}^m)}_{m\in \mathbb{N}}$ be an estimator satisfying Assumption 2. We then have the following consistency result. For all $x\in \mathcal{X},\delta >0$ and $\alpha >0$, there exists $N\in \mathbb{N}$ such that for all $n\ge N$ we can find $M_n\in \mathbb{N}$ such that for all $m\ge M_n$ we have that(6) $$\mathbb{P}\left(\left|{\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)(x)-f_{\text{AVE}(X\to Y)}(x)\right|>\delta \right)\le \alpha .$$(6)

Apart from the LSCM structure, the above result does not rely on any particular distributional properties of the data. Assumptions 1 and 2 do not impose strong restrictions on the data-generating process and hold true for several model classes, including linear and nonlinear models. In Appendix D, we provide sufficient conditions under which these assumptions are true.

2.3.2 An Example LSCM

To illustrate the consistency result in Theorem 1, we now consider a simple example with one covariate (d = 1) and two hidden variables ($\mathcal{l}=2$).

Example 1

(Latent Gaussian process and a linear average causal effect). Let $\mathit{\zeta },\mathit{\psi },{\mathit{\xi }}^t,{\mathit{\epsilon }}^t$, $t\in \mathbb{N}$, be independent versions of a univariate stationary spatial Gaussian process with mean 0 and covariance function $u\mapsto \hspace{0.17em}\text{exp}\hspace{0.17em}(-\frac{1}{2}|\left|u\right|{|}_2)$. For notational simplicity, let $\overline{\mathbf{H}}$ and $\tilde{\mathbf{H}}$ denote the respective first and second coordinate process of H. We define a marginal distribution over H and conditional distributions $\mathbf{X} | \mathbf{H}$ and $\mathbf{Y} | (\mathbf{X},\mathbf{H})$ by specifying that for all $(s,t)\in {\mathbb{R}}^2\times \mathbb{N}$,$$\begin{array}{cc}{H}_s^t\hfill & =({\overline{H}}_s^t,{\tilde{H}}_s^t)=({\zeta }_s,1+\frac{1}{2}{\zeta }_s+\frac{\sqrt{3}}{2}{\psi }_s),\hfill \\ X_s^t\hfill & =\hspace{0.17em}\text{exp}\hspace{0.17em}(-|\left|s\right|{|}_2^2/1000)+(0.2+0.1·\hspace{0.17em}\text{sin}\hspace{0.17em}(2\pi t/100))\hfill \\ \hfill & \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}·{\overline{H}}_s^t·{\tilde{H}}_s^t+0.5·{\xi }_s^t,\hfill \\ Y_s^t\hfill & =(1.5+{\overline{H}}_s^t·{\tilde{H}}_s^t)·X_s^t+{({\overline{H}}_s^t)}^2+\left|{\tilde{H}}_s^t\right|·{\epsilon }_s^t.\hfill \end{array}$$

Interventions on X, Y, or H are defined as in Definition 1. In this LSCM, the average causal effect $f_{\text{AVE}(X\to Y)}$ is the linear function $x\mapsto {\beta }_0+{\beta }_{1}x$, with ${\beta }_0:=\mathbb{E}[{({\overline{H}}_0^1)}^2]=1$ and ${\beta }_1:=1.5+\mathbb{E}[{\overline{H}}_0^1·{\tilde{H}}_0^1]=2$. We define a spatial sampling scheme ${(s_i)}_{i\in \mathbb{N}}$ for every $j\in \mathbb{N}$ and $k\in \{1,\dots ,25\}$ by $s_{25·(j-1)+k}=(j,k)$. Given a sample $({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)={(X_s^t,Y_s^t)}_{(s,t)\in \{s_1,\dots ,s_n\}\times \{1,\dots ,m\}}$ from $(\mathbf{X},\mathbf{Y})$, we construct an estimator of $f_{\text{AVE}(X\to Y)}$ by(7) $${\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)(x)=\frac{1}{n}\sum _{i=1}^n(1x) {\widehat{\beta }}_{\mathit{OLS}}^m({\mathbf{X}}_{s_i}^m,{\mathbf{Y}}_{s_i}^m),$$(7) where ${\widehat{\beta }}_{\text{OLS}}^m({\mathbf{X}}_{s_i}^m,{\mathbf{Y}}_{s_i}^m)\in {\mathbb{R}}^2$ is the OLS estimator for the linear regression at spatial location s_i , that is of ${\mathbf{Y}}_{s_i}^m=(Y_{s_i}^1,\dots ,Y_{s_i}^m)$ on ${\mathbf{X}}_{s_i}^m=(X_{s_i}^1,\dots ,X_{s_i}^m)$ (we assume that the regression includes an intercept term). It follows by Propositions 1 and 2 (see in particular Example 4 and Remark 6 in Appendix E) that Assumptions 1 and 2 are satisfied. ² Hence, (7) is a consistent estimator of $f_{\text{AVE}(X\to Y)}$.

Figure 3 illustrates our procedure using a numerical experiment based on Example 1. ³ The example shows that we can estimate causal effects even under complex influences of the latent process H. To construct the estimator ${\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}$, we have used that the influence of $(\mathbf{X},\mathbf{H})$ on Y is linear in X. However, we do not assume knowledge of the particular functional dependence of Y on H; we obtain consistency under any influence of the form $Y_s^t=f_1(H_s^t)·X_s^t+f_2(H_s^t,{\epsilon }_s^t)$, see Proposition 2.

Fig. 3 Results for applying our methodology to Example 1. The left panel shows a sample dataset of $(\mathbf{X},\mathbf{Y},\mathbf{H})$ observed at the spatial grid ${\{1,\dots ,25\}}^2$ and at several time instances. The middle panel illustrates our method applied to the same dataset. The average causal effect, our inferential target, is indicated by a green line. Due to confounding by $H_s^t$, a standard nonlinear regression (red curve) severely overestimates the causal influence of $X_s^t$ on $Y_s^t$. By regressing $Y_s^t$ on $X_s^t$ in each location separately (thin blue lines), and aggregating the results into a final estimate (thick blue line), all spatial confounding is removed. In the right panel, we investigate the consistency result from Theorem 1 empirically. For increasing n and m, we generate several datasets $({\mathbf{X}}_{n,i}^m,{\mathbf{Y}}_{n,i}^m),i=1,\dots ,100$, compute estimates ${\widehat{\beta }}_i^{nm}$ of the causal coefficients β, and use these to compute empirical error probabilities $\widehat{\mathbb{P}}(||{\widehat{\beta }}^{nm}-\beta |{|}_2>\delta )$. In the above plot, we have chosen $\delta =0.2$. As n and m increase, the error probability tends toward zero.

2.3.3 Extensions

Our methodology can be extended in several directions. In Appendix B, we provide details on how to model the influence of observed (time- and space-varying) confounders and temporally lagged causal effects of X on Y. We furthermore argue that our method also applies in situations where the roles of time and space are interchanged, that is, when the hidden confounders are time-varying, but remain static across space. The extension which includes observed confounders is furthermore explored empirically in Appendix F.1.

3 Testing for the Existence of Causal Effects

The previous section has been concerned with the quantification and estimation of the causal effect of X on Y. In this section, we introduce hypothesis tests for this effect being zero. We consider the null hypothesis$$\begin{array}{cc}{H}_0:\hfill & (\mathbf{X},\mathbf{Y})\mathrm{ }\text{come}\mathrm{ }\text{from}\mathrm{ }\text{an}\mathrm{ }\text{LSCM}\mathrm{ }\text{with}\text{ a }\text{function}\mathrm{ }f\hfill \\ \hfill & \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\text{that is constant w}.\mathrm{r}.\mathrm{t}.X_s^t,\hfill \end{array}$$which formalizes the assumption of “no causal effect of X on Y” within the LSCM framework. We construct a hypothesis test for H ₀ using data resampling. Our approach acknowledges the existence of spatial dependence in the data without modeling it explicitly. It thus does not rely on distributional assumptions apart from the LSCM structure.

For the construction of a resampling test, we closely follow the setup presented in Pfister et al. (2018). We require a data permutation scheme which, under the null hypothesis, leaves the distribution of the data unaffected. In particular, it must preserve the dependence between X and Y that is induced by H. The idea is to permute observations of Y corresponding to the same (unobserved) values of H. Since H is assumed to be constant within every spatial location, this is achieved by permuting Y along the time axis. Let $({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)$ be the observed data. For every $(\mathbf{x},\mathbf{y})\in {\mathbb{R}}^{(d+1)\times n\times m}$ and every permutation σ of the elements in $\{1,\dots ,m\}$, let $\sigma (\mathbf{x},\mathbf{y})\in {\mathbb{R}}^{(d+1)\times n\times m}$ denote the permuted array with entries ${(\sigma (x,y))}_s^t=(x_s^t,y_s^{\sigma (t)})$. We then have the following exchangeability property.

Proposition 3

(Exchangeability). For any permutation σ of the elements in $\{1,\dots ,m\}$, we have that, under H ₀, $\sigma ({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)$ is equal in distribution to $({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)$.

Proposition 3 is the cornerstone for the construction of a valid resampling test. Under the null hypothesis, we can compute pseudo-replications of the observed sample $({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)$ using the permutation scheme described above. Given any test statistic $\widehat{T}:{\mathbb{R}}^{(d+1)\times n\times m}\to \mathbb{R}$, we obtain a p-value for H ₀ by comparing the value of $\widehat{T}$ calculated on the original dataset with the empirical null distribution of $\widehat{T}$ obtained from the resampled datasets. The choice of $\widehat{T}$ determines the power of the test. More formally, let $M:=m!$ and let ${\sigma }_1,\dots ,{\sigma }_M$ be all permutations of the elements in $\{1,\dots ,m\}$. By Proposition 3, each σ_i yields a new dataset with the same distribution as $({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)$. Let $B\in \mathbb{N}$ and let $k_1,\dots ,k_B$ be independent, uniform draws from $\{1,\dots ,M\}$. For every $(\mathbf{x},\mathbf{y})$, we define$$p_{\widehat{T}}(\mathbf{x},\mathbf{y}):=\frac{1+\left|\right\{b\in \{1,\dots ,B\}:\widehat{T}({\sigma }_{k_b}(\mathbf{x},\mathbf{y}))\ge \widehat{T}(\mathbf{x},\mathbf{y})\left\}\right|}{1+B},$$and construct for every $\alpha \in (0,1)$ a test ${\phi }_{\widehat{T}}^{\alpha }:{\mathbb{R}}^{(d+1)\times n\times m}\to \{0,1\}$ of H ₀ defined by ${\phi }_{\widehat{T}}^{\alpha }=1:\iff p_{\widehat{T}}\le \alpha$. ⁴ The following level guarantee for ${\phi }_{\widehat{T}}^{\alpha }$ follows directly from (Pfister et al. 2018, prop. B.4).

Corollary 1

(Level guarantee of resampling test). Assume that for all $k,\mathcal{l}\in \{1,\dots ,B\},k\cancel{=}\mathcal{l}$, it holds that, under H ₀, $\mathbb{P}(\widehat{T}({\sigma }_k({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m))=\widehat{T}({\sigma }_{\mathcal{l}}({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)))=0$. Then, for every $\alpha \in (0,1)$, the test ${\phi }_{\widehat{T}}^{\alpha }$ has correct level α.

Corollary 1 ensures valid test level for a large class of test statistics. The particular choice of test statistic should depend on the alternative hypothesis that we seek to have power against. Within the LSCM model class, it makes sense to quantify deviations from the null hypothesis using functionals of the average causal effect, that is, $T=\psi (f_{\text{AVE}(X\to Y)})$ for some suitable function ψ. As a test statistic, we then use the plug-in estimator $\widehat{T}({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)=\psi ({\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)).$ An implementation of the above testing procedure is contained in our code package, see Section 1.4. A power-analysis can be found in Appendix F.3.

4 Conflict and Forest Loss in Colombia

We return to the problem of conflict (X) and forest loss (Y). As discussed in Section 1.3, there may exist several confounders of the (potential) causal effect of X on Y. We believe that many of these vary at a relatively low temporal frequency (e.g., population density, market infrastructure), justifying the application of the methods developed above.

4.1 Data Description and Preprocessing

Our analysis is based on two main datasets: (i) a remote sensing-based forest loss dataset for the period 2000–2018, which identifies annual forest loss at a spatial resolution of $30\mathrm{m}\times 30\mathrm{m}$ using Landsat satellites (Hansen et al. 2013). Here, forest loss is defined as complete canopy removal. (ii) Spatially explicit information on conflict events from 2000 to 2018, based on the Georeferenced Event Dataset (GED) from the Uppsala Conflict Data Program (UCDP) (Croicu and Sundberg 2015). In this dataset, a conflict event is defined as “an incident where armed force was used by an organized actor against another organized actor, or against civilians, resulting in at least one direct death at a specific location and a specifc date”. Such events were identified through global newswire reporting, global monitoring of local news, and other secondary sources such as reports by non-governmental organizations (for information on the data collection as well as control for quality and consistency of the data, please refer to Croicu and Sundberg 2015). We homogenized these datasets through aggregation to a spatial resolution of $10 \text{km}\times 10 \text{km}$ by averaging the annual forest loss within each grid, and by counting all conflict events occurring in the same year and within the same grid. As a proxy for accessibility, we additionally calculated, for each spatial grid, the average Euclidean distance to the closest road segment, using spatial data from https://diva-gis.org containing all primary and secondary roads in Colombia. We regard this variable as relatively constant throughout the considered time-span.

4.2 Quantifying the Causal Influence of Conflict on Forest Loss

We assume that $(\mathbf{X},\mathbf{Y})$ come from an LSCM as defined in Definition 2. Since $X_s^t$ is binary, we can characterize the causal influence of X on Y by $T:=f_{\text{AVE}(X\to Y)}(1)-f_{\text{AVE}(X\to Y)}(0)$, that is, the difference in expected forest loss $\mathbb{E}[Y_s^t]$ under the respective interventions enforcing conflict ($X_s^t:=1$) and peace ($X_s^t:=0$). Positive values of T correspond to an augmenting effect of conflict on forest loss and negative values correspond to a reducing effect. Our goal is to estimate T, and to test the hypothesis $H_0:T=0$ (no causal effect of X on Y). To construct an estimator of the average causal effect of the form (5)(5) $${\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)(x):=\frac{1}{n}\sum _{i=1}^n{\widehat{f}}_{Y|X}^m({\mathbf{X}}_{s_i}^m,{\mathbf{Y}}_{s_i}^m)(x),$$(5) , we require estimators of the conditional expectations $x\mapsto f_{Y|(X,H)}(x,h)$. Since $X_s^t$ is binary, we use simple sample averages of the response variable. To make the resulting estimator of $f_{\text{AVE}(X\to Y)}$ well-defined, we omit all locations which do not contain at least one observation from each of the regimes $X_s^t=0$ and $X_s^t=1$. More precisely, let $({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)$ be the observed dataset. We then use the estimator(8) $${\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)(x)=\frac{1}{\left|{\mathcal{I}}_n^m\right|}\sum _{i\in {\mathcal{I}}_n^m}\frac{1}{\left|\right\{t:X_{s_i}^t=x\left\}\right|}\sum _{t:X_{s_i}^t=x}{Y}_{s_i}^t,$$(8)

$x\in \{0,1\}$, where ${\mathcal{I}}_n^m:=\{i\in \{1,\dots ,n\} : \exists t_0,t_1\in \{1,\dots ,m\}\mathrm{ }\text{such}\mathrm{ }\text{that}\mathrm{ }{X}_{s_i}^{t_0}=0\mathrm{ }\text{and}\mathrm{ }{X}_{s_i}^{t_1}=1\}$. To test H ₀, we use the resampling test from Section 3 with $\widehat{T}={\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}(1)-{\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}(0)$. In Appendix F.4, we argue that, under additional assumptions on the underlying LSCM, the above estimator is approximately unbiased. Note, however, that even if the above estimator is biased, this does not affect the level guarantee of our testing procedure—we obtain a valid test level for any test statistic $\widehat{T}$ satisfying the assumptions of Corollary 1.

4.3 Alternative Assumptions on the Causal Structure

To emphasize the relevance of the assumed causal structure, we compare our method with two alternative approaches based on different assumptions about the ground truth: Model 1 assumes no confounders of $(\mathbf{X},\mathbf{Y})$ and Model 2 assumes that the only confounder is the observed process W (mean distance to a road). In reality, we expect the existence of several confounders in addition to W, for example, population density or market infrastructure. Even though none of the models may be a precise description of the data-generating mechanism, we therefore regard both Models 1 and 2 as less realistic than the LSCM. In both models we can, similarly to Definition 3, define the average causal effect of X on Y. Under Model 1, $f_{\text{AVE}(X\to Y)}$ coincides with the conditional expectation of $Y_s^t$ given $X_s^t$, which can be estimated simply using sample averages (as is done in Figure 1 left). Under Model 2, $f_{\text{AVE}(X\to Y)}$ can, analogously to Proposition 2, be computed by adjusting for the confounder W. For each $x\in \{0,1\}$, we obtain an estimate ${\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}(x)$ by calculating sample averages of Y across different subsets $\{(s,t)\in {\mathbb{R}}^2\times \mathbb{N} : X_s^t=x, W_s^t\in {\mathcal{W}}_j\},j\in \mathcal{J}$ (we here construct these by considering 100 equidistant quantiles of W), and subsequently averaging over the resulting values. In both models, we furthermore test the hypothesis of no causal effect of X on Y using approaches similar to the ones presented in Section 3. Under the LSCM assumption, we have constructed a permutation scheme that permutes the values of Y along the time axis, to preserve the dependence between Y and H, see Proposition 3. Similarly, we construct a permutation scheme for Model 2 by permuting observations of Y corresponding to similar values of the confounder W (i.e., values within the same quantile range). Under the null hypothesis corresponding to Model 1, X and Y are (unconditionally) independent, and we therefore permute the values of Y completely at random. Strictly speaking, the permutation schemes for Models 1 and 2 require additional exchangeability assumptions on Y in order to yield valid tests. In Appendix G, we repeat the analysis for Model 1 using a spatial block-permutation to account for the spatial dependence in Y, and obtain similar results.

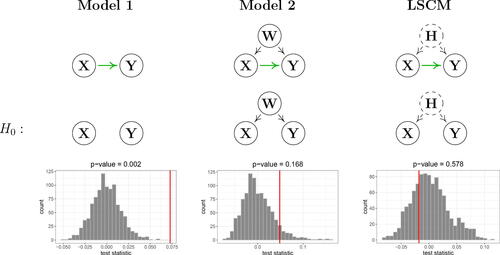
4.4 Results

The results of applying our method and the two alternative approaches to the entire study region are depicted in Figure 4. Under Model 1, there is an enhancing, highly significant causal effect of conflict on forest loss ($\widehat{T}=0.073$, P = 0.002). When adjusting for accessibility (quantified by W, Model 2), the size of the estimated causal effect shrinks, and becomes insignificant ($\widehat{T}=0.049$, P = 0.168). (Note that we have considered other confounders, too, yet obtained similar results. For example, when adjusting for population density, which we consider as moderately temporally varying, we obtain $\widehat{T}=0.038$ and P = 0.214.) When applying the methodology proposed in this article, that is, adjusting for all time-invariant confounders, the estimated effect swaps sign ($\widehat{T}=-0.018,P=0.578$), but is insignificant. We also tested for spatial spill-over effects by modeling causal effects that are spatially lagged by up to one or two pixels, respectively. In both cases, the effect was negative and insignificant (results not shown here). One reason for the above non-finding could be the time delay between the proposed cause (conflict) and effect (forest loss). To account for this potential issue, we also test for a causal effect of X on Y that is temporally lagged by one year, that is, we use an estimator similar to (8)(8) $${\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}({\mathbf{X}}_n^m,{\mathbf{Y}}_n^m)(x)=\frac{1}{\left|{\mathcal{I}}_n^m\right|}\sum _{i\in {\mathcal{I}}_n^m}\frac{1}{\left|\right\{t:X_{s_i}^t=x\left\}\right|}\sum _{t:X_{s_i}^t=x}{Y}_{s_i}^t,$$(8) , where we compare the average forest loss succeeding conflict events with the average forest loss succeeding non-conflict events. Again, the estimated influence of X on Y is negative and insignificant ($\widehat{T}=-0.0293$, P = 0.354). Additionally, we perform alternative versions of the last two tests to account for potential autocorrelation in the response variable, by adopting a temporal block-permutation scheme. In both cases, the test is insignificant, see Appendix G.

Fig. 4 Testing for a causal influence of conflict (X) on forest loss (Y) using our method (right) and two alternative approaches (left and middle) which are based on different and arguably less realistic assumptions on the causal structure. The process W corresponds to the mean distance to a road, and H represents unobserved time-invariant confounders. Each of the above models gives rise to a different expression for the test statistic $\widehat{T}={\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}(1)-{\widehat{f}}_{\text{AVE}(X\to Y)}^{nm}(0)$ (indicated by red vertical bars), see Sections 4.2 and 4.3. The gray histograms illustrate the empirical null distributions of $\widehat{T}$ under the respective null hypotheses obtained from 999 resampled datasets. The results show that our conclusions about the causal influence of conflict on forest loss strongly depend on the assumed causal structure: under Model 1, there is a positive, highly significant effect ($\widehat{T}=0.073$). When adjusting for the confounder W, the effect size decreases and becomes insignificant ($\widehat{T}=0.049$). When applying our proposed methodology, the estimated effect is negative ($\widehat{T}=-0.018$).

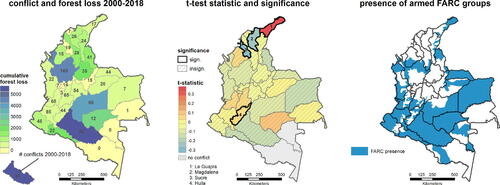
The above analysis provides an estimate for the average causal effect, see Equation (3)(3) $$f_{\text{AVE}(X\to Y)}(x):=\mathbb{E}[f(x,H_0^1,{\epsilon }_0^1)].$$(3) , which, in particular, averages over space. Given that Colombia is a country with high ambiental and socio-economic heterogeneity, we furthermore conduct an analysis at the department level (see Figure 5). In fact, there is considerable spatial variation in the estimated causal effects, with significant positive as well as negative effects (Figure 5 middle). This variation may be seen as evidence for an interaction effect between conflict and the assumed hidden confounders. In most departments, the estimated causal effect is negative (although mostly insignificant), meaning that conflict tends to decrease forest loss. The strongest positive and significant causal influence is identified in the La Guajira department ($\widehat{T}=0.398$, P = 0.047). Although this region is commonly associated with semi-arid to very dry conditions, most conflicts occured in the South-Western areas, at the beginning of Caribbean tropical forests (see Figure 1). In fact, these zones have also been also identified by Negret et al. (2019) as having been strongly affected by deforestation pressure in the wake of conflict. Interestingly, the neighboring Magdalena department shows the opposite effect ($\widehat{T}=-0.218$, P = 0.004). The positive effect in the department of Huila ($\widehat{T}=0.095$, P = 0.023) is again in line with the findings by Negret et al. (2019) (based on a visual inspection of their attribution maps). Out of the 8 departments that are mostly controlled by FARC (Figure 5 right), 6 have a negative test statistic, meaning that conflict reduces forest loss. This can be explained in part by the internal governance of this group, where forest cover was a strategic advantage for both their own protection as well as for cocaine production. Overall, of course, the peace-induced acceleration of forest loss has to be discussed with caution, and should not be interpreted reversely as if conflict per se is a measure of environmental protection (Clerici et al. 2020).

Fig. 5 Regional analysis of conflict and forest loss in Colombia. The left panel shows the total forest loss and the total number of conflict events 2000–2018 at department level. The most severe incidences of forest loss occur in the northern Andean forests and on the northern borders of the Amazon region. In the middle panel, we report for each department estimates $\widehat{T}$ and test results for $H_0:T=0$, using the methodology described in Sections 2 and 3. We used a test level of $\alpha =0.05$, and report significances without multiple-testing adjustment. In most departments, the estimated causal effect is negative (blue, conflict reduces forest loss), although mainly insignificant. We identify four departments with statistically significant results, hereof two with a positive causal effect (La Guarija and Huila) and two with a negative causal effect (Magdalena and Sucre). In total, there are 8 departments that are mostly controlled by FARC (above 75% FARC presence, right panel). Out of these, 6 departments have a negative test statistic (conflict reduces forest loss).

4.5 Interpretation in Light of the Colombian Peace Process

In late 2012, negotiations that later would be known as the “Colombian peace process” started between the then president of Colombia and the strongest group of rebels, the FARC, lasting until 2016. Peace was declared by both parties upon a revised agreement in October 2016, and became effective in 2017. ⁵ The negotiations marked a steadily decreasing number of conflicts (Figure 6, left). Since this decrease is the result of governmental intervention, rather than a natural resolution of local tensions, the peace process provides an opportunity to verify the intervention effects estimated in Section 4.4. As can be seen in Figure 6 (right), Colombia experienced a steep increase in the total forest loss in the final phase of the peace negotiations. Although there may be several other factors which have contributed to this development, we observe that these results align with our previous finding of an overall negative causal effect of conflict on forest loss ($\widehat{T}<0$).

Fig. 6 Number of conflicts (left) and forest loss (right) in the years 2000–2018 in Colombia. In the right panel, the height of the curve at $x+0.5$ indicates the forest loss between years x and x + 1. Shaded areas mark the Colombian peace process (2012–2016).

5 Conclusions and Future Work

In this article, we have investigated the relationship between conflict and forest loss in Colombia based on yearly measurements from 2000 to 2018. Our methodology allows for a causal rather than a purely predictive analysis. We find that conflicts are predictive of exceedances in forest loss, but we find no significant evidence of a causal relation when analyzing this problem on country level: once all (time-invariant) confounders are adjusted for, there is a negative but insignificant correlation between conflict and forest loss. Our analysis on department level suggests that this nonfinding could be due to locally varying effects of opposite directionality, which would approximately cancel out in our final estimate. In most departments, we find negative (mostly insignificant) effects, although we also identify a few departments where conflict seems to have increased forest loss. It would be interesting to furthermore explore these differences in causal dependence, for example, by adjusting for socio-political factors. The overall negative influence of conflict on forest loss estimated by our method is in line with the observation that during the final phase of the peace process, which stopped many of the existing conflicts, the total forest loss in Colombia has increased. However, these results should be interpreted with caution. Overall, we find that, once all time-invariant confounders are adjusted for, conflicts have only weak explanatory power for predicting forest loss, and the potential causal effect is therefore likely to be small, compared to other drivers of forest loss. Furthermore, our results rely on the assumption that all latent confounders are time-invariant, which, in practice, can only be expected to hold approximately. In Appendix F.1, we explore how our estimator is affected by temporal variation in the latent confounders.

To analyze the relation between conflict and forest loss, we have introduced a novel causal framework for spatio-temporal data. From a methodological perspective, this article contains three main contributions: the definition of a class of causal models for multivariate spatio-temporal stochastic processes, a procedure for estimating causal effects within this model class, and a nonparametric hypothesis test for the overall existence of such effects. Our method allows for the influence of arbitrarily many latent confounders, as long as these confounders do not vary across time (or space). We prove asymptotic consistency of our estimator, and verify this finding empirically using simulated data. Our results hold under weak assumptions on the data generating process, and do not rely on any particular distributional properties of the data. We prove sufficient conditions under which these rather general assumptions hold true. The proposed testing procedure is based on data resampling and provably obtains valid level in finite samples.

Acknowledgments

This work contributes to the Global Land Programme, and was supported by Carlsberg Foundation (JP) and a research grant (18968) from VILLUM FONDEN (RC, JP). MDM thanks ESA for funding the Earth System Data Lab. We are grateful to Steffen Lauritzen, Niels Richard Hansen and Niklas Pfister for valuable comments on the methodology, and to Lina Estupinan-Suarez and Alejandro Salazar for helpful discussions on the case study. We thank two anonymous referees and the associate editor for many helpful comments.

Supplementary Material

The supplementary material is structured as follows. Appendix A contains a review of existing causal methodology, Appendix B explores several extensions of our methods, and Appendix C proposes an alternative definition of the average causal effect, our inferential target. In Appendix D, we provide sufficient conditions for Assumptions A1 and A2, and Appendix E provides two examples of data generating processes which satisfy these assumptions. Appendix F contains several simulation experiments which investigate the numerical performance of our methods, Appendix G shows results of the case study where we use adapted versions of our testing procedure, and Appendix H contains all proofs.

Additional information

Funding

This work contributes to the Global Land Programme, and was supported by Carlsberg Foundation (JP) and a research grant (18968) from VILLUM FONDEN (RC, JP). MDM thanks ESA for funding the Earth System Data Lab. We are grateful to Steffen Lauritzen, Niels Richard Hansen and Niklas Pfister for valuable comments on the methodology, and to Lina Estupinan-Suarez and Alejandro Salazar for helpful discussions on the case study. We thank two anonymous referees and the associate editor for many helpful comments.

Notes

1 We are grateful to Steffen Lauritzen for emphasizing this viewpoint.

2 Strictly speaking, Example 4 and Remark 6 in Appendix E show that (L1)–(L3) are satisfied for bounded basis functions. We are confident that the same holds true in the current example.

3 In this example, a standard regression approach overestimates the causal effect. Similarly, one can construct examples where the causal effect would be underestimated.

4 Two-sided tests can be obtained using $p_{\widehat{T},2-\text{sided}}:=\min (1,2·\min (p_{\widehat{T}},p_{-\widehat{T}}))$, for example.

5 The agreement was signed only by the FARC, while other guerilla groups remain active.