Dynamic Causal Effects Evaluation in A/B Testing with a Reinforcement Learning Framework

Abstract

A/B testing, or online experiment is a standard business strategy to compare a new product with an old one in pharmaceutical, technological, and traditional industries. Major challenges arise in online experiments of two-sided marketplace platforms (e.g., Uber) where there is only one unit that receives a sequence of treatments over time. In those experiments, the treatment at a given time impacts current outcome as well as future outcomes. The aim of this article is to introduce a reinforcement learning framework for carrying A/B testing in these experiments, while characterizing the long-term treatment effects. Our proposed testing procedure allows for sequential monitoring and online updating. It is generally applicable to a variety of treatment designs in different industries. In addition, we systematically investigate the theoretical properties (e.g., size and power) of our testing procedure. Finally, we apply our framework to both simulated data and a real-world data example obtained from a technological company to illustrate its advantage over the current practice. A Python implementation of our test is available at https://github.com/callmespring/CausalRL. Supplementary materials for this article are available online.

Keywords:

• A/B testing
• Causal inference
• Online experiment
• Online updating
• Reinforcement learning
• Sequential testing

1 Introduction

A/B testing, or online experiment is a business strategy to compare a new product with an old one in pharmaceutical, technological, and traditional industries (e.g., google, Amazon, or Facebook). It has become the gold standard to make data-driven decisions on a new service, feature, or product. For example, in web analytics, it is common to compare two variants of the same webpage (denote by A and B) by randomly splitting visitors into A and B and then contrasting metrics of interest (e.g., click-through rate) on each of the splits. There is a growing literature on developing A/B testing methods (see e.g., Kharitonov et al. 2015; Johari et al. 2017; Yang et al. 2017, and the references therein). The key idea of these approaches is to apply causal inference methods to estimating the treatment effect of a new change under the assumption of the stable unit treatment value assumption (SUTVA, Rubin 1980; Imbens and Rubin 2015; Wager and Athey 2018, and the references therein). SUTVA precludes the existence of the interference effect such that the response of each subject in the experiment depends only on their own treatment and is independent of others’ treatments. Despite its ubiquitousness, however, the standard A/B testing is not directly applicable for causal inference under interference (Zhou et al. 2020).

In this article, we focus on the setting where there is only one unit (or system) in the experiment that receives a sequence of treatments over time. In many applications, the treatment at a given time can impact future outcomes, leading SUTVA being invalid. These studies frequently occur in the two-sided markets (intermediary economic platforms having two distinct user groups that provide each other with network benefits) that involve sequential decision making over time. As an illustration, we consider evaluating the effects of different order dispatching strategies in ride-sharing companies (e.g., Uber) for large-scale fleet management. See our real data analysis in Section 5 for details. These companies form a typical two-sided market that enables efficient interactions between passengers and drivers (Rysman 2009). With the rapid development of smart mobile phones and internet of things, they have substantially transformed the transportation landscape of human beings (Jin et al. 2018). Order dispatching is one of the most critical problems in online ride-sharing platforms to adapt the operation and management strategy to the dynamics in demand and supply. At a given time, an order dispatching strategy not only affects the platform’s immediate outcome (e.g., passengers’ answer time, drivers’ income), but also impacts the spatial distribution of drivers in the future. This in turn affects the platform’s future outcome. The no interference assumption is thus, violated.

A fundamental question of interest that we consider here is how to develop valid A/B testing methods in the presence of interference. Solving this fundamental question faces at least three major challenges. (i) The first one lies in establishing causal relationship between treatments and outcomes over time, by taking the carryover effect into consideration. Most of the existing A/B testing methods are ineffective. They fail to identify the carryover effect, leading the subsequent inference being invalid. See Section 3.1 for details. (ii) The second one is that running each experiment takes a considerable time. The company wishes to terminate the experiment as early as possible in order to save both time and budget. As such, the testing hypothesis needs to be sequentially evaluated online as the data are being collected, and the experiment shall be stopped in accordance with a predefined stopping rule as soon as significant results are observed. (iii) The third one is that treatments are desired to be allocated in a manner to maximize the cumulative outcomes or to detect the alternative more efficiently. The testing procedure shall allow the treatment to be adaptively assigned. Addressing these challenges requires the development of new tools and theory for A/B testing and causal effects evaluation.

1.1 Contributions

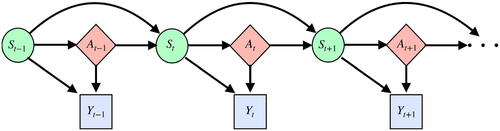
We summarize our contributions as follows. First, to address the challenge mentioned in (i), we introduce a reinforcement learning (RL, see, e.g., Sutton and Barto 2018, for an overview) framework for A/B testing. RL is suitable framework to handle the carryover effects over time. In addition to the treatment-outcome pairs, it is assumed that there is a set of time-varying state confounding variables. We model the state-treatment-outcome triplet by using the Markov decision process (MDP, see, e.g., Puterman 1994) to characterize the association between treatments and outcomes across time. Specifically, at each time point, the decision maker selects a treatment based on the observed state variables. The system responds by giving the decision maker a corresponding outcome and moving into a new state in the next time step. In this way, past treatments will have an indirect influence on future rewards through its effect on future state variables. See Figure 1 for an illustration. In addition, the long-term treatment effects can be characterized by the value functions (see Section 2.1 for details) that measure the discounted cumulative gain from a given initial state. Under this framework, it suffices to evaluate the difference between two value functions to compare different treatments. Our proposal gives an example of how to utilize some state-of-the-art machine learning tools, such as reinforcement learning, to address a challenging statistical inference problem for making business decisions.

Fig. 1 Causal diagram for MDP under settings where treatments depend on current states only. $(S_t,A_t,Y_t)$ represents the state-treatment-outcome triplet. Solid lines represent causal relationships.

Second, to address the challenges mentioned in (ii) and (iii), we propose a novel sequential testing procedure for detecting the difference between two value functions. Our proposed test integrates reinforcement learning and sequential analysis (see e.g., Jennison and Turnbull 1999, and the references therein) to allows for sequential monitoring and online updating.¹ Meanwhile, our proposal contributes to each of these two areas as well.

• To the best of our knowledge, this is the first work on developing valid sequential tests in the RL framework. Our work is built upon the temporal-difference learning method based on function approximation (see e.g., Sutton, Szepesvári, and Maei 2008). In the computer science literature, convergence guarantees of temporal difference learning have been derived by Sutton, Szepesvári, and Maei (2008) under the setting of independent noise and by Bhandari, Russo, and Singal (2018) for Markovian noise. However, uncertainty quantification and asymptotic distribution of the resulting value function estimators have been less studied. Such results are critical for carrying out A/B testing. Recently, Luckett et al. (2020) outlined a procedure for estimating the value under a given policy. Shi et al. (2021) developed a confidence interval for the value function. However, these method do not allow for sequential monitoring or online updating.

• Our proposal is built upon the α-spending approach (Lan and DeMets 1983) for sequential testing. We note that most test statistics in classical sequential analysis have the canonical joint distribution (see eq. (3.1) in Jennison and Turnbull 1999) and their associated stopping boundary can be recursively updated via numerical integration. However, in our setup, test statistics no longer have the canonical joint distribution. This is due to the existence of the carryover effects in time. We discuss this in detail in Section 3.4. As such, the numerical integration approach is not applicable to our setting. To resolve this issue, we propose a bootstrap-assisted procedure to determine the stopping boundary. It is much more computationally efficient than the classical wild bootstrap algorithm (Wu 1986, see Section 3.4 for details). The resulting test is generally applicable to a variety of treatment designs, including the Markov design, the alternating-time-interval design and the adaptive design (see Section 3.3 for details).

Third, we systematically investigate the asymptotic properties of our testing procedure. We show that our test not only maintains the nominal Type I error rate, but also has nonnegligible powers against local alternatives. In particular, we show that when the sieve method is used for function approximation in temporal difference learning, undersmoothing is not needed to guarantee that the resulting value estimator has a tractable limiting distribution. This occurs because sieve estimators of conditional expectations are idempotent (Newey, Hsieh, and Robins 1998). It implies that the proposed test will not be overly sensitive to the choice of the number of basis functions. To our knowledge, these results have not been established in the existing RL framework. Please see Section 3.3 for details.

Finally, our proposal addresses an important business question in ride-sharing companies. In particular, our methodology allows the company to evaluate different policies more accurately in the presence of carryover effects. It also allows the company to terminate the online experiment earlier and to evaluate more policies within the same time frame. These policies have the potential to improve drivers’ salary and meet more customer requests, providing a more efficient transportation network. Please see Section 5 for details.

1.2 Related Work

There is a huge literature on RL in the computer science community such that various algorithms are proposed for an agent to learn an optimal policy and interact with an environment. Recently, a few methods have been developed in the statistics literature on learning the optimal policy in mobile health applications (Ertefaie 2014; Luckett et al. 2020; Hu et al. 2020; Liao, Qi, and Murphy 2020). In addition, there is a growing literature on adapting reinforcement learning to develop dynamic treatment regimes in precision medicine, to recommend treatment decisions based on individual patients’ information (Murphy 2003; Chakraborty, Murphy, and Strecher 2010; Qian and Murphy 2011; Zhao et al. 2012; Zhang et al. 2013; Song et al. 2015; Zhao et al. 2015; Zhu et al. 2017; Zhang et al. 2018; Wang et al. 2018; Shi et al. 2018a, 2018b; Mo, Qi, and Liu 2020; Meng et al. 2020).

Our work is closely related to the literature on off-policy evaluation, whose objective is to estimate the value of a new policy based on data collected by a different policy. Existing literature can be cast into model-based methods, importance sampling (IS)-based and doubly-robust procedures. Model-based methods first fit an MDP model from data and then compute the resulting value function. The estimated value function might suffer from a large bias due to potential misspecification of the model. Popular IS based methods include Thomas, Theocharous, and Ghavamzadeh (2015), Thomas and Brunskill (2016), and Liu et al. (2018). These methods reweight the observed rewards with the density ratio of the target and behavior policies. The value estimate might suffer from a large variance, due to the use of importance sampling. Doubly-robust methods (see, e.g., Jiang and Li 2016; Kallus and Uehara 2019) learn the Q-function as well as the probability density ratio and combine these estimates properly for more robust and efficient value evaluation. However, both IS and doubly-robust methods required the treatment assignment probability (propensity score) to be bounded away from 0 and 1. As such, they are inapplicable to the alternating-time-interval design, which is the treatment allocation strategy in our real data application (see, Section 5 for details).

In addition to the literature on RL, our work is also related to a line of research on causal inference with interference. Most of the works studied the interference effect across different subjects (see e.g., Hudgens and Halloran 2008; Pouget-Abadie et al. 2019; Li et al. 2019; Zhou et al. 2020; Reich et al. 2020). That is, the outcome for one subject depends on the treatment assigned to other subjects as well. To the contrary, our work focuses on the interference effect over time. We also remark that most of the aforementioned methods were primarily motivated by research questions in psychological, environmental and epidemiological studies, so their generalization to infer time dependent causal effects in two-sided markets remains unknown.

Finally, we remark that there is a growing literature on evaluating time-varying causal effects (see e.g., Robins 1986; Sobel and Lindquist 2014; Boruvka et al. 2018; Ning, Ghosal, and Thomas 2019; Rambachan and Shephard 2019; Viviano and Bradic 2019; Bojinov and Shephard 2020). However, none of the above cited works used a RL framework to characterize the treatment effects. In particular, Bojinov and Shephard (2020) proposed to use IS based methods to test the null hypothesis of no (average) temporal causal effects in time series experiments. Their causal estimand is different from ours since they focused on p lag treatment effects, whereas we consider the long-term effects characterized by the value function. Moreover, their method requires the propensity score to be bounded away from 0 and 1, and thus, it is not valid for our applications. In addition, these method do not allow for sequential monitoring.

1.3 Organization of the Article

The rest of the article is organized as follows. In Section 2, we introduce a potential outcome framework to MDP and describe the causal estimand. Our testing procedure is introduced in Section 3. In Section 4, we demonstrate the effectiveness of our test via simulations. In Section 5, we apply the proposed test to a data from an online ride-hailing platform to illustrate its usefulness. Finally, we conclude our article in Section 6.

2 Problem Formulation

2.1 A Potential Outcome Framework for MDP

For simplicity, we assume that there are only two treatments (actions, products), coded as 0 and 1, respectively. For any $t\ge 0$, let ${\overline{a}}_t={(a_0,a_1,\dots ,a_t)}^{\top }\in {\{0,1\}}^{t+1}$ denote a treatment history vector up to time t. Let $\mathbb{S}$ denote the support of state variables and S₀ denote the initial state variable. We assume $\mathbb{S}$ is a compact subset of ${\mathbb{R}}^d$. For any $({\overline{a}}_{t-1},{\overline{a}}_t)$, let $S_t^{*}({\overline{a}}_{t-1})$ and $Y_t^{*}({\overline{a}}_t)$ be the counterfactual state and counterfactual outcome, respectively, that would occur at time t had the agent followed the treatment history ${\overline{a}}_t$. The set of potential outcomes up to time t is given by$$W_t^{*}({\overline{a}}_t)=\{S_0,Y_0^{*}(a_0),S_1^{*}(a_0),\dots ,S_t^{*}({\overline{a}}_{t-1}),Y_t^{*}({\overline{a}}_t)\}.$$

Let $W^{*}={\cup }_{t\ge 0,{\overline{a}}_t\in {\{0,1\}}^{t+1}}{W}_t^{*}({\overline{a}}_t)$ be the set of all potential outcomes.

A deterministic policy π is a time-homogeneous function that maps the space of state variables to the set of available actions. Following π, the agent will assign actions according to π at each time. We use $S_t^{*}(\pi )$ and $Y_t^{*}(\pi )$ to denote the associated potential state and outcome that would occur at time t had the agent followed π. The goodness of a policy π is measured by its (state) value function,$$V(\pi ;s)=\sum _{t\ge 0}{\gamma }^t\mathbb{E}\{Y_t^{*}(\pi )|S_0=s\},$$where $0<\gamma <1$ is a discount factor that reflects the tradeoff between immediate and future outcomes. The value function measures the discounted cumulative outcome that the agent would receive had they followed π. Note that our definition of the value function is slightly different from those in the existing literature (see, e.g., Sutton and Barto 2018). Specifically, $V(\pi ;s)$ is defined through potential outcomes rather than the observed data.

Similarly, we define the Q function by$$Q(\pi ;a,s)={\displaystyle \sum _{t\ge 0}{\gamma }^t}\mathbb{E}\{Y_t^{*}(\pi (a))|S_0=s\},$$where $\pi (a)$ denotes a time-varying policy where the initial action equals to a and all other actions are assigned according to π.

The goal of A/B testing is to compare the difference between the two treatments. Toward that end, we focus on two nondynamic (state-agnostic) policies that assign the same treatment at each time point. We remark that this is nontraditional in RL where the goal is to build a policy that depends on the state. For these two nondynamic policies, we use their value functions (denote by $V(1;·)$ and $V(0;·)$) to measure their long-term treatment effects. Meanwhile, our proposed method is equally applicable to the dynamic policy scenario as well. To quantitatively compare the two policies, we introduce the Conditional Average Treatment Effect (CATE) and Average Treatment Effect (ATE) based on their value functions in the following definitions. These two definitions relate RL to causal inference.

Definition 1.

Conditional on the initial state $S_0=s$, CATE is defined by the difference between two value functions, that is, $\text{CATE}(s)=V(1;s)-V(0;s)$.

Definition 2.

For a given reference distribution function $\mathbb{G}$ that has a bounded density function on $\mathbb{S}$, ATE is defined by the integrated difference between two value function, that is, $\text{ATE}={\int }_s\{V(1;s)-V(0;s)\}\mathbb{G}(ds).$

The focus of this paper is to test the following hypotheses:$$H_0:{\tau }_0=\text{ATE}\le 0\hspace{1em}\text{versus}\hspace{1em}{H}_1:{\tau }_0=\text{ATE}>0.$$

When H₀ holds, the new product is no better than the old one on average and is not of practical interest.

2.2 Identifiability of ATE

One of the most important question in causal inference is the identifiability of causal effects. In this section, we present sufficient conditions that guarantee the identifiability of the value function.

We first introduce two conditions that are commonly assumed in multi-stage decision making problems (see e.g., Murphy 2003; Robins 2004; Zhang et al. 2013). We need to use the notation $Z_1\perp \mathrm{}\mathrm{}\perp Z_2|Z_3$ to indicate that Z₁ and Z₂ are independent conditional on Z₃. In practice, with the exception of S₀, the set $W^{*}$ cannot be observed, whereas at time t, we observe the state-action-outcome triplet $(S_t,A_t,Y_t)$. For any $t\ge 0$, let ${\overline{A}}_t={(A_0,A_1,\dots ,A_t)}^{\top }$ denote the observed treatment history.

(CA) Consistency assumption: $S_{t+1}=S_{t+1}^{*}({\overline{A}}_t)$ and $Y_t=Y_t^{*}({\overline{A}}_t)$ for all $t\ge 0$.

(SRA) Sequential randomization assumption: $A_t\perp \mathrm{}\mathrm{}\perp W^{*}|S_t,$ ${\{S_j,A_j,Y_j\}}_{0\le j<t}$.

The CA requires that the observed state and outcome correspond to the potential state and outcome whose treatments are assigned according to the observed treatment history. It generalizes SUTVA to our setting, allowing the potential outcomes to depend on past treatments. The SRA implies that there are no unmeasured confounders and it automatically holds in online randomized experiments, in which the treatment assignment mechanism is prespecified. In SRA, we allows A_t to depend on the observed data history $S_t,{\{S_j,A_j,Y_j\}}_{0\le j<t}$ and thus, the treatments can be adaptively chosen.

We next introduce two conditions that are unique to the reinforcement learning setting.

(MA) Markov assumption: there exists a Markov transition kernel $\mathcal{P}$ such that for any $t\ge 0,{\overline{a}}_t\in {\{0,1\}}^{t+1}$ and $\mathcal{S}\subseteq {\mathbb{R}}^d$, we have $\text{Pr}\{S_{t+1}^{*}({\overline{a}}_t)\in \mathcal{S}|W_t^{*}({\overline{a}}_t)\}=\mathcal{P}(\mathcal{S};a_t,S_t^{*}({\overline{a}}_{t-1})).$

(CMIA) Conditional mean independence assumption: there exists a function r such that for any $t\ge 0,{\overline{a}}_t\in {\{0,1\}}^{t+1}$, we have $\mathbb{E}\{Y_t^{*}({\overline{a}}_t)|S_t^{*}({\overline{a}}_{t-1}),W_{t-1}^{*}({\overline{a}}_{t-1})\}=r(a_t,S_t^{*}({\overline{a}}_{t-1}))$.

We make a few remarks. First, these two conditions are central to the empirical validity of reinforcement learning (RL). Specifically, under these two conditions, one can show that there exists an optimal time-homogenous stationary policy whose value is no worse than any history-dependent policy (Puterman 1994). This observation forms the foundation of most of the existing state-of-the-art RL algorithms.

Second, when CA and SRA hold, it implies that the Markov assumption and the conditional mean independence assumption hold on the observed data as well,(1) $$\text{Pr}(S_{t+1}\in \mathcal{S}|A_t,S_t,{\{S_j,A_j,Y_j\}}_{0\le j<t})=\mathcal{P}(\mathcal{S};A_t,S_t),$$(1) (2) $$\mathbb{E}(Y_t|A_t,S_t,{\{S_j,A_j,Y_j\}}_{0\le j<t})=r(A_t,S_t).$$(2)

As such, $\mathcal{P}$ corresponds to the transition function that defines the next state distribution conditional on the current state-action pair and r corresponds to the conditional expectation of the immediate reward as a function of the state-action pair.

Assumption (1) is commonly assumed in the existing reinforcement learning literature (see e.g., Ertefaie 2014; Luckett et al. 2020). It is testable based on the observed data. See the goodness-of-fit test developed by Shi et al. (2020). In practice, to ensure the Markov property is satisfied, we can construct the state by concatenating measurements over multiple decision points till the Markovian property is satisfied.

Assumption (2) implies that past treatments will affect future response only through its impact on the future state variables. In other words, the state variables shall be chosen to include those that serve as important mediators between past treatments and current outcomes. By Assumption (1), this assumption is automatically satisfied when Y_t is a deterministic function of $(S_t,A_t,S_{t+1})$ that measures the system’s status at time t + 1. The latter condition is commonly imposed in the reinforcement learning literature and is stronger than (2).

To conclude this section, we derive a version of Bellman equation for the Q function under the potential outcome framework. Specifically, for $a\prime ,a\in \{0,1\}$, let $Q(a\prime ;a,·)$ denote the Q function where treatment a is assigned at the initial decision point and treatment $a\prime$ is repeatedly assigned afterwards. By definition, we have $V(a;s)=Q(a;a,s)$ for any (a, s).

Lemma 1.

Under MA, CMIA, CA, and SRA, for any $t\ge 0,a\prime \in \{0,1\}$ and any function $\phi :\mathbb{S}\times \{0,1\}\to \mathbb{R}$, we have $\mathbb{E}[\{Q(a\prime ;A_t,S_t)-Y_t-\gamma Q(a\prime ;a\prime ,S_{t+1})\}\phi (S_t,A_t)]=0$.

Lemma 1 implies that the Q-function is estimable from the observed data. Specifically, an estimating equation can be constructed based on Lemma 1 and the Q-function can be learned by solving this estimating equation. Note that $V(a,s)=Q(a;a,s)$ and τ₀ is completely determined by the value function V. As a result, ${\tau }_0=$ATE is identifiable.

Note that the positivity assumption is not needed in Lemma 1. Our procedure can thus, handle the case where treatments are deterministically assigned. This is due to MA and CMIA that assume the system dynamics are invariant across time. To elaborate this, note that the discounted value function is completely determined by the transition kernel $\mathcal{P}$ and the reward function r. These quantities can be consistently estimated under certain conditions, regardless of whether the treatments are deterministically assigned or not. Consequently, the value can be consistently estimated even when the treatment assignments are deterministic. We formally introduce our testing procedure in the next section.

3 Testing Procedure

We first introduce a toy example to illustrate the limitations of existing A/B testing methods. We next present our method and prove its consistency under a variety of different treatment designs.

3.1 Toy Examples

Existing A/B testing methods can only detect short-term treatment effects, but fail to identify any long-term effects. To elaborate this, we introduce two examples below.

Example 1.

$S_t=0.5{\epsilon }_t,Y_t=S_t+\delta A_t$ for any $t\ge 1$ and $S_0=0.5{\epsilon }_0$.

Example 2.

$S_t=0.5S_{t-1}+\delta A_t+0.5{\epsilon }_t$, Y _t = S_t for any $t\ge 1$ and $S_0=0.5{\epsilon }_0$.

In both examples, the random errors ${\left\{{\epsilon }_t\right\}}_{t\ge 0}$ follow independent standard normal distributions and the parameter δ describes the degree of treatment effects. When δ = 0, H₀ holds. Suppose $\delta >0$. Then H₁ holds. In Example 1, the observations are independent and there are no carryover effects at all. In this case, both the existing A/B tests and the proposed test are able to discriminate H₁ from H₀. In Example 2, however, treatments have delayed effects on the outcomes. Specifically, Y_t does not depend on A_t , but is affected by $A_{t-1}$ through S_t . Existing tests will fail to detect H₁ as the short-term conditional average treatment effects $\mathbb{E}(Y_t|A_t=1,S_t)-\mathbb{E}(Y_t|A_t=0,S_t)=0$ in this example. As an illustration, we conduct a small experiment by assuming the decision is made once at T = 500, and report the empirical rejection probability of the classical two-sample t-test that is commonly used in online experiments, a more complicated test based on the double machine learning method (DML, Chernozhukov et al. 2017) that is widely employed for inferring causal effects, and the proposed test. It can be seen the competing methods do not have any power under Example 2.

3.2 An Overview of the Proposal

We present an overview of our proposal in this section. As commented before, we adopt a reinforcement learning framework to address the limitations of existing A/B testing methods and characterize the long-term treatment effects. First, we estimate τ₀ based on a version of temporal difference learning. The idea is to apply basis function approximations to solve an estimating equation derived from Lemma 1. Specifically, let $\mathcal{Q}=\{{\Psi }^{\top }(s){\beta }_a:{\beta }_a\in {\mathbb{R}}^q\}$ be a large linear approximation space for $Q(a;a,s)=V(a,s)$, where $\Psi (·)$ is a vector containing q basis functions on $\mathbb{S}$. The dimension q is allowed to grow with the number of samples T to alleviate the effects of model misspecification. Let us suppose $Q\in \mathcal{Q}$ for a moment. Set the function $\psi (s,a)$ in Lemma 1 to $\Psi (s)\mathbb{I}(a=a\prime )$ for $a\prime =0,1$, there exists some ${\mathit{\beta }}^{*}={({\beta }_0^{*\top },{\beta }_1^{*\top })}^{\top }$ such that$$\begin{array}{c}\mathbb{E}\left[\right\{{\Psi }^{\top }(S_t){\beta }_a^{*}-Y_t-\gamma {\Psi }^{\top }(S_{t+1}){\beta }_a^{*}\}\Psi (S_t)\mathbb{I}(A_t=a)]=0,\\ \forall a\in \{0,1\},\end{array}$$where $\mathbb{I}(·)$ denotes the indicator function. The above equations can be rewritten as $\mathbb{E}({\mathbf{\Sigma }}_t{\mathit{\beta }}^{*})=\mathbb{E}{\mathit{\eta }}_t$, where ${\mathbf{\Sigma }}_t$ is a block diagonal matrix given by$$\begin{array}{c}{\mathbf{\Sigma }}_t=\left[\begin{array}{cc}\Psi (S_t)\mathbb{I}(A_t=0)& \\ \hspace{1em}{\{\Psi (S_t)-\gamma \Psi (S_{t+1})\}}^{\top }& \\ & \Psi (S_t)\mathbb{I}(A_t=1)\\ & {\{\Psi (S_t)-\gamma \Psi (S_{t+1})\}}^{\top }\end{array}\right]\hspace{1em}\\ \text{and}\hspace{1em}{\mathit{\eta }}_t=\{\Psi {(S_t)}^{\top }\mathbb{I}(A_t=0)Y_t,\Psi {(S_t)}^{\top }\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\\ \mathbb{I}(A_t=1)Y_t{\}}^{\top }.\end{array}$$

Let $\widehat{\mathbf{\Sigma }}(t)=t^{-1}\sum _{j<t}{\mathbf{\Sigma }}_j$ and $\widehat{\mathit{\eta }}(t)=t^{-1}\sum _{j<t}{\mathit{\eta }}_j$. It follows that $\mathbb{E}\{\widehat{\mathbf{\Sigma }}(t){\beta }^{*}\}=\mathbb{E}\{\widehat{\mathit{\eta }}(t)\}$. This motivates us to estimate ${\mathit{\beta }}^{*}$ by$$\widehat{\mathit{\beta }}(t)={\{{\widehat{\beta }}_0^{\top }(t),{\widehat{\beta }}_1^{\top }(t)\}}^{\top }={\widehat{\mathbf{\Sigma }}}^{-1}(t)\widehat{\mathit{\eta }}(t).$$

ATE can thus, be estimated by the plug-in estimator $\widehat{\tau }(t)={\int }_s{\Psi }^{\top }(s)\{{\widehat{\beta }}_1(t)-{\widehat{\beta }}_0(t)\}\mathbb{G}(ds)$. We remark that there is no guarantee that $\widehat{\mathbf{\Sigma }}(t)$ is always invertible. However, its population limit, $\mathbf{\Sigma }(t)$ is invertible for any t (see Lemma 3 in the supplementary materials). Consequently, for sufficiently large t, $\widehat{\mathbf{\Sigma }}(t)$ is invertible with large probability. In cases where $\widehat{\mathbf{\Sigma }}(t)$ is not invertible, we may add a ridge penalty to compute the resulting estimator. See Appendix D.4 of Shi et al. (2021) for details.

Second, we use $\widehat{\tau }(t)$ to construct our test statistic at time t. Let(3) $$\mathit{U}={\left\{-{\int }_{s\in \mathbb{S}}\Psi {(s)}^{\top }\mathbb{G}(ds),{\int }_{s\in \mathbb{S}}\Psi {(s)}^{\top }\mathbb{G}(ds)\right\}}^{\top }.$$(3)

It follows that $\widehat{\tau }(t)=\mathit{U}\widehat{\mathit{\beta }}(t)$. We will show that $\sqrt{t}\{\widehat{\mathit{\beta }}(t)-{\mathit{\beta }}^{*}\}$ is multivariate normal. This implies that $\sqrt{t}\{\widehat{\tau }(t)-{\tau }_0\}$ is asymptotically normal. Its variance can be consistently estimated by$${\widehat{\sigma }}^2(t)={\mathit{U}}^{\top }{\widehat{\mathbf{\Sigma }}}^{-1}(t)\widehat{\mathbf{\Omega }}(t){\{{\widehat{\mathbf{\Sigma }}}^{-1}(t)\}}^{\top }\mathit{U},$$as t grows to infinity, where ${\widehat{\mathbf{\Sigma }}}^{-1}(t)\widehat{\mathbf{\Omega }}(t){\{{\widehat{\mathbf{\Sigma }}}^{-1}(t)\}}^{\top }$ is the sandwich estimator for the variance of $\sqrt{t}\{\widehat{\mathit{\beta }}(t)-{\mathit{\beta }}^{*}\}$, and that$$\widehat{\mathbf{\Omega }}(t)=\frac{1}{t}\sum _{j=0}^{t-1}\left\{\begin{array}{c}\Psi (S_j)(1-A_j){\widehat{\epsilon }}_{j,0}\hfill \\ \Psi (S_j)A_j{\widehat{\epsilon }}_{j,1}\hfill \end{array}\right\}{\left\{\begin{array}{c}\Psi (S_j)(1-A_j){\widehat{\epsilon }}_{j,0}\hfill \\ \Psi (S_j)A_j{\widehat{\epsilon }}_{j,1}\hfill \end{array}\right\}}^{\top },$$ where ${\widehat{\epsilon }}_{j,a}$ is the temporal difference error $Y_j+\gamma {\Psi }^{\top }(S_{j+1}){\widehat{\beta }}_a-{\Psi }^{\top }(S_j){\widehat{\beta }}_a$ whose conditional expectation given $(A_j=a,S_j)$ is zero asymptotically (see Lemma 1). This yields our test statistic $\sqrt{t}\widehat{\tau }(t)/\widehat{\sigma }(t)$, at time t. For a given significance level $\alpha >0$, we reject H₀ when $\sqrt{t}\widehat{\tau }(t)/\widehat{\sigma }(t)>z_{\alpha }$, where $z_{\alpha }$ is the upper α-th quantile of a standard normal distribution.

Third, we integrate the α-spending approach with bootstrap to sequentially implement our test (see Section 3.4). The idea is to generate bootstrap samples that mimic the distribution of our test statistics, to specify the stopping boundary at each interim stage. Suppose that the interim analyses are conducted at time points $T_1<\cdots <T_K=T$. We focus on the setting where both K and ${\left\{T_k\right\}}_k$ are predetermined, as in our application (see Section 5 for details). To simplify the presentation, for each $1\le k<K$, we assume $T_k/T\to c_k$ for some constants $0<c_1<c_2<\cdots <c_{K-1}<1$. To better understand our algorithm, we investigate the limiting distribution of our test statistics at these interim stages in the next section.

Finally, we remark that for simplicity, we use the same Q-function model at each interim stage. This works when ${\left\{T_k\right\}}_k$ are of the same order of magnitude, which is the case in our real data application where $T_1=T_K/2$. Alternatively, one could allow q to grow with k. The testing procedure can be similarly derived.

3.3 Asymptotic Properties Under Different Treatment Designs

We consider three treatment allocation designs that can be handled by our procedure as follows:

• (D1). Markov design: $\text{Pr}(A_t=1|S_t,{\{S_j,A_j,Y_j\}}_{0\le j<t})=b^{(0)}(S_t)$ for some function $b^{(0)}(·)$ uniformly bounded away from 0 and 1.

• (D2). Alternating-time-interval design: $A_{2j}=0,A_{2j+1}=1$ for all $j\ge 0$.

• (D3). Adaptive design: For $T_k\le t<T_{k+1}$ for some $k\ge 0,\text{Pr}(A_t=1|S_t,{\{S_j,A_j,Y_j\}}_{0\le j<t})=b^{(k)}(S_t)$ for some $b^{(k)}(·)$ that depends on ${\{S_j,A_j,Y_j\}}_{0\le j<T_k}$ and is uniformly bounded away from 0 and 1 almost surely. We set $T_0=0$.

Here, D2 is a deterministic design and is widely used in industry (see our real data example and this technical report²). D1 and D3 are random designs. D1 is commonly assumed in the literature on reinforcement learning (Sutton and Barto 2018). D3 is widely employed in the contextual bandit setting to balance the tradeoff between exploration and exploitation. These three settings cover a variety of scenarios in practice.

In D3, we require $b^{(k)}$ to be strictly bounded between 0 and 1. Suppose an ϵ-greedy policy is used, that is, $b^{(k)}(s)=ϵ/2+(1-ϵ){\widehat{\pi }}^{(k)}(s)$, where ${\widehat{\pi }}^{(k)}$ denotes some estimated optimal policy. It follows that $ϵ/2\le b^{(k)}(s)\le 1-ϵ/2$ for any s. Such a requirement is automatically satisfied. Meanwhile, other adaptive strategies are equally applicable (see e.g., Zhang et al. 2007; Hu, Zhu, and Hu 2015; Metelkina and Pronzato 2017).

For any behavior policy b in D1–D3, define $S_t^{*}({\overline{b}}_{t-1})$ and $Y_t^{*}({\overline{b}}_t)$ as the potential outcomes at time t, where ${\overline{b}}_t$ denotes the action history assigned according to b. When b is a random policy as in D1 or D3, definitions of these potential outcomes are more complicated than those under a deterministic policy (see Appendix S3, supplementary materials for details). When b is a stationary policy, it follows from MA that ${\{S_{t+1}^{*}({\overline{b}}_t)\}}_{t\ge -1}$ forms a time-homogeneous Markov chain. When b follows the alternating-time-interval design, both ${\{S_{2t}^{*}({\overline{b}}_{2t-1})\}}_{t\ge 0}$ and ${\{S_{2t+1}^{*}({\overline{b}}_{2t})\}}_{t\ge 0}$ form time-homogeneous Markov chains.

To study the asymptotic properties of our test, we need to introduce assumptions C1–C3 and move them and their corresponding detailed discussions to Appendix S4, supplementary materials. In C1, we require the above mentioned Markov chains to be geometrically ergodic. Geometric ergodicity is weaker than the uniform ergodicity condition imposed in the existing reinforcement learning literature (see e.g., Bhandari, Russo, and Singal 2018; Zou, Xu, and Liang 2019). In C2, we impose conditions on the set of basis functions $\Psi (·)$ such that $\Psi (·)$ is chosen to yield a good approximation for the Q function. It is worth mentioning that we only require the approximation error to decay at a rate of $o(T^{-1/4})$ instead of $o(T^{-1/2})$. In other words, “undersmoothing” is not required and the value estimator has a well-tabulated limiting distribution even when the bias of the Q-estimator decays at a rate that is slower than $O(T^{-1/2})$. This result has a number of importation implications. First, it suggests the proposed test will not be overly sensitive to the choice of the number of basis functions. Such a theoretical finding is consistent with our empirical observations in Section 4.3. Second, the number of basis functions could be potentially selected by minimizing the prediction loss of the Q-estimator via cross-validation. We also present examples of basis functions that satisfy C2 in Appendix S4.2, supplementary materials. In C3, we impose some mild conditions on the action value temporal-difference error, requiring their variances to be nondegenerate.

Let $\{Z_1,\dots ,Z_K\}$ denote the sequence of our test statistics, where $Z_k=\sqrt{T_k}\widehat{\tau }(T_k)/\widehat{\sigma }(T_k)$. In the following, we study their joint asymptotic distributions. We also present an estimator of their covariance matrix that is consistent under all designs.

Theorem 1

(Limiting distributions). Assume C1–C3, MA, CMIA, CA, and SRA hold. Assume all immediate rewards are uniformly bounded variables, the density function of S₀ is uniformly bounded on $\mathbb{S}$ and q satisfies $q=o(\sqrt{T}/\hspace{0.17em}\text{log}\hspace{0.17em}T)$. Then under D1, D2 or D3, we have

• ${\left\{Z_k\right\}}_{1\le k\le K}$ are jointly asymptotically normal;

• their asymptotic means are nonpositive under H₀;

• their covariance matrix can be consistently estimated by some $\widehat{\mathbf{\Xi }}$, whose (k₁, k₂)-th element ${\widehat{\Xi }}_{k_1,k_2}$ equals$$\sqrt{\frac{T_{k_1}}{T_{k_2}}}\frac{{\mathit{U}}^{\top }{\widehat{\mathbf{\Sigma }}}^{-1}(T_{k_1})\widehat{\mathbf{\Omega }}(T_{k_1}){\{{\widehat{\mathbf{\Sigma }}}^{-1}(T_{k_2})\}}^{\top }\mathit{U}}{\widehat{\sigma }(T_{k_1})\widehat{\sigma }(T_{k_2})}.$$

This theorem forms the basis of our sequential testing procedure, which we elaborate in the next section.

3.4 Sequential Monitoring and Online Updating

To sequentially monitor our test, we need to specify the stopping boundary ${\left\{b_k\right\}}_{1\le k\le K}$ such that the experiment is terminated and H₀ is rejected when Z_k > b_k for some k.

First, we use the α spending function approach to guarantee the validity of our test. It requires to specify a monotonically increasing function $\alpha (·)$ that satisfies $\alpha (0)=0$ and $\alpha (T)=\alpha$. Some popular choices of the α spending function include(4) $$\begin{array}{c}{\alpha }_1(t)=2-2\Phi \{{\Phi }^{-1}(1-\alpha /2)\sqrt{T/t}\}\hspace{1em}\text{and}\\ {\alpha }_2(t)=\alpha {(t/T)}^{\theta }\hspace{1em}\text{for} \theta >0,\end{array}$$(4) where $\Phi (·)$ denotes the normal cumulative distribution function. Adopting the α spending approach, we require b_k ’s to satisfy(5) $$\text{Pr}({\cup }_{j=1}^k\{Z_j>b_j\})=\alpha (T_k)+o(1),\hspace{1em}\forall 1\le k\le K.$$(5)

Suppose there exist a sequence of information levels ${\left\{{\mathcal{I}}_k\right\}}_{1\le k\le K}$ such that(6) $$\text{cov}(Z_{k_1},Z_{k_2})=\sqrt{{\mathcal{I}}_{k_1}/{\mathcal{I}}_{k_2}}+o(1),$$(6) for all $1\le k_1\le k_2$. Then the sequence ${\left\{Z_k\right\}}_{1\le k\le K}$ satisfies the Markov property. The stopping boundary can be efficiently computed based on the numerical integration method detailed in Section 19.2 of Jennison and Turnbull (1999). However, in our setup, condition (6) might not hold when adaptive design is used. As commented in the introduction, this is due to the existence of carryover effects in time. Specifically, when treatment effects are adaptively generated, the behavior policy at difference stages are likely to vary. Due to the carryover effects in time, the state vectors at difference stages have different distribution functions. As such, the asymptotic distribution of the test statistic at each interim stage depends on the behavior policy. Consequently, the covariance $\text{cov}(Z_{k_1},Z_{k_2})$ is a very complicated function of k₁ and k₂ (see e.g., the form of ${\widehat{\Xi }}_{k_1,k_2}$ in Theorem 1) that cannot be represented by (6). Consequently, the numerical integration method is not applicable.

Next, we outline a method based on the wild bootstrap (Wu 1986). Then we discuss its limitation and present our proposal, a scalable bootstrap algorithm to determine the stopping boundary. The idea is to generate bootstrap samples ${\{{\widehat{Z}}^{\text{MB}}(t)\}}_t$ that have asymptotically the same joint distribution as ${\{\sqrt{t}{\widehat{\sigma }}^{-1}(t)(\widehat{\tau }(t)-{\tau }_0)\}}_t$. By the requirement on ${\left\{b_k\right\}}_k$ in (5), we obtain$$\begin{array}{c}\text{Pr}\left\{Z_k>b_k|\underset{1\le j<k}{\max }(Z_j-b_j)\le 0\right\}\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}=\frac{\alpha (T_k)-\alpha (T_{k-1})}{1-\alpha (T_{k-1})}+o(1).\end{array}$$

To implement the test, we thus, recursively calculate the threshold ${\widehat{b}}_k$ as follows,(7) $$\begin{array}{c}{\text{Pr}}^{*}\left\{{\widehat{Z}}^{\text{MB}}(t_k)>{\widehat{b}}_k|\underset{1\le j<k}{\max }({\widehat{Z}}^{\text{MB}}(t_j)-{\widehat{b}}_j)\le 0\right\}\\ \hspace{1em}=\frac{\alpha (T_k)-\alpha (T_{k-1})}{1-\alpha (T_{k-1})},\end{array}$$(7) where ${\text{Pr}}^{*}$ denotes the probability conditional on the data, and reject H₀ when $Z_k^{*}>{\widehat{b}}_k$ for some k. In practice, the above conditional probability can be approximated via Monte Carlo simulations. This forms the basis of the bootstrap algorithm.

Specifically, let ${\left\{{\zeta }_t\right\}}_{t\ge 0}$ be a sequence of iid mean-zero, unit variance random variables independent of the observed data. Define(8) $${\widehat{\mathit{\beta }}}^{\text{MB}}(t)={\widehat{\mathbf{\Sigma }}}^{-1}(t)\left[\frac{1}{t}\sum _{j<t}{\zeta }_j\left\{\begin{array}{c}\Psi (S_j)(1-A_j){\widehat{\epsilon }}_{j,0}\\ \Psi (S_j)A_j{\widehat{\epsilon }}_{j,1}\end{array}\right\}\right],$$(8) where ${\widehat{\epsilon }}_{t,a}$ is the temporal difference error defined. Based on ${\widehat{\mathit{\beta }}}^{\text{MB}}(t)$, one can define the bootstrap sample ${\widehat{Z}}^{\text{MB}}(t)=\sqrt{t}{\widehat{\sigma }}^{-1}(t){\mathit{U}}^{\top }{\widehat{\mathit{\beta }}}^{\text{MB}}(t)$. Based on the definition of $\widehat{\sigma }(t)$, it is immediate to see that each ${\widehat{Z}}^{\text{MB}}(t)$ follows a standard normal distribution conditional on the data.

We remark that although the wild bootstrap method is developed under the iid settings, it is valid under our setup as well. This is due to that under CMIA, $\widehat{\mathit{\beta }}(t)-{\mathit{\beta }}^{*}$ forms a martingale sequence with respect to the filtration $\{(S_j,A_j,Y_j):j<t\}$. It guarantees that the covariance matrices of ${\widehat{\mathit{\beta }}}^{\text{MB}}(t)$ and $\widehat{\mathit{\beta }}(t)$ are asymptotically equivalent. As such, the bootstrap approximation is valid.

However, calculating ${\widehat{\mathit{\beta }}}^{\text{MB}}(T_k)$ requires $O(T_k)$ operations. The time complexity of the resulting bootstrap algorithm is $O(B{T}_k)$ up to the k-th interim stage, where B is the total number of bootstrap samples. This can be time consuming when ${\{T_k-T_{k-1}\}}_{k=1}^K$ are large. To facilitate the computation, we observe that in the calculation of ${\widehat{\mathit{\beta }}}^{\text{MB}}$, the random noise ζ_t is generated upon the arrival of each observation. This is unnecessary as we aim to approximate the distribution of $\widehat{\mathit{\beta }}(·)$ only at finitely many time points $T_1,T_2,\dots ,T_K$.

Finally, we present our bootstrap algorithm to determine ${\left\{b_k\right\}}_{1\le k\le K}$, based on Theorem 1. Let ${\left\{e_k\right\}}_{1\le k\le K}$ be a sequence of iid $N(0,I_{4q})$ random vectors, where I_J stands for a J × J identity matrix for any J. Let $\widehat{\mathbf{\Omega }}(T_0)$ be a zero matrix. At the k-th stage, we compute the bootstrap sample$${\widehat{Z}}_k^{*}=\frac{{\mathit{U}}^{\top }{\widehat{\mathbf{\Sigma }}}^{-1}(T_k)}{\sqrt{T_k}\widehat{\sigma }(T_k)}\sum _{j=1}^k{\{T_j\widehat{\mathbf{\Omega }}(T_j)-T_{j-1}\widehat{\mathbf{\Omega }}(T_{j-1})\}}^{1/2}{e}_j.$$

A key observation is that, conditional on the observed dataset, the covariance of ${\widehat{Z}}_{k_1}^{*}$ and ${\widehat{Z}}_{k_2}^{*}$ equals$$\begin{array}{c}\frac{{\mathit{U}}^{\top }{\widehat{\mathbf{\Sigma }}}^{-1}(T_{k_1})}{\sqrt{T_{k_1}{T}_{k_2}}\widehat{\sigma }(T_{k_1})\widehat{\sigma }(T_{k_2})}\left[\sum _{j=1}^{k_1}\left\{T_j\widehat{\mathbf{\Omega }}(T_j)-T_{j-1}\widehat{\mathbf{\Omega }}(T_{j-1})\right\}\right]\\ \hspace{1em}\times {\{{\widehat{\mathbf{\Sigma }}}^{-1}(T_{k_2})\}}^{-1}\mathit{U}={\widehat{\Xi }}_{k_1,k_2}.\end{array}$$

By Theorem 1, the covariance matrices of ${\left\{Z_k\right\}}_k$ and ${\left\{Z_k^{*}\right\}}_k$ are asymptotically equivalent. In addition, the limiting distributions of ${\left\{Z_k\right\}}_k$ and ${\left\{Z_k^{*}\right\}}_k$ are multivariate normal with zero means. As such, the joint distribution of ${\left\{Z_k\right\}}_{1\le k\le K}$ can be well approximated by that of ${\left\{Z_k^{*}\right\}}_{1\le k\le K}$ conditional on the data. The rejection boundary can thus, be computed in a similar fashion as in (7).

Theorem 2

(Type-I error). Suppose that the conditions of Theorem 1 hold and $\alpha (·)$ is continuous. Then the proposed thresholds satisfy $\text{Pr}({\cup }_{j=1}^k\{Z_j>{\widehat{b}}_j\})\le \alpha (T_k)+o(1)$, for all $1\le k\le K$ under H₀. The equality holds when ${\tau }_0=0$.

Theorem 2 implies that the Type-I error rate of the proposed test is well controlled. When $\text{ATE}=0$, the equality in Theorem 2 holds. The rejection probability achieves the nominal level under H₀. We next investigate the power property of our test.

Theorem 3

(Power). Suppose that the conditions of Theorem 2 hold. Assume ${\tau }_0\gg T^{-1/2}$, then $\text{Pr}({\cup }_{j=1}^k\{Z_j>{\widehat{b}}_j\})\to 1$. Assume ${\tau }_0=T^{-1/2}h$ for some h > 0. Then $\underset{T\to \infty }{\lim }[\text{Pr}({\cup }_{j=1}^k\{Z_j>{\widehat{b}}_j\})-\alpha (T_k)]>0$.

Combining Theorems 2 and 3 yields the consistency of our test. The second assertion in Theorem 3 implies that our test has nonnegligible powers against local alternatives converging to H₀ at the $T^{-1/2}$ rate. When the signal decays at a slower rate, the power of our test approaches 1.

Algorithm 1 The testing procedure

Input: number of basis functions q, number of bootstrap samples B, an α spending function $\alpha (·)$.

Initialize: $T_0=0,\mathcal{I}=\{1,2,\dots ,B\}$. Set $\widehat{\mathbf{\Omega }}$, ${\widehat{\mathbf{\Omega }}}^{*}$, ${\widehat{\mathbf{\Sigma }}}_0,{\widehat{\mathbf{\Sigma }}}_1$ to zero matrices, and $\widehat{\mathit{\eta }}$, ${\widehat{S}}_1,\dots ,{\widehat{S}}_B$ to zero vectors.

Compute U according to (3), using either Monte Carlo methods or numerical integration, where $0_q$ denotes a zero vector of length q.

For k = 1 to K:

Step 1. Online update of ATE.

For $t=T_{k-1}$ to $T_k-1$:

${\widehat{\mathbf{\Sigma }}}_a=(1-t^{-1}){\widehat{\mathbf{\Sigma }}}_a+t^{-1}\Psi (S_t)\mathbb{I}(A_t=a){\{\Psi (S_t)-\gamma \Psi (S_{t+1})\mathbb{I}(A_{t+1}=a)\}}^{\top }$, a = 0, 1;

${\widehat{\mathit{\eta }}}_a=(1-t^{-1}){\widehat{\mathit{\eta }}}_a+t^{-1}\Psi (S_t)\mathbb{I}(A_t=a)Y_t$.

Set ${\widehat{\beta }}_a={\widehat{\mathbf{\Sigma }}}_a^{-1}{\widehat{\mathit{\eta }}}_a$ for $a\in \{0,1\}$ and $\widehat{\tau }={\mathit{U}}^{\top }\widehat{\mathit{\beta }}$.

Step 2. Online update of the variance estimator.

Initialize ${\widehat{\mathbf{\Omega }}}^{*}$ to a zero matrix.

For $t=T_{k-1}$ to $T_k-1$:

${\widehat{\epsilon }}_{t,a}=Y_t+\gamma {\Psi }^{\top }(S_{t+1}){\widehat{\beta }}_a-{\Psi }^{\top }(S_t){\widehat{\beta }}_a$ for a = 0, 1;

${\widehat{\mathbf{\Omega }}}^{*}={\widehat{\mathbf{\Omega }}}^{*}+{\{\Psi {(S_t)}^{\top }(1-A_t){\widehat{\epsilon }}_{t,0},\Psi {(S_t)}^{\top }{A}_t{\widehat{\epsilon }}_{t,1}\}}^{\top }\{\Psi {(S_t)}^{\top }(1-A_t){\widehat{\epsilon }}_{t,0},\Psi {(S_t)}^{\top }{A}_t{\widehat{\epsilon }}_{t,1}\}$.

Set $\widehat{\mathbf{\Sigma }}$ to a block diagonal matrix by aligning ${\widehat{\mathbf{\Sigma }}}_0$ and ${\widehat{\mathbf{\Sigma }}}_1$ along the diagonal of $\widehat{\mathbf{\Sigma }}$;

Set $\widehat{\mathbf{\Omega }}=T_k^{-1}(T_{k-1}\widehat{\mathbf{\Omega }}+{\widehat{\mathbf{\Omega }}}^{*})$ and the variance estimator ${\widehat{\sigma }}^2={\mathit{U}}^{\top }{\widehat{\mathbf{\Sigma }}}^{-1}\widehat{\mathbf{\Omega }}{\left\{{\widehat{\mathbf{\Sigma }}}^{-1}\right\}}^{\top }\mathit{U}$.

Step 3. Bootstrap test statistic.

For b = 1 to B:

Generate $e_k^{(b)}\sim N(0,I_{4q})$;

${\widehat{S}}_b={\widehat{S}}_b+{\widehat{\mathbf{\Omega }}}^{*1/2}{e}_k^{(b)}$;

${\widehat{Z}}_b^{*}=T_k^{-1/2}{\widehat{\sigma }}^{-1}{\mathit{U}}^{\top }{\widehat{\mathbf{\Sigma }}}^{-1}{\widehat{S}}_b$;

Set z to be the upper $\{\alpha (t)-|{\mathcal{I}}^c|/B\}/(1-|{\mathcal{I}}^c|/B)$-th percentile of ${\left\{{\widehat{Z}}_b^{*}\right\}}_{b\in \mathcal{I}}$.

Update $\mathcal{I}$ as $\mathcal{I}\leftarrow \{b\in \mathcal{I}:{\widehat{Z}}_b^{*}\le z\}$;

Step 4. Reject or not?

Reject the null if $\sqrt{T_k}{\widehat{\sigma }}^{-1}\widehat{\tau }>z$.

Since we use a linear basis function to approximate the Q-function, the regression coefficients $\widehat{\mathit{\beta }}(t)$ as well as their covariance estimator can be online updated as batches of observations arrive at the end of each interim stage. As such, our test can be implemented online. We summarize our procedure in Algorithm 1. Recall that q is the number of basis functions. As the kth interim stage, the time complexities of Steps 1–3 in Algorithm 1 are dominated by $O\{q^2(T_k-T_{k-1})+q^3\},O\{q^2(T_k-T_{k-1})+q^3\}$ and $O(B{q}^2+q^3)$, respectively. As such, the time complexity of Algorithm 1 is dominated by $O(BK{q}^2+T{q}^2+K{q}^3)$. In contrast, one can show that the classical wild bootstrap algorithm would take at least $\Omega (BT{q}^2+K{q}^3)$ number of flops and is much more computationally intensive when $T\gg K$, which is case in phase 3 clinical trials and our real data application.

To conclude this section, we remark that a few bootstrap algorithms have been developed in the RL literature for policy evaluation. Specifically, Hanna, Stone, and Niekum (2017) and Hao et al. (2021) proposed to use bootstrap for uncertainty quantification in off-policy evaluation. These algorithms require the number of trajectories to diverge to infinity to be consistent and are thus, not applicable to our setting where there is only one trajectory in the experiment. In addition, they are developed in offline settings and do not allow online updating. Ramprasad et al. (2021) developed a bootstrap algorithm for policy evaluation in online settings. Their algorithm generates bootstrap samples upon the arrival of each observation and is thus, more computationally intensive than the proposed algorithm.

4 Simulation Study

4.1 Settings and Implementation

Simulated data of states and rewards was generated as follows,$$\begin{array}{c}{S}_{1,t}=(2A_{t-1}-1)S_{1,(t-1)}/2+S_{2,(t-1)}/4+\delta A_{t-1}+{\epsilon }_{1,t},\\ S_{2,t}=(2A_{t-1}-1)S_{2,(t-1)}/2+S_{1,(t-1)}/4+\delta A_{t-1}+{\epsilon }_{2,t},\\ Y_t=1+(S_{1,t}+S_{2,t})/2+{\epsilon }_{3,t},\end{array}$$where the random errors ${\left\{{\epsilon }_{j,t}\right\}}_{j=1,2,0\le t\le T}$ are iid $N(0,{0.5}^2)$ and ${\left\{{\epsilon }_{3,t}\right\}}_{0\le t\le T}$ are iid $N(0,{0.3}^2)$. Let $S_t={(S_{1,t},S_{2,t})}^{\top }$ denote the state at time t. Under this model, treatments have delayed effects on the outcomes, as in Example 2. The parameter δ characterizes the degree of such carryover effects. When δ = 0, ${\tau }_0=0$ and H₀ holds. When $\delta >0$, H₁ holds. Moreover, τ₀ increases as δ increases.

We set K = 5 and $(T_1,T_2,T_3,T_4,T_5)=(300,375,450,$ $525,600)$. The discounted factor γ is set to 0.6 and $\mathbb{G}$ is chosen as the initial state distribution. We consider three behavior policies, according to the designs D1–D3, respectively. For the behavior policy in D1, we set $b^{(0)}(s)=0.5$ for any $s\in \mathbb{S}$. For the behavior policy in D3, we use an ϵ-greedy policy and set $b^{(k)}(s)=ϵ/2+(1-ϵ)\mathbb{I}(\Psi {(s)}^{\top }({\widehat{\beta }}_1(T_k)-{\widehat{\beta }}_0(T_k))>0),$ with $ϵ=0.1$, for any $k\ge 1$ and $s\in \mathbb{S}$.

For each design, we further consider five choices of δ, corresponding to $0,0.05,0.1,0.15$ and 0.2. The significance level α is set to 0.05 in all cases. To implement our test, we choose two α-spending functions, corresponding to ${\alpha }_1(·)$ and ${\alpha }_2(·)$ given in (4). The hyperparameter θ in ${\alpha }_2(·)$ is set to 3. The number of bootstrap sample is set to 1000. In addition, we consider the following polynomial basis function, $\Psi (s)=\Psi (s_1,s_2)={(1,s_1,s_1^2,\dots ,s_1^J,s_2,s_2^2,\dots ,s_2^J)}^{\top }$, with J = 4.

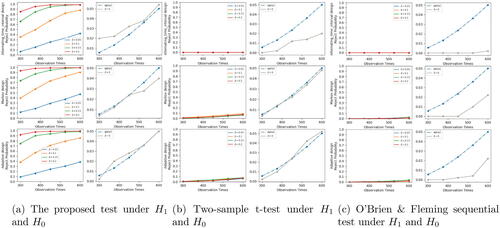
All experiments run on a MacBook Pro with a dual-core 2.7 GHz processor. Implementing a single test takes one second. Figures 2(a) and S1(a) (see Appendix S1, supplementary materials) depict the empirical rejection probabilities of our test statistics at different interim stages under H₀ and H₁ with different combinations of δ, $\alpha (·)$ and the designs. These rejection probabilities are aggregated over 500 simulations. We also plot ${\alpha }_1(·)$ and ${\alpha }_2(·)$ under H₀. Based on the results, it can be seen that under H₀, the Type-I error rate of our test is well-controlled and close to the nominal level at each interim stage in most cases. Under H₁, the power of our test increases as δ increases, showing the consistency of our test procedure.

Fig. 2 Empirical rejection probabilities of our test and the two-sample t-test with $\alpha (·)={\alpha }_1(·)$ and of the O’Brien and Fleming sequential test developed by Kharitonov et al. (2015). The left panels depicts the empirical Type-I error and the right panels depicts the empirical power. Settings correspond to alternating-time-interval, adaptive and Markov designs, from top to bottom plots.

4.2 Comparison with Baseline Methods

To further evaluate our method, we first compare it with the classical two-sample t-test and a modified version of modified versions of the O’Brien and Fleming sequential test developed by Kharitonov et al. (2015). We remark that the current practice of policy evaluation in most two-sided marketplace platforms is to employ classical two-sample t-test. Specifically, for each T_k , we apply the t-test to the data ${\{A_t,Y_t\}}_{0\le t\le T_k}$ and plot the corresponding empirical rejection probabilities in Figures 2(b) and S1(b). Figure 2(c) depicts the empirical rejection probabilities of the modified version of the O’Brien and Fleming sequential test. We remark that such a test requires equal sample size $T_1=T_k-T_{k-1}$ for $k=2,\dots ,K$ and is not directly applicable to our setting with unequal sample size. To apply such a test, we modify the decision time and set $(T_1,T_2,T_3,T_4,T_5)=(120,240,360,480,600)$. As shown in these figures, all these tests fail to detect carryover effects and do not have power at all.

We next compare the proposed test with the test based on the V-learning method developed by Luckett et al. (2020). As we have commented, V-learning does not allow sequential testing. So we focus on settings where the decision is made once at T = 600. In addition, V-learning requires the propensity score to be bounded away from 0 and 1. To meet the positivity assumption, we generate the actions according to the Markov design where $\text{Pr}(A_t=1|S_t)=\text{sigmoid}(\theta S_{1,t}+\theta S_{2,t})$. Both tests require to specify the discounted factor γ. We fix $\gamma =0.8$. Results are reported in Figure 3(a), aggregated over 500 simulations. It can be seen for large θ, the test based on V-learning cannot control the Type-I error and has smaller power than our test when δ is large. This is because V-learning uses inverse propensity score weighting. In cases where θ is large, the propensity score can be close to zero or one for some sample values, making the resulting test statistic unstable.

Fig. 3 (a) Empirical rejection probabilities of the proposed test and the test based on V-learning. (b) Empirical rejection probabilities of the proposed test and the test derived based on analysis of crossover trials. The shaded area corresponds to the interval $[0.05-1.96\text{MCE},0.05+1.96\text{MCE}]$ where MCE denotes the Monte Carlo error $\sqrt{0.05\times 0.95/500}$.

Finally, we compare the proposed test with a t-test based on analysis of crossover trials (see e.g., Jones and Kenward 1989). We remark that such a test requires the data to be generated from crossover designs and cannot be applied under D1, D2 or D3. In addition, most crossover trials require to recruit multiple subjects/patients to estimate the carryover effect. The resulting tests are not directly applicable to our setting where only one subject receives a sequence of treatments over time. In Appendix S1, supplementary materials, we develop a t-test for the carryover effect under our setting, based on analysis of $2\times 2$ crossover trials. For simplicity, we focus on settings where the decision is made once at T = 600. In Figure 3(b), we report the empirical rejection probabilities of such a test and the proposed test under several crossover designs with different number of blocks. Please refer to Appendix S1, supplementary materials for more details about the design and the test. It can be seen that the proposed test is more powerful in most cases.

4.3 Sensitivity Analysis

In Section 4.1, we set the number of polynomial basis function J to 4. We also tried some other values of J by setting J to 3 and 5. Results are reported in Figure S2 (see Appendix S1, supplementary materials). It can be seen that the resulting tests have very similar performance and is not sensitive to the choice of J. In Appendix S1, supplementary materials, we fixed J to 4 and tried some other values of $\gamma \in$ (0.1, 0.3, 0.5, 0.9). Results are reported in Figure S3, supplementary materials. It can be seen that our test controls the Type-I error in most cases. In addition, its power increases with γ. This is consistent with the following observation: γ characterizes the balance between the short-term and long-term treatment effects. Under the current setup, there is no short-term treatment effects. The value difference increases with γ. It is thus, expected that our test has better power properties for large values of γ.

5 Real Data Application

We apply the proposed test to a real dataset from a large-scale ride-sharing platform. The purpose of this study is to compare the performance of a newly developed order dispatching strategy with a standard control strategy used in the platform. For a given order, the new strategy will dispatch it to a nearby driver that has not yet finished their previous ride request, but almost. In comparison, the standard control assigns orders to drivers that have completed their ride requests. The new strategy is expected to reduce the chance that the customer will cancel an order in regions with only a few available drivers. It is expected to meet more call orders and increase drivers’ income on average.

The experiment is conducted at a given city from December 3 to December 16. Dispatch strategies are executed based on alternating half-hourly time intervals. We also apply our test to a data from an A/A experiment (which compares the baseline strategy against itself), conducted from November 12 to November 25. Note that it is conducted at a different time period from the A/B experiment. The A/A experiment is employed as a sanity check for the validity of the proposed test. We expect that our test will not reject H₀ when applied to this dataset, since the two strategies used are essentially the same.

Both experiments last for two weeks. Thirty-minutes is defined as one time unit. We set K = 8 and $T_k=48\times (k+6)$ for $k=1,\dots ,8$. That is, the first interim analysis is performed at the end of the first week, followed by seven more at the end of each day during the second week. We discuss more about the experimental design in Appendix S2.2. We choose the overall drivers’ income in each time unit as the response. The new strategy is expected to reduce the answer time of passengers and increase drivers’ income. Three time-varying variables are used to construct the state. The first two correspond to the number of requests (demand) and drivers’ online time (supply) during each 30-minute time interval. These factors are known to have large impact on drivers’ income. The last one is the supply and demand equilibrium metric. This variable characterizes the degree that supply meets the demand and serves as an important mediator between past treatments and future outcomes.

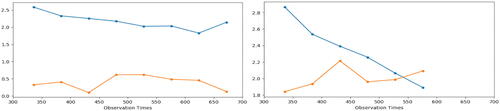
To implement our test, we set $\gamma =0.6$, B = 1000 and use a fourth-degree polynomial basis for $\Psi (·)$, as in simulations. We use ${\alpha }_1(·)$ as the spending function for interim analysis and set $\alpha =0.05$. The test statistic and its corresponding rejection boundary at each interim stage are plotted in Figure 4. It can be seen that our test is able to conclude, at the end of the 12th day, that the new order dispatch strategy can significantly increase drivers’ income. When applied to the data from the A/A experiment, we fail to reject H₀, as expected. We remark that early termination of the A/B experiment is beneficial to both the platform and the society. First, take this particular experiment as an example, we find that the new strategy reduces the answer time of orders by 2%, leading to almost 2% increment of drivers’ income. If we were to wait until Day 14, drivers would lose 2% income and customers would have to wait longer on two days. The benefits are considerable by taking the total number of drivers and customers in the city into account. In addition, the platform can benefit a lot from the increase in the driver income, as they take a fixed proportion of the driving fee from all completed trips. Second, the platform needs to conduct a lot of A/B experiments to investigate various policies. A reduction in the experiment duration facilitates the process, allowing the platform to evaluate more policies within the same time frame. These policies have the potential to further improve the driver income and the customer satisfaction, providing safer, quicker and more convenient transportation.

Fig. 4 Our test statistic (the orange line) and the rejection boundary (the blue line) in the A/A (left plot) and A/B (right plot) experiments.

For comparison, we also apply the two-sample t-test to the data collected from the A/B experiment. The corresponding p-value is 0.18. This result is consistent with our findings. Specifically, the treatment effect at a given time affects the distribution of drivers in the future, inducing interference in time. As shown in the toy example (see Section 3.1), the t-test cannot detect such carryover effects, leading to a low power. Our procedure, according to Theorem 2, has enough powers to discriminate H₁ from H₀.

6 Discussion

First, we remark that our focus is to compare the long-term treatment effects between two nondynamic policies. Meanwhile, the proposed method can be easily extended to handle dynamic policies as well. We discuss this further in Appendix S2.1, supplementary materials.

Second, in our real data application, the design of experiment is determined by the company and we are in the position to analyze the data collected based on such a design. It is important and interesting to design experiments to identity the treatment effect efficiently, but it is beyond the scope of the current paper. In addition, it is worth mentioning that the 30-minute-interval design is adopted by the company to optimize the performance of the resulting A/B test. We consider a few toy examples to elaborate in Appendix S2.2, supplementary materials.

Third, in the current setup, we assume the dimension of the state is fixed whereas the number of basis functions diverges to infinity at a rate that is slower than T. In Appendix S2.3, supplementary materials, we extend our proposal to settings with high-dimensional state information. In that case, we recommend to include a rich class of basis functions to ensure that the Q-function can be well-approximated. The number of basis functions is allowed to be much larger than T. To handle high-dimensionality, we first adopt the Dantzig selector (Candes and Tao 2007) which directly penalizes the Bellman equation to compute an initial estimator. We next develop a decorrelated estimator to reduce the bias of the initial estimator and outline the corresponding testing statistic.

Finally, we focus on causal effects evaluation in online experiments where the treatment generating mechanism is predetermined. Under these settings, there are no unmeasured confounders that confound the action-outcome or the action-next state relationship. Another equally important problem is to study off-policy evaluation in our application. We discuss this further in Appendix S2.4, supplementary materials.

Supplementary Materials

The supplementary materials contain technical assumptions, proofs, additional simulation results, extensions to high-dimensional models and dynamic policies, and discussions on the experimental design, off-policy evaluation and some related works.

Notes

Table 1 Powers of t-test, DML-based test and the proposed test under Examples 1 and 2, with T = 500, $\delta =0.1$. ${\left\{A_t\right\}}_t$ follow iid Bernoulli distribution with success probability 0.5.

		Example 1		Example 2
t-test 0.76	DML-based test 1	Our test 0.98	t-test 0.04	DML-based test 0.06	Our test 0.73

Acknowledgments

The authors thank the AE, and the reviewers for their constructive comments, which have led to a significant improvement of the earlier version of this article.

Additional information

Funding

Shi’s research was partially supported by the LSE’s Research Support Fund in 2021. Song’s research was partially supported by grants from NSF-DMS-1555244 and 2113637.

Notes

1 Our test statistic and its stopping boundary are updated as batches of new observations arrive without storing historical data.

2 https://eng.lyft.com/experimentation-in-a-ridesharing-marketplace-b39db027a66e