Factor Modeling for Clustering High-Dimensional Time Series

Abstract

We propose a new unsupervised learning method for clustering a large number of time series based on a latent factor structure. Each cluster is characterized by its own cluster-specific factors in addition to some common factors which impact on all the time series concerned. Our setting also offers the flexibility that some time series may not belong to any clusters. The consistency with explicit convergence rates is established for the estimation of the common factors, the cluster-specific factors, and the latent clusters. Numerical illustration with both simulated data as well as a real data example is also reported. As a spin-off, the proposed new approach also advances significantly the statistical inference for the factor model of Lam and Yao. Supplementary materials for this article are available online.

Keywords:

• Eigenanalysis
• Idiosyncratic components
• k-means clustering algorithm
• Strong and weak factors

1 Introduction

One of the primary tasks of data mining is clustering. While most clustering methods are originally designed for independent observations, clustering a large number of time series gains increasing momentum (Esling and Agon, 2012), due to mining large and complex data recorded over time in business, finance, biology, medicine, climate, energy, environment, psychology, multimedia and other areas (Table 1 of Aghabozorgi, Shirkhorshid, and Wah, 2015). Consequently, the literature on time series clustering is large; see Liao (2005), Aghabozorgi, Shirkhorshid, and Wah (2015), Maharaj, D’Urso, and Caiado (2019) and the references therein. The basic idea is to develop some relevant similarity or distance measures among time series first, and then to apply the standard clustering algorithms such as hierarchical clustering or k-means method. Most existing similarity/distances measures for time series may be loosely divided into two categories: data-based and feature-based. The data-based approaches define the measures directly based on observed time series using, for example, L₂- or, more general, Minkowski’s distance, or various correlation measures. Alonso and Peña (2019) proposed a generalized cross-correlation as a similarity measure, which takes into account cross-correlation over different time lags. Dynamic time warping can be applied beforehand to cope with time deformation due to, for example, shifting holidays over different years (Keogh and Ratanamahatana, 2005). The feature-based approaches extract relevant features from observed time series data first, and then define similarity/distance measures based on the extracted features. The feature extraction can be carried out by various transformations such as Fourier, wavelet or principal component analysis (sec. 2.3 of Roelofsen, 2018). The features from fitted time series models can also be used to define similarity/distance measures (Yao et al., 2000; Frühwirth-Schnatter and Kaufmann, 2008). Attempts have also been made to define the similarity between two time series by measuring the discrepancy between the two underlying stochastic processes (Kakizawa, Shumway, and Taniguchi, 1998; Khaleghi et al., 2016). Other approaches include Zhang (2013) which clusters time series based on the parallelism of their trend functions, and Ando and Bai (2017) which represents the latent clusters in terms of a factor model. So-called “subsequence clustering” occurs frequently in the literature on time series clustering; see Keogh and Lin (2005) and Zolhavarieh, Aghabozorgi, and Teh (2014). It refers to clustering the segments from a single long time series, which is not considered in this article.

The goal of this study is to propose a new factor model based approach to cluster a large number of time series into different and unknown clusters such that the members within each cluster share a similar dynamic structure, while the number of clusters and their sizes are all unknown. We represent the dynamic structures by latent common and cluster-specific factors, which are both unknown and are identified by the difference in factor strength. The strength of a factor is measured by the number of time series which influence and/or are influenced by the factor (Chamberlain, 1983). The common factors are strong factors as each of them carries the information on most (if not all) time series concerned. The cluster-specific factors are weak factors as they only affect the time series in a specific cluster.

Though our factor model is similar to that of Ando and Bai (2017), our approach is radically different. First, we estimate strong factors and all the weaker factors in the manner of one-pass, and then the latent clusters are recovered based on the estimated weak factor loadings. Ando and Bai (2017) adopted an iterative least squares algorithm to estimate factors/factor loadings and latent cluster structure recursively. Second, our setting allows the flexibility that some time series do not belong to any clusters, which is often the case in practice. Third, our setting allows the dependence between the common factors and cluster-specific factors while Ando and Bai (2017) imposed an orthogonality condition between the two; see Remark 1(iv) in Section 2.

The methods used for estimating factors and factor loadings are adapted from Lam and Yao (2012). Nevertheless substantial advances have been made even within the context of Lam and Yao (2012): (i) we remove the artifact condition that the factor loading spaces for strong and weak factors are perpendicular with each other, (ii) we allow weak serial correlations in idiosyncratic components in the model, which were assumed to be vector white noise by Lam and Yao (2012), and, more significantly, (iii) we propose a new and consistent ratio-based estimator for the number of factors (see Step 1 and also Remark 3(iii) in Section 3).

The rest of the article is organized as follows. Our factor model and the relevant conditions are presented in Section 2. We elaborate explicitly why it is natural to identify the latent clusters in terms of the factor strength. The new clustering algorithm is presented in Section 3. The clustering is based on the factor loadings on all the weak factors; applying a K-means algorithm using a correlation-type similarity measure defined in terms of the loadings. The asymptotic properties of the estimation for factors and factor loadings are collected in Section 4. Section 5 presents the consistency the proposed factor-based clustering algorithm with error rates. Numerical illustration with both simulated and a real data example is reported in Section 6. We also provide some comments in Section 7. All technical proofs are presented to a supplementary materials.

We always assume vectors in column. Let $\left|\right|\mathbf{a}\left|\right|$ denote the Euclidean norm of vector $\mathbf{a}$. For any matrix $\mathbf{G}$, let $\mathcal{M}(\mathbf{G})$ denote the linear space spanned by the columns of $\mathbf{G}\equiv (g_{i,j}),\left|\right|\mathbf{G}\left|\right|$ the square root of the largest eigenvalue of ${\mathbf{G}}^{\top }\mathbf{G},\left|\right|\mathbf{G}|{|}_{\min }$ the square root of the smallest eigenvalue of ${\mathbf{G}}^{\top }\mathbf{G}$, $\left|\mathbf{G}\right|$ the matrix with $\left|g_{i,j}\right|$ as its (i, j)th element. We write $a\asymp b$ if $a=O(b)$ and $b=O(a)$. We use $C,C_0$ to denote generic constants independent of p and n, which may be different at different places.

2 Models

Let ${\left\{{\mathbf{y}}_t\right\}}_{1\le t\le n}$ be a weakly stationary $p\times 1$ vector time series, that is, $E{\mathbf{y}}_t$ is a constant independent of t, and all elements of $\text{cov}({\mathbf{y}}_{t+k},{\mathbf{y}}_t)$ are finite and dependent on k only. Suppose that ${\mathbf{y}}_t$ consists of d + 1 latent segments, that is, (1) $${\mathbf{y}}_t^{\top }=({\mathbf{y}}_{t,1}^{\top },\dots ,{\mathbf{y}}_{t,d}^{\top },{\mathbf{y}}_{t,d+1}^{\top }),$$(1) where ${\mathbf{y}}_{t,1},\dots ,{\mathbf{y}}_{t,d+1}$ are, respectively, $p_1,\dots ,p_{d+1}$-vector time series with $p_1,\dots ,p_d\ge 1,p_{d+1}\ge 0$, and $$p_1+\cdots +p_d=p_0,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{p}_0+p_{d+1}=p.$$

Furthermore, we assume the following latent factor model with d clusters: (2) $$\begin{array}{c}{\mathbf{y}}_t=\mathbf{A}{\mathbf{x}}_t+(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array}){\mathbf{z}}_t+{\mathit{\epsilon }}_t,\\ \mathbf{B}=\text{diag}({\mathbf{B}}_1,\dots ,{\mathbf{B}}_d),\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\mathbf{z}}_t^{\top }=({\mathbf{z}}_{t,1}^{\top },\dots ,{\mathbf{z}}_{t,d}^{\top }),\end{array}$$(2) where $\mathbf{A}$ is a $p\times r_0$ matrix with rank r₀, ${\mathbf{x}}_t$ is r₀-vector time series representing r₀ common factors and $|\text{var}({\mathbf{x}}_t)|\ne 0,{\mathbf{B}}_j$ is $p_j\times r_j$ matrix with rank r_j, ${\mathbf{z}}_{t,j}$ is r_j-vector time series representing r_j factors for ${\mathbf{y}}_{t,j}$ only and $|\text{var}({\mathbf{z}}_{t,j})|\ne 0$, $\mathbf{0}$ stands for a $p_{d+1}\times r$ matrix with all elements equal to 0, $r=r_1+\cdots +r_d$, and ${\mathit{\epsilon }}_t$ is an idiosyncratic component in the sense of Chamberlain (1983) and Chamberlain, and Rothschild (1983) (see below). Note that in the model above, we only observe permuted ${\mathbf{y}}_t$ (i.e., the order of components of ${\mathbf{y}}_t$ is unknown) while all the terms on the RHS of (2) are unknown.

By (2), the p₀ components of ${\mathbf{y}}_t$ are grouped into d clusters ${\mathbf{y}}_{t,1},\dots ,{\mathbf{y}}_{t,d}$, while the $p_{d+1}$ components of ${\mathbf{y}}_{t,d+1}$ do not belong to any clusters. The jth cluster ${\mathbf{y}}_{t,j}$ is characterized by the cluster-specific factor ${\mathbf{z}}_{t,j}$, in addition to the dependence on the common factor ${\mathbf{x}}_t$. The goal is to identify those d latent clusters from observations ${\mathbf{y}}_1,\dots ,{\mathbf{y}}_n$. Note that all p_j, r_j and d are also unknown.

We always assume that the number of the common factors and the number of cluster-specific factors for each cluster remain bounded when the number of time series p diverges. This reflects the fact that the factor models are only appealing when the numbers of factors are much smaller than the number of time series concerned. Furthermore, we assume that the number of time series in each cluster p_i diverges at a lower order than p and the number of clusters d diverges as well. See Assumption 1.

Assumption 1.

${\max }_{0\le i\le d}\left\{r_i\right\}<C<\infty$, $r\asymp d=O(p^{\delta })$, and $p_i\asymp p^{1-\delta }$ for $i=1,\dots ,d$, where C > 0 and $\delta \in (0,1)$ are constants independent of n and p.

The strength of a factor is measured by the number of time series which influence and/or are influenced by the factor. Each component of ${\mathbf{x}}_t$ is a common factor. It is related to most, if not all, components of ${\mathbf{y}}_t$ in the sense that the most elements of the corresponding column of $\mathbf{A}$ (i.e., the factor loadings) are nonzero. Hence, it is reasonable to assume (3) $$\left|\right|{\mathbf{a}}_j|{|}^2\asymp p,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}j=1,\dots ,r_0,$$(3) where ${\mathbf{a}}_j$ is the jth column of $\mathbf{A}$. This is in the same spirit of the definition for the common factors by Chamberlain, and Rothschild (1983). Denoted by ${\mathbf{b}}_i^j$ the ith column of the $p_j\times r_j$ matrix ${\mathbf{B}}_j$. In the same vein, we assume that (4) $$\left|\right|{\mathbf{b}}_i^j|{|}^2\asymp p^{1-\delta },\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}i=1,\dots ,r_j\text{and}j=1,\dots ,d,$$(4) as each cluster-specific factor for the jth cluster is related to most of the $p_j\asymp p^{1-\delta }$ (Assumption 1) time series in the cluster. Note that the factor strength can be measured by constant $\delta \in [0,1]$: $\delta >0$ in (4) indicates that factors ${\mathbf{z}}_t=({\mathbf{z}}_{t,1},\dots ,{\mathbf{z}}_{t,d})$ are weaker than factors ${\mathbf{x}}_t$ which corresponds to δ = 0; see (3).

Conditions (3) and (4) are imposed under the assumption that all the factors remain unchanged as p diverges, all the entries of covariance matrices below are bounded, $$\begin{array}{c}{\mathbf{\Sigma }}_x(k)=\text{cov}({\mathbf{x}}_{t+k},{\mathbf{x}}_t),\hspace{1em}{\mathbf{\Sigma }}_z(k)=\text{cov}({\mathbf{z}}_{t+k},{\mathbf{z}}_t),\\ {\mathbf{\Sigma }}_{x,z}(k)=\text{cov}({\mathbf{x}}_{t+k},{\mathbf{z}}_t),\hspace{1em}{\mathbf{\Sigma }}_{z,x}(k)=\text{cov}({\mathbf{z}}_{t+k},{\mathbf{x}}_t),\end{array}$$and, furthermore, ${\mathbf{\Sigma }}_x(k)$ and ${\mathbf{\Sigma }}_z(k)$ are full-ranked for $k=0,1,\dots ,k_0$, where $k_0\ge 1$ is an integer. Then conditions (3) and (4) are equivalent to (6) and (7) in Assumption 3 after the orthogonal normalization to be introduced now in order to make model (2) partially identifiable and operationally tractable.

In model (2) $\mathbf{A},\mathbf{B},{\mathbf{x}}_t$ and ${\mathbf{z}}_t$ are not uniquely defined, as, for example, $(\mathbf{A},{\mathbf{x}}_t)$ can be replaced by $(\mathbf{AH},{\mathbf{H}}^{-1}{\mathbf{x}}_t)$ for any $r_0\times r_0$ invertible matrix $\mathbf{H}$. We argue that this lack of uniqueness gives us the flexibility to choose appropriate $\mathbf{A}$ and $\mathbf{B}$ to facilitate our estimation more readily. Assumption 2 specifies both $\mathbf{A}$ and $\mathbf{B}$ to be half-orthogonal in the sense that the columns of $\mathbf{A}$ or $\mathbf{B}$ are orthonormal, which can be fulfilled by, for example, replacing the original $(\mathbf{A},{\mathbf{x}}_t)$ by $(\mathbf{H},\mathbf{V}{\mathbf{x}}_t)$, where $\mathbf{A}=\mathbf{HV}$ is a QR decomposition of $\mathbf{A}$. Even under Assumption 2, $\mathbf{A}$ and $\mathbf{B}$ are still not unique. In fact that only the factor loading spaces $\mathcal{M}(\mathbf{A}),\mathcal{M}({\mathbf{B}}_i)$ are uniquely defined by (2). Hence $\mathbf{A}{\mathbf{A}}^{\top }=\mathbf{A}{({\mathbf{A}}^{\top }\mathbf{A})}^{-1}{\mathbf{A}}^{\top }$, that is, the projection matrix onto $\mathcal{M}(\mathbf{A})$, is also unique.

Assumption 2.

${\mathbf{A}}^{\top }\mathbf{A}={\mathbf{I}}_{r_0},$ ${\mathbf{B}}_j^{\top }{\mathbf{B}}_j={\mathbf{I}}_{r_j}$ for $1\le j\le d$, and it holds for a constant $q_0\in (0,1)$ that (5) $$\left|\right|\mathbf{A}{\mathbf{A}}^{\top }(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})\left|\right|\le q_0.$$(5)

Furthermore for $j=1,\dots ,d$, $\text{rp}({\mathbf{B}}_j){\{\text{rp}({\mathbf{B}}_j)\}}^{\top }$ cannot be written as a block diagonal matrix with at least two blocks, where $\text{rp}({\mathbf{B}}_j)$ denotes any row-permutation of ${\mathbf{B}}_j$.

Condition (5) implies that the columns of $(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})$ do not fall entirely into the space $\mathcal{M}(\mathbf{A})$ as otherwise one cannot distinguish ${\mathbf{z}}_t$ from ${\mathbf{x}}_t$. It is automatically fulfilled if ${\mathbf{A}}^{\top }(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})=0$ which is a condition imposed in Lam and Yao (2012). Finally the last condition in Assumption 2 ensures that the number of clusters d is uniquely defined.

Assumption 3.

Let ${\mathbf{y}}_t,{\mathbf{x}}_t$, and ${\mathbf{z}}_t$ be strictly stationary with the finite fourth moments. As $p\to \infty$, it holds for $k=0,1,\dots ,k_0$ that (6) $$\left|\right|{\mathbf{\Sigma }}_x(k)\left|\right|\asymp p\asymp \left|\right|{\mathbf{\Sigma }}_x(k)|{|}_{\min },$$(6) (7) $$\left|\right|{\mathbf{\Sigma }}_z(k)\left|\right|\asymp p^{1-\delta }\asymp \left|\right|{\mathbf{\Sigma }}_z(k)|{|}_{\min },$$(7) (8) $$\begin{array}{c}\left|\right|{\mathbf{\Sigma }}_x{(k)}^{-1/2}{\mathbf{\Sigma }}_{x,z}(k){\mathbf{\Sigma }}_z{(k)}^{-1/2}\left|\right|\le q_0<1,\\ \hspace{1em}\left|\right|{\mathbf{\Sigma }}_z{(k)}^{-1/2}{\mathbf{\Sigma }}_{z,x}(k){\mathbf{\Sigma }}_x{(k)}^{-1/2}\left|\right|\le q_0<1,\end{array}$$(8) (9) $$\left|\right|{\mathbf{\Sigma }}_{x,z}(k)\left|\right|=O(p^{1-\delta /2}),\hspace{1em}\left|\right|{\mathbf{\Sigma }}_{z,x}(k)\left|\right|=O(p^{1-\delta /2}).$$(9)

Furthermore, ${\mathbf{y}}_t$ is ψ-mixing with the mixing coefficients satisfying $\sum _{t\ge 1}t\psi {(t)}^{1/2}<\infty$, and $\text{cov}({\mathbf{x}}_t,{\mathit{\epsilon }}_s)=0$, $\text{cov}({\mathbf{z}}_t,{\mathit{\epsilon }}_s)=0$ for any t and s.

Remark 1.

(i) The factor strength is defined in terms of the orders of the factor loadings in (3) and (4). Due to the orthogonalization specified in Assumption 2, they are transformed into the orders of the covariance matrices in (6) and (7). See also Remark 1 in Lam and Yao (2012). Nevertheless, the factor strength is still measured by the constant $\delta \in [0,1]$: the smaller δ is, the stronger a factor is. The common factors in ${\mathbf{x}}_t$ are the strongest with δ = 0, and the cluster-specific factors in ${\mathbf{z}}_t$ are weaker with $\delta \in (0,1)$. In (2) ${\mathit{\epsilon }}_t$ represents the idiosyncratic component of ${\mathbf{y}}_t$ in the sense that each component of ${\mathit{\epsilon }}_t$ only affects the corresponding component and a few other components of ${\mathbf{y}}_t$ (i.e., δ = 1), which is implied by Assumptions 4. Hence, the strength of ${\mathit{\epsilon }}_t$ is the weakest. The differences in the factor strength make ${\mathbf{x}}_t,{\mathbf{z}}_t$, and ${\mathit{\epsilon }}_t$ on the RHS of (2) (asymptotically) identifiable. To simplify the presentation, we assume that all the components of ${\mathbf{z}}_t$ are of the same strength (i.e., all pi are of the same order). See the real data example in Section 6.2 for how to handle the cluster-specific factors of different strengths.

(ii) Model (2) is similar to that of Ando and Bai (2017). However, we do not require that the common factor ${\mathbf{x}}_t$ and the cluster-specific factor ${\mathbf{z}}_t$ are orthogonal with each other in the sense that $\frac{1}{n}\sum _{1\le t\le n}{\mathbf{x}}_t{\mathbf{z}}_t^{\top }=0$, which is imposed by Ando and Bai (2017). Furthermore, we allow the idiosyncratic term ${\mathit{\epsilon }}_t$ to exhibit weak autocorrelations (Assumption 4), instead of complete independence as in Ando and Bai (2017).

We now impose some structure assumptions on the idiosyncratic term ${\mathit{\epsilon }}_t$ in model (2).

Assumption 4.

Let ${\mathit{\epsilon }}_t=\mathbf{G}{\mathbf{e}}_t$, where $\mathbf{G}$ is a p × p constant matrix with $\left|\right|\mathbf{G}\left|\right|$ bounded from above by a positive constant independent of p. Furthermore, one of the following two conditions holds.

1. ${\mathbf{e}}_t$ is MA($\infty$), that is, ${\mathbf{e}}_t={\sum }_{s=0}^{\infty }{\varphi }_s{\mathit{\eta }}_{t-s}$, where ${\sum }_{s=0}^{\infty }\left|{\varphi }_s\right|<\infty$, ${\mathit{\eta }}_t={({\eta }_{t,1},\dots ,{\eta }_{t,p})}^{\top }$, and ${\eta }_{t,i}$ being iid across t and i with mean 0, variance 1 and $E({\eta }_{t,i}^4)<\infty$.

2. ${\mathbf{e}}_t={(e_{t,1},\dots ,e_{t,p})}^{\top }$ consists of p independent weakly stationary univariate time series, $E({\mathbf{e}}_t)=0$, and ${\min }_{1\le i\le p}E{e}_{t,i}^2>0$. Furthermore, ${\tilde{\mathit{e}}}_i=(e_{1,i},\dots ,e_{n,i})$ satisfies (10) $$\underset{{}_{\beta \ge 1,1\le i\le p,\left|\right|\mathbf{a}\left|\right|=1}}{\max }{\beta }^{-1/2}{\left\{\mathbb{E}\right|{\tilde{\mathit{e}}}_i^{\top }\mathbf{a}{|}^{\beta }\}}^{1/\beta }\le C_0.$$(10)

Remark 2.

In Assumption 4, (i) assumes that ${\mathbf{e}}_t$ is a linear process with the same serial correlation structure across all the components. (ii) allows some nonlinear serial dependence, the dependence structures for different components may differ. But then the sub-Gaussian condition (10) is required.

3 A Clustering Algorithm

With available observations ${\mathbf{y}}_1,\dots ,{\mathbf{y}}_n$, we propose below an algorithm (in five steps) to identify the latent d clusters. To this end, we introduce some notation first. Let $\overline{\mathbf{y}}=\frac{1}{n}{\sum }_{t=1}^n{\mathbf{y}}_t$, (11) $${\widehat{\mathbf{\Sigma }}}_y(k)=\frac{1}{n}\sum _{t=1}^{n-k}({\mathbf{y}}_{t+k}-\overline{\mathbf{y}}){({\mathbf{y}}_t-\overline{\mathbf{y}})}^{\top },\hspace{1em}\widehat{\mathit{M}}=\sum _{k=0}^{k_0}{\widehat{\mathbf{\Sigma }}}_y(k){\widehat{\mathbf{\Sigma }}}_y{(k)}^{\top },$$(11) where $k_0\ge 0$ is a pre-specified integer in Assumption 3.

• Step 1(Estimation for the number of factors.) For $0\le k\le k_0$, let ${\widehat{\lambda }}_{k,1}\ge \cdots \ge {\widehat{\lambda }}_{k,p}\ge 0$ be the eigenvalues of matrix ${\widehat{\mathbf{\Sigma }}}_y(k){\widehat{\mathbf{\Sigma }}}_y{(k)}^{\top }$. For a pre-specified positive integer $J_0\le p$, put ${\widehat{R}}_0=1$ and (12) $${\widehat{R}}_j=\sum _{k=0}^{k_0}{\widehat{\lambda }}_{k,j}/\sum _{k=0}^{k_0}{\widehat{\lambda }}_{k,j+1},\hspace{1em}1\le j\le J_0.$$(12) We say that ${\widehat{R}}_s$ attains a local maximum if ${\widehat{R}}_s>\max \{{\widehat{R}}_{s-1},{\widehat{R}}_{s+1}\}$. Let ${\widehat{R}}_{{\widehat{\tau }}_1}$ and ${\widehat{R}}_{{\widehat{\tau }}_2}$ be the two largest local maximums among ${\widehat{R}}_1,\dots ,{\widehat{R}}_{J_0-1}$. The estimators for the numbers of factors are then defined as (13) $${\widehat{r}}_0=\min \{{\widehat{\tau }}_1,{\widehat{\tau }}_2\},\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\widehat{r}}_0+\widehat{r}=\max \{{\widehat{\tau }}_1,{\widehat{\tau }}_2\}.$$(13)

• Step 2(Estimation for the loadings for common factors.) Let ${\widehat{\mathit{\gamma }}}_1,\dots ,{\widehat{\mathit{\gamma }}}_p$ be the orthonormal eigenvectors of matrix $\widehat{\mathbf{M}}$, arranged according to the descending order of the corresponding eigenvalues. The estimated loading matrix for the common factors is (14) $$\widehat{\mathbf{A}}=({\widehat{\gamma }}_1,\dots ,{\widehat{\mathit{\gamma }}}_{{\widehat{r}}_0}).$$(14)

• Step 3(Estimation for the loadings for cluster-specific factors.) Replace ${\mathbf{y}}_t$ by $({\mathbf{I}}_p-\widehat{\mathbf{A}}{\widehat{\mathbf{A}}}^{\top }){\mathbf{y}}_t$ in (11), and repeat the eigenanalysis as in Step 2 above but now denote the corresponding orthonormal eigenvectors by ${\widehat{\mathit{\zeta }}}_1,\dots ,{\widehat{\mathit{\zeta }}}_p$. The estimated loading matrix for the cluster-specific factors is (15) $$\widehat{\mathbf{B}}=({\widehat{\mathit{\zeta }}}_1,\dots ,{\widehat{\mathit{\zeta }}}_{\widehat{r}}).$$(15)

• Step 4(Identification for the components not belonging to any clusters.) Let ${\widehat{\mathbf{b}}}_1,\dots ,{\widehat{\mathbf{b}}}_p$ denote the row vectors of $\widehat{\mathbf{B}}$. Then the identified index set for the components of ${\mathbf{y}}_t$ not belonging to any clusters is (16) $${\widehat{\mathfrak{J}}}_{d+1}=\{j:1\le j\le p,|\left|{\widehat{\mathbf{b}}}_j\right||\le {\omega }_p\},$$(16) where ${\omega }_p>0$ is a constant satisfying the conditions ${\omega }_p=o(p^{\delta /2-1/2}),p^{-1/2}{\omega }_p^{-1}=o(1)$ and $\frac{p^{\delta }{n}^{-1}r+p^{-\delta }}{p^{1-\delta }{\omega }_p^2}=o(1).$

• Step 5 (K-means clustering.) Denote by $\widehat{d}$ the number of eigenvalues of $\left|\widehat{\mathbf{B}}{\widehat{\mathbf{B}}}^{\top }\right|$ greater than $1-{\hspace{0.17em}\log \hspace{0.17em}}^{-1}n$, which is taken as an upper bound of the number of clusters. Let ${\widehat{p}}_0=p-\left|{\widehat{\mathfrak{J}}}_{d+1}\right|$, and $\widehat{\mathbf{F}}$ be the ${\widehat{p}}_0\times \widehat{r}$ matrix obtained from $\widehat{\mathbf{B}}$ by removing the rows with their indices in ${\widehat{\mathfrak{J}}}_{d+1}$. Let ${\widehat{\mathbf{f}}}_1,\dots ,{\widehat{\mathbf{f}}}_{{\widehat{p}}_0}$ denote the ${\widehat{p}}_0$ rows of $\widehat{\mathbf{F}}$. Let $\widehat{\mathbf{R}}$ be the ${\widehat{p}}_0\times {\widehat{p}}_0$ matrix with the $(\mathcal{l},m)$th element $${\widehat{\rho }}_{\mathcal{l},m}=\left|{\widehat{\mathbf{f}}}_{\mathcal{l}}^{\top }{\widehat{\mathbf{f}}}_m\right|/{({\widehat{\mathbf{f}}}_{\mathcal{l}}^{\top }{\widehat{\mathbf{f}}}_{\mathcal{l}}·{\widehat{\mathbf{f}}}_m^{\top }{\widehat{\mathbf{f}}}_m)}^{1/2},\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}1\le \mathcal{l},m\le {\widehat{p}}_0.$$

Perform the K-means clustering (with L²-distance) for the ${\widehat{p}}_0$ rows of $\widehat{\mathbf{R}}$ to form the d clusters, where $d\le \widehat{d}$ is chosen such that the within-cluster-sum of L²-distances (to the cluster center points) are stabilized.

Remark 3.

(i) The ratio-based estimation in Step 1 is new. By Theorem 3 in Section 4, it holds ${\widehat{r}}_0\to r_0$ and $\widehat{r}\to r$ in probability. The existing approaches use the ratios of the ordered eigenvalues of matrix $\widehat{\mathbf{M}}$ instead (Lam and Yao, 2012; Chang, Gao, and Yao, 2015; Li, Wang, and Yao, 2017); leading to an estimator which may not be consistent. See Example 1. Note that Lam and Yao (2012) shows that their estimator ${\tilde{r}}_0$ fulfills the relation $P({\tilde{r}}_0\ge r_0)\to 1$ only.

(ii) The intuition behind the estimators in (12) is that the eigenvalues ${\lambda }_{k,1}\ge \cdots \ge {\lambda }_{k,p}(\ge 0)$ of matrix ${\mathbf{\Sigma }}_y(k){\mathbf{\Sigma }}_y{(k)}^{\top }$, where ${\mathbf{\Sigma }}_y(k)=\text{cov}({\mathbf{y}}_{t+k},{\mathbf{y}}_t)$, satisfy the conditions $$\begin{array}{c}{\lambda }_{k,i}^{-1}=o({\lambda }_{k,j}^{-1})\text{and}{\lambda }_{k,j}^{-1}=o({\lambda }_{k,\mathcal{l}}^{-1})\text{for\hspace{0.17em}}1\le i\le r_0,\\ \hspace{1em}{r}_0<j\le r_0+r\text{\hspace{0.17em}and\hspace{0.17em}}\mathcal{l}>r_0+r.\end{array}$$

This is implied by the differences in strength among the common factor ${\mathbf{x}}_t$, the cluster specific factors ${\mathbf{z}}_{t,i}$, and the idiosyncratic components ${\mathit{\epsilon }}_t$; see Theorem 3. Note that we use the ratios of the cumulative eigenvalues in (12) in order to add together the information from different lags k. In practice, we set k₀ to be a small integer such as $k_0\le 5$, as the significant autocorrelation occurs typically at small lags. The results do not vary that much with respect to the value of k₀ (see the simulation results in Section 6.1). We truncate the sequence $\left\{{\widehat{R}}_j\right\}$ at J₀ to alleviate the impact of “0/0”. In practice, we may set $J_0=p/4$ or $p/3$.

(iii) Step 3 removes the common factors first before estimating $\mathbf{B}$, as Lam and Yao (2012) showed that weak factors can be more accurately estimated by removing strong factors from the data first.

(iv) Once the numbers of strong and weak factors are correctly specified, the factor loading spaces are relatively easier to identify. In fact $\mathcal{M}(\widehat{\mathbf{A}})$ is a consistent estimator for $\mathcal{M}(\mathbf{A})$. However, $\mathcal{M}(\widehat{\mathbf{B}})$ is a consistent estimator for $\mathcal{M}\{({\mathbf{I}}_p-\mathbf{A}{\mathbf{A}}^{\top })(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})\}$ instead of $\mathcal{M}\{(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})\}$. See Theorem 2 in Section 4. Furthermore the last $p_{d+1}$ rows of $({\mathbf{I}}_p-\mathbf{A}{\mathbf{A}}^{\top })(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})$ are no longer 0. Nevertheless when the elements in $\mathbf{A}{\mathbf{A}}^{\top }$ and $\mathbf{B}{\mathbf{B}}^{\top }$ have different orders, those $p_{d+1}$ zero-rows can be recovered from $\widehat{\mathbf{B}}$ in Step 4. See Theorem 5 in Section 5.

(v) Given the block diagonal structure of $\mathbf{B}$ in (2), the d clusters would be identified easily by taking the (i, j)th element of $\left|\mathbf{B}{\mathbf{B}}^{\top }\right|$ as the similarity measure between the ith and the jth components, or by simply applying the K-means method to the rows of $\left|\mathbf{B}{\mathbf{B}}^{\top }\right|$. However, applying the K-means method directly to the rows of $\mathbf{B}$ will not do. Theorems 2 and 4 indicate that the block diagonal structure, though masked by asymptotically diminishing “noise”, still presents in $\widehat{\mathbf{B}}{\widehat{\mathbf{B}}}^{\top }$ via a latent row-permutation of $\widehat{\mathbf{B}}$. Accordingly the cluster analysis in Step 5 is based on the absolute values of the correlation-type measures among the rows of $\widehat{\mathbf{F}}{\widehat{\mathbf{F}}}^{\top }$ which is an estimator for $\mathbf{B}{\mathbf{B}}^{\top }$.

(vi) In Step 5, we search for the number of clusters d by the “elbow method” which is the most frequently used method in K-means clustering. Nevertheless $\widehat{d}$ provides an upper bound for d; see Theorem 6. Our empirical experiences indicate that $\widehat{d}=d$ holds often especially when r_j, $1\le j\le d$, are small. See Tables 7 and 8 in Section 6.1. Note that $\mathbf{B}{\mathbf{B}}^{\top }$ is a block diagonal matrix with d blocks and all the nonzero eigenvalues equal to 1. Therefore the dominant eigenvalue for each of the latent d blocks in $\widehat{\mathbf{B}}{\widehat{\mathbf{B}}}^{\top }$ is greater than or at least very close to 1. Moreover, by Perron-Frobenius’s theorem, the largest eigenvalue of $\left|{\mathbf{B}}_j{\mathbf{B}}_j^{\top }\right|$, that is, the so-called Perron-Frobenius eigenvalue, is strictly greater than the other eigenvalues of $\left|{\mathbf{B}}_j{\mathbf{B}}_j^{\top }\right|$ under the last condition in Assumption 2. This is the intuition behind the definition of $\widehat{d}$.

Example 1.

Consider a simple model of the form (2) in which ${\mathit{\epsilon }}_t\equiv 0,r_0=1, r=2,{\mathbf{A}}^{\top }(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})=\mathbf{0}$ and $$\begin{array}{c}{x}_t=p^{1/2}(u_{1,t}+a_1{u}_{1,t-1}+u_{2,t}+a_2{u}_{2,t-1}),\\ z_{1,t}=p^{1/2-\delta /2}(u_{2,t}+a_2{u}_{2,t-1}),\\ z_{2,t}=p^{1/2-\delta /2}(u_{3,t}+a_3{u}_{3,t-1}),\end{array}$$where $a_1,a_2,a_3$ are constants, and $u_{i,t}$, for different i, t, are independent and N(0, 1). Let $\mathbf{M}=\sum _{0\le k\le 1}{\mathbf{\Sigma }}_y(k){\mathbf{\Sigma }}_y{(k)}^{\top }$, and ${\lambda }_1\ge {\lambda }_2\ge {\lambda }_3$ be the three largest eigenvalues of $\mathbf{M}$. It can be shown that ${\lambda }_1\asymp p^2,{\lambda }_3=p^{2-2\delta }\{{(1+a_3^2)}^2+a_3^2\}$ and ${\lambda }_2\asymp p^{2-\delta }$ provided ${(a_1-a_2)}^2(1-a_1{a}_2)\ne 0$. Hence, ${\lambda }_1/{\lambda }_2\asymp {\lambda }_2/{\lambda }_3\asymp p^{\delta }$. This shows that $r_0(=1)$ or $r(=2)$ cannot be estimated stably based on the ratios of the eigenvalues of $\widehat{\mathbf{M}}$ for this example. In fact, let two $p\times 3$ matrices ${\mathbf{U}}_0$ and ${\mathbf{U}}_1$ be the eigenvectors of ${\mathbf{\Sigma }}_y(0){\mathbf{\Sigma }}_y{(0)}^{\top }$ and ${\mathbf{\Sigma }}_y(1){\mathbf{\Sigma }}_y{(1)}^{\top }$. When ${(a_1-a_2)}^2(1-a_1{a}_2)\ne 0,{\mathbf{U}}_0$ and ${\mathbf{U}}_1$ are different while ${\mathbf{U}}_0{\mathbf{U}}_0^{\top }={\mathbf{U}}_1{\mathbf{U}}_1^{\top }$.

4 Asymptotic Properties on Estimation for Factors

Theorem 1 and Remark 4 show that in the absence of weak factor ${\mathbf{z}}_t$, the estimation for the strong factor loading space $\mathcal{M}(\mathbf{A})$ achieves root-n convergence rate in spite of diverging p. Since only the factor loading space $\mathcal{M}(\mathbf{A})$ is uniquely defined by (2) (see the discussion below Assumption 2), we measure the estimation error in terms of its (unique) projection matrix $\mathbf{A}{\mathbf{A}}^{\top }$.

Theorem 1.

Let Assumptions 1–4 hold. Let $p,n\to \infty ,n=O(p)$ and $p^{\delta }=o(n)$. Then it holds that (17) $$\Vert \stackrel{\mathbf{⁁}}{\mathbf{A}}{\stackrel{\mathbf{⁁}}{\mathbf{A}}}^{\top }-\mathbf{A}{\mathbf{A}}^{\top }\Vert =O_p(n^{-1/2}+p^{-\delta /2}).$$(17)

Assumption 2 ensures that the rank of matrix ${\mathbf{B}}_{*}\equiv ({\mathbf{I}}_p-\mathbf{A}{\mathbf{A}}^{\top })(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})$ is r. Denote by ${\mathbf{P}}_{A_{\perp }B}={\mathbf{B}}_{*}{({\mathbf{B}}_{*}^{\top }{\mathbf{B}}_{*})}^{-1}{\mathbf{B}}_{*}^{\top }$ the projection matrix onto $\mathcal{M}\{({\mathbf{I}}_p-\mathbf{A}{\mathbf{A}}^{\top })(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})\}$ of which $\mathcal{M}(\widehat{\mathbf{B}})$ is a consistent estimator, see Theorem 2, and also Remark 3(iv).

Theorem 2.

Let Assumptions 1–4 hold. Let $p,n\to \infty ,n=O(p),p^{\delta }r=o(n)$. Then it holds that (18) $$\left|\right|\widehat{\mathit{B}}{\widehat{\mathit{B}}}^{\top }-{\mathbf{P}}_{A_{\perp }B}\left|\right|=O_p(p^{\delta /2}{n}^{-1/2}+p^{-\delta /2})$$(18)

and (19) $$\left|\right|\widehat{\mathit{B}}{\widehat{\mathit{B}}}^{\top }-{\mathbf{P}}_{A_{\perp }B}|{|}_F=O_p(p^{\delta /2}{n}^{-1/2}{r}^{1/2}+p^{-\delta /2}).$$(19)

Theorem 3 specifies the asymptotic behavior for the ratios of the cumulated eigenvalues used in estimating the numbers of factors in Step 1 in Section 3. It implies that ${\widehat{r}}_0\to r_0,\widehat{r}\to r$ in probability provided that $J_0>r_0+r$ is fixed.

Theorem 3.

Let Assumptions 1–4 hold. Let $p,n\to \infty ,n=O(p),p^{\delta }r=o(n)$. For ${\widehat{R}}_j$ defined in (12), it holds for some constant C > 0 that (20) $$\underset{n,p\to \infty }{\lim }P({\widehat{R}}_j<C)=1\hspace{1em}\text{for}j=1,\dots ,r_0-1,$$(20) (21) $${\widehat{R}}_{r_0}^{\mathrm{ }-1}=O_p(p^{-2\delta }),\hspace{1em}{\widehat{R}}_{r_0+r}^{\mathrm{ }-1}=O_p(n^{-2}{p}^{2\delta }),$$(21) (22) $$\underset{n,p\to \infty }{\lim }P({\widehat{R}}_j<C)=1\hspace{1em}\text{for}j=r_0+1,\dots ,r_0+r-1,\text{and}$$(22) (23) $${\widehat{R}}_j=O_p(1)\hspace{1em}\text{for}j=r_0+r+1,\dots ,r_0+r+s,$$(23) where s is a positive fixed integer.

Remark 4.

It is worth pointing out that the block diagonal structure of $\mathbf{B}$ is not required for Theorems 1–3. On the other hand, if ${\mathbf{A}}^{\top }(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})=0$ and $\left\{{\mathbf{x}}_t\right\}$ and $\left\{{\mathbf{z}}_t\right\}$ are independent, the term $p^{-\delta /2}$ on the RHS of (17)–(19) disappears.

5 Asymptotic Properties on Clustering

Assumption 5.

The elements of $\mathbf{A}{\mathbf{A}}^{\top }$ are of the order $O(p^{-1})$, and $\left|\right|{\mathbf{b}}_i|{|}^2\asymp p^{\delta -1}$ for $1\le i\le p_0$, where ${\mathbf{b}}_i$ denotes the ith row of matrix $\mathbf{B}$.

The orthogonalization ${\mathbf{A}}^{\top }\mathbf{A}={\mathbf{I}}_{r_0}$ implies that the average of the squared elements of $\mathbf{A}$ is $O(p^{-1})$. Since r₀ is finite, it is reasonable to assume that the elements of $\mathbf{A}{\mathbf{A}}^{\top }$ are $O(p^{-1})$. As $\mathbf{B}$ is a block-diagonal matrix with blocks $\left\{{\mathbf{B}}_j\right\}$ and ${\mathbf{B}}_j^{\top }{\mathbf{B}}_j={\mathbf{I}}_{r_j}$, the squared elements of ${\mathbf{B}}_j$ are of the order $p_j^{-1}\asymp p^{-(1-\delta )}$ in average. As r_j is bounded, it is reasonable to assume $\left|\right|{\mathbf{b}}_i|{|}^2\asymp p^{\delta -1}$. Assumption 5 ensures that $({\mathbf{I}}_p-\mathbf{A}{\mathbf{A}}^{\top })(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})$ is asymptotically a block diagonal matrix; see Theorem 4. This enables to recover the block diagonal structure of $\mathbf{B}$ based on $\widehat{\mathbf{B}}$ which provides a consistent estimator for the space $\mathcal{M}\{({\mathbf{I}}_p-\mathbf{A}{\mathbf{A}}^{\top })(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})\}$ (Theorem 2), and also to separate the components of ${\mathbf{y}}_t$ not belonging to any clusters. See Theorems 5–7 .

Theorem 4.

Let Assumptions 1–2 and 5 hold. Divide matrix $(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})({\mathbf{B}}^{\top },\mathbf{0})-{\mathbf{P}}_{A_{\perp }B}$ into $(d+1)\times (d+1)$ blocks, and denote its (i, j)th block of the size $p_i\times p_j$ by ${\mathbf{V}}_{i,j}$. Then as $p\to \infty$, $\left|\right|{\mathbf{V}}_{i,j}|{|}_F=O_p(p^{-1}{p}_i^{1/2}{p}_j^{1/2})=O_p(p^{-\delta })$.

Theorem 5.

Let the conditions of Theorem 2 and Assumption 5 hold. For ${\widehat{\mathfrak{J}}}_{d+1}$ defined in (16), it holds that (24) $$\frac{|{\mathfrak{J}}_{d+1}^c\cap {\widehat{\mathfrak{J}}}_{d+1}|}{p^{1-\delta }}=O_p(n^{-1}r{p}^{\delta }+p^{-\delta }),\hspace{1em}\text{and}$$(24) (25) $$\frac{|{\mathfrak{J}}_{d+1}\cap {\widehat{\mathfrak{J}}}_{d+1}|}{\left|{\mathfrak{J}}_{d+1}\right|}=1+O_p\left(\frac{p^{\delta }r{n}^{-1}+p^{-\delta }}{p_{d+1}{\omega }_p^2}\right),$$(25) where ω_p is given in (16). Furthermore, $\frac{p^{\delta }r{n}^{-1}+p^{-\delta }}{p_{d+1}{\omega }_p^2}=o(1)$ provided that $p^{1-\delta }/p_{d+1}=O(1)$.

Theorem 6.

Let the conditions of Theorem 5 hold, and $p^{\delta }r{\hspace{0.17em}\log \hspace{0.17em}}^{2}n=o(n)$. Then $P(\widehat{d}\ge d)\to 1,$ as $n,p\to \infty$.

Remark 5.

Theorem 5 shows that most the components belonging to the d clusters will not be classified as not belonging to any clusters (see (24)). Furthermore most the components not belonging to any clusters will be correctly identified (see (25)). Theorem 6 shows that the probability of under-estimating d converges to 0.

To investigate the errors in the K-means clustering, let $\mathbf{R}=(|r_{\mathcal{l},m}|)$ be the $p_0\times p_0$ matrix with $$r_{\mathcal{l},m}={\mathbf{b}}_{\mathcal{l}}^{\top }{\mathbf{b}}_m/{({\mathbf{b}}_{\mathcal{l}}^{\top }{\mathbf{b}}_{\mathcal{l}}·{\mathbf{b}}_m^{\top }{\mathbf{b}}_m)}^{1/2},\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}1\le \mathcal{l},m\le p_0.$$

We assume that d is known. Let ${\mathfrak{O}}_d$ be the set consisting of all $p_0\times p_0$ matrices with d distinct rows. Put (26) $${\mathbf{D}}_0=\arg \underset{{}_{\mathbf{D}\in {\mathfrak{O}}_d}}{\min }\left|\right|\mathbf{R}-\mathbf{D}|{|}_F^2.$$(26)

For any p₀-vector $\mathbf{g}$ with its elements taking integer values between 1 and d, let $$\begin{array}{c}{\mathfrak{O}}_d(\mathbf{g})=\{\mathbf{D}\in {\mathfrak{O}}_d:\text{two rows of\hspace{0.17em}}\mathbf{D}\text{\hspace{0.17em}are the same if and}\\ \hspace{1em}\text{only if the corresponding two}\mathrm{ }\text{elements}\mathrm{ }\text{of}\mathrm{ }\mathbf{g}\text{\hspace{0.17em}are}\mathrm{ }\text{the}\mathrm{ }\text{same}\}.\end{array}$$

Note that the d distinct rows of ${\mathbf{D}}_0$ would be the centers of the d clusters identified by the K-means method based on the rows of $\mathbf{R}$. However $\mathbf{R}$ is unknown, we identify the d clusters based on its estimator $\widehat{\mathbf{R}}$; see Step 5 of the algorithm in Section 3. The clustering based on $\widehat{\mathbf{R}}$ can only be successful if that based on $\mathbf{R}$ is successful, that is, ${\mathbf{D}}_0\in {\mathfrak{O}}_d({\mathbf{g}}_0)$, where ${\mathbf{g}}_0$ is the p₀-vector with 1 as its first p₁ elements, 2 as its next p₂ elements, $\dots$, and d as its last p_d elements. Given the block diagonal structure of $\mathbf{B}$, condition ${\mathbf{D}}_0\in {\mathfrak{O}}_d({\mathbf{g}}_0)$ is likely to hold.

For any p₀-vector $\mathbf{g}$ with its elements taking integer values between 1 and d, it partitions $\{1,\dots ,p_0\}$ into d subset. Let $\tau (\mathbf{g})$ denote the number of misclassified components by partition g.

Assumption 6.

${\mathbf{D}}_0\in {\mathfrak{O}}_d({\mathbf{g}}_0)$. For some constant c > 0, $$\underset{{}_{\mathbf{D}\in {\mathfrak{O}}_d(\mathbf{g})}}{\min }\left|\right|\mathbf{R}-\mathbf{D}|{|}_F^2\ge ||\mathbf{R}-{\mathbf{D}}_0|{|}_F^2+c\tau (\mathbf{g})p^{1-\delta }.$$

Theorem 7.

Let the conditions of Theorem 5 and Assumption 6 hold. The number of clusters d is assumed to be known. Denoted by $\widehat{\tau }$ the number of misclassified components of ${\mathbf{y}}_t$ by the K-means clustering in Step 5. Then as $n,p\to \infty$, (27) $$\widehat{\tau }/p=O_p(p^{-\delta /2}).$$(27)

Remark 6.

Theorem 7 implies that the misclassification rate of the K-means method converges to 0, though the convergence rate is slow (see (27)). However, a faster rate is attained when ${\mathbf{A}}^{\top }(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})=0$, and $\left\{{\mathbf{x}}_t\right\}$ and $\left\{{\mathbf{z}}_t\right\}$ are independent, as then $\widehat{\tau }/p=O_p(n^{-1/2}{r}^{1/2})$. See also Remark 4. Assumption 6 requires that $\left|\right|\mathbf{R}-\mathbf{D}|{|}_F^2$ increases as the number of misplaced members of this partition $\tau (\mathbf{g})$ becomes large, which is necessary for the K-means method.

6 Numerical Properties

6.1 Simulation

We illustrate the proposed methodology through a simulation study with model (2). We draw the elements of $\mathbf{A}$ and ${\mathbf{B}}_j$ independently from $U(-1,1)$. All component series of ${\mathbf{x}}_t$ and ${\mathbf{z}}_t$ are independent and AR(1) and MA(1), respectively, with Gaussian innovations. All components of ${\mathit{\epsilon }}_t$ are independent MA(1) with $N(0,0.25)$ innovations. All the AR and the MA coefficients are drawn randomly from $U\{(-0.95,-0.4)\cup (0.4,0.95)\}$. The standard deviations of the components of ${\mathbf{x}}_t$ and ${\mathbf{z}}_t$ are drawn randomly from U(1, 2).

We consider following two scenarios with $r_0=r_1=\cdots =r_d=2$ and $p_1=\cdots =p_d$:

• Scenario I: n = 400, d = 5 and $p_{d+1}=p_1$. Hence, r = 10 and $p=6p_1$.

• Scenario II: n = 800, d = 10 and $p_{d+1}=5p_1$. Hence, r = 20 and $p=15p_1$.

The numbers of factors r₀ and r are estimated based on the ratios ${\widehat{R}}_j$ in (13) with $k_0=1,\dots ,5$ and $J_0=[p/4]$ in (12). For the comparison purpose, we also report the estimates based on the ratios of eigenvalues of $\widehat{\mathbf{M}}$ in (11) also with $k_0=0,\dots ,5$, which is the standard method used in literature and is defined as in (13) but now with ${\widehat{R}}_j={\tilde{\lambda }}_j/{\tilde{\lambda }}_{j+1}$ instead, where ${\tilde{\lambda }}_1\ge \cdots \ge {\tilde{\lambda }}_p\ge 0$ are the eigenvalues of $\widehat{\mathbf{M}}$. See, for example, Lam and Yao (2012). For each setting, we replicate the experiment 1000 times.

The relative frequencies of ${\widehat{r}}_0=r_0$ and ${\widehat{r}}_0+\widehat{r}=r_0+r$ are reported in Tables 1–2. Overall the method based on the ratios of the cumulative eigenvalues ${\widehat{R}}_j$ provides accurate and robust performance and is not sensitive to the choice of k₀. The estimation based on the eigenvalues of $\widehat{\mathbf{M}}$ with $k\ge 1$ is competitive for r₀, but is considerably poorer for $r_0+r$ in Scenario II. Using $\widehat{\mathbf{M}}$ with k = 0 leads to weaker estimates for r₀ in Scenario I.

Table 1 The relative frequencies of ${\widehat{r}}_0=r_0$ and ${\widehat{r}}_0+\widehat{r}=r_0+r$ in a simulation for Scenario I with 1000 replications, where ${\widehat{r}}_0$ and $\widehat{r}$ are estimated by the ${\widehat{R}}_j$-based method (13), and the ratios of the eigenvalues of $\widehat{\mathbf{M}}$.

Estimation	${\widehat{r}}_0=r_0$				${\widehat{r}}_0+\widehat{r}=r_0+r$
method	$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$	$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$
${\widehat{R}}_j$ $(k_0=1)$	0.742	0.785	0.787	0.808	1	1	1	1
${\widehat{R}}_j$ $(k_0=2)$	0.762	0.792	0.799	0.823	0.999	1	1	1
${\widehat{R}}_j$ $(k_0=3)$	0.766	0.787	0.793	0.823	0.999	1	1	1
${\widehat{R}}_j$ $(k_0=4)$	0.753	0.783	0.790	0.821	0.998	1	1	1
${\widehat{R}}_j$ $(k_0=5)$	0.751	0.779	0.782	0.816	0.998	1	1	1
$\widehat{\mathbf{M}}$ $(k_0=0)$	0.707	0.749	0.761	0.758	1	1	1	1
$\widehat{\mathbf{M}}$ $(k_0=1)$	0.754	0.791	0.790	0.788	0.985	0.993	0.989	0.971
$\widehat{\mathbf{M}}$ $(k_0=2)$	0.774	0.802	0.807	0.826	0.977	0.993	0.998	0.998
$\widehat{\mathbf{M}}$ $(k_0=3)$	0.783	0.801	0.807	0.829	0.953	0.989	0.992	0.996
$\widehat{\mathbf{M}}$ $(k_0=4)$	0.786	0.799	0.805	0.830	0.929	0.979	0.982	0.991
$\widehat{\mathbf{M}}$ $(k_0=5)$	0.781	0.797	0.804	0.828	0.916	0.965	0.976	0.979

Table 2 The relative frequencies of ${\widehat{r}}_0=r_0$ and ${\widehat{r}}_0+\widehat{r}=r_0+r$ in a simulation for Scenario II with 1000 replications, where ${\widehat{r}}_0$ and $\widehat{r}$ are estimated by the ${\widehat{R}}_j$-based method (13), and the ratios of the eigenvalues of $\widehat{\mathbf{M}}$.

Estimation	${\widehat{r}}_0=r_0$				${\widehat{r}}_0+\widehat{r}=r_0+r$
method	$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$	$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$
${\widehat{R}}_j$ $(k_0=1)$	0.985	0.989	0.996	0.993	1	1	1	1
${\widehat{R}}_j$ $(k_0=2)$	0.985	0.984	0.992	0.990	1	1	1	1
${\widehat{R}}_j$ $(k_0=3)$	0.983	0.981	0.989	0.988	0.999	1	1	1
${\widehat{R}}_j$ $(k_0=4)$	0.980	0.974	0.986	0.985	0.998	1	1	1
${\widehat{R}}_j$ $(k_0=5)$	0.976	0.973	0.984	0.985	0.998	1	1	1
$\widehat{\mathbf{M}}$ $(k_0=0)$	0.976	0.991	0.998	0.993	1	1	1	1
$\widehat{\mathbf{M}}$ $(k_0=1)$	0.985	0.990	0.996	0.993	0.638	0.647	0.642	0.646
$\widehat{\mathbf{M}}$ $(k_0=2)$	0.986	0.985	0.992	0.990	0.705	0.780	0.801	0.818
$\widehat{\mathbf{M}}$ $(k_0=3)$	0.984	0.981	0.989	0.989	0.638	0.734	0.762	0.771
$\widehat{\mathbf{M}}$ $(k_0=4)$	0.980	0.976	0.985	0.988	0.597	0.689	0.722	0.723
$\widehat{\mathbf{M}}$ $(k_0=5)$	0.978	0.973	0.985	0.987	0.569	0.660	0.694	0.702

It is noticeable that the performance of the estimation for the number of common factor r₀ in Scenario II is better than Scenario I. This is due to the fact the difference in the factor strength between the common factor ${\mathbf{x}}_t$ and the cluster-based factor ${\mathbf{z}}_t$ in Scenario II is larger than Scenarios I. In contrast, the results hardly change with different values of p₁.

Recall ${\mathbf{P}}_{A\perp B}$ is the projection matrix onto the space $\mathcal{M}\{({\mathbf{I}}_p-\mathbf{A}{\mathbf{A}}^{\top })(\begin{array}{c}\mathbf{B}\\ \mathbf{0}\end{array})\}$; see Theorem 2 and also Remark 3(iv). Tables 3–4 contain the means and standard deviations of the estimation errors for the factor loading spaces $\left|\right|\widehat{\mathbf{A}}{\widehat{\mathbf{A}}}^{\top }-\mathbf{A}{\mathbf{A}}^{\top }|{|}_F$ and $\left|\right|\widehat{\mathbf{B}}{\widehat{\mathbf{B}}}^{\top }-{\mathbf{P}}_{A\perp B}|{|}_F$, where $\widehat{\mathbf{A}}$ is estimated by the eigenvectors of the matrix $\widehat{\mathbf{M}}$ in (11) with $k_0=1,\dots ,5$, see Step 2 of the algorithm stated in Section 3. See also Step 3 there for the similar procedure in estimating $\mathbf{B}$. For the comparison purpose, we also include the estimates obtained with $\widehat{\mathbf{M}}$ replaced by ${\widehat{\mathbf{\Sigma }}}_y(k){\widehat{\mathbf{\Sigma }}}_y{(k)}^{\top }$ with $k=0,1,\dots ,5$. Tables 3–4 show clearly that the estimation based on $\widehat{\mathbf{M}}$ is accurate and robust with respect to the different values of k₀. Furthermore using a single-lagged covariance matrix for estimating factor loading spaces is not recommendable. The error $\left|\right|\widehat{\mathbf{A}}{\widehat{\mathbf{A}}}^{\top }-\mathbf{A}{\mathbf{A}}^{\top }|{|}_F$ in Scenario I is larger than the error in Scenarios II. This is due to the larger sample size n in Scenario II. See Theorem 1. In contrast, Theorem 2 shows that the error rate of $\left|\right|\widehat{\mathbf{B}}{\widehat{\mathbf{B}}}^{\top }-{\mathbf{P}}_{A\perp B}\left|\right|$ contains the term $p^{\delta /2}{n}^{-1/2}$. While n is larger in Scenario II, so is $p^{\delta }$. This explains why the error $\left|\right|\widehat{\mathbf{B}}{\widehat{\mathbf{B}}}^{\top }-{\mathbf{P}}_{A\perp B}|{|}_F$ in Scenario II is also larger than that in Scenario I.

Table 3 The means and standard deviations (in parentheses) of $\left|\right|\widehat{\mathbf{A}}{\widehat{A}}^{\top }-\mathbf{A}{\mathbf{A}}^{\top }|{|}_F$ and $\left|\right|\widehat{\mathbf{B}}{\widehat{\mathbf{B}}}^{\top }-{\mathbf{P}}_{A\perp B}|{|}_F$ in a simulation for Scenario I with 1000 replications, where $\widehat{\mathbf{A}}$ is estimated by the eigenvectors of $\widehat{\mathbf{M}}$ in (11) (with $k_0=1,\dots ,5$), or by those of ${\widehat{\mathbf{\Sigma }}}_y(k){\widehat{\mathbf{\Sigma }}}_y{(k)}^{\top }$ (for $k=0,1,\dots ,5$), and $\widehat{\mathbf{B}}$ is estimated in the similar manner.

Estimation	$\left|\right|\widehat{\mathbf{A}}{\widehat{\mathbf{A}}}^{\top }-\mathbf{A}{\mathbf{A}}^{\top }|{|}_F$				$\left|\right|\widehat{\mathbf{B}}{\widehat{\mathbf{B}}}^{\top }-{\mathbf{P}}_{A\perp B}|{|}_F$
method	$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$	$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$
$\widehat{\mathbf{M}}$ $(k_0=1)$	0.237(0.101)	0.219(0.077)	0.212(0.077)	0.205(0.069)	0.508(0.061)	0.491(0.043)	0.486(0.043)	0.482(0.039)
$\widehat{\mathbf{M}}$ $(k_0=2)$	0.229(0.092)	0.215(0.072)	0.210(0.073)	0.203(0.065)	0.511(0.056)	0.495(0.042)	0.491(0.042)	0.487(0.038)
$\widehat{\mathbf{M}}$ $(k_0=3)$	0.228(0.089)	0.215(0.071)	0.211(0.072)	0.204(0.064)	0.517(0.055)	0.501(0.042)	0.498(0.042)	0.493(0.038)
$\widehat{\mathbf{M}}$ $(k_0=4)$	0.229(0.089)	0.216(0.071)	0.212(0.072)	0.205(0.064)	0.523(0.055)	0.507(0.043)	0.503(0.042)	0.499(0.039)
$\widehat{\mathbf{M}}$ $(k_0=5)$	0.230(0.088)	0.217(0.070)	0.214(0.073)	0.206(0.064)	0.528(0.055)	0.511(0.043)	0.508(0.043)	0.503(0.039)
${\widehat{\mathbf{\Sigma }}}_y(0){\widehat{\mathbf{\Sigma }}}_y{(0)}^{\top }$	0.264(0.122)	0.234(0.088)	0.222(0.086)	0.213(0.077)	0.501(0.077)	0.478(0.050)	0.470(0.049)	0.466(0.044)
${\widehat{\mathbf{\Sigma }}}_y(1){\widehat{\mathbf{\Sigma }}}_y{(1)}^{\top }$	0.292(0.117)	0.283(0.101)	0.281(0.105)	0.274(0.096)	0.994(0.083)	0.976(0.075)	0.973(0.072)	0.969(0.072)
${\widehat{\mathbf{\Sigma }}}_y(2){\widehat{\mathbf{\Sigma }}}_y{(2)}^{\top }$	0.414(0.187)	0.411(0.181)	0.414(0.181)	0.405(0.180)	2.27(0.139)	2.26(0.139)	2.26(0.131)	2.25(0.139)
${\widehat{\mathbf{\Sigma }}}_y(3){\widehat{\mathbf{\Sigma }}}_y{(3)}^{\top }$	0.621(0.312)	0.614(0.303)	0.632(0.309)	0.610(0.306)	2.31(0.154)	2.30(0.152)	2.30(0.152)	2.29(0.150)
${\widehat{\mathbf{\Sigma }}}_y(4){\widehat{\mathbf{\Sigma }}}_y{(4)}^{\top }$	0.775(0.352)	0.767(0.336)	0.800(0.361)	0.764(0.348)	2.35(0.163)	2.34(0.158)	2.34(0.161)	2.33(0.158)
${\widehat{\mathbf{\Sigma }}}_y(5){\widehat{\mathbf{\Sigma }}}_y{(5)}^{\top }$	0.885(0.359)	0.881(0.347)	0.894(0.358)	0.868(0.350)	2.39(0.169)	2.37(0.158)	2.36(0.164)	2.36(0.164)

NOTE: Both r₀ and r are assumed to be known.

Table 4 The means and standard deviations (in parentheses) of $\left|\right|\widehat{\mathit{A}}{\widehat{\mathit{A}}}^{\top }-\mathbf{A}{\mathbf{A}}^{\top }|{|}_F$ and $\left|\right|\widehat{\mathit{B}}{\widehat{\mathit{B}}}^{\top }-{\mathbf{P}}_{A\perp B}|{|}_F$ in a simulation for Scenario II with 1000 replications, where $\widehat{\mathbf{A}}$ is estimated by the eigenvectors of $\widehat{\mathbf{M}}$ in (11) (with $k_0=1,\dots ,5$), or by those of ${\widehat{\mathbf{\Sigma }}}_y(k){\widehat{\mathbf{\Sigma }}}_y{(k)}^{\top }$ (for $k=0,1,\dots ,5$), and $\widehat{\mathbf{B}}$ is estimated in the similar manner.

Estimation	$\left|\right|\widehat{\mathbf{A}}{\widehat{\mathbf{A}}}^{\top }-\mathbf{A}{\mathbf{A}}^{\top }|{|}_F$				$\left|\right|\widehat{\mathbf{B}}{\widehat{\mathbf{B}}}^{\top }-{\mathbf{P}}_{A\perp B}|{|}_F$
method	$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$	$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$
$\widehat{\mathbf{M}}$ $(k_0=1)$	0.118(0.027)	0.116(0.027)	0.115(0.026)	0.113(0.025)	0.720(0.040)	0.705(0.034)	0.701(0.033)	0.699(0.032)
$\widehat{\mathbf{M}}$ $(k_0=2)$	0.119(0.027)	0.117(0.027)	0.117(0.026)	0.115(0.025)	0.735(0.043)	0.718(0.035)	0.714(0.035)	0.711(0.033)
$\widehat{\mathbf{M}}$ $(k_0=3)$	0.121(0.027)	0.120(0.027)	0.119(0.026)	0.117(0.025)	0.748(0.045)	0.729(0.037)	0.725(0.036)	0.722(0.034)
$\widehat{\mathbf{M}}$ $(k_0=4)$	0.123(0.028)	0.122(0.027)	0.121(0.027)	0.119(0.025)	0.758(0.047)	0.739(0.038)	0.734(0.037)	0.731(0.035)
$\widehat{\mathbf{M}}$ $(k_0=5)$	0.124(0.028)	0.123(0.027)	0.122(0.027)	0.120(0.025)	0.767(0.048)	0.746(0.038)	0.741(0.038)	0.738(0.036)
${\widehat{\mathbf{\Sigma }}}_y(0){\widehat{\mathbf{\Sigma }}}_y{(0)}^{\top }$	0.119(0.029)	0.114(0.026)	0.113(0.025)	0.111(0.024)	0.677(0.036)	0.665(0.031)	0.662(0.031)	0.661(0.030)
${\widehat{\mathbf{\Sigma }}}_y(1){\widehat{\mathbf{\Sigma }}}_y{(1)}^{\top }$	0.169(0.048)	0.168(0.049)	0.166(0.046)	0.165(0.047)	1.48(0.080)	1.45(0.073)	1.44(0.071)	1.44(0.069)
${\widehat{\mathbf{\Sigma }}}_y(2){\widehat{\mathbf{\Sigma }}}_y{(2)}^{\top }$	0.277(0.121)	0.277(0.122)	0.274(0.114)	0.276(0.125)	3.29(0.101)	3.28(0.099)	3.27(0.098)	3.27(0.103)
${\widehat{\mathbf{\Sigma }}}_y(3){\widehat{\mathbf{\Sigma }}}_y{(3)}^{\top }$	0.456(0.249)	0.455(0.249)	0.450(0.240)	0.444(0.247)	3.32(0.106)	3.31(0.105)	3.30(0.106)	3.30(0.105)
${\widehat{\mathbf{\Sigma }}}_y(4){\widehat{\mathbf{\Sigma }}}_y{(4)}^{\top }$	0.626(0.329)	0.621(0.314)	0.610(0.306)	0.604(0.309)	3.35(0.119)	3.33(0.112)	3.32(0.114)	3.32(0.112)
${\widehat{\mathbf{\Sigma }}}_y(5){\widehat{\mathbf{\Sigma }}}_y{(5)}^{\top }$	0.729(0.337)	0.730(0.330)	0.725(0.337)	0.723(0.338)	3.37(0.123)	3.36(0.114)	3.34(0.118)	3.35(0.115)

NOTE: Both r₀ and r are assumed to be known.

In the sequel, we only report the results with ${\widehat{r}}_0$ and $\widehat{r}$ estimated by (13), and the factor loading spaces estimated by the eigenvectors of $\widehat{\mathbf{M}}$. We always set $k_0=5$. We examine now the effectiveness of Step 4 of the algorithm. Note that the indices of the components not belonging to any clusters are identified as those in ${\widehat{\mathfrak{J}}}_{d+1}$ in (16), which is defined in terms of a threshold ${\omega }_p=o(p^{\delta /2-1/2})$. We experiment with the three choices of this tuning parameter, namely ${\omega }_{p1}={(\widehat{r}/p)}^{1/2}/\hspace{0.17em}\ln \hspace{0.17em}p$, ${\omega }_{p2}={\{\widehat{r}/(p\hspace{0.17em}\ln \hspace{0.17em}p)\}}^{1/2}$ and ${\omega }_{p3}={\{\widehat{r}/(p\hspace{0.17em}\ln \hspace{0.17em}\hspace{0.17em}\ln \hspace{0.17em}p)\}}^{1/2}$. Recall ${\mathfrak{J}}_{d+1}^c$ contains all the indices of the components of ${\mathbf{y}}_t$ belonging to one of the d clusters. The means and standard deviations of the two types of misclassification errors $E_1=|{\mathfrak{J}}_{d+1}^c\cap {\widehat{\mathfrak{J}}}_{d+1}|/\left|{\mathfrak{J}}_{d+1}^c\right|$ and $E_2=|{\mathfrak{J}}_{d+1}\cap {\widehat{\mathfrak{J}}}_{d+1}^c|/\left|{\mathfrak{J}}_{d+1}\right|$ over the 1000 replications are reported in Tables 5–6. Among the three choices, ${\omega }_{p2}$ appears to work best as the two types of errors are both small. The increase in the errors due to the estimation for r₀ and r is not significant.

Table 5 The means and standard deviations (in parentheses) of the error rates $E_1=|{\mathfrak{J}}_{d+1}^c\cap {\widehat{\mathfrak{J}}}_{d+1}|/\left|{\mathfrak{J}}_{d+1}^c\right|$ and $E_2=|{\mathfrak{J}}_{d+1}\cap {\widehat{\mathfrak{J}}}_{d+1}^c|/\left|{\mathfrak{J}}_{d+1}\right|$ in a simulation for Scenario I with 1000 replications with the three possible choices of threshold ω_p in (16), and the numbers of factors r₀ and r either known or to be estimated.

		r0 and r are known				r0 and r are estimated
		$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$	$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$
${\omega }_{p1}$	E1	0.007(0.007)	0.006(0.005)	0.005(0.003)	0.005(0.003)	0.006(0.007)	0.005(0.006)	0.005(0.004)	0.004(0.007)
${\omega }_{p2}$		0.073(0.021)	0.067(0.014)	0.064(0.012)	0.061(0.010)	0.067(0.024)	0.062(0.022)	0.058(0.016)	0.057(0.023)
${\omega }_{p3}$ Z ${\omega }_{p3}$		0.259(0.031)	0.244(0.021)	0.237(0.017)	0.231(0.015)	0.256(0.033)	0.240(0.026)	0.232(0.018)	0.227(0.023)
${\omega }_{p1}$	E2	0.279(0.152)	0.216(0.119)	0.201(0.107)	0.194(0.097)	0.380 (0.247)	0.328(0.255)	0.321(0.264)	0.297(0.254)
${\omega }_{p2}$		0.000(0.003)	2e-5(0.0006)	1.3e-5(0.0004)	0.000(0.002)	0.050(0.096)	0.051(0.101)	0.057(0.111)	0.050(0.108)
${\omega }_{p3}$		0.000(0.000)	0.000(0.000)	0.000(0.000)	0.000(0.000)	0.000(0.001)	0.000(0.000)	0.000(0.000)	0.000(0.000)

Table 6 The means and standard deviations (in parentheses) of the error rates $E_1=|{\mathfrak{J}}_{d+1}^c\cap {\widehat{\mathfrak{J}}}_{d+1}|/\left|{\mathfrak{J}}_{d+1}^c\right|$ and $E_2=|{\mathfrak{J}}_{d+1}\cap {\widehat{\mathfrak{J}}}_{d+1}^c|/\left|{\mathfrak{J}}_{d+1}\right|$ in a simulation for Scenario II with 1000 replications with the three possible choices of threshold ω_p in (16), and the numbers of factors r₀ and r either known or to be estimated.

		r0 and r are known				r0 and r are estimated
		$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$	$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$
${\omega }_{p1}$	E1	0.003(0.004)	0.003(0.002)	0.002(0.002)	0.002(0.001)	0.003(0.004)	0.002(0.002)	0.002(0.002)	0.002(0.001)
${\omega }_{p2}$		0.049(0.013)	0.046(0.009)	0.044(0.007)	0.042(0.006)	0.049(0.013)	0.046(0.009)	0.044(0.007)	0.042(0.007)
${\omega }_{p3}$		0.185(0.019)	0.179(0.014)	0.174(0.012)	0.171(0.010)	0.185(0.019)	0.179(0.015)	0.174(0.012)	0.171(0.010)
${\omega }_{p1}$	E2	0.208(0.083)	0.202(0.069)	0.226(0.072)	0.252(0.070)	0.221(0.118)	0.218(0.119)	0.235(0.104)	0.261(0.100)
${\omega }_{p2}$		0.000(0.003)	0.000(0.000)	0.000(0.000)	0.000(0.000)	0.001(0.005)	0.001(0.009)	0.001(0.009)	0.001(0.011)
${\omega }_{p3}$		0.000(0.000)	0.000(0.000)	0.000(0.000)	0.000(0.000)	0.000(0.000)	0.000(0.000)	0.000(0.000)	0.000(0.000)

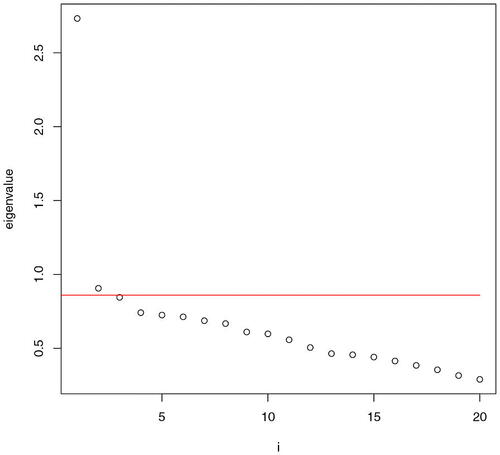
In the sequel, we only report the results with ${\omega }_{p2}={\{\widehat{r}/(p\hspace{0.17em}\ln \hspace{0.17em}p)\}}^{1/2}$. In Step 5, we estimate $\widehat{d}$ as an upper bound for d. As r_j = 2 for $j=1,\dots ,d,\widehat{d}=d$ occurs almost surely in our simulation. See Tables 7–8. Then the $\widehat{d}$ clusters are obtained by performing the K-means clustering for the ${\widehat{p}}_0$ rows of $\widehat{\mathbf{R}}$, where ${\widehat{p}}_0=p-\left|{\widehat{\mathfrak{J}}}_{d+1}\right|$. As the error rates in estimating ${\mathfrak{J}}_{d+1}^c$ has already been reported in Tables 5–6, we concentrate on the components of ${\mathbf{y}}_t$ with indices in ${\widehat{\mathfrak{J}}}_{d+1}^c\cap {\mathfrak{J}}_{d+1}^c$ now, and count the number of them which were misplaced by the K-means clustering, that is, $\widehat{\tau }$. Both the means and the standard deviations of the error rates $\widehat{\tau }/|{\widehat{\mathfrak{J}}}_{d+1}^c\cap {\mathfrak{J}}_{d+1}^c|$ over 1000 replications are reported in Tables 7–8. We also report the relative frequencies of $\widehat{d}=d$. Tables 7–8 show clearly that the K-means clustering identifies the latent clusters very accurately, and the difference in performance due to the estimating $(r_0,r)$ is also small.

Table 7 The means and Standard Deviations (STD) of the error rates $\widehat{\tau }/|{\widehat{\mathfrak{J}}}_{d+1}^c\cap {\mathfrak{J}}_{d+1}^c|$ and the relative frequencies of $\widehat{d}=d$ in a simulation for Scenario I with 1000 replications with the numbers of factors r₀ and r either known or to be estimated.

	r0 and r are known				r0 and r are estimated
	$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$	$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$
mean	1.7e-5	0	2.8e-6	0	0.0037	0.0029	0.0037	0.0034
STD	0.0003	0	8.9e-5	0	0.0134	0.0072	0.0101	0.0167
$\widehat{d}=d$	1	1	1	1	1	0.999	1	0.999

Table 8 The means and Standard Deviations (STD) of the error rates $\widehat{\tau }/|{\widehat{\mathfrak{J}}}_{d+1}^c\cap {\mathfrak{J}}_{d+1}^c|$ and the relative frequencies of $\widehat{d}=d$ in a simulation for Scenario II with 1000 replications with the numbers of factors r₀ and r either known or to be estimated.

	r0 and r are known				r0 and r are estimated
	$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$	$p_1=25$	$p_1=50$	$p_1=75$	$p_1=100$
mean	0	0	0	0	8e-6	0.0002	0.0003	0.0005
STD	0.0003	0	0	0	0.0001	0.0036	0.0046	0.0075
$\widehat{d}=d$	1	1	1	1	1	1	1	1

6.2 Real Data Illustration

We consider the daily returns of the stocks listed in S&P500 in December 31, 2014–December 31, 2019. By removing those which were not traded on every trading day during the period, there are p = 477 stocks which were traded on n = 1259 trading days. Those stocks are from 11 industry sectors:

Table

1. Communication Services	2. Consumer Discretionary
3. Consumer Staples	4. Energy
5. Financials	6. Health Care
7. Industrials	8. Information Technology
9. Materials	10. Real Estate
11. Utilities

The conventional wisdom suggests that the companies in the same industry sector share some common features. We apply the proposed 5-step algorithm in Section 3 to the return series to cluster those 477 stocks into different groups.

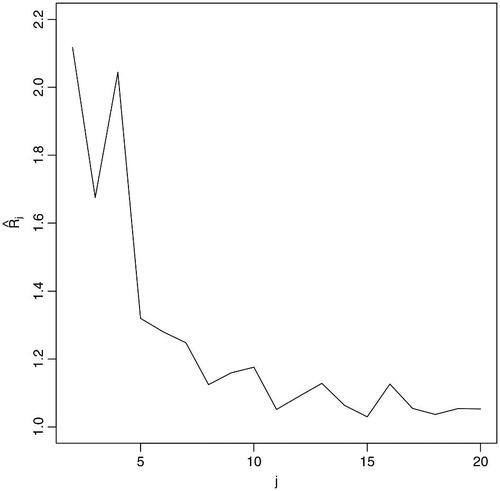
Step 1 is to estimate the numbers of strong factors and cluster-specific weak factors. To this end, we calculate ${\widehat{R}}_j$ as in (12) with $k_0=5$. It turns out ${\widehat{R}}_1=32.53$ is much larger than all the others, while ${\widehat{R}}_j$ for $j\ge 2$ are plotted in Figure 1. By (13), ${\widehat{r}}_0=1$ and ${\widehat{r}}_0+\widehat{r}=4$. Note that the estimates for ${\widehat{r}}_0$ and ${\widehat{r}}_0+\widehat{r}$ are unchanged with $k_0=1,\dots ,4$. While the existence of ${\widehat{r}}_0=1$ strong and common factor is reasonable, it is most unlikely that there are merely $\widehat{r}=3$ cluster-specific weak factors. Note that estimators in (13) are derived under the assumption that all the r cluster-specific (i.e., weak) factors are of the same factor strength; see Remark 1(ii) in Section 2. In practice weak factors may have different degrees of strength; implying that we should also take into account the 3rd, the 4th, the 5th largest local maximum of ${\widehat{R}}_j$. Hence, we take ${\widehat{r}}_0+\widehat{r}=16$ (or perhaps also 10 or 13), as Figure 1 suggests that there are 3 factors with factor strength ${\delta }_1>0$, and further 12 factors with strength ${\delta }_2\in ({\delta }_1,1)$.

Fig. 1 Plot of ${\widehat{R}}_j$ against j for $2\le j\le 20$.

With ${\widehat{r}}_0=1$ and $\widehat{r}=15$, we proceed to Steps 2 & 3 of Section 3 and obtain the estimator $\widehat{\mathbf{B}}$ as in (15). Setting ${\omega }_p={\{\widehat{r}/(p\hspace{0.17em}\ln \hspace{0.17em}p)\}}^{1/2}$, $\left|{\widehat{\mathfrak{J}}}_{d+1}\right|=11$, that is, 11 stocks do not appear to belong to any clusters, where ${\widehat{\mathfrak{J}}}_{d+1}$ is defined as in (16) in Step 4. Leaving those 11 stocks out, we perform Step 5, that is, the K-means clustering for the ${\widehat{p}}_0=477-11=466$ rows of matrix $\widehat{\mathbf{R}}$. From Figure 2 we choose $\widehat{d}=3$. But we also consider $\widehat{d}=9$ and $\widehat{d}=11$ as two more examples.

Fig. 2 The eigenvalues of $\left|\widehat{\mathit{B}}{\widehat{\mathit{B}}}^{\top }\right|$ when ${\widehat{r}}_0=1$ and $\widehat{r}=15$. The red line is $1-{\hspace{0.17em}\log \hspace{0.17em}}^{-1}n$.

To present the identified d clusters, we define $11\times d$ matrix with $n_{ij}/n_i$ as its (i, j)th element, where n_i is the number of the stocks in the ith industry sector, and n_ij is the number of the stocks in the ith industry sector which are allocated in the jth cluster. Thus, $n_{ij}/n_i\in [0,1]$ and $\sum _j{n}_{ij}/n_i=1$.

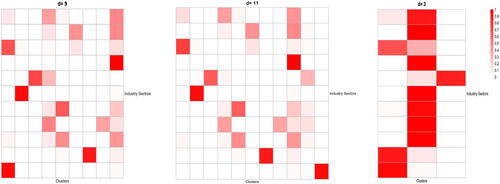
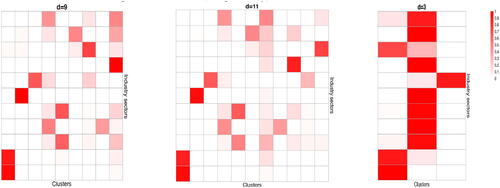
The heat-maps of this $11\times d$ matrix for $d=\widehat{d}=9$ is presented in Figure 3. The first cluster mainly consists of the companies in Consumer Staples, and Utilities, Clusters 2 and 3 contain the companies in, respectively, Health Care and Financials, Cluster 4 contains mainly some companies in Communication Service and Information Technology, Cluster 5 consists of the companies in Industrials and Materials, Cluster 6 are mainly the companies in Consumer Discretionary, Cluster 7 are mainly the companies in Real Estate. Cluster 8 is mainly the companies from Information Technology, Cluster 9 contains almost all companies in Energy and a small number of companies from each of 5 or 6 different sectors. To examine how stable the clustering is, we also include the results for d = 11 and d = 3 in Figure 3. When d is increased from 9 to 11, the original Cluster 1 is divided into new Clusters 1 and 11 with the former consisting of Consumer Staples, and the latter being Utilities. Furthermore the original Cluster 4 splits into new Clusters 4 and 10, while the other 7 original clusters are hardly changed. With d = 3, most companies in each of the 11 sectors stay in one cluster. For example, most companies in Financials are always in a separate group.

Fig. 3 Heat-maps of the distributions of the stocks in each of the 11 industry sectors (corresponding to 11 rows) over d clusters (corresponding to d columns), with $d=9,11,$ and 3. The estimated numbers of the common and cluster-specific factors are, respectively, ${\widehat{r}}_0=1$ and $\widehat{r}=15$.

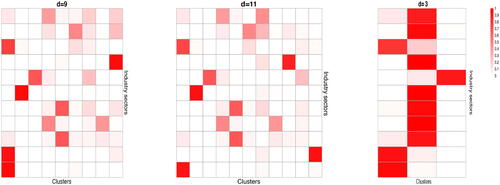
If we take ${\widehat{r}}_0=1$ and $\widehat{r}=9,\left|{\widehat{\mathfrak{J}}}_{d+1}\right|=12$ and ${\widehat{p}}_0=477-12=465$. The clustering results with $d=9,11$ and 3 are presented in is presented in Figure 4. The first cluster mainly consists of the companies in Consumer Staples, Real Estate and Utilities, Clusters 2 and 3 contain the companies in, respectively, Health Care and Financials, Cluster 4 contains mainly some companies in Communication Service and Information Technology, Cluster 5 consists of the companies in Industrials and Materials, Cluster 6 are mainly the companies in Consumer Discretionary, Cluster 7 is a mixture of a small number of companies from each of 5 or 6 different sectors, Cluster 8 is mainly the companies from Information Technology, Cluster 9 contains almost all companies in Energy. To examine how stable the clustering is, we also include the results for d = 11 and d = 3 in Figure 4. When d is increased from 9 to 11, the original Cluster 1 is divided into new Clusters 1 and 11 with the former consisting of Consumer Staples and Utilities sectors, and the latter being Real Estate sector. Furthermore the original Cluster 7 splits into new Clusters 7 and 10, while the other 7 original clusters are hardly changed. With d = 3, most companies in each of the 11 sectors stay in one cluster.

Fig. 4 Heat-maps of the distributions of the stocks in each of the 11 industry sectors (corresponding to 11 rows) over d clusters (corresponding to d columns), with $d=9,11,$ and 3. The estimated numbers of the common and cluster-specific factors are, respectively, ${\widehat{r}}_0=1$ and $\widehat{r}=9$.

If we take ${\widehat{r}}_0=1$ and $\widehat{r}=12$, the estimated ${\widehat{\mathfrak{J}}}_{d+1}$ is unchanged. The clustering results with $d=9,11,$ and 3 are presented in Figure 5. Comparing with Figure 4, there are some striking similarities: First the clustering with d = 3 are almost identical. For d = 9, the profiles of Clusters 2, …, 6, 8, and 9 are not significantly changed while Clusters 1 and 7 in Figure 4 are somehow mixed together in Figure 5. With d = 11, the profiles of Clusters 2 – 6, 8 – 10 in the two figures are about the same while Clusters 7 and 11 are mixed up across the two figures.

Fig. 5 Heat-maps of the distributions of the stocks in each of the 11 industry sectors (corresponding to 11 rows) over d clusters (corresponding to d columns), with $d=9,11,$ and 3. The estimated numbers of the common and cluster-specific factors are, respectively, ${\widehat{r}}_0=1$ and $\widehat{r}=12$.

The analysis above indicates that the companies in the same industry sector tend to share similar dynamic structure in the sense that they are driven by the same cluster-specific factors. Our analysis is reasonably stable as most the clusters do not change substantially when the number of the weaker factors chooses different values $\widehat{r}=9,\widehat{r}=12$, or $\widehat{r}=15$.

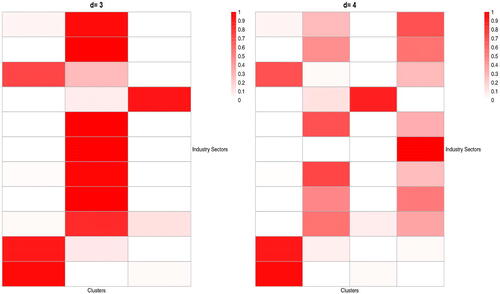
We also apply method of Ando and Bai (2017) to this dataset; leading to the same estimate ${\widehat{r}}_0=1$, but smaller estimates $\widehat{r}=4$ and $\widehat{d}=4$. The clustering results for $\widehat{d}=3$ and $\widehat{d}=4$ are presented in Figure 6 which similar to the right parts in Figures 3–5, though the method of Ando and Bai (2017) puts energy companies as a separate group. In contrast, our method puts financial companies as a separate group. Note that classical papers in Finance (e.g., Berger and Ofek, 1995; Denis, Denis, and Yost, 2002; Lemmon, Roberts, and Zender, 2008) often eliminate financial companies from other companies.

Fig. 6 Heat-maps of the distributions of the stocks in each of the 11 industry sectors (corresponding to 11 rows) over d clusters (corresponding to d columns) based on Ando and Bai (2017).

7 Miscellaneous Comments

Robustness

We identify and distinguish common factors and cluster-specific factors by the different factor strengths, that is, common factors are strong with δ = 0, and cluster-specific factors are weak with $\delta >0$. However if, for example, one of the common factors has the same strength as the cluster-specific factors, the number of the strong factor is then $r_0-1$ and the number of the weak factors is r + 1. In this case, the estimated $r_0, r$ and the factor loading spaces will all be wrong. Nevertheless a common factor has nonzero loadings on the most components of ${\mathbf{y}}_t$, hence, those loadings must be extremely small in order to be a weak factor. Therefore, its impact on the estimation of the number of clusters, and the misclassification rates is minor. Simulation results in supplementary materials support this assertion.

Heterogeneous factor strength

We assume two factor strengths: p for common factors and $p^{1-\delta }$ for cluster-specific factors. If there are s different strengths $p^{1-{\delta }_1},\dots ,p^{1-{\delta }_s}$ among the cluster-specific factors, we can search for the s largest local maximums among ${\widehat{R}}_1,\dots ,{\widehat{R}}_{J_0-1}$ in Step 1. Moreover, Step 2 should be repeated s times to estimate s factor loadings corresponding to different factor strengths. While the asymptotic results can be extended accordingly, small values such as $s\le 3$ are sufficient for most practical applications.

Estimation for r_j and ${\mathbf{B}}_j$

When we cluster the time series correctly in Steps 4–5, we obtain the estimator for ${\mathbf{B}}_j$ from $\widehat{\mathit{B}}$ directly. We can also run Step 1 on each cluster to estimate r_j. Theorem 3 ensures the consistency of those estimates. Although Theorem 7 ensures that most of time series can be clustered correctly, there may be a cluster obtained in Step 5 which is not accuracy enough. It remains an open problem to evaluate how the clustering error is propagated into the estimation for r_j and ${\mathbf{B}}_j$.

Supplementary Materials

All the technical proofs are presented in an online supplementary which also contains additional simulation results. We also provide the dataset and codes in Section 6 in an online supplementary.

Acknowledgments

We would like to thank three reviewers, the associate editor and the editor for their comments and suggestions. We would like to thank Professor Tomohiro Ando and Professor Jushan Bai for kindly providing us with the computer code for the simulations in Ando and Bai (2017).

Disclosure Statement

There are no relevant competing interests to declare.

Additional information

Funding

Bo Zhang is partially supported by National Natural Science Funds of China No.12001517 & 72091212, National Key R&D Program of China-2022YFA1008000, USTC Research Funds of the Double First-Class Initiative YD2040002005 and The Fundamental Research Funds for the Central Universities WK2040000026 & WK2040000027. Guangming Pan is partially supported by MOE Tier 2 grant 2018-T2-2-112 and MOE Tier 1 grant RG76/21 at the Nanyang Technological University, Singapore. Qiwei Yao is partially supported by EPSRC (UK) Research grant EP/V007556/1. Wang Zhou is partially supported by a grant A-8000440-00-00 at the National University of Singapore.