Addressing Multiple Detection Limits with Semiparametric Cumulative Probability Models

Abstract

Detection limits (DLs), where a variable cannot be measured outside of a certain range, are common in research. DLs may vary across study sites or over time. Most approaches to handling DLs in response variables implicitly make strong parametric assumptions on the distribution of data outside DLs. We propose a new approach to deal with multiple DLs based on a widely used ordinal regression model, the cumulative probability model (CPM). The CPM is a rank-based, semiparametric linear transformation model that can handle mixed distributions of continuous and discrete outcome variables. These features are key for analyzing data with DLs because while observations inside DLs are continuous, those outside DLs are censored and generally put into discrete categories. With a single lower DL, CPMs assign values below the DL as having the lowest rank. With multiple DLs, the CPM likelihood can be modified to appropriately distribute probability mass. We demonstrate the use of CPMs with DLs via simulations and a data example. This work is motivated by a study investigating factors associated with HIV viral load 6 months after starting antiretroviral therapy in Latin America; 56% of observations are below lower DLs that vary across study sites and over time. Supplementary materials for this article are available online including a standardized description of the materials available for reproducing the work.

EYWORDS:

• HIV
• Limit of detection
• Ordinal regression model
• Transformation model

1 Introduction

Detection limits (DLs) are not uncommon in biomedical research and other fields. For example, radiation doses may only be detected above a certain threshold (Wing et al.1991), antibody concentrations may not be measured below certain levels (Wu et al.2001), and X-rays may have lower limits of detection (Pan et al.2017). In HIV research, viral load can only be detected above certain levels. To complicate matters, DLs often vary by assay and may change over time.

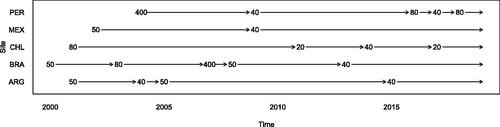
As a motivating example, we consider estimating the association between patient factors at initiation of antiretroviral therapy (ART) and viral load 6 months after starting ART among adults with HIV. Viral load (VL) measures the amount of virus circulating in a person with HIV. A high VL after ART initiation may indicate nonadherence or an ineffective regimen that should be switched. We study the association between VL 6 months after ART initiation and variables measured at ART initiation (baseline). The data include 5301 adults living with HIV starting ART at one of 5 study centers in Latin America between 2000 and 2018. The DLs for the outcome VL differed by site and calendar time. Figure 1 shows the most frequent lower DL values for each year and at each site. There are five distinct lower DLs in this database: 20, 40, 50, 80, and 400 copies/mL. A total of 2992 (56%) patients had 6-month VL censored at a DL: 45%, 54%, 52%, 65%, and 57% at study sites in Argentina, Brazil, Chile, Mexico, and Peru, respectively.

Figure 1: The changes of most frequent DL values every year at each study site over time.

A traditional analysis in the HIV literature would dichotomize VL as detectable or undetectable and perform logistic regression (Jiamsakul et al.2017). There are a few issues that make this analysis less than ideal. First, all VLs above the DL (nearly half of all observations) would be collapsed into a “detectable” category resulting in well-known loss of information due to dichotomizing continuous variables (Fedorov, Mannino, and Zhang 2009). Second, because the DL varies with time and by site, the analyst is forced to dichotomize at the largest DL (in this case 400 copies/mL) or else perform an analysis where values above the DL at one site are treated differently than they would be treated at another site. For example, a VL of 300 copies/mL measured in Mexico in 2005 would be measured as “$<400$” that same year in Peru; assigning this value as “$<400$” results in lost information but leaving it as “detectable” would make the outcome variable different across time and sites.

Another common approach for handling DLs is substitution, where all nondetects are imputed with a single constant and a linear regression model is fit. The imputed constant may be, for example, the DL itself, DL/2, DL/$\sqrt{2}$ (Hornung and Reed 1990; Lubin et al.2004; Helsel 2011), or the expectation of the measurement conditional on being outside the DL under some assumed parametric model (Garland et al.1993). For example, DL/2 corresponds to the expectation of a uniform distribution between 0 and the DL. Although simple, these substitution approaches typically result in biased estimation, underestimated variances, and thus sometimes wrong conclusions (Baccarelli et al.2005; Fiévet and Della Vedova 2010). With multiple DLs, additional questions arise about whether to assign all values below any DL the same constant or to use the same function of the DL (e.g., 400/2 = 200 copies/mL for all values below any DL, or DL/2); there are obvious problems with either approach.

A more parametric analysis might assume that the VL follow a specified distribution (e.g., log-normal distribution) and fit the censored data likelihood or multiply impute values below the DL from the assumed distribution to obtain estimated regression coefficients (Baccarelli et al.2005; Harel, Perkins, and Schisterman 2014). However, distributional assumptions for values below the DL are strong and untestable; goodness of fit of a parametric model inside DLs does not ensure goodness of fit outside the DLs. These parametric assumptions may be particularly dangerous in settings with high rates of censoring such as our HIV application (Lubin et al.2004; Zhang et al.2009).

To avoid strong parametric assumptions, nonparametric methods such as Kaplan–Meier, score, and rank-based methods have been proposed in two-sample comparisons (Helsel 2011). Zhang et al. (2009) explored the use of the Wilcoxon rank sum test, other weighted rank tests, Gehan and Peto-Peto tests, and a novel nonparametric method for location-shift inference with DLs. Although attractive for two-sample tests, these nonparametric methods generally do not permit inclusion of covariates.

In this manuscript, we propose a new approach for analyzing data subject to multiple detection limits. Data with DLs effectively follow a mixture distribution, where those below a lower DL can be thought of as belonging to a discrete category, those above an upper DL belonging to another discrete category, while those inside the DLs are continuous. Whether discrete or continuous, the values are orderable. In earlier work, Liu et al. (2017) showed that continuous response variables can be modeled using a popular model for ordinal outcomes, namely the cumulative probability model (CPM), also known as the ‘cumulative link model’ (Agresti 2013). CPMs are a type of semiparametric linear transformation model (Zeng and Lin 2007), in which the continuous response variable after some unspecified monotonic transformation is assumed to follow a linear model, and the transformation is nonparametrically estimated. These models are very flexible and can handle a wide variety of outcomes, including variables with DLs. Importantly, when fitting CPMs to data with DLs, minimal assumptions are made on the distribution of the response variable outside the DLs as these models are based on ranks, and values below/above DLs are simply the lowest/highest rank values. Because of their relationship to the Wilcoxon rank sum test (McCullagh 1980), the CPM can be thought of as a semiparametric extension to permit covariates to the approaches that Zhang et al. (2009) found effective for handling DLs in two-sample comparisons. Finally, as will be shown, because CPMs model the conditional cumulative distribution function (CDF), it is easy to extract many different measures of conditional association from a single fitted model, including conditional quantiles, conditional probabilities, odds ratios, and probabilistic indexes, which permits flexible and compatible interpretation.

Methods proposed by Cai and Cheng (2004) and Shen (2011) could also be used to fit semiparametric linear transformation models for data with DLs. Specifically, these authors developed methods to address doubly censored data, of which data subject to both lower and upper DLs are a special case. Like CPMs, these methods are robust and powerful approaches. Unfortunately, implementation of the methods of Cai and Cheng (2004) and Shen (2011) is rare/nonexistent in practice, perhaps because of the complexity of fitting these models and a lack of software. These methods estimate model parameters using estimating equations. In contrast, the CPM that we present obtains nonparametric maximum likelihood estimates that are more efficient than those of Cai and Cheng (2004) and Shen (2011) while making the same assumptions.

In Section 2, we review the CPM, illustrate its use for simple settings where there is a lower and/or upper DL for all subjects, and then show how CPMs can be extended to address multiple DLs. We also propose a new method for estimating the conditional quantile from a CPM. In Section 3, we illustrate and demonstrate the advantages of the proposed approach applied to our HIV study with multiple detection limits. In Section 4, we demonstrate the performance of our method and compare it to other approaches with simulations. The final section contains a discussion of the strengths and limitations of our method and future work. An R package, multipleDL, permits fitting CPMs in settings with multiple DLs.

2 Methods

2.1 Cumulative Probability Models

Transformation is often needed for the regression of a continuous outcome variable Y to satisfy model assumptions, but specifying the correct transformation can be difficult. In a linear transformation model, the outcome is modeled as $Y=H({\beta }^{T}X+ϵ)$, where $H(·)$ is an unknown monotonically increasing transformation, X is a vector of covariates, and $ϵ$ follows a known distribution with CDF $F_{ϵ}$. This linear transformation model can be equivalently expressed in terms of the conditional CDF, $$\begin{array}{c}F(y|X)\equiv \mathrm{\text{Pr}}(Y\le y|X)=\mathrm{\text{Pr}}[ϵ\le H^{-1}(y)-{\beta }^{T}X|X]\hfill \\ =F_{ϵ}[H^{-1}(y)-{\beta }^{T}X].\hfill \end{array}$$

Let $G=F_{ϵ}^{-1}$ and $\alpha =H^{-1}$; $\alpha (·)$ is monotonically increasing but otherwise unknown. Then (1) $$\begin{array}{c}G[F(y|X)]=\alpha (y)-{\beta }^{T}X,\hfill \end{array}$$(1) where G serves as a link function and the model becomes a cumulative probability model (CPM). The intercept function $\alpha (y)$ is the transformation of the response variable such that $\alpha (Y)={\beta }^{T}X+ϵ.$ The $\beta$ coefficients indicate the association between the response variable and covariates: fixing other covariates, a positive/negative ${\beta }_j$ means that an increase in $X_j$ is associated with a stochastic increase/decrease in the distribution of the response variable.

In the CPM (1), the intercept function $\alpha (y)$ can be nonparametrically estimated with a step function (Zeng and Lin 2007; Liu et al.2017). This allows great model flexibility. Consider an iid dataset $\{(y_i,x_i):i=1,\dots ,n\}$. The nonparametric likelihood is (2) $$\begin{array}{c}\prod _{i=1}^n\left[F(y_i|x_i)-F(y_i^{-}|x_i)\right],\hfill \end{array}$$(2) where $F(y_i^{-}|x_i)=\underset{t\uparrow y_i}{\mathrm{\text{lim}}}F(t|x_i)$. In nonparametric maximum likelihood estimation, the probability mass given any x will be distributed over the discrete set of observed outcome values. Thus, we only need to consider functions for $\alpha (·)$ such that $F(y|x_i)$ is a discrete distribution over the observed values. Let J be the number of distinct outcome values, denoted as $a_1<\cdots <a_J$. Let $S=\{a_1,\dots ,a_J\}$. These serve as the anchor points for the nonparametric likelihood. Let ${\alpha }_j=\alpha (a_j)$; then ${\alpha }_1<\cdots <{\alpha }_J$. The nonparametric likelihood (2) can be written as (3) $$\begin{array}{c}L(\beta ,\mathbf{\alpha })=\prod _{i:y_i=a_1}{F}_{ϵ}({\alpha }_1-{\beta }^T{x}_i)\hfill \end{array}$$(3) (3) $$\begin{array}{c}\times \prod _{j=2}^{J-1}\prod _{i:y_i=a_j}\left[F_{ϵ}({\alpha }_j-{\beta }^T{x}_i)-F_{ϵ}({\alpha }_{j-1}-{\beta }^T{x}_i)\right]\hfill \\ \times \prod _{i:y_i=a_J}\left[1-F_{ϵ}({\alpha }_{J-1}-{\beta }^T{x}_i)\right].\hfill \end{array}$$(3)

Maximizing (3), we obtain the nonparametric maximum likelihood estimates (NPMLEs), $(\widehat{\beta },\widehat{\mathit{\alpha }})$, where $\widehat{\mathit{\alpha }}=({\widehat{\alpha }}_1,\dots ,{\widehat{\alpha }}_{J-1})$. Note the multinomial form of the likelihood (3); because the probabilities in a multinomial likelihood add to one, ${\alpha }_J$ is not estimated. Note also that the likelihood in (3) is identical to that of cumulative link models for ordinal data if the outcome Y is treated as ordinal with categories $\{a_1,\dots ,a_J\}$. Liu et al. (2017) and Tian et al. (2020) have shown that CPMs can be fit to and work well for continuous responses ($J=n$) and mixed types of responses. Under mild conditions including boundedness of the response variable, CPM estimates are consistent and asymptotically normal, with variance consistently estimated with the inverse of the information matrix (Li et al.2023). The NPMLEs and their estimated variances can be efficiently computed with the orm() function in the rms package in R (Harrell 2020), which takes advantage of the tridiagonal nature of the Hessian matrix using Cholesky decomposition (Liu et al.2017).

CPMs have several nice features. Some widely used regression methods model only one aspect of the conditional distributions (e.g., conditional mean for linear regression and conditional quantile for quantile regression). With the NPMLEs $(\widehat{\beta },\widehat{\mathit{\alpha }})$, we can estimate the conditional CDFs as $\widehat{F}(y|x)=F_{ϵ}({\widehat{\alpha }}_j-{\widehat{\beta }}^{T}x)$ where j is the index such that $a_j=\mathrm{\text{max}}\{a\in S:a\le y\}$; standard errors can be obtained by the delta method. Since conditional CDFs are directly modeled, other characteristics of the distribution, such as the conditional quantiles and conditional expectations, can be easily derived (Liu et al.2017). Depending on the choice of link function, $\beta$ may be interpretable; for example, with the logit link function, exp $(\beta )$ is an odds ratio. Probabilistic indexes (De Neve, Thas, and Gerds 2019), which are defined as $\mathrm{\text{Pr}}(Y_1<Y_2|X_1,X_2)$, can also be easily derived; for example, with the logit link, $P(Y_1<Y_2|X_1,X_2)={\left[1+\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(-{(X_2-X_1)}^T\beta )\right]}^{-1}$. With the transformation $\alpha (·)$ nonparametrically estimated, CPMs are invariant to any monotonic transformation of the outcome; therefore, no pre-transformation is needed. With a single binary covariate and the logit link function, the score test for the CPM is nearly identical to the Wilcoxon rank sum test (McCullagh 1980); see supplementary materials S1.1. Because only the order of the outcome values but not the specific values matter when estimating $\beta$ in the CPM, it can handle any ordinal, continuous, or a mixture of ordinal and continuous distributions, which can be useful for analyzing data with DLs.

2.2 Single Detection Limits

In this section, we first present our method for the simple scenario that there is a single lower DL and/or a single upper DL. We will describe the general approach for multiple DLs in the next section.

Consider a dataset with a lower DL, l, and an upper DL, u. The outcome Y is observed if it is inside the DLs (i.e., $l\le Y\le u$) or censored if it is outside the DLs. The J distinct values of the observed outcomes are denoted as $l\le a_1<\cdots <a_J\le u$. When there are no observations outside the DLs, these values are treated as ordered categories in CPMs and they are the anchor points in the nonparametric likelihood (3), and correspondingly there are $J-1$ alpha parameters, ${\alpha }_1<\cdots <{\alpha }_{J-1}$. With observations outside the DLs, the likelihood (3) needs to be modified accordingly.

When there are observations below the lower DL, we do not know their values except that they are $<l$. As there is no way to distinguish them, we treat them as a single category, denoted as $a_0$. Note that $a_0$ is not a value but a symbol for the additional category below $a_1$. The nonparametric likelihood for a subject outcome censored at the lower DL l is $$\begin{array}{c}\mathrm{\text{Pr}}(Y_i<l|X_i=x_i)=F_{ϵ}({\alpha }_0-{\beta }^T{x}_i),\hfill \end{array}$$where ${\alpha }_0$ is the extra alpha parameter corresponding to category $a_0$ such that ${\alpha }_0<{\alpha }_1$. Because $a_1$, the previously lowest category, now has a category below it, the nonparametric likelihood for a subject with $y_i=a_1$ becomes $$\begin{array}{c}{F}_{ϵ}({\alpha }_1-{\beta }^T{x}_i)-F_{ϵ}({\alpha }_0-{\beta }^T{x}_i).\hfill \end{array}$$

Similarly, when there are observations above the upper DL, they are also treated as a single category, denoted as $a_{J+1}$, which is a symbol for the additional category above $a_J$. The nonparametric likelihood for a subject censored at the upper DL u is $$\begin{array}{c}\mathrm{\text{Pr}}(Y_i>u|X_i=x_i)=1-F_{ϵ}({\alpha }_J-{\beta }^T{x}_i).\hfill \end{array}$$

Because $a_J$ is no longer the highest category, ${\alpha }_J$ will need to be estimated, and the likelihood for a subject with $y_i=a_J$ is now $$\begin{array}{c}{F}_{ϵ}({\alpha }_J-{\beta }^T{x}_i)-F_{ϵ}({\alpha }_{J-1}-{\beta }^T{x}_i).\hfill \end{array}$$

Put together, with observed data subject to a single lower DL and a single upper DL, the CPM likelihood is (4) $$\begin{array}{c}\begin{array}{c}L(\beta ,\mathbf{\alpha })=\prod _{i:y_i=a_0}{F}_{ϵ}({\alpha }_0-{\beta }^T{x}_i)\hfill \end{array}\\ \begin{array}{c}\times \prod _{j=1}^J\prod _{i:y_i=a_j}\left[F_{ϵ}({\alpha }_j-{\beta }^T{x}_i)-F_{ϵ}({\alpha }_{j-1}-{\beta }^T{x}_i)\right]\hfill \\ \times \prod _{i:y_i=a_{J+1}}\left[1-F_{ϵ}({\alpha }_J-{\beta }^T{x}_i)\right],\hfill \end{array}\end{array}$$(4) which is equivalent to (3) except with two new anchor points, $a_0$ and $a_{J+1}$. Therefore, (4) is maximized in an identical manner to (3), with outcomes below the lower DL and outcomes above the upper DL simply assigned to categories $a_0$ and $a_{J+1}$, respectively.

In summary, when there are data censored below the lower DL, we add a new anchor point $a_0<a_1$ and a new parameter ${\alpha }_0$; when there are data censored above the upper DL, we add a new anchor point $a_{J+1}>a_J$ and a new parameter ${\alpha }_J$. The alpha parameters to be estimated are $({\alpha }_1,\dots ,{\alpha }_{J-1})$ when there are no DLs or no data censored at DLs, $({\alpha }_0,{\alpha }_1,\dots ,{\alpha }_{J-1},{\alpha }_J)$ when both categories $a_0$ and $a_{J+1}$ are added, $({\alpha }_0,{\alpha }_1,\dots ,{\alpha }_{J-1})$ when only $a_0$ is added, and $({\alpha }_1,\dots ,{\alpha }_{J-1},{\alpha }_J)$ when only $a_{J+1}$ is added.

In practice, one can fit the NPMLE in these settings using the orm() function by setting outcomes below the lower DL to some arbitrary number $<l$ and outcomes above the upper DL to some arbitrary number $>u$. Note that unlike single imputation approaches for dealing with DLs, the CPM estimation procedure is invariant to the choice of these numbers assigned to values outside the DLs. The CPM (1) assumes that after some unspecified transformation, the outcome follows a linear model both within and outside the DLs. In contrast, parametric approaches to deal with DLs assume the full distribution of the outcome conditional on covariates is known, both within and outside DLs. Hence, CPMs make much weaker assumptions than fully parametric approaches.

2.3 Multiple Detection Limits

We now consider the general situation where data may be collected from multiple study sites. A site may have no DL, only one DL, or both lower and upper DLs. Each site may have different lower DLs and different upper DLs, which may change over time.

Every subject has a vector X of covariates and three underlying random variables $(Y,C_L,C_U)$, where Y is the true outcome and $C_L<C_U$ are the lower and upper DLs. When there is no upper DL, $C_U=\infty$, and when there is no lower DL, $C_L=-\infty$. $C_L$ and $C_U$ are assumed to be independent of Y conditional on X; the vector X may contain variables for study sites or calendar time. This non-informative censoring assumption is typically plausible as DLs are determined by available equipment/assays.

We assume the CPM (1) holds for all subjects. Due to DLs, we may not always observe Y. Instead, we only observe $(Z,\Delta )$, where $Z=\mathrm{\text{max}}(\mathrm{\text{min}}(Y,C_U),C_L)$ and $\Delta$ is a variable indicating whether Y is observed or censored at a DL: $\Delta =1$ and $Z=Y$ if Y is observed, $\Delta =L$ and $Z=C_L$ if $Y<C_L$, and $\Delta =U$ and $Z=C_U$ if $Y>C_U$.

Given a dataset $\{(z_i,{\delta }_i;x_i)\}$ ($i=1,\dots ,n$), we first determine how many anchor points are needed to support the nonparametric likelihood of the CPM. Let J be the number of distinct values of $z_i$ among those with ${\delta }_i=1$; they are denoted as $a_1<\cdots <a_J$. For data without any DLs, these points are the anchor points for the nonparametric likelihood, and they are effectively treated as ordered categories in a CPM. Let $S=\{a_1,\dots ,a_J\}$ be the set of these values. When there are data with ${\delta }_i=L$, let l be the smallest $z_i$ with ${\delta }_i=L$. Similarly, when there are data with ${\delta }_i=U$, let u be the largest $z_i$ with ${\delta }_i=U$. If $l\le a_1$, we add a category into S below $a_1$, denoted as $a_0$; note that it is not a value but a symbol for the additional category in S below $a_1$. Similarly, if $u\ge a_J$, we add $a_{J+1}$ into S, which is a symbol for the additional category above $a_J$. Depending on the data, the number of ordered categories can be J, $J+1$, or $J+2$.

Consider the situation where both $a_0$ and $a_{J+1}$ have been added to S (i.e., $S=\{a_0,a_1,\dots ,a_J,a_{J+1}\}$). When ${\delta }_i=1$, the nonparametric likelihood for $(z_i,1)$ is (5) $$\begin{array}{c}{F}_{ϵ}({\alpha }_j-{\beta }^T{x}_i)-F_{ϵ}({\alpha }_{j-1}-{\beta }^T{x}_i),\hfill \end{array}$$(5) where j is the index such that $a_j=z_i$. When ${\delta }_i=L$, the nonparametric likelihood for $(z_i,L)$ is (6) $$\begin{array}{c}\mathrm{\text{Pr}}(Y<z_i|x_i)=\{\begin{array}{cc}{F}_{ϵ}({\alpha }_0-{\beta }^T{x}_i),& (z_i=l)\\ F_{ϵ}({\alpha }_j-{\beta }^T{x}_i),& (z_i\ne l)\end{array}\hfill \end{array}$$(6) where j is the index such that $a_j=\mathrm{\text{max}}\{a\in S:a<z_i\}$ when $z_i\ne l$. When ${\delta }_i=U$, the nonparametric likelihood for $(z_i,U)$ is (7) $$\begin{array}{c}\mathrm{\text{Pr}}(Y>z_i|x_i)=\{\begin{array}{cc}1-F_{ϵ}({\alpha }_J-{\beta }^T{x}_i),& (z_i=u)\\ 1-F_{ϵ}({\alpha }_{j-1}-{\beta }^T{x}_i),& (z_i\ne u)\end{array}\hfill \end{array}$$(7) where j is the index such that $a_j=\mathrm{\text{min}}\{a\in S:a>z_i\}$ when $z_i\ne u$. The overall nonparametric likelihood is the product of these individual likelihoods over all subjects. Note that if there are no uncensored observations between two lower (or upper) DLs, the two DLs are effectively treated as the same DL. A toy example to illustrate our definition is provided in supplementary materials Table S1.

Slight modifications will be applied when no or only one additional category is added to S. When there is no need to add $a_0$ to S (i.e., when $l>a_1$ or there are no lower DLs), only the second row in the likelihood (6) for $(z_i,L)$ will be employed, and the likelihood for $(z_i,1)$ with $z_i=a_1$ is $F_{ϵ}({\alpha }_1-{\beta }^T{x}_i)$. When there is no need to add $a_{J+1}$ to S (i.e., when $u<a_J$ or there are no upper DLs), only the second row in the likelihood (7) for $(z_i,U)$ will be employed, and the likelihood for $(z_i,1)$ with $z_i=a_J$ is $1-F_{ϵ}({\alpha }_{J-1}-{\beta }^T{x}_i)$.

Similar to the likelihood of CPM for data without DLs, the individual likelihoods presented above involve either one alpha parameter or two adjacent alpha parameters. As a result, the Hessian matrix continues to be tridiagonal, allowing us to use Cholesky decomposition to solve for the NPMLEs and efficiently estimate their variances using asymptotic approximations from which p-values and confidence intervals (CIs) can be computed. We have developed an R package, multipleDL available on the Comprehensive R Archive Network (CRAN), which uses the optimizing() function in the rstan package to maximize the likelihood (Stan Development Team 2020).

As mentioned in the Introduction, there are other existing techniques for fitting semiparametric linear transformation models with doubly censored data (Cai and Cheng 2004; Shen 2011). Similar to our proposed CPMs, both of these methods assume a model of the form of (1) with known $C_L$ and $C_U$, and with $\alpha (y)$ nonparametrically estimated using a step function. These two methods rely on estimating equations expressed with counting process notation. Both methods consistently estimate $\beta$ and $\alpha (y)$ under the same assumptions as the CPM, but they are less efficient than our NPMLE, which attains the semiparametric efficiency bound (Li et al.2023). The method of Shen (2011) treats the left-censored data below lower detection limits as left-truncated, thus, discarding information. The approach of Cai and Cheng (2004) also loses efficiency as individuals only contribute information for times between $C_L$ and $C_U$; for example, if an observation is observed between $C_L$ and $C_U$, when estimating $\alpha (y)$ for $y<C_L$, this observation is not used even though it is known that it was above the lower detection limit. Details are given in supplementary materials S1.3, and simulations comparing CPMs to these approaches are presented in Section 4.

2.4 Interpretable Quantities and Conditional Quantiles

Interpretation of results after fitting CPMs to outcomes with DLs is similar to settings without DLs. Depending on the link function, $\beta$ may be directly interpretable. The conditional CDF, probabilistic indexes, and conditional quantiles are also easily derived. Note, however, that without additional assumptions on the distribution of the outcome outside DLs, conditional expectations cannot be estimated.

We now describe how to infer conditional quantiles from a CPM fitted on data with DLs. The conditional CDF from a CPM for a given x can be computed as $\widehat{F}(y|x)=F_{ϵ}({\widehat{\alpha }}_j-{\widehat{\beta }}^{T}x)$ where j is the index such that $a_j=\mathrm{\text{max}}\{a\in S:a\le y\}$; if there is no $a\in S$ such that $a\le y$, then $\widehat{F}(y|x)=0$. For ease of presentation, we fix x and let $P_j=\widehat{F}(a_j|x)$ ($j=0,1,\dots ,J,J+1$); for convenience, let $P_{-1}=0$. Our goal is to define a quantile function $\widehat{Q}(p)$, where $0<p<1$, for the conditional distribution given x.

The quantile function for a CDF $F(·)$ is typically defined as $Q(p)=\mathrm{\text{inf}}\{z:F(z)\ge p\}$. A plug-in estimator for an estimated CDF, $\widehat{F}$, is ${\widehat{Q}}_0(p)=\mathrm{\text{inf}}\{z:\widehat{F}(z)\ge p\}$. When applied to our setting, ${\widehat{Q}}_0(p)=a_j$ when $P_{j-1}<p\le P_j$. This estimator may not be suitable for CPMs because $\widehat{F}(·)$ is a step function and therefore ${\widehat{Q}}_0(p)$ only takes values at the anchor points, which can be undesirable for continuous outcomes, especially when there is a large gap between adjacent anchor points.

Liu et al. (2017) proposed to estimate quantiles for CPMs with linear interpolation. Specifically, given a fixed p, let $j=j(p)$ be the index such that $P_{j-1}<p\le P_j$. When $p>P_0$, $j\ge 1$ and define ${\widehat{Q}}_1(p)=a_{j-1}+(p-P_{j-1})/(P_j-P_{j-1})\times (a_j-a_{j-1})$, which is a linear interpolation between $a_{j-1}$ and $a_j$. When $p\le P_0$, ${\widehat{Q}}_1(p)$ is set to be $a_0$. Recall that $a_0$ is not a value but a symbol for being below the lower DL, l; we thus relabel it as “$<l$”, so when $p\le P_0$, ${\widehat{Q}}_1(p)=$ “$<l$”. For the linear interpolation between $a_0$ and $a_1$, we set $a_0$ to be l. Similarly, $a_{J+1}$ is labeled “$>u$” and assigned the value u for the linear interpolation between $a_J$ and $a_{J+1}$. ${\widehat{Q}}_1(p)$ is illustrated as the dashed line in Figure 2. An alternative definition is to interpolate between $a_j$ and $a_{j+1}$: ${\widehat{Q}}_2(p)=a_j+(p-P_{j-1})/(P_j-P_{j-1})\times (a_{j+1}-a_j)$ when $p<P_J$ and ${\widehat{Q}}_2(p)=a_{J+1}=$ “$>u$” when $p\ge P_J$. ${\widehat{Q}}_2(p)$ is illustrated as the dotted lines in Figure 2. For continuous data without DLs, ${\widehat{Q}}_1(p)$ and ${\widehat{Q}}_2(p)$ converge as the sample size increases. However, they are problematic for continuous data with DLs because ${\widehat{Q}}_1(p)<a_{J+1}$ for all $p<1$ and ${\widehat{Q}}_2(p)>a_0$ for all $p>0$ even though there are nonzero estimated probabilities at the lower DL $a_0$ and upper DL $a_{J+1}$.

Figure 2: Illustration of three approaches for conditional quantiles. The dataset has a lower DL 0.5, an upper DL 2, and five observed values of y: 0.7, 0.86, 1, 1.5, 1.8. Thus, $S=\{\mathrm{`}<0.5\prime ,0.7,0.86,1,1.5,1.8,\mathrm{`}>2\prime \}$. The dashed lines are for ${\widehat{Q}}_1(p)$, the dotted lines are for ${\widehat{Q}}_2(p)$, the solid black lines are for $\widehat{Q}(p)$, and the solid gray lines are for the empirical CDF. Here, $\widehat{Q}(p)={\widehat{Q}}_1(p)=\mathrm{`}<0.5\prime$ when $p<\widehat{F}(0.5|x)$, and $\widehat{Q}(p)={\widehat{Q}}_2(p)=\mathrm{`}>2\prime$ when $p>\widehat{F}(2|x)$.

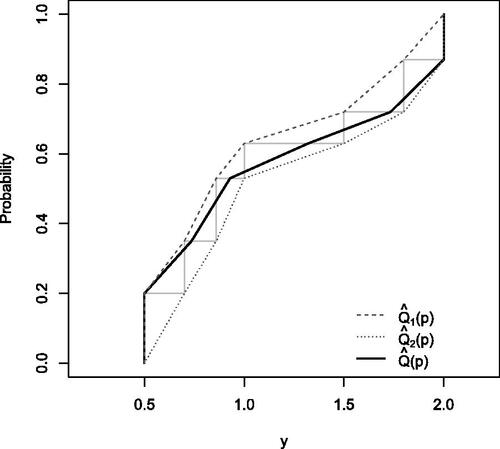
We propose a new quantile estimator as a weighted average between ${\widehat{Q}}_1(p)$ and ${\widehat{Q}}_2(p)$, (8) $$\begin{array}{c}\widehat{Q}(p)=(1-w){\widehat{Q}}_1(p)+w{\widehat{Q}}_2(p),\hfill \end{array}$$(8) where $w=w(p)=(p-P_0)/(P_J-P_0)$ when $P_0<p<P_J$, 0 when $p\le P_0$, and 1 when $p\ge P_J$. This definition is shown as the black curve in Figure 2. Note that $\widehat{Q}(p)$ equals ${\widehat{Q}}_1(p)=$ “$<l$” when $p\le P_0$, and equals ${\widehat{Q}}_2(p)=$ “$>u$” when $p\ge P_J$. It can be shown that similar to ${\widehat{Q}}_1(p)$ and ${\widehat{Q}}_2(p)$, $\widehat{Q}(p)$ is also piecewise linear with transition points at $P_j$ ($j=0,1,\dots ,J$). Note that with multiple DLs, the definition seamlessly applies with l and u being the smallest lower and largest upper DLs, respectively. In situations where there is only a lower DL or an upper DL, our definition of $\widehat{Q}(p)$ is similar. Confidence intervals for conditional quantiles can be estimated by applying a weighted linear interpolation to the confidence intervals of the conditional CDF in a similar manner (Liu et al.2017).

3 Application

We fit a CPM to study factors associated with viral load 6 months after starting ART in Latin America among 5301 adults with HIV, as described in the Introduction. Our CPM included age, sex, study center, probable route of HIV infection, the indicator that the patient had an AIDS event prior to ART initiation, their CD4 count and viral load at ART initiation (baseline), the ART regimen that they started, the calendar year of ART initiation, and the time between their baseline VL and the 6-month VL measurement. (The baseline VL was the measurement closest to ART initiation within a window of –180 to 30 days; the 6-month VL was the measurement closest to 180 days within a window of $\pm$90 days.) Baseline CD4 was square-root transformed and baseline VL was log ${}_{10}$ transformed. The CPM used a logit link function. The response variable, 6-month VL, had $J=1283$ distinct observed values.

Results are shown in Table 1. With the logit link, the $\beta$ parameters can be interpreted as log odds ratios and are presented as odds ratios along with 95% CIs. p-values are likelihood ratio test p-values. The results suggest that study center, route of infection, prior AIDS event, baseline CD4, baseline VL, ART regimen, months to VL measurement, and calendar year are all associated with VL at 6 months. For example, holding other variables constant, a 10-fold increase in VL at baseline is associated with a 44% increase in the odds of having a higher VL at 6 months (95% CI 34%–54%). Initiating a more modern ART regimen based on integrase strand transfer inhibitors (INSTIs) resulted in a 45% decreased odds of having a higher 6-month VL (95% CI 25%–60% decreased odds) compared with regimens based on older non-nucleoside reverse transcriptase inhibitors (NNRTIs). This result was seen after fixing all other variables, including calendar year of ART initiation. In addition, holding all other variables constant, a person starting ART one calendar year later had an estimated 11% lower odds of having a higher 6-month VL (95% CI 9%–12%).

Table 1: The $\beta$ coefficients in CPMs can be interpreted as log odds ratios.

Predictor	Odds ratio (95% CI)	p-value
Age (per 10 years)	0.98 (0.93, 1.03)	0.418
Sex		0.201
Male (reference)	1
Female	0.90 (0.76, 1.06)
Study center		$<0.001$
Peru (reference)	1
Argentina	1.26 (0.98, 1.61)
Brazil	1.07 (0.91, 1.26)
Chile	1.07 (0.90, 1.26)
Mexico	0.59 (0.49, 0.70)
Route of infection		0.408
Homosexual/Bisexual (reference)	1
Heterosexual	0.96 (0.83, 1.10)
Other/unknown	0.79 (0.62, 1.01)
Prior AIDS event		0.001
No (reference)	1
Yes	1.24 (1.09, 1.41)
Baseline CD4 (per 1 square root cells/$\mu$ L)	1.09 (1.08, 1.10)	$<0.001$
Baseline VL (per 1 ${\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}}_{10}$ copies/mL)	1.44 (1.34, 1.54)	$<0.001$
ART regimen		0.007
NNRTI-based (reference)	1
INSTI-based	0.55 (0.40, 0.75)
PI-based	1.10 (0.95, 1.29)
Other	2.57 (1.28, 5.16)
Months to VL measure	0.95 (0.92, 0.98)	0.002
Calendar year	0.89 (0.88, 0.91)	$<0.001$

NOTE: We show the odds ratio (95% confidence interval) and p-value for the predictors included in the model.

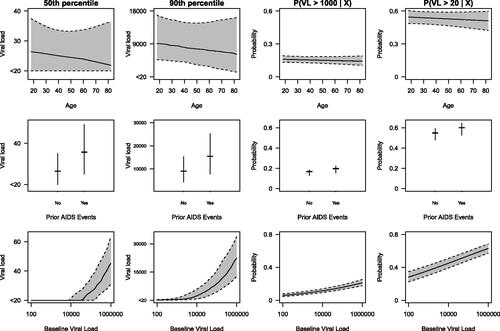
Quantiles and cumulative probabilities are also easily extracted from the CPM. The first row of Figure 3 shows the estimated conditional 50th and 90th percentiles of 6-month VL and the conditional probabilities for 6-month VL being greater than 1000 and 20 copies/mL as functions of age. The plots show that VL at 6 months is fairly similar across age after fixing the other covariates. The second row of Figure 3 contains the estimated conditional quantiles and probabilities as functions of whether a patient had an AIDS event prior to starting ART. People with a prior AIDS event (36%) tended to have a higher VL at 6 months. The third row of Figure 3 are the estimated conditional quantiles and probabilities as functions of baseline VL. People with a higher baseline VL tended to have a higher VL at 6 months. The smallest DL is 20 copies/mL, and all VL values less than this DL belong to the smallest ordered category, which we label as “$<20$”. The flat line at “$<20$” in the lower left plot suggests that for those with a baseline VL $<10,000$ copies/mL, the estimated median 6-month VL, as well as its 95% confidence interval, is $<20$ copies/mL. Note that our analyses make no attempt to estimate the specific values below the lower DL because the data contain no information on values below 20 copies/mL.

Figure 3: The estimated conditional 50th and 90th percentiles of 6-month VL and the conditional probability of 6-month VL being greater than 1000 and 20 as functions of age (top row), prior AIDS events (middle row), and baseline VL (bottom row) while keeping other covariates at their medians (for continuous variables) or modes (for categorical variables) based on our method.

Figures S1 and S2 of the supplementary materials show diagnostic plots examining model fit using probability-scale residuals (Shepherd, Li, and Liu 2016). From QQ-plots, the logit link function appears reasonable and yields a higher log-likelihood than other link functions considered (probit, loglog, and cloglog). Residual-by-predictor plots show no strong relationship between residuals and continuous predictor variables, suggesting model fit may be adequate. Supplementary materials Table S2 and Figure S3 show results from a similar CPM, except with continuous covariates expanded using restricted cubic splines to relax linearity assumptions as a sensitivity analysis. The results are fairly similar.

From Table 1, we note that 6-month VL was similar across all study centers except for the center in Mexico. In sensitivity analyses, we repeated the analyses of Table 1 comparing results using data only from Mexico ($n=1030$) versus using data pooled across the other four sites ($n=4271$). Results are in Table S3 in supplementary materials. The only association that substantially differed between Mexico and the other sites was the association with initial ART regimen. In Mexico, patients starting an INSTI- versus an NNRTI-based regimen tended to have similar 6-month viral loads (OR = 1.0, 95% CI 0.51–1.93), whereas at the other sites, those starting an INSTI- versus an NNRTI-based regimen tended to have lower 6-month viral loads (OR = 0.50, 95% CI 0.36–0.71). Interestingly, among patients starting an INSTI-based regimen, most at our Mexican site used a different drug (bictegravir) than those at the other four sites (dolutegravir). Because the study covers nearly 20 years, as an additional sensitivity analysis we compared estimates among those starting ART from 2000 to 2009 ($n=1372$) versus those starting ART from 2010 to 2018 ($n=3929$). Results are in Table S4 in supplementary materials. Estimated odds ratios were fairly similar between the time periods with two exceptions: First, the odds ratio for our Chilean site changed quite a bit, with starting ART in Chile pre-2010 associated with higher viral loads (OR for Chile vs. Peru = 2.34, 95% CI 1.45–3.77) whereas after 2010 associated with lower viral loads (OR = 0.87, 95% CI 0.72–1.05). Second, the odds ratio for INSTI-based regimens appeared to differ pre- versus post-2010 (OR for INSTI- vs. NNRTI-based ART = 1.75, 95% CI 0.46–6.65 pre-2010; OR = 0.57, 95% CI 0.41–0.78 post-2010). Pre-2010, use of INSTI-based regimens was rare (hence, the wide confidence interval) and likely among people with worse health as a sort of experimental salvage drug.

For comparison, we also analyzed the data using competing approaches for addressing DLs described earlier. First, we fit logistic regression to 6-month VL values dichotomized as $<400$ versus $\ge 400$ copies/mL, corresponding to the highest DL. Results are in Table S5 of supplementary materials. The $\beta$ coefficients in the CPM and the logistic regression model represent identical quantities on the latent logistic distribution scale, the location shift due to covariates (Agresti 2013). Whereas the logistic regression estimates arise from a single dichotomization of the outcome variable, the CPM estimates can be thought of as weighted averages of log odds ratio estimates for all possible orderable dichotimizations of the observed response values (Foresi and Peracchi 1995). In our HIV application, the CPM and the logistic regression model tended to give similar estimates of the $\beta$ coefficients, although there were some differences and 95% CIs from the CPM tended to be narrower, as expected. For example, the odds ratios for the cumulative probability and logistic regression models for prior AIDS were 1.24 and 1.27, respectively. However, the 95% confidence interval (on the log odds ratio scale) was 29% narrower with the CPM than with the logistic regression model. The odds ratios for an INSTI- versus NNRTI-based regimen were 0.55 and 0.44 for the CPM and the logistic regression model, respectively, whereas the width of the 95% CI (log odds ratio scale) for the CPM was 36% narrower.

We also fit a full likelihood-based model assuming the outcome variable was normally distributed after ${\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}}_{10}(·)$ transformation (supplementary materials Table S6). Note that even the log-transformed 6-month VL was still quite skewed (supplementary materials Figure S4), and hence the assumptions of this fully parametric approach are questionable. The parameters in this approach and those from the CPM with the logit link are not directly comparable because they are on different scales; however, the directions of associations were similar.

4 Simulations

Extensive simulations of CPMs with continuous data have been reported elsewhere (Liu et al.2017; Tian et al.2020). Here we present a limited set of simulations investigating the performance of CPMs with data subject to multiple DLs.

Data were generated for sample sizes of $n=150$ and $n=900$ such that the outcome Y followed a normal linear model after log-transformation in the following manner: $$\begin{array}{c}Y=\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(Y^{*}),\text{where}{Y}^{*}=X\beta +ϵ,\beta =1,X\sim N({\mu }_x,1),\hfill \\ \text{and}ϵ\sim N(0,1).\hfill \end{array}$$

Data were simulated to mimic a setting with three equal-sized sites, where the DL of Y and the mean of X, ${\mu }_x$, could vary by site. We considered the following five scenarios:

1. No DL, ${\mu }_x=0$ for all sites.

2. Lower DLs 0.16, 0.30, and 0.50 for the three sites (about 17%, 20%, and 20% censored), and ${\mu }_x=-0.5,0,$ and 0.5 for site 1, 2, and 3, respectively.

3. Upper DLs 0.16, 0.30, and 0.50 for the three sites (about 90%, 80%, and 70% censored), and ${\mu }_x=0$ for all sites.

4. Lower DLs 0.2, 0.3, and $-\infty$ (13%, 20%, and 0% censored) and upper DLs at $\infty$, 4, and 3.5 (0%, 19%, and 16% censored) for the three sites, and ${\mu }_x=0$ for all sites.

5. Lower DLs 0.4, 1.0, and 2.5 (38%, 50%, and 62% censored), and ${\mu }_x=-0.5,0,$ and 0.5 for site 1, 2, and 3, respectively.

Additional simulations considered scenario 2 with (i) $\beta =0$ to evaluate Type I error; (ii) link function misspecification; (iii) misspecification of the functional form of the model; (iv) comparison with other methods for handling DLs.

CPMs were fit to the observed data $\{X,Y\}$ without using any knowledge of the correct transformation or $Y^{*}$. We simulated 10,000 replications under each scenario. Bias, root mean squared error (RMSE), and coverage of 95% CIs were estimated with respect to $\beta$, conditional quantiles for $X=\{0,1\}$, and conditional CDFs for $X=\{0,1\}$. The choice of quantile and CDF levels varied based on the simulation scenario to ensure that we were estimating a quantity that could be well-estimated based on the scenario-specific detection limits. Specifically, in scenarios 2 and 5, because of the high censoring rates, we estimated the quantiles at $p=0.03$ and 0.9 (i.e., the 3rd and 90th percentiles) and CDFs at $y=0.10$ and 3.0, respectively.

Table 2 shows results under correctly specified models (i.e., probit link function and X correctly included). CPMs resulted in nearly unbiased estimation and good CI coverage for $\beta$, conditional quantiles $Q(·|X=x)$, and conditional CDFs $F(·)|X=x)$ for all five scenarios. As the sample size increased, both the bias and RMSE decreased. The RMSE for $\beta$ tended to be higher in scenarios with substantial censoring (e.g., scenario 5), as expected. In a simulation under scenario 2 with $\beta$ set to zero, the Type I error rate was preserved with both $n=150$ and $n=900$ (coverage of 95% confidence intervals of 0.948 and 0.947, respectively, and approximately uniformly distributed p-values, supplementary materials Figure S5).

Table 2: Simulation results for multiple DLs.

	$n=150$			$n=900$
Parameter	Bias	RMSE	Coverage	Bias	RMSE	Coverage
Scenario 1
$\beta$	0.018	0.106	0.945	0.004	0.041	0.947
$Q(0.5|X=0)$	–0.005	0.115	0.956	–0.002	0.046	0.947
$Q(0.5|X=1)$	0.032	0.396	0.955	0.003	0.163	0.941
$F(1.5|X=0)$	0.002	0.044	0.951	0.000	0.018	0.954
$F(1.5|X=1)$	–0.003	0.049	0.953	–0.002	0.020	0.944
Scenario 2
$\beta$	0.019	0.106	0.958	0.003	0.041	0.962
$Q(0.5|X=0)$	–0.002	0.117	0.964	–0.001	0.047	0.969
$Q(0.5|X=1)$	0.026	0.395	0.950	0.001	0.160	0.949
$F(1.5|X=0)$	0.002	0.045	0.963	0.001	0.017	0.962
$F(1.5|X=1)$	–0.003	0.050	0.948	–0.001	0.020	0.955
Scenario 3
$\beta$	0.037	0.186	0.948	0.005	0.068	0.954
$Q(0.03|X=0)$	0.305	0.307	0.953	0.000	0.014	0.952
$Q(0.03|X=1)$	–0.008	0.036	0.953	0.007	0.046	0.955
$F(0.10|X=0)$	0.000	0.000	0.933	0.000	0.000	0.952
$F(0.10|X=1)$	0.000	0.000	0.945	0.000	0.000	0.947
Scenario 4
$\beta$	0.018	0.110	0.957	0.005	0.044	0.953
$Q(0.5|X=0)$	–0.004	0.115	0.958	–0.002	0.046	0.947
$Q(0.5|X=1)$	0.036	0.410	0.972	0.005	0.166	0.955
$F(1.5|X=0)$	0.002	0.045	0.945	0.000	0.018	0.947
$F(1.5|X=1)$	–0.002	0.050	0.970	–0.002	0.021	0.947
Scenario 5
$\beta$	0.023	0.123	0.930	0.005	0.047	0.934
$Q(0.9|X=0)$	–0.010	0.555	0.940	–0.010	0.224	0.946
$Q(0.9|X=1)$	0.312	1.985	0.964	0.115	0.792	0.952
$F(3.0|X=0)$	–0.001	0.031	0.941	–0.001	0.013	0.929
$F(3.0|X=1)$	–0.001	0.059	0.956	0.002	0.025	0.954

Supplementary materials Table S7 shows the performance of CPMs for the data generated in scenario 2 under moderate and severe link function misspecification. Link function misspecification is equivalent to misspecification of the distribution of $ϵ$ because $F_{ϵ}=G^{-1}$. Specifically, we fit CPMs with logit and loglog link functions. Compared to the correct probit link, the logit is moderate misspecification (similar shape and skewness as the true distribution of $ϵ$), while the loglog represents severe misspecification (very different shape and skewness from the true distribution of $ϵ$). The performance of CPMs was reasonable with moderate link function misspecification with bias for the conditional median and the conditional CDF $F(1.5|X=x)$ under 6% and coverage of 95% CI generally close to 0.95 with $n=150$, although as low as 0.85 with $n=900$. With severe link function misspecification, the performance of CPMs was noticeably worse, with bias as high as 8% and coverage as low as 0.46 for the conditional median at $X=1$. CPMs, like other regression models, were not very robust to model misspecification due to leaving out a variable (details in supplementary materials Table S8).

Table 3 shows results under scenario 2 with $n=900$ comparing CPMs with some widely used approaches for handling DLs, specifically single imputation with $l/2$, single imputation with $l/\sqrt{2}$, multiple imputation, and fully parametric maximum likelihood estimation (MLE). For all non-CPM approaches, we first correctly assumed that the outcome variable followed a log-normal distribution. With the imputation approaches, unobserved values were imputed, then a linear regression model was fit on the log-transformed outcome to obtain the $\beta$ estimate, and median regression was used to estimate conditional medians. In multiple imputation, the correct tail distribution was used for imputing data and 10 iterations were performed for each dataset. For the MLE approach, the medians were computed using the estimated parameters of the fully parametric model. As expected, the MLE performed the best with the lowest bias and RMSE, and highest efficiency because the distributional assumptions matched the true distribution. The performance of multiple imputation was similar to that of the MLE, but with higher RMSE. As a semiparametric method, the CPM also resulted in minimal bias and correct coverage, but had slightly larger variance and RMSE. In contrast, the single imputation estimators were biased and tended to have poor coverage, especially for estimating $\beta$. We also evaluated the approaches under misspecification of the transformation. Specifically, we generated data in a manner similar to scenario 2 except using a different transformation, $Y=\text{Inv‐}{\chi }^2(\Phi (Y^{*}/2),5)$, where $\Phi$ is the probability density function of the standard normal distribution, and $\text{Inv‐}{\chi }^2(·,5)$ is the inverse of the CDF for a Chi-square distribution with degrees of freedom equal to 5. Lower DLs were set to be 2, 3, and 4 (corresponding to approximately 14%, 23%, and 30% censored) for sites 1, 2, and 3, respectively. The non-CPM approaches assumed a normal linear model after an incorrectly specified log-transformation. As shown in the lower half of Table 3, only the CPM resulted in unbiased estimates, because it is the only approach that does not require pre-transformation or strict distributional assumptions.

Table 3: Comparison of CPM with common approaches for addressing DLs under with the unknown transformation correctly and incorrectly specified.

Method	Truth	Bias(%)	Empirical SE	RMSE	Coverage
Correct transformation
CPM
$\beta$	1	0.428	0.040	0.041	0.941
$Q(0.5|X=0)$	1	–0.115	0.046	0.045	0.963
$Q(0.5|X=1)$	2.718	0.092	0.165	0.165	0.937
Single imputation with $\mathit{\text{dl}}/\sqrt{2}$
$\beta$	1	–14.501	0.027	0.147	0.000
$Q(0.5|X=0)$	1	8.431	0.041	0.094	0.461
$Q(0.5|X=1)$	2.718	–5.825	0.148	0.217	0.804
Single imputation with $\mathit{\text{dl}}/2$
$\beta$	1	–8.003	0.028	0.085	0.233
$Q(0.5|X=0)$	1	3.122	0.041	0.051	0.905
$Q(0.5|X=1)$	2.718	–3.650	0.149	0.179	0.901
Multiple imputation
$\beta$	1	0.071	0.034	0.034	0.958
$Q(0.5|X=0)$	1	–0.060	0.035	0.035	0.957
$Q(0.5|X=1)$	2.718	0.059	0.127	0.127	0.949
MLE
$\beta$	1	0.859	0.034	0.035	0.965
$Q(0.5|X=0)$	1	1.254	0.041	0.043	0.959
$Q(0.5|X=1)$	2.718	–0.062	0.151	0.154	0.947
Incorrect transformation
CPM
$\beta$	1	0.483	0.040	0.041	0.941
$Q(0.5|X=0)$	4.354	–0.119	0.067	0.067	0.960
$Q(0.5|X=1)$	5.976	–0.004	0.109	0.109	0.935
Single imputation with $\mathit{\text{dl}}/\sqrt{2}$
$\beta$	1	–69.388	0.009	0.694	0.000
$Q(0.5|X=0)$	4.354	–1.482	0.058	0.087	0.813
$Q(0.5|X=1)$	5.976	–1.870	0.101	0.151	0.812
Single imputation with $\mathit{\text{dl}}/2$
$\beta$	1	–62.696	0.011	0.627	0.000
$Q(0.5|X=0)$	4.354	–6.560	0.073	0.295	0.028
$Q(0.5|X=1)$	5.976	–0.842	0.107	0.118	0.919
Multiple imputation
$\beta$	1	–68.150	0.011	0.682	0.000
$Q(0.5|X=0)$	4.354	–2.206	0.049	0.108	0.506
$Q(0.5|X=1)$	5.976	–2.028	0.082	0.146	0.711
MLE
$\beta$	1	–66.964	0.011	0.670	0.000
$Q(0.5|X=0)$	4.354	–1.677	0.059	0.094	0.807
$Q(0.5|X=1)$	5.976	0.926	0.099	0.113	0.912

Finally, we compared our method with two existing methods for fitting semiparametric linear transformation models to doubly censored data (Cai and Cheng 2004; Shen 2011). The efficiency gains of our method over these other approaches are seen in Table 4, which compares estimates of $\beta$ with data generated under a proportional hazards model under various levels of censoring similar to those in scenarios 2–5. (Details are in the supplementary materials S3.1.) For scenario 1 (no censoring) and scenarios 2, 4, and 5 (all have some left-censoring), the bias of the CPM was similar to that of the other two approaches, but the empirical standard error and RMSE was lower for the CPM. The improved efficiency was particularly notable as the proportion of censored observations increased. For example, in scenario 2 (approximately 20% left-censored) with $n=900$, the empirical SE for our estimator of $\beta$ was 0.040 compared to 0.054 and 0.051 for the estimators of Cai and Cheng (2004) and Shen (2011), respectively. Under scenario 5 (approximately 50% left-censored) with $n=900$, the empirical SE for our estimator was 0.044 compared to 0.069 for both of the other estimators. Under scenario 3 (approximately 80% right-censored), the empirical SE and RMSE for $\beta$ were smaller for the method of Shen (2011) with $n=150$ but they were approximately the same between our method and that of Shen (2011) with $n=900$. This finding is similar to that observed by Liu et al. (2017) with uncensored data generated under a proportional hazards model, where with small sample sizes Cox regression had lower RMSE for estimating $\beta$ than CPM, but similar RMSE as the sample size increased. Under scenario 3, the RMSE for the estimator of Cai and Cheng (2004) was higher than the other two methods.

Table 4: Simulation results for multiple DLs comparing CPMs with the methods proposed by Cai and Cheng (2004) (labeled Cai) and Shen (2011) (labeled Shen).

	$n=150$			$n=900$
	CPM	Cai	Shen	CPM	Cai	Shen
Scenario 1
Bias(%)	4.386	3.271	3.098	0.316	0.398	0.482
Empirical SE	0.149	0.173	0.153	0.056	0.067	0.060
RMSE	0.155	0.176	0.156	0.056	0.067	0.060
Scenario 2
Bias(%)	2.287	2.021	0.906	–0.320	0.223	0.245
Empirical SE	0.111	0.136	0.132	0.040	0.054	0.051
RMSE	0.113	0.137	0.132	0.041	0.054	0.051
Scenario 3
Bias(%)	3.553	3.497	–6.132	0.613	0.535	–1.527
Empirical SE	0.223	0.249	0.191	0.085	0.093	0.082
RMSE	0.225	0.251	0.200	0.085	0.094	0.083
Scenario 4
Bias(%)	2.079	1.014	1.307	0.508	0.318	0.333
Empirical SE	0.117	0.137	0.135	0.045	0.056	0.051
RMSE	0.119	0.138	0.136	0.045	0.056	0.051
Scenario 5
Bias(%)	2.817	3.495	1.457	–0.319	0.276	0.288
Empirical SE	0.122	0.180	0.194	0.044	0.069	0.069
RMSE	0.125	0.184	0.195	0.045	0.069	0.069

5 Discussion

In this article, we have described an approach to address multiple detection limits in response variables using CPMs. We illustrated the method with a study looking at factors associated with HIV viral load after antiretroviral therapy initiation, where a large percentage of people had measurements below lower detection limits, which varied over time and by study site. CPMs have several advantages over commonly employed approaches for addressing DLs. They make minimal distributional assumptions, they yield interpretable parameters, and they are invariant to the value assigned to measures outside DLs. Any values outside the lowest/highest DLs are simply assigned to the lowest/highest ordinal categories, and estimation proceeds naturally. From simulation studies we saw that CPMs performed well, even with high censoring rates and relatively small sample sizes, and that they were more generally more efficient than previously proposed methods for fitting semiparametric transformation models to censored data.

Our focus has been on addressing settings with multiple detection limits. However, as highlighted in Section 2.2, CPMs are an effective analysis approach that can also be easily applied to address response data subject to a single detection limit. The supplementary materials contain an example analysis using HIV data subject to a single detection limit (Section S2.2) and a set of simulations demonstrating the excellent performance of CPMs in settings with a single detection limit (Section S3.2).

CPMs have some limitations. Because we do not make distributional assumptions outside DLs, we are not able to estimate conditional expectations after fitting a CPM; however, with DLs, conditional quantiles are probably more reasonable statistics to report anyway. Although CPMs do not make distributional assumptions on the response variable, the link function must still be specified, which corresponds to making an assumption on the distribution of the response variable after an unspecified transformation. Performance can be poor with severe link function misspecification; however, CPMs appear to be fairly robust to moderate misspecification. Note that the latent variable is typically assumed to follow a standard distribution (e.g., standard normal or standard logistic). If in our model, for example, after an unspecified transformation the data are assumed to follow a normal distribution with variance ${\sigma }^2$, then the transformation is simply a rescaling of what it would be if the latent variable distribution had variance 1. Specifically, if $H^{-1}(Y)={\beta }^{T}X+ϵ$ with $ϵ\sim N(0,1)$, and $H_1^{-1}(Y)={\gamma }^{T}X+\delta$ with $\delta \sim N(0,{\sigma }^2)$, then $H^{-1}(y)=H_1^{-1}(y)/\sigma$ and $\beta =\gamma /\sigma$. Similarly, if the model had an intercept term, for example, $H_2^{-1}(Y)={\gamma }_0+{\gamma }^{T}X+\delta$ with $\delta \sim N(0,{\sigma }^2)$, the intercept term would also be absorbed by the transformation: $H^{-1}(y)=\left[H_2^{-1}(y)-{\gamma }_0\right]/\sigma$. Notice that ${\gamma }_0$ and $\sigma$ are not identifiable in these latent variable models where we leave $H(·)$ unspecified. By assuming the latent variable follows a standard distribution, the $\beta$ coefficient is more interpretable than it would be otherwise. For example, suppose we assumed that $H_1^{-1}(Y)={\gamma }^{T}X+\delta$ with $\delta \sim \text{logistic}(0,2)$. Then $\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(\gamma /2)$ (not $\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(\gamma )$) would have the usual odds ratio interpretation for a 1-unit increase in X.

Further research could consider extensions of CPMs to handle clustered or longitudinal data with DLs. The website, https://github.com/YuqiTian35/DetectionLimitCode, contains code for our application examples and simulations. The website also contains a synthetic dataset similar to the original dataset on which our application analysis code can be run. Our R package, multipleDL, currently handles probit, logit, loglog, and cloglog link functions.

Supplementary Materials

Supplementary materials include details about the relationship between CPMs and the Wilcoxon test, a demonstration of the likelihood in a toy example with multiple detection limits, extended descriptions of other approaches for fitting semiparametric transformation models with censoring, additional results for the HIV viral load study, additional simulation results, and a second application in a setting with a single detection limit.

Acknowledgments

The authors gratefully acknowledge CCASAnet investigators for providing data for the HIV study.

Disclosure Statement

The authors report there are no competing interests to declare.

Additional information

Funding

This study was supported by funding from the U.S. National Institutes of Health, grants R01 AI093234 and U01 AI069923.