Efficient Stochastic Generators with Spherical Harmonic Transformation for High-Resolution Global Climate Simulations from CESM2-LENS2

Abstract

Earth system models (ESMs) are fundamental for understanding Earth’s complex climate system. However, the computational demands and storage requirements of ESM simulations limit their utility. For the newly published CESM2-LENS2 data, which suffer from this issue, we propose a novel stochastic generator (SG) as a practical complement to the CESM2, capable of rapidly producing emulations closely mirroring training simulations. Our SG leverages the spherical harmonic transformation (SHT) to shift from spatial to spectral domains, enabling efficient low-rank approximations that significantly reduce computational and storage costs. By accounting for axial symmetry and retaining distinct ranks for land and ocean regions, our SG captures intricate nonstationary spatial dependencies. Additionally, a modified Tukey g-and-h (TGH) transformation accommodates non-Gaussianity in high-temporal-resolution data. We apply the proposed SG to generate emulations for surface temperature simulations from the CESM2-LENS2 data across various scales, marking the first attempt of reproducing daily data. These emulations are then meticulously validated against training simulations. This work offers a promising complementary pathway for efficient climate modeling and analysis while overcoming computational and storage limitations. Supplementary materials for this article are available online, including a standardized description of the materials available for reproducing the work.

KEYWORDS:

• Emulator
• Global temperature
• Low-rank approximation
• Nonstationary spatial structure
• Tukey g-and-h transformation

1 Introduction

Earth system models (ESMs) are complex mathematical equations that describe and simulate the transformation and interaction of energy and materials within the Earth’s climate system. Their development is grounded in the fundamental laws of physics, fluid dynamics, and chemistry, necessitating the identification and quantification of physical processes represented through mathematical equations (National Oceanic and Atmospheric Administration (NOAA) 2022). ESMs are indispensable tools in both scientific research and government policymaking, enabling a deeper understanding and more accurate predictions of Earth’s systems. For example, the Intergovernmental Panel on Climate Change (IPCC) used datasets from the Coupled Model Intercomparison Project’s fifth (CMIP5) and sixth (CMIP6) phases (Taylor, Stouffer, and Meehl 2012; Eyring et al. 2016) to compile their fifth and sixth synthesis assessment reports on climate change.

Despite their significance, ESMs have limitations as approximations of the Earth’s complex system. They are sensitive to changes in model inputs, such as physics parameters and emission scenarios, which need being assessed. Additionally, distinguishing between model errors and the effects of internal variability, which arises from atmospheric, oceanic, land, and cryospheric processes and their interactions, is challenging with a limited number of simulations (Kay et al. 2015). This underscores the need for multiple climate simulations to comprehensively characterize Earth’s system. The Community Earth System Model (CESM, Kay et al. 2015) is one such model designed to study climate change while accounting for internal climate variability.

Running ESMs is a time-consuming process, even with the support of powerful supercomputers. Scientists partition the planet into thousands of three-dimensional grids. Within each grid cell, they specify variables and conditions, employ computers to solve equations, propagate results to neighboring cells, and then iterate the above procedure with the updated variables and conditions. The whole process is repeated through time steps of different scales, which is the temporal resolution. The spatial resolution of the model is determined by the size of the grid cell, with smaller sizes yielding higher resolution but requiring more time. Generating multiple climate simulations demands weeks and even months of computational resources, exclusively available to several research institutes globally (Huang et al. 2023). Furthermore, while modern computational power allows for the generation of climate simulations, storing them is constrained by technological limitations, resource availability, and cost considerations. For instance, the storage requirement for CMIP5 data exceeds 2.5 Petabytes, incurring significant expenses for institutions like the National Center for Atmospheric Research (NCAR), a prominent U.S. research center for Earth Systems science. Consequently, budget constraints may necessitate the abandonment of partial data or higher resolutions (Guinness and Hammerling 2018).

Emulators play a crucial role in providing rapid approximations for computationally demanding model outputs and serve as effective surrogates for the original model. Specifically, emulators are statistical models that undergo proper training using a set of existing simulations and are then employed to approximate simulations for unexplored inputs. Over the past few decades, emulators have found widespread application, including assessing the sensitivity of various physical parameters (Oakley and O’Hagan 2002, 2004) and performing model calibration (Kennedy and O’Hagan 2001; Chang et al. 2014). Within the climate research community, emulators have been extensively developed to evaluate the influence of physics parameters (Sacks, Schiller, and Welch 1989), emission scenarios (Castruccio and Stein 2013; Castruccio et al. 2014), and the internal variability (Jeong et al. 2019; Hu and Castruccio 2021) on climate model outputs. These emulators enable efficient exploration of model behavior and facilitate a deeper understanding of complex climate systems.

Stochastic generators (SGs, Jeong et al. 2018), as a type of emulator for quantifying internal variability uncertainty, align closely with our requirements. SGs are spatio-temporal models adeptly tailored with a limited number of climate simulations, capable of generating numerous annual and monthly simulations across extensive and high-resolution domains at any moment (Jeong et al. 2018, 2019; Castruccio et al. 2019; Tagle et al. 2020), yet daily scale remains elusive to this date. Their implementation is affordable and even efficient, albeit at the expense of detailed physical mechanisms. SGs require the storage of only model parameters, enabling them to generate simulations that capture the general behavior of the original climate simulations. It is essential to distinguish SGs from compression methods (Baker et al. 2017; Underwood et al. 2022), which effectively reduce data volume using compression algorithms. While compression methods store and recover compressed data, they are designed for reconstructing individual data rather than generating new simulations. Moreover, the storage requirements for compression methods tend to increase with additional simulations.

SGs typically use Gaussian processes (GPs) and auto-regressive models to capture the intricate spatio-temporal dependencies among climate simulations driven by underlying physical mechanisms. While SGs offer several advantages, they face notable challenges when emulating ESMs. First, global climate simulations, which need the technique of SGs, involve extensive high-resolution data. Inference with GPs on such data can be computationally prohibitive, often requiring time on the order of data size cubed. Addressing this computational challenge can draw inspiration from existing techniques such as low-rank approximations (Cressie and Johannesson 2008; Banerjee et al. 2008), composite likelihoods (Vecchia 1988; Guinness 2021), stochastic partial differential equations (Rue, Martino, and Chopin 2009; Bolin, Simas, and Xiong 2023), covariance tapering (Kaufman, Schervish, and Nychka 2008) and their combinations (Datta et al. 2016). Second, global climate simulations frequently exhibit nonstationary spatial dependence. The covariance structure can vary significantly with latitude while may remain relatively stationary along the longitude, which is called axial symmetry (Jones 1963) and has been noticed and discussed by Stein (2007), Stein (2008) and Jun and Stein (2008). Additionally, the smoothness and variance of data can change between land and ocean at the same latitude (Castruccio and Guinness 2017; Jeong et al. 2018). A well-defined covariance function based on geodesic distance rather than chordal distance is needed to model the nonstationary spatial dependence structure. The use of chordal distance may cause physically unrealistic distortions (Jeong, Jun, and Genton 2017). Lastly, global climate simulations with high temporal resolutions, such as monthly and daily scales, may deviate from Gaussian assumptions when studying temporal evolution. To address this, the Tukey g-and-h (TGH) transformation has been employed to Gaussianize the data, striking a balance between model flexibility and simplicity (Yan and Genton 2019; Jeong et al. 2019).

For global surface temperature simulations from the CESM2-LENS2 data, which are newly published in the climate community and face the above-mentioned challenges, we propose a novel SG. Our SG serves as a pragmatic complement to CESM2, offering the capability to rapidly generate an unlimited number of emulations closely resembling simulations. Central to our method is the utilization of the spherical harmonic transformation (SHT)—the well-known spherical counterpart of the Fourier transformation, allowing us to efficiently transition global simulations from the spatial to the spectral domain. Moreover, it unlocks a practical low-rank approximation strategy, using spherical harmonics as available multi-resolution basis functions that are naturally suitable for global data. The modeling in the spectral domain ushers in significant reductions in both computational and storage costs. By judiciously retaining distinct ranks for land and ocean regions and applying a general assumption of axial symmetry, our SG captures the intricate nonstationary spatial dependence among different latitudes and between land and ocean regions. Furthermore, the employment of a modified TGH transformation equips our SG to effectively model the temporal dependence of simulations, accommodating the non-Gaussianity inherent in high-temporal-resolution data. In our case study, we apply these principles to construct SGs and generate emulations for the surface temperature simulations, spanning annual, monthly, and even daily scales. We meticulously illustrate and compare the generated emulations against the training simulations, both through visual inspection and quantitative metrics. Notably, our work marks a significant advancement by being the first to generate, display, and evaluate emulations at a daily scale.

The remainder of the article is structured as follows. In Section 2, we provide an overview of temperature simulations across annual, monthly, and daily scales. Section 3 delves into the intricate procedures involved in constructing an SG using the SHT and generating emulations. The generated emulations, along with comparisons to the training simulations, are showcased in Section 4. Finally, Section 5 encapsulates our conclusions and outlines avenues for future research.

2 CESM2-LENS2 Data

The Community Earth System Model version 2 Large Ensembles (CESM2-LENS2), as detailed in Rodgers et al. (2021), is a recently released extensive ensemble of climate change projections. It originates from the CESM2 and serves as a valuable resource for studying the sensitivity of internal climate fluctuations to greenhouse warming. This ensemble comprises 100 individual members, operating at a spatial resolution of ${0.9375}^{°}\times {1.25}^{°}$ (latitude × longitude), spanning the temporal domain from 1850 to 2100, and generated through a combination of diverse oceanic and atmospheric initial states. CESM2-LENS2 draws upon CMIP6 historical forcing, spanning the period from 1850 to 2014, and integrates the Shared Socioeconomic Pathways 370 (SSP370) future radiative forcing (RF, an influential factor in climate system describing the difference between incoming and outgoing sun radiation) from 2015 to 2100. The SSP scenarios, introduced in response to the sixth IPCC report, encompass a range of socioeconomic developments and atmospheric greenhouse gas concentration pathways (O’Neill et al. 2014; Riahi et al. 2017). Notably, SSP370 represents a medium-to-high emission scenario, projecting an additional RF of 7 ${\text{Wm}}^{-2}$ by the year 2100 under the social development pathway of regional rivalry.

The choice of CESM2-LENS2 in our study is motivated by several factors. First, it provides comprehensive and credible global climate simulations at high resolutions, which often pose storage challenges. Second, its ample ensemble size allows for effective training and evaluation of our SG. Third, despite generating considerable interest within the climate community (Kay et al. 2022; Muñoz et al. 2023; Dong, Peings, and Magnusdottir 2023), CESM2-LENS2 has yet to gain widespread attention in the field of statistics. This article marks the first introduction of an SG, extending to daily scales, to complement CESM2-LENS2. Both CESM2-LENS2 and SSP370 RF are readily accessible from the NCAR and Zenodo websites, respectively. Our analysis focuses on global surface temperatures for the period 2015–2100, encompassing all $192\times 288=55,296$ grid points in space. Existing literature (Jeong et al. 2018, 2019; Huang et al. 2023) has demonstrated that fewer than ten ensembles are sufficient to construct an efficient SG for a climate variable. Therefore, we select training simulations from a subset of 20 members micro-initialized from the year 1251, with each member created through random perturbations of the atmospheric potential temperature field. These members are assumed to be independent from each other. We aggregate the ensembles at annual, monthly, and daily scales, despite their original availability at a three-hourly resolution. Consequently, each annual, monthly, and daily aggregated temperature simulation comprises approximately 4.75 million ($192\times 288\times 86$), 57.07 million, and 1.73 billion data points, respectively.

Let $y_t^{(r)}(L_i,l_j)$ denote the temperature in Celsius at latitude L_i, longitude l_j, time point t after year 2014, and ensemble r, where $i=1,\dots ,I$ (I = 192), $j=1,\dots ,J$ (J = 288), $t=1,\dots ,T$, and $r=1,\dots ,R$. The value of T varies depending on the temporal resolution chosen, with possible values of 86, 1032, or 31,390. Similarly, let x_t represent the RF at time t for all ensembles, as they are generated with the same external forcing. We use members 11 to 17 (out of 20) to illustrate certain data characteristics. The justification for the number of ensembles will be further discussed in Figure 3(a), using an index for goodness-of-fit. Let $y_{A,t}^{(r)}(L_i,l_j)$ be the annually aggregated temperature at grid point (L_i, l_j), year $t+$2014 and ensemble r. Consequently, the ensemble mean and standard deviation at (L_i, l_j) and $t+$2014 are denoted as ${\overline{y}}_{A,t}(L_i,l_j)=R^{-1}{\sum }_{r=1}^R{y}_{A,t}^{(r)}(L_i,l_j)$ and $y_{A,t}^{\text{sd}}(L_i,l_j)=\{R^{-1}{\sum }_{r=1}^R(y_{A,t}^{(r)}(L_i,l_j)-{\overline{y}}_{A,t}(L_i,l_j){)}^2{\}}^{1/2}$, respectively. Figure 1(a) and (b) depict maps of ${\overline{y}}_{A,9}(L_i,l_j)$ and $y_{A,9}^{\text{sd}}(L_i,l_j)$. The maps align with the intuitive understanding that temperature generally decreases with increasing latitude. The surface temperatures in the Himalayas and Andes ranges are lower than in surrounding regions. Numerical instabilities occur near the two pole regions. Additionally, the surface temperature at the tropical Pacific Ocean exhibits larger variation across ensembles due to the climate phenomenon called El Niño–Southern Oscillation.

Fig. 1 Illustration of simulations with different scales. (a) and (b) are maps of the ensemble mean and standard deviation of the annually aggregated temperature in the year 2023. Two black “×” marks indicate grid points located at coordinates $(40.05,43.75)$ and $(-30.63,170.00)$, designating points on land (GL) and ocean (GO), respectively. (c) shows annual temperature time series at GL and GO, where each ensemble is represented by a distinct color. (d) shows the monthly temperature time series at GL and GO, where the black curves are ensemble means. (e)–(g) are histograms of annual, monthly and daily temperature simulations at GL and GO, which have been detrended by ensemble means. Only data of years 2020, 2040, 2060, 2080, and 2100 are used in daily data.

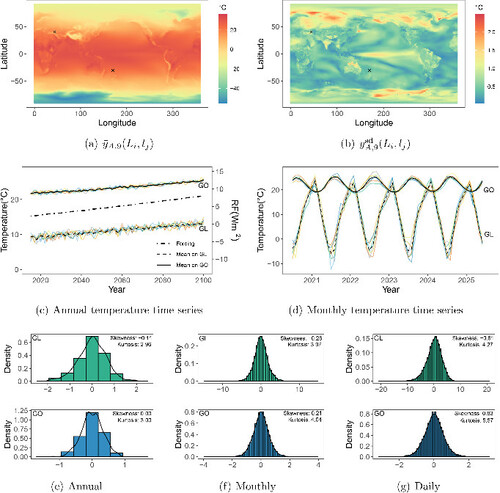
Let ${\{y_{A,t}^{(r)}(L_i,l_j)\}}_{t=1}^T$ represent the annual temperature trajectory of ensemble r at (L_i, l_j). Figure 1(c) illustrates these time series for both GL (land) and GO (ocean) locations, that is, ${\{y_{A,t}^{(r)}(\text{GL})\}}_{t=1}^T$ and ${\{y_{A,t}^{(r)}(\text{GO})\}}_{t=1}^T$, alongside their respective ensemble means ${\{{\overline{y}}_{A,t}(\text{GL})\}}_{t=1}^T$ and ${\{{\overline{y}}_{A,t}(\text{GO})\}}_{t=1}^T$. Take ${\{y_{A,t}^{(r)}(\text{GL})\}}_{t=1}^T$ as an example. All ensembles exhibit a shared increasing trend, influenced by the RF also depicted in Figure 1(c). Moreover, each ensemble exhibits its unique shape, signifying the presence of uncertainty among ensembles. These motivate us to develop an SG incorporating both deterministic and stochastic factors. Similarly, Figure 1(d) provides monthly temperature time series of years 2021–2025 at GL and GO, along with their respective ensemble means. They experience alternating peaks and valleys because they are situated in the northern and southern hemispheres, respectively. In comparison to annual data, Figure 1(d) exhibits a clear seasonality, which is a common feature in monthly and daily data. The seasonality of surface temperature varies across grid points and remains consistent among all ensembles at a fixed grid point. Notably, from Figure 1(c) and (d), both the uncertainty and the variation are more pronounced at GL.

Figure 1(e)–(g) demonstrate histograms, skewness and kurtosis of the detrended annual, monthly and daily temperature simulations at GL and GO, respectively. For example, the top panel of Figure 1(e) displays the histogram of ${\{y_{A,t}^{(r)}(\text{GL})-R^{-1}{\sum }_{r=1}^R{y}_{A,t}^{(r)}(\text{GL})\}}_{r=1,\dots ,R;t=1,\dots ,T}$ and its skewness and kurtosis. The close-to-zero skewness and the close-to-three kurtosis enable a Gaussian assumption when we model R time series ${\{y_{A,t}^{(r)}(\text{GL})-R^{-1}{\sum }_{r=1}^R{y}_{A,t}^{(r)}(\text{GL})\}}_{t=1}^T$, with an auto-regression. In contrast, the histograms in Figure 1(f) and (g) tend to be skewed and heavy-tailed. Figure S1 presents the skewness and kurtosis for time series across all global grid points. The degree of skewness and the presence of heavy tails become more pronounced with increasing temporal resolution. The non-Gaussianity is particularly severe in the band region below latitude $-{60}^{°}$, termed as Band, and the North Pole region, where the surface temperature simulations exhibit numerical instabilities. The reason will be discussed in Section 4.2. These observations underscore the necessity for additional transformations and parameters to Gaussianize the monthly and daily simulations, as the first two moments alone are insufficient to characterize data with greater temporal complexity.

3 Stochastic Generator Methodology

In this section, we detail the procedures of constructing an SG and generating emulations for the temperature simulations described in Section 2. Leveraging the SHT, our proposed SG offers efficient and adaptable capabilities for dealing with global climate simulations that exhibit: (a) a substantial size in terms of the number of observations in space and time; (b) nonstationary spatial dependencies among latitudes and land/ocean regions; and (c) non-Gaussian temporal trajectories.

The data characteristics outlined in Section 2 underscore the deterministic chaotic nature inherent in climate models (Lorenz 1963; Branstator and Teng 2010; Castruccio and Genton 2018), which motivates us to decouple the data into deterministic and stochastic components as follows: (1) $$y_t^{(r)}(L_i,l_j)=m_t(L_i,l_j)+\sigma (L_i,l_j)Z_t^{(r)}(L_i,l_j).$$(1)

Here, m_t and σ are deterministic functions responsible for the mean trend and standard error, respectively, and are shared across all ensembles. $Z_t^{(r)}(L_i,l_j)$ is the stochastic component at grid point (L_i, l_j), time point t, and ensemble r. Given the expansive parameter space, simultaneously inferring both the deterministic and stochastic components would be computationally infeasible. Therefore, we adopt a two-stage approach, commonly employed in existing work (Castruccio and Genton 2018; Jeong et al. 2019; Huang et al. 2023). First, we evaluate $m_t(L_i,l_j)$ and $\sigma (L_i,l_j)$ at each grid point, making the independence assumption regarding ${\{Z_t^{(r)}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J;t=1,\dots ,T;r=1,\dots ,R}$. Subsequently, we analyze the dependence structure of $Z_t^{(r)}(L_i,l_j)$ by detrending and rescaling $y_t^{(r)}(L_i,l_j)$ with the estimate of $m_t(L_i,l_j)$ and $\sigma (L_i,l_j)$, respectively.

3.1 Deterministic Component of SG

In the first stage of constructing the SG, we focus on determining the mean trend m_t. It is crucial that the mean trend is both simple enough to minimize the storage requirements for parameters and informative enough to capture the physical relationships between simulations and essential covariates. Let $y_t^{(r)}(L_i,l_j)$ represent the annually aggregated temperature data. Previous research (Castruccio et al. 2014; Huang et al. 2023) has shown its dependence on the RF trajectory and adopted an infinite distributed lag model: $$\begin{array}{c}{m}_t(L_i,l_j)={\beta }_0(L_i,l_j)+{\beta }_1(L_i,l_j)x_t\\ \hspace{1em}+{\beta }_2(L_i,l_j)\{1-\rho (L_i,l_j)\}\sum _{s=1}^{\infty }\rho {(L_i,l_j)}^{s-1}{x}_{t-s},\end{array}$$where ${\beta }_0(L_i,l_j)$ is the intercept, ${\beta }_1(L_i,l_j)$ and ${\beta }_2(L_i,l_j)$ are slopes for the current and past RFs, respectively. Lag weights ${\beta }_2(L_i,l_j)\{1-\rho (L_i,l_j)\}\rho {(L_i,l_j)}^{s-1}$ decrease the impact of past RFs exponentially by $\rho (L_i,l_j)\in [0,1]$. Moreover, if $y_t^{(r)}(L_i,l_j)$ represents the monthly aggregated temperature data, additional harmonic terms ${\{\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(2\pi \mathit{\text{tk}}/12),\hspace{0.17em}\mathrm{\text{sin}}\hspace{0.17em}(2\pi \mathit{\text{tk}}/12)\}}_{k=1}^{K_M}$ should be included to fit the interannual cycle as shown in Figure 1(d). That is, $$\begin{array}{c}{m}_t(L_i,l_j)={\beta }_0(L_i,l_j)+{\beta }_1(L_i,l_j)x_{\lceil t/12\rceil }\\ \hspace{1em}+{\beta }_2(L_i,l_j)\{1-\rho (L_i,l_j)\}\sum _{s=1}^{\infty }\rho {(L_i,l_j)}^{s-1}{x}_{\lceil t/12\rceil -s}\\ \hspace{1em}+\sum _{k=1}^{K_M}\{a_k(L_i,l_j)\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}\left(\frac{2\pi \mathit{\text{tk}}}{12}\right)\\ \hspace{1em}+b_k(L_i,l_j)\hspace{0.17em}\mathrm{\text{sin}}\hspace{0.17em}\left(\frac{2\pi \mathit{\text{tk}}}{12}\right)\},\end{array}$$ which would also be applied to the daily aggregated temperature by replacing K_M and $t/12$ with K_D and $t/365$, respectively. The larger the value of K_M (or K_D), the higher the frequency the harmonic terms can present. For the deterministic component, $\{{\beta }_0(L_i,l_j),{\beta }_1(L_i,l_j),{\beta }_2(L_i,l_j),\rho (L_i,l_j),\sigma (L_i,l_j),$ $a_1(L_i,l_j),\dots ,a_K(L_i,l_j),b_1(L_i,l_j),\dots ,b_K(L_i,l_j){\}}_{i=1,\dots ,I;j=1,\dots ,J}$ are all $(5+2K)\mathit{\text{IJ}}$ parameters to be evaluated and stored, where K can take values of 0, K_M, and K_D to represent the annual, monthly and daily temperature, respectively. With the independence assumption, we can efficiently estimate the parameters of the deterministic component in parallel for each grid point. The detailed inferential process is given in Section S3.1 of the supplementary materials.

3.2 Stochastic Component of SG

Now, we sequentially model the spatial and temporal dependence of the stochastic component $Z_t^{(r)}(L_i,l_j)$, which is a general principle for analyzing space-time data (Stein 2007; Castruccio and Genton 2018) to bypass the prohibitive computation.

3.2.1 Modeling the Spatial Dependence

The inference of the spatial dependence should consider several crucial factors: (a) The simulations are extensive; (b) The simulations encompass the entire globe, making the use of chordal distance inappropriate (Jeong, Jun, and Genton 2017); and (c) The simulations exhibit nonstationarity among different latitudes and between land and ocean regions. Given these considerations, we propose using the SHT (Jones 1963; Stein 2007, 2008), which involves expanding the stochastic component $Z_t^{(r)}(L_i,l_j)$ with spherical harmonics: (2) $$Z_t^{(r)}(L_i,l_j)=\sum _{q=0}^{Q-1}\sum _{m=-q}^q{(s_t^{(r)})}_q^m{H}_q^m(L_i,l_j)+{\epsilon }_t^{(r)}(L_i,l_j).$$(2)

In (2), ${\left\{H_q^m\right\}}_{q=0,1,2,\dots ;m=-q,\dots ,q}$ is a complete set of orthonormal basis functions defined in ${\mathcal{L}}^2({\mathbb{S}}^2)$ and indexed by integer degree q and order m, where ${\mathcal{L}}^2({\mathbb{S}}^2)$ is the Hilbert space consisting of squared-integrable functions on the sphere ${\mathbb{S}}^2$. The spherical harmonic $H_q^m$ is a complex-valued function with a closed form $H_q^m(L_i,l_j)=\sqrt{\frac{2q+1}{4\pi }\frac{(q-m)!}{(q+m)!}}{P}_q^m(\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}{\theta }_i)\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(\iota m{\psi }_j)$, where ${\iota }^2=-1,({\theta }_i,{\psi }_j)=(-\pi L_i/180+\pi /2,\pi l_j/180)$ is a reparameterization of (L_i, l_j) and $P_q^m$ is the associated Legendre polynomial of degree q and order m, such that $H_q^{-m}={(-1)}^m\overline{H_q^m}$. Corresponding to the $H_q^m,{(s_t^{(r)})}_q^m$ is the complex-valued spherical harmonic coefficient satisfying ${(s_t^{(r)})}_q^{-m}={(-1)}^m\overline{{(s_t^{(r)})}_q^m}$. The norm of ${(s_t^{(r)})}_q^m$, that is, $\left|\right|{(s_t^{(r)})}_q^m|{|}_2=\sqrt{{\mathfrak{R}}^2\left\{{(s_t^{(r)})}_q^m\right\}+{\mathfrak{I}}^2\left\{{(s_t^{(r)})}_q^m\right\}}$, indicates the energy gathered at degree q and order m. More details about spherical harmonics and their application on spectrum and differentiability analysis are given in Section S3.2.1 of the supplementary materials. Q is an integer ranging from 0 to $Q_{\mathrm{\text{max}}}$, with $Q_{\mathrm{\text{max}}}=\mathrm{\text{min}}\{I-1,(J+1)/2\}$ derived in Section S3.2.2 and determined by the spatial resolution of the data. The denser the grid points are, the higher the frequency they capture, and the larger the value of $Q_{\mathrm{\text{max}}}$ could be. For CESM2-LENS2, $Q_{\mathrm{\text{max}}}=144$. The term ${\epsilon }_t^{(r)}(L_i,l_j)$ accounts for the remaining information and is assumed to be independent and follow $\mathcal{N}(0,v^2(L_i,l_j))$. In a physical sense, (2) translates ${\{Z_t^{(r)}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$ from the spatial domain to ${\left\{{(s_t^{(r)})}_q^m\right\}}_{q=0,\dots ,Q-1;l=-q,\dots ,q}$ in the spectral domain. In a statistical sense, with $Q\ll \sqrt{\mathit{\text{IJ}}}$, (2) provides a low-rank approximation for the stochastic process Z_t, where ${(s_t)}_q^m$ serves as a random coefficient and Q trades off the quality of approximation against the computational complexity.

We provide Figure 2 to facilitate the understanding of SHT. Figure 2(a) shows a set of stochastic components in the spatial domain, that is, ${\{Z_9^{(1)}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$, which is obtained by detrending and rescaling the annually aggregated temperature at year 2023 and ensemble one with ensemble mean and standard error in Figure 1(a) and (b), respectively. After applying the SHT, Figure 2(b) presents the pattern of ${\left\{{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}}_{10}\right|\left|{(s_9^{(1)})}_q^m\right|{|}_2\}}_{q=0,1,\dots ,Q_{\mathrm{\text{max}}};m=-q,\dots ,q}$, which indicates the energy allocation in the spectral domain. The energy is more concentrated at lower degrees of lower frequencies, gradually decreasing as the degree increases. The decay rate reflects the differentiability property of the data, as detailed in Section S3.2.1 of the supplementary materials. Figure 2(c)–(e) show the influence of Q on the loss of using SHT for a single set of stochastic components. Section S3.2.3 provides a more comprehensive illustration of the general approximation performance. In essence, a larger value of Q retains more information and provides a better approximation. Additionally, the spatial structure of surface temperature varies significantly between land and ocean.

Fig. 2 Demonstration of SHT. (a) shows a set of stochastic component ${\{Z_9^{(1)}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$ in the spatial domain. (b) indicates energy allocation of (a) in spectral domain. (c)–(e) depict the absolute values of ${\{{\epsilon }_9^{(1)}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$ in (2) with Q = 36, 72, and 116, respectively. (f) depicts the absolute values of ${\{{\epsilon }_9^{(1)}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$ obtained by using LatticeKrig with 13,658 bases of 6 levels, where $13,658>{116}^2=13,456$.

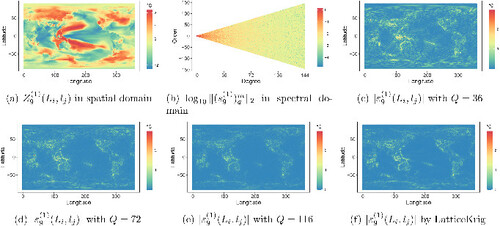
We compare SHT with two popular bases used in low-rank approximations, empirical orthogonal functions (EOFs) and those in LatticeKrig (Nychka et al. 2016), as detailed in Section S3.2.4. EOFs, as data-driven basis functions, lack a closed form and must be stored. Their evaluation involves computing and eigen-decomposing an IJ × IJ matrix, leading to constraints on computational time and resources. Figure 2(e) and (f) illustrate comparable approximation performance of SHT and LatticeKrig on $Z_9^{(1)}(L_i,l_j)$ with similar numbers of bases. However, LatticeKrig entails more time for parameter tuning selection and coefficient calculation, along with greater storage requirements. For a more detailed and comprehensive comparison, readers are referred to Section S3.2.4. We emphasize the advantages of employing the spherical harmonics to represent substantial global climate simulations: (a) Natural basis functions. Spherical harmonics are eigenfunctions of the Laplace-Beltrami operator, making them well-suited for analyzing spherical data of various variables, as well as their spectrum; (b) Easily available multi-resolution basis functions. Spherical harmonics have a closed form, which saves the procedures for getting bases, conserves the memory for storing them, and facilitates the derivation of special forms of covariance under certain assumptions. Their resolutions are automatically multiple, eliminating the need for researchers to manually allocate knots or tuning parameters. Instead, one can simply select a degree Q to control the level of detail; (c) Efficient coefficient calculation. As shown in Section S3.2.2, both the SHT and its inverse can be efficiently calculated with a computational time $O(Q^3)$. Moreover, this computational time can be further reduced to $O(Q^2)$ by parallel computing. On a MacBook with a 3.2 GHz Apple M1 Pro processor with ten cores, performing the SHT with $Q=Q_{\mathrm{\text{max}}}$ in Figure 2 takes about 3 sec, and the inverse SHT with Q = 36, 72, and 144 take no more than 0.06, 0.3, and 2 sec, respectively.

Next, we model the spatial dependence structure, which is assumed to remain consistent over time. The covariance between $Z_t^{(r)}(L_i,l_j)$ and $Z_t^{(r)}(L_{i\prime },l_{j\prime })$ is (3) $$c\{(L_i,l_j),(L_{i\prime },l_{j\prime })\}=\mathbf{H}{(L_i,l_j)}^{\top }\mathbf{K}\overline{\mathbf{H}(L_i,l_j)}+{\delta }_{i=i\prime }{\delta }_{j=j\prime }{v}^2(L_i,l_j),$$(3) where $\mathbf{K}={\mathbf{K}}_t^{(r)}=\mathrm{E}\left\{{\mathbf{s}}_t^{(r)}{({\mathbf{s}}_t^{(r)})}^{\mathrm{H}}\right\}$ is a $Q^2\times Q^2$ covariance matrix of ${\left\{{(s_t^{(r)})}_q^m\right\}}_{q=0,1,\dots ,Q;m=-q,\dots ,q},\mathrm{H}$ is the operator of conjugate transpose, $\mathbf{H}(L_i,l_j)$ and ${\mathbf{s}}_t^{(r)}$ are vectors consisting of basis functions and spherical harmonic coefficients, indexed by $(q^2+q+m+1)$. Specifically, the $(q^2+q+m+1)$th elements of $\mathbf{H}(L_i,l_j)$ and ${\mathbf{s}}_t^{(r)}$ are $H_q^m(L_i,l_j)$ and ${(s_t^{(r)})}_q^m$, respectively.

Further examining the structure of K, it is evident that the stochastic component in Figure 2(a) exhibits strong heterogeneity across different latitudes, as observed in previous studies of global climate data (Stein 2007; Jeong et al. 2018; Huang et al. 2023). Consequently, the commonly used isotropic assumption for Euclidean data is no longer appropriate. Instead, we adopt the assumption of axial symmetry, which posits that only data on the same latitude are stationary (Jones 1963). This leads to the covariance $c\{(L_i,l_j),(L_{i\prime },l_{j\prime })\}$ becoming a function of L_i (θ_i), $L_{i\prime }$ (${\theta }_{i\prime }$), and $|l_j-l_{j\prime }|$ ($|{\psi }_j-{\psi }_{j\prime }|$, the central angle between points (L_i, l_j) and $(L_{i\prime },l_{j\prime })$ expressed in chordal distance). Using a simple derivation outlined in Jones (1963), we have (4) $$\begin{array}{c}c(L_i,L_{i\prime },|l_j-l_{j\prime }|)\\ \hspace{1em}=\sum _{q=0}^{Q-1}\sum _{q\prime =0}^{Q-1}\sum _{m=-q}^q{k}_{\mathit{\text{qq}}\prime m}{H}_q^m({\theta }_i,0)H_{q\prime }^m({\theta }_{i\prime },0)\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(\iota m|{\psi }_j-{\psi }_{j\prime }|)\end{array}$$(4) with $\mathrm{E}\left\{{(s_t^{(r)})}_q^m{(s_t^{(r)})}_{q\prime }^{m\prime }\right\}={\delta }_{m=m\prime }{k}_{\mathit{\text{qq}}\prime m}$. It means that axial symmetry assumes dependence only on coefficients of the same order. Thus, K becomes a sparse matrix, consisting of $Q^2+{(Q-1)}^2+\cdots +1^2=Q^3/3+Q^2/2+Q/6$ nonzero elements.

However, from Figures 1 and 2, we still observe heterogeneity between land and ocean data on the same latitude. The stochastic components on land and ocean exhibit different spatial structures, requiring different numbers of basis functions to capture them adequately. Therefore, we propose replacing (2) by (5) $$\begin{array}{c}{Z}_t^{(r)}(L_i,l_j)={\delta }_{(L_i,l_j)\in {\mathcal{S}}_l}\sum _{q=0}^{Q_l-1}\sum _{m=-q}^q{(s_t^{(r)})}_q^m{H}_q^m(L_i,l_j)\\ \hspace{1em}+{\delta }_{(L_i,l_j)\in {\mathcal{S}}_o}\sum _{q=0}^{Q_o-1}\sum _{m=-q}^q{(s_t^{(r)})}_q^m{H}_q^m(L_i,l_j)+{\epsilon }_t^{(r)}(L_i,l_j),\end{array}$$(5) where ${\mathcal{S}}_o$ (${\mathcal{S}}_l$) represents the set of grid points over the ocean (land) and Q_o (Q_l) denotes the value of Q for ocean (land). We ignore the continuity of temperature changes between land and ocean, since (5) is formulated on grid points and our target is not to predict at new points. Accordingly, the covariance $c(L_i,L_i,|l_j-l_{j\prime }|)$ is given by plugging the Q values of (L_i, l_j) and $(L_{i\prime },l_{j\prime })$ into (4). We present the process of choosing appropriate values for Q_o and Q_l in Section 4.

3.2.2 Modeling the Temporal Dependence

Next, we investigate the temporal dependence within the vector time series ${\left\{{\mathbf{s}}_t^{(r)}\right\}}_{t=1}^T$ in the spectral domain. We will employ an auto-regressive model, but with two additional operations: converting the coefficients to real-valued ones and Gaussianizing them using the TGH transformation. Specifically, for the complex-valued vector ${\mathbf{s}}_t^{(r)}$ with the special structure of ${(s_t^{(r)})}_q^{-m}={(-1)}^m\overline{{(s_t^{(r)})}_q^m}$, we first linearly transform it into a real-valued vector: $$\begin{array}{c}{\tilde{\mathbf{s}}}_t^{(r)}={\mathbf{A}}^{-1}{\mathbf{s}}_t^{(r)}=[{(s_t^{(r)})}_0^0,\mathfrak{I}\{{(s_t^{(r)})}_1^1\},{(s_t^{(r)})}_1^0,\mathfrak{R}\{{(s_t^{(r)})}_1^1\},\dots ,\\ \hspace{1em}\mathfrak{I}\left\{{(s_t^{(r)})}_{Q-1}^{Q-1}\right\},\dots ,\mathfrak{R}\left\{{(s_t^{(r)})}_{Q-1}^{Q-1}\right\}{]}^{\top },\end{array}$$where both A and its inverse are $Q^2\times Q^2$ sparse matrices with known structures. For example, in the case of Q = 2, A and ${\mathbf{A}}^{-1}$ can be represented as $$\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& \iota & 0& -1\\ 0& 0& 1& 0\\ 0& \iota & 0& 1\end{array}\right)\hspace{1em}\text{and}\hspace{1em}\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& -\iota /2& 0& -\iota /2\\ 0& 0& 1& 0\\ 0& -1/2& 0& 1/2\end{array}\right),$$ respectively. For simplicity, we denote the $(q^2+q+m+1)$th element of ${\tilde{\mathbf{s}}}_t^{(r)}$ as ${({\tilde{s}}_t^{(r)})}_q^m$. Consequently, we have $Z_t^{(r)}(L_i,l_j)=\mathbf{H}{(L_i,l_j)}^{\top }\mathbf{A}{\tilde{\mathbf{s}}}_t^{(r)}+{\epsilon }_t^{(r)}(L_i,l_j)$, where ${\mathbf{A}}^{\top }\mathbf{H}(L_i,l_j)$ and ${\tilde{\mathbf{s}}}_t^{(r)}$ are vectors of bases and coefficients, respectively. Under the assumption of axial symmetry, the covariance of ${\tilde{\mathbf{s}}}_t^{(r)}$, denoted as ${\tilde{\mathbf{K}}}_0=\mathrm{E}({\tilde{\mathbf{s}}}_t^{(r)}{\tilde{\mathbf{s}}}_t^{(r)\top })$, is also a sparse matrix. Specifically, $\mathrm{E}\left\{{({\tilde{s}}_t^{(r)})}_q^m{({\tilde{s}}_t^{(r)})}_{q\prime }^{m\prime }\right\}=\mathrm{E}\left\{{({\tilde{s}}_t^{(r)})}_q^{-m}{({\tilde{s}}_t^{(r)})}_{q\prime }^{-m\prime }\right\}={\tilde{k}}_{\mathit{\text{qq}}\prime m}{\delta }_{m=m\prime }{\delta }_{m\ge 0}$. The derivation is given in Section S3.3 of supplementary materials. The matrix ${\tilde{\mathbf{K}}}_0$ consists of $2Q^3/3+Q/3$ nonzero elements and only $Q^3/3+Q^2/2+Q/3$ ones need to be stored. If $Z_t^{(r)}(L_i,l_j)$ represents the stochastic component of annually aggregated temperature, it is reasonable to assume the Gaussianity of ${\{Z_t^{(r)}(L_i,l_j)\}}_{t=1}^T$, and therefore, the Gaussianity of ${\left\{{\tilde{\mathbf{s}}}_t^{(r)}\right\}}_{t=1}^T$. This allows us to model it with a vector auto-regressive model of order P (VAR(P)): ${\tilde{\mathbf{s}}}_t^{(r)}={\sum }_{p=1}^P{\mathbf{\Phi }}_p{\tilde{\mathbf{s}}}_{t-p}^{(r)}+{\mathit{\xi }}_t^{(r)}$, where ${\mathit{\xi }}_t^{(r)}\stackrel{\text{iid}}{\sim }{\mathcal{N}}_{Q^2}(\mathbf{0},\mathbf{U})$ and $\mathbf{U}={\tilde{\mathbf{K}}}_0-{\sum }_{p=1}^P{\mathbf{\Phi }}_p{\tilde{\mathbf{K}}}_0{\mathbf{\Phi }}_p^{\top }-{\sum }_{p=1}^P{\sum }_{p\prime \ne p}^P{\mathbf{\Phi }}_p{\tilde{\mathbf{K}}}_{|p\prime -p|}{\mathbf{\Phi }}_{p\prime }^{\top }$ with ${\tilde{\mathbf{K}}}_{|p\prime -p|}=\mathrm{E}({\tilde{\mathbf{s}}}_{t-p}^{(r)}{\tilde{\mathbf{s}}}_{t-p\prime }^{(r)\top })$.

However, as in Sections 2 and S2, when $Z_t^{(r)}(L_i,l_j)$ is the stochastic component of the monthly or daily aggregated temperature, the Gaussianity assumption for time series ${\{Z_t^{(r)}(L_i,l_j)\}}_{t=1}^T$ at most grid points (L_i, l_j) may not hold. It implies that ${\left\{{({\tilde{s}}_t^{(r)})}_q^m\right\}}_{t=1}^T$ at some (q, m) pairs are not Gaussian and motivates us to employ a modified TGH transformation. Denote by ${\mathcal{S}}_{\mathit{\text{gh}}}$ the set of (q, m) such that ${\left\{{({\tilde{s}}_t^{(r)})}_q^m\right\}}_{t=1}^T$ rejects the Gaussianity. We model the coefficients with a TGH auto-regressive model: ${\check{\mathbf{s}}}_t^{(r)}={\sum }_{p=1}^P{\mathbf{\Phi }}_p{\check{\mathbf{s}}}_{t-p}^{(r)}+{\mathit{\xi }}_t^{(r)}$, where the $(q^2+q+m+1)$th element of ${\check{\mathbf{s}}}_t^{(r)}$ is (6) $${({\check{s}}_t^{(r)})}_q^m=\{\begin{array}{cc}{\lambda }_q^m{\tau }_{g_q^m,h_q^m}^{-1}\{{({\tilde{s}}_t^{(r)})}_q^m/{\omega }_q^m\},& \text{if}\hspace{1em}(q,m)\in {\mathcal{S}}_{\mathit{\text{gh}}},\\ {({\tilde{s}}_t^{(r)})}_q^m,& \text{if}\hspace{1em}(q,m)\notin {\mathcal{S}}_{\mathit{\text{gh}}},\end{array}$$(6) with ${\tau }_{g_q^m,h_q^m}(s)={(g_q^m)}^{-1}\{\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(g_q^{m}s)-1\}\hspace{0.17em}\mathrm{\text{exp}}\hspace{0.17em}(h_q^m{s}^2/2)$. Compared to the regular TGH, the one in (6) removes a location parameter and introduces a scale parameter ${\lambda }_q^m$. The former is due to the zero-mean ${\left\{{({\tilde{s}}_t^{(r)})}_q^m\right\}}_{t=1,\dots ,T;r=1,\dots ,R}$. The later ensures the standard deviation of ${\left\{{({\check{s}}_t^{(r)})}_q^m\right\}}_{t=1,\dots ,T;r=1,\dots ,R}$ to be equal to that of ${\left\{{({\tilde{s}}_t^{(r)})}_q^m\right\}}_{t=1,\dots ,T;r=1,\dots ,R}$. Four additional parameters describing characteristics beyond the first two moments are to be stored. Based on (6), the covariance matrix of ${\mathit{\xi }}_t^{(r)}$ is $\mathbf{U}={\check{\mathbf{K}}}_0-{\sum }_{p=1}^P{\mathbf{\Phi }}_p{\check{\mathbf{K}}}_0{\mathbf{\Phi }}_p^{\top }-{\sum }_{p=1}^P{\sum }_{p\prime \ne p}^P{\mathbf{\Phi }}_p{\check{\mathbf{K}}}_{|p-p\prime |}{\mathbf{\Phi }}_{p\prime }^{\top }$, where both ${\check{\mathbf{K}}}_0=\mathrm{E}({\check{\mathbf{s}}}_t^{(r)}{\check{\mathbf{s}}}_t^{(r)\top })$ with $\mathrm{E}\left\{{({\check{s}}_t^{(r)})}_q^m{({\check{s}}_t^{(r)})}_{q\prime }^{m\prime }\right\}=\mathrm{E}\left\{{({\check{s}}_t^{(r)})}_q^{-m}{({\check{s}}_t^{(r)})}_{q\prime }^{-m\prime }\right\}={\check{k}}_{\mathit{\text{qq}}\prime m}{\delta }_{m=m\prime }{\delta }_{m\ge 0}$ and ${\check{\mathbf{K}}}_{|p-p\prime |}=\mathrm{E}({\check{\mathbf{s}}}_{t-p}^{(r)}{\check{\mathbf{s}}}_{t-p\prime }^{(r)\top })$ have sparse structures under the assumption of axial symmetry.

Furthermore, we assume that ${\mathbf{\Phi }}_p$ is a diagonal matrix with the $(q^2+q+m+1)$th diagonal element denoted as ${({\varphi }_p)}_q^m$, which neglects the cross dependence between ${\left\{{({\tilde{s}}_t^{(r)})}_q^m\right\}}_{q=0,\dots ,Q-1;m=-q,\dots ,q}$. This assumption enables the independent and parallel evaluation of ${\left\{{({\varphi }_p)}_q^m\right\}}_{p=1}^P$ across q and m and ensures U to inherit the same sparse structure from ${\check{\mathbf{K}}}_0$ and ${\check{\mathbf{K}}}_{|p-p\prime |}$. We briefly validated it in Section S3.4 by testing the significance of the first temporal lag of the cross-correlation. The proportion of p-values less than 0.05 is nearly zero, indicating negligible cross-dependence. The details about the parameter estimation are given in Section S3.5.

3.3 Emulation with SG

The procedures of constructing an SG for the monthly and daily simulations from CESM2-LENS2 is summarized in Algorithm S1 of Section S3.6. We assume that the tuning parameters K, Q_l, Q_o, and P are known. More details about their selection will be provided in Section 4. In Stage 1, we calculate and store a total of $(5+2K)\mathit{\text{IJ}}$ parameters in the deterministic component. In Step 1) of Stage 2, although we use different Q values for land and ocean data to evaluate $v(L_i,l_j)$, we still need coefficients up to $Q\prime =\mathrm{\text{max}}(Q_l,Q_o)$. The number of stored parameters in Stage 2 is $\mathit{\text{IJ}}+(4+P)Q{\prime }^2+(Q{\prime }^3/3+Q{\prime }^2/2+Q\prime /3)$. Therefore, the total number of parameters is of the order $O(\mathit{\text{IJ}}+Q{\prime }^3)$. For the annually aggregated temperature, there is no need to perform a TGH transformation in Step 3) of Stage 2. Consequently, ${\mathcal{S}}_{\mathit{\text{gh}}}$ is an empty set, and only $\mathit{\text{IJ}}+\mathit{\text{PQ}}{\prime }^2+(Q{\prime }^3/3+Q{\prime }^2/2+Q\prime /3)$ parameters are needed for the stochastic component. In summary, we develop an SG by training on simulations of size IJRT and store it for generating unlimited emulations using at most $(6+2K)\mathit{\text{IJ}}+(4+P)Q{\prime }^2+(Q{\prime }^3/3+Q{\prime }^2/2+Q\prime /3)$ memorized parameters.

Here, we contrast the storage requirements of our SG with that of another efficient SG proposed by Huang et al. (2023) (referred to as HCBG-SG) for surface temperature simulations from LENS1 (Kay et al. 2015). HCBG-SG was primarily developed within the spatial domain and required memorization of $(2K+P_H+8)\mathit{\text{IJ}}+6I+2$ parameters. This consisted of $(5+2K)\mathit{\text{IJ}}$ parameters for the deterministic component, $P_H\mathit{\text{IJ}}$ parameters for evaluating the temporal dependence with P_H representing the selected order for the auto-regressive model, 3IJ parameters for TGH transformation, and $6I+2$ parameters for assessing the nonstationary spatial dependence. The storage advantage of our SG stems from its modeling in the spectral domain rather than the spatial domain, with $Q{\prime }^2\ll \mathit{\text{IJ}}$. Taking the case of $P=P_H=1$ and $Q\prime =70$ as an example, which maximizes storage requirements of our SG for all temporal resolutions, the daily HCBG-SG necessitates additional 25,747 parameters. However, for annual simulations, which do not need a TGH, HCBG-SG needs 120,541 fewer parameters. A further comparison of their performance is presented in Section 4.

In Algorithm 1, we outline the procedures for generating monthly and daily temperature emulations for CESM2-LENS2. Note that a Cholesky decomposition should be performed on U when generating ${\check{\mathbf{s}}}_t^{(r\prime )}$, which may be time-consuming if $Q\prime$ is not small. However, the sparse structure of U avoids the possible computational limitation. For the annually aggregated temperature, we can simply remove Step (b) in Stage 2 and replace ${\tilde{\mathbf{s}}}_{\mathit{\text{SG}},t}^{(r\prime )}$ in Step (c) with ${\check{\mathbf{s}}}_{\mathit{\text{SG}},t}^{(r\prime )}$.

Algorithm 1

Emulation with SG

Input: $\rho (L_i,l_j),{\beta }_0(L_i,l_j),{\beta }_1(L_i,l_j),{\beta }_2(L_i,l_j),a_1(L_i,l_j)$,…, $a_K(L_i,l_j),b_1(L_i,l_j)$,…, $b_K(L_i,l_j),\sigma (L_i,l_j),v(L_i,l_j),{\lambda }_q^m,{\omega }_q^m,g_q^m,h_q^m,{({\varphi }_1)}_q^m,\dots ,{({\varphi }_P)}_q^m,i=1,\dots ,I,j=1,\dots ,J,q=0,\dots ,Q_o-1,m=-q,\dots ,q$, U, Q_l, Q_o, K, P, $\mathbf{A}\in {\mathbb{R}}^{Q_o^2\times Q_o^2},R\prime$.

Stage 1: Preliminary

1) For each grid point (L_i, l_j), calculate ${\{m_t(L_i,l_j)\}}_{t=1}^T$ with given parameters of the deterministic component, $i=1,\dots ,I$ and $j=1,\dots ,J$.

Stage 2: Emulation

For $r\prime =1,\dots ,R\prime$:

1) generate ${\check{\mathbf{s}}}_{\mathit{\text{SG}},-(p-1)}^{(r\prime )}\sim {\mathcal{N}}_{Q_o^2}(\mathbf{0},\mathbf{U}),p=1,\dots ,P$,

2) for $t=1,\dots ,T$:

(a) generate ${\mathit{\xi }}_{\mathit{\text{SG}},t}^{(r\prime )}\sim {\mathcal{N}}_{Q_o^2}(\mathbf{0},\mathbf{U})$, and calculate ${\check{\mathbf{s}}}_{\mathit{\text{SG}},t}^{(r\prime )}={\sum }_{p=1}^P{\Phi }_p{\check{\mathbf{s}}}_{\mathit{\text{SG}},t-p}^{(r\prime )}+{\mathit{\xi }}_{\mathit{\text{SG}},t}^{(r\prime )}$,

(b) calculate ${\tilde{\mathbf{s}}}_{\mathit{\text{SG}},t}^{(r\prime )}$, where ${({\tilde{s}}_{\mathit{\text{SG}},t}^{(r\prime )})}_q^m={\omega }_q^m{\tau }_{g_q^m,h_q^m}\{{({\check{s}}_{\mathit{\text{SG}},t}^{(r\prime )})}_q^m/{\lambda }_q^m\}$,

(c) calculate ${\mathbf{s}}_{\mathit{\text{SG}},t}^{(r\prime )}=\mathbf{A}{\tilde{\mathbf{s}}}_{\mathit{\text{SG}},t}^{(r\prime )}$, and perform the inverse SHT on ${\mathbf{s}}_{\mathit{\text{SG}},t}^{(r\prime )}$ with (5) to obtain ${\{\text{invSHT}({\mathbf{s}}_{\mathit{\text{SG}},t}^{(r\prime )})(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$,

(d) generate ${\epsilon }_{\mathit{\text{SG}},t}^{(r\prime )}(L_i,l_j)\sim \mathcal{N}(0,\widehat{v}{(L_i,l_j)}^2),i=1,\dots ,I;j=1,\dots ,J$;

(e) generate emulations $$y_{\mathit{\text{SG}},t}^{(r\prime )}(L_i,l_j)=m_t(L_i,l_j)+\sigma (L_i,l_j)\{\text{invSHT}({\mathbf{s}}_{\mathit{\text{SG}},t}^{(r\prime )})(L_i,l_j)$$ $$\hspace{1em}+{\epsilon }_{\mathit{\text{SG}},t}^{(r\prime )}(L_i,l_j)\}.$$

Output: ${\{y_{\mathit{\text{SG}},t}^{(r\prime )}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J;r\prime =1,\dots ,R\prime }$.

4 Case Study: CESM2-LENS2

In this section, we develop emulators and generate emulations for surface temperature simulations from CESM2-LENS2 using the proposed algorithms. We delve into the implementation of our SG (referred to as SHT-SG in this section), covering the choice of tuning parameters and the modeling of the dependence structure, and the assessment of their performance. Additionally, we include the results of HCBG-SG for comparison. Discussion about the monthly SG is presented in Section S4.2 of the supplementary materials to save space.

The assessment of an SG relies on the specific purpose for which the emulator is intended (Castruccio et al. 2014). Our main goal is to generate emulations that closely resemble the given simulations. To achieve this, our SG should efficiently decouple and capture the deterministic and stochastic components of the data. First, the estimated mean trend ${\widehat{m}}_t$ should mimic and extract the variation of the ensemble mean in the simulations. After adding the stochastic component, the variability of emulations should be similar to the internal variability observed in simulations. Therefore, we will discuss two key factors: goodness-of-fit and variability, quantified with $${\mathrm{I}}_{\text{fit}}(L_i,l_j)=\frac{\sum _{r=1}^R\sum _{t=1}^T\{y_t^{(r)}(L_i,l_j)-{\widehat{m}}_t(L_i,l_j){\}}^2}{R/(R-1)\sum _{r=1}^R\sum _{t=1}^T\{y_t^{(r)}(L_i,l_j)-{\overline{y}}_t(L_i,l_j){\}}^2}$$

and $${\mathrm{I}}_{\text{uq}}(L_i,l_j)=\frac{\text{CRA}\{y_{\mathit{\text{SG}},t}^{(1)}(L_i,l_j),\dots ,y_{\mathit{\text{SG}},t}^{(R)}(L_i,l_j)\}}{\text{CRA}\{y_t^{(1)}(L_i,l_j),\dots ,y_t^{(R)}(L_i,l_j)\}},$$respectively. Given a grid point (L_i, l_j), the index ${\mathrm{I}}_{\text{fit}}(L_i,l_j)$ compares ${\widehat{m}}_t(L_i,l_j)$ with $2K+4$ parameters with the ensemble mean ${\overline{y}}_t(L_i,l_j)=R^{-1}{\sum }_{r=1}^R{y}_t^{(r)}(L_i,l_j)$ with T parameters among all ensembles and time points. The closer the ${\mathrm{I}}_{\text{fit}}$ value to 1, the better the ability of the SG to capture the variability of the ensemble mean. Index ${\mathrm{I}}_{\text{uq}}$, a measure proposed in Huang et al. (2023), leverages the concept of functional data depths (López-Pintado and Romo 2009). In particular, we treat ${\{y_{\mathit{\text{SG}},t}^{(r\prime )}(L_i,l_j)\}}_{r\prime =1}^R$ as R functions of t at (L_i, l_j) and measure the interquartile range (Sun and Genton 2011) of these functions using the central region area (CRA). Then, ${\mathrm{I}}_{\text{uq}}(L_i,l_j)$ is the uncertainty qualification of ${\{y_{\mathit{\text{SG}},t}^{(r\prime )}(L_i,l_j)\}}_{r\prime =1}^R$ against that of ${\{y_t^{(r)}(L_i,l_j)\}}_{r=1}^R$. A value of ${\mathrm{I}}_{\text{uq}}$ close to 1 suggests that the variability of the generated emulations closely reflects the internal variability of the training simulations.

Moreover, we will visually and numerically compare various statistical characteristics of the emulations to those of simulations. This ensures that our emulations faithfully capture the essential features of the temperature data from CESM2-LENS2. For example, at each grid point, we compare the empirical distribution of ${\{y_{\mathit{\text{SG}},t}^{(r\prime )}(L_i,l_j)\}}_{t=1,\dots ,T;r\prime =1,\dots ,R}$ to that of ${\{y_t^{(r)}(L_i,l_j)\}}_{t=1,\dots ,T;r=1,\dots ,R}$ by the Wasserstein distance (Santambrogio 2015), which is denoted as ${\text{WD}}_S(L_i,l_j)$. Similarly, we calculate the Wasserstein distance between the empirical distribution of ${\{y_{\mathit{\text{SG}},t}^{(r\prime )}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J;r\prime =1,\dots ,R}$ and ${\{y_t^{(r)}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J;r=1,\dots ,R}$ at each time point t, which is denoted as ${\text{WD}}_T(t)$.

4.1 Annually Aggregated Temperature

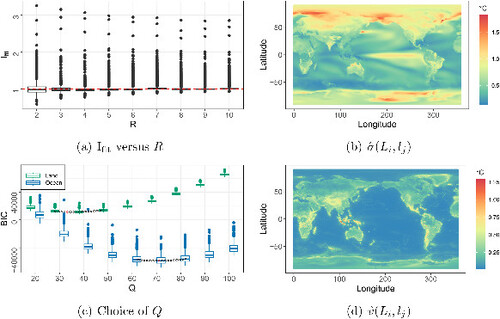
First, we evaluate the deterministic component m_t and σ of the annually aggregated temperature simulations ${\{y_t^{(r)}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J;t=1,\dots ,T;r=1,\dots ,R}$, with a total of T = 86 time points. Figure 3(a) presents boxplots of ${\{{\mathrm{I}}_{\text{fit}}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$ for different values of R. These values tend to get closer to 1 as R increases, and they stabilize after $R\ge 7$, which means that using seven training simulations is sufficient to stabilize the inference. Therefore, we select R = 7 for the subsequent analysis. The corresponding ${\{{\mathrm{I}}_{\text{fit}}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$ values are shown in Figure S5(a), with a median value of 1.001. Temperature can be fitted well at most grid points. Furthermore, Figure 3(b) displays the map of $\widehat{\sigma }(L_i,l_j)$, illustrating the nonstationarity of the data. It is evident that larger variations of surface temperatures are observed over land.

Fig. 3 Inference process for the annual SG. (a) shows boxplots of ${\{{\mathrm{I}}_{\text{fit}}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$ for different values of R. (b) is the map of the estimated standard deviation ${\{\widehat{\sigma }(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$. (c) shows boxplots of ${\{{\text{BIC}}_{*,t}^{(r)}(Q)\}}_{r=1,\dots ,R;t=1,\dots ,T}$ for different values of Q, where $*$ takes “l” and “o”. Points × show medians of BIC values. The red points indicate the minimum values. (d) is the map of ${\{\widehat{v}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$.

Then, we perform the SHT on the stochastic component, necessitating the selection of appropriate values for Q_l and Q_o. Based on the Gaussian assumption of ${\epsilon }_t^{(r)}(L_i,l_j)$, we propose a Bayesian information criterion (BIC) for ${\{Z_t^{(r)}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$ at time t of ensemble r: $$\begin{array}{c}{\text{BIC}}_{*,t}^{(r)}(Q)=\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(n_{*})Q^2+n_{*}\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(2\pi )\\ \hspace{1em}+{\delta }_{(L_i,l_j)\in {\mathcal{S}}_{*}}\sum _{i=1}^I\sum _{j=1}^J\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}\{{\widehat{v}}^2(L_i,l_j)\}\\ \hspace{1em}+{\delta }_{(L_i,l_j)\in {\mathcal{S}}_{*}}\sum _{i=1}^I\sum _{j=1}^J{\left\{\frac{{\epsilon }_t^{(r)}(L_i,l_j)}{\widehat{v}(L_i,l_j)}\right\}}^2,\end{array}$$where ${\widehat{v}}^2(L_i,l_j)={(\mathit{\text{RT}})}^{-1}{\sum }_{r=1}^R{\sum }_{t=1}^T\{{\epsilon }_t^{(r)}(L_i,l_j){\}}^2$. When $*$ takes “o”, the above BIC with $n_o={\sum }_{i=1}^I{\sum }_{j=1}^J{\delta }_{(L_i,l_j)}\in {\mathcal{S}}_o$ helps select an appropriate Q_o for $Z_t^{(r)}(L_i,l_j)$ over the ocean. Similarly, when $*$ is “l”, it leads to the determination of Q_l. Figure 3(c) illustrates boxplots of ${\left\{{\text{BIC}}_{*,t}^{(r)}\right\}}_{r=1,\dots ,R;t=1,\dots ,T}$ against different values of Q, revealing a substantial discrepancy in preferred Q values between land and ocean. The stochastic components on land exhibit a preference for a smaller Q value compared to those on the ocean. This might seem counterintuitive, given that Figure 2(c) and (d) suggest that the stochastic component on land requires more harmonic terms for a better approximation. However, it is essential to note that the introduction of Q aims not only for accurate approximation but also to strike a balance between accuracy and the number of parameters, leading to improved model selection. Examining the boxplots for land, the improvement gained by including additional terms does not fully compensate for the associated drawbacks, such as increased storage requirements and accumulated errors from evaluation. The subsequent Figure 4(d) and (e) further validate this model selection result. Finally, the × points in Figure 3(c) suggest selecting Q_l = 35 and Q_o = 69 to minimize the medians of BIC for land and ocean, respectively.

Fig. 4 Temporal and spatial dependence structure. (a) is the map of the estimated ${\left\{{({\varphi }_1)}_q^m\right\}}_{q=0,\dots ,Q_o-1;m=-q,\dots ,q}$ for the annual simulations. (b) is the first 69 rows and columns of ${\tilde{\mathbf{K}}}_0$ empirically evaluated by ${(\mathit{\text{RT}})}^{-1}{\sum }_{r=1}^R{\sum }_{t=1}^T{\tilde{\mathbf{s}}}_t^{(r)}{\tilde{\mathbf{s}}}_t^{(r)\top }$ and denoted as ${\tilde{\mathbf{K}}}_{\text{emp}}$. (c) is the first 69 rows and columns of ${\tilde{\mathbf{K}}}_0$ evaluated under the axial symmetric assumption and denoted as ${\tilde{\mathbf{K}}}_{\text{axl}}$. (d) and (e) show empirical and fitted auto-covariance at latitudes $-{11.8}^{°}$ and ${36.3}^{°}$, respectively.

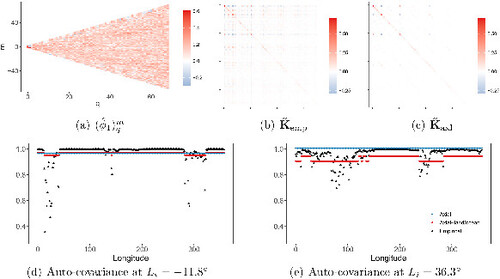
In Figure 3(d), we further analyze the values of $\widehat{v}(L_i,l_j)$, which serves as an assessment of the low-rank approximation on (L_i, l_j). There are several regions on land that exhibit significantly larger $\widehat{v}(L_i,l_j)$: (a) High-altitude regions such as the Himalayas and the Andes ranges with altitudes exceeding 3500 meters above sea level; and (b) Regions characterized by diverse topography, such as the Indonesian archipelago, encompassing islands, mountains, and coastal areas. These geographic factors contribute to a more complex spatial and temporal structure in surface temperature in these regions. To capture more details, one may consider including additional covariates in the deterministic component and choosing specific values of Q for these regions in the stochastic component. These considerations are avenues for future exploration.

Next, we assess the temporal dependence by fitting ${\left\{{({\tilde{s}}_t^{(r)})}_q^m\right\}}_{t=1,\dots ,T;r=1,\dots ,R}$ with the VAR(P) model. For each (q, m), we suggest to choose P by minimizing ${\text{BIC}}_q^m(P)=P\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}\{(T-P)R\}+R(T-P)\{\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}(2\pi )+1\}+R(T-P)\hspace{0.17em}\mathrm{\text{log}}\hspace{0.17em}({({\widehat{u}}_q^m)}^2)$, where ${({\widehat{u}}_q^m)}^2=R^{-1}{(T-P)}^{-1}{\sum }_{r=1}^R{\sum }_{t=P+1}^T\{({\tilde{s}}_t^{(r)}{)}_q^m-{\sum }_{p=1}^P{({\widehat{\varphi }}_p)}_q^m{({\tilde{s}}_{t-p}^{(r)})}_q^m{\}}^2$. For briefness, we use the conditional log-likelihood (given ${({\tilde{s}}_1^{(r)})}_q^m,\dots ,{({\tilde{s}}_P^{(r)})}_q^m$) rather than an exact log-likelihood in the above BIC. The proportions of $P=1,\dots ,5$ are 99.3%, 0.2%, 0.2%, 0.1%, and 0.2%, respectively. Therefore, we opt for P = 1 for the annual case. Figure 4(a) further demonstrates the estimates of ${\left\{{({\varphi }_1)}_q^m\right\}}_{q=0,\dots ,Q_o-1;m=-q,\dots ,q}$.

Finally, we evaluate the spatial dependence by examining the matrix ${\tilde{\mathbf{K}}}_0$. Figure 4(b) and (c) show top-left corners of two evaluations of ${\tilde{\mathbf{K}}}_0$. ${\tilde{\mathbf{K}}}_{\text{emp}}$ is the sample covariance matrix of ${\tilde{\mathbf{s}}}_t^{(r)}$, forming a dense $Q_o^2\times Q_o^2$ matrix. In contrast, ${\tilde{\mathbf{K}}}_{\text{axl}}$ is a sparse matrix. The sparsity of ${\tilde{\mathbf{K}}}_{\text{axl}}$ would be inherited by U, facilitating storage and enabling fast Cholesky decomposition using efficient algorithms (Furrer and Sain 2010). Figure 4(d) and (e) display empirical and fitted covariances for $Z(L_i,l_j)$ and $Z(L_i,l_{j+1})$, specifically the auto-covariance ${\left\{\text{cov}\right\{Z(L_i,l_j),Z(L_i,l_{j+1})\left\}\right\}}_{j=1}^{J-1}$ at $L_i=-{11.8}^{°}$ and ${36.3}^{°}$. These plots highlight the distinction between the proposed separate SHT for land and ocean (5) (Axial-land/ocean) and the original SHT (2) (Axial). The empirical auto-covariance over the ocean appears almost flat, supporting the assumption of axial symmetry over the ocean. In contrast, the auto-covariance over land significantly differs from that over the ocean. This difference is not captured by the fitted covariance of Axial, which selects Q = 77 via BIC. Axial-land/ocean fits the covariance separately for land and ocean, resulting in segmented lines in Figure 4(d) and (e). However, land temperature exhibits a complex and nonstationary dependence structure, with covariance weakening as one moves farther inland. This intricacy warrants further investigation in future research.

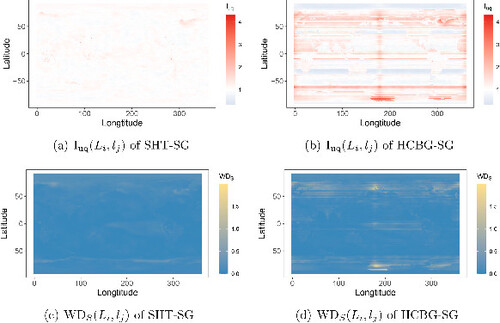
Inputting the above-estimated parameters, we generate $R\prime =R=7$ emulations with Algorithm 1. Each emulation takes approximately 30 sec to produce without parallel computation. Additionally, we include emulations generated by HCBG-SG for comparison, with detailed implementation procedures shown in the supplementary materials. Figure 5(a) and (b) compare ${\mathrm{I}}_{\text{uq}}$ values for the proposed SHT-SG and HCBG-SG, with median values of 1.013 and 1.085, respectively. Our emulations can successfully capture the variability of simulations at most grid locations, including polar regions. A high-${\mathrm{I}}_{\text{uq}}$ region near the location $(50.00,300.00)$ is caused by the poor evaluation of the mean trend, which is discussed in Section S4.1.1 of the supplementary materials. Figure 5(b) shows a poor spatial continuity for HCBG-SG, which may be caused by the independent evaluation of parameters at each latitude and a relatively weak model of dependence across latitudes. A similar pattern can be seen in Figure 5(d), which depicts the map of ${\text{WD}}_S$ for HCBG-SG, with a median value of 0.076. The ${\text{WD}}_S$ values for SHT-SG in Figure 5(c), which are closer to zero with a median value of 0.062, provide further evidence of the similarity between our emulations and the simulations. From Figure 5, geographic factors have no obvious impact on both two SGs regarding ${\mathrm{I}}_{\text{uq}}$ and ${\text{WD}}_S$ values. The ${\text{WD}}_T$ values for SHT-SG and HCBG-SG are comparable, with medians 0.126 and 0.108, respectively. In the supplementary materials, we further compare other basic statistical characteristics of our emulations to those of the simulations by replicating the procedures outlined in Figure 1.

Fig. 5 (a) and (b) are maps of ${\{{\mathrm{I}}_{\text{uq}}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$ for the annual temperature emulations. (c) and (d) are maps of ${\{{\text{WD}}_S(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$ for the annual temperature emulations.

4.2 Daily Aggregated Temperature

Now, we develop an SG for the daily aggregated temperature simulations with $T=31,390$. Analyzing such a vast amount of data presents a computational challenge. Therefore, we adopt a strategy similar to Huang et al. (2023) to perform inference only on data for the years 2020, 2040, 2060, 2080, and 2100. The procedure of inference closely follows that of the monthly case. Therefore, we put the details of development to Section S4.3 of the supplementary materials and focus on assessing the performance of the emulations and a further exploration of data characteristics.

For the daily data, we choose K_D = 4, Q_l = 36, Q_o = 68, and P = 1. The choice of $K_D>K_M=3$ reveals the presence of more complex fluctuations in daily time series, requiring harmonic terms with higher frequencies in the model. The more structured and higher ${({\widehat{\varphi }}_1)}_q^m$ in Figure S14(f) indicates a stronger dependence among time points. The performance of our SG, both with and without the use of TGH (referred to as SHT-SG(with TGH) and SHT-SG(without TGH), respectively), along with HCBG-SG, is illustrated in Figure 6. For better demonstration, indices larger than maximum values in Figure 6(a) and (c) are excluded from Figure 6(b) and (d), respectively. Comparing emulations generated by HCBG-SG with those of SHT-SG(with TGH), the latter illustrates a closer resemblance to simulations, greater robustness in numerically unstable regions, and better spatial continuity. From Figure 6(f), the incorporation of TGH in our SG results in an improvement in ${\text{WD}}_S$. The empirical distribution of emulations from SHT-SG(with TGH) is closer to that of simulations, aligning with the correct assumption. This advantage may not be apparent in Figure 6(e), as ${\mathrm{I}}_{\text{uq}}$ is used mainly for assessing the variabilities of emulations.

Fig. 6 Performance assessment of $R\prime =7$ daily emulations generated by various methods. (a) and (b) are maps of ${\{{\mathrm{I}}_{\text{uq}}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$ for the SHT-SG(with TGH) and HCBG-SG, respectively. (c) and (d) are maps of ${\{{\text{WD}}_S(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$ for SHT-SG(with TGH) and HCBG-SG, respectively. Points × represent four testing grid points TGL=$(-2.36,10.00)$, TGO=$(-30.63,10.00)$, TGN=$(-56.07,10.00)$, and TGB=$(-64.55,10.00)$. (e) and (f) are boxplots of ${\{{\mathrm{I}}_{\text{uq}}(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$ and ${\{{\text{WD}}_S(L_i,l_j)\}}_{i=1,\dots ,I;j=1,\dots ,J}$ for comparing the SHT-SG(with TGH) and SHT-SG(without TGH).

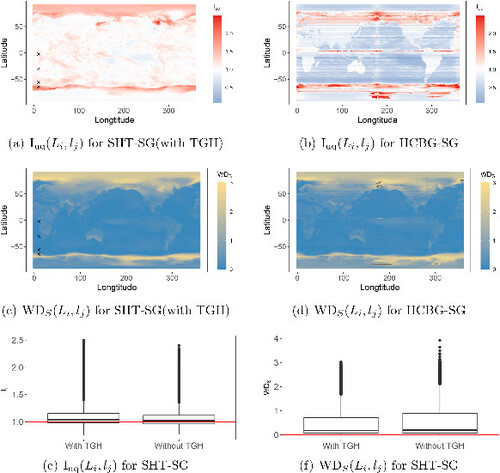
As in the monthly case, the daily emulations exhibit challenges in accurately representing certain regions, notably the North Pole and the Band regions. These regions display larger ${\mathrm{I}}_{\text{uq}}$ values, indicating higher uncertainty. Additionally, they may deviate from the behavior observed in the simulations, as reflected by the larger ${\text{WD}}_S$ values. Moreover, ${\text{WD}}_S$ values are generally higher over land compared to ocean areas, which may be attributed to the complex spatial and temporal structures and larger variation of the temperature on land.

We further explore these by intuitively displaying and comparing simulations and emulations at four testing grid points selected from the southern hemisphere with the same longitude in Figure 7. TGL is a land point near the equator. In Figure 7(a), temperature simulations on TGL exhibit larger variability but can be well replicated by the emulations. TGO is an ocean point in the middle latitudes. From Figure 7(b), temperature simulations on TGO have smaller variability overall, with relatively larger variability at peaks and valleys of each year. These patterns can also be observed at emulations on TGO. TGN is also an ocean point in the middle latitudes, but very close to the Band region. In Figure 7(c) (and Figure S14(a)), some temperature simulations exhibit sudden drops at a few days in year 2020, which leads to an overestimate of $\widehat{\sigma }(\mathrm{T}\mathit{\text{GN}})$, and hence a relatively higher variability in the emulations. Despite this, with ${\mathrm{I}}_{\text{uq}}(\mathrm{T}\mathit{\text{GN}})=1.200$ and ${\text{WD}}_S(\mathrm{T}\mathit{\text{GN}})=0.078$, the abnormal drops do not significantly affect these indices. Both ${\mathrm{I}}_{\text{uq}}$ and ${\text{WD}}_S$ exhibit a certain tolerance to isolated “outliers”. TGB is an ocean point within the Band region. Compared with the scenarios in Figure 7(c), temperature simulations at TGB display much more rapid and significant fluctuations at lots of time slots in years 2020, 2040, and 2060. In contrast, in years 2080 and 2100, the temperature simulations behave as other grid points on ocean with small variability. As shown in Figure S14(b), simulations at the North Pole region exhibit similar patterns, that is, surface temperature experiences sharp fluctuations on numerous days. According to the explanation kindly provided by NCAR, these temperature fluctuations are caused by the way of data generation. Specifically, the surface temperature in simulations is the spatial average of the surface temperature of whatever medium is in the grid box, whether it is water, land, or sea ice. Grid points at Band and North Pole regions undergo a dynamic transition, shifting back and forth between being partial sea ice and being open ocean. Consequently, sometimes we get the temperature of sea ice, and sometimes we get the temperature of the top layer of the ocean (or a mixture of the two). Combining this with Figure S14, the numerical instabilities exhibit four features: they do (a) not occur in each ensemble; (b) not happen during a fixed period; (c) not vary within a similar extent; and 4) not exhibit a consistent pattern across different grid points. Therefore, although the high ${\mathrm{I}}_{\text{uq}}$ and ${\text{WD}}_S$ values at the North Pole and Band regions directly stem from the inadequate assumption of a fixed $\widehat{\sigma }$ over time, developing an SG that can accurately model the temperature fluctuations in these two regions is a challenge.

Fig. 7 Comparison of daily emulations and simulations at four testing grid points. The black solid curves are ensemble means for simulations and emulations. The red dashed curves are ${\widehat{m}}_t$ s.

5 Conclusion and Future Work

In this article, we presented an efficient SG for global temperature simulations from the newly published CESM2-LENS2. With at most $O(\mathit{\text{IJ}}+Q_o^3)$ parameters to be stored, an unlimited number of emulations of size O(IJT), even at a daily scale, can be generated to help with the investigation of climate internal variability. Such a saving of computational time and resources comes from the use of SHT, which expands data with $Q_o^2\ll \mathit{\text{IJ}}$ spherical harmonics and represents a practical low-rank approximation on the sphere. By customizing Q values for grid points on land and ocean and leveraging the axial symmetry, the proposed SG can properly capture the complex nonstationary dependencies among different latitudes and land/ocean regions. To account for the non-Gaussian nature of the high-resolution time series, we introduced a modified TGH transformation into the SG. In our case study, we developed SGs based on R = 7 annually, monthly and daily aggregated simulations, respectively. We evaluated the efficiency and accuracy of the proposed SG by comparing the generated emulations to the original simulations and emulations generated by Huang et al. (2023) using various indexes and visual inspections.

While the proposed SGs have demonstrated commendable performance, there remains room for further enhancements: (a) Including altitude factors in both the deterministic and stochastic components. The influence of altitude has been evident in the inference process and the performance of emulations. Surface temperatures are sensitive to altitude (Castruccio and Genton 2016); (b) Improving the efficiency of SG on land, particularly for monthly and daily simulations. The larger variability observed in these cases suggests the need for more suitable models and additional factors to account for the complicated spatial and temporal structures on land; (c) Replacing the constant standard error with a temporal-varying one, denoted as σ_t. For simulations with higher temporal resolution, the assumption of a constant σ leads to an overestimate of standard error, further amplifying the variability of emulations, especially on land; and (d) Extending the current work to include hourly simulations. Hourly data may exhibit more intriguing characteristics, and exploring their emulation presents an opportunity for further investigation and understanding.

Beyond surface temperature, the idea of constructing an SG with SHT can be extended to various climate variables such as wind speed and atmospheric gas concentrations. After the removal of the deterministic component, the stochastic component can be efficiently expanded using spherical harmonics. The model in the spectral domain is contingent on the specific nature of the variable, which may ask for including other influential factors. Moreover, for variables that may exhibit interdependence, such as temperature and precipitation, exploring methods for their joint modeling in the spectral domain is also of interest. Investigating regional climate change, especially on land, is crucial for several reasons. On the one hand, climate change does not affect all regions equally. On the other hand, different regions have varying levels of vulnerability to climate change, for example, extreme weather events, sea-level rise, or precipitation patterns. Local communities, governments, and businesses may be interested in how specific areas are being impacted so that they can adapt and plan for the future. Therefore, another possible extension is to build an SG for high-resolution climate simulations on a specific region.

Supplementary Materials

Additional information about the CESM2-LENS2 data, inference process, derivation, validation, and results for the case studies are contained in the online supplementary materials. (.pdf file)

The R code and instructions for downloading, processing the data, and reproducing the results in the article are available at the GitHub repository: https://github.com/SpatialTemporalStats/LENS2_Emulator_Reproducibility_Materials

Disclosure Statement

The authors report there are no competing interests to declare.