Modeling of hyper-adaptability: from motor coordination to rehabilitation

Abstract

Hyper-adaptability is an ability of humans and animals to adapt to large-scale changes in the nervous system or the musculoskeletal system, such as strokes and spinal cord injuries. Although this adaptation may involve similar neural processes with normal adaptation to usual environmental and body changes in daily lives, it can be fundamentally different because it requires ‘construction’ of the neural structure itself and ‘reconstitution’ of sensorimotor control rules to compensate for the changes in the nervous system. In this survey paper, we aimed to provide an overview on how the brain structure changes after brain injury and recovers through rehabilitation. Next, we demonstrated the recent approaches used to apply computational and neural network modeling to recapitulate motor control and motor learning processes. Finally, we discussed future directions to bridge the gap between conventional physiological and modeling approaches to understand the neural and computational mechanisms of hyper-adaptability and its applications to clinical rehabilitation.

GRAPHICAL ABSTRACT

Keywords:

• Rehabilitation
• motor control theory
• neural networks

1. Introduction

Humans can adapt to different environments. Focusing on motor ability, we could move our arms to reach an external object and dexterously manipulate various shapes. We can even learn new motor tasks, such as sports skills. For example, if a mismatch occurs between the planned movement and realized movement (i.e. prediction error), humans could learn and adjust their motor command to adapt to the environment. This adaptive motor ability stems from the sensory-motor systems, redundancy of the human body, and brain function. When the human brain or spinal cord is damaged, motor function is severely impaired. However, the human brain has a great potential to adapt to these changes and overcome motor impairment. ‘Hyper-adaptability’ is defined as an animal's ability to adapt to large-scale and irreversible changes in the nervous or musculoskeletal system (e.g. brain/spinal cord injury). To introduce the concept of ‘hyper-adaptability,’ we focused on how humans regain their motor function after sustaining a brain injury.

Hyper-adaptability differs from normal adaptation in daily life (i.e. fatigue) in that this requires ‘reconstruction of the neural structure’ and ‘reconstitution of the sensorimotor control rules.’ After sustaining a spinal cord injury, for example, primates could utilize various indirect corticomotoneuronal pathways, the bilateral motor-related cortical areas, and mesolimbic structures, which are not otherwise used for the direct control of motor movements under normal physiological conditions [1]. By recruiting and exploring these latent neural circuits that are not typically used under normal conditions, the brain might use new control mechanisms through a re-optimization process. To fully understand hyper-adaptability (i.e. the mechanism underlying reconstruction of the neural structure and reconstitution of sensorimotor control rules), integration of multidisciplinary approaches, including conventional neurophysiological methodologies and computational neuroscience approaches is necessary. In other words, theoretical control modeling and neural network modeling are important to describe the general principles of the adaptation processes.

In this survey paper, we aimed to examine the phenomenon occurring after brain damage caused by stroke or traumatic injury to introduce the concept of hyper-adaptability. First, we provide an overview on how the brain function changes after a brain injury and how it recovers through rehabilitation. These physiological studies were also reviewed previously [1]. Furthermore, to understand the mechanism of hyper-adaptation and apply it for rehabilitation therapy, computational approaches are needed. Next, we showed the computational modeling of motor control, which is a possible candidate to explain hyper-adaptability. Then, we reviewed the recent advances in neural network modeling approaches for motor control and introduced the previous physiological experiments to validate the efficacy of these approaches. Finally, we discussed future directions to clarify the neural and computational mechanism of hyper-adaptability and its application to clinical rehabilitation.

2. Reconstruction of neural networks and reconstitution of control rules for hyper-adaptability

When humans move their body to perform a task, many parts of the human brain play important roles. Sensory information integrated in the parietal association area of the brain and the network between parietal area, premotor cortex, and primary motor cortex (M1) are involved in planning a motor command. This planned motor command is sent to the brainstem and the spinal cord through the corticospinal tract. Subcortical systems involve low-dimensional motor primitives (known as synergies) to generate muscle activity. When humans learn a new motor skill, these nervous systems are utilized for adaptation. In the normal adaptation, the cerebellum, basal ganglia, and cerebral cortex are thought to play specialized roles in supervised learning, reinforcement learning, and unsupervised learning, respectively [2].

When performing a motor task, humans plan and execute motor commands under a constraint condition. In this context, the goal of the task, surrounding environments, and dynamics of the musculoskeletal system determine the constraint conditions and cost function. The human brain can learn motor commands, which give less value to the cost function and satisfy the constraint condition. However, if the cerebral cortex, cerebellum, and basal ganglia are damaged (i.e. stroke or traumatic brain injuries), how can our nervous system adapt to this large-scale and irreversible change in the nervous system itself? Under this circumstance, it is mandatory to utilize other latent neural circuits, which emerged during development but less activated in a normal state, and all existing elements such as synergy to adapt to drastic change. In the next section, we reviewed the previous studies on the neurophysiological changes after brain injuries and what the type of rehabilitation intervention performed. Furthermore, we introduced how the brain networks change by rehabilitation to understand the role of hyper-adaptability after a brain damage.

2.1. Change of neural networks after a brain injury

When the brain is damaged by stroke or traumatic brain injury, neurons in the damaged area are lost, and if it involves the corticospinal tracts, hemiplegia occurs. These motor impairments are caused by physical damages and indirect behavioral changes following the physical damage. For example, the previous study investigated how the affected brain area of adult squirrel monkeys changes after a focal ischemic infarct in M1 [3]. They reported that the movements formerly represented in the infarcted zone did not reappear in the surrounding zone when the monkey did not receive extensive behavioral training. This is a direct effect of brain damage on motor function.

In addition to the direct physical effects, brain damage also causes secondary impairments. For example, many motor-impaired patients show behavioral change called ‘learned non-use’ after experiencing a stroke [4]. They pointed out that this behavioral suppression is caused by the experience of effortful movement and unsuccessful motor attempts. Further loss of function in the affected brain area occurs in the case of disuse of the affected limb.

Furthermore, the balance of transcallosal inhibitory activity between the affected and unaffected motor cortices changes after the onset of stroke [5,6]. A previous study [6] investigated the generation of a voluntary movement by the paretic hand of the patients who had ischemic subcortical infarction. They found an abnormally high interhemispheric inhibition from M1 of the unaffected hemisphere to the M1 of the affected side. A functional magnetic resonance imaging study also revealed that the interhemispheric functional connectivity between the cortical motor areas is reduced and correlates with the severity of motor impairment [7]. Damage to the brain causes impairment in the descending pathways from the brain to the spinal cord. Although the spinal cord is undamaged, the excitation level of motor neurons in the spinal cord cannot be properly controlled. This results in increased stretch reflex (spasticity) and muscle tonus, muscle weakness, or impaired muscle coordination. These results clearly demonstrate that brain damage causes functional impairment not only due to the direct focal damage but also due to the plastic changes in the entire nervous system.

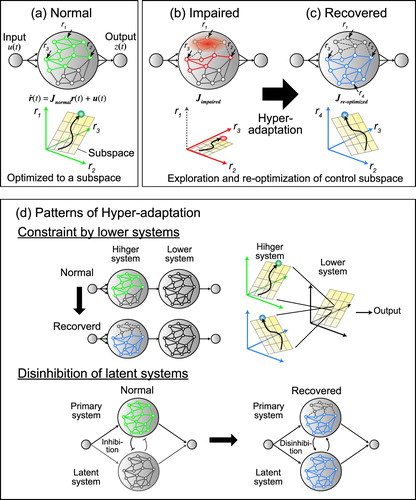
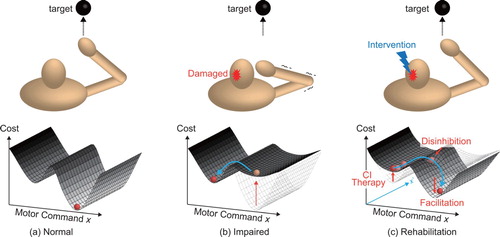
These findings suggest that brain injury often causes difficulty in limb movement, and it imposes a long-term constraint when deciding the appropriate motor commands to accomplish a motor task. Figure 1 shows a schematic diagram of the comparison between moving a hand to a target under normal and impaired states. In the normal state, humans could learn and execute appropriate motor commands, which minimize the ‘cost function,’ generally indicating the effectiveness of a motor command under the given environmental and body dynamics (lower is preferable), as shown in Figure 1(a). However, when irreversible changes occur in the brain network (e.g. abnormal interhemispheric inhibition), it is considered to be an additional motor constraint. In particular, the previous motor commands, which used to be sufficient under normal conditions, are no longer appropriate solutions solution during the impaired state. Thus, humans need to choose different motor commands to accomplish the task although it requires a higher cost (Figure 1(b)). In the next section, we introduce the type of rehabilitation performed for motor impaired post-stroke patients.

Figure 1. Schematic diagram of motor control. (a) Humans can choose appropriate motor commands under the cost function provided by the environmental and body dynamics. (b) When the brain is damaged, cost function is changed so that humans need to choose different motor strategies. (c) Rehabilitation intervention aims to reshape the cost function and encourage the individual to hyper-adapt to learn a new motion strategy.

2.2. Neuro-rehabilitation for motor recovery

Constraint-induced movement (CI) therapy is widely used in rehabilitation to overcome the learned non-use of the effected limb [8]. As described in the former section, behavioral suppression of movement in the affected limb prolongs the non-use of the said limb, resulting in the reduction in the volume of the brain region for body representation. In CI therapy, patients are encouraged to use their affected limb by inducing constraints on the unaffected limb. This intensive and repetitive practice can induce use-dependent plasticity to reorganize brain structure. The previous study [9] investigated how the hand representation area changes after CI therapy is applied to the chronic stroke patients with cortical lesions or subcortical lesions that involved the internal capsule. The internal capsule is the region where the corticospinal tract passes, and damage to this area impairs limb movement. Authors used transient magnetic stimulation (TMS) to investigate evoked movements to identify how the hand representation area changes in stroke patients after CI therapy. They found that the cortical representation area of the affected limb became significantly larger than that before CI therapy [9]. The CI therapy limits the unaffected limb movement, and this prevents the formulation and execution of motor commands under the impaired state. In this situation, the CI therapy is considered to increase the cost of the motor commands, which are used in the impaired state to encourage the patient to explore better motor commands (Figure 1(c)).

Some facilitation techniques are also used in stroke rehabilitation, such as repetitive facilitation exercise and neuro-developmental training. In the repetitive facilitation exercise, physical therapists provide physical stimulation (flexion or extension of the targeted joint) as the patient intends to move his or her affected hand [10]. This technique aims to elevate the excitation level of impaired descending motor tracts and encourage patients to initiate movement. Similarly, facilitation based on the Bobath concept uses facilitation techniques [11]. They also emphasized that the afferent information from the limb is important to improve body awareness. The timing of muscle synergy activation from a sitting position to a standing position improved and was similar to that of healthy individuals when the physical therapists provided facilitation based on the Bobath concept [12]. Facilitation techniques are thought to change the shape of the cost function to enable the motor-impaired patients to relearn new motor commands. In this way, the role of the facilitation provided by the physical therapists is considered to encourage the patient to seek different motor commands under the modified neural network (Figure 1(c)).

Another possible methodology to improve motor impairment is the use of transcranial direct current stimulation (tDCS). tDCS involves the application of a weak direct current through the scalp to change the excitability of the cortex. Anodal and cathodal stimulation are used, respectively, for excitation and inhibition of the target brain area [13]. There are two possible strategies for stroke rehabilitation: one strategy is to provide anodal stimulation to the affected sphere to increase excitability, and the other strategy is to provide cathodal stimulation in an unaffected hemisphere to decrease inhibition in this area. This is expected to improve unbalanced interhemispheric inhibition. Repetitive transcranial magnetic stimulation (rTMS) involves the induction of motor unit potentials in the cortex. A low-frequency rTMS (<1 Hz) inhibits the excitation of the targeted area, while a high-frequency rTMS (>5 Hz) increase the excitation [14]. These techniques modify the neural networks of the inter- and intra-hemisphere to improve the interhemispheric inhibition. As a result, the motor-impaired patients are able to avoid local minimum motor commands and explore the landscape of cost function to find a global minimum solution (Figure 1(c)).

Bimanual training is also suggested to be effective for motor restoration [15]. In contrast to CI therapy, patients with stroke are asked to move both affected and unaffected limbs. Previous study [16] investigated the effect of bimanual arm training on the patients who had upper extremity spastic hemiparesis following a single cortical or subcortical ischemic stroke. In this way, activation of the unaffected hemisphere increased, and it may unmask the uncrossed corticospinal projections to the affected limb. This uncrossed corticospinal projections are the latent neural subsystems, which are not used in the normal state. Fady et al. also showed that the muscle activities of the affected limb became similar to those of healthy individuals when the patients with cortical and subcortical stroke used the unaffected limb to support the affected limb [17]. The advantage of bimanual training to CI therapy is that bimanual training is applicable to patients with more severe movement disorders. The bimanual training aims to improve the abnormal interhemispheric inhibition and to prompt the usage of latent neural sub systems to allow the motor-impaired patient to use different motor strategies (Figure 1(c)).

As discussed in the previous section, humans have difficulties to move their limb after a brain damage (Figure 1(b)). Rehabilitation interventions help the motor-impaired patients to seek better solutions under the additional constraints imposed by the brain injury. CI therapy and facilitation techniques contribute to reshaping the cost function by limiting the limb movement or guiding the patient to perform limb movements appropriately. Modifying the neural network by tDCS and bimanual training encourages the patient to use the latent neural network, which is not typically used in the normal state, and to explore different motion commands. Therefore, the rehabilitation intervention could be interpreted as reshaping the cost function to prompt the utilization of latent neural networks and encourage the patient to seek new motor commands. In the next section, we showed how reorganization occurs in neural networks and how motor control rules are reconstituted.

2.3. Changes in neural network and motor control rules while motor recovery

As mentioned in the previous section, rehabilitation therapies help motor-impaired patients of motor impairments to regain motor functions. In this section, we reviewed the different changes occurring in the brain that are induced by rehabilitation and how humans improve motor performance. The human brain has the plasticity to reorganize neural networks even after a brain injury. Nudo et al. showed that reorganization of hand representation in M1 occurs after rehabilitative training [3]. While recovering, the squirrel monkey showed improvements in their ability to retrieve more food from the well placed in front of them. This plastic change occurs not only at the damaged brain area but also at the adjacent and even remote areas. In patients with stroke at the M1, the finger motor representation in M1 is evoked in the adjacent dorsal area of the lesion [18]. The other previous study used NIRS to examine the brain activity during gait rehabilitation of patients with stroke at the cerebral cortex [19]. During the gait rehabilitation of patients with stroke, the activation of premotor cortice is enhanced in the affected hemisphere. These findings imply that different brain areas are activated largely in patients with stroke than in healthy individuals due to the reorganization of neural structure to compensate for the motor deficit.

Moreover, patients who recovered from stroke utilized motor pathways different from those of those healthy individuals to achieve movement [20]. A previous study investigated the patients who recovered their motor ability after experiencing ischemic infarct of the internal capsule. When the brain activity assessed using PET, the blood flow in the motor-related areas, such as the premotor cortex and the primary sensorimotor cortex, of the patients' unaffected side of the brain was increased compared with that of healthy individuals. This finding implies that patients with stroke exhibit cerebral cortex reorganization to utilize the uncrossed corticospinal tract from the unaffected hemisphere to re-generate motor commands.

As the patients with stroke receive rehabilitation, they improve motor performance utilizing the residual motor function. For example, although the cerebral cortex is damaged, humans could still use the subcortical systems to achieve the movement. The muscle activity involved in an animal locomotion could be decomposed into small sets of primitives called muscle synergy [21]. Muscle synergies can be preserved in the cortical stroke patients between the affected and unaffected limbs to perform a variety of tasks and movements [22,23]. Fewer numbers of muscle synergies in locomotion are also reported in post-stroke patients with hemiparesis secondary to a single unilateral stroke than in healthy individuals [24]. Changes in the activation timing of muscle synergies observed during the sit-to-stand motion in stroke patients occurs in the cerebral cortex [25]. These studies imply that animals could utilize the existing low dimensional subspace of motor commands such as muscle synergies to accomplish motor tasks despite brain damage.

When environmental and body dynamics are provided, the normal adaptation process enables humans to learn and choose motor commands under the given cost function (Figure 1(a)). However, when the brain is damaged (e.g. large-scale and irreversible changes), the motor commands that humans used in the normal condition requires more cost due to the inhibition of brain activity and changes in muscle property, such as muscle spasticity. To regain the motor function after these irreversible changes, normal adaptation may not enough because humans may insist on using the high-cost motor commands, which is the local minimum solution under the impaired cost function (Figure 1(b)). In order to obtain better motor commands, the hyper-adaptation process reshapes the cost function by modifying the neural network. In such a way, the patients can utilize the preserved low-dimensional subspace of body dynamics and explore different motion strategies (Figure 1(c)). In this context, rehabilitation intervention is considered to reorganize the brain network including employment of the latent subsystem by guiding the patients to utilize preserved low-dimensional subspace (e.g. muscle synergies). In the next chapter, we will introduced the framework of the motor control theories to possibly explain the process of hyper-adaptability.

3. Motor control theories for hyper-adaptability

In this section, we provided an overview of the control schemes, and discussed the potential control framework suitable to explain the hyper-adaptability. We introduced the concept of weak and strong anticipation, and explained how these control schemes based on these two concepts can explain the process of motor control and neurorehabilitation, and discussed the potential control framework suitable to study hyper-adaptability as introduced in the previous sections. In summary, to determine the suitable pathways to understand the control mechanisms underlying the hyper-adaptability, we discussed two types of theoretical frameworks, strong and weak anticipation; if a model of the target/environment dynamics is provided for the prediction of the future, it is said to be weak anticipation; if it is not given, but the prediction arises from systematic lawfulness based on the real-time coupling between environmental dynamics, body dynamics and internal dynamics, it is said to be strong anticipation [26].

3.1. Types of motor control theories: weak and strong anticipation

A surprising aspect of neuroscience and neurorehabilitation is that motor control is one of the most complex and difficult tasks that the human brain is responsible for. The sheer number of factors, for example, high degrees of freedom of body parts, that must be managed to execute even the simplest physical task stands in sharp contrast to the unconscious ease with which we perform complex tasks. The confusion has only grown as engineering-based robotics techniques have been found singularly lacking in the face of the unavoidable sensory delays, persistent noise, and imprecise sensing ubiquitous to biological systems. Therefore, discussing the topic of motor control in organisms requires a relaxation of constraints and biases imported from control theory and engineering.

To overcome the inevitable time-delay in the sensory-motor systems, which would otherwise make simple tasks impossible, we need to predict or anticipate the next moment of environmental dynamics as well as body dynamics. Anticipation allows an individual to obtain information about the environment because errors between the anticipated and actual feedback from the body can be used to measure and improve the motor controller, or can be a simple source of instability. Furthermore, functions to induce anticipation are strongly related to the ability to adapt to the new environmental dynamics or impaired dynamics of body parts. In examining how organisms achieve this, Stepp and Turvey made a distinction between control methods based on ‘weak’ and ‘strong’ anticipation [26] (Table 1).

Table 1. Summary of weak and strong anticipation.

	Weak anticipation	Strong anticipation
Basic mechanism	Prediction of motor outcomes with internal models to estimate the body state for generation of motor commands	Synchronization of internal dynamics with body and environmental dynamics to reinforce motor commands
Normal adaptation	Updating of internal models to produce appropriate motor commands	No need to tune the parameters
Hyper adaptation	May not to be applicable	Reshaping of RNNs to find the global minimum
Examples	Optimal feedback control, MOSAIC	Anticipating synchronization, outfielder problems

Weak anticipation methods use a mathematical model of the system under control to explicitly calculate its future state. This allows appropriate control signals to be formulated in down streams based on this future state, rather than waiting for delayed feedback from the body. Weak anticipation methods include feedforward and feedback models such as Smith predictors, MOSAIC [27], and optimal feedback control (OFC) models [28]. From the control engineering point of view, the feedback delay between brain and body is a source of instability, and the feedforward (internal) model plays a role of stabilizing the feedback loops.

All of the weak anticipation-based control frameworks need to construct an explicit model of the body dynamics as an internal model to simulate the outcomes of motor commands. Characteristically, a weakly anticipating predictor's performance is maximized where the system under control and its environment are fully understood, and drops when this characterization is uncertain or incorrect.

As an example of weak anticipation, the MOSAIC [27] model is an extended version of OFC and suggests that the brain encodes many contextual models that represent different physical tasks. By observing sensory cues, a MOSAIC-based system can select a forward and inverse model suited to the current environmental context or begin the process of learning a new one if none matches. The functional hypothesis of MOSAIC is that these models can collectively approximate a prediction for any given scenario, although the number and diversity of models that would be required are still under debate. Nonetheless, all weak anticipation methods must contend with the difficulty of constructing a forward model not only for the (highly complex) human body, but also for every possible interaction between the body and the environment.

By contrast, strong anticipation does not posit the existence of a predictive model, but that anticipation arises out of the real-time coupling of the organism (or artificial system) with its environment [26]. The controller or internal dynamics does not act as a predictor in isolation for changing environment or target dynamics, but only in concert with the sensors and actuators of the body. Thus, the brain-body system as a whole anticipates the future states of environmental or target dynamics. In contrast to the weak anticipation, there is no single internal dynamics that represents the external dynamics. For example, the controllers developed by Alverez-Aguirre et al. [29] and Eberle et al. [30] do not model the feedback delay of the controlled system, but automatically adapt to the length of delay without parameter changes via the phenomenon of anticipating synchronization [31]. Anticipation for the future state of the target dynamics was made possible, without using the internal model of the target dynamics, by out of the resonance between the internal dynamics of the body and the actual body dynamics itself. This provides a new perspective for engineering-inspired models of human motor control, which traditionally take the sensors and actuators (muscles) as fixed priors that do not contribute to the ability to anticipate, and would indicate a dynamical system approach for neuroscience and neurorehabilitation. In later sections, we showed how a strong anticipation can be implemented in the control scheme to interact with the environmental dynamics, and how the strong anticipation via anticipating synchronization (one particular branch) allows us to have a simple oscillator model capable of predicting the environmental dynamics and body dynamics.

3.1.1. Optimal feedback controller: an example of weak anticipation

As an example of the weak anticipation framework, an attempt to explain the motor control comes in the form of optimal feedback control (OFC) (for example, see [28]). In principle, one desired state of body kinematics (e.g. desired velocity and position) is input to the controller of the OFC, and the controller also receives the input from the feedback loops, which encodes the discrepancy between the sensory feedback from the musculoskeletal systems (body) and the predicted state from the internal model of the body. In practice, the state estimator combines the incoming afferent sensory feedback and an outcome prediction of outgoing motor commands through an internal forward model to construct an optimal estimate of the body's current state by tuning the feedback gain in the controller.

In the OFC, a motor variance is hypothesized to be a result of a ‘minimum intervention’ principle, where the feedback controller only corrects the feedback gain parameters for task-relevant deviations. Motor planning of feedback gain should proceed, depending on task goals [32,33]. Once movement is initiated, motor commands are generated by an OFC with the estimated state and planned feedback gain.

The motor planning itself is context dependent; Cluff and Scott showed that the motor system can produce a spectrum of corrective responses that depend on the behavioral goal of the motor task [33]. This also indicates that the internal model is needed to simulate the environmental and body dynamics to determine the motor planning prior to the motor execution. Once a motor plan has been specified, motor commands are generated by an OFC that uses a state estimator to combine sensory feedback and forward sensory prediction (based on an efference copy of the motor command) in order to correct motor errors. In summary, in terms of a whole control scheme, ‘weak anticipation’ model of the OFC includes (a) perception (b) simulation (c) motor planning and (d) optimal functions.

3.1.2. Anticipating synchronization-based control scheme: an example of strong anticipation

The optimal feedback model can stabilize the control to achieve a goal, overcoming the time delay in the sensory-motor system by the internal model of the body. However, this stable control is achieved by the precise representation of body dynamics within the internal model to simulate the body dynamics. Thus, if the body dynamics is altered due to the brain damage, it goes beyond the functions of the OFC to exhibit the adaptation for a new body dynamics. In addition, when the target has a certain dynamics, and humans are engaged to trace a target, the future state of the target cannot be predicted, requiring another internal model that represents and simulates the target dynamics.

Thus, here still remains the questions; (1) how humans can smoothly follow the target dynamics, predicting the future state of its dynamics, and (2) the robustness of the internal model of the body when it is damaged. We considered that the framework of strong anticipation, i.e. dynamical real-time coupling of internal dynamics with the target/body dynamics, can shed a light into the questions above.

Although the potential implementations of strong anticipation are very diverse one, in particular, the strong anticipation is applicable to the problem of human motor control: anticipating synchronization. Let us think of the situation in which an agent (follower) is anticipating the environmental dynamics (leader). In the original AS framework, ‘leader’ system is showing the autonomous dynamics as a function of time. The ‘follower’ system has the identical autonomous dynamics and is the coupling term that tries to minimize the difference to the state of the leader system. This AS Framework can be considered as a variation in the synchronization between dynamical systems where the ‘follower’ system synchronizes with the future of the ‘leader’ system instead of its present state [31]. Synchronization of the follower with the future state of the leader is not a violation of causality but relies on the fact that a deterministic dynamical system's current state is strongly determined by its past. Intuitively, the leader and follower systems have the same autonomous dynamics, and are running autonomously as a function of time; in the follower system, the coupling term to minimize the difference to the state of the leader, the self-feedback delay of the follower (‘memory’ of the follower's past state) plays a role in ‘pushing’ the autonomous dynamics of the follower to synchronize with the future state of the leader.

From here, we focused on the detailed formulation of the AS-based strong anticipation. Mathematically speaking, let us describe the leader system as $x\left(t\right)$, and the follower system as $y\left(t\right)$. Both systems share the same autonomous dynamics of $f\left(x\right)$ as shown in Equations (1(1) $\begin{array}{rl}\dot{x}\left(t\right)& =f\left(x\right(t\left)\right)\end{array}$(1) ) and (2(2) $\begin{array}{rl}\dot{y}\left(t\right)& =f\left(y\right(t\left)\right)+K\left[x\right(t)-y(t-\tau \left)\right]\end{array}$(2) ). It was shown that anticipation could be induced in the follower systems by adding a time-delayed coupling $K[x-y(t-\tau \left)\right]$ (Equation 2(2) $\begin{array}{rl}\dot{y}\left(t\right)& =f\left(y\right(t\left)\right)+K\left[x\right(t)-y(t-\tau \left)\right]\end{array}$(2) ) in which K is a coupling parameter and τ denotes the degree of self-feedback delay. (1) $\begin{array}{rl}\dot{x}\left(t\right)& =f\left(x\right(t\left)\right)\end{array}$(1) (2) $\begin{array}{rl}\dot{y}\left(t\right)& =f\left(y\right(t\left)\right)+K\left[x\right(t)-y(t-\tau \left)\right]\end{array}$(2) The coupling accelerates the time evolution of the follower until it ‘catches up’ with the leader; as shown by Hayashi et al. [34], the coupling term with the time delay is related to the renormalization of the follower's time step to be longer, leading to the faster evolution of the follower dynamics. As a result, the follower system can synchronize with the future state of the leader system, $y\left(t\right)=x(t+\tau )$, steadily within a certain range of K and τ. Anticipating synchronization was first demonstrated in identical leader/follower autonomous dynamics, but it was subsequently established that this is a sufficient, but not necessary condition for stable anticipation [35,36]. Mathematically speaking, internal models of the body or target are not necessary, as shown in Equation (2(2) $\begin{array}{rl}\dot{y}\left(t\right)& =f\left(y\right(t\left)\right)+K\left[x\right(t)-y(t-\tau \left)\right]\end{array}$(2) ) in which $f\left(x\right)$ does not have to be the exact match of $f\left(x\right)$ in Equation (1(1) $\begin{array}{rl}\dot{x}\left(t\right)& =f\left(x\right(t\left)\right)\end{array}$(1) ), i.e. autonomous dynamics of the leader and the follower does not have to be exactly the same. If the autonomous dynamics of the follower is sufficiently similar to that of the leader, the follower can anticipate the future state of the leader. Thus, as long as the follower's behavior is sufficiently similar to that of the leader there will be some region in which the anticipating manifold $y\left(t\right)=x(t+\tau )$ is stable and can be used to predict the leader [35,37].

Oguchi and Nijmeijer used an AS follower system to act as a nonlinear predictor in a delayed-feedback control problem, although this required an explicit internal model of the feedback delay [29,38]. However, this still falls short of the potential of anticipating synchronization to deliver robust anticipation without reliance on computational modeling of the external dynamics.

To develop a human model that can trance the chaotic target, Eberle et al. developed a framework for a novel ‘parallel’ controller (Figure 2), extending the AS paradigm where the predictive capacity is linked directly to feedback delay [30]. From the motor control perspective, as shown in Figure 2, the target signals, $x\left(t\right)$, are directed toward the parallel system, one signal goes to the proportional control in which the delayed feedback from the body (plant) is subtracted and multiplied by the gain parameter, k. Therefore, the end-effector, $y\left(t\right)$, is designed to trace the target dynamics with the sensory-motor delay. Meanwhile, the same target signal, $x\left(t\right)$, goes into the internal dynamics, and another feedback loop is implemented to generate errors as input signals to the internal dynamics. Having those two parallel control units with the feedback loops driven by the target dynamics, original motor commands from the minimum feedback model are reinforced by the motor commands from the internal dynamics.

Figure 2. Block diagram of the ‘parallel’ system: internal dynamics $g(\cdot )$ condition the behavior of the body $h(\cdot )$ such that it can be coupled with the target $f(\cdot )$ and predict its output such that $x(t+\tau )=y\left(t\right)$. Green elements represent intrinsic elements of the body and target, while yellow elements are added to enable anticipation.

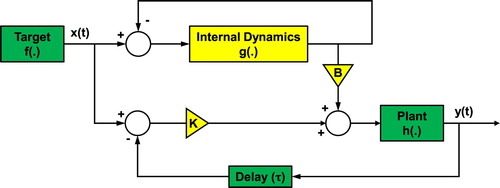
Here, the internal dynamics is not used to predict the body motion, but to change the dynamical behavior of the real body such that it can become the target's follower and predict the future state of the target. Crucially, the parallel system could predict a chaotically moving external target despite the absence of a target model. Unlike previous implementations within the optimal feedback control framework, the internal dynamics does not output a prediction of the plant state, and there is no need to adjust the gain parameters in the controller. The body's response is a result of the resonance between the two parallel feedback loops (Figure 3). This synchronization-based adaptation occurs rapidly, meaning that the framework of the AS based control scheme is highly adaptive by nature to the changing environment and changes of the body dynamics.

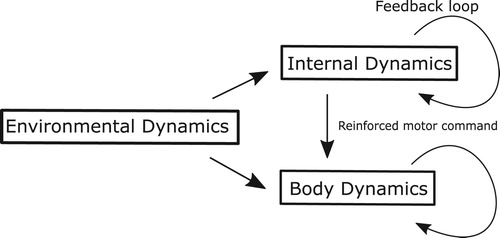
Figure 3. Schematic illustration of the parallel model based on anticipating synchronization. Environmental dynamics drives both internal dynamics and body dynamics. Internal dynamics with the feedback loops will reinforce the original motor commands. Note that the internal dynamics is not internal models of environmental or body dynamics, just a band of oscillators. We discussed the possibility of using recurrent neural networks (RNNs) as internal dynamics.

A further extension of the framework was demonstrated [39], where the internal dynamics was represented by a bank of simple oscillators while maintaining the predictive behavior for the environmental dynamics. Surprisingly, as the nature of strong anticipation, neither an exact model of the target nor the body is required for the robotic hand to trace the chaotic motion of the target, i.e. anticipation for the target dynamics. In other words, the bank of oscillators as an internal dynamics could represent the plant and target dynamics in the parallel configuration and reinforce the motor commands to control the body coordination, compensating the time delay in the sensory-motor system and predicting the future state of target dynamics.

To summarize the mathematical formulation of the AS-based anticipating synchronization, let us give a comprehensive discussion below. In the control framework based on the AS, for the target motion representing the environmental dynamics, the harmonic oscillators could induce the resonance of the body dynamics so that the body coordination status can be used to predict the future state of the target dynamics (Figure 3). Again, the bank of harmonic oscillators in isolation is not the model of the body or target dynamics. Thus, the ability to trace the chaotic target in synchronization naturally emerged from the systematic lawfulness of the configuration as shown in Figure 3.

The ability to encode the internal dynamics in the form of oscillatory dynamics is of interest given that such systems are ubiquitous in biological organisms. Similar properties are exhibited by certain recurrent neural networks (RNNs) that seek to represent the dynamical properties of the human brains. Thus, these networks might represent an ideal platform for control based on strong anticipation for more complex dynamics, because a bank of non-linear oscillators can be a rich source of the non-linear dynamics spanning a variety of landscape of cost functions.

3.2. Control theories for normal adaptation

So far, control frameworks based on weak and strong anticipation were introduced to mainly explain how they work in terms of control. Here, we extend our approach of two theoretical frameworks to discuss the adaptation process in motor learning where participants are asked to learn a new environmental or body dynamics.

For example, let us think of the reaching task as shown in Figure 1 under the unknown force field, and how humans can learn or adapt to this new environmental dynamics of the force field. In the OFC, while reaching the target, the force field induces the discrepancy between the predicted state of body parts and the actual state of these parts (sensory-prediction errors). Initially, the gain parameters in the feedback controller will be tuned, an internal model of the force field will be generated, and the motor commands will be generated to compensate for the sensory-prediction errors. On the other hand, the AS-based strong anticipation was initially validated in manual tracking of non-chaotic targets, with and without programmed feedback delays in the visual-motor systems [40]. Participants were asked to track a chaotically moving target presented on a computer monitor by means of controlling a similar on-screen object. The task success of adapting to the introduced time delay in the visual feedback required anticipation on the part of the participant. Stepp showed that (a) participants are able to synchronize with a chaotic target, even with some amount of applied delay; (b) the degree of anticipation to the target dynamics varies systematically with applied time delay, and (c) this systematic dependence of anticipation is the primary feature of systems exhibiting anticipating synchronization. Validation of the AS-based strong anticipation in various experimental paradigms should be explored further to explain the motor adaptation of humans in the future.

3.3. Control theories for hyper-adaptability

In this section, let us focus on the adaptation mechanism when the neural networks in the brain are damaged. In the case of OFC, depending on the damaged area, perception, simulation of body dynamics, motor planning, and optimal functions will be affected; therefore, the efference copy and predicted state of the body coordination will also be affected [41]. However, the OFC itself does not have the explicit functions to recover those damages or may not be developed to have functions in order to resolve the damage to the neural networks.

On the other hand, AS-based strong anticipation has been shown to work even in cases where the body dynamics is not modeled. Therefore, the function could be restored after damage to the internal dynamics by much simpler adaptations to the closed loops of feedback between the body and the brain. Since a simple follower system can anticipate a complex leader, the remaining functional neurons representing the internal dynamics could be repurposed to resume anticipating the body's dynamics, utilizing the ability of self-organization. The AS coupling without invoking the need for a ‘diagnostic function’ can selectively repair the original internal dynamics.

This autonomous ability of the strong anticipation may be compatible with the usage of recurrent neural networks, RNNs (please see the following sections) as more adaptive internal dynamics. Using the harmonic oscillators, we showed that the internal dynamics can be resonanced with the target and body dynamics to anticipate the future state of the target dynamics. If the simple harmonic oscillators are replaced with the RNNs, the internal dynamics will be enriched as a reservoir of the nonlinear dynamics and the ability to repair itself, when damaged, will be more enhanced as the closed loops within the networks will have a higher function to induce resonanced states with the body and environmental dynamics (Figure 3).

From the perspective of the reshaping neural networks for hyper-adaptation, when the brain reorganizes neural networks by disinhibiting the pre-existing neural network that is normally suppressed (Figure 1), an internal dynamics based on RNNs can rapidly change its dynamical behavior to explore the landscape of cost functions (please see the following sections for details). When RNNs are embedded within an AS-based internal model, the systematic lawfulness of the control configuration (Figure 3) would allow the RNNs to find the global minimum of the cost functions. That is, physical intervention to the body dynamics can stimulate the feedback loops between the brain and the body to induce the reshaping of the RNNs for the global minimum of the cost functions as shown in Figure 1. In this section of motor control theories for hyper-adaptability, we provided an overview of the two main frameworks, namely, weak and strong anticipation, discussing the basic mechanisms of how they function and consequence for motor adaptation. Although the discussion on weather the parallel model should be used to implement the RNN as an internal dynamics needs to be clarified, the RNN would have a higher affinity with the idea of strong anticipation since it states that organisms like human beings anticipate events by continuously coupling their own (cognitive or somatic) processes to the dynamics of the environment. To induce the motor coordination for a given purpose, quite a few control frameworks would be able to achieve a goal; however, the mechanisms themselves can be different. Thus, as in the following sections, the physiological experiments conducted to measure the activity of neurons will play an important role to validate the extracted dynamics against the motor coordination and to discuss further the control framework used in the motor coordination of humans.

4. Neural network modeling of hyper-adaption

In the previous sections, we reviewed the examples of hyper-adaptability in humans after stroke or traumatic brain injuries and discussed the applicability of control theories (weak and strong anticipation) in understanding the mechanisms of hyper-adaptability. These behavioral and theoretical considerations highlighted the ‘reconstruction’ of neural structures, which is essential for hyper-adaptation and differentiate it from normal adaptation. To understand the circuit mechanism of hyper-adaptability, it is necessary to establish neural network models that can recapitulate the behavioral change during hyper-adaptation. In addition, such neural network modeling also provides useful insights into physiological observations during hyper-adaptation. In the previous section, we attempted to apply the recurrent neural networks to replace a control process (i.e. internal dynamics). Here, we more generally discuss how recent advances of neural network modeling can be used to understand the circuit mechanisms of hyper-adaptability.

4.1. Neural network modeling of sensory-motor systems

Neural network modeling has emerged as a powerful tool to emulate the neural functions and to infer their circuit mechanisms, such as sensory processing [42], decision making [43], and motor control [44–46]. One of the biggest successes is the application of feedforward neural networks (i.e. networks that only have feedforward connections) to recapitulate a neural processing of ventral stream in the visual system [42]. Such a feedforward network was successfully trained to identify objects in a large dataset of images (ImageNet). An advantage of neural network modeling is that once the network is sufficiently trained, researchers can ‘look inside’ the network, including synaptic connections and network structures, to get insights for critical structure, which achieves the desired functions. For example, the trained network of the ventral stream demonstrated that the neural responses of layers in the network were surprisingly similar to those recorded from the visual system, indicating the hierarchical and serial processing in the ventral stream.

However, in contrast to a huge success of the feedforward networks in modeling of the sensory system, their application to the motor system has not been successful. One of the potential reasons is that the motor control is fundamentally based on the interaction between top-down motor commands and feedback information. The ultimate goal of motor system is not to ‘represent’ some behavioral parameters, but to ‘generate’ a temporal, i.e. dynamic, pattern of motor outputs, such as muscle activation patterns [47]. Unlike a feedforward network, an RNN contains recursive connections that allow the past states of neurons to influence their current state, and it can generate a temporal pattern of motor outputs. In the RNN, the activity of the network ($\mathit{r}$) can be viewed as a differential equation of the input ($\mathit{u}$) and the own network activity: (3) $\dot{\mathit{r}}\left(t\right)=\mathit{J}\mathit{r}\left(t\right)+\mathit{u}\left(t\right)$(3) where $\mathit{J}$ represents the system dynamics that defines how the network activity develops over time.

4.2. RNN modeling of motor control, preparation and learning

Recent development of neural recording techniques from a large-scale neural structure allows us to find a neural state which represents patterns of population neural activity rather than the individual neurons. For example, when monkeys make a reaching to spatial target, each neuron in the motor areas shows a wide variety of patterns of activity, which does not seem to consistently represent any specific motor parameters, such as muscle activity or hand position [48]. However, when a dimensional reduction technique (e.g. PCA and jPCA) is applied to high-dimensional neural activity, the population activity can be successfully expressed as a combination of smaller sets of population activity that can be expressed as a low-dimensional subspace of neural activity [49]. This finding indicates that a population of motor cortex neurons are not independently activated but regulated to reflect the body and behavioral constraints. Interestingly, when an RNN was trained to reproduce muscle activity that was experimentally recorded from monkeys during reaching, similar low-dimensional subspaces of neural activity spontaneously appeared in the RNN although it was not explicitly required [46]. This result suggested that in a normal state, the network connections in the motor cortex can be optimized to perform motor tasks, and the network dynamics of the motor cortex is confined to a low-dimensional subspace (Figure 4(a), a yellow plane). Similar results were found when the RNN was trained to reproduce the arm velocity during reaching rather than the muscle activity [50].

Figure 4. Schematic illustration of the network modeling of normal state and hyper-adaptability.

What is the functional implication of the low-dimensional subspace of the network dynamics of motor cortex? Recent studies have suggested that there are at least two advantages of the low-dimensional dynamics in the motor system: separation of multiple processes and facilitation of motor learning. Firstly, it can separate the neural processes for motor execution from those that should not affect motor outputs directly, such as motor preparation. For example, motor preparation facilitates the performance (speed and accuracy) of the forthcoming motor behaviors, but the neural activity involved in the motor preparation should not evoke motor outputs before the start signal arrives. Therefore, the process for motor execution and preparation should be separated although both are processed in the same motor cortical neurons. Kaufman et al. (2014) demonstrated that the preparatory activity in the motor cortex spanned a neural subspace that is orthogonal to a subspace for motor output [51]. This finding suggests that motor preparation can be made without affecting the motor outputs. This separation of output null (motor preparation) and output-potent (motor execution) dimensions allows the network to perform multiple processes simultaneously and independently. The RNN modeling of motor preparation and execution activity replicates these subspaces that are located orthogonally. More interestingly, the neural states in the preparatory and execution subspaces were not randomly related, but they were tightly related to each other [44]. This modeling results suggested that the low-dimensional dynamics of the motor cortex can create several subspaces separately for the multiple neural functions and ‘gate’ them from one space to the other (e.g. from motor preparation to motor execution).

Another advantage of the existence of low-dimensional dynamics in the motor system is that it can facilitate motor learning and adaptation. Accumulating evidence showed that the low-dimensional subspace of motor cortex dynamics was consistent across multiple behaviors [52], over a long period of time [53,54], and during motor learning [54]. Using a brain-computer interface (BCI) technique in monkeys, Sadtler et al. examined how quickly monkeys can adapt to novel BCI mappings (i.e. mappings between neural activity and cursor movements), which are designed to be within or outside of the original subspace of the motor cortex dynamics [55]. Their results showed that monkeys could readily learn to control the cursor when the change was within the original subspace, whereas they were less able to learn the new mapping if it was outside of the original subspace. To understand the circuit mechanisms that cause the difference in the motor learning ability, Feulner and Clopath (2020) trained RNNs and compared their adaptability to change of the BCI mapping within and outside of the original subspace [45]. Their results showed that RNN can predict error feedback signal more correctly when the change was within the original subspace than when it was outside of the original subspace and resulted in the better learning performance, suggesting that the low-dimensional subspace provided a constraint to correctly estimate the error feedback for motor learning. These results give functional implications for the existence of the low-dimensional subspaces of the motor cortex.

4.3. Perspectives for RNN modeling of hyper-adaptability

In the previous section, we reviewed the recent advances regarding the neural dynamics of the motor system and applications of RNN modeling to determine the underlying network mechanisms. Here, we further discuss how to employ these approaches to investigate the neural mechanisms of hyper-adaptability.

Figure 4 shows a schematic illustration to explain possible scenarios about how the network changes during hyper-adaptability. First, in a normal situation, the network dynamics is optimized to body and behavioral constraints and confined to a low-dimensional subspace (Figure 4(a)). During normal adaptation (e.g. force field adaptation), network weights are changed but the low-dimensional subspace is preserved [54]. Then, if the network is damaged by stroke or traumatic brain injuries, a part of the network can be lost, and this prevents the neural state from fully exploring the original subspace and causes motor impairments (Figure 4(b)). To recover from the impairments, the network needs to explore a large range of networks, including latent networks, which were less active in a normal state ($r4$ in Figure 4(c)). After that, the network also needs to re-optimize its dynamics to obtain the new control subspace to recover motor function. Note that, in the recovered state, the optimized subspace is not necessarily the same as that of the original activity pattern (e.g. the activity of neurons $r2$ and $r3$ are different from the normal state), but their activity could be re-optimized for the new network structure including recruited the latent networks (e.g. $r4$). In this scenario, in order to identify the mechanism that causes the hyper-adaptability, it is important to determine the factor that regulates or facilitates the re-optimization of neural dynamics from the normal state to the recovered state.

Previous studies have demonstrated some common principles that explain the changes in the neural dynamics in the recovered state (Figure 4(d)). First, functional recovery can be constrained by subspaces of lower motor systems, such as the brainstem and spinal cord (Figure 4(d) top). For example, muscle synergies, which are believed to be predominantly implemented in the subcortical systems [56–59], can be preserved after a cortical stroke [22,23]. This result suggests that the network dynamics of a lower system might constrain a control space where the higher system needs to explore to re-optimize the network dynamics during hyper-adaptation. This constraint might help the motor system to achieve faster and robust learning similar to the BCI motor learning within the original subspace [45,55].

Second, hyper-adaptation sometimes caused disinhibition to employ latent networks that are less active in a normal state (Figure 4(d) bottom). After stroke or spinal cord injuries, indirect corticomotoneuronal pathways such as propriospinal and cortico-rubral pathways are recruited to achieve functional recovery [60–62]. In addition, ipsilateral motor areas, which are usually less activated during unilateral limb movements, are activated to increase the interhemispheric interaction after spinal cord injuries [63,64]. Interestingly, these latent neural circuits are mostly phylogenetically and developmentally older systems, but they are preserved in developed nervous systems. These observations are consistent with basic principles proposed by Gerald Edelman that development and plasticity of the central neural system occurs in a bottom-up manner through a natural selection of neuronal groups rather than in a top-down manner [65]. From a neural network perspective, the hyper-adaptation can be viewed as a bottom-up process to reproduce a neural development with (1) the extensive exploration of the nervous system and (2) selection or reoptimization of the neural dynamics to achieve behavioral goals.

It is of interest how the latent, normally suppressed, circuits are recruited and the entire dynamics is reoptimized. The neural interactions can be investigated by combining a large-scale neural recordings and statistical techniques to infer the causal interactions, such as Granger causality, or dynamical causal modeling. However, all of these methods are based on the correlational estimates of neural interactions, and they cannot accurately deal with the problem of confounders like common input or recurrent connectivity [66]. Perich and Rajan recently proposed a novel approach to describe the interactions of neural networks using data-driven RNN modeling [67]. This technique trains RNN models to match not only the final outputs with target outputs, but also the network activity with ‘teacher’ activity, which is experimentally recorded. Using this approach, they successfully recapitulate the changes in the neural dynamics of the whole brain recordings from larval zebrafish and identify a putative interaction between habenula and the raphe nucleus during adaptation to inescapable stress [68]. Critically, these neural network modeling approaches provide useful insights into the mechanistic change during the hyper-adaptation because these data-driven RNN can explicitly model the latent network, which is suppressed during normal states and is difficult to model with conventional RNN training algorithms.

5. Future direction to understand the neural mechanisms for hyper-adaptability

Hyper-adaptability is the ability of the human to bridge the gap that occurs in the brain-body system by reconstruction of their neural structure and reconstitution of motor principle. Although humans have the capability to learn new motor skills under the given environments and musculoskeletal systems utilizing the existing neural networks, hyper-adaptability becomes important to relearn motor functions after the brain is severely damaged. In this survey paper, we reviewed how the human brain changes after injury and how the rehabilitation methodology induces motor recovery. When the neural networks are injured due to brain damage, humans are unable to utilize conventional neural networks. In the context of hyper-adaptability, rehabilitation intervention is considered to modify the neural networks and to encourage the use of latent neural circuits, which humans do not use in the normal state.

To prompt hyper-adaptation, the motor-impaired patients could explore different motor strategies in the latent neural networks by utilizing the low-dimensional subspace of the musculoskeletal systems (e.g. muscle synergy). As previous studies suggested, motor-impaired patients after brain injury could utilize muscle synergies preserved in the spinal cord [23–25], and the activation of muscle synergies improve by rehabilitation [12]. Identifying the existing muscle synergy structure and utilizing them in rehabilitation would be beneficial for restoring the motor function of the patients with motor impairment. Furthermore, it is worthwhile to examine the effects of a combination of different intervention methods, such as CI therapy, disinhibition, and facilitation. To fully utilize these rehabilitation methods, it is necessary to understand how neural network models change through rehabilitation after a brain injury.

One promising approach is the application of neural network models to recapitulate the process of functional recovery after motor dysfunctions. This approach can be divided into two steps: (1) building network models to reproduce intact behavior (forward engineering) and (2) ‘breaking’ the model to analyze the internal structure and emulate the motor impairments and recovery processes (reverse engineering). Michaels et al. (2020) showed that the inhibition of a part of hierarchical RNNs showed unique patterns of motor deficits similar to those observed in animal experiments [69]. Other studies also demonstrated that deactivation of brain areas could be emulated by the deactivation of motor control models, such as the optimal feedback control model [70,71]. The network model approaches (such as hierarchical RNNs and other variants) will be more critical to bridge the gap between the theoretical predictions and physiological observations.

Another feasible application of neural network models is to understand the development and evolution of the central nervous system. To understand the reorganization of neural systems for a large-scale change in the nervous system (i.e. hyper-adaptability), it is important to consider how the latent neural structures are recruited and reoptimized to adapt to the change of the nervous system and body. How these latent neural structures are selected and preserved during development and across species is a fundamental question in neuroscience [65,72]. Training and testing network models could provide a mechanistic explanation of the development and preservation of latent structures and recruitment while recovering from the nervous system impairment.

One limitation of network modeling is that training algorithms are not biologically plausible. Trained RNNs can recapitulate the animal behaviors and neural dynamics, but most of the previous studies used biologically less feasible algorithms, such as backpropagation through time [73], transfer learning [74], and data-driven RNN modeling [67]. This prevented us from considering the time-course of the learning process with regard to the adaptation of animals. Recently, biologically more plausible algorithms have been proposed, such as Hebbian learning [75]. These algorithms might provide useful insights into the time-course of development and adaptation, including hyper-adaptability. Further development and investigation are warranted.

In terms of neurorehabilitation, the process of regaining motor control in impaired parts of the body can be considered as reshaping the neural networks and reconstituting the control scheme in the brain. Although some parts of the neural networks are damaged, using the framework of the strong anticipation, we suggest that the nature of the nonlinear reservoir of RNN as an internal dynamics and low dimensional space based on synergy from the muscle allow the reshaping of the RNN for a rapid adaptation of the new body. The former is generated by the resonance of the RNN with the body dynamics based on the AS control framework, and the latter by the constraint of body kinematics and dynamics through sensory-motor feedback loops. It could be more important to identify the robustness or adaptability of each latent neural systems to unravel the neural mechanism of hyper-adaptation and leverage them for rehabilitation.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the JSPS KAKENHI [grant numbers JP19H05729, JP18H01405, JP19H03975 and JP19H05311].

Notes on contributors

Harry Eberle

Henry Eberle received a Meng in Artificial Intelligence and Cybernetics and a PhD in Cybernetics at the University of Reading in 2019. He is currently a postdoctoral researcher in the Aspire CREATe group at University College London, where he researches shared control for assistive navigation in crowds. His interests include human-machine cooperation, reservoir computing, and robustness in intelligent systems.

Yoshikatsu Hayashi

Yoshikatsu Hayashi has received a BSc in Cell biology from University of Tokyo, Japan and a PhD in Statistical physics of soft matter from Lund University, Sweden in 2004. Currently, he is an associate professor of biomedical engineering in the School of Biological Sciences, University of Reading. He is interested in physics of complex systems, behavioral science, and neuroscience.

Ryo Kurazume

Ryo Kurazume is a Professor at the Graduate School of Information Science and Electrical Engineering, Kyushu University. He received his MEng and PhD in Mechanical Engineering from Tokyo Institute of Technology in 1989 and 1998. He was a director of the Robotics Society of Japan (RSJ) from 2009 to 2011 and 2013 to 2015, and the Society of Instrument and Control Engineers (SICE) from 2013 to 2015, and a division head of the Japan Society of Mechanical Engineers (JSME) Robotics and Mechatronics Division in 2019. He is a director of the Japan Society of Mechanical Engineers (JSME) from 2021 to 2023. He received JSME Robotics and Mechatronics Academic Achievement Award in 2012, RSJ Fellow in 2016, SICE System Integration Division Academic Achievement Award in 2017, JSME Fellow in 2018, and SICE Fellow in 2019. His current research interests include legged robot control, computer vision, multiple mobile robots, service robots, care technology, and biometrics.

Tomohiko Takei

Tomohiko Takei received BS degree in integrated human studies, and MS and PhD degrees in human and environmental studies from Kyoto University in 2002, 2004 and 2008, respectively. Since 2018, he has been a program-specific associate professor in the Hakubi Center for Advanced Research/ Graduate School of Medicine, Kyoto University. His research interests include neural mechanisms for motor control and motor learning.

Qi An

Qi An received his BE, ME, and PhD degrees in Engineering from The University of Tokyo in 2009, 2011 and 2014, respectively. From 2012, he is a JSPS Research Fellowship for Young Scientists (DC1). From 2015 to 2020, he was Assistant Professor of The University of Tokyo. He is a visiting researcher in RIKEN from 2015. Currently, he is Associate Professor of Kyushu University from 2020. His research interests are rehabilitation robotics and human biomechanics.