Model predictive control of legged and humanoid robots: models and algorithms

ABSTRACT

Model predictive control (MPC) of legged and humanoid robotic systems has been an active research topic in the past decade. While MPC for robotic systems has a long history, its paradigm such as problem formulations and algorithms has changed along with the recent drastic progress in robot hardware, computational processors, and algorithms. This survey paper reviews recent progress on MPC for legged and humanoid robotics from the following three points of view. First, we review a variety of dynamical models of robotic systems used in the MPC formulation. Second, we give an overview of MPC algorithms, particularly focusing on suitable ones for robotic problems. Finally, we introduce methods and applications of MPC for practical robotic problems from MPC based on reduced-order models to recent progress on MPC based on whole-body models.

GRAPHICAL ABSTRACT

KEYWORDS:

• Legged robot
• humanoid robot
• motion planning
• model predictive control

1. Introduction

1.1. Growing utilization of MPC in legged and humanoid robotics

Legged and humanoid robots have seen considerable technological advances in the past two decades. Two major factors have contributed to the development of legged robot research: hardware and control technology. For quadruped robots, hardware platforms such as LittleDog [1], have facilitated research on rough terrain locomotion. Recently, more advanced robots, such as HyQ [2], ANYmal [3], MIT Cheetah [4], and Mini Cheetah [5], have been developed by different research institutes. For bipedal and humanoid robots, many significant research achievements using hardware platforms, such as the HRP series [6–8], TORO [9], Atlas [10], TALOS [11], E2-DR [12], and Cassie [13], have been reported in the literature.

Advanced control technology is crucial for drawing maximum performance from robotic hardware. However, the traditional methodology based on offline motion planning and linear control is incapable of sufficiently harnessing hardware performance and responding swiftly to a dynamically changing environment. Model predictive control (MPC), on the other hand, enables trajectory generation in nonlinear domain and full utilization of kinematic movable range and torque limits. Moreover, frequent replanning of motion reflecting the current state makes the robot more robust against disturbances. Therefore, the application of MPC to legged robotic systems has been a subject of active research in the past decade. Notably, 19 out of 28 workshop papers presented during the legged robotics workshop in ICRA2022 included the keywords ‘model predictive’ or ‘receding horizon’, of which 9 were directly focused on MPC [14].

Table 1 summarizes legged robotic systems reported in the literature that use MPC to realize certain functions. The columns of the table detail, from left to right, the year of publication, the dynamical model, the problem formulation and/or the solution method, the parameter setting, and the name of the robot. Cells containing information that could not be found in the original paper are left empty. The definitions of abbreviations are listed at the bottom of the table. In early research of legged robotics, MPC was been used for online walking pattern generation of bipedal and humanoid robots to improve responsiveness to disturbances and user commands. Although not all methods proposed during this period are referred to as MPC, we included them in the table as they are based on a similar concept. Following the DARPA Robotics Challenge held from 2013 to 2015, more studies that attempt to use MPC for whole-body control have been published. In recent years, the application of MPC to both biped and quadruped robots has seen a dramatic increase, where MPC is used for online trajectory generation as well as for whole-body control. In a broad sense, the term ‘online’ means that the planned trajectory is updated at a certain frequency inside of a feedback loop. The actual update frequency for MPC varies considerably across robotic systems and ranges from 10 Hz to 1 kHz, as shown in Table 1. In exceptional cases, the update is synchronized with walking steps [20,24,42].

1.2. Focus and organization of this survey

The objective of this survey paper is to provide an extensive review of recent progress in the theory, implementation, and application of model predictive control techniques to legged and humanoid robotics. Several well-written survey papers [49–52] and handbook articles [53–55] on motion planning and control of legged and humanoid robots exist in the literature. Among them, [54] surveyed MPC for adaptive walking pattern generation and [55] discussed multi-contact MPC with a predetermined contact sequence. However, as mentioned previously, the application of MPC to legged and humanoid robots has increased rapidly ever since the publication of these surveys, and several important theoretical and technical developments have not been addressed in the existing surveys. The original contribution of this paper is twofold. First, we reviewed numerical algorithms of MPC that are particularly efficient for robotic problems, which is often discussed in research on MPC robotic applications but has not been extensively reviewed yet in the aforementioned surveys. Second, we provide an extensive survey of the recent developments in MPC for legged and humanoid robots including the most recent topics such as contact-implicit and whole-body MPC. The target period for this survey is approximately two decades, from the early 2000s to the present. To ensure reliability, we have avoided citing papers that have appeared only on pre-print servers such as arXiv.

Table 1. Summary of legged robot systems that utilizes MPC.

Ref.	Year	Model	Prob./method	N	T	Rate	Platform
[15]	2002	LIPM	–${}^{\ast 1}$	–	–	–	H6
[16]	2003	LIPM	LQR	320	1.6	–	HRP-2P
[17]	2006	LIPM	LQR	160	1.6	25[Hz]	HRP-2
[18]	2011	LIPM	LQR	300	1.5	1[kHz]	HRP-3L-JSK
[19]	2013	WBD	iLQG	16	0.5	33[Hz]	Atlas${}^{\ast 2}$
[20]	2013	LIPM	DDP	–	–	per step	Atlas${}^{\ast 2}$
		WBD	QP	–${}^{\ast 3}$	–	1[kHz]
[21]	2014	LIPM	QP	5	2.5	–	Atlas${}^{\ast 2}$
		WBD	QP	–${}^{\ast 3}$		–
[22]	2014	WBD	QP	10	0.05	–	TORO${}^{\ast 2}$
[23]	2015	WBD	DDP	25	0.5	20[Hz]	HRP-2
[24]	2016	LIPM	DDP	–	–	per step	Atlas
		WBD	QP	–${}^{\ast 3}$		500[Hz]
[25]	2016	CD + WBK	SQP	–	–	offline	Atlas
		WBD	QP	–${}^{\ast 3}$	–	800[Hz]
[26]	2017	SRBD	NLP (fmincon)	$<4^{\ast 4}$	–	–	Cheetah${}^{\ast 2}$
[27]	2017	LIPM	SQP	$2^{\ast 5}$	1.6	200[Hz]	HRP-2
[28]	2017	SRBD + WBK	SLQ	$2^{\ast 4}$	0.8–1.2	60[Hz]	HyQ
[29]	2018	LIPM	QP	$1^{\ast 5}$	0.75	20[Hz]	E2-DR
[30]	2018	SRBD	QP	10–16	0.33 – 0.5	25 – 50[Hz]	Cheetah 3
[31]	2018	WBD	iLQR/SQP	125	0.5	80–175[Hz]	HyQ, ANYmal
[32]	2019	SRBD	NLP (Ipopt)	–	–	40 – 80[Hz]	Cheetah 3
[33]	2019	LIPM	QP	–	–		HRP-4
		WBD	QP	–${}^{\ast 3}$	–
[34]	2020	SRBD	NLP (Ipopt)	–	–	100–200[Hz]	Mini Cheetah
[35]	2020	SRBD	QP	–${}^{\ast 3}$	–	500[Hz]	Mini Cheetah
[36]	2020	WBD	DDP	15	0.3	50[Hz]	CB-i
[37]	2020	LIPM	QP	–	1.6	100[Hz]	HRP-4, NAO
[38]	2021	SRBD + WBK	SLQ	–	–	20–50[Hz]	Wheeled ANYmal
[39]	2021	SRBD + WBK	SLQ	–	–	20–50[Hz]	ANYmal
[40]	2021	CD + WBK	SLQ	–	1.0	70[Hz]	ALMA
[41]	2021	LIPM	QP	$3^{\ast 5}$	0.9	400[Hz]	ANYmal
[42]	2021	LIPM${}^{\ast 6}$	QP	–	–	per step	Cassie
[43]	2021	LIPM${}^{\ast 7}$	SQP	31	1.55	200[Hz]	COMAN${}^{\ast 2}$
[44]	2021	WBD	DDP	100	1.0	60[Hz]	TALOS
[45]	2021	SRBD	SQP	50	2.0	25[Hz]	HyQ
		WBC	QP	–${}^{\ast 3}$	–	250[Hz]
[46]	2022	CD	NLP (Ipopt)	–	–	16[Hz]	iCub
[47]	2022	WBD	DDP	100	1.0	60[Hz]	TALOS
[48]	2022	SRBD	MPCC (Ipopt)	–	–	10[Hz]	Mini Cheetah
		WBC	QP	–${}^{\ast 3}$	–	500[Hz]
LIPM	linear inverted pendulum mode			CD	centroidal dynamics
SRBD	single rigid-body dynamics			WBK(D)	whole-body kinematics (dynamics)
(S)QP	(sequential) quadratic programming			LQR	linear-quadratic regulator
DDP	differential dynamic programming			NLP	nonlinear programming
iLQR(G)	iterative linear-quadratic regulator (Gaussian)
SLQ	sequential linear quadratic (general term that includes DDP, iLQR, and iLQG)
MPCC	mathematical programming with complementarity constraints

Notes: *1  similar to Kajita's preview control, but not explicitly mentioned.

*2 in simulation.

*3 QP-based inverse dynamics without prediction.

*4 steps in stance phases.

*5 steps in walking steps.

*6 called H-LIP in the referenced work.

*7 with height variation and angular momentum.

The organization of the rest of this survey is as follows. In Section 2, a brief review of dynamical systems of legged robots is provided. In Section 3, the theory and algorithms for MPC are reviewed from a general perspective. In Section 4, MPC methods specific to legged and humanoid robots are reviewed. Section 5 presents concluding remarks and future prospects.

2. Dynamical system models of legged robots

2.1. Dynamical models with different levels of detail

Because legged robots have many degrees of freedom, a mathematical model that fully describes its dynamic and kinematic characteristics can be very high-dimensional and complex. It is, therefore, unrealistic to rely entirely on such complex models for implementing MPC with a long prediction horizon, for which real-time update is a strong requirement. For capturing and utilizing the dynamics of legged robots in different levels of detail, mathematical models with various degrees of abstraction and dimensionality have been proposed. The complexity of a model strongly influences the computational complexity of MPC algorithms and the variety of motions that can be generated. In the following, models widely used for MPC are briefly reviewed in the complex-to-simple order.

2.2. Whole-body dynamics

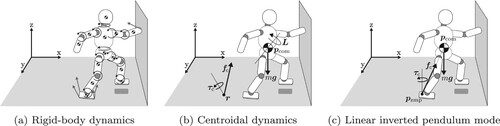
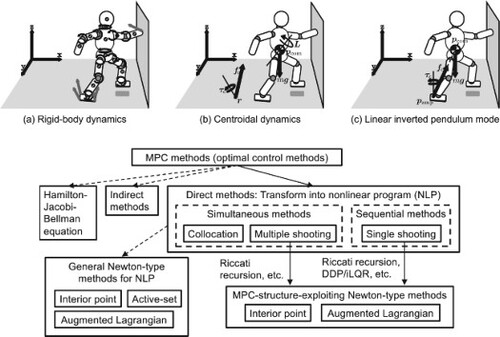
The whole-body dynamics (WBD, also known as rigid-body dynamics or multi-body dynamics) is a model that represents a robot as a floating-base mechanical system comprising multiple rigid bodies connected by joints (see Figure 1(a)). Its equation of motion is expressed as follows. (1) $\begin{array}{r}M\left(\mathit{q}\right)\dot{\mathit{v}}+h(\mathit{q},\mathit{v})=S^{\mathsf{T}}\mathit{\tau }+J(\mathit{q}{)}^{\mathsf{T}}\mathit{\lambda }\end{array}$(1) Here, $\mathit{q}$, $\mathit{v}$, and $\mathit{\tau }$ are the generalized coordinate, velocity, and torque of the system, M is the inertia matrix, h is the Coriolis-centrifugal term, S is the selection matrix that specifies actuated joints, and J is the contact Jacobian. The domain of the generalized coordinate $\mathit{q}$ is $\mathrm{S}\mathrm{E}\left(3\right)\times {\mathbb{R}}^{n_{\mathrm{j}}}$, where $n_{\mathrm{j}}$ is the number of joints. Here, the orientation of the base link is parameterized either by a unit quaternion or Euler angles. The contact force vector $\mathit{\lambda }$ is a concatenation of all contact forces; $\mathit{\lambda }=[{\mathit{\lambda }}_1^{\mathsf{T}},{\mathit{\lambda }}_2^{\mathsf{T}},\dots ,{\mathit{\lambda }}_{n_{\mathrm{c}}}^{\mathsf{T}}{]}^{\mathsf{T}}$, where ${\mathit{\lambda }}_i$ is the contact force acting on the ith contact point. In rigid contact model, the contact force $\mathit{\lambda }$ is determined to satisfy the complementarity between contact force and contact acceleration at each contact point. Moreover, to avoid slipping, each contact force must be inside the friction cone associated with that contact point. See, for example, [56] for more details on the whole-body dynamics.

Figure 1. Dynamical models with different dimensionality.

2.3. Centroidal dynamics

The centroidal dynamics equation given below describes the dynamics of the center of mass and the total angular momentum (see Figure 1(b)). (2) $\begin{array}{rl}m{\ddot{\mathit{p}}}_{\mathrm{c}\mathrm{o}\mathrm{m}}& ={\mathit{f}}_{\mathrm{c}}-m\mathit{g}\\ \dot{\mathit{L}}& ={\mathit{\tau }}_{\mathrm{c}}+(\mathit{r}-{\mathit{p}}_{\mathrm{c}\mathrm{o}\mathrm{m}})\times {\mathit{f}}_{\mathrm{c}}\end{array}$(2) Here, ${\mathit{p}}_{\mathrm{c}\mathrm{o}\mathrm{m}}$ and $\mathit{L}$ are the position of the center of mass (CoM, also called the center of gravity, CoG) and the total angular momentum with respect to the CoM. Moreover, ${\mathit{f}}_{\mathrm{c}}$ is the total contact force and ${\mathit{\tau }}_{\mathrm{c}}$ is the total contact moment around the point of application $\mathit{r}$, which can be chosen arbitrarily. The 6D vector consisting of ${\mathit{f}}_{\mathrm{c}}$ and ${\mathit{\tau }}_{\mathrm{c}}$ is called the total contact wrench.

The centroidal dynamics can be rigorously derived from the whole-body dynamics (1(1) $\begin{array}{r}M\left(\mathit{q}\right)\dot{\mathit{v}}+h(\mathit{q},\mathit{v})=S^{\mathsf{T}}\mathit{\tau }+J(\mathit{q}{)}^{\mathsf{T}}\mathit{\lambda }\end{array}$(1) ) without approximation. The relationship between the whole-body and centroidal dynamics is well described in [57].

One difficulty of the centroidal dynamics is that the relationship between the angular momentum $\mathit{L}$ and the robot's posture is not explicit. A frequently used approach is the single rigid-body dynamics (SRBD) approximation which expresses the angular momentum as $\mathit{L}=I\mathit{\omega }$, where I and $\mathit{\omega }$ are the base link's inertia tensor and angular velocity, respectively. This approximation is only valid if the inertia tensor does not change drastically depending on the robot's posture, and therefore, is often used for MPC of quadrupeds with light-weight legs [26,30]. One limitation of single rigid-body approximation is that it cannot express movements involving dynamical changes of the inertia tensor, such as changing the posture in the air [58].

2.4. Contact models

With the whole-body and centroidal dynamics models, the contacts are often modeled as constraints on the kinematics. When the contact sequence (e.g. gait patterns and contact points) is given, the contacts are typically expressed as equality constraints. Let $r\left(\mathit{q}\right)$ and $\overline{r}$ be the stacks of positions of bodies in contacts and given contact points, respectively. The contact constraint is then given by (3) $\begin{array}{r}r\left(\mathit{q}\right)-\overline{\mathit{r}}=0.\end{array}$(3) Alternatively, one can consider contact velocity or contact acceleration constraints, i.e. time derivative and second time derivatives of (3(3) $\begin{array}{r}r\left(\mathit{q}\right)-\overline{\mathit{r}}=0.\end{array}$(3) ), respectively. Note that instead of the position $r\left(\mathit{q}\right)$ and given contact point $\overline{r}$, the distance between the body and point (e.g. the height of a foot from the ground) or its time derivative is also utilized to determine the horizontal contact positions through the MPC optimization.

In contrast, when the planning problem involves the decision-making on the contact sequence, the underlying dynamics must be modeled so that various possibilities can be considered in the problems. A typical way is to model the contact dynamics using the complementarity constraints [59]. An intuitive example of the complementarity constraints expresses on/off of a point contact: (4) $\begin{array}{r}\phi \left(\mathit{q}\right)\ge 0,f_N\ge 0,\phi \left(q\right)f_N=0,\end{array}$(4) where $\phi \left(\mathit{q}\right)$ denotes the distance between the robot's body and the environment, and $f_N$ denotes the corresponding normal contact force. While the complementarity constraints can rigorously model the unilateral aspect of contacts, the optimization problems are generally hard to solve. More computationally tractable but inaccurate contact models have been proposed to mitigate such difficulties [31,60,61]. These models can be regarded as soft contact models and approximations of the complementarity constraints. Neunert et al. [31,60] modeled the contacts via a mass-spring-damper system, which is simple but leads to a stiff dynamical system and inaccuracy. Todorov [61] proposed an analytically invertible and differentiable contact model used in MuJoCo simulator [62]. However, it still lacks physical accuracy compared with the rigorous rigid contact models, e.g. allowing penetration between rigid objects, as seen in a contact model comparison of [63].

2.5. Linear inverted pendulum mode

The linear inverted pendulum mode, initially proposed in [64], describes the movement of the CoM as a linear second-order ordinary differential equation (ODE). Initially proposed as a 2D dynamical model, it has been generalized extensively in later studies [65]. The LIPM can be directly derived from the centroidal dynamics with an additional assumption that no tilting moment act around the CoM. Some earlier studies claim that the LIPM is valid only under the lumped mass assumption; that is, the whole mass is concentrated around the CoM, but this assumption is, though sufficient, not necessary. Its derivation can be found in [50].

The 3D LIPM equation is expressed as follows. (5) $\begin{array}{r}{\ddot{\mathit{p}}}_{\mathrm{c}\mathrm{o}\mathrm{m}}=\frac{1}{T^2}({\mathit{p}}_{\mathrm{c}\mathrm{o}\mathrm{m}}-{\mathit{p}}_{\mathrm{z}\mathrm{m}\mathrm{p}})-\mathit{g}\end{array}$(5) Here, ${\mathit{p}}_{\mathrm{c}\mathrm{o}\mathrm{m}}$ is the CoM, ${\mathit{p}}_{\mathrm{z}\mathrm{m}\mathrm{p}}$ is the ZMP, $\mathit{g}=[0,0,g{]}^{\mathsf{T}}$ is the acceleration of gravity, and T is an arbitrary constant (more generally, it can be time-varying). In a simple setup where the CoM maintains a constant height h from the ground, the condition that the z-component of ${\ddot{\mathit{p}}}_{\mathrm{c}\mathrm{o}\mathrm{m}}$ is 0 gives $T=\sqrt{\frac{h}{g}}$. Because the LIPM is a second-order linear ODE, it yields a closed-form solution. This characteristic is extremely useful for planning long trajectories with a small number of decision variables.

The LIPM has been used extensively for walking pattern generation and stabilization control of bipedal and humanoid robots. Theoretically, the LIPM is applicable not only to bipedal locomotion but to general-legged locomotion. However, its application to non-biped robots such as quadrupeds is relatively rare (see Section 4.1).

2.6. Stability criteria based on contacts

It is essential to consider contact stability in the planning and control of legged locomotion. That is, generated trajectories must be supported by the distribution of valid contact forces. The CoM-based static stability criterion was used in early studies. Namely, the robot is statically stable if the ground projection of its CoM is inside the support region. However, this conservative stability criterion inevitably leads to static walking, which is impractical in terms of walking speed. For dynamic walking, the ZMP-based stability criterion is used instead. The ZMP (zero (tilting) moment point) or the CoP (center of pressure) is a point at which the tangential components of the net contact moment are zero. In coplanar contact cases (i.e. when all contact points lie on a single common plane), the condition that the ZMP is inside the convex hull of contact points is a necessary condition for surface contact stability. It is not generally sufficient because it neglects friction constraint (in other words, it assumes that the friction coefficient is large enough). Consideration of friction was discussed in [65]. For non-coplanar contact cases, the feasible set of the ZMP or total contact wrench can be still defined but are difficult to compute explicitly. Instead, some recent studies treated contact forces of multiple contact points as decision variables and impose contact stability constraints in optimization.

The CoM-based static stability is too conservative, while the ZMP/contact wrench-based criteria merely ensure the existence of valid contact force distribution at every instant. A theoretical framework that treats true dynamical stability (a property of a dynamical system that its state can be kept inside a bounded region indefinitely) in the context of legged locomotion has been developed as the capturability theory [66]. The robot is said to be in an N-step capturable state if it can be brought to a halt within N walking steps. In particular, the robot is 0-step capturable if the instantaneous capture point (ICP) is inside the support region. It is a natural extension of the classical CoM-based static stability criterion. The capturability criterion is used to ensure the closed-loop stability of MPC [37].

3. MPC algorithms

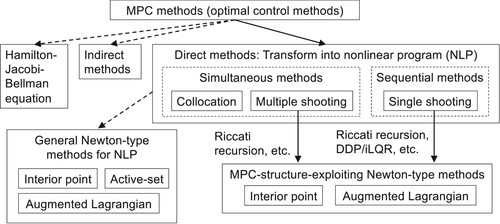
Before reviewing the robotic applications of MPC, we provide an overview of MPC algorithms. Figure 2 shows the classification of solution approaches to MPC problems, i.e. optimal control problems (OCPs). As shown in Figure 2, the solution approaches to MPC problems are roughly divided into three methods: the Hamilton-Jacobi-Bellman equation (dynamic programming), indirect methods (e.g. Pontryagin's maximum principle), and direct methods. However, the two former approaches are difficult to use for practical robotic problems that involve nonlinear and high-dimensional constrained MPC problems. Therefore, this survey focuses on the direct methods in which the MPC problems are transformed into nonlinear programs (NLPs) and solved by numerical optimization techniques.

Figure 2. Overview of solution approaches of MPC.

3.1. Linear MPC

If the dynamical system and constraints are linear and the cost function is quadratic, the MPC is classified as linear MPC. The NLPs of the direct methods are then reduced to quadratic programs (QPs). Dedicated QP solvers have been developed, such as active-set [67,68], interior point [69–71], and alternating direction method of multipliers (ADMM)-based methods [72]. Their efficiency typically depends on problem settings, e.g. numbers of optimization variables and inequality constraints. A comprehensive review of QP solvers for MPC can be found in [73].

3.2. Nonlinear MPC

If the dynamical systems or constraints are nonlinear or the cost function is nonconvex, the MPC optimization problem is classified as a nonlinear (or nonconvex) MPC problem. A challenge in nonlinear MPC is that we must solve an NLP problem within a predefined sampling time of MPC, which is typically small as shown in Table 1. Refs. [74,75] are pioneer works on nonlinear MPC. These two works utilize tangential predictors to track the solution manifold of the NLP and perform only one inexact Newton iteration to update the solution at each time. Such ideas were further studied in [76,77].

On the other hand, improving the computational speed of solving the NLPs arising in nonlinear MPC has gained attention. In particular, the Newton-type methods such as sequential quadratic programming (SQP) methods and (nonlinear) interior point (IP) methods (specifically, primal-dual IP method) [78] have been developed along with efficient general-purpose NLP solvers such as Snopt [79] and Ipopt [80]. Developments in active-set QP solvers for MPC, such as [67] and [68], have also pushed the efficiency of SQP methods for MPC. SQP methods, particularly with active-set QP solvers, can leverage warm-start but lack efficiency for large-scale problems. However, IP methods can treat large-scale problems efficiently while they cannot leverage warm-start. These general-purpose NLP solvers or SQP methods with active-set QP solvers still lack computational efficiency. Therefore, it is still challenging to implement real-time MPC for fast, large-scale, and complicated robotic systems.

3.3. Structure-exploiting Newton-type methods for nonlinear MPC problems

To further improve the computational efficiency of nonlinear MPC, researchers have attempted to exploit the structure of the NLP problems of the direct methods of MPC. The NLP problems for MPC, particularly of single shooting and multiple-shooting methods, have special structures [81,82]. As the multiple-shooting method is more suitable for nonlinear MPC than the single shooting methods in terms of computational speed and convergence property [82], we show an example of the structured NLP of the multiple-shooting method. Let N be the length of the horizon, ${\mathit{x}}_0,\cdots ,{\mathit{x}}_N$ and ${\mathit{u}}_0,\cdots ,{\mathit{u}}_{N-1}$ be the state and control input of the system over the horizon, and $\overline{\mathit{x}}$ be the given initial state. Then, the NLP is given as (6a) $\begin{array}{rl}& \underset{{\mathit{x}}_0,\dots ,{\mathit{x}}_N,{\mathit{u}}_0,\dots ,{\mathit{u}}_{N-1}}{min}{V}_N\left({\mathit{x}}_N\right)+\sum _{i=0}^{N-1}{l}_i({\mathit{x}}_i,{\mathit{u}}_i)\end{array}$(6a) (6b) $\begin{array}{rl}& \mathrm{s}.\mathrm{t}.{\mathit{x}}_0=\overline{\mathit{x}},\end{array}$(6b) (6c) $\begin{array}{rl}& {\mathit{x}}_{i+1}=f_i({\mathit{x}}_i,{\mathit{u}}_i),i=0,\dots ,N-1,\end{array}$(6c) (6d) $\begin{array}{rl}& g_i({\mathit{x}}_i,{\mathit{u}}_i)\le 0,i=0,\dots ,N-1,\end{array}$(6d) (6e) $\begin{array}{rl}& g_N\left({\mathit{x}}_N\right)\le 0,\end{array}$(6e) where $V_N\left({\mathit{x}}_N\right)$ denotes the given terminal cost function $l_i({\mathit{x}}_i,{\mathit{u}}_i)$ denotes the given cost function, (6c(6c) $\begin{array}{rl}& {\mathit{x}}_{i+1}=f_i({\mathit{x}}_i,{\mathit{u}}_i),i=0,\dots ,N-1,\end{array}$(6c) ) denotes the discrete-time state equation, and (6d(6d) $\begin{array}{rl}& g_i({\mathit{x}}_i,{\mathit{u}}_i)\le 0,i=0,\dots ,N-1,\end{array}$(6d) ) and (6e(6e) $\begin{array}{rl}& g_N\left({\mathit{x}}_N\right)\le 0,\end{array}$(6e) ) denote the given inequality constraints. Note that we can obtain the NLP for the single shooting method by eliminating ${\mathit{x}}_i$ from the decision variables via (6b(6b) $\begin{array}{rl}& \mathrm{s}.\mathrm{t}.{\mathit{x}}_0=\overline{\mathit{x}},\end{array}$(6b) ) and (6c(6c) $\begin{array}{rl}& {\mathit{x}}_{i+1}=f_i({\mathit{x}}_i,{\mathit{u}}_i),i=0,\dots ,N-1,\end{array}$(6c) ). Here, we treat the inequality constraints (6d(6d) $\begin{array}{rl}& g_i({\mathit{x}}_i,{\mathit{u}}_i)\le 0,i=0,\dots ,N-1,\end{array}$(6d) ) and (6e(6e) $\begin{array}{rl}& g_N\left({\mathit{x}}_N\right)\le 0,\end{array}$(6e) ) using the IP methods. Let $\mathrm{\Delta }{\mathit{x}}_0,\cdots ,\mathrm{\Delta }{\mathit{x}}_N$, $\mathrm{\Delta }{\mathit{u}}_0,\cdots ,\mathrm{\Delta }{\mathit{u}}_{N-1}$ be the Newton steps of ${\mathit{x}}_0,\cdots ,{\mathit{x}}_N$, ${\mathit{u}}_0,\cdots ,{\mathit{u}}_{N-1}$. The computation of the Newton steps, which is one of the most time-consuming aspects of the Newton-type iteration, can then be reduced to the following QP subproblem [82]: (7a) $\begin{array}{rl}& \underset{\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_0,\dots ,\mathrm{\Delta }{\mathit{x}}_N,\\ \mathrm{\Delta }{\mathit{u}}_0,\dots ,\mathrm{\Delta }{\mathit{u}}_{N-1}\end{array}}{min}\frac{1}{2}{\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_N\\ 1\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}{P}_N& p_N\\ p_N^{\mathrm{T}}& 1\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_N\\ 1\end{array}\right]\\ & +\frac{1}{2}{\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_i\\ \mathrm{\Delta }{\mathit{u}}_i\\ 1\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{ccc}{Q}_i& S_i& q_i\\ S_i^{\mathrm{T}}& R_i& r_i\\ q_i^{\mathrm{T}}& r_i^{\mathrm{T}}& 1\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_i\\ \mathrm{\Delta }{\mathit{u}}_i\\ 1\end{array}\right]\end{array}$(7a) (7b) $\begin{array}{rl}& \mathrm{s}.\mathrm{t}.\mathrm{\Delta }{\mathit{x}}_0=\overline{\mathit{x}},\end{array}$(7b) (7c) $\begin{array}{rl}& \mathrm{\Delta }{\mathit{x}}_{i+1}=A_i\mathrm{\Delta }{\mathit{x}}_i+B_i\mathrm{\Delta }{\mathit{u}}_i+b_i,i=0,\dots ,N-1,\end{array}$(7c) where $A_i:={\mathrm{\nabla }}_{x}f({\mathit{x}}_i,{\mathit{u}}_i)$, $B_i:={\mathrm{\nabla }}_{u}f({\mathit{x}}_i,{\mathit{u}}_i)$. The coefficient matrices in the quadratic cost function of (7a(7a) $\begin{array}{rl}& \underset{\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_0,\dots ,\mathrm{\Delta }{\mathit{x}}_N,\\ \mathrm{\Delta }{\mathit{u}}_0,\dots ,\mathrm{\Delta }{\mathit{u}}_{N-1}\end{array}}{min}\frac{1}{2}{\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_N\\ 1\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}{P}_N& p_N\\ p_N^{\mathrm{T}}& 1\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_N\\ 1\end{array}\right]\\ & +\frac{1}{2}{\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_i\\ \mathrm{\Delta }{\mathit{u}}_i\\ 1\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{ccc}{Q}_i& S_i& q_i\\ S_i^{\mathrm{T}}& R_i& r_i\\ q_i^{\mathrm{T}}& r_i^{\mathrm{T}}& 1\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_i\\ \mathrm{\Delta }{\mathit{u}}_i\\ 1\end{array}\right]\end{array}$(7a) ) are derived from the derivatives of the Lagrangian of the NLP (6a(6a) $\begin{array}{rl}& \underset{{\mathit{x}}_0,\dots ,{\mathit{x}}_N,{\mathit{u}}_0,\dots ,{\mathit{u}}_{N-1}}{min}{V}_N\left({\mathit{x}}_N\right)+\sum _{i=0}^{N-1}{l}_i({\mathit{x}}_i,{\mathit{u}}_i)\end{array}$(6a) ) and some matrix manipulations related to IP methods. Here, we omitted the detailed derivations of the coefficient matrices, but they can be found, e.g. in [78,82,83]. According to (7a(7a) $\begin{array}{rl}& \underset{\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_0,\dots ,\mathrm{\Delta }{\mathit{x}}_N,\\ \mathrm{\Delta }{\mathit{u}}_0,\dots ,\mathrm{\Delta }{\mathit{u}}_{N-1}\end{array}}{min}\frac{1}{2}{\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_N\\ 1\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}{P}_N& p_N\\ p_N^{\mathrm{T}}& 1\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_N\\ 1\end{array}\right]\\ & +\frac{1}{2}{\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_i\\ \mathrm{\Delta }{\mathit{u}}_i\\ 1\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{ccc}{Q}_i& S_i& q_i\\ S_i^{\mathrm{T}}& R_i& r_i\\ q_i^{\mathrm{T}}& r_i^{\mathrm{T}}& 1\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_i\\ \mathrm{\Delta }{\mathit{u}}_i\\ 1\end{array}\right]\end{array}$(7a) ), the arising QP subproblems of IP methods take the same structure as unconstrained time-varying linear-quadratic OCPs. Note that we can have the same QP subproblems in the inner iterations of Augmented Lagrangian (AL) methods. Efficient MPC algorithms that leverage the unconstrained LQR structure to compute the Newton steps were proposed in [83–86].

3.3.1. Riccati recursion

Riccati recursion [83], which corresponds to dynamic programming for the linear-quadratic OCP (7a(7a) $\begin{array}{rl}& \underset{\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_0,\dots ,\mathrm{\Delta }{\mathit{x}}_N,\\ \mathrm{\Delta }{\mathit{u}}_0,\dots ,\mathrm{\Delta }{\mathit{u}}_{N-1}\end{array}}{min}\frac{1}{2}{\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_N\\ 1\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}{P}_N& p_N\\ p_N^{\mathrm{T}}& 1\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_N\\ 1\end{array}\right]\\ & +\frac{1}{2}{\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_i\\ \mathrm{\Delta }{\mathit{u}}_i\\ 1\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{ccc}{Q}_i& S_i& q_i\\ S_i^{\mathrm{T}}& R_i& r_i\\ q_i^{\mathrm{T}}& r_i^{\mathrm{T}}& 1\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_i\\ \mathrm{\Delta }{\mathit{u}}_i\\ 1\end{array}\right]\end{array}$(7a) ), has gained popularity both in MPC and robotics communities as it can compute the Newton step in $O\left(N\right)$ computational burden. This contrasts the general NLP solvers and SQP methods with active-set QP solvers in which the Newton step computation typically requires $O\left(N^3\right)$ time-complexity. In the MPC community, IP methods are typically used with Riccati recursion for inequality constraints [83]. An efficient open-source IP solver with Riccati recursion is developed in [70], and a nonlinear MPC toolbox based on it is developed in [87].

Treating the equality constraints, which often represent the contact constraints as stated in Section 2.4, with the Riccati recursion-type methods is another issue because IP methods cannot be used. A simple way is to use AL methods [88], which generally lack convergence speed, however. Variants of the Riccati recursion-type methods to treat the equality constraints have been proposed [28,89–91].

3.3.2. Differential dynamic programming

Riccati recursion-based Newton's methods are often interpreted as differential dynamic programming (DDP) [92] in the robotics community. Also, its Gauss-Newton counterpart is called an iterative linear quadratic regulator (iLQR) [93]. Variants of DPP and iLQR have been proposed, such as sequential linear quadratic (SLQ) [28] and feasible-driven DDP [94]. In robotic applications, a variant of IP methods [95] is often used to treat inequality constraints with DDP-type methods. AL methods are also used, e.g. [88,96], because they have the same unconstrained LQR structure as (7a(7a) $\begin{array}{rl}& \underset{\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_0,\dots ,\mathrm{\Delta }{\mathit{x}}_N,\\ \mathrm{\Delta }{\mathit{u}}_0,\dots ,\mathrm{\Delta }{\mathit{u}}_{N-1}\end{array}}{min}\frac{1}{2}{\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_N\\ 1\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}{P}_N& p_N\\ p_N^{\mathrm{T}}& 1\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_N\\ 1\end{array}\right]\\ & +\frac{1}{2}{\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_i\\ \mathrm{\Delta }{\mathit{u}}_i\\ 1\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{ccc}{Q}_i& S_i& q_i\\ S_i^{\mathrm{T}}& R_i& r_i\\ q_i^{\mathrm{T}}& r_i^{\mathrm{T}}& 1\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\mathit{x}}_i\\ \mathrm{\Delta }{\mathit{u}}_i\\ 1\end{array}\right]\end{array}$(7a) ) in the inner Newton-type iteration.

If the MPC problem is deterministic, DDP-type methods are almost identical to the Riccati recursion-based Newton (or Gauss-Newton) method for the single shooting method (see Chapter 8 of [82]). From this point of view, it is easy to implement ‘DDP/iLQR-like methods with inequality constraints’ in deterministic MPC by using the Riccati recursion to solve the QP subproblems of nonlinear IP methods. This is considered challenging in the robotics community [88,95]. Further, it is trivial to implement ‘multiple shooting DDP/iLQR-like methods’ just by using the Riccati recursion in solving the QP subproblems of multiple shooting NLPs [81]. This is also recognized as nontrivial in the robotics community [94].

3.4. MPC with hybrid systems/complementarity constraints

When the contact sequence and contact timings are fixed in MPC, e.g. when a higher-level contact planner provides them, MPC can be implemented by the above numerical methods, in principle. In contrast, when MPC involves the decision-making on the contact sequence, the robotic systems with contacts have to be modeled such as a hybrid system [97] or using complementarity constraints as stated in Section 2.4. The aforementioned numerical methods are then no longer applicable. Alternatively, the approximated soft contact models introduced in Section 2.4 are used to incorporate the decision-making on the contact sequence into MPC even with the above numerical methods. However, it has limitations as reviewed in Section 2.4. Its applications are introduced later in Section 4.3.2.

When the robotic systems are modeled as hybrid systems, MPC is typically implemented as a mixed-integer program (MIP) [98], in which the discrete variables are introduced explicitly. However, MIPs are hard to implement in real time owing to exponentially growing computational time [98]. Recently, suboptimal solution methods [99,100] and MPC-specific solution methods [101,102] have been studied. When the robotic systems are modeled using the complementarity constraints, the resultant OCP is often termed as contact-implicit trajectory optimization (CITO), whose pioneer work is [103]. A solution method of the CITO is using mathematical programs with complementarity constraints (MPCC) [104], which solves the optimization problems under complementarity constraints. The MPCC approach was first utilized for the CITO in [105]. However, MPCC inherently lacks constraint qualifications such as linear independence constraint qualification (LICQ), which causes numerical ill-conditionings [104]. Moreover, numerical alleviations for such problems [106] often lead to undesirable stationary points [107]. An alternative approach for the CITO is bilevel optimization (BO) methods [103,108–110], whose solution can be a solution to MPCC under certain conditions [111]. However, BO problems also involve combinatorial structure and are therefore hard to solve in general [112].

3.5. MPC of switched systems

Even when the contact sequence is given, we can further optimize the contact timings or switching times, which is classified as OCP of switched systems [113,114]. A classical solution approach for OCP of switched systems is to decompose the optimization problem into two stages: one is for switching times and the other is for state and control trajectory [113,115]. This two-stage approach has been successfully applied for offline motion planning [116,117]. However, it lacks computational speed and a local convergence guarantee, making it difficult to realize MPC. Another approach is to optimize the switching times, state, and control simultaneously in Newton-type methods [114]. In [114], the simultaneous optimization problems were solved by the off-the-shelf NLP solvers such as [80]. However, their applications are also limited to offline trajectory optimization due to inefficient computation of the general NLP solvers, and it is still challenging to optimize the contact timings online.

4. MPC applications for legged robots

4.1. MPC with LIPM

For bipedal robots, MPC based on the LIPM has been widely used. This model is linear to the horizontal position of the CoM and is time-invariant if the CoM is constrained in a plane. The ZMP is equivalent to the center of pressure on the sole and must lie within the convex hull of the foot support region. MPC is used to plan a CoM trajectory that satisfies this ZMP constraint.

As an early approach, instead of explicitly considering the ZMP constraint, a method was proposed to minimize the error with the reference ZMP trajectory [16,118]. This method, also called preview control [119], is computationally efficient because the solution is written in closed form using the solution of the Riccati equation. However, inequality constraints cannot be considered. The reference ZMP trajectory is determined based on the footstep sequence obtained in the preprocessing footstep planning [53]. Graph search [120] is widely used for footstep planning [121,122], but mathematical optimizations have also been used in recent years [123,124]. Many extensions have been made to CoM trajectory generation based on preview control; for example, in [125], the angular momentum trajectory was generated simultaneously with the CoM trajectory.

Owing to improved computational performance and efficient QP solvers, linear MPC that explicitly considers inequality constraints of ZMP has come into use [126]. See [54] for a survey of linear MPC for bipedal robots. Linear MPC is formulated as QP and solved in real time by coarsening the horizon sample. Some MPCs impose an equality constraint on the capture point or DCM at the horizon terminal, which is specific to MPCs based on the LIPM [29,37]. As the CoM height changes along a predefined trajectory, the system becomes linear time-varying, which can be solved with linear MPC without significant change in computational cost [127]. Control inputs at sampling points within the horizon are often used as decision variables, but several attempts have been proposed to reduce the dimension of the variables. For example, in [29], the ZMP trajectory was expressed as a polynomial function, and the coefficients of the polynomial function are used as decision variables. In addition, in [21,42,128,129], by analytically solving the linear differential equation of the LIPM, the CoM at the timing of footstep switching was derived in closed form, eliminating the fine sampling within the horizon.

A major extension of linear MPC in bipedal walking is the simultaneous planning of CoM trajectory and foot placement sequence [29,37,128,130]. In [131], $l_1$- and $l_{\mathrm{\infty }}$-norm were used in the regularization of foot placement instead of the commonly used $l_2$-norm, so that the foot placement modification is sparse. Linear MPCs that can simultaneously plan CoM trajectory and foot placement sequence have also been proposed, using the first-order dynamics of the DCM instead of the LIPM [132,133]. In [133], the angular momentum trajectory was also planned with the CoM trajectory and foot placement sequence, using the dynamics of the DCM. Furthermore, MPCs beyond the framework of linear MPCs have also been proposed for planning foot placement [27,132], although they can no longer be formulated as QP. In [132], the MPC was represented as an MIP by approximating the trigonometric functions required to describe the foot orientation as piecewise linear functions with 0–1 variables [123]. In [27], the nonlinear MPC was solved by SQP, taking into account the nonconvex constraints representing the obstacle avoidance of the feet. There are also some methods [18,24,134,135] in which the foot placement modification was treated in a different computational process other than the MPC for CoM trajectory generation.

Another major extension of linear MPC in bipedal walking is to account for external forces in the robot's hands. In linear MPC, external forces are treated in different ways; in [136] they were included in the state of the LIPM, in [33] they were included in the control input, and in [137] they were considered as offsets of the model. In [138], whether hand contact is necessary to avoid a fall due to disturbances was determined in linear MPC by introducing slack variables in ZMP's inequality constraints. Morisawa et al. [139] extended the LIPM by introducing a point corresponding to ZMP that accounts for hand contacts and represented the dynamics of multi-contact motion as a linear system.

The dynamics of bipedal walking become nonlinear if the horizontal and vertical positions of the CoM are considered as state variables. Some MPCs treat nonlinear systems and plan the three-dimensional trajectory of the CoM [140–142]. In [140], DDP was applied to plan the CoM trajectory, omitting ZMP's inequality constraints. In [141], using the three-dimensional position of the CoM as decision variables, the ZMP constraints were expressed as quadratic constraints, and the nonconvex quadratically constrained quadratic program (QCQP) was solved by the SQP method. In [142], by setting bounds on the LIPM time constant, the nonlinearity caused by the CoM vertical motion was avoided, and the three-dimensional CoM trajectory and foot placement sequence were simultaneously planned using linear MPC.

As a supplement, we present several methods for planning bipedal CoM trajectory without using linear MPC, formulated as QP. In [134,143,144], the CoM trajectory was efficiently planned by integrating the first-order dynamics of the capture point or DCM in the reverse direction. In [135,145], an analytical solution to the linear MPC problem with boundary conditions was derived. MPCs based on the LIPM have been applied mainly to bipedal and humanoid robots, but have also been applied to quadruped robots [41,129,146,147].

4.2. MPC with centroidal dynamics and SRBD models

The LIPM does not explicitly consider friction constraints on contact forces and is, therefore, inappropriate for handling non-coplanar contacts. The centroidal dynamics [148] is a model based on the Newton-Euler equation for solving this problem and is widely used in humanoid and quadrupedal robots.

4.2.1. Application to humanoid robots

The centroidal dynamics model is used to plan and control humanoid multi-contact motion in which the feet and hands make non-coplanar contacts. See survey [55] for some MPCs in humanoid multi-contact motion. The difficulty of the centroidal dynamics model compared to the LIPM is that it has nonlinearity in the rotational dynamics [55].

Several MPC-based methods [22,149–154] that mitigate this nonlinearity in some way and avoid MPC with computationally expensive nonconvex optimization are presented. In [22], the nonlinear terms in the rotational dynamics were neglected to construct a linear MPC, formulated as a QP, under the contact force constraints. Audren et al. [149] focused on the fact that the rotational dynamics can be represented as a linear system by predetermining the CoM vertical motion. In [150], the rotational dynamics were approximated linearly by assuming a convex region for the CoM and by treating the upper bound of the angular momentum. Fernbach et al. [151] eliminate the nonlinear term in the rotational dynamics by representing the CoM trajectory as a Bezier curve parameterized by a one-degree-of-freedom decision variable. In [152], nonlinear trajectory optimization was attributed to QCQP by expressing the nonlinear term in rotational dynamics as the difference between two convex functions. In [153], a linear MPC is constructed with a system that linearizes the rotational dynamics while considering the effect of the angular momentum generated by the motion of each link. In [150,154], the friction constraints at each contact point were integrated and converted to CoM acceleration constraints, and CoM acceleration was used instead of contact forces as the decision variables for linear MPC to reduce the dimension of the variables.

In contrast, MPCs that use NLP solvers to solve nonconvex optimization have also emerged. Because nonconvex optimization is computationally expensive, the early methods were positioned as offline trajectory optimization rather than online MPC. In [155–157], trajectory generation of CoM and angular momentum under a centroidal dynamics model was formulated as a nonlinear optimization and solved offline by an off-the-shelf SQP solver. Nonlinear trajectory optimization can recently be solved online with the MPC scheme owing to improvements in computational performance and optimization algorithms. In [57], nonlinear MPC with learned kinematic reachability was solved by the multiple-shooting method using the OCP solver. In [46], the centroidal trajectory and contact position sequence were simultaneously planned online considering a nonlinear centroidal dynamics model.

Furthermore, by using a full-body model for kinematic constraints and a centroidal dynamics model for dynamic constraints, a method of simultaneously planning centroidal and joint position trajectories while avoiding high-dimensional full-body dynamics has been proposed [155]. Chignoli et al. [158] further imposed constraints on the speed-torque relationship of the actuators.

4.2.2. Application to quadrupedal robots

Centroidal dynamics-based MPCs were also applied for quadrupedal robots which typically involve point contacts in their feet. Existing quadrupedal robots, such as MIT Mini Cheetah, were designed such that the weights of limbs are small relative to the whole-body weight. For such hardware, the single rigid-body dynamics (SRBD) model is a simple and powerful model that can simplify the MPC optimization problem while accurately capturing the dynamics. Di Carlo et al. [30] achieved fast and highly dynamic motion of a quadrupedal robot via a fast linear MPC in which the robot dynamics were approximated by the (linearized) SRBD model, and the contact forces of feet (i.e. ground reaction forces (GRFs)) were treated as the control input to the SRBD model. When the weights of limbs are negligibly small compared with the base and a lower-level joint controller can track the GRFs from MPC quickly, the SRBD-based simplified model can be accurate. Ding et al. [159] further improved the SRBD-based linear MPC in terms of linearization of the rotation and achieved acrobatic motion on a quadrupedal robot. In [160], because the nonlinearity of rotational dynamics is due to the cross-product, the nonlinear trajectory optimization was solved by alternately solving two types of QPs with one variable fixed in the cross-product term.

Nonlinear MPC is also applied with the SRBD and centroidal dynamics models. Refs. [26,32,34] incorporated the contact positions as the optimization variables in the linearized SRBD-based MPC of [30]. The resultant optimization problem was nonlinear; therefore, a nonlinear MPC was implemented for the problem. Rathod et al. [45] formulated a nonlinear MPC with a nonlinear SRBD model to capture the nonlinear rotational dynamics and achieved quadrupedal walking that can traverse over a large obstacle only with on-board embedded computation. Further, Refs. [28,95] applied nonlinear MPC for the nonlinear SRBD and full-body kinematics model, in which the GRFs and joint velocities were treated as the control input to the dynamical systems. In [40], instead of the nonlinear SRBD model, the centroidal momentum matrix (CMM) [148] was used with the full-kinematics in nonlinear MPC, which is the same formulation of the offline trajectory optimization of [155]. The CMM enabled us to consider the exact CoM dynamics, including the weights of limbs in MPC, while the SRBD-based methods ignored it. The full-kinematic model (and the CMM) are versatile so that they can realize dynamic loco-manipulation tasks [40] of ALMA [161], locomotion under safety constraints [39], and wheeled-legged control [38]. In contrast to the aforementioned research assuming the predefined contact sequence, recent research reported the successful online CITO [48] with the centroidal dynamics model with some simplifications on the problem, e.g. frictional complementarity constraints were neglected.

4.3. MPC with full-body models (whole-body MPC)

4.3.1. Developments in rigid-body dynamics algorithms

MPC with whole-body (full-body) dynamics, called whole-body MPC, had been challenging owing to the large problem size of the NLP and the high computational cost of the whole-body dynamics and their derivatives. Therefore, early studies on whole-body MPC were limited, e.g. linear MPC based on linearly approximated dynamics, as studied in the computer graphics community [162]. This has come closer to reality owing to the developments in computational algorithms of the whole-body dynamics and their derivatives, namely, rigid-body dynamics algorithms [56]. Well-known rigid-body dynamics algorithms are the recursive Newton-Euler algorithm (RNEA) [163] for inverse dynamics computation and the articulated body algorithm (ABA) [164] for forward dynamics computation. Carpentier et al. [165] proposed efficient forward dynamics computation under a closed-kinematic chain or rigid contacts.

For MPC, the computational efficiency of derivatives of rigid-body dynamics is also critical. Neunert et al. [166] proposed automatics differentiation of the RNEA and ABA. Carpentier et al. [167] proposed analytical derivatives of the RNEA and ABA and achieved faster computation than the automatic differentiation. Singh et al. [168] further improved the computational efficiency of the analytical derivatives using spatial vector algebra. Also, Ayusawa and Yoshida [169] proposed analytical derivatives of forward and inverse dynamics computations. Nganga and Wensin [170] proposed an automatic differentiation of the second-order derivatives rigid-body dynamics in direct OCPs to improve the convergence speed of the Newton-type method with the exact Hessian, which is an extension of [171].

Some software have been developed to efficiently compute rigid-body dynamics and their derivatives. RobCoGen [172] is an open-source C++ code-generation tool supporting the RNEA, ABA, and automatic differentiations of these algorithms [166]. Pinocchio [173] is an open-source C++ library for RNEA, ABA, and the analytical derivatives of the RNEA and ABA [167].

4.3.2. State-of-the-art and challenges

Researchers can try the whole-body MPC because of the above developments in dynamics and their derivatives computation. Because the whole-body MPC is based on accurate full-body robot dynamics, it can achieve energy-efficient, reasonable, and highly dynamic motions for various problems. The whole-body MPC does not involve limitations on hardware platforms, working environment, and desired tasks, which can arise in MPC based on reduced-order models, i.e. the SRBD and centroidal dynamics models, due to the problem approximations. In the following, we introduce the researches that successfully implemented the whole-body MPC. The following MPC methods utilized Riccati recursion (specifically iLQR) to perform Newton-type iteration efficiently.

Refs. [23,31,36] formulated whole-body MPC problems with approximated soft contact models that are introduced in Section 2.4. Ref. [23] was the first study that realized the whole-body MPC in both simulation and real robot hardware. It utilized the analytically invertible and smooth contact model of [61]. Ishihara et al. [36] utilized the same contact model and proposed a hierarchical MPC strategy based on a singular perturbation technique to improve the control performance for fast dynamics. Neunert et al. [31] implemented whole-body MPC with a contact model approximation based on the mass-spring-damper model. Neunert et al. [31] also leveraged the automatic differentiation of the rigid-body dynamics proposed in [166] while [23] relied on slower finite differentiation. As stated in Section  2.4, these studies based on approximated contact models do not require the prespecified contact sequence and enable fast dynamics computation while lacking the solution's accuracy. Note that the offline trajectory optimization based on these contact models has also been studied, e.g. early in the computer graphics community [174].

In contrast, Refs. [94,175] formulated whole-body MPC problems taking the rigid contacts into account under the given contact sequence. Specifically, the rigid collisions and contact acceleration constraints were explicitly considered as utilized for the offline trajectory optimization in [176]. Further, Mastalli et al. [94] leveraged the efficient derivative computations of rigid-body dynamics of [167]. Dantec et al. [44,47] realized whole-body MPC of a humanoid robot using the algorithm of [94]. These rigid contact-based MPC can determine the control action by taking the future impact dynamics (i.e. instantaneous changes in the state due to impacts) into account, which cannot be achieved in the aforementioned MPC based on reduced-order models.

While whole-body MPC has been implemented in various robotic problems, computational challenges remain. First, the full-body dynamics involve high nonlinearity, which requires many Newton-type iterations and reduces the reliability of the numerical optimization solvers. For example, Dantec et al. [44] proposed to give an initial guess using the histories of the MPC solutions to improve the too-slow convergence speed of the whole-body MPC. Further, the computational burdens of dynamics and their derivatives and that of the Newton-type iterations still requires a long computational time, particularly compared with the simple SRBD model in which the computational cost of dynamics and Newton-type iterations is small.

4.4. Software for MPC of robotic systems

The robotic MPC problems, particularly in complicated models such as the centroidal dynamics model with full-kinematics or whole-body dynamics, involve complicated and variable MPC problem structures due to contacts. Moreover, rigid-body kinematics and dynamics calculations are required in solving optimization problems, which are difficult to implement only with the general NLP modeling tool [177] or nonlinear MPC tool [87]. Dedicated software for robotic MPC problems has been developed to interface with these difficulties. Control-toolbox [178] is a toolbox that implements MPC algorithms such as iLQR and SQP and has interfaces for rigid-body library RobCoGen [172]. ocs2 [179] is a collection of optimal control solvers such as the iLQR-type method for switched systems [180] and SQP methods. In ocs2, an approximated IP method [95] and AL methods are implemented to treat constraints. It also supports interfacing the switched systems, i.e. robotic systems with contacts, and has robotic MPC examples such as MPC with the SRBD/centroidal dynamics model and the full-kinematics model using Pinocchio [173]. Crocoddyl [94] implemented iLQR-type methods for whole-body dynamics with rigid contacts in which Pinocchio was used to efficiently compute rigid-body dynamics and their derivatives. It can treat box constraints on the control input efficiently. robotic [181] implemented the same whole-body dynamics with rigid contacts model based on Pinocchio as Crocoddyl. It utilized the nonlinear IP method for general inequality constraints and implemented the multiple-shooting method with Riccati recursion.

5. Conclusion

This survey paper reviewed the recent development of model predictive control methods in legged and humanoid robotics. Section 2 gave an overview of dynamical models of robotic systems. Section 3 reviewed MPC algorithms that are particularly suitable for robotic problems. Section 4 reviewed MPC methods for legged and humanoid robots. In the following, we point out open problems in the MPC of robotic systems.

First, ensuring the closed-loop stability is an unsolved problem. It is particularly difficult in whole-body MPC compared to trajectory generation MPC based on the reduced-order models because we must handle high-dimensional models with a short prediction horizon (due to the heavy computation cost). Some recent studies on combining control Lyapunov functions with MPC [182] and imposing passivity in whole-body control [183–185] are expected to provide insights to tackling this issue.

Second, reducing the computation cost of MPC is still an everlasting problem, particularly with on-board computation. In the MPC based on reduced-order models, there is a low-level controller that determines joint commands from the solution to MPC. It will be then a practical way to compensate for the computational inefficiency of MPC via the low-level controller such as the control barrier function [186] as presented in [39]. Whole-body MPC is challenging even with off-board computation. Recent advances in rigid-body algorithms such as [165,168,170] will potentially reduce the computational burden of whole-body MPC.

The third problem is robustness against disturbances and model mismatches. This is particularly problematic in whole-body MPC since the control commands are directly sent to the actuators. In contrast, MPC based on the reduced-order models are inherently inaccurate and the low-level controllers such as QP-based whole-body controllers typically try to compensate for the modeling error. Possible approaches are robust MPC [187,188] and stochastic MPC [189], in which the uncertainties are explicitly considered in the MPC formulation. Other possibilities are data-driven approaches such as the combination of MPC and adaptive-control [190,191] or reinforcement learning methods [192].

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by JSPS KAKENHI [grant number JP22J11441].

Notes on contributors

Sotaro Katayama

Sotaro Katayama received Bachelor of Engineering Science, Master of Informatics, and Ph.D. in Informatics from Kyoto University, Kyoto, Japan, in 2017, 2019, and 2022, respectively. His research interest includes model predictive control of robotic systems.

Masaki Murooka

Masaki Murooka received the BE, MS, and PhD degrees in information science and technology from The University of Tokyo, Japan, in 2013, 2015, and 2018, respectively. He was a project assistant professor in the Department of Mechano-Informatics at The University of Tokyo from 2018 to 2020. He joined the CNRS-AIST Joint Robotics Laboratory in the National Institute of Advanced Industrial Science and Technology (AIST) in 2020 as a researcher. His research interest includes the motion planning and control of humanoid robots.

Yuichi Tazaki

Yuichi Tazaki received Dr. Eng degree in control engineering from the Tokyo Institute of Technology, Tokyo, Japan, in 2008. Since 2016, he has been an associate professor at Kobe University, Japan. His research interests include autonomous vehicles, mobile robots, and humanoid robots.