Classification into Two-Parameter Exponential Populations with a Common Guarantee Time

SYNOPTIC ABSTRACT

Let Π₁, Π₂, …, Π_k be k (≥2) exponential populations with unknown scale parameters σ₁, σ₂, …, σ_k, respectively, and an unknown but common location parameter μ. First, we consider the estimation of scale parameters when an isotonic ordering among the scale parameters is present. We show the superiority of a class of mixed estimators over the maximum likelihood estimators of scale parameters under a scale-invariant loss function. Bayes and generalized Bayes estimates of scale parameters are obtained assuming proper and improper prior distributions, respectively. As an application of these new estimators, we have considered the problem of classifying an observation into one of k populations under order restrictions on scale parameters. Classification rules are proposed based on mixed estimators. We also derive plug-in Bayes classification rules and likelihood ratio-based classification rules. Extensive simulations are performed to compare these rules with respect to the expected probability of correct classification. An application of the classification rules is done on a real data set.

Key Words and Phrases:

• Bayes estimator
• best affine equivariant estimator
• likelihood ratio
• mixed estimator
• probability of correct classification.

Mathematics Subject Classification:

• 62H30
• 62F30

1. Introduction

Suppose an observation x has come from one of k (≥2) populations Π₁, Π₂, …, Π_k but the exact population is unknown. The random variable X_i corresponding to Π_i is exponentially distributed with an unknown location parameter μ and unknown scale parameter σ_i, (i = 1, 2, …, k). The probability density function (pdf) of the random variable X_i is (1) where Suppose an observation x has to be classified into one of these k populations. As an example, suppose a rocket is launched from a surface (ground or sea). At a certain stage of launching, process failure has occurred due to damage to an individual component out of two major components. It is known that the failure rate of one component is greater than that of another component. From the observed failure time, we need to identify which particular component may have failed.

The problem of estimation of the parameters of several shifted exponential distributions having a common location parameter μ but different scale parameters has received considerable attention from many researchers. For this model, Pal and Sinha (1990) compared the risk of maximum likelihood estimate (MLE), modified MLE, and uniformly minimum variance unbiased estimator (UMVUE) of μ in terms of Pitman measure of closeness. They proposed a class of estimators of μ dominating over the MLE under a particular condition. For this model, the testing on the parameter μ has been studied by Chang, Lin, and Pal (2013). Recently, when the scale parameters are ordered, Tripathi, Kumar, and Misra (2014) derived estimators of μ improving over the modified MLE and the UMVUE derived by Ghosh and Razmpour (1984). As far as we know, there are no studies on the estimation of the ordered scale parameters for this model.

The problem of classification of an observation into one-parameter exponential populations was first studied by Basu and Gupta (1974). For this model, Adegboye (1993) showed that the probability of misclassification of an observation depends on the ratio of the scale parameters only. They established that the plug-in Bayes classification rule is superior to the Fisher's discriminant rule. Basu and Gupta (1977) extended the results of Basu and Gupta (1974) to k (≥2) two-parameter exponential distributions and proposed the likelihood-ratio criterion–based rules. They also derived rules based on a Bayes predictive approach. Wakaki (1998) considered the problem of classification of an observation into one of the two multivariate elliptical populations with different mean vectors and different covariance matrices. He used the asymptotic distribution of the classification statistic to express the conditional probabilities of misclassification of an observation. In recent years, classification rules of an observation into k (≥2) populations have been improved using additional information on the parameters. Long and Gupta (1998) first improved the linear classification rules for classifying an observation into one of the two multivariate normal populations with identity matrices as covariance matrices. They also assumed an ordering between the components of the mean vectors. They showed that the proposed rule is better than the linear discriminant rule of Anderson (1951). When the mean vectors are assumed to be restricted to a cone, Fernández, Rueda, and Salvador (2006) developed improved classification rules. For two univariate normal populations having a common mean but different variances, Jana and Kumar (2015) showed that the classification rule based on the Graybill Deal estimator of the common mean performs better than other rules in terms of expected probability of misclassification (EPM). They also proposed rules when variances are ordered. Conde, Fernández, and Salvador (2005) improved classification rules proposed by Basu and Gupta (1974) for two exponential populations, assuming that the mean of the first population is greater than that of the second population. Jana, Kumar, and Misra (2014) proposed a class of classification rules that includes the rule proposed by Conde et al. (2005). To the best of our knowledge, the classification rule for the exponential distribution having an unknown common mean and ordered scale parameters has not been studied in literature. We shall consider an example where such ordering among the scale parameters arises. Consider an electronic water purifier machine. Due to stepwise removal of impurities at k different steps, the average longevity of components is expected to be in an increasing order, though the minimum guarantee time will be the same for each of the components due to the terms and conditions of the manufacturer.

Suppose independent random samples are taken from k exponential populations having a common unknown location parameter μ and unknown scale parameters σ₁, σ₂, …, σ_k, respectively, where the scale parameters are assumed to follow an ordering; 0 < σ₁ ≤ σ₂ ≤ … ≤ σ_k < ∞. In Section 2 of this article, we have considered the problem of estimating scale parameters. For the case k = 2, mixed estimators are proposed and shown to dominate over the unrestricted MLEs for specific range of the mixing parameter. Further, we derive Bayes and generalized Bayes estimates of scale parameters with respect to a gamma prior and a noninformative prior distribution, respectively. The loss function is the squared error. The problem of estimating ratio of scale parameters is also considered and a class of affine equivariant estimators is derived. Risk functions of all proposed estimators are compared numerically.

In Section 3, the problem of classification of an observation into one of two exponential populations is considered under isotonic ordering among scale parameters. Several rules are proposed using estimators proposed in Section 2. Likelihood-based classification rules are also derived under order restrictions. These rules are further extended to the case k ≥ 3. Finally, the performance of these rules is then compared numerically with respect to the expected probability of correct classification.

2. Estimation Under Restrictions on Scale Parameters

Define as a random sample from the population Π_i, (i = 1, 2, …, k) and these random samples are mutually independent. Suppose and . The statistic is complete and sufficient for , where . Note that Z and are independently distributed with the probability density functions and (2) respectively, where p = ∑^k_{i = 1}n_iσ_i^{− 1}. Under the ordering, the isotonic regression of s with appropriate weights n_is are given by the following min–max formula (see Barlow, Bartholomew, Bremner, & Brunk, 1972). where For k = 3, using the pool-adjacent-violators algorithm (Barlow et al., 1972), the MLE of , when σ₁ ≤ σ₂ ≤ σ₃, is obtained as follows: When no such ordering between the parameters is present, Ghosh and Razmpour (1984) derived the UMVUE and the modified MLE of μ given by and respectively. Assuming the ordering σ₁ ≤ σ₂ ≤ … ≤ σ_k, Tripathi et al. (2014) proposed the following isotonic version of the unrestricted modified MLE: (3) For two populations, in the presence of the restriction σ₁ ≤ σ₂, they derived the estimators and improving over the estimators and of μ, respectively, where and We utilize these estimators to propose new classification rules in Section 3.

2.1. Mixed Estimators

We shall use the existing basic estimators to propose a class of mixed estimators for the scale parameters of the exponential distributions when an additional information among the parameters is known. Katz (1963) first proposed a mixed estimator of the ordered probabilities of successes (say, θ₁ and θ₂), where 0 < θ₁ ≤ θ₂ ≤ 1. They showed that any estimator of the parameter satisfying P_θ(δ₁ > δ₂) > 0, for all θ ∈ Θ, is dominated by the mixed estimator based on where δ_1α = min (δ₁, αδ₁ + (1 − α)δ₂) and δ_2α = max (δ₂, (1 − α)δ₂ + αδ₁). Kumar and Sharma (1988) proposed the mixed estimators of the ordered scale parameters of two normal distributions. For two exponential distributions having known location parameters, Vijayasree and Singh (1993) considered mixed estimators and obtained minimal complete class among the class of estimators. Following these, we propose the mixed estimators based on the MLE of the scale parameters. The usual MLEs of σ₁, σ₂ are (4) respectively. We define the following mixed estimators when the ordering σ₁ ≤ σ₂ is known: (5) (6) Note that when α = n₁/(n₁ + n₂), the estimator is the restricted MLE of σ₁ and when α = n₂/(n₁ + n₂), the estimator is the restricted MLE of σ₂. We denote the restricted MLE of σ_i by σ^rm_i for i = 1, 2. Now, we compare the risk of estimator δ_i of the parameter σ_i with respect to the loss function (7) We have the following results.

Theorem 1.

Let and be the MLE and the mixed estimators of σ_i as defined in (4(4) )–(6(6) ). Suppose denotes the risk of the estimator σ*_i in estimating σ_i for i = 1, 2. Then for all 0 < σ₁ ≤ σ₂,

(i)	α ∈ [α1, 1], where α1 = n1/(n1 + n2), n1 ≥ 1, n2 ≥ 1,
(ii)	, α ∈ [α2, 1], where α2 = n2/(n1 + n2), n1 ≥ 1, n2 ≥ 1,
(iii)	For α ∈ [0, 1], and n1 = n2 = n, and .

Proof.

(i) Suppose is the joint pdf of T₁ and T₂. The difference in risk of and is where I_S(.) denote the indication function defined over the region S = {(T₁, T₂): 0 < n₁T₂ < n₂T₁ < ∞}. Now on substituting t₁ = n₁yz/n₂, t₂ = y and solving the inner integral, we have (8) where Let g(z) = (n₁ + n₂)((1 + α)z + 1 − α) − 2(n₁z + n₂ρ). Clearly, g is an increasing function of z for α ≥ α₁. The function g achieves zero value at Note that z₀ < 1. Since g is an increasing function and it is nonnegative on [z₀, ∞) for all α ≥ α₁, we conclude g(z) > 0 for z > 1 and α > α₁. Therefore, the integrand of (8(8) ) is negative. Hence Δ₁ < 0 and this completes the proof.

The proofs of (ii) and (iii) follow in a similar fashion.

Remark 1.

The right-hand side of (8(8) ) is a function of ρ only. Hence, the risk difference of the estimators and of the parameter σ_i for i = 1, 2 depends on the parameters only through ρ.

2.2. Bayes and Generalized Bayes Estimators

Now we consider the Bayes estimation of the scale parameters assuming a known prior distribution of the scale parameters. Consider the noninformative prior density of the parameters (σ₁, σ₂) as given by Π(σ₁, σ₂) = 1/(σ₁σ₂), 0 < σ₁ ≤ σ₂ < ∞. The joint PDF of and is given by The marginal probability density function of is given by and the posterior probability density of given is where is the normalizing constant. With respect to the scale equivariant squared error loss function (7(7) ), the generalized Bayes estimator for σ₁ is the mean of the posterior distribution. (9) where R₁ = {(σ₁, σ₂): 0 < σ₁ ≤ σ₂ < ∞}. Suppose s = t₁/t₂. Using the transformations t₁/σ₁ = ss₁s₂, t₂/σ₂ = s₂, we evaluate the integral and the generalized Bayes estimator of σ₁ as (10) Similarly, the generalized Bayes estimator of σ₂ is given by (11)

Similarly, assuming the inverse gamma prior distribution of σ_i with probability density function for i = 1, 2, the Bayes estimators of σ₁ and σ₂ are (12) and (13) respectively. We apply these estimators to propose classification rules in Section 3 of this article.

2.3. Affine Equivariant Estimators

In this section, we consider the estimation of the parameter ρ = σ₁/σ₂ under the loss function (14) where δ is an estimator of the parameter ρ. Consider the affine group of transformations Then under the transformations the family of distributions remains invariant and we have X_i(1) transforms to a_iX_i(1) + b_i and T_i transforms to a_iT_i. The complete sufficient statistic of (μ, σ₁, σ₂) is (Z, T₁, T₂). Let T = T₁/T₂, Then we have the following result.

Theorem 2.

The estimator c_*T improves the estimator cT if c < c_* and the estimator c^*T improves cT if c > c^*. The class of estimators {cT: c_* ≤ c ≤ c^*} forms an admissible class within estimators of the form cT for estimating ρ.

Proof.

The loss function (14(14) ) will be invariant if δ transforms to We have where a₁, a₂ > 0 and . The form of the scale equivariant estimator is δ_c(T) = cT, where c > 0. The risk is minimum when where ρ = σ₁/σ₂ ∈ (0, 1]. Since φ(ρ) is a decreasing function of ρ for n₂ > 3, and . An application of the Brewster and Zidek (1974) technique shows that the estimator improves the estimator cT if c^* < c, the estimator improves cT if c_* > c and the estimator δ_c is admissible among all δ_c if c^* ≤ c ≤ c^*.

We apply these estimators to evaluate the EPC given in Eq. (16(16) ) of the forthcoming section when the parameters are unknown.

2.4. Numerical Comparisons

We shall now provide the risk comparison of the estimators of σ₁ with respect to the loss function (7(7) ) using simulation. The risk calculations are based on 50,000 generations of random samples from each of two exponential populations. We denote the risk of the estimator δ by R(δ). The risk of the estimators of the parameters σ_i (i = 1,2) are functions of ρ = σ₁/σ₂ only. In Table 1, for a fixed value of σ₂ = 1, the risks of the estimators of σ₁ are reported considering different values of ρ and for different sample sizes such as (n₁, n₂) = (3, 3), (6, 6), (9, 9), (12, 12), (9, 12), (12, 9). We observe the following conclusions.

Table 1. Risk performance of proposed estimators of σ₁.

	(n1, n2) = (3, 3)				(n1, n2) = (6, 6)
ρ			R(σ^rm1)	R(δ^gb1)			R(σ^rm1)	R(δ^gb1)
0.1	0.3344	0.3312	0.3318	0.5799	0.1661	0.1661	0.1661	0.3313
0.2	0.3346	0.3207	0.3228	0.5708	0.1663	0.1651	0.1656	0.3255
0.3	0.3348	0.3076	0.3094	0.5651	0.1664	0.1606	0.1624	0.322
0.4	0.335	0.298	0.2956	0.5619	0.1665	0.1535	0.1566	0.3209
0.5	0.3352	0.2939	0.2834	0.5604	0.1664	0.1461	0.1492	0.3218
0.6	0.3353	0.2946	0.273	0.5599	0.1664	0.1412	0.1415	0.3242
0.7	0.3354	0.2996	0.2645	0.56	0.1663	0.1406	0.1348	0.3278
0.8	0.3356	0.3082	0.2581	0.5607	0.1662	0.1447	0.1297	0.332
0.9	0.3357	0.3196	0.2533	0.5617	0.1662	0.1534	0.1263	0.3366
1	0.3357	0.3333	0.25	0.5628	0.1661	0.166	0.1246	0.3414
	(n1, n2) = (9, 9)				(n1, n2) = (12, 12)
ρ			R(σ^rm1)	R(δ^gb1)			R(σ^rm1)	R(δ^gb1)
0.1	0.1105	0.1105	0.1105	0.2195	0.0831	0.0831	0.0831	0.1591
0.2	0.1104	0.1103	0.1104	0.2157	0.0832	0.0832	0.0832	0.1565
0.3	0.1102	0.1092	0.1096	0.2129	0.0831	0.0828	0.0829	0.1544
0.4	0.1102	0.1056	0.1071	0.2117	0.0831	0.0811	0.0819	0.1532
0.5	0.1101	0.1003	0.1027	0.2125	0.0831	0.0775	0.0792	0.1536
0.6	0.1101	0.095	0.0973	0.215	0.0831	0.0728	0.0752	0.1558
0.7	0.1101	0.0922	0.0918	0.2191	0.0831	0.0693	0.0706	0.1595
0.8	0.1101	0.0936	0.0873	0.2241	0.0832	0.0691	0.0664	0.1645
0.9	0.1101	0.0996	0.0842	0.2298	0.0832	0.0736	0.0635	0.1705
1	0.1101	0.1104	0.0828	0.236	0.0832	0.0831	0.0624	0.177
	(n1, n2) = (9, 12)				(n1, n2) = (12, 9)
ρ			R(σ^rm1)	R(δ^gb1)			R(σ^rm1)	R(δ^gb1)
0.1	0.1097	0.1097	0.1097	0.2177	0.0824	0.0824	0.0824	0.1597
0.2	0.1096	0.1095	0.1096	0.2128	0.0824	0.0823	0.0823	0.1576
0.3	0.1095	0.1086	0.1089	0.2091	0.0823	0.0815	0.0818	0.1562
0.4	0.1095	0.1053	0.1066	0.2069	0.0823	0.0794	0.0804	0.1561
0.5	0.1095	0.099	0.1018	0.2065	0.0822	0.0764	0.0779	0.1576
0.6	0.1095	0.0918	0.0953	0.2081	0.0822	0.0738	0.0746	0.1607
0.7	0.1095	0.086	0.0884	0.2114	0.0822	0.0733	0.071	0.165
0.8	0.1095	0.084	0.0825	0.2162	0.0822	0.0766	0.068	0.1702
0.9	0.1095	0.0873	0.0786	0.222	0.0822	0.0843	0.066	0.176
1	0.1095	0.0958	0.077	0.2286	0.0822	0.0964	0.0652	0.182

1.	The restricted MLE σrm1 of the scale parameter σ1 performs better than estimators , and δgbi for moderate and large values of ρ and the estimator σrm1 has the lowest risk for equal sizes as well as for unequal sizes samples.
2.	The estimators and σrm1 have similar risk performance when ρ is very low. The risk of each of the estimators decreases as ρ increases.
3.	If σ1 is close to σ2, the relative percentage improvement of the estimator σrm1 over the estimator is 25%.

Table 2 shows the risks of the estimators of the parameter σ₂ for various values of n₁, n₂, σ₂, where σ₁ is fixed as one. We have evaluated the risks of the estimators considering size of the samples as (n₁, n₂) = (3, 3), (6, 6), (9, 9), (12, 12), (9, 12), (12, 9). We mention the following observations.

Table 2. Risk performance of proposed estimators of σ₂.

	(n1, n2) = (3, 3)				(n1, n2) = (6, 6)
σ2			R(σ^rm2)	R(δ^gb2)			R(σ^rm2)	R(δ^gb2)
1.1	0.3302	0.2945	0.2503	0.2896	0.1652	0.1443	0.126	0.1312
1.2	0.3302	0.2751	0.2561	0.3003	0.1652	0.1343	0.1297	0.1405
1.3	0.3302	0.2659	0.2624	0.3093	0.1652	0.131	0.1339	0.1486
1.4	0.3303	0.2625	0.2688	0.3167	0.1651	0.1312	0.1379	0.1555
1.5	0.3303	0.2627	0.2747	0.323	0.1651	0.1332	0.1417	0.1615
1.6	0.3304	0.2648	0.2802	0.3282	0.1651	0.1361	0.145	0.1666
1.7	0.3304	0.268	0.2852	0.3326	0.1651	0.1391	0.1479	0.1709
1.8	0.3304	0.2718	0.2897	0.3363	0.1651	0.1421	0.1505	0.1746
1.9	0.3304	0.2758	0.2938	0.3395	0.165	0.145	0.1526	0.1778
2	0.3305	0.2797	0.2974	0.3421	0.165	0.1475	0.1544	0.1805
	(n1, n2) = (9, 9)				(n1, n2) = (12, 12)
σ2			R(σ^rm2)	R(δ^gb2)			R(σ^rm2)	R(δ^gb2)
1.1	0.1108	0.0951	0.0852	0.0795	0.0828	0.0697	0.0636	0.0562
1.2	0.1108	0.089	0.0883	0.0868	0.0828	0.0656	0.0664	0.062
1.3	0.1108	0.0881	0.0917	0.0932	0.0828	0.0657	0.0693	0.0674
1.4	0.1108	0.0896	0.095	0.0989	0.0828	0.0676	0.0721	0.0721
1.5	0.1108	0.092	0.0978	0.1039	0.0828	0.0701	0.0744	0.0763
1.6	0.1108	0.0947	0.1003	0.1081	0.0828	0.0725	0.0763	0.0798
1.7	0.1108	0.0972	0.1023	0.1117	0.0828	0.0746	0.0778	0.0829
1.8	0.1108	0.0995	0.1039	0.1148	0.0828	0.0763	0.0789	0.0854
1.9	0.1108	0.1014	0.1052	0.1174	0.0828	0.0777	0.0798	0.0876
2	0.1107	0.1031	0.1063	0.1196	0.0828	0.0788	0.0805	0.0894
	(n1, n2) = (9, 12)				(n1, n2) = (12, 9)
σ2			R(σ^rm2)	R(δ^gb2)			R(σ^rm2)	R(δ^gb2)
1.1	0.0828	0.0787	0.0659	0.0655	0.1111	0.0865	0.0826	0.0665
1.2	0.0829	0.0711	0.0681	0.0707	0.1111	0.084	0.0863	0.0743
1.3	0.0829	0.0688	0.0706	0.0754	0.1111	0.0854	0.0904	0.0817
1.4	0.0829	0.0691	0.0729	0.0794	0.1112	0.0885	0.0942	0.0883
1.5	0.0829	0.0706	0.0749	0.0828	0.1112	0.092	0.0975	0.0942
1.6	0.0829	0.0724	0.0766	0.0857	0.1112	0.0953	0.1002	0.0994
1.7	0.0829	0.0741	0.0779	0.0881	0.1112	0.0982	0.1025	0.1039
1.8	0.0829	0.0757	0.079	0.0901	0.1112	0.1006	0.1042	0.1077
1.9	0.0829	0.0771	0.0798	0.0918	0.1112	0.1026	0.1057	0.111
2	0.0829	0.0783	0.0805	0.0932	0.1112	0.1043	0.1068	0.1139

1.	The estimators and σrm2 are uniformly better than the MLE for all values of the parameter σ2. There is a substantial improvement when σ1 and σ2 are close to each other. For moderate values of σ2, the generalized Bayes estimator σgb2 is also better than the MLE .
2.	For small size samples, when ρ is close to one, the estimator σrm2 has the lowest risk than all proposed estimators; however, for the large sample, both the estimators σrm2 and σgb2 have similar risk performance.
3.	For unequal as well as for equal size samples, when ρ is close to one, the estimator σgb2 performs better than estimator .

3. Classification Rules

In this section, we present the classification rules to classify an observation using the estimators derived in the previous section. Suppose x is an observation that is to be classified into one of the populations Π₁, Π₂, …, Π_k. Assume that the priori probability that an observation comes from the ith population is q_i, i = 1, 2, …, k, where ∑^k_{i = 1}q_i = 1. If an observation actually comes from one population and we assign it to another population, then it is considered as misclassified. Suppose C(i|j) denotes the cost of misclassification where i, j = 1, 2, …, k and i ≠ j. The performance of the classification rules is measured with respect to the expected probability of correct classification (EPC). Let P(i|j) denote the probability of classifying an observation into the ith population when it actually belongs to the jth population. Then the EPC is ∑^k_{i = 1}q_iP(i|i) and the expected cost of misclassification (ECM) is ∑_{i ≠ j}q_jP(i|j)C(i|j). When all parameters are known, minimizing the ECM, Anderson (1951) derived the Bayes classification rule: Classify x into Π_i if First, we consider the classification rules for two exponential populations with a common location but ordered scale parameters and then for k (≥2) such populations.

3.1. Rules for Two Populations

In this subsection, we study the rule for classifying an observation x into two populations Π₁ and Π₂ assuming C(1|2) = C(2|1) and q₁ = q₂. When the parameters are known, the usual classification rule is as follows: Classify the observation x into Π₁ if and only if U(x) ≤ 0, where (15) The probabilities of correct classification P(1|1) and P(2|2) can be expressed as and respectively, where l = log ρ/(ρ − 1), and F_Y is the distribution function of an exponentially distributed random variable with mean equal to one. Therefore, the expected probability of correct classification is (16) When the parameters are unknown, we plug in the estimators and propose the classification rule, R₁.

• R₁: Classify the observation x into Π₁ if and only if U₁(x) ≤ 0, where The rule based on the mixed estimators of the parameters σ₁ and σ₂ is given by R^(α)₂.

• R^(α)₂: Classify the observation x into Π₁ if and only if U^(α)₂(x) ⩽ 0, where

Since the distribution of (Z − x) is independent of μ, the distributions of the classification statistic U₁(x) and U^(α)₂(x) are independent of μ.

Remark 2.

The EPC does not depend on the location parameter. The classification rule proposed by Basu and Gupta (1977) is different from the above rule, since the MLE Z of the common location parameter μ has been used in the proposed rule.

We have the following result on the individual probability of correct classification.

Theorem 3.

The probability P(1|1) of the rule R₁, is greater than P(1|1) corresponding to the rule R⁽⁰⁾₂.

Proof.

We have to show that P(U₁(x) ⩽ 0|X ∈ Π₁) ⩾ P(U⁽⁰⁾₂(x) ⩽ 0|X ∈ Π₁). Note that under the condition n₂T₁ < n₁T₂, and and therefore the classification functions U₁(x) and U⁽⁰⁾₂(x) are equal. Also, if n₂T₁ > n₁T₂, then the classification statistic U⁽⁰⁾₂(x) = −U₁(x). The difference between the probabilities of correct classification into population Π₁ corresponding to the rule R₁ and R⁽⁰⁾₂ is (17) where D = {(T₁, T₂): n₂T₁ > n₁T₂}, (18) and is the cumulative distribution function of the random variable (T₁, T₂). When the observation belongs to Π₁, the distribution of U = (x − Z) is given by the probability density function where p = n₁/σ₁ + n₂/σ₂. Therefore, the integrand in (17(17) ) is reduced to 1 − 2(1 + pσ₁)⁻¹ exp {g(t₁, t₂)}, which is negative since g(t₁, t₂) > 0. The proof follows immediately.

The comparison of the rules, when the observation is correctly classified into second population, is established here.

Theorem 4.

The probability P(2|2) of rule R₁, is less than the probability P(2|2) corresponding to the rule R⁽⁰⁾₂.

Proof.

We have to show that P(U₁(x) > 0|X ∈ Π₂) ⩽ P(U⁽⁰⁾₂(x) > 0|X ∈ Π₂). The difference between the probabilities of correct classification into Π₂ corresponding to the rule R₁ and R^(α)₂ is (19) where D and g(t₁, t₂) are defined in (18(18) ). When the observation belongs to Π₂, the distribution of V = (x − Z) is given by the probability density function Therefore, the integrand in (19(19) ) is reduced to 2(1 + pσ₂)⁻¹ exp {g(t₁, t₂)} − 1, which is negative since g(t₁, t₂) < 0. The proof follows immediately.

Theorem 5.

The ordered classification rule R⁽⁰⁾₂ is better than the usual classification rule R₁ with respect to the EPC.

Proof.

It is sufficient to show From Eqs. (17(17) ) and (19(19) ), we have Since σ₁ ≤ σ₂, we have Δ₁ + Δ₂ ≤ 0. Thus the proof follows.

Theorems 3, 4, and 5 also hold when we have to classify a sample y₁, y₂, …, y_m of size m > 1 coming from the same population. In this case, we use the sufficient statistic ∑^m_{i = 1}y_i, instead of x for classification. The proof follows in a similar way since ∑^m_{i = 1}y_i/m follows Exp(μ, σ₁/m) if the sample belongs to Π₁ and ∑^m_{i = 1}y_i/m follows Exp(μ, σ₂/m) if the sample belongs to Π₂.

We also propose classification rules based on these Bayes estimators of the scale parameters. Plugging in estimators δ^gb₁, δ₂^gb and in (15(15) ), we have the classification rule R₃. Similarly, the rule R₄ is obtained substituting the estimators δ^b₁, δ₂^b, and for the parameters in (15(15) ). The comparison of the rules R₁, R⁽⁰⁾₂, R₃, and R₄ is carried out in the numerical comparison section.

3.2. Likelihood Ratio-Based Rule

We derive the likelihood ratio-based classification rule (LR rule) following Anderson (2003) through the testing procedure of a composite hypothesis versus its alternative composite hypothesis. To classify an observation x, we test the hypothesis H₁: belong to Π₁ and belong to the population Π₂ versus the alternative hypothesis H₂: belong to Π₁ and belong to population Π₂. The likelihood ratio is given by (20) where , and Suppose r = (n₁ + 1)⁻¹ and s = (n₂ + 1)⁻¹. Under the hypothesis H₁, the MLEs of μ, σ₁, and σ₂ are , and respectively and under the hypothesis H₂, the MLEs of μ, σ₁, and σ₂ are and , respectively. Therefore, the LR rule, say, R₅, is as follows:

• R₅: Classify x into Π₁ if λ^* ≥ c else classify x into Π₂, where (21) The cutoff point c should be chosen such that the EPC is high. We determine the cutoff point using the bootstrap method.

3.3. Rules for k Populations

We consider k(≥2) exponential populations Π_is with unknown scale parameters σ₁, σ₂, …, σ_k and a common unknown location parameter μ. Suppose the prior probabilities that an observation may come from exactly one of these k populations are equal. An observation x has to be classified into one of these k populations. When the parameters are known, the classification function related to the ith and jth population is (22) Plugging in the MLEs , and of the parameters μ, σ_i, and σ_j, respectively, the estimated classification function is If the prior probabilities are known, then the classification rule, say, R_m, is as follows:

• R_m: Classify the observation x into Π_i if u_ij(x) > 0 for j = 1, …, k, i ≠ j.

Now we consider that random variables associated with the k exponential populations Π_is have unknown scale parameters but they follow a simple order restriction 0 < σ₁ ≤ σ₂ ≤ … ≤ σ_k < ∞. Under this ordering, the isotonized version estimators of the parameters are mentioned in Section 2. Corresponding to the estimators and , we get the classification rule R_IR.

• R_IR: Classify the observation x into Π_i if u_ij(x) > 0 for j = 1, …, k, i ≠ j, where We discuss the performance of the rules for k = 3 in the following subsection.

3.4. Numerical Comparisons

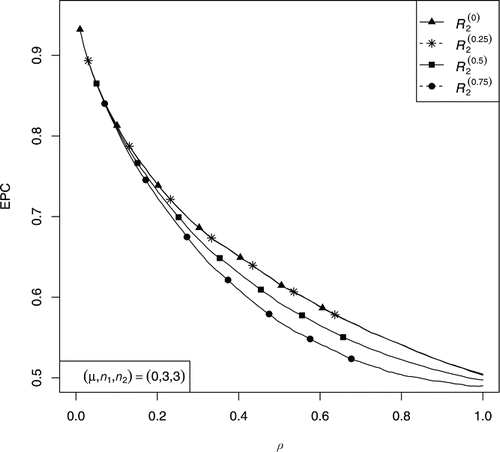
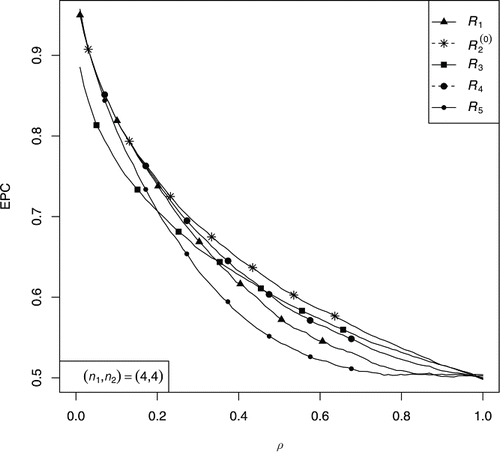
In this section, we describe the results of comprehensive simulation study considering 50,000 replications. We compare the classification rules with respect to EPC. The probability of correct classification corresponding to each classification rule is estimated using the frequency definition of probability. Firstly, we perform the classification into two exponential populations and predict the results. The plot of the EPC of the rules R^(α)₂ for several values of α is shown in Figure 1. Among these rules based on the mixed estimators, the rule corresponding to α = 0 is the best rule. We have chosen the cutoff point c = 1.6 for the classification rule R₅ in Figure 2. The following conclusions are drawn from the plot of the EPC of rules R₁, R⁽⁰⁾₂, R₃, R₄, and R₅ as shown in Figure 2.

Figure 1. EPC of rule R^(α)₂ for different values of α.

Figure 2. Plot of the EPC corresponding to classification rules vs. ρ.

1.	The rule R4 based on the restricted MLEs of σis is better than the usual rule R1.
2.	The classification rule R(0)2 has the highest EPC among all classification rules and therefore for application, it is the best rule among all proposed rules.
3.	For high and moderate values of ρ, the rule R3 is better than the usual rules R1 and R5, however, the rule R3 has lower EPC than both rules R1 and R(0)2 for small values of ρ.
4.	If ρ is close to zero or one, the performance of rules R1, R(0)2, and R3 is equally good.
5.	For large sample sizes, all classification rules exhibit more or less the similar performance.

We define the relative percentage improvement of EPC for the rule R_i over the rule R₁ by In Table 3, the relative percentage improvements of the EPC of the rules over the usual rule R₁ are mentioned for the equal size samples as well as for the unequal size samples. The rules R⁽⁰⁾₂ and R₄ always show improvement over the usual rule R₁ and among the classification rules R⁽⁰⁾₂ and R₄, rule R⁽⁰⁾₂ is better. For small sample size and for moderate values of ρ, the amount of improvement is 7–10%. Therefore, for classifying an observation, we recommend the rule R⁽⁰⁾₂ based on the mixed estimators of the scale parameters corresponding to α = 0 for all values of ρ.

Table 3. Relative improvement of EPC of the ordered rules over the usual rule.

	(n1, n2) = (3, 3)			(n1, n2) = (6, 6)			(n1, n2) = (12, 12)
ρ	RI21	RI31	RI41	RI21	RI31	RI41	RI21	RI31	RI41
0.1	0.3572	−6.2586	0.1786	0.006	−4.0732	0.003	0	−1.4169	0
0.2	1.8415	−4.0888	0.9207	0.2994	−3.3121	0.1497	0.0039	−1.3693	0.002
0.3	4.0702	−1.1206	2.0351	1.3131	−1.7668	0.6566	0.1249	−0.9157	0.0625
0.4	6.4406	2.22	3.2203	3.1183	0.4337	1.5591	0.7098	−0.1183	0.3549
0.5	8.158	4.8422	4.079	5.1822	3.0665	2.5911	1.9747	1.1624	0.9873
0.6	8.7325	6.2825	4.3662	6.5505	4.9169	3.2752	3.5163	2.8506	1.7581
0.7	8.1254	6.4496	4.0627	6.6775	5.478	3.3387	4.4613	3.8065	2.2306
0.8	6.3361	5.229	3.1681	5.929	5.1501	2.9645	4.377	3.8706	2.1885
0.9	3.4588	2.801	1.7294	3.5724	3.2244	1.7862	2.8181	2.5222	1.409
1	0.2147	0.0582	0.1074	0.419	0.3238	0.2095	−0.1197	−0.3033	−0.0599
	(n1, n2) = (3, 6)			(n1, n2) = (3, 9)			(n1, n2) = (3, 12)
ρ	RI21	RI31	RI41	RI21	RI31	RI41	RI21	RI31	RI41
0.1	0.3572	−6.2586	0.1786	0.006	−4.0732	0.003	0	−1.4169	0
0.2	1.8415	−4.0888	0.9207	0.2994	−3.3121	0.1497	0.0039	−1.3693	0.002
0.3	4.0702	−1.1206	2.0351	1.3131	−1.7668	0.6566	0.1249	−0.9157	0.0625
0.4	6.4406	2.22	3.2203	3.1183	0.4337	1.5591	0.7098	−0.1183	0.3549
0.5	8.158	4.8422	4.079	5.1822	3.0665	2.5911	1.9747	1.1624	0.9873
0.6	8.7325	6.2825	4.3662	6.5505	4.9169	3.2752	3.5163	2.8506	1.7581
0.7	8.1254	6.4496	4.0627	6.6775	5.478	3.3387	4.4613	3.8065	2.2306
0.8	6.3361	5.229	3.1681	5.929	5.1501	2.9645	4.377	3.8706	2.1885
0.9	3.4588	2.801	1.7294	3.5724	3.2244	1.7862	2.8181	2.5222	1.409
1	0.2147	0.0582	0.1074	0.419	0.3238	0.2095	−0.1197	−0.3033	−0.0599
	(n1, n2) = (6, 3)			(n1, n2) = (9, 3)			(n1, n2) = (12, 3)
ρ	RI21	RI31	RI41	RI21	RI31	RI41	RI21	RI31	RI41
0.1	0.3572	−6.2586	0.1786	0.3225	−3.7114	0.1613	0.2583	−3.0896	0.1291
0.2	1.8415	−4.0888	0.9207	1.6051	−1.9517	0.8026	1.4885	−1.4604	0.7442
0.3	4.0702	−1.1206	2.0351	3.8149	0.767	1.9075	3.6094	1.3395	1.8047
0.4	6.4406	2.22	3.2203	6.0434	3.5063	3.0217	5.8755	4.0261	2.9378
0.5	8.158	4.8422	4.079	8.0463	6.2658	4.0232	7.6168	6.2753	3.8084
0.6	8.7325	6.2825	4.3662	8.8039	7.5897	4.4019	8.6998	7.8581	4.3499
0.7	8.1254	6.4496	4.0627	8.2503	7.5752	4.1252	8.2219	7.6464	4.1109
0.8	6.3361	5.229	3.1681	6.3959	6.229	3.198	6.5352	6.2482	3.2676
0.9	3.4588	2.801	1.7294	3.455	3.5089	1.7275	3.8379	3.7021	1.919
1	0.2147	0.0582	0.1074	0.148	0.111	0.074	0.346	0.244	0.173

Now we consider the case for classifying an observation into one of the three populations, assuming that the costs of misclassifications are equal and q_i = 1/3 for i = 1, 2, 3. In Table 4, the EPC of an observation is listed for fixed values of ρ₁( = σ₁/σ₂) and ρ₂( = σ₂/σ₃) and for different configuration of the samples. For each value of ρ₁, the first and the second rows of Table 4 represent the EPC of the rules R_m and R_IR, respectively. We observed the following conclusions.

Table 4. EPC of rules R₁ and R_IR for three populations.

	(n1, n2, n3) = (4, 4, 4)				(n1, n2, n3) = (8, 8, 8)
↓ρ1 ρ^→2	0.25	0.5	0.75	1	0.25	0.5	0.75	1
0.25	0.6175	0.5361	0.4932	0.4716	0.6373	0.556	0.5072	0.4847
	0.6053	0.4975	0.4153	0.357	0.6354	0.5392	0.4477	0.3752
0.5	0.539	0.4567	0.4094	0.385	0.5582	0.4784	0.428	0.4005
	0.4963	0.3967	0.3211	0.2666	0.5377	0.4477	0.365	0.2999
0.75	0.4961	0.4096	0.3631	0.3441	0.5083	0.4274	0.3731	0.3488
	0.4082	0.3139	0.2415	0.19	0.4365	0.3531	0.2746	0.2108
1	0.4743	0.3847	0.3443	0.3322	0.4862	0.4004	0.3485	0.3327
	0.3433	0.2517	0.1822	0.1344	0.352	0.2737	0.1969	0.1369
	(n1, n2, n3) = (4, 4, 8)				(n1, n2, n3) = (4, 8, 4)
↓ρ1 ρ^→2	0.25	0.5	0.75	1	0.25	0.5	0.75	1
0.25	0.6227	0.5413	0.4928	0.4721	0.6256	0.5416	0.4944	0.4724
	0.6133	0.5132	0.4251	0.3601	0.6188	0.5091	0.4207	0.3572
0.5	0.543	0.4627	0.4119	0.3863	0.5455	0.4614	0.4116	0.3864
	0.5036	0.4116	0.3314	0.271	0.5169	0.4158	0.3352	0.2781
0.75	0.5009	0.4172	0.3645	0.3418	0.4978	0.4107	0.362	0.3429
	0.4154	0.3293	0.2515	0.1914	0.4226	0.3284	0.2532	0.1998
1	0.4819	0.3936	0.3446	0.331	0.4751	0.386	0.3429	0.3319
	0.3504	0.2664	0.191	0.134	0.3505	0.2609	0.1899	0.1417
	(n1, n2, n3) = (8, 8, 4)				(n1, n2, n3) = (8, 4, 8)
↓ρ1 ρ^→2	0.25	0.5	0.75	1	0.25	0.5	0.75	1
0.25	0.6326	0.5478	0.4999	0.4803	0.6296	0.5496	0.5008	0.4789
	0.6274	0.5178	0.4291	0.3686	0.6223	0.5238	0.4351	0.3716
0.5	0.5532	0.4686	0.4174	0.3941	0.5502	0.4716	0.4205	0.3934
	0.5304	0.4283	0.3479	0.2933	0.5126	0.4223	0.3424	0.283
0.75	0.5038	0.4164	0.3652	0.3465	0.5057	0.4241	0.3697	0.3447
	0.4294	0.3341	0.2585	0.2072	0.4182	0.3335	0.2561	0.195
1	0.4793	0.388	0.3433	0.3335	0.4854	0.3976	0.3464	0.3319
	0.346	0.2552	0.1835	0.137	0.3438	0.2613	0.1832	0.1251
	(n1, n2, n3) = (8, 4, 4)				(n1, n2, n3) = (4, 8, 8)
↓ρ1 ρ^→2	0.25	0.5	0.75	1	0.25	0.5	0.75	1
0.25	0.6329	0.5522	0.5001	0.4779	0.6296	0.5496	0.5008	0.4789
	0.6297	0.533	0.4389	0.3659	0.6223	0.5238	0.4351	0.3716
0.5	0.5544	0.4747	0.4208	0.394	0.5502	0.4716	0.4205	0.3934
	0.527	0.4367	0.3511	0.2849	0.5126	0.4223	0.3424	0.283
0.75	0.5066	0.4238	0.3688	0.3452	0.5057	0.4241	0.3697	0.3447
	0.4314	0.3475	0.2671	0.2043	0.4182	0.3335	0.2561	0.195
1	0.4847	0.3973	0.346	0.3336	0.4854	0.3976	0.3464	0.3319
	0.3595	0.2796	0.2025	0.1439	0.3438	0.2613	0.1832	0.1251

1.	For low values of ρ1 and ρ2, the EPC is more than 60% for small as well for large size samples.
2.	For fixed values of ρ2, as ρ1 increases the EPC decreases. Similarly, when ρ1 is fixed, EPC decreases with respect to ρ2.
3.	The performance of the classification rule significantly increases as the sample size increases.
4.	The rule Rm dominates the classification rule RIR in terms of EPC.

Hence, we recommend the rule R_m based on the MLE for classifying an observation into one of the three exponential populations.

For two exponential populations, we show an application of the proposed rule using a real data set given in Barlow et al. (1972, p. 271).

Example:

Consider the following data representing the operational times (in hours) between successive failures of air conditioning equipments in two aircrafts (plane 7915 and plane 8044).

• Plane 7915 (sample size n₁ = 9): 359, 9, 12, 270, 603, 3, 104, 2, 438

• Plane 8044 (sample size n₂ = 10): 487, 18, 100, 7, 98, 5, 85, 91, 43, 230

Barlow et al. (1972) showed that the sample values fit exponential distribution. The equality of the common location parameter is justified at a 10% significance level. Suppose the expected lifetime of the air-conditioner used in plane 8044 is greater than that of the air-conditioner used in plane 7915. The samples corresponding to planes 7915 and 8044 can then be assumed as samples from two exponential populations with a common location μ and different scale parameters σ₁ and σ₂, respectively. We want to classify the observation x = 130. Suppose the exact population is unknown due to faulty record-keeping. For the given data, using the symbols as defined in Section 2, we have X = 2, T₁ = 1782, and T₂ = 1144. Since T₁/n₁ > T₂/n₂, the ordered classification rule R⁽⁰⁾₂ as defined in Subsection 3.1 must show better performance than rule R₁. The classification statistic U⁽⁰⁾₂(x) has value −0.0761. Therefore, we classify the observation 130 into the plane 7915 using the rule R⁽⁰⁾₂.

4. Conclusion

In this article, we have introduced mixed estimators of scale parameters of two exponential distributions with an unknown but common location parameter. We have also derived Bayes and generalized Bayes estimators of scale parameters with respect to a gamma prior and a noninformative prior, respectively, when the loss function is the squared error. For the invariant loss function, the risk improvements of the ordered estimators over the usual estimators are also noticed. Using the Bayes estimators, the restricted MLE, modified MLE, and mixed estimators, we suggested rules for classification of an observation into two populations. For two populations, we have shown that the rule based on the mixed estimator is better than the usual classification rule and other ordered rules in terms of EPC. In addition, we have numerically obtained the EPC of the rules for classifying an observation into more than two populations. Although the restricted MLEs of the scale parameters have lower risk than that of the other estimators, use of the mixed estimators of the scale parameters with mixing constant zero in the classification rule provides higher EPC than the rule based on restricted MLEs for the purpose of classification.

Acknowledgements

The authors are thankful to the referee and the editor for the valuable comments, which have substantially improved the article.