Abstract
I begin by stating a small set of troublesome but pervasive educational issues. While these have remained in the background during our work, they have served as the impetus for developing and reflecting on possible roles for computer technology in classrooms. In the remaining sections of the paper I propose that the computer can serve as an effective mediator between action and symbol. After setting the scene in the Laboratory for Making Things, I give an extended example of how computer-as-mediator contributes to learning when played out in this rather unusual classroom.
Resumen
Abro este artículo con algunas cuestiones pedagógicas incómodas y persistentes que, si bien han permanecido en segundo plano durante nuestro trabajo, han constituido el incentivo necesario para reflexionar y actuar sobre las posibles funciones de la tecnología digital en el aula. En las secciones siguientes, propongo que el ordenador puede constituir un mediador eficaz entre la acción y el símbolo. Tras explicar el contexto de El laboratorio para hacer cosas, se detalla un extenso ejemplo del modo en que el ordenador, como factor mediador, contribuye al aprendizaje cuando se incorpora a un aula tan peculiar.
Palabras clave:
I begin by stating a small set of troublesome but pervasive educational issues. I argue that while these issues have a long history, they are illuminated if we look critically at possible roles for computer technology in the classroom. I propose that the computer can be used both to enhance and to resolve the generative tension between action and symbol. I give an extended example of how these moves contribute to learning when played out in a rather unusual classroom.
The literature points to numerous ways in which my proposal is supported by past research. For instance, to assume that ‘knowledge’ and ‘information’ are equivalent can be destructive to learning. ‘Information’ lies quietly in books, is gathered from others or ‘accessed via the web’. Instead, I and others argue that ‘knowledge’ is actively developed through experience, interpretation, constructions, questions, failures and successes (Vossoughi & Bevan, Citation2014). In fact, children can be active makers and builders of knowledge, but they are often asked to become passive consumers — the target of selected others’ goods and information (Osberg, Biesta, & Cilliers, Citation2008; Papavlasopoulou, Giannakos, & Jaccheri, Citation2014). Furthermore, children are also makers and builders of things. In that context, ‘grasping’ is not a metaphor as in grasping an idea, the truth. For children living in an unstable, unpredictable world in flux, literally grasping, holding, holding still, holding on, is a persistent need (Vossoughi & Bevan, Citation2014). However, for children whose worlds are spinning too fast already, and who are vulnerable to a sense of loss of place — in space, in a family, in a community — uses of the computer for speedy access to vast spaces and quick, efficient, packaged-up, ready-to-go information may be more confounding than useful.
Looking back through the literature for how and where to place these more contemporary issues, I was surprised to find that Dewey had already been there. I refer in particular to a brief article titled ‘The Way Out of Educational Confusion’, published originally in 1931 as a pamphlet by Harvard University Press (Archambault, Citation1964). Consider, for example, an often-quoted comment by Seymour Papert (Citation2005):Footnote1
There cannot be a problem that is not a problem of something. (Dewey, Citation1931/1964, quoted in Archambault, Citation1964, p. 422)
You can’t think about thinking without thinking about thinking about something. (Papert, Citation2005, p. 366)
More specifically, the work discussed here shares obvious aspects with the current Maker Movement, both harking back to Dewey and his emphasis on ‘learning by doing’. For instance, Osberg et al. (Citation2008) say:
Dewey solves this problem by understanding knowledge and learning in terms of action or more accurately, transaction. (p. 222)
However, there are important differences. The core of the Maker Movement seems well described by the following quote:
Give the pupils something to do, not something to learn; and the doing is of such a nature as to demand thinking; learning naturally results. (Dewey, Citation1916, p. 191)
While we are also encouraging students to be ‘doing’ and to be ‘makers’, the focus of our workFootnote2 is both broader and more specific compared with the current Maker Movement. We are developing contexts that build on learning as a function of the generative tension between action and symbol. We encourage students to move back and forth between, on one hand, using hands-on action with materials in real time and space, and on the other, making by creating descriptions/representations that serve as ‘instructions’ in the virtual space of the computer.
Background: the laboratory for making things
Our work with young children began in 1985 as a project and a place that we called The Laboratory for Making Things (Bamberger, Citation1991). It took up residence in the Graham and Parks Alternative Public School in Cambridge, Massachusetts (MA), in the United States. The project was initially motivated by my interest in a well-recognized but poorly understood phenomenon: Children who are virtuosos at building and fixing complicated things in the everyday world around them (bicycles, plumbing, car motors, musical instruments and music, games and gadgets, or a club house out of junk from the local construction site) are often children who are having trouble learning in school. These are children who have the ability to design and build complex systems, who are experts at devising experiments to analyse and test problems confronted on the way, and who can learn by extracting features and principles from the successful workings of the things they make. But they are also children who are often described as having trouble working within the discrete spaces of common symbolic expressions — numbers, graphs, simple calculations, written language.
With ‘knowledge’ in schools mostly measured by the student’s ability to work with and understand conventional symbolic expressions, it is not surprising that attention focuses on what these children cannot do. Instead of seeing them as virtuosos, they are seen as ‘failing to learn’. Thus, my primary question was this: if we could better understand the nature of the knowledge the children were bringing to what they do so effectively, could we help them use this knowledge to succeed in the classroom as well?Footnote3
Getting started
Work at the Graham and Parks School began in the fall of 1985. Susan Jo Russell, who had been a classroom teacher and was now completing her PhD in technology and education, joined me in starting the project. The school, in a working class neighbourhood of Cambridge, MA, is named after Sondra Graham, a social activist and former member of the Cambridge School Committee, and Rosa Parks, well known for the role she played in the struggle for equal rights in the 1960s. The core of the student population mirrored the diverse population of Cambridge, and in addition included most of the Haitian Creole speaking children in the city. We began with the teachers. All the teachers in the school (grades K–8) were sent an invitation to join the project. We described it as an opportunity to think together about children’s learning through sharing puzzles and insights from the classroom. Twelve teachers signed up, with a core group of eight becoming regular participants. We had expected the initial planning period to last perhaps two months, but the teachers felt ready to bring children to the Lab only after we had worked together for close to six months. As it turned out, those six months were critical in shaping the form that the Lab took.
The Lab, a large, empty room in the school, was gradually ‘furnished’ with a great variety of materials for designing and building structures that work — gears and pulleys, LegoTM blocks, pattern blocks and large building blocks, Cuisenaire rods, batteries and buzzers for building simple circuitry, foam core, wood and glue for model house construction, as well as drums and keyboards for making music. And the 10 Apple IIe computers took their place as another medium for building structures that worked and that made sense — what we came to call ‘working systems’.Footnote4 The children renamed the room the ‘Design Lab’. Some 250 children ranging in age from six to 14 participated in Lab activities over a period of about four years.
It was a month into working with the teachers that the Apple computers arrived. Unpacking and putting them together was a necessary first step towards helping the teachers gain a feeling of intimacy with the machines. Learning the computer language Logo was a further step towards this sense of intimacy, and it had a surprising spin-off: perhaps because the computer was still a totally new medium in 1985, the teachers shed their initial fears and became fascinated, instead, with their own and one another’s confusions around their interactions with the machine. Probing their confusions came to be seen as a source of insight: what was the basis of the confusion and how could you find out?
This new productive source for inquiry had another unexpected spin-off. Stories from the classroom turned to children’s confusions and how to understand them: making the assumption that no matter what a child said or did, it was making sense to her, the question was, how could we find the sense she was making? As Mary Briggs put it, ‘I hear a child saying this really weird thing, but if only I could look out from where that child is looking, it would make perfect sense’.
Watching the children at work (see ), we often saw learning going on that grew out of the children’s easy moves between hands-on and computer-based thinking and making. While the learning was often elusive, it suggested a possible general design for children’s future projects that would both encourage and perhaps make more explicit the learning that we had begun to see happening in the Lab.
Learning from the children, our goal became to provide an environment in which making occurred in a variety of media (Lego™ cars, geometric blocks, huge cardboard gears, pulleys, foam core houses, drums for playing rhythms), along with using the Apple computers as a platform for construction (graphics, music, quiz programs, puzzles). We would design projects that differed in the kinds of objects/materials used, that utilized differing sensory modalities, that held the potential for differing modes of description (graphic, symbolic), but that shared conceptual underpinnings (Bamberger, Citation1991).
In designing this environment, we were drawing on what we had found in the past to be the effective learning strategies that children were bringing with them from outside of school: to learn by noticing and drawing out principles from the success of the objects and the actions that worked. Here again we find a connection to Dewey:
It is possible to find problems and projects that come within the scope and capacities of the experience of the learner and which have a sufficiently long span so that they raise new questions, introduce new and related undertakings, and create a demand for fresh knowledge … [N]oting the bearing and function of things acquired … has the advantage of being of the kind followed in study and learning outside of school walls where data and principles do not offer themselves in isolated segments with labels already affixed. (Dewey, Citation1931/1964, p. 423)
A cluster of interrelated questions also emerged. We asked: how do children (or any of us) learn to turn continuously moving, organized actions — clapping a rhythm, bouncing a ball, circling gears — into static, discrete, symbolic descriptions that are meant to represent our experience of these objects and our sensory/action mastery of them? How do we learn to make descriptions that hold still to be looked at ‘out there’? And why is this important?
Osberg et al. (Citation2008) make the relevant point when they argue that ‘knowledge’ in school is commonly measured and is recognized when it becomes an ‘accurate representation’ (p. 213). In this way, knowledge, by implication, is no longer accepted when embodied in action but only when it becomes ‘spatial’. As Osberg et al. (Citation2008) state:
it can be argued that schooling is organized around a representational epistemology: one which holds that knowledge is an accurate representation of something that is separate from knowledge itself. Since the object of knowledge is assumed to exist separately from the knowledge itself, this epistemology can also be considered ‘spatial’. (p. 213)
In the Lab, the computer played a role as mediator in addressing these questions. As Papert (Citation2005) sees it, the computer is a ‘transitional object’. While the computer was used as another medium for designing and building working systems, there were stunning differences in its everyday use and function in the children’s designing. Indeed, the differences created a potentially generative tension between making things with hands-on materials and making things with the computer.
For example, in the hands-on situation, makers begin with action and rarely, if at all, make verbal or written descriptions of what they know how to do. In the computer situation, makers must begin by describing what they want to happen in a symbolic programming language. Once made, the description is meant to become what they have described — symbol becomes digitized object/action!
Also by contrast, descriptions written on paper remain static. The individual reading the description must put its described pieces together and often needs to ask, ‘Did I get it right?’ In this regard the computer has a unique capability: you are not left in doubt; descriptions sent to the computer immediately turn into the things or actions described by the programming language; the feedback regarding ‘Did I get it right?’ is provided almost automatically.
Sometimes, however, the computer becomes a strangely reflecting playground as the programmed instructions produce provocative surprises. These are the critical moments of learning. You ask yourself, ‘Wow, I wonder why that happened?’ ‘What does that tell me about how I’m understanding the problem?’ ‘How do I probe this puzzlement?’
The children needed time to notice and play with these surprises. Rather than turning away as if they had failed, they made experiments to interrogate what had happened — much as they knew how to do in fixing their bikes or the LegoTM cars they made in the Lab.
But the computer experiments had a special quality: because descriptions became (virtual) actions, the relationship between symbol and action could be tested. Indeed, chasing surprises, tracing the paths that led to them, turned out to be a very productive way for the children to explore their own understandings and confusions. Much as it had been with the teachers during the six months before the children joined in, interrogating their confusions was often a critical and exciting step towards insight. Strange encounters of a special kind.
Thus, rather than joining hand-made and computer-made systems to construct a single working system (such as using the computer to control a LegoTM robot), we urged the children to pay attention to differences in the kinds of things that inhabited these two worlds. How did the differences between these design worlds influence what they thought of to think about; what was different in the kinds of problems, confusions and puzzles they encountered as they moved from the familiar hands-on, real-time/space world to the virtual computer world? Confronting the potential tension generated by these differences, rather than avoiding them, turned out also to be important in helping the children move more effectively between their ‘smart hands’ and the symbolic text-oriented school world.
Working in the Lab, the children also noticed and helped us notice moments, often caught on the fly, when the moves back and forth — between action in real time/space and virtual action in computer space — revealed surprising similarities. And, as we had hoped, the seeing of similarities (‘Hey, that reminds me of what we did …’) often led to the emergence of a shared powerful principle that was previously hidden. As I will show, capturing these insights and the discussions that led to them produced some of the most significant learning for both the children and the teacher-researchers.
Emerging ideas
The back-and-forth movement between materials, sensory modalities and modes of description resulted in certain kinds of ideas becoming part of the Lab culture, illuminating the children’s designing, building and understanding across all the media. Three of these ideas were particularly present:
The notion of a ‘procedure’ which initially developed in their computer designing but was found useful in designing hand-made systems as well.
The sense that it is useful and interesting to look for ‘patterns’ which germinated in hand-made designing but seeped into computer designing.
Closely related to both of the above, the idea of grouping or ‘chunking’ and their boundaries.
Chunking initially grew out of a specific need to work with the continuousness of music. But its usefulness crept into designing with other materials as well. Issues around ‘chunking’ became surprisingly evident in children’s often heard, but rather unexpected question. As one student examined another student’s many-pieced construction, we would hear him or her ask, ‘But what’s a THING, here?’
A day in the life of the Design Lab
Once a week after school we worked for two hours in the Lab with six nine- and 10-year old children. I worked together with Mary Briggs, the special education teacher in the school. Mary had selected the six children from among the many others she worked with, because she believed they would particularly thrive in the Design Lab environment. She knew the children well, as she worked with each of them on a daily basis. The six children were Rachel, Rosa, Steve, Laf, Simon and Leah.
For me it came as a kind of revelation to realize how hard it is to really make contact with a child, to become intimate with his or her thinking so as to learn from it — especially a child for whom life in school has not been especially rewarding. Most of all I came to appreciate the work of teachers: what a huge difference there is between thinking and talking about schooling, and actually being there — living there, doing it every single day, not just once a week for an afternoon. Working with Mary and the children was an intense learning experience — learning that has influenced almost everything I have done since.
Gears and rhythm
Working in the Logo Lab (a section of the Artificial Intelligence Lab at MIT directed by Seymour Papert), I had designed, with the help of others, a music version of the programming language Logo, originally designed by Papert and collegues. It was called MusicLogo and, along with Logo, was up and running in the Design Lab for the children to use. While Logo was commonly used for programming graphics, with MusicLogo available, the children could work in multiple media — sometimes doing graphics, sometimes doing music. The idea was much like working with hands-on design projects: by moving across media and sensory modalities but keeping the underlying means of procedural designing a constant present, shared principles could seep out. Thus, shaping actions and objects in quite different media could be seen as sharing structural design.
For example, the same computer procedure and the principles behind it (particularly recursion) were used to print a ‘count-down’ (10–9–8–7 …), to make a synthesizer drum play a faster and faster beat and to make a synthesizer clarinet play a descending scaleFootnote5: the countdown procedure is a typical Logo procedure. The faster drum beat and the descending scale procedures are typical MusicLogo procedures.
A COUNTDOWN
TO COUNTDOWN :START :DONE
IF :START = :DONE STOP
PRINT :START
COUNTDOWN :START – 1 :DONE
END
Running the COUNTDOWN procedure with inputs of 12 and 1, the computer will print out the following:
COUNTDOWN 12 1
12
11
10
9
8
7
6
5
4
3
2
1
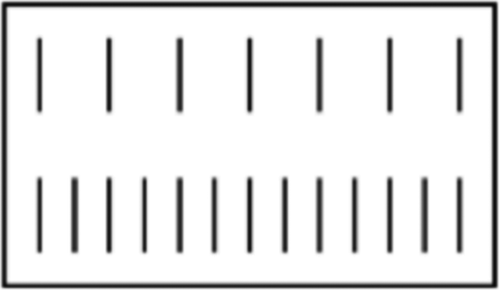
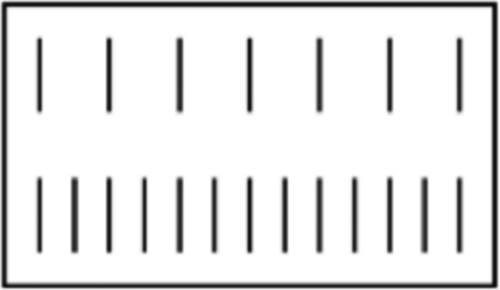
A FASTER BEAT (see )
Figure 2. A spatial analogue graphic representation of the time of the drum doing the faster beat procedureFootnote7.

TO FASTER :START :DONE
IF :START = :DONE STOP
BOOM :START
FASTER :START – 1 :DONE
END
FASTER 12 1
A DESCENDING SCALE (see )
TO DOWNPITCH :START :DONE
IF :START = :DONE STOP
PLAY :START – 1 :DONE
DOWNPITCH :START – 1
END
DOWNPITCH 12 1
The gears
Gears also played an important role in the Lab as a means for helping children see and feel shared principles across media and sensory modalities — e.g., kinds of fast and slow, a counting unit, periodicity (see ).
As Seymour Papert has pointed out:
The gear, as well as connecting with the formal knowledge of mathematics, it also connects with the ‘body knowledge’, the sensorimotor schemata of a child. You can BE the gear, you can understand how it turns by projecting yourself into its place and turning with it. It is this double relationship — both abstract and sensory — that gives the gear the power to carry powerful mathematics into the mind. The gear acts, here, as a transitional object. (Papert, 1980, p. viii)
My hunch was that moving between clapping rhythms and playing with gears could be a particularly lively playground for making this ‘double relationship’ manifest. On this particular Wednesday afternoon we moved through several activities — from drumming, to walking, to playing with very large cardboard gears, to clapping, and eventually to ‘telling’ the computer how to ‘play’ drum patterns using MusicLogo. The gears were designed by Arthur GansonFootnote6 and built by a group of slightly older children.Footnote7
Mary asked the children as we moved over to the gears, ‘Now how could these gears, the walking and the drumming we did sort of be alike?’ Rachel, one of the students in the group, was standing by the gears, her hands actually being the gears as she talked (see ). As she turned the gears, watching them go around, she spontaneously made a proposal. The interaction includes Rosa and Steve, another two students in the group.
Oh, it’s a math problem. Like this one has (counting teeth on the smaller gear) one, two, three, four, five, six, seven, eight — and you bring the eight around four times to get it [the bigger gear] all the way around once. Now how many teeth does that one [bigger gear] have?
24.
No. Four times eight, 32. And the small one goes around four times when that one goes around once.
(changing the focus) But I wanna know which one of those wheels is going the fastest.
The smaller one.
Both of them are going at the same speed.
(to Steve) You say the smaller one?
Yah, the smaller one is going around four times and it’s fastest.
But Rachel said same speed.
Because look, you can’t make this one go faster. Every time this is going … Oh, you mean how fast it’s going around?
Well, I don’t know, what do you think?
What kind of fastness do you mean?
What are the choices?
Like for one kind of fastest you could say … like you could go … like (pointing to meshing of teeth) how each teeth goes in like that, ya know? And one kind of fastest you could say how long it takes for this one to go around. (Rachel has, in fact, described the difference between linear and angular velocities.)
Hmmm. So if you say it’s the kind of fastness with the teeth?
The smaller one.
No, they both are going the same speed.
OK. And what about if you say which goes around the fastest?
The smallest one.
Clapping the gears
At this moment, Arthur Ganson, who was also working with the children that day, saw a connection. This time, Leah also participated in the conversation.
So what is the rhythm of those gears?
The rhythm of that gear? Someone want to play it?
Yah, how about playing it?
I’ll play it. (He turns the gears around as if making them ‘play’.)
Yah, how would you play that rhythm?
Like this … hmmm (see ).
Yah. Which is the small gear?
The one that’s going … (taps with her right hand)
In clapping, Leah’s hands acted out the 4:1 relationship of the two gears. That is, each tap of her left hand is the bigger gear going around once; each group of four taps of her right hand is the smaller gear going around four times (see ).
Arthur’s spur-of-the-moment question neatly brought together the seemingly disparate materials, modalities and means of description with which the children had been working. Leah’s clapping was a kind of metaphor-in-action for the relative motions of the two meshed gears — she had become the gears. For Rachel the motion of the two gears embodied principles of ratio and ‘kinds of fastness’. And yet, hiding behind each student’s moves from one medium and mode of expression to another were shared principles. Perhaps the most generalizable shared principle was the fundamental idea of a ‘unit’ accumulating to make related ‘periodicities’ — what the group of children had been calling simply ‘beats’.
Leah and Rachel were demonstrating the hunch we had had from the beginning: children who are having difficulties learning in school can learn in profound ways by extracting principles from the successful workings of their built objects and their actions on and with them. The question still was, as it had been from the beginning, could we help the children make working, functional connections in the tension between what they knew how to do already in action, and the know-about as expressed in more general symbolic form (see also Ryle, Citation1949)? Rachel was clearly on the way; Leah was making moves in that direction; but what about the others? Could the computer and MusicLogo enable more students to mediate between action knowledge and symbolic knowledge?
The computer as mediator
While Arthur’s specific question and Leah’s response were unplanned events, they had been prepared by our juxtaposing the activities of clapping rhythms and working with the gears. The next activity was definitely planned in advance. It reflected our earlier intention of using the computer as mediator between action and symbol. The question was: could the children use the computer as a vehicle for effectively moving between the actions of the gears, their own body actions in clapping/drumming, and now, the numeric-symbolic instructions given to the computer? In short, could they transform the results of their own continuous body actions into discrete, symbolic expressions that would, in turn, become computer procedures for generating virtual sound/actions? This would be a prime example of confronting the tension between action and symbol.
The new task I put to the children was: ‘Can you get the computer synthesizer drums to play what Leah clapped? Except, to begin with, we’ll make it a little easier’. Using two hands as Leah had, I tapped out a simpler 2:1 rhythm. The children all clapped the two-layered rhythm, as well (see ).
The children had already become familiar with procedural programming and with the meanings of numbers in doing Logo graphics — what we called ‘teaching the computer’. Now the children would need to give meaning to numbers in this new MusicLogo context. What were the links between the actions and sounds the children made in clapping, the numbers used in doing ordinary arithmetic, numbers used in doing graphics Logo and now numbers used as instructions to the computer indicating the temporal relations between synthesized drumbeats?
The children were also used to conversations when they got stuck while building; they would explain to one another or to an adult what they were trying to do to get something to work. However, descriptions of such real-time building didn’t usually include symbolic/numeric expressions even after the act. Thus, what the children engaged in would now be reversed compared with what the children were used to: Instead of reflecting back to make descriptions after the fact and after the act, they would need to describe, as instructions to the computer, what they wanted to happen before the act. And instructions must be in the symbolic form of a computer language — i.e., Logo. These were some of the issues as we moved to the computers and to the next task.
An example: Laf invents an experiment
MusicLogo could make the synthesizer play two different drum sounds called BOOM or PING, respectively. The number of numbers in a list that follow BOOM or PING determines how many sounds, BOOMs or PINGs, should be played in all. The numbers themselves determine the ‘duration’ of each event. Or more exactly, the proportional relations of the time from one sound attack to the next.
To help the children get started, I typed the following instructions and we listened (PM is the command for PlayMusic; CM is the command for ClearMusic):
BOOM [8 8 8 8 8 8 8] PM
We heard seven BOOM sounds, each with a duration of ‘8’. However, at this point the children still had to discover what ‘8’ meant. I gave another example, saying, ‘This one will go faster’:
BOOM [6 6 6 6 6 6 6 6] PM
Now I want to make a still faster one.
(who had not participated in the discussion up to now): But the lower you get the faster it gets.
You answered my question before I asked it.
Laf’s psychic.
Do 1 1 1 1 1 1.
What do ya think will happen?
If you put all ones, it’ll go fast.
Jeanne types:
BOOM [1 1 1 1 1 1 1] PM
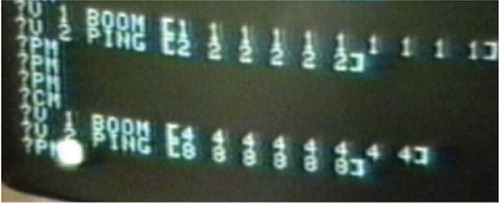
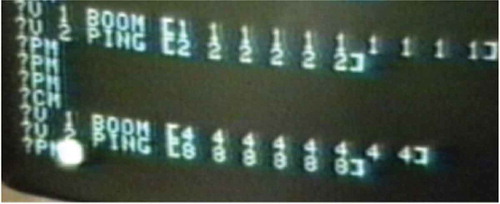
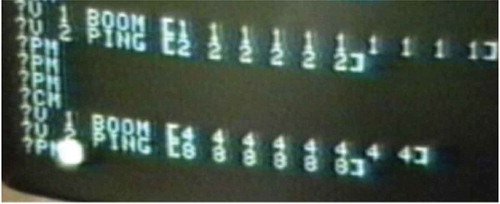
And it did ‘go fast’. I also showed the children how Logo could play BOOM and PING together, each in a separate ‘voice’ (see ).
From Action to Symbol: An Example
As the children went to work on their computers, I went around to work with Laf. Laf was a quintessential example of a child for whom to ‘grasp an idea’ was literally a physical experience. All of us seek ways of holding on to a new idea. But for most children, especially those growing up living in an unstable, unpredictable world, grasping, holding still, is a persistent need. Laf’s explorations to find out how numbers could ‘teach’ the computer to play the drums made that quite clear. And like probably so many times before, I almost missed it.
Laf talked very little. It was in the Lab that we discovered his most notable quality: integrity. Unlike more school-smart children, he would just turn off rather than going through the motions to get a right answer. He needed to understand for himself. However, on this occasion, as on so many others in watching a child work, I learned that we adults often need to slow down in order to catch up with another’s thinking.
Sitting down next to Laf, I saw that he was determinedly, slowly, persistently, typing either BOOM or PING, each followed by a single list of 1s and 2s (see ).
Despite my best intentions I found it difficult to find reason in what Laf was doing. Only later, looking at the video of the whole session, did I realize how wrong I was. Because I was focusing on my task — to make two levels of beats in a 2:1 relationship, I missed the significance of Laf’s lists of BOOMs and PINGs. True to his integrity, Laf had designed an organized experiment to answer questions he had silently put to himself: What is the difference between BOOM and PING and between 1 and 2 in this context? What exactly do these numbers do? And how can I find out? Listening, participating in his own experiment, he confirmed his previous understanding; the contrast between the very fast 1s and the slower 2s was eminently hearable.
To further confirm his understanding, Laf followed the numbers on the screen. Tapping with his finger along with the 1s and 2s, relating his own actions to the computer’s sound and virtual actions (see ), Laf was literally, physically grasping the meaning of the 1s and 2s. Attentively and patiently, he continued until the whole screen had been traversed (see ). Looking back, I see this as a first example of coordinating symbol with sound and action. The numbers stood still, the beats were sounding/moving, and Laf’s ‘finger-drumming’ was marking each of them in action as time went on.
Figure 11. Finger drumming. (See video in Supplemental File online to watch Laf’s finger drumming.).

Starting with what he knew already (‘The lower you get the faster it gets … If you put all 1s, it’ll go fast’), he tested that knowledge in action. Perhaps like a scientist working with the puzzling behaviour of molecules, Laf needed to differentiate between two closely related but slightly different elements (‘1’ and ‘2’). And like the scientist, he needed repetition — a critical sample size of each element repeated over sufficient time, and in a controlled environment where their differences and similarities could be clearly perceived as regularities.
Having observed instances of his essential elements behaving over a sufficiently long time, and having confirmed that the behaviours of ‘1’ and ‘2’ do not vary between the BOOM context and the PING context, Laf found that the ‘joints’ where the 1s and 2s met produced the revealing moments: the 1s went too fast for him to follow, so he waited each time for the 2s to begin (see and listen to the supplemental video file online).
Laf was using his available resources to do the work of making meaning. He had invented a way to use the computer and MusicLogo as mediators between the virtual world of symbols and his actions in real-time/space. And in retrospect, he taught me how important it is to be able to slow down and take the time to repeat so as literally to practise grasping meaning.
But there was more. Building on his experiment, Laf now used what he had learned to make a whole piece of music. The piece was made up of alternating rows of BOOMs and PINGs and 1s and 2s. Not surprisingly, he named his Logo procedure TO LAF (see ).
Seeing and hearing what Laf had made, Mary gathered the children’s attention:
Mary: Shhhh … Laf is going to play his piece.
Looking very excited, Laf said, ‘Here we go again’, and he typed: LAF PM.
Laf’s procedure filled the Lab as the children listened attentively all the way to the end. The usually quiet Laf looked triumphant and the children clapped in appreciation.
Moving farther towards symbolic representation
The biggest surprises came the next week, when the children returned to the Lab. Clearly feeling comfortable enough with the meaning of 1s and 2s, and perhaps learning from what he had seen and heard the other children doing, Laf went on to make the two-voiced experiment I had suggested — BOOM in one voice (V 1) and PING in the other voice (V 2). Beginning with the familiar 1s and 2s, he also surprisingly moved ahead to make a further 1:2 relationship — 4:8 (see ).
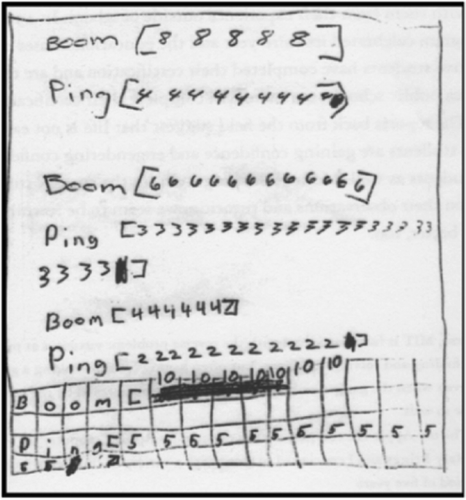
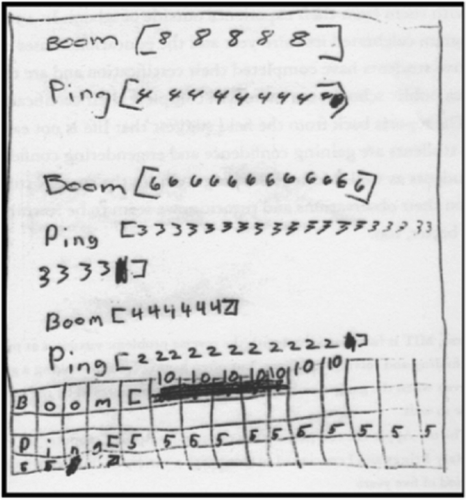
The biggest surprise came when, at the end of the session, Laf went on to make a whole table of possible 2:1 drumming examples (see ).
In we see Laf’s representation of BOOMs and PINGs consistently playing together in 2:1 ratios: 8:4, 6:3, 4:2, 10:5. Laf’s first experiment, which had seemed to me at the time a rather mindless activity, turns out to have been a playground for gathering, grasping, mulling over and finally developing and giving meaning to a whole symbolic table of shared 2:1 drumming ratios. As further evidence of the importance Laf gives to representing time passing, notice that with each pair, the PINGs, playing twice as fast (4s) as the BOOMs (8s), also have twice as many iterations as the BOOMs. Thus, each pair of BOOMs and PINGs will come out together — equal in total time.
The computer literally becomes a mediator helping to integrate symbol, sound and action. Through building his initial interactive experiment, his repeated runs of 1s and 2s, Laf built himself a powerful idea. Following his quiet, steady work patiently, we see one child’s process of slowly transforming his continuous actions into evolving static images, culminating in the invention of a fully developed symbolic representation.
But wait: on the basis of this table, it was easy to assume that in building on, generalizing upon his previous experiments with 1s and 2s, Laf had developed the powerful idea of ratio. But notice the difference between the form of my static representation of ratio and Laf’s representation of repeatable BOOMs and PINGs (see ).
Put most simply, I have imposed upon Laf’s invention the traditional representation of ratio. In that process, I have taken away time and action! Laf has carefully marked each action, each iteration, as he moves through time and action onto paper space. Each of the numbers in Laf’s table reflects an action or a reaction: his finger drumming as he follows the computer’s ‘performance’. My ratio representation, 6:3, 10:5, has obliterated actual iterations in motion and time, collapsed them into a single symbolic representation — many events have become one.
The table shown in does not actually show Laf grasping the concept of ratio. Rather, it is a snapshot in an evolutionary process of learning. We are seeing a moment on-the-way to an ‘abstracting process’: continuous actions in time extracted, made discrete, held still gradually transforming into the symbolic expressions that we teach in school. As Werner (Citation1957) pointed out:
Abstraction can be defined as a mental activity by means of which parts of a unit are detached from the whole and separate qualities — color, form, etc. — are experienced in isolation. (p. 234)
I argue that Laf’s insights depend deeply on an environment that exploits the computer in a way that is unique to it: the computer as a medium in which a symbol defines itself by becoming what it does. To paraphrase Papert, Laf used the computer as a ‘transitional object’. His continuing participation in this productive tension between action and symbol could later yield the powerful idea of ratio.
Conclusions
The activities described in these stories are not intended as recommendations to be literally copied — e.g., ‘a curriculum’, or even ‘what to do in class tomorrow’. Nor are they intended as a general recommendation for how the computer may be effectively used in classrooms. The stories are meant rather as examples of a context and an approach to learning.
To recapitulate, the examples of children at work have helped to illustrate that knowledge is actively developed through experience, interpretation, constructions, questions, failures, successes. The examples are perhaps most relevant for those children whose personal, powerful know how is failing them in school largely because it has no way of coming in off the street into the classroom. As mentioned at the beginning of this article, for children living in an unstable, unpredictable world in flux, literally grasping, holding, holding still, holding on, is a persistent need. These are children who often feel that school is irrelevant and reciprocally are made to perceive themselves as irrelevant, peripheral, in school settings.
In sum, I argue that the computer may play a special role as a resource for inquiry and invention when students can build on what they know how to do already, while working within a conceptual space and at a pace that they can grasp. In this environment, instead of becoming passive consumers — the target of selected others’ goods and information — children can potentially become makers of new knowledge of which they can feel proud. And through this empowerment they may also discover strategies for learning how to learn within the school world and beyond.
Conocimiento basado en la acción y conocimiento simbólico. El equipo informático como mediador
Empiezo con algunas cuestiones pedagógicas incómodas pero persistentes. Propongo que, aunque estas cuestiones tienen una larga historia, podemos arrojar luz sobre ellas cuando analizamos críticamente las posibles funciones de la tecnología digital en las aulas. Propongo que el equipo informático puede utilizarse para mejorar y resolver la tensión generativa entre acción y símbolo. Ofrezco un ejemplo extenso de la contribución de estos enfoques al aprendizaje cuando se realizan en un contexto de clase algo peculiar.
La bibliografía revela múltiples contextos en los que mi propuesta está respaldada por investigaciones anteriores. Por ejemplo, asumir que ‘conocimiento’ e ‘información’ son términos equivalentes puede resultar destructivo para el aprendizaje. La ‘información’ descansa pasiva en los libros, o es recopilada por terceros, o ‘se accede a ella’ a través de Internet. Por el contrario, hay quienes, como yo, defienden que el ‘conocimiento’ se desarrolla de manera activa a través de la experiencia, de interpretaciones, construcciones, preguntas, fracasos y éxitos (Vossoughi & Bevan, Citation2014). De hecho, para algunos niños cuyos mundos giran ya con demasiada rapidez a su alrededor y están expuestos a un sentimiento de desubicación — en el espacio, en la familia, en la comunidad — el uso de la tecnología digital para un acceso inmediato a espacios inmensos y a una información igualmente inmediata, empaquetada y lista para llevar, puede resultar más desconcertante que útil.
Al revisar la literatura buscando cómo y dónde localizar estas cuestiones más contemporáneas, me sorprendió descubrir que John Dewey ya lo había hecho. Me refiero en particular a un breve artículo titulado The way out of educational confusion (El camino para salir de la confusión educativa) publicado en 1931 en forma de panfleto por la editorial Harvard University Press (Archambault, Citation1964). Pensemos, por ejemplo, en el comentario de Seymour Papert (Citation2005) tan frecuentemente citadoFootnote1:
No puede haber un problema que no sea un problema de algo. (Dewey, Citation1931/1964, citado en Archambault, Citation1964, p. 422, traducción propia)
No se puede pensar sobre el pensamiento sin pensar sobre el pensamiento sobre algo. (Papert, Citation2005, p. 366, traducción propia)
En particular, el trabajo que detallamos en este artículo comparte algunos aspectos obvios con el actual movimiento maker, ambos reminiscentes del énfasis de Dewey sobre ‘el aprendizaje basado en la acción’. Por ejemplo, en Osberg et al. (Citation2008), se afirma:
Dewey resuelve su problema considerando el conocimiento y el aprendizaje como acción o, más exactamente, transacción. (p. 222, traducción propia)
Sin embargo, existen diferencias importantes. Esta cita parece describir muy bien la esencia del movimiento maker:
Da a los alumnos algo que hacer, no algo que aprender; el proceso de hacer algo exige la reflexión y, por tanto, el aprendizaje ocurre de manera natural. (Dewey, Citation1916, p. 191, traducción propia).
Aunque también aquí se fomenta que los alumnos ‘hagan’ y sean ‘hacedores’, en enfoque principal de nuestro trabajoFootnote2 es a la vez más amplio y más específico comparado con el actual movimiento maker. Estamos desarrollando contextos en los que se desarrolla el aprendizaje como función de la tensión generativa entre la acción y el símbolo. Animamos a los estudiantes a moverse libremente entre el trabajo práctico con materiales en tiempo y espacio reales, por un lado, y por el otro, crear y elaborar descripciones/representaciones que ejercen la función de ‘instrucciones’ en el espacio virtual del ordenador.
Antecedentes: el laboratorio para hacer cosas
Nuestro trabajo con niños pequeños comenzó en 1985 como un proyecto en un lugar que denominamos El laboratorio para hacer cosas (Bamberger, Citation1991). Se ubicó en la escuela Graham and Parks Alternative Public School de Cambridge, Massachusetts (MA), en Estados Unidos. El proyecto fue instigado inicialmente por mi interés en un fenómeno muy reconocido, pero poco comprendido: los niños que son virtuosos en la creación y reparación de objetos complejos en el mundo cotidiano que les rodea (bicicletas, tuberías, motores, instrumentos musicales y música, juegos y artilugios o una casa club construida con los restos de unas obras locales) suelen ser aquellos que tienen problemas de aprendizaje en la escuela. Estos son niños que tienen la capacidad de diseñar y construir sistemas complejos, que son expertos en el diseño de experimentos para analizar y solucionar los problemas con los que se encuentran en el proceso, y que pueden aprender extrayendo características y principios del buen funcionamiento de aquello que construyen. Pero son también niños que suelen describirse como alumnos con problemas para trabajar en el espacio discreto de las expresiones simbólicas comunes: números, gráficos, cálculos simples o lenguaje escrito.
Dado que, en las escuelas, el ‘conocimiento’ suele medirse principalmente a través de la capacidad del estudiante para comprender y trabajar con estas expresiones simbólicas convencionales, no es de extrañar que la atención se centre en aquello que no pueden hacer. En lugar de considerarlos virtuosos, se considera que ‘fracasan en el aprendizaje’. Por lo tanto, mi pregunta principal es la siguiente: si pudiésemos comprender mejor la naturaleza del conocimiento al que los niños recurren para hacer lo que hacen con tanta eficacia, ¿podríamos ayudarles a utilizar ese mismo conocimiento para ser eficaces también en el aula?Footnote3
Los comienzos
El trabajo en Graham and Parks School comenzó en otoño de 1985. Susan Jo Rusell, maestra de escuela que estaba completando su doctorado en tecnología y educación, me acompañó en la puesta en marcha del proyecto. La escuela, en un barrio de trabajadores de Cambridge, MA, recibió su nombre en honor de Sondra Graham, una activista social y anterior miembro del Consejo escolar de Cambridge, y de Rosa Parks, famosa por su papel en la lucha por los derechos de la mujer en la década de los 60. El núcleo de la población estudiantil del centro reflejaba la diversidad de la población de Cambridge, e incluía también gran parte de los niños de la ciudad cuya lengua era el criollo haitiano. Comenzamos con los docentes del centro. Se invitó a todos los docentes (grados K–8) a incorporarse al proyecto, que describimos como una oportunidad para pensar juntos sobre el aprendizaje infantil compartiendo dificultades y puntos de vista de sus clases respectivas. Se apuntaron doce maestros y maestras, de los cuales ocho se convirtieron en participantes habituales. Esperábamos que el periodo inicial de planificación durara unos dos meses, pero los maestros no se sintieron preparados para traer a los niños al laboratorio hasta después de haber trabajado juntos casi seis meses. Esos seis meses resultaron críticos para darle al laboratorio la forma que finalmente adquirió.
Fuimos ‘amueblando’ gradualmente el laboratorio, una sala vacía del centro, con gran variedad de materiales para diseñar y construir estructuras funcionales: engranajes y poleas, bloques LegoTM, piezas para patrones y bloques de construcción, regletas Cuisenaire, baterías y timbres para construir circuitos básicos, espuma, madera y cola para construir modelos de casas, así como baterías y pianos para crear música. Y los equipos Apple IIe de aquel entonces ocuparon su lugar como un medio más para construir estructuras que funcionasen y tuviesen sentido; lo que denominamos ‘sistemas funcionalesFootnote4’. Los niños rebautizaron el aula como ‘Laboratorio de diseño’. Unos 250 niños y adolescentes de entre seis y 14 años participaron en las actividades del laboratorio durante un periodo de unos cuatro años.
Los equipos Apple llegaron cuando llevábamos un mes trabajando con los docentes. El primer paso para ayudar a los maestros a sentirse cómodos con las máquinas fue desembalarlas y montarlas. El paso siguiente fue el aprendizaje del lenguaje de programación Logo, que tuvo unas repercusiones sorprendentes. Tal vez porque los equipos informáticos constituían todavía un medio totalmente nuevo en 1985, los docentes se libraron de sus miedos iniciales y pasaron a sentirse fascinados por su propia confusión y la de sus compañeros sobre su relación con las máquinas. Sus indagaciones sobre esta confusión pasaron a considerarse una fuente de conocimiento: ¿Qué era lo que causaba la confusión y cómo podían averiguarlo?
Esta nueva y productiva fuente de indagación tuvo otro resultado inesperado. Las historias provenientes del aula pasaron a ser confusiones de los alumnos y había que averiguar cómo comprenderlas. Teniendo en cuanta que cualquier cosa que el alumno dijese o hiciese, tenía sentido para él o ella, la pregunta era: ¿Cómo podríamos averiguar cuál era ese sentido? Como ya dijo Mary Briggs, ‘Oigo a un niño decir algo muy extraño, pero si pudiese ponerme en su lugar y adoptar su mirada, tendría perfecto sentido’.
Cuando observábamos trabajar a los niños (), veíamos con frecuencia el aprendizaje que tenía lugar y que surgía de los movimientos fluidos del niño entre la acción y el razonamiento práctico y basado en el ordenador. Si bien el aprendizaje seguía siendo esquivo, sugería un posible diseño general para futuros proyectos que fomentarían y quizás harían más explícito el aprendizaje que habíamos visto surgir en el laboratorio.
Al tiempo que aprendíamos de los chicos, nuestro objetivo se transformó en ofrecerles un entorno en el que el proceso de ‘hacer’ ocurría con gran variedad de medios (vehículos Lego™, bloques geométricos, enormes engranajes de cartón, poleas, casas de espuma de poliuretano, tambores para establecer ritmos, etc.), así como con el uso de los equipos Apple como una plataforma de construcción (gráficos, música, cuestionarios, puzles, etc.). Diseñábamos proyectos que diferían en los tipos de objetos y materiales utilizados, que hacían uso de distintas modalidades sensoriales, que tenían potencial para distintos modelos descriptivos (gráficos o simbólicos), pero que compartían los mismos fundamentos conceptuales (Bamberger, Citation1991).
Al diseñar este entorno, recurríamos a las estrategias de aprendizaje que traían los niños con ellos de fuera de la escuela y que había resultado eficaces en el pasado: aprender observando y extrayendo principios del funcionamiento correcto de los objetos y las acciones que creaban. Y aquí, de nuevo, encontramos una conexión con Dewey:
Es posible encontrar problemas y proyectos que entran en el ámbito y las capacidades de la experiencia del alumno y que tienen un alcance suficientemente largo para que surjan nuevas preguntas, se introduzcan nuevas tareas relacionadas y se cree una demanda de conocimientos nuevos … Observando la orientación y función de lo adquirido … tiene la ventaja de ser del mismo tipo que se sigue en el estudio y el aprendizaje fuera de las aulas, donde los datos y los principios no se presentan en segmentos aislados con etiquetas adjudicadas de antemano. (Dewey, Citation1931/1964, p. 423, traducción propia)
Surgió también un conjunto de preguntas interrelacionadas. Nos preguntamos: ¿Cómo aprenden los niños (o cualquiera de nosotros) a convertir ciertas acciones organizadas en movimiento continuo — como un repiqueteo rítmico, el rebote de una pelota, el movimiento de un engranaje de ruedas dentadas — en descripciones simbólicas estáticas y discretas con las que tratan de representar nuestra experiencia de esos objetos y nuestro dominio sensorial/actual de ellos? ¿Cómo aprendemos a hacer descripciones que permanecen estáticas para ser observadas ‘allá afuera’? Y, ¿por qué es esto importante?
En Osberg et al. (Citation2008) se indica algo relevante cuando se afirma que el ‘conocimiento’ en los centros escolares suele evaluarse y reconocerse cuando se convierte en una ‘representación precisa’ (p. 213, traducción propia). Y así, el conocimiento, por implicación, ya no es aceptado cuando se encarna en la acción, sino solo cuando se convierte en ‘espacial’. Como se afirma en Osberg et al. (Citation2008),
podemos afirmar que la escolarización se organiza alrededor de una epistemología representacional, que defiende que el conocimiento es una representación precisa de algo que es distinto del propio conocimiento. Puesto que se asume que el objeto del conocimiento existe con independencia del propio conocimiento, esta epistemología también puede considerarse ‘espacial’ (p. 213, traducción propia).
En el laboratorio, los equipos informáticos desempeñaron un papel mediador para tratar de responder a estas preguntas. Como sugiere Papert (Citation2005), los ordenadores son ‘objetos transitorios’. Aunque estos equipos se utilizaron como un medio más para diseñar y construir sistemas funcionales, observamos diferencias sorprendentes en su uso cotidiano y su función en los diseños creados por los niños. De hecho, estas diferencias crearon una tensión generativa potencial entre la creación de objetos con materiales físicos y crear cosas con los ordenadores.
Por ejemplo, en el caso de la creación práctica, los ‘hacedores’ comienzan con la acción, y raramente o nunca elaboran descripciones verbales o escritas de lo que saben hacer. En el caso de los ordenadores, los ‘hacedores’ deben comenzar describiendo aquello que quieren que suceda en un lenguaje de programación simbólico. Una vez hecho esto, la descripción se convierte en lo que han descrito; el símbolo se convierte en el objeto/la acción digitalizada.
Por el contrario, las descripciones escritas en papel permanecen estáticas. El individuo que lee la descripción debe unir todas las piezas y, por lo general, pregunta ‘¿Lo he entendido bien?’ En este sentido, el ordenador tiene una capacidad única: no cabe duda; las descripciones que se introducen en el ordenador se convierten de inmediato en aquellos objetos o acciones descritos en el lenguaje de programación. La confirmación buscada con ese ‘¿Lo he entendido bien?’ se obtiene casi automáticamente.
Sin embargo, en ocasiones, el ordenador se convierte en un juego de reflejos, cuando las instrucciones programadas producen sorpresas provocativas. Estos son los momentos críticos de aprendizaje. Nos preguntamos, ‘¿Qué ha podido pasar?’ ‘¿Qué me dice esto sobre el modo en que estoy entendiendo el problema?’ ‘¿Cómo puedo solucionar esta perplejidad?’
Los niños requerían un tiempo para reconocer y jugar con estas sorpresas. En lugar de darles la espalda como si hubiesen fracasado, hacían experimentos para averiguar qué había pasado, de un modo muy similar al que sabían cómo reparar sus bicicletas o los coches LegoTM que habían construido en el laboratorio.
Pero los experimentos con los ordenadores tenían una cualidad especial. Puesto que las descripciones se convertían en acciones (virtuales), podía comprobarse la relación entre el símbolo y la acción. De hecho, investigando las sorpresas surgidas, retomando los caminos que conducían a ellas, resultó un proceso muy productivo en el que los niños exploraban sus propios conocimientos y confusiones. Del mismo modo que había sucedido con los docentes en los seis meses anteriores a la llegada de los niños, la interrogación de su propia confusión resultó con frecuencia un elemento crítico y un paso fascinante hacia el conocimiento. Encuentros extraños de un tipo muy especial.
Así pues, en lugar de unir las actividades manuales y los sistemas creados con los ordenadores para construir un único sistema funcional (como podría ser el uso del ordenador para controlar un robot construido con piezas LegoTM), pedimos a los niños que se fijasen en las diferencias en los tipos de cosas que habitaban cada uno de estos mundos. ¿Cómo influían estas diferencias en lo que pensaban para reflexionar? ¿Qué diferencias había en el tipo de problemas, confusión o dificultades a las que se enfrentaban cuando pasaban de la actividad manual más familiar, en tiempo y espacio reales, al mundo virtual de los ordenadores? Confrontar la posible tensión generada por estas diferencias, en lugar de evitarla, resultó también un factor importante para ayudar a los niños a moverse con más eficacia entre sus ‘manos sabias’ y el mundo escolar simbólico y orientado hacia el texto.
En su trabajo en el laboratorio, los niños observaban y nos ayudaron a observar momentos, generalmente percibidos sobre la marcha, en que los movimientos entre la acción en un tiempo y un espacio reales, y la acción virtual en un espacio informático, revelaron semejanzas sorprendentes. Y, como cabía esperar, la observación de estas semejanzas (‘Esto me recuerda algo que hicimos …’) con frecuencia condujo a la emergencia de un fuerte principio compartido que previamente había estado oculto. Como demostraré, capturar estas percepciones y las discusiones que conducían a ellas, produjo parte del aprendizaje más significativo para ambas partes, niños y docentes.
Ideas emergentes
El movimiento entre materiales, modalidades sensoriales, y modos descriptivos, hizo que cierto tipo de ideas llegasen a formar parte de la cultura del laboratorio, iluminando los diseños realizados por los niños, sus construcciones y sus conocimientos en todos los medios utilizados. Tres de estas ideas eran particularmente persistentes:
La noción de un ‘procedimiento’ inicialmente desarrollado en el diseño informático, pero que también resultó útil en el diseño de sistemas manuales.
El sentido de que buscar los ‘patrones’ que se generan en los diseños manuales y que luego se filtran a los diseños informáticos puede resultar útil e interesante.
Estrechamente relacionado con lo anterior, la idea de agrupamiento o desglosamiento, y sus límites.
El desglosamiento surgió inicialmente por la necesidad de trabajar con la continuidad de la música. Pero su utilidad se infiltró también en el diseño con otros materiales. Las cuestiones surgidas sobre el ‘desglosamiento’ resultaron sorprendentemente evidentes en una pregunta formulada con frecuencia, pero bastante inesperada. Mientras un alumno examinaba la construcción compleja de un compañero, le oímos preguntar: ‘Pero ¿cuál es la COSA, aquí?’
Un día en la vida del laboratorio de diseño
Una vez por semana, después de las clases, trabajábamos en el laboratorio con seis niños de nueve y 10 años. Yo trabajaba con Mary Biggs, profesora de educación especial en la escuela. Mary había seleccionado los seis niños de entre los muchos con los que trabajaba porque creía que podían beneficiarse particularmente del entorno en el laboratorio. Conocía bien a los niños, puesto que trabajaba con ellos a diario. Los seis niños eran Rachel, Rosa, Steve, Laf, Simon y Leah.
Para mí, fue una revelación darme cuenta de lo difícil que es establecer contacto con un niño, establecer una relación íntima con su pensamiento para poder aprender de él, especialmente los niños o niñas para quienes la vida en la escuela no ha sido particularmente gratificante. Sobre todo, llegué a apreciar el trabajo de los docentes: existe una diferencia abismal entre reflexionar y conversar sobre la escuela y estar allí en la práctica; vivir allí, ejercer la docencia todos los días y no solo un día a la semana, durante la tarde. El trabajo con Mary y los niños fue una experiencia de aprendizaje muy intensa; un aprendizaje que ha influido prácticamente en todo lo que he hecho desde entonces.
Engranajes y ritmos
Durante nuestro trabajo en el laboratorio de Logo (una sección del Laboratorio de Inteligencia Artificial de MIT dirigida por Seymour Papert), diseñé, con la ayuda de otros, una versión musical del lenguaje de programación Logo, diseñado originalmente por Papert y su equipo. Lo denominamos MusicLogo y, junto con el lenguaje Logo, los niños podían utilizarlo en el laboratorio de diseño. Mientras que Logo se utilizaba habitualmente para programar gráficos, con MusicLogo, los niños podían trabajar con múltiples medios: en ocasiones haciendo gráficos, otras veces haciendo música. La idea era trabajar en proyectos prácticos de diseño, moviéndose entre medios y modalidades sensoriales, pero manteniendo unos fundamentos de diseño de procesos de los que podían extraerse los principios subyacentes compartidos. Así pues, dando forma a objetos y acciones con medios tan distintos podía considerarse una manera de compartir un diseño estructural.
Por ejemplo, se hizo uso de un mismo procedimiento informático y los principios subyacentes (en particular, la recurrencia) para producir una ‘cuenta atrás’ (10–9–8–7 …), para que un sintetizador de batería tocase un ritmo creciente y para que un sintetizador de clarinete tocase una escala descencenteFootnote5. El procedimiento de cuenta atrás es típico de Logo, mientras que el ritmo creciente de batería y la escala descendente son procedimientos típicos de MusicLogo.
PROCEDIMIENTO DE CUENTA ATRÁS (COUNTDOWN)
TO COUNTDOWN :START :DONE
IF :START = :DONE STOP
PRINT :START
COUNTDOWN :START – 1 :DONE
END
Si ejecutamos el procedimiento COUNTDOWN con las entradas 12 y 1, la pantalla mostrará:
COUNTDOWN 12 1
12
11
10
9
8
7
6
5
4
3
2
1
RITMO CRECIENTE(FASTER, véase )
Figura 2. Una representación gráfica espacial y analógica del tiempo en el que se realiza un ritmo de batería creciente.

TO FASTER :START :DONE
IF :START = :DONE STOP
BOOM :START
FASTER :START – 1 :DONE
END
FASTER 12 1
ESCALA DESCENDENTE (DOWNPITCH, véase )
TO DOWNPITCH :START :DONE
IF :START = :DONE STOP
PLAY :START – 1 :DONE
DOWNPITCH :START – 1
END
DOWNPITCH 12 1
Engranajes
Los engranajes también desempeñaron un papel importante en el laboratorio como elemento de ayuda para que los niños pudiesen visualizar y sentir principios compartidos entre los distintos medios y modalidades sensoriales; es decir, distintos tipos de ritmos rápidos y lentos, unidades de conteo, periodicidad, etc. (véase ).
Como dijo Seymour Papert:
El engranaje, además de conectar con el conocimiento formal de las matemáticas, conecta también con el ‘lenguaje corporal’, el esquema sensoriomotor del niño. El niño puede SER el engranaje, puede comprender cómo gira proyectándose en el lugar de este y girando con él. Esta doble relación, abstracta y sensorial, confiere al engranaje el poder de facilitar una matemática mental robusta. El engranaje actúa aquí como objeto transicional. (Papert, 1980, p. viii, traducción propia)
Mi intuición me decía que experimentar con distintos ritmos y jugar con los engranajes podría ser una manera especialmente entretenida de hacer manifiesta esta ‘doble relación’. Un miércoles por la tarde, habíamos realizado diversas actividades: tocamos la batería, caminamos, jugamos con enormes engranajes de cartón, creamos ritmos con las manos y, por último, ‘dictamos’ al ordenador cómo tocar distintos ritmos de batería utilizando MusicLogo. Los engranajes fueron diseñados por Arthur GansonFootnote6 y construidos por un grupo de niños algo mayores7.
Cuando nos dirigíamos a los engranajes, Mary preguntó a los niños: ‘¿En qué podrían parecerse estos engranajes a lo que hemos hecho antes, como caminar o tocar la batería?’ Rachel, una de las alumnas del grupo, estaba de pie junto a los engranajes, y sus manos eran los engranajes mientras hablaba (). Mientras giraba los engranajes y los veía dar vueltas, hizo una propuesta de manera espontánea. En la interacción intervienen Rosa y Steve, otros dos alumnos del grupo.
Es un problema matemático. Esta tiene (cuenta el número de dientes de la rueda pequeña) uno, dos, tres, cuatro, cinco, seis, siete, ocho … Tienes que hacer girar esta rueda cuatro veces para que esta otra [la rueda grande] de una vuelta completa. ¿Cuántos dientes tiene esta [la rueda grande]?
24.
No, 4 × 8 = 32. Y la rueda pequeña da cuatro vueltas cuando la grande da una vuelta.
(cambia de enfoque) Pero yo quiero saber cuál de las dos va más rápido.
La pequeña.
Las dos van a la misma velocidad.
(se dirige a Steve) ¿Tú dices que la más pequeña?
Sí, la más pequeña gira cuatro veces y va más rápido.
Pero Rachel dice que van a la misma velocidad.
Mira, no puedes hacer que esta vaya más rápido. Cada vez que esta va … Ah, ¿quieres decir cuál de las dos gira más rápido?
Pues, no sé. ¿Tú qué crees?
¿A qué clase de rapidez te refieres?
¿Qué clases hay?
Un tipo de rapidez, podríamos decir … (indica el encaje de los dientes) cómo va encajando cada diente así, ¿lo ves? Y otro tipo de rapidez podría ser el tiempo que tarda esta rueda en dar una vuelta (Rachel está describiendo la diferencia entre velocidad lineal y velocidad angular).
Mmm. ¿Y si nos referimos a la rapidez de los dientes?
La más pequeña.
No, las dos van a la misma velocidad.
OK. ¿Y cuál de las dos da gira más rápido?
La más pequeña.
Marcando el ritmo de los engranajes con las manos
En ese momento, Arthur Ganson, que ese día trabajaba con los niños, percibió una conexión. Esta vez, Leah también participa en la conversación.
Entonces, ¿qué ritmo llevan las ruedas?
Esa rueda. ¿Alguien quiere tocar el ritmo al que gira esa rueda?
Sí, ¿Qué ritmo lleva esa rueda?
Yo lo haré. Os lo enseño. (Hace girar la rueda para demostrar su ‘ritmo’).
Sí, pero ¿cómo representaríamos este ritmo?
Así … mmm (véase ).
Sí. ¿Y la rueda pequeña?
Esa va así … (golpea la mesa con la mano derecha)
Dando palmadas en la mesa, Lea representa la relación 4:1 entre las dos ruedas. Es decir, cada palmada con la mano izquierda representa una vuelta de la rueda grande, mientras que las cuatro palmadas de la mano derecha representan las cuatro vueltas de la rueda pequeña (véase ).
La pregunta instintiva de Arthur vinculó materiales, modalidades y descripciones en apariencia dispares, con los que los niños habían estado trabajando. Las palmadas de Leah eran una especie de metáfora en acción de los movimientos de las dos ruedas del engranaje; había personificado el engranaje. Para Rachel, el movimiento de las dos ruedas representaba los principios de proporcionalidad y de ‘tipos de velocidad’. Y, sin embargo, detrás de esa alternancia de medios y formas de expresión, se esconden principios compartidos. Tal vez el principio compartido más generalizable sea la idea fundamental de la acumulación de ‘unidades’ para crear ‘periodicidades’ relacionadas, que los niños denominaron ‘ritmos’.
Leah y Rachel demostraron la intuición que tuvimos desde el principio: niños que tenían dificultades de aprendizaje en la escuela podrían alcanzar un aprendizaje profundo extrayendo los principios a partir del funcionamiento de los objetos que construían y de sus acciones en ellos y con ellos. La pregunta que seguía sin respuesta, como al principio, era si podíamos ayudar a los niños a establecer conexiones prácticas y funcionales en la tensión entre lo que ya sabían hacer en la práctica y su conocimiento sobre ello expresado de una forma más simbólica (Ryle, Citation1949). Quedaba claro que Rachel iba por buen camino y Leah se iba acercando, pero ¿y los demás? ¿Podrían los ordenadores y MusicLogo ayudar a más niños a establecer ese vínculo entre el conocimiento basado en la acción y el conocimiento simbólico?
El ordenador como factor mediador
Aunque la pregunta específica que Arthur formuló y la respuesta de Leah no habían sido planificados, ambos habían surgido de nuestras actividades yuxtapuestas de representación de ritmos con las palmas y del trabajo con los engranajes. La actividad siguiente sí estaba planificada de antemano. Reflejaba nuestra intención inicial de utilizar el ordenador como mediador entre la acción y el símbolo. La pregunta que nos formulábamos era: ¿Podrían los niños utilizar el ordenador como un vehículo efectivo para moverse entre las acciones de los engranajes, sus propias acciones corporales tocando la batería o dando palmadas y juegos de palmadas y, ahora, con las instrucciones simbólico-numéricas que se introducen en el ordenador? En definitiva, ¿podrían transformar los resultados del estudio continuo de sus acciones corporales en expresiones simbólicas discretas que, a su vez, se convertirían en procedimientos informáticos para generar acciones/sonidos virtuales? Este sería un ejemplo excelente de confrontación de la tensión entre el símbolo y la acción.
La nueva tarea que planteamos a los chicos fue la siguiente: ‘¿Podéis hacer que el sintetizador de batería del ordenador toque el ritmo que Leah ha marcado con las palmas? Pero, para empezar, lo haremos un poco más fácil’. Utilizando las dos manos como lo había hecho Leah, marqué un ritmo sencillo 2:1. Todos los niños repitieron el ritmo con las palmas (véase ).
Los chicos ya estaban familiarizados con la programación de procesos y con el significado de los números para elaborar gráficas Logo; lo que denominábamos ‘enseñar al ordenador’. Ahora, tenían que dar significado a esos números en el nuevo contexto de MusicLogo. ¿Cuáles eran los vínculos entre las acciones y los sonidos que hacían con las manos, los números que utilizaban en operaciones aritméticas simples, los números que utilizaban para crear gráficas en Logo y los que utilizaban como instrucciones en el ordenador para indicar las relaciones temporales entre los ritmos producidos por el sintetizador?
También estaban acostumbrados a conversar cuando se quedaban atascados durante una actividad. Se explicaban unos a otros o a un adulto lo que trataban de hacer para que algo funcionase. No obstante, las descripciones que utilizaban de esa construcción en tiempo real no solían incluir expresiones simbólicas o numéricas ni siquiera después de la actividad. Así pues, lo que los niños iban a hacer ahora sería lo inverso de lo que estaban acostumbrados a hacer: en lugar de reflexionar después para describir algo después de la acción y después del acto, ahora tendrían que describir primero, a modo de instrucciones para el ordenador, lo que querían que sucediese, antes de que suceda. Y las instrucciones tenían que adoptar la forma simbólica de un lenguaje de programación, Logo. Estas son algunas de las cuestiones que surgieron cuando nos dirigíamos hacia los ordenadores y la siguiente tarea.
Un ejemplo: Laf inventa un experimento
MusicLogo podía hacer que el sintetizador tocase dos sonidos distintos de batería denominados PING y BOOM respectivamente. La cantidad de números en la lista que sigue a BOOM y PING determina cuantos sonidos, BOOM o PING, producirá en total el sintetizador. Los números en sí mismos determinan la ‘duración’ de cada evento. O, más exactamente, las relaciones de proporcionalidad de tiempo de un golpe de sonido al siguiente.
Para ayudar a los niños a arrancar, introduje las siguientes instrucciones en el ordenador y escuchamos el resultado (PM es el comando para que se inicie la música, PlayMusic, y CM para detenerla, ClearMusic):
BOOM [8 8 8 8 8 8 8] PM
Escuchamos siete sonidos BOOM de una duración de ‘8’ cada uno. No obstante, los chicos todavía tenían que descubrir el significado de ‘8’. Entonces introduje otro ejemplo y les dije ‘Este irá más rápido’:
BOOM [6 6 6 6 6 6 6 6] PM
Ahora yo quiero hacer uno más rápido todavía.
(que no había participado en la discusión hasta ahora): Pero cuanto más pequeño sea el número más rápido va.
Has respondido a mi pregunta antes de que la haga.
Laf es adivino.
Haz 1 1 1 1 1 1.
¿Qué crees que pasará?
Si pones todo unos, irá muy rápido.
Jeanne escribe:
BOOM [1 1 1 1 1 1 1] PM
Y, en efecto, iba muy rápido. A continuación, les enseñé cómo Logo tocaba los sonidos BOOM y PING a la vez, cada uno con su propia ‘voz’ (véase ).
De la acción al símbolo: un ejemplo
Mientras los chicos se ponían manos a la obra con los ordenadores, yo hice lo propio con Laf. Laf era el ejemplo paradigmático del alumno que, cuando ‘comprendía una idea’ era literalmente una experiencia física. Todos tratamos de capturar y asimilar una idea nueva, pero para la mayor parte de los niños, sobre todo los que viven en un mundo inestable e impredecible, la necesidad de asimilar y conservar algo es persistente. Las exploraciones de Laf para averiguar cómo los números podían ‘enseñar’ al ordenador a tocar la batería lo dejaban bien claro. Y como seguramente había pasado muchas veces, casi lo paso por alto.
Laf hablaba muy poco. En el laboratorio descubrimos su cualidad más notoria: su integridad. A diferencia de otros niños con mayor pericia escolar, en lugar de seguir la rutina de tratar de dar con la respuesta correcta, simplemente desconectaba. Necesitaba comprender las cosas por sí mismo. Sin embargo, en esta ocasión, como en tantas otras en las que contemplaba a otros compañeros realizar una tarea, me di cuenta de que los adultos necesitamos levantar el pie del acelerador más a menudo para poder conectar con el pensamiento de los demás.
Sentado junto a Laf, vi que escribía BOOM y PING una y otra vez, despacio, con decisión y persistencia, seguidos por una sola lista de unos y doses (véase ).
A pesar de mis esfuerzos, no veía razón alguna en lo que hacía Laf. No fue hasta más tarde, analizando los vídeos de la sesión, cuando me di cuenta de lo equivocado que estaba. Estaba centrado en mi tarea y, mientras ejecutaba mis dos niveles de ritmo en una relación de 2:1, me perdía el significado de las listas de BOOM y PING de Laf. Fiel a su integridad, Laf había diseñado un experimento organizado para responder a las preguntas que silenciosamente se había formulado a sí mismo: ¿Cuál es la diferencia entre BOOM y PING y entre 1 y 2 en este contexto? ¿Qué hacen exactamente estos números? ¿Cómo puedo averiguarlo? Escuchando, participando en su propio experimento, confirmó sus conocimientos recién adquiridos: podía oír el contraste entre los rapidísimos 1 y los 2, más lentos.
Para reafirmar sus conocimientos, Laf seguía los números en la pantalla. Golpeando con el dedo sobre la serie de 1 y 2, vinculaba sus propias acciones al sonido y las acciones virtuales del ordenador (véase ). Literalmente, Laf estaba asimilando físicamente el significado de los números 1 y 2. Con atención y paciencia, continuó con la tarea hasta haber completado toda la pantalla (véase ). Echando la vista atrás, veo esta acción como el primer ejemplo de coordinación del símbolo con el sonido y la acción. Los números permanecían inmóviles, mientras que el sonido expresaba un ritmo sonoro en movimiento y Laf, golpeando la pantalla con el dedo, marcaba cada uno de ellos en acción mientras estos se sucedían.
Figura 11. Tamborileo con el dedo. (Véase el archivo complementario en línea para observar el tamborileo con el dedo realizado por Laf.).

Figura 12. Representaciones de BOOM, and PING, 1 y 2, llenan la pantalla (ver el archivo complementario en línea).

Comenzando con lo que ya conocía (‘Cuanto menor es el número, más rápido va … Si pones todo de 1, irá muy rápido’), comprobó ese conocimiento en acción. Tal vez como un científico que observa desconcertado el comportamiento de las moléculas, Laf necesitaba diferenciar entre dos elementos estrechamente relacionados, pero ligeramente distintos (el ‘1’ y el ‘2’). Y como el científico, necesitaba una repetición, un tamaño crítico de muestra de cada elemento repetido durante el tiempo suficiente y en un entorno controlado en el que podía percibir claramente las diferencias y semejanzas como algo regular.
Tras haber observado las suficientes instancias de esos elementos esenciales durante un tiempo suficientemente largo, y tras haber confirmado que los comportamientos de las cifras 1 y 2 no variaban en los diferentes contextos de BOOM y PING, Laf observó que los puntos de coincidencia de las dos secuencias de 1 y 2 producían momentos de gran revelación: los 1 iban demasiado rápido para poder seguirlos, así que esperó a la secuencia de 2 para comenzar (véase y el archivo de vídeo suplementario disponible en línea).
Laf hizo uso de los recursos que tenía a su alcance para la tarea de crear significado. Inventó una manera de utilizar el ordenador y MusicLogo como mediadores entre el mundo virtual de los símbolos y sus acciones en el tiempo/espacio real. Retrospectivamente, me enseñó la importancia de ser capaz de desacelerar y tomarse el tiempo de repetir para practicar literalmente la asimilación del significado.
Pero eso no fue todo. Para desarrollar su experimento, Laf utilizó lo que había aprendido para crear una pieza de música completa. La pieza estaba formada por líneas alternas de BOOM y PING y secuencias de 1 y 2. No es extraño que llamara a su procedimiento TO LAF (PARA LAF, véase ).
Cuando Mary vio y oyó la creación de Laf, llamó la atención de sus compañeros:
Mary: ¡chiss! … Laf va a tocar su pieza.
Entusiasmado, Laf exclamó: ‘Ahí va otra vez’, y escribió LAF PM.
El procedimiento creado por Laf llenó el laboratorio y los niños escucharon con atención hasta el final. El habitualmente discreto Laf tenía un aspecto triunfante y sus compañeros le aplaudieron con ganas.
Avanzando hacia la representación simbólica
La mayor sorpresa se produjo la semana siguiente, cuando los niños regresaron al laboratorio. Claramente cómodo con el significado de las series numéricas 1 y 2, y tal vez habiendo aprendido de lo que vio hacer a los demás niños, Laf se puso manos a la obra con el experimento a dos voces que les había sugerido, BOOM (V1) y PING (V2). Comenzó con las secuencias ya familiares de 1 y 2, pero sorprendentemente avanzó hasta una nueva relación del tipo 1:2; 4:8 (véase ).
Pero nuestra mayor sorpresa fue cuando, a final de la sesión, Laf procedió a elaborar una tabla completa de posibles ejemplos de tamborileos 2:1 (véase ).
En la se pueden observar las representaciones de BOOM y PING sonando consistentemente a la vez en proporciones de 2:1; 8:4, 6:3, 4:2, 10:5. El primer experimento de Laf, que en ese momento me pareció una actividad sin sentido, resultó haber sido un preludio en el que reunir, asumir, considerar y finalmente desarrollar y dar significado a toda una tabla simbólica de proporciones rítmicas de 2:1. Como una muestra más de la importancia conferida por Laf a la representación del paso del tiempo, cabe resaltar que, con cada par, los PING, que suenan el doble de rápido (secuencias de 4) que los BOOM (secuencias de 8), también tienen el doble de iteraciones que los BOOM. Por tanto, cada pareja de BOOM y PING aparecen a la vez, igualados en el tiempo total.
El ordenador se convierte literalmente en un mediador que ayuda a integrar el símbolo, el sonido y la acción. Desarrollando su experimento interactivo inicial, sus iteraciones de las series de 1 y 2, Laf se construyó una idea poderosa. Siguiendo con paciencia su trabajo tranquilo y constante, podemos observar el proceso de transformación de sus acciones continuas en imágenes estáticas en desarrollo, que culminan en la invención de una representación simbólica totalmente desarrollada.
Pero esperen: sobre la base de esta tabla, era fácil asumir que, al desarrollar y generalizar sus experimentos previos con secuencias de l y 2, Laf desarrolló la poderosa idea de proporción. Pero nótese la diferencia entre la forma de mi representación estática de la proporción y la representación de las repeticiones de BOOM y PING de Laf (véase ).
Sencillamente, sobre la invención de Laf, había impuesto la representación tradicional de la proporción. En este proceso, he eliminado el tiempo y la acción. Laf marcó cuidadosamente cada acción, cada iteración, mientras pasaba del tiempo y la acción al espacio del papel. Cada uno de los números de su tabla refleja una acción o reacción: su repiqueteo con el dedo, acompañando la ‘actuación’ del ordenador. Mi representación proporcional, 6:3, 10:5, ha eclipsado las iteraciones reales en el tiempo y en movimiento, condensadas en una única representación simbólica; muchos eventos se han convertido en uno.
La tabla que se ilustra en la no muestra en realidad cómo Laf asimila el concepto de proporción, sino que constituye una instantánea de un proceso evolutivo de aprendizaje. Vemos un momento del camino hacia un ‘proceso abstracto’. La extracción de acciones continuas, hechas discretas, inmovilizadas en una transformación gradual en las expresiones simbólicas que enseñamos en la escuela. Como señaló Werner (Citation1957):
La abstracción puede definirse como una actividad mental a través de la cual las partes de una unidad se desprenden del todo y sus cualidades particulares — color, forma, etc. — se experimentan de forma aislada (p. 234, traducción propia).
Propongo que el conocimiento de Laf es profundamente dependiente de un entorno que el ordenador explora a su modo, modo único y particular: el ordenador es un medio en el que el símbolo se define a sí mismo convirtiéndose en lo que hace. Parafraseando a Papert, Laf utiliza el ordenador como un ‘objeto transicional’. Su participación continua en la tensión productiva entre acción y símbolo podría producir más tarde la poderosa idea de proporción.
Conclusiones
Las actividades que se describen en estas historias no pretenden ser recomendaciones para su reproducción literal ‘en el currículum’, ni siquiera pretenden indicar ‘qué hacer mañana en clase’. Tampoco pretenden ser una recomendación de cómo utilizar los ordenadores con eficacia en las aulas. Estas historias pretender ser meros ejemplos de un contexto y de un enfoque hacia el aprendizaje.
Por resumir, los ejemplos descritos del trabajo de los niños nos han ayudado a ilustrar que el conocimiento se desarrolla activamente a través de la experiencia, la interpretación, las construcciones, las preguntas, los fracasos y los éxitos. Los ejemplos mostrados tal vez sean más relevantes para niños cuyo poderoso know how, su conocimiento personal, les falla en la escuela, en gran parte porque no encuentra una manera de pasar de la calle a la clase. Como se ha mencionado al principio del artículo, para niños que viven un mundo inestable e impredecible, en flujo continuo, poder asimilar, mantener, detener y mantenerse es una necesidad persistente. Estos niños suelen sentir que la escuela es irrelevante y, de manera recíproca, se les hace percibir a sí mismos como irrelevantes, periféricos, en un entorno escolar.
En definitiva, defiendo que el ordenador puede desempeñar un papel especial como recurso para la exploración y la invención cuando los estudiantes son capaces de desarrollar lo que ya saben hacer, mientras trabajan en un espacio conceptual y a un ritmo que pueden asimilar. En este entorno, en lugar de convertirse en consumidores pasivos, recipientes de información y bienes provenientes de otros, los niños tienen la posibilidad de convertirse en constructores de nuevo conocimiento del que pueden sentirse orgullosos. Y, a través de este empoderamiento, también pueden descubrir estrategias para aprender cómo aprender en el mundo escolar y fuera de él.
RIYA_A_1401316_SM8254.mov
Download QuickTime Video (1.4 MB)Disclosure statement
No potential conflict of interest was reported by the author. / Los autores no han referido ningún potencial conflicto de interés en relación con este artículo.
Supplemental data
Supplemental data for this article can be accessed here.
Notes
1. Seymour Papert (1928–2016) was a professor in the Artificial Intelligence Lab and the Director of the Logo Lab at the Massachusetts Institute of Technology (MIT). He was the primary developer of the Logo computer language.
2. This work was carried out under the direction of the author together with the invaluable help of Mary Briggs, the Special Education teacher in the school.
3. There is a clear relationship between what I am calling ‘action knowledge’ in contrast to ‘symbolic knowledge’ and Ryle’s ‘knowing how’ and ‘knowing that’ (Ryle, Citation1949).
4. The 10 Apple IIe computers were donated by Apple Computer.
5. In the procedures that follow, the colon symbol (called ‘dots’) indicates a variable as input.
6. Arthur Ganson, a kinetic sculptor, had designed both the materials and the tools with which the children had worked.
7. A spatial analogue representation of the computer drum playing the faster beat procedure.
1. Seymour Papert (1928–2016) fue profesor en Laboratorio de inteligencia artificial y director del Laboratorio Log en el Massachusetts Institute of Technology (MIT). Fue el primer desarrollador del lenguaje de programación Logo.
2. Este trabajo fue realizado bajo la dirección del autor, con la inestimable ayuda de Mary Briggs, la profesora de educación especial de la escuela.
3. Existe una relación clara entre lo que llamo ‘conocimiento basado en la acción’, en contraposición al ‘conocimiento simbólico’ y lo que Ryle denomina ‘saber cómo’ y ‘saber qué’ (Ryle, Citation1949).
4. Los 10 equipos Apple IIe fueron donados por Apple Computer.
5. En los procedimientos que se detallan, el símbolo ‘:’ (‘dos puntos’) indica una variable como entrada.
6. Arthur Ganson, un escultor cinético, diseñó los materiales y las herramientas con las que trabajaron los niños.
7. Representación analógica espacial de la batería electrónica tocando el ritmo rápido.
References / Referencias
- Archambault, R. D. (1964). John Dewey on education: Selected writings. New York, NY: The Modern Library.
- Bamberger, J. (1991). The laboratory for making things: Developing multiple representations of knowledge. In D. A. Schön (Ed.), The reflective turn: Case studies in and on educational practice (pp. 37–62). New York, NY: Teachers College Press.
- Dewey, J. (1916). Democracy and education: An introduction to the philosophy of education. New York, NY: The Free Press.
- Dewey, J. (1931/1964). The way out of educational confusion. In R. D. Archambault (Ed.), John Dewey on education: Selected Writings (pp. 422–426). New York, NY: The Modern Library.
- Osberg, D., Biesta, G., & Cilliers, P. (2008). From representation to emergence: Complexity’s challenge to the epistemology of schooling. Educational Philosophy and Theory, 40, 213–227. doi:10.1111/j.1469-5812.2007.00407.x
- Papavlasopoulou, S., Giannakos, M., & Jaccheri, M. L. (2014). Empirical studies on the maker movement, a promising approach to learning: A literature review. Entertainment Computing, 18, 57–78. doi:10.1016/j.entcom.2016.09.002
- Papert, S. (2005). You can’t think about thinking without thinking about thinking about something. Contemporary Issues in Technology and Teacher Education, 5, 366–367.
- Ryle, G. (1949). The concept of mind. Chicago, IL: University of Chicago Press.
- Vossoughi, S., & Bevan, B. (2014). Making and tinkering: A review of the literature. National Research Council Committee on Successful Out-of-School STEM Learning. Retrieved from https://sites.nationalacademies.org/cs/groups/dbassesite/documents/webpage/dbasse_089888.pdf
- Werner, H. (1957). Comparative psychology of mental development. New York, NY: International University Press.