A unified vector optimization problem: complete scalarizations and applications

Abstract

The aim of this article is to introduce and analyse a general vector optimization problem in a unified framework. Using a well-known nonlinear scalarizing function defined by a solid set, we present complete scalarizations of the solution set to the vector problem without any convexity assumptions. As applications of our results we obtain new optimality conditions for several classical optimization problems by characterizing their solution set.

Keywords:

• vector optimization
• efficiency
• approximate efficiency
• scalarization
• weak efficiency
• strict efficiency
• optimality conditions

AMS Subject Classifications:

• 90C26
• 90C29
• 90C30
• 90C46

1. Introduction

In most real-life problems, optimization problems concern the minimization of several criterion functions simultaneously. Very often, no single point minimizing all criteria at once may be found, and therefore other concepts of optimality arise. Among them, the so-called weak efficient, efficient, strict efficient or proper efficient solutions are discussed in the literature.

By algorithmic and theoretical purposes, one needs to describe the whole solution set to a vector optimization problem via scalarization. For instance, given a function f: K ⊆ ℝ ⁿ  → ℝ ^m , if we are interested in its weakly efficient minima with respect to the nonnegative orthant in ℝ ^m , E _W , one desires to know under which conditions, the equivalence

holds. Assuming the convexity of K, it is well-known that such an equivalence (1) is true whenever each component of f is convex, but it is still true under weaker assumption as shown in [9,22]. The authors in [9], for m = 2, established a necessary and sufficient condition under which the equivalence (1) is satisfied; such a condition is the convexity of the set , where cone(A) means the smallest cone containing the set A (for general m ∈ ℕ, the convexity is only sufficient to satisfy the equivalence (1). In spite of this fact, solving the vector optimization problem via the equivalence (1) (giving rise to the weighting method) requires to know p* in advance. This is the main drawback of the procedure. In fact, by taking the function f(x) = x = (x ₁, x ₂), and K = {(x ₁, x ₂) ∈ ℝ²: x ₁ + x ₂ ≥ 1}, we get, for given , p* ≠ 0,

Here E _W  = {(x ₁, x ₂) ∈ ℝ²: x ₁ + x ₂ = 1}. A way to choose the parameter p* is discussed in [5] under the boundedness from below of ⟨ p*, f(·)⟩ on K.

One purpose of this article is to provide an alternative approach by using a nonlinear scalarizing function which already appears in the literature, without any convexity assumption. This will be carried out by introducing a general vector optimization problem which encompasses most notions of solutions well-known in the literature: efficiency, weak efficiency, strict efficiency as well as proper efficiency.

Furthermore, since most algorithmic procedures yield feasible points near to the exact solution, we are also interested in approximate solutions. Thus, we introduce an approximate vector optimization problem and find scalar representations of its solution set.

The outline of this article is as follows. In Section 2 we formulate the unified vector optimization problem and discuss its generality. Section 3 introduces the scalarizing function and recalls its useful properties under very mild conditions. Section 4 is devoted to describe the scalarization procedure for (approximate) efficiency by establishing complete scalarizations under a more general assumption, termed (B). Section 5 provides optimality conditions for specific optimization problems and gives several examples. In Section 6, the main conclusions are presented.

2. A unified vector optimization problem

Throughout this article Y will be a real topological vector space and X a real Banach space. Given a nonempty set S ⫋ Y, a nonempty set K ⊆ X and a function f: K → Y, we are interested in the problem

The set of such vectors is denoted by E _S  = E _S (K), and each one of its elements is called a (global) S-minimizer of f on K.

If 0 ∈ S, one can realize that problem (𝒫) reduces to find such that for all x ∈ K; whereas if 0 ∉ S and then for all .

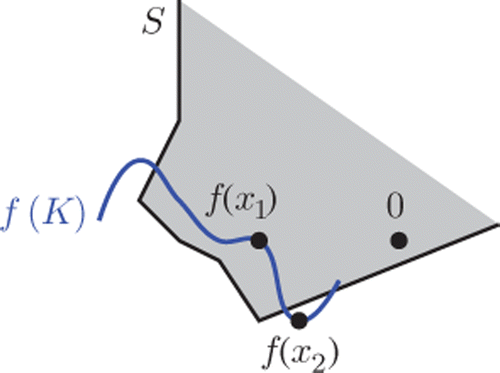
We emphasize the generality of problem (𝒫) from the economic point of view since the preference relation can be given on X and determined by a certain function f (e.g. a utility function) or/and on Y by a set S which is not necessarily a cone. An instance of this fact is illustrated in Figure 1, where one easily sees that x ₁ ∉ E _S and x ₂ ∈ E _S .

Figure 1. Illustration of problem (𝒫).

Since most numerical procedures or location methods, like the iterative and heuristic ones, yield feasible points near to the exact solution, we are interested in the following notion of approximate solution.

Given ϵ ≥ 0 and 0 ≠ q ∈ Y, we consider the following approximated problem associated with (𝒫):

where S is any set satisfying S + ℝ₊₊ q ⊆ S, where ℝ₊₊ ≐ ]0, +∞[. We denote by E _S (ϵq) the solution set to (𝒫(ϵq)). Thus, the previous inclusion implies that:

Consequently,

When f is a real-valued function we denote by E(f, ϵ) the set of ϵ-solutions, that is, if and only if for all x ∈ K. The above approximate problem is defined in Kutateladze's sense [23]. In [33], several notions of approximate solutions are discussed.

If we consider the classical framework of vector spaces ordered by a proper convex cone {0} ≠ P ⊆ Y we obtain the following well-known notions of optimality.

In what follows, given any ∅ ≠ A ⊆ Y, we denote by 𝒞(A), int A, cl A and ∂A the complement, the topological interior, the topological closure and the boundary of A respectively. We say that A is solid if int A ≠ ∅ . A convex cone P is called pointed if l(P) ≐ P ∩ (−P) = {0}. If

•	S = P, the solutions are termed ‘ideal’ or ‘strong’ minima of f and the solution set is denoted by E P ;
•	(int P ≠ ∅) S = 𝒞(−int P), the solutions are called ‘weakly efficient’ minima of f and for the set of solutions we use E W ;
•	S = 𝒞(−P) ∪ l(P), the solutions are said to be ‘efficient’ minima of f and we set E S  ≐ E;
•	S = 𝒞(−P) ∪ {0} (P nonpointed), such solutions are named ‘weakly strict efficient’ minima of f, in this case E S  ≐ E W1;
•	S = 𝒞(−P), such solutions are named ‘strict efficient’ minima of f and the solution set is denoted by E 1.

In addition, we can also study proper efficiency. In fact:

•	is a ‘Henig proper efficient’ minimum for f if there exists a proper convex cone D ⊆ Y with nonempty interior satisfying P∖l(P) ⊆ int D such that with S = 𝒞(−D) ∪ l(D). The set of such minima is denoted by E 2.
•	is a ‘proper efficient’ minimum for f if there exists a closed convex set A ⫋ Y with nonempty interior satisfying 0 ∈ ∂A and A + (P∖{0}) ⊆ int A such that with S = 𝒞(−int A). The set of such minima is denoted by E 3. Note that A + (P∖{0}) ⊆ int A implies the pointedness of P.

Since l(P) ∪ 𝒞(−P) ⊆ 𝒞(−int P) and l(D) ∪ 𝒞(−D) ⊆ l(P) ∪ 𝒞(−P) we have E ₂ ⊆ E ⊆ E _W . In the case E _P  ≠ ∅, we get E _P  = E. On the other hand: E ₁ ⊆ E _W1 ⊆ E; E = E _W1 whenever P is pointed; E _W  = E _P provided P is a closed halfspace (see Lemma 2.5 of [8]); E ₁ = E _W1 whenever f is injective. Moreover, when P is pointed every Henig proper efficient solution is also proper efficient.

The set E ₃ has been studied in [32], see the references therein for more details; whereas the notion of strict efficiency is further developed in [11].

We point out that in [18] Ha introduces the following unified vector optimization problem: find ā ∈ A (Q-minimal point of A) such that

where Q is an arbitrary proper open cone (with apex at the origin). It is clear that the above problem can be considered as a particular case of (𝒫) by setting f to be the identity, K = A, X = Y and S = 𝒞(−Q). Notice that we neither require S to be a cone nor closedness, see Figure 2. The unified formulation (2) allowed the author to deal with strong efficiency, weak efficiency and proper efficiency (except efficiency itself). A characterization of Q-minimal points is established in [18, Proposition 21.10] as minima of a scalar function involving the signed (or oriented) distance functional, which is different from the scalarizing function employed in the subsequent sections. In addition, by means of the same signed distance functional, Fermat rule for Q-minimal points are provided in terms of the Ioffe approximate and Clarke coderivatives for set-valued vector optimization problems. Thus, the scope of Ha's paper is different from the present one. We also note that Lagrange optimality conditions without any convexity assumption for problem (𝒫) are derived in [10], via Mordukhovich subdifferential, by using the scalarizing function recalled in the following section.

Figure 2. Illustration of problem (𝒫) satisfying Assumption (B).

As we shall see in Section 5, problem (𝒫) categorizes optimization problems given by a not necessarily pre-order relation. Such nontransitive preferences are very interesting in mathematical economics, see [26] and the references therein. Moreover, problem (𝒫(ϵq)) encompasses several notions of ϵ-efficiency, in particular the Q(ϵ)-efficiency concept introduced by Gutiérrez et al. in [17], which already unifies the approximated solutions in vector optimization.

3. The nonlinear scalarizing function

A nonlinear scalarizing function, that nowadays is having a great impact in the development of a theoretical and algorithmic treatment of vector optimization problems, is a particular Minkowski-type function which is known under different names in several areas of applied mathematics. Especially, such a scalarizing function has been considered in optimization theory by several authors. For instance, we refer to [1,25] for mathematical economics; [13,21,24,27,31] for vector solutions; [19,20] for set solutions [15,16] for approximate solutions; [6] for fuzzy optimality conditions; and [7] for computing ϵ-efficient solutions. Among others, a previous paper which studies such a scalarizing function is [12], although a similar function already appeared in [29, Example 2, p. 139].

In the sequel, q ∈ Y, q ≠ 0 and A ⊆ Y is a proper set, that is, ∅ ≠ A ≠ Y. Set ℝ₊ ≐ [0, +∞[, ℝ₊₊ ≐ ]0, +∞[. Let ∅ ≠ P ⊆ Y. We say that P is a cone if ℝ₊ P = P and P a conic set if ℝ₊₊ P = P.

Definition 3.1

Let ξ _q,A : Y → ℝ ∪ {±∞} be defined by

We use the convention inf ∅ = +∞. It is well-known that such a function has many useful properties of separation and monotonicity which play a central role in the proofs of the main results of the above-mentioned works. We emphasize that a good account of its properties is given in [14,32].

A useful property is that ξ _q,A (y + tq) = ξ _q,A (y) + t for all y ∈ Y and t ∈ ℝ. Now we recall some additional properties which are used to establish complete scalarizations of problem (𝒫) in the subsequent sections. Proposition 3.2 can be deduced from the proof of [14, Theorem 2.3.1] which is presented for a closed set A.

Firstly, we need directions of the recession cone of a nonempty set A ⊆ Y, A _∞ ≐ { y ∈ Y: a + ℝ₊₊ y ⊆ A, ∀a ∈ A}, then A + A _∞ = A.

Proposition 3.2

Let λ ∈ ℝ, q ≠ 0, The following assertions hold:

a.	{ y ∈ Y: ξ q,A (y) < λ} = ]−∞, λ[q − A; thus If, in addition, A + ℝ++ q ⊆ A ⫋ Y:
b.	λq − int A ⊆ { y ∈ Y: ξ q,A (y) < λ} ⊆ λq − A ⊆ { y ∈ Y: ξ q,A (y) ≤ λ} ⊆ λq − cl A;
c.	{ y ∈ Y: ξ q,A (y) = λ} ⊆ λq − ∂A.

From the preceding proposition we obtain the next corollary.

Corollary 3.3

Let q ∈ Y, q ≠ 0, A ⫋ Y.

a.	Assume that cl A + ℝ++ q ⊆ A, then
b.	Assume that int A ≠ ∅ and A + ℝ++ q ⊆ int A, then

Figure 2 illustrates the previous results by considering S = A. Taking into account that [cl A + ℝ₊₊ q ⊆ A and A + ℝ₊₊ q ⊆ int A] ⇔ cl A + ℝ₊₊ q ⊆ int A, we have the following result.

Corollary 3.4

Let q ∈ Y, q ≠ 0, A ⫋ Y.

a.	If cl A + ℝ++ q ⊆ int A, then for all λ ∈ ℝ, { y ∈ Y: ξ q,A (y) = λ} = λq − ∂A; { y ∈ Y: ξ q,A (y) > λ} = λq − int 𝒞(A); { y ∈ Y: ξ q,A (y) ≤ λ} = λq − cl A; { y ∈ Y: ξ q,A (y) ≥ λ} = λq − cl 𝒞(A); { y ∈ Y: ξ q,A (y) < λ} = λq − int A.
b.	If cl A + ℝ++ q ⊆ A and cl A is convex, then ξ q,A is convex.

Remark 3.5

Note that cl A + ℝ₊₊ q ⊆ int A implies that q ∈ (cl A)_∞. On the other hand, the condition A + int P ⊆ A ≠ Y, with P being any convex cone with nonempty interior, implies cl A + ℝ₊₊ q ⊆ int A ∀q ∈ int P. Indeed, by [3, Lemma 2.5], we obtain

Moreover, A + int P ⊆ A ⇔ cl(A) + int P ⊆ A.

Lemma 3.6

Let ∅ ≠ A ⊆ Y and P ⊆ Y be any proper convex cone with nonempty interior. Then, for all q ∈ int P,

Proof

It is a consequence of Corollary 3.3 and [3, Lemma 2.5].▪

Lemma 3.7

Suppose that A, B ⊆ Y, such that B + B ⊆ B. Let y, y′ ∈ Y and q ∈ Y.

a.	If y − y′ ∈ −B, then ξ q,B−A (y) ≤ ξ q,B−A (y′).
b.	If y − y′ ∈ −int B, then ξ q,B−A (y) < ξ q,B−A (y′).

Proof

By definition ξ _q,B−A (y) = inf{t ∈ ℝ: y ∈ tq + A − B} for every y ∈ Y. We only prove (b) since (a) is similar. Since y − y′ ∈ −int B there exists ϵ < 0 such that y − y′ − ϵq ∈ −B. Thus, if t ∈ ℝ is such that y′ ∈ tq − (B − A), then

since B + B ⊆ B. It follows that ξ _q,B−A (y) ≤ ϵ + t and hence ξ _q,B−A (y) < ξ _q,B−A (y′).▪

4. Scalarizations for a unified vector optimization problem

Following the notations introduced in the previous sections, we establish scalarizing conditions for the problems

and

where ϵ ≥ 0, q ∈ Y, q ≠ 0, ∅ ≠ K ⊆ X and f: K → Y by introducing families of scalar optimization problems which will describe the solution set to (𝒫) and (𝒫(ϵq)), denoted by E _S and E _S (ϵq), respectively. This will be carried out through the scalarizing function discussed in the previous section.

According to [24, Definition 3.1, p. 95], given a family G of functions g: Y → ℝ, we say that G is a complete scalarization for (𝒫) if for every x ∈ E _S there exists g ∈ G such that x ∈ E(g ○ f) and E(g ○ f) ⊆ E _S , where E(g ○ f) denotes the solution set to (𝒮𝒫):

Equivalently, G (a family of functions from Y to ℝ) is a complete scalarization for (𝒫) if and only if there exists G′ ⊆ G such that

Similar representations will be established for (𝒫(ϵq)).

In this section we consider sets satisfying the so-called free-disposal assumption (S + P = S) introduced by Debreu [4] in the setting of mathematical economics.

ASSUMPTION (A) P ⊆ Y is a proper (not necessarily closed or pointed) convex cone with nonempty interior, and S ⫋ Y is such that 0 ∈ ∂S and S + int P = int S, or equivalently, S + int P ⊆ S, or equivalently, cl S + int P ⊆ S.

Since then, several conditions related to Assumption (A) have been considered in economic theory and optimization. More precisely, given a closed convex cone P, we say that a closed set S ⫋ Y satisfies the free-disposal Assumption (P) [2,32] if S + P = S; whereas S satisfies the strong free-disposal Assumption (P _S ) [32]: if S + (P∖{0}) = int S, or equivalently, S + (P∖{0}) ⊆ int S.

Obviously, when 0 ∈ ∂S, int S ≠ ∅ and int P ≠ ∅, we get (P _S ) ⇒ (P) ⇒ (A). Certainly, the set S = 𝒞(−P) ∪ l(P) satisfies S + P = S, but in general, it is not closed; whereas S = 𝒞(−P) ∪ {0} satisfies (A), but it is nonclosed and S + P ≠ S whenever P is nonpointed.

Throughout this section we impose the following assumption on S which is more general than Assumption (A) since no convex cone P is involved.

ASSUMPTION (B) 0 ≠ q ∈ Y, and S ⫋ Y is a (not necessarily closed) set such that 0 ∈ ∂S and cl(𝒞(−S)) + ℝ₊₊ q ⊆ int 𝒞(−S).

It is clear that, the condition 0 ∈ ∂S can be assumed, after a translation, whenever S ≠ Y. Moreover, under this assumption, int 𝒞(−S) ≠ ∅ ≠ int S, because of S ≠ Y and we have the equivalence

By virtue of Remark 3.5, if P and S satisfy Assumption (A) then S fulfills Assumption (B) for every q ∈ int P since S + int P ⊆ S ⇔ cl S + int P ⊆ S ⇔ 𝒞(−S) + int P ⊆ 𝒞(−S), as one can check easily. We recall that Assumption (A) holds for a wide class of (not necessarily closed) sets including those classical models:

Notice that any set S satisfying 0 ∈ ∂S and S + P = S fulfills Assumption (A) provided int P ≠ ∅, but such an equality is not verified by S = 𝒞(−P) ∪ {0} when P is not pointed.

If, instead, S is closed and satisfies Assumption (P _S ), then S fulfills Assumption (B) for every q ∈ P∖{0}. This allows us to deal with proper efficiency (E ₃), where S = 𝒞(−int A) for some closed convex set A such that 0 ∈ ∂A and A + (P∖{0}) ⊆ int A. Here, P may have empty interior.

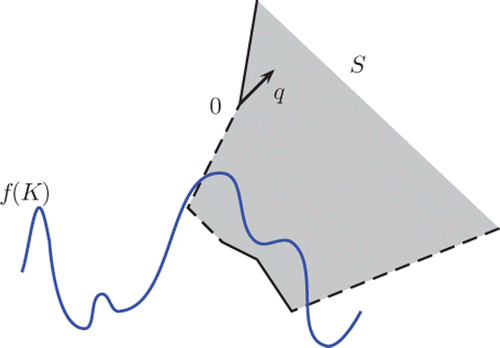
The previous remarks point out the generality of our problem (𝒫) due to geometric structure of S under Assumption (B), since S could not be a cone or not a convex set as shown in Figure 2.

Remark 4.1

If cl S + ℝ₊₊ q ⊆ int S, then S + ℝ₊₊ q = cl S + ℝ₊₊ q = int S, and so int(cl S) = int S, cl(int S) = cl S. Similar expressions hold for 𝒞(−S).

The next two main theorems characterize when a point belongs to E _S (resp. E _S (ϵq)) in terms of (resp. ) under Assumption (B).

Theorem 4.2

Suppose that q and S satisfy Assumption (B). Let , the following assertions are equivalent:

a.
b.	and

Proof

It is clear that since 0 ∈ ∂S. On the other hand, by Corollary 3.4(a),

and if , one obtains

(a) ⇒ (b): Let . Then for all , x ∈ K. By (4) we have since 0 ∈ ∂S. It is clear that and by (5), .

(b) ⇒ (a): Take as in (b). Suppose that . Then there exists such that

Thus, from the hypothesis, , that is, by (5). On the other hand, by (4), we have . Therefore, which contradicts (6).▪

In particular, we deduce that Lemma 5.2 in [32] follows from (a) ⇒ (b) in the previous theorem by taking S such that E _S  = E ₃.

Before continuing, some remarks are in order.

Remark 4.3

i.	It may happen that the set in (b) be empty (this occurs for instance when S = 𝒞(−P)) with P being closed: in such a situation (S = 𝒞(−P)) Theorem 4.2 reduces to We will discuss related points later on.
ii.	When 0 ∈ S (some classical models have been described before), (b) of the previous theorem admits the following formulation:

Now, we establish a similar characterization for the problem (𝒫(ϵq)). Notice that it also provides another characterization for ϵ = 0.

Theorem 4.4

Suppose that q and S satisfy Assumption (B). Let us consider problem (𝒫(ϵq)) with ϵ ≥ 0, and . The following assertions are equivalent:

a.
b.	and

Proof

Since , by Corollary 3.4(a), we have

(a) ⇒ (b): Let . Then for all . Thus, by (7), since 0 ∈ ∂S. Moreover, when one gets , that is, . Again, from Corollary 3.4(a) we obtain

which concludes the proof.

(b) ⇒ (a): take as in (b). Suppose that Then there exists such that whence, by (7), , and so, by Corollary 3.4(a), we have for all x′ ∈ K since . It follows that . From (b) we get which contradicts the hypothesis. Hence ▪

Remark 4.5

We point out that taking into account that if and only if , the implication of Theorem 4.2 may be obtained by using a similar reasoning to that employed in the proof of Theorem 2.3.6 in [14] about nonconvex separation (where Assumption (B) substitutes (i) of [14, Theorem 2.3.6]). A similar argument can be used to prove the ‘if part’ of Theorem 4.4.

Next example shows the inclusion in Theorem 4.4(b) for ϵ > 0 may be strict.

Example 4.6

Take and f: K → ℝ², f(x) = (x, x + 2) if and f(x) = (x, 0) if 0 ≤ x ≤ 2. Let , and ϵ = 2. It is clear that 0 ∈ E _S (ϵq), in addition,

However

since

and

taking into account that , (ξ _q,𝒞(−S) ○ f)(−1) = 2 and .

A simpler equivalence than those in Theorems 4.2 and 4.4 can be obtained under an additional assumption on S.

Theorem 4.7

Consider problem (𝒫(ϵq)) and suppose that q and S satisfy Assumption (B). Let . Then,

Consequently if, in addition, S is closed then

a.
b.

Proof

The first implication is in Theorem 4.4.

For the second we proceed as follows. If on the contrary , then for some x ∈ K, . Then, . Thus, . By assumption,

Hence, if δ > ϵ then , a contradiction.

The third implication is obtained by taking the limit as δ goes to ϵ in (𝒫(δq)).▪

By considering (𝒫(ϵq)), we deduce that Theorem 4.4 extends and refines Theorems 4.5 and 5.1(a) in [16]. In addition, the first part of Theorem 4.7 extends Theorem 5.1 of [16]; whereas the second part can be applied to S = 𝒞(−int P) when P is any (not necessarily closed or pointed) convex cone; or to S = P when P is a closed halfspace; or to S = 𝒞(−P∖{0}) = 𝒞(−P) ∪ {0} when P = Q ∪ {0} with Q being open and convex satisfying tQ ⊆ Q for all t > 0 (then P is a convex cone). The latter case recovers Theorem 5.2 in [16]. The special case of weak efficiency treated in Theorem 4.5 in [16], is a consequence of the previous theorem.

The examples below show that under the assumptions given in Theorem 4.7 the implication may be false when S is not closed.

Example 4.8

Consider S = 𝒞(−P) ∪ {(0, 0)} where P = {(x, y) ∈ ℝ²: x ≥ 0, y > 0}. Let f be a function from K = ℝ to Y = ℝ² defined by

and take q = (1, 1), ϵ = 1. Then, q and S satisfy Assumption (B) and it is easy to check that since . On the other hand, taking into account that 𝒞(−S) = P and we easily compute

Thus,

that is, , and therefore ∀δ > ϵ = 1. Note that E _S (0) = {0}.

Example 4.9

Consider S = P with P = {(x, y) ∈ ℝ²: x > 0, y ≥ 0} ∪ {(0, 0)}. Let f, q and ϵ be as in the previous example. Then, we see that since . However, we can also check that and so ∀δ > ϵ = 1. Note that E _S (0) = E _S  = ∅.

In order to obtain complete scalarizations for E _S , we need the next theorem.

Theorem 4.10

Suppose that q and S satisfy Assumption (B).

a.	If ∅ ≠ A ⊆ E S , then
b.	If 0 ∈ S and S + [cl(𝒞(−S))∖𝒞(−S)] ⊆ S then,

Proof

a.	Since for each , for all , we obtain by Proposition 3.2, for all x ∈ K. Thus, (ξ q,−f(A)+𝒞(−S) ○ f)(x) ≥ 0 for all x ∈ K. Since , we get The same reasoning also proves
b.	It only remains to prove the inclusion. Let and with . By Theorem 4.2, . Hence, for every x ∈ K with x ≠ x′, , and so x′ ∈ E S since 0 ∈ S.▪

Remark 4.11

Taking into account the previous results, we point out that Theorem 4.10(a) applies when P is any (not necessarily closed or pointed) convex cone with nonempty interior, to S = P; S = 𝒞(−int P); 𝒞(−P) ∪ l(P); 𝒞(−P) ∪ {0}; 𝒞(−P) being q ∈ int P; whereas (b) applies when P is any (not necessarily pointed) closed convex cone with nonempty interior, to S = 𝒞(−int P); 𝒞(−P) ∪ l(P); 𝒞(−P) ∪ {0} being q ∈ int P.

Theorem 4.12

Suppose that q and S satisfy Assumption (B) and consider (𝒫(ϵq)), ϵ ≥ 0. Assume that 𝒞(−S) + 𝒞(−S) ⊆ 𝒞(−S) and S is closed. If ∅ ≠ A ⊆ K then

Proof

Let and . Then, there exists x ∈ K, , such that . By the closedness of S, Lemma 3.7(b) implies that

It follows that , which contradicts the assumption.▪

Remark 4.13

When P is any (not necessarily closed or pointed) convex cone, the previous theorem can be applied to S = 𝒞(−int P), and to S = P provided P is a closed halfspace. In addition, it also applies when S = 𝒞(−P∖{0}) = 𝒞(−P) ∪ {0} where P = Q ∪ {0} is pointed with Q being open and convex set satisfying tQ ⊆ Q for all t > 0.

We are ready to state our main result of complete scalarization for (𝒫) which is a consequence of Theorems 4.10 and 4.12.

Theorem 4.14

Suppose that q and S satisfy Assumption (B). Assume that E _S  ≠ ∅.

a.	If 0 ∈ S and S + [cl(𝒞(−S))∖𝒞(−S)] ⊆ S, then
b.	If S is closed and 𝒞(−S) + 𝒞(−S) ⊆ 𝒞(−S), then

5. Some applications

In this section, we present three important applications of our results: the first one develops complete characterizations of the well-known notions of solutions to vector optimization as described in Section 1, say weakly efficient, efficient, proper efficient, strict efficient, etc. The second application shows that our Problem (𝒫) also subsumes the notion of ϵ-efficiency recently introduced in [17]. Finally, as a third application we deal with a nontransitive relation since the set S, which models the vector optimization problem, is neither convex nor a cone; thus, the results established in [31] are improved.

5.1. Complete scalarizations for the classical problems

In this section, we apply the previous results to establish new optimality conditions and characterize different types of well-known efficient solutions.

From now on, we consider vector optimization problems defined by a solid convex cone P as described in Section 1.

Let q ∈ int P. From Theorem 4.2, Remark 4.3 and Lemma 3.6, we can prove the following results.

Corollary 5.1

Let . Then,

a.
b.	⇔
c.	⇔
d.	⇔
e.	⇔ .
f.	Denoting by ℋ(P) to be the family of all proper convex cones D with nonempty interior satisfying P∖l(P) ⊆ int D, we get (q ∈ P∖l(P)),
g.	Denoting by 𝒟(P) to be the family of all closed convex sets A satisfying 0 ∈ ∂A and A + (P∖{0}) ⊆ int A, we get (q ∈ P∖{0}),

When P is closed and pointed, Part (c) was earlier proved in [20, Corollary 4.9]. The optimality conditions proved in [31, Section 6] are related to that in Theorem 4.2, different from those expressed in the previous result.

Next result, whose proof follows from Theorem 4.7 and Corollary 5.1, provides some characterizations for a point to be in E _S when S = 𝒞(−int P), S = P, S = 𝒞(−P) ∪ {0} or S = 𝒞(−P). In particular, we recover Corollary 5.5 in [16] and extend Lemma 5.2(ii) of [32]. The last equality of Part (a1) is really interesting since it says that approximate weakly efficient solutions can be approximated by efficient solutions.

Corollary 5.2

The following assertions hold.

a.	Let ϵ ≥ 0. Then, (a1)  ⇔ ; (a2) E(ξ q,−f(K)+P  ○ f, ϵ) ⊆ E W (ϵq).
b.	if, in addition, P is closed, then (b1) (b2) (b3) (b4)

Proof

• (a1) follows from Theorem 4.7 and (a2) results by particularizing S = 𝒞(−int P) in Theorem 4.12.

• (b1) is a consequence of the following equivalence:

  and the closedness of P, along with Corollary 3.3; (b2) results from (d) of Corollary 5.1; (b3) is Remark 4.3(i).

  To prove (b4), we write

  We use the closedness of P and Corollary 3.3 to conclude with the desired result.▪

The next example shows that the closedness of P is necessary in (b1), (b2), (b3) and (b4).

Example 5.3

Let f be a function from ℝ to ℝ² defined by

Let P = {(x, y) ∈ ℝ² : x, y > 0} ∪ {(0, 0)} and q = (1, 1). It is clear that E _P  = ∅ and E = E ₁ = E _W1 = (−∞, 0]. However (b4) is false because −1 ∈ E(ξ _{f(−1−𝒞(−P)} ○ f) since (ξ _{q,−f(−1)+𝒞(−P)} ○ f)(x) = 0 if x ≤ 0 and (ξ _{q,−f(−1)+𝒞(−P)} ○ f)(x) > 0 if x > 0. In addition, (b1), (b2) and (b3) do not hold since (ξ _q,−f(0)+P  ○ f)(−1) = 0, (ξ _{q,−f(−1)+P}  ○ f)(0) > 0 and f(0) ≠ f(−1).

From Corollary 5.2 we deduce Corollary 4.8(a) in [11].

By particularizing Theorem 4.14 to our classical models, we obtain complete scalarization for E _W , E, E ₁, E _W1, E ₂ and E ₃.

Corollary 5.4

Let P ⊆ Y be a (not necessarily pointed ) convex cone with nonempty interior and q ∈ int P.

a.	If E W  ≠ ∅ then
b.	If P is closed and E ≠ ∅ then
c.	If P is closed and E W1 ≠ ∅ then
d.	If P is closed and E 1 ≠ ∅ then
e.	Let ℋ(P) be as in Corollary 5.1, we get where E(D) corresponds to the efficient solution set for D instead of P.
f.	Let 𝒟(P) be as in Corollary 5.1, we get

Proof

By taking into account Remark 4.11, the corollary is a consequence of Theorem 4.14. Notice the equality of (c) may also be obtained from Corollary 5.1(d) since if and only if . Part (d) trivially holds by Remark 4.3(i) since if and only if .

The remaining part follows from Corollary 5.1.▪

The first part in (a) of the above result was established in the proof of [24, Theorem 3.4, p. 96]; whereas the second part was proved in [16, Theorem 5.11] for P pointed. Observe also that (a) is sharper than Theorem 3.1 in [28] when restricted to single-valued functions.

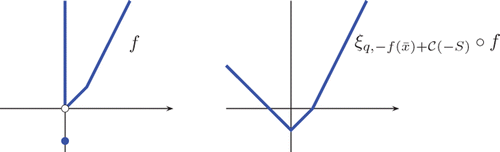
We cannot expect an equality in Corollary 5.4 for E _P even when P is closed. Indeed, take , q = (1, 1) and f: ℝ → ℝ² defined by f(x) = (−1, −x − 1) if x ≤ −1, f(x) = (x, 0) if −1 < x < 0 and f(x) = (x, x) if x ≥ 0. We have E _P  = {−1} and E(ξ _{q,−f(−1)+𝒞(−P)} ○ f, K) = ] −∞, 0].

Remark 5.5

In [11, Corollary 4.14] a free boundary Stefan problem is discussed taking into account the definitions introduced in [21]. Exactly, the scalarizing function is computed. We point out that according to previous results (see, e.g. Theorem 4.7 and Corollary 5.2) we may obtain optimality conditions for the (approximate) free boundary Stefan problem.

5.2. About Q( ϵ )-efficiency

Recently, a new ϵ-efficiency notion in vector optimization was introduced in [17] which is more general than that (C, ϵ)-efficiency discussed by the same authors in [15] (see more details in [17, Remark 2.1]).

We show that our problem (𝒫) also subsumes such approximated solutions, and so new optimality conditions will be obtained as applications of our results established in Section 4.

Throughout this section, we consider Y to be a real topological vector space (note that additionally local convexity of Y was needed in [17]), P ⊆ Y to be a proper pointed convex cone.

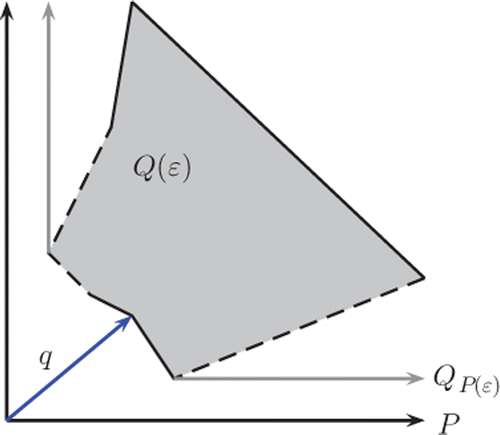
Following the notations in [17], let Q _P : ℝ₊ → 2 ^P be defined by Q _P (ϵ) = Q(ϵ) + P∖{0} for all ϵ ∈ ℝ₊ where Q: ℝ₊ → 2 ^P is a proper set-valued map (Q(ϵ) ≠ ∅ for all ϵ ∈ ℝ₊). From the pointedness of P, we obtain that 0 ∉ Q _P (ℝ₊) and Q _P (ϵ) + ℝ₊ p ⊆ Q _P (ϵ) for all p ∈ P ( Figure 4).

Figure 3. Illustration of f and in Example 4.8.

Figure 4. Illustration of Q _P (ϵ).

Definition 5.6 17

Let M ⊆ Y and ϵ ∈ ℝ₊. y ∈ M is a Q(ϵ)-efficient point of M, y ∈ E(M, Q(ϵ)), if (M − y) ∩ (−Q _P (ϵ)) = ∅

As stated in Remark 2.1 of [17], the above-approximated notion of efficiency can be considered as an extension of several approximated solutions, and when applied to the vector optimization problem (V-P)

we obtain the notion of Q(ϵ)-efficient solution of (V-P) as follows: is Q(ϵ)-efficient solution of (V-P), denoted by , if .

Lemma 5.7

if and only if with S = 𝒞(−Q _P (ϵ)).

From now on, we denote by S ₁ = 𝒞(−Q _P (ϵ)). Note that 0 ∈ S ₁ and we have two cases:

• Case I 0 ∈ ∂S ₁.

  It is not much interesting from the point of view of approximate solutions since if 0 ∈ ∂S ₁, then cl(Q _P (ϵ)) = cl(P). Indeed, it is clear that cl(Q _P (ϵ)) ⊆ cl(P) (note that Q _P (ϵ) ⊆ P). Conversely, if p ∈ cl(P) then p = p + 0 ∈ cl(Q _P (ϵ)) since 0 ∈ cl(Q _P (ϵ)).

• Case II 0 ∈ int S ₁.

  Since Q _P (ϵ) ⊆ P we can chose q ∈ P∖{0} such that 0 ∈ ∂(q + S ₁) (note q depends on Q(ϵ)).

Thus, if S ₂ ≐ q + S ₁ then Problem (𝒫) for S = S ₁ can be rewritten as follows:

By Lemma 5.7, , for ϵ = 1, and thus (𝒫₁) coincides with 𝒫(ϵq)) for ϵ = 1. Moreover, S ₂ + ℝ₊₊ q ⊆ S ₂, q ∈ int S ₂ and 0 ∈ ∂S ₂. From 𝒞(−S ₂) = −q + Q _P (ϵ), we can easily deduce that Assumption (B) for problem 𝒫₁) holds if, and only if

In particular, if P is solid and q ∈ int P, by Remark 3.5, the inclusion (8) is always satisfied and, by Lemma 3.6 the scalarizing function for problem (𝒫₁) satisfies:

(note that ξ _q,A−q (·) = ξ _q,A (·) − 1).

As particular cases of Theorems 4.4 and 4.7 we obtain new characterizations for Q(ϵ)-efficiency under the solidness of P.

Corollary 5.8

Let us consider problem (𝒫₁), q ∈ int P and . The following assertions are equivalent:

a.
b.	and

Corollary 5.9

Consider problem (𝒫₁) and q ∈ int P. Let . Then,

Consequently if, in addition, Q _P (ϵ) is open then

a.
b.

Corollaries 5.8 and 5.9 can be considered more interesting than Corollaries 5.1 and 5.2 of [17] since from the practical point of view the scalarizing function could be easily computed (since such a functional can be reduced to a max function, see [15] and the references therein) and the assumptions on Q _P (ϵ) could be relaxed.

On the other hand, the authors in [17] establish necessary or sufficient conditions for Q(ϵ)-efficiency where P is pointed and not necessarily solid; instead, they consider a scalarizing function satisfying suitable separation properties. See Definitions 3.1 and 4.1 in [17] and compare with Proposition 3.2(a) and (b) respectively.

5.3. About a nontransitive preference relation

We now provide a geometric condition on q and S satisfying Assumption (B) by considering preferences that are not necessarily transitive (examples are given in [31]), it means that nonconvex cones are involved giving rise to such preferences.

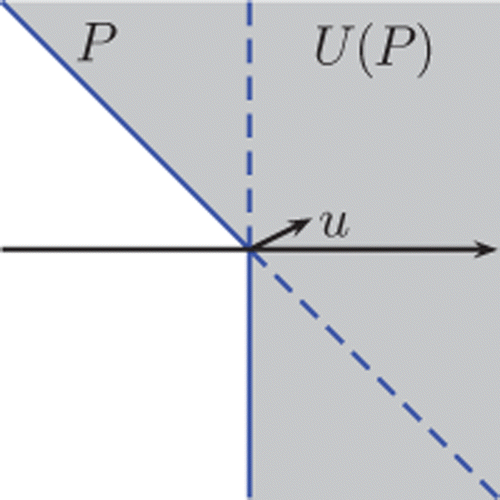
Following notations used in [31], we consider Y a Banach space (although Y to be a real topological vector space suffices) and say that a set S ⊆ Y is strongly star-shaped if there exists u ∈ int S such that u + ℝ₊ y does not intersect the boundary ∂S of the set S more than once for each y ∈ Y. The set of points u, which enjoy this property is denoted by Ker_* S. That is, Ker_* S ≐ {u ∈ int S: (u + ℝ₊ y) ∩ ∂S = {z} or ∅ for each y ∈ Y } = {u ∈ int S: (u + ℝ₊ y) ∩ ∂S = {z} or u + ℝ₊ y ⊆ int S for each y ∈ Y }.

A set S ⊆ Y is star-shaped if there exists u ∈ S such that αu + (1 − α)x ∈ S for all x ∈ S and α ∈ [0, 1]. We denote by Ker S = {u ∈ S: αu + (1 − α)a ∈ S, ∀α ∈ [0, 1], ∀a ∈ S} = {u ∈ S: u + α(a − u) ∈ S, ∀α ∈ [0, 1], ∀a ∈ S}. Note that, in general, Ker_* S ⊆ Ker S.

Lemma 5.10 [30, Proposition 5.18]

Let S ⫋ Y. If S is closed, then Ker_* S ⊆ Ker S.

It is easy to check that if S is a conic set, that is, αS = S for any α > 0, or equivalently ℝ₊₊ S = S, then 𝒞(S), int S, ∂S and Ker_* S are also conic sets.

Proposition 5.11

Let S ⫋ Y be a conic proper set. Then the following assertions hold.

a.	S + ℝ++ q ⊆ S ⇔ S + ℝ+ q ⊆ S ⇔ S + q ⊆ S,
b.	Ker S = S ∞,
c.	If Ker* S ⊆ Ker S, then u and S satisfy Assumption (B) for all u ∈ Ker* S.

Proof

a.	The equivalences are straightforward.
b.	Ker S = {u ∈ S: αu + (1 − α)S ⊆ S, ∀α ∈ [0, 1]}. Since S is conic, Ker S = {u ∈ S: αu + S ⊆ S, ∀α ∈ [0, 1]} = {u ∈ S: u + S ⊆ S} and from (a), the conclusion follows.
c.	Let u ∈ Ker* S. By assumption, u ∈ Ker S. From (a) it follows that int S + u ⊆ int S. Since cl S = int S ∪ ∂S we need to check that ∂S + u ⊆ int S. Let y ∈ ∂S. Since u ∈ Ker* S, we have [u + ℝ+(y − u)] ∩ ∂S = { y}. On the other hand, u + α(y − u) ∈ S for all α ∈ (0, 1) since u ∈ Ker S. Thus, u + α(y − u) ∈ int S for α ∈ (0, 1). In particular, , and taking into account that S is conic the proof is concluded by (3).

▪

The previous proposition allows us to state the following result which ensures the applicability of our approach developed in Section 4.

Proposition 5.12

Suppose that P is a closed conic set and strongly star-shaped. Then P + Ker_* P ⊆ int P. In particular, if u ∈ Ker_* P, P and u satisfy Assumption (B).

Consequently, we obtain a class of sets which satisfy Assumption (B) and point out that the definition of weakly minimal, minimal and proper minimal considered in [31] can be rewritten as minimal solutions of problem (𝒫) where f is the identity function on (a suitable) S (e.g. S = 𝒞(−int P) for weakly minimal points). Thus, according to Proposition 5.12, it is easy to check that the results given in Section 5 of [31] could be improved and extended by those results established in Section 4 under Assumption (B) and P not necessarily closed and/or conic (note that the scalarizing function considered in [31] p _u,P where u ∈ U(P) ≐ {u ∈ Ker_* P: for each y ∈ Y, y + ℝu ⫅̸ P}, see Figure 5, coincides with ξ _u,P ). Moreover, optimality conditions for approximate solutions in the framework of [31] can also be given.

Figure 5. Illustration of u ∈ U(P).

6. Conclusions

We have provided an alternative approach to study several efficient notions via an abstract optimization problem. By using a well-known nonlinear function and considering the standard procedure of scalarization we obtain optimality conditions for several classical efficient notions without any convexity assumption. This has been carried out by considering a solid set which satisfies an assumption of free-disposal type.

The main result lies in establishing complete characterizations of the solution sets to the (approximate) vector optimization problems. Moreover, many instances satisfying our assumptions are exhibited, showing the wide applicability of our results.

It would be interesting to obtain new characterizations without solidness on S in order to include ordering cones such as , , 1 ≤ p < ∞, for instance. On the other hand, applications of our complete scalarizations to derive convergence results and analysing Q _P (ϵ)-efficiency for set-valued maps Q and Q _P not necessarily with values into the power set of P would be welcome.

Acknowledgements

The authors wish to thank both referees for their constructive criticism which allowed to improve the presentation of this article. This research, for the first author, was supported in part by CONICYT-Chile through FONDECYT 110-0667 and BASAL Projects, CMM, Universidad de Chile. Part of the research of the second author was accomplished during a visit to the Department of Mathematical Engineering at University of Concepción supported by Ministerio de Educación y Ciencia (Spain), grant PR2007-0064. The author wishes to thank her hosts and the University of Concepción for the hospitality. The research was also partially supported by Ministerio de Ciencia e Innovación (Spain) under projects MTM2009-09493 and Ingenio Mathematica (i-MATH) CSD2006-00032 (Consolider-Ingenio 2010).