One decade of multi-objective calibration approaches in hydrological modelling: a review

Abstract

One decade after the first publications on multi-objective calibration of hydrological models, we summarize the experience gained so far by underlining the key perspectives offered by such approaches to improve parameter identification. After reviewing the fundamentals of vector optimization theory and the algorithmic issues, we link the multi-criteria calibration approach with the concepts of uncertainty and equifinality. Specifically, the multi-criteria framework enables recognition and handling of errors and uncertainties, and detection of prominent behavioural solutions with acceptable trade-offs. Particularly in models of complex parameterization, a multi-objective approach becomes essential for improving the identifiability of parameters and augmenting the information contained in calibration by means of both multi-response measurements and empirical metrics (“soft” data), which account for the hydrological expertise. Based on the literature review, we also provide alternative techniques for dealing with conflicting and non-commeasurable criteria, and hybrid strategies to utilize the information gained towards identifying promising compromise solutions that ensure consistent and reliable calibrations.

Citation Efstratiadis, A. & Koutsoyiannis, D. (2010) One decade of multi-objective calibration approaches in hydrological modelling: a review. Hydrol. Sci. J. 55(1), 58–78.

Une décennie d'approches de calage multi-objectifs en modélisation hydrologique: une revue

Résumé Une décennie après les premières publications sur le calage multi-objectifs des modèles hydrologiques, nous résumons l'expérience acquise jusqu'ici en soulignant les perspectives clefs offertes par de telles approches pour améliorer l'identification des paramètres. Après la revue des éléments fondamentaux de la théorie de l'optimisation de vecteurs et des problèmes algorithmiques, nous relions l'approche de calage multi-critères avec les concepts d'incertitude et d'équifinalité. Spécifiquement, le cadre multi-critères permet de reconnaître et de gérer des erreurs et des incertitudes, et d'identifier les principales solutions comportementales selon des compromis acceptables. En particulier pour des modèles ayant un paramétrage complexe, une approche multi-objectifs devient essentielle pour améliorer l'identification des paramètres et augmenter l'information contenue dans le calage au moyen de mesures à réponses multiples et de métriques empiriques (données “molles”), qui tiennent compte de l'expertise hydrologique. Sur la base d'une revue de la littérature, nous fournissons également des techniques alternatives pour gérer les critères contradictoires et incommensurables, et des stratégies hybrides pour utiliser l'information obtenue durant l'identification de compromis prometteurs qui assurent des calages cohérents et fiables.

Key words:

• multi-objective evolutionary algorithms
• multiple responses
• uncertainty
• equifinality
• hybrid calibration
• soft data

Mots clefs:

• algorithmes évolutifs multi-objectifs
• réponses multiples
• incertitude
• équifinalité
• calage hybride
• données molles

1 INTRODUCTION

Even today, a common practice of parameter estimation in hydrological modelling is built on the hypothesis that a unique set of parameter values exists that ensures a “global optimum” fitting of the computed model responses to the observed ones. This involves the formulation of a scalar performance criterion (objective function) that measures the differences between the two sets (i.e. simulated and observed values), the determination of lower and upper bounds for the model parameter values (control variables), and the selection of a robust searching procedure (algorithm) to optimize the parameters with respect to the aforementioned criterion. This automatic calibration practice was significantly favoured by the great improvement of computer capabilities (in terms of both memory and processing speed), as well as by the development of advanced nonlinear optimization methods, most of which were implemented within evolutionary schemes. Such methods have been proved effective and efficient against the various peculiarities (e.g. multiple peaks at all scales, discontinuous first derivatives, extended flat areas, long and curved multi-dimensional ridges, etc.) of the highly non-convex response surfaces, which derive from the typical fitting measures used within hydrological calibration. These issues are thoroughly analysed in the classic work of Duan et al. (1992; see also Beven, 2001, pp. 219–222).

Despite the progress of the “algorithmic” component of the parameter estimation procedure, it was soon recognized that the above approach has many drawbacks, since it may result in a black-box mathematical game that fails to ensure satisfactory predictive capacity and realistic parameter values. Thus, many researchers demonstrated the necessity for establishing a more powerful paradigm that takes into account the inherent multi-objective nature of the calibration problem and the major role of model errors and uncertainties (Gupta et al., 1998). This issue became more imperative due to the expansion of complex modelling schemes (semi- or fully-distributed) to represent multiple fluxes and reflect the spatial heterogeneities of the hydrological mechanisms and their related attributes across a river basin. Several studies (e.g. Mroczkowski et al., 1997; Refsgaard, 1997; Gupta et al., 1998; Kuczera & Mroczkowski, 1998; Franks et al., 1999) revealed the utility of conditioning hydrological models on multiple responses (or various aspects of each single response), in order to reduce uncertainties and provide more faithful predictions. Moreover, the hypothesis of parameter set uniqueness, where the global calibration paradigm is founded, has been intensively disputed in favour of the so-called “equifinality” concept (Beven & Binley, 1992; Beven, 1993), where multiple model and parameter configurations are considered as acceptable simulators of the real-world system.

Accordingly, during the past years, much attention has been given to employing vector (instead of scalar) search techniques to optimize the model parameters. This allows for incorporating multiple criteria within calibration to provide a number of alternative parameter sets that are optimal, on the basis of the Pareto-dominance concept explained below (Section 2.1). Madsen & Khu (2002) report that early attempts are found in the work of Harlin (1991), who formulated an iterative procedure that focuses on different process descriptions and associated performance measures. However, the use of automatic routines employing Pareto-based calibration was only established in the last decade, after the pioneering work by Yapo et al. (1998), while multi-objective optimization approaches appeared in water resources technology a few years earlier (Ritzel et al., 1994; Cieniawski et al., 1995; Halhal et al., 1997).

Here we review the recent history of multi-objective hydrological calibration and its usefulness towards establishing more faithful and consistent models. The following section presents the mathematical background of multi-objective optimization and the relevant computer tools. Next, we introduce the concepts of uncertainty and equifinality as well as their relationship with the parameter estimation procedure. In the following section we investigate five key issues of multiple objective model fitting, taking into account the experience obtained from characteristic examples from literature. The possible drawbacks as well as the future perspectives of multi-objective calibration are discussed in the closing section.

2 MULTI-OBJECTIVE SEARCH: MATHEMATICAL BACKGROUND AND COMPUTER TOOLS

2.1 Fundamental notions

A multi-objective search problem involves the simultaneous optimization (for convenience, minimization) of m numerical measures that represent the components (criteria) of a vector objective function f ( x ) = [f ₁( x ), f ₂( x ), … f_m ( x )], with respect to a vector of control variables x ∈ X, where X ⊆ R ⁿ is the feasible control space; assuming unconstrained optimization, except for the control variable bounds (which is the typical configuration in hydrological calibration problems), the feasible space becomes a hyper-rectangle in R ⁿ .

When the criteria are conflicting, there is no feasible point that optimizes all of them simultaneously. In that case, we look for acceptable trade-offs rather than a unique solution, according to the fundamental concept of Edgeworth-Pareto optimality (commonly referred to as Pareto optimality), introduced within welfare economics theory at the end of 19th century. In particular, we define a vector of control variables x * to be Pareto optimal if there does not exist another feasible vector x such that f_i ( x ) ≤ f_i ( x *) for all i= 1, …, m and f_i ( x ) < f_i ( x *) for at least one i. The above definition implies that x * is Pareto optimal if there is no feasible vector that would improve some criterion without causing a simultaneous deterioration of at least one other criterion.

The concept of Pareto optimality leads to a set of feasible vectors, called the Pareto set and symbolized as X*⊂ X; all Pareto optimal vectors x *∈ X* are called non-inferior or non-dominated. The image of the non-dominated set in the objective space is called the Pareto front, denoted as F*. In the absence of further information, all non-dominated solutions are assumed equivalent or, according to the formal mathematical terminology, indifferent. However, within real-world decision-making, it is usually required to determine a single solution from the Pareto set; the latter is called the best-compromise solution and is either selected by “intuition” or systematically, i.e. on the basis of external criteria or by maximizing a utility function, which allows the comparison of all alternative solutions, even the indifferent ones, on the basis of a scalar measure (Cohon, 1978, pp. 164–173).

2.2 Classical approaches through aggregating schemes

Optimization problems involving multiple and conflicting objectives have been traditionally handled by combining the objectives into a scalar function and, next, solving the equivalent single-optimization problem to identify the best-compromise solution. The combination schemes, usually referred to as aggregating functions, are the oldest mathematical programming approaches, since they originate from the Kuhn-Tucker conditions for non-dominated solutions (Cohon, 1978, pp. 77–82). The characteristics of the optimal solution are expressed using multipliers (e.g. the weighting method), target-values (e.g. goal-programming, goal-attainment and ϵ-constraint methods) or priorities (e.g. lexicographic ordering). By changing the arguments of the aggregating function (e.g. the weighting coefficients), one can obtain alternative solutions from the Pareto set.

The above approach to multi-objective optimization has some serious disadvantages. The major problems are its subjectivity (e.g. in choosing weights) and the fact that it hides the competitions among the conflicting criteria. Additionally, a step-by-step approximation of representative trade-offs is computationally inefficient or even, in the case of non-convex Pareto fronts, infeasible. Finally, when incommensurate criteria are involved, the use of aggregation schemes without appropriate scaling results in extremely rough response surfaces.

2.3 Multi-objective evolutionary algorithms (MOEAs)

Evolutionary algorithms (EAs) are well-established tools for handling nonlinear optimization problems of any complexity. Their key feature is the parallel search of the feasible space, through a set (population) of randomly generated points that evolves on the basis of stochastic transition schemes, e.g. the genetic operators. Their multi-objective versions aim to spread the population along the Pareto front instead of converging around a single optimum. For this purpose, some essential adaptations are implemented with the original selection mechanisms of EAs, by assigning dummy fitness values to the individuals, to guide the search mechanism towards well-distributed non-dominated solutions.

Early multi-objective evolutionary attempts appeared in the mid-1980s. The first is the Vector Evaluated Genetic Algorithm (VEGA) by Shaffer (1984), where the population is divided into sub-sets, each one evolving according to a different criterion; thus, for a problem with m objectives, m sub-populations, each of size N/m, are generated, assuming a population of N points. These sub-populations are then shuffled together to get a new population, on which the genetic operators are employed. However, clear Pareto approaches (commonly referred as first-generation techniques), using the dominance concept, were developed in the mid-1990s. The most representative were the Multi-Objective Genetic Algorithm (MOGA; Fonseca & Fleming, 1993), the Nondominated Sorting Genetic Algorithm (NSGA; Srinivas & Deb, 1994) and the Niched-Pareto Genetic Algorithm (NPGA; Horn et al., 1994). Their common strategy involves the assignment of dummy fitness functions on the basis of Pareto ranking or slight variations of it (Goldberg, 1989, pp. 99–101), and fitness sharing, which enables diversity to be maintained and avoids convergence to single solutions (Coello Coello, 2005).

More recent advances on MOEAs, known as second-generation approaches, introduce the notion of elitism that denotes the use of an archive or external population to retain the non-dominated individuals found so far that eliminate the risk to be lost due to random effects. In addition, they aim to provide more efficient ranking and clustering schemes used within the fitness evaluation procedure. Some of the most popular algorithms, according to the state-of-the-art review of Coello Coello (2005), are the Strength Pareto Evolutionary Algorithm (SPEA; Zitzler & Thiele, 1999) and its successor SPEA II (Zitzler et al., 2001), the Pareto Archive Evolution Strategy (PAES; Knowles & Corne, 2000), the Nondominated Sorting Genetic Algorithm II (NSGA II; Deb et al., 2002), the Pareto Envelope-based Selection Algorithm (PESA; Corne et al., 2001) and the Micro Genetic Algorithm (Coello Coello & Pulido, 2001). An extended and systematically updated repository containing MOEA references and tools is available at www.lania.mx/∼ccoello/EMOO/.

The contribution of hydrologists in the development of MOEAs is not negligible. Significant progress was made at the University of Arizona, initially with the Multi-objective Complex Evolution (MOCOM) algorithm (Yapo et al., 1998) and the Multi-objective Shuffled Complex Evolution Metropolis algorithm (MOSCEM; Vrugt et al., 2003a). The former is a first-generation multi-objective optimizer that employs Pareto ranking within a simplex-based pattern in the objective space. The MOSCEM algorithm is an extended version of the SCEM-UA method for uncertainty assessment (Vrugt et al., 2003b), and merges the strength of complex shuffling with the probabilistic covariance-based search strategy of the Metropolis algorithm and the fitness assignment procedure employed within the SPEA algorithm (Zitzler & Thiele, 1999). Reed et al. (2003) proposed an enhanced version of the NSGA-II method, called ϵ-NSGA-II, where they employ ϵ-dominance archiving, adaptive population sizing and automatic termination to minimize the need for extensive parameter calibration. Notably, the concept of ϵ-dominance allows users to specify the precision with which they want to quantify each objective to optimize. The procedure was also built within a parallelization framework, which radically improves the efficiency and reliability of the multi-objective search (Tang et al., 2007). Another example is the Multi-objective Evolutionary Annealing-Simplex method (MEAS; Efstratiadis & Koutsoyiannis, 2008), which implements a generalized definition of dominance to effectively handle problems with more than two criteria, and also imposes feasibility bounds on the objective space. This allows rejection of non-dominated solutions that lie on the outer ends of the Pareto front, thus focusing only on trade-offs with practical interest.

3 uncertainty, EQUIFINALITY and multi-objective calibration of hydrological models

3.1 The concepts of uncertainty and equifinality in hydrological modelling

Uncertainty is a structural and inevitable characteristic of all hydrological processes, arising from the intrinsic complexity of the related natural systems. In water resources engineering, the management of uncertainty is of major interest, and necessary to account for the risk within planning (e.g. uncertainty in the design variables) and decision-making (e.g. uncertainty in the forecasts; Montanari, 2007). Yet, the wide use of deterministic tools for hydrological predictions introduces additional burden to uncertainty handling. Uncertainty originates from the inherent complexity of natural mechanisms, as well as from errors and inappropriate assumptions within the entire modelling procedure. These errors or assumptions, forming the so-called “epistemic” uncertainty, span from the field observations to the conceptualization of processes and the parameter estimation strategy. Specifically, epistemic uncertainty is related to the following factors: (a) measurement errors; (b) use of over-parameterized model structures, whose complexity is inconsistent with the available information about the system behaviour; (c) inappropriate representation of the temporal and spatial variability of model inputs, which are obtained either from processed data (e.g. discharge records based on stage information) or point observations (e.g. precipitation, temperature); (d) poor identification of initial and boundary conditions; (e) non-informativeness of calibration data with regard to the entire system regime; (f) use of statistically inconsistent fitting criteria (e.g. error metrics not accounting for heteroscedasticity); (g) weaknesses of nonlinear optimization algorithms on rough and high-dimensional response surfaces; and (h) inconsistent assumption of parameters constant in time whilst the environment is changing, e.g. due to urbanization, deforestation, stream lining and other human interventions (Beven & Binley, 1992; Wagener & Gupta, 2005; Rosbjerg & Madsen, 2005; Engeland et al., 2005; Efstratiadis et al., 2008; Beven et al., 2008). Evidently, models are, by nature, imperfect representations of the real world and thus model uncertainty, even though it may be decreased in some of the above components, will be always present.

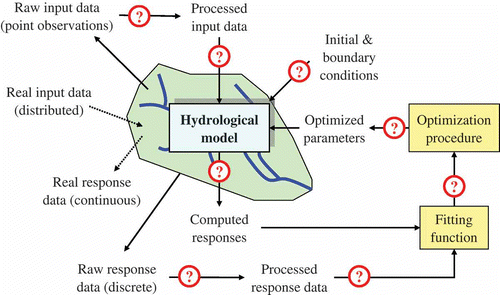
The classical paradigm of model fitting on observations through automatic optimization based on a single performance criterion conceals all above issues, since the entire procedure degenerates to a “computational trick” of recycling errors and uncertainties (Fig. 1). Yet, non-expert users often adopt such a black-box approach, which may result in: (a) ostensible best-fitted parameter values that are inconsistent with their physical interpretation; (b) poor predictive model capacity against an independent control period (validation); and (c) unreasonable regimes of model responses that are not controlled by measurements (e.g. evapotranspiration, underground losses) as well as internal model variables (e.g. soil and groundwater storage) (Refsgaard, 1997; Wagener et al., 2001; Rozos et al., 2004; Efstratiadis et al., 2008). All the above are contrary to the targets of the traditional manual calibration, which requires a comprehensive understanding of the model, the real system and the data, to ensure reliable results (Boyle et al., 2000).

Fig. 1 An automatic calibration procedure – a black-box game of recycling errors and uncertainties.

The context examined so far reveals a typical conflict in hydrological modelling, where the principle of consistency (i.e. building models that are consistent with the behaviour of the real system) has been generally accepted as a working paradigm instead of the principle of optimality, since the latter is too weak against uncertainties (Seibert & McDonnell, 2002; Wagener & Gupta, 2005; Beven, 2006). The limitations of the unique parameter set concept have been emphasized by Beven & Binley (1992) and Beven (1993), who introduced the term “equifinality” to illustrate the existence of multiple “behavioural” parameter sets, which are all acceptable albeit not equivalent, on the basis of different conceptualizations, data and fitting criteria. It is clearly admitted that equifinality arises from uncertainty (Freer et al., 1996), thus making it impossible to identify a “global” optimal simulator that definitely better reproduces the entire hydrological regime of a river basin. Even when assuming a specific structure and a single performance measure (a scalar calibration function) it remains difficult to locate a unique solution whose measure differs significantly from other feasible ones across the search space. Such poor parameter identifiability may result in considerable uncertainty in the model outputs and, also, preclude relating of the optimized parameter values with the observable characteristics of the basin (Vrugt et al., 2003b).

Current advances in hydrological research provide a variety of computational techniques to deal with these drawbacks and quantify the model predictive uncertainty, by seeking for promising trajectories of its outputs on the basis of different parameter sets. So far, the most common uncertainty assessment procedure is the Generalized Likelihood Uncertainty Estimation (GLUE), proposed by Beven & Binley (1992) and applied in a wide range of hydrological and environmental models. Founded on a quasi-Bayesian framework of uncertainty, it employs Monte Carlo simulation, assuming a known prior distribution of the parameter values, in order to identify behavioural parameter sets according to either a single or multiple, appropriately combined, likelihood measures. Next, the empirical cumulative likelihood weighted distribution of simulations is used to estimate quantiles for model predictions at any time step (Beven, 2001, pp. 234–240).

While the GLUE method estimates the global uncertainty of predictions, without reference to the individual effects of the input, parameter and model structure components, other approaches attempt to handle them individually. These include multi-normal approximations (Kuczera & Mroczkowski, 1998), simple uniform random sampling (Uhlenbrook et al., 1999), Markov Chain Monte Carlo methods (Kuczera & Parent, 1998; Thiemann et al., 2001; Vrugt et al., 2003b; Engeland et al., 2005), meta-Gaussian techniques (Montanari & Brath, 2004), sequential data assimilation (Vrugt et al., 2005), multi-model averaging methods (Ajami et al., 2007) and coupled schemes (Blasone at al., 2008). For instance, the Shuffled Complex Evolution Metropolis (SCEM-UA) algorithm by Vrugt et al. (2003b) is a combined uncertainty assessment and parameter optimization procedure, based on a modified version of the SCE method for global optimization. It is Bayesian in nature and operates by merging the strengths of the Metropolis algorithm, controlled random search, competitive evolution and complex shuffling, to continuously update the prior distribution and evolve the sampler to the posterior target distribution (Feyen et al., 2008). Moreover, the simultaneous optimization and data assimilation (SODA) method by Vrugt et al. (2005) aims for a joint assessment of the uncertainty of model parameters and observations (Montanari, 2007).

Regardless of their background, most of the above procedures do not enable incorporating the user's experience in parameter estimation, which is the key advantage of manual calibration. They are generally too complicated for non-experts, whilst some of them (especially when employing random sampling) are computationally inefficient, thus being impractical for models with complex parameterization. Additionally, they imply considerable subjectivity with respect to the selection of prior probability distributions, likelihood functions and cut-off thresholds (Stedinger et al., 2008). Inappropriate configurations may result in overestimation of uncertainty, thus providing prediction ranges that are comparable to those computed through statistical uncertainty measures (e.g. confidence limits) of the observed responses. Hence, the almost negligible dissemination of similar approaches in problems of the every day engineering practice and the reluctance to provide uncertainty estimation results to decision-makers and stakeholders is not surprising. Besides, the scientific community remains sceptical, if not divided, about the concepts of uncertainty and equifinality and the proper use of Bayesian inference methods in hydrological modelling, as implied from several recent discussions (Beven, 2006; Pappenberger & Beven, 2006; Hamilton, 2007; Hall et al., 2007; Todini & Montovan, 2007; Montanari, 2007; Andréassian et al., 2007; Todini, 2007; Sivakumar, 2008; Beven et al., 2008).

3.2 The multi-objective calibration paradigm

Despite the criticism of the equifinality concept, hydrologists agree now that is impossible to formulate a unique modelling structure and assign a unique parameter set to it, thus identifying the globally optimal simulator of all processes of a river basin using a unique objective function. In fact, more than three decades of research have demonstrated that it is impossible to assign an appropriate formal error structure for the model residuals and, on the basis of the latter, detect a particular statistical measure that is better suited for fitting model outputs to observations (e.g. Diskin & Simon, 1977; Sorooshian et al., 1983; Yapo et al., 1996). This is because the non-systematic interaction of uncertainties and errors within all modelling aspects precludes defining a statistically-proper fitting function and, consequently, making a statistically-correct choice for the model parameters (Gupta et al., 1998).

In reality, any parameter estimation procedure through data-fitting is inherently multi-objective. Let e (θ) = {e ₁(θ), e ₂(θ), …, e_M (θ)} represent the model residuals, i.e. the departures of the observed responses from the computed ones, where θ is the vector of parameters. We can evidently define calibration as the simultaneous minimization of the absolute departures │e_i (θ)│ with respect to θ, i.e.:

(1)

where Θ is the feasible parameter space, expressing the prior uncertainty of parameters. Given that hydrological models are, as discussed before, imperfect simulators of complex natural systems, the above vector optimization problem is ill-posed. This prevents the possibility of finding a utopian solution, namely a specific parameter set that simultaneously minimizes all residuals. However, on the basis of the Pareto optimality notion, we can locate a subset of the feasible parameter space Θ* ⊂ Θ, which contains the non-dominated vectors of parameters, while the rest of the space is captured by the dominated vectors, corresponding to non-acceptable trade-offs of the residuals.

The above formulation entails the separate minimization of all model residuals, whose number is impractically large; for instance, given a single observable response to fit, the problem dimension is equal to the calibration horizon. This makes the interpretation of their trade-offs impossible, since the Pareto front becomes too extended, if not tending to cover the entire M-dimensional objective space (Coello Coello, 2005). Moreover, the magnitudes of the individual residuals e_i (θ) are directly related through the model structure, thus equation (1)(1) is not properly defined in multi-objective terms (Gupta et al., 1998). So, instead of minimizing residuals themselves, we can correctly state a multi-objective configuration of the calibration problem, assuming a limited number of fitting criteria that account for representative aspects of the model performance with regard to the behaviour of the hydrological system. Therefore, the problem is reduced to:

(2)

where g_i [ e (θ)] are scalar performance measures that ideally should be approximately uncorrelated and preserve the information contained in the observations, and m is the reduced dimension, with m << M. The above problem is handled using either an aggregating or a multi-objective evolutionary approach to identify a single solution or a Pareto optimal set, respectively. While the first strategy is typically employed in practice, the second one is definitely more integrated, since it allows for investigating possible conflicts between the components of the vector objective function (equation 2(2)).

From a mathematical point-of-view, all parameter sets that are non-dominated with respect to criteria g_i correspond to equivalently optimal (in the Pareto sense) solutions of equation (2)(2). This reveals that equifinality (mainly as treated within the GLUE framework) and dominance are closely related (but not identical), since both seek feasible model configurations that are then distinguished in two categories corresponding to acceptable or not acceptable representations of the physical system. But while the GLUE method utilizes subjective criteria to differentiate the behavioural simulators from the non-behavioural ones, the multi-objective paradigm is founded on a stricter notion, i.e. the principle of dominance, for evaluating alternative solutions. Moreover, in GLUE, the behavioural solutions are not equivalent since they are classified according to the likelihood function. As shown in Fig. 2, a non-dominated solution obtained through multi-objective analysis is not necessarily behavioural and vice versa. On the other hand, formal Bayesian inference techniques do not differentiate behavioural from non-behavioural models—they only give a tiny likelihood to poor simulators. Further discussion on the comparison of the above approaches is provided in Section 4.3.

Fig. 2 Graphical examples illustrating Pareto-optimal and behavioural solutions in the objective space, for two hypothetical problems of simultaneous minimization of two criteria [f ₁, f ₂] with smooth (left diagram) and steep (right diagram) trade-offs. Vector e  = [e ₁, e ₂] indicates limits of acceptability, i.e. cut-off thresholds for distinguishing behavioural and non-behavioural solutions.

4 critical issues IN multi-objective calibration

Multi-objective calibration has received great attention in the last decade, as indicated in Table 1, where we quote representative case studies from the literature. For each one, we provide synoptic information about the application area, the modelling framework, the number of parameters and criteria to optimize, and the calibration strategy. We distinguish between pure Pareto-based approaches, where a set of non-dominated solutions is detected using a MOEA, and aggregating ones, where a unique compromise parameter set is identified on the basis of multiple criteria embedded in a scalar performance function. We note that, while most of early studies focused on lumped rainfall–runoff models, there is a growing number of recent studies on semi-distributed and distributed schemes, usually involving a small portion of the total model parameters (Madsen, 2003; Ajami et al., 2004; Muleta & Nicklow, 2005; Vrugt et al., 2005; Kunstmann et al., 2006). The spatial scale of applications varies from experimental basins of a few hectares (Seibert & McDonnell, 2002; Meixner et al., 2002; Tang et al., 2006) to very large basins of thousands of square kilometres (Schoups et al., 2005a; Cheng et al., 2005a; Engeland et al., 2006; Feyen et al., 2008). Most applications use two or three objectives, and only a few explore more criteria, ranging from statistical fitting functions to empirical and fuzzy metrics (Schoups et al., 2005a; Parajka et al., 2007; Efstratiadis et al., 2008; Moussa & Chahinian, 2009). Finally, only few items of the wide spectrum of second-generation multi-objective evolutionary tools have been tested in hydrological calibration applications (NSGA-II, SPEA-II, ϵ‐NSGA). We have found only two studies which compare their performance characteristics (Tang et al., 2006, 2007).

Table 1  Characteristic applications of multiobjective calibration of hydrological models (pure Pareto approaches are annotated with *)

Reference	Study basin(s)	Model	Problem formulation (parameters and objectives)	Calibration method(s)
*Yapo et al. (1998)	Leaf River, USA (1950 km^2)	SAC-SMA	13 parameters, 2 objectives (RMSE, HMLE)	MOCOM-UA
Seibert (2000)	Lilla Tivsjön (12.8 km^2) and Tärnsjö (14.0 km^2), Sweden	HBV	10 parameters, 2 objectives (fuzzy measures combining EF for runoff and CD for groundwater levels)	Modified genetic algorithm
Madsen (2000)	Tryggevaelde, Denmark (130 km^2)	MIKE 11/NAM	9 parameters, 4 objectives (overall volume error, RMSE, RMSE of peak and low flows)	Weighted SCE-UA
Yu & Tang (2000)	Gao-Oing Creek, Taiwan (3257 km^2)	HBV	9 parameters, 3 objectives (RMSE, MPE, fuzzy MPE-based function for 11 flow stages)	SCE-UA
*Liong et al. (2001)	UBT, Singapore (6.11 km^2)	HydroWorks	8 parameters, 2 objectives (overall volume error, peak discharge error)	VEGA, MOGA, NSGA, ACGA with NN
*Madsen & Khu (2002)	Tryggevaelde, Denmark (130 km^2)	MIKE 11/NAM	9 parameters, 2 objectives (RMSE of high and low flows)	Weighted SCE-UA, PROSCE
*Beldring (2002)	Sæternbekken, Norway (6.32 km^2)	Physically-based rainfall–runoff model	11 parameters, 3 objectives (EF of runoff and two groundwater level series)	MOCOM-UA
Seibert & McDonnell (2002)	Maimai M8, New Zealand (3.8 ha)	3-box lumped conceptual model	16 parameters, 3 fuzzy functions (one based on runoff and two groundwater level series, and two rules based on “soft” data)	Modified genetic algorithm
Cheng et al. (2002)	Shuangpai, China (10 594 km^2)	Xinanjiang	16 parameters, 3 objectives (peak value, peak time, total runoff volume)	Multiple objective GA
*Meixner et al. (2002)	Emerald Lake, Sequoia National Park, USA (120 ha)	Alpine Hydrochemical Model (AHM)	15 parameters, 4 objectives (sub-sets of 21 chemical and hydrological criteria)	MOCOM-UA, combined with sensitivity analysis
*Madsen (2003)	Karup, Denmark (440 km^2)	MIKE-SHE	12 parameters, 2 objectives (RMSE of runoff, avg. RMSE of 17 groundwater level series)	Weighted SCE-UA
*Vrugt et al. (2003a)	Leaf River, USA (1950 km^2)	SAC-SMA	13 parameters, 2 objectives (RMSE for driven and non-driven parts of hydrograph)	MOCOM-UA, MOSCEM-UA
Ajami et al. (2004)	Illinois River, USA (1645 km^2)	Multiple structures of SAC-SMA	13 parameters, 2 objectives (RMSE and Log-RMSE for fitting on high and low flows)	Multi-step calibration with SCE-UA
*Schoups et al. (2005b)	San Joaquin Valley, USA (1400 km^2)	MOD-HMS	10 parameters, 3 objectives (RMSE of water table, annual pumping and subsurface drainage)	SCEM-UA, MOSCEM-UA
Muleta & Nicklow (2005)	Big Creek, USA (133 km^2)	SWAT	16 parameters, 2 objectives (RMSE of runoff and sediment yield)	Sensitivity analysis, GA, GLUE
*Khu & Madsen (2005)	Tryggevaelde, Denmark (130 km^2)	MIKE 11/NAM	9 parameters, 4 objectives (overall volume error, RMSE, RMSE of peak and low flows)	NSGA-II with Pareto preference ordering
*Schoups et al. (2005a)	Yaqui Valley, Mexico (6800 km^2)	Integrated surface water-groundwater model	10 parameters, 4 objectives (RMSE of water table, aquifer head, drainage volume and canal seepage volume)	MOSCEM-UA
Cheng et al. (2005a)	Shuangpai Reservoir, China (10 594 km^2)	Xinanjiang	16 parameters, 3 objectives (peak value, peak time, total runoff volume)	Serial and parallel GAs
*Engeland et al. (2006)	Saone, France (11 700 km^2)	Ecomag	10 parameters, 7 objectives for calibration, 15 independent objectives for validation (EF of 22 runoff series)	MOCOM-UA
*Tang et al. (2006)	Leaf River, USA (1950 km^2)	SAC-SMA	13 parameters, 2 objectives (RMSE & RMSE with Box-Cox transformation)	NSGA-II, SPEA-II, MOSCEM-UA
*Tang et al. (2006)	Shale Hills, USA (19.8 ha)	Integrated surface-subsurface model	13 parameters, 2 objectives (RMSE, RMSE of peak and low flows)	NSGA-II, SPEA-II, MOSCEM-UA
Kunstmann et al. (2006)	Ammer River, Germany (710 km^2); Alpine catchment	WaSiM (distributed model)	37 parameters, 8 objectives (EF at 8 discharge gauges, using transformed flows)	PEST (two-step approach)
Rouhani et al. (2007)	Grote Nete, Belgium (383 km^2)	SWAT	10 parameters, 5 objectives (bias, RMSE for total and slow flow, quick flow maxima and slow flow minima)	Manual calibration
Moussa et al. (2007)	Gardon d'Anduze, France (543 km^2)	ModSpa	5 parameters, 7 objectives (EF, bias and CC of 7 runoff series)	Single and multi-site manual calibration
*De Vos & Rientjes (2007)	Geer River, Belgium (494 km^2)	HBV	10 parameters, 3 objectives (RMSE, log-RMSE and MSDE)	NSGA-II
*Bekele & Nicklow (2007)	Big Creek, USA (133 km^2)	SWAT (two calibration scenarios)	16 parameters, 2 objectives per scenario (RMSE and log-RMSE of runoff; RMSE and log-RMSE of sediment yield; RMSE of runoff and sediment yield)	NSGA-II
*Tang et al. (2007)	Leaf River, USA (1950 km^2)	SAC-SMA	13 parameters, 2 objectives (RMSE and RMSE with Box-Cox transformation)	Serial and parallel implementations of ϵ-NSGA-II
*Confesor & Whittaker (2007)	Calapooia, USA (963 km^2)	SWAT	139 parameters, 2 objectives (RMSE and MAE of daily flows)	NSGA-II (cluster of 24 parallel computers)
*Parajka et al. (2007)	320 Austrian catchments	Modified HBV (with semi-distributed structure)	14 parameters, 2 objectives (weighted function of EF and bias of runoff, time ratio with poor snow cover simulation)	Weighted SCE-UA, MOSCEM-UA
Kim et al. (2007)	North River, Virginia (973 km^2)	HSPF	11 parameters, 6 objectives (MSE of daily flows, 50% of lowest flows exceed., 10% of highest flows exceed., storm peaks, seasonal volume, storm volume)	Manual and automatic calibration, using the PEST software
*Fenicia et al. (2007a)	Hesperange, Luxemburg (288 km^2)	FLEX (simple & complex structure)	8 to 11 parameters, 3 objectives (RMSE, log-RMSE and CC of runoff)	MOSCEM-UA, SCA (stepped calibration)
*Fenicia et al. (2007b)	Hesperange, Luxemburg (288 km^2)	HBV-96	9 parameters, 2 objectives accounting for the low and high portions of the hydrographs	MOSCEM-UA
Efstratiadis et al. (2008)	Boeoticos Kephissos, Greece (1956 km^2)	HYDROGEIOS (surface water, groundwater and water management model)	99 parameters, 40 objectives (EF and bias of 7 runoff series, penalties to control flow interruption events and unrealistic trends of groundwater level series)	Hybrid, using the evolutionary annealing-simplex method
*Khu et al. (2008)	Karup, Denmark (440 km^2)	MIKE-SHE	11 parameters, 5 to 9 objectives (RMSE of runoff, avg. RMSE and st.dev. of residuals for representative piezometric series, after grouping of multisite data)	Preference ordering genetic algorithm (POGA)
Feyen et al. (2008)	Morava, Austria, Czech Rep. and Slovak Rep. (∼10 000 km^2)	LISFLOOD (three calibration scenarios)	9 parameters (lumped or semi-distributed over 7 sub-basins), 3 objectives per hydrograph (bias, EF and CD) with transformed flows	SCEM-UA
*Moussa & Chahinian (2009)	Gardon d' Anduze, France (543 km^2)	Lumped, two-reservoir-layer model, event-based	7 parameters, 1 to 3 objectives resulting from 6 fitting criteria (global and relative bias, global and relative RMSE, global and relative peak flow error)	Multi-step aggregation method for 29 flood events
RMSE: root mean square error; log-RMSE: RMSE of logarithmically transformed data; HMLE: heteroscedastic maximum likelihood error; EF: Nash-Sutcliffe efficiency; CD: coefficient of determination; CC: coefficient of correlation; MPE: mean absolute percentage error; MAE: mean absolute error; MSDE: mean square derivative error.

Taking into account the rich experience of this last decade, we next discuss five key issues of multi-objective calibration, also attempting to propose some guidelines for appropriate use of such approaches to ensure faithful and reliable models.

4.1 Preservation of the principle of parsimony in complex models

The principle of parsimony is a key notion in modelling, where model parameters are estimated by fitting computed outputs to observed data. It aims to represent the model structure with as few parameters as possible and accepts that simpler parameterizations are preferred from more complex ones, provided that both ensure similarly good fitting. Specifically, in hydrological modelling, several investigations about the practical use of this concept (e.g. Beven, 1989; Jakeman & Hornberger, 1993; Ye et al., 1997; Uhlenbrook et al., 1999; Perrin et al., 2001) concluded that parsimony is the guise for well-posed models. Specifically, in the case of lumped conceptual schemes, up to five or six parameters can be identified from time series of external system variables (e.g. rainfall, streamflow) through single-objective calibration approaches (Wagener et al., 2001; see also earlier discussions by Dawdy & O'Donnell, 1965, and Kirkby, 1975). Attempts to use additional parameters, in the absence of supplementary data to support them, usually fail to notably improve the model fitting and result in poorly identified parameters (Gupta & Sorooshian, 1983; Hornberger et al., 1985; Kuczera & Mroczkowski, 1998). In this manner, model complexity, defined as the formulation of non-parsimonious (over-parameterized) structures, becomes a key origin of equifinality, thus increasing uncertainty within the parameter estimation procedure. Additionally, the use of such structures reveals a critical problem known as over-fitting, which is recognized by the surprisingly poor validation of a model with significantly good fitting in calibration.

Yet, the preservation of parsimony is questionable in modern modelling tools with distributed or semi-distributed structures and, thus, with a large number of parameters for representing the spatial heterogeneities of both basin characteristics and forcing data. Similar difficulties arise when hydrological models are coupled with water management schemes to provide forecasts of inflows and abstractions at multiple sites (Efstratiadis et al., 2008). Distributed schemes are founded on small-scale physics, which, in theory, would allow for obtaining all parameter values from field data, thus avoiding calibration effort. However, the idea that the natural heterogeneity could be modelled without calibration based on field measurements of physically meaningful properties in a detailed spatial scale is fundamentally flawed and unrealistic. For this reason, some modellers employ an intermediate strategy, aiming to optimize a small portion of parameters, while the rest of them are approximated on the basis of known properties of the basin (e.g. Refsgaard, 1997; Muleta & Nicklow, 2005). In contrast, semi-distributed models do not hide the fact that they are conceptual in nature. Yet, they involve calibration of many more free variables, if compared to analogous schemes with lumped or semi-lumped parameterization (Ajami et al., 2004).

In the case of complex models with many parameters, multi-objective calibration provides a favourable framework for preserving parsimony and thus reducing uncertainty. This presupposes the increase of independent information contained in calibration, by introducing additional outputs for model fitting or by improving the knowledge already available, e.g. using different data periods to identify different parameters (Wagener et al., 2001). As a first approach, and extending the empirical rule expressed for lumped models, we should retain a ratio of about 1:5 to 1:6 between the number of criteria and the number of parameters to optimize, to provide a parsimonious representation of the multi-objective calibration problem. Typically, significant effort is required to formulate uncorrelated criteria that really add new information, based on the available measures, as further analysed in the following sub-section.

A deeper inspection of the above framework reveals the need for fundamental changes to the classical rainfall–runoff modelling strategy, assumed so far as a staged procedure where conceptualization (i.e. the representation of system dynamics through parametric equations) precedes calibration (Beven, 2001, p. 4). This approach has little flexibility, since the model structure and, subsequently, the number of parameters, is a priori specified. Yet, for poorly measured hydrosystems, it is impossible to have sufficient information to formulate the number of criteria that is necessary to justify the detail of the adopted delineation. An efficient way to avoid this is to disconnect the schematization, involving the spatial detail of process description (which is imposed by the specific scope of study), from parameterization, which assigns the model free variables to the characteristics of the physical system (Efstratiadis et al., 2008). However, in most known distributed tools schematization dictates parameterization, since parameters refer to contiguous spatial elements, usually grid cells, whose number is typically huge. Not only does this contrast the principle of parsimony but also makes optimization inefficient, due to the curse of dimensionality and the large time effort of simulation. In groundwater modelling, the problem is typically addressed through regularization techniques, i.e. by using spatial zonation patterns through the aquifer or by constraining parameters to preferred values or relationships. While such approaches are widely used to obtain a unique solution to the inverse problem, an oversimplified parameterization dramatically reduces the model accuracy at local scales (Moore & Doherty, 2006; see also discussion by Hunt et al., 2007).

4.2 Model fitting on multiple responses

Fully- and semi-distributed models estimate the basin fluxes at multiple sites (grid and sub-basin scale, respectively) while conjunctive simulation schemes, i.e. surface–groundwater models, hydrochemical models and sediment transport models, provide estimations for multiple processes. When systematic measurements exist for those variables, the role of multi-objective calibration becomes evident, in order to maximize the model predictive capacity by fitting its parameters to the corresponding data. The advantages of “conditioning” the model parameters on multiple responses are extensively discussed by Gupta et al. (1998). In addition, Kuczera & Mroczkowski (1998) use the term joint calibration to describe a suitable framework for compromising between model complexity and the principle of parsimony. In the absence of major structural errors, this approach enhances the calibration procedure with additional information about the physical system, thereby leading to a better identification of the model parameters (Boyle et al., 2000).

Following the terminology of Madsen (2003), the multi-objective fitting function may be formulated on the basis of the following three types of information:

	multi-variable data: different observable fluxes that are reproduced by conjunctive simulation schemes, including flows, piezometric levels, sediment load, geochemical tracers, distributed soil moisture, etc.;
	multi-site data: historical records obtained from a number of gauges within the river basin, which measure the same variable and are reproduced by semi- or fully-distributed schemes;
	multi-response models: independent criteria accounting for various aspects of a single process (typically discharge), which is reproduced even by lumped conceptual schemes.

In particular, the last type of information originates from the same historical sample, which is utilized from different points of view. This approach aims to ensure a satisfactory agreement of the specific components making up the observed discharge series, and not an average good match across all flow ranges (Yapo et al., 1998; Madsen, 2000; Moussa & Chahinian, 2009). It is in full accordance with a manual calibration strategy, where the expert hydrologist follows a trial-and-error approach to reproduce all features of a hydrograph, regarding both flow quantity and timing. Moreover, focusing on different aspects ensures more realistic and robust parameter values, given that different parameters activate different hydrological mechanisms, which are finally reflected on the shape of the hydrograph (Rouhani et al., 2007).

A multi-objective fitting strategy should not be restricted to systematic measurements for all variables involved in calibration. Even sparse observations, or rough estimations about the average quantities or their long-term fluctuation, are useful to enhance the information contained in calibration and reduce uncertainties. This issue becomes critical when the number of the observed variables is insufficient to support the number of parameters. In that case, the hydrologist should take advantage of his experience to “invent” empirical criteria so as to be compatible with the principle of parsimony in parameterization. Seibert & McDonnell (2002) introduced the term “soft data” to characterize the qualitative rather than the quantitative knowledge about the behaviour of a basin, in contradistinction to “hard data”, namely measurements derived from well-recorded variables. This approach represents a new dimension to calibration that favours the dialogue between experimentalists and modellers, ensures reasonableness and consistency of internal model structures and simulations, and also helps to specify realistic parameter ranges. Moreover, it helps in providing reliable simulations for model responses and internal variables that are not controlled by measurements, e.g. evapotranspiration, moisture storage, groundwater storage, underground losses, etc.

While hard data are typically represented by statistical fitting functions (e.g. RMSE, efficiency), the incorporation of soft data within calibration is implemented through empirical or fuzzy metrics, which are introduced as independent components of the multi-objective function (e.g. Yu & Yang, 2000; Seibert & McDonnell, 2002; Cheng et al., 2002; Rozos et al., 2004; Parajka et al., 2007; Efstratiadis et al., 2008). This certainly increases the effort of calibration and provides less attractive results with regard to an approach that is merely based on hard data. Nevertheless, this is the cost paid to obtain a better overall model performance and ensure consistency within all of its aspects (Seibert & McDonnell, 2002).

The effects on model predictive capacity of conditioning its responses on multiple objectives have been also examined within uncertainty assessment approaches, employing the GLUE technique (Lamb et al., 1998; Blazkova et al., 2002; Freer et al., 2004; Mo & Beven, 2004; Blazkova & Beven, 2004; Zhang et al., 2006; Choi & Beven, 2007; Gallart et al., 2007). In some of the above studies, this involved the evaluation of the performance of TOPMODEL against discharge, water table and saturated area observations, through appropriate likelihood measures. All concluded that the use of internal catchment information definitely helped to narrow the posterior distributions for the related parameters. Yet, only the last paper, by Gallart et al. (2007), reports that the uncertainty of the predicted discharges has been significantly restricted.

The above reveals a common misconception with regard to multi-objective calibration, which is that as more information about the system becomes available, the uncertainty of predictions is definitely reduced. Kuczera & Mroczkowski (1998) highlight this danger, indicating that the improvement of the parameter identifiability mainly depends on how the model structure interacts with each response, and less on the amount of data itself. In addition, a consistent formulation of the multi-objective calibration problem is far form being a straightforward task. For instance, the criteria are not expected to be uncorrelated (since the basin fluxes are mutually correlated with precipitation and evapotranspiration) and are also related with commensurability and uncertainty issues. A proper evaluation of the information content of additional observations, as well as the development of a generalized approach that may allow us to benefit from different types of information (including multi-site observations and soft data), remains an open issue in hydrological research (Beven, 2006; Montanari, 2007; Khu et al., 2008).

4.3 Recognition of model errors and uncertainties

The limitations of a model can be empirically addressed within a multi-objective calibration framework, by investigating the trade-offs between the different objectives of the Pareto optimal solutions (Gupta et al., 1998). Although, from a statistical point-of-view, it is difficult to isolate the different categories of errors from parameter uncertainty (Rosbjerg & Madsen, 2005), an irregular shape of the Pareto front is a usual evidence of ill-posed models. For instance, significant trade-offs in fitting two or more objectives may indicate that the model is wrongly parameterized (Schoups et al., 2005a,b). In addition, an asymmetrically extended spread of the Pareto solutions along one particular axis indicates considerably high uncertainty in reproducing the processes that are controlled by the corresponding criterion. Similarly, the generation of very steep fronts, almost resembling right angles (Fig. 2, right) denotes the sensitivity of parameters to the corresponding criteria, since a small perturbation of the parameter values, in the direction of improving one criterion, leads to significant deterioration of the others (Efstratiadis & Koutsoyiannis, 2008). Valuable information about the possible model errors is also provided by deriving the ranges of non-dominated parameter sets, as well as the ranges of the simulated responses (“envelopes”) against the criteria. For instance, when these envelopes fail to enclose all observed values of a hydrograph, an expert hydrologist can easily recognize whether this failure is due to an inappropriate model structure (e.g. by examining which specific parts of the hydrograph systematically remain out of the Pareto-optimal range) or inaccurate data. In contrast, a single-objective calibration would not allow recognition of whether the departures of the modelled outputs from the observations are due to structural (or data) errors or a statistically inconsistent fitting function.

In some cases, the increased information provided after employing a multi-objective framework may even lead to rejection of an inappropriate model, which would appear as proper against a single criterion. An interesting example is given by Choi & Beven (2007), who attempted to fit TOPMODEL in an experimental catchment in Korea, taking advantage of both annual and seasonal (30 day) calibration data. While the model showed good performance (by means of efficiency) at the annual level, no model implementations were found that were behavioural over all multi-period clusters and all performance measures (mainly in dry periods). The authors claimed that the model rejection strategy of their GLUE approach served to focus attention on possible model deficiencies, thus making it necessary to add more parameters for the description of the time-varying recession and evapotranspiration processes.

Since the Pareto set can be used to generate envelopes that contain all acceptable (according to the dominance concept) model outputs, multi-objective calibration has some links with Bayesian inference methods for uncertainty assessment. Yet, there are also key differences, as Engeland et al. (2006) explain, especially with respect to the GLUE method. First, Bayesian methods evaluate the uncertainty around a single performance measure, namely the likelihood function, while a multi-objective context requires at least two criteria to make sense. The GLUE framework also allows combining multiple objectives, provided that they can be expressed in terms of likelihoods—yet, the evaluation of these objectives is not based on the principle of dominance but on arbitrary acceptability thresholds. Thus, the behavioural solutions are searched inside a hyperrectangle in the m-dimensional objective space (containing both dominated and non-dominated sets), whereas Pareto optimal solutions are searched across hypersurfaces of dimension m– 1, i.e. in a much restricted area. Their cross-section determines a sub-set that encloses solutions that are simultaneously non-dominated and behavioural, while in the case of very steep Pareto fronts one should further restrict its limits to seek for promising trade-offs (Fig. 2). Finally, when new objectives are included, while in a Bayesian inference approach the parameter uncertainty possibly decreases (or remains unchanged), the Pareto set definitely extends, thus resulting in increased uncertainty. This is a known characteristic of multi-objective theory, where criteria are considered as degrees of freedom and not as constraints. Indeed, on the basis of Pareto optimality, if one solution outperforms another one against even a single criterion, then the two alternatives are indifferent. Therefore, by adding criteria, the existing non-dominated set not only remains non-dominated, but spreads across the new dimensions. For this reason, and given that even state-of-the-art multi-objective optimization algorithms incur serious performance deterioration in high-dimensional objective spaces, it is not practical to employ Pareto-based optimization on the basis of more than three to four criteria. Otherwise, it is necessary to implement some form of aggregation of objectives, e.g. through clustering techniques (Khu et al., 2008), or even review the concept of dominance as the only evaluation principle, by employing some kind of filtering among indifferent solutions (Efstratiadis & Koutsoyiannis, 2008).

4.4 Handling non-commeasurable fitting criteria

Several studies seek a single parameter set that ensures satisfactory performance against all conflicting criteria, namely an intermediate solution from the Pareto front. However, approximating this front through a MOEA and then manually picking up a suitable solution on the basis of external-empirical criteria is time-consuming, not well-understood and thus far away from the usual practice. On the other hand, the traditional manipulation through an equivalent single-objective optimization approach (e.g. weighting method) involves many more difficulties than when optimizing a particular criterion. Some of the practical drawbacks of the so-called aggregating approaches have been already discussed in Section 2.2. Specifically, within a calibration problem involving many criteria, it is necessary to broadly specify the desirable characteristics of the best-compromise solution, through suitable configuration of the scalar objective function. But in some cases, it is even hard to recognize whether two criteria are conflicting or not, since their behaviours differentiate across the feasible parameter space. Further problems arise when the criteria are non-commeasurable, which requires proper scaling to avoid over-emphasis of specific components of the objective function, in contrast to others (Madsen, 2000). Obviously, an incautious formulation of the problem may result in asymmetrically good fitting for some criteria in contrast to the rest of them (solutions lying in the extremes of the Pareto front), unless limits of acceptability are imposed, as shown in Fig. 2. It is interesting to notice that, in some cases, it is desirable to focus on specific criteria in order to obtain more accurate predictions at local rather than global scales. For instance, Pappenberger et al. (2007) used a vulnerability-weighted approach to ensure better calibration of a flood inundation model to locations that are of particular interest to flood planners and risk assessors.

Scaling problems occur when dealing with variables measured in different units (e.g. runoff and groundwater level), when combining dimensional measures with non-dimensional ones, and when combining statistical and empirical or fuzzy measures. The different criteria require assigning proper transformations, most typically weighting coefficients. The latter may be either empirically determined (Cheng et al., 2005; Rouhani et al., 2007; Parajka et al., 2007), or specified analytically at the beginning of the evolution procedure, according to the properties of the initial population (Madsen, 2000, 2003; Moussa & Chahinian, 2009), or manually re-evaluated during optimization, taking into account the progress achieved so far and the conflicts to compromise (Rozos et al., 2004; Kim et al., 2007; Efstratiadis et al., 2008). Fuzzy multi-objective functions are also used that ensure flexibility and allow for combining criteria that are not directly analogous (Yu & Tang, 2000; Seibert & McDonnell, 2002; Cheng et al., 2002, 2006). All of the above approaches are in accordance with the hybrid calibration paradigm for selecting a single “balanced” solution.

In general, the aggregation of criteria leads to significantly high complexity of the objective function, thus formulating non-convex response surfaces of irregular geometry. In that case, even the most sophisticated global optimization methods are possible to trap, thus failing to locate a suitable compromise that ensures satisfactory performance against all criteria. This negates all the benefits discussed so far, regarding multi-criteria calibration. In this respect, hybrid strategies taking advantage of the strengths of both manual and automatic calibration, can be most suitable approaches for such problems (Boyle et al., 2000). These allow guiding “by hand” the search towards acceptable compromises, since an expert hydrologist easily recognizes the conflicts of criteria. In contrast, a black-box algorithmic procedure, which evolves on the basis of an aggregating scalar function, has no insight on the trade-offs of criteria and thus may converge to solutions with unsatisfactory performance. Characteristic studies involving hybrid manipulations of the multi-criteria problem (Ajami et al., 2004; Kunstmann et al., 2006; Rouhani et al., 2007; Moussa et al., 2007; Efstratiadis et al., 2008; Moussa & Chahinian, 2009) are included in Table 1.

4.5 Identifying a best-compromise parameter set

While multi-objective calibration provides new perspectives to the parameter estimation problem, the detection of a unique parameter set, to be utilized for hydrological planning, management and forecasting, remains a common practice. This is confirmed by the recent calibration studies (Table 1), where many of them attempt to identify the most “prominent” solution against the conflicting criteria, usually following a semi-automatic strategy, where the hydrological experience plays a key role. In contrast to the black-box approaches of the 1990s, the current trend favours the incorporation of the user's judgment in order to retrieve a good compromise among the multiple non-dominated solutions. This major issue was comprehensively addressed by Boyle et al. (2000), who proposed a hybrid calibration procedure comprising two steps. In the first step, an automatic search of the feasible parameter space is implemented, to define a representative sample of Pareto optimal parameter steps, on the basis of user-selected criteria that measure different aspects of the closeness of the model outputs and observations. In the second step, the solutions having unacceptable trade-offs are rejected, and additional criteria (both objective and subjective) are introduced to narrow the search space, also accounting for the overall statistical characteristics of the model responses (e.g. long-term biases and overall residual variance).

Madsen et al. (2002) investigated three strategies that utilize multiple objectives and allow user intervention on different levels and different stages in the calibration process, specifically:

	a generic search routine, where the user specifies the priorities to be given to certain objectives that are aggregated into one measure which is then optimized automatically;
	a method using different automatic search techniques (cluster analysis, simulated annealing and multi-criteria optimization) in combination with different calibration objectives, which requires user intervention at different stages in the calibration process;
	a knowledge-based expert system, reflecting the course of a trial-and-error effort of experienced hydrologists, where user intervention is required for subjective evaluation of different calibration criteria.

These different methods focused on different aspects of the examined model responses, but none of them proved superior with respect to all criteria considered.

Several recent studies focus on the exploitation of the valuable information provided by vector optimization approaches and the development of guidelines for selecting the best-suited parameter set among multiple non-dominated ones. Rozos et al. (2004) used several empirical criteria for evaluating Pareto optimal solutions, including the overall model performance against all the measured responses as well as the likelihood of the unmeasured ones, the consistency of the optimized parameters against their broad physical interpretation, and the model predictive capacity, i.e. the performance of each non-dominated solution in validation. With regard to the last issue, it was not surprising that the majority of the solutions obtained within calibration were clearly rejected, since their performance was significantly deteriorated when moved to another time period (i.e. validation). This reveals a serious drawback of multi-objective calibration, which seems to be rather inefficient at providing solutions that remain non-dominated (or approximately non-dominated) across different control periods, since the Pareto set obtained on the basis of a specific data set is obviously non-unique. On the other hand, the existence of satisfactory trade-offs against different criteria and different periods are strong evidence of the robustness of the best-compromise solution (Efstratiadis & Koutsoyiannis, 2009; cf. Choi & Beven, 2007).

Although manual strategies take full advantage of the hydrological experience, they are very time-consuming and too difficult to computerize. Thus, some recent approaches have focused on developing effective and “friendly” filtering tools and embedding them within multi-objective search. For instance, Schoups et al. (2005a,b) used various procedures for identifying the best-compromise solution, including the minimization of the Euclidean distance in the normalized objective function space. They claimed that the optimal choice depends on the individual interests as defined by the user, thus emphasizing the decision-making process rather than the hydrological problem. Khu & Madsen (2005) proposed an automatic routine, based on multi-objective genetic algorithms and Pareto preference ordering, which enables one to sift through the numerous Pareto optimal solutions and retain a short-list of preferred ones for further investigation; this list contains non-dominated solutions that remain non-dominated in different subspace combinations of the objective functions space. Finally, Fenicia et al. (2007a) combined vector optimization with a stepped calibration strategy to explore the deficiencies of the model structure and determine a solution that is consistent with the data available.

5 synopsis and discussion

The progress in integrated representation of hydrological processes through detailed modelling tools has highlighted the weaknesses of automatic, single-objective calibration approaches. At the same time, as models become more complex, multi-objective strategies for parameter estimation have exhibited several strong points; they: (a) ensure parsimony, namely consistency between the number of criteria against parameters to optimize, thus improving their identifiability; (b) fit the distributed responses of models on multiple measurements (“hard” data), also enhancing the information contained in calibration on the basis of “soft” data, derived through expert knowledge; (c) recognize the uncertainties and structural errors related to the model configuration and the parameter estimation procedure; (d) effectively handle criteria of different scales or criteria having contradictory performance; and (e) utilize the experience obtained after investigating the trade-offs of criteria for identifying a best-compromise solution, which should be consistent with the existing knowledge (i.e. experience and data). Such strategies are advantageous even for calibrating simple models with a few parameters, because by taking into account various objectives (both quantitative and qualitative), they ensure consistency against multiple aspects of the system under study.

In this last decade, significant progress was made with regard to different components of the multi-objective calibration problem, including: (a) the algorithmic manipulation; (b) the formulation of objectives; (c) the interpretation of non-dominated solutions and the guidance to a best-compromise choice, and (d) the link with uncertainty assessment approaches. Still, there are many open issues that have been recognized after the experience gained by employing the multi-objective framework in a wide spectrum of applications.

Specifically, recent advances in computer science provide a number of robust multi-objective optimization tools, typically employed as adaptations of genetic algorithms. Yet their dissemination in real-world hydrological applications is relatively poor and thus there is much research to be done on comparative tests in challenging calibration problems. The definition of appropriate procedures for evaluating MOEAs remains a challenging task in optimization science (Zitzler et al., 2003; Coello Coello, 2005). The calibration problems of hydrological models certainly present difficulties not usually faced in other technological areas. First, the computational time needed for a single simulation run in complex models, makes it impossible to approach the Pareto front with reasonable effort. Second, there is too little experience on multi-dimensional objective spaces, while a calibration problem may involve a large number of fitting criteria, either statistical or empirical. In reality, not all of them are by nature conflicting and the trade-offs appearing are mainly due to ill-posed structures and deficient data. However, as more objectives are included in the calibration, the set of Pareto optimal solutions tends to be impractically extended; thus, it is necessary to provide guidelines for determining a limited number of criteria that are best suited for Pareto analysis (Meixner at al., 2002). For example, Khu et al. (2008) proposed a framework for classifying multi-site measurements into groups according to temporal dynamics.

A multi-objective approach does not necessarily guarantee the detection of calibrations that are acceptable from a hydrological perspective. In fact, because of the past emphasis on finding the “best” model (in either a global- or Pareto-optimal sense, both based on fitting metrics requiring systematic measurements), there has been little consideration of whether this optimal model is actually a consistent simulator according to an expert hydrologist (Choi & Beven, 2007). Thus, the attention is now given to soft data, usually expressed through empirical criteria that also reflect the expert knowledge on the system under study. This allows for controlling different modelling aspects from a macroscopic point-of-view, e.g. to ensure realistic fluctuations of internal model variables (Efstratiadis et al., 2008). It also offers a means to partially handle the huge uncertainty resulting from the complexity of model parameterizations in contrast to data scarcity, which is a global engineering problem that is getting increasingly severe. Yet, we emphatically note that soft data are auxiliary information and cannot substitute measurements; moreover, a “bulimic” use of empirical criteria that are not supported by some kind of documentation may lead to over-constraining the feasible parameter space and thus underestimating uncertainty. Actual research should provide more guidance on the effective combination of statistical and expert-based evaluation procedures.

The assessment of the richness of information derived by Pareto-based calibration approaches also offers additional research perspectives. For instance, the interpretation of the irregularities of the trade-off curves has been little investigated. There are also many practical issues that remain open, such as the development of a hybrid calibration framework supporting interactive computerized facilities, for filtering through numerous Pareto-optimal solutions to detect the most promising ones. This last option may be related to the non-uniqueness property of the Pareto set—a critical point to which no attention has been given so far. For instance, a cross-validation on different data subsets may help to significantly reduce the number of solutions ensuring acceptable trade-offs through different control periods (Efstratiadis & Koutsoyiannis, 2009). Yet, since this is often not feasible, it is essential to provide a framework to effectively combine (and explain) the results obtained from multiple calibration periods, in order to improve the model predictions (Beven et al., 2008).

Many argue that the real challenge in hydrology is the development of a generalized uncertainty assessment framework that will allow hydrological models to profit from different types of information (e.g. Hamilton, 2007; Montanari, 2007). Indeed, state-of-the-art research is actually focused on the integrated handling of parameter estimation and uncertainty assessment, using multiple objectives within Bayesian inference techniques (Vrugt et al., 2003b, 2005). Until now, the experience has been restricted to elementary models and it is difficult to predict their success in more demanding applications as well as their dissemination in the everyday engineering practice. Yet, the major problem is not only technical but also philosophical; a generally agreed definition of uncertainty is missing, as is a generally-accepted assessment of whether the existing approaches over- or underestimate the uncertainty of predictions (Beven, 2006; Andréassian et al., 2007; Hall et al., 2007; Todini & Montovan, 2007; Beven et al., 2008). In this obscure environment, it is difficult to predict the success of a unified approach to model calibration and uncertainty assessment following the multi-criteria paradigm, which requires subjective decisions and is based on qualitative considerations (i.e. soft data).

Acknowledgements

The preliminary research for this paper was done within the PhD dissertation of the first author entitled “Non-linear methods in multi-objective water resource optimization problems, with emphasis on the calibration of hydrological models” (http://www.itia.ntua.gr/en/docinfo/838/) and supported by the scholarship project “Heracleitos”. The project was co-funded by the European Social Fund (75%) and National Resources (25%). We are grateful to Hoshin Gupta and Keith Beven for their useful and constructive comments, critiques and suggestions, which helped us to substantially improve the paper.