Analytical procedures for weekly hydrological droughts: a case of Canadian rivers

Abstract

Two entities of importance in hydrological droughts, viz. the longest duration, L_T , and the largest magnitude, M_T (in standardized terms) over a desired time period (which could also correspond to a specific return period) T, have been analysed for weekly flow sequences of Canadian rivers. Analysis has been carried out in terms of week-by-week standardized values of flow sequences, designated as SHI (standardized hydrological index). The SHI sequence is truncated at the median level for identification and evaluation of expected values of the above random variables, E(L_T ) and E(M_T ). SHI sequences tended to be strongly autocorrelated and are modelled as autoregressive order-1, order-2 or autoregressive moving average order-1,1. The drought model built on the theorem of extremes of random numbers of random variables was found to be less satisfactory for the prediction of E(L_T ) and E(M_T ) on a weekly basis. However, the model has worked well on a monthly (weakly Markovian) and an annual (random) basis. An alternative procedure based on a second-order Markov chain model provided satisfactory prediction of E(L_T ). Parameters such as the mean, standard deviation (or coefficient of variation), and lag-1 serial correlation of the original weekly flow sequences (obeying a gamma probability distribution function) were used to estimate the simple and first-order drought probabilities through closed-form equations. Second-order probabilities have been estimated based on the original flow sequences as well as SHI sequences, utilizing a counting method. The E(M_T ) can be predicted as a product of drought intensity (which obeys the truncated normal distribution) and E(L_T ) (which is based on a mixture of first- and second-order Markov chains).

Citation Sharma, T. C. & Panu, U. S. (2010) Analytical procedures for weekly hydrological droughts: a case of Canadian rivers. Hydrol. Sci. J. 55(1), 79–92.

Procédures d'analyse de sécheresses hydrologiques hebdomadaires: le cas de rivières Canadiennes

Résumé Deux caractéristiques importantes des sécheresses hydrologiques, à savoir la plus longue durée, L_T , et la plus grande magnitude, M_T (en termes standardisés) sur une durée souhaitée (qui pourrait aussi correspondre à une période de retour spécifique) T, ont été analysées pour des séquences hebdomadaires de débits de rivières au Canada. L'analyse a été faite en termes de séquences hebdomadaires des valeurs standardisées des débits, appelées IHS (indices hydrologiques standardisés). La séquence d'IHS est tronquée au niveau de la médiane pour l'identification et l'évaluation des espérances des caractéristiques précédentes considérées comme variables aléatoires, E(L_T ) et E(M_T ). Les séquences d'IHS ont tendance à être fortement auto-corrélées et sont représentées par des modèles auto-régressifs d'ordre 1, d'ordre 2 ou avec moyenne mobile d'ordre 1,1. Le modèle de sécheresse basé sur le théorème des valeurs extrêmes de variables aléatoires s'est révélé être moins satisfaisant pour la prévision de E(L_T ) et de E(M_T ) sur une base hebdomadaire. Cependant le modèle a bien fonctionné sur des bases mensuelle (faiblement Markovienne) et annuelle (aléatoire). Une procédure alternative basée sur une chaîne de Markov du deuxième ordre a donné des prévisions de E(L_T ) satisfaisantes. Des paramètres comme la moyenne, l'écart type (ou coefficient de variation) et l'auto-corrélation de décalage 1 des séquences originales de débits hebdomadaires (suivant une loi de probabilité Gamma) ont été utilisés pour estimer les probabilités simples et du premier ordre des sécheresses via des équations finies. Les probabilités du deuxième ordre ont été estimées sur la base des séquences originales de débits ainsi que des séquences d'IHS en utilisant une méthode de comptage. E(M_T ) peut être prévue comme le produit de l'intensité de la sécheresse (qui suit la distribution normale tronquée) et de E(L_T ) (qui est basée sur un mélange de chaînes de Markov de premier et de deuxième ordres).

Key words:

• conditional probabilities
• standardized hydrological index
• Markov chain
• weekly flow

Mots clefs:

• probabilités conditionnelles
• indice hydrologique standardisé
• chaîne de Markov
• débit hebdomadaire

INTRODUCTION

Analysis of hydrological droughts on a weekly basis offers useful information for scheduling planting and watering activities of cereal crops (growing period 12–15 weeks) and vegetable crops (growing period 3–10 weeks), water rationing during water shortage periods, and other exigency-related planning of water supply and distribution on a short-term basis. For example, consider a river equipped with a reservoir to provide a town with drinking water supplies and to provide the cereal and vegetable crops with supplemental irrigation water. During a drought period, it is desirable to know the likelihood of the drought continuing until the onset of rains. It is known a priori that delayed rains during the up coming season are normally scanty, and thus for drought mitigation purposes an adequate irrigation scheduling plan for cereal crops and a water rationing plan for town dwellers are required. Under such circumstances, formulations of drought statistics (duration and magnitude) based on either an annual or a monthly basis may lend limited information as these statistics cannot be scaled down in a direct multiplicative manner. For example, if a 100-year drought persists for 4 years, it does not mean that all the 208 (= 4 × 52) weeks will be under the grip of drought. It is expected that a much smaller number of weeks shall be affected by persistent drought, a number which can be obtained through drought analysis of weekly flow sequences, as developed in this paper.

Droughts can be identified using several drought indices such as the Standardized Precipitation Index (SPI) or the Palmer Drought Severity Index (PDSI) (Hayes, 2002). The SPI operates on the simple principle of standardization and normalization of precipitation values at the time period chosen for analysis, such as monthly, bimonthly, or a 3-, 6-, 12-, 24-, 48-month basis (McKee et al., 1993, 1995; Edwards & McKee, 1997; Guttman, 1999; Sirdas & Sen, 2003). For example, a monthly SPI series is obtained using month-by-month standardization (subtraction of monthly means and division by monthly standard deviations) of precipitation values and then normalizing them. Such a series can be truncated at the mean level and the resultant periods below the truncation level are indicative of drought conditions. Note that a non-normalized series truncated at the median level is equivalent to a normalized series at the mean level. During a drought period the sum of absolute SPIs below the chosen truncation level is termed the magnitude (Hayes, 2002; Sirdas & Sen, 2003). It is noted that the above sum (i.e. the magnitude) in the hydrological drought context has been referred to as “severity” since the early days of drought research (Yevjevich, 1967) and until recently (Sharma & Panu, 2008). Likewise, the term “intensity” (ratio of severity to duration) has been used interchangeably with magnitude (Dracup et al., 1980; Panu & Sharma, 2002). Use of the term magnitude in the hydrological drought context seems to be gaining momentum (Timilsena et al., 2007; Lopez-Moreno et al., 2009). In view of the changing trend in the nomenclature of drought parameters, the term magnitude shall be used in place of severity, and the ratio of magnitude to duration shall be termed drought intensity in this study.

Identification of drought events depends on selection of the truncation level. Thus, in view of the adopted practice for the analysis of SPI, the median value of the flow sequence will be used as the desired truncation level in this study. Since this paper deals with streamflow sequences rather than precipitation sequences, the Standardized Hydrological Index, SHI, is defined virtually parallel to SPI. However, it must be noted that the SHI is a standardized sequence (mean 0 and variance 1) but not a normalized one. In the case of SHI, drought probabilities change in tandem with the probability distribution function (pdf) of the data, which is reflected in changed behaviour of the drought duration and magnitude. The data are not transformed so their original form remains undistorted and the pdf is preserved, which is a desirable feature. On an annual basis, the treatment of three common pdfs of SHI, viz. normal, gamma, and lognormal distributions, for drought analysis is well documented in Sharma (2000). The theorem of extremes of random numbers of random variables (Todorovic & Woolhiser, 1975) has been found to be a powerful tool for the prediction of the hydrological drought parameters of SHI series on annual and monthly streamflow sequences of Canadian rivers (Panu & Sharma, 2009; Sharma & Panu, 2008). For the prediction of dry and wet spells on a daily basis, the concepts of Markov chains were found to be promising (Chin, 1976, 1977).

Deficits below the chosen truncation level, recognized as drought events, form the runs. Consequently, two entities are associated with each drought event: the duration, L, of the negative run, hereafter referred to as the drought duration; and the corresponding magnitude, D, equal to the cumulative deficit run-sum, hereafter referred to as the drought magnitude. As the drought analysis is carried out in the standardized domain of the flow sequences, the drought magnitude, D, is termed the standardized magnitude M. It can be deduced that drought magnitude, D = σM (Yevjevich, 1967), where σ is the standard deviation of the sequence under consideration. This paper attempts the prediction of the average drought duration, E(L_T ) over a time period (which could also correspond to a specific return period) T, and corresponding standardized magnitude, E(M_T ) (E stands for expected value) on a weekly basis using the flow data of Canadian rivers and involving the conceptual framework of SHI. The main objective of this study is to evaluate, on a weekly basis, the applicability of those drought prediction models that have been built on the premise of the theorem of extremes of random numbers of random variables and are reported in the literature to perform well on annual and monthly bases, and, furthermore, in the case of an anomaly to adapt alternative models based on the concepts of Markov chains.

FLOW DATA ACQUISITION AND PRELIMINARY ANALYSIS

The data for the analysis are natural (i.e. unregulated) and uninterrupted flow records of 18 rivers across Canada (Fig. 1) and are listed in Table 1. The data for these stations and the corresponding periods were used to study hydrological droughts on monthly and annual bases (Sharma & Panu, 2008; Panu & Sharma, 2009). These studies were conducted using the existing concepts and notions of stochastic theory for evaluating the drought characteristics in the highly seasonal flow regimes of Canadian rivers. Encouraged by the success of concepts incorporated within models for predicting the behaviour of the annual or monthly hydrological droughts, it was considered logical to use the same database for the characterization of droughts on a weekly basis. The major considerations for the selection of stations and the period of data were the same as reported earlier by Sharma & Panu (2008); for example, the existence of natural flow regimes with continuous records and unaffected by human intervention, with a minimal need for data infilling. Additional statistical analyses involving trend, homogeneity and consistency were used to further statistically screen the data sets. Thus, daily flow data for these 18 rivers were extracted from the Canadian Hydrologic Data Base (HYDAT; Environment Canada, 2005). The selected rivers are representative of a wide range of drainage basins (37 km² to 32 400 km²) and a period of the historical database (1919–2005) which required virtually no data infilling. Daily flows were transformed to weekly flows such that each of the first 51 weeks would be composed of 7 days while the 52nd week would contain the remainder of days. That is, the last week of the year would comprise of 8 or 9 (during a leap year) days.

Fig. 1 Spatial location across Canada of all hydrometric stations used in the analysis (source: Environment Canada).

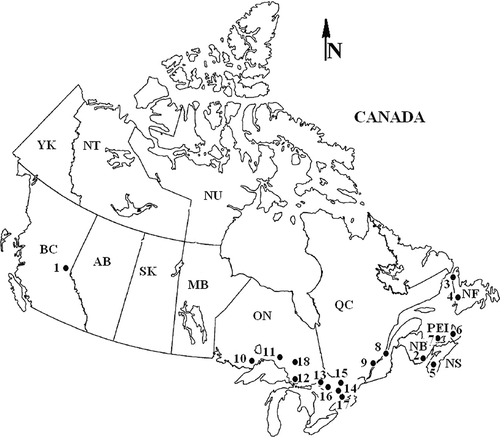
Table 1  Summary of statistical parameters of flow sequences (weekly) of rivers across Canada

Station number	River name	Record (years)	Area (km^2)	μ (m^3/s)	cv	γ	ρ	ρ1	Model type
BC08KB001	Fraser River	1951–05	32400	816.9	0.90	1.30	0.92	0.73	AR-1
1**	at Shelley								(0.73)
NB01AQ001	Lepreau River	1919–05	239	7.24	1.09	2.91	0.60	0.51	AR-1
2	at Lepreau								(0.51)
NF02YC001	Torrent River	1960–05	624	24.50	1.12	2.95	0.73	0.59	AR-2
3	at Bristol Pool								(0.67, –0.12)
NF02YL001	Upper Humber River	1953–05	2110	79.38	1.09	2.25	0.71	0.49	AR-2
4	at Reidville								(0.53, –0.09)
NS01DG003	Beaverbank River	1922–00	96.9	2.99	1.09	2.20	0.55	0.46	AR-1
5	at Kinsac								(0.46)
NS01FB001	Northeast Margaree River	1929–05	368	17.11	0.97	2.44	0.65	0.46	AR-2
6	at Margaree Valley								(0.44, –0.05)
PE01CA003	Carruthers River	1962–05	46.8	0.94	1.32	4.19	0.66	0.53	AR-1
7	at St. Anthony								(0.53)
QC02PJ007	Beaurivage River	1951–96	709	13.95	1.46	3.24	0.68	0.48	AR-1
8	at Sainte-Etienne								(0.48)
QC02PL001	Becancour River	1923–68	1410	30.62	1.32	3.24	0.72	0.63	AR-2
9	at Lyster,								(0.69, −0.09)
ON02AB008	Neebing River	1954–05	187	1.63	1.88	3.91	0.67	0.67	AR-2*
10	at Thunder Bay								(0.63, –0.07)
ON02BB003	Pic River	1971–05	4270	52.70	1.19	2.68	0.77	0.76	AR-2*
11	at Marathon								(0.82, –0.07)
ON02BF002	Goulais River	1968–05	1160	18.46	1.29	3.37	0.74	0.73	AR-2*
12	at Searchmont								(0.83, –0.14)
ON02CF007	Whitson River	1961–05	272	3.04	1.53	4.36	0.67	0.69	AR-2*
13	at Chelmsford								(0.78, –0.11)
ON02DD013	La Vase River	1975–05	70.4	0.92	1.51	3.31	0.61	0.49	AR-1
14	at North Bay								(0.49)
ON02DD014	Chippewa Creek	1975–05	37.3	0.61	1.12	2.87	0.60	0.45	AR-1
15	at North Bay								(0.45)
ON02DD015	Commanda Creek	1975–05	106	1.71	2.07	2.88	0.71	0.60	AR-1
16	at Commanda								(0.60)
ON02EA010	North Magnetawan River	1969–05	149	2.75	1.29	3.27	0.63	055	AR-2*
17	at Pickerel Lake								(0.56, −0.02)
ON04JC003	Shekak River	1951–86	3290	36.17	1.20	2.58	0.87	0.85	ARMA(1,1)
18	at Highway #11								(0.76, −0.40)
The station identifier in the first column is prefixed by the provincial identifier (BC, NB, NF, NS, PE, QC and ON, respectively denoting the provinces of British Columbia, New Brunswick, Newfoundland, Prince Edward Island, Quebec and Ontario in which a particular river is metered). ** The number indicates the location of the station on Fig. 1. With the model type, parameters Φ1, Φ2 or θ1 are shown in parentheses; for AR-1 process only Φ1, for AR-2 Φ1 and Φ2, and for ARMA (1,1) Φ1 and θ1 are shown. * means AR-2 was still inadequate as the Portmanteau statistic exceeded marginally the critical value (at 5% level of significance and 23 degrees of freedom).

Identification of probability distribution and dependence structure of weekly flow sequences

The analysis of drought parameters using probability theory generally begins with the identification of the probability distribution function (pdf) of the drought variable (weekly flows) and its dependence structure. For identifying the pdf of the weekly flows, the product moment and L-moment relationships (Vogel & Fennessey, 1993; Hosking & Wallis, 1997) were used. For each river, values of statistics such as the mean (μ), standard deviation (σ) or coefficient of variation (cv) and skewness (γ) were computed (Table 1) and necessary plots were graphed in terms of product moment and L-moments. The analysis revealed that a two-parameter gamma pdf fits the weekly flow data reasonably well.

Once a suitable pdf fitting the weekly flow sequences is obtained, the underlying dependence structures of these flow sequences can be investigated. That is, if x_y,t is the flow in the tth week (t = 1, 2, 3,…, 52) of the yth year (1 ≤ y ≤ N) then the standardized series u_y,t  = (x_y,t – μ _t )/σ _t with μ _t and σ _t respectively being the mean and standard deviation of the tth week, is rendered as weakly stationary with mean zero and variance 1. Since the u_y,t series is assumed stationary, it can be designated as e_i with i ranging from 1 to n = N ×52. It is recognized that e_i is a standardized series but not a normalized one, since its generic source x_{y, t} is generally non-normal for weekly flow sequences and, as stated earlier, in the present case it is the gamma distribution. The e_i (or alternately SHI) sequence was subjected to autocorrelation analysis to uncover the presence of any Markovian or other higher-order persistence. Such analysis demonstrated that the e_i sequence resembles either order-1 autoregressive (AR-1; e_i  = Φ₁ e_{i- 1} + a_i ), or order-2 autoregressive (AR‐2; e_i  = Φ₁ e_{i- 1} + Φ₂ e_{i- 2 +} a_i )], or an autoregressive moving average order –1,1 (ARMA (1,1); e_i – Φ ₁ e_{i- 1} = a _i – θ₁ a_{i −1}) process, with some notable exceptions in data sets from northern Ontario rivers. In the above relationships, Φs are autoregressive parameters, θ is a moving average parameter in the ARMA model, and a_i is a random component with mean zero and constant variance σ_a ². The model identification and associated parameters were estimated using a procedure due to Box & Jenkins (1976) wherein the randomness of the a_i component was affirmed by Portmanteau statistic involving the first 25 autocorrelations. It should be noted that the concepts of time series analysis advanced by Box & Jenkins (1976) are not constrained on the normal pdf of the data. However, it is preferable that the data be normally distributed for ease in the statistical interpretation of the parameters, and for diagnostic checking of residuals for ascertaining the adequacy of the model. Rivers in northern Ontario (Table 2) appear to generally show persistence beyond AR-2 in the e_i sequences. Such persistence is attributed to significant storage effects caused by the presence of a large number of lakes and wetlands in watersheds of this region. Rivers passing through or originating from lakes would have significant storage-driven carryover effects, so causing flows to fall behind by multiple weeks. In a nutshell, it is prudent to regard the first approximation of the memory component in the weekly flows to lag by up to 2 weeks, and hence AR-1 and AR-2 could be considered to model the SHI or e_i sequences.

Table 2  Summary of observed and predicted weekly values of E(L _T ) with q = 0.5, gamma pdf of weekly flows

Station identifier*	Memory form	N (year)	e 0	LT -ob (week)	ρ	LT -pr (week)	ρ 1	LT -pr (week)
BC08KB001	AR(1)	55	−0.27	37	0.92	43	0.73	24
NB01AQ001	AR(1)	87	−0.32	29	0.60	21	0.51	18
NF02YC001	AR(2)	46	−0.32	27	0.73	23	0.59	19
NF02YL001	AR(2)	53	−0.32	31	0.71	23	0.49	17
NS01DG003	AR(1)	79	−0.32	29	0.55	19	0.46	17
NS01FB001	AR(2)	77	−0.29	23	0.65	22	0.46	17
PE01CA003	AR(1)	44	−0.36	38	0.66	20	0.53	17
QC02PJ007	AR(1)	46	−0.38	22	0.68	21	0.48	16
QC02PL001	AR(2)	46	−0.36	27	0.72	23	0.63	20
ON02AB008	AR(2)	52	−0.41	23	0.67	22	0.67	22
ON02BB003	AR(2)	35	−0.35	41	0.77	24	0.76	23
ON02BF002	AR(2)	38	−0.35	37	0.74	23	0.73	23
ON02CF007	AR(2)	45	−0.39	44	0.67	21	0.69	22
ON02DD013	AR(1)	31	−0.39	23	0.61	18	0.49	16
ON02DD014	AR(1)	31	−0.33	30	0.60	18	0.49	15
ON02DD015	AR(1)	31	−0.34	36	0.71	21	0.60	18
ON02EA010	AR(2)	37	−0.35	36	0.63	19	0.55	17
ON04JC003	ARMA(1,1)	36	−0.34	42	0.87	32	0.85	30
LT -ob and, LT -pr respectively mean observed and predicted T-week (T = 52 × N weeks) drought duration in weeks using a gamma pdf of weekly flows. *The station identifiers are the same as defined in Table 1.

ASSESSING THE PREDICTION OF WEEKLY E(L_T )

The theorem of extremes of random numbers of random variables, coupled with the theory of runs, is well documented in the hydrological literature (Todorovic & Woolhiser, 1975) and has been successfully used for the analysis and prediction of hydrological droughts on an annual basis (Sen, 1980a; Guven, 1983; Sharma, 1998, 2000). The theorem also provides satisfactory estimates of E(L_T ) and E(M_T ) on a monthly (Sharma & Panu, 2008) and an annual (Panu & Sharma, 2009) basis in Canadian environments. One important feature of this theorem is that E(L_T ) can be predicted first, and then can be transformed into E(M_T ) through the relationship E(M_T ) = I E(L_T ) (Sharma & Panu, 2008). Therefore, it is logical to apply the above theorem to the weekly flow sequences because the monthly and weekly flow sequences can be regarded as nearly similar, both being periodic stochastic, and through the standardization procedure both sequences are transformed into stationary e_i (i.e. SHI) series. The probabilistic relationships for the estimation of E(L_T ) and the associated parameters emanating from the theorem and theory of runs were developed by Sen (1980a) and are briefly presented as follows:

(1)

(2)

where q is the probability of any week being a drought week and q_q is the conditional probability of the present drought week given that the previous week was also a drought week. The value of q is dependent on the pdf, the coefficient of variation, cv, of the flow sequence, and the truncation level, e ₀. The value of q_q is dependent on the pdf of the flow sequence, ρ₁ of the standardized series, e_i or ρ of the original weekly flow series, and e ₀.

The procedure for determining q entails the use of the standard normal probability integral in which the integration is accomplished up to the truncation level, e ₀. That is, if a standardized time series e_i is normally distributed then the probability q = P(e ≤ e ₀) = P(z ≤ z ₀) can be evaluated as:

(3)

where z is a standardized normal variate with mean 0 and variance 1 (a notation common in statistical texts). The value of q can also be obtained directly from standard normal probability tables.

For the gamma pdf, which represents a mild skew in the data, the normalized standard variate can be obtained using following equation (Sharma, 1998, 2000):

(4)

Succinctly, once the pdf of the weekly flow series is identified (say the gamma pdf), its cv and ρ are estimated from the original weekly flow sequence. The series is then standardized week-by-week and the resulting series (e_i series) is truncated at a level such that the probability q = 0.5. The value of e ₀ is computed by setting z_g  = 0 in equation (4)(4). For example, in Table 1 for the Fraser River (station BC08KB001), the value of z_g  = 0 and cv = 0.89 yields e ₀ = −0.27. In other words, the median level of truncation in the e_i series of the gamma distributed weekly flows of the Fraser River corresponds to e ₀ = −0.27. A week with e_i less than or equal to −0.27 shall be recognized as a drought week. If the flows had obeyed a normal pdf, the e ₀ would be equal to 0.0 by setting q = 0.5 in equation (3)(3).

The conditional probability, q_q or p_p , is related to ρ₁ or ρ through the following relationship reported by Sen (1976, 1977):

(5)

(6)

where p means the simple probability of any week being wet; p_p means conditional probability of a wet week given that the previous week was also wet. Similar notations apply for q and q_q . It is noted that q_q= q and p_p  = p for independent or random streamflow sequences, or when drought spells display characteristics of random occurrences. As an illustration, for the Fraser River with the gamma pdf, cv = 0.87, e ₀ = −0.27, ρ = 0.92 and q = 0.5 yields q_q  = 0.87 through the numerical integration of equation (5)(5). Truncation levels e ₀ corresponding to the median level were determined by setting z_g  = 0 in equation (4)(4) for all rivers and are summarized in Table 2. The values of e_i above the truncation level were designated as 1 (w, i.e. wet) and below as 0 (d, i.e. deficit or drought), thus one obtains a series of 1s and 0s. The longest run of the 0s corresponds to the longest drought duration, which was determined by a counting method (Sen, 1980b) and is also equivalent to the observed value of E(L_T ). Likewise, the highest sum of negative values (in a negative run) represents the observed E(M_T ), which was computed by summing the negative values (e_i – e ₀) in absolute terms. It can be perceived that the sample size n = 52N weeks, where N is the number of years, represents a time period of T = n weeks. To estimate conditional probabilities in equations (5)(5) and (6(6)), both values of lag-1 autocorrelation (ρ as well as ρ₁) were used to improve upon the prediction of E(L_T ) by matching it to its observed counterpart.

Concluding remarks on the prediction results of weekly E(L_T )

At the median level of truncation in all rivers (except for the Fraser River, BC08KB001) with either the value of ρ or ρ₁ and regardless of the memory structure embedded in the weekly flow sequences, the values of E(L_T ) generally represent under-prediction, as summarized in Table 2. Since flow sequences of approximately half of the rivers (Table 1) were found to follow AR-2 or ARMA(1,1), such a mismatch in model identification is justifiable in view of the inherent complicity of the memory in weekly flow sequences. However, it is difficult to explain the discrepancy (i.e. under-prediction) for the rivers having AR-1 type memory in weekly sequences. It is worth noting that drought parameters obtained based on AR-1 type memory for monthly flow sequences turned out to be satisfactory (Sharma & Panu, 2008). Because there is a strong commonality of memory behaviour of AR-1 type between the monthly and weekly flows, a reasonable correspondence between predicted and observed values of E(L_T ) is expected for weekly flows in such rivers. The only difference between the AR-1 structure of the stochastic component of the weekly and monthly sequences has been the degree of strength in the persistence (i.e. the parameter Φ₁ being >0.45 in weekly series against about 0.20 in monthly flow series). This degree of persistence in the AR-1 type model for monthly and weekly flow sequences can be ascribed to be the major cause of this discrepancy. Stated another way, the model structure based on the theorem of extremes of random numbers of random variables is strictly applicable to random (annual flow) or weak Markovian (monthly flow) drought variables. In a nutshell, an unsatisfactory response for weekly flow sequences, though obeying the Markovian type (AR-1) persistence (nearly half of the rivers) is intriguing to state the least, which warrants further investigation and analysis, as presented in the following sections.

PROPOSED MARKOV CHAIN MODEL

Based on the concept of Markov chains (Chin, 1976, 1977), the following methodology is proposed for the estimation of drought duration E(L_T ). The relationships based on earlier research efforts (Sharma, 2000; Sharma & Panu, 2008; Panu & Sharma, 2009) have been utilized for estimation of drought magnitude E(M_T ).

Estimation of drought duration, E(L_T ) in terms of simple and conditional probabilities

From the preceding analysis, each e_i series of the analysed rivers has been found to follow either an order-1 or order-2 type of autoregressive process. An alternative approach of Markov chains is also investigated and presented below.

When the e_i series is cut off at a truncation level e ₀, the values above the truncation level are positive or in the wet (w) state, and those below are negative or in the drought (d) state. So the e_i series can be transformed into a sequence of discrete states in terms of w and d (say for example: wwwddddwwwwdd). One can define the following notations for probabilities, designated by P( ); P(d) (simple probability), i.e. the probability of any week being a drought week at a given truncation level = q; P(d│d) (conditional probability) i.e. the probability of any week being a drought week given that the previous week was also a drought week (first-order persistence) = q_q ; P(d│d,d) (conditional probability), i.e. the probability of any week being a drought week given that the previous two weeks were also drought weeks (second-order persistence) = q_qq . The same applies to the wet state, i.e. p = P(w); p_p = P(w│w); and p_pp = P(w│w,w). Likewise, p_qq = P(w│d,d); q_p= P(d│w); and q_qp= P(d│d,w). The simple and conditional probabilities sum to 1 as follows:

Consider a sequence wwwwdwwddwdddww---d (which contains k number of letters w and/or d with a minimum value of k = 3), then to designate the occurrence of a wet or a dry week, one needs respectively to express it as: dwd or wdw. The probability distribution of lengths in drought and wet spells can be described by a well known geometric distribution (Mathier et al., 1992). Invoking the above geometric law into a second-order Markov chain, the following equations can be derived (Chin, 1976, 1977) for L = 1, 2, 3, …, j.

To obtain the probability of just one drought week (L = 1; i.e. wdw), the week should be followed and preceded by at least a wet week; for example, refer to the first occurrence of d in the above sequence:

(7)

Likewise, to obtain the probability of a spell of two drought weeks (L = 2; i.e. wddw), such a drought spell must be preceded and followed by at least a wet week. For example, referring to the drought spell containing two successive ds in the sequence above:

(8)

Similarly, regarding the probability of a spell of three drought weeks (L = 3; i.e. wdddw), such a drought spell must be preceded and followed by at least a wet week. For example, referring to the drought spell containing three successive ds in the above sequence:

(9)

In general, the probability of a drought spell of L = 2, 3, 4, …, j is:

(10)

For a Markov chain of the first order, P(d│d,w) = P(d│d); P(d│d,d) = P(d│d) and P(w│d,d) = P(w│d) so that equation (10)(10) reduces to:

(11)

Using a counting or enumeration method, sufficiently accurate estimates of p, q_p , q_qp , q_qq , and p _q can be obtained from the historical data with sample size n > 1000 (Chin, 1977). It should be noted that more rigorous and elaborate equations for determination of P(L = j); j = 2, 3, 4… have also been developed by Sen (1990) involving the concepts of tree diagram, conditional and recursive probabilities, which may provide another route to involving Markov chains in the analysis.

The exceedence probability for a T-week period is 1/T. Therefore if the drought duration, L (when taken as dummy variable) for a T-week period is greater than or equal to j weeks, then for a second-order Markov chain, equation (10)(10) can be expressed as follows:

(12)

where, j has a value such that the area to the right of it in the geometric probability curve is 1/T. Equation (12)(12) can be summed as follows:

(13)

Note that the term (1 – q_qq ) cancels out with p_qq in the numerator while summing, and since p_qq  = 1 – q_qq , a solution of equation (13)(13) for j (knowing that p = 1 – q), becomes:

(14)

The value of j in equation (14)(14) corresponds to the T-week period and, therefore, it can be construed as an estimate of the expected value of drought length and can be expressed as E(L_T ). It is apparent from equation (14)(14) that only four parameters are needed for a second-order Markov chain process. Parameters p, q_p and q_q can be estimated from the information on cv, ρ and e ₀, using a counting method and the closed-form equations (5)(5) and (6(6)). However, no such closed-form equations can be found for the estimation of second-order parameters, viz. q_qp and q_qq , hence they are estimated by a counting method described below.

A counting method for estimation of simple and conditional probabilities

The parameters q, q _p , q _qq and q _qp can be estimated by a counting method (Sen, 1980b, 1990) using the sequence of 1s and 0s which was obtained by truncating the e_i series at the desired truncation level of e ₀ (such that the q value is equal to 0.5). It is to be noted that, for convenience, in calculations the letters d and w are respectively replaced by 0 and 1. Consider a number of scenarios involving occurrences of zeros as follows: as isolated single zeros (say n ₁), as two consecutive zeros, i.e. “00” (say n ₂), and as three consecutive zeros, i.e. “000” (say n ₃). Knowing that the total sample size is n, then q = n ₁/n, q_q  = n ₂/n ₁, and q_qq  = n ₃ /n ₂. Since there are only two numerals, 1 and 0, so the number of 1s = (n – n ₁). The number of pairs “11” occurring in succession (i.e. 1 precedes 1) is counted (say n ₄). Therefore, p_p  = n ₄/(n – n ₁) and hence q _p  = (1 – p _p ). Similarly the number of pairs such as “01” (0 precedes 1, say n ₅) and “001” (00 precedes 1) are counted (say n ₆) which can be used to estimate the value of q_qp as n ₆ /n ₅. By following the above method, the second-order parameters (q_qq and q_pq ) were also estimated from the original flow series truncated at the median level. Thus, there are two estimates for each of the parameters q_qq and q_pq for subsequent analyses.

DISCUSSION OF RESULTS OF THE MARKOV CHAIN MODEL

Comparative analysis of predicted and observed drought duration, E(L_T )

For each river, the truncation level, e ₀ corresponding to the probability, q = 0.5 (truncation at the median level) was computed as shown in Table 2 . Using ρ₁ and equations (5)(5) and (6(6)), the first order conditional probabilities q_q and q_p for each river were computed. Parameters q_qq and q_qp were estimated by a counting method using the series e_i . For each river the values of E(L_T ) as summarized in Table 3 were predicted from equation (14)(14) using parameters q_qq and q_qp .

Table 3  Summary of observed and predicted weekly values of E(L _T ) with q = 0.5, gamma pdf of weekly flows and second-order Markov chain model

Station identifier	N (year)	e 0	LT -ob (week)	LT -pr (week)
				ρ1 and qqq , q qp (ei series)	ρ (original) and qqq , qqp (ei series)	ρ and qqq , q qp (original flow series)
1	2	3	4	5	6	7
BC08KB001	55	−0.27	37	31	39	67
NB01AQ001	87	−0.32	29	26	27	35
NF02YC001	46	−0.32	27	24	24	33
NF02YL001	53	−0.32	31	20	21	29
NS01DG003	79	−0.32	29	24	24	37
NS01FB001	77	−0.29	23	24	24	36
PE01CA003	44	−0.36	38	25	26	40
QC02PJ007	46	−0.38	22	20	20	27
QC02PL001	46	−0.36	27	22	23	32
ON02AB008	52	−0.41	23	21	21	54
ON02BB003	35	−0.35	41	29	32	63
ON02BF002	38	−0.35	37	29	29	49
ON02CF007	45	−0.39	44	26	29	45
ON02DD013	31	−0.39	23	19	20	34
ON02DD014	31	−0.33	30	19	19	28
ON02DD015	31	−0.34	36	25	26	36
ON02EA010	37	−0.35	36	23	24	38
ON04JC003	36	−0.34	42	34	36	62
L T -ob and, LT -pr respectively means observed and predicted T-week (T = 52 × N year) drought duration in weeks using a gamma pdf of weekly flow sequences. The station identifier in column 1 is the same as defined in Table 1.

Corresponding to ρ₁, it is apparent from column 5 in Table 3 that almost all values are underpredicted. To ameliorate the underprediction, ρ₁ was replaced by ρ, which has marginally improved the prediction of values for E(L_T ) but underprediction still persists (column 6, Table 3). To further improve upon the persistence of underprediction of L_T -pr (week), parameters q_qq and q_qp were estimated from the original flow sequence by truncating it at the median level. In other words, all parameters are estimated based on the original flow sequences. This new set of parameters resulted in overprediction of E(L_T ) as shown in column 7 of Table 3. It is clearly evident that a balance can be struck if appropriate values of parameters are sought. The most sensitive parameter in the aforesaid parameters is q_qq ; a slight change in its value causes a dramatic change in E(L_T ). Therefore, a rational estimate of parameters q_qq and q_qp can be considered as an average of values obtained from the above two routes (i.e. based on standardized as well as the original sequences, Table 4). Since ρ (based on the original data) proved to be a better estimator of first-order conditional probabilities (q_q and q_p ), it was retained in the final analysis. It was noted that the value of q_q ranged from 0.68 to 0.87 (mean = 0.75) _. Likewise, q_qq ranged from 0.78 to 0.90 (mean = 0.83) and q_qp ranged from 0.66 to 0.83 (mean = 0.74). For prediction purposes, it must be mentioned that a number of sub-samples were considered from the available original data set for each river to increase the sample size for assessing the adequacy of fit. For illustration, such a set of sub-samples is presented for two rivers in Table 4. In this manner 62 sub-samples were formulated from the 18 rivers in question, resulting in a large number of points that are plotted in Fig. 2.

Table 4  An illustration for computing the observed and predicted weekly values of E(L _T ) at q = 0.5, and using the second-order Markov chain model

Station identifier	N (Year)	Period of sub-sample	qq , qp and e 0*	qqq, , qqp and e 0**	LT -ob (week)	LT -pr (week)
1	2	3	4	5	6	7
Fraser River at Shelley, BC08KB001	55	1955–05	0.87, 0.13 and –0.27	0.703, 0.888, and –0.20	37	43
	30	1951–80			37	38
	27	1951–77			34	37
	28	1978–05			31	37
Upper Humber at Reidville, NF02YL001	53	1953–05	0.75, 0.25, and −0.32	0.704, 0.776 and −0.31	31	24
	27	1953–79			17	21
	26	1980–05			20	21
	30	1953–82			16	21
	40	1953–92			20	23
* the value of e 0 was computed from equation (4)(4) with q = 0.5
** the value of e 0 was obtained from the SHI sequences (i.e. ei series) which were obtained from the observed flow series such that q = 0.5.

Fig. 2 Comparison of predicted and observed drought durations, E(L_T ).

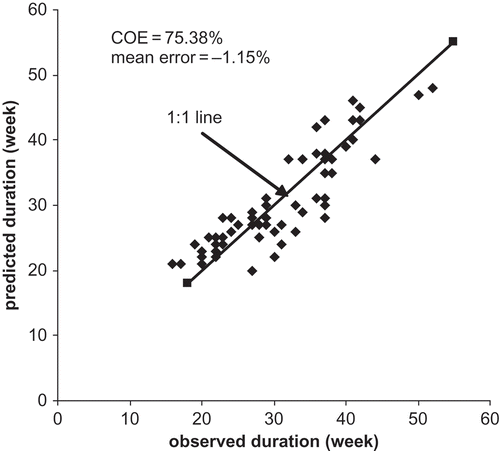
The quality of fit in Fig. 2 was assessed through the coefficient of efficiency (COE) statistic and mean error as reported in earlier papers by Sharma & Panu (2008), and Panu & Sharma (2009). The value of the COE for the scatter of points (predicted and observed values of E(L_T ) ) on the 1:1 line in Fig. 2 was about 75% and the mean error of prediction was less than –1.5%. This plot therefore indicates a reasonable ability of the second-order Markov chain model to simulate and predict the T-week drought durations at the median level of truncation in the SHI sequences. A point to be noted in context of the second-order parameter q_qq is that the parameter was greater than q_q by almost 2% to 20%, with a mean of 10%. In the absence of any other estimate of q_qq , one can assume the value of this parameter is equal to 1.10q_q , and further, the parameter q_pq is far less sensitive in influencing the prediction behaviour, and therefore its conservative estimate can be taken as equal to q_q .

Comparison of predicted and observed standardized drought magnitude, E(M_T )

As stated earlier, the drought magnitudes were computed from the standardized series and are consequently denoted as standardized drought magnitudes, E(M_T ), which were estimated from the following linkage relationship (Sharma, 1998, 2000):

(15)

where │ │ means an absolute value and I stands for the drought intensity that can be estimated using the following relationship (Sen, 1977):

(16)

Note that equation (16)(16) is based on the truncated normal distribution of deficits. Furthermore, the equation is valid for dependent as well as independent hydrological sequences as it only needs the estimate of simple probability, q, and corresponding e ₀ for evaluation of I. In the case of the river identified as BC08KB001, the value of q for the normal pdf is 0.39 (column 4, Table 5) at the median level of truncation (i.e. e ₀ = –0.27). The corresponding value of I (equation 16(16)) results as 0.71. The predicted values of E(M_T ) were computed (column 6, Table 5) through equation (15)(15) by using I as calculated above and multiplying by L_T–pr (column 5). 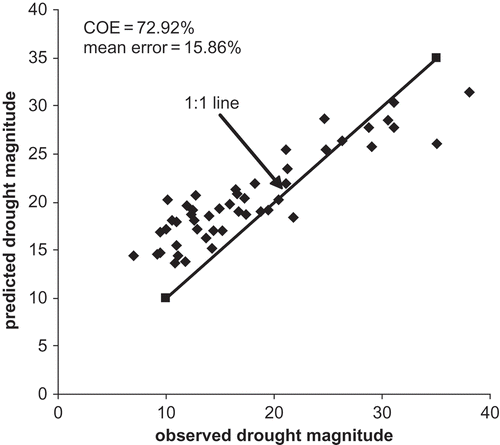The predicted values, designated as M_T–pr (column 6, Table 5), were compared with the corresponding observed values, M_T -ob (column 7, Table 5). The scatter of the points about the 1:1 line (Fig. 3) resulted in a significant overprediction (mean error ≈ 16% and COE ≈ 73%) that leaves ample scope for amelioration. A review of Fig. 3 reveals that the E(M_T ) in the lower range are being over predicted by the model, whereas in the higher range they appear to be satisfactory.

Table 5  An illustration of the table for computing observed and predicted E(M _T ) at the median level of truncation based on the truncated normal distribution of I and gamma pdf of E(L _T )

Station identifier	N	Sub-sample	e 0, q, I (eq.16)	LT -pr	MT -pr	MT -ob	LT -pr-1*	MT -pr-1**	Remark
1	2	3	4	5	6	7	8	9	10
BC08KB001	55	1951–05	−0.27,0.39, 0.71	42.86	30.43	24.66	39.13	27.78	AR-1 to be used
	30	1951–80		37.76	26.81	29.09	34.69	24.63
	27	1951–77		36.87	26.18	26.31	34.18	24.27
	28	1978–05		37.18	26.40	24.77	34.30	24.35
NF02YL001	53	1953–05	−0.32,0.37, 0.69	23.69	16.35	13.76	21.34	14.72	AR-1 to be used
	27	1953–79		21.02	14.50	9.24	18.99	13.10
	26	1980–05		20.87	14.40	11.75	18.11	12.49
	30	1953–82		21.44	14.79	9.46	11.00	7.59
ON02CF007	38	1968–05	−0.39,0.36, 0.67	35.05	23.48	21.29	35.05	23.48	AR-2 to be used
	30	1968–97		32.62	21.85	18.20	32.62	21.85
	30	1976–05		32.62	21.85	21.15	32.62	21.85
ON04JC003	36	1951–86	−0.34,0.37, 0.69	45.5	31.40	38.02	31.40	31.40	AR-2 to be used
	30	1951–80		43.90	30.29	31.12	30.295	30.29
*Predicted values of LT with AR-1 or AR-2 type model as shown in column 10.
**Predicted values of MT based on values of LT as given in column 8.

Fig. 3 Comparison of predicted and observed magnitudes (L_T , second-order Markov chain).

The higher values of E(M_T ) correspond to rivers located in northern Ontario, where flow sequences generally have memory content extending beyond the second order. Generally for other rivers the memory is confined up to the second order (Table 1). Thus the rivers can be divided into two groups, Group 1 comprising rivers with memory content up to the second order: BC08KB001 to QC02PL008 and three rivers, ON02DD013, ON02DD014, and ON02DD015, from northern Ontario (Table 1). The remaining rivers, ON02AB008, ON02BB003, ON02BF002, ON02CF007, ON02EA010 and ON04JC003 (Table 1) from northern Ontario with memory content extending beyond the second order are classified in Group 2. The E(M_T ) (= I E(L_T )) values for rivers in Group 1 were predicted by calculating L_T based on the first-order Markov chain model. For rivers in Group 2, the predicted values of E(M_T ) were computed using E(L_T ) values based on the second-order Markov chain assumption. For the first-order Markov chain model, the E(L_T ) can be computed using equation (14)(14) with q_qq  = q_q and q_qp  = q_q . The value of I remains unchanged as it is a function of e ₀ and q only. The new set of predicted values for E(L_T ) are designated as L_T -pr-1 (column 8 in Table 5) and the corresponding standardized magnitudes as M_T -pr-1 (column 9). 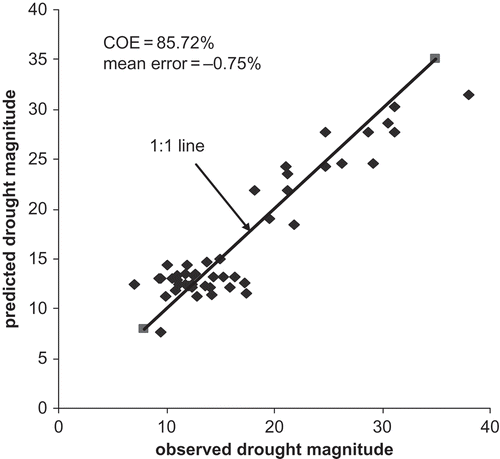The values of M_T -pr-1 were plotted (Fig. 4) against their observed counterparts (column 7 in Table 5). It is apparent from this plot that the degree of prediction has improved significantly, as is evident from the value of the COE ≈ 86% and the mean error of prediction being nearly zero (≈ –0.70%). Thus, it is reasonable to state that drought magnitudes on a weekly basis can be modelled adequately by using E(L_T ) values obtained from a mixture of the first- and second-order Markov chain models, depending upon the order of the memory content inherent in the flow sequences.

Fig. 4 Comparison of predicted and observed magnitudes (L_T , first- and second-order Markov chain).

The present study alludes to an observation that modelling drought magnitude, although more complex compared to duration, can be tracked by a mixture of Markovian models. In hydrological analysis, the mixing of Markovian models representing various states is not uncommon. For example, the Markov mixture model hypothesis was proposed by Jackson (1975) for generating synthetic streamflows with long droughts. Likewise, for modelling the differential persistence in high and low flows, a scheme of complex Markov models was successfully used by Bayazit (1982) and Bayazit & Bulu (1988).

Computation of E(L_T ) and E(M_T ) – an illustration of the proposed methodology

Consider the Torrent River (NF02YC001) with the following statistics: mean flow μ = 24.50 m³/s, ρ = 0.73, and σ = 17.15 m³/s. It is noted that the value of σ was obtained as the average value of 52 weekly values because each week in the drought sequence has a different σ and an averaged value is a suitable estimate (Sharma & Panu, 2008) for such a calculation. Based on the regional analysis of Canadian rivers, one can consider the second-order conditional probability q_qq to be 1.1 q_q , as stated earlier, and likewise, the second-order conditional probability q_qp equals q_q . One needs to estimate the drought duration (weeks) and the magnitude (m³) for a time period of 100 years (T = 5200 weeks). Analysis of weekly and monthly flow sequences of Canadian rivers shows that they exhibit mild skew and fit well to the gamma pdf. Annual flow sequences can be approximated by the normal law of probability.

For drought analysis, consider a weekly flow sequence exhibiting persistence characteristics that can be described by the second-order Markov chain. For such a weekly flow sequence, one can proceed with the gamma pdf, the value of simple drought probability, q = 0.5, and the truncation level at the median based on the long-term flow sequence. The value of e ₀ equal to –0.32 from equation (4)(4), is obtained by substituting the value of the standardized normal variate, z _g  = 0.0. At the median level in the standardized domain, therefore, the truncation level equals –0.32. Likewise, using ρ = 0.73 in equations (5)(5) and (6(6)), the values of q_q (numerical integration) and q_p are obtained as 0.76 and 0.24, respectively. As described above, the values of q_qq and q _qp can, respectively, be taken as 0.84 (10% greater than q_qq ) and 0.76 (same as q_q ). Thus, one obtains a value of E(L_T ) approximately equal to 37 weeks for T = 5200 weeks (by putting q = 0.5, q_p = 0.24, q_qq  = 0.76, and q_qq  = 0.84, into equation (14)(14)). Alternatively, one can state that a 100-year drought is expected to last for 37 weeks for the Torrent River. Likewise, by putting appropriate values into the above equations a 50-year drought is expected to last for 33 weeks.

For calculating E(M_T ), one first needs to identify the order of persistence in the drought sequences. Since the Torrent River can be adequately modelled using the AR-2 model, E(M_T ) should be computed using E(L_T ), which is based on the first-order Markov chain. Putting appropriate values into equation (14)(14), one can determine E(L_T ) = 24.57 (≈ 25 weeks). Thus, E(M_T ) ≈ 0.69 × E(L_T ) ≈ 17.0 (note that I = 0.69 is based on the normal pdf at e ₀ = –0.32). The drought magnitude, E(D_T ), or the total shortfall of water in volumetric units, i.e., σ E(M_T ) = 17.15 × 17 × (7 × 24 × 3600) m³ = 1.76 × 10⁸ m³. It is noted that since σ has the unit of m³/s, a multiplier (7 × 24 × 3600) is needed to convert a week into seconds. Likewise, using a first-order Markov chain, one obtains E(L_T ) for a 50-year drought to be ≈ 22 weeks with the corresponding E(D_T ) of 1.55 × 10⁸ m³. If the estimates of E(M_T ) are obtained based on the second-order Markov chain model, then the corresponding E(D_T ) would turn out to be 2.70 × 10⁸ and 2.40 × 10⁸ m³, respectively, for 100- and 50-year droughts. These values represent a substantial overprediction, and are too conservative for design purposes. The drought magnitude calculations for rivers in northern Ontario, such as the Shekak River (ON04JC003), shall be based on E(L_T ) using the second-order Markov chain because the memory terms for this river are represented by the ARMA(1,1) model, which is equivalent to the AR process of order greater than 2 (Box & Jenkins, 1976).

CONCLUSIONS

The analysis of drought duration and magnitude can best be accomplished using a second-order Markov chain on the weekly standardized flow sequences (e_i ) referred to as the standardized hydrological sequences (SHI). The term SHI is analogous to SPI (standardized precipitation index) commonly used in the context of meteorological droughts. A drought event is recognized when the value of the index falls below the long-term median value of the e_i sequence. Results of the present analysis indicate that weekly river flow sequences in Canada tend to fit well the gamma probability distribution function. It is noted that the e_i sequence, while displaying the characteristics of a stationary stochastic process tends to obey an AR-1, AR-2 or ARMA-1,1 process. The theorem of extremes of random numbers of random variables, which proved to be a reliable model for predicting T‐year drought parameters (E(L_T ) and E(M_T )) on an annual- and monthly-basis, is less satisfactory on a weekly basis. As an alternative, the second-order Markov chain model performed well for predicting T‐year drought durations and drought magnitudes. The model, while being simple in mathematical form, requires the information on the simple, first- and second-order conditional probabilities. The simple drought probability q, and first-order conditional probability q_q were obtained from closed-form equations using the information on cv and ρ of the weekly flow sequences. The second-order conditional probabilities, viz., q_qq and q_qp were obtained from the original flow sequences as well as the SHI (e_i ) sequences. The averaged values of the aforesaid parameters from both sequences were found to be optimal for performing reliable estimates of E(L_T ). The value of E(M_T ) was best estimated using a trivial yet simple relationship, E(M_T ) = I E(L_T ) with the value of drought intensity, I, dependent on the truncation level at the median and its corresponding probability for the normal pdf. The E(L_T ) estimates based on the first-order Markov chain in the aforesaid relationship responded better for rivers with memory content up to second order. Other rivers with higher orders of memory content tend to resonate well with the second-order Markov chain based E(L_T ) values.

Acknowledgements

The partial financial support of the Natural Sciences and Engineering Research Council of Canada for this project is gratefully acknowledged.