Flood frequency analysis using historical data: accounting for random and systematic errors

Abstract

Flood frequency analysis based on a set of systematic data and a set of historical floods is applied to several Mediterranean catchments. After identification and collection of data on historical floods, several hydraulic models were constructed to account for geomorphological changes. Recent and historical rating curves were constructed and applied to reconstruct flood discharge series, together with their uncertainty. This uncertainty stems from two types of error: (a) random errors related to the water-level readings; and (b) systematic errors related to over- or under-estimation of the rating curve. A Bayesian frequency analysis is performed to take both sources of uncertainty into account. It is shown that the uncertainty affecting discharges should be carefully evaluated and taken into account in the flood frequency analysis, as it can increase the quantiles confidence interval. The quantiles are found to be consistent with those obtained with empirical methods, for two out of four of the catchments.

Citation Neppel, L., Renard, B., Lang, M., Ayral, P.-A., Coeur, D., Gaume, E., Jacob, N., Payrastre, O., Pobanz, K. & Vinet, F. (2010) Flood frequency analysis using historical data: accounting for random and systematic errors. Hydrol. Sci. J. 55(2), 192–208.

Résumé Ce papier présente une analyse fréquentielle des crues basée sur un échantillon de crues collecté sur une période systématique et sur une période historique. Elle est appliquée sur plusieurs petits bassins versants méditerranéens. Après le recensement et la collecte des données sur les crues historiques, plusieurs modèles hydrauliques ont été construits pour prendre en compte l'évolution géomorphologique des cours d'eau. Des courbes de tarage pour les périodes récentes et historiques ont été construites et utilisées pour estimer les débits de crues avec leurs incertitudes. Ces incertitudes prennent en compte deux types d'erreurs: (a) une erreur aléatoire liée à la lecture de la hauteur d'eau, et (b) une erreur systématique liée à une sur ou sous estimation de la courbe de tarage. Un modèle bayésien d'analyse fréquentielle est développé pour prendre en compte ces deux sources d'incertitudes. Il est montré que les incertitudes affectant les débits doivent être prise en compte dans l'analyse fréquentielle des crues car elles peuvent significativement modifier les intervalles de confiance des quantiles. Les quantiles de crues obtenus semblent concordant avec les estimations de formules empiriques pour deux des quatre bassins étudiés.

Key words:

• historical flood
• Bayesian flood frequency analysis
• discharge errors
• Mediterranean catchment

Mots clefs:

• crues historiques
• analyse fréquentielle bayésienne des crues
• incertitude sur les débits
• bassin versant Méditerranéen

1 INTRODUCTION

The most widely used method for flood frequency analysis is to estimate the parameters of a probability distribution using a sample of observed flood events. As discharge time series are often short compared to the recurrence interval of the quantiles of interest, this method is highly sensitive to the sampled data. In France, for example, the longer uninterrupted discharge series provide 40–50 years of data, with only a couple of series longer than 80 years (Renard, 2006), whereas flood-risk areas are defined on the basis of a design event with a recurrence interval of at least 100 years. One way of reducing the resulting uncertainties is to extend the observation period by augmenting the systematic observations with historical flood events or palaeofloods. A number of applications, e.g. Llasat et al. (2005) in Catalonia, Naulet et al. (2005) on the Ardèche River (France), and Payrastre et al. (2005, 2006) on small watersheds in the Aude River system (France), demonstrate the improvement offered by this method compared to methods using only the systematic observation period. Brazdil et al. (2006) provide a more detailed assessment of flood risk that takes account of historical flood events in Europe.

A first difficulty with this approach lies in the estimation of empirical flood frequencies from a sample made of both systematic and censored data. Indeed, historical discharge data are not exhaustive: only events exceeding a given threshold of perception (possibly varying over time) are reported. Hirsh & Stedinger (1987) and Naulet (2002) propose ways of computing empirical flood frequencies with a mixed systematic/censored sample. A second difficulty is to quantify the discharge of historical flood events, as this information is often subject to considerable uncertainty, which must be taken into consideration in estimating flood frequency. Moreover, such an error is not limited to historical floods; it also affects more recent exceptional events for which only posterior estimates of discharge are available (Gaume et al., 2004; Sheffer et al., 2008). It can be considered that the data on historical flood events are marred by random errors related to readings of the staff gauge, and both historical and recent flood events are marred by systematic errors arising from over- or under-estimation of the rating curve.

This paper presents a frequency analysis method that takes these two sources of error into account for floods in both the historical and systematic periods. The approach presented was developed under the INONDHIS-LR project (Neppel et al., 2007), funded by the French Ministry of Ecology. The second section presents the study area and the data. The third section describes the frequency analysis models, with an application to a Mediterranean catchment. The results of the analysis are further discussed in the fourth section.

2 STUDY AREA AND DATA

2.1 Location of the study area

The INONDHIS-LR project studies 10 Mediterranean catchments: two in the Hérault River system, four in the Aude and four in the Gard watershed. This paper considers the latter catchments, particularly the catchment of the Gardon d'Anduze River at Anduze, which has an area of 540 km², making it, along with the Gardon d'Alès (320 km²), one of the main tributaries of the Gard River, which drains a total area of about 2000 km² into the Rhône River (Fig. 1).

Fig. 1 Overview of the Gard River, and the four study catchments (1 to 4).

The two main tributaries of the Gardon d'Anduze are the Gardon de Saint-Jean (154 km²) and the Gardon de Mialet (219 km²). Their catchments are bounded on the north by the crests of the Cévennes range, which can exceed 1000 m NGF (NGF = nivellement général de la France, the altitude reference system of France's National Geographical Institute, IGN) in altitude, and their outlets lie at altitudes around 100 m. Given the steep gradients of the catchments and the torrential rainfall characteristic of the Mediterranean rim in autumn, these streams are the site of devastating floods (Ayral, 2004; Marchandise, 2007).

The four catchments in the Gard system are instrumented by gauging stations belonging to the Grand Delta flood forecasting department (FFD), formerly the flood warning department (FWD), founded in 1892. The purpose of these measurements was not to compile a time series of discharge data for hydrological analysis, but to provide flood warning. Managers were therefore interested in the flood crest levels rather than in discharge per se, which explains the virtual absence of gaugings (there are only two low-flow gaugings at the Anduze station). The possibilities for gauging discharge during flood events are severely limited by the high flow velocity. This is why a majority of hydrometric stations in the Mediterranean region are not gauged beyond the 2-year flood (Lang et al., 2006). The Grand Delta FFD allowed the authors of this paper to use the topographical surveys conducted in 2003 for all catchments in the Gard River system, with longitudinal profiles and latitudinal profiles from 40 to 300 m apart.

2.2 Available historical data

The work of identifying historical information, collecting it from archives and subjecting it to critical analysis was conducted in conjunction with historians and geographers. The methods used are not described in this paper; for a description, see Cœur et al. (2002) or Naulet et al. (2005). The data relate either to flood crest levels or to the morphology of the Gardon.

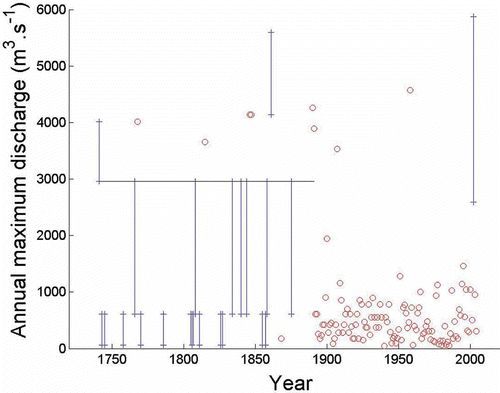
For this sector, a total of 249 useable flood crest measurements were found, the oldest dating from 1741. When their positions were given with respect to a landmark still in existence, it became possible to place them in the NGF system. Some archives provided only censored information owing to the lack of precision of observations, e.g. “the water level is above the bridge parapet”. Figure 2 lists all the flood events found for the Gardon d'Anduze; the series is incomplete for the 1741–1891 period (high water mark, threshold level not exceeded, measurement recorded as an interval) and complete since 1892. The FFD archives contributed greatly: the entire series of daily water-level measurements were found for the four catchments studied, dating back to the founding of FWD in 1892. The past positions and zero levels of the staff gauges were reconstructed, partly from correspondence between FFD engineers and the observers assigned to each sector, and partly from breaks in the time series of low-water levels.

Fig. 2 Floods on the Gardon d'Anduze River at Anduze (1741–2005). Circles correspond to events whose water level is known with high precision. Intervals represent the uncertainty due to imperfect knowledge of the water level reached during the event. The horizontal line is the perception threshold.

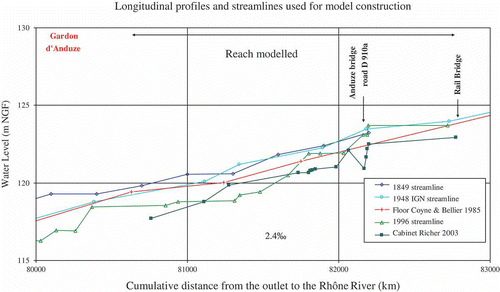
Historical information on the morphology of the Gardon stems from technical studies for hydraulic works and reports on major hydrometeorological events. The plans, consisting of longitudinal profiles and a few latitudinal profiles, show the crest levels of known major flood events. The period from 1845–1850 to the present, was marked by a deepening of the streambeds, by more than 3 m in some areas. This phenomenon, which has also been demonstrated in a nearby area through the analysis of lichens (Gob et al., 2008), results from an incision in the gravelly alluvium, and the gradual scouring out of this material once the sedimentary build-up in the channels had stopped in these catchments. As in most watercourses in the Rhône watershed, the process seems irreversible as from the 1950s. Figure 3 presents a 3‐km stretch of the Gardon d'Anduze at Anduze. Comparing the oldest useable profile, dating from 1849, to that produced in the 2003 survey, it can be seen that the river bed has sunk by approximately 2 m on the downstream side of the Anduze bridge.

Fig. 3 Longitudinal profile of the Gardon d'Anduze River at Anduze.

2.3 Example of reconstruction of flood discharges at Anduze

Estimates of flood discharge are based on hydraulic modelling of a reach of about 2 km length. The river bed was fairly stable at the downstream end between the 1849 and 1985 profiles (Fig. 3), then deepened by about 1.5 m between 1985 and 2003. We therefore use two models: a “recent” model based on the 2003 topographical surveys supplemented by Cemagref's 2006 surveys and applied to the period from 1985 onward, and an “historical” model obtained by raising the river bed floor by 1.50 m. In view of the consistency between the 1849 and 1985 profiles, the latter is considered to be representative of the streambed topography for the historical period. The historical profiles collected did not allow reconstruction of the river's topographical past with sufficient precision to refine the hydraulic models further.

Discharge estimates are based on numerical solutions of Barré de Saint Venant's free surface runoff equations (Chow, 1960), in a one-dimensional simulation using the Manning-Strickler discharge formula. The software used was RUBARBE (Paquier & Khodashenas, 2002), which divides the river's geometry into a low-flow channel and a flood plain. The software makes it possible to model a change from sub-critical flow to torrential flow.

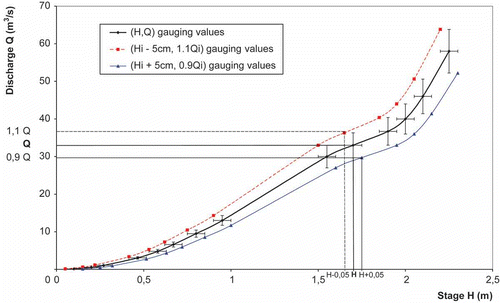
The first step in hydraulic modelling is to calibrate the model, i.e. to determine the Manning coefficients. The calibration procedure is performed in two steps (main channel/flood plain), and is described in greater detail in Renouf et al. (2005) and Lang et al. (2006). For the main channel, calibration is performed using stream gaugings. A first Manning coefficient is estimated based on the (water level, discharge) observations. An uncertainty of ±5 cm for water level and ±10% for discharge is then considered. A second calibration procedure is performed using the values (water level minus 5 cm, discharge plus 10%) and (water level plus 5 cm, discharge minus 10%). This leads to an interval for the Manning coefficient in the main channel, which corresponds to an envelope curve of the rating curve (Fig. 4). This approach is applied with the two gaugings available at Anduze, corresponding to low discharges in the main channel. The corresponding Manning's coefficient ranges from 1/30 to 1/20. In the flood plain, no measurements were available, so the Manning's coefficient is restricted to the interval 1/20–1/10, based on field observations and the configuration of the flood plain (see correspondence tables, Barnes, 1967).

Fig. 4 Envelope curves of the stage–discharge relationship.

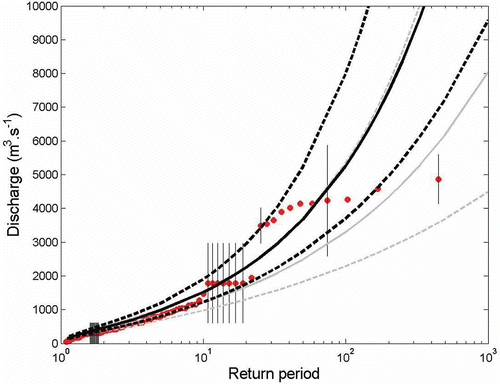
The second step is to construct rating curves in the staff gauge cross-section. For each model (historical and recent), the primary relationship between discharge and water level is determined, then a range for this relationship is derived from the uncertainty bounds on the Manning coefficient, as explained in Fig. 4. Figure 5 presents the rating curves obtained. One can see on Fig. 5 that the upper limit of the rating curve described by the rating curve error model does not correspond to the previous one by hydraulic sensitivity analysis (i.e. the envelope curve related to the sensitive analysis on Manning coefficient). The hydraulic analysis showed that if supercritical flow appears in the neighbourhood of the bridge for the three curves (upper, central and lower) for Q = 4000, 5000 and 6000 m³/s, respectively, the position of the hydraulic jump is either just in front of the flood scale (upper curve) or upstream of the flood scale (central and lower curves). The former case leads to an equivocal relationship between stage and discharge, but a large uncertainty remains on the exact location of the hydraulic jump. As such, a hypothetical upper limit yields values that are much too high in terms of specific discharge, and are considered to be overestimated. The rating curve error model was therefore calibrated without the hydraulic jump.

Fig. 5 Historical and recent rating curves.

Once the rating curves have been constructed for both recent and historical models, the sample of flood-level measurements is used to construct the sample of discharge values. Figure 2 shows the series of reconstructed discharge values from 1741 to 2005. Discharge values were estimated using the central rating curves in Fig. 5 (the uncertainty related to a possible systematic rating curve error is therefore not represented in Fig. 2). It may be observed that this data series is made of several data types:

	Point-values (circles) correspond to water-level data known with high precision. Discharge values corresponding to such data are therefore solely affected by the uncertainty stemming from rating curve errors (not represented in Fig. 2).
	Intervals correspond to water-level data known with limited precision. The information therefore consists of lower and upper bounds for the water level reached during the flood. This water-level interval can be transformed into a discharge interval using the central rating curve.
	The perception threshold (horizontal line) corresponds to the water level ensuring the exhaustiveness of historical data collection. In other words, it can be ensured that water levels did not exceed the perception threshold during years with no available information in Fig. 2 (otherwise, such an event would have been recorded in the historical archives).

The five highest flood levels recorded at Anduze are those of: 1958 (7.6 m; 4575 m³/s), 1861 which ranged between 7 m (4100 m³/s) and 8.2 m (5600 m³/s), 1890 (7.1 m; 4260 m³/s), 1846 and 1847 (7.0 m; 4135 m³/s). For the flood event of 9 September 2002, the gauge reading was initially recorded as 7.60 m in the FWD survey, but a review led to it being adjusted to, and ultimately validated at 5.60 m with hydraulic modelling, as the initial reading proved inconsistent with the high-water marks available in the vicinity. The interpretation adopted jointly with the FFD is that the reading was taken upstream of the Anduze road bridge, whereas the gauge is downstream. Given the very rough profile of the channel, the hydraulic model yields an estimate of 3500 m³/s with a very large error interval (2590–5870 m³/s). It should be noted that the value of 6180 m³/s that would have been obtained at Anduze (540 km²) at a flood crest of 7.60 m would also have been inconsistent from a hydrological standpoint when compared with the discharge estimate made by the FFD further downstream at Russans (1515 km²), which gave a range of 6000–6800 m³/s. The discharge interval used (2590–5870 m³/s) agrees with other estimates performed by DDE (2003) and the engineering firm ISL (2005), which range from 3000 to 3400 m³/s.

The flood of 9 September 2002 merits more detailed analysis, because this event caused 23 deaths and an estimated €1.2 billion in damage (Huet et al., 2003). In the upstream part of the Gardon d'Anduze catchment, this flood is not listed as a major event, while that of 1958 remains the biggest since 1741. This is consistent with the rainfall pattern that caused the 2002 flood, which was characterised by very high accumulations on the intermediate part of the catchment (Delrieu et al., 2004), in contrast to the event of 1958, when the greatest cumulative rainfall was located in the foothills of the Cévennes range, upstream from Anduze (Jacquet, 1959). On the downstream part of the catchment, the flood is noteworthy for its geographical scope and an epicentre of over 600 mm at Lédignan (Neppel et al., 2003). However, a palaeohydrological analysis by Sheffer et al. (2008) in the canyons of the Gardon shows that the 2002 flood level has been exceeded at least five times over the last 500 years, based on sediment traces and dating of organic and mineral particles.

3 FREQUENCY ANALYSIS OF FLOOD DATA

3.1 Cumulative density function of annual maximum discharge

The aim is to estimate flood quantiles from the samples collected for the recent and historical periods. This estimate needs to take account of the fact that the data are incomplete and that the discharge values are estimated using a hydraulic model and subject to considerable uncertainty.

The estimation of flood quantiles can be based on data extracted from two distinct sampling approaches. The peak-over-threshold (POT) approach uses flood peaks exceeding a predefined threshold. Since the exhaustiveness of data from the historical period is related to a perception threshold, it seems natural to use a POT approach, with a first exceedence threshold equal to the perception threshold during the historical period, and a second, lower exceedence threshold during the systematic period. An example of POT analysis of historical data can be found in the paper by Parent & Bernier (2003). Alternatively, historical data can also be included in the analysis of annual maxima (AM, see e.g. Naulet et al., 2006). The perception threshold is considered as a censoring threshold in this case. In this study, we opted for the AM approach.

The “pros” and “cons” of each approach for analysing historical data are still unclear. An obvious drawback of the AM approach would be the loss of data if two (or more) floods happened to exceed the perception threshold within the same year. However, this is unlikely to occur with high perception thresholds. In particular, this did not occur in the data set studied in this paper. A formal evaluation of the relative merits of the AM and POT approaches for analysing historical data would be of great interest; however, it is considered to lie beyond the scope of the present paper and is left for future work.

Let X_t be the random variable representing the “true” annual maximum discharge at the gauging station for year t (t = 1, …, T). Throughout this paper, variables in upper case denote random variables, while lower case is used for realizations (observations). Extreme value theory suggests using a generalized extreme value (GEV) distribution to model such data (e.g. Embrecht et al., 1997). The probability density function f (pdf) and the cumulative density function F (cdf) of a GEV (μ, λ, ξ), where μ, λ and ξ are the location, scale and shape parameters, respectively, are given by:

(1)

The case ξ = 0 corresponds to the Gumbel distribution, and is equal to the limit of equation (1)(1) when ξ → 0:

(2)

The main task of frequency analysis is to estimate the parameter vector θ = (μ, λ, ξ). A Bayesian approach is used in this paper (e.g. Gelman et al., 1995). Standard frequency analyses usually neglect the possible errors corrupting observed data. In this case, the posterior distribution p( θ │ x ) is simply obtained by combining prior information on the distribution of the parameters p(θ) and the likelihood of the observations vector x  = (x_t ) _t=1,…,n , written as p( x │θ):

(3)

where the symbol ∝ denotes proportionality. Note that we use the standard Bayesian notation p(·│·) to denote the pdf of a conditional distribution (e.g. Gelman et al., 1995).

3.2 Error model

Unfortunately, the assumption that observed runoff data are error-free is untenable in most applications involving historical data. An error model is needed that links the “true” runoff X_t (which is unknown, but whose distribution is wanted) with the “observed” runoff (derived from a hydraulic model). Further notation needs to be defined for this purpose.

Let H_t be the “true” water level reached during the highest flood of year t, and the corresponding observed level. When the historical information collected is deemed accurate enough, or for data in the systematic measurement period, the error affecting observed water level may be neglected, this leads to the assumption . However, incomplete information may lead to relaxation of this assumption, by simply assuming the true level is contained in an interval. This can be formalized as follows:

(4)

Using the above convention, the observed level is the centre of the interval of length 2l_t . Importantly, it will be assumed that the errors δ_t are independent from year to year. The rationale behind this assumption is that such errors are due to incompleteness or inconsistency of the historical information. The error made at year t should therefore not impact on the error at year t +1, since it only depends on the availability and consistency of historical information.

Runoff data are then derived by applying the rating curve obtained from the hydraulic model to the observed levels. Since several rating curves may be used, let denote the kth rating curve (k = 1, …, N_c ). The term is an approximation of the “true” rating curve ψ(h) linking the true runoff with the true water level. The following error model will be used to describe the error made during this approximation:

(5)

This multiplicative error model is justified by the common observation that absolute rating curve errors (differences between true and estimated discharges) increase with the discharge value (e.g. Reitan & Petersen-Overleir, 2009; Thyer et al., 2009). Contrary to water-level errors, the rating curve error is systematic, i.e. all runoff data included in the period of validity of the kth rating curve are affected by the same multiplicative error, γ_k. This error model is a particular case of the rating curve error model proposed by Kuczera (1996).

Combining equations (4)(4) and (5)(5) allows the relationship between true and observed runoff to be derived as follows:

(6)

The superscript (k) has been introduced to recall the rating curve used to derive the observed runoff . Since the additive water level error, δ_t, is included in the interval [–l_t , l_t ], the resulting additive runoff error, ϵ_t, is included in the interval

The error model in equation (6)(6) shows that observed runoff is affected by two different types of error: multiplicative systematic errors stemming from the estimated rating curve, and independent event-specific errors stemming from the imperfect knowledge of the water level reached during historical floods.

3.3 Parameter estimation

In order to perform the Bayesian estimation of the GEV parameters, the likelihood of the observations needs to be derived. In a first step, inverting equation (6)(6) gives the following relationship:

(7)

It is then possible to demonstrate that , the distribution of the random variable , conditional on errors γ_k and ϵ_t, is a (see Appendix 1).

The explicit treatment of errors leads to the introduction of additional unknown terms in the inference, namely vectors γ = (γ₁, …, γ_Nc) and ε = (ε ₁, …, ε _T ). The length of vector, γ, is equal to the number of rating curves, N_c , used to reconstruct past discharges, which is likely to remain relatively small. However, the length of vector ε can theoretically be equal to the total number of years included in the analysis, T. In practice, some components of ε can be fixed at zero, corresponding to flood events whose water levels are assumed to be known without any error (circles in Fig. 2).

There are two options for treating these additional unknown terms: they can be included in the list of parameters to be estimated, or alternatively, they can be integrated out from the conditional distribution, prior to the inference (e.g. Kuczera, 1992). In this paper, a mixed approach is adopted: parameter vector γ is included in the inference, but ϵ is integrated out as follows:

Application of equation (8) requires the definition of a prior probability distribution for the error term ε_t . Since ε_t is assumed to be included in the interval [a_t , b_t ], a natural choice is to use the uniform distribution on this interval. This choice is particularly interesting because it allows the integration in equation (8) to be performed analytically (see Appendix 2). Under this assumption, the distribution of an observation , conditional on errors γ_k only, is given by the following pdf:

(9)

Note that, in the particular case where ϵ _t is forced to zero (no water-level-related error), the conditional pdf is simply given by:

(10)

which appears to be the limit of the right-hand side of equation (9)(9) when a_t → b_t.

Equations (9)(9) and (10)(10) can then be used to derive the likelihood function of the whole set of observations, x . For a given rating curve (k), let S_k be the set of years included in the period of validity of the rating curve for which an observation is available (with either point or interval water-level data, corresponding to circles and intervals in Fig. 2). Let us further assume that n_k years correspond to censored data, i.e. the only available information is that the annual maximum flood did not exceed the perception threshold, u_k . Lastly, it is assumed that annual maxima are independent and identically distributed. Under these assumptions, following Reis & Stedinger (2005), the likelihood function is proportional to:

(11)

In equation (11)(11), the term is the cdf of the GEV distribution evaluated at the perception threshold, and corresponds to the contribution of a censored data (i.e. below the threshold) to the likelihood. The term corresponds to the contribution of an observation to the likelihood. It is evaluated with equation (9)(9) or (10)(10) for interval or point data, respectively.

Assuming prior independence, the posterior pdf can then be derived (up to a constant of proportionality) as follows:

(12)

In this case study, the joint prior distribution of the three GEV parameters is obtained by assuming their prior independence and by using very broad, uniform distributions for location (μ) and scale (λ) parameters. For the shape parameter, ξ, we use a Gaussian distribution centred on zero with a standard deviation of 0.3, which means that the interval [–0.6, 0.6] contains over 90% of the prior density. Such a prior distribution for the shape parameter is similar to the “geophysical prior” of Martins & Stedinger (2000). Thus:

(13)

The assumption of prior independence is mainly used here for convenience. However, since flat priors are used for the location and scale parameters in order to reflect the lack of prior knowledge on these parameters, it seems natural not to introduce any form of dependence between them. Importantly, prior independence does not imply that the parameter posterior distributions will be independent (i.e. the parameter estimates might be dependent). Moreover, methods for specifying an informative prior distribution (without necessarily using the assumption of prior independence) have been proposed (e.g. Coles & Powell, 1996; Renard et al., 2006a; Ribatet et al., 2006) and could be used within this inference framework.

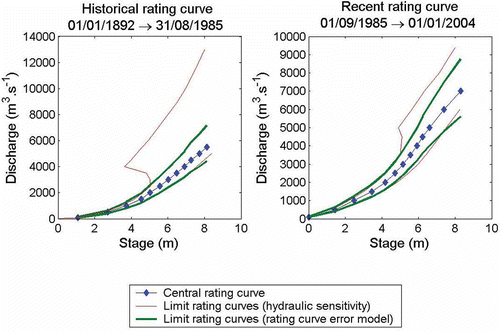
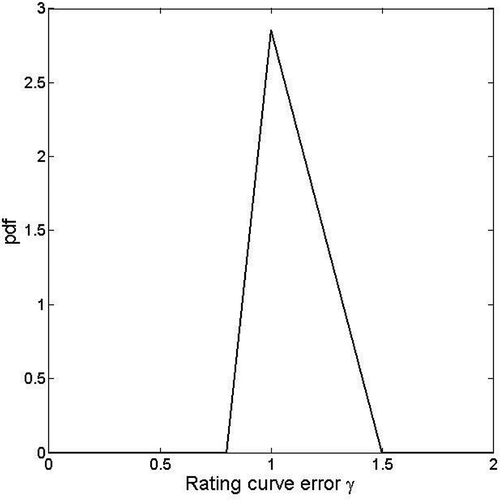
The prior distributions of rating curve error parameters, γ, remain to be specified. This can be done using the results of the hydraulic sensitivity study (Fig. 5). More accurately, a triangular prior distribution is used (Fig. 6). The mode of this distribution is obtained for γ = 1 (no error), while the base expands between values min and max. These values are determined so that the corresponding rating curves (thick lines in Fig. 4) roughly match the limits given by the hydraulic sensitivity analysis. In this case study, these values (min, max) are equal to (0.8, 1.3) for the historical rating curve and (0.8, 1.25) for the recent rating curve. Note that the choice of such a triangular distribution is somewhat arbitrary. Alternative assumptions may be used (e.g. O'Connell et al., 2002; O'Connell, 2005). However, this choice is a delicate issue, since a hydraulic sensitivity analysis does not provide the full distribution of the rating curve error. This would require a more in-depth probabilistic assessment of the propagation of errors in the hydraulic model. This is considered to lie beyond the scope of this paper and is left for future work.

Fig. 6 Illustration of a triangular prior pdf for the rating curve error parameter, γ.

Lastly, Markov chain Monte Carlo (MCMC) algorithms are applied to the posterior distribution, equation (12)(12), making it possible to estimate the parameters and derived quantities, including flood quantiles. We used the two-stage MCMC strategy proposed by Renard et al. (2006b). We refer to that paper for a detailed description of the algorithms used. The first stage of the algorithm is an adaptive Gibbs sampler (Geman & Geman, 1984), which is used to perform a preliminary exploration of the posterior distribution properties (notably in terms of posterior covariance). In a second step, a standard Metropolis sampler (Metropolis & Ulam, 1949; Metropolis et al., 1953) is used, with a Gaussian jump distribution whose covariance matrix is specified using the preliminary exploration performed at stage one. The Metropolis sampler is run during 100 000 iterations, with the first half of the iterations being considered as a burn-in period and therefore discarded. Convergence was assessed by evolving four parallel chains and verifying that the Gelman-Rubin criteria (Gelman et al., 1995) were close to one for all inferred quantities.

3.4 Results

The modelled series (Fig. 2) stems from two information sources: (a) data from the flood warning gauge at Anduze (1892–2005), and (b) data from the historical survey, covering the 1741–1891 period. The systematic period is exceptionally long at this site, lasting over 100 years. Over the historical period, the perception threshold was taken to be 2961 m³/s, corresponding to the station's alert level. It should be remembered that discharge values are reconstructed on the basis of one recent (post-1985) and one historical (pre-1985) rating curve.

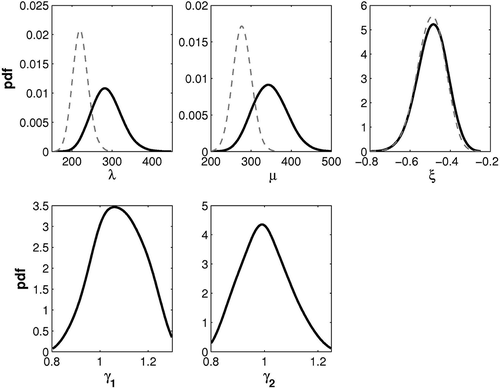
In a first step, the posterior distribution of GEV parameters obtained with the whole data set (1741–2005) was evaluated. Figure 7 compares the posterior pdfs obtained when systematic/ independent errors are accounted for (thick black lines) or ignored (thin grey lines). It shows that the location- and scale-parameter estimates are highly sensitive to the treatment of errors affecting data. Conversely, the shape parameter remains similar: this can be explained by the fact that the shape parameters of observed and true runoffs are identical (see Appendix 1) to the error model, equation (7)(7), assumed in this study. The posterior pdfs of the multiplicative error terms γ₁ and γ₂ contain the value 1: the probabilistic model identifies no systematic rating curve error.

Fig. 7 Posterior pdfs of GEV parameters λ, μ, ξ, and of rating curve error parameters γ₁ and γ₂, obtained with the whole data set (1741–2005). Thick black lines: systematic and independent errors accounted for; dashed lines: systematic and independent errors ignored.

In a second step, the impact of additional historical information was evaluated by comparing quantiles obtained using the 1892–2005 data with quantiles obtained using the whole 1741–2005 data set (Fig. 8). Note that the treatment of systematic/independent errors is identical in both cases, with all errors being accounted for. Using historical (pre-1892) data appreciably changes the estimated quantiles, owing to the presence of many events in the vicinity of 4000 m³/s. The fit with empirical frequencies is not very satisfactory, but given the shape suggested by these empirical frequencies, it seems likely that no curve would fit these points convincingly.

Fig. 8 GEV distribution of annual maxima at Anduze, with 90% posterior intervals. Thick lines: whole period (1741–2005); thin lines: systematic period (1892–2005); circles: empirical frequencies.

3.5 Sensitivity analysis

In Section 3.4, we illustrated the impact of errors affecting discharge estimates when historical information is included in the inference. In this sensitivity analysis, several quantities were fixed prior to the inference: (a) the width of the triangular prior (Fig. 6) for systematic rating curve errors; (b) the width of the discharge uncertainty intervals due to independent errors affecting water level (intervals in Fig. 2); and (c) the value of the perception threshold. A sensitivity analysis was carried out to evaluate whether modifications of these predefined quantities significantly impact the estimated quantiles.

Sensitivity to the triangular prior for rating curve errors is studied by increasing/decreasing the width of the triangle base. More precisely, the original triangle with base [a, b] is replaced by a triangle with base [a′, b′] defined by:

(14)

where z corresponds to an inflation factor: when z = 0, the interval [a, b] is unchanged; when z = 1, the width of the interval is doubled; when z = –1, the interval collapses to the single point 1. The latter case yields a Dirac prior distribution, which corresponds to ignoring the rating curve systematic error.

Sensitivity to the intervals describing independent discharge errors, ε _t , equation (6)(6), makes use of a similar inflation factor, except that the value 1 in equation (14)(14) is replaced by the centre of the interval [a, b]:

(15)

Lastly, the sensitivity to the choice of the perception threshold, u, is studied by increasing/decreasing the value of u. When u is decreased, the historical information is preserved, but its exhaustiveness occurs for a lower discharge. Therefore, in some sense, decreasing the perception threshold tests the robustness of the inference when the exhaustiveness assessment is unduly optimistic. Conversely, when u is increased, all historical floods becoming smaller than u are discarded from the analysis.

Results from the sensitivity analysis are shown in Fig. 9 and yield interesting observations:

Fig. 9 Sensitivity of 0.9- and 0.99-quantile posterior estimates. Circles: posterior medians, bars: 90% posterior intervals. (a) Sensitivity to the prior for systematic rating curve errors; (b) sensitivity to the width of intervals describing independent errors; (c) sensitivity to the perception threshold. “Recent” denotes results with data from the period 1892–2005 (with rating curve errors accounted for).

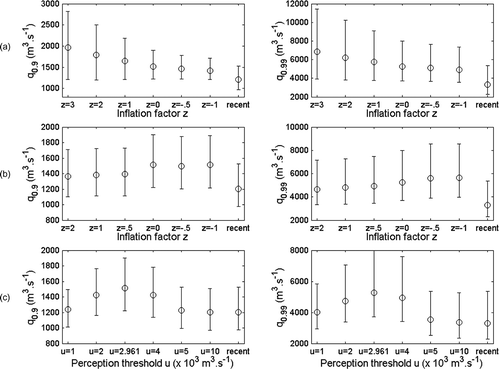
1. The prior for rating curve systematic errors exerts a significant influence on the estimated quantiles. In particular, the uncertainty strongly increases with the prior width. This demonstrates the influence of the chosen prior distributions on the estimates, and calls for further research to derive meaningful priors from the hydraulic analysis.

2. Independent discharge errors stemming from imprecise knowledge of the water levels appear to impact on the results to a lesser extent. In particular, ignoring these errors (z = –1) leaves the original estimated quantiles (z = 0) almost unchanged.

3. The choice of perception threshold also exerts a significant influence on the inference, with the estimated quantiles being affected by both increases and decreases of the threshold. As expected, the inference using historical information becomes similar to the inference for using solely the data from the recent period when the threshold reaches high levels (u = 5000 or 10 000 m³ s⁻¹).

Although interesting, these observations should not be extrapolated beyond this particular case study. In particular, the relative influence of systematic and independent errors might be case-specific. This will be established in future work.

4 DISCUSSION

The approach detailed for the Anduze catchment was also applied to the other four catchments of the Gard River described in Section 2. For all of these catchments, the following conclusions may be drawn. First, the use of historical data shows that Frechet-type distributions seem to represent flood discharge distributions better than the Gumbel distribution. For these catchments, the posterior distributions of the shape coefficient indicate that the coefficients are significantly different from zero, ranging from –0.25 at Alès to –0.5 at Anduze. The high values of the shape coefficient for the two main tributaries of the Gardon d'Anduze (Mialet and St-Jean) are consistent with the estimates at Anduze. We reached the same conclusions here as those obtained by Naulet et al. (2005) for the Ardèche River and Payrastre et al. (2005) for four catchments of the Aude River system. Thus, even when the systematic period is exceptionally long (>100 years) the distributions of discharge values are clearly modified when historical floods are taken into account. Table 1 presents the estimates of the 10-year and 100-year quantiles for the four catchments with their respective confidence intervals. It can be seen that the ratio of the 100-year quantiles for the historical period to those for the systematic period ranges from 1.1 for the Gardon de Mialet to 1.85 for the Gardon d'Anduze at Anduze. This indicates once again the importance of taking historical flood data into consideration in the predetermination of flood volumes, even when long systematic time series are available.

Table 1  The 10-year and 100-year quantiles (in m³ s⁻¹) estimated on the basis of the systematic and historical periods, and their 90% confidence intervals (in italics)

Catchment (area)	Systematic period:		Historical period:
	Q 10 ± IC 90% (m^3 s^−1)	Q 100 ± IC 90% (m^3 s^−1)	Q 10 ± IC 90% (m^3 s^−1)	Q 100 ± IC 90% (m^3 s^−1)
Anduze (540 km^2)	1070 +240/–170	2780 +1680/–800	1460 +360/–290	5130 +2650/–1540
Alès (320 km^2)	690 +370/–80	1330 +550/–530	770 +130/–120	1650 +480/–340
Mialet (219 km^2)	250 +90/–60	1170 +1110/–460	270 +80/–60	1250 +770/–420
Saint-Jean (154 km^2)	300 +80/–60	920 +680/–300	360 +100/–70	1480 +900/–480

Examination of the confidence intervals of the quantiles shows that, in contrast to what one might expect, these intervals can become wider when historical floods are taken into account compared to the systematic period alone. This result may be due to the high level of uncertainty affecting the highest historical floods and to the model used for systematic errors.

The specific 100-year flood discharge values obtained when the historical period is used range from 5 to 10 m³ s⁻¹ km⁻², a standard order of magnitude for Mediterranean catchments. More specifically, we tried to compare our estimates of 100-year flood discharge (Q ₁₀₀) with other approaches (Table 2). The empirical relationships established for the Gard region by Bressand & Golossof (1996) give:

(15)

where Q _rare and Q _exc give orders of magnitude for 100-year and 1000-year flood discharge (m³/s), respectively, for a catchment with a surface area, A (km²).

Table 2  Comparison of specific discharge estimates (m³ s⁻¹ km⁻²) for 100-year quantiles or major floods on the Gardon River

Catchment (area)	Q 100 with historical data	Q rare │ Q exc. (Bressand & Golossof, 1996)	Q max (Stanescu, 2004)	Shyreg model (Arnaud et al., 2007)
Anduze (540 km^2)	9.5	6.2 │ 10.4	7.8	3.8
Alès (320 km^2)	5.2	7.1 │ 11.8	10	5.1
Mialet (219 km^2)	5.7	7.8 │ 13.0	12.8	5.4
Saint-Jean (154 km^2)	9.6	8.5 │ 14.2	13.9	6.4

Our estimates of Q ₁₀₀ using the historical data lie in an interval of –30% to +50% with respect to Q _rare. The historical 100-year flood discharge is higher than these estimates for the Anduze and Saint-Jean du Gard catchments. In addition, except in the case of the Gardon d'Anduze, these specific 100-year discharge values are below the highest regional curves of specific discharge values Q _max from major floods in Europe, constructed by Stanescu (2004) from a database of more than 700 flood events.

The specific discharge estimate of Q ₁₀₀ issued from a regional stochastic rainfall generator mixed with a rainfall–runoff model (Arnaud et al., 2007), called the Shyreg model, presents fewer variations among the four catchments. It seems more logical as the four basins have similar climatic and morphometric characteristics. The Q ₁₀₀ estimates at Ales and Mialet are similar, as large differences between historical and Shyreg approaches are observed at St-Jean (9.6 vs 6.4) and especially at Anduze (9.5 vs 3.8). Large uncertainties in discharge estimates could explain such differences. Additional studies, based on both historical and regional approaches, are needed to better understand the advantages and limits of each kind of information.

5 CONCLUSIONS

A three-step procedure has been used to estimate discharge from major floods on the various Gardon catchments.

First, a historical survey identified and collected data on historical floods. The recent period is particularly rich in information on the studied catchments: the archives of daily discharge readings preserved by the flood forecasting department (FFD) allowed us to reconstruct the time series back to 1892, when the FFD was created. Information in the archives of the Gard region allowed us to supplement the Anduze time series with 29 un-indexed flood events that occurred between 1741 and 1891. In view of this research, we can guarantee that the sample is complete for all floods since 1741 that exceeded the 1892 alert level.

These data were then used to reconstruct flood discharge series and their uncertainty, based on a hydraulic model. Several models were constructed for each site in order to take account, to the greatest extent possible, of geomorphological changes in the river beds and changes in flood gauges during the period analysed. Recent and historical rating curves were constructed. For a given water-level reading, they output a central discharge value with an uncertainty interval that takes account of the roughness of the channel in the reach considered. When this is added to the uncertainty affecting water-level readings, the overall uncertainty for the largest floods can be very high, with the relative error of the reconstructed discharge values reaching 100% in some cases.

Lastly, a Bayesian frequency analysis was performed in order to analyse the sample of recent and historical maxima, accounting for additive and multiplicative errors affecting discharge values due respectively to random error in water-level readings and systematic rating curve error.

The use of historical flood data yielded mixed results. It lengthens the study period, but the reconstructed discharge values are, in some cases, subject to very high uncertainty, which is due, among other things, to the rating curves and also affects recent discharge values. This demonstrates the need to improve discharge measurement, notably by increasing the number of flood gauges, so as to reduce the sources of uncertainty, at least for recent discharge values. When this uncertainty affecting discharge is taken into account in the probabilistic model, the confidence intervals for quantiles are in some cases higher when historical flood data are used than when the analysis is based solely on the recent discharge series. This demonstrates the need for careful evaluation of the various sources of uncertainty in order to assess the impact of using historical flood data and for their integration in the probabilistic model. In addition, the historical quantiles have been found to be of the same order of magnitude as those obtained through regional empirical methods, for two of the four studied catchments.

Acknowledgements

The authors would like to thank the French Ministry of Ecology for supporting this research in the framework of the RDT research programme, and the two anonymous reviewers for their helpful comments.

Appendix 1

The aim is to derive the distribution of , conditionally on errors γ_k and ε_t . For this purpose, we write the cdf of at a given value x as:

(A1)

Since X_t ∼ , equation (A1)(A1) yields:

(A2)

The latter expression is equal to the cdf of a evaluated at x.

Appendix 2

The aim is to perform the following integration:

(A3)

Assuming p(ε _t ) is a uniform distribution on [a_t , b_t ] yields:

(A4)

Using the substitution :

(A5)