Reply to the Discussion of “Assessment and review of the hydraulics of storage flood routing 70 years after the presentation of the Muskingum method” by M. Perumal

The Discussion of M. Perumal (2010) is welcome, for it gives the opportunity to further analyse various, truly or apparently, controversial aspects of the Muskingum method, and also to rectify certain related misconceptions.

1. ON THE DISCUSSER'S INTRODUCTORY REMARKS

Perumal (2010) (henceforth, also the Discusser) criticizes the author, in essence, for not having presented the Discusser's work adequately in the (already 19-pages long) review (Koussis, 2009). This could be, perhaps, partly true because one has to be selective in the choice of references, noting that apparently some findings have been made, seemingly independently, by various authors. Therefore, giving appropriate credits to the earliest sources is difficult. However, it will be demonstrated that the Discusser fails to give credit to the work of others). Frankly however, given the volume of publications on the topic of the Muskingum and related methods, I am surprised that other hydrologists, who have contributed in this field, have not voiced more similar critique.

Then, Perumal claims to be the first to have brought out the interpretation of the Muskingum method according to Apollov et al. (1969) ¹ I respond to this claim in detail in Section 3 herein, yet, what matters is the original work of Apollov et al. itself; hence my reference that “Apollov et al. (1969) give an elegant derivation of equation (31), already presented in 1960.”

2. ON “TRADITIONAL PRESENTATION OF THE MUSKINGUM STORAGE EQUATION”

When the Discusser criticizes the traditional presentation of the Muskingum storage equation, he is “forcing open doors”. I thought that it was clear that I did not advocate the traditional way of presenting the Muskingum method. I referred to it for the sake of completeness and as a preparation for a more rational, hydraulics-based derivation, after discussing certain of its weaknesses. Curiously, Perumal admits that much when he writes: “The only way to overcome this paradoxical illusion is to develop the linear form of the Muskingum storage equation using hydrodynamic principles based on the extension of the Kalinin-Miljukov (K-M) theory (Apollov et al., 1964) as illustrated by the author in his paper and this writer (Perumal, 1992b),” yet portrays the author's position as supporting the traditional presentation. This is exactly contrary to what is written in the review paper, Section 2, The Muskingum Method and its Traditional Presentations:

The above approaches can be criticised in that their assumptions are not as intuitive as the textbooks imply. For example, ad hoc splitting of storage into prism and wedge storage and relating it to different flows cannot be justified on the grounds of physics. On the other hand, the application of the linear Muskingum model has been proven widely successful. This fact may not be attributed to chance. On the contrary, we must conclude that the linear storage–discharge relationship has at least an approximate basis in the hydraulics. Hence, a derivation consistent with wave motion must be possible, with justified assumptions, e.g. as in the derivation of the Kalinin & Miljukov (1958) routing method, which is firmly grounded on hydraulics.

Perumal characterizes the traditional approach presented by Chow as having “logical flaws.” This assessment is, in my opinion, unnecessarily harsh, for its logic does not suffer, but the assumptions necessary for arriving at the linear form of the Muskingum storage equation (7)(R7) (a linear discharge–depth relation at the in- and outflow sections and the splitting of the total storage in the reach to prism and wedge storage) are not really understandable without a direct link to the linearized wave-mechanistic description of a hydraulically consistent derivation, such as that of the approaches of Kalinin-Miljukov and of the author.

In the same section, Perumal states that his flood routing work has proven that the linear Muskingum storage equation is superior to nonlinear ones such as, e.g. equations (8)(R8) and (12) listed in Koussis (2009). The experience at Monash University is that equation (12) fits well the, generally, nonlinear catchment response; therefore, the RORB watershed model of Monash University incorporates that equation. Tung (1986) also demonstrates the appropriateness of equation (12). My own experience is that consideration of nonlinearity in river routing benefits accuracy (see the example in Koussis, 1980). Euler & Koussis (1973) and Price (1973) were probably the first to use storage routing schemes with discharge-dependent coefficients, but not the only ones (see Koussis, 2009, Section 5):

Of course, the enhanced performance of nonlinear storage routing has attracted the interest of hydrologists for some time (e.g. Koussis, 1975, 1978; Miller & Cunge, 1975; Ponce & Yevjevich, 1978; Chang et al., 1983; Koussis & Osborne, 1986; Cappelaere, 1997; Tang et al., 1999). This is also demonstrated in comparisons of storage routing results with solutions of the complete equations (e.g. Koussis, 1975; Miller & Cunge, 1975; Weinmann, 1977; Weinmann & Laurenson, 1979; Todini, 2007).

An advantage of nonlinear Muskingum-type routing schemes lies in their ability to reproduce well the steep rise of the flood wave that linear models fail to do (Koussis, 1980). Their disadvantage lies in the small mass balance error that they suffer. These positive and negative features are stated in the paper as follows:

However, ad hoc devised nonlinear versions of schemes derived from linear storage routing models inevitably suffer mass balance errors (Ponce & Yevjevich, 1978; Koussis, 1980; Cappelaere, 1997), despite their better shape response. Equation (18) with constant C and θ conserves mass because it is consistent with the linear equations (6) and (7)(R7) from which it is derived. In contrast, versions of equation (18) in which the parameters are simply re-interpreted as discharge-dependent, or as time-dependent, fail to conserve mass because they are not compatible with equations (6) and (7)(R7).

Weinmann's (1977) routing example – shown in Fig. 1 herein and also reported by Weinmann & Laurenson (1979) – further demonstrates the aforementioned contrast in the behaviour of linear and nonlinear routing models and lends support to the use of (mainly) a flow-dependent kinematic wave celerity. Weinmann considered a rapidly rising flood wave (rate of rise of the inflow wave ∼1 m/h) in a trapezoidal prismatic channel, with a fairly mild slope S_o  = 2 × 10^‐4 and Manning's n = 0.04; the cross-section has a base width b = 50 m and side slopes 1 V:1.5 H. The slope ratio (Koussis & Chang, 1982) SR = −(∂y/∂x)/S_o  ≈ (∂y/∂t)/cS_o is ∼1. The inflow hydrograph was of the form of Q(t) = Q_b  + (Q_p  – Q_b ) (t/t_p )^β exp[β(1 – t/t_p )], with Q_b  = 100 m³/s, Q_p  = 1000 m³/s, t_p  = 10 h and β = 6.67. Routing was carried out for 40 km using the St Venant equations, a model referred to as the generalized kinematic wave model (a Muskingum-Cunge linear routing model with the refined exponential scheme, which in this particular case, θ = 0, reduces to the Kalinin-Miljukov model) and the diffusive-wave equivalent model developed by Koussis (1975) (referred to as Kinematic Model Corrected for Dynamic Effects – KCD). The latter is the nonlinear kinematic wave model corrected for wave diffusion (by matching the routing scheme's numerical to the physical diffusion coefficient) outlined in the review article: (i) stage–discharge conversions are based on the flow rating formula of Jones; and (ii) the kinematic wave celerity c(Q) is computed via the Jones formula.

Fig. 1 Comparison of routing solutions of the St Venant equations and of two diffusive-wave equivalent models, for a rapidly rising wave through a prismatic channel of trapezoidal cross-section (from Weinmann, 1977).

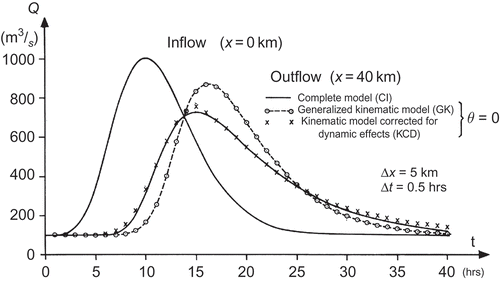
Based on this simulation, a realistic, yet still conservative limit for the application of the method outlined above and in the review paper appears to be SR = –(∂y/∂x)/S_o  ≈ (∂y/∂t)/cS_o  ≤ 0.5, at least.

3. ON “MATCHED DIFFUSIVITY THEORY”

The Discusser writes: “Based on the K-M extension theory (Apollov et al., 1964), it is now clear that McCarthy's (1938) Muskingum method has the inherent capability to attenuate the inflow hydrograph and there is no necessity to invoke the matched diffusivity concept to link the Muskingum parameters to channel and flow characteristics.”

Here, again, the Discusser is “forcing open doors.” Of course, the Muskingum and similar methods, such as the method of Kalinin-Miljukov, are inherently capable of wave diffusion and, hence, attenuation; this capability derives from their spatially lumped nature. By solving (for a convenient analytical inflow function) the ordinary differential equation resulting from the elimination of storage between equations (6) and (7)(R7), or by convolving equation (35) with the inflow, one can readily show that the resulting outflow has a lower peak value, is broader and its centre of gravity is delayed; also, mass (volume) is conserved. Moreover, Apollov et al. (1969) have shown, and the review paper drew attention to it, that the weighting coefficient θ can be linked directly to the channel morphology in this manner. But the review paper also states:

Viewed from Cunge's perspective, it is the second-order truncation error of the particular discrete representation of the kinematic wave equation that endows the Muskingum flood routing scheme with the ability to account for wave attenuation and diffusion. From the perspective of Koussis, the Muskingum method's hydraulic diffusion property is inherent to the Muskingum equations themselves: through the spatial lumping, the discharge is defined only at the end-sections of the reach, not continuously, while the uneven (θ ≠ 0.5, see equation (23)) splitting of a point-discharge between two cross-sections allows flexible control of the diffusion. In either case, equation (23) provides the value of θ that yields physically proper results in the sense of the CDE, equation (3)(R3), and is used in Muskingum-Cunge routing.

Perhaps Perumal simply misinterpreted this specific part of my review; however his next criticism is entirely unjustified.

The Discusser writes:

One may also question the logic of the matched diffusivity theory from the consideration that if one uses the matching of the numerical CDE, arrived as an approximation of the kinematic wave equation, with that of the physical CDE of Hayami's equation (Hayami, 1951), then it is expected that matching should be applicable in all ranges of the applicability of the physical CDE. But in the reality, it is well known that this matching is applicable only in a small range of applicability of the physical CDE. Therefore, the inadequacy of the matched diffusivity theory to interpret the Muskingum method is obvious.

The expectation of Perumal that the CDE, equation (21), derived from discretizing the kinematic wave equation and subsequent diffusion matching should ensure complete equivalence to the physical CDE, equation (3),(R3) without the lateral flow term, is incorrect (also incorrect is that the matching range is small). The reason for this is given in the review paper's Section 3.2, Estimation of θ in the Muskingum-Cunge CDE-equivalent model, as follows:

A point that has not been raised in the literature is that equation (21) is not a true CDE-equivalent. It is an upstream-controlled, single-reach CDE. Contrary to the physical CDE, equation (21) cannot accommodate a downstream boundary condition (neither can the Muskingum method). This inability is due to the numerical CDE's derivation from the first-order kinematic wave equation or the zero- and first-order Muskingum equations, which are incompatible with downstream control.

Thus, one reason has to do with the downstream boundary condition. The second is numerical and has to do with two things: (a) the remainder of equation (21), and (b) the fundamental flow status that underpins the development of the Muskingum routing scheme. The physical CDE obviously does not have a remainder, therefore equations (3)(R3) and (21) cannot be entirely equivalent. The leading term of the remainder of equation (21) is the third-order derivative that gives rise to the unphysical oscillations, which are absent from the response of the diffusive wave model (see, e.g. equation (34) in Dooge, (1973), and the solution of Szymkiewicz, (2002), in the review paper). The fundamental flow status underpinning the development of the Muskingum routing scheme is dominance of the kinematic wave mode over wave diffusion; the condition on the grid Peclet number P = <c_k>Δx/D ≥ 2 reflects this dominance and restricts the weighting coefficient to positive values, θ ≥ 0 (up to ½ or 1, depending on the traditional or the exponential scheme, respectively, for P → ∞).

Perumal's statement “It is this writer's hunch that Cunge (1969) had openly discredited the McCarthy's Muskingum storage theory, by equating the reach storage to sum of prism and wedge storages, based on Chow's (1959) representation of the storage equation” is, at the very least, a poor choice of words. Obviously, I am not entitled to speak for the hydrological community, nor can I speak for Jean Cunge. Nevertheless, I consider that the matched artificial diffusion method neither discredits the very respected Muskingum storage concept of McCarthy nor deprives its inventor of the credit due to him. The diffusion matching simply provides a sound wave-mechanics framework for additionally interpreting storage routing and also a convenient means to estimate θ, but not the only one, as pointed out in the review paper (p. 51): “We have shown, following four different avenues, that the Muskingum method's weighting coefficient θ can be estimated from equation (24) (equation (31)).”

This Reply gives the opportunity to present yet another variation on the theme of the derivation of the weighting coefficient θ, starting from the Muskingum method's equations (6) and (7)(R7) of the review article, which are restated here as equations (R1)(R1) and (R2)(R2) for convenience:

(R1)

(R2)

Upon elimination of the storage between equations (R1)(R1) and (R2)(R2), we obtain the ordinary differential equation:

(R3)

written in this particular form to facilitate solving for the weighting coefficient:

(R4)

We then develop the outflow and all derivatives in Taylor series to second order about the inflow section, at the space coordinate x, for the time t. The notation used is q _in(t) = q(x; t) and q _out(t) = q(x + Δx; t) = q(x;t)  + (∂q/∂x)Δx + (∂² q/∂x ²)Δx ²/2 + R(Δx ³), where R is the remainder of the series with the leading term containing ∂³ q/∂x ³, which is henceforth omitted from the equations. Thus, we obtain for the first term in the numerator of equation (R4)(R4), q _in – q _out = −(∂q/∂x)Δx − (∂² q/∂x ²) Δx ²/2. For the first spatial derivative in this last expression, we use the linear diffusion-wave equation (CDE in the review paper), which we restate here for convenience:

(R5)

(R5a)

so that the difference between inflow and outflow becomes:

Because the relationship for the weighting coefficient, equation (R4)(R4), contains also temporal derivatives, we convert the second spatial derivatives to second temporal derivatives through the use of the kinematic wave equation. The latter is equation (R5)(R5) with the right-hand side set equal to zero:

(R7)

It can be verified that the approximate conversion mentioned above yields and . With these conversion relations for the second derivatives, we can restate equation (R6) as follows:

(R8)

Proceeding similarly, and also recalling that Δx/c_k  = K, we can write the following expression for the last term in the numerator of equation (R4)(R4):

(R9)

Entering equations (R8)(R8) and (R9)(R9) into the numerator of equation (R4)(R4) cancels the first derivative term and leaves as result simply . The denominator of equation (R4)(R4) contains flow derivatives; therefore, keeping only terms up to second order (derivatives), yields Kd(q _in  – q _out)/dt = (Δx/c_k ) ∂/∂t[q – q – (∂q/∂x) Δx]  =  (Δx/c_k )² ∂ ² q/∂t ².

Finally, substituting the two last derived expressions into equation (R4)(R4) gives the well-known relationship for the weighting factor (equation (23) in the review article):

(R10)

Also this derivation shows that it is possible to estimate the weighting coefficient θ without resorting to the matching of numerical (artificial) and physical diffusion, yet it requires additional considerations to demarcate the Muskingum method's range of validity. In the matched artificial diffusion method, it is obvious that the routing scheme's range of validity must be limited, because it derives from the discretization of the kinematic wave equation, which is a truncated convection–diffusion wave equation. This fact leads naturally to the conclusion that, for this truncation to be tolerable, the flow must be quasi-kinematic, a condition requiring that the second term on the right-hand side of equation (R10)(R10) be small (hence the lower limit of P = c_k Δx/D = 2). This restriction holds also for the derivation just presented, although its necessity is somewhat hidden, becoming apparent only in the conversion of the second derivatives. Furthermore, we note that a similar argumentation must be applied in the case of the Kalinin-Miljukov method as well, which assumes that the elemental waves travel from the inflow section to its midpoint without attenuation, which tacitly assumes quasi-kinematic flow. Of course, the same holds for the extension of the Kalinin-Miljukov derivation to the Muskingum method of Apollov et al. (1969). Such limitation, however, which derives from the omission of diffusion, is not mentioned in the literature. The omission of diffusion in the Kalinin-Miljukov method's requisite conversion of a temporal relationship at a cross-section to a spatial relationship at a fixed time was pointed out in the review paper (middle of second paragraph of that section) as follows: “Then, ignoring attenuation, it holds that that depth passed ΔT time units earlier through a section at a distance <c_k > ΔT.”

The following brief exposition continues the analysis of Kalinin-Miljukov and highlights the elegance of the derivation by Apollov et al. (1969) of the Muskingum method's weighting coefficient, with reference to Figure 5(b) of the review paper and minor explanatory additions of mine placed inside backslashes, / … /.

Assuming a linear variation of the discharge and of the depth over a reach of prismatic /strictly, rectangular/ cross-sections of length L > L _KM = unit reach length of the Kalinin-Miljukov method, it follows that the flow area A_m at the midpoint of that reach, L/2, uniquely determines the water storage in that reach: S = L A_m . According to the analysis of Kalinin & Miljukov (1958), also the flow rate at the end of L _KM – denoted here by q* – is related to the depth and area at the midpoint of the reach. The storage in L is thus S(q*), and by linking q* to the in- and outflow of the reach L we can obtain a relationship of the Muskingum-type. Linear interpolation on the flows yields: q* = q _out + (q _in – q _out)[(0.5L – L _KM)/L], /and, since the depth is also assumed to vary linearly over L , there exists a linear flow–area relationship, so that their ratio <c_k > = q*/A_m is the constant wave celerity, which is related to the average wave travel time K = L/<c_k >. \Therefore, S = L_M A_m  = L q*/<c_k > = K q* = K{q _out + (q _in  – q _out) [(0.5L – L _KM)/L]}. Then, by defining the Muskingum method's weighting coefficient as θ = (0.5L – L _KM)/L, we gain the storage equation (7)(R7) of the review paper S = K[θq _in + (1 – θ)q _out], with θ given by equation (24) or equation (31). Apollov et al. (1969) also point out the flow-dependence of θ.

With this elegant derivation of Apollov et al. as backdrop, the approach outlined by Perumal in his Discussion appears immediately as essentially the same. The only difference lies in that the, at first unspecified, cross-section and the length identified as KM by Perumal are the end-section and length of the unit reach, respectively, as the result for θ reveals (setting θ = 0 yields L _KM). But the original derivation rests on the intuitive hydraulic concepts of the Kalinin-Miljukov method and stands in stark contrast to the lengthy mathematical manipulations detailed in Perumal (1994a).

Now, I would like to return to the issue of not adequately referencing the Discusser's work and to consider specifically his 1989 publication entitled Unification of Muskingum difference schemes, which compares an exponential, or refined routing scheme that I have studied to the classical, fractional Muskingum routing scheme.

Perumal claims that both schemes are in fact identical. To prove this, he restates the coefficients of the traditional (fractional) and the refined (exponential) routing schemes, equations (18)–(20) and (37) in the review paper (or, Perumal's equations (D5)–(D7) and (D1)–(D4)), respectively, in terms of the Courant and Peclet (or Reynolds) numbers and shows that they yield identical equations. Thus, thinks Perumal, the two schemes are one and the same, and, therefore, the work of Koussis (1980) is incorrect. Before presenting substantive counter-arguments, first an objection on formal grounds: If the two schemes were identical, how does Perumal conclude (contradicting himself) that the traditional scheme scores better than the refined one in a comparative example?

The rebuttal in substantive terms is as follows. Perumal's algebra is correct and his argument would be valid if the true, field-value of the hydraulic diffusion coefficient D would be given by equation (5)(R5) of the review paper (or by Perumal's equation (D10)), repeated here (ignoring the Froude-number term), to facilitate the discussion:

(R11)

However, the question changes in cases in which measured hydrographs are available; important then is the behaviour of the two schemes and their optimal parameters. The line of argument of Perumal misses the cardinal point that the two schemes are numerically different, so that, when the value of the weighting coefficient is not given theoretically, they give different results and will have a generally (slightly) different behaviour. We will return to this point, after considering the particular case of θ = 0.

To further clarify the point above, let us consider an actual reservoir, whence θ = 0 for both the fractional and the exponential scheme; further, to keep the problem as simple as possible, we also linearize the storage–outflow curve. If we now use these two schemes to route an inflow wave through the reservoir, we obtain two (slightly) different outflow hydrographs. We may also contrive a still simpler problem: the linear reservoir has been receiving a constant inflow over an extended period – whence the outflow equals the constant inflow – until the inflow is suddenly terminated. As stated in Chang et al. (1984), calculating the emptying of the reservoir by the two schemes reveals that only the refined scheme matches the exact, analytical solution.

Next, we examine a problem in which measured inflow and outflow hydrographs for a certain river reach are available and we seek the best constant parameters K and θ, e.g. by minimizing the sum of the squared deviations computed from measured outflow values. This case is different from the previous one. An optimization procedure, involving routing with both schemes, will yield different θ values for the two schemes, owing to their different makeup (in the case of the refined scheme, the θ value will also depend on the Courant number; note also that θ can take on values greater than 1/2, up, but not equal to 1, without causing instability). This is exactly where Perumal went wrong in comparing the two schemes shown in Table 1 of Perumal (1989), and, of course, his conclusions are wrong as well. It is surprising that Perumal repeated the same mistake, after Chang et al. (1984) pointed it out in their response to the discussion by Perumal & Seth (1984). But even if a unique θ value were estimated following the traditional storage-weighted flow loop-minimization method, the routing results would differ, due to the different make-up of the schemes. Ferrick et al. (1984) and Bowen et al. (1989) give details on the exponential scheme.

I do not advocate the exponential scheme as necessarily the one of choice, although it derives from a good discretization of the analytical solution, which is superior to a simple discretization of the differential equation (Seus & Rösl, 1972, p. 43), mainly due to its more complex structure that makes grid design more difficult. Nash (1959), however, suggests that it allows using longer time steps than the fractional scheme. In addition, its upper stability limit is θ = 1, C = 1 for kinematic wave behaviour (conditionally stable in 0.5 ≤ θ ≤ 1), in agreement with the model's SRF (Koussis, 1983), while the traditional, fractional scheme is stable for θ ≤ 0.5.

In two different places in the review paper, I have drawn attention to the need not to lose sight of the actual physical system, implying that a model is just a simplified replica of a complex reality. The end of Section 2 reads:

Although the implied “small variation” about an initial flow is not plausible for floods, it is useful in developing a rational framework for the approximate solution of the flood propagation problem.

In the last paragraph of Section 3, I unequivocally caution, regarding the theoretical estimation of the weighting coefficient θ by equation (24) or equation (31):

In using this estimator, we must keep in mind the simplifications made in its derivation, and the same holds for K and τ. Judgement is required because the assumptions are drastic: prismatic channel unaffected by erosion and sediment deposition, linearisation (small flow variation) and straight-line flow profiles in the reach.

A personal remark is in order here. When I saw Perumal's 1989 paper, I decided not to comment on that work, as he and I had already discussed these matters on the occasion of the paper of Chang et al. (1983). Surprisingly, Perumal (1989) referenced his discussion to Chang et al., but not the response of its authors. This time however, I felt differently because of Perumal's insistence that I reference his work, and because it should be made clear that repeating a wrong argument does not make it right; this statement applies directly to the point of contention in Section 4 herein.

It can be demonstrated that Perumal (2010) is selective in giving credit to the work of others. This started with the extension of the method of Kalinin-Miljukov by Apollov et al. (1969). Figure 1 in Perumal (1994a,b) is shown without reference to Apollov et al., yet follows directly from the passage therein, p. 73, that I translate here:

In a prismatic streambed and for a linear variation of the water stage along the stream, the amount of water (W) in the reach of length l ₁ is functionally related linearly to the average stage (H) in this reach. Under the considered conditions, this water stage (H) is located in the middle of the reach (l ₁/2) and is uniquely related to the flow rate Q_l crossing the monitoring station that is located at a distance l downstream of the monitoring station, the stage of which is the average stage H. It therefore holds that H = f(Q_l ), or W = ϕ(Q_l ).

Figure 5(b) in the review paper is the sketch the writer made during his doctoral research (early 1970s) in his copy of Apollov et al. (1969). Perumal simply reversed the derivation of Apollov et al., posing the problem as locating the weighted-discharge section, and did not cite the preceding relevant derivation in Wong's dissertation (1984) (Chapter 2) and Figure 2.3 therein. The following are additional examples of the same attitude.

Perumal (1994b) presented the transformed Jones formula (equation (34) in the review) used in the routing method developed by Koussis (1975) in his dissertation, without referring to the latter (the method has been outlined in the review and is sketched out, with an example, in Section 2 herein). Generally, Perumal mentions only Weinmann (1977), who detailed the method of Koussis, including the programme's flow chart, and Weinmann & Laurenson (1979), who summarized it. But also in his 1989 note Perumal failed to give credit to Kundzewicz (1984), who, in his Comment on Chang et al. (1983), established the link between the fractional and the exponential schemes via the Padé approximation, although Perumal & Seth (1984) wrote a comment on that article. Finally, Perumal & Sahoo (2007) should have presented their – otherwise useful – findings on the variable parameter Muskingum routing method, after giving credit also to Koussis (1975, 1976) and to Weinmann (1977), which they failed to do.

4. ON THE NEGATIVE VALUE OF θ

Perumal argues against my position that negative θ values are not reasonable, characterizing the reason given – namely, that storage cannot decline while the inflow rises – as a pretext. As proof of the opposite, he mentions that the system response function of the Muskingum model, equation (35), ensures a positive outflow for a negative θ value. First of all, this statement is completely irrelevant to the question posed; the discussion is not about the negative outflows (see below). In contrast, the argument that storage cannot decline while the inflow rises is entirely logical; it is grounded in physics. (Dooge, 1973, and Wong, 1984, explain how θ < 0 can be interpreted in the use of the model.) Perumal's reference to Szilagyi's (1992) work displays exactly this misconception. Szilagyi comments on a case where the outflow peaks before the inflow and outflow hydrographs intersect, characterizing this situation as physically unrealistic and attributing such apparent field occurrences to measurement errors. He concludes that, in such cases, the optimum value of the weighting parameter becomes negative because of inadequacies of the techniques applied for measuring water stages or/and calculating corresponding discharges. In other words, unlike Perumal, Szilagyi is aware that such flow behaviour is physically impossible. In this context, it is worth pointing out that the observed occurrence reported by Szilagyi could be also attributed, in principle, to unmonitored lateral surface- and groundwater inflows; in that case, the model behaviour could be brought in to compliance with physics by including a lateral flow term.

5. ON THE INITIAL DIP

Perumal claims to have, finally, discovered the cause of the formation of initial dip in the Muskingum solution in the use of “a long reach as a single reach of the Muskingum method.” Perumal has made this discovery “using the interpretation of the Muskingum method based on the extension of the K-M theory (Apollov et al., 1964)” and “Based on the direct derivation of the Muskingum method from the St Venant equations, . . . ”. Perumal errs in this case as well. Negative outflow values result as soon as the reach length exceeds the unit reach length of the Kalinin-Miljukov method, or, for even the slightest positive value of θ, as the Muskingum model's SRF, equation (35), shows. It is indeed surprising that Perumal did not recognise θ > 0 as the cause for the unphysical oscillations from his own simulations; in Perumal (1994b) the dip and the oscillations are prominent in the single-reach solution (θ large) and tend to diminish as the spatial resolution increases. This initial dip is inherent in the Muskingum model's system response function, equation (35); it is caused by the presence of the last term on the right-hand side that contains the Dirac pulse. We must therefore conclude that, if we insist on eliminating the train of unphysical oscillations generated by the initial dip and do not accept masking the problem by “skipping” over the region of negative outflows, which usually causes a small mass balance inconsistency, then we have two options: (i) to use a series of reservoirs, as does the Kalinin-Miljukov method, or (ii) to choose the alternative, mathematically correct diffusive wave solution of Szymkiewicz (2002). Of course, in the second case one loses the convenience of the recursive solution of Muskingum-type or storage routing schemes.

6. ON THE RATING CURVE FOR UNSTEADY OPEN-CHANNEL FLOW

The review paper mentions only the, so-called, Jones formula as a practically useful and convenient approximation of the linear 1-D momentum equation (written as a flow formula, via the equations of Manning, Chezy, or Darcy-Weisbach) for linking discharge and stage at a section. The writer is aware of attempts to improve the Jones formula, among which are also the proposals of Perumal & Ranga-Raju (1999) and Perumal et al. (2004). The recent study of Dottori et al. (2009), on estimating discharge in unsteady flow from stage observations, has shown that formulas that also involve a second temporal derivative of the stage, such as the one proposed by the Discusser, are prone to numerical oscillations.

The author (Koussis, 2010) points out that Henderson (1963, 1966) improved the not strictly correct basis of the Jones formula, while maintaining that formula's basic practical format (the shortcoming of the Jones formula derive from its use of the kinematic wave approximation in converting the spatial to the temporal depth derivative, thus ignoring attenuation of the wave). Henderson corrected the rating formula of Jones for wave subsidence (in the wave crest region) by adding the small fixed term 2r ^‐2/3, i.e. Q/Q_o  = [1 + ∂y/∂t/(<c>S_o ) + 2r ^‐2/3]^1/2, where r is the ratio of the bed slope to the “wave slope” S_w  = 2y _crest/L, with L the wave length, r = S_o /S_w  = S_o /(2y _crest/L). A judicious estimation of S_w is neither difficult (e.g. L can be estimated as <c_k > × (time of wave rise)) nor has strong implications, since typically r > 10 and thus 2r ^‐2/3 is small. Indeed, Henderson (1966) had already derived a formula with the second temporal derivative of stage (equation (9-57), p. 379), also including approximations for the inertial terms at Froude numbers less than ∼0.7 (equations (9-64) and (9-65), p. 381), but insisted on applying the fixed-term correction only to the crest region (see equations (9-92) and (9-94), p. 393). Henderson was careful not to adopt generally the form with the second derivative, despite considering prismatic channels. It must be mentioned that the seeds of Henderson's analysis are present in the text of Forchheimer (1930), which became known to English-speakers probably through Gilcrest's (1967) article.

I contend that the Jones formula, with Henderson's correction, can infer transient flow in open channels with good accuracy from at-a-section stage observations, when the kinematic wave celerity is computed on the looped rating curve. Computing the kinematic wave celerity based on the rating relationship for uniform (or steady) flow, c_k (Q _o) = dQ_o /dA| _x=const., gives good results as long as the flow conditions are quasi-kinematic. But when the flow departs markedly from the KW status, the Jones formula should be evaluated with c_k (Q) computed on the looped rating curve. An indication of the correctness of computing the kinematic wave celerity on the loop-shaped rating curve is that c_k (Q _max) = 0: the maximum discharge does not propagate downstream! However, care must be exercised in the iterative calculation of c_k , to ensure convergence (Koussis, 1975; Weinmann, 1977; Weinmann & Laurenson, 1979; Ferrick et al., 1984; Perkins & Koussis, 1996).

It is also useful to add a note regarding the Calculation of depths (Section 4.1 in the review paper). As an alternative to computing depth (or stage) hydrographs at the inflow and outflow sections, one can determine the mean depth in the reach by recalling that the Muskingum storage equation S = K [θq _in + (1 – θ)q _out], is equivalent to the geometric storage equation S = L <A> ( equation (13) in the review), as the representative cross-sectional area <A> is related to the weighted discharge <q> = θq _in + (1 – θ)q _out at steady flow (Wong, 1984). This procedure avoids working with the Jones formula and corresponds roughly to computing the depth in the reach's mid-section in a staggered grid, as suggested by Cunge (1969). However, iterations cannot be avoided, as flow formulas are implicit in y even for steady-state conditions:

where F is the Froude number, F = q ²/gA ³. Equation (R12) can be readily evaluated by writing for the surface slope dy/dx = dq/dx/<c_k >B and calculating the flow derivative as (q _out – q _in)/L at any desired time level, assuming that Δq/Δx under corresponding steady-state and transient conditions differ little:

Having completed the routing calculations, the flows are known and so is <q> = <q_ss >, hence one only needs to solve the implicit equation (R14) iteratively for the depth <y>:

The author realized the utility of the Muskingum concept in this simple calculation of the depth in reviewing, for the purpose of this reply, Wong's (1984) analysis of the Muskingum method. Contrary to Perumal's method (1994a), this hydraulics-based method does not imply a linear depth profile, which may not exist in a long reach. As the review explained, if the upstream condition is a depth hydrograph, its conversion to an inflow hydrograph must be accomplished via the Jones formula, and similarly for the reverse outflow conversion; Perumal's work ignores these conversions.

7. SETTING THE RECORD STRAIGHT

A minor, but disturbing point is Perumal's imputation that I stopped studying the subject matter at ca. 1986. This is grossly inaccurate. My own publications referenced in the review reach 1998 (Koussis et al., 1998). Other research of mine, in which the matched artificial diffusion/dispersion method is used (Syriopoulou & Koussis, 1991; García-Delgado & Koussis, 1997; Koussis et al., 2003b) has been alluded to, without explicit reference, because it concerns mass transport in aquifers and is indirectly relevant to flood routing (see the last sentence in the penultimate paragraph of Section 9, Epilogue: “the same principle is used to model longitudinal transport in aquifers, first splitting the transport along and transverse to the streamlines, yielding extremely efficient 2-D models.”). In addition, new research on the matched diffusion/dispersion schemes, again in relation to mass transport in aquifers, was presented at the 2003 and 2008 EGU conferences, while flood routing was the subject of Koussis et al. (2003a), Mazi & Koussis (2006) and of my Comment (Koussis, 2010).

8. CONCLUDING REMARKS

I want to express my admiration for the sense of the essential in early works, as exemplified not only by such classical papers as McCarthy (1938) and Kalinin & Miljukov (1958), or by the fundamental work of Lighthill & Whitham (1955), but also by papers such as Henderson's (1963), which displays a magnificent understanding of flood hydraulics, and also a sound measure for applications; the latter characterizes NERC's (1975) publication as well.

The issues related to the Muskingum method that the Discusser has raised have been clarified in past works on the subject, and also in the review article.

Note for a Correction in the Review paper (Koussis, 2009):

In equation (37) of the review paper (Koussis, 2009) coefficient a ₂ is incorrect, for which I apologise. The correct equation (37) is written as follows:

Notes

¹Perumal's Discussion uses another translation of Apollov et al., published in 1964.