Balance between calibration objectives in a conceptual hydrological model

Abstract

Three different measures to determine the optimum balance between calibration objectives are compared: the combined rank method, parameter identifiability and model validation. Four objectives (water balance, hydrograph shape, high flows, low flows) are included in each measure. The contributions of these objectives to the specific measure are varied to find the optimum balance between the objectives for each measure. The methods are applied to nine middle-sized catchments, using a typical conceptual hydrological model. The results indicate that differences in the optimum balance between the combined rank method and parameter identifiability on the one hand, and model validation on the other, are considerable. The theoretical optimum balance would be a situation without trade-off between single objectives. For some catchments and measures, this situation is closely approximated. On average, the performance of combined rank method is somewhat better than that of parameter identifiability (respectively 3.6% and 5.0% below the theoretical optimum), where the performance of model validation is considerably lower (22.4% below the theoretical optimum). These results are supported by additional validation tests which gave robust results for the combined rank measure and the parameter identifiability measure, and less robust results for the model validation measure.

Citation Booij, M. J. & Krol, M. S. (2010) Balance between calibration objectives in a conceptual hydrological model. Hydrol. Sci. J. 55(6), 1017–1032.

Résumé

On compare trois mesures différentes pour déterminer l'équilibre optimal entre des objectifs de calage: la méthode des rangs combinés, l'identifiabilité des paramètres et la validation du modèle. Quatre objectifs (bilan en eau, forme de l'hydrogramme, hauts débits, bas débits) sont utilisés dans chaque mesure. Les contributions de ces objectifs à chaque mesure sont modifiées pour trouver l'équilibre optimal entre les objectifs pour chaque mesure. Les méthodes sont appliquées à neuf bassins de taille moyenne, en utilisant un modèle hydrologique conceptuel commun. Les résultats indiquent que les différences sur l'équilibre optimal sont considérables entre d'un côté la méthode des rangs combinés et l'identifiabilité des paramètres, et de l'autre la validation du modèle. L'équilibre optimal théorique correspondrait à une situation sans compromis entre les objectifs pris séparément. Pour certains bassins et certaines mesures, cette situation peut être approchée assez finement. En moyenne, la performance de la méthode des rangs combinés est meilleure que celle de la méthode d'identifiabilité (respectivement à 3.6% and 5.0% de l'optimum théorique), alors que celle de la validation du modèle est nettement moindre (à 22.4% de l'optimum théorique). Ces résultats sont corroborés par des tests de validation complémentaires montrant des résultats robustes pour la méthode des rangs combinés et la méthode d'identifiabilité, et des résultats moins robustes pour la méthode de validation du modèle.

Key words:

• calibration objectives
• combined rank measure
• parameter identifiability
• model validation
• HBV model
• Meuse basin

Mots clefs:

• objectifs de calage
• mesure des rangs combinés
• identifiabilité des paramètres
• validation de modèle
• modèle HBV
• bassin de la Meuse

INTRODUCTION

Hydrological models have been applied extensively in water resources management for purposes such as flood forecasting (for an overview, see Cloke & Pappenberger, 2009), low-flow simulation (e.g. Smakhtin et al., 1998; Engeland & Hisdal, 2009), and climate impact studies (e.g. Akhtar et al., 2008; Steele-Dunne et al., 2008; Yu & Wang, 2009). Often, these models are based on conceptual representations of the physical processes in the rainfall–runoff transformation lumped at (sub-)basin level (lumped conceptual models, e.g. Bergström, 1995). Generally, the parameters of these models cannot be derived from catchment characteristics measured in the field and, therefore, calibration of these parameters is required. Calibration implies that parameters are selected in such a way that observed hydrological behaviour is simulated by the model as closely as possible (Sorooshian & Gupta, 1995). The usefulness of models for application depends on the robustness of the model, i.e. the insensitivity of model results to uncertainties in data used in the model set-up and calibration. An important factor determining the robustness of such a model is the model performance under different calibration and validation conditions. Other important factors influencing the robustness of models are extrapolation behaviour and propagation of uncertainties.

The purpose of simulation determines which hydrological behaviour should be simulated well in the calibration and validation of the model. Simulation of high flows is important in the context of flood safety, whereas simulation of low flows is important for river-related functions, such as agriculture, navigation and drinking water supply. Both purposes might be important in the context of integrated river basin management. Depending on the simulation purpose, appropriate objective functions should be chosen and used to select the conceptual model parameters. Commonly used objective functions are the root mean square error and the Nash-Sutcliffe coefficient (Nash & Sutcliffe, 1970). Most hydrological modelling studies focus on high-flow simulation or simulation of the discharge regime and, hence, objective functions that emphasize the corresponding components of the hydrograph are used. Low-flow simulation and related objective functions receive less attention. However, low flows may cause serious problems to society, necessitating a thorough understanding of low-flow behaviour as well (see e.g. De Wit et al., 2007).

When multiple purposes are of interest (e.g. in the case of reservoir operation), the calibration problem should be considered in a multi-objective framework (Yapo et al., 1998; Madsen, 2000; see Efstratiadis & Koutsoyiannis, 2010, for an excellent review of this topic). This can be done using no-preference multi-objective methods that independently optimize multiple objectives and reveal a set of solutions that represent the trade-off between the objectives involved (i.e. a Pareto front, see e.g. Yapo et al., 1998; Khu & Madsen, 2005; Schoups et al., 2005; Fenicia et al., 2007a). Alternatively, multi-objective functions can be used, which commonly transform and aggregate single-objective functions into one function, resulting in a single-objective optimisation problem. Multi-objective functions implicitly or explicitly involve a balance between single-objective functions, depending on their relative importance, represented in their weighting. This is in contrast to Pareto optimization, where relative weighting is not necessary. Recent examples of calibration procedures for hydrological models using multi-objective functions are given by Schoups et al. (2005), Cheng et al. (2005) and Deckers et al. (2010). In general, a multi-objective function aggregates a number of single-objective functions using weights; see, for example, Lindström (1997) and Oudin et al. (2006) for the case of two single-objective functions, and Madsen (2003) and Schoups et al. (2005) for a general formulation. Weights also can be implicitly incorporated when combining two (e.g. Akhtar et al., 2009) or more (see Deckers et al., 2010) single-objective functions. Gupta et al. (2009) show that, actually, the Nash-Sutcliffe coefficient is already a multi-objective function by decomposing it into three distinctive components representing the correlation, bias and a measure of relative variability in the simulated and observed values. Madsen (2000) proposed the use of the Euclidean distance as an aggregated measure, with transformation constants as weights. Fuzzy multi-objective functions are another way to combine single-objective functions. Herein, each objective function is transferred into a membership function according to personal preferences (e.g. Yu & Yang, 2000; Cheng et al., 2005). In general, these approaches do not elucidate which balance between different single objectives to choose and assume a certain balance between different objectives. The optimum balance between objectives obviously depends on the simulation purpose of the model user and the importance of the different functions in the modelled system. An alternative way to determine this balance is to use an aggregated measure, for instance a scaled multi-objective function (Deckers et al., 2010), or to use multi-model approaches (Duan et al., 2007; Marshall et al., 2007) or multiple parameterizations within a fixed model structure (Oudin et al., 2006; Fenicia et al., 2007b). This enables an objective determination of the optimum balance between single-objective functions according to the underlying method, without subjectively choosing a balance. This can be useful when information about the importance of different objectives is not available, or when the user does not want to make any explicit decisions on this issue. It should be noted that the choice of single-objective function is still a subjective one. The focus of this paper is on aggregated measures. Although individual aggregated measures have been used before, a comparison of different aggregated measures to assess the optimality of the balance according to mutual objectives has not been done.

The optimum balance between different objectives is sometimes close to being perfect so that all objectives are simulated very well by the model. However, probably more frequently, the optimum balance is far from perfect resulting in a poor simulation of one or more parts of the hydrograph. If the model is calibrated using only one single-objective function (Nash-Sutcliffe coefficient or root mean square error), the results may look very good, but poor simulation of specific parts of the hydrograph, e.g. low flows, may be hidden. The measures to identify the optimum balance between calibration objectives will not solve this problem. However, they will unveil the failure of the model to simulate one or more parts of the hydrograph and thus serve as a diagnostic tool for non-satisfactory model performance contributing to the aims of this special issue on The Court of Miracles of Hydrology (Andréassian et al., 2010). Given these possible model deficiencies, the measures can be used to identify the optimum balance between different objectives.

The aim of this paper is to determine the optimum balance between different objectives based on three different (aggregated) measures developed by the authors: a combined rank measure, parameter identifiability and model validation. Here, the combined rank measure serves as a kind of reference method, to which the other two methods are compared. First, the study area consisting of a set of nine sub-basins of the Meuse basin in Western Europe is described, followed by a brief outline of the conceptual hydrological model used (HBV) and its recent application to the Meuse. In the remaining sections, the methodology, including the calibration method, objective functions and the three measures, are described. The results are discussed and, finally, conclusions are drawn.

STUDY AREA AND DATA

The Meuse basin

The Meuse basin covers an area of approximately 33 000 km², including parts of France, Luxembourg, Belgium, Germany, and The Netherlands. About 60% of the Meuse basin is used for agricultural purposes (including pastures) and 30% is forested. The average annual precipitation ranges from 1000–1200 mm/year in the Ardennes to 700–800 mm/year in the Dutch and Flemish lowlands. The maximum altitude is just below 700 m a.s.l. Snowmelt is not a major factor for the discharge regime of the Meuse. The average discharge of the Meuse at the outlet is approximately 350 m³/s and this corresponds to an annual precipitation surplus of almost 400 mm/year. Precipitation is uniformly distributed over the year. The seasonal variation in discharge is a reflection of the variation in evapotranspiration (Booij, 2005). Nine sub-basins of the Meuse basin with observed discharge data and without upstream neighbours are investigated.

Meteorological and hydrological data

Daily precipitation, temperature, potential evapotranspiration and discharge data for the period 1968–1997 are used. The potential evapotranspiration has been calculated using the Penman-Monteith equation. The precipitation, temperature and potential evapotranspiration series are corrected for elevation and prepared for 15 sub-basins using data provided by KMI (Belgian Royal Meteorological Institute) and Météo France, similarly to Booij (2005). The discharge series at nine sub-basin outflow points have been obtained from SETHY/WACONDAH (Belgium) and DIREN Lorraine (France).

THE HBV MODEL FOR THE MEUSE RIVER

The hydrological model HBV is used in this study to model the rainfall–runoff process in the Meuse basin. The considerations which have led to the choice of HBV can be found in Booij (2005). HBV is a conceptual model of river basin hydrology which simulates river discharge using precipitation, temperature and potential evapotranspiration as input. The model consists of a precipitation routine representing rainfall, snow accumulation and snowmelt; a soil moisture routine determining actual evapotranspiration and overland and subsurface flow; a fast flow routine representing stormflow; a slow-flow routine representing subsurface flow; a transformation routine for flow delay and attenuation; and a routing routine for river flow (Bergström, 1995). The parameters that are most important for calibration and model skill are described below. A detailed description of the most recent version of HBV (HBV96) is given in Lindström et al. (1997).

The most important parameters occur in the soil moisture, fast-flow and slow-flow routines. The main parameters in the soil moisture routine are: FC (maximum soil moisture storage, mm); LP (the fraction of FC above which potential evapotranspiration occurs and below which evapotranspiration will be linearly reduced); and BETA (to determine the relative contribution to runoff from 1 mm of precipitation at a given soil moisture deficit). The main parameters in the fast-flow routine are: ALFA (the measure of nonlinearity for fast-flow; for ALFA = 0, fast-flow is the outflow from a linear reservoir and for ALFA > 0, fast-flow becomes more and more nonlinear); k_f (a recession coefficient for the fast-flow reservoir); and PERC (drainage from the fast-flow reservoir to the slow-flow reservoir when sufficient water is available). The main parameters related to the slow-flow routine are: k_s (a recession coefficient for the slow-flow reservoir); and CFLUX (the maximum value for capillary flow).

The HBV model has been applied recently to the Meuse basin to assess the impact of climate change on river flooding with three spatial model resolutions: lumped as one sub-basin, 15 sub-basins and 118 sub-basins (Booij, 2005). The differences between average and extreme discharge behaviour modelled by the two distributed models (15 vs 118 sub-basins) were found to be small. Therefore, the model with 15 sub-basins (HBV-15) is used here to simulate the river flow behaviour where each sub-basin is modelled in a lumped way. The schematization of HBV-15 for the Meuse basin upstream of Borgharen is shown in Fig. 1. This schematization is slightly different from that of Booij (2005), because improved climatological data and additional discharge data (12 stations instead of five) could be used. This adapted schematization has also been used by Leander et al. (2005) and Leander & Buishand (2007). Nine sub-basins without upstream neighbours and with observed discharge data (nos 1, 2, 5, 6, 8, 10, 11, 12 and 13 in Fig. 1) are used to investigate the balance between different objectives for different sub-basins. Some characteristics of these sub-basins are summarized in Table 1.

Fig. 1 Location and schematization of the Meuse basin upstream of Borgharen in HBV-15 with numbers referring to sub-basin names. 1: Meuse source–Meuse St Mihiel; 2: Chiers; 3: Meuse St Mihiel–Meuse Stenay; 4: Meuse Stenay–Meuse Chooz; 5: Semois; 6: Viroin; 7: Meuse Chooz–Meuse Namur; 8: Lesse; 9: Sambre; 10: Ourthe; 11: Amblève; 12: Vesdre; 13: Mehaigne; 14: Meuse Namur–Meuse Borgharen; 15: Jeker.

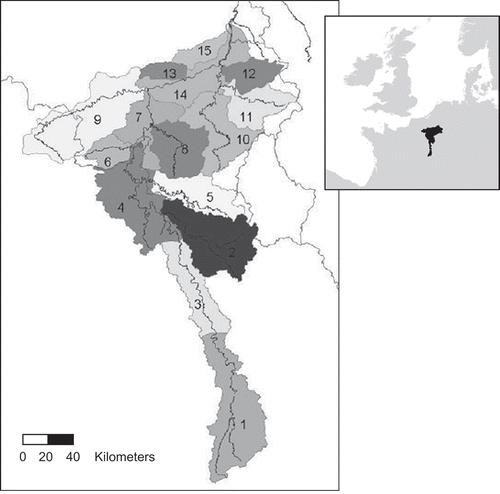
Table 1  Characteristics of nine sub-basins

Sub-basin	Size (km^2)	Slope (m/m)	Mean discharge* (m^3/s)	Mean annual precip.* (mm/year)	Lithology
Meuse Lorraine	2540	0.4 × 10^-3	29.7	922	Limestone, siltstone, sandstone
Chiers	2207	1.0 × 10^-3	26.6	918	Siltstone, sandstone
Semois	1235	1.5 × 10^-3	25.9	1201	Sandstone, siltstone
Viroin	526	2.0 × 10^-3	7.9	991	Quartzite, limestone
Lesse	1311	5.0 × 10^-3	17.4	983	Quartzite, phylitte, shales, limestone
Ourthe	1597	3.7 × 10^-3	22.2	971	Quartzite, phylitte, schists, limestone
Amblève	1050	5.0 × 10^-3	18.6	1094	Quartzite, phylitte
Vesdre	685	8.0 × 10^-3	10.3	1097	Phylitte, quartzite, limestone
Mehaigne	346	2.0 × 10^-3	2.4	789	Limestone, sands
*Period 1968–1998.

MONTE CARLO SIMULATION AND SINGLE-OBJECTIVE FUNCTIONS

Monte Carlo simulation

Following Harlin & Kung (1992) and Seibert (1999), Monte Carlo simulation (MCS) is applied for model calibration to nine sub-basins. The MCS is a technique in which, through numerous model simulations, a best objective function value is sought by using randomly generated parameter values within a pre-defined model parameter space. The most important aspects of MCS are: the selection of calibration parameters; the determination of prior parameter spaces; the selection of probability distributions for the calibration parameters; the determination of the number of simulations to be carried out; and the selection of the objective function(s). The first four steps are described in this sub-section and the last step, being the focus of this study, is described in the remaining part of this section.

In this study we aim to develop a robust hydrological model, which is able to adequately simulate different aspects of the hydrograph and not merely high or low flows. Therefore, model parameters which are of influence on these different aspects should be selected for calibration. In previous HBV studies, much experience has been gained in demonstrating the most sensitive model parameters (e.g. Harlin & Kung, 1992; Seibert, 1999; Lidén & Harlin, 2000; Merz & Blöschl, 2004; Booij, 2005), and these studies were used to determine the model parameters for calibration. This resulted in the selection of eight calibration parameters that require optimization, while for the remaining model parameters default values are used (SMHI, 1999). The transformation routine for flow delay and attenuation (with parameter MAXBAS) is used with a default parameter value of one, since the response time of each of the nine sub-basins is less than the time step of the model of one day. Moreover, the routing routine of the HBV model is omitted since in this study no sub-basins had to be linked.

The model parameter space is determined by evaluating model parameter ranges applied in former HBV studies (e.g. Harlin & Kung, 1992; Seibert, 1999; Lidén & Harlin, 2000; Booij, 2005; Akhtar et al., 2008; Deckers et al., 2010), taking into account physical and mathematical constraints (e.g. the model can act unrealistically for a given model parameter value due to the mathematical implementations in the model). For random generation of parameter values in MCS, a uniform distribution is applied, because a limited amount of information concerning the uncertainty of the parameters is available. More efficient methods for sampling the parameter space exist (e.g. Markov chain Monte Carlo, see Gilks et al., 1996). The selected model parameters and parameter ranges are given in Table 2

Table 2  Model parameters and their minimum and maximum values used in the Monte Carlo simulation

Parameter value	FC (mm)	BETA (−)	LP (−)	ALFA (−)	Kf (d^-1)	Ks (mm/d)	PERC (mm/d)	CFLUX (mm/d)
Minimum	150	1	0.2	0.1	0.005	0.005	0.1	0.1
Maximum	500	3	1	1.5	0.1	0.1	2.5	2.5

.

To be certain that the entire model parameter space is examined and to permit statistical treatment of the results, a sufficient number of runs should be executed. Following the approach of Harlin & Kung (1992), Lidén & Harlin (2000) and Steele-Dunne et al. (2008), the number of model simulations is set at 10 000. This number of simulations is confirmed as reasonable by Shrestha et al. (2009), who found that statistics for testing convergence were stable after 5000–10 000 simulations for an HBV model study with nine calibration parameters. Similarly to Booij (2005), the data period 1968–1998 is split into a calibration period (1968–1984) and a validation period (1985–1998). The calibration period is used for the first (combined rank measure) and second (parameter identifiability) methods to assess the optimum balance between the four different objectives. Both calibration and validation period are used for the third method (model validation).

Single-objective functions (SOF)

For proper calibration and evaluation of a model, Madsen (2000) states that, in the case of “… simulating the hydrological behaviour of the catchment as closely as possible”, usually four different objectives are considered. These are: (1) a good water balance, (2) a good overall agreement of the shape of the hydrograph, (3) a good agreement of high flows, and (4) a good agreement of low flows. Since in this study the objective of model calibration is to simulate all aspects of the hydrograph adequately, a single-objective function (SOF) is selected for each objective. For Objective 1, the relative volume error (RVE) is selected, for Objective 2 – the Nash-Sutcliffe coefficient (NS), for Objective 3 – the relative mean error in modelling 10-year and 100-year return values (RMERV), and for Objective 4 – the relative mean absolute error in modelling low flows (RMAEL). These four SOFs are presented in equations (1–4).

(1)

(2)

(4)

where i is the time step; T is the total number of time steps; Q is the discharge; subscripts o, m and t stand for observed, modelled and threshold, respectively; and RV(y) is the y-year return value of the annual maximum discharge using the Gumbel extreme value distribution. The RVE and RMERV vary between –∞ and ∞, but perform best when a value of zero is generated; NS ranges between –∞ and 1, with higher values indicating a better agreement between observed and modelled values and 1 being a perfect fit; and RMAEL varies between 0 and ∞ with a perfect value of zero. For the calculation of RMAEL a 31-day moving average window is applied and a threshold discharge value of .

A disadvantage of RMERV is that it relies on the assumption that annual maximum discharges are Gumbel distributed. However, previous studies on extreme discharges have shown that this is a reasonable assumption (e.g. Booij, 2005; Leander & Buishand, 2007; Akhtar et al., 2008). Moreover, the parameters of the Gumbel distribution are estimated using the average and standard deviation of the annual maximum discharges and, thus, RMERV provides an estimation of the average fit of annual maximum discharges. Many alternative criteria can be used, such as a weighted form of the Nash-Sutcliffe coefficient (e.g. Hundecha & Bardossy, 2004), or criteria assessing the goodness of fit of annual maximum discharges (e.g. Ashagrie et al., 2006). The choice of the threshold for RMAEL results in different numbers of values being evaluated depending on the hydrological regime of the catchment. This makes a comparison between catchments difficult, but is not a limitation for the aggregated measures used in this study. Also, for low flows, alternative criteria might be used such as the Nash-Sutcliffe coefficient with logarithmically-transformed discharges (e.g. Engeland & Hisdal, 2009), or criteria assessing the goodness of fit of discharge deficits (e.g. De Wit et al., 2007).

MEASURES TO IDENTIFY OPTIMUM BALANCE

In this study, three methods are used to set model parameters. In the combined rank measure method, the model is calibrated by selecting parameters optimizing a multi-objective function using Monte Carlo simulation. The relative importance of single-objective functions is taken as a degree of freedom. In the second method, the identifiability of parameters is assessed, and optimized by varying the relative importance of the SOFs, yielding an optimum parameter set as a by-product. In the third method, model validation is assessed by comparing model performance for calibration and validation periods, and optimized by varying the relative importance of the SOFs, yielding an optimum parameter set as a by-product. We denote the selected relative importance of the SOFs the “optimum balance” between the SOFs, according to the method used.

Combined rank measure

We constructed the combined rank measure in two steps:

Step 1: the SOF values are ranked in descending performance order and each rank number is scaled with the total number of simulations, N, thus obtaining N values between 0 and 1. For the SOFs RVE and RMERV this means that values close to 0 are given a scaled rank number: r _RVE and r _RMERV, respectively, close to 1, and vice versa. For NS, high values, and for RMAEL, low values are given a scaled rank number: r _NS and r _RMAEL, respectively, close to 1.

Step 2: the combined rank measure, R, for each simulation run, n, is defined as:

(5)

The optimum simulation run, R*, of N runs is determined by:

(6)

The parameter set corresponding to R* is assumed to be a well-performing parameter set taking into account the four objectives, but is not necessarily an optimum parameter set for each SOF. The combined rank measure implicitly incorporates weights when combining the four SOFs in a similar way to that described in Deckers et al. (2010). This is in contrast to the methods in which weights have to be assigned explicitly to different objectives, e.g. in a linear way (Madsen, 2003), or in a fuzzy way (Yu & Yang, 2000).

The optimum balance between calibration objectives determined with the combined rank measure is represented by the scaled rank numbers (or relative weights) of the SOFs corresponding to the optimum simulation run, R*. However, to determine the optimum balance for the other two measures (parameter identifiability and model validation), the contributions of the SOFs to the combined rank measure need to be varied. The relative weights of the SOFs within the combined rank measure are varied by adding constants between 0 and 1 to the scaled rank numbers, i.e. λ_RVE, λ_NS, λ_RMERV, λ_RMAEL = 0, 0.25, 0.5, 0.75 and 1, respectively. In this way, objective functions become more decisive in the combined rank measure (e.g. having a value of 0 added) than others (e.g. having a value of 1 added) and vice versa. Then, the total number of combinations of adapted scaled rank numbers (i.e. {r _RVE + λ_RVE, r _NS + λ_NS, r _RMERV + λ_RMERV, r _RMAEL , + λ_RMAEL}) for each simulation run is 5⁴ = 625. Several combinations are expected to lead to the same optimum simulation run and, thus, the same scaled rank numbers representing the same balance between objectives. Therefore, the total number of different evaluated “balances” is expected to be less than 625.

Parameter identifiability

This method is based on the identifiability of all eight calibrated parameters. In the literature, several methods for the determination of the parameter identifiability have been proposed. Bastidas et al. (1999) discuss the multi-objective generalized sensitivity analysis (MOGSA) algorithm for parameter identifiability analysis. Wagener et al. (2003) use the marginal probability distribution of a parameter as an indicator of the parameter identifiability in their dynamic identifiability analysis (DYNIA) method. Doherty & Hunt (2009) defined two statistics for parameter identifiability based on singular value decomposition of the weighted sensitivity matrix, the elements of which express the sensitivity of each model output to each parameter. For practical reasons, in this work, a relatively simple and intuitive method to determine parameter identifiability is used. The method is slightly related to the above-mentioned methods, since it also expresses parameter identifiability as the sensitivity of the objective function to parameter variations.

We determined the identifiability of a parameter by the sensitivity of the combined rank measure, R, to the parameter. This is illustrated in Fig. 2, which shows the combined rank measure as a function of scaled parameter value for an identifiable parameter and a non-identifiable parameter.

Fig. 2 Combined rank measure as a function of scaled parameter value for: (a) identifiable parameter and (b) non-identifiable parameter. The points within the squares are used in the calculation of the identifiability of a parameter.

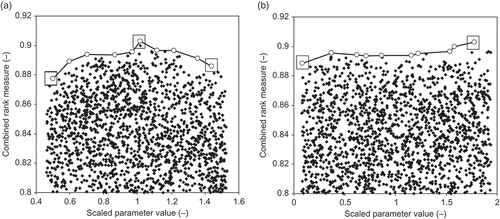
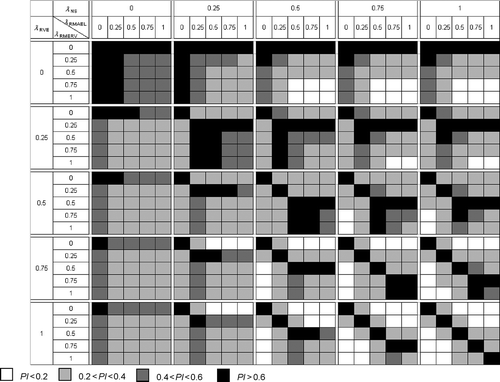
A parameter is identifiable when the maximum value of the combined rank measure is found within the prior parameter space; it is non-identifiable when the maximum value of the combined rank measure is found at the border of the prior parameter space and thus, possibly, is located outside the prior parameter space. The prior parameter space, S, is subdivided into 10 blocks of equal length and, for each parameter sub-space, s, the maximum value for the combined rank measure, R _max(s), is determined. The maximum of these 10 values and the values for s = 1 and s = 10 are used in the calculation of the parameter identifiability, PI (see also Fig. 2), for identifiable parameters:

(7)

where is the average parameter value within the parameter space, S. In the example of Fig. 2, PI = 0.040 for the identifiable parameter. The total parameter identifiability is the sum of all individual parameter identifiabilities. In this method, model parameters are set by maximizing PI, in varying the constants λ adding to the scaled rank numbers.

Model validation

The third method to assess the optimum balance between the four different objectives uses data from a period other than the calibration period, i.e. the validation period, to evaluate the model performance for different conditions than the calibrated ones. The model performance for the validation period cannot be assessed with the combined rank measure since only one simulation run is made for each balance. Therefore, we compared the model performance for the calibration and validation periods using the average difference between the SOFs under calibration (cal) and validation (val) conditions, ME:

(8)

The difference in the RMAEL value between the calibration and validation is corrected for the difference in the length of the calibration and validation period. Since RVE and RMERV are in %, only NS and RMAEL need to be multiplied by 100. A positive value for ME means that the model performs better in the validation than in the calibration, and vice versa. In this method, model parameters are set by maximizing ME, in varying the constants λ adding to the scaled rank numbers.

RESULTS AND DISCUSSION

Combined rank measure

The calibration results using the combined rank measure are shown in Table 3. The SOF values corresponding to the maximum value of the combined rank measure are obviously less than the optimum value obtained in a single-objective optimisation (with a scaled rank of 1), but differences are generally smaller than 10% except for RMAEL. This is confirmed by the large R* values for each sub-basin; only for the Viroin sub-basin is R* smaller than 0.9 obtained. This means that the trade-off between the SOFs is limited and, generally, SOF values belonging to the top 5–10% of all simulated SOF values are obtained when using the combined rank measure. Different SOFs determine R* for the different sub-basins, where NS is the most limiting SOF (for four out of nine sub-basins). No relationship between limiting SOFs and physical basin characteristics (e.g. size, slope, lithology) could be identified.

Table 3  Single-objective function values from calibration for maximum value of combined rank measure (comb.) and for maximum value of each single-objective function (optimum) and maximum value of combined rank measure (R*) for nine sub-basins

Sub-basin	NS (−)		|RVE| (%)		RMAEL (−)		|RMERV| (%)		R* (−)
	Comb.	Opt.	Comb.	Opt.	Comb.	Opt.	Comb.	Opt.
Meuse L.	0.755^#	0.810	0.631	0.001	0.337	0.274	8.041	0.004	0.913
Chiers	0.776	0.816	1.572^#	0.013	9.487	9.267	2.565	0.015	0.984
Semois	0.877	0.897	0.277	0.000	0.289	0.243	6.504^#	0.007	0.951
Viroin	0.891	0.915	1.115	0.001	3.511^#	3.067	6.147	0.040	0.871
Lesse	0.871	0.902	0.535	0.004	0.267^#	0.199	2.617	0.020	0.959
Ourthe	0.851	0.885	0.684^#	0.001	0.221	0.176	5.798	0.005	0.949
Amblève	0.832^#	0.879	0.710	0.002	0.187	0.158	6.746	0.035	0.948
Vesdre	0.731^#	0.790	0.237	0.002	0.246	0.192	2.463	0.024	0.959
Mehaigne	0.597^#	0.655	8.813	5.989	0.446	0.321	2.366	0.032	0.978
^#SOF determining R*.

Parameter identifiability

Figure 3 shows the contribution of the different HBV parameters to the total parameter identifiability for the balance between calibration objectives for which the maximum identifiability is obtained. The total identifiability varies strongly between different sub-basins. The Mehaigne sub-basin has the smallest total identifiability, which might be explained by the relatively poor quality of the discharge data, as illustrated by a small optimum NS value and a high optimum RVE value (Table 3). The Vesdre and, to a lesser extent, the Meuse Lorraine and the Ourthe sub-basins have relatively larger total identifiabilities. The other five sub-basins have comparable total identifiabilities. For some sub-basins (e.g. the Semois and the Lesse), the maximum identifiability is achieved for equal contributions of the SOFs to the combined rank measure, while for other sub-basins (e.g. the Chiers and the Viroin), contributions vary.

Fig. 3 Contribution of calibration parameters to total identifiability for balance between calibration objectives with maximum total parameter identifiability for nine sub-basins. Dotted lines indicate total parameter identifiability for λ_RVE = λ_NS =λ_RMERV = λ_RMAEL = 0.

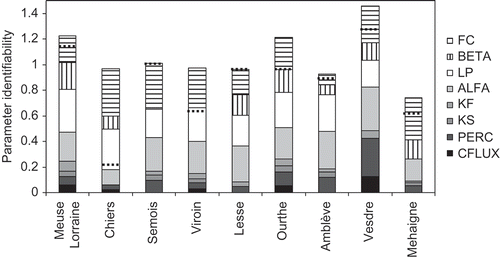
The soil moisture routine parameters FC and LP and the fast flow routine parameter ALFA show the largest contribution to the total parameter identifiability (about 75% averaged over all sub-basins). This large contribution would be expected based on sensitivity analyses in previous HBV studies, although the contributions of the soil moisture routine parameter BETA (about 10% on average) and, in particular, the fast flow routine parameter, k_f (about 3% on average) are less than expected. Contributions of parameters to the total identifiability vary considerably between different sub-basins: for instance, that for FC is between 9% for the Amblève and approx. 40% for the Chiers and the Mehaigne. The non-identifiability of LP for the Mehaigne may partly explain the large contribution of FC for this sub-basin. Furthermore, the contribution of PERC for the Vesdre is considerably larger than for other sub-basins. The contributions of different parameters to the total identifiability for different sub-basins should ideally be explained from differences in physical basin characteristics. However, this is almost impossible here, because HBV parameters can only be related indirectly to physical characteristics and several additional uncertainties (e.g. input, model structure and scale-related uncertainties) are implicitly incorporated in the relationship between the combined rank measure and parameter values determining the identifiability.

This noise in the identifiability relationships is also illustrated in Fig. 4, where the balance between four objectives, when choosing parameters according to the maximum identifiability of the three most identifiable parameters (FC, LP and ALFA) for nine sub-basins, is given. One would expect a rather good balance between calibration objectives for the “general” parameter FC, influencing all discharge regimes, an important role for NS and RMERV for fast-flow parameter ALFA and possibly a more important role for RVE and RMAEL with respect to evapotranspiration parameter LP. Indeed, Fig. 4 shows a good balance for FC was found for six out of nine sub-basins, (except for the Viroin, Vesdre and in particular Lesse). The deviation for the Viroin might be caused by the poor simulation of low flows and the consequent focus of the combined rank measure on RMAEL paying less attention to other SOFs (here RVE). For the Lesse, FC is important only for SOFs related to the water balance and not for SOFs related to the hydrograph shape, which may be explained by the relatively low discharge variability of this river. High scaled rank numbers for NS and RMERV for ALFA are found for all sub-basins, with only the Viroin and Amblève showing some trade-off with respect to RVE and, in particular, RMAEL. The behaviour for LP is more unclear and only the Meuse Lorraine sud and the Amblève show some of the expected trade-off behaviour. Overall, four out of nine sub-basins show hardly any trade-off behaviour (for FC, but also for LP and ALFA) and the other five sub-basins show contradictory results for the three parameters.

Fig. 4 Balance between four objectives expressed as scaled rank number for maximum identifiability of each of three parameters for nine sub-basins.

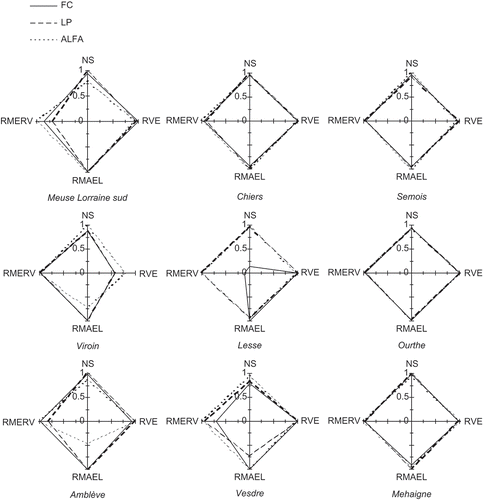
As an example, Fig. 5 shows the total parameter identifiability as a function of balance between the four objectives for the Amblève sub-basin. It may be observed that incorporation of objective functions (constant of 0 added to scaled rank number) in the combined rank measure, emphasizing a good water balance (RVE) and a good agreement of high flows (RMERV), always results in high total identifiability for this sub-basin. Furthermore, RMAEL seems to be more important for the identifiability than NS, although NS is used as objective function in most hydrological modelling studies and low-flow related objective functions are much less incorporated.

Fig. 5 Total parameter identifiability (PI) as a function of balance between four objectives expressed as constants added to scaled rank numbers (λ_RVE, λ_NS, λ_RMERV, λ_RMAEL) for the Amblève sub-basin.

Model validation

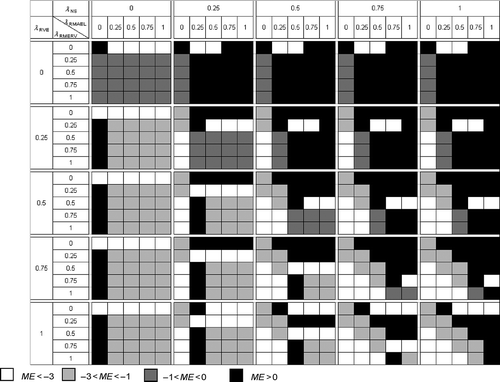
Table 4 gives the SOF values for the calibration and validation and corresponding improvements (+) or deteriorations (–) in the validation compared to the calibration (ME) when using the maximum value of the combined rank measure as calibration criterion. Also, the maximum ME value for a specific balance is given, representing the maximum possible improvement in the validation compared to the calibration, and being the third measure for the determination of the optimum balance. All sub-basins have a positive maximum ME value, where four out of nine sub-basins have a positive ME value for the parameter set corresponding to the maximum value of the combined rank measure in the calibration. Most sub-basins have ME values around 0 for this latter case; relatively large (positive) values are obtained only for the Chiers and Viroin.

Table 4  Single-objective function values for calibration for maximum value of combined rank measure (cal.) and validation (val.) and related ME value (for equal importance of the SOFs) and maximum ME value (varying the importance of SOFs) for nine sub-basins

Sub-basin	NS (−)		|RVE| (%)		RMAEL (−)		|RMERV| (%)		ME (%)
	Cal.	Val.	Cal.	Val.	Cal.	Val.	Cal.	Val.		Max.
Meuse L.	0.755	0.798	0.631	5.486	0.337	0.297	8.041	4.015	−0.49	3.01
Chiers	0.776	0.682	1.572	6.259	9.487	0.400	2.565	26.268	13.56	20.28
Semois	0.877	0.925	0.277	3.889	0.289	0.277	6.504	11.667	−4.92	97.98
Viroin	0.891	0.916	1.115	4.243	3.511	0.275	6.147	12.271	21.01	27.02
Lesse	0.871	0.918	0.535	0.965	0.267	0.219	2.617	19.732	−2.95	59.58
Ourthe	0.851	0.928	0.684	0.652	0.221	0.236	5.798	0.062	−3.69	6.31
Amblève	0.832	0.899	0.710	0.356	0.187	0.161	6.746	6.451	1.03	3.57
Vesdre	0.731	0.765	0.237	1.842	0.246	0.149	2.463	11.121	5.17	17.08
Mehaigne	0.597	0.660	8.813	2.103	0.446	0.416	2.366	8.057	−0.41	8.90

Similarly to Fig. 5, Fig. 6 shows the ME value as a function of balance between the four objectives for the Amblève sub-basin. Improvement of model performance in the validation compared to the calibration (black boxes) is obtained for a mixture of balances, where a more important role for RVE and a less important role for NS generally leads to higher ME values.

Fig. 6 Model validation (ME) as a function of balance between four objectives expressed as constants added to scaled rank numbers (λ_RVE, λ_NS, λ_RMERV, λ_RMAEL) for the Amblève sub-basin.

Comparison of methods for determination of optimum balance

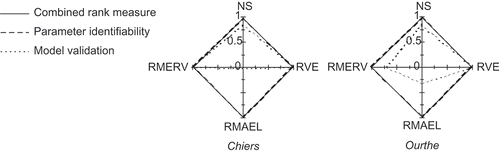
Figure 7 shows the balance between the four objectives for the model parameter set according to the three measures (combined rank measure, parameter identifiability and model validation). Note that the combined rank measure serves as a kind of reference method, to which the other two methods can be compared. Differences in balance between the combined rank measure and parameter identifiability on the one hand, and model validation on the other, are considerable, in particular for the Semois, Lesse, Ourthe and Vesdre sub-basins, where the mutual differences between the combined rank measure and parameter identifiability are smaller. The model validation measure tends to force balances towards water volume-related objectives (RVE and RMAEL), especially for the above mentioned four sub-basins. This can be partly explained by the difference in discharge variability under calibration and validation conditions. In particular for the Semois, Lesse and Ourthe (compared to the other six sub-basins), the variability is much greater in the validation period (20–30%) resulting in relatively poor performances for hydrograph shape-related objectives in the validation (in particular RMERV). This is obviously not supporting the robustness of the HBV model calibrated over this period for these sub-basins.

Fig. 7 Balance between four objectives expressed as scaled rank number for maximum values of three measures (combined rank measure, parameter identifiability and model validation) for nine sub-basins.

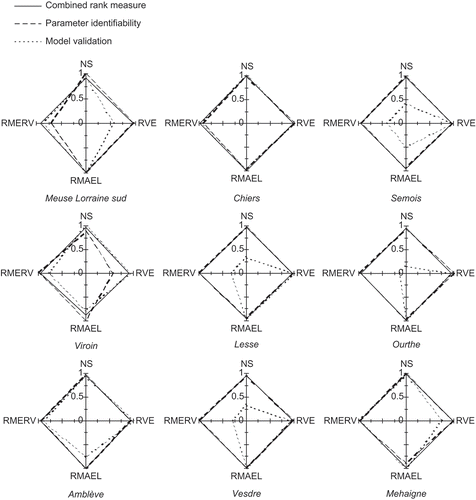
Besides the assessment of the optimum balance between different objectives based on three different measures for each sub-basin, the three measures can be compared. This enables one to use a particular measure for specific targeted model applications or for basins with specific climatological and hydrological characteristics, or to choose one measure for all hydrological modelling studies with conceptual hydrological models. The theoretically optimum balance situation would be one without trade-off, so that every objective is fulfilled as much as possible (r _RVE = r _NS = r _RMAEL = r _RMERV = 1). This would mean a “perfect rhombus” in Fig. 7. For some sub-basins and some measures, this situation is closely approximated (e.g. the combined rank measure and model validation measure for the Chiers are within 2% of the optimum balance). On average, the performance of the parameter identifiability is close to that of the combined rank measure (respectively, 5.0% and 3.6% from optimum performance), where the model validation performance is considerably poorer (22.4% from optimum performance). Since the implementation of the combined rank measure is less complicated than that of the parameter identifiability measure, and the results for the latter measure are sensitive to the definition of identifiability, the combined rank measure is recommended here for use in future studies.

This recommendation is supported by an additional validation test for two sub-basins. In this test, the 10 000 generated parameter sets for the calibration period are applied to the validation period. This enables an assessment of the temporal transposibility of the parameter sets and a subsequent validation of the three different measures. The Chiers and Ourthe sub-basins are selected for this purpose, since they showed rather distinct optimum balances between calibration objectives for the three measures in the calibration period. Figure 8 shows the results of the three different measures for the Chiers and Ourthe for the validation period. It demonstrates that differences in balance between the combined rank measure and parameter identifiability on the one hand, and model validation on the other, are considerable for the Ourthe as has been observed for the calibration period. However, the results for the Chiers in Fig. 8 show this difference as well, where differences between the three measures were very small in the calibration period. The model validation measure tends to force balances for the Chiers away from the objective function related to low flows (RMAEL). This is caused by the large increase in the value of RMAEL in the validation period compared to the calibration period, which in turn is the result of less pronounced low flows in the validation period compared to the calibration period (difference of 45%). This results in a maximum value of ME for a balance where RMAEL is not important and therefore the balance is far from optimum. A similar, although less pronounced, result for ME is found for the Ourthe. It can thus be concluded that the combined rank measure and the parameter identifiability measure show robust and good results in the validation period. The model validation measure is much less robust and very sensitive to the climatological and hydrological conditions represented by the calibration and validation periods.

Fig. 8 Balance between four objectives expressed as scaled rank number for maximum values of three measures (combined rank measure, parameter identifiability and model validation) for Chiers and Ourthe sub-basins in the validation period.

CONCLUSIONS

Three different measures to determine the optimum balance between calibration objectives have been compared using the conceptual hydrological model HBV. Differences in the resulting optimum balance between the combined rank method and parameter identifiability on the one hand, and model validation on the other, were found to be considerable. As could be expected, on average, the performance of the combined rank method is somewhat closer to the theoretically optimum balance (i.e. a situation without trade-off) than that of the parameter identifiability, since the combined rank measure is a kind of reference method to which the other two methods are compared. The performance of the model validation is considerably less than the theoretical optimum. These results are supported by an additional validation test for two sub-basins, where the combined rank measure and the parameter identifiability measure show robust and good results and the model validation measure is much less robust and very sensitive to the climatological and hydrological conditions. The results are believed not to be restricted to the conceptual model used here. In particular, trade-offs between calibration objectives as expressed by the combined rank measure and differences between calibration and validation conditions as expressed by the model validation measure are typical for conceptual hydrological models. The parameter identifiability measure and its results are less general since the parameters examined and hence their identifiability are unique for HBV. However, lessons learned regarding the relation between type of parameter (e.g. fast response parameter) and trade-off behaviour (e.g. more focus on hydrograph shape-related objectives) can be applied to other conceptual models as well.

Regarding the individual measures, several interesting results were found. Application of the combined rank measure generally resulted in values for the SOFs belonging to the top 5–10% of all simulated SOF values. This indicates a small trade-off between different objectives when using this multiple objective function, which is confirmed by the small average difference between the simulated and theoretically optimum balance. Application of the parameter identifiability measure generally resulted in expected relatively large identifiabilities of important parameters of the hydrological model, although the identifiability of one parameter in the fast flow routine of the model was much less than expected. This is partly caused by the interdependence of this parameter and another, very well-identifiable, parameter in this routine of the model. One might argue that almost all identifiability in the fast flow routine is caught by this well-identifiable parameter. Application of the model validation measure resulted in four out of nine sub-basins having better validation than calibration results for the parameter set corresponding to the maximum value of the combined rank measure in the calibration. The validation results of the other five sub-basins were slightly less than the calibration results. For the optimum balance corresponding to the maximum value of the model validation measure for all sub-basins validation results were better than calibration results. Overall, it can be concluded that the model is robust considering the issue of simulation under different temporal (calibration and validation periods) and spatial (different sub-basins) conditions. Obviously, for model calibration purposes the model validation measure can not be used since a validation step is necessary.

Acknowledgements

Meteorological data were provided by KMI (Belgium) and Météo France. Discharge data were obtained from SETHY/WACONDAH (Belgium) and DIREN Lorraine (France).