Prediction of hydrological drought durations based on Markov chains: case of the Canadian prairies

Abstract

Hydrological drought durations (lengths) in the Canadian prairies were modelled using the standardized hydrological index (SHI) sequences derived from the streamflow series at annual, monthly and weekly time scales. The rivers chosen for the study present high levels of persistence (as indicated by values exceeding 0.95 for lag-1 autocorrelation in weekly SHI sequences), because they encompass large catchment areas (2210–119 000 km²) and traverse, or originate in, lakes. For such rivers, Markov chain models were found to be simple and efficient tools for predicting the drought duration (year, month, or week) based on annual, monthly and weekly SHI sequences. The prediction of drought durations was accomplished at threshold levels corresponding to median flow (Q50) (drought probability, q = 0.5) to Q95 (drought probability, q = 0.05) exceedence levels in the SHI sequences. The first-order Markov chain or the random model was found to be acceptable for the prediction of annual drought lengths, based on the Hazen plotting position formula for exceedence probability, because of the small sample size of annual streamflows. On monthly and weekly time scales, the second-order Markov chain model was found to be satisfactory using the Weibull plotting position formula for exceedence probability. The crucial element in modelling drought lengths is the reliable estimation of parameters (conditional probabilities) of the first- and second-order persistence, which were estimated using the notions implicit in the discrete autoregressive moving average class of models. The variance of drought durations is of particular significance, because it plays a crucial role in the accurate estimation of persistence parameters. Although, the counting method of the estimation of persistence parameters was found to be unsatisfactory, it proved useful in setting the initial values and also in subsequent adjustment of the variance-based estimates of persistence parameters. At low threshold levels corresponding to q < 0.20, even the first-order Markov chain can be construed as a satisfactory model for predicting drought durations based on monthly and weekly SHI sequences.

Editor D. Koutsoyiannis; Associate editor C. Onof

Citation Sharma, T.C. and Panu, U.S., 2012. Prediction of hydrological drought durations based on Markov chains in the Canadian prairies. Hydrological Sciences Journal, 57 (4), 705–722.

Résumé

La durée des sécheresses hydrologiques dans les Prairies canadiennes a été modélisée en utilisant des séries de l'indice hydrologique normalisé (IHN), issues de séries de débits annuels, mensuels et hebdomadaires. Les rivières choisies pour l'étude présentent des niveaux de persistance élevés (qui se traduisent par les valeurs supérieures à 0,95 de l'auto-corrélation de rang 1 des séries d'IHN hebdomadaires), car elles drainent de grands bassins versants (2210–119000 km²), et traversent ou proviennent de lacs. Pour ces rivières, les modèles de chaine de Markov se sont avérés des outils simples et efficaces pour prédéterminer les sécheresse de durée (en années, mois ou semaines) à partir des séries d'IHN annuelles, mensuelles ou hebdomadaires. La prédétermination des durées de sécheresse a été réalisée pour des niveaux de seuils correspondant dans les séries d'IHN au niveau de dépassement du débit médian allant de Q50 (probabilité de sécheresse, q = 0,5) jusqu'à Q95 (probabilité de sécheresse, q = 0,05). Pour la prédétermination des durées de sécheresses annuelles le modèle de chaine de Markov d'ordre 1 ou aléatoire a donné des résultats acceptables, sur la base de la formule de position de Hazen pour la probabilité au dépassement, du fait de la faible taille des séries annuelles. Aux pas de temps mensuels et hebdomadaires, c'est la chaine de Markov d'ordre 2 qui a donné des résultats satisfaisants, en utilisant la formule de Weibull pour la probabilité au dépassement. L'élément crucial dans la modélisation des durées de sécheresse est la fiabilité de l'estimation des paramètres (probabilités conditionnelles) de persistance de premier et second ordre, qui ont été estimés en utilisant les notions implicites dans la classe des modèles discrets à moyenne mobile autorégressive. La variance des durées de sécheresse a une importance particulière, car elle joue un rôle crucial pour l'estimation précise des paramètres de persistance. Bien que la méthode de comptage de l'estimation des paramètres de persistance n'ait pas été très satisfaisante, elle a été utile pour établir les valeurs initiales et également pour l'ajustement ultérieur de l'estimation basée sur la variance des paramètres de persistance. Pour des niveaux de seuil bas correspondant à q < 0, 20, même la chaine de Markov d'ordre 1 peut âtre interprétée comme un modèle satisfaisant pour prédéterminer les durées de sécheresse sur la base de séries d'IHN mensuelles et hebdomadaires.

Key words:

• discrete autoregressive moving average (DARMA) models
• drought duration
• second-order Markov chain
• standard hydrological index (SHI)

Mots clefs:

• modèles discrets à moyenne mobile autorégressive (DARMA)
• durée de sécheresse
• chaine de Markov d'ordre 2
• indice hydrologique normalisé

INTRODUCTION

Modelling of hydrological droughts using the threshold level approach advanced by Yevjevich (1967) has been pursued by researchers for predicting the drought of longest duration (L_T ) over a period of T time units (year, month and week). The analytical tools used in modelling include: the theory of runs, the theorem of extremes of random numbers of random variables (Todorovic and Woolhiser 1975, Sen 1980), hereafter referred to as the “extreme number theorem”; Markov chains (Sharma and Panu 2010); and discrete autoregressive moving average (DARMA) schemes (Chung and Salas 2000, Cancelliere and Salas 2010). Streamflow has been the hydrological variable commonly used to study hydrological droughts, with the probability distribution function (pdf) of flows assumed to obey normal, gamma or lognormal distributions. In a majority of hydrological drought studies, threshold level (also referred to herein as cut-off level) is chosen as the long-term mean or median of streamflow time series. On a monthly or weekly basis, the mean or median flows for respective months or weeks are taken as threshold levels. Essentially, a major reason for using the threshold level at q = 0.5 (median level) is to support the notion that parameters of duration and magnitude of a drought at high threshold levels may turn out to be conservative and, thus, provide a rational basis for designing water storage systems. However, threshold levels such as q = 0.4, 0.3, 0.2, 0.1 and 0.05 also have relevance in terms of the recognition of physical prevalence of droughts and the consequent water resources management, such as rationing (e.g. curtailment of water supply hours, regulating water for kitchen gardening and washing). The threshold level at q = 0.05 means that flows are being cut off at a level such that 5% flows are below this level (or 95% flows are above it) on a flow duration curve. Such a low threshold level relates to extreme drought conditions that lead to an acute lack of moisture in the atmosphere, and signifies the existence of widespread ground-level dry conditions. Vis-à-vis a high threshold level, such as q = 0.5 or 0.4, the droughts are mild, their onset may not be readily visible and the consequences may have occurred unnoticed. Therefore, there is a need to extend analysis and modelling of drought at the threshold levels representing low flows rather than mean or median levels.

Sharma and Panu (2010, 2012) suggested the use of a standardized hydrological index (SHI) as a measure for defining and modelling hydrological droughts. The SHI _i (= (x_i  – μ)/σ; with mean μ and standard deviation σ) represents a standardized value of the time series of the drought variable such as streamflow, x_i . It should be noted that the concept of SHI is analogous to SPI (standardized precipitation index, Mckee et al. 1993), as used in the context of meteorological droughts, except that SPI represents a standardized and normalized entity (converted into an equivalent normal probability variate), whereas SHI is only a standardized entity and thus implicitly inherits the non-normal character of the flow series. The SHI sequence turns out to be virtually stationary, and can be used as a platform for modelling and prediction of the drought duration, or length, L_T .

Droughts are frequent in the Canadian prairies, encompassing the provinces of Alberta, Saskatchewan and Manitoba, and their impacts on agriculture and the beef industry are widely recognizable. Therefore, a need exists for the analysis of hydrological droughts and associated durations and magnitudes in the prairie region. In turn, suitable relationships for predicting the expected hydrological drought lengths, E(L_T ), based on annual, monthly and weekly flow series, are required at threshold levels corresponding to the drought probabilities, q ranging from 0.5 to 0.05.

A streamflow time series that is largely from the Canadian prairies forms the basis for the analysis. These rivers are typical in the sense that the persistence features are very strong and therefore offer unique challenges and opportunities for analysis and modelling of drought durations. In earlier studies, Sharma and Panu (2008, 2010) analysed E(L_T ) for rivers displaying modest levels of persistence, where the parameters of Markov chain models were estimated using the trivial counting- (or enumeration-) based method. However, the use of that method for the estimation of model parameters on rivers reported herein resulted in significant under-prediction of E(L_T ). Consequently, the need arose to improvise a parameter estimation technique which, in turn, would improve the predictions of E(L_T ), and a DARMA-based method of parameter estimation was therefore considered relevant.

The DARMA models were developed by Jacobs and Lewis (1977) and are similar to the autoregressive integrated moving average (ARIMA) models developed by Box and Jenkins (1976). The characteristic difference between these two classes of models is that, while the former take only discrete values of the variable (0, 1, 2 ..., e.g. dry state as 0 and wet state as 1), the latter take continuous values (such as daily flows in a river). Though analogous to the ARIMA class of models, the DARMA models contain autoregressive and moving-average components, with the parameters estimated from the autocorrelation function of the sequences of the discrete values. The statistical properties of DARMA model parameters are well documented (Jacobs and Lewis 1977, Chang et al. 1984). A major focus of this paper is the estimation of parameters involving DARMA concepts in the Markov chain models for reliably predicting E(L_T ) at monthly and weekly time scales.

FLOW DATA ACQUISITION AND PRELIMINARY ANALYSIS

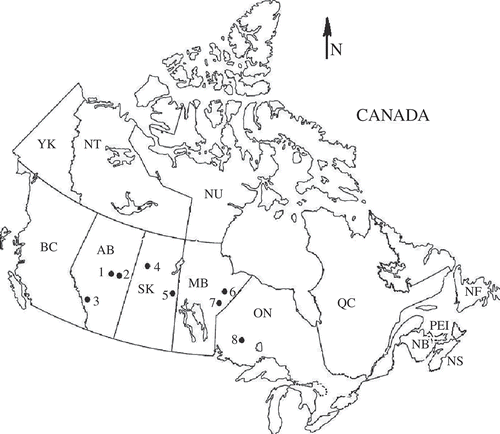
Data for the analysis constitute natural (i.e. unregulated) and uninterrupted flow records of the seven rivers situated in the Canadian prairies (Fig. 1), and the English River in northwestern Ontario, chosen because its persistence characteristics are similar to the prairie rivers and thus provide an additional data set to corroborate the results. The major distinguishing feature of these rivers is a high value of lag-1 autocorrelation (ρ₁) ranging from 0.4 to 0.997 (Table 2) for monthly and weekly flow sequences, and a large catchment size ranging from 2210 to 119 000 km². The daily and monthly flow data for these eight rivers were extracted from the Canadian Hydrological database of Environment Canada (EC 2009) and, subsequently, the daily flows were converted into weekly flows (52 weeks in a year) following a procedure described in Sharma and Panu (2010). The need for data infilling was minimal (except for the Islands Lake River) and, wherever missing data existed, they were infilled, either using a standard correlation technique, or through extrapolation of monthly or weekly hydrographs (Panu et al. 2003). Since monthly and weekly flows tend to be highly correlated, the infilled data are presumed to be reasonably accurate, at least for the purpose of the study. Daily flow records of the Island Lake River contain a large number of gaps that could not reliably be infilled by the aforesaid methods. This precluded the reliable assimilation of daily flows into weekly flows and, therefore, the weekly analysis for drought purposes could not be conducted on this river.

Fig. 1 Location of hydrometric stations used in the analysis.

The names and relevant details of the selected rivers with a historical database of between 35 and 98 years are summarized in Table 1, together with statistics, such as mean, μ, coefficient of variation, cv and lag-1 autocorrelation, ρ₁, of the annual flow data. As is apparent from this table, the rivers selected for the study represent diversity in terms of flow regimes (annual flows), with cv ranging from 0.13 to 0.76 and ρ₁ from 0.02 (random or virtually no annual carry-over effect) to 0.62 (high degree of annual carry-over effect). Such a large variability in the flow regimes offers a significant advantage in testing the model hypothesis and deducing inferences based on the model outputs.

Table 1  Particulars of the rivers chosen for the study with salient statistical features based on annual flows (see Fig. 1 for locations)

No.	Name of river and location	Period of record	Area (km^2)	Mean (m^3/s)	cv	γ	ρ1 (Model)
1	Athabasca River at Athabasca (54°43′ 20″N, 113°17′10″W)	1941–2008 (N = 57)	74 600	426.21	0.23	0.97	0.16 (Random)
2	Beaver River at cold Lake Reserve (52°21′18″N, 10°13′2″W)	1956–2008 (N = 53)	14 505	18.76	0.76	1.33	0.37 (AR-1)
3	Bow River at Banff (51°10′ 30″N, 115°34′10″W)	1911–2008 (N = 98)	2 210	39.23	0.13	0.09 (normal)	0.02 (Random)
4	Churchill River above (56°38′ 47″N, 104°44′ 05″W)	1964–2008 (N = 45)	119 000	275.61	0.39	0.88	0.62 (AR-1)
5	Sturgeon–Weir River at outlet of Amisk Lake (54°26′20″N, 103°10′30″ W)	1961–1995 (N = 35)	14 600	46.97	0.43	0.97	0.62 (AR-1)
6	Gods River below Allen Rapids (55°01′35″N, 93°50′10″W )	1948–1993 (N = 46)	25 900	161.41	0.27	0.54 (normal)	0.31 (AR-1)
7	Islands Lake River near Island Lake (54°03′ 34″N, 94°39′34″ )	1934–1994 (N = 61)	14 000	86.37	0.28	0.23 (normal)	0.27 (AR-1)
8	English River at Umfreville, Ontario (49°52′ 30″N, 91°27′30″)	1922–1908 (N = 87)	6 230	58.24	0.34	0.33 (normal)	0.19 (Random)
cv: coefficient of variation, γ: skewness, and ρ1: lag-1 serial correlation of annual stream flow sequences.

Table 2  Summary of autocorrelations of SHI and salient statistical parameters of monthly and weekly flow (non-stationary) sequences

River	μ* (m^3/s)	Monthly flows					Weekly flows
		cv ^†	γ	ρ1	ρ2	ρ ^‡	cv ^†	γ	ρ1	ρ2	ρ^‡
Athabasca	424.56	0.35	1.25	0.61	0.45	0.73	0.42	1.26	0.819	0.644	0.901
Beaver	18.63	1.02	1.83	0.81	0.68	0.64	1.11	1.92	0.921	0.814	0.871
Bow	39.09	0.24	0.71	0.49	0.27	0.66	0.31	0.92	0.726	0.521	0.916
Churchill	275.27	0.44	0.87	0.96	0.90	0.93	0.45	0.87	0.996	0.986	0.994
Sturgeon	46.91	0.49	1.13	0.97	0.91	0.94	0.49	1.14	0.997	0.990	0.995
Gods	161.29	0.38	0.55	0.96	0.87	0.93	0.34	0.52	0.995	0.986	0.996
Islands	86.19	0.38	0.89	0.88	0.72	0.81	–	–	–	–	–
English	58.10	0.52	0.55	0.78	0.58	0.65	0.54	1.24	0.968	0.899	0.961
*μ is the average of 365 daily values.
^†cv is computed as the ratio of the average of 12 monthly or 52 weekly standard deviations to their means of the respective periods; likewise γ is the average value of 12 months or 52 weeks.
^‡ρ is lag-1 autocorrelation of the original non-stationary series of monthly or weekly flows, whereas ρ1 and ρ2 are lag-1 and lag-2 autocorrelations from the SHI (standardized) series.

Persistence characteristics of annual SHI sequences

Based on the standard statistical test for lag-1 autocorrelation, ρ₁ (95% confidence interval =±1.95/√n), it can be stated that rivers in the prairies, except the Athabasca and the Bow, present significant carry-over effect from year to year. The English River also tends to display a negligible level of persistence. This was further confirmed by transforming the annual flow series into SHI _i or e_i series (SHI _i  =e_i  =(x_i – μ)/σ), to which either a random or an autoregressive order-1 (AR-1) model fitted satisfactorily (Table 1). Therefore, on an annual basis, a model that accounts for first-order persistence (in addition to independent or random) occurrences of successive drought events is needed for modelling the drought durations.

Persistence characteristics of monthly and weekly SHI sequences

The monthly and weekly flow series were standardized by removing the periodicity through month-by-month or week-by-week standardization, such that the resulting series u_{y ,t}  = {(x_y,t  – μ _t )/σ _t } is stationary with mean zero and unit standard deviation. In this expression, x_{y ,t} is the yth year flow (y = 1, 2, 3, …, n; i.e. n year of data record) and the tth month or week (t = 1, 2, 3, …, 12, or t = 1, 2, 3, …, 52), and μ _t and σ _t are the mean and standard deviation, respectively, corresponding to the tth flows. The entity u_{y ,t} is a standardized term and is therefore tantamount to SHI _i with i ranging from 1 to y × t. The values of the first two autocorrelations (ρ₁ and ρ₂) are indicative of the highly persistent nature of SHI _i sequences at monthly, as well as weekly, time scales. In fact, at the weekly time scale, the values of ρ₁ and ρ₂ reach 0.997 (Table 2). The value of lag-1 autocorrelation (ρ) in the non-standardized (original) monthly or weekly flow series is also high, suggesting that flows are strongly persistent. Other relevant information that emerges from Table 2 is that γ and cv also tend to be closely tied through a relationship γ =2cv, implying that monthly and weekly flow series can be described by the use of a gamma pdf, in conformity with earlier investigations by Sharma and Panu (2008, 2010).

Before attempting Markov chain models of varying orders, it is prudent to fit the autoregressive moving average (ARMA) family of models to SHI _i sequences, to make a preliminary assessment of the order of the memory contained in these sequences. The fitting procedures of ARMA models (Box and Jenkins 1976) indicate that models up to autoregressive order-2 (AR-2) are adequate for monthly SHI _i sequences. The adequacy of fit of models to data was assessed using the Portmanteau statistic, based on the first 25 values of the autocorrelations in the series of residuals, as prescribed in Box and Jenkins (1976). For weekly SHI _i sequences, the AR-2 model was found adequate for very strongly-persistent SHI _i sequences of two rivers (Gods and Sturgeon), while even AR-3 or ARMA (1,1) models were found inadequate for the remaining rivers. Since, the Gods and Sturgeon rivers (having the highest degree of persistence) are adequately captured by the memory structure of the AR-2 model, the remaining rivers (characterized by a slightly lower level of persistence) can reasonably be presumed to follow a regime of the AR-2 model. It is noted that the rivers with a relatively high memory content either originate in lakes, or pass through lakes and, therefore, carry-over impacts tend to be delayed for up to two weeks and sometimes slightly beyond two weeks.

The AR(2) model appeared to dominate the persistence features; therefore, in the discrete (specifically in binary) domain its counterpart Markov chain-2 model was considered as the first choice for estimating monthly, as well as weekly, drought lengths. Since monthly SHI _i sequences tend to display a smaller degree of persistence (smaller values of ρ₁), it makes sense to consider the first-order Markov chain (Markov chain-1) model to estimate month-scale drought durations. On a weekly time scale, since some rivers exhibit a tendency to possess memory beyond second-order, it is sensible to consider the use of the Markov chain-3 type of models to describe the underlying persistence structure. In summary, the first-, second- and third-order Markov chain models are considered as competing candidates for the prediction of drought durations at monthly and weekly time scales.

MARKOV CHAIN MODELS—RELEVANT PRELIMINARIES

From the preliminary analysis described above, it is reasonable to consider that a generalized third-order Markov chain model (Markov chain-3) can be hypothesized for weekly SHI _i sequences that can be reduced to Markov chain-2 or Markov chain-1, or even random (independent) model, for other time scales. The model structure is briefly explained as follows.

When the SHI _i or e_i series is cut off at a threshold level e ₀, the values above that level are positive, or in wet (w) state, and those below the level are negative, or in drought (d) state. So, the e_i series can be transformed into a sequence of discrete states in terms of w and d (for example, wwwddddwwwwdd). One can define the following notations for probabilities:

‐	P(d) (simple probability), the probability of any week being a drought week at a given threshold level =q;
‐	P(d|d) (conditional probability), the probability of any week being a drought week given that the previous week was also a drought week (first-order persistence) =qq ;
‐	P(d|d,d) (conditional probability), the probability of any week being a drought week given that the previous two weeks were also drought weeks (second-order persistence) =qqq .

Likewise, for third-order probabilities, P(d|d,d,d) =q_qqq and P(w|d,d,d) =p_qqq . Similarly, p = P(w); p_p = P(w|w); and p_pp = P(w|w,w) and, likewise, p_qq = P(w|d,d); q_p = P(d|w); q_qp = P(d|d,w); q_qqp = P(d|d,d,w), and so on. The simple and conditional probabilities sum to 1 for the zero-, first-, second- and third-order dependence, respectively, as follows:

(1a)

(1b)

(1c)

(1d)

The probability distribution of drought lengths and wet spells in a sequential occurrence (such as wwwwdwwddwddddww---d) can be deduced by using the first principles of simple and conditional probabilities (Sharma and Panu 2010). Since the memory terms are being considered up to the third-order in the weekly SHI _i sequences, the Markov chain-3 equations can be derived by using the geometric law of probabilities (Todorovic and Woolhiser 1975, Chin 1977, Sen 1990, Mathier et al. 1992). By using the analogy and detail of model derivation (equation (3)(3)) for the Markov chain-2 model (Sharma and Panu 2010), the following forms of Markov chain model can be derived.

Markov chain-3:

(2)

Equation (2)(2) can be reduced to a lower-order Markov chain as follows:

Markov chain-2:

(3)

Markov chain-1:

(4)

Random model:

(5)

It is emphasized that T is taken as the sample size (n) of the river under consideration such that the probability of exceedence is equal to 1/n, which is equivalent to an empirical estimate of the return period through the Weibull plotting position (= 1/(n + 1) ≈ 1/n = 1/T). Such a simplification for computing the probability of exceedence in drought investigations is not uncommon (e.g. Burn et al. 2004, Yoo et al. 2008). The Weibull plotting position formula is generally applicable for a large sample size, which is readily available for the monthly and weekly analysis of streamflows. For a small sample size, such as annual flows, the Hazen plotting position formula (= (2m – 1)/2n = 1/2n; m = 1, Viessman and Lewis 2003) was found to be more reliable in the present study, and is discussed later. It can be seen from 2–4 that four, three and two parameters, respectively, are needed for Markov chain-3, Markov chain-2 and Markov chain-1 models, for a given level of q and sampling period, T. For a random model (also referred to as Markov chain-0), no additional parameter is needed, other than already known q and T. These parameters can be estimated from the historical data using a counting method. The SHI _i (or e_i ) sequences can be truncated at the levels corresponding to q = 0.5, 0.45, 0.4, 0.35, 0.3, 0.25, 0.2, 0.15, 0.10 and 0.05 to represent droughts of varying severity. The truncated levels at a step level equal to 0.05 offer an advantage of increased sample size for testing the adequacy of the hypothesized model.

Estimation of simple and conditional probabilities (i.e. persistence parameters)

The parameters q, q_q , q_p , q_qq and q_qp can be estimated (Sen 1990) by counting the occurrences of w and d that are obtained by truncating the e_i sequences at the desired threshold level e ₀ (such that q is equal to 0.5, or any other chosen value of q). Sufficiently accurate estimates of q, q_p , q_qp , q_qq , q_qqq and q_qqp can be obtained from the historical data with sample size n > 1000 (Chin 1977). The calculations were effectively accomplished by writing a program in Visual Basic on the Microsoft Excel framework.

It is noted that stable and reliable estimates of probabilities require a large sample size (Chin 1977). On an annual time scale, the sample size is generally small; therefore, a difficulty may arise in obtaining reliable estimates of the probabilities. In this situation, approximate first-order probabilities (q_p , q_q ) may be obtained from the following closed-form equation (Sen 1977):

(6)

where z ₀ is the cut-off level as a standard normal variate (such as 0, –0.2, –0.3) corresponding to the value of q. When SHI _i sequences follow the normal pdf, then, at q = 0.5, the value of z ₀ =0 (likewise, at q = 0.05, z ₀ =–1.65) is obtained from the standard normal probability table. When the SHI _i sequence is gamma distributed, then the standardized cut-off level SHI₀ (= e ₀) should be first converted to z ₀ and then inserted in equation (6)(6) to obtain the estimate of q_q . The following simple Wilson-Hilferty transform (Viessman and Lewis 2003) can also be used to obtain the values of z ₀ for SHI₀ based on the gamma pdf of streamflows:

(7)

where z ₀ and e ₀ are the standardized normal and standardized gamma variates, respectively, and γ is the coefficient of skewness.

A value of q_p can be obtained from the trivial relationship, q_p  =(1 – p_p ) and p_p can be computed from equation (6)(6) by replacing q with p and q_p with p_p . In the above equation, ρ₁ is lag-1 autocorrelation and v is the dummy variable of integration. At the level of q = 0.5, it can be noted that q_p = (1 – q_q ). However, it should be noted that there are no known closed-form equations in the literature for estimating second- and higher-order probabilities, such as q_qp , q_qq , q_qqq and q_qqp .

RESULTS AND DISCUSSION

The prediction of E(L_T ) using Markov chain models involving two pertinent methods of parameter estimation is presented. First, the utility and limitation of the counting method and subsequently the DARMA-based procedure involving run length for the estimation of relevant model parameters is explored and discussed.

Predicting E(L_T )—Markov chain models (parameters by counting method)

Case of annual SHI sequences

For analysis, annual SHI _i sequences were truncated at the level SHI₀ (or e ₀) such that q attains the value of 0.5. Various values of e ₀ were tried out, to arrive at the exact value of q by counting and computing the ratio in the observed SHI _i sequence. Because of the limitation of sample size, the exact value of 0.5 was difficult to attain at any pre-selected level of e ₀. The same difficulty was experienced at all threshold probability levels from 0.5 to 0.05. To elucidate the point, the case of the Churchill River (a typical river displaying persistence at the annual level) is presented. The nearest q value to q = 0.5 that could be identified from the annual SHI _i sequence was 0.51 and the corresponding cut-off level in terms of SHI₀ (= e ₀) was –0.15. At this cut-off level, q_q and q_p were estimated by ratios (counting method) as 0.78 and 0.22, respectively. The exercise was repeated for all truncation levels and the nearest values of q that could be obtained were: 0.46 (instead of 0.45), 0.40 (0.40), 0.33 (0.35), 0.30 (0.30), 0.24 (0.25), 0.19 (0.20), 0.14 (0.15), 0.11 (0.10), 0.052 (0.05). The respective e ₀ values obtained were –0.27, –0.41, –0.48, –0.56, –0.73, –0.88, –1.03, –1.08 and –1.22. The values of nearest q (by ratios of observed) at median (q = 0.5) level and the corresponding e ₀ for all rivers studied are shown in Table 3. For a normally-distributed SHI sequence at q = 0.5, a value of e ₀ =0 should be obtained. It can be seen from Table 3 that e ₀ values are close to 0 for the Bow, Gods and English rivers, suggesting their proximity to the normal pdf. For the other rivers, the e ₀ values are less close to 0 and suggest the non-normal pdf of flow sequences for these rivers.

Table 3  Summarized values of threshold levels, conditional probabilities, observed (L _T -ob) and predicted, E(L _T ) at the threshold level corresponding to q = 0.5 for annual drought lengths

River	T (year)	Flow ratio *	e 0 -ob	Counting method		LT -ob (year) ^†	E(LT ), (year)		Model used
				q	q q		Markov-1 or random ^‡	Extreme ^§
Athabasca	57	0.97	−0.15	0.51	0.59	6(1998−2003)	6(5)	6	Random
Beaver	53	0.77	−0.29	0.51	0.78	16(1980–1995)	11(8)	10	Markov-1
Bow	98	1.01	0.04	0.50	0.49	7(2000–2006)	7(6)	6	Random
Churchill	43	0.94	−0.15	0.51	0.78	8(1988–1995)	10(8)	9	Markov-1
Sturgeon	35	0.88	−0.27	0.49	0.59	7(1987–1993)	6(5)	6	Markov-1
Gods	41	0.94	−0.04	0.50	0.61	7(1987–1993)	7(5)	6	Markov-1
Islands	61	0.96	−0.20	0.51	0.48	6(1939–1944)	6(5)	5	Markov-1
English	87	0.98	−0.05	0.51	0.57	6(1979–1984)	6(6)	6	Random
*ratio of median flow to mean flow (annual).
^†values in parentheses represent drought duration.
^‡values in parentheses are based on the Weibull plotting position formula; those without parentheses are based on the Hazen plotting position formula.
^§values were computed using the extreme number theorem.

The other difficulty encountered pertains to the value of q_q , which is crucial for the estimation of E(L_T ) in equation (4)(4). It was noticed that, at low cut-off levels, such as q = 0.10 and 0.05, q_q by counting method turned out to be 0, which hindered the computation of E(L_T ). The problem was salvaged by inserting ρ₁ and z ₀ in equation (6)(6) to obtain an estimate of q_q . Since z ₀ is a standard normal variate corresponding to e ₀, a relationship is required to convert e ₀ into z ₀. For the rivers in close proximity, with normal pdf, a trivial relationship e ₀ =z ₀ will work, but for the rivers with flows falling in the skewed probability regime, prior knowledge of the pdf of flows is needed. Since the level of skewness (γ) is mild, annual flows can be presumed to follow a gamma probability distribution. The hypothesis of gamma pdf emanates from the studies for Canadian rivers (Sharma and Panu 2008, 2010), in which monthly and weekly flows are shown to exhibit gamma probability distribution. In most instances, when flow sequences at small time scales (say daily, weekly, monthly) are aggregated to the annual level, the skewness is significantly reduced, making the annual flow sequences obey the normal pdf very closely. If mild skewness is still present, then it can be easily tackled by using the gamma pdf. Therefore, equation (7)(4) was used to transform e ₀ to z ₀ by involving q and γ and, thereby, q_q was estimated. The need for estimating q_p by this method did not arise as the counting method was able to provide some positive values of this parameter.

The e ₀ values derived as above at various q levels were used to truncate the annual SHI _i sequences to determine the observed drought lengths (L_T -ob). The predicted values of E(L_T ) were obtained by the Markov chain-1 model (equation (4)(4)) or random model (equation (5)(5)), depending on the persistence feature imbibed in the SHI _i sequence. For example, in the rivers with insignificant persistence, q_q is not required and therefore equation (5)(5) was used. It is noted that in equations (4)(4) and (5)(5), the exceedence probability was computed using the Weibull plotting position formula. According to the persistence behaviour of SHI _i sequences (Table 1), the predicted and observed values of L_T at q at the 0.5 level are shown in Table 3.

It can be seen from Table 3 that the drought lengths predicted using the Weibull method (shown in parentheses) tend to be under-predicted. Note the under-prediction of E(L_T ) by almost 8 years for the Beaver River. This is because of the starkly different characteristics of this river compared to the other rivers—for example, flows are highly skewed (γ =1.33), year-to-year variability (cv =0.76) is high, and the median flow is 77% of the mean annual flow, compared to the other rivers with median flow of 88% or more of the mean annual flow (Table 3) and cv < 0.43 (Table 1). A close examination of the flow data for the Beaver River suggests that a long period of drought that occurred during 1980–1995, with a tendency to break in 1985, could reduce the value of L_T -ob to 11 years. Such unusual behaviour of drought duration at the median level for the Beaver River places the L_T -ob value to be an outlier. However, at lower threshold values (q = 0.45–0.05), the predicted values of E(L_T ) for this river compared fairly well, as depicted in Fig. 2.

Fig. 2 Comparison of L_T -ob and E(L_T ) on an annual time scale by Markov chain-1 or random model: (a) Hazen plotting position, and (b) Weibull plotting position.

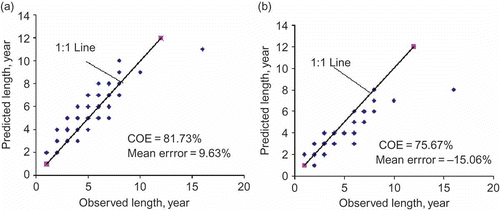
The adequacy of fit of predictions based on the chosen model was evaluated using two performance statistics, the coefficient of efficiency, COE (Nash and Sutcliffe 1970) and the associated mean error of prediction as was demonstrated in earlier publications (Sharma and Panu 2008, 2010). The COE statistic for the plot was found ≈76% with under-prediction of the order of 15% (mean error =–15.06%). In order to improve the under-prediction issue, the exceedence probability was computed by the Hazen plotting position formula i.e. exceedence probability (=1/2n, Viessman and Lewis 2003). For small sample sizes, the utility of the Hazen formula has been discussed by Gumbel (1958). Using the Hazen formula, the value of T (=2 × n) in equations (4)(4) and (5)(5) and the resultant E(L_T ) values tend to be larger comparable to the observed counterpart as revealed by the plot (Fig. 2(a)) and increase in COE by 6% (COE =81.73%) with a slight over-prediction to 9.63%. Most importantly the correspondence between L_T -ob and E(L_T ) was improved at the median level (Table 3, column 8, without parentheses). Furthermore, a slight over-prediction is a desirable feature for mobilizing resources and storage-size design to combat the drought situations. Therefore, for small sample sizes as commonly encountered in annual flow series; the Hazen formula tends to be more reliable than the Weibull formula for Markov chain analysis of drought lengths.

Panu and Sharma (2009) have used the extreme number theorem to predict the T-year drought duration on an annual basis. The theorem is strictly applicable to the random structure of SHI _i sequences but could be used when a weak persistence exists. For illustrative purposes, the results based on this theorem to predict E(L_T ) at the cut-off level of q = 0.5 are shown in Table 3, where it is apparent that the values of E(L_T ) are under-predicted. However, when the theorem was used at all threshold levels for predicting E(L_T ), the COE turned out to be close to 83% (82.55%) with under-prediction to 7.5% (mean error =–7.53%). Though the COE has increased, a slight under-prediction is still present. In a nutshell, the extreme number theorem appears to be competitive, although it is computationally more rigorous and mathematically involved. Further, it is noted that the equations (Panu and Sharma 2009) in the method based on the extreme number theorem are not straightforward and require numerical integration, unlike the Markov chain model, in which equations (4)(4) and (5)(5) are trivial, efficient and relatively intelligible.

On an annual time scale and based on the above results, it can be conjectured that Markov chain models in combination with the Hazen formula tend to provide better prediction of drought lengths. For pragmatic reasons, the Markov chain models (order 1 or 0) can be used for predicting the hydrological drought lengths on an annual basis, with the exceedence probability computed from the Hazen formula. As noted earlier, the rivers originating in lakes or passing through lakes tend to show first-order persistence in the annual SHI _i sequences, whereas the SHI _i of rivers unaffected by the storage impacts of lakes tend to be independent or random in the stochastic sense. As a consequence, rivers draining large catchment areas that are riddled with lakes experience longer drought years, which is clearly evident from the predicted values of E(L_T ) shown in Table 3.

The best interpretation of droughts in agriculturally intensive regions of the Canadian prairies can be made from the drought behaviour of the Bow River, which is located around the latitude of 51°N. The river has near normal pdf of streamflows with negligible persistence in terms of SHI _i sequences. Two major historical droughts have occurred on this river, one from 1939 to 1945 (7 years) with the intensity (= magnitude/duration) of 0.96 and a recent one from 2000 to 2006 (7 years) with 0.91 intensity. The severe drought years were 1941 and 1945, with drought intensity of 1.67 and 1.73, respectively, during the 1940s spell, and 2001 (drought intensity of 2.1) in the more recent period. Bearing in mind that the intensity of drought in a year is equivalent to SHI of that year, the drought of 2001 with such high intensity can be classified as extreme drought (in view of normal pdf of flows, SPI < –2 and SHI =SPI (i.e. standardized precipitation index). It is recognized that drought severity has also been classified as mild, moderate, severe and extreme, based on the values of SPI (Nalbantis and Tsakiris 2009). Such an extreme drought was starkly evident in terms of devastation of crops, forages and water supplies over much of the regions in the Canadian prairies (Rannie 2006). It is known that severe to extreme droughts are often considered as harbingers of extensive forest fires that occur in the boreal forests of central and eastern Canada (Scott and Sauchym 2006). The other extreme drought year observed was 1949, with a SHI value or intensity equal to 2.17. Since the drought of 1949 was an isolated event, its impacts were not widespread because of the occurrence of succeeding wet years.

Table 4  Illustration of calculations for monthly and weekly drought lengths for Athabasca River, parameters estimated by counting method

q	LT -ob	Markov parameters									E(LT )
		e 0	qq	qp	qqq	qqp	α1	α2			1*	2^†
Monthly drought parameters (T = 684):
0.50	22	−0.17	0.77	0.23	0.81	0.62	1.05	0.77			18	21
0.45	22	−0.30	0.72	0.29	0.78	0.55	1.08	0.71			15	18
0.40	19	−0.44	0.71	0.19	0.74	0.63	1.04	0.85			14	15
0.35	14	−0.57	0.68	0.17	0.72	0.59	1.06	0.82			12	13
0.30	10	−0.66	0.64	0.15	0.66	0.60	1.03	0.91			11	11
0.25	9	−0.76	0.59	0.14	0.62	0.54	1.05	0.87			9	10
0.20	8	−0.86	0.55	0.11	0.55	0.57	1.00	1.04			8	8
0.15	8	−0.97	0.48	0.09	0.54	0.52	1.13	0.96			6	7
0.10	5	−1.06	0.41	0.07	0.43	0.39	1.05	0.91			5	5
0.05	5	−1.27	0.35	−0.04	0.34	0.36	0.97	1.06			4	4
		e 0	qq	qp	qqq	qqp	qqqq	qqqp	α1	α2	1*	2^†	3^‡
Weekly drought parameters (T = 2964):
0.50	44	−0.17	0.85	0.15	0.88	0.70	0.89	0.78	1.04	0.80	34	40	44
0.45	42	−0.32	0.85	0.13	0.86	0.78	0.87	0.78	1.01	0.91	33	35	37
0.40	42	−0.43	0.82	0.12	0.84	0.75	0.86	0.75	1.03	0.89	29	31	34
0.35	41	−0.53	0.81	0.11	0.83	0.73	0.84	0.76	1.03	0.88	26	28	30
0.30	35	−0.61	0.78	0.10	0.80	0.74	0.81	0.74	1.03	0.93	22	24	25
0.25	22	−0.71	0.76	0.08	0.77	0.71	0.79	0.73	1.01	0.92	20	21	22
0.20	20	−0.81	0.72	0.07	0.74	0.68	0.77	0.64	1.03	0.92	17	17	20
0.15	18	−0.91	0.68	0.06	0.70	0.64	0.72	0.63	1.03	0.91	14	15	16
0.10	16	−1.04	0.65	0.04	0.68	0.58	0.70	0.64	1.05	0.85	12	13	14
0.05	2**	−1.21	0.60	0.02	0.63	0.55	0.71	0.45	1.05	0.87	9	9	11
* Markov chain-1 model, ^† Markov chain-2 model, and ^‡ Markov chain-3 model.

Case of monthly SHI sequences

Based on the aforementioned discussion, the monthly SHI _i sequences were truncated at the level e ₀ such that corresponding q values range from 0.5 to 0.05 (median and downwards) with a step of 0.05. In view of there being sufficiently large samples of observed records at the monthly and weekly time scales, no difficulty was encountered in attaining the exact value of q. Likewise; no difficulty was noticed in estimating the values of first- and second-order probabilities (i.e. non-occurrence of zero values for probabilities by the counting method). The E(L_T ) values were predicted using Markov chain-2 and Markov chain-1 models and compared with the observed counterparts (L_T -ob). For illustrative purpose, the detailed computations for the Athabasca River are summarized in Table 4.

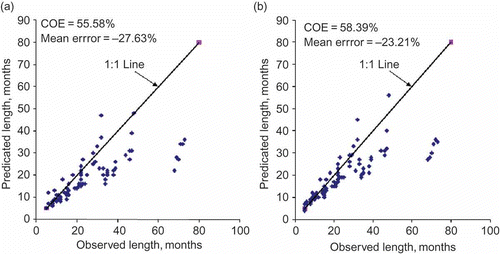
The predicted, E(L_T ) and observed drought length (L_T -ob) are plotted in Fig. 3, from which it is evident that the Markov chain-2 or Markov chain-1 models are under-predicting the drought lengths. However, the performance of the Markov chain-2 model appears to be marginally better (COE =58.39%, mean error =–23.21%) than the Markov chain-1 model (COE =55.58%, mean error =–27.63%). The correspondence between observed and predicted drought lengths was satisfactory only at low threshold levels, viz. 0.20, 0.15, 0.10 and 0.05. At high threshold levels, particularly at 0.5 (median level) and 0.4 the discrepancy was highly conspicuous. One reason for this discrepancy in the prediction of E(L_T ) can be ascribed to the high sensitivity of the parameter q_q (first-order situation) or q_qq (second-order situation) because one requires a large sample size (>1000) for stable parameters (Chin 1977). Because the above parameter appears as a logarithmic function in the denominator of equations (3)(3) and (4)(4), a small numerical change in its value makes a significant change in its logarithmic value and thus markedly changes the prediction of E(L_T ). This is not the case for other parameters, such as q, q_p or q_qp , because they appear in the numerator and are multiplied by T. The logarithm of the product thus changes marginally, even with significant change in the values of the above parameters. Another plausible reason could be ascribed to values of L_T -ob, which are relatively insensitive to minor variations in the cut-off level e ₀. To elucidate the point, for the Churchill River, if the SHI _i sequence is cut off at a level (e ₀ =–0.20 or –0.40), the value of L_T -ob is still the same, i.e. 47 months. In fact, when e ₀ was changed from –0.17 to –0.70, the L_T -ob changed from 48 to 46, or nearly remained constant at the level of 47 months. Among other reasons, one can argue that the Markov chain-1 or Markov chain-2 model represents an over-simplification of the long memory processes in such river flows. In other words, it can be stated that there is a scope for improving the estimates of parameters or inducting alternate models that are capable of simulating the strong short-term and/or weak long-term persistence in flow series.

Fig. 3 Comparison of monthly L_T -ob and E(L_T ) using (a) Markov chain-1 and (b) Markov chain-2 models.

At this point, the extreme number theorem-based method was also applied to estimate the E(L_T ) values in monthly SHI _i sequences similar to the annual SHI _i sequences. The model predicted L_T values that were shorter than those obtained by Markov chain models. This observation further affirmed that, in the situation of a strong first-order persistence (ρ₁ being high), the extreme number theorem-based method does not work well and, therefore, is applicable only to weakly persistent or random sequences of the drought variable.

Case of weekly SHI sequences

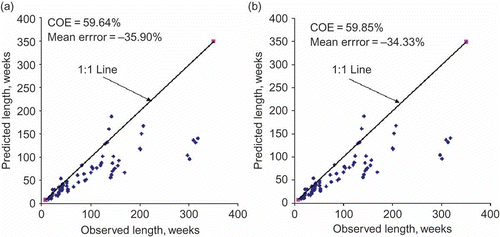
Following the model fitting procedures of the ARMA family, the weekly SHI _i sequences tended to have complex memory components. For example, two rivers exhibit second-order memory while the remaining rivers were found to possess third-order memory or even beyond. Therefore it is reasonable to consider Markov chain-3 and Markov chain-2 models as a first choice for modelling drought lengths. The observed and predicted L_T values obtained are plotted in Fig. 4 and the relevant detailed computations are summarized in Table 4 for the case of the Athabasca River. From Fig. 4, it is apparent that under-prediction is common, but interestingly there is no appreciable gain in fitting the Markov chain-3 model over the Markov chain-2 one in terms of COE (59.85% vs 59.64%) and the mean error of prediction (–34.33% vs –35.90%). In view of the above discussion, it was considered prudent to examine the potential of the Markov chain-1 model and, accordingly, the analysis was repeated. Although the performance indices for the Markov chain-1 model were slightly inferior (COE =57.20%, mean error =–39.14%), it could not be totally ruled out. Considering the computational time and effort required to estimate the additional parameters, an extension of the analysis to the Markov chain-3 model did not appear reasonable. However, a slight edge of the Markov chain-2 model in terms of improvement in COE by nearly 3% and a reduction in mean error by nearly 5% over the Markov chain-1 model, is a worthy consideration. In other words, the Markov chain-2 and Markov chain-1 models still appear to be potential candidates for prediction of drought lengths at the weekly time scale.

The monthly and weekly analyses revealed that major disagreements exist between predicted and observed drought lengths at higher threshold levels, viz. q ≥ 0.20. At low threshold levels, i.e. q < 0.20, the discrepancies between the predicted drought lengths are less pronounced. At higher threshold levels, if the estimates of conditional probabilities q_q , q_qq and q_qqq are adjusted upwards by 1 to 10%, the predicted drought lengths, or E(L_T ), would increase accordingly, thereby exhibiting almost parity with the observed counterparts. This observation provided an impetus for the development of a procedure or method that would be capable of estimating the aforesaid parameters with a reasonable accuracy to yield E(L_T ) comparable to the observed counterparts. It must be mentioned that the estimation of q_q and q_qq presented an equally intriguing problem in rivers with smaller drainage areas and much lower degrees of persistence (Sharma and Panu 2010). However, the problem was salvaged by computing these parameters from SHI _i sequences and original (non-stationary) flow series. The value of q_q in the prediction equation was taken as obtained from the non-stationary weekly streamflow series. The value of q_qq was taken as an average of the values obtained from the non-stationary flow series and SHI_i sequences. Initially, the same strategy was also used for the rivers under question, but it resulted in little improvement for the under-prediction problem. In fact, in almost all cases, the values of the above parameters were nearly the same in both non-stationary flow series and SHI _i sequences. The above route of parameter estimation turned out not to be a successful approach. Hence, recourse was taken to the DARMA-based method of parameter estimation, which involves the variance-based relationships as follows.

It is noted that, since the memory structure of weekly SHI sequences falls in regimen beyond AR-1, the extreme number theorem was not utilized to model the weekly drought lengths. The validity of the extreme number theorem is ascribed up to the first-order dependence and, therefore, its utility is strictly true for data series at the annual time scale. At the monthly time scale, since the degree of persistence was very strong, even being in the region of AR-1 for some rivers, the results from the extreme value theorem were less encouraging.

Predicting E(L_T )—Markov chain models (parameters by DARMA-based procedure involving run lengths)

The above parameters, viz. q_q , q_p and q_qq , can be estimated by using the algorithms based on DAR(1) and DARMA(1,1) models. In the realm of DARMA models, the sequences of binary values 0 (drought) and 1 (wet) are formed by truncating SHI _i sequences at the desired cut-off levels. The sequence of 0 and 1 forms a time series, which is subjected to autocorrelation analysis in a similar manner as was conducted in classical ARMA models (Box and Jenkins 1976). The autocorrelation function of time series of 0 and 1 forms the basis for identification of the DARMA model. It has been shown by Chang et al. (1984) that the DAR (1) model is equivalent to the Markov chain-1 model and the estimates of parameters q_q and q_p can be obtained as follows.

(8)

(9)

where r ₁ is the lag-1 autocorrelation in the time series of 0 and 1 and π₀ is the ratio of the drought lengths to the sum of drought and wet lengths, which is obtained by the relationship

(10)

where L ₀ is the average (mean) length of drought periods (length of runs of 0s) and L ₁ is the average length of wet periods (or length of runs of 1s). To elucidate the point, the monthly SHI _i sequence of the Athabasca River was truncated at the median level (q = 0.5) and the time series of 0s and 1s was obtained. The number of drought runs, N_d was counted as 78 with the total lengths of drought months as 344 over these 78 runs. Therefore, L ₀ (= 344/78 =4.41) and, likewise, the number of wet runs was counted as 77 with a total of 340 wet months resulting in L ₁ (= 340/77 =4.42) and thus, π₀ =0.5 {= 4.41/(4.41 + 4.42)}. Almost invariably, it was noticed that the value of π₀ turned out to be close to the value of q. The autocorrelation function, i.e. r ₁, r ₂ and r ₃, can be computed with the values of the binary time series x_t denoted by 00111000001111 (x ₁ =0, x ₂ =0, x ₃ =1, x ₄ =1, and so on) using the formula documented in Box and Jenkins (1976). The values of r ₁, r ₂ and r ₃ were found to be 0.548, 0.442 and 0.365, respectively. Therefore, values of q_q  = 0.774 {= r ₁ + (1 – r ₁)π₀ =0.548 + (1 – 0.548)0.5} and, likewise, q_p  = 0.226 {=(1 – r ₁)(1 – π₀) =(1 – 0.548)(1 – 0.5)} were obtained. These revised estimates are nearly the same (Table 5) as those computed by the counting method (Table 4). Therefore, when these new parameter estimates were inserted in equation (4)(1d) for the Markov chain-1 model, the E(L_T ) values resulted in no significant improvement. In summary, it can be stated that the estimates of parameters q_p and q_q obtained using the DAR(1)-based procedure were found to be marginally better compared to the counting method.

Table 5  Illustration of calculations for monthly and weekly drought lengths for Athabasca River using revised estimates (DAR-1, variance based) of parameters

q	LT -ob	Markov parameters *					Monthly E(LT )
		e 0	qq′	qp′	qq	qp	1^†	2 ^‡
Monthly drought parameters (T = 684):
0.50	22	−0.17	0.81	0.19	0.77	0.23	21	25
0.45	22	−0.30	0.78	0.18	0.72	0.23	18	21
0.40	19	−0.44	0.75	0.17	0.71	0.19	16	18
0.35	14	−0.57	0.71	0.16	0.69	0.17	13	14
0.30	10	−0.66	0.65	0.15	0.64	0.15	11	12
0.25	9	−0.76	0.59	0.14	0.59	0.14	9	9
0.20	8	−0.86	0.53	0.12	0.54	0.11	7	8
0.15	8	−0.97	0.52	0.09	0.48	0.10	7	7
0.10	5	−1.06	0.39	0.07	0.41	0.07	5	5
0.05	5	−1.27	0.39	0.03	0.42	0.03	4	4
		e 0	qq′	qp′	qq	qp	Weekly E(LT )
Weekly drought parameters (T = 2964):							1^†	2^‡
	44	−0.17	0.89	0.11	0.85	0.15	46	57
	42	−0.32	0.88	0.10	0.85	0.13	41	50
	42	−0.43	0.87	0.09	0.82	0.12	36	42
	41	−0.53	0.85	0.08	0.81	0.11	32	36
	35	−0.61	0.81	0.08	0.78	0.10	26	28
	22	−0.71	0.78	0.07	0.76	0.08	21	23
	20	−0.81	0.75	0.06	0.72	0.07	18	19
	18	−0.91	0.70	0.05	0.68	0.06	15	16
	16	−1.04	0.68	0.04	0.64	0.04	13	13
	14	−1.21	0.64	0.02	0.60	0.02	10	10
*value of qq and qp as determined by the DAR (1) mean length method.
^†Markov chain-1 model, ^‡ Markov chain-2 model,
Remarks: for monthly droughts, α1 =1.04 and α2 =0.88; for weekly droughts, α1 =1.025 and α2 =0.88;
qqq ′ =α1 qq ′; qqp′ =α2 qqq ′

For additional investigations, it is desirable to involve the DARMA (1,1) model and, therefore, the need arose for the estimation of the MA parameter. A simple test for the existence of the MA component in the DARMA (1,1) model is to evaluate and examine the value of the parameter β (Chung and Salas 2000). The DARMA (1,1) model contains two parameters, viz. ρ (as estimated above by r ₁) representing the AR component and β to represent the MA component. A low value of β close to 0 alludes to the insignificant role of the MA component in the DARMA (1,1) model and thus suggests the adequacy of the DAR(1) model for fitting the data. For almost all the highly correlated flow ridden rivers, as noted earlier, the value of parameter β ranged from 0.011 to 0.07 (in all cases of the chosen truncation levels), thus signifying that the role of the MA component is rather marginal. Therefore, the above indicators lend support to the notion that any attempt to involve DARMA (1,1) is likely to be marginally gainful. Further, the fitting of the DARMA (1,1) model is embroiled with cumbersome procedure, unlike the DAR(1) model.

In order to ameliorate E(L_T ) values as mentioned earlier, efforts should be directed to increase the value q_q , which in turn is expected to raise the estimates of E(L_T ). Therefore, the following relationships involving the mean μ _l and variance σ _l ² of the drought lengths are considered for computing the parameter. It can be shown that μ _l and σ _l ² of drought lengths can be expressed (Sen 1977) in terms of q_q as follows:

(11)

(12)

Therefore, the μ _l (designated as L ₀) and variance σ _l ² (designated as VL₀) were computed from the observed drought run lengths. By inserting values of L ₀ in equation (11)(11), the estimates of q_q turned out to be almost the same as those obtained by the counting method (or equation (8)(8)). Due to apparent lack of improvement in the estimate of q_q , it became necessary to take recourse to equation (12)(12), where the estimation of q_q explicitly involves the consideration of variance or second-order moments.

By inserting VL₀ values in equation (12)(12), the revised estimate of q_q (denoted as q_q′) was obtained. It is noted that the solution of equation (12)(12) requires an iterative procedure (solving a quadratic equation) that can easily be carried out. The q_q′ values thus computed were found to be slightly higher than the estimates of q_q obtained from equation (8)(8) in the majority of the rivers. It is only at a low threshold level that these estimates sometimes were found to be slightly less than, or equal to, the values obtained by equation (8)(8). As stated earlier, the higher values of q_q in the form of q_q′ are desired and therefore this route of parameter estimation involving variance appears to be more robust. Based on the estimates of q_q′, q and p (p = 1 – q), the estimate of q_p′ was revised using the following equation (Sen 1977):

(13)

The estimates q_q′ and q_p′ for the Athabasca River are shown in Table 5 along with the values of q_q and q_p obtained using the DAR(1)-based procedure involving the mean lengths of drought and wet periods.

Prediction of E(L_T ) by the Markov chain-1 model with revised parameters: case of monthly and weekly SHI sequences

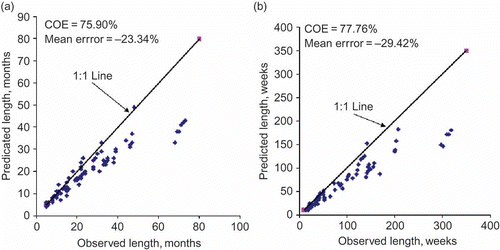
The values of revised parameters q_q′ and q_p′ were inserted in equation (4)(1d) and the values of E(L_T ) predicted. A representation of the estimates for the Athabasca River is shown in Table 5 and plotted against the observed counterparts in Fig. 5. It is apparent from Fig. 5 that the Markov chain-1 model still appears unsatisfactory because of significant under-prediction (–23.34%) although the value of COE has improved to 75.90% for monthly drought lengths. A similar scenario is also noticeable for the weekly droughts where the under-prediction and COE values are –29.42% and 77.60%, respectively (Fig. 5). When these parameters were estimated based on the counting method, the under-prediction was further accentuated (i.e. –27.63% for monthly and –39.14% for weekly) and the value of COE was far less (COE =55.58% for monthly and 57.20% for weekly) as displayed in Fig. 3. Although amelioration of parameters by involving the variance does improve the value of COE, there still remains a significant under-prediction, which is a cause for concern.

Fig. 4 Comparison of weekly L_T -ob and E(L_T ) using: (a) Markov chain-2 and (b) Markov chain-3 models.

Fig. 5 Comparison of (a) monthly and (b) weekly L_T -ob and E(L_T ) using Markov chain-1 model with revised estimates of parameters.

Prediction of E(L_T ) by the Markov chain-2 model with revised parameters: case of monthly and weekly SHI sequences

Despite the use of different methods of estimation of parameters, the results of the Markov chain-1 model did not improve the prediction of drought lengths, for either the monthly or the weekly time scales, which prompted the use of second-order Markov chain models for simulating the behaviour of drought lengths. That in turn spurred the need for estimating the second-order probabilities.

In general, it should be realized that there is a lack of closed-form equations for the estimation of second-order probabilities, similar to equations (12)(12) and (13)(13) for first-order probabilities. Therefore, a simple rule of thumb was adopted in which the new estimate of q_qq (denoted by q_qq′) was set equal to α₁ q_q′. Where, α₁ =q_qq /q_q ; q_qq and q_q are obtained using the counting method (Table 4). For a given river, the value of α₁ was computed at all threshold levels and the average value used for predicting E(L_T ). For monthly SHI _i sequences of all rivers, the values of α₁ ranged from 1.02 to 1.10 (2–10%) whereas for the weekly SHI _i sequences, α₁ was in a much smaller range of 1.005–1.05 (0.5–5%). In the case of monthly SHI _i sequences, the values of α₁ turned out to be clearly within the above range, but for weekly SHI _i sequences it was not so clear (for instance α₁ =1.005 means there is hardly any difference between q_qq and q_q ). In such cases, the values of α₁ were determined through trial and error by matching the predicted values, E(L_T ) with the observed counterparts.

Another parameter that needs to be estimated is q_qp′ (i.e. the revised estimate of q_qp ). For SHI _i sequences of all rivers, the parameter q_qp can be expressed as q_qp  =α₂ q_qq . The value of α₂ ranged from 0.75 to 0.90 in the case of monthly SHI _i sequences and from 0.85 to 0.95 in weekly SHI _i sequences. These values of α₂ were used to obtain the estimates of q_qp′ (i.e. q_qp′ =α₂ q_qq′). For each river, it should be noted that α₂ is the averaged value based on all cut-off levels. The parameter q_qp′ appears in the numerator of equation (3)(3), which makes it less sensitive, and consequently minor variations in α₂ make little difference in the results. The most crucial parameter is q_qq′ and in turn α₁, which must be determined accurately because it has a pronounced impact on the prediction of E(L_T ). The value of α₁ was found to be smaller for rivers with a high degree of persistence (such as the Churchill, Gods and Sturgeon rivers), compared to those with smaller values of q_q .

The predicted values of E(L_T ) obtained using the computed parameters obtained by the above noted procedure are plotted against the observed counterparts in Fig. 6 . From Fig. 6, it apparent that the value of COE has increased sharply to 93.33%, with a significant drop in the associated mean error of prediction (–0.63%) for monthly drought lengths. Likewise, these statistics also improved significantly for weekly drought lengths (e.g. COE =93.26% and mean error prediction =–0.06%). A high quality of fit depicted by the scatter of points about the 1:1 line (Fig. 6) therefore suggests that the Markov chain-2 model is more appropriate for simulating the drought periods for monthly flow series with a high degree of persistence. As far as weekly droughts are concerned, the second-order persistence seems to be appropriate, in view of the previous research efforts of Sharma and Panu (2010), where the weekly flow series of Canadian rivers with much smaller drainage areas along with smaller values of autocorrelations displayed memory to second-order. When the drainage areas are large with associated larger values of autocorrelations, one should expect memory components to go beyond the second-order. Such a fact became apparent when weekly SHI _i sequences were fitted in the ARMA type of models using the autocorrelation function method (Box and Jenkins 1976). In view of the rigor and uncertainty involved in the estimation of the second-order persistence parameter q_qq and its high sensitivity towards the prediction of E(L_T ), the second-order Markov chain model can be construed as adequate for modelling drought lengths, even on a weekly time scale.

Fig. 6 Comparison of (a) monthly and (b) weekly L_T -ob and E(L_T ) using Markov chain-2 with revised estimates of parameters.

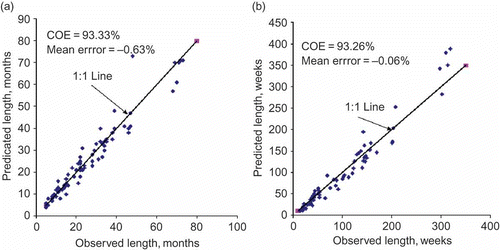
An interesting point to note is that for the prediction of monthly and weekly drought durations at the cut-off levels q below 0.20, the Markov chain-1 and Markov chain-2 models were found to differ only marginally. In other words, at low cut-off levels for the prediction of monthly and weekly drought durations, there is no significant error even with the Markov chain-1 model. Furthermore, the role of the revised estimates of parameters also turned out to be minimal. In fact, at low cut-off levels, the estimates of persistence parameters by the counting method turn out to be fairly robust, requiring no further adjustments. Since low cut-off levels are no less important in the prediction of drought durations, because they signify the pervasion of droughts in a tangible form, the counting method of parameter estimation should also be considered reliable. Some contingency planning measures to combat drought effects can be launched based on the predictions at such low levels. Significant differences in terms of method of computing the parameters and the order of a model were noticed at cut-off levels of q > 0.20, and in particular about median values, i.e. q = 0.45 and 0.5.

It is to be noted that the problem of under-prediction of extreme drought lengths using the flow generation technique is well documented (Askew et al. 1971, Jackson 1975, Panu and Sharma 2002). Jackson (1975) even suggested a method for solving the problem by adjusting the parameters in the flow generation techniques. The method suggested in this paper is simpler and is based on the observed drought lengths and autocorrelations of the binary series (drought =0s and wet =1s). The variance of drought lengths forms an important link in the estimation of persistence parameters, which are crucial for the prediction of E(L_T ).

CONCLUSIONS

The rivers investigated for drought properties in this paper flow through the Canadian prairies and represent a typical scenario for modelling of drought lengths, as they present a high level of persistence, draining relatively large areas and, at times, passing through or originating in lakes. For such rivers, Markov chain models are simple tools for predicting the T-year drought lengths based on annual, monthly and weekly SHI _i sequences. A major problem encountered in drought modelling pertains to the estimation of reliable persistence parameters q_q and q_qq , which are very sensitive towards prediction of drought lengths. The counting method of estimating these parameters resulted in significant under-prediction, though they are useful in providing initial estimates. For the estimation of parameters, the DAR (1)-based procedure using mean lengths of drought and wet periods was also equally deficient in yielding reliable predictions of drought lengths. However, the variance of drought lengths (using SHI _i sequences) provided a good basis for yielding a more accurate estimate of q_q (denoted by q_q′). The second-order persistence parameter q_qq′ can be adjusted with the same ratio (α₁ =q_qq/q_q ), as was obtained by the counting method. The values of α₁ were found to range from 1.02 to 1.10 for monthly drought lengths and from 1.005 to 1.05 for weekly drought lengths. Likewise, the parameter q_qp′ was adjusted using the ratio α₂ (= q_qp /q_qq , these estimates are based on the counting method). The values of α₂ turned out to be varying respectively from 0.75 to 0.90 for monthly droughts and from 0.85 to 0.95 for weekly droughts. Since the parameters q_p′ and q_qp′ are less sensitive, their estimates based on the method of counting (i.e. q_p′ =q_p and q_qp′ =q_qp ) can also serve this purpose satisfactorily.

On an annual time scale, the Markov chain-1 or random model (Markov chain-0) model worked satisfactorily in predicting drought lengths, i.e. E(L_T ), with exceedence probability computed from the Hazen plotting position formula. On a monthly time scale, both the Markov chain-1 and the extreme number theorem-based method resulted in under-prediction, which was adequately ameliorated by the use of the Markov chain-2 model. On a weekly time scale, the Markov chain-2 model proved satisfactory in predicting drought lengths, and higher Markov chain models showed no significant gain. Since the extreme number theorem-based method is designed for AR-1 or random SHI sequences, it was not applied to weekly droughts because of a strong presence of second- or higher-order persistence. Succinctly, in view of the highly persistent nature of flows, the drought lengths on monthly and weekly time scales can be satisfactorily predicted using the Markov chain-2 model. The exceedence probability computations using the Weibull plotting position formula were found adequate for prediction of monthly and weekly drought lengths. The Markov chain model structure is simple and efficient, although the persistence parameters q_q and q_qq need to be estimated with the utmost precision. At low threshold levels corresponding to q < 0.20, the Markov chain-1 model was also found satisfactory for predicting drought lengths on monthly and weekly time scales, with parameters estimated from the counting method.

Acknowledgements

The partial financial support of the Natural Sciences and Engineering Research Council of Canada for this project is gratefully acknowledged.